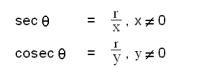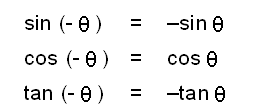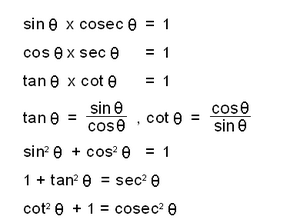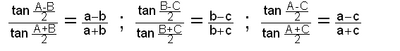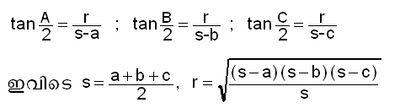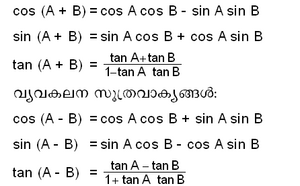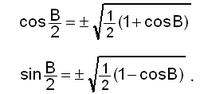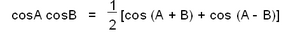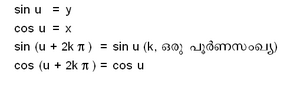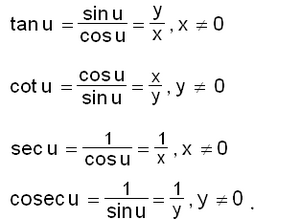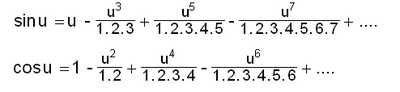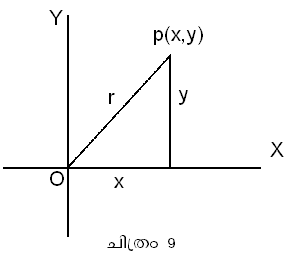This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ത്രികോണമിതി
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
ഉള്ളടക്കം |
ത്രികോണമിതി
Trigonometry
ത്രികോണങ്ങളെയും ത്രികോണമിതീയ ഫലനങ്ങളെയും കുറിച്ചുള്ള പഠനം. ത്രികോണത്തിലെ കോണങ്ങള്‍ (angles) തമ്മിലും കോണങ്ങളും വശങ്ങളും തമ്മിലുമുള്ള ബന്ധങ്ങളാണ് ത്രികോണമിതിയുടെ അടിസ്ഥാനം. എന്നാല്‍, വാസ്തവിക സംഖ്യകളുടെ (real numbers) ത്രികോണമിതീയ ഫലനങ്ങള്‍, സമ്മിശ്ര സംഖ്യകളുടെ (complex numbers) ത്രികോണമിതീയ ഫലനങ്ങള്‍, ത്രികോണമിതീയ ശ്രേണികള്‍ എന്നിവയെക്കുറിച്ചുള്ള പഠനങ്ങളും ഇന്ന് ത്രികോണമിതിയിലുള്‍പ്പെടുന്നു. ജ്യാമിതീയ സ്വഭാവത്തില്‍നിന്ന് വിശ്ളേഷക സ്വഭാവത്തിലേക്കുള്ള രൂപാന്തരമാണ് ത്രികോണമിതിയുടെ വികാസത്തിലെ ശ്രദ്ധേയമായ അംശം.
ത്രികോണമിതിയെ പ്രധാനമായും സമതല ത്രികോണമിതി (Plane trigonometry), ഗോളീയ ത്രികോണമിതി (Spherical trigonometry) എന്നീ രണ്ട് വിഭാഗങ്ങളായി തരംതിരിച്ചിട്ടുണ്ട്.
ത്രികോണമിതിയുടെ വളര്‍ച്ച
പ്രാചീന ത്രികോണമിതി
പ്രാചീന ജനങ്ങളുടെ പ്രായോഗിക ആവശ്യങ്ങള്‍ക്കുവേണ്ടിയാണ് ആദ്യകാലത്ത് ത്രികോണമിതീയാശയങ്ങള്‍ ഉടലെടുത്തത്. ത്രികോണാകൃതിയിലുള്ള കൃഷിസ്ഥലങ്ങളുടെ അളവ്, വിസ്തീര്‍ണം എന്നിവ നിര്‍ണയിക്കുന്നതിനും കെട്ടിടങ്ങള്‍, പിരമിഡുകള്‍ തുടങ്ങിയവയുടെ നിര്‍മാണത്തിനും പിന്നീട് ഭൂസര്‍വേക്കും ത്രികോണരൂപങ്ങളെക്കുറിച്ചുള്ള അറിവ് അത്യന്താപേക്ഷിതമായിത്തീര്‍ന്നു. തുടര്‍ന്ന്, ജ്യോതിശ്ശാസ്ത്രപഠനങ്ങള്‍ക്ക്, പ്രത്യേകിച്ച് ജ്യോതിര്‍ഗോളങ്ങളുടെ സ്ഥാനം, ചലനദിശ തുടങ്ങിയവ നിര്‍ണയിക്കാന്‍ ത്രികോണമിതീയാശയങ്ങള്‍ പ്രയോഗക്ഷമമാണെന്ന് ജ്യോതിശ്ശാസ്ത്രജ്ഞര്‍ കണ്ടെത്തിയതോടെ ഖഗോളീയ ത്രികോണമിതിക്ക് വര്‍ധിച്ച പ്രാധാന്യമാണ് കൈവന്നത്.
ഈജിപ്ത്, ബാബിലോണിയ, ഗ്രീസ്
ത്രികോണമിതീയ ശാസ്ത്രപഠനങ്ങള്‍ക്ക് 3500 വര്‍ഷത്തിലേറെ പഴക്കമുണ്ടെന്നാണ് കരുതപ്പെടുന്നത്. പ്രാചീന ഈജിപ്തിലും മെസപ്പൊട്ടേമിയയിലുമാണ് ഈ ഗണിതശാസ്ത്രശാഖയുടെ ഉദ്ഭവമെന്ന് അനുമാനിക്കപ്പെടുന്നു. പ്രാചീന ഈജിപ്തുകാരും ബാബിലോണിയക്കാരും ത്രികോണത്തിന്റെ സവിശേഷതകളെ സംബന്ധിച്ച് ജ്യാമിതീയ വിശകലനം നടത്തിയിരുന്നു. ഡിഗ്രിയിലും മിനിറ്റിലും സെക്കന്‍ഡിലും ഇവര്‍ കോണളവുകളെ നിര്‍ണയിച്ചിട്ടുണ്ട്. അഹ്മസ് പാപ്പിറസ് (ബി.സി. 1650) എന്ന പ്രാചീന ഈജിപ്ഷ്യന്‍ ഗ്രന്ഥത്തില്‍, പിരമിഡുകളെ സംബന്ധിച്ച വിവരങ്ങളില്‍ ഒരു മട്ടത്രികോണത്തിന്റെ വശങ്ങളുമായി ബന്ധപ്പെട്ട ചില സമസ്യകള്‍ രേഖപ്പെടുത്തിയിട്ടുള്ളതായി കാണാം. മട്ടത്രികോണങ്ങളെക്കുറിച്ചുള്ള പഠനങ്ങളില്‍ ഗ്രീക്കുകാരുടെ പങ്കും ശ്രദ്ധേയമാണ്. ഒരു വസ്തുവും അതിന്റെ നിഴലിന്റെ നീളവും തമ്മിലുള്ള അംശബന്ധത്തിലൂടെ വസ്തുവിന്റെ ഉയരം കണക്കാക്കാന്‍ ഇവര്‍ക്ക് സാധിച്ചിട്ടുണ്ട്. ഗ്രീക്ക് തത്ത്വചിന്തകനും ഗണിതശാസ്ത്രജ്ഞനുമായിരുന്ന തേലീസ് (ബി.സി. 634-546) സമദ്വിഭുജ ത്രികോണത്തിന്റെ പാദകോണങ്ങള്‍ തുല്യങ്ങളാണെന്ന് തെളിയിച്ചതായി കാണാം. ത്രികോണമിതീയ തത്ത്വങ്ങളും ത്രികോണമിതീയ ഫലനപ്പട്ടികകളും ശാസ്ത്രീയമായ രീതിയില്‍ ആദ്യമായി തയ്യാറാക്കിയത് ഹിപ്പാര്‍ക്കസ് (ബി.സി. 2-ാം ശ.) ആണ്. ഗോളീയ മട്ടത്രികോണങ്ങളെക്കുറിച്ചുള്ള ചില സൂത്രവാക്യങ്ങളും ഇദ്ദേഹം ആവിഷ്കരിച്ചിട്ടുണ്ട്. ടോളമിയുടെ (100-170) അല്‍മജെസ്റ്റില്‍ സൈന്‍, കൊസൈന്‍ എന്നീ ഫലനങ്ങളുടെ പട്ടിക, സൈന്‍ നിയമം, ത്രികോണ നിര്‍ധാരണം, സൂത്രവാക്യങ്ങള്‍ എന്നിവയെല്ലാം വിവരിച്ചിട്ടുണ്ട്. ഗോളീയ ത്രികോണങ്ങള്‍ക്ക് ആദ്യമായി നിര്‍വചനം നല്കിയത് മെനലേയസ് (10-ാം ശ.) ആണ്. മെനലേയസ് സിദ്ധാന്തം ഗോളീയ ത്രികോണ നിര്‍ധാരണത്തിനുപയോഗപ്പെടുന്നു. എന്‍ജിനീയറിങ്, ഭൂസര്‍വേ എന്നീ മേഖലകളില്‍ ത്രികോണമിതീയാശയങ്ങള്‍ ഉപയോഗപ്പെടുത്താന്‍ ഹെറോണിന് (2-ാം ശ.) കഴിഞ്ഞിട്ടുണ്ട്. നാസിര്‍-അല്‍-ദിന്‍-അല്‍-തുസി (1201-47) എന്ന പേര്‍ഷ്യന്‍ ജ്യോതിശ്ശാസ്ത്രജ്ഞനാണ് സമതല, ഗോളീയ ത്രികോണമിതീയാശയങ്ങളെ ജ്യോതിശ്ശാസ്ത്രമേഖലയില്‍നിന്നു വേര്‍പെടുത്തി പ്രത്യേക വിഭാഗങ്ങളാക്കി ക്രോഡീകരിച്ചത്.
ഭാരതത്തില്‍
4-ാം ശ. വരെ ഭാരതീയ ഗണിതശാസ്ത്രജ്ഞര്‍ ജ്യോതിശ്ശാസ്ത്രപഠനങ്ങള്‍ക്കു മാത്രമാണ് ത്രികോണമിതീയാശയങ്ങള്‍ ഉപയോഗിച്ചിരുന്നത്. ആര്യഭടന്‍ (5-ാം ശ.), ബ്രഹ്മഗുപ്തന്‍ (7-ാം ശ.), വരാഹമിഹിരന്‍ (6-ാം ശ.), ഭാസ്കരാചാര്യര്‍ (1114-85), മാധവന്‍ (1340-1425), നീലകണ്ഠസോമയാജി (1465-1545) എന്നിവര്‍ ത്രികോണമിതിയുടെ വളര്‍ച്ചയ്ക്ക് അമൂല്യമായ സംഭാവന നല്കിയവരാണ്. ആര്യഭടനാണ് ത്രികോണമിതീയ ഫലനങ്ങളിലൊന്നായ സൈനിന് (sine) സദൃശമായ 'ജ്യാ' എന്ന പേര് ('ജ്യാ'എന്നാല്‍ R sin θ ആണ്. R = 3438' ആയിട്ടാണ് എടുത്തിട്ടുള്ളത്) ആദ്യമായി നല്കിയത്. ജ്യാ എന്നത് 'ജിബാ' എന്നും 'ജെയ്ബ്' എന്നും പരിവര്‍ത്തിതമായി. തുടര്‍ന്ന്, ജെയ്ബിന്റെ ലത്തീന്‍പദമായ 'സൈനസി'ല്‍ നിന്ന് സൈന്‍ എന്ന പദം നിഷ്പന്നമായി. ബ്രഹ്മഗുപ്തന്റെ കൃതികളില്‍ സൈന്‍, കൊസൈന്‍ നിയമങ്ങളെക്കുറിച്ച് പരാമര്‍ശിച്ചിട്ടുണ്ട്. ത്രികോണമിതീയ വാക്യമായ sin (A + B) = sin A cos B + cos A sin B ആ മാധവന്‍ വികസിപ്പിച്ചെടുത്തിട്ടുണ്ട്. മുസ്ലിം പണ്ഡിതന്മാരിലൂടെയാണ് ഭാരതത്തില്‍ ഗോളീയ ത്രികോണമിതി വികാസം പ്രാപിച്ചത്. അല്‍-ബത്താനി (850-929), അബൂള്‍ വെഫാ (940-998) എന്നിവരുടെ കൃതികളിലും സൈന്‍, കൊസൈന്‍ നിയമങ്ങളും ത്രികോണമിതീയ പട്ടികയും കാണുന്നുണ്ട്. ശകരവര്‍മന്റെ സദ്രത്നമാലയില്‍ R tan, R cos, R sec,R cosec ഇവയ്ക്ക് സദൃശമായ ആശയങ്ങളും കാണുന്നുണ്ട്.
യൂറോപ്പില്‍
15-ാം ശ.-ത്തോടെയാണ് യൂറോപ്പില്‍ ത്രികോണമിതീയാശയങ്ങളും സിദ്ധാന്തങ്ങളും രൂപംകൊള്ളാന്‍ തുടങ്ങിയത്. അടിസ്ഥാന നിയമങ്ങള്‍ ചിട്ടപ്പെടുത്തി ത്രികോണമിതിയെ സ്വതന്ത്ര ഗണിതശാഖയാക്കി ആദ്യം അവതരിപ്പിച്ചത് യൊഹാന്‍ മ്യൂളര്‍ (1436-76) ആണ്. തുടര്‍ന്ന് കോപ്പര്‍നിക്കസ് (1473-1543), റാറ്റിക്സ് (1514-76) എന്നിവര്‍ മട്ടത്രികോണത്തിന്റെ വശങ്ങളുടെ അനുപാതമായി ത്രികോണമിതീയ ഫലനങ്ങളെ നിര്‍വചിച്ചു. ഗ്രഹങ്ങളുടെ ചലനത്തോടനുബന്ധിച്ചുള്ള പ്രശ്ന നിര്‍ധാരണങ്ങള്‍ക്ക് കോപ്പര്‍നിക്കസ് ത്രികോണമിതീയ നിയമങ്ങളുപയോഗിച്ചിട്ടുള്ളതായി കാണാം. ആറ് ത്രികോണമിതീയ ഫലനങ്ങളെയും ഒരേ കൃതിയില്‍ ആദ്യമായി ഉപയോഗപ്പെടുത്തിയത് ബീജഗണിതജ്ഞനായിരുന്ന വിയറ്റെ (1540-1603) ആണ്. ആധുനിക ത്രികോണമിതിയില്‍ ഏതാനും സര്‍വസമങ്ങള്‍ ഇദ്ദേഹം തയ്യാറാക്കിയിട്ടുണ്ട്. കൂടാതെ സമതല, ഗോളീയ ത്രികോണ നിര്‍ധാരണത്തിനുള്ള പല സൂത്രവാക്യങ്ങളും വികസിപ്പിച്ചെടുക്കുകയും ചെയ്തു.
പ്രാഥമിക ത്രികോണമിതീയ ആശയങ്ങള്‍
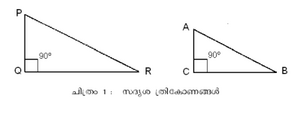
സദൃശ (similar)ത്രികോണങ്ങളുടെ സവിശേഷതകളാണ് പ്രാഥമിക ത്രികോണമിതി പഠനങ്ങള്‍ക്ക് അടിസ്ഥാനം. ആകൃതിയില്‍ ഒരുപോലെയും വലുപ്പത്തില്‍ വ്യത്യാസമുള്ളതുമായ ത്രികോണങ്ങളാണ് സദൃശ ത്രികോണങ്ങള്‍. ഈജിപ്തിലെ പിരമിഡുകളുടെ ഉയരം, നിഴല്‍ ഗണനരീതിയിലൂടെ തേലീസ് കൃത്യമായി നിര്‍ണയിച്ചു. ഇത് സദൃശ ത്രികോണപഠനം സുഗമമാക്കി.
ചിത്രം (1)-ല്‍ Δ PQR ,Δ ABCഎന്നിവ സദൃശ ത്രികോണങ്ങളാണ്. ത്രികോണങ്ങള്‍ സദൃശങ്ങളാണെങ്കില്‍ സമസ്ഥാനീയ (corresponding) വശങ്ങള്‍ ആനുപാതികമായിരിക്കും എന്ന നിയമത്തില്‍നിന്നും,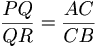 
ചിത്രം (1). ഇതില്‍ നിന്ന് എന്നു ലഭിക്കുന്നു. ഈ രീതിയിലൂടെ ഒരു വസ്തുവിന്റെ നേരിട്ടളക്കുവാന്‍ കഴിയാത്ത ഉയരം നിര്‍ണയിക്കാവുന്നതാണ്.
ആധുനിക ത്രികോണമിതീയ ആശയങ്ങള്‍
ആധുനിക ത്രികോണമിതീയാശയങ്ങള്‍ 17-ാം ശ.-ത്തോടെയാണ് വികാസം പ്രാപിച്ചത്. ഗോളീയ ത്രികോണ നിര്‍ധാരണങ്ങള്‍ക്ക് ജോണ്‍ നേപ്പിയര്‍ (1550-1617) കണ്ടുപിടിച്ച നിയമങ്ങള്‍ (നേപ്പിയര്‍ നിയമങ്ങള്‍) ഏറെ പ്രയോജനകരമാണ്. ത്രികോണമിതീയ ഫലനങ്ങളുടെ ആവര്‍ത്തികതാ (periodicity) സ്വഭാവങ്ങളെക്കുറിച്ച് ആദ്യമായി പ്രതിപാദിച്ചത് തോമസ് ഫാന്റേറ്റ് ലയ്നി (18-ാം ശ.) ആണ്. ഹൈപ്പര്‍ബോളീയ ഫലനങ്ങളെക്കൂടി ത്രികോണമിതിയുടെ പരിധിയില്‍ ലാംബെര്‍ട്ട് (1728-77) ഉള്‍പ്പെടുത്തി. വാലിസ് (1616-1703), ദ് മ്വാവ്റ് (1667-1754), ഓയ്ലര്‍ (1707-83), കെപ്ളര്‍ (1571-1630) ഫൂറിയെ (1768-1830), ഗൌസ് (1777-1855), ഹെര്‍ഷല്‍ (19-ാം ശ.) തുടങ്ങിയവരും ത്രികോണമിതീയാശയങ്ങള്‍ ചിട്ടപ്പെടുത്തിയിട്ടുണ്ട്. വിശ്ളേഷണ മേഖലയുടെ ഒരു ശാഖയായിട്ടാണ് ത്രികോണമിതിയെ ഓയ്ലര്‍ വീക്ഷിച്ചത്. സമ്മിശ്ര ചരങ്ങളുടെ ഫലനങ്ങളായി ത്രികോണമിതീയ ഫലനങ്ങളെ സാമാന്യവത്കരിക്കാന്‍ ഇദ്ദേഹത്തിനു കഴിഞ്ഞു. ഫൂറിയെ വികസിപ്പിച്ചെടുത്തത്രികോണമിതീയ ശ്രേണികള്‍ പ്രയോജനപ്പെടുത്തി ഗണിതീയ ഭൗതികത്തിലെ പല സമസ്യകളും നിര്‍ധാരണം ചെയ്യാന്‍ സാധിക്കുന്നു.
മുന്‍കാലങ്ങളില്‍ നിര്‍മാണപ്രവര്‍ത്തനങ്ങള്‍, സര്‍വേ, നാവിക വിദ്യ, ജ്യോതിശ്ശാസ്ത്രം തുടങ്ങിയ മേഖലകളില്‍ മാത്രമായി ത്രികോണമിതിയുടെ ഉപയോഗം ഒതുങ്ങിയിരുന്നു. ഇന്ന് കലനം, വിശ്ളേഷണം, ബീജഗണിതം എന്നീ ഗണിതശാഖകളിലും ശബ്ദം, വൈദ്യുതി, പ്രകാശികം തുടങ്ങിയ ഭൌതികമേഖലകളില്‍ ആവര്‍ത്തികതാ പ്രതിഭാസങ്ങള്‍ വിശകലനം ചെയ്യുന്നതിനും അവശ്യമാര്‍ഗമായി ത്രികോണമിതി പ്രയോജനപ്പെടുന്നു.
സമതല ത്രികോണമിതി
സമതലത്തിലെ ത്രികോണങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് സമതലത്രികോണമിതി. മൂന്ന് അസമരേഖാ ബിന്ദുക്കളെ (non-collinear points) മൂന്ന് രേഖാഖണ്ഡങ്ങളാല്‍ യോജിപ്പിക്കുന്ന രൂപമാണ് ത്രികോണം. ഒരു ത്രികോണം, അതുള്‍ക്കൊള്ളുന്ന പ്രതലത്തെ ആശ്രയിച്ചാണിരിക്കുന്നത്. ത്രികോണത്തിന്റെ മൂന്നുവശങ്ങളും മൂന്നുകോണങ്ങളും ഇതിന്റെ അംഗ(elements)ങ്ങളാണ്. ഒരു സമതലത്തില്‍ ത്രികോണത്തിനകത്തെ കോണങ്ങളുടെ തുക 180° ആണ് (യൂക്ളിഡിയന്‍ ജ്യാമിതി).
കോണങ്ങള്‍ (Angles)
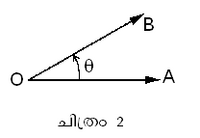
ഒരു നേര്‍രേഖ അതിലുള്ള ഒരു ബിന്ദുവിനെ കേന്ദ്രീകരിച്ച് പരിക്രമിക്കുമ്പോഴുണ്ടാകുന്ന അളവ്. കോണം ഡിഗ്രിയിലോ റേഡിയനിലോ അളക്കാവുന്നതാണ്. ചിത്രം 2-ല്‍ O എന്നത് ശീര്‍ഷ(vertex)മാണ്. ശീര്‍ഷത്തിന് ചുറ്റുമുള്ള കോണം (ഒരു പരിക്രമണം) 360° ആയിട്ടാണ് കണക്കാക്കുന്നത്. 360°ക്കു തുല്യമാണ് 2 റേഡിയന്‍. ഒരു പരിക്രമണത്തെ 360 ഡിഗ്രിയായും ഒരു ഡിഗ്രിയെ 60 മിനിറ്റായും ഒരു മിനിറ്റിനെ 60 സെക്കന്‍ഡായും ഭാഗിച്ചിട്ടുണ്ട്. നേര്‍രേഖ O കേന്ദ്രമാക്കി അപ്രദക്ഷിണ ദിശയില്‍ സഞ്ചരിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന കോണങ്ങള്‍ ധനാത്മകവും പ്രദക്ഷിണ ദിശയില്‍ സഞ്ചരിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന കോണങ്ങള്‍ ഋണാത്മകവുമായിരിക്കും. കോണങ്ങള്‍ മൂന്നുതരമുണ്ട്. കോണം 90° ആണെങ്കില്‍ അതിനെ മട്ടകോണം എന്നും 90°യില്‍ കുറവാണെങ്കില്‍ ന്യൂനകോണം എന്നും 90°യില്‍ കൂടുതലാണെങ്കില്‍ അധികകോണം എന്നും പറയുന്നു. ഭാരതീയ ജ്യോതിശ്ശാസ്ത്രഗ്രന്ഥങ്ങളില്‍ ഡിഗ്രിക്ക് 'ഭാഗ' എന്നും മിനിറ്റിന് 'കല' എന്നും സെക്കന്‍ഡിന് 'വികല' എന്നുമാണ് സംജ്ഞകള്‍.
കോണങ്ങളുടെ ത്രികോണമിതീയ ഫലനങ്ങള്‍
ഒരു മട്ടത്രികോണത്തിന്റെ വശങ്ങളുടെ അംശബന്ധമായി ത്രികോണമിതീയ ഫലനങ്ങളെ നിര്‍വചിക്കാവുന്നതാണ്. ഒരു കോണ്‍ 90° ഉള്ള ത്രികോണമാണ് മട്ടത്രികോണം. സൈന്‍ (sine), കൊസൈന്‍ (cosine), ടാന്‍ജെന്റ് (tangent) എന്നിവയും അവയുടെ വ്യുത്ക്രമങ്ങളായ കൊസീക്കന്റ്, സീക്കന്റ്, കോടാന്‍ജെന്റ് എന്നിവയും ചേര്‍ന്നുള്ള ആറ് ത്രികോണമിതീയ ഫലനങ്ങള്‍ (Trigonometric functions) ഉണ്ട്. ലഘുരൂപത്തില്‍ ഇവയെ സൈന്‍ (sin), കോസ് (cos), ടാന്‍ (tan), കൊസീക്ക് (cosec), സീക്ക് (sec), കോട്ട് (cot) എന്നിങ്ങനെ എഴുതാം.
ABCഎന്ന മട്ടത്രികോണത്തില്‍, ആ എന്ന ന്യൂനകോണത്തിന്റെ ത്രികോണമിതീയ ഫലനങ്ങള്‍ പട്ടിക 1-ല്‍ കൊടുത്തിരിക്കുന്നു.
കോണത്തിന്റെ മൂല്യത്തിനനുസരിച്ച് ഫലനങ്ങളുടെ വിലയ്ക്കു മാറ്റം വരുന്നതാണ്. വശങ്ങളുടെ നീളം എന്തുതന്നെ ആയിരുന്നാലും ഒരേ കോണത്തിന്റെ ത്രികോണമിതീയ ഫലനങ്ങള്‍ സ്ഥിരമായിരിക്കും. കൂടാതെ, ഒരു ന്യൂനകോണത്തിന്റെ ഏതു ത്രികോണമിതീയ ഫലനവും ആ കോണത്തിന്റെ പൂരകകോണത്തിന്റെ സഹഫലനത്തിനു (cofunction) തുല്യമായിരിക്കും. അതായത്, sin C = cos B,cos C = sin B,tan C =cot B എന്നും ചിത്രത്തില്‍ നിന്നു കിട്ടുന്നതാണ്.
ഒരു മട്ടത്രികോണത്തിന്റെ ഒരു വശവും ഒരു കോണവും തന്നിട്ടുണ്ടെങ്കില്‍ ആ കോണത്തിനനുയോജ്യമായ ഫലനത്തിന്റെ സഹായത്താല്‍ മറ്റുള്ള ഏതു വശവും കണ്ടുപിടിക്കുവാന്‍ സാധിക്കുന്നതാണ്.
ഒരു ന്യൂനകോണത്തിനെ ആധാരമാക്കിയുള്ള ത്രികോണമിതീയ ഫലനങ്ങളാണ് മുകളില്‍ വിശദീകരിച്ചത്. ഏതു തരം കോണത്തിനെയും ആധാരമാക്കിയുള്ള ത്രികോണമിതീയ ഫലനങ്ങള്‍ വിശദീകരിക്കാന്‍ ബീജഗണിതാശയങ്ങള്‍ സഹായിക്കുന്നു.
സമതല ത്രികോണത്തിലെ ഒരു ബിന്ദുവിനെ കുറിക്കാന്‍ സംഖ്യകളുടെ ക്രമിതയുഗ്മം (ordered pair) ഉപയോഗിക്കുന്നു.
ചിത്രം 4-ല്‍ XOX',YOY' എന്നീ ഋജുരേഖകള്‍ പരസ്പരം O എന്ന ബിന്ദുവില്‍ സന്ധിക്കുന്നു. XOX', YOY' ഇവ രണ്ടിനേയും നിര്‍ദേശാങ്കാക്ഷങ്ങള്‍ എന്നു പറയുന്നു. ഈ അക്ഷങ്ങള്‍ സമതലത്തെ നാല് പാദ(quadrant) ങ്ങളായി വിഭജിക്കുന്നു.
ഈ നിര്‍വചനങ്ങളില്‍നിന്ന് നാല് പാദങ്ങളിലുമുള്ള ത്രികോണമിതീയ ഫലനങ്ങള്‍ കണ്ടുപിടിക്കാം.
ഋണകോണങ്ങളുടെ ത്രികോണമിതീയ ഫലനങ്ങള്‍ ഇപ്രകാരമാണ്.
അടിസ്ഥാന ത്രികോണമിതീയ സര്‍വസമങ്ങള്‍ (Identities)
പ്രധാനപ്പെട്ട ത്രികോണമിതീയ സര്‍വസമങ്ങള്‍ ചുവടെ ചേര്‍ക്കുന്നു.
ത്രികോണ നിര്‍ധാരണം
ത്രികോണത്തിന്റെ ആറ് അംഗങ്ങളില്‍ മൂന്നെണ്ണം (അതില്‍ ഒന്നെങ്കിലും വശം ആയിരിക്കണം) തന്നിരുന്നാല്‍ ശേഷിച്ചവ ത്രികോണ നിര്‍ധാരണത്തിലൂടെ കണ്ടെത്താം.
ത്രികോണ നിര്‍ധാരണത്തിന് പ്രധാനപ്പെട്ട മൂന്ന് നിയമങ്ങളാണ് സാധാരണ ഉപയോഗിക്കാറുള്ളത്.
സൈന്‍ നിയമം
ഒരു ത്രികോണത്തിന്റെ വശങ്ങള്‍ അവയ്ക്കെതിരെയുള്ള കോണങ്ങളുടെ സൈനുകള്‍ക്ക് ആനുപാതികങ്ങളാണ്.
അതായത് [[Image:ഈ സമീകരണം സൈന്‍ നിയമം എന്നറിയപ്പെടുന്നു. സൈന്‍ നിയമത്തിന്റെ ഉപപ്രമേയങ്ങള്‍ മോള്‍വീഡ് സമീകരണങ്ങള്‍ എന്നറിയപ്പെടുന്നു.
ഒരു ത്രികോണത്തിന്റെ രണ്ട് വശങ്ങളും ഒരു കോണവും തന്നിരുന്നാല്‍ ബാക്കിയുള്ളവ കാണാന്‍ സൈന്‍ നിയമം ഉപയോഗിക്കുന്നു.
കൊസൈന്‍ നിയമം
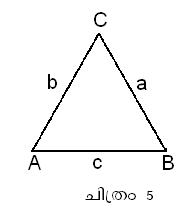
ത്രികോണം ABC-യില്‍ (ചിത്രം 5)
a2 = b2 + C2-2bc cos A
b2 = c2 + a 2-2ca cos B
c2 = a2 + b2-2ab cos C
ഇവ കൊസൈന്‍ നിയമങ്ങള്‍ എന്നറിയപ്പെടുന്നു.
ഒരു ത്രികോണത്തിന്റെ രണ്ട് വശങ്ങളും അവ ഉള്‍ക്കൊള്ളുന്ന കോണവും തന്നിരുന്നാല്‍ മൂന്നാമത്തെ വശം കാണാന്‍ കൊസൈന്‍ നിയമം സഹായിക്കുന്നു.
ടാന്‍ജെന്റ് നിയമം
ടാന്‍ജെന്റ് നിയമം മൂന്ന് രൂപത്തില്‍ എഴുതാം.
(a,b,c എന്നിവ A,B,c കോണങ്ങള്‍ക്ക് എതിരെയുള്ള വശങ്ങളാണ്).
ഒരു ത്രികോണത്തിന്റെ വശങ്ങള്‍ മാത്രം തന്നിരുന്നാല്‍ കോണങ്ങള്‍ കണ്ടുപിടിക്കാന്‍ അര്‍ധ-കോണ ടാന്‍ജെന്റ് നിയമം ഉപയോഗിക്കുന്നു.
ത്രികോണ വിസ്തീര്‍ണം
ഒരു ത്രികോണത്തിന്റെ വിസ്തീര്‍ണം കാണുന്നതിന് മൂന്ന് സൂത്രവാക്യങ്ങള്‍ ഉപയോഗിക്കാവുന്നതാണ്.
ᐃ ചിഹ്നം ത്രികോണവിസ്തീര്‍ണത്തെ സൂചിപ്പിക്കുന്നു.
കൂടാതെ 
എന്ന സൂത്രവാക്യവും ഉപയോഗിക്കുന്നുണ്ട്. ഈ സൂത്രവാക്യം 'ഹെറോണ്‍ സൂത്രം' (Heron's formula) എന്നറിയപ്പെടുന്നു.
സംയുക്ത (compound) കോണങ്ങളുടെ സൂത്രവാക്യങ്ങള്‍
സംയുക്ത കോണങ്ങളുടെ സൂത്രവാക്യങ്ങളെ രണ്ടായി തരംതിരിക്കാം.
1. സങ്കലന സൂത്രവാക്യങ്ങള്‍ 2. വ്യവകലന സൂത്രവാക്യങ്ങള്‍
സങ്കലന സൂത്രവാക്യങ്ങള്‍:
ഇരട്ട കോണങ്ങള്‍, അര്‍ധ കോണങ്ങള്‍ എന്നിവയെക്കുറിച്ചുള്ള സൂത്രവാക്യങ്ങളാണ്,
എന്നു ലഭിക്കുന്നു. ഈ സൂത്രവാക്യങ്ങള്‍ കലന(Calculus)ത്തിലെ പ്രശ്ന നിര്‍ധാരണങ്ങള്‍ക്ക് വളരെ പ്രയോജനപ്പെടുന്നു.
ഇവ അര്‍ധകോണ സൂത്രവാക്യങ്ങളാണ്.
പരിവര്‍ത്തന സൂത്രവാക്യങ്ങള്‍ (Conversion formula)
സമാനയന സൂത്രവാക്യങ്ങള്‍ (Reduction formula)
സമാനയന സൂത്രവാക്യങ്ങളുടെ സഹായത്തോടെ, ഏതു കോണത്തിന്റെ ത്രികോണമിതീയ ഫലനവും 45°-യില്‍ കുറവായ ധനകോണങ്ങളുടെ ഫലനമായി എഴുതാന്‍ സാധിക്കും.
ത്രികോണമിതിയുടെ സാമാന്യവത്കരണം
കോണങ്ങളുടെ ത്രികോണമിതീയ ഫലനങ്ങളെക്കുറിച്ചുള്ള പഠനങ്ങളാണ് മുമ്പ് ത്രികോണമിതിയില്‍ ഉള്‍പ്പെട്ടിരുന്നത്. പിന്നീട് വിവിധ ശാസ്ത്ര ശാഖകളിലുണ്ടായ പുരോഗതി, നൂതന ത്രികോണമിതീയാശയങ്ങള്‍ക്ക് രൂപംനല്കുവാന്‍ സഹായകമായിത്തീര്‍ന്നു.
വാസ്തവിക സംഖ്യകള്‍
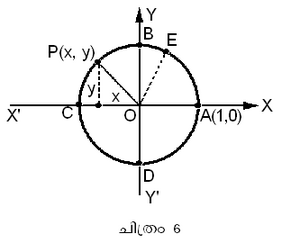
ത്രികോണമിതിയുടെ ആധുനിക പ്രയോഗങ്ങളില്‍, വാസ്തവിക സംഖ്യകളുടെയും സമ്മിശ്ര സംഖ്യകളുടെയും ത്രികോണമിതീയ ഫലനങ്ങള്‍ പ്രയോജനപ്പെടുന്നു. ഒരു വാസ്തവിക സംഖ്യയെ ഒരു വൃത്തീയ ചാപത്തിന്റെ നീളമായി പ്രതിനിധാനം ചെയ്യുന്നതുവഴി, ഒരു വാസ്തവികസംഖ്യയും നിര്‍ദിഷ്ട കോണവും തമ്മിലുള്ള ബന്ധത്തെ ആവിഷ്കരിക്കുവാന്‍ സാധിക്കുന്നു. ആരം ഒരു ഏകകം ആയുള്ള ഒരു വൃത്തത്തെ പരിഗണിക്കാം (ചിത്രം 6).
ചിത്രത്തില്‍ x2 + y2 = 1. u എന്ന ഓരോ വാസ്തവിക സംഖ്യയ്ക്കും വൃത്തത്തില്‍ AP എന്ന ചാപം ഉണ്ട്. u എന്ന വാസ്തവിക സംഖ്യകൊണ്ട് p(x, y) എന്ന ബിന്ദു നിര്‍വചിക്കാം.
ത്രികോണമിതീയ ഫലനങ്ങള്‍ ആവര്‍ത്തികത (periodicity) സ്വഭാവമുള്ളവയാണെന്ന് വ്യക്തമാണ്. sin,cos എന്നിവയുടെ ആവര്‍ത്തികത (periodicity) 2πtanയും ഫലനത്തിന്റെ ആവര്‍ത്തികത π ഉം ആണ്.
മുകളില്‍ വിശദീകരിച്ചവയില്‍ നിന്ന്,
u എന്ന വാസ്തവിക സംഖ്യയുടെ ത്രികോണമിതീയ ഫലനങ്ങള്‍, u റേഡിയന്‍ അളവുള്ള കോണത്തിന്റെ ത്രികോണമിതീയ ഫലനങ്ങള്‍ക്കു തുല്യമായിരിക്കുമെന്ന് വ്യക്തമാകുന്നു.
എന്നു കിട്ടും.
വാസ്തവികസംഖ്യകളുടെ ത്രികോണമിതീയ ഫലന ശ്രേണികള്‍ ഇപ്രകാരമാണ്.
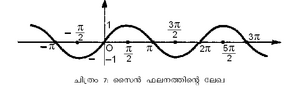
ത്രികോണമിതീയ ഫലനങ്ങളുടെ ലേഖ (graph)
ത്രികോണമിതീയ ഫലനങ്ങളുടെ പല സവിശേഷതകളും ലേഖയില്‍നിന്നു മനസ്സിലാക്കാന്‍ സാധിക്കുന്നു. സൈന്‍ ഫലനത്തിന്റെ ലേഖയില്‍നിന്ന് (ചിത്രം 7) ഫലനം തരംഗസ്വഭാവമുള്ളതാണെന്നു വ്യക്തമാണ്.
എന്നിവയുടെ ലേഖകള്‍ താഴെ കൊടുക്കുന്നു.
വൃത്തീയ ഫലനങ്ങള്‍ക്ക് തരംഗിത സ്വഭാവമുള്ളതിനാല്‍ ഗണിതീയ ഭൌതികത്തില്‍ ഇവയ്ക്കു മുഖ്യസ്ഥാനമുണ്ട്. വൈദ്യുതി, ശബ്ദം, പ്രകാശം, പെന്‍ഡുലങ്ങളുടെ ദോലനം എന്നിവയിലെ പല പ്രതിഭാസങ്ങളെയും കുറിച്ചു പഠിക്കാന്‍ ഇവ പ്രയോജനപ്പെടുന്നു.
ഫൂറിയെ വിശ്ലേഷണം. ഫൂറിയെ ശ്രേണി(Fourier series) യെക്കുറിച്ചുള്ള സിദ്ധാന്തം, ഇവയുടെ പ്രയോഗങ്ങള്‍ എന്നിവയെസംബന്ധിച്ച പഠനമാണ് ഫൂറിയെ വിശ്ളേഷണത്തില്‍ ഉള്‍പ്പെടുന്നത്. സൈന്‍, കൊസൈന്‍ എന്നീ ആവര്‍ത്തനഫലനങ്ങളെ ഒരു ശ്രേണികൊണ്ട് വ്യക്തമാക്കുന്ന രീതിയാണ് ഫൂറിയെ ശ്രേണിയിലുള്ളത്. y = a0+(a1 sinx+b1 cosx)+(a2 sin2x+b2+b2 cos 2x)+.... ഈ രൂപത്തിലുള്ള ത്രികോണമിതീയ ശ്രേണിയാണ് ഫൂറിയെ ശ്രേണി. ജോസഫ് ഫൂറിയെ ആണ് ഈ ശ്രേണി ആവിഷ്കരിച്ചത്.
(a0, a1, b1, b2 .... ഇവ അചരങ്ങളാണ്).
ഫൂറിയെ ശ്രേണിയിലെ ഗുണാങ്ക(coefficient)ത്തിന്റെ സാമാന്യരൂപം,
. ഇതില്‍ f(x) എന്ന ഫലനത്തിന്റെ അന്തരാളം(-π,π) ആണ്. താപനിലയെക്കുറിച്ചുള്ള പഠനത്തിനാണ് ഫൂറിയെ ആദ്യമായി ഈ ശ്രേണി ആവിഷ്കരിച്ചത്. ആധുനിക വിശ്ളേഷണ മേഖലയില്‍ ഈ ശ്രേണിക്ക് മുഖ്യ പങ്കുണ്ട്.
സമ്മിശ്രസംഖ്യകളുടെ ത്രികോണമിതീയ ഫലനങ്ങള്‍
സമ്മിശ്ര സംഖ്യകളുടെ ത്രികോണമിതീയഫലനങ്ങള്‍ നിര്‍വചിക്കാവുന്നതാണ്.
x + iyഎന്ന സമ്മിശ്രസംഖ്യയുടെ ആലേഖം ചിത്രം 9-ല്‍നിന്ന് ലഭിക്കുന്നതാണ്. (ഇവിടെ x,y എന്നിവ വാസ്തവിക സംഖ്യകളും i എന്നത് കല്പിത സംഖ്യ imaginary number-യും ആണ്.) സമ്മിശ്രസംഖ്യകളെ ഒരു സമതലത്തിലെ ബിന്ദുക്കളായി പരിഗണിക്കുന്ന ചിത്രമാണ് ആര്‍ഗന്‍ഡ് ആരേഖം (Argand diagram).
ഓരോ സമ്മിശ്രസംഖ്യ (z = x + iy)യ്ക്കും (x,y) എന്നൊരു ബിന്ദു കാര്‍ട്ടീഷ്യന്‍ നിര്‍ദേശാങ്ക വ്യവസ്ഥയിലുണ്ട്; നേരേ മറിച്ചും. ഏതു സമ്മിശ്രസംഖ്യയും r(cos θ + i sin &theata;) എന്ന രൂപത്തില്‍ എഴുതാവുന്നതാണ് (r,θ വാസ്തവിക സംഖ്യകള്‍). സമ്മിശ്രസംഖ്യകളുടെ ത്രികോണമിതീയ ഫലനങ്ങളെക്കുറിച്ചുള്ള തിയറമാണ് ദ് മ്വാവ്റ് തിയറം. ഫ്രഞ്ച് ഗണിതശാസ്ത്രജ്ഞനായ അബ്രഹാം ദ് മ്വാവ്റ് (1667-1754) ആണ് ഇത് കണ്ടുപിടിച്ചത്. [r(cos θ+ i sin θ )]n = rn (cos θ + i sin n θ). ഇത് ദ് മ്വാവ്റ് തിയറം എന്നറിയപ്പെടുന്നു . സംയുക്തകോണങ്ങളുടെ സൈന്‍, കൊസൈന്‍ ഫലനങ്ങള്‍ കാണുന്നതിനും സമ്മിശ്രസംഖ്യകളുടെ വര്‍ഗമൂലം (root) കാണുന്നതിനും ഈ തിയറം സഹായകമാണ്.
സമ്മിശ്ര സംഖ്യകളെക്കുറിച്ച് ഓയ്ലറും ചില സൂത്രവാക്യങ്ങള്‍ കണ്ടുപിടിച്ചിട്ടുണ്ട്. അവ താഴെക്കൊടുക്കുന്നു.
എക്സ്പൊണന്‍ഷ്യല്‍ ശ്രേണീരൂപത്തിലുള്ള ഈ ഫലനങ്ങളില്‍നിന്ന് ഇവയുടെ മൂല്യങ്ങള്‍ കാണാവുന്നതാണ്.
ഹൈപ്പര്‍ബോളിക ഫലനങ്ങളാണ്,
പ്രതിലോമ ത്രികോണമിതീയ ഫലനങ്ങള്‍
ഒരു ത്രികോണമിതീയ ഫലനത്തിന്റെ മൂല്യം 'x' തന്നാല്‍ ഫലനത്തിന്റെ കോണമോ വാസ്തവിക സംഖ്യയോ സൂചിപ്പിക്കാന്‍ പ്രതിലോമ (inverse) ത്രികോണമിതീയ ഫലനങ്ങളുപയോഗിക്കുന്നു. ഉദാ. sin-1x,cos-1x മുതലായവ.
ഗോളീയ ത്രികോണമിതി (Spherical trigonometry)
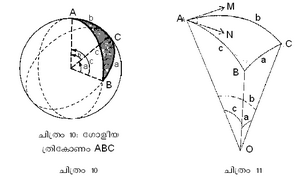
ഗോളീയ ത്രികോണങ്ങളുടെ വശങ്ങള്‍, കോണങ്ങള്‍ എന്നിവയെ സംബന്ധിച്ചുള്ള പഠനങ്ങളാണ് ഗോളീയ ത്രികോണമിതിയിലുള്‍പ്പെടുന്നത്. ഭൗമബിന്ദുക്കള്‍ ശീര്‍ഷങ്ങളായി (vertix) വരുന്നവയും സൂര്യന്‍, ഗ്രഹങ്ങള്‍, നക്ഷത്രങ്ങള്‍ തുടങ്ങിയ ഖഗോള വസ്തുക്കളിലെ ബിന്ദുക്കള്‍ ശീര്‍ഷങ്ങളായി വരുന്നവയും ആയ രണ്ടുതരം ഗോളീയ ത്രികോണങ്ങള്‍ പ്രത്യേകം പ്രാധാന്യമര്‍ഹിക്കുന്നു. മൂന്ന് മഹാവൃത്തങ്ങളുടെ (great circle) ചാപങ്ങള്‍ പരസ്പരം ഛേദിക്കുമ്പോഴുണ്ടാകുന്ന ത്രികോണമാണ് ഗോളീയ ത്രികോണം. ഒരു ഗോളത്തിന്റെ കേന്ദ്രത്തിലൂടെ കടന്നുപോകുന്ന തലം ഉപരിതലത്തില്‍ രചിക്കുന്ന വൃത്തമാണ് മഹാവൃത്തം.
മഹാവൃത്തങ്ങളുടെ ചാപമാണ് ഗോളീയ ത്രികോണത്തിന്റെ വശമായി കണക്കാക്കുന്നത്. ചിത്രത്തില്‍ AB,BC,AC എന്നിവ ഈ ത്രികോണത്തിന്റെ വശങ്ങളാണ്; ഇവയുടെ അളവുകള്‍ പ്രസക്ത വശങ്ങള്‍ (ചാപങ്ങള്‍) ഗോളകേന്ദ്രത്തില്‍ സമ്മുഖമാക്കുന്ന (subtend) കോണത്തിന്റെ അളവിന് ആനുപാതികമായിരിക്കും. അതിനാല്‍ ഒരു ഗോളീയ ത്രികോണത്തിന്റെ മൂന്ന് കോണങ്ങളുടെയും മൂന്ന് വശങ്ങളുടെയും അളവിന്റെ മാനദണ്ഡം കേന്ദ്രത്തിലെ കോണങ്ങളാണ്. ഇത്തരം ത്രികോണങ്ങളുടെ കോണങ്ങളുടെ തുക 180°-യില്‍ കൂടുതലും 540°-യില്‍ കുറവും ആയിരിക്കും.
ഗോളീയ മട്ടത്രികോണം
ഒരു ഗോളീയത്രികോണത്തിലെ ഏതെങ്കിലമൊരു കോണം മാത്രം 90° ആണെങ്കില്‍ അത്തരം ത്രികോണങ്ങളെ ഗോളീയമട്ടത്രികോണമെന്നു പറയുന്നു. ഒരു ഗോളീയ ത്രികോണത്തില്‍ മൂന്നു മട്ടകോണങ്ങള്‍ വരെയുണ്ടാകാം.
സൂത്രവാക്യങ്ങള്‍
സമതല ത്രികോണമിതീയാശയങ്ങളുപയോഗിച്ച് ഗോളീയ മട്ടത്രികോണ സൂത്രവാക്യങ്ങള്‍ കാണാവുന്നതാണ്. ജോണ്‍ നേപ്പിയര്‍ (1550-1617) കണ്ടുപിടിച്ച നേപ്പിയര്‍ നിയമങ്ങളുടെ സഹായത്താല്‍ ഗോളീയ മട്ടത്രികോണങ്ങളിലെ സമസ്യകള്‍ നിര്‍ധാരണം ചെയ്യാന്‍ സാധിക്കുന്നു.
നേപ്പിയര്‍ നിയമം (Napier's rule)
a,b,90°-A,90°-C,90°-B എന്നിവ ABC എന്ന ഗോളീയ മട്ടത്രികോണത്തിലെ നേപ്പിയര്‍ ഘടക(Napier parts)ങ്ങളാണ്. ഈ ഭാഗ(part)ങ്ങള്‍ ഒരു വൃത്തത്തിന്റെ അഞ്ച് സെക്ടറുകളിലാണ് അടയാളപ്പെടുത്തിയിരിക്കുന്നത്. a ഒരു പ്രത്യേക ഭാഗമായി (particular part) പരിഗണിച്ചാല്‍ b യും 90°-B യും സമീപഭാഗ(adjacent pats)ങ്ങളെന്നും 90°-C യും 90°-A യും എതിര്‍ഭാഗ(opposite parts) ങ്ങളെന്നും പറയുന്നു. ഈ ഭാഗങ്ങളുടെ സഹായത്താല്‍ നേപ്പിയര്‍ നിയമം നിര്‍വചിക്കാം.
ഒരു പ്രത്യേക ഭാഗത്തിന്റെ സൈന്‍ ഫലനം, സമീപ ഭാഗങ്ങളുടെ ടാന്‍ജെന്റുകളുടെ ഗുണനഫലത്തിന് തുല്യവും എതിര്‍ഭാഗങ്ങളുടെ കൊസൈനുകളുടെ ഗുണനഫലത്തിന് തുല്യവുമായിരിക്കുമെന്നതാണ് നേപ്പിയര്‍ നിയമം. ഈ നിയമങ്ങളില്‍ നിന്ന് ഗോളീയ മട്ടത്രികോണത്തിലെ പ്രധാനപ്പെട്ട ചില സൂത്രവാക്യങ്ങള്‍ തെളിയിച്ചെടുക്കാന്‍ സാധിക്കും.
ഗോളീയ ത്രികോണമിതിയുടെ പ്രയോജനം
ജ്യോതിശ്ശാസ്ത്രം, സമുദ്രസഞ്ചാരം എന്നീ മേഖലകളില്‍ ഗോളീയ ത്രികോണമിതീയാശയങ്ങള്‍ക്ക് മുഖ്യ പങ്കാണുള്ളത്. ജ്യോതിര്‍ഗോളങ്ങളുടെ ചലനത്തെക്കുറിച്ചു മനസ്സിലാക്കാന്‍ ഈ ശാസ്ത്രശാഖ സഹായിക്കുന്നു. ഖഗോള വസ്തുവും (celestial bodies) ശിരോബിന്ദു(zenith)വും ഖഗോള ഉത്തരധ്രുവവും ശീര്‍ഷങ്ങളായുള്ള ഗോളീയ ത്രികോണങ്ങളുടെ പഠനങ്ങള്‍ക്ക് ഗോളീയ ത്രികോണമിതീയാശയങ്ങളും സൂത്രവാക്യങ്ങളും വളരെ പ്രയോജനപ്പെടുന്നവയാണ്. ഖഗോള അക്ഷാംശം (Celestial latitude), ഖഗോള രേഖാംശം (Celestial longitude)എന്നീ കോണീയ ദൂരങ്ങള്‍ നിര്‍ണയിക്കുന്നതിനും സാധിക്കുന്നു. ഖഗോളവസ്തുക്കളുടെ ദിഗംശവും (Azimuth) ഉന്നതി(Altitude)യുമായി ബന്ധപ്പെട്ട പ്രശ്ന നിര്‍ധാരണങ്ങള്‍ക്ക് നേപ്പിയര്‍ നിയമം പ്രയോജനപ്പെടുന്നു.
