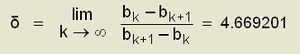This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കയോസ് സിദ്ധാന്തം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
കയോസ് സിദ്ധാന്തം
വാനശാസ്ത്രം, ദ്രവബലതന്ത്രം, കാലാവസ്ഥാപഠനം തുടങ്ങിയ ശാഖകളില് ഉരുത്തിരിഞ്ഞുവന്ന ഒരു മൗലികാശയമാണ് കയോസ്. ചില നിയത (deterministic)പ്രഭാവങ്ങളില് പ്രവചനീയത നഷ്ടപ്പെടുന്ന സാഹചര്യങ്ങള് ഉണ്ടാവാനിടയുണ്ടെന്ന കണ്ടെത്തലാണ് ഇതിന്റെ ആധാരം. ഹെന്റി പോയ്ന്കറെ എന്ന പ്രശസ്ത ഗണിത ശാസ്ത്രജ്ഞന് ബലതന്ത്രത്തിലെ വിഷമം പിടിച്ച മൂവസ്തുചലനപ്രശ്നം (three body motion) (ഉദാ. അന്യോന്യാകര്ഷണത്തിനു വിധേയമായി സൂര്യന്, ഭൂമി, ചന്ദ്രന് ഇവയുടെ ചലനം) നിര്ധരിക്കാന് ശ്രമിക്കുകയായിരുന്നു. ന്യൂട്ടന്റെ വ്യുത്ക്രമവര്ഗ (inverse square)നിയമമനുസരിച്ച് ഗുരുത്വാകര്ഷണം പ്രവര്ത്തിക്കുമ്പോള് മൂന്നു വസ്തുക്കളടങ്ങുന്ന ഇത്തരമൊരുവ്യൂഹം എങ്ങനെ ചലിക്കും എന്നായിരുന്നു അദ്ദേഹം പഠിക്കാന് ശ്രമിച്ചത്. ചില പ്രാരംഭികാവസ്ഥകളില്, മൂവസ്തുവ്യൂഹത്തിന്റെ കക്ഷ്യകള് അനാവര്ത്തിത(non-periodic)മാണെന്ന് അദ്ദേഹം കണ്ടുപിടിച്ചു. രണ്ട് വസ്തുവ്യൂഹത്തില് ആവര്ത്തിത കക്ഷ്യ (periodic orbit)കള് ഉണ്ടെന്ന് ന്യൂട്ടണ് ഇതിന് മുന്പ് തെളിയിച്ചിട്ടുണ്ട്. 1898ല് യാക്ക് ഹദമാര്ദ് (Jacques Hadamard) എന്ന ഗണിതജ്ഞന്, സ്ഥിരമായ നെഗറ്റീവ് വക്രത (negative curvature) ഉള്ള ഒരു പ്രതലത്തില്, ഘര്ഷണ രഹിത(frictionless)മായി ചലിക്കുന്ന സ്വതന്ത്രകണത്തിന്റെ ചലനം അനിയതം ആണെന്ന് തെളിയിച്ചു.
ഏറെക്കാലം കയോസ് പഠനം ഗണിതജ്ഞരുടെ കുത്തകയായിരുന്നു. എര്ഗോഡിക്ക് (Ergodic) സിദ്ധാന്തം എന്ന പേരിലാണ് കയോസിനെ ഭരിക്കുന്ന പല അടിസ്ഥാന സിദ്ധാന്തങ്ങളും അവര് ആവിഷ്കരിച്ചത്. 1961ല് ഇ.എന്. ലോറെന്സ് (E.N. Lorenz) ആവിഷ്കരിച്ച കാലാവസ്ഥാ മോഡലില് കയോസ് ഉണ്ടെന്ന് അദ്ദേഹം കണ്ടുപിടിച്ചതോടെയാണ് ഇതിനെ സംബന്ധിച്ച് ഒരു നൂതനാവബോധം സാര്വത്രികമായത്.
പ്രാരംഭികാവസ്ഥ നിര്ദിഷ്ടകമാണെങ്കില് ഏതൊരു വ്യൂഹത്തിന്റെയും ഗതി എന്താകുമെന്ന് കൃത്യതയോടെ വിവരിക്കാമെന്നതാണ് സാമ്പ്രദായിക ഭൗതികത്തില് നിയതത്വം (determinism)എന്നതുകൊണ്ട് വിവക്ഷിക്കുന്നത്. പിയറെ ലപ്ലാസ് (Pierre Laplace)ആണ് ഇക്കാര്യത്തിന് ഏറെ ഊന്നല് നല്കിയത്. ഇതുപ്രകാരം ഒരു വ്യൂഹത്തിന്റെ ചലനചരിത്രം ചുരുള് നിവര്ത്താന് പ്രാരംഭിക വ്യവസ്ഥകളും പ്രസക്തമായ സമവാക്യങ്ങളും മതിയാവും. എന്നാല് ഇപ്പറഞ്ഞത് രേഖീയ (Linear)വ്യൂഹങ്ങളെ സംബന്ധിച്ചിടത്തോളം ശരിയാണെങ്കിലും അരേഖീയ(non-linear)വ്യൂഹങ്ങളുടെ കാര്യത്തില് ഇത് ശരിയല്ല. ഒരു വ്യൂഹത്തിന്റെ പ്രാരംഭികാവ്യവസ്ഥകള് നിര്ദേശിക്കുമ്പോളുണ്ടാകാനിടയുള്ള പിശക് രേഖീയ വ്യൂഹത്തില് സ്ഥിരമായി നിലകൊള്ളും എന്നാല് അരേഖീയത ഉണ്ടെങ്കില്, പോകപ്പോകെ എത്ര ചെറിയ ഒരു പിശകും അനേക മടങ്ങ് വര്ധിക്കാനുള്ള സാഹചര്യം കണ്ടേക്കാം. ക്ലാസ്സിക്കല് വ്യൂഹങ്ങളില് പ്രവചനീയത അപ്രത്യക്ഷമാകുന്നതിന് അവശ്യം വേണ്ട സവിശേഷതയാണ് അരേഖീയത. എന്നാല് അരേഖീയത ഉള്ളതുകൊണ്ടുമാത്രം കയോസ് ഉണ്ടാകുമെന്ന് ഉറപ്പിക്കുവാന് സാധ്യമല്ല.
ഒരു വ്യൂഹത്തിന്റെ ബലതന്ത്രം പഠിക്കുന്നതിന് അതിന്റെ അവസ്ഥ(state)യെ സൂചിപ്പിക്കുന്ന എല്ലാ സ്വതന്ത്ര ചരങ്ങളെയും തിരിച്ചറിയേണ്ടതുണ്ട്. ത്രിമാന സ്പേസില് ചലിക്കുന്ന ഒരു കണത്തിന്റെ സ്ഥാനം അടയാളപ്പെടുത്താന് മൂന്നു സംഖ്യകള് അല്ലെങ്കില് നിര്ദേശാങ്കങ്ങള് ആവശ്യമാണ്. 10 കണങ്ങള് അടങ്ങിയ വ്യൂഹമാണെങ്കില് 10x 3 = 30 ചരങ്ങള് ആവശ്യമാണ്. ച കണങ്ങളുള്ള വ്യൂഹത്തിന്റെ ചലനം വിവരിക്കാന് 3N ചരങ്ങള് വേണം. ചലനം എങ്ങോട്ടെന്ന് അറിയണമെങ്കില് സ്ഥാനസൂചകങ്ങള്ക്കു പുറമേ വേഗതകളും വേണ്ടിവരും. ത്രിമാനങ്ങളില് മൂന്നു വേഗതകളും ഓരോ കണത്തിനും അനുവദനീയമാണ്. ഇങ്ങനെ മൊത്തം ആറു ചരങ്ങള് ഓരോ കണത്തിനും പ്രസക്തമാകുന്നു. 6ച ചരങ്ങളാണ് ച കണവ്യൂഹത്തെ വിവരിക്കുക. ഈ സംഖ്യകള്ക്ക് സ്വാതന്ത്യ്രത്തിന്റെ മാനങ്ങള് (Degrees of Freedom)എന്നാണ് പേര്. 6N മാനങ്ങളുള്ള ഒരു സ്പേസിനെ വിഭാവനം ചെയ്താല് അതിലെ ഓരോ ബിന്ദുവിനും 6ച നിര്ദേശാങ്കങ്ങള് ഉണ്ടാകും. വ്യൂഹങ്ങളുടെ അവസ്ഥയെ ഈ സ്പേസിലെ (ഇതിനെ അവസ്ഥാ സ്പേസ് എന്നു വിളിക്കാം) ബിന്ദുവിനെക്കൊണ്ട് പ്രതിനിധീകരിക്കാം. ഒരു നിയോജകമണ്ഡലത്തിലെ ലക്ഷക്കണക്കിനാളുകളെ പ്രതിനിധീകരിച്ച് ഒരു ജനപ്രതിനിധി നിയമസഭയില് ഇരിക്കുന്നു. അതുപോലെ, വ്യൂഹചലനം പഠിക്കുന്നതിന്, അവസ്ഥാ സ്പേസില് "വ്യൂഹബിന്ദു' (System point) ചേലിക്കുന്നത് പരിശോധിച്ചാല് മതി. കൃത്യമായ ആവൃത്തിയോടെ ദോലനം നടത്തുന്ന ഒരു ഏകമാന ഹാര്മോണിക് ദോലകം (one dimensional harmonic oscillator)എടുക്കുക. ഇതിന് ഒരു സ്വതന്ത്രമാനവും ഒരു വേഗതയും ഉണ്ട്. ഇതിന്റെ അവസ്ഥാ സ്പേസ് (state or phase space), ദ്വിമാനം(two dimension) ആണ്. പരസ്പര ലംബമായ രണ്ട് ദിശകളില് (x,y അക്ഷങ്ങളില്) ഈ മൂല്യങ്ങളെ അടയാളപ്പെടുത്താം. രേഖീയ ദോലകമെന്നും വിളിക്കപ്പെടുന്ന ഈ വ്യൂഹത്തിന്റെ വ്യൂഹബിന്ദു അവസ്ഥാ സ്പേസില് ദീര്ഘവൃത്താ(ellipse)കൃതിയിലുള്ള കക്ഷ്യയില് ചലിക്കുന്നു (ചിത്രം 1). കക്ഷ്യയുടെ അക്ഷ ദൈര്ഘ്യങ്ങള് ദോലകത്തിന്റെ ഊര്ജത്തെ ആശ്രയിച്ചിരിക്കുന്നു. പൂര്ണ കൃത്യതയോടെ ഈ കക്ഷ്യയെ നിര്ണയിക്കാന് കഴിയുന്നു. പ്രസക്തവ്യൂഹം രേഖീയമായതിനാലാണ് ഇത് സാധിക്കുന്നത്. ഊര്ജം എത്ര ആയിരുന്നാലും, ഇതിന്റെ വ്യൂഹബിന്ദു ഒരു നിശ്ചിത ദീര്ഘവൃത്തത്തിലായിരിക്കും എന്നാണ് പ്രവചനീയത വിവക്ഷിക്കുക. രേഖീയ ദോലകം സമാകലനീയ (integrable)വ്യൂഹമാണ്. പ്രാരംഭികാവസ്ഥ എന്തായിരുന്നാലും ഭാവിചലനത്തെ കൃത്യമായി പ്രവചിക്കാമെന്നതാണ് ഇത്തരം വ്യൂഹങ്ങളുടെ അല്ലെങ്കില് മോഡലുകളുടെ സവിശേഷത. ക്ലാസ്സിക്കല് ബലതന്ത്രത്തില് ഊര്ജഫലന(energy function)ത്തിന് ഹാമില്ട്ടോണിയന് (Hamiltonian) എന്നാണ് പേര്. രേഖീയ ദോലകത്തിന്റെ ഹാമില്ട്ടോണിയന് സമാകലനീയമാണെന്ന് പറയുന്നു.
ഒരു ചെറിയ വിക്ഷോഭ(perturbation)ത്തിന് ഒരു സമാകലനീയ വ്യൂഹത്തെ അസമാകലനീയ(non-integrable)മാക്കാന് കഴിഞ്ഞേക്കാം. പുതിയ ഹാമില്ട്ടോണിയന് അസമാകലനീയമാവാന് രണ്ട് വ്യവസ്ഥകള് അനുസരിക്കണം:
1. വിക്ഷോഭം ചെറുതായിരിക്കണം.
2. മൂല (original)ഹാമില്ട്ടോണിയന്റെ ആവൃത്തി (frequency)കള് അസമ്മേയം (incommensurate) ആയിരിക്കണം.
രേഖീയ ദോലകങ്ങള്ക്ക് ഒരു ആവൃത്തിയേ ഉള്ളു. രണ്ട് മാനങ്ങളില് ചലിക്കുന്ന ദോലകത്തിന് രണ്ട് ആവൃത്തികളുണ്ട്. ഇവ പൂര്ണസംഖ്യകളോ, അല്ലെങ്കില് പൂര്ണസംഖ്യകളുടെ അനുപാതത്തിലോ ആണെങ്കില് സമ്മേയം(commensurate) ആണെന്നും, അങ്ങനെ അല്ലെങ്കില് അസമ്മേയം (incommensurate) ആണെന്നും പറയുന്നു. ആവൃത്തികളില് ഒരെണ്ണമെങ്കിലും അപരിമേയ(irrational)മാണെങ്കില്, അവ അസമ്മേയമാണ്. അസമാകലനീയതയുടെ മേല്പറഞ്ഞ വ്യവസ്ഥകള് പാലിക്കപ്പെട്ടാല് വ്യൂഹബിന്ദു അവസ്ഥാ സ്പേസില് ഒരു ടോറസി(torus)ല് ചലിക്കും. ത്രിമാനങ്ങളില് നിര്മിക്കുന്ന ടോറസിന് ഉഴുന്നുവടയുടെ ആകൃതിയാണുള്ളത്. ചിലതൊഴികെ, മറ്റെല്ലാ പ്രാരംഭികാവസ്ഥകള്ക്കും അനുസൃതമായി വ്യൂഹബിന്ദു ടോറസില് നിശ്ചിതമായ ഒരു കക്ഷ്യ വരയ്ക്കും. ഒഴിവാക്കിയ പ്രാരംഭികാവസ്ഥകളുടെ കാര്യത്തില്, വ്യൂഹബിന്ദു ടോറസില് "അലഞ്ഞുതിരിഞ്ഞു' കൊണ്ടിരിക്കും. നിശ്ചിതമല്ലാത്ത ഒരു കക്ഷ്യയാവും ഈ സാഹചര്യത്തില് ടോറസില് ആലേഖിതമാവുക. ഇപ്പറഞ്ഞ കാര്യങ്ങളെ സമാഹരിക്കുന്ന പ്രസ്താവമാണ് സുപ്രസിദ്ധമായ കൊള്മൊഗൊറോഫ് ആര്ണോള്ഡ് മോസര് (KAM-കാം) തിയറം. ഇത്തരത്തിലുള്ള ഒരു "തെണ്ടിത്തിരയലാ'ണ് മൂവസ്തുചലനത്തില് പൊയ്ന്കറെ കണ്ടുപിടിച്ചത്.
ഹാമില്ട്ടോണിയന് വിവരണം അസാധ്യമായതരത്തിലുള്ള വ്യൂഹങ്ങളാണ് സ്ഥൂലപ്രകൃതിയില് ധാരാളമായി കണ്ടുവരുന്നത്. ഊര്ജവ്യയം (dissipation) ഉള്ള വ്യൂഹങ്ങള് ഉദാഹരണം ഒരു വ്യയകാരി വ്യൂഹം (dissipative system)ചലിച്ചുതുടങ്ങുമ്പോള്, കുറെനേരത്തേക്ക് ചാഞ്ചല്യങ്ങള് (transient) സജീവമാകുന്നു. ഇവ അപ്രത്യക്ഷമാകുമ്പോള് ചലനം ദൃഢ (steady)മാകുന്നു. ഈഘട്ടത്തില്, വ്യൂഹബിന്ദു അവസ്ഥാ സ്പേസില് ആകര്ഷണകാരി (attractor) എന്നുവിളിക്കുന്ന ഭാഗത്താവും സ്ഥിതി ചെയ്യുക. ആകര്ഷണകാരി ഒരു ബിന്ദുവോ ഒരു പ്രദേശ(region) മോആവാം. ആകര്ഷണകാരി ബിന്ദുവാണെങ്കില് അതിന് സ്ഥിരബിന്ദു (fixed point) എന്നു പറയുന്നു. ഒരു പെന്ഡുലത്തിന്റെ സ്ഥിരബിന്ദു അതിന്റെ വിശ്രമബിന്ദുവാണ് (resting point). പെന്ഡുലത്തിന്റെ താങ്ങി(support)ന്മേല് ഉണ്ടാകുന്ന ഘര്ഷണം മൂലം, ക്രമേണ അത് വിശ്രമബിന്ദുവിലേക്ക് ചെല്ലുന്നു. പലതരം യാന്ത്രികദോലകങ്ങള്, വൈദ്യുത സര്ക്യൂട്ടുകള് തുടങ്ങിയവയിലെ ദോലനങ്ങളുടെ മോഡലാണ് വാന്ഡെര് പോള് ദോലകം (van der pol oscillator). ഇതില് ഒരു സവിശേഷരീതിയിലുള്ള ഘര്ഷണവും ദോലനം ചെയ്യുന്ന ഒരു ബാഹ്യബിന്ദുവും ഒരേസമയം പ്രവര്ത്തിക്കുന്നു. ദോലകത്തിന്റെ അനുനാദ (resonant)ആവൃത്തി പ്രയുക്തബലത്തിന്റെ ആവൃത്തിയോട് ഏകദേശം തുല്യമാണെങ്കില് പ്രയുക്തബല ആവൃത്തിയില് ചലനം ആവര്ത്തിച്ചുകൊണ്ടിരിക്കും. ഇതില് ആകര്ഷണകാരി ഏകക (unit) വ്യോസാര്ധമുള്ള ഒരു വൃത്തമാണ്. സീമാചക്രം (limit cycle)എന്നാണ് ഇത് അറിയപ്പെടുന്നത്. ആകര്ഷണകാരിക്ക് ഒരു മാനം (dimension) ഉണ്ട്. ആകര്ഷണകാരി സ്ഥിരബിന്ദുവാണെങ്കില് മാനം, dA= 0 ഉം, സീമാചക്രമാണെങ്കില് dA = 1 ഉം, ഒരു സാധാരണ ടോറസ് (ദ്വിമാനപ്രതലം) ആണെങ്കില് dA = 2 ഉം ആയിരിക്കും. ആകര്ഷണകാരിയുടെ മാനം dA , ഒരു സൂചക പരിമാണമാണ്. ഭിന്നസംഖ്യ മാനമായുള്ള ആകര്ഷണകാരികളാണ് അപരിചിത ആകര്ഷണകാരി(strange attractor)കള് ഭിന്നസംഖ്യാമാനത്തിന് ഫ്രാക്ടല് (fractal) മാനം എന്നു പറയും. കയോസ് പ്രദര്ശിപ്പിക്കുന്ന വ്യൂഹങ്ങളുടെ ആകര്ഷണകാരികള് ഫ്രാക്ടലുകള് ഫ്രാക്ടല് മാനമുള്ളത് ആണ്. ഫ്രാക്ടല് മാനം ചിലപ്പോള് അപരിമേയ സംഖ്യയുമാവാം.
കയോസെന്ന് വിശേഷിപ്പിക്കുന്നത്, ആകസ്മികത (chance)യ്ക്കും അനിവാര്യത (necessity)യ്ക്കും ഇടയിലുള്ള ഒരു ചലനരീതിയാണ്. ഇതിനെ വിവരിക്കാന് അവസ്ഥാസ്പേസാണ് ഉത്തമം. അവസ്ഥാ സ്പേസിലെ ഒരു ആകര്ഷണകാരിയില് വ്യൂഹബിന്ദു മുന്പോട്ടും പുറകോട്ടും, മേലോട്ടും കീഴോട്ടും യാതൊരു വ്യവസ്ഥയുമില്ലാതെ ചലിക്കുന്നുവെങ്കില്, കയോസിലെത്തി എന്ന് തീരുമാനിക്കാം. പ്രസ്തുത ആകര്ഷണകാരി അപരിചിത ഇനത്തില്പ്പെട്ടതായിരിക്കുംതാനും. കയോട്ടിക് അവസ്ഥയില്പ്പോലും വ്യൂഹബിന്ദു ഒരിക്കലും ഒന്നില്ക്കൂടുതല് തവണ ഒരേ സ്ഥാനത്തുകൂടി കടന്നുപോവില്ല. അപരിചിത ആകര്ഷണകാരിയില് പഥങ്ങള് നിബിഡ(dense)മായി നിറഞ്ഞുനില്ക്കും. പ്രാരംഭികവ്യവസ്ഥകള്ക്കനുസരിച്ചാണ് കയോസില് എത്തുകയോ, എത്താതിരിക്കുകയോ ചെയ്യുക എന്ന കാര്യം അടിവരയിട്ടു പറയേണ്ടതാണ്. ഈ വ്യവസ്ഥകളില് അല്പം മാറ്റം വന്നാല് വ്യൂഹബിന്ദു മിക്കവാറും അപരിചിത ആകര്ഷണകാരി വിട്ടുപോകാനിടയുണ്ട്. വ്യാമിശ്രം (mixing), ഏകദേശ ആവര്ത്തനമുള്ള കക്ഷ്യകള് (quasi periodic orbits), പ്രാരംഭിക വ്യവസ്ഥകളിന്മേലുള്ള അതിസൂക്ഷ്മ ആശ്രയത്വം (sensitive dependence) ഇവയാണ് കയോട്ടിക്ക് ചലനത്തിന്റെ ലക്ഷണങ്ങള്. R1, R2 രണ്ട് പ്രദേശങ്ങള്. ഇവ എത്രയും ചെറുതാകട്ടെ, സഞ്ചാരപഥം R1ലൂടെ കടന്നുപോകുന്നുണ്ടെങ്കില് കാലാന്തരത്തില് R2വിലൂടെയും കടന്നുപോകും എന്ന സവിശേഷതയാണ് വ്യാമിശ്രം സൂചിപ്പിക്കുന്നത്. ഏകദേശ ആവര്ത്തനമെന്ന് പറഞ്ഞാല്, ഒരേ പ്രദേശത്തിലൂടെ കൂടെക്കൂടെ, തികച്ചും യാദൃച്ഛികരീതിയില്, സഞ്ചാരപഥം കടന്നുപോകുന്നുവെന്നര്ഥം. എന്നാല് പഥം അതിന്മേല്ത്തന്നെ കൂട്ടിമുട്ടുന്നുമില്ല. പ്രാരംഭിക വ്യവസ്ഥകളില് മാറ്റം ഉണ്ടായാല്, ഇതിന്റെ ആകൃതിയും പ്രകൃതിയും വ്യത്യാസപ്പെട്ടേക്കും. ഉദാഹരണമായി, ഒരു ദീര്ഘവൃത്താകൃതിയിലുള്ള കക്ഷ്യ, ഹൈപ്പര് ബോളിക്ക് കക്ഷ്യയായി അനന്തതയിലേക്ക് നിഷ്ക്രമിച്ചെന്നുവരാം. കൃത്യമായി പറഞ്ഞാല് സമീപസ്ഥമായ ബിന്ദുക്കളില് നിന്നാരംഭിക്കുന്ന രണ്ട് സഞ്ചാരപഥങ്ങള് തമ്മില് എക്സ്പോണെന്ഷ്യല് നിരക്കില് പരസ്പരം അകന്നുപോവുകയാണ് കയോസില് സംഭവിക്കുന്നത്. കയോസില്ലെങ്കില്, സമീപസ്ഥ പഥങ്ങള് സമീപസ്ഥങ്ങളായിത്തന്നെ നില്ക്കും, എത്ര സമയം കഴിഞ്ഞാലും രണ്ടു കക്ഷ്യകള് തമ്മില് തുടക്ക (+ = 0) ത്തിലുള്ള അകലം S0 ആണെങ്കില്, t സെക്കണ്ട് കഴിയുമ്പോള് അകലം S(t) = Soeλt എന്ന നിരക്കില് വര്ധിക്കുന്നു. ഇവിടെ S യ്ക്ക് വ്യതിചലന (divergence) നിരക്ക് അല്ലെങ്കില് ല്യാപ്പുനോവ് വര്ഗം (Lyapunov exponent)എന്ന് പറയുന്നു. കയോട്ടിക് ചലനത്തിന് അവശ്യം വേണ്ടത് ഒരു പോസിറ്റീവ് ല്യാപ്പുനോവ് വര്ഗമാണ്. ല്യാപ്പുനോവ് വര്ഗം നെഗറ്റീവാണെങ്കില് കയോസിന് സാധ്യതയില്ല.
കേവലമൊരു ഗണിതപ്രശ്നമായി കയോസ് പഠിക്കാവുന്നതാണ്. അവിച്ഛിന്ന (continuous) മാതൃകകളെക്കാള് ഇതിനെളുപ്പം വിച്ഛിന്ന (discrete) മാതൃകകളാണ്.x(t) യുടെ അര്ഥം സമയം - t ലെ x ന്റെ മൂല്യം എന്നാണല്ലോ. ഇവിടെ t ഒരു അവിച്ഛിന്നം (variable) ആണ്. സമയത്തെ (t) വ്യതിരിക്ത ഘടകങ്ങളാക്കുമ്പോള് പോസിറ്റീവ് പൂര്ണസംഖ്യകളുടെ ഒരു ശ്രണി ആണ് ലഭിക്കുക: n = 0,1, 2, 3, ... x(t) യെ അവിച്ഛിന്നീകരിച്ചെഴുതുന്നത് xnഎന്നാണ്.xn ന്റെ മൂല്യങ്ങളാണ് x1, x2 ... എന്നിവയുടെ ശ്രണി. മുകളില് കൊടുത്തിട്ടുള്ള (t) യ്ക്കുപകരം sn എന്നെഴുതുക. അപ്പോള് s2 = Soeλt എന്ന് ലഭിക്കുന്നു. ഒരു നിയത മോഡലില്, xn ന്റെ മൂല്യത്തില്നിന്ന് xn+1ന്റെ മൂല്യം നിര്ണയിക്കാം.xn+1, xn ന്റെ ഫലനം (function) ആണെന്നു പറയാം. ഇത്തരമൊരു സംബന്ധ(relation)ത്തിന് മാപ്പ് (map) എന്ന് പറയാറുണ്ട്. കയോസ് സിദ്ധാന്തത്തില് കയോസിലെത്താനായി പല മാര്ഗങ്ങളും ഉപയോഗിക്കുന്നുണ്ടെങ്കിലും, കയോസ് പ്രദര്ശിപ്പിക്കുന്ന ഏറ്റവും സരളമായ ഗണിത മോഡല് ലോജിസ്റ്റിക്ക് മാപ്പ് (Logistic Map) ആണ്. ഇതിനെ താഴെക്കുറിക്കുന്ന രീതിയില് നിര്വചിക്കാം.
xn+1 = bxn (1-xn)
പൂജ്യത്തിനും ഒന്നിനും ഇടയില് കിടക്കുന്ന ഒരു ചരമാണ് x. b യെ നിയന്ത്രണരാശി (control parameter) എന്ന് വിളിക്കുന്നു. b ക്ക് പൂജ്യത്തിനും നാലിനും ഇടയില് ചലിക്കാം. ഒരു കൂട്ടം ജീവികളുടെ സംഖ്യയില് ഉണ്ടാകുന്ന മാറ്റത്തെ ചിത്രീകരിക്കുന്ന ഒരു സമീകരണ(equation)മാണിത്. (n + 1)-ാമത്തെ തലമുറയിലെ മുയലുകളുടെ എണ്ണം തൊട്ടുമുമ്പുള്ള തലമുറയിലെ എണ്ണത്തിന്റെ (xn) അനുപാതത്തിലാണ്. എന്നാല് ഭക്ഷ്യവസ്തുക്കളുടെ ദൗര്ലഭ്യംമൂലം കുറെ എണ്ണം ചത്തുപോകുന്നു. ഈ വസ്തുതയെ സൂചിപ്പിക്കുകയാണ് xn2ലുള്ള പദം (term)ചെയ്യുന്നത്.
n ന്റെ മൂല്യം ക്രമമായി വര്ധിപ്പിച്ചാല് ഒരു സീമാ മൂല്യ(limiting value)ത്തിലെത്തും. ഇതിനെ x' എന്ന് കുറിക്കുക. x' ഒരു സ്ഥിരബിന്ദുവിനെ പ്രതിനിധീകരിക്കുന്നു. എന്നു വച്ചാല്,.
അതായത്, b, 1നും 3നും ഇടയിലായിരിക്കുന്നിടത്തോളം ഈ സ്ഥിരബിന്ദു സ്ഥിരമാണ്. b യെ 3നുമേല് വര്ധിപ്പിച്ചാല് രണ്ട് ബിന്ദുക്കള്ക്കിടയില് വ്യൂഹബിന്ദു ദോലനംചെയ്യും. ഈ മാറ്റം സംഭവിക്കുന്നത് b = 3.2ലാണ്. ഇതിന് രണ്ടാകല് (bifurcation) എന്നു പറയുന്നു. ദോലനങ്ങളുടെ ആവര്ത്തനകാലം (period) ഇരട്ടിക്കുകയാണ് ചെയ്യുന്നത്. ആവര്ത്തനകാലം ഇരട്ടിക്കല് (period doubling)എന്ന് ഇതിന് പറയുന്നു. ദോലനത്തിന്റെ ഒരു ചക്ര(cycle)ത്തിനുപകരം ഇപ്പോള് ഇരട്ടി ആവര്ത്തനകാലമുള്ള "രണ്ട്' ചക്രം (two-cycle) ലഭിക്കുന്നു. അടുത്തഘട്ടം നാലിരട്ടിയാക(quadrupling)ലാണ്. ആവര്ത്തനകാലം നാലിരട്ടിയാകുന്ന ഈ സംഭവം നടക്കുന്നത് യ = 3.5 ആകുമ്പോഴാണ്; അനുബന്ധിത ചക്രത്തിന് "നാല്ചക്രം' (four-cycle)എന്ന് പറയുന്നു. ഇതുപോലുള്ള ഓരോ മാറ്റത്തിലും ആവര്ത്തനകാലം ഇരട്ടിക്കുന്നു. ഇരട്ടിക്കല് പ്രതിഭാസത്തെ വിശദമാക്കുന്ന ചിത്രമാണ് x' ഉം b യും തമ്മിലുള്ള ഗ്രാഫ് (ചിത്രം 2). b, 3.5699456 എന്ന മൂല്യത്തെ തൊടുമ്പോള് ഗ്രാഫിലെ ശാഖ(branch)കളുടെ സംഖ്യ അനന്തമാകുന്നു. ആദ്യത്തെ ഇരട്ടിക്കല് നടക്കുമ്പോള്, അതുവരെ ഒരു ശാഖയായി പെരുമാറിയിരുന്ന x'- b ഗ്രാഫില് രണ്ട് ശാഖകള് പ്രത്യക്ഷപ്പെടുന്നതായി ചിത്രം 2 വ്യക്തമാക്കുന്നു. ഇവിടെ സൂചിപ്പിച്ച "അനന്തശാഖീകരണം' കയോസിന്റെ പടിവാതില് തുറക്കുന്നു. ആവര്ത്തനകാലം ഇരട്ടിക്കല് മാര്ഗം എന്നാണ് കയോസിലേക്കുള്ള ഈ വഴി(rout)ക്ക് നല്കിയിട്ടുള്ള നാമം. bk ഉം bk+1ഉം അടുത്തടുത്തുള്ള ഇരട്ടിക്കല് യ മൂല്യങ്ങളാണെങ്കില് ഇവ തമ്മിലുള്ള തിരശ്ചീന അകലം (horizontal distnace)ഒരു സീമ(limit)യിലേക്ക് അഭിസരി(converge)ക്കുന്നു:
മിച്ചല് ഫെയ്ഗെന്ബാമാ(Mitchell Feigenbaum)ണ് ഈ മൂല്യം ആദ്യമായി നിര്ണയിച്ചത്. ഇതിന് ഫെയ്ഗെന് ബാം സ്ഥിരാങ്കം എന്ന് പറയുന്നു. വിവിധതരം കയോട്ടിക് വ്യൂഹങ്ങളുടെ മൂല്യം ഇതുതന്നെ ആയതിനാല്, ഈ സീമയ്ക്ക് ഒരു സാര്വത്രികത (universality) ഉണ്ട്. ഇടവിട്ടിടവിട്ട് ഉണ്ടാകുന്ന അസ്ഥ (Intermitt-ancy), ഏകദേശ ആവര്ത്തനക്രമം (quasi periodicity), സന്നിഗ്ധാവസ്ഥ (crisis) തുടങ്ങിയ വേറെ മാര്ഗങ്ങളിലൂടെ കയോട്ടിക് അവസ്ഥയെ പ്രാപിക്കുന്ന വ്യൂഹങ്ങളും മോഡലുകളും ഉണ്ട്.
ഒരു കയോട്ടിക് ആകര്ഷണകാരിയില് അസ്ഥിരമായ ആവര്ത്തിത കക്ഷ്യ(unstable periodic orbit)കള് അനന്തമായ തോതിലുണ്ട്. ഇവയിലൊരെണ്ണം തിരഞ്ഞെടുത്ത് സഞ്ചാരം ആരംഭിക്കുന്ന വ്യൂഹബിന്ദു ഉടനെ വേറൊരു സദൃശകക്ഷ്യയിലേക്ക് വഴുതിവീഴുന്നു. മൊത്തത്തിലുള്ള അസ്ഥിരതയായി ഈ പ്രഭാവത്തെ വ്യാഖ്യാനിക്കാവുന്നതാണ്. വളരെ ചെറിയ വിക്ഷോഭങ്ങള്ക്ക് വിധേയമാക്കി അസ്ഥിരകക്ഷ്യകളില് ഒന്നിനെ സ്ഥിരതയുള്ളതാക്കി രൂപാന്തരപ്പെടുത്താമത്ര. കയോസ് നിയന്ത്രണം എന്നാണ് ഈ വിദ്യയ്ക്ക് പറയുക. വിക്ഷുബ്ധദ്രവ (turbulent fluid)ങ്ങള്, ദോലനീയ (oscillating) രാസപ്രവര്ത്തനങ്ങള്, ഹൃദയപേശികള് തുടങ്ങിയ വ്യൂഹങ്ങളില് കയോസ് നിയന്ത്രണം സാധിച്ചിട്ടുണ്ട്.
സാര്വത്രികമായി കാണുന്ന പ്രതിഭാസമായ കയോസ് വാനശാസ്ത്രം, വിക്ഷോഭപഠനം, ഇലക്ട്രാണിക്സ്, ഫോട്ടോണിക്സ്, കാലാവസ്ഥാശാസ്ത്രം, ധനതത്ത്വശാസ്ത്രം, ഫൈനാന്സ്, ജിയോളജി, കാര്ഡിയോളജി, എപിഡെമിയോളജി തുടങ്ങിയ വ്യത്യസ്തങ്ങളായ മണ്ഡലങ്ങളില് ഉള്പ്പെട്ടിട്ടുണ്ട്. കാലാവസ്ഥയെ നിര്ണയിക്കുന്ന ഘടകങ്ങള് തികച്ചും കയോട്ടിക് ആയതിനാല് കൃത്യമായ കാലാവസ്ഥാ പ്രവചനം അസാധ്യമാണെന്ന് 1963ല് ലോറന്സ് (Lorenz) വികസിപ്പിച്ച ഗണിതശാസ്ത്ര മാതൃക വ്യക്തമാക്കുന്നു. അന്തരീക്ഷ വാതകപ്രവാഹങ്ങള് പ്രാരംഭിക വ്യവസ്ഥകളിന്മേലുള്ള സൂക്ഷ്മ ആശ്രയത്വം നിലനിര്ത്തുന്നതിനാല് അന്തിമഫലങ്ങള് ശരിയായി കണക്കാക്കാനാവില്ല. പ്രസിദ്ധമായ "ചിത്രശലഭ പ്രഭാവം' (Butterfly effect)എന്ന രൂപകത്തിലൂടെ കാരണവും കാര്യവും തമ്മിലുള്ള അനുപാതരഹിതവും അരേഖീയവുമായ ബന്ധമാണ് ലോറന്സ് നിര്ധാരണം ചെയ്യുന്നത്.
സമകാലീന സാമൂഹ്യശാസ്ത്രതത്വചിന്താ രംഗത്തും കയോസ് സിദ്ധാന്തം സ്വാധീനമുണ്ടാക്കിയിട്ടുണ്ട്. ആഗോള സാമ്പത്തിക പ്രവര്ത്തനങ്ങള്, വിശേഷിച്ചും ധനകാര്യഓഹരി കമ്പോളങ്ങള് കയോട്ടിക് സിദ്ധാന്തത്തിന്റെ മാതൃകയില് വിശകലനം ചെയ്യാനുള്ള ശ്രമങ്ങള് ആരംഭിച്ചിട്ടുണ്ട്. സൂക്ഷ്മതലപ്രതിഭാസങ്ങളെ ഭരിക്കുന്ന ഭൗതിക സിദ്ധാന്തമായ ക്വാണ്ടം ബലതന്ത്ര മൊരു രേഖീയശാസ്ത്രമാണെങ്കിലും ഇതില് സംഭാവ്യത(probability)യ്ക്ക് മൗലികമായ പങ്കുണ്ട്. അതിനാല് കയോസിന്റെ അടിസ്ഥാന തത്വമായ യാദൃച്ഛികത ക്വാണ്ടം ബലതന്ത്രത്തില് സ്വാഭാവികമായിത്തന്നെ ഉണ്ടെന്ന് പറയാം.
എന്നാല് ന്യൂടോണിയന് ബലതന്ത്രത്തിന്റെയും ഡാര്വീനിയന് പരിണാമസിദ്ധാന്തത്തിന്റെയും മൗലിക നിയമങ്ങള് അപ്രസക്തമായി എന്നു സ്ഥാപിക്കുന്നതിനു വേണ്ടി കയോസ് സിദ്ധാന്തത്തെ ഉപയോഗിക്കുന്ന പ്രവണത ഉത്തരാധുനിക ചിന്തകര്ക്കിടയില് വ്യാപകമായിട്ടുണ്ട്. ക്വാണ്ടം ബലതന്ത്രത്തെപ്പോലെതന്നെ കയോസ് സിദ്ധാന്തവും ദെക്കാര്ത്തിയന്ന്യൂട്ടോണിയന് സിദ്ധാന്തത്തെയും അത് ഉത്പാദിപ്പിക്കുന്ന അടിസ്ഥാനലോക ബോധത്തെയും അപ്രസക്തമാക്കുന്നില്ലെന്നും പുതിയ ശാസ്ത്രീയരീതികളുടെ ദുരുപയോഗത്തിനെതിരെ ജാഗ്രത പാലിക്കേണ്ടതുണ്ടെന്നുമാണ് ഊര്ജതന്ത്ര നോബല് ജേതാവായ "സ്റ്റീഫന് വെയ്ന്ബര്ഗ്' അഭിപ്രായപ്പെടുന്നത്.
(ഡോ. കെ. ബാബുജോസഫ്, സ.പ.)