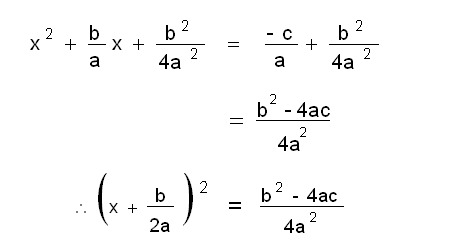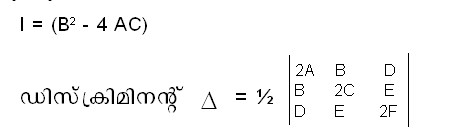This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ദ്വിഘാത സമവാക്യങ്ങള്‍
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(New page: ദ്വിഘാത സമവാക്യങ്ങള്‍ ഝൌമറൃമശേര ലൂൌമശീിേ ചരങ്ങളുടെ ഏറ്റവും കൂടിയ ഘ...) |
|||
| (ഇടക്കുള്ള 9 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | ദ്വിഘാത സമവാക്യങ്ങള്‍ | + | =ദ്വിഘാത സമവാക്യങ്ങള്‍= |
| - | + | Quadratic equations | |
ചരങ്ങളുടെ ഏറ്റവും കൂടിയ ഘാതം രണ്ട് ആയിട്ടുള്ള ബീജീയ സമവാക്യങ്ങള്‍. ദ്വിഘാത സമവാക്യങ്ങളില്‍ ഒന്നോ അതിലധികമോ ചരങ്ങള്‍ ഉണ്ടാകാം. സ്ഥലങ്ങളുടെയും വസ്തുക്കളുടെയും നീളം, വീതി, വിസ്തീര്‍ണം വൈദ്യുതിപ്രവാഹ തീവ്രതയും താപനഷ്ടവും, വിദ്യുത്-കാന്തിക തരംഗപ്രവാഹം തുടങ്ങിയ നിരവധി പ്രതിഭാസങ്ങളുമായി ബന്ധപ്പെട്ട സമസ്യകള്‍ നിര്‍ധാരണം ചെയ്യുന്നതിന് ദ്വിഘാത സമവാക്യങ്ങള്‍ പ്രയോജനപ്പെടുന്നു. | ചരങ്ങളുടെ ഏറ്റവും കൂടിയ ഘാതം രണ്ട് ആയിട്ടുള്ള ബീജീയ സമവാക്യങ്ങള്‍. ദ്വിഘാത സമവാക്യങ്ങളില്‍ ഒന്നോ അതിലധികമോ ചരങ്ങള്‍ ഉണ്ടാകാം. സ്ഥലങ്ങളുടെയും വസ്തുക്കളുടെയും നീളം, വീതി, വിസ്തീര്‍ണം വൈദ്യുതിപ്രവാഹ തീവ്രതയും താപനഷ്ടവും, വിദ്യുത്-കാന്തിക തരംഗപ്രവാഹം തുടങ്ങിയ നിരവധി പ്രതിഭാസങ്ങളുമായി ബന്ധപ്പെട്ട സമസ്യകള്‍ നിര്‍ധാരണം ചെയ്യുന്നതിന് ദ്വിഘാത സമവാക്യങ്ങള്‍ പ്രയോജനപ്പെടുന്നു. | ||
| - | + | '''ചരിത്രം'''. പ്രാചീനകാലം മുതല്‍ ദ്വിഘാത സമവാക്യങ്ങളെക്കുറിച്ചുള്ള പഠനം നടന്നിരുന്നു. ബാബിലോണിയയിലെ ക്യൂനിഫോം ഗണിതപ്പട്ടികയില്‍ ഇവയെക്കുറിച്ചുള്ള പരാമര്‍ശമുണ്ട്. ഹമുറബി രാജവംശക്കാലത്തെ (ബി.സി. 1800-1600) രേഖകളാണിവ. ചതുഷ്ഘാത (quartic) സമവാക്യങ്ങള്‍ ദ്വിഘാത സമവാക്യങ്ങളിലൂടെ നിര്‍ധാരണം ചെയ്യാന്‍ ഈജിപ്തുകാര്‍ക്ക് കഴിഞ്ഞിരുന്നു. ഒരു പുരാതന (ബി.സി. 1700) ബാബിലോണിയന്‍ ഗണിത ഗ്രന്ഥത്തില്‍, ദ്വിഘാത സമവാക്യങ്ങള്‍ x+x<sup>-1</sup>=a എന്ന രൂപത്തിലും അജ്ഞാതരാശികള്‍ x ± y=a; x.y=a എന്ന രൂപത്തിലും കൊടുത്തിരിക്കുന്നതായി കാണാം. | |
| - | + | ഒരു ചരമുള്ള ദ്വിഘാത സമവാക്യങ്ങളുടെ (ax<sup>2</sup>+bx+c= 0) നിര്‍ധാരണങ്ങള്‍ [[Image:p599a1pqr.png]]കണ്ടുപിടിച്ചത് യവനരാണെന്ന് അനുമാനിക്കപ്പെടുന്നു. വര്‍ഗപൂര്‍ത്തീകരണ രീതിയെയാണ് ഇവര്‍ അവലംബിച്ചത്. യൂക്ലിഡിന്റെ ''എലിമെന്റ്സി''ല്‍ (ബി.സി. 300) ഈ നിര്‍ധാരണങ്ങള്‍ കാണാം. ചൈനക്കാര്‍ ക്രിസ്തുവര്‍ഷാരംഭത്തിനു മുമ്പുതന്നെ ദ്വിഘാത സമവാക്യങ്ങളുടെ നിര്‍ധാരണ രീതികള്‍ സ്വായത്തമാക്കി. 2ax=[[Image:p599a2pqr.png]] | |
| + | എന്ന ദ്വിഘാത സൂത്രവാക്യം കണ്ടെത്തിയത് ഭാരതീയരായിരുന്നുവെന്ന് അനുമാനമുണ്ട്. അറബിഗണിതജ്ഞരില്‍ പ്രമുഖനായ മുഹമ്മദ് ബിന്‍ മൂസ അല്‍-ഖവാരിസ്മി(സു. 780-850)യുടെ ''അല്‍-ജബര്‍ വാല്‍-മുഖാബല'' എന്ന ബീജഗണിതഗ്രന്ഥത്തില്‍ ഈ സമവാക്യങ്ങള്‍ പഠനവിധേയമാക്കിയിട്ടുണ്ട്. 16-ാം ശ.-ത്തോടെ ഏതു വിഭാഗത്തിലുമുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ക്ക് നിര്‍ധാരണങ്ങള്‍ കണ്ടെത്തുവാന്‍ സാധിച്ചതായി കാണാം. | ||
| - | + | '''വര്‍ഗീകരണം'''. ചരങ്ങളുടെ എണ്ണത്തെ അടിസ്ഥാനമാക്കിയാണ് ദ്വിഘാത സമവാക്യങ്ങളെ സാധാരണയായി വര്‍ഗീകരിക്കുന്നത്. ഓരോ വിഭാഗത്തിനും അതിനെ പ്രതിനിധാനം ചെയ്യുന്ന ഒരു പൊതു സമവാക്യം ഉണ്ട്. | |
| - | + | '''ഒരു ചരം മാത്രമുള്ളവ'''. ഒരു ചരമുള്ള എല്ലാ ദ്വിഘാത സമവാക്യങ്ങളെയും ax<sup>2</sup>+bx+c=0 (a ≠0) എന്ന സമവാക്യംകൊണ്ട് സൂചിപ്പിക്കാം. വര്‍ഗപൂര്‍ത്തീകരണ രീതിയിലൂടെ ഈ സമവാക്യം നിര്‍ധാരണം ചെയ്യുമ്പോള്‍ x-ന്റെ മൂല്യം കിട്ടും. | |
| - | + | ax<sup>2</sup>+bx+c= 0 → (1) (a,b,c സ്ഥിര സംഖ്യകള്‍). | |
| - | ഇതില്‍ നിന്ന് | + | ഇതില്‍ നിന്ന് ax<sup>2</sup>+bx=-c → (2) |
| - | (2) നെ | + | (2) നെ a കൊണ്ട് ഹരിച്ച് ഇരുവശത്തും b<sup>2</sup>/4a<sup>2</sup> കൂട്ടിയാല്‍ |
| - | + | [[Image:p600apqr.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
ഇരുഭാഗത്തും വര്‍ഗമൂലമെടുത്ത് പുനഃക്രമീകരിച്ചാല്‍ | ഇരുഭാഗത്തും വര്‍ഗമൂലമെടുത്ത് പുനഃക്രമീകരിച്ചാല്‍ | ||
| + | [[Image:temp_san.png]] | ||
| + | എന്നു കിട്ടുന്നു. ദ്വിഘാത സൂത്രവാക്യം എന്ന് ഇതറിയപ്പെടുന്നു. | ||
| - | + | ഇവിടെ ± എന്ന അടയാളം x-ന്റെ വ്യത്യസ്ത മൂല്യങ്ങളെ സൂചിപ്പിക്കുന്നു. ചില സാഹചര്യങ്ങളില്‍ ഈ മൂല്യങ്ങള്‍ സമവുമാകാം. നിര്‍ധാരണമൂല്യങ്ങള്‍ തിരിച്ചറിയാന്‍ ഉപകരിക്കുന്നതിനാല്‍, b<sup>2</sup>-4ac യെ ഡിസ്ക്രിമിനന്റ് (Discriminant) എന്നു വിശേഷിപ്പിക്കുന്നു. Δ (ഡെല്‍റ്റാ) എന്ന ചിഹ്നം ഉപയോഗിച്ചാണ് ഇത് സൂചിപ്പിക്കുന്നത്. Δ യുടെ മൂല്യം കണ്ടെത്തുന്നതിലൂടെ x-ന്റെ മൂല്യങ്ങള്‍ വാസ്തവിക സംഖ്യകളാണോ സമ സംഖ്യകളാണോ അസമ സംഖ്യകളാണോ പരിമേയ സംഖ്യകളാണോ അപരിമേയ സംഖ്യകളാണോ എന്നൊക്കെ തിരിച്ചറിയാന്‍ സാധിക്കുന്നു. | |
| - | + | Δ= b<sup>2</sup>-4ac > 0 ആണെങ്കില്‍ മൂല്യങ്ങള്‍ വാസ്തവികവും (real) അസമവും ആണ്. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | Δ < 0 ആണെങ്കില്‍ രണ്ട് മൂല്യങ്ങളും സമ്മിശ്രം (complex) | ||
ആണ് | ആണ് | ||
| - | + | Δ = 0 ആണെങ്കില്‍ മൂല്യങ്ങള്‍ വാസ്തവികവും സമവും ആണ്. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | പൂര്‍ണ വര്‍ഗമല്ലായെങ്കില്‍ മൂല്യം ധനമായിരിക്കുമ്പോള്‍ അപരിമേയ സംഖ്യകളും ഋണമാവുമ്പോള്‍ സമ്മിശ്ര സംഖ്യകളും Δ പൂര്‍ണവര്‍ഗമാണെങ്കില്‍ പരിമേയ ഭിന്ന സംഖ്യകളും ആയിരിക്കും ചരത്തിന്റെ മൂല്യങ്ങള്‍. | |
| - | + | ദ്വിഘാത സമവാക്യ നിര്‍ധാരണത്തിന് ഘടക സിദ്ധാന്തവും പ്രയോജനപ്രദമാണ്. | |
| - | + | ഉദാ. ഒരു ദ്വിഘാത സമവാക്യത്തെ x<sup>2</sup>-(a+b)x+ab= 0 എന്ന രൂപത്തില്‍ എഴുതാമെങ്കില്‍ (x-a) (x-b) = 0 എന്ന് ഘടകങ്ങളായി എഴുതാം. അതില്‍നിന്ന് x = a അല്ലെങ്കില്‍ x = b എന്നു കിട്ടും. നിര്‍ധാരണ മൂല്യങ്ങള്‍ വെവ്വേറെ കാണാതെതന്നെ അവയെ സംബന്ധിച്ച വിവരങ്ങള്‍ മനസ്സിലാക്കാന്‍ മറ്റു ചില സിദ്ധാന്തങ്ങളും പ്രയോജനപ്പെടുന്നുണ്ട്. | |
| - | + | '''സിദ്ധാന്തം 1 ''' | |
| - | + | ax<sup>2</sup>+bx+c= 0 എന്ന ദ്വിഘാത സമവാക്യത്തില്‍ ചരം x-ന്റെ മൂല്യങ്ങള്‍ ''α,β'' ആണെങ്കില്‍ ''α'' +''β''=-b/a യും ''αβ''=c/aആയിരിക്കും. | |
| - | + | '''സിദ്ധാന്തം 2''' | |
| - | + | മൂല്യങ്ങള്‍ അറിയാമെങ്കില്‍ താഴെപ്പറയുന്ന സിദ്ധാന്തം ഉപയോഗിച്ച് ദ്വിഘാത സമവാക്യം രൂപവത്കരിക്കാവുന്നതാണ്. | |
| - | + | ax<sup>2</sup>+bx+c= 0 എന്ന സമവാക്യത്തില്‍ x-ന്റെ മൂല്യങ്ങള്‍ ''α'' ,''β'' എന്നിവയാണെങ്കില്‍, | |
| - | + | ax<sup>2</sup>+bx+c ≡a(x-''α'')(x-''β'') | |
| - | + | ≡ a{x<sup>2</sup>-(''α''+''β'')x+''αβ''} എന്നു കിട്ടും. ഇതിലൂടെ സമവാക്യം രൂപപ്പെടുത്താം. | |
| - | + | '''രണ്ട് ദ്വിഘാത സമവാക്യങ്ങളുടെ പൊതു മൂല്യം'''. രണ്ട് ദ്വിഘാത സമവാക്യങ്ങളുടെ പൊതുമൂല്യം കാണുന്നതിന് താഴെപ്പറയുന്ന വ്യവസ്ഥകള്‍ അനുയോജ്യമാണ്. | |
| - | + | ax<sup>2</sup>+bx+c= 0 → (1) (a≠0), | |
| - | + | a'x<sup>2</sup> +b'x+ c' = 0 → (2) (a'≠0) എന്ന രണ്ട് ദ്വിഘാത സമവാക്യങ്ങള്‍ പരിഗണിക്കുക. ഇവിടെ (ca' - c'a)<sup>2</sup> = (ab'- a'b) (bc'- b'c) എന്ന വ്യവസ്ഥ പാലിക്കപ്പെട്ടാല്‍, (1)നും (2)നും α എന്ന ഒരു പൊതുനിര്‍ധാരം ഉണ്ടായിരിക്കും. | |
| - | + | [[Image:p600a5pqr.png]] | |
| - | + | '''രണ്ട് ചരങ്ങളുള്ളവ'''. രണ്ട് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങളുടെ സാമാന്യരൂപമാണ്, | |
| - | + | Ax<sup>2</sup>+Bxy+Cy<sup>2</sup>+Dx+Ey+F = 0. | |
| - | + | ഇവിടെ നിശ്ചര(invariant)ത്തെ 'I' എന്ന ചിഹ്നംകൊണ്ട് കുറിക്കുന്നു. | |
| - | + | [[Image:p600a7pqr.png]] | |
| - | + | I,Δ എന്നിവയിലൂടെ x,y എന്നീ രണ്ട് ചരങ്ങളുടെയും മൂല്യങ്ങള്‍ കാണാന്‍ സാധിക്കും. | |
| - | + | ഇതുപോലെ രണ്ടിലേറെ ചരങ്ങളുള്ള സമവാക്യങ്ങളും നിര്‍ധരിക്കാന്‍ സാധിക്കുന്നതാണ്. | |
| - | + | '''ദ്വിഘാത സമവാക്യങ്ങളും ഗ്രാഫും'''. ദ്വിഘാത സമവാക്യങ്ങളെ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ പല ജ്യാമിതീയ രൂപങ്ങളും രൂപപ്പെടുന്നു. ഒന്നും രണ്ടും ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങളെ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ രേഖകളോ കോണിക ഛേദങ്ങളായ വൃത്തങ്ങള്‍, ദീര്‍ഘവൃത്തങ്ങള്‍ (എലിപ്സുകള്‍), പരാബൊളകള്‍, ഹൈപ്പര്‍ബോളകള്‍ എന്നിവയോ രൂപം കൊള്ളുമെന്ന് ദെക്കാര്‍ ത്തെ തെളിയിച്ചിട്ടുണ്ട്. x<sup>2</sup>-y<sup>2</sup> = 0 എന്ന സമവാക്യം പരസ്പരം കൂട്ടിമുട്ടുന്ന രണ്ട് ഋജു രേഖകളെയും x<sup>2</sup>+y<sup>2</sup> = a വൃത്തത്തെയും [[Image:p600a8pqr.png]]ഹൈപ്പര്‍ബോളയെയും ദീര്‍ഘവൃത്തത്തെയും y<sup>2</sup>=4ax പരാബൊളയെയും ആണ് പ്രതിനിധാനം ചെയ്യുന്നത്. | |
| - | + | ഒരു ചരമുള്ള രണ്ട് ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ ചിത്രീകരിക്കുന്ന രീതി താഴെ ചേര്‍ക്കുന്നു. | |
| - | + | Δ < 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തെ സ്പര്‍ശിക്കുന്നില്ല. | |
| - | + | Δ = 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തെ സ്പര്‍ശിക്കുന്നു (സമ ബിന്ദുക്കളില്‍). | |
| - | + | Δ > 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തില്‍ രണ്ട് വ്യത്യസ്ത ബിന്ദുക്കളില്‍ സന്ധിക്കുന്നു. | |
| - | + | രണ്ട് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ രേഖപ്പെടുത്തിയാല്‍ കോണിക പരിച്ഛേദങ്ങളാണ് ലഭിക്കുക. ഇവിടെ നിശ്ചര(I)ത്തിന്റെയും ഡിസ്ക്രിമിനന്റിന്റെയും (Δ) മൂല്യങ്ങളില്‍നിന്ന് വക്രങ്ങളുടെ സ്വഭാവം മുന്‍കൂട്ടി അറിയാന്‍ സാധിക്കുന്നു. മൂന്ന് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ ഉണ്ടാകുന്ന പ്രതലത്തെ ദ്വിഘാതി പ്രതലം (Quadratic surface) എന്നു വിളിക്കുന്നു. ഈ പ്രതലത്തിന്റെ ഓരോ തല(plane)വും കോണിക പരിച്ഛേദമായിരിക്കും. f(x,y,z)=k എന്നതാണ് ഇവയുടെ സാമാന്യ രൂപം. ദ്വിഘാതി പ്രതലങ്ങളില്‍ കോണികവും സിലിണ്ടര്‍ ആകൃതിയും ഉള്ള പ്രതലങ്ങള്‍ക്ക് ഡിജനറേറ്റ് ക്വാഡ്രിക്സ് (Degenerate quadrics) അഥവാ കോണ്‍കോയ്ഡുകള്‍ എന്നാണ് സംജ്ഞ. ഒരേ ഫോക്കസ് ഉള്ള മൂന്ന് ക്വാഡ്രിക് പ്രതലങ്ങളുടെ വ്യൂഹത്തെ സംനാഭി ദ്വിഘാതി (Confocal quadric) എന്നു വിശേഷിപ്പിക്കുന്നു. ഇതിന്റെ[[Image:pno601aaaa.png]] സമവാക്യം എന്നാണ്. A യുടെയും B യുടെയും C യുടെയും മൂല്യങ്ങള്‍ സമമാകുമ്പോള്‍ ക്വാഡ്രിക്കിന് ഗോളാകൃതി സിദ്ധിക്കുന്നു. | |
Current revision as of 09:23, 24 മാര്‍ച്ച് 2009
ദ്വിഘാത സമവാക്യങ്ങള്‍
Quadratic equations
ചരങ്ങളുടെ ഏറ്റവും കൂടിയ ഘാതം രണ്ട് ആയിട്ടുള്ള ബീജീയ സമവാക്യങ്ങള്‍. ദ്വിഘാത സമവാക്യങ്ങളില്‍ ഒന്നോ അതിലധികമോ ചരങ്ങള്‍ ഉണ്ടാകാം. സ്ഥലങ്ങളുടെയും വസ്തുക്കളുടെയും നീളം, വീതി, വിസ്തീര്‍ണം വൈദ്യുതിപ്രവാഹ തീവ്രതയും താപനഷ്ടവും, വിദ്യുത്-കാന്തിക തരംഗപ്രവാഹം തുടങ്ങിയ നിരവധി പ്രതിഭാസങ്ങളുമായി ബന്ധപ്പെട്ട സമസ്യകള്‍ നിര്‍ധാരണം ചെയ്യുന്നതിന് ദ്വിഘാത സമവാക്യങ്ങള്‍ പ്രയോജനപ്പെടുന്നു.
ചരിത്രം. പ്രാചീനകാലം മുതല്‍ ദ്വിഘാത സമവാക്യങ്ങളെക്കുറിച്ചുള്ള പഠനം നടന്നിരുന്നു. ബാബിലോണിയയിലെ ക്യൂനിഫോം ഗണിതപ്പട്ടികയില്‍ ഇവയെക്കുറിച്ചുള്ള പരാമര്‍ശമുണ്ട്. ഹമുറബി രാജവംശക്കാലത്തെ (ബി.സി. 1800-1600) രേഖകളാണിവ. ചതുഷ്ഘാത (quartic) സമവാക്യങ്ങള്‍ ദ്വിഘാത സമവാക്യങ്ങളിലൂടെ നിര്‍ധാരണം ചെയ്യാന്‍ ഈജിപ്തുകാര്‍ക്ക് കഴിഞ്ഞിരുന്നു. ഒരു പുരാതന (ബി.സി. 1700) ബാബിലോണിയന്‍ ഗണിത ഗ്രന്ഥത്തില്‍, ദ്വിഘാത സമവാക്യങ്ങള്‍ x+x-1=a എന്ന രൂപത്തിലും അജ്ഞാതരാശികള്‍ x ± y=a; x.y=a എന്ന രൂപത്തിലും കൊടുത്തിരിക്കുന്നതായി കാണാം.
ഒരു ചരമുള്ള ദ്വിഘാത സമവാക്യങ്ങളുടെ (ax2+bx+c= 0) നിര്‍ധാരണങ്ങള്‍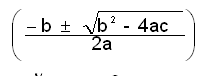 
കണ്ടുപിടിച്ചത് യവനരാണെന്ന് അനുമാനിക്കപ്പെടുന്നു. വര്‍ഗപൂര്‍ത്തീകരണ രീതിയെയാണ് ഇവര്‍ അവലംബിച്ചത്. യൂക്ലിഡിന്റെ എലിമെന്റ്സില്‍ (ബി.സി. 300) ഈ നിര്‍ധാരണങ്ങള്‍ കാണാം. ചൈനക്കാര്‍ ക്രിസ്തുവര്‍ഷാരംഭത്തിനു മുമ്പുതന്നെ ദ്വിഘാത സമവാക്യങ്ങളുടെ നിര്‍ധാരണ രീതികള്‍ സ്വായത്തമാക്കി. 2ax=
എന്ന ദ്വിഘാത സൂത്രവാക്യം കണ്ടെത്തിയത് ഭാരതീയരായിരുന്നുവെന്ന് അനുമാനമുണ്ട്. അറബിഗണിതജ്ഞരില്‍ പ്രമുഖനായ മുഹമ്മദ് ബിന്‍ മൂസ അല്‍-ഖവാരിസ്മി(സു. 780-850)യുടെ അല്‍-ജബര്‍ വാല്‍-മുഖാബല എന്ന ബീജഗണിതഗ്രന്ഥത്തില്‍ ഈ സമവാക്യങ്ങള്‍ പഠനവിധേയമാക്കിയിട്ടുണ്ട്. 16-ാം ശ.-ത്തോടെ ഏതു വിഭാഗത്തിലുമുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ക്ക് നിര്‍ധാരണങ്ങള്‍ കണ്ടെത്തുവാന്‍ സാധിച്ചതായി കാണാം.
വര്‍ഗീകരണം. ചരങ്ങളുടെ എണ്ണത്തെ അടിസ്ഥാനമാക്കിയാണ് ദ്വിഘാത സമവാക്യങ്ങളെ സാധാരണയായി വര്‍ഗീകരിക്കുന്നത്. ഓരോ വിഭാഗത്തിനും അതിനെ പ്രതിനിധാനം ചെയ്യുന്ന ഒരു പൊതു സമവാക്യം ഉണ്ട്.
ഒരു ചരം മാത്രമുള്ളവ. ഒരു ചരമുള്ള എല്ലാ ദ്വിഘാത സമവാക്യങ്ങളെയും ax2+bx+c=0 (a ≠0) എന്ന സമവാക്യംകൊണ്ട് സൂചിപ്പിക്കാം. വര്‍ഗപൂര്‍ത്തീകരണ രീതിയിലൂടെ ഈ സമവാക്യം നിര്‍ധാരണം ചെയ്യുമ്പോള്‍ x-ന്റെ മൂല്യം കിട്ടും.
ax2+bx+c= 0 → (1) (a,b,c സ്ഥിര സംഖ്യകള്‍).
ഇതില്‍ നിന്ന് ax2+bx=-c → (2)
(2) നെ a കൊണ്ട് ഹരിച്ച് ഇരുവശത്തും b2/4a2 കൂട്ടിയാല്‍
ഇരുഭാഗത്തും വര്‍ഗമൂലമെടുത്ത് പുനഃക്രമീകരിച്ചാല്‍
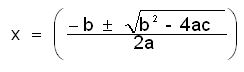എന്നു കിട്ടുന്നു. ദ്വിഘാത സൂത്രവാക്യം എന്ന് ഇതറിയപ്പെടുന്നു.
ഇവിടെ ± എന്ന അടയാളം x-ന്റെ വ്യത്യസ്ത മൂല്യങ്ങളെ സൂചിപ്പിക്കുന്നു. ചില സാഹചര്യങ്ങളില്‍ ഈ മൂല്യങ്ങള്‍ സമവുമാകാം. നിര്‍ധാരണമൂല്യങ്ങള്‍ തിരിച്ചറിയാന്‍ ഉപകരിക്കുന്നതിനാല്‍, b2-4ac യെ ഡിസ്ക്രിമിനന്റ് (Discriminant) എന്നു വിശേഷിപ്പിക്കുന്നു. Δ (ഡെല്‍റ്റാ) എന്ന ചിഹ്നം ഉപയോഗിച്ചാണ് ഇത് സൂചിപ്പിക്കുന്നത്. Δ യുടെ മൂല്യം കണ്ടെത്തുന്നതിലൂടെ x-ന്റെ മൂല്യങ്ങള്‍ വാസ്തവിക സംഖ്യകളാണോ സമ സംഖ്യകളാണോ അസമ സംഖ്യകളാണോ പരിമേയ സംഖ്യകളാണോ അപരിമേയ സംഖ്യകളാണോ എന്നൊക്കെ തിരിച്ചറിയാന്‍ സാധിക്കുന്നു.
Δ= b2-4ac > 0 ആണെങ്കില്‍ മൂല്യങ്ങള്‍ വാസ്തവികവും (real) അസമവും ആണ്.
Δ < 0 ആണെങ്കില്‍ രണ്ട് മൂല്യങ്ങളും സമ്മിശ്രം (complex) ആണ്
Δ = 0 ആണെങ്കില്‍ മൂല്യങ്ങള്‍ വാസ്തവികവും സമവും ആണ്.
പൂര്‍ണ വര്‍ഗമല്ലായെങ്കില്‍ മൂല്യം ധനമായിരിക്കുമ്പോള്‍ അപരിമേയ സംഖ്യകളും ഋണമാവുമ്പോള്‍ സമ്മിശ്ര സംഖ്യകളും Δ പൂര്‍ണവര്‍ഗമാണെങ്കില്‍ പരിമേയ ഭിന്ന സംഖ്യകളും ആയിരിക്കും ചരത്തിന്റെ മൂല്യങ്ങള്‍.
ദ്വിഘാത സമവാക്യ നിര്‍ധാരണത്തിന് ഘടക സിദ്ധാന്തവും പ്രയോജനപ്രദമാണ്.
ഉദാ. ഒരു ദ്വിഘാത സമവാക്യത്തെ x2-(a+b)x+ab= 0 എന്ന രൂപത്തില്‍ എഴുതാമെങ്കില്‍ (x-a) (x-b) = 0 എന്ന് ഘടകങ്ങളായി എഴുതാം. അതില്‍നിന്ന് x = a അല്ലെങ്കില്‍ x = b എന്നു കിട്ടും. നിര്‍ധാരണ മൂല്യങ്ങള്‍ വെവ്വേറെ കാണാതെതന്നെ അവയെ സംബന്ധിച്ച വിവരങ്ങള്‍ മനസ്സിലാക്കാന്‍ മറ്റു ചില സിദ്ധാന്തങ്ങളും പ്രയോജനപ്പെടുന്നുണ്ട്.
സിദ്ധാന്തം 1
ax2+bx+c= 0 എന്ന ദ്വിഘാത സമവാക്യത്തില്‍ ചരം x-ന്റെ മൂല്യങ്ങള്‍ α,β ആണെങ്കില്‍ α +β=-b/a യും αβ=c/aആയിരിക്കും.
സിദ്ധാന്തം 2
മൂല്യങ്ങള്‍ അറിയാമെങ്കില്‍ താഴെപ്പറയുന്ന സിദ്ധാന്തം ഉപയോഗിച്ച് ദ്വിഘാത സമവാക്യം രൂപവത്കരിക്കാവുന്നതാണ്.
ax2+bx+c= 0 എന്ന സമവാക്യത്തില്‍ x-ന്റെ മൂല്യങ്ങള്‍ α ,β എന്നിവയാണെങ്കില്‍,
ax2+bx+c ≡a(x-α)(x-β)
≡ a{x2-(α+β)x+αβ} എന്നു കിട്ടും. ഇതിലൂടെ സമവാക്യം രൂപപ്പെടുത്താം.
രണ്ട് ദ്വിഘാത സമവാക്യങ്ങളുടെ പൊതു മൂല്യം. രണ്ട് ദ്വിഘാത സമവാക്യങ്ങളുടെ പൊതുമൂല്യം കാണുന്നതിന് താഴെപ്പറയുന്ന വ്യവസ്ഥകള്‍ അനുയോജ്യമാണ്.
ax2+bx+c= 0 → (1) (a≠0),
a'x2 +b'x+ c' = 0 → (2) (a'≠0) എന്ന രണ്ട് ദ്വിഘാത സമവാക്യങ്ങള്‍ പരിഗണിക്കുക. ഇവിടെ (ca' - c'a)2 = (ab'- a'b) (bc'- b'c) എന്ന വ്യവസ്ഥ പാലിക്കപ്പെട്ടാല്‍, (1)നും (2)നും α എന്ന ഒരു പൊതുനിര്‍ധാരം ഉണ്ടായിരിക്കും.
രണ്ട് ചരങ്ങളുള്ളവ. രണ്ട് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങളുടെ സാമാന്യരൂപമാണ്,
Ax2+Bxy+Cy2+Dx+Ey+F = 0.
ഇവിടെ നിശ്ചര(invariant)ത്തെ 'I' എന്ന ചിഹ്നംകൊണ്ട് കുറിക്കുന്നു.
I,Δ എന്നിവയിലൂടെ x,y എന്നീ രണ്ട് ചരങ്ങളുടെയും മൂല്യങ്ങള്‍ കാണാന്‍ സാധിക്കും.
ഇതുപോലെ രണ്ടിലേറെ ചരങ്ങളുള്ള സമവാക്യങ്ങളും നിര്‍ധരിക്കാന്‍ സാധിക്കുന്നതാണ്.
ദ്വിഘാത സമവാക്യങ്ങളും ഗ്രാഫും. ദ്വിഘാത സമവാക്യങ്ങളെ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ പല ജ്യാമിതീയ രൂപങ്ങളും രൂപപ്പെടുന്നു. ഒന്നും രണ്ടും ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങളെ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ രേഖകളോ കോണിക ഛേദങ്ങളായ വൃത്തങ്ങള്‍, ദീര്‍ഘവൃത്തങ്ങള്‍ (എലിപ്സുകള്‍), പരാബൊളകള്‍, ഹൈപ്പര്‍ബോളകള്‍ എന്നിവയോ രൂപം കൊള്ളുമെന്ന് ദെക്കാര്‍ ത്തെ തെളിയിച്ചിട്ടുണ്ട്. x2-y2 = 0 എന്ന സമവാക്യം പരസ്പരം കൂട്ടിമുട്ടുന്ന രണ്ട് ഋജു രേഖകളെയും x2+y2 = a വൃത്തത്തെയും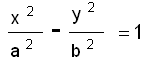 
ഹൈപ്പര്‍ബോളയെയും ദീര്‍ഘവൃത്തത്തെയും y2=4ax പരാബൊളയെയും ആണ് പ്രതിനിധാനം ചെയ്യുന്നത്.
ഒരു ചരമുള്ള രണ്ട് ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ ചിത്രീകരിക്കുന്ന രീതി താഴെ ചേര്‍ക്കുന്നു.
Δ < 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തെ സ്പര്‍ശിക്കുന്നില്ല.
Δ = 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തെ സ്പര്‍ശിക്കുന്നു (സമ ബിന്ദുക്കളില്‍).
Δ > 0 എങ്കില്‍ ഗ്രാഫ് x അക്ഷത്തില്‍ രണ്ട് വ്യത്യസ്ത ബിന്ദുക്കളില്‍ സന്ധിക്കുന്നു.
രണ്ട് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ രേഖപ്പെടുത്തിയാല്‍ കോണിക പരിച്ഛേദങ്ങളാണ് ലഭിക്കുക. ഇവിടെ നിശ്ചര(I)ത്തിന്റെയും ഡിസ്ക്രിമിനന്റിന്റെയും (Δ) മൂല്യങ്ങളില്‍നിന്ന് വക്രങ്ങളുടെ സ്വഭാവം മുന്‍കൂട്ടി അറിയാന്‍ സാധിക്കുന്നു. മൂന്ന് ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള്‍ ഗ്രാഫില്‍ രേഖപ്പെടുത്തുമ്പോള്‍ ഉണ്ടാകുന്ന പ്രതലത്തെ ദ്വിഘാതി പ്രതലം (Quadratic surface) എന്നു വിളിക്കുന്നു. ഈ പ്രതലത്തിന്റെ ഓരോ തല(plane)വും കോണിക പരിച്ഛേദമായിരിക്കും. f(x,y,z)=k എന്നതാണ് ഇവയുടെ സാമാന്യ രൂപം. ദ്വിഘാതി പ്രതലങ്ങളില്‍ കോണികവും സിലിണ്ടര്‍ ആകൃതിയും ഉള്ള പ്രതലങ്ങള്‍ക്ക് ഡിജനറേറ്റ് ക്വാഡ്രിക്സ് (Degenerate quadrics) അഥവാ കോണ്‍കോയ്ഡുകള്‍ എന്നാണ് സംജ്ഞ. ഒരേ ഫോക്കസ് ഉള്ള മൂന്ന് ക്വാഡ്രിക് പ്രതലങ്ങളുടെ വ്യൂഹത്തെ സംനാഭി ദ്വിഘാതി (Confocal quadric) എന്നു വിശേഷിപ്പിക്കുന്നു. ഇതിന്റെ
സമവാക്യം എന്നാണ്. A യുടെയും B യുടെയും C യുടെയും മൂല്യങ്ങള്‍ സമമാകുമ്പോള്‍ ക്വാഡ്രിക്കിന് ഗോളാകൃതി സിദ്ധിക്കുന്നു.
