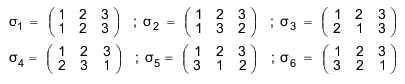This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗ്രൂപ്പ് സിദ്ധാന്തം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→ആമുഖം) |
(→ഗ്രൂപ്പ് സിദ്ധാന്തം) |
||
| വരി 1: | വരി 1: | ||
==ഗ്രൂപ്പ് സിദ്ധാന്തം== | ==ഗ്രൂപ്പ് സിദ്ധാന്തം== | ||
| + | |||
Group Theory | Group Theory | ||
അമൂര്ത്ത ബീജഗണിത (Abstract Algebra) ത്തിലെ ഒരു പ്രധാന ശാഖ. ഒരു ഗ്രൂപ്പിന്റെ ഏത് രണ്ടംഗങ്ങളെയും ചില വ്യവസ്ഥകള് പാലിക്കുന്ന ക്രിയയ്ക്ക് വിധേയമാക്കാന് സാധിക്കും. ഈ ക്രിയ സങ്കലനമോ ഗുണനമോ വേറെ ക്രിയയോ ആകാം. | അമൂര്ത്ത ബീജഗണിത (Abstract Algebra) ത്തിലെ ഒരു പ്രധാന ശാഖ. ഒരു ഗ്രൂപ്പിന്റെ ഏത് രണ്ടംഗങ്ങളെയും ചില വ്യവസ്ഥകള് പാലിക്കുന്ന ക്രിയയ്ക്ക് വിധേയമാക്കാന് സാധിക്കും. ഈ ക്രിയ സങ്കലനമോ ഗുണനമോ വേറെ ക്രിയയോ ആകാം. | ||
| - | |||
===ആമുഖം=== | ===ആമുഖം=== | ||
ഗ്രൂപ്പ് സിദ്ധാന്തം എ.ഡി. 20-ാം ശ.-ത്തിലാണ് പ്രാധാന്യം നേടിയത്. പ്രാചീന സംസ്കാരങ്ങളില്ത്തന്നെ സമമിതി (symmetry) എന്ന ആശയം ഉണ്ടായിരുന്നു. ഈജിപ്തിലെ ഭിത്തികളിലെ കലാത്മകമായ ചിത്രങ്ങളില് 'സമമിതി' എന്ന ആശയം പ്രകടമായിട്ടുണ്ട്. ഈ 'സമമിതി'കളെ ഗ്രൂപ്പെന്ന സങ്കല്പംകൊണ്ട് വ്യക്തമാക്കാം. യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) എന്ന സുപ്രസിദ്ധ ഗണിതശാസ്ത്രജ്ഞന് ബഹുഭുജങ്ങള് (polygons), സമബഹുഫലകങ്ങള് (regular polyhedra) എന്നിവയെപ്പറ്റി പഠിച്ചിട്ടുണ്ട്. പക്ഷേ, ഗ്രൂപ്പ് എന്ന ആശയം എ.ഡി. 18-ാം ശ.-ത്തിലാണ് ആദ്യമായി ഉടലെടുത്തത്. ജോസഫ് ലൂയി ലഗ്റാഞ്ജ് (എ.ഡി. 1736-1813) ഗ്രൂപ്പുകളെപ്പറ്റി പരാമര്ശിച്ചിട്ടുണ്ട്. അതിനുശേഷം അഗസ്റ്റിന് ലൂയി കാഷി (1789-1857) ക്രമചയങ്ങളുടെ ഗ്രൂപ്പുകളെ പരിഗണിച്ചു. എന്നാല്, ഗ്രൂപ്പുകള്ക്ക് പ്രാധാന്യം ഉണ്ടാകാന് ഒരു പ്രത്യേക കാരണമുണ്ടായിരുന്നു. ബീജഗണിതത്തില് 4-ാം ഘാതം വരെയുള്ള സമീകരണങ്ങളെ കരണികള് ഉപയോഗിച്ച് നിര്ധാരണം ചെയ്യാം. അതായത്, സങ്കലനം, വ്യവകലനം, ഗുണനം, ഹരണം, ഘാതം, മൂലം ഇവ ഉപയോഗിച്ച് നിര്ധാരണമൂല്യത്തെ സൂചിപ്പിക്കാന് സാധിക്കും. പക്ഷേ, 5-ാം ഘാതത്തിലെ സമീകരണത്തിന് അത് സാധ്യമല്ല. ആബെല് (1802-29) എന്ന നോര്വീജിയന് ഗണിതശാസ്ത്രജ്ഞന് ഇത് തെളിയിച്ചു. എന്തുകൊണ്ടാണ് ഇത് സാധ്യമാകാത്തത് എന്നുള്ള കാര്യം ഗ്രൂപ്പ് സിദ്ധാന്തം ഉപയോഗിച്ച് ഇവാരിസ്ത് ഗാല്വ (1811-32) എന്ന ഗണിതജ്ഞന് അനന്യസാധാരണമായ രീതിയില് വിശദമാക്കി. അതിനുശേഷമാണ് ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ നൈസര്ഗികമായ പ്രാധാന്യം ഗണിതശാസ്ത്രജ്ഞന്മാര് മനസ്സിലാക്കുകയും ഗ്രൂപ്പ് സിദ്ധാന്തം പഠനത്തിന് വിധേയമാക്കുകയും ചെയ്തത്. ഇപ്പോള് അമൂര്ത്തബീജഗണിതത്തിന്റെ ലളിതവും അടിസ്ഥാനപരവുമായ ഒരു ശാഖയാണ് ഗ്രൂപ്പ് സിദ്ധാന്തം. ഗണിതത്തിന്റെ പല ശാഖകളിലും, ഭൗതികം, രസതന്ത്രംപോലുള്ള ഇതര ശാസ്ത്രങ്ങളിലും, ഗ്രൂപ്പ് സിദ്ധാന്തം പ്രയോജനപ്പെടുത്താവുന്നതാണ്. | ഗ്രൂപ്പ് സിദ്ധാന്തം എ.ഡി. 20-ാം ശ.-ത്തിലാണ് പ്രാധാന്യം നേടിയത്. പ്രാചീന സംസ്കാരങ്ങളില്ത്തന്നെ സമമിതി (symmetry) എന്ന ആശയം ഉണ്ടായിരുന്നു. ഈജിപ്തിലെ ഭിത്തികളിലെ കലാത്മകമായ ചിത്രങ്ങളില് 'സമമിതി' എന്ന ആശയം പ്രകടമായിട്ടുണ്ട്. ഈ 'സമമിതി'കളെ ഗ്രൂപ്പെന്ന സങ്കല്പംകൊണ്ട് വ്യക്തമാക്കാം. യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) എന്ന സുപ്രസിദ്ധ ഗണിതശാസ്ത്രജ്ഞന് ബഹുഭുജങ്ങള് (polygons), സമബഹുഫലകങ്ങള് (regular polyhedra) എന്നിവയെപ്പറ്റി പഠിച്ചിട്ടുണ്ട്. പക്ഷേ, ഗ്രൂപ്പ് എന്ന ആശയം എ.ഡി. 18-ാം ശ.-ത്തിലാണ് ആദ്യമായി ഉടലെടുത്തത്. ജോസഫ് ലൂയി ലഗ്റാഞ്ജ് (എ.ഡി. 1736-1813) ഗ്രൂപ്പുകളെപ്പറ്റി പരാമര്ശിച്ചിട്ടുണ്ട്. അതിനുശേഷം അഗസ്റ്റിന് ലൂയി കാഷി (1789-1857) ക്രമചയങ്ങളുടെ ഗ്രൂപ്പുകളെ പരിഗണിച്ചു. എന്നാല്, ഗ്രൂപ്പുകള്ക്ക് പ്രാധാന്യം ഉണ്ടാകാന് ഒരു പ്രത്യേക കാരണമുണ്ടായിരുന്നു. ബീജഗണിതത്തില് 4-ാം ഘാതം വരെയുള്ള സമീകരണങ്ങളെ കരണികള് ഉപയോഗിച്ച് നിര്ധാരണം ചെയ്യാം. അതായത്, സങ്കലനം, വ്യവകലനം, ഗുണനം, ഹരണം, ഘാതം, മൂലം ഇവ ഉപയോഗിച്ച് നിര്ധാരണമൂല്യത്തെ സൂചിപ്പിക്കാന് സാധിക്കും. പക്ഷേ, 5-ാം ഘാതത്തിലെ സമീകരണത്തിന് അത് സാധ്യമല്ല. ആബെല് (1802-29) എന്ന നോര്വീജിയന് ഗണിതശാസ്ത്രജ്ഞന് ഇത് തെളിയിച്ചു. എന്തുകൊണ്ടാണ് ഇത് സാധ്യമാകാത്തത് എന്നുള്ള കാര്യം ഗ്രൂപ്പ് സിദ്ധാന്തം ഉപയോഗിച്ച് ഇവാരിസ്ത് ഗാല്വ (1811-32) എന്ന ഗണിതജ്ഞന് അനന്യസാധാരണമായ രീതിയില് വിശദമാക്കി. അതിനുശേഷമാണ് ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ നൈസര്ഗികമായ പ്രാധാന്യം ഗണിതശാസ്ത്രജ്ഞന്മാര് മനസ്സിലാക്കുകയും ഗ്രൂപ്പ് സിദ്ധാന്തം പഠനത്തിന് വിധേയമാക്കുകയും ചെയ്തത്. ഇപ്പോള് അമൂര്ത്തബീജഗണിതത്തിന്റെ ലളിതവും അടിസ്ഥാനപരവുമായ ഒരു ശാഖയാണ് ഗ്രൂപ്പ് സിദ്ധാന്തം. ഗണിതത്തിന്റെ പല ശാഖകളിലും, ഭൗതികം, രസതന്ത്രംപോലുള്ള ഇതര ശാസ്ത്രങ്ങളിലും, ഗ്രൂപ്പ് സിദ്ധാന്തം പ്രയോജനപ്പെടുത്താവുന്നതാണ്. | ||
11:37, 10 ഡിസംബര് 2015-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ഗ്രൂപ്പ് സിദ്ധാന്തം
Group Theory
അമൂര്ത്ത ബീജഗണിത (Abstract Algebra) ത്തിലെ ഒരു പ്രധാന ശാഖ. ഒരു ഗ്രൂപ്പിന്റെ ഏത് രണ്ടംഗങ്ങളെയും ചില വ്യവസ്ഥകള് പാലിക്കുന്ന ക്രിയയ്ക്ക് വിധേയമാക്കാന് സാധിക്കും. ഈ ക്രിയ സങ്കലനമോ ഗുണനമോ വേറെ ക്രിയയോ ആകാം.
ആമുഖം
ഗ്രൂപ്പ് സിദ്ധാന്തം എ.ഡി. 20-ാം ശ.-ത്തിലാണ് പ്രാധാന്യം നേടിയത്. പ്രാചീന സംസ്കാരങ്ങളില്ത്തന്നെ സമമിതി (symmetry) എന്ന ആശയം ഉണ്ടായിരുന്നു. ഈജിപ്തിലെ ഭിത്തികളിലെ കലാത്മകമായ ചിത്രങ്ങളില് 'സമമിതി' എന്ന ആശയം പ്രകടമായിട്ടുണ്ട്. ഈ 'സമമിതി'കളെ ഗ്രൂപ്പെന്ന സങ്കല്പംകൊണ്ട് വ്യക്തമാക്കാം. യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) എന്ന സുപ്രസിദ്ധ ഗണിതശാസ്ത്രജ്ഞന് ബഹുഭുജങ്ങള് (polygons), സമബഹുഫലകങ്ങള് (regular polyhedra) എന്നിവയെപ്പറ്റി പഠിച്ചിട്ടുണ്ട്. പക്ഷേ, ഗ്രൂപ്പ് എന്ന ആശയം എ.ഡി. 18-ാം ശ.-ത്തിലാണ് ആദ്യമായി ഉടലെടുത്തത്. ജോസഫ് ലൂയി ലഗ്റാഞ്ജ് (എ.ഡി. 1736-1813) ഗ്രൂപ്പുകളെപ്പറ്റി പരാമര്ശിച്ചിട്ടുണ്ട്. അതിനുശേഷം അഗസ്റ്റിന് ലൂയി കാഷി (1789-1857) ക്രമചയങ്ങളുടെ ഗ്രൂപ്പുകളെ പരിഗണിച്ചു. എന്നാല്, ഗ്രൂപ്പുകള്ക്ക് പ്രാധാന്യം ഉണ്ടാകാന് ഒരു പ്രത്യേക കാരണമുണ്ടായിരുന്നു. ബീജഗണിതത്തില് 4-ാം ഘാതം വരെയുള്ള സമീകരണങ്ങളെ കരണികള് ഉപയോഗിച്ച് നിര്ധാരണം ചെയ്യാം. അതായത്, സങ്കലനം, വ്യവകലനം, ഗുണനം, ഹരണം, ഘാതം, മൂലം ഇവ ഉപയോഗിച്ച് നിര്ധാരണമൂല്യത്തെ സൂചിപ്പിക്കാന് സാധിക്കും. പക്ഷേ, 5-ാം ഘാതത്തിലെ സമീകരണത്തിന് അത് സാധ്യമല്ല. ആബെല് (1802-29) എന്ന നോര്വീജിയന് ഗണിതശാസ്ത്രജ്ഞന് ഇത് തെളിയിച്ചു. എന്തുകൊണ്ടാണ് ഇത് സാധ്യമാകാത്തത് എന്നുള്ള കാര്യം ഗ്രൂപ്പ് സിദ്ധാന്തം ഉപയോഗിച്ച് ഇവാരിസ്ത് ഗാല്വ (1811-32) എന്ന ഗണിതജ്ഞന് അനന്യസാധാരണമായ രീതിയില് വിശദമാക്കി. അതിനുശേഷമാണ് ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ നൈസര്ഗികമായ പ്രാധാന്യം ഗണിതശാസ്ത്രജ്ഞന്മാര് മനസ്സിലാക്കുകയും ഗ്രൂപ്പ് സിദ്ധാന്തം പഠനത്തിന് വിധേയമാക്കുകയും ചെയ്തത്. ഇപ്പോള് അമൂര്ത്തബീജഗണിതത്തിന്റെ ലളിതവും അടിസ്ഥാനപരവുമായ ഒരു ശാഖയാണ് ഗ്രൂപ്പ് സിദ്ധാന്തം. ഗണിതത്തിന്റെ പല ശാഖകളിലും, ഭൗതികം, രസതന്ത്രംപോലുള്ള ഇതര ശാസ്ത്രങ്ങളിലും, ഗ്രൂപ്പ് സിദ്ധാന്തം പ്രയോജനപ്പെടുത്താവുന്നതാണ്.
ഗ്രൂപ്പുകള്
ബീജഗണിതത്തിലെ ഒരു ആധാര തത്ത്വമാണ് ദ്വിചരക്രിയ (Binary operation). X ഒരു അശൂന്യഗണം (non-empty) എന്നിരിക്കട്ടെ. X-ലെ ഏത് രണ്ടംഗങ്ങള്ക്കും സംഗതമായി (corresponding to) ഗണത്തിലെ ഒരംഗം നിര്വചിക്കുന്നതിനെയാണ് ദ്വിചരക്രിയ എന്നുപറയുന്നത്. അതായത്. X x X-ല് നിന്നും X-ലേക്കുള്ള ഒരു ഫലനമാണ് ദ്വിചരക്രിയ. ഉദാഹരണമായി N = {1,2,3, ...} എന്നിരിക്കട്ടെ. N-ല് സങ്കലനം എന്ന ക്രിയ നിര്വചിക്കാം. '+' എന്ന ചിഹ്നംകൊണ്ടാണ് അതിനെ സൂചിപ്പിക്കുന്നത്.
N-ലെ a,b എന്ന ഏത് അംഗങ്ങള്ക്കും a + b എന്ന സങ്കലനഫലമുണ്ട്. അതുപോലെ N-ലെ a,b എന്ന ഏത് അംഗങ്ങള്ക്കും 'x' എന്ന ഗുണനം നിര്വചിക്കാം. മ,യ ഇവയുടെ ഗുണനഫലം മഃയ ആണ്.
A = {1, 2, 3} എന്നിരിക്കട്ടെ. A - ക്ക് 6 ക്രമചയങ്ങള് ഉണ്ട്. ഈ ക്രമചയങ്ങളെ ![]() എന്ന രീതിയില് സൂചിപ്പിക്കാം. ഇവിടെ a1, a2, a3 എന്നിവ ഏതെങ്കിലും ക്രമത്തില് എഴുതപ്പെട്ട 1,2,3 എന്ന സഖ്യകളാണ്. ഇങ്ങനെ കിട്ടുന്ന ക്രമചയങ്ങള് ഇപ്രകാരമാണ്.
എന്ന രീതിയില് സൂചിപ്പിക്കാം. ഇവിടെ a1, a2, a3 എന്നിവ ഏതെങ്കിലും ക്രമത്തില് എഴുതപ്പെട്ട 1,2,3 എന്ന സഖ്യകളാണ്. ഇങ്ങനെ കിട്ടുന്ന ക്രമചയങ്ങള് ഇപ്രകാരമാണ്.
σ, τ എന്നീ ക്രമചയങ്ങളുടെ ഗുണനഫലമായ എന്ന ക്രമചയത്തെ ഇങ്ങനെ നിര്വചിക്കാം. ആദ്യം എന്ന ക്രമചയത്തെ നിര്വചിക്കുക. പിന്നീട് എന്ന ക്രമചയം നിര്വചിക്കുക. അപ്പോള് കിട്ടുന്ന ക്രമചയമാണ് .
ഉദാഹരണമായി
എന്നുകിട്ടും.