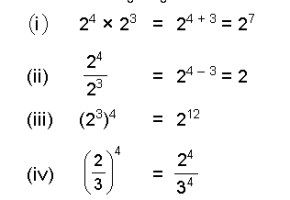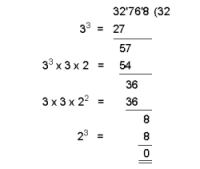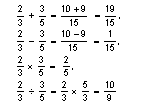This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

അങ്കഗണിതം

Arithmetic

വാസ്തവിക ധനസംഖ്യകളെയും അവയുടെ പ്രയോഗത്തെയും പറ്റി പ്രതിപാദിക്കുന്ന ഗണിതശാഖ. ബീജഗണിതത്തിന്റെ മുന്നോടിയാണ് ഇത്. അമൂര്‍ത്തമായ ഏറെ സങ്കല്പങ്ങള്‍ അങ്കഗണിതത്തിലില്ല. സാധാരണജീവിതത്തില്‍ ആവശ്യമായ ഗണിതമാണിത്. മനുഷ്യസംസ്കാരത്തിന്റെ ആവശ്യങ്ങളനുസരിച്ച് വികസിച്ചതാണ് ഈ ഗണിതശാഖ. ആടുമാടുകളുടെയും ആയുധങ്ങളുടെയും എണ്ണം തിട്ടപ്പെടുത്താന്‍ പ്രാചീനമനുഷ്യന് കഴിഞ്ഞിരുന്നില്ല. സംഖ്യാസമ്പ്രദായം അവന് പരിചയമില്ലായിരുന്നു. ഓരോന്നിനോടും ഇണങ്ങിച്ചേരുംവിധം (ഒന്നിനൊന്ന് അനുയോഗം) ഓരോ കല്ല് കണക്കിലെടുക്കുകയായിരുന്നിരിക്കണം അന്നു പതിവ്. ചെറിയവരകള്‍ ഉപയോഗിച്ചും കൈവിരലുകളില്‍ എണ്ണം പിടിച്ചും ഇന്നത്തെ രീതിയിലേക്ക് ആ ഗണനസമ്പ്രദായം പരിഷ്കരിക്കപ്പെട്ടു.

അങ്കഗണിതത്തിന് അരിത്മെറ്റിക് (Arithmetic) എന്നാണ് ഇംഗ്ളീഷിലുള്ള പേര്. സംഖ്യയെന്നര്‍ഥമുള്ള അരിത്മോസ് എന്ന ഗ്രീക്കുപദത്തിന്റെ തദ്ഭവമാണ് അരിത്മെറ്റിക്.

അങ്കഗണിതത്തില്‍ മൌലികമായി നാലു ക്രിയകളുണ്ട്: കൂട്ടല്‍ (സങ്കലനം), കുറയ്ക്കല്‍ (കിഴിക്കല്‍, വ്യവകലനം), ഗുണിക്കല്‍ (പെരുക്കല്‍, ഗുണനം), ഹരിക്കല്‍ (ഹരണം). ഇവയുടെ പ്രയോഗം, ഘടകക്രിയ, ലഘുതമസാധാരണഗുണിതം (ലസാഗു), ഉത്തമസാധാരണഘടകം (ഉസാഘ) എന്നിവയും ഭിന്നിതങ്ങളുടെ പ്രയോഗം, അനുപാതം, ത്രൈരാശികം, മാനനിര്‍ണയം, വ്യാവസായികഗണിതം, ശതമാനം, പലിശ, സ്റ്റോക് നിക്ഷേപങ്ങള്‍, ബില്‍ ഡിസ്ക്കൌണ്ട് -- എന്നീ പ്രായോഗികപ്രാധാന്യമുള്ള വിഷയങ്ങളുമാണ് അങ്കഗണിതത്തില്‍ പ്രതിപാദിക്കുന്നത്.

വ്യാവസായികകാര്യങ്ങളില്‍ ഇടപെടാനായി വേണ്ടത്ര ഗണിത പരിശീലനം കിട്ടുന്നതിനും യുക്തിപരീക്ഷണമെന്ന നിലയില്‍ മാനസികമായ അച്ചടക്കമുണ്ടാകുന്നതിനും അങ്കഗണിതം ആവശ്യമാണ്. ഗുണനപ്പട്ടിക ഹൃദിസ്ഥമാക്കുന്നതുകൊണ്ട് നിത്യോപയോഗമുള്ള കണക്കുകള്‍ എളുപ്പത്തില്‍ ചെയ്യാന്‍ കഴിയും.

ഗണിതചിഹ്നങ്ങളുടെ കണ്ടുപിടിത്തം. അങ്കഗണിതത്തില്‍ ഉപയോഗിക്കുന്ന ചിഹ്നങ്ങളാണ് +, –, ണ്മ, ÷ എന്നിവ. ഇവ യഥാക്രമം കൂട്ടല്‍, കുറയ്ക്കല്‍, ഗുണിക്കല്‍, ഹരിക്കല്‍ എന്നീ ഗണിതക്രിയകളെ സൂചിപ്പിക്കുന്നു. '+' എന്ന സങ്കലനചിഹ്നവും '–' എന്ന വ്യവകലനചിഹ്നവും ജോഹാന്‍ വിഡ്മാന്‍ എന്ന ഗണിതശാസ്ത്രജ്ഞന്‍ 1489-ല്‍ പ്രസിദ്ധം ചെയ്ത അങ്കഗണിതം (Arithmetic) എന്ന ഗ്രന്ഥത്തിലാണ് ആദ്യമായി അച്ചടിയില്‍ പ്രത്യക്ഷപ്പെട്ടതെന്ന് വിശ്വസിക്കപ്പെടുന്നു. ഇംഗ്ളീഷ് ഗണിതശാസ്ത്രജ്ഞനായ വില്യം ഔട്രഡ് (1574-1660) പ്രസിദ്ധപ്പെടുത്തിയ ക്ളാവിസ് മാത്തമാറ്റിക്ക (Clavis Mathematica, 1631) എന്ന ഗ്രന്ഥമാണ് '്x' എന്ന ഗുണനചിഹ്നം ഉള്‍ക്കൊള്ളുന്ന അച്ചടിഗ്രന്ഥങ്ങളില്‍ ഏറ്റവും പഴയതായി അറിയപ്പെടുന്നത്. 1668-ല്‍ ജോണ്‍പെല്‍ (1610-1685) ലണ്ടനില്‍ പ്രസിദ്ധംചെയ്ത ഒരു ഗ്രന്ഥത്തിലാണ് '÷' എന്ന ഹരണചിഹ്നം ആദ്യമായി പ്രയോഗിച്ചുകാണുന്നത്. '=' എന്ന സമചിഹ്നം ആദ്യമായി അച്ചടിച്ചുകണ്ടത് റോബര്‍ട്ട് റിക്കോര്‍ഡ് 1557-ല്‍ പ്രസിദ്ധം ചെയ്ത ആള്‍ജിബ്ര എന്ന ഗ്രന്ഥത്തിലാണ്.

ഘാതം (Exponent). ഒരു സംഖ്യയെ അതുകൊണ്ടുതന്നെ ഗുണിക്കുന്ന ക്രിയയെ സൂചിപ്പിക്കുന്ന സമ്പ്രദായമാണ് ഘാതക്രിയകൊണ്ടുദ്ദേശിക്കുന്നത്. ഉദാ. 2 x 2 x 2 = 2³. ഇതില്‍ 2 പാദവും (base), 3 അതിന്റെ ഘാതവുമാണ്. ഘാതക്രിയാനിയമങ്ങള്‍ താഴെ ചേര്‍ക്കുന്നു:

ഓരോ ഘാതക്രിയയുടെയും വ്യാഖ്യാനം എഴുതി ഈ നിയമങ്ങള്‍ തെളിയിക്കാവുന്നതാണ്. നിസര്‍ഗസംഖ്യകളെ സംബന്ധിച്ച് ഇവ തെളിയിക്കാന്‍ ഈ മാര്‍ഗം സ്വീകാര്യമാണെങ്കിലും, ഭിന്നിതങ്ങളെയും ഋണാത്മകഘാതങ്ങളെയും സംബന്ധിച്ച് ചില വ്യാഖ്യാനങ്ങളുടെ അടിസ്ഥാനത്തില്‍ മാത്രമേ ഈ നിയമങ്ങള്‍ പ്രയോഗക്ഷമമാകുന്നുള്ളു. അഥവാ, ഈ നിയമങ്ങള്‍ സ്വീകാര്യമാകുന്നവിധത്തിലാണ് ഋണാത്മകഘാതം നിര്‍വചിക്കപ്പെട്ടിരിക്കുന്നത്. അതായത്, 2^-8 എന്നു പറഞ്ഞാല്‍  ; 2°, എന്നുവേണ്ട ഏതു സ്ഥിരസംഖ്യയ്ക്കും (പൂജ്യം ഒഴികെ) 0 ഘാതമാണെങ്കില്‍ അതിന്റെ ഫലം 1 ആയിരിക്കും.

ബീജീയ നിയമങ്ങള്‍ (Algebraic laws). നിസര്‍ഗ സംഖ്യകളെ സംബന്ധിച്ചിടത്തോളം അപ്രധാനമാണെങ്കിലും ബീജഗണിതത്തില്‍ പ്രാധാന്യമുള്ള ഗണിതക്രിയാനിയമങ്ങളുണ്ട്; വിനിമേയനിയമം (Commutative law), സാഹചര്യനിയമം (Associative law), വിതരണനിയമം (Distributive law) എന്നിവ. വ്യത്യസ്തക്രിയകളെ ആധാരമാക്കി ഈ നിയമങ്ങള്‍ നിര്‍വചിക്കാവുന്നതാണ്. ഇവിടെ കൂട്ടല്‍, ഗുണിക്കല്‍ എന്നിവയെ സംബന്ധിച്ചു മാത്രമേ വ്യവഹരിക്കുന്നുള്ളു.

(i) വിനിമേയ നിയമം. പദങ്ങളുടെ (terms) ക്രമം മാറ്റിയിട്ടാലും ഫലത്തില്‍ മാറ്റമില്ല.

ഉദാ. 3 + 5 = 5 + 3 (സങ്കലന വിനിമേയനിയമം)

3 x 5 = 5 x 3 (ഗുണനാത്മക വിനിമേയനിയമം)

(ii) സാഹചര്യനിയമം. രണ്ടിലേറെപദങ്ങള്‍ (terms) തമ്മിലുള്ള ക്രിയയില്‍ ഈ രണ്ടെണ്ണം എടുത്തിട്ടാണ് ക്രിയ മുഴുമിപ്പിക്കുന്നത്. ആദ്യത്തെ രണ്ടെണ്ണം തമ്മിലുള്ള ക്രിയയ്ക്കുശേഷം ആ ക്രിയാഫലവും മൂന്നാമത്തെ പദവും തമ്മിലുള്ള ക്രിയ ചെയ്യുന്നു; ഇതിനുപകരം രണ്ടും മൂന്നും ചേര്‍ത്തതിനുശേഷം ആ ഫലവും ആദ്യത്തെ പദവും തമ്മില്‍ ക്രിയ ചെയ്യുന്നു. ഇങ്ങനെ രണ്ടു തരത്തില്‍ ചെയ്യുന്നതുകൊണ്ട് ഫലത്തില്‍ വ്യത്യാസം വന്നേക്കാം. എന്നാല്‍ നിസര്‍ഗസംഖ്യകളെ സംബന്ധിച്ച് വ്യത്യാസമില്ല.

(iii) വിതരണ നിയമം. രണ്ടു ക്രിയകള്‍ ഉള്‍പ്പെടുന്നതാണ് ഈ നിയമം.

ഉദാ. 3 + (5+7) = 3 + 5 + 3 + 7

സാധാരണ സംഖ്യകളെ സംബന്ധിച്ചിടത്തോളം ക്രമവിനിമേയനിയമം, സാഹചര്യനിയമം, വിതരണനിയമം എന്നീ ബീജീയാശയങ്ങള്‍ക്കു വലിയ പ്രസക്തിയില്ല. പൂജ്യം കൊണ്ടുള്ള ഹരണമൊഴിച്ച് മറ്റെല്ലാ ക്രിയകളും ചെയ്യാവുന്നതാണ്. അങ്കഗണിതത്തില്‍ ഇവ എടുത്തുപറയേണ്ടതില്ല. വിപുലമായ ആധുനികഗണിതശാഖയായി അങ്കഗണിതം വളര്‍ന്നു വന്നിട്ടുള്ളതില്‍ ഈ നിയമങ്ങള്‍ക്കു പ്രാധാന്യമുണ്ട്.

ഘടകക്രിയ (Factorisation). ഏതു പൂര്‍ണസംഖ്യയും അതിന്റെ അവിഭാജ്യഘടകങ്ങളുടെ ഗുണിതമായി പിരിച്ചെഴുതാന്‍ കഴിയും. ഒന്നാം സ്ഥാനത്തെ അക്കം ഇരട്ടസംഖ്യയാണെങ്കില്‍ 2-ഉം അക്കങ്ങളുടെ ആകത്തുകയെ 3 കൊണ്ടു കൃത്യമായി ഹരിക്കാന്‍ കഴിയുമെങ്കില്‍ 3-ഉം ഒന്നാം സ്ഥാനത്ത് 0, 5 എന്നിവയാണെങ്കില്‍ 5-ഉം ഘടകമായിരിക്കും. ഇത്തരം സൂചനകള്‍കൊണ്ട് ഘടകങ്ങള്‍ കണ്ടുപിടിക്കാന്‍ കഴിയും.

ലസാഗു, ഉസാഘ (L.C.M.,G.C.D). നിര്‍ദിഷ്ടമായ സംഖ്യകള്‍ എല്ലാം ഘടകമായിരിക്കുന്ന ഏറ്റവും ചെറിയ സംഖ്യയാണ് ലഘുതമ സാധാരണ ഗുണിതം (ലസാഗു); ഈ സംഖ്യകളെ കൃത്യമായി ഹരിക്കാവുന്ന ഏറ്റവും വലിയ ഘടകമാണ് ഉത്തമ സാധാരണ ഘടകം (ഉസാഘ). ചുരുങ്ങിയത് രണ്ടെണ്ണത്തെയെങ്കിലും ഹരിക്കാവുന്ന ഘടകങ്ങള്‍ കണ്ടുപിടിച്ച് അവയെ ഗുണിച്ചാല്‍ ലസാഗു കിട്ടും. ഉദാ. ആദ്യത്തെ ഘടകം ആയ 2 ഉസാഘയും 2 x 2 x 8 x 5 x 9 = 1440 ലസാഗുവുമാണ്.

ഭിന്നിതം (fraction). ഭിന്നിതങ്ങള്‍ രണ്ടുതരമുണ്ട്: ക്രമഭിന്നിതം, അക്രമഭിന്നിതം. ഹാര്യം ഹാരകത്തെക്കാള്‍ ചെറുതാണെങ്കില്‍, അഥവാ ഭിന്നിതത്തിന്റെ മൂല്യം ധനാത്മകവും 1-നേക്കാള്‍ കുറവുമാണെങ്കില്‍ ആ ഭിന്നിതം ക്രമവും മറിച്ചാണെങ്കില്‍ അക്രമവുമാണ്. രണ്ടു ഭിന്നിതങ്ങള്‍ കൂട്ടുമ്പോഴും കുറയ്ക്കുമ്പോഴും അവയുടെ ഹാരകങ്ങളുടെ ലസാഗുവിലേക്ക് രണ്ടു ഹാര്യങ്ങളും ക്രമപ്പെടുത്തുന്നു. ഗുണിക്കുമ്പോള്‍ ഹാര്യങ്ങള്‍ തമ്മിലും ഹാരകങ്ങള്‍ തമ്മിലും ഗുണിച്ചുകിട്ടുന്നവയുടെ ഭിന്നിതമായിരിക്കും ഫലം. ഹരിക്കുന്നതിന് ഹാരകഭിന്നിതത്തിന്റെ വ്യുത്ക്രമംകൊണ്ടു ഗുണിക്കുകയാണ് ചെയ്യുന്നത്. ഉദാ.

വര്‍ഗമൂലം, ഘനമൂലം (Square root,Cube root). 4 x 4 = 16, 2 x 2 x 2 = 8. അതുകൊണ്ട് 16-ന്റെ വര്‍ഗമൂലം 4, 8-ന്റെ ഘനമൂലം 2. 762129-ന്റെ വര്‍ഗമൂലവും 32768-ന്റെ ഘനമൂലവും കാണാം. ദശാംശബിന്ദുവില്‍നിന്ന് 2 അ ക്കങ്ങള്‍ വീതം ഇരുവശത്തേക്കും തുടര്‍ച്ചയായി അടയാളപ്പെടുത്തുക. 76-ല്‍ താഴെയുള്ള ഏറ്റവം വലിയ വര്‍ഗമാണ് 8² = 64. വലതുവശത്ത് 8 എഴുതുന്നു. 64 കഴിച്ച് ശിഷ്ടം 12. അടുത്ത രണ്ടക്കങ്ങള്‍ (21) താഴേക്കു ചേര്‍ത്തെഴുതുമ്പോള്‍ 1221 ആകുന്നു. 8-ന്റെ 2 ഇരട്ടി ഇടതുവശത്തെഴുതി 7-ഉം കൂടി 167 ആയി.

167-നെ 7 കൊണ്ടു ഗുണിക്കുമ്പോള്‍ 1221-ല്‍ താഴെ 1169 കിട്ടും; 168-നെ 8 കൊണ്ടു ഗുണിച്ചാല്‍ 1221-ല്‍ കവിയും. അതുകൊണ്ട് വലതുവശത്ത് 87 ആയി. വീണ്ടും ഇടതുവശത്ത് 87-ന്റെ 2 ഇരട്ടി 174 എന്നെഴുതുന്നു. 1743-നെ 3 കൊണ്ടു ഗുണിച്ചാല്‍ 5229 ആയി; 1744-നെ 4 കൊണ്ടു ഗുണിച്ചാല്‍ 5229-ല്‍ കവിയും. കൃത്യമായി നില്ക്കുന്നതിനാല്‍ 873 ആണ് വര്‍ഗമൂലം. കൃത്യമല്ലാതെ വന്നാല്‍ ഈ പ്രക്രിയ തുടര്‍ന്നു ചെയ്യാം.

ഘനമൂലം നിര്‍ണയിക്കുന്ന മാര്‍ഗം. സംഖ്യയുടെ ഒന്നാം സ്ഥാനം ഘനസ്ഥാനം; പിന്നെ രണ്ടു സ്ഥാനങ്ങള്‍ കഴിഞ്ഞാല്‍ വീണ്ടും ഘനസ്ഥാനം; പിന്നെ രണ്ടു സ്ഥാനങ്ങള്‍ കഴിഞ്ഞ് വീണ്ടും എന്നിങ്ങനെ തുടരുന്നു. ഇടത്തേ അറ്റത്തെ ഘനസ്ഥാന (32)ത്തുനിന്നു ഘനം 3³ കളഞ്ഞു ശിഷ്ടം കാണുക. അടുത്ത ഒരു സ്ഥാനം താഴേക്കിറക്കുന്നു. 57 ആയി. വലതുവശത്തു ചേര്‍ത്ത സംഖ്യയുടെ വര്‍ഗ(3²)ത്തെ 3 കൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന 3² x 3 കൊണ്ട് 57-നെ ഹരിച്ചാലുണ്ടാകുന്ന ഹരണഫലം 2; അതുകൊണ്ട് 3-നെ 2² കൊണ്ട് ഗുണിച്ച് ആ സംഖ്യകൊണ്ട് 36-നെ ഹരിച്ചുണ്ടാകുന്ന ഫലം 3 കണ്ടുപിടിക്കുക. ഈ 3 കൊണ്ട് 3 x 2²-നെ ഗുണിച്ച് 36-ല്‍ നിന്നു കുറയ്ക്കുന്നു. ശിഷ്ടം 0. അടുത്ത ഘനസ്ഥാനം 8 താഴേയ്ക്കിറക്കുന്നു. 2³ ഈ 8-ല്‍ നിന്നു കുറയ്ക്കുമ്പോള്‍ ശിഷ്ടം 0 ആയതിനാല്‍ ഘനമൂലം 32 തന്നെ.

അനുപാതം (Proportion). 3, 5 എന്നിവയുടെ അംശബന്ധവും (Ratio) 6, 10 എന്നിവയുടെ അംശബന്ധവും തുല്യമാണ്: . ഈ സംഖ്യകള്‍ ഒരേ അനുപാതത്തിലാണെന്നര്‍ഥം.

ത്രൈരാശികം. അനുപാതത്തെ ആധാരമാക്കിയാണ് ത്രൈരാശികം ചെയ്യുന്നത്. ഒരനുപാതത്തിലെ മൂലകങ്ങളില്‍ ഏതെങ്കിലും മൂന്നെണ്ണം അറിഞ്ഞാല്‍ നാലാമത്തേത് കണ്ടുപിടിക്കാം.

x/5=6/10, x = 6 x 5/10 =3

മാനനിര്‍ണയം (Mensuration). വസ്തുക്കളുടെ വിസ്തീര്‍ണം, ഘനമാനം, ചുറ്റളവ് എന്നിവ കണക്കാക്കുന്ന അങ്കഗണിതശാഖ. വ്യാസാര്‍ധം r ആയിട്ടുള്ള വൃത്തത്തിന്റെ പരിധി πr², വിസ്തീര്‍ണം πr²; r സമതലവ്യാസാര്‍ധവും h ഉയരവുമുള്ള വൃത്തസ്തംഭത്തിന്റെ പ്രതലവിസ്തീര്‍ണം 2πrh + 2πr²; ഘനമാനം πr²h; r വ്യാസാര്‍ധവുമുള്ള ഗോളത്തിന്റെ പ്രതലവിസ്തീര്‍ണം 4πr², ഘനമാനം 4/3πr³; h ഉയരവും l ചരിവുനീളവും r സമതല വ്യാസാര്‍ധവുമുള്ള സ്തൂപിക(cone)യുടെ പ്രതലവിസ്തീര്‍ണം πrl+ πr²; ഘനമാനം 1/3πr²h. ഈ വ്യഞ്ജകങ്ങള്‍ കണ്ടെത്തിയിട്ടുള്ളത് ബീജഗണിതം, കലനം എന്നീ ഗണിതശാഖകളിലൂടെയാണ്. പ്രായോഗികവശം മാത്രമേ അങ്കഗണിതത്തിലുള്ളു.

വ്യാവസായിക ഗണിതം. 100-ന് ഇത്രയെന്ന കണക്കാണ് ശതമാനം. % എന്ന ചിഹ്നംകൊണ്ടാണ് ശതമാനം രേഖപ്പെടുത്തുക. മുതല്‍ സംഖ്യ (P), n വര്‍ഷത്തേക്ക് r ശ.മാ. ലഘുപലിശയ്ക്കിട്ടാല്‍ മുതലും പലിശയും കൂടി P+ P x n x r/100 = P(1+nr/100)ആയിത്തീരും. കൂട്ടുപലിശയാണെങ്കില്‍ p(1+r/100)ആണ് പലിശയടക്കം മുതല്‍. അങ്കഗണിതനിയമങ്ങള്‍ പ്രയോജനപ്പെടുത്തി മറ്റു വ്യാവസായികഗണിതവും സാധിക്കുന്നു.

കൂട്ടല്‍, കുറയ്ക്കല്‍, ഗുണനം, ഹരണം, വര്‍ഗനിര്‍ണയം, വര്‍ഗമൂലനിര്‍ണയം, ഘനനിര്‍ണയം, ഘനമൂലനിര്‍ണയം എന്നീ എട്ടു ക്രിയകളെ ഭാരതീയരായ പൂര്‍വികന്മാര്‍ പരികര്‍മാഷ്ടകമെന്നു പറഞ്ഞിരുന്നു. ഭാസ്കരാചാര്യരുടെ ലീലാവതി എന്ന ഗണിതഗ്രന്ഥത്തില്‍ ഈ ക്രിയകള്‍ വിവരിച്ചിട്ടുണ്ട്. നോ: അംശബന്ധം, അനുപാതം; ആള്‍ജിബ്ര; മാനനിര്‍ണയം; ലീലാവതി; സംഖ്യാപദ്ധതികള്‍