This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോണം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
കോണം
Angle
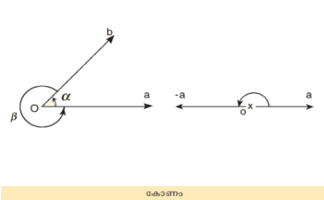
സമതല ജ്യാമിതിയില്‍ ഒരു ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്‍വരകളുടെ ജോടി. രേഖകളെ കോണത്തിന്റെ വശങ്ങളെന്നും ബിന്ദുവിനെ ശീര്‍ഷം (vertex) എന്നും പറയുന്നു. a,b എന്നിവ O എന്ന ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്‍രേഖകളാണെങ്കില്‍ ഇവ ഉള്‍ക്കൊള്ളുന്ന കോണം (a.b) എന്നുരേഖപ്പെടുത്താം. (a,b) -ഉം (b,a) -ഉം വ്യത്യസ്‌ത കോണങ്ങളാണ്‌. ചിത്രത്തില്‍ അവയെ ക്രമത്തില്‍ α, β എന്നിവകൊണ്ട്‌ സൂചിപ്പിച്ചിരിക്കുന്നു. ഈ സൂചനയനുസരിച്ചും കോണം നിര്‍വചിക്കപ്പെടാറുണ്ട്‌. Oa, Ob എന്നീ രേഖകളുടെ സമതലത്തില്‍ O എന്ന ബിന്ദുവിനെ ആധാരമാക്കി b യിലെത്താന്‍ a യ്‌ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണമാണ്‌ (a,b) എന്ന കോണം; അതുപോലെ a യിലെത്താന്‍ b യ്‌ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണം (b.a). ഈ പരിമാണങ്ങളെ ക്രമത്തില്‍ α, β എന്നിങ്ങനെ ഇവിടെ കണക്കാക്കിയിരിക്കുന്നു. ശീര്‍ഷത്തിലൂടെ കടന്നുപോകുന്ന ഒരു നേര്‍വരയുടെ ഒരു ഭാഗം a എന്നാണെങ്കില്‍ മറുവശം '-a' എന്നുകണക്കാക്കപ്പെടുന്നു; ഈ രണ്ടുവശങ്ങളുടെ ജോടി സൂചിപ്പിക്കുന്ന കോണത്തെ (a,-a) എന്നും. കോണം ഡിഗ്രിയായും റേഡിയന്‍ ആയും അളക്കാറുണ്ട്‌. ഡിഗ്രി 'º' എന്നും റേഡിയന്‍ 'c' എന്നും അടയാളപ്പെടുത്തുന്നു. ശീര്‍ഷത്തിനു ചുറ്റുമുള്ള കോണം 360 ഡിഗ്രിയായി കണക്കാക്കുന്നതുകൊണ്ട്‌, (a,a) പൂജ്യമോ 360° യോ ആകാം; (a,-a) എന്നത്‌ 180º. ശീര്‍ഷത്തിന്റെ ചുറ്റുമുള്ള കോണം 2𝜋 റേഡിയന്‍ ആയി കണക്കാക്കുമ്പോള്‍ (a,a) പൂജ്യം റേഡിയനോ 2𝜋 റേഡിയനോ ആകുന്നു; (a,-a) 𝜋 റേഡിയനും. അതായത്‌ 360º ക്കു തുല്യമാണ്‌ 2𝜋 റേഡിയന്‍; x 
റേഡിയന്‍ ഡിഗ്രിക്കും, അഥവാ y 
ഡിഗ്രി റേഡിയനും തുല്യം. 90º-യില്‍ കുറഞ്ഞ കോണത്തെ ന്യൂനകോണം (acute angle) എന്നും 90º-യില്‍ കൂടിയതിനെ ബൃഹത്‌കോണം (obtuse angle) എന്നും 90º ആണെങ്കില്‍ മട്ടകോണം (right angle) എന്നും വിളിക്കുന്നു.
