This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗോളീയ ജ്യോതിശ്ശാസ്ത്രം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
ഉള്ളടക്കം |
ഗോളീയ ജ്യോതിശ്ശാസ്ത്രം
Spherical Astronomy
ഭൂമിയെ കേന്ദ്രബിന്ദുവാക്കിക്കൊണ്ടുള്ള സാങ്കല്പിക (ആകാശ) ഗോളത്തില് ഗ്രഹങ്ങള്, നക്ഷത്രങ്ങള്, ധൂമകേതുക്കള് തുടങ്ങിയവയുടെ സ്ഥാനം, ദിശ, സഞ്ചാരപഥം എന്നിവയെപ്പറ്റി പ്രതിപാദിക്കുന്ന ശാസ്ത്രശാഖ.
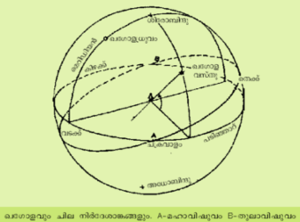
ജ്യോതിശ്ശാസ്ത്രത്തിന് മനുഷ്യസംസ്കാരത്തോളം തന്നെ പഴക്കമുണ്ട്. ഓരോ സംസ്കാരത്തിന്റെയും പുരാണങ്ങളില് നക്ഷത്രങ്ങളും ഗ്രഹങ്ങളും നക്ഷത്രവ്യൂഹങ്ങളും കഥാപാത്രങ്ങളാണ്. പൗരാണിക കാലം മുതല്ക്കുതന്നെ നക്ഷത്രങ്ങളുടെയും ഗ്രഹങ്ങളുടെയും സൂര്യന്റെയും മറ്റും ചലനങ്ങള് മനസ്സിലാക്കാന് ഖഗോള സങ്കല്പം ഉണ്ടായിരുന്നതായി കാണാം. അനന്തമായ വ്യാസമുള്ള ഈ ഗോളത്തില് ആകാശത്തില് കാണുന്ന എല്ലാ വസ്തുക്കളും പതിച്ചിരിക്കുന്നതായി തോന്നുന്നു. ഖഗോളവുമായി താരതമ്യപ്പെടുത്തുമ്പോള് ഭൂമിയുടെ വ്യാസം അവഗണിക്കാമെന്നതുകൊണ്ട് എല്ലാ പ്രായോഗികാവശ്യങ്ങള്ക്കും നിരീക്ഷകന് ഭൂമിയുടെ ഏതു സ്ഥലത്തുനിന്നാലും അയാള് ഖഗോളത്തിന്റെ കേന്ദ്രബിന്ദുവിലാണെന്നു കണക്കാക്കാം. ഖഗോളം ദിവസം ഒരു പ്രാവശ്യം ഭൂമിക്കു ചുറ്റും കറങ്ങുന്നതായി തോന്നുന്നു. നക്ഷത്രങ്ങള് വളരെ അകലെ സ്ഥിതിചെയ്യുന്ന സൂര്യന്മാരാണെന്നും, ഗ്രഹങ്ങള് സൗരയൂഥത്തിലെ അംഗങ്ങളാണെന്നും, കറങ്ങുന്നത് ഖഗോളമല്ല, മറിച്ച് ഭൂമിയാണെന്നും അറിയാവുന്ന ഇക്കാലത്തും ആകാശഗോളങ്ങളുടെ ചലനങ്ങള് മനസ്സിലാക്കാന് ഖഗോളസങ്കല്പം ജ്യോതിശ്ശാസ്ത്രജ്ഞന്മാര് ഉപയോഗിക്കുന്നുണ്ട്. ആകാശത്ത് ചിതറിക്കാണുന്ന നക്ഷത്രങ്ങളില് ചില പ്രത്യേക രൂപങ്ങള് സങ്കല്പിച്ചിരിക്കുന്നു. ഇവ രാശികള് (constellations) എന്നറിയപ്പെടുന്നു.
നക്ഷത്രരാശികള് (Constellations)
നക്ഷത്രരാശികള് (Constellations): തെളിഞ്ഞ ഒരു രാത്രിയില് ആകാശത്ത് ഏതാണ്ട് 3000 നക്ഷത്രങ്ങളെ കാണാം. ഇത്രയും തന്നെ എണ്ണം ഖഗോളത്തിന്റെ മറ്റേ അര്ധഗോളത്തിലും ദൃശ്യമാണ്. അതായത് ഏകദേശം 6000 നക്ഷത്രങ്ങള് മനുഷ്യന്റെ നഗ്നനേത്രങ്ങള്കൊണ്ട് കാണാന് സാധിക്കും. ഒരു ബൈനോക്കുലറോ ദൂരദര്ശിനിയോ ഉപയോഗിച്ചാല് ഇതിന്റെ പതിന്മടങ്ങ് നക്ഷത്രങ്ങളെ കാണാന് സാധിക്കും. ദൂരദര്ശിനിയുടെ വലുപ്പം കൂടുന്തോറും കൂടുതല് കൂടുതല് നക്ഷത്രങ്ങളെ കാണാനാവും. നക്ഷത്രങ്ങള് ഭൂമിയില് നിന്നും പ്രകാശവര്ഷങ്ങള് അകലെയായതുകൊണ്ട് ദൂരദര്ശിനികള് വഴി നോക്കിയാല്പ്പോലും നക്ഷത്രങ്ങള് ബിന്ദുക്കളായിത്തന്നെ കാണപ്പെടുന്നു.
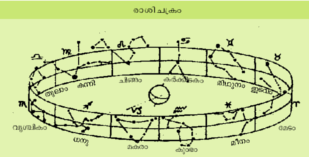
ആകാശത്തേക്ക് പെട്ടെന്നു നോക്കുന്ന ഒരാള്ക്ക് നക്ഷത്രങ്ങള് പല ഭാഗത്തായി ചിതറിക്കിടക്കുന്നതുപോലെ തോന്നുമെങ്കിലും ദീര്ഘകാലത്തെ നിരീക്ഷണ ഫലമായി നക്ഷത്രങ്ങളെ കൂട്ടങ്ങളായി കാണാനും പരിചിത രൂപങ്ങളുമായി താരതമ്യപ്പെടുത്തി പേരുകള് നല്കാനും ഇടയായി. ഉദാ. സിംഹം (ചിങ്ങം-Leo), തേള് (വൃശ്ചികം -Scorpio ), മീന് (മീനം-Pisces), തുടങ്ങിയ പേരുകള് നൂറ്റാണ്ടുകളായി ലോകമെങ്ങും അറിയപ്പെടുന്നു. ഇങ്ങനെയുള്ള നക്ഷത്രസമൂഹങ്ങളെ രാശികള് (constellations) എന്നു വിളിക്കുന്നു. ഓരോ സംസ്കാരത്തിന്റെയും ചരിത്രത്തിന്റെയും പുരാണങ്ങളുടെയും അടിസ്ഥാനത്തില് ഇവയുടെ പേരുകള് പലതാണ്. ഇന്റര്നാഷണല് അസ്ട്രോണമിക്കല് യൂണിയന് (IAU) അംഗീകരിച്ച 88 രാശികളാണുള്ളത്. ഇവയില് ഏറ്റവും പ്രധാനപ്പെട്ടത് സൂര്യന്റെയും ചന്ദ്രന്റെയും ഗ്രഹങ്ങളുടെയും പാതയില് കാണപ്പെടുന്ന സൗരരാശികള് (Zodiac Constellations) 12 എണ്ണമാണ്: ചിങ്ങം (Leo), കന്നി (Virgo), തുലാം (Libra), വൃശ്ചികം (Scorpio), ധനു (Sagittarius), മകരം (Capricon), കുംഭം (Aquarius), മീനം (Pisces), മേടം (Aries), ഇടവം (Taurus), മിഥുനം (Gemini), കര്ക്കടകം (Cancer) എന്നിവ. ആധുനിക ജ്യോതിശ്ശാസ്ത്രത്തിലെ ലിയോ (Leo), വിര്ഗോ (Virgo) തുടങ്ങിയ നക്ഷത്രവ്യൂഹങ്ങളും മലയാളം കലണ്ടറിലെ മാസങ്ങളെ നിര്വചിക്കാന് ഉപയോഗിക്കുന്ന ചിങ്ങം, കന്നി ഇത്യാദി സൗരരാശികളും തമ്മില് പ്രധാനമായ ഒരു വ്യത്യാസമുണ്ട്. സൂര്യന് കടന്നുപോകുന്ന പാതയിലുള്ള നക്ഷത്രവ്യൂഹങ്ങളാണ് ലിയോ, വിര്ഗോ തുടങ്ങിയവ എന്നതു ശരിതന്നെ. എന്നാല് ഇവയെക്കൂടാതെ ഒഫ്യൂക്കസ് (Ophiuchus) എന്ന രാശിയിലൂടെയും സൂര്യന് കടന്നുപോകുന്നു. ചിങ്ങം, കന്നി തുടങ്ങിയവയ്ക്ക് ഖഗോളത്തില് ഒരേ വലുപ്പമാണ് (30 ഡിഗ്രി) നല്കിയിരിക്കുന്നതെങ്കില് ആധുനിക നക്ഷത്രച്ചാര്ട്ടുകളില് ഇത് വ്യത്യസ്തമാണ്. സൂര്യനും ചന്ദ്രനും ഗ്രഹങ്ങളും ആകാശത്തില് ഒരു രാശിയില് നിന്നും മറ്റൊരു രാശിയിലേക്ക് മാറിക്കൊണ്ടിരിക്കുന്നതായി കാണാം. സൂര്യന് ഒരു രാശിയില് ഉദ്ദേശം 30 ദിവസം കാണപ്പെടുന്നു. ഈ കാലഘട്ടത്തെ മാസം എന്നു പറയുന്നു. ഉദാഹരണത്തിന് ചിങ്ങമാസത്തില് സൂര്യന് ചിങ്ങം രാശിയിലും കന്നിമാസത്തില് കന്നിരാശിയിലും 30 ദിവസത്തോളം വീതം നിലകൊള്ളുന്നു. എന്നാല് സൂര്യന് എല്ലാ രാശിയിലും തുല്യസമയമല്ല ചെലവഴിക്കുന്നത്. സൂര്യനു ചുറ്റുമുള്ള ഭൂമിയുടെ പാത ദീര്ഘവൃത്തമായിരിക്കുന്നതുകൊണ്ടാണ് ഇതു സംഭവിക്കുന്നത്. ഭൂമി സൗരസമീപകത്തില് (perihieon) വളരെ വേഗത്തിലും സൗരോച്ചത്തില് (aphelion) വളരെ സാവധാനവും സഞ്ചരിക്കുന്നതുകൊണ്ട് ധനുരാശിയില് സൂര്യന് ഏറ്റവും കുറഞ്ഞ സമയവും (ഉദ്ദേശം 28-29 ദിവസം) മിഥുനം രാശിയില് ഏറ്റവും കൂടിയ സമയവും (ഉദ്ദേശം 32 ദിവസം) ചെലവഴിക്കുന്നു. ഖഗോളത്തിലെ മറ്റൊരു പ്രധാനവിഭജനം ചന്ദ്രന്റെ സഞ്ചാരപഥത്തിനെ 27 നാളുകളായി വിഭജിച്ചി രിക്കുന്നതാണ്. ഭൂമിക്കു ചുറ്റുമുള്ള യാത്രയില് ദിവസവും 131/3o വീതം ചന്ദ്രന് ഖഗോളത്തില് സഞ്ചരിക്കുന്നു. ഓരോ ദിവസത്തെയും സ്ഥാനത്തെ അശ്വതി, ഭരണി, കാര്ത്തിക തുടങ്ങി ഓരോ നാളുകള് സൂചിപ്പിക്കുന്നു. ഖഗോളത്തില് സ്ഥാനനിര്ണയത്തിനും ദിശാനിര്ണയത്തിനും ഭൂമിയുടെ ചലനങ്ങള് മനസ്സിലാക്കേണ്ടതത്യാവശ്യമാണ്.
ഭൂമിയുടെ ചലനങ്ങളും ഖഗോളവും
ഹിപ്പാര്ക്കസ് തുടങ്ങിയ പൗരാണിക ജ്യോതിശ്ശാസ്ത്രജ്ഞര് ധരിച്ചിരുന്നത് ആകാശം ഭൂമിക്കു ചുറ്റുമുള്ള പൊള്ളയായ ഗോളമാണെന്നും നക്ഷത്രങ്ങള് അതില് ഒട്ടിച്ചുവച്ച ബിന്ദുക്കളാണെന്നുമായിരുന്നു. ഈ ഗോളത്തിനകത്ത് സഞ്ചരിക്കുന്ന മറ്റു ഖഗോളവസ്തുക്കളാണ് സൂര്യനും ചന്ദ്രനും ഗ്രഹങ്ങളും. ഭൂമിയുടെ ഭ്രമണം കിഴക്കോട്ടായതുകൊണ്ട് ഖഗോളം പടിഞ്ഞാറോട്ട് തിരിയുന്നതായി തോന്നുന്നു. ഭൂമിയുടെ യഥാര്ഥ ദിനചലനം (diurnal motion) കൊണ്ട് ആകാശത്തിന്റെ മിഥ്യയായ ദിനചലനം നമുക്കനുഭവപ്പെടുന്നു. ഖഗോളത്തിന്റെ വ്യവസ്ഥ മനസ്സിലാക്കാന് ആദ്യം ഭൂമിയുടെ ഭ്രമണത്തെയും സ്വയം ഭ്രമണാക്ഷത്തെയും കുറിച്ച് മനസ്സിലാക്കേണ്ടിയിരിക്കുന്നു.
ഭൂമി ഒരു ഭ്രമണം പൂര്ത്തിയാക്കാന് 23 മ. 56 മി. 6 സെ. സമയമെടുക്കുന്നു. സൂര്യനെ ചുറ്റുന്നതുകൊണ്ട് സൂര്യനെ അപേക്ഷിച്ച് ഭ്രമണം പൂര്ത്തിയാക്കാന് ഭൂമിക്ക് 24 മണിക്കൂര് വേണം. ഭൂമിയുടെ അച്ചുതണ്ട് ഖഗോളത്തില് രണ്ടു ബിന്ദുക്കളില്ക്കൂടി കടന്നുപോവുന്നു. ഈ രണ്ടു ബിന്ദുക്കളെ ഉത്തരഖഗോള ധ്രുവം (north celestial pole) എന്നും ദക്ഷിണഖഗോള ധ്രുവം (south celestial pole) എന്നും പറയുന്നു. ഖഗോളധ്രുവങ്ങള്ക്ക് വളരെയടുത്തുള്ള നക്ഷത്രങ്ങള് ദിനചലനംകൊണ്ട് ഈ ധ്രുവങ്ങള്ക്കു ചുറ്റും ചെറിയ വൃത്തങ്ങള് ചമയ്ക്കുന്നതായി അനുഭവപ്പെടുന്നു. എന്നാല് ഖഗോള ധ്രുവങ്ങളില് നിന്നും അകന്ന നക്ഷത്രങ്ങള് ദിനചലനത്തില് വളരെ ദൂരം സഞ്ചരിക്കുന്നതായി തോന്നും. ഖഗോളധ്രുവങ്ങള് ദൃശ്യമാകുന്നത് നിരീക്ഷകന്റെ അക്ഷാംശമനുസരിച്ചാണ്. ഭൂമിയില് ഉത്തരധ്രുവത്തില് നില്ക്കുന്ന നിരീക്ഷകന് ഉത്തരഖഗോളധ്രുവം നേരെ തലയ്ക്കു മുകളിലും മധ്യരേഖയില് നില്ക്കുന്ന ആളിന് ഖഗോളധ്രുവങ്ങള് ചക്രവാളത്തിലും കാണപ്പെടുന്നു. ഇതിനു രണ്ടിനും ഇടയില് നില്ക്കുന്ന നിരീക്ഷകന് ഉത്തരധ്രുവം നിരീക്ഷകന്റെ അക്ഷാംശത്തിന്റെ അളവില് ചക്രവാളത്തില്നിന്നും ഉയര്ന്നു കാണുന്നു. ഉദാഹരണമായി അക്ഷാംശം 8.3o യിലുള്ള തിരുവനന്തപുരത്തുള്ള നിരീക്ഷകന് ഉത്തരഖഗോള ധ്രുവം 8.3o ചക്രവാളത്തില്നിന്നും ഉയര്ന്നു കാണുന്നു. എന്നാല് ഉത്തരാര്ധഗോളത്തിലെവിടെനിന്നു നോക്കിയാലും ഉത്തരഖഗോളധ്രുവം എല്ലായ്പ്പോഴും ദൃശ്യമായിരിക്കും. അതുപോലെ തന്നെ ദക്ഷിണഖഗോള ധ്രുവം എല്ലായ്പ്പോഴും അദൃശ്യമായിരിക്കുകയും ചെയ്യും. ധ്രുവപ്രദേശത്തിന്റെ എത്രശതമാനമാണ് ദൃശ്യ/അദൃശ്യമായിരിക്കുന്നത് എന്നത് നിരീക്ഷകന്റെ അക്ഷാംശരേഖാംശങ്ങളെ ആശ്രയിച്ചിരിക്കും. ധ്രുവനക്ഷത്രം (Pole Star - Polaris) ദിനചലനങ്ങള്ക്കനുസരിച്ച് മാറ്റമില്ലാതെ ആകാശത്തില് കാണപ്പെടുന്നു. ഭൂമധ്യരേഖയ്ക്കു സമാന്തരമായി ഖഗോളത്തിലൂടെയുള്ള സാങ്കല്പിക രേഖയെ ഖഗോള മധ്യരേഖയെന്നു പറയുന്നു. ഭൂമിയുടെ ഉപരിതലത്തില് അക്ഷാംശരേഖകള് സങ്കല്പിച്ചിട്ടുള്ളതുപോലെ ഖഗോള മധ്യരേഖയ്ക്കു സമാന്തരമായി തെക്കും വടക്കുമുള്ള രേഖകളാണ് അപക്രമങ്ങള് (declinations) എന്ന പേരിലറിയപ്പെടുന്നത്. നക്ഷത്രം ആകാശത്തില് ഖഗോള മധ്യരേഖയില് നിന്ന് എത്രകണ്ട് തെക്കോട്ടോ വടക്കോട്ടോ മാറിയാണ് കാണുന്നതെന്ന് അറിയാന് അപക്രമം സഹായിക്കുന്നു. ഉത്തരഖഗോളധ്രുവത്തിന്റെ അപക്രമം +90o യും ദക്ഷിണഖഗോള ധ്രുവത്തിന്റെത് 90ബ്ബയുമാണ്. 8.3o അക്ഷാംശത്തിലുള്ള തിരുവനന്തപുരത്തു നില്ക്കുന്ന നിരീക്ഷകന്റെ നേരെ തലയ്ക്കു മുകളിലായി കാണപ്പെടുന്ന നക്ഷത്രത്തിന്റെ അപക്രമം 8.3o യാണ്. തിരുവാതിര നക്ഷത്രത്തിന്റെ അപക്രമം +7o24' ഉം (7 ഡിഗ്രി 24 മിനിറ്റ്-മിനിറ്റ് ഒരു ഡിഗ്രിയുടെ അറുപതിലൊരു ഭാഗമാണ്) തൃക്കേട്ടയുടേത് 26o 19'-ഉം ആണ്. ഭൂമിയിലെ രേഖാംശത്തിനു സമമായി ഖഗോളത്തിലുള്ളത് വിഷുവാംശം (right ascension) ആണ്. എന്താണിതെന്നു മനസ്സിലാക്കാന് ആകാശത്തില് സൂര്യന്റെ സഞ്ചാരപഥമായ ക്രാന്തിവൃത്തത്തിന്റെ സ്ഥാനം അറിയണം. ക്രാന്തിവൃത്തം ഖഗോള മധ്യരേഖയുമായി 23.5o ചെരിഞ്ഞാണ് സ്ഥിതിചെയ്യുന്നത്. ഈ രണ്ടു വൃത്തങ്ങള് ഖഗോളത്തില് രണ്ടു ബിന്ദുക്കളില് കൂട്ടിമുട്ടുന്നു. വിഷുവങ്ങള് (equinoxes) എന്നാണിവയുടെ പേര്. ഈ ബിന്ദുക്കളില് സൂര്യനെത്തുമ്പോള് ഭൂമിയിലെല്ലായിടത്തും പകലും രാത്രിയും ഒരേ ദൈര്ഘ്യമുള്ളതായിരിക്കും. മാര്ച്ച് 21-ന് മഹാവിഷുവ(Vernal equinox)വും സെപ്. 22-ന് തുലാവിഷുവ(Autumn equinox)വും ആണ്. ലണ്ടനിലെ ഗ്രീനിച്ചില് കൂടി കടന്നുപോകുന്ന രേഖാംശത്തെ 0o ആയി കണക്കാക്കുന്നതുപോലെ ഖഗോളത്തില് വിഷുവാംശം ആരംഭിക്കുന്നത് മഹാവിഷുവത്തില് നിന്നാണ്. വിഷുവാംശം രേഖപ്പെടുത്തുന്നത് 0 മുതല് 24 വരെ മണിക്കൂറുകളായിട്ടാണ് (ഒരു മണിക്കൂര് 15o ക്കു തുല്യമാണ്).
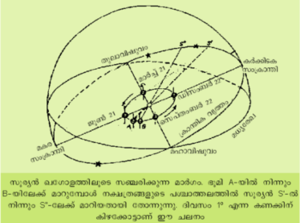
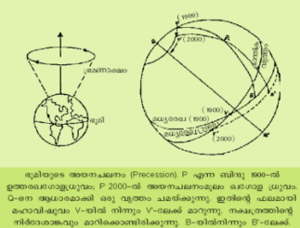
ഭൂമിയുടെ ഭ്രമണാക്ഷത്തിന്റെ ചലനമാണ് അയനചലനം (precession). ഭൂമിയുടെ ഭ്രമണാക്ഷം 25,800 സംവത്സരം കൊണ്ട് ക്രാന്തികവൃത്തത്തിന്റെ ലംബത്തിനു ചുറ്റും പമ്പരത്തിന്റെ തണ്ടു കറങ്ങുന്നതുപോലെ തിരിയുന്നു. തന്മൂലം ക്രാന്തികവൃത്തവും ഖഗോള മധ്യരേഖയുമായി കൂട്ടിമുട്ടുന്ന ബിന്ദുക്കള് ഖഗോളത്തില് പടിഞ്ഞാറോട്ട് മാറിമാറിവരുന്നു. ഉദ്ദേശം 1500 വര്ഷങ്ങള്ക്കു മുന്പ് കൊല്ലവര്ഷം ആരംഭിക്കുന്ന കാലത്ത് മഹാവിഷുവം മേടം 1-നായിരുന്നു. ഇതു നാം വിഷുവായി മേടമാസത്തില് ആഘോഷിക്കുന്നു. എന്നാല് ഭൂമിയുടെ അയനചലനം കൊണ്ട് മഹാവിഷുവം ഇന്ന് മീനം രാശിയിലാണ് കാണുന്നത്.
മഹാവിഷുവത്തില് നിന്നും എത്ര കിഴക്കോട്ടോ പടിഞ്ഞാറോട്ടോ നീങ്ങിയാണു ഖഗോളവസ്തു എന്നു കാണിക്കുന്ന അളവാണ് വിഷുവാംശം (right ascension). ഭൂഗോളത്തില് രേഖാംശം അടയാളപ്പെടുത്തുന്നതുമാതിരി കിഴക്കോട്ടാണ് വിഷുവാംശം അടയാളപ്പെടുത്തുന്നത്. ഇതു മണിക്കൂറിലാണ് പറയുക. ഉദാ. തിരുവാതിര നക്ഷത്രം വിഷുവാംശം 5 മ. 32.5 മിനിറ്റിലും (മഹാവിഷുവത്തില് നിന്നും ഉദ്ദേശം 83o കിഴക്കോട്ടു മാറി), രോഹിണി 4 മ. 33 മിനിറ്റിലും (മഹാവിഷുവത്തില് നിന്നും 68o കിഴക്ക്), ചിത്തിര 13 മ. 22.6 മിനിറ്റിലും (195o കിഴക്ക്) കാണപ്പെടുന്നു. വിഷുവാംശവും അപക്രമവും അറിയാമെങ്കില് ഖഗോളത്തിലെ ഏതൊരു വസ്തുവിന്റെയും സ്ഥാനം നിര്ണയിക്കാനാവും.
നിര്ദേശാങ്ക വ്യവസ്ഥ (Coordinate System)
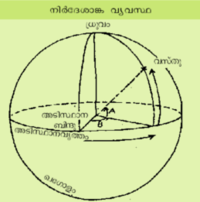
നിര്ദേശാങ്ക വ്യവസ്ഥ (Coordinate System): ഖഗോളത്തിലെ ഒരു അടിസ്ഥാന മഹാവൃത്തത്തെയും ഈ മഹാവൃത്തത്തിലെ ഒരു ബിന്ദുവിനെയും അടിസ്ഥാനമാക്കി ഖഗോളത്തിലെ ഒരു വസ്തുവിന്റെയോ ഏതെങ്കിലുമൊരു ബിന്ദുവിന്റെയോ ദിശയോ സ്ഥാനമോ രണ്ടു ഗോളീയ നിര്ദേശാങ്കങ്ങള് (spherical coordinates) ഉപയോഗിച്ച് കണക്കാക്കാനുതകുന്ന വ്യവസ്ഥയെയാണ് ഖഗോളനിര്ദേശാങ്ക വ്യവസ്ഥ (Celestial coordinate system) എന്നു പറയുന്നത്. ഇതില് ഒരു നിര്ദേശാങ്കം (A) ഖഗോളവസ്തുവിന്റെ കോണീയദൂരം (angular distance) ആണ്. ഇത് അളക്കുന്നത് അടിസ്ഥാനവൃത്തത്തിനു ലംബമായി നിര്ദിഷ്ട വസ്തുവിലൂടെയും അടിസ്ഥാന വൃത്തത്തിന്റെ ധ്രുവത്തിലൂടെയും കടന്നുപോകുന്ന ഒരു മഹാവൃത്തത്തെ ആസ്പദമാക്കിയാണ്. മറ്റേ നിര്ദേശാങ്കം (B) ഒരു അടിസ്ഥാന ബിന്ദു (zero point)വും ധ്രുവത്തിലൂടെയും നിര്ദിഷ്ട വസ്തുവിലൂടെയും കടന്നുപോവുന്ന മഹാവൃത്തവും തമ്മിലുള്ള കോണീയ ദൂരമാണ്.
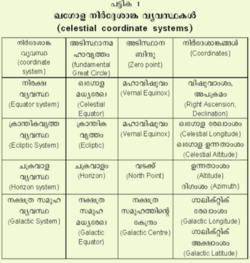
നിരീക്ഷിക്കുന്ന വസ്തുവിനനുസരിച്ച് പ്രധാനമായും നാലു നിര്ദേശാങ്ക വ്യവസ്ഥകളുണ്ട്: ചക്രവാള വ്യവസ്ഥ (horizon or horizontal system), നിരക്ഷ വ്യവസ്ഥ (equator system), ക്രാന്തിക വൃത്തവ്യവസ്ഥ (ecliptic system), നക്ഷത്ര സമൂഹ വ്യവസ്ഥ (galactic system).
ഒരു ഗോളത്തിന്റെ കേന്ദ്രബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഏതൊരു തലവും ഗോളത്തെ ഖണ്ഡിക്കുന്നത് ഒരു വൃത്തത്തിലാണ്. ഇതിനെ മഹാവൃത്തം (great circle) എന്നു പറയുന്നു. കേന്ദ്രബിന്ദുവില്ക്കൂടി കടന്നുപോകാത്ത മറ്റ് ഏതൊരു തലവും ഗോളത്തെ ഖണ്ഡിക്കുന്ന വൃത്തത്തിനെ ലഘുവൃത്തം (small circle) എന്നു പറയുന്നു. മഹാവൃത്തത്തിന്റെ വ്യാസം എപ്പോഴും ഗോളത്തിന്റെ വ്യാസത്തിനു തുല്യമായിരിക്കും. എന്നാല് ലഘുവൃത്തത്തിന്റെ വ്യാസം എല്ലായ്പ്പോഴും ഗോളത്തിന്റെ വ്യാസത്തെക്കാള് ചെറുതായിരിക്കും.
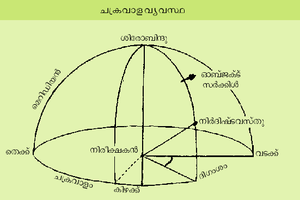
ചക്രവാളവ്യവസ്ഥ
ഈ വ്യവസ്ഥയിലെ അടിസ്ഥാന മഹാവൃത്തം ചക്രവാള (horizon)മാണ്. ഈ തലത്തിനു ലംബമായി നിരീക്ഷകനിലൂടെ കടന്നുപോകുന്ന രേഖ ഈ വൃത്തത്തെ രണ്ടു ബിന്ദുക്കളില് സന്ധിക്കുന്നു. ഇതില് നിരീക്ഷകന്റെ നേരെ തലയ്ക്കു മുകളിലുള്ളത് ശിരോബിന്ദു(Zenith)വും താഴെയുള്ളത് അധോബിന്ദു (nadir)വുമാണ്. തെക്കുവടക്കു ദിക്കുകളെ യോജിപ്പിച്ചുകൊണ്ട് ശിരോബിന്ദുവിലൂടെ കടന്നുപോകുന്ന രേഖയാണ് മെറിഡിയന് (Meridian). ഉന്നതി (altitude), ദിഗംശം (azimuth) എന്നിവയാണ് നിര്ദേശാങ്കങ്ങള്. ചക്രവാളത്തില് നിന്ന് നിര്ദിഷ്ട വസ്തുവിലേക്കുള്ള കോണീയദൂരമാണ് ഉന്നതി. ശിരോബിന്ദുവിലൂടെയും വസ്തുവിലൂടെയും കടന്നുപോകുന്ന മഹാവൃത്തമാണ് ഓബ്ജക്റ്റ് സര്ക്കിള് (Object circle) എന്നറിയപ്പെടുന്നത്. ശിരോബിന്ദുവിലൂടെയും വസ്തുവിലൂടെയും കടന്നുപോകുന്ന രേഖകള് തമ്മിലുള്ള കോണീയദൂരമാണ് ശിരോബിന്ദു അകലം (zenith angle). ദിഗംശം എന്നത് വടക്കു ദിക്കില് നിന്നും എത്രമാത്രം കിഴക്കാണ് വസ്തു സ്ഥിതിചെയ്യുന്നതെന്നു കാണിക്കുന്ന കോണീയ അളവാണ്. ഒരു വസ്തുവിന്റെ ഈ വ്യവസ്ഥയിലുള്ള നിര്ദേശാങ്കങ്ങള് ഭൂമി തിരിയുന്നതനുസരിച്ച് മാറിക്കൊണ്ടിരിക്കും എന്നത് ശ്രദ്ധേയമാണ്.
നിരക്ഷവ്യവസ്ഥ
ഭൂമധ്യരേഖയാണ് ഈ വ്യവസ്ഥയുടെ അടിസ്ഥാന മഹാവൃത്തം. ഖഗോളധ്രുവങ്ങള്, ശിരോബിന്ദു എന്നിവയിലൂടെ കടന്നുപോകുന്ന മഹാവൃത്തമാണ് മെറിഡിയന്. ധ്രുവങ്ങള്, നിര്ദിഷ്ട വസ്തു എന്നിവയിലൂടെ കടന്നുപോകുന്ന മഹാവൃത്തം, ഹോരാവൃത്തം (hour circle) എന്നറിയപ്പെടുന്നു. ഹോരാവൃത്തവും മെറിഡിയനും തമ്മിലുള്ള കോണീയ ദൂരമാണ് ഹോരാംശം (hour angle). ഖഗോള മധ്യരേഖ, ഡിഗ്രികള്ക്കു പകരം മണിക്കൂര് (24), മിനിറ്റ് (60), സെക്കന്റ് (60) എന്നിങ്ങനെയാണ് വിഭജിച്ചിരിക്കുന്നത്. ഹോരാകോണമളക്കുന്നത് ഈ മൂന്നളവുകള് ഉപയോഗിച്ചാണ്.
നിരക്ഷവ്യവസ്ഥയിലെ നിര്ദേശാങ്കങ്ങള് വിഷുവാംശവും അപക്രമവുമാണ് (വിഭാഗം 2 നോക്കുക). വിഷുവാംശം രേഖപ്പെടുത്തുന്നതും മണിക്കൂര്, മിനിറ്റ്, സെക്കന്റ് എന്നീ ക്രമത്തിലാണ്. മെറിഡിയന് കടന്ന് കിഴക്കോട്ടുപോകുന്ന വസ്തുവിന്റെ വിഷുവാംശം കൂടിക്കൂടി വരുന്നു. അതായത് മെറിഡിയന് കടക്കുന്നതിനു മുന്പ് വസ്തുവിന്റെ വിഷുവാംശം ഋണവും കടന്നതിനുശേഷം ധനവുമാണ് മെറിഡിയന്, വിഷുവാംശം 0 മ. ആണ്. അപക്രമം അളക്കുന്നത് ഡിഗ്രിയിലാണ്. ഖഗോള മധ്യരേഖയില് നിന്നും ഹോരാവൃത്തത്തിലൂടെ ഉത്തരധ്രുവത്തിലേക്കു നീങ്ങുന്തോറും അപക്രമം വര്ധിച്ചു വരുന്നു. ദക്ഷിണധ്രുവത്തിലേക്കു പോകുന്തോറും അപക്രമം കുറഞ്ഞുവരുന്നു. ഒരു വസ്തുവിന്റെ അപക്രമം ഉത്തരാര്ധഗോളത്തില് ധനവും ദക്ഷിണാര്ധഗോളത്തില് ഋണവുമാണ്.
വിഷുവാംശം അളക്കുന്നതിനുള്ള അടിസ്ഥാന ബിന്ദു മഹാവിഷുവമാണ്. അതായത് മഹാവിഷുവമായ മാര്ച്ച് 21 വിഷുവാംശം 0 മണിക്കൂറും തുലാവിഷുവമായ സെപ്തംബര് 22 വിഷുവാംശം 12 മണിക്കൂറും ആയിരിക്കും. വിഷുവാംശം 6 മണിക്കൂറും 18 മണിക്കൂറും എന്നത് കര്ക്കടക സംക്രാന്തി (summer solstice)യും മകര സംക്രാന്തി (winter solstice)യുമായ ജൂണ് 21-ഉം ഡിസംബര് 22-ഉം ആണ്.
ക്രാന്തിവൃത്തവ്യവസ്ഥ
സൗരയൂഥത്തില് സംഭവിക്കുന്ന പ്രതിഭാസങ്ങള് വിശദീകരിക്കുവാന് ഈ വ്യവസ്ഥ ഉപയോഗിക്കുന്നു. ക്രാന്തിവൃത്ത രേഖാംശം, ക്രാന്തിവൃത്ത അക്ഷാംശം എന്നിവയാണ് നിര്ദേശാങ്കങ്ങള്. ആദ്യകാലത്ത് ഗ്രഹങ്ങളെക്കുറിച്ച് പഠിക്കുന്നതിനാണ് ഈ വ്യവസ്ഥ നിര്ദേശിക്കപ്പെട്ടത്. സന്ധ്യാസമയത്ത് ആകാശത്തേക്കു നോക്കിയാല് അസ്തമിക്കുന്ന സൂര്യന്, ചന്ദ്രന്, ഉജ്ജ്വലമായി പ്രകാശിക്കുന്ന ഗ്രഹങ്ങള് (ചൊവ്വ, വ്യാഴം, ശുക്രന് എന്നിവ) ഒരു നേര്രേഖയില് കാണാം. ക്രാന്തികവൃത്തവ്യവസ്ഥയുടെ ആവിര്ഭാവത്തിനു കാരണം ഇതാണ്. ഈ വസ്തുക്കളെല്ലാം രേഖാംശം എന്ന പൊതുനിര്ദേശാങ്കത്തിന്റെ വിവിധ സ്ഥാനങ്ങളിലാണെന്നു കാണാം. മഹാവിഷുവത്തില് നിന്നും ക്രാന്തികവൃത്തത്തിലൂടെ കിഴക്കോട്ട് എത്രദൂരം അകലെയാണെന്നു കാണിക്കുന്ന കോണീയ അളവാണ് ക്രാന്തിവൃത്തരേഖാംശം. വസ്തുവിന്റെ ക്രാന്തിവൃത്തത്തില് നിന്നുള്ള കോണീയദൂരമാണ് ക്രാന്തിവൃത്ത അക്ഷാംശം. ക്രാന്തിവൃത്തത്തിന്റെ ഉത്തര ദക്ഷിണധ്രുവങ്ങള് ക്രാന്തിവൃത്തത്തില്നിന്നും 90o അകലെയുള്ള രണ്ടു ബിന്ദുക്കളാണ്. ക്രാന്തിവൃത്തം മധ്യരേഖയുമായി 23o27'8.26 ചരിവുള്ളതിനാല് ഖഗോള ധ്രുവങ്ങളില് നിന്നും അത്രയും അകലെയാണ് ക്രാന്തിവൃത്ത ധ്രുവങ്ങള്.
ക്രാന്തിവൃത്തവ്യവസ്ഥ ഭൂമിയുടെ പരിക്രമണത്തെ അടിസ്ഥാനമാക്കിയുള്ളതാണ്. എന്നാല് നിരക്ഷവ്യവസ്ഥയാകട്ടെ, സ്വന്തം അച്ചുതണ്ടിലുള്ള ഭൂമിയുടെ ഭ്രമണത്തെ ആസ്പദമാക്കിയും. കൂടുതലായി ഉപയോഗിച്ചുവരുന്നത് നിരക്ഷവ്യവസ്ഥയാണെങ്കിലും ഗ്രഹങ്ങളെക്കുറിച്ചു പഠിക്കുന്നതിനും ഗ്രഹാന്തര പേടകങ്ങളുടെ സ്ഥാനവും ചലനവും വിവരിക്കുന്നതിനും ക്രാന്തികവൃത്തവ്യവസ്ഥ ഇപ്പോഴും ഉപയോഗിക്കുന്നു.
നക്ഷത്രവ്യൂഹവ്യവസ്ഥ
ഗാലക്സികളുടെ പഠനത്തിന്, പ്രത്യേകിച്ചും ഓപ്റ്റിക്കല്, റേഡിയോ, ഗാമാ എന്നീ തരംഗദൈര്ഘ്യത്തില് ഗാലക്സികളുടെ കാന്തിമാനത്തെക്കുറിച്ചുള്ള പഠനത്തിന് ഗാലക്സിയെ ആധാരമാക്കിക്കൊണ്ടുള്ള ഒരു വ്യവസ്ഥയാണ് ഭൂമിയുടെ ദിനചലനത്തെയും വാര്ഷിക ചലനത്തെയും അടിസ്ഥാനമാക്കിയുള്ള വ്യവസ്ഥകളെക്കാള് അഭികാമ്യം. ഇവിടെ ഗാലക്റ്റിക് മധ്യരേഖ (galactic equator) അടിസ്ഥാന വൃത്തം. ആകാശഗംഗയുടെ മധ്യത്തിലൂടെ കടന്നുപോകുന്ന മഹാവൃത്തമാണ് ഗാലക്റ്റിക് മധ്യരേഖ. ഖഗോള മധ്യരേഖയുമായി ഏകദേശം 62o ചെരിവുണ്ട് ഈ മധ്യരേഖയ്ക്ക്. ഈ രണ്ടു മധ്യരേഖകളും കൂട്ടിമുട്ടുന്ന രണ്ടു ബിന്ദുക്കള് അക്വില (Aquila), മോണോസെറസ് (Monocerus) എന്നീ രണ്ടു രാശികളിലാണ്. ഗാലക്റ്റിക് ധ്രുവങ്ങള് ഖഗോളധ്രുവങ്ങളില് നിന്നും 62o അകലെയാണ്. ഉത്തരധ്രുവം വിഷുവാംശം 12 മ. 49 മിനിറ്റിലും അപക്രമം +27.4o യിലും ദക്ഷിണധ്രുവം 0 മ. 49 മി., 27.4o എന്നീ നിര്ദേശാങ്കങ്ങളിലുമാണ്. ഭൂമിയുടെ ഉപരിതലത്തില് സങ്കല്പിച്ചിട്ടുള്ളതുപോലെ മധ്യരേഖയ്ക്കു സമാന്തരമായി 0o മുതല് 90o (ധ്രുവങ്ങള്) വരെ തെക്കും വടക്കുമുള്ള സാങ്കല്പിക രേഖകളാണ് ഗാലക്റ്റിക് അക്ഷാംശരേഖകള്. ഗാലക്സിയുടെ ധ്രുവങ്ങളില്ക്കൂടിയും ഗാലക്സിയുടെ കേന്ദ്രഭാഗത്തുള്ള ധനുരാശിയിലെ (Sagittarius) അതീവ തീവ്രതയുള്ള റേഡിയോ വികിരണങ്ങളുത്സര്ജിക്കുന്ന സഗിറ്റാറിയസ് A എന്ന നക്ഷത്രത്തിലൂടെയും കടന്നുപോകുന്ന മഹാവൃത്തമാണ് അടിസ്ഥാന മെറിഡിയന്. സഗിറ്റാറിയസ് A യുടെ വിഷുവാംശം 17 മ. 42.4 മി. അപക്രമം 28o 55' എന്നിങ്ങനെയാണ്. രേഖാംശം അളക്കുന്നത് ഡിഗ്രിയിലാണ്: 0 മുതല് 360 വരെ.
നക്ഷത്രങ്ങളുടെ കാന്തിമാനം(Magnitude)
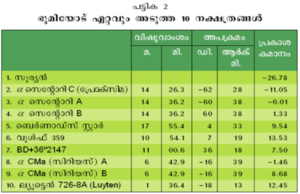
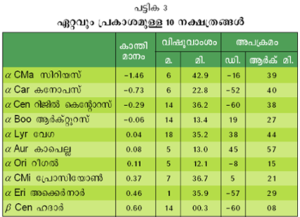
നക്ഷത്രങ്ങളുടെ കാന്തിമാനം (Magnitude): ദൂരദര്ശിനിയുടെയും മറ്റു സാങ്കേതിക വിദ്യകളുടെയും ആവിര്ഭാവത്തിനു മുമ്പ് നഗ്നനേത്രങ്ങള്ക്കു ദൃശ്യമായ നക്ഷത്രങ്ങളെ അവയുടെ പ്രത്യക്ഷകാന്തിമാനം (apparent brightness) അനുസരിച്ച് തരം തിരിച്ചിരുന്നു. ബി.സി. രണ്ടാം ശ.-ത്തില് ഹിപ്പാര്ക്കസ് നക്ഷത്രങ്ങളെ ആറു വിഭാഗങ്ങളായി തരം തിരിച്ചു. ഇതില് ഏറ്റവും പ്രകാശം കൂടിയവയെ കാന്തിമാനം 1 എന്നും നഗ്നനേത്രങ്ങള്കൊണ്ട് കഷ്ടിച്ചു കാണാന് കഴിയുന്നവയെ 6 എന്നും കണക്കാക്കി. (പ്രകാശത കൂടുന്നതനുസരിച്ച് മാനം കുറയുന്നു എന്ന കാര്യം ശ്രദ്ധിക്കുക) ഇതില് ആദ്യത്തെ വിഭാഗം നക്ഷത്രങ്ങളുടെ പ്രകാശത (brightness), അവസാനത്തെ വിഭാഗം നക്ഷത്രങ്ങളുടെ പ്രകാശതയുടെ നൂറിരട്ടിയാണ്. 1856-ല് നോര്മന് ആര്. ഭോഗ്സണ് അടുത്തടുത്ത രണ്ടു വിഭാഗം നക്ഷത്രങ്ങളുടെ പ്രകാശതയുടെ അനുപാതം ആണെന്നു കാണിക്കുകയുണ്ടായി. ഇതനുസരിച്ച് സൂര്യന്റെ കാന്തിമാനം-26.78, പൂര്ണചന്ദ്രന്റേത്-11, ശുക്രന്റേത്-4 ആണ്. ഭൂമിയില് ഇപ്പോഴുള്ള ഏറ്റവും വലിയ ദൂരദര്ശിനി ഉപയോഗിച്ച് പ്രകാശമാനം 24 വരെയുള്ള നക്ഷത്രങ്ങളെ കാണാന് കഴിയും. എന്നാല് ഉപഗ്രഹ ദൂരദര്ശിനിവഴി പ്രകാശമാനം 31 വരെയുള്ള വസ്തുക്കളെ നിരീക്ഷിക്കാന് കഴിയുന്നുണ്ട്.
പ്രത്യക്ഷകാന്തിമാനം നക്ഷത്രത്തിന്റെ യഥാര്ഥ പ്രകാശതയെക്കുറിച്ച് ശരിയായ വിവരം നല്കുന്നില്ല. ഒരു നക്ഷത്രത്തിന്റെയോ പ്രകാശിക്കുന്ന മറ്റു വസ്തുക്കളുടെയോ യഥാര്ഥ പ്രകാശത അളക്കുന്ന തോതാണ് കേവല കാന്തിമാനം. നക്ഷത്രങ്ങള് 10 പാര്സെക് (32.56 പ്രകാശവര്ഷം) അകലെ സ്ഥിതിചെയ്താല് അതിന്റെ പ്രത്യക്ഷ കാന്തിമാനം എത്രയാണോ അതാണ് ആ നക്ഷത്രത്തിന്റെ കേവലകാന്തിമാനമായി കണക്കാക്കപ്പെടുന്നത്. ഒരു നക്ഷത്രത്തിന്റെ പ്രത്യക്ഷ-കേവല കാന്തിമാനങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യം താഴെ കൊടുക്കുന്നു.
m - M = 5 log r -5
ഇവിടെ m പ്രത്യക്ഷകാന്തിമാനവും
M കേവലകാന്തിമാനവും
r നക്ഷത്രത്തിലേക്കുള്ള ദൂരം, പാര്സെകിലുമാണ്.
അതിനാല് ഒരു നക്ഷത്രത്തിന്റെയോ മറ്റേതെങ്കിലും ഖഗോളവസ്തുവിന്റെയോ പ്രത്യക്ഷ കാന്തിമാനവും കേവല കാന്തിമാനവും അറിയാമെങ്കില് നക്ഷത്രത്തിലേക്കുള്ള യഥാര്ഥ ദൂരം കണ്ടുപിടിക്കാവുന്നതാണ്.
നക്ഷത്ര ചാര്ട്ടുകള് (Star Charts)
നക്ഷത്ര ചാര്ട്ടുകള് (Star Charts). ഓരോ നക്ഷത്രസമൂഹത്തിലെയും ഏറ്റവും പ്രകാശമുള്ള നക്ഷത്രങ്ങളെ ഗ്രീക്ക് അക്ഷരം കൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്. ഏറ്റവും പ്രകാശമുള്ളത് ആല്ഫാ (α) രണ്ടാമത്തേത് ബീറ്റാ (β), മൂന്നാമത്തേത് ഗാമാ (γ)... അങ്ങനെ പോകുന്നു ഈ ക്രമം. ഉദാ. വൃശ്ചികം (Scorpio) രാശിയിലെ ഏറ്റവും പ്രകാശമാനമായ നക്ഷത്രമാണ് തൃക്കേട്ട (α - Scorpii) നക്ഷത്രചാര്ട്ടുകളില് പൊതുവേ മുകള് ഭാഗം വടക്കിനെയും, കീഴ്ഭാഗം തെക്കിനെയും സൂചിപ്പിക്കുന്നു. എന്നാല് സാധാരണ ജ്യോഗ്രഫി മാപ്പുകളില് നിന്നും വ്യത്യസ്തമായി ഇടതുഭാഗം കിഴക്കിനെയും വലതുഭാഗം പടിഞ്ഞാറിനേയും സൂചിപ്പിക്കുന്നു. ചാര്ട്ടുകള് തലയ്ക്കുമുകളില് പിടിച്ച് മുകളിലേക്കു നോക്കുമ്പോള് ഇടവും വലവും ശരിയായി വരും.
ആദ്യത്തെ നക്ഷത്ര കാറ്റലോഗ് പ്രസിദ്ധീകരിച്ചത് ടോളമിയാണ്. ബി.സി. 2-ാം ശ.-ത്തില് അല്മജസ്റ്റ് (Almagest) എന്ന പുസ്തകത്തിലാണിതു പ്രത്യക്ഷപ്പെട്ടത്. ആകെ 1025 നക്ഷത്രങ്ങളെപ്പറ്റി ഇതില് പ്രതിപാദിച്ചിരിക്കുന്നു. 250 വര്ഷം മുമ്പ് ഹിപ്പാര്ക്കസ് കണക്കുകൂട്ടി കണ്ടുപിടിച്ച വളരെ പ്രകാശമുള്ള നക്ഷത്രങ്ങളുടെ സ്ഥാനമാണിതില് കൊടുത്തിരിക്കുന്നത്. 17-ാം ശ.-ത്തിനു മുന്പ് വളരെ പ്രചാരത്തിലിരുന്ന ആധികാരികമായ ഒരു നക്ഷത്ര കാറ്റലോഗാണിത്.
1799 മുതല് 1875 വരെ ജീവിച്ചിരുന്ന ഫ്രെഡറിക് വില്യം ഒഗസ്റ്റ് ആര്ഗെലണ്ഡര് എന്ന ജ്യോതിശ്ശാസ്ത്ര പ്രൊഫസറുടെ മേല്നോട്ടത്തില് നിര്മിക്കപ്പെട്ടതാണ് ഇപ്പോഴുപയോഗിക്കപ്പെടുന്നതില് വച്ച് ഏറ്റവും പഴയ കാറ്റലോഗ്. 72 മി.മീ. ദൂരദര്ശിനിയുപയോഗിച്ച് 3,20,000 നക്ഷത്രങ്ങളുടെ സ്ഥാനവും പ്രകാശമാനവും അദ്ദേഹം കണക്കാക്കി. ബോണര് ഡൂര്ഷ് മുഷ്റ്റെറൂങ് (Bonner Durch Musterung) എന്ന പേരില് അറിയപ്പെടുന്ന ഈ കാറ്റലോഗില് ഉത്തരധ്രുവത്തിനും അപക്രമം 42-നും ഇടയ്ക്കുള്ള, പ്രകാശമാനം 9.5-ല് കൂടുതലുള്ള നക്ഷത്രങ്ങളാണുള്ളത്. ആകാശത്തിലെ ഏതാണ്ട് മുഴുവന് ഭാഗവും ഉള്പ്പെടുത്തിക്കൊണ്ട് മറ്റു രണ്ടു കാറ്റലോഗുകള് കൂടി പുറത്തിറക്കുകയുണ്ടായി. എല്ലാ കാറ്റലോഗിലും കൂടി ആകെ ഒരു ദശലക്ഷത്തോളം നക്ഷത്രങ്ങള് വരും.
ഇതു കൂടാതെ ദൂരദര്ശിനികളുടെ ക്ഷമത മെച്ചപ്പെട്ടതോടെ കൂടുതല് നക്ഷത്രങ്ങളെയും ആകാശത്തിന്റെ കൂടുതല് ഭാഗങ്ങളിലെ നക്ഷത്രങ്ങളെയും മറ്റും ഉള്ക്കൊള്ളിച്ചുകൊണ്ടുള്ള നിരവധി കാറ്റലോഗുകള് ലഭ്യമായി. വളരെയധികം പ്രചാരമുള്ള ഒന്നാണ് എസ്.എ.ഓ. (S.A.O) എന്ന കാറ്റലോഗ്. സ്മിത്ത്സോണിയന് അസ്ട്രോഫിസിക്കല് ഒബ്സര്വേറ്ററി (Smithsonian Astrophysical Observatory) 1960-ല് പുറത്തിറക്കിയതാണിത്. 9-ല്ക്കൂടുതല് പ്രകാശമാനമുള്ള നക്ഷത്രങ്ങളുടെ സ്ഥാനം, മാഗ്നിറ്റ്യൂഡ്, ചലനം, സ്പെക്ട്രം തുടങ്ങിയ വിവരങ്ങളടങ്ങിയ വിലയേറിയ ഒരു ഗ്രന്ഥമാണിത്. പലോമര് അറ്റ്ലസ് (Palomar Observatory) എന്ന ഗ്രന്ഥത്തിലുള്ക്കൊള്ളിച്ചിട്ടുള്ള നക്ഷത്രങ്ങള് അപക്രമം-20 വരെയുള്ളവയാണ്. ദക്ഷിണാര്ധഗോളത്തിലുള്ള നക്ഷത്രങ്ങളുടെ വിവരം താരതമ്യേന കുറവാണെന്നുവേണം ഇതില്നിന്നു മനസ്സിലാക്കാന്.ആസ്റ്റ്രേലിയയിലെ സൈഡിങ് സ്പ്രിങ് നിരീക്ഷണകേന്ദ്രവും (Siding Spring Observatory), ചിലിയിലെ യൂറോപ്യന് സതേണ് ഒബ്സര്വേറ്ററി (European Southern Observatory) യും ആകാശത്തിന്റെ ശേഷിച്ച ഭാഗത്തെ നക്ഷത്രങ്ങളുടെ കാറ്റലോഗ് തയ്യാറാക്കുന്നതില് വ്യാപൃതരാണ്. കൃത്രിമോപഗ്രഹങ്ങളുപയോഗിച്ചുള്ള നിരീക്ഷണങ്ങള് കുറച്ചുകൂടി മെച്ചപ്പെട്ട കാറ്റലോഗുകള് തയ്യാറാക്കുവാന് സാഹചര്യമൊരുക്കിയിട്ടുണ്ട്. 1990 മുതല് ഇത്തരത്തിലൊരു സംരംഭം ആരംഭിച്ചു. ആയിരക്കണക്കിനു നക്ഷത്രങ്ങളുടെ സ്ഥാനവും ചലനവും മറ്റും നല്കാന് ഹിപ്പാര്കോസ് എന്ന ഉപഗ്രഹത്തിനു സാധിച്ചു. സ്പേസ് ടെലിസ്കോപ്പ് സെന്ററിന്റെ (Space Telescope Centre) ആഭിമുഖ്യത്തില് ഇത്തരം പരിപാടികള് വളരെ ഊര്ജസ്വലമായി നടന്നുവരികയാണ്.
(ഡോ. എസ്.ആര്. പ്രഭാകരന് നായര്; ബി. ബാല)