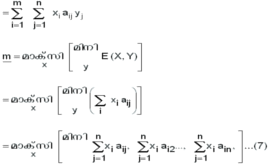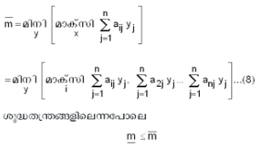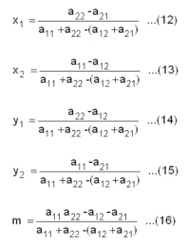This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗെയിം സിദ്ധാന്തം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
ഗെയിം സിദ്ധാന്തം
Game Theory
ഗണിതശാസ്ത്രതത്ത്വങ്ങള് മത്സരരംഗത്ത് ഉപയോഗിക്കുന്നതിനു വേണ്ടി ആവിഷ്കൃതമായ സിദ്ധാന്തം. ഒരു മത്സരത്തിന്റെ അവസാനഫലം അതില് പങ്കെടുക്കുന്ന ഓരോരുത്തരുടെയും നീക്കങ്ങളെ ആശ്രയിച്ചിരിക്കുമെങ്കില് അതിനെ ഒരു ഗെയിമായിക്കരുതാം. ഇത്തരം മത്സരരംഗങ്ങള് സാമ്പത്തികമോ കളികളുമായി ബന്ധപ്പെട്ടതോ രാഷ്ട്രീയമോ യുദ്ധസംബന്ധമോ ആവാം.
ഗെയിം സിദ്ധാന്തത്തിന്റെ ഉപജ്ഞാതാവ് ജോണ് ഫൊണ് ന്യൂമാന് ആണ്. ഇതിന്റെ രൂപരേഖ ആദ്യമായി വെളിച്ചം കണ്ടത് 1928-ല് നോട്ടിങ്ഗാമിലെ ഗണിതശാസ്ത്രസമിതിയോഗത്തില് ഇദ്ദേഹം അവതരിപ്പിച്ച ഒരു പ്രബന്ധത്തിലാണ്. 1944-ല് ജോണ് ഫൊണ് ന്യൂമാനും ഓസ്കാര് മോര്ഗെന്സ്റ്റയ്നും ചേര്ന്നവതരിപ്പിച്ച പ്രസിദ്ധമായ തിയറി ഒഫ് ഗെയിംസ് ആന്ഡ് ഇക്കണോമിക്സ് ബിഹേവിയര് എന്ന പ്രസിദ്ധീകരണത്തെത്തുടര്ന്നാണ് ഇതിന്റെ വിപ്ലവകരമായ വളര്ച്ച. വലിയ നഷ്ടങ്ങളില് ചെറുതു തിരഞ്ഞെടുക്കുക (minimax principle) എന്ന അടിസ്ഥാന ആശയമാണ് ന്യൂമാന് ഉപയോഗപ്പെടുത്തിയത്. ഗെയിമുകളുടെ അമൂര്ത്തമായ മാതൃകാരൂപങ്ങളിലാണ് ഈ സിദ്ധാന്തം കരുപ്പിടിപ്പിച്ചിരിക്കുന്നത്. ആദ്യകാലങ്ങളില് ചതുരംഗം, പോക്കര്, ബ്രിഡ്ജ്, പകിടകളി തുടങ്ങിയവ അപഗ്രഥിക്കാനാണിതുപയോഗിച്ചത്. ഇപ്പോള് ധനതത്ത്വശാസ്ത്രം, രാഷ്ട്രമീമാംസ, സാമൂഹിക ശാസ്ത്രം, മാനേജ്മെന്റ് വിജ്ഞാനീയം, ലീനിയര് പ്രോഗ്രാമിങ്, ഓപ്പറേഷന്സ് റിസര്ച്ച് തുടങ്ങിയ ഒട്ടേറെ മേഖലകളിലും, മിക്കവാറും എല്ലാ ശാസ്ത്രശാഖകളിലും ഗെയിം സിദ്ധാന്തം ഉപയോഗിച്ചുവരുന്നു. ഒരു ഗെയിം ജയിക്കാനുള്ള പ്രാവീണ്യം, കരുനീക്കങ്ങള് എന്നിവ ഇതില് പ്രതിപാദിക്കുന്നില്ല. മറിച്ച് ഒരു ഗെയിം തുടര്ച്ചയായി കളിച്ചാല് അവയുടെ ഭാവവും പ്രവര്ത്തനക്രമവും ഫലവും എങ്ങനെയായിരിക്കണമെന്നുള്ള പഠനമാണിത്. ബീജഗണിതം, മെഷര് തിയറി തുടങ്ങിയ ഗണിതശാസ്ത്ര ശാഖകളിലെ ആശയങ്ങള് ഇതില് ഉള്ക്കൊണ്ടിട്ടുണ്ട്.
ഗെയിം സിദ്ധാന്തമനുസരിച്ച് ഒരു മത്സരരംഗം ഗെയിം ആകണമെങ്കില് അവ ഇനിപ്പറയുന്ന വ്യവസ്ഥകള്ക്ക് വിധേയമായിരിക്കണം. 1. പങ്കെടുക്കുന്നവരുടെ എണ്ണം പരിമിതമായിരിക്കണം. 2. ഓരോ കളിക്കാരനും പരിമിതമായ നീക്കങ്ങളുടെ ഒരു പട്ടിക ലഭ്യമായിരിക്കണം. രണ്ടു കളിക്കാരുടെ പട്ടിക ഒരുപോലെ ആയിരിക്കണമെന്നില്ല. 3. പട്ടികയിലെ നീക്കങ്ങളില്നിന്ന് ഓരോ നീക്കം കളിക്കാര് ഉപയോഗിക്കുന്നു. എതിരാളിയുടെ നീക്കം എന്തായിരിക്കുമെന്ന് മുന്കൂട്ടി അറിയാന് മാര്ഗമുണ്ടായിരിക്കില്ല. 4. ഓരോ നീക്കത്തിനും ഒരു പ്രതിഫലവിഹിതം കളിക്കാര്ക്കു ലഭിക്കും. പ്രതിഫലം നഷ്ടമാണെങ്കില് ഋണസംഖ്യ (negative number) കളായി കാണിക്കും.
എത്ര ആളുകള് വേണമെങ്കിലും ഒരു ഗെയിമില് പങ്കെടുക്കാം. രണ്ടു പേരുള്ള ഗെയിമാണ് കൂടുതല് ഗവേഷണവിധേയമായിട്ടുള്ളത്. കൂടുതല് ആളുകളുണ്ടെങ്കില് കൂട്ടം പിരിച്ച് രണ്ടുപേരുള്ള ഗെയിമാക്കിമാറ്റാന് മിക്കപ്പോഴും സാധിക്കും.
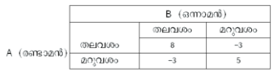
രണ്ടുപേരുള്ള ഗെയിമില് ഒരാള്ക്കു ലഭിക്കുന്ന പ്രതിഫലത്തുകകള് ഒരു 'മാട്രിക്സ്' രൂപത്തില് എഴുതാന് കഴിയും. പ്രതിഫലമാട്രിക്സ് തന്നിട്ടുണ്ടെങ്കില് ഗെയിമിന്റെ പൂര്ണരൂപംതന്നെ മനസ്സിലാക്കാന് കഴിയും. ഒരാള്ക്കു കിട്ടുന്ന പ്രതിഫലം മറ്റേയാളുടെ നഷ്ടമാകുമ്പോള് ആ ഗെയിമിനെ 'പൂജ്യം-തുക-ഗെയിം' (zero-sum-game) എന്നു പറയുന്നു. ഉദാ. 1. രണ്ടുപേര് നാണയമെറിഞ്ഞു കളിക്കുന്നു എന്നിരിക്കട്ടെ. ഒരുപോലെ തലവശം വീണാല് രണ്ടാമതു കളിക്കുന്ന ആളിന് എട്ട് രൂപയും ഒരുപോലെ മറുവശം വീണാല് അഞ്ച് രൂപയും പ്രതിഫലം കിട്ടും. അല്ലാത്തപക്ഷം മൂന്ന് രൂപ ഒന്നാമതു കളിക്കുന്ന ആളിന് കൊടുക്കണം. പ്രതിഫല മാട്രിക്സ് താഴെക്കൊടുത്തിരിക്കുന്നു.
ഇത് ഒരു 2 x 2 പൂജ്യം-തുക-ഗെയിമാണ്. കോളങ്ങള് B യുടെ നീക്കങ്ങളും നിരകള് A യുടെ നീക്കങ്ങളും കാണിക്കുന്നു. A യ്ക്കു കിട്ടുന്ന തുകകളാണ് മാട്രിക്സില് ഉള്ളത്; നെഗറ്റീവ് സംഖ്യകള് B യ്ക്കു കൊടുക്കേണ്ടതും. A യ്ക്കു എട്ട് രൂപ കിട്ടുമ്പോള് B യ്ക്കു എട്ട് രൂപ നഷ്ടം വരുമെന്നുള്ളതുകൊണ്ടാണ് ഇത് പൂജ്യം-തുക-ഗെയിമാകുന്നത്. ഇത്തരം ഗെയിമുകളില് B യുടെ മാട്രിക്സ് കിട്ടാന് A യുടെ മാട്രിക്സിലെ സംഖ്യകളുടെ ഋണസംഖ്യകളെഴുതിയാല് മതിയാവും. ഇത്തരം ഗെയിമുകളില് കളിക്കാര്ക്കെല്ലാം കൂടിയുള്ള ആകെ ധനത്തില് മാറ്റമൊന്നും വരുന്നില്ല. ഒരു പുതിയ വിനിമയം നടക്കുന്നു എന്നു മാത്രം.
പട്ടികയിലെ നീക്കങ്ങളെ അങ്ങനെതന്നെ ഉപയോഗിക്കുമ്പോള് അവയെ ശുദ്ധതന്ത്രങ്ങള് എന്നു പറയാം. ചെസ്സ് (ചതുരംഗം) ശുദ്ധതന്ത്രങ്ങള് മാത്രമുപയോഗിക്കുന്ന ഒരു ഗെയിമാണ്. നാണയത്തിന്റെ തലവശവും മറുവശവും രണ്ടു ശുദ്ധതന്ത്രങ്ങളാണ്.
അനുകൂല സന്ദര്ഭം നിശ്ചയിച്ച് നീക്കം ഉപയോഗിക്കുമ്പോള് അതിനെ മിശ്രതന്ത്രമെന്നു പറയാം. A ക്ക് A1, A2 എന്ന രണ്ടു ശുദ്ധതന്ത്രങ്ങളുണ്ട്; ഒരു നാണയം എറിഞ്ഞ് തലവശം വീണാല് A1 ഉപയോഗിക്കുമെന്നും മറുവശം വീണാല് A2 ഉപയോഗിക്കുമെന്നും വച്ചാല് അതു മിശ്രതന്ത്രമായി. മിശ്രതന്ത്രമാകുമ്പോള് അതിനോടു ചേര്ന്ന് സംഭാവ്യതകള് കൂടി കാണും. തുക ഒന്ന് (1) ആയിവരുന്ന 'm' ധനവാസ്തവിക സംഖ്യ (positive real number) കളുടെ ഒരു ഗണമാണ് മിശ്രതന്ത്രം.
1 + x + ... + xm= 1 ... (1)
xi ≥0, i = 1,2, ...m
ആയാല് (x1,x2, ...xm) എന്ന ഗണം ഒരു മിശ്രതന്ത്രം ആകും. 'm' എന്ന സംഖ്യ കളിക്കാരന്റെ ശുദ്ധതന്ത്രങ്ങളുടെ എണ്ണമാണ്.
xr=1 ... (2)
xi=0, j ≠ r എന്നത്
r ശുദ്ധതന്ത്രമാണ്. മേല്ക്കാണിച്ച കളിക്കാരന് ശുദ്ധതന്ത്രങ്ങളുടെ എണ്ണം 'm' ആണെങ്കിലും മിശ്രതന്ത്രങ്ങളുടെ എണ്ണം അനന്തമായിരിക്കും എന്ന് ശ്രദ്ധിക്കുക. രണ്ടുപേരുടെ ഗെയിമില് ഒരാള്ക്ക് 'm' ശുദ്ധതന്ത്രങ്ങളും മറ്റേ ആള്ക്ക് 'n' ശുദ്ധതന്ത്രങ്ങളും ഉണ്ടെങ്കില് പ്രതിഫല മാട്രിക്സിന്റെ വലുപ്പം m x n ആയിരിക്കും.
ഒരു ഗെയിമില് ഏറ്റവും മെച്ചപ്പെട്ട തന്ത്രങ്ങള് ഏതെന്ന് കണ്ടുപിടിക്കുകയാണ് ഗെയിം സിദ്ധാന്തത്തിന്റെ ലക്ഷ്യം. മിനിമാക്സി അല്ലെങ്കില് മാക്സിമിനി രീതികളനുസരിച്ചാണ് മെച്ചപ്പെട്ട തന്ത്രങ്ങള് നിശ്ചയിക്കുന്നത്. ഒരു കളിക്കാരനു കിട്ടാവുന്ന ഏറ്റവും മോശമായ പ്രതിഫലങ്ങള് അവലംബിച്ച് അതിലെ ഏറ്റവും മെച്ചപ്പെട്ടതു തിരഞ്ഞെടുക്കുന്നതാണ് മാക്സിമിനി രീതി. ഓരോ കളിയിലും വരാവുന്ന വലിയ നഷ്ടങ്ങളിലെ ചെറുതു തിരഞ്ഞെടുക്കുന്നതിനെ മിനിമാക്സിരീതി എന്നുപറയുന്നു.
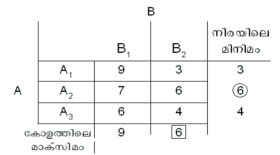
ഉദാ. 2 ഒരു ഗെയിമിന്റെ പ്രതിഫലമാട്രിക്സ് താഴെക്കാണുന്ന പ്രകാരമാണെന്നിരിക്കട്ടെ.
ഓരോ കളിക്കാരനും അവനവന്റെ സ്ഥിതി മെച്ചപ്പെടുത്തത്തക്കവിധമായിരിക്കുമല്ലോ കളിക്കുന്നത്. A യുടെ പ്രതിഫലം കുറവായിരിക്കത്തക്കവണ്ണമേ B കളിക്കുകയുള്ളൂ. A തിരഞ്ഞെടുക്കുന്നത് A1 ആണെങ്കില് B എടുക്കുന്നത് B2 ആയിരിക്കും. A എടുക്കുന്നത് A1 ആയാലും B എടുക്കുന്നത് B2 തന്നെ ആയിരിക്കും. B ഏതെടുത്താലും ഓരോ അവസരത്തിലും മിനിമം പ്രതിഫലത്തുകയെങ്കിലും A ക്കു ലഭിക്കും. നിരയിലെ മിനിമം സംഖ്യകളായിരിക്കും ഇവ. ഇതിലെ മാക്സിമം നേടാനായിരിക്കുമല്ലോ A-യുടെ ശ്രദ്ധ. അതായത്, Aക്ക് എപ്പോഴും മാക്സിമിനി എടുക്കുന്നതാണ് ഗുണകരം.
B യുടെ കണക്കുകൂട്ടലില് B1 കളിച്ചാല് വരാവുന്ന മാക്സിമം നഷ്ടം 9 ആണ്. B2 കളിച്ചാല് 6-ഉം. ഇതില് മിനിമം എടുക്കാനായിരിക്കും ആയുടെ ശ്രദ്ധ. അതുകൊണ്ട് അയാളുടെ മെച്ചപ്പെട്ട തന്ത്രം B2 ആണ്. ഇക്കാര്യം തന്നെ ഗണിതചിഹ്നങ്ങളുപയോഗിച്ച് എഴുതാം.
'm' നിരകളും 'n' കോളങ്ങളുമുള്ള പ്രതിഫല മാട്രിക്സിനെ എന്നു ![]() സൂചിപ്പിക്കാം.
സൂചിപ്പിക്കാം.
എന്നിരിക്കട്ടെ. 'p' നിരയിലെ മിനിമം സംഖ്യയായിരിക്കും ![]() (p നിരയിലെ മറ്റൊരു സംഖ്യ)
(p നിരയിലെ മറ്റൊരു സംഖ്യ)
പക്ഷേ, ars 's' കോളത്തിലെ മാക്സിമം സംഖ്യയാണ്
രണ്ടും കൂടിയാകുമ്പോള് ![]() എന്നുവരും.
എന്നുവരും.
അതായത്,
ഇവ രണ്ടും ഒന്നായി വരുന്ന ഗെയിമുകളെ നിര്ധാരണം ചെയ്യാമെന്നും ![]() -നെ ഗെയിമിന്റെ മൂല്യമെന്നും പറയുന്നു.
-നെ ഗെയിമിന്റെ മൂല്യമെന്നും പറയുന്നു. ![]() ആയാല് ഗെയിം ഭേദപ്പെട്ടതാണെന്നു പറയുന്നു.
ആയാല് ഗെയിം ഭേദപ്പെട്ടതാണെന്നു പറയുന്നു.
![]() ഇവ ഒന്നായി വരുന്ന ബിന്ദുവിനെ ഗെയിമിന്റെ നിശ്ചിത ബിന്ദു എന്നുവിളിക്കുന്നു. ai0j0 ആണ് നിശ്ചിത ബിന്ദുവെങ്കില് A യുടെ മെച്ചപ്പെട്ട തന്ത്രം i0 യും B യുടെ മെച്ചപ്പെട്ട തന്ത്രം j0 ആണ്. പ്രതിഫലമാട്രിക്സിലെ നിരകളിലെ മിനിമം സംഖ്യകളുടെ മാക്സിമവും കോളങ്ങളിലെ മാക്സിമം സംഖ്യകളിലെ മിനിമവും ആണിത്; ആ ബിന്ദുവില്ക്കൂടി കടക്കുന്ന നിരയും കോളവും മെച്ചപ്പെട്ട തന്ത്രങ്ങളും. നിശ്ചിത ബിന്ദുവിലെ സംഖ്യാ ഗെയിമിന്റെ മൂല്യമാണിത്.
ഇവ ഒന്നായി വരുന്ന ബിന്ദുവിനെ ഗെയിമിന്റെ നിശ്ചിത ബിന്ദു എന്നുവിളിക്കുന്നു. ai0j0 ആണ് നിശ്ചിത ബിന്ദുവെങ്കില് A യുടെ മെച്ചപ്പെട്ട തന്ത്രം i0 യും B യുടെ മെച്ചപ്പെട്ട തന്ത്രം j0 ആണ്. പ്രതിഫലമാട്രിക്സിലെ നിരകളിലെ മിനിമം സംഖ്യകളുടെ മാക്സിമവും കോളങ്ങളിലെ മാക്സിമം സംഖ്യകളിലെ മിനിമവും ആണിത്; ആ ബിന്ദുവില്ക്കൂടി കടക്കുന്ന നിരയും കോളവും മെച്ചപ്പെട്ട തന്ത്രങ്ങളും. നിശ്ചിത ബിന്ദുവിലെ സംഖ്യാ ഗെയിമിന്റെ മൂല്യമാണിത്.
നിശ്ചിത ബിന്ദു എല്ലാ ഗെയിമിനുമുണ്ടായിരിക്കണമെന്നില്ല. നിശ്ചിതബിന്ദു വ്യക്തമായി കിട്ടുന്ന ഗെയിമുകള്ക്ക് നിര്ധാരണം എളുപ്പമാണ്. എന്നാല് നിശ്ചിതബിന്ദു അതുല്യ (unique)മായിരിക്കണമെന്നില്ല.
ഉദാ. 3.
i. രണ്ടുപേര് ഒരു നാണയമെറിഞ്ഞു കളിക്കുന്നു എന്നിരിക്കട്ടെ. രണ്ടുപേര്ക്കും ഒരു പോലെയുള്ള വശം ലഭിച്ചാല് രണ്ടാമതു കളിക്കുന്ന ആള്ക്ക് ഒരു തുക ലഭിക്കും; ഇല്ലെങ്കില് മറ്റെ യാള്ക്കും. പ്രതിഫല മാട്രിക്സ് ഇപ്രകാരമായിരിക്കും.
ഇത് ഒരു പൂജ്യം-തുക-ഗെയിമാണ്. നിശ്ചിതബിന്ദു ഇല്ല.
2. ഒന്നാമത്തെ ഉദാഹരണത്തില് പിന്മാറാനുള്ള അവസരം കൂടികൊടുക്കുന്നു എന്നിരിക്കട്ടെ. പിന്മാറുന്ന ആള്ക്ക് പകുതി പ്രതിഫലം കിട്ടും. രണ്ടുപേരും മാറിയാല് ആര്ക്കുമൊന്നുമില്ല. പ്രതിഫല മാട്രിക്സ് താഴെക്കൊടുക്കുന്നു.
ഇപ്പോള് നിശ്ചിതബിന്ദു ഉണ്ട്. ഗെയിം ഭേദപ്പെട്ടതാണ്; മൂല്യം പൂജ്യവും.
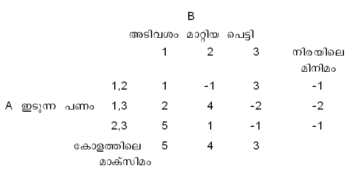
3. ഒരു 3x3 ഗെയിം നോക്കാം. 3 പെട്ടികള് 1, 2, 3 എന്ന് അടയാളപ്പെടുത്തിയിരിക്കുന്നു. അവയുടെ അടിവശം മാറ്റാവുന്നതാണ്. A അടയാളപ്പെടുത്തിയ തുകവീതം ഏതെങ്കിലും 2 പെട്ടികളിലിടുന്നു. B ഏതെങ്കിലും ഒരു പെട്ടിയുടെ അടിവശം മാറ്റുന്നു. പരസ്പരനീക്കങ്ങള് അറിയുന്നുമില്ല. 2 പെട്ടികളിലുള്ള പണത്തിന്റെ തുക A യ്ക്കു ലഭിക്കും. അടിവശം മാറ്റിയ പെട്ടിയിലേത് B ക്കും. A ക്ക് ഇടാവുന്ന തുകകളുടെ വ്യത്യസ്ത സാധ്യതകള് 1,2; 1, 3; 2, 3 എന്നിങ്ങനെയാണ്. A യ്ക്കു കിട്ടാവുന്ന തുകകള് മാട്രിക്സ് രൂപത്തില് കൊടുക്കാം.
A ഇടുന്ന തുകകള് 1, 2 ആണെന്നിരിക്കട്ടെ. അടിവശം മാറ്റിയപെട്ടി 1 ആണെങ്കില് A ക്കു കിട്ടുന്ന തുക = 1 + 2 = 1. അടിവശം മാറ്റയതു 2 ആണെങ്കില് A ക്ക് കിട്ടുന്ന തുക = 1 2 = 1. അടിവശം മാറ്റിയതു 3 ആണെങ്കില് A ക്കു കിട്ടുന്ന തുക = 1 + 2 = 3. ഇങ്ങനെ മറ്റു കോളങ്ങളും നിറയ്ക്കാം. ഇതിലും നിശ്ചിതബിന്ദു ഇല്ല,
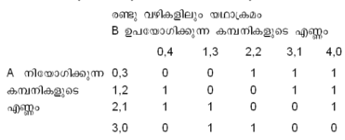
3. രണ്ടു പട്ടാളമേധാവികള് ഒരു പട്ടണത്തിലെത്താന് ശ്രമിക്കുന്നു. A യുടെ കീഴില് 3 കമ്പനികളും B യുടെ കീഴില് 4 കമ്പനികളും ഉണ്ട്. രണ്ടു വഴികളാണ് പട്ടണത്തിലേക്കുള്ളത്. A എത്താന് ശ്രമിക്കുകയും ആ തടയുകയുമാണെന്നു കരുതാം. A ക്കു 3 കമ്പനികളും ഒന്നിച്ചോ വെവ്വേറെയോ അയയ്ക്കാം. ഒരു കമ്പനി മുറിച്ചയയ്ക്കാന് പാടില്ല. B ക്കും ഒന്നിച്ചോ വെവ്വേറെയോ അയാളുടെ 4 കമ്പനികളും പ്രതിരോധത്തിനുപയോഗിക്കാം. ഏതെങ്കിലുമൊരു വഴിയില് A-യുടെ കമ്പനികളുടെ എണ്ണം B യുടേതിനെക്കാള് കൂടിയാല് A-ക്ക് ആ വഴി ഉപയോഗിച്ച് ലക്ഷ്യത്തിലെത്താമെന്നു വയ്ക്കാം. ലക്ഷ്യത്തിലെത്തുമെങ്കില് പ്രതിഫലം 1 എന്നും അല്ലെങ്കില് 0 എന്നും വച്ചാല് പ്രതിഫല പട്ടിക താഴെക്കൊടുത്തിരിക്കുന്ന പ്രകാരമായിരിക്കും.
എല്ലാ നിരകളിലും കുറഞ്ഞ സംഖ്യ പൂജ്യവും കൂടിയ സംഖ്യ 1-ഉം ആയതിനാല് നിശ്ചിത ബിന്ദു ഇല്ല.
നിരകളുടെയോ കോളങ്ങളുടെയോ ആധിപത്യം (പ്രമുഖത-dominance) ഉപയോഗിച്ച് വലിയ മാട്രിക്സുകളെ ചുരുക്കാന് സാധിക്കും. താഴെ കൊടുത്തിരിക്കുന്ന പ്രതിഫല മാട്രിക്സ് നോക്കുക.
A ഏതു തന്ത്രമുപയോഗിക്കുമ്പോഴാണ് B-ക്കു കുറഞ്ഞ നഷ്ടം വരുന്നത്. II ഉപയോഗിക്കുമ്പോഴാണ് എന്നു വ്യക്തം. അതുകൊണ്ട് B-യുടെ II-ാം തന്ത്രമാണ് I-നെക്കാള് പ്രബലമായത്. അഥവാ, II-ാം തന്ത്രം I-നെക്കാള് ആധിപത്യമുള്ളതാണ്.
(-2<3, 1<4) B-യുടെ I-ാം തന്ത്രം വലിയ ഗുണമില്ലാത്തതിനാല് എടുത്തുമാറ്റാം. അതുപോലെ III, IV ഇവ പരിശോധിച്ചു നോക്കുമ്പോള് III ആണ് ആധിപത്യമുള്ളത് എന്നു കിട്ടുന്നു. അതുകൊണ്ട് IV നീക്കിക്കളയാം. ഇപ്പോള് മാട്രിക്സ് ചുരുങ്ങി ഇപ്രകാരമാകുന്നു.
A-യുടെ ഭാഗത്തു നിന്നു നോക്കുമ്പോള് A യ്ക്കു കൂടുതല് തുക കിട്ടുന്നതാണു നല്ലത്. 1>2, 2>3. അതുകൊണ്ട് A യുടെ II-നാണ് ആധിപത്യം. I മാറ്റിനിര്ത്താം. ഇപ്പോള് പ്രതിഫല മാട്രിക്സ്
ഇപ്പോള് 1<2. അതുകൊണ്ട് ബലം കുറഞ്ഞ B യുടെ മൂന്നാം തന്ത്രം മാറ്റുക. അങ്ങനെ A-യുടെ II, B-യുടെ II ഇവ മെച്ചപ്പെട്ട തന്ത്രങ്ങളായും 1 എന്നത് ഗെയിമിന്റെ മൂല്യമായും അനുമാനിക്കാം. നിശ്ചിതബിന്ദുരീതി ഉപയോഗിച്ചാലും ഇതുതന്നെ കിട്ടും.
ഒരു ഗെയിമില് നിശ്ചിതബിന്ദു ഇല്ലാതെ വരുമ്പോഴാണ് മിശ്രതന്ത്രങ്ങളുപയോഗിക്കുന്നത്. അപ്പോള് സംഭാവ്യത ഉപയോഗിച്ച് അ യുടെയും ആ യുടെയും പ്രതീക്ഷാമൂല്യങ്ങള് (expected values) കണ്ടുപിടിച്ചശേഷം അവയിലെ മാക്സിമിനിയോ മിനിമാക്സിയോ കണ്ടുപിടിച്ചാണ് ഗെയിം നിര്ധാരണം ചെയ്യുന്നത്.
A-യുടെ മിശ്രതന്ത്രം X = (x1, x2, x3....xm)ഉം
B-യുടെ മിശ്രതന്ത്രം Y = (y1, y2, y3....yn)ഉം
ആണെങ്കില്
A പ്രതീക്ഷിക്കുന്ന
പ്രതിഫലം = E (X, Y)
ന്യൂമാന്റെ അടിസ്ഥാന സൂത്രമനുസരിച്ച് ഏതൊരു ഗെയിമിനും ഒരു മൂല്യം ഉണ്ട്. ഈ മൂല്യത്തിന്റെ മിശ്രതന്ത്രങ്ങള് X0, Y0 ആണെങ്കില് അവയ്ക്കു താഴെപ്പറയുന്ന ഗുണങ്ങളുണ്ടായിരിക്കണം.
1. ഒരു കളിക്കാരന് മെച്ചപ്പെട്ട തന്ത്രം മാത്രം ഉപയോഗിക്കുമ്പോള് മറ്റെയാള് അയാളുടെ മെച്ചപ്പെട്ട തന്ത്രത്തില് നിന്നും വ്യതിചലിച്ചാല് അങ്ങനെ മാറുന്ന ആളുടെ പ്രതിഫലം കുറയുകയേയുള്ളൂ; കൂടുകയില്ല.
2. ഒരു കളിക്കാരന് മെച്ചപ്പെട്ട തന്ത്രം സ്ഥിരമായി ഉപയോഗിച്ചാല് മറ്റെയാള് മിശ്രതന്ത്രങ്ങള് എങ്ങനെ ഉപയോഗിച്ചാലും ഗെയിമിന്റെ മൂല്യത്തിനു മാറ്റം വരികയില്ല.
മിശ്രതന്ത്രങ്ങളുടെ സംഭവ്യതകള് കണ്ടുപിടിക്കാന് സൂത്രങ്ങള് (formulas) തന്നെ ഉണ്ടാക്കിയെടുക്കാം.
2 x 2 ഗെയിം എടുക്കാം.
A-യുടെ മിശ്രതന്ത്രം (x1,x2); B-യുടെ മിശ്രതന്ത്രം (y,sub>1</sub>, y2) എന്നിരിക്കട്ടെ. ഗെയിമിന്റെ മൂല്യം m ആണെങ്കില് A യുടെ പ്രതീക്ഷാലാഭം
എന്നാല് ഇവയിലെ സമവാക്യരൂപം തന്നെ ഉപയോഗിച്ചാല്
പ്രതിഫല മാട്രിക്സ് 2 x 2 നെക്കാള് വലുതാണെങ്കില് ആധിപത്യരീതി ഉപയോഗിച്ച് അതിനെ ചെറുതാക്കി 2x 2 വലുപ്പമാക്കി മേല്പറഞ്ഞ സൂത്രമുപയോഗിച്ചാല് മതിയാകും.
ഉദാ. പ്രതിഫല മാട്രിക്സ്
ക, കകക കോളങ്ങളില് 1 < 3, 6 < 7, 55, അതുകൊണ്ട്, ക, കകക ഇവയില് ആധിപത്യമുള്ളത് ക ആണ്.
കക, കകക നിരകളില് 6 > 5, 2 > 1 ആയതുകൊണ്ട് കക ആണ് ആധിപത്യമുള്ളത്.
മുന് സൂത്രങ്ങളുപയോഗിച്ചാല് (12, 13, 14, 15, 16)
ാ = 4 എന്നുകിട്ടും.
അ-യുടെ മെച്ചപ്പെട്ട മിശ്രതന്ത്രം യും
ആ-യുടെ മെച്ചപ്പെട്ട മിശ്രതന്ത്രം യും ആണ്.
ഗെയിമിന്റെ മൂല്യം-4.
രണ്ടുപേരുള്ള ഗെയിമില് ഒരാള്ക്കു രണ്ടും എതിരാളിക്ക് എത്രവേണമെങ്കിലും തന്ത്രങ്ങളുണ്ടെങ്കില് 2x ി അഥവാ ിx 2 ഗെയിമുകള് ലഭിക്കുന്നു. ഇത്തരം ഗെയിമുകളെ ആധിപത്യരീതിയില് 2x 2 ആക്കി മാറ്റുകയോ ഓരോ 2x 2 ഉപമാട്രിക്സുകളെടുത്ത് അവയുടെ മിശ്രതന്ത്രങ്ങള് ഉപയോഗിച്ച് മെച്ചപ്പെട്ടത് എടുക്കുകയോ ചെയ്യാം. 'ി' വലിയ സംഖ്യ ആണെങ്കില് ഉപമാട്രിക്സുകളുടെ സംഖ്യ കൂടുമെന്നുള്ളതുകൊണ്ട് അപ്രായോഗികത ഉണ്ടാകാം. അത്തരം സന്ദര്ഭങ്ങളില് ഗ്രാഫ് രീതിയാണ് മെച്ചം.
ഈ ഗെയിമിന് വ്യക്തമായ നിശ്ചിതബിന്ദു ഇല്ല. ആധിപത്യരീതിയില് ചുരുക്കാനും വിഷമമാണ്. അ, 'ഃ' എന്ന സംഭാവ്യതയോടുകൂടി നീക്കം ക തിരഞ്ഞെടുക്കുന്നു എന്നിരിക്കട്ടെ. അപ്പോള് കക-ന്റെ സംഭാവ്യത 1ഃ ആയിരിക്കുമല്ലോ. ആ, ക എടുക്കുമ്പോള് അ യുടെ പ്രതീക്ഷാ പ്രതിഫലം ്യ=ഃ+2(1ഃ)
=2ഃ
ന്റെ വില പൂജ്യത്തിനും 1-നും ഇടയ്ക്കായിരിക്കുന്നതുകൊണ്ട് ഒരു യൂണിറ്റ് അകലത്തില് രണ്ട് ്യ അക്ഷങ്ങള് വരച്ച് അതില് പ്രതിഫലത്തിനുള്ള യൂണിറ്റുകള് അടയാളപ്പെടുത്തി ഗ്രാഫ് വരയ്ക്കാം.
ആ ക-ാം തന്ത്രം ഉപയോഗിക്കുമ്പോള്
അ യുടെ പ്രതിഫല രേഖ ്യ=2ഃ ആണ്.
ഈ രേഖ വരയ്ക്കാന്x=0, ്യ=2;
ഃ=1, ്യ=1 എന്നു കാണുക.
അതായത് പ്രതിഫലരേഖ അ യുടെ ക-ാം തന്ത്ര അക്ഷത്തില് 1 എന്ന ബിന്ദുവില്ക്കൂടിയും കക-ാം തന്ത്ര അക്ഷത്തില് 2 എന്ന ബിന്ദുവില്ക്കൂടിയും പോകുന്നു. അതുപോലെ ആ-യുടെ കക-ാം തന്ത്രത്തിനനുസരിച്ചുള്ള അ യുടെ പ്രതിഫലരേഖ യഥാക്രമം 3, 1 എന്ന ബിന്ദുവില്ക്കൂടി പോകുന്നു. പ്രതിഫലമാട്രിക്സിലെ സംഖ്യകള് തന്നെയാണിവ. മെച്ചപ്പെട്ട തന്ത്രം തിരഞ്ഞെടുക്കാന് ഈ രേഖകളുടെ സമാഹാരത്തിന്റെ താഴെയുള്ള അതിര്ത്തി (ജഝഞട) കണ്ടുപിടിക്കുക. ഏറ്റവും ഉയര്ന്ന ബിന്ദുവാണ് എടുക്കേണ്ടത് (ഞ).
B-യുടെ കക, കകക തന്ത്രങ്ങള്ക്കനുസരണമായാണ് മെച്ചപ്പെട്ട തന്ത്രങ്ങള് തരുന്നത്.
നേരത്തേ ഉപയോഗിച്ച സൂത്രങ്ങളുപയോഗിച്ചോ ഗ്രാഫില് നിന്നുതന്നെയോ അ യുടെ മെച്ചപ്പെട്ട തന്ത്രങ്ങള്
എന്നും
B യുടെ മെച്ചപ്പെട്ട തന്ത്രങ്ങള് എന്നും
ഗെയിമിന്റെ മൂല്യം എന്നും ലഭിക്കും.
ഇതുവരെ കൊടുത്തിട്ടുള്ള രീതികള് ഉപയോഗിച്ചാലും നിര്ധാരണം ചെയ്യാന് കഴിയാത്ത ഗെയിമുകള്ക്കു ലീനിയര് പ്രോഗ്രാമിങ് തുടങ്ങിയ രീതികളും പ്രയോഗിക്കാറുണ്ട്.
ഇലക്ട്രോണിക്സിന്റെ സഹായത്തോടെ ധാരാളം മെഷീന് ഗെയിമുകള് വിപണിയിലുണ്ട്. കംപ്യൂട്ടര് ഗെയിമുകള് എന്നറിയപ്പെടുന്ന ഇവ മനുഷ്യന് കളിക്കുന്ന ഗെയിമുകളോളം രസമുള്ളവയല്ലെങ്കിലും ഗെയിം സിദ്ധാന്തത്തിലെ പല ചോദ്യങ്ങള്ക്കും ഉത്തരം ലഭിക്കാനായി ഭാവിയില് ഉപയോഗിച്ചേക്കാം. ഗെയിം സിദ്ധാന്തത്തിലെ പല ഗവേഷണപ്രശ്നങ്ങളും വളരെ വലുപ്പമുള്ള മാട്രിക്സുകളില് ചെന്നെത്തുന്നതുകൊണ്ട് അതിന്റെ ഭാവിയിലെ പ്രയോജനങ്ങള് തീര്ച്ചയായും കംപ്യൂട്ടറിന്റെ കഴിവുകളെ ആശ്രയിച്ചുകൂടിയാണിരിക്കുന്നത്.
(ഡോ. സിസിലി സക്കറിയാസ്)