അഭികേന്ദ്രസരണം

\sin a\ Convergence

ഗണിതശാസ്ത്രത്തില്‍, ഒരു പരിമാണം മറ്റൊരു പരിമാണത്തോട് അടുക്കുന്ന അവസ്ഥ. പരിമാണങ്ങളുടെ സീമോന്‍മുഖമായ പ്രയാണമാണ് അഭികന്ദ്രസരണം; സീമാവിമുഖമായത് അപകേന്ദ്രസരണവും. അനുക്രമങ്ങള്‍, ശ്രേണികള്‍, ഫലനങ്ങള്‍ തുടങ്ങിയ ഗണിതശാസ്ത്രപരിമാണങ്ങള്‍ക്കെല്ലാം ഈ സ്വഭാവസവിശേഷതയുണ്ട്. ഗണിതശാഖയായ അനാലിസിസിലെ ഒരു മുഖ്യവിഷയമാണ് അഭികേന്ദ്രസരണം.

പരിബന്ധമില്ലാതെ വര്‍ധിക്കുന്ന ഒരു ശ്രേണിയിലെ തുടര്‍ച്ചയായുള്ള പദങ്ങളുടെ ആകെത്തുക ഒരു സീമയിലേയ്ക്കടുക്കുന്നെങ്കില്‍ ആ ശ്രേണി അഭികേന്ദ്രസരകമെന്നു പറയുന്നു. ഒരു ബിന്ദു അതിന്റെ പഥത്തിലൂടെ നീങ്ങിക്കൊണ്ട് മറ്റൊരു സ്ഥിരബിന്ദുവിലേക്ക് അടുക്കുമ്പോള്‍ ചരബിന്ദുവും സ്ഥിരബിന്ദുവും തമ്മിലുള്ള ദൂരം പൂജ്യത്തിനോടടുക്കുന്നു. ആ ചരബിന്ദു അഭികേന്ദ്രസരകം ആണെന്നു പറയാം. ഒരു വക്രരേഖ അതിന്റെ അനന്തസ്പര്‍ശകത്തോട് അഭികേന്ദ്രസരകമാണെന്നു പറയുന്നത്, ആ രേഖയില്‍ നിന്ന് സ്പര്‍ശകത്തിലേക്കുള്ള ദൂരം പൂജ്യത്തിനോട് അടുക്കുമ്പോഴാണ്. ഒരു രേഖ മറ്റൊന്നിനോട് അഭികേന്ദ്രസരകമാണെന്നു പറഞ്ഞാല്‍ ആ രേഖ നീട്ടിക്കൊണ്ടുപോയാല്‍ മറ്റേ രേഖയില്‍ മുട്ടുമെന്നാണര്‍ഥം.

നിരപേക്ഷ അഭികേന്ദ്രസരണം. ശ്രേണീപദങ്ങളുടെ നിരപേക്ഷമൂല്യങ്ങള്‍ കൊണ്ടുണ്ടാകുന്ന ശ്രേണി അഭികേന്ദ്രസരകമാണെങ്കില്‍, ആദ്യത്തെ ശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരകം ആണ്. Σa_n എന്ന ശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരകമാകുമ്പോള്‍ (1+a_n) എന്ന അനന്തഗുണിതം നിരപേക്ഷ അഭികേന്ദ്രസരകമാണെന്നു പറയുന്നു

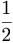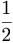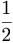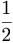1 - $\frac{1} {2}$ + $\frac{1} {2}$ ₂ - $\frac{1} {2}$ ₃ +.........+ (-1)^n-1 $\frac{1} {2}$ _n+......

ഒരു നിരപേക്ഷ അഭികേന്ദ്രസരകശ്രേണിയാണ്;

1 + 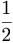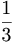$\frac{1} {2}$ + $\frac{1} {3}$ +... അഭികേന്ദ്രസരകമല്ല. എന്നാല്‍

1 - 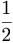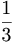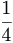$\frac{1} {2}$ + $\frac{1} {3}$ - $\frac{1} {4}$ +....... അഭികേന്ദ്രസരകമാണ്. ഈ സ്ഥിതിവിശേഷത്തിന് സോപാധിക അഭികേന്ദ്രസരണം (conditional convergence) എന്നു പറയുന്നു. ജ്യാമിതീയ ശ്രേണി (Geometric series) ആയ 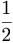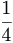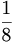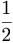$\frac{1} {2}$ + $\frac{1} {4}$ + $\frac{1} {8}$ + ... + $\frac{1} {2}$ _n +.... യുടെ ആദ്യത്തെ n പദങ്ങളുടെ ആകെത്തുക 1- 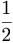$\frac{1} {2}$ _n ആണ്.

അഭികേന്ദ്രസരണവൃത്തം. സമ്മിശ്രസംഖ്യാതലത്തിലെ (complex numbers) ഘാതശ്രേണികളെ (power series) അഭികേന്ദ്രസരകമാക്കുന്ന ബിന്ദുക്കള്‍ ചേര്‍ന്ന് പരിധിയായിരിക്കുന്ന വൃത്തമാണ് അഭികേന്ദ്രസരകവൃത്തം. നിരപേക്ഷ അഭികേന്ദ്രസരകമാകുന്നത് വ്യാസാര്‍ധമുള്ള വൃത്തത്തിന്‍മേലും അതിനകത്തുമാണ്; പുറമേ അപകേന്ദ്രസരകവും.

ഏകതാന (uniform) അഭികേന്ദ്രസരണം.ഒരു ശ്രേണിയുടെ തീരുമാനിക്കപ്പെടാവുന്നത്ര വിദൂരമായ ഒരു പദം മുതല്‍ തുടര്‍ന്നെല്ലാംകൂടി ആശിക്കുന്നത്ര ചെറുതായിരിക്കാനുള്ള സാധ്യതയുണ്ടെങ്കില്‍ ആ ശ്രേണി ഏകതാന അഭികേന്ദ്രസരകമാണ്. (a,b) എന്ന അന്തരാളത്തില്‍ --- ഒരു ധനവാസ്തവികസംഖ്യയായിരിക്കെ, k എന്നൊരു നില മുതല്‍ n > k, x (a,b) യിലെ ഏതു ബിന്ദുവുമായിരിക്കെ,-/---------//ആകുമെങ്കില്‍-/------/ശ്രേണി ഏകതാന അഭികേന്ദ്രസരകം ആണ്. ഒരു നില മുതല്‍ എല്ലാം എടുക്കുന്നതിനുപകരം അവിടം മുതല്‍ ഏതെങ്കിലും രണ്ടുപദങ്ങള്‍, അതായത്-/--------// ഉം -/------/തമ്മിലുള്ള നിരപേക്ഷ വ്യത്യാസം ഏറ്റവും ചുരുങ്ങിയിരുന്നാലും വ്യവസ്ഥ പൂര്‍ണമാകുന്നു. ഉദാ. (-3, 3) അന്തരാളത്തില്‍ -3 < x < 3, f(x) = 1 / (1 - x/3), //----------// പോലെ ദോലനസ്വഭാവമുള്ള ശ്രേണികള്‍ (oscillating seris) ഉണ്ട്.

അഭികേന്ദ്രസരണ പരീക്ഷണങ്ങള്‍. 1. പൊതുതത്ത്വം. ----എന്നൊരു ധനവാസ്തവികസംഖ്യ തന്നാല്‍, n-ന് N-നേക്കാള്‍ വലിയ എല്ലാ നിസര്‍ഗസംഖ്യകള്‍ക്കും യോജിക്കുന്ന തരത്തില്‍----നെ അപേക്ഷിച്ചുള്ള ഒരു നിസര്‍ഗസംഖ്യ N = N() ഉണ്ടായിരിക്കണം. ഇത് a_1 + a_2 + ... a_n ... എന്ന ശ്രേണിയുടെ അഭികേന്ദ്രസരണത്തിന് അവശ്യവും മതിയായതുമായ (necessary and sufficient) വ്യവസ്ഥയാണ്.

2. താരതമ്യപരീക്ഷണം (Comparison Test).

(a) a_n----o,b_n---o: kn-നെ ആശ്രയിക്കാത്ത നിസര്‍ഗ സംഖ്യ, n > N ആയിരിക്കെ ആകുന്ന വിധത്തിലുള്ള ഒരു നിസര്‍ഗസംഖ്യ ച;അഭികേന്ദ്രസരകം. ഇത്രയും വ്യവസ്ഥകളില്‍, അഭികേന്ദ്രസരകമാണ്. ഇവിടെ ;അപകേന്ദ്രസരകമായിരിക്കയും മറ്റു വ്യവസ്ഥകള്‍ ഉണ്ടായിരിക്കുകയുമാണെങ്കില്‍, അപകേന്ദ്രസരകമാണ്.

(b) a_n---o;b_n----o;k, m n-നെ ആശ്രയിക്കാത്ത ധനസംഖ്യകള്‍ n>N, k<a_n/b_n< m ആകുന്നവിധം n > N; ഈ വ്യവസ്ഥകള്‍ അനുസരിച്ചാല്‍ --b_nഅഭികേന്ദ്രസരകമോ അപകേന്ദ്രസരകമോ ആകുന്നതിനുസരിച്ച് --a_n ഉം അതുപോലെ അതേ ക്രമത്തിലാകും.

3. അംശബന്ധപരീക്ഷണം അഥവാ ദാലെംബര്‍ പരീക്ഷണം. a_n > o, n+1 / മി = p

ആണെങ്കില്‍, , a_n,p < 1 ആകുമ്പോള്‍ അഭികേന്ദ്രസരകവും p >1 ആകുമ്പോള്‍ അപകേന്ദ്രസരകവുമായിരിക്കും.

4. കോഷി പരീക്ഷണം. , സീമ എങ്കില്‍ , p < 1 ആകുമ്പോള്‍ അഭികേന്ദ്രസരകവും p > 1 ആകുമ്പോള്‍ അപകേന്ദ്രസരകവുമായിരിക്കും.

5. പൊതുപരീക്ഷണം അഥവാ കുമ്മര്‍ പരീക്ഷണം. a_n>o; യ b_n>o, അപകേന്ദ്രസരകം എന്നു സങ്കല്പിക്കുക.

സീമ-----ആയിരിക്കും. k > o അല്ലെങ്കില്‍ k < o അനുസരിച്ച് അഭികേന്ദ്രസരകമോ അപകേന്ദ്രസരകമോ ആയിരിക്കും.

5. റാബി പരീക്ഷണം.------------------- ആകുമ്പോള്‍

എന്നു സങ്കല്പിക്കുക. എന്നാല്‍ q > 1 അഥവാ q < 1 ആയിരിക്കുന്നതനുസരിച്ച് അഭികേന്ദ്രസരകമോ അപകേന്ദ്രസരകമോ ആകും.

6. ഗോസ് പരീക്ഷണം. റാബി പരീക്ഷണത്തില്‍ q-ന്റെ മൂല്യം 1 ആയാല്‍ ആ പരീക്ഷണംകൊണ്ട് ഒരു പ്രയോജനവും ഉണ്ടാകുന്നില്ല. അതിനാല്‍ ഗോസ് അത് അല്പം പരിഷ്കരിച്ചു:

ആണെങ്കില്‍ 1-നേക്കാള്‍ വലുതോ ചെറുതോ ആകുന്നതനുസരിച്ച്അഭികേന്ദ്രസരകമോ അപകേന്ദ്രസരകമോ ആയിത്തീരും.

ഈ പരീക്ഷണങ്ങളുടെ പരിഷ്കരിച്ച പതിപ്പുകളായി പലതും വേറെയുണ്ട്. നിരപേക്ഷ അഭികേന്ദ്രസരണത്തിനും ഏകതാന അഭികേന്ദ്രസരണത്തിനും പരീക്ഷണങ്ങളുണ്ട്.

8. ആബല്‍ പരീക്ഷണം. ധനാത്മകവും ഏകദിഷ്ടവും (monotonic) ആയ ഫലനമാണ്; അഭികേന്ദ്രസരകം. എന്നാല്‍ -ഉം അഭികേന്ദ്രസരകമാണ്.

9. വെയര്‍സ്റ്റ്രോസ് പരീക്ഷണം. അഭികേന്ദ്രസരകം; എങ്കില്‍ എന്ന വ്യവസ്ഥയില്‍ഏകതാന അഭികേന്ദ്രസരകമാണ്.

10. ഘാതശ്രേണികള്‍.

ആയിരിക്കട്ടെ. എങ്കില്‍ |x| < R ആകുമ്പോള്‍ അഭികേന്ദ്രസരകവും |x| > R ആകുമ്പോള്‍ അപകേന്ദ്രസരകവുമായിരിക്കും. R അഭികേന്ദ്രസരണ വ്യാസാര്‍ധമാണ്. ഉം,-------- R അഭികേന്ദ്രസരണവ്യാസാര്‍ധവും ആയിരിക്കെ, ------ ഏകതാന അഭികേന്ദ്രസരകമാകും.

യുഗ്മശ്രേണികള്‍ക്കും (double series) ഇത്തരം പരീക്ഷണങ്ങള്‍ ഉണ്ട്. നോ: അനന്തശ്രേണികള്‍, അനലിറ്റിക് നമ്പര്‍ തിയറി, അനാലിസിസ്, അനുക്രമം, ഫലനം

അഭികേന്ദ്രസരണം

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

അഭികേന്ദ്രസരണം

താളിന്റെ അനുബന്ധങ്ങള്‍

സ്വകാര്യതാളുകള്‍

ഉള്ളടക്കം

തിരയൂ

പണിസഞ്ചി