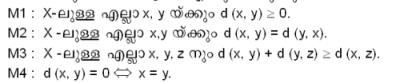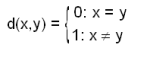This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ടോപ്പോളജി
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
ടോപ്പോളജി
Topology
ആധുനിക ഗണിതശാസ്ത്രത്തിന്റെ ഒരു ശാഖ. 20-ാം ശ. -ത്തിന്റെ ആദ്യവര്‍ഷങ്ങളിലാണ് ഈ ശാഖ സ്വതന്ത്ര വളര്‍ച്ച പ്രാപിച്ചത്. വസ്തുവിന്റെ ജ്യാമിതീയ സവിശേഷതകളേക്കാള്‍, സമരൂപ വിരൂപണം(homomorphic deformation) കൊണ്ട് ആ വസ്തുവില്‍ മാറ്റമില്ലാതെ തുടരുന്ന ഗുണവിശേഷങ്ങളാണ് ടോപ്പോളജിയില്‍ പഠനവിഷയമാക്കുന്നത്. അതിനാല്‍ 'സ്പേയ്സിന്റെ ഗുണധര്‍മങ്ങളെക്കുറിച്ചുള്ള പഠനം' എന്ന് ടോപ്പോളജിയെ നിര്‍വചിക്കാം. ഗണിതീയ വിശ്ലേഷണം (analysis), ജ്യാമിതീയ ഘടന എന്നീ മേഖലകളിലെ ചില പ്രശ്നങ്ങളാണ് ഈ ശാഖയുടെ വളര്‍ച്ചയ്ക്ക് തുടക്കം കുറിച്ചത്. ഗണിതശാസ്ത്രത്തിന്റെ വിവിധ നൂതന ശാഖകളില്‍ ഇന്ന് ടോപ്പോളജി ഉപയുക്തമാക്കുന്നുണ്ട്. ഫലന വിശ്ലേഷണം (Functional analysis), വാസ്തവിക വിശ്ലേഷണം (Real analysis), ത്രിവിമീയ ജ്യാമിതി (Three dimensional geometry) തുടങ്ങിയ ഒട്ടേറെ ശാഖകളിലും ടോപ്പോളജി ഒരു അടിസ്ഥാന ഘടകമായി മാറിക്കഴിഞ്ഞു.
ടോപ്പോളജിക്ക് രണ്ടു പ്രധാന ശാഖകളാണുള്ളത്; പൊതു (General) ടോപ്പോളജിയും ബീജീയ (Algebraic) ടോപ്പോളജിയും. ഗണിത വിശ്ലേഷണവുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങള്‍ കൈകാര്യം ചെയ്യാനുള്ള വിശാലമായ ഒരു വേദി എന്ന നിലയ്ക്കാണ് പൊതു ടോപ്പോളജി വികസിച്ചു വന്നത്. ജ്യാമിതീയ പഠനത്തില്‍ നിന്നുണ്ടായ പ്രശ്നങ്ങള്‍ കൈകാര്യം ചെയ്യുന്ന ശാഖയാണ് ബീജീയ ടോപ്പോളജി. ഗ്രൂപ്പ് തിയറി ഉള്‍പ്പെടെയുള്ള സിദ്ധാന്തങ്ങള്‍ ഉപയോഗപ്പെടുത്തുന്നു എന്നതാണ് ബീജീയ ടോപ്പോളജിയുടെ സവിശേഷത.
പൊതു ടോപ്പോളജി. വാസ്തവിക സംഖ്യാ ഫലനങ്ങളുടെ പഠനമാണ് ഈ ശാഖയുടെ വികാസത്തിനു പ്രചോദനം നല്‍കിയത്; പ്രധാനമായും സന്തത (continuous) ഫലനങ്ങളുടെ പഠനം. കുറേക്കൂടി അമൂര്‍ത്തമായ തലത്തില്‍ സന്തത ഫലനങ്ങളെ വീക്ഷിക്കാനുള്ള ശ്രമം പൊതു ടോപ്പോളജിയില്‍ ദൃശ്യമാണ്. സന്തത സ്വഭാവം വ്യക്തമാക്കാന്‍ അവശ്യം വേണ്ട ഘടകങ്ങളുടെ അന്വേഷണം പുതിയ സ്പേയ്സിന്റെ ആവിഷ്ക്കാരത്തിലേക്കു നയിക്കുന്നു. ടോപ്പോളജീയ സ്പേയ്സ്, മെട്രിക് സ്പേയ്സ് എന്നിവ ഇത്തരത്തില്‍ നിര്‍വചിക്കപ്പെട്ടവയാണ്. വാസ്തവിക സംഖ്യകളുടെ ഫലനത്തെ ഇത്തരം അമൂര്‍ത്ത തലങ്ങളിലെ ഫലനങ്ങളുടെ ഒരു പ്രത്യേക ഇനമായി കണക്കാക്കാമെന്നതാണ് ഈ അമൂര്‍ത്തവത്ക്കരണത്തിന്റെ പ്രസക്തി.
മെട്രിക് സ്പേയ്സ്. സംഖ്യകള്‍ തമ്മിലുള്ള ദൂരം എന്നത് സന്തത ഫലനങ്ങളുടെ നിര്‍വചനത്തിലും ശ്രേണികളുടെ അഭിസരണത്തിലും (convergence) ഉപയോഗപ്പെടുത്തുന്ന ഒരു ആശയമാണ്. ഉദാഹരണത്തിന് {an} എന്ന വാസ്തവിക സംഖ്യാശ്രേണിയുടെ അഭിസരണം പരിഗണിക്കുക. ഈ ശ്രേണി ι എന്ന വാസ്തവിക സംഖ്യയിലേക്ക് അഭിസരണം ചെയ്യുന്നു എന്നതിനര്‍ഥം {an} ഉം l ഉം തമ്മിലുള്ള ദൂരം ക്രമേണ കുറഞ്ഞു കുറഞ്ഞ് {an}എന്ന ശ്രേണി l നോട് എത്ര വേണമെങ്കിലും അടുത്തു വരുന്നു എന്നതാണ്. ഇതിനെ കൂടുതല്‍ കൃത്യമായി പറയുന്നത് താഴെ കൊടുക്കും വിധം ആണ്.
ഏതൊരു വാസ്തവിക സംഖ്യ ε > 0 തന്നിരുന്നാലും അതിനോടു ബന്ധപ്പെട്ട് N എന്ന ഒരു പൂര്‍ണസംഖ്യ താഴെപ്പറയുന്ന നിബന്ധന അനുസരിക്കുന്നതായി ഉണ്ടാകണം.
നിബന്ധന : n ≥ N ആണെങ്കില്‍ | an − l | < εആണ്.
ഇവിടെ | an − l | എന്നത് an ഉം l ഉം തമ്മിലുള്ള ദൂരം ആണ് എന്നു കണക്കാക്കാം. വാസ്തവിക സംഖ്യകള്‍ തമ്മിലുള്ള ദൂരം ഇപ്രകാരമാണ് നിര്‍വചിക്കപ്പെട്ടിരിക്കുന്നത്. ഇവിടെ ശ്രദ്ധേയമായ മറ്റൊരു കാര്യം ദൂരം എന്ന ആശയം കൊണ്ട് ഒരു ശ്രേണിയുടെ അഭിസരണം വ്യക്തമാക്കാം എന്നതാണ്. അതായത് | an − l | < εഎന്ന നിബന്ധന an ഉം l ഉം തമ്മിലുള്ള ദൂരം < ε എന്നു മാറ്റി എഴുതാവുന്നതാണ്. ഈ ദൂരത്തെ d (an, l) എന്ന് സൂചിപ്പിച്ചാല്‍ മുകളില്‍ പറഞ്ഞ നിബന്ധന d (an, l) < ε എന്നാകും.
ഈ പ്രസ്താവന, രേഖീയ സംഖ്യകളല്ലാത്ത ഒരു ഗണത്തിലും ദൂരം എന്ന ആശയം നിലവിലുണ്ടെങ്കില്‍ ശ്രേണികളുടെ അഭിസരണം പ്രതിപാദിക്കാന്‍ ഉപയോഗപ്പെടും. അത്തരം ഒരു ഗണ (set) ത്തില്‍ ദൂരം എന്ന ആശയം നിര്‍വചിക്കപ്പെട്ടിരിക്കണം. ഈവിധത്തിലുള്ള പരിഗണനയാണ് മെട്രിക് തലം എന്ന ആശയത്തിന് രൂപം നല്‍കിയത്. ദൂരം എന്ന ആശയത്തിന്റെ അമൂര്‍ത്തീകരണമാണ് മെട്രിക് എന്നതുകൊണ്ട് അര്‍ഥമാക്കുന്നത്. മെട്രിക്കിന്റെ നിര്‍വചനം ഇപ്രകാരമാണ്:
X ഒരു അശൂന്യ ഗണം (Non empty set) ആണെന്നിരിക്കട്ടെ. R വാസ്തവിക സംഖ്യകളുടെ ഗണവും d: X × X → R ഒരു ഫലനവും ആകട്ടെ. താഴെപ്പറയുന്ന നിബന്ധനകള്‍ പൂര്‍ത്തിയാക്കുന്നു എങ്കില്‍ d ഒരു മെട്രിക് ആണ് എന്നു പറയുന്നു.
X-ല്‍ ഇങ്ങനെ ഒരു മെട്രിക്, d, നിര്‍വചിച്ചിട്ടുണ്ടെങ്കില്‍ (X,d) എന്ന ജോടിയെ ഒരു മെട്രിക് സ്പേയ്സ് എന്നു വിളിക്കുന്നു.
ഉദാഹരണത്തിന് വാസ്തവിക സംഖ്യകളുടെ ഗണത്തില്‍ d(x,y) = | x − y | ഒരു മെട്രിക് ആണ്.
പലതരത്തില്‍ മെട്രിക് നിര്‍ദേശിക്കപ്പെടാം. ഉദാഹരണത്തിന് X ഏതെങ്കിലുമൊരു അശൂന്യ ഗണം ആകട്ടെ.x,y ഇവ X -ല്‍ ആണെങ്കില്‍
എന്നത് X ലെ ഒരു മെട്രിക് ആണ്. വാസ്തവിക സംഖ്യാഗണത്തിന്റെ വര്‍ഗമായ R2 ലെ ചില മെട്രിക്കുകള്‍ താഴെക്കൊടുക്കുന്നു. ഇവയില്‍ x = (x1x2),y=(y1y2) എന്നിരിക്കട്ടെ.
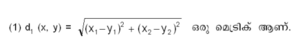ഇതിനെ യൂക്ളിഡിയന്‍ മെട്രിക് എന്നു പറയുന്നു.
സന്തത ഫലനങ്ങള്‍. മെട്രിക് തലങ്ങളില്‍ ദൂരം എന്ന ആശയം ഉള്ളതുകൊണ്ട് ശ്രേണികളുടെ അഭിസരണം പരിഗണിക്കാവുന്നതാണ്. അതുപോലെ തന്നെ ഫലനങ്ങളുടെ സന്തതത്വവും ഇത്തരം സ്പേയ്സുകളില്‍ പ്രതിപാദിക്കാവുന്നതാണ്.
രേഖീയ സംഖ്യകളുടെ ഒരു ഫലനമായ f ന്റെ സന്തതത്വം ഒരു ബിന്ദുവില്‍ പ്രകടമാക്കുന്ന രീതി ശ്രദ്ധിക്കുക.x0 എന്ന ബിന്ദുവില്‍ f സന്തതമാണെന്നതിന്റെ അര്‍ഥം x എന്ന ബിന്ദു x0 നോട് അടുക്കുന്തോറും f(x), f(x0) നോട് അടുക്കുന്നു എന്നാണ്. ഈ സാമീപ്യം വിടവില്ലാതെ തുടരും എന്നതാണ് സന്തതഫലനങ്ങളുടെ സ്വഭാവം. ഇവിടെ സാമീപ്യം മനസ്സിലാക്കുന്നത് ദൂരം ഉപയോഗിച്ചാണ്. ദൂരം മെട്രിക് ഉപയോഗിച്ചും വ്യക്തമാക്കുന്നു. അപ്പോള്‍ f(x), f(x0) നോട് സമീപമാണെന്നത് d(f(x), f(x0)) ചെറുതാണ് എന്നതിനു തുല്യമാണ്.
ഈ രീതിയില്‍ (X,d1), (Y,d2) ഇവ മെട്രിക് സ്പേയ്സുകളും f : X → Y ഒരു ഫലനവും ആണെങ്കില്‍ f ന്റെ സന്തതത്വം ഇങ്ങനെ പ്രകടമാക്കാം. d1(x, x0) ചെറുതാകുന്തോറും d2 (f(x), f(x0)) എത്രവേണമെങ്കിലും ചെറുതായിക്കൊണ്ടിരിക്കുമെങ്കില്‍ f എന്ന ഫലനം x0 എന്ന ബിന്ദുവില്‍ സന്തതം ആണ് എന്നു പറയാം. കൂടുതല്‍ കൃത്യതയോടെ പറഞ്ഞാല്‍ ഏതൊരു വാസ്തവിക സംഖ്യ ε>0 തന്നിരുന്നാലും അതുമായി ബന്ധപ്പെടുത്തി δ> 0 എന്ന ഒരു വാസ്തവിക സംഖ്യ താഴെപ്പറയുന്ന നിബന്ധന പാലിച്ച് ഉണ്ടാകുമെങ്കില്‍ f എന്ന ഫലനം x0 എന്ന ബിന്ദുവില്‍ സന്തതമാണ്.
നിബന്ധന: d1 (x,x0) < δ ആണെങ്കില്‍ d2 (f(x), f(x0)) < ε ആയിരിക്കും.
സാമീപ്യം. സാമീപ്യം എന്ന ആശയത്തെ കൂടുതല്‍ കൃത്യതയോടെ നിര്‍വചിച്ചാല്‍ സന്തതസ്വഭാവം വ്യക്തമാക്കാന്‍ ഈ ആശയം മതിയാകും എന്നു കാണാം. ഉദാഹരണത്തിന് f(x), f(x0)ന് സമീപം ആണ് എന്നതിനെ f(x), f(x0) ന്റെ ഒരു സാമീപ്യ മേഖലയില്‍ ആണ് എന്നും പറയാം. അങ്ങനെ ഓരോ ബിന്ദുവിനും സാമീപ്യ മേഖലകള്‍ നിര്‍ണയിച്ചാല്‍ അതിന്റെ അടിസ്ഥാനത്തില്‍ ശ്രേണികളുടെ അഭിസരണം, ഫലനങ്ങളുടെ സന്തതത്വം ഇവ പരിഗണിക്കാവുന്നതാണ്. ഇത്തരം ഒരു സമീപനമാണ് പൊതു ടോപ്പോളജിയില്‍ സ്വീകരിച്ചിട്ടുള്ളത്. ദൂരം എന്ന ആശയത്തില്‍ നിന്നാണ് സാമീപ്യം എന്ന ആശയം ഉടലെടുക്കുന്നതെങ്കിലും, സാമീപ്യം എന്ന ആശയം സ്വതന്ത്രമായി വ്യവഹരിക്കാവുന്നതാണ്. ഈ ദിശയിലുള്ള ശ്രമമാണ് പൊതു ടോപ്പോളജിയിലൂടെ പ്രകടമാകുന്നത്. 1906-ല്‍ ഫ്രെഷെ (Frechet) യുടെ മെട്രിക് സ്പേയ്സിനെപ്പറ്റിയുള്ള പഠനം, 1909-ല്‍ റീസ്സിന്റെ സീമാബിന്ദുക്കളെപ്പറ്റിയുള്ള പഠനം, 1913-ലെ വെയ്ലിന്റെ സാമീപ്യങ്ങളെ ആശ്രയിച്ചുള്ള സ്പേയ്സുകളുടെ പഠനം എന്നിവയാണ് ഈ ദിശയിലുള്ള ആദ്യ ശ്രമങ്ങള്‍. 1914-ല്‍ ഹൗസ്ഡോര്‍ഫ് രചിച്ച പ്രബന്ധത്തില്‍ ടോപ്പോളജീയ സ്പേയ്സ് കൂടുതല്‍ വ്യക്തതയോടെ നിര്‍വചിച്ചു. ഇതോടെ പൊതു ടോപ്പോളജി കൂടുതല്‍ പ്രയോഗക്ഷമമായി മാറുകയും ചെയ്തു.
ടോപ്പോളജീയ സ്പേയ്സ്. X ഒരു അശൂന്യ ഗണവും &tatu;എന്നത് X-ന്റെ ഉപഗണങ്ങളുടെ ഒരു സമൂഹവും (class) ആണെന്നിരിക്കട്ടെ. താഴെപ്പറയുന്ന നിബന്ധനകള്‍ പാലിച്ചാല്‍ X ലുള്ള ഒരു ടോപ്പോളജിയാണ് τ എന്നുപറയാം.
X എന്ന ഗണവും അതിലെ τ എന്ന ടോപ്പോളജിയും ചേര്‍ന്ന ജോടിയെ (X,τ) എന്നു സൂചിപ്പിക്കുന്നു. ഇതിനെ ഒരു ടോപ്പോളജീയ സ്പേയ്സ് എന്നു പറയുന്നു.
(X,τ) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെങ്കില്‍ τ ലെ അംഗങ്ങളെ വിവൃത ഗണങ്ങള്‍ (open sets) എന്നു പറയും. (T1), (T2),(T3) എന്നീ ടോപ്പോളജിയുടെ നിബന്ധനകളെ വിവൃത ഗണങ്ങളുടെ സ്വഭാവമായി വിവരിക്കാം.
(4) R, വാസ്തവിക സംഖ്യകളുടെ ഗണം ആണെന്നിരിക്കട്ടെ. (a,b) എന്നത് a മുതല്‍ b വരെയുള്ള വാസ്തവിക സംഖ്യകളുടെ ഗണം ആണ്. a,b എന്നീ അഗ്രബിന്ദുക്കള്‍ ഉള്‍പ്പെട്ടിട്ടില്ലാത്തതിനാല്‍ ഇതിനെ ഒരു വിവൃത അന്തരാളം എന്നു പറയുന്നു. വിവൃത അന്തരാളങ്ങളുടെ യോഗം ആയി വരുന്ന ഗണങ്ങള്‍ R ന്റെ ഒരു ടോപ്പോളജിയാണ്. R, φ ഇവ വിവൃത അന്തരാളങ്ങളായി കണക്കാക്കാം. ഈ ടോപ്പോളജി R ന്റെ സാധാരണ ടോപ്പോളജി എന്നാണ് അറിയപ്പെടുന്നത്.
(5) ഏതു മെട്രിക് സ്പേയ്സും ഒരു ടോപ്പോളജിയ സ്പേയ്സ് ആയി പരിഗണിക്കാം. മെട്രിക് രൂപം നല്‍കുന്ന ഒരു ടോപ്പോളജി ഓരോ മെട്രിക് സ്പേയ്സിലും നിര്‍വചിക്കാവുന്നതാണ്. ഇതു താഴെപ്പറയുന്ന പ്രകാരം നിര്‍വചിക്കാം.
(X,d) ഒരു മെട്രിക് സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. x എന്നത് X ലെ ഒരംഗവും r എന്നത് ഒരു ധന സംഖ്യയും ആണെങ്കില്‍ Sr (x) = {y ∈X : d (x,y) < r} എന്നത് X ന്റെ ഒരു ഉപഗണം ആണ്. ഇതിനെ ഒരു വിവൃത ഗോളം എന്നുപറയുന്നു. Sr (x) എന്ന വിവൃത ഗോളത്തിന്റെ ആരം r ഉം കേന്ദ്രം r ഉം ആണ്. ഇത്തരം വിവൃത ഗോളങ്ങളുടെ യോഗത്തെ മെട്രിക് സ്പേയ്സിലെ വിവൃത ഗണങ്ങള്‍ എന്നു പറയുന്നു. Sr (x) എന്നതും ഈ അര്‍ത്ഥത്തില്‍ ഒരു വിവൃത ഗണം ആണ്. X ഉം φ ഉം വിവൃത ഗണങ്ങള്‍ ആണെന്നു കാണാം. ഈ വിവൃത ഗണങ്ങളുടെ സമൂഹം X ന്റെ ഒരു ടോപ്പോളജിയാണ്. ഇതിനെ മെട്രിക് ടോപ്പോളജി എന്നു പറയുന്നു.
X ഏതെങ്കിലും ഒരു അശൂന്യ ഗണം ആണെന്നിരിക്കട്ടെ.
τ1 = {X,φ} എന്നത് X ലെ ഒരു ടോപ്പോളജി ആണ്. ഇതിനെ അവിവിക്ത (Indiscrete) ടോപ്പോളജി എന്നു പറയുന്നു. τ2 എന്നത് X ന്റെ എല്ലാ ഉപഗണങ്ങളുടേയും സമൂഹമാണെങ്കില്‍ τ2 ഉം ഒരു ടോപ്പോളജിയാണ്. τ2 നെ വിവിക്ത (Discrete) ടോപ്പോളജി എന്നു പറയുന്നു. X ലെ ഏതൊരു ടോപ്പോളജിയും ഇവയുടെ ഇടയിലായിരിക്കും. അതായത് X ലെ ഏതൊരു ടോപ്പോളജി τ യും τ1≤τ≤τ2 എന്ന നിബന്ധന പാലിക്കും.
വിവൃത ഗണങ്ങളും സംവൃത ഗണങ്ങളും. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. ലെ അംഗങ്ങളെ വിവൃത ഗണങ്ങള്‍ എന്നാണ് പറയുന്നതെന്ന് നേരത്തെ വ്യക്തമാക്കിയിരുന്നു. വിവൃത ഗണങ്ങളുടെ പൂരകങ്ങളെ (രീാുഹലാലി) സംവൃത ഗണങ്ങള്‍ എന്നു പറയുന്നു. (ത,) എന്ന ടോപ്പോളജീയ സ്പേയ്സില്‍ ത, ള ഇവ വിവൃതങ്ങളും സംവൃതങ്ങളും ആണ്. വിവൃത ഗണങ്ങള്‍ പാലിക്കേ വ്യവസ്ഥകള്‍ അടിസ്ഥാനപ്പെടുത്തിയാണ് ടോപ്പോളജി നിര്‍വചിച്ചിരിക്കുന്നത്. ഈ വ്യവസ്ഥകള്‍ക്കു പകരം സംവൃത ഗണങ്ങള്‍ പാലിക്കേ വ്യവസ്ഥകള്‍ ഉപയോഗിച്ചും ടോപ്പോളജി നിര്‍വചിക്കാം. സംവൃത ഗണങ്ങള്‍ പാലിക്കേ വ്യവസ്ഥകള്‍ ഇവയാണ്. ഠ1' : ത, ള ഇവ സംവൃത ഗണങ്ങള്‍ ആണ്. ഠ2' : സംവൃത ഗണങ്ങളുടെ ഏതു സംഗമവും (ശിലൃേലെരശീിേ) സംവൃത ഗണം ആണ്. ഠ3' : സംവൃത ഗണങ്ങളുടെ ഏതു പരിമിത യോഗവും സംവൃത ഗണം ആണ്. ആഭ്യന്തരവും സംവൃതവും. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സും അ ഡ്ഡ ത ഉം ആണെന്നു സങ്കല്പിക്കുക. അ സംവൃതമോ വിവൃതമോ ആകണമെന്നില്ല. ള ഡ്ഡ അ ആകയാല്‍ അ യ്ക്ക് വിവൃത ഉപഗണം ഉ് എന്നു കിട്ടുന്നു. അ യുടെ വിവൃത ഉപഗണങ്ങളുടെ യോഗം അ യുടെ ഉപഗണവും, വിവൃത ഗണവും ആണ്. ഇതിനെ അത്ഥ എന്നാണ് സൂചിപ്പിക്കുക. അത്ഥ എന്നത് അ യുടെ ഏറ്റവും വലിയ വിവൃത ഉപഗണം ആണ്. അ തന്നെ വിവൃത ഗണം ആണെങ്കില്‍ അത്ഥ = അ ആണ്. അത്ഥ യെ അ യുടെ ആഭ്യന്തരം എന്നു പറയുന്നു. അ ഡ്ഡ ത എന്നതില്‍നിന്ന് അ യ്ക്ക് സംവൃതമായ അധിഗണങ്ങള്‍ ഉ് എന്നു വ്യക്തമാകുന്നു. ഇത്തരം സംവൃത അധിഗണങ്ങളുടെ സംഗമം ഒരു സംവൃതഗണവും അ യുടെ അധിഗണവും ആണ്. ഇതിനെ എന്നാണ് സൂചിപ്പിക്കുന്നത്. നെ അ യുടെ സംവൃതം (രഹീൌൃല) എന്നു പറയുന്നു. അ ഉള്‍ക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ സംവൃത ഗണമാണ് . അ ഒരു സംവൃത ഗണമാണെങ്കില്‍ = അ ആണ്. സംവൃതം സംബന്ധിച്ച ചില പ്രമേയങ്ങള്‍ പ്രമേയം 1. ത ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. അ, ആ ഇവ ത ന്റെ ഉപഗണങ്ങള്‍ ആണെങ്കില്‍ താഴെപ്പറയുന്ന പ്രസ്താവനകള്‍ ശരിയാണ്.
സംവൃത ക്രിയ ഉപയോഗിച്ച് ടോപ്പോളജി നിര്‍വചിക്കാവുന്നതാണ്. അടുത്ത പ്രമേയം ഇതിന്റെ രീതി വ്യക്തമാക്കുന്നു. പ്രമേയം 2. ത ഒരു അശൂന്യഗണം ആണെന്നു സങ്കല്പിക്കുക. അ ണ്ണ എന്നത് ത ന്റെ ഉപഗണങ്ങള്‍ തമ്മിലുള്ള ഒരു ബന്ധം ആണെന്നിരിക്കട്ടെ. താഴെപ്പറയുന്ന നിബന്ധനകള്‍ പാലിക്കുന്നു എന്നു കരുതുക.
അപ്പോള്‍ അ = എന്ന വ്യവസ്ഥ പാലിക്കുന്ന ഉപഗണങ്ങള്‍ സംവൃത ഗണങ്ങള്‍ ആകുന്ന ഒരു ടോപ്പോളജി ത ന് ഉാവും. മാത്രമല്ല ഈ ടോപ്പോളജീയ സ്പേയ്സില്‍ അ എന്ന ഉപഗണത്തിന്റെ സംവൃതം മുകളില്‍ തന്നിട്ടുള്ള എന്ന ഗണം ആകുകയും ചെയ്യും. സാമീപ്യം എന്ന ആശയം ടോപ്പോളജീയ സ്പേയ്സില്‍ വളരെ പ്രയോജനകരമാണ്. ത ഒരു ടോപ്പോളജീയ സ്പേയ്സും ഃ ക്ട ത ഉം ആണെന്നിരിക്കട്ടെ. ഃ അംഗമായുള്ള ഒരു വിവൃത ഗണം ഉള്‍ക്കൊള്ളുന്ന ഏതു ഗണത്തേയും ഃ ന്റെ ഒരു സാമീപ്യം എന്നു പറയാം. ഉദാഹരണമായി ഞ എന്നത് വാസ്തവിക സംഖ്യകളുടെ ഗണം സാധാരണ ടോപ്പോളജി ഉള്‍പ്പെടുത്തി കണക്കാക്കുക. 0 എന്ന അംഗത്തിന്റെ സാമീപ്യങ്ങളാണ് (1,1), (2,1), (2,3) തുടങ്ങിയവ. ആധാരവും ഉപ ആധാരവും. ഒരു ടോപ്പോളജീയ സ്പേയ്സിലെ വിവൃത ഉപഗണങ്ങള്‍ ആണ് അതിലെ ടോപ്പോളജി നിര്‍ണയിക്കുന്നത്. വിവൃത ഉപഗണങ്ങള്‍ പാലിക്കുന്ന വ്യവസ്ഥകള്‍ പ്രകാരം സംഗമം, യോഗം എന്നിവയിലൂടെ വീും വിവൃതഗണങ്ങള്‍ സൃഷ്ടിക്കപ്പെടുന്നു. ഉദാഹരണത്തിന് അ, ആ എന്നിവ വിവൃത ഗണങ്ങള്‍ ആണെങ്കില്‍ അ ശ്ശ ആ, അ ശ്ള ആ എന്നിവയും വിവൃത ഗണങ്ങള്‍ ആണ്. വിവൃത ഉപഗണങ്ങള്‍ മുഴുവന്‍ ഇപ്രകാരം ചെറിയ ഒരു ഉപഗണ സമൂഹത്തില്‍ നിന്നും സൃഷ്ടിച്ചെടുക്കാനുള്ള അന്വേഷണം ആണ് ആധാരം, ഉപ ആധാരം തുടങ്ങിയ ആശയങ്ങളിലേക്ക് എത്തിക്കുന്നത്. (ത, ) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. യ ഡ്ഡ ആകട്ടെ. ലെ ഏത് അംഗവും യ ലെ അംഗങ്ങളുടെ യോഗം ആണെങ്കില്‍ യ യെ (ത, ) യുടെ ഒരു ആധാരം എന്നു പറയുന്നു. മറ്റൊരുതരത്തില്‍ പറഞ്ഞാല്‍ യുടെ ഉപഗണമായ യ താഴെപ്പറയുന്ന വ്യവസ്ഥകള്‍ പാലിച്ചാല്‍ അത് യുടെ ഒരു ആധാരം ആണ്. (ശ) ശ്ശ ആ = ത, (ശശ) ആ1, ആ2 ക്ട യ ആണെങ്കില്‍ ആ1 ശ്ള ആ2 യ ലെ അംഗങ്ങളുടെ ഒരു യോഗം ആണ്. ഒരു ടോപ്പോളജി വ്യക്തമാക്കാന്‍ അതിന്റെ എല്ലാ വിവൃതഗണങ്ങളും പറയുന്നതിനു പകരം അതിന്റെ ഒരു ആധാരം നല്‍കിയാല്‍മതി എന്നതാണ് ആധാരം എന്ന ആശയത്തിന്റെ പ്രാധാന്യം. ചെറിയ ഗണ സമൂഹം ക്ൊ ടോപ്പോളജി നിര്‍ണയിക്കുന്ന പ്രക്രിയ കുറേക്കൂടി മുന്നോട്ടു കാുെപോയാല്‍ ലഭിക്കുന്നതാണ് ഉപ ആധാരം. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സും ട ഡ്ഡ ഉം ആകട്ടെ. ട ലെ അംഗങ്ങളുടെ സംഗമം ആയി വരുന്ന ഗണങ്ങള്‍ യുടെ ഒരു ആധാരം ആണെങ്കില്‍ നെ യുടെ ഒരു ഉപ ആധാരം എന്നു പറയുന്നു. ഉദാഹരണത്തിന് വാസ്തവിക സംഖ്യാഗണത്തിന്റെ ടോപ്പോളജി പരിഗണിക്കുക. യ = (മ, യ) : മ < യ} എന്നത് ഈ ടോപ്പോളജിയുടെ ഒരു ആധാരം ആണ്. അതുപോലെ ട = ന്ദ , യ) : യ ക്ട ഞ} ശ്ശ (മ, ന്ദ ) : മ ക്ട ഞ} എന്നത് ഈ ടോപ്പോളജിയുടെ ഒരു ഉപ ആധാരം ആണ്. സന്തത ഫലനങ്ങള്‍. സന്തത ഫലനങ്ങള്‍ കൈകാര്യം ചെയ്യാനുള്ള ഒരു വേദി എന്ന നിലയിലാണ് ടോപ്പോളജീയ സ്പേയ്സുകള്‍ പ്രയോജനപ്പെടുന്നത്. സാമീപ്യം എന്ന ആശയം ഉപയോഗിച്ച് സന്തതസ്വഭാവം വ്യക്തമാക്കുന്നത് എങ്ങനെ എന്നു നോക്കാം. ത, ഥ ഇവ ടോപ്പോളജീയ സ്പേയ്സും ള : ത ണ്ണ ഥ ഒരു ഫലനവും ആണെന്നിരിക്കട്ടെ. ഢ എന്നത് ഥ യുടെ ഏതു വിവൃത ഉപഗണം ആണെങ്കിലും ള 1 (ഢ)എന്നത് ത -ന്റെ ഒരു വിവൃത ഉപഗണം ആണെങ്കില്‍ ള എന്ന ഫലനം സന്തതം ആണ് എന്നു പറയുന്നു. ഞ വാസ്തവിക സംഖ്യാഗണവും ള : ഞ ണ്ണ ഞ ഒരു സന്തതഫലനവും ആണെന്നിരിക്കട്ടെ. ഞ ന് സാധാരണ ടോപ്പോളജി നല്‍കിയാല്‍ ടോപ്പോളജീയ സ്പേയ്സിലെ സന്തത ഫലനത്തിന്റെ നിര്‍വചനം സാധാരണ സന്തത ഫലനത്തിന്റെ നിബന്ധനയ്ക്കു സമാനമാണെന്നു കാണാം. സമരൂപത. ടോപ്പോളജീയ സ്പേയ്സുകള്‍ തമ്മിലുള്ള ഘടനാപരമായ സമാനത കൈകാര്യം ചെയ്യാനും സന്തത ഫലനങ്ങള്‍ ആണ് ഉപയോഗിക്കുന്നത്. രു ടോപ്പോളജീയ സ്പേയ്സുകള്‍ സമരൂപങ്ങളായി കണക്കാക്കുന്നത് അവയ്ക്ക് ഒരേ ഘടന ഉള്ളപ്പോഴാണ്. അതായത് രു ഗണങ്ങളും അവയുടെ വിവൃത ഉപഗണങ്ങളും പരസ്പരം ഏകൈക പ്രതിലോമത്തില്‍ (ീില ീ ീില രീൃൃലുീിറലിരല) ആയിരിക്കണം. സമരൂപതയുടെ നിര്‍വചനം ഇപ്രകാരം നല്‍കാം. ത, ഥ ഇവ ടോപ്പോളജീയ സ്പേയ്സും ള : ത ണ്ണ ഥ ഒരു ബൈജക്റ്റീവ് ഫലനവും ആണെന്നിരിക്കട്ടെ. ള ഉം ള 1 ഉം സന്തത ഫലനങ്ങള്‍ ആണെങ്കില്‍ ത, ഥ ഇവ സമരൂപങ്ങളാണ് എന്നു പറയുന്നു. ഈ സന്ദര്‍ഭത്തില്‍ ള എന്ന ഫലനത്തെ ഒരു സമരൂപത (വീാീാീൃുവശാ) എന്നും പറയുന്നു. രു ടോപ്പോളജീയ സ്പേയ്സുകള്‍ സമരൂപങ്ങളാണെങ്കില്‍ അവ ടോപ്പോളജീയമായി ഒരുപോലെ പ്രവര്‍ത്തിക്കും എന്നാണ് വിവക്ഷ. വിവിധതരം ടോപ്പോളജികള്‍. സാധാരണ പരിഗണിക്കാറുള്ള ചില ടോപ്പോളജികളെ ഇവിടെ പരാമര്‍ശിക്കാം. (ശ) ആപേക്ഷിക ടോപ്പോളജി. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സും ഥഡ്ഡ ത ഉം ആണെന്നിരിക്കട്ടെ. ഥ യ്ക്ക് ത ന്റെ ടോപ്പോളജിയില്‍ നിന്ന് ലഭ്യമാകുന്ന ഒരു ടോപ്പോളജി ഉ്. ഇതിനെ ഥ യുടെ ആപേക്ഷിക ടോപ്പോളജി എന്നു പറയുന്നു. ആപേക്ഷിക ടോപ്പോളജിയില്‍ ഥ യുടെ ഒരു ഉപഗണമായ അ വിവൃതം ആകണമെങ്കില്‍ താഴെപ്പറയുന്ന നിബന്ധന പാലിക്കണം. അ = ഥ ശ്ള ഏ ആകുംവിധം ഏ എന്ന വിവൃത ഗണം ല്‍ ഉാകണം. മറ്റൊരുതരത്തില്‍ പറഞ്ഞാല്‍ ഥേ = ഥ ശ്ള ഏ : ഏ ക്ട } എന്നത് ഥ യുടെ ഒരു ടോപ്പോളജി ആണ്. ഇതിനെ ഥ യുടെ ആപേക്ഷിക ടോപ്പോളജി എന്നു പറയുന്നു. ഥ യെ ത ന്റെ ഒരു ഉപതലം എന്നും പറയാറ്ു. (ശശ) ഗുണന ടോപ്പോളജി. ത, ഥ ഇവ ടോപ്പോളജീയ സ്പേയ്സുകളാണെങ്കില്‍ ത ഃ ഥ ല്‍ ത, ഥ ഇവയില്‍ നിന്നു ലഭ്യമായ ഒരു ടോപ്പോളജി നിര്‍വചിക്കാന്‍ കഴിയും. ഡ, ഢ ഇവ യഥാക്രമം ത, ഥ ഇവയിലെ വിവൃതഗണങ്ങള്‍ ആണെങ്കില്‍ ഡ ഃ ഢ ആധാരത്തിലെ അംഗം ആകുംവിധം ആണ് ത ഃ ഥ ലെ ടോപ്പോളജി നിര്‍ണയിക്കുന്നത്. അതായത് യ = ഡ ഃ ഢ : ഡ, ഢ ഇവ യഥാക്രമം ത, ഥ ഇവയില്‍ വിവൃതം ആണ്} എന്നത് ഒരു ആധാരം ആയി ത ഃ ഥ ല്‍ കിട്ടുന്ന ടോപ്പോളജിയെ ഗുണന ടോപ്പോളജി എന്നു പറയുന്നു. ഈ ടോപ്പോളജി മറ്റൊരു രൂപത്തിലും പ്രതിപാദിക്കാം. ട = ത്ര ഃ ഢ : ഢ, ഥ ലെ വിവൃതഗണം} ശ്ശ ഡ്ര ഃ ഥ : ഡ, ത ലെ വിവൃത ഗണം} എന്നത് ഉപആധാരം ആയി ത ഃ ഥ ല്‍ കിട്ടുന്ന ടോപ്പോളജിയും മുകളില്‍ കൊടുത്ത ഗുണന ടോപ്പോളജി തന്നെ ആണ്. രാമത്തെ രീതിയിലുള്ള പ്രതിപാദനത്തിന് അനന്തഗുണനത്തിലേക്ക് കൂടി വ്യാപിക്കാം എന്ന സവിശേഷത ഉ്. ത = ു തശ എന്നത് ഒരു അനന്തഗുണനഫലം ആണെന്നു കരുതുക. ഓരോ തശ ഉം ടോപ്പോളജീയ സ്പേയ്സ് ആണെങ്കില്‍ ത ല്‍ ഗുണന ടോപ്പോളജി നിര്‍വചിക്കാനാവും. ജശ : ത ണ്ണ തശ പ്രൊജക്ഷന്‍ഫലനം ആണെങ്കില്‍ ട = ജശ1 (ഡശ) : ഡശ , തശ ലെ വിവൃതഗണം} ഉപആധാരം ആയി ത ല്‍ കിട്ടുന്ന ടോപ്പോളജി ആണ് ത ലെ ഗുണന ടോപ്പോളജി. (ശശശ) ഹരണ ടോപ്പോളജി. ത ഒരു ഗണവും ജ ഒരു സമതാബന്ധവും (ലൂൌശ്മഹലിരല ൃലഹമശീിേ) ആണെങ്കില്‍ സമതാഗണങ്ങളുടെ സമൂഹത്തെ ത ന്റെ ജ ഹരണഫലം എന്നാണ് പറയുന്നത്. ഇത് ത / ജ എന്ന് എഴുതുന്നു. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെങ്കില്‍ ത / ജ ല്‍ ഒരു ടോപ്പോളജി ത ല്‍ നിന്നും ലഭ്യമാണ്. ഇത് നിര്‍വചിക്കാന്‍ ത ല്‍ നിന്ന് ത / ജ യിലേക്കുള്ള ഹരണഫലനം ഉപയോഗപ്പെടുത്തുന്നു. ു : ത ണ്ണ ത / ജ ആകട്ടെ ഈ ഹരണഫലനം. ഃ ക്ട ത ആണെങ്കില്‍ ു(ഃ) എന്നത് ഃ ഉള്‍ക്കൊള്ളുന്ന സമതാഗണം ആണ്. ഇവിടെ ജേ = ണ്ര ഡ്ഡ ത / ജ : ു1 (ണ) ക്ട } എന്നത് ത / ജ ലെ ഒരു ടോപ്പോളജി ആണ്. ഇതിനെ ഹരണ ടോപ്പോളജി എന്നു പറയുന്നു. ഹരണ ടോപ്പോളജി മറ്റൊരു രീതിയിലും നിര്‍വചിക്കാം. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സും ള : ത ണ്ണ അ, അ റേഞ്ചായുള്ള ഒരു ഫലനവും ആണെന്നിരിക്കട്ടെ. അപ്പോള്‍ ൂ = ഏ ഡ്ഡ അ : ള 1 (ഏ) ക്ട } എന്നത് അ -ലെ ഒരു ടോപ്പോളജി ആണ്. ഇതിനേയും ഹരണ ടോപ്പോളജി എന്നു പറയാം. ടോപ്പോളജീയ സവിശേഷതകള്‍ (ഠീുീഹീഴശരമഹ ുൃീുലൃശേല). പലപ്പോഴും ചില സവിശേഷതകള്‍ ഉള്ള ടോപ്പോളജീയ സ്പേയ്സുകള്‍ ആണ് പ്രായോഗികമായി ഉപകരിക്കപ്പെടുന്നത്. ഉദാഹരണത്തിന് വാസ്തവിക സംഖ്യകളുടെ ടോപ്പോളജീയ സ്പേയ്സിന്റെ ഒരു സവിശേഷതയാണ് അവിച്ഛിന്നത (രീിിലരലേറില). (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. ത -നെ സംഗമം ശൂന്യമായ രു അശൂന്യ വിവൃതഗണങ്ങളുടെ യോഗം ആയി എഴുതാന്‍ സാധ്യമല്ല എങ്കില്‍ ത -നെ ഒരു അവിച്ഛിന്ന സ്പേയ്സ് എന്നു വിളിക്കുന്നു. വാസ്തവിക സംഖ്യാതലം, ഞ, സംഗമം ശൂന്യമായ രു അശൂന്യ വിവൃതഗണങ്ങളുടെ യോഗം ആയി എഴുതാന്‍ പറ്റാത്തതാണ്. എന്നാല്‍ എണ്ണല്‍ സംഖ്യകളുടെ ഗണം ഞ ന്റെ ഒരു ഉപസ്പേയ്സായി കണക്കാക്കിയാല്‍ അത് അവിച്ഛിന്നം അല്ല. അവിച്ഛിന്ന തലങ്ങള്‍ക്ക് പല പ്രത്യേകതകളും ഉ്. ഉദാഹരണത്തിന് ത ഒരു അവിച്ഛിന്ന സ്പേയ്സ് ആണെങ്കില്‍ ത ല്‍ നിന്ന് മുകളില്‍ പറഞ്ഞ എണ്ണല്‍ സംഖ്യാസ്പേയ്സിലേക്കുള്ള ഏതു സന്തത ഫലനവും ഒരു സ്ഥിരസംഖ്യാഫലനം (രീിമിെേ ളൌിരശീിേ) ആണ്. വാസ്തവിക സംഖ്യാസ്പേയ്സില്‍ ഇല്ലാത്തതും എന്നാല്‍ ഏതു സംവൃത അന്തരാളം, ധമ,യപ യ്ക്കും ഉള്ളതുമായ ഒരു സവിശേഷതയാണ് കോംപാക്റ്റ്നെസ്. ഒരു തരത്തിലുള്ള പരിമിതത്വമാണ് ഇതിലൂടെ പ്രകടമാകുന്നത്. (ത, ) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ ഏ = ഏശ : ശക്ടക}, ത ലെ വിവൃതഗണങ്ങളുടെ ഒരു സമൂഹം ആകട്ടെ. ത = ശ്ശ ഏശ ആണെങ്കില്‍ ഏ യെ ത ന്റെ ഒരു ആവരണം എന്നു പറയുന്നു. ത ന്റെ ഏതു ആവരണത്തിലും ഒരു പരിമിത ഉപആവരണം ഉങ്കിെല്‍ ത ഒരു കോംപാക്റ്റ് സ്പേയ്സ് ആണ് എന്നു പറയുന്നു. ത ഒരു പരിമിത ഗണം ആണെങ്കിലും, ഒരു പരിമിത സമൂഹം ആണെങ്കിലും ത കോംപാക്റ്റ് സ്പേയ്സ് ആണ്. വാസ്തവിക സംഖ്യാസ്പേയ്സിന്റെ എല്ലാ കോംപാക്റ്റ് ഉപസ്പേയ്സുകളും ഹെയ്ന്‍- ബോറല്‍ (ഒലശില ആീൃലഹ) പ്രമേയം വഴി ലഭ്യമാണ്. അതു പ്രകാരം സംവൃതവും പരിമേയവും (യീൌിറലറ) ആയ ഉപസ്പേയ്സുകള്‍ മാത്രമാണ് വാസ്തവിക സംഖ്യാസ്പേയ്സിന്റെ കോംപാക്റ്റ് ആയ ഉപസ്പേയ്സുകള്‍. വേര്‍തിരിവ് ആക്സിയങ്ങള്‍ (ടലുമൃമശീിേ മഃശീാ). ടോപ്പോളജീയ സ്പേയ്സിനെ അവയിലുള്ള വിവൃത ഗണങ്ങളുടെ ലഭ്യതയുടെ അടിസ്ഥാനത്തില്‍ ഠ0, ഠ1, ഠ2, ഠ3, ഠ4 എന്നിങ്ങനെ വിവിധ തട്ടുകളിലായി തരംതിരിക്കാറ്ു. (ത,) ഒരു ടോപ്പോളജീയ സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. ഃ, ്യ ഇവ ത ലെ ഏതെങ്കിലും രു വ്യത്യസ്ത അംഗങ്ങള്‍ ആകട്ടെ. ഃ ഉള്‍ക്കൊള്ളുന്നതും ്യ അംഗമല്ലാത്തതുമായ ഒരു ഗണമോ ്യ ഉള്‍ക്കൊള്ളുന്നതും ഃ അംഗമല്ലാത്തതുമായ ഒരു ഗണമോ ല്‍ ഉങ്കിെല്‍, (ത,) ഒരു ഠ0 - സ്പേയ്സ് ആണ് എന്നു പറയുന്നു. ഃ ഉള്‍പ്പെടുന്നതും ്യ അംഗമല്ലാത്തതുമായ ഒരു വിവൃത ഗണവും, ്യ ഉള്‍പ്പെടുന്നതും ഃ അംഗമല്ലാത്തതുമായ ഒരു വിവൃത ഗണവും ത ന് ഉങ്കിെല്‍ ത നെ ഒരു ഠ1 സ്പേയ്സ് എന്നു പറയുന്നു. എല്ലാ ഠ1 സ്പേയ്സും ഠ0 സ്പേയ്സ് ആണെന്നത് വ്യക്തമാണ്. ഃ അംഗമായ ഒരു വിവൃത ഗണവും, ്യ അംഗമായ മറ്റൊരു വിവൃത ഗണവും പരസ്പരം സംഗമം ശൂന്യമായതായി ഉങ്കിെല്‍ ത നെ ഒരു ഠ2 സ്പേയ്സ് എന്നു വിളിക്കുന്നു. ഇവിടെ എല്ലാ ഠ2 സ്പേയ്സും ഠ1 സ്പേയ്സാണ് എന്നത് വ്യക്തമാണ്. എല്ലാ മെട്രിക് സ്പേയ്സുകളും ഠ2 സ്പേയ്സ് ആണെന്നതും എളുപ്പത്തില്‍ തെളിയിക്കാവുന്നതാണ്. (ത,) ഒരു ഠ1 സ്പേയ്സ് ആണെന്നിരിക്കട്ടെ. ഃ ക്ട ത ഉം എ എന്നത് ഃ അംഗമല്ലാത്ത ഏതെങ്കിലും ഒരു സംവൃത ഗണവും ആണെന്നിരിക്കട്ടെ. സംഗമം ശൂന്യമായ അ, ആ എന്നീ വിവൃത ഗണങ്ങള്‍ ഃ ക്ട അ, എ ഡ്ഡ ആ ആകുംവിധം ഉങ്കിെല്‍ ത നെ ഒരു ഠ3 സ്പേയ്സ് എന്നു വിളിക്കുന്നു. എല്ലാ ഠ3 സ്പേയ്സും ഠ2 സ്പേയ്സ് ആണെന്ന് കാണാവുന്നതാണ്. (ത,) ഒരു ഠ1 സ്പേയ്സും, അ, ആ ഇവ സംഗമം ശൂന്യമായ ഏതെങ്കിലും രു സംവൃത ഗണങ്ങളും ആണെന്നിരിക്കട്ടെ. ഏ,ഒ ഇവ സംഗമം ശൂന്യമായ വിവൃത ഗണങ്ങളും അ ഡ്ഡ ഏ, ആ ഡ്ഡ ഒ എന്നീ വ്യവസ്ഥകള്‍ പാലിക്കുന്നതും ആയി ഉങ്കിെല്‍ ത ഒരു ഠ4 സ്പേയ്സ് ആണെന്നു പറയുന്നു. എല്ലാ ഠ4 സ്പേയ്സും ഠ3 സ്പേയ്സ് ആണെന്ന് കാണാവുന്നതാണ്. എല്ലാ മെട്രിക് സ്പേയ്സും ഠ4 സ്പേയ്സ് ആണ് എന്നു കാണാം. ത = 1, 2}, = ത്ര, ഷ} ആണെങ്കില്‍ (ത, ) മുകളില്‍ പറഞ്ഞ ഒരു ഠശ സ്പേയ്സിലും പെടുന്നില്ല. 2. ബീജീയ ടോപ്പോളജി. ടോപ്പോളജീയ സ്പേയ്സിനെ സംബന്ധിച്ച പഠനത്തില്‍ ബീജഗണിത ആശയങ്ങള്‍ ഉള്‍പ്പെടുത്തി കൈകാര്യം ചെയ്യുന്ന ശാഖയാണ് ബീജീയ ടോപ്പോളജി. ഇവിടെ കൈകാര്യം ചെയ്യപ്പെടുന്ന പ്രശ്നങ്ങള്‍ പൊതു ടോപ്പോളജിയില്‍ പരിഗണിക്കുന്നവയില്‍ നിന്ന് പലപ്പോഴും വ്യത്യസ്തമാണ്. പൊതു ടോപ്പോളജിയിലും ജ്യാമിതിയിലും ഉത്ഭവിക്കുന്ന ചില പ്രശ്നങ്ങള്‍ക്ക് ഉചിതമായ നിര്‍ധാരണം ബീജീയ സങ്കേതങ്ങളില്‍ക്കൂടി പലപ്പോഴും ലഭ്യമാണ്. സ്ഥിരബിന്ദു (ളശഃലറ ുീശി) പ്രശ്നങ്ങള്‍, സമരൂപതാപ്രശ്നങ്ങള്‍ എന്നിവ പലപ്പോഴും ബീജീയ ടോപ്പോളജിയുടെ സിദ്ധാന്തങ്ങള്‍ ഉപയോഗിച്ച് എളുപ്പത്തില്‍ കൈകാര്യം ചെയ്യാറ്ു. ഉദാഹരണത്തിന് ഞ2 ഉം ഞ3 ഉം സമരൂപങ്ങളല്ല എന്നു തെളിയിക്കണമെന്നിരിക്കട്ടെ. അവ തമ്മില്‍ ഒരു സമരൂപത നിലവിലില്ല എന്നു തെളിയിക്കാന്‍ ഫലനങ്ങള്‍ ഉപയോഗിച്ച് എളുപ്പമല്ല. ബീജീയടോപ്പോളജിയില്‍ ഇത് തെളിയിക്കുന്നത് ഓരോ സ്പേയ്സിനേയും ഓരോ ഗ്രൂപ്പുമായി ബന്ധിപ്പിച്ചാണ്. ഈ ബന്ധം സമരൂപത സംരക്ഷിക്കുന്നതാകണം. അപ്പോള്‍ ഞ2 നെ ബന്ധപ്പെടുത്തുന്ന ഗ്രൂപ്പും ഞ3 നെ ബന്ധപ്പെടുത്തുന്ന ഗ്രൂപ്പും സമരൂപം അല്ലെങ്കില്‍ ഞ2 ഉം ഞ3 ഉം സമരൂപം അല്ല എന്നു കിട്ടും. ഹോമോളജി ഗ്രൂപ്പ് എന്ന ആശയം ആണ് ഇവിടെ പ്രയോഗിക്കുന്നത്. ഹോമോളജി ഗ്രൂപ്പ്, ഹോമോട്ടോപ്പി ഗ്രൂപ്പ് എന്നീ ഗ്രൂപ്പുകള്‍ ആണ് സാധാരണയായി ടോപ്പോളജീയ സ്പേയ്സുമായി ബന്ധപ്പെട്ട് പരിഗണിക്കാറുള്ളത്. ഹോമോട്ടോപ്പി. ടോപ്പോളജീയ സ്പേയ്സിലെ സന്തതഫലനങ്ങള്‍ തമ്മില്‍ ഉള്ള ഒരു ബന്ധമാണ് ഹോമോട്ടോപ്പി. ത, ഥ ഇവ ടോപ്പോളജീയ സ്പേയ്സുകളും ള, ഴ : ത ണ്ണ ഥ സന്തതഫലനങ്ങളും ആണെന്നിരിക്കട്ടെ. ക = ധ0,1പ ആകട്ടെ. എ: ത ഃ ക ണ്ണ ഥ എന്ന ഒരു സന്തതഫലനം താഴെപ്പറയുന്ന നിബന്ധനപ്രകാരം ഉങ്കിെല്‍ ള ഉം ഴ ഉം തമ്മില്‍ ഹോമോട്ടോപ്പി ബന്ധം ഉ് എന്നു പറയുന്നു. നിബന്ധന: എല്ലാ ഃ ക്ട ത നും, എ(ഃ,0) = ള (ഃ) എല്ലാ ഃ ക്ട ത നും എ(ഃ,1) = ഴ(ഃ) എ നെ ള, ഴ ഇവ തമ്മിലുള്ള ഒരു ഹോമോട്ടോപ്പി എന്നും പറയുന്നു. പ്രാമാണിക ഗ്രൂപ്പ് (എൌിറമാലിമേഹ ഴൃീൌു). ടോപ്പോളജീയ സ്പേയ്സിന്റെ പഠനത്തില്‍ പ്രയോഗിക്കപ്പെടുന്ന ഒരു ഗ്രൂപ്പാണ് പ്രാമാണിക ഗ്രൂപ്പ് (എൌിറമാലിമേഹ ഴൃീൌു) എന്ന പേരില്‍ അറിയപ്പെടുന്നത്. ഈ ഗ്രൂപ്പിന്റെ സ്വഭാവത്തില്‍ നിന്ന് അതു നല്‍കുന്ന ടോപ്പോളജീയ സ്പേയ്സിനെ സംബന്ധിച്ച് കുറേ കാര്യങ്ങള്‍ വ്യക്തമാക്കാന്‍ സാധിക്കും. ക = ധ0,1പ എന്ന സംവൃത അന്തരാളത്തില്‍ നിന്നും ത എന്ന ടോപ്പോളജീയ സ്പേയ്സിലേക്കുള്ള സന്തതഫലനങ്ങളില്‍ നിന്നാണ് ഈ ഗ്രൂപ്പ് രൂപപ്പെടുന്നത്. ഇത്തരം സന്തതഫലനങ്ങളെ പഥം എന്നു പറയുന്നു. ൌ : ക ണ്ണ ത ഒരു പഥം ആണെങ്കില്‍ ൌ(0), ൌ(1) ഇവയെ യഥാക്രമം ൌ എന്ന പഥത്തിന്റെ ആദ്യബിന്ദു എന്നും അവസാനബിന്ദു എന്നും പറയുന്നു. ൌ (0) = ഃ0, ൌ (1) = ഃ1 ആണെങ്കില്‍ ഃ0 ല്‍ നിന്ന് ഃ1ലേക്കുള്ള ഒരു പഥമാണ് ൌ. ഃ0, ഃ1 ക്ട ത ഉം ൌ, ് ഇവ ഃ0 ല്‍ നിന്ന് ഃ1 ലേക്കുള്ള പഥങ്ങളും ആണെന്നിരിക്കട്ടെ. എ : ക ഃ ക ണ്ണ ത എന്നത് ൌ ല്‍ നിന്ന് ് -ലേക്കുള്ള ഒരു ഹോമോട്ടോപ്പി ആണെന്നിരിക്കട്ടെ. ഉപരിയായി ഓരോ ക്ട ക യ്ക്കും എ (0, ) = ഃ0, എ (1,) = ഃ1 എന്നീ വ്യവസ്ഥകള്‍ കൂടി പാലിക്കുന്നു എങ്കില്‍ എ നെ ഒരു പഥ ഹോമോട്ടോപ്പി എന്നു പറയുന്നു. അപ്പോള്‍ ൌ,് ഇവ പഥ ഹോമോട്ടോപ്പിക് ആണ് എന്നും പറയാം. ഃ0, ഃ1, ഃ2 ഇവ ത എന്ന ടോപ്പോളജീയ സ്പേയ്സിലെ ബിന്ദുക്കളും ൌ, ് ഇവ യഥാക്രമം ഃ0 ല്‍ നിന്ന് ഃ1 ലേക്കും ഃ1 ല്‍ നിന്ന് ഃ2 ലേക്കുള്ള പഥങ്ങളും ആണെന്നിരിക്കട്ടെ. അപ്പോള്‍ ൌ, ് ഇവയുടെ കൂടിച്ചേരല്‍ വഴി ൌ.് എന്ന ഒരു പഥം സൃഷ്ടിക്കപ്പെടുന്നു. ൌ.് നിര്‍വചിക്കപ്പെടുന്നത് ഇപ്രകാരമാണ്. ക്ട ധ0,1പ ആണെങ്കില്‍ (ൌ.്) () = ൌ(2) : 0 ക്ഷ ക്ഷ 1/2
്(21) : 1/2 ക്ഷ ക്ഷ 1
ൌ.് ഒരു പഥം ആണെന്ന കാര്യം വ്യക്തമാണ്. അതുപോലെ തന്നെ വ്യക്തമാണ് ൌ.് യുടെ ആദ്യബിന്ദു ഃ0 ഉം അവസാനബിന്ദു ഃ2 ഉം ആണെന്നതും. ൌ എന്ന ഒരു പഥത്തിന്റെ ആദ്യബിന്ദുവും അവസാനബിന്ദുവും ഃ0 എന്ന ഒരേ ബിന്ദു ആണെങ്കില്‍ ൌ-നെ ഒരു ലൂപ്പ് എന്നു വിളിക്കുന്നു. കൂടുതല്‍ കൃത്യമായി ഃ0 ല്‍ ഉള്ള ഒരു ലൂപ്പ് എന്നു പറയാം. ഃ0-ലുള്ള ഏതു ജോടി ലൂപ്പുകളും തമ്മില്‍ ഒരു ഗുണനം സാധ്യമാണ്. ഈ ഗുണനക്രിയ ആണ് പ്രാമാണിക ഗ്രൂപ്പിന്റെ അടിസ്ഥാനമായ ക്രിയ. ത ഒരു ടോപ്പോളജീയ സ്പേയ്സും ഃ0 ക്ട ത ഉം ആണെങ്കില്‍ ത ന്റെ ഃ0 ആധാരമായുള്ള പ്രാമാണിക ഗ്രൂപ്പിനെ ു (ത, ഃ0) എന്നാണ് സൂചിപ്പിക്കുന്നത്. ഇതിലെ അംഗങ്ങള്‍ ഃ0 ലുള്ള ലൂപ്പുകളുടെ ഹോമോട്ടോപ്പിക സമൂഹങ്ങള്‍ ആണ്. ൌ എന്ന ലൂപ്പിന്റെ ഹോമോട്ടോപ്പിക സമൂഹത്തെ ധൌപ എന്ന് സൂചിപ്പിച്ചാല്‍ ു (ത, ഃ0) ലെ ഗുണനക്രിയ ധൌപ . ധ്പ = ധൌ.്പ എന്ന് നിര്‍വചിക്കാം. ഇവിടെ ധൌ.്പ എന്നത് ൌ.് എന്ന ലൂപ്പിന്റെ ഹോമോട്ടോപ്പിക സമൂഹം ആണ്. ഈ ക്രിയയില്‍ ു (ത, ഃ0) ഒരു ഗ്രൂപ്പാണ് എന്നത് തെളിയിക്കാവുന്നതാണ്. ഇതാണ് പ്രാമാണിക ഗ്രൂപ്പ്.
X പഥ അവിച്ഛിന്നം (path connected) ആണെങ്കില്‍ π (X,x0) എന്ന പ്രാമാണിക ഗ്രൂപ്പ് x0-ല്‍ നിന്നും സ്വതന്ത്രമായിരിക്കും. അതായത് x0, x1∈ X ആണെങ്കില്‍ π (X, x0) ഉം π (X,x1) ഉം സമരൂപഗ്രൂപ്പുകളായിരിക്കും. ഇത്തരം സന്ദര്‍ഭങ്ങളില്‍ π (X,x0) നെ π(X) എന്നു പറയാം. ഉദാഹരണത്തിന് വാസ്തവിക സംഖ്യാസ്പേയ്സിന്റെ പ്രാമാണിക ഗ്രൂപ്പ് ഒരംഗം മാത്രമുള്ള കേവല ഗ്രൂപ്പാണ്. എന്നാല്‍ S1 = {(x,y)∈R×R :x2 + y2 = 1} എന്ന വൃത്തത്തിന്റെ പ്രാമാണിക ഗ്രൂപ്പ് Z എന്ന പൂര്‍ണ സംഖ്യാഗ്രൂപ്പിന് സമരൂപം ആണ്.
ഹോമോളജി ഗ്രൂപ്പ്. ടോപ്പോളജീയ സ്പേയ്സിന്റെ പഠനത്തില്‍ ഉപയോഗപ്പെടുത്തുന്ന മറ്റൊരു ഗ്രൂപ്പാണ് ഹോമോളജി ഗ്രൂപ്പ്. ഇത് പ്രാമാണിക ഗ്രൂപ്പിനേക്കാള്‍ കൂടുതല്‍ സങ്കീര്‍ണമായുള്ള ഒന്നാണ്. അതുകൊണ്ട് ഇവ കൂടുതല്‍ പ്രയോജനകരവും ആണ്. പ്രാമാണിക ഗ്രൂപ്പില്‍ക്കൂടി വ്യക്തമാകാത്ത പല സ്വഭാവവിശേഷങ്ങളും ഹോമോളജി ഗ്രൂപ്പില്‍ക്കൂടി വ്യക്തമാക്കാന്‍ സാധിക്കും. ഉദാഹരണത്തിന് R2, R3 എന്നിവയുടെ പ്രാമാണിക ഗ്രൂപ്പുകള്‍ സമരൂപങ്ങളാണ്. അതിനാല്‍ R2, R3 എന്നീ ടോപ്പോളജീയ സ്പേയ്സുകള്‍ സമരൂപങ്ങള്‍ ആണോ എന്ന പ്രശ്നം പ്രാമാണിക ഗ്രൂപ്പ് ഉപയോഗിച്ച് പരിഹരിക്കാന്‍ സാധിക്കുന്നില്ല. എന്നാല്‍ ഹോമോളജി ഗ്രൂപ്പില്‍ ഇവ തമ്മിലുള്ള വ്യത്യാസം പ്രതിഫലിക്കുന്നുമുണ്ട്. R2, R3 എന്നിവയുടെ ഹോമോളജി ഗ്രൂപ്പുകള്‍ സമരൂപങ്ങള്‍ അല്ല എന്നു കാണാവുന്നതാണ്. ഇതില്‍ നിന്ന് ആ സ്പേയ്സുകള്‍ സമരൂപങ്ങള്‍ അല്ല എന്ന് സിദ്ധിക്കുന്നു.
ബീജീയ ടോപ്പോളജി പരിഗണിക്കുന്ന മറ്റൊരു പ്രശ്നം പ്രതലങ്ങളെ സംബന്ധിച്ചുള്ളതാണ്. പ്രതലങ്ങളും വര്‍ഗീകരണം ഉള്‍പ്പെടെയുള്ള പ്രശ്നങ്ങളും കാര്യക്ഷമമായി ഈ ശാഖയില്‍ കൈകാര്യം ചെയ്യുന്നുണ്ട്. ജ്യാമിതീയ ടോപ്പോളജി എന്ന പേരിലും ഈ ശാഖ അറിയപ്പെടുന്നു.
(ഡോ. എസ്. മാധവന്‍, ഡോ. എ.ആര്‍. രാജന്‍)
