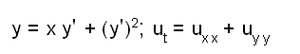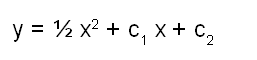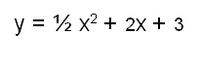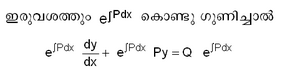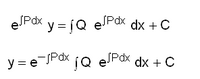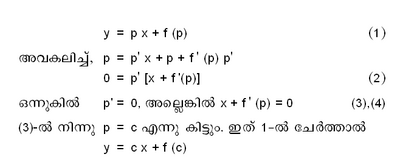This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അവകലസമവാക്യം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
ഉള്ളടക്കം[മറയ്ക്കുക]
|
അവകലസമവാക്യം
Differential equation
ഒരു ഗണിതശാസ്ത്രശാഖ. ഫലനങ്ങളും അവയുടെ അവകലജങ്ങളും (dirivatives) തമ്മിലുള്ള ബന്ധത്തെ കുറിക്കുന്ന സമവാക്യം. സാധാരണ അവകല സമവാക്യങ്ങള് (Ordinary Differential Equations), ആംശിക അവകല സമവാക്യങ്ങള് (Partial Differential Equations) എന്നീ വിഭാഗങ്ങളായി അവകല സമവാക്യങ്ങളെ തരം തിരിക്കാവുന്നതാണ്.
ആമുഖം
y = f(x) അഥവാ u = f(x,y,.....t) എന്ന ഒന്നോ അതിലധികമോ ചരങ്ങളുടെ ഒരു ഫലനം നേരിട്ടറിവില്ല; എന്നാല് ളന്റെ അവകലജങ്ങള് ഒരു സമവാക്യം അനുസരിക്കുന്നു എന്നറിയാം; ഈ നിലയില് ഫലനം കണ്ടുപിടിക്കേണ്ട ആവശ്യം ശുദ്ധഗണിതത്തിലും പ്രയുക്തഗണിതത്തിലും പലപ്പോഴും ഉദ്ഭവിക്കുന്നു. ഉദാ. ഒരു വക്രത്തിന്റെ വക്രതാ-ആരം (radius of curvature) തന്നിരുന്നാല് വക്രം കാണുക; ഒരു വസ്തുവിന്റെ സ്ഥാനവും പ്രവേഗവും ത്വരണ(acceleration)വും തമ്മില് ബന്ധിപ്പിക്കുന്ന ഒരു സമവാക്യത്തില്നിന്നും അതിന്റെ ഗതി നിര്ണയിക്കുക; ഒരു റേഡിയോ ആക്ടീവ് പദാര്ഥത്തിന്റെ ക്ഷയനിരക്ക് അറിയാമെങ്കില് അര്ധായൂസ് കാണുക; തുടങ്ങിയ പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യാന് അവകല സമവാക്യങ്ങള് പ്രയോജനപ്പെടുന്നു.
ഒരു സ്വതന്ത്രചരം മാത്രമുള്ള അവകല സമവാക്യങ്ങളെ [ഉദാ:y = f(x)] സാധാരണ അവകല സമവാക്യങ്ങള് എന്നു പറയുന്നു. ഈ സമവാക്യങ്ങളുടെ സാമാന്യരൂപം F(x,y,y',y",y"'....y(n) = 0 എന്നാണ്. ്y യുടെ അവകലജങ്ങളാണ് y',y",y"'....y(n)
രണ്ടോ അതില് കൂടുതലോ സ്വതന്ത്ര ചരങ്ങളുള്ള അവകല സമവാക്യങ്ങളെ [ഉദ. u = f(x,y,...,t)] ആംശിക അവകല സമവാക്യങ്ങള് എന്നാണ് പറയുന്നത്. ഇവയുടെ സാമാന്യരൂപം F(x,y,u,ux,y,uxx,uxy= +uyy)= 0 അവകലജ കോടി (order), രണ്ട് ആയിട്ടുള്ളതും x,y എന്നീ രണ്ട് സ്വതന്ത്രചരങ്ങളുള്ളതുമായ സമവാക്യത്തിന്റെ സാമാന്യരൂപമാണിത്.
എന്നിവ u എന്ന ഫലനത്തിന്റെ ആംശിക അവകലജങ്ങളാണ്.
ഒന്നിലധികം ഫലനങ്ങളുടെ അവകലജങ്ങള് ഉള്പ്പെട്ട സമവാക്യ വ്യൂഹങ്ങളും ഉണ്ടാകാം. അവ യൗഗപദിക (simultaneous) അവകല സമവാക്യങ്ങള് എന്നറിയപ്പെടുന്നു.
ഒരു അവകലസമവാക്യത്തിലുള്ള അവകലജങ്ങളില് ഏറ്റവും ഉയര്ന്ന അവകലജകോടി ആണ് ആ വാക്യത്തിന്റെ കോടി.
എന്നിവയുടെ കോടി ക്രമത്തില് 1, 2 ആണ്. (അവകലസമവാക്യങ്ങള്ക്ക് ഡിഗ്രിയും നിര്വചിക്കാറുണ്ട്; അതത്ര പ്രധാനമല്ല).
അവകലസമവാക്യം അനുസരിക്കുന്ന ഫലനങ്ങള് കണ്ടുപിടിക്കുന്ന ക്രിയയ്ക്ക് നിര്ധാരണം (solving) എന്നും നിര്ധരിച്ചു കിട്ടുന്ന ഫലത്തിനു നിര്ധാരം (solution) എന്നും പറയുന്നു.
നിര്ധാരണ തത്ത്വങ്ങള്
ആദ്യം സാധാരണ അവകല സമവാക്യങ്ങള് ചര്ച്ച ചെയ്യാം. ഒരു n-ാം കോടി സമവാക്യത്തിന്റെ നിര്ധാരണത്തില് n സമാകലന (integration) ക്രിയകള് അന്തര്ഭവിച്ചിരിക്കുന്നു; ഓരോ സമാകലനവും ഓരോ അനിയതസ്ഥിരം (arbitrary constant) കൊണ്ടുവരികയും ചെയ്യും. അതിനാല് n-ാം കോടി സമവാക്യത്തിന്റെ നിര്ധാരത്തില് n സ്വതന്ത്ര അനിയത സ്ഥിരങ്ങള് ഉള്പ്പെട്ടിരിക്കും.
[y = f(x,c1,c2.....,cnഎന്നപോലെ]. ഈ സാമാന്യനിര്ധാരം (General solution) ഒരൊറ്റ ഫലനമല്ല, ഒരു ഫലനകുലം (family of function) ആണ്. ഉദാ. y11 = x എന്നു തന്നിരുന്നാല് നേരെ രണ്ടു സമാകലനംമൂലം
എന്നു സാമാന്യനിര്ധാരം കിട്ടും. അനിയതസ്ഥിരങ്ങള്ക്കു വില സ്വീകരിച്ചാല് കിട്ടുന്ന ഓരോ ഫലനവും സമവാക്യത്തിന്റെ ഒരു വിശേഷനിര്ധാരം (Particular solution) ആണെന്നു പറയുന്നു. മേല് ഉദാഹരണത്തില് c1 = 2, c2 = 3 എന്നു സ്വീകരിച്ചാല്
എന്ന് ഒരു വിശേഷനിര്ധാരം കിട്ടുന്നു. ഇവിടെ സാമാന്യനിര്ധാരത്തില്പ്പെടാത്ത യാതൊരു ഫലനവും സമവാക്യം അനുസരിക്കയില്ലെന്ന് ഏറെക്കുറെ സ്പഷ്ടമാണ്.
എന്നാല് എല്ലാ അവകലസമവാക്യങ്ങളും ഇങ്ങനെ നേരെ സമാകലിച്ചു നിര്ധരിക്കാവുന്നവയല്ല. ആ സ്ഥിതിയില് ി അനിയതസ്ഥിരങ്ങള് ഉള്പ്പെട്ട സാമാന്യനിര്ധാരം കിട്ടിയാലും, അതില്പ്പെടാത്ത മറ്റു നിര്ധാരങ്ങള് ഇല്ലെന്നു തീരുമാനിച്ചുകൂടാ; ഉണ്ടാകാം എന്നു താഴെ ഒരു ഉദാഹരണത്തില് കാണാം.
ഭൗതികശാസ്ത്രങ്ങളില് അവകലസമവാക്യങ്ങള് ഉപയോഗിക്കുന്നിടത്തെല്ലാംതന്നെ സാമാന്യനിര്ധാരമല്ല, ചില വ്യവസ്ഥകള് അനുസരിക്കുന്ന വിശേഷനിര്ധാരങ്ങള് ആണ് ആവശ്യം. ഉദാ. ഒരു രേഖയില് സഞ്ചരിക്കുന്ന കണത്തിന്റെ ത്വരണം മ എന്നു തന്നിരുന്നാല് അതിന്റെ ഗതി നിര്ണയിക്കാന്
എന്നു കണ്ടുവച്ചതുകൊണ്ടായില്ല; b,c എന്നിവ നിശ്ചയിക്കാന് വേണ്ട ദത്തങ്ങള് (data) കൂടി വേണം. t = 0 എന്ന നിമിഷത്തില് അതായത് ആരംഭത്തില്, s = d, s' = v എന്നു കണത്തിന്റെ സ്ഥാനവും പ്രവേഗവും അറിയാമെങ്കില്
എന്നു നിര്ണയിക്കാം. d,v എന്നിവയെ ഇവിടെ പ്രാരംഭവിലകള് (initial values) എന്നും; ഇവ ശരിയായി വരുന്ന നിര്ധാരം കണ്ടുപിടിക്കുന്നതിലുള്ള പ്രശ്നങ്ങളെ 'പ്രാരംഭ വിലപ്രശ്നങ്ങള്' എന്നും പറയുന്നു (ആംശിക അവകലസമവാക്യങ്ങളെ സംബന്ധിച്ചാകുമ്പോള് അതിര്വിലകള് -Boundary valuesഎന്നു പറയുകയാണ് പതിവ്).
അസ്തിത്വ പ്രമേയങ്ങള്
എല്ലാ അവകലസമവാക്യങ്ങള്ക്കും നിര്ധാരം ഉണ്ടായിരിക്കണമെന്നില്ല; സമവാക്യം അനുസരിക്കുന്ന യാതൊരു ഫലനവും ഇല്ലെന്നുവരാം.
എന്നു ശരിയാകുന്ന യാതൊരു y-ഉം ഇല്ല; കാരണം, അവകലജത്തിന് അവശ്യം ഉണ്ടായിരിക്കേണ്ട ഇടവില സ്വഭാവം (intermediate value property) സിഗ്നം ഫലനത്തിനില്ല. (x-ന്റെ വില 0 ത്തെക്കാള് വലുതാണെങ്കില് 1 ഉം, 0 ത്തെക്കാള് ചെറുതാണെങ്കില് 1 ഉം, 0 ആണെങ്കില് 0 ഉം വിലവരുന്ന ഫലനത്തെ സിഗ്നം x എന്നു പറയുന്നു). ഇത്തരം പ്രത്യുദാഹരണങ്ങള് എടുത്തുകാട്ടാനുണ്ടെന്നല്ലാതെ സാധാരണ കൈകാര്യം ചെയ്യേണ്ടിവരുന്നവയല്ലെങ്കിലും, അവകലസമവാക്യങ്ങള്ക്കു നിര്ധാരം ഉണ്ടായിരിക്കാന് വേണ്ട വ്യവസ്ഥകള് അറിഞ്ഞിരിക്കേണ്ടത് സിദ്ധാന്തദൃഷ്ടിയില് ആവശ്യമാണ്. ഇത്തരം വ്യവസ്ഥകള് നിര്ദേശിക്കുന്ന പ്രമേയങ്ങള് അസ്തിത്വപ്രമേയങ്ങള് (Existence theorems) എന്നറിയപ്പെടുന്നു. അതുപോലെതന്നെ തന്നിരിക്കുന്ന പ്രാരംഭവ്യവസ്ഥകള് അനുസരിക്കുന്ന നിര്ധാരം ഒന്നിലധികമില്ലെന്ന് ഉറപ്പു വരുത്തുന്ന പ്രമേയങ്ങളും വേണ്ടിവരും. ഇവയ്ക്ക് ഏകമാത്രതാ പ്രമേയങ്ങള് (Uniqueness theorems) എന്നു പറയുന്നു.
17-ാം ശ.-ത്തില് ന്യൂട്ടനും ലൈബ്നിസും കലനം എന്ന ഗണിതശാഖ വളര്ത്തിയെന്നു പറയപ്പെടുന്ന കാലം മുതല് അവകല സമവാക്യങ്ങള് പഠിച്ചും ഉപയോഗിച്ചും പോന്നിരുന്നെങ്കിലും 1820-ല് ആണ് ആദ്യമായി ഒരു അസ്തിത്വപ്രമേയം സ്ഥാപിക്കപ്പെട്ടത്. കോഷി എന്ന ഗണിതശാസ്ത്രജ്ഞനാണ് ഇതിന്റെ ഉപജ്ഞാതാവ്. പിന്നീട് നിര്ധാരണരീതികള് പോലെതന്നെ ഏകമാത്രതാ അസ്തിത്വപ്രമേയങ്ങളും അവകലസമവാക്യപഠനത്തില് പ്രാധാന്യം അര്ഹിക്കുന്നു.
നിര്ധാരണം
ഏത് അവകല സമവാക്യവും നിര്ധരിക്കാന് തക്ക യാതൊരു സാമാന്യരീതിയും ഇല്ല. ഒട്ടേറെ മാനകരൂപങ്ങള്ക്ക് നിര്ധാരണരീതികള് ഏര്പ്പെടുത്തിയിട്ടുണ്ട്. മറ്റുള്ളവയ്ക്കു മനോധര്മത്തെ ആശ്രയിക്കയേ തരമുള്ളു. പ്രായോഗിക പ്രശ്നങ്ങളില് ഏകദേശനം (approximation) വഴി ഇഷ്ടഫലനം (desired function) കാണാനുള്ള രീതികളും ആവിഷ്കരിക്കപ്പെട്ടിട്ടുണ്ട്.
ഒന്നാം കോടി സമവാക്യങ്ങള്
ഒന്നാം കോടി സമവാക്യത്തിന്റെ സാമാന്യരൂപം F(x,y,y') = 0 എന്നാണ്. നിര്ധരിച്ച് y' കാണാമെങ്കില്, y' = f (x,y) എന്ന രൂപം കിട്ടും. ഈ സാമാന്യരൂപത്തില് ഒന്നാം കോടി സമവാക്യം പോലും നിര്ധരിക്കാന് മാര്ഗമില്ല. ചില പ്രത്യേക രൂപത്തിലുള്ളവയ്ക്കു നിര്ധാരണരീതികള് താഴെ സൂചിപ്പിക്കുന്നു.
ചരങ്ങള് വേര്പെടുത്താവുന്നവ
M dx = N dy,M x-ന്റെ ഫലനം, N y യുടെ ഫലനം. ഇതാണ് സമവാക്യം എങ്കില്, നേരെ സമാകലിച്ച്
എന്നു കാണാം. ഇവിടെ വരുന്ന സമാകലങ്ങള് സാധാരണ ഫലനങ്ങളായി എഴുതുന്നത് ക്ളേശകരമോ, ചിലപ്പോള് അസാധ്യമോ, ആണെന്നു വരാം. എങ്കിലും, നിര്ധാരം സമാകലരൂപത്തില് എഴുതാന് കഴിഞ്ഞാല് നിര്ധാരണം ഏറെക്കുറെ പൂര്ത്തിയായി. ആവശ്യമെങ്കില് സമാകലലക്ഷണങ്ങള് ഉപയോഗിച്ച് സംഖ്യാത്മകരീതിയില് നിര്ധാരഫലനത്തെപ്പറ്റി അറിയേണ്ട കാര്യങ്ങള് ഏകദേശം കാണുകയും ചെയ്യാം. ഇതിനും പുറമേ പലപ്പോഴും y = f(x,c)എന്നു പ്രത്യക്ഷഫലനരൂപത്തില് നിര്ധാരം എഴുതാന് കഴിഞ്ഞില്ലെന്നു വരാം. f(x,y,c) = 0 എന്ന് x-ന്റെ പരോക്ഷഫലനമായിട്ട് y കണ്ടാലും നിര്ധാരണം പൂര്ത്തിയായി എന്നു കരുതാം.
ഒരു ചരം പ്രത്യക്ഷത്തില് ഉള്പ്പെടാത്തവ
y'=f(x)അഥവാ y' = f(y). ഇവിടെ ചരങ്ങള് വേര്പെടുത്താന് കഴിയുന്നു.
രേഖീയ രൂപം
Linear Form y' + Py = Q;P,Q xന്റെ ഫലനങ്ങള്. ഇഷ്ടഫലനവും അവകലജവും രേഖീയ ചേരുവ(linear combination)യില് മാത്രം വരുന്നതാണ് രേഖീയം എന്ന പേരിനു ഹേതു; ചേരുവയിലെ ഗുണാങ്കങ്ങള് x-ന്റെ മാത്രം ഫലനങ്ങളായിരിക്കയും വേണം. ഇവിടെ
എന്നാകും. ഇടതുവശത്തെ രണ്ടാമത്തെ പദം y യുടെ അവകലജമാണ്; വലതുവശം x-ന്റെ മാത്രം ഫലനവും. അതിനാല് സമാകലിച്ച്,
എന്ന് സാമാന്യനിര്ധാരം ഉണ്ടാക്കുന്നു. തന്ന സമവാക്യം നേരെ സമാകലിക്കാന് ഇവിടെ നിവൃത്തിയില്ല. കാരണം, ഇടതുവശത്ത് xഉം x-ന്റെ അജ്ഞാതഫലനം y-ഉം ഉള്പ്പെട്ടിരിക്കുന്നു. എന്നാല് കൊണ്ടു ഗുണിച്ചുകഴിഞ്ഞാല്, y എന്തായാലും, ഇടതുവശം നേരെ സമാകലിക്കാവുന്ന രൂപത്തിലായി. ഇത്തരം ഗുണകങ്ങള്ക്ക് സമാകലനഗുണകങ്ങള് (integrating factor) എന്നാണ് പേര്.
ബെര്ണോലി സമവാക്യം എന്നു പേരുള്ള
എന്ന രൂപം z = y1-nഎന്ന ചരം-മാറ്റം (transformation) മൂലം രേഖീയ രൂപത്തിലാക്കി നിര്ധരിക്കാം.
സമഘാത (Homogeneous) സമവാക്യം
M dy = N dx,M,N എന്നിവ രണ്ടും ഒരേ ഡിഗ്രിയിലുള്ള x,y-യുടെ സമഘാതഫലനങ്ങള്. ഇത് y= vx എന്ന പ്രതിഷ്ഠാപനം (substitution) മൂലം ചരങ്ങള് വേര്പെടുത്താവുന്ന രൂപത്തിലാക്കി നിര്ധരിക്കാം.
ക്ളേയ്റോ സമവാക്യം
y = p x + f(p),p = y' (ഇവിടെ p എന്നത് എഴുതാന് സൌകര്യത്തിനുവേണ്ടി മാത്രമാണു സ്വീകരിക്കുന്നത്).
എന്ന സാമാന്യനിര്ധാരം സിദ്ധിക്കുന്നു. അതേ സമയം, (1), (4) എന്നിവയില്നിന്ന് p ഒഴിവാക്കിയാല് കിട്ടുന്ന ഫലവും ഒരു നിര്ധാരം ആണ്. ഇതാണ് വിചിത്ര നിര്ധാരം (Singular solution). സാമാന്യനിര്ധാരത്തില് c-യ്ക്ക് വില സ്വീകരിച്ചാല് കിട്ടാവുന്നതല്ല വിചിത്രനിര്ധാരം എന്ന് താഴെ ചേര്ക്കുന്ന ഉദാഹരണം വ്യക്തമാക്കുന്നു.
സാമാന്യനിര്ധാവും വിചിത്രനിര്ധാരവും തമ്മിലുള്ള ബന്ധം മനസ്സിലാക്കാന് ജ്യാമിതീയ ചിത്രണം പ്രയോജനപ്പെടുത്താം.താഴെവരുന്ന അസ്ത്ത്വപ്രമേയത്തിലെന്നപോലെ പലപ്പോഴും പ്രതിപാദനസൗകര്യത്തിനുവേണ്ടി ജ്യാമതീയഭാഷ ഉപയോഗ്ക്കാറുണ്ട്.(M)ഒരു രേഖാ-കുലത്തെയാണ് കുറിക്കുന്നത്.ആദിബിന്ദുവില് നിന്ന് എല്ലാ രേഖകളുടെയും ദൂരം a ആണ്.അതിനാല്(N)കുറിക്കുന്ന വൃത്തം രേഖാകുലത്തിന്റെ ആവരണം(Envelope)ആണെന്നു വരുന്നു.(M)എന്ന കുലത്തിന്റെ ആവരണം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയും(L)എന്ന സമവാക്യത്തിന്റെ വിചിത്രനിര്ധാരം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയും താരതമ്യപ്പെടുത്തി നോക്കിയാല് സാരാംശത്തില് രണ്ടും ഒന്നുതന്നെയാണ്,ലിപികള് മാത്രമേ വ്യത്യാസമുള്ളു.വിചിത്ര നിര്ധാരത്തിന്റെ നിര്വചനം തന്നെ 'സാമാന്യനിര്ധാരം കുരിക്കുന്ന വക്രകുലത്തിന്റെ ആവരണം'.എന്നാണ്;ആവരണം ഇല്ലെങ്കില് വിചിത്രനിര്ധാരവും ഇല്ല.
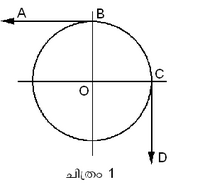
സാമാന്യനിര്ധാരം, വിചിത്രനിര്ധാരം എന്നിവ കൂടാതെ സാമാന്യനിര്ധാരത്തില്പ്പെട്ട വിശേഷനിര്ധാരങ്ങളുടെയും വിചിത്രനിര്ധാരത്തിന്റെയും അംശങ്ങള് യഥായോഗ്യം കൂട്ടിയിണക്കി എത്ര നിര്ധാരങ്ങള് വേണമെങ്കിലും കെട്ടിച്ചമച്ചെടുക്കാം. ഉദാ. ചിത്രം 1-ല് കാണുന്നപോലെ ക്രമത്തില് AB,BC,CD എന്ന അര്ധരേഖ വൃത്തപാദം, അര്ധരേഖ എന്നിവ കൂട്ടിച്ചേര്ത്താല് കിട്ടുന്ന വക്രത്തില് എവിടെയും (L) ശരിയാകും. അതുകൊണ്ട് ആ വക്രവും ഒരു നിര്ധാരത്തെ കുറിക്കുന്നു.
ഒന്നാം കോടി സമവാക്യത്തെ സംബന്ധിച്ച ഒരു ഏകമാത്രാസ്തിത്വപ്രമേയം, മാതൃക എന്ന നിലയില്, പ്രസ്താവിക്കുക മാത്രം ചെയ്യാം; ഉപപത്തി വിട്ടുകളയുന്നു.
എന്നൊക്കുന്ന ഒരു k ഉണ്ട്, എങ്കില്, (x0,y0) R-ലെ ഏതൊരു ആന്തരിക ബിന്ദു ആയാലും y1 = f(x,y) എന്ന അവകല സമവാക്യത്തിന് x0,y0 ല്കൂടി പോകുന്ന ഒരു ഏകമാത്ര നിര്ധാരം ഉണ്ട്.
(2)-ലുള്ള വ്യവസ്ഥയെ ലിപ്ഷിത്സ് (Lipschitz) വ്യവസ്ഥ എന്നു പറയുന്നു. R-ല് fyസന്തതമാണെങ്കില് ഈ വ്യവസ്ഥ തീര്ച്ചയായും നിറവേറും; അല്ലെങ്കിലും നിറവേറിയെന്നു വരാം.
അസ്തിത്വപ്രമേയങ്ങള് കൊണ്ടുള്ള നേട്ടത്തിന് ഒരുദാഹരണം:
എന്ന റിക്കാറ്റി (Riccati) സമവാക്യം സാമാന്യരൂപത്തില് നിര്ധരിക്കാന് ഒരു വഴിയും ഇതുവരെ അറിവില്ല. എങ്കിലും ഇതിന്റെ നിര്ധാരങ്ങളെക്കുറിച്ചു പല പ്രമേയങ്ങളും ഉണ്ട്.
(ഏതെങ്കിലും നാലു നിര്ധാരങ്ങളായ വജ്രാനുപാതം-cross-ratio- സ്ഥിരമാണെന്നും മറ്റും). അസ്തിത്വപ്രമേയം മൂലം P,Q,R സന്തതമായിരിക്കുമ്പോഴെങ്കിലും, അതിനു നിര്ധാരം ഉണ്ടെന്നു തെളിയുന്നു.
ഒന്നിനുമേല് കോടി സമവാക്യങ്ങള്
ഈ വകുപ്പില് ഏറ്റവും കൂടുതല് ഉപയോഗത്തില് വരുന്നതും പഠനവിഷയമായിട്ടുള്ളതും രേഖീയ സമവാക്യങ്ങളാണ്. ഒന്നാം കോടിക്കു രേഖീയത നിര്വചിച്ചപോലെതന്നെയാണ് രേഖീയതയുടെ സാമാന്യനിര്വചനം; അവകലജങ്ങള് ഒന്നിനുമേല് കോടിയിലുള്ളവയും വരാമെന്നു മാത്രം.
എന്നാണ് n-ാം കോടി രേഖീയ സമവാക്യത്തിന്റെ സാമാന്യരൂപം. പ്രതിപാദനസൌകര്യം പ്രമാണിച്ച്, ഇവിടെ രണ്ടാം കോടി സമവാക്യമാണു ചര്ച്ച ചെയ്യപ്പെടുന്നതെങ്കിലും പ്രമേയങ്ങളെല്ലാംതന്നെ, സാമാന്യവത്കരിച്ചാല്, ഏതു കോടിക്കും ശരിയാകും.
എന്നത് L(y) = Q എന്നെഴുതിയാല് L രേഖീയ കാരകം (Linear Operator) ആണ്. ഘ L(y) = 0 എന്നത് L(y) = Q -നോട് ബന്ധപ്പെട്ട സമഘാത രേഖീയ സമവാക്യം ആണെന്നു പറയുന്നു. ഇത് Q = 0 എന്നാകുമ്പോഴുള്ള വിശേഷസ്ഥിതി ആണെന്നും കരുതാം.
രണ്ടാം കോടി രേഖീയ സമവാക്യങ്ങള്ക്ക് ഒരു ഏകമാത്രാസ്തിത്വപ്രമേയം താഴെ പറയുന്നു:
I എന്ന സാന്ത(finite)മോ അനന്തമോ ആയ തുറന്ന അന്തരാള(open interval)ത്തില് P1,P2,Q സന്തതമാണ്;x0 I-ലെ ഒരു ബിന്ദുവും സ0, സ1 തന്നിട്ടുള്ള സംഖ്യകളും ആണ്, എങ്കില്
L(y) = Q എന്നതിന് Φ(x0) = k0,Φ'(x0) =k1 എന്ന പ്രാരംഭ വ്യവസ്ഥകള് അനുസരിക്കുന്ന ഒരു ഏകമാത്ര നിര്ധാരം y = Φ(x) ഉണ്ട്.
L(y) = 0 എന്നതിന്റെ നിര്ധാരം കാണുന്ന രീതി താഴെ വിവരിക്കുന്നു. ഗുണാങ്കങ്ങള് സന്തതമാണെന്നു സങ്കല്പിക്കേണ്ടതുണ്ട്: u1,u2 അതിന്റെ രണ്ടു നിര്ധാരങ്ങള് ആണെങ്കില്, c1,c2 എന്ന സ്ഥിരങ്ങള് എന്തായാലും, c1 u1 + c2 u2 എന്നതും ഒരു നിര്ധാരമാണ്; മറിച്ച് u1,u2 രേഖീയമായി അനാശ്രിതമാണെങ്കില്, y = c1 u1 +c2 u2എന്നു വരത്തക്കവണ്ണം c1,c2 എന്ന സ്ഥിരങ്ങള് കാണാം.
ഇതില് ആദ്യഭാഗം L രേഖീയകാരകമായതുകൊണ്ട് സിദ്ധിക്കുന്നു; മറിച്ചുള്ള ഉപപത്തി വിട്ടുകളയുന്നു. നേരത്തെ നിര്വചിച്ച പ്രകാരം രണ്ട് അനിയത സ്ഥിരങ്ങള് ഉള്പ്പെടുത്തിയതിനാല് c1 u1 + c2 u2 സാമാന്യനിര്ധാരമാണ്. മാത്രമല്ല ഇതിലുള്പ്പെടാത്ത നിര്ധാരങ്ങള് ഇല്ലതാനും. രേഖീയ സമവാക്യങ്ങള്ക്ക് വിചിത്രനിര്ധാരമേ ഇല്ല.
I-ല് X0 എന്നൊരു ബിന്ദു സ്വീകരിച്ചാല്
u1(x0) = 0,u1'(x0) = 1,U2'(x0) = 0എന്ന പ്രാരംഭവ്യവസ്ഥകള് അനുസരിക്കുന്ന U1,U2 എന്ന രണ്ടു നിര്ധാരങ്ങള് L(y) = 0 ത്തിനുണ്ടെന്ന് അസ്തിത്വപ്രമേയം മൂലം സിദ്ധിക്കും; ഇവ അനാശ്രിതമാണെന്നു തെളിയിക്കാനും സാധിക്കും.
ഇങ്ങനെL(y) = 0 ത്തിനു രണ്ടു വിശേഷനിര്ധാരങ്ങള് ഉണ്ടെന്നും അവയില്നിന്നു സാമാന്യനിര്ധാരം കാണാമെന്നും അറിയാമെങ്കിലും ഇത്തരം ഏതൊരു സമവാക്യത്തിനും രണ്ടു വിശേഷനിര്ധാരങ്ങള് കാണാന് പര്യാപ്തമായ രീതികളൊന്നുമില്ല. പരീക്ഷിച്ചു നോക്കി നിര്ധാരങ്ങള് കാണാന് കഴിഞ്ഞെന്നു വരാം. എന്നാല്
എന്നതില് a1,a2 എന്നിവ സ്ഥിരങ്ങളാണെങ്കില് രണ്ട് അനാശ്രിത നിര്ധാരങ്ങള് തീര്ച്ചയായും കാണാം.
ആയിത്തീരും. er x പൂജ്യമാകാത്തതിനാല്,
എന്ന വര്ഗിക സമവാക്യം ഉണ്ടാകുന്നു. ഈ സമവാക്യത്തിന്റെ മൂലങ്ങള് r1 ,r2എന്നാണെങ്കില് Screen short എന്ന അനാശ്രിത നിര്ധാരങ്ങളും തന്മൂലം
എന്ന സാമാന്യനിര്ധാരവും കിട്ടുംr1 ,r2 എന്നിവ തുല്യമോ മിശ്രസംഖ്യകളോ ആണെങ്കില് ചില പ്രത്യേക ഉപായങ്ങള് വേണ്ടിവരുന്നവ എടുത്തുപറയുന്നില്ല. ഈ സ്ഥിതിയില് നിര്ധാരത്തില് ഘാതാങ്കീയ (exponential) ഫലനത്തിനു പുറമേ ഘാതങ്ങളോ അഥവാ വൃത്തീയ (circular) ഫലനങ്ങളോ ഉള്പ്പെട്ടിരിക്കും.
(c1 + c2X)eax അഥവാ (c1cos β x + c2 sin β x)eax എന്ന പോലെ. അങ്ങനെ L (y) = 0 ത്തിന്റെ സഹായക (Auxiliary) സമവാക്യം എന്നു വിളിക്കപ്പെടുന്ന (T) നിര്ധരിച്ചാല് L(y) = 0 ത്തിന്റെ സാമാന്യനിര്ധാരം കാണാം. അവകലസമവാക്യത്തിന്റെ കോടി n ആണെങ്കില് സഹായകസമവാക്യം n-ാം ഡിഗ്രി ആയിരിക്കും; അതു നിര്ധരിക്കാന് ഏകദേശനം ആണ് മാര്ഗം.
അസമഘാത സമവാക്യം
L(y) = Q എന്നതിന്റെ ഒരു വിശേഷ നിര്ധാരം y1 സാമാന്യനിര്ധാരം
എന്നിവ അറിയാമെങ്കില് അതിന്റെ സാമാന്യനിര്ധാരം ∈+ y1 ആയിരിക്കും.
അങ്ങനെ ø + y1 , L (y) = Q ന്റെ നിര്ധാരമാണ്. ഏതു നിര്ധാരവും ഇതില് ഉള്പ്പെട്ടിരിക്കയും ചെയ്യും. കാരണം,y2 ഏതെങ്കിലുമൊരു നിര്ധാരമാണെങ്കില്
L(y) = Q ന്റെ ഒരു വിശേഷനിര്ധാരംy1 കാണുക എന്ന പ്രശ്നം അവശേഷിക്കുന്നു. മിക്കപ്പോഴും പരീക്ഷിച്ചുനോക്കി ഒരു നിര്ധാരം കാണാന് കഴിയും. L(y) = 0 ത്തിനു കണ്ടുപിടിച്ചിട്ടുള്ള u1 + u2എന്ന രണ്ടു നിര്ധാരങ്ങളില്നിന്ന് ഒരു y1 കാണാനും വഴിയുണ്ട്.
ചില പ്രത്യേക രണ്ടാം കോടി സമവാക്യങ്ങള്
സരള ഹാര്മോണിക സമവാക്യം
ചിത്രം:Screen Short എന്ന സഹായക സമവാക്യം നിര്ധരിച്ച് y = c1 cos kx + c4 sin kx എന്നു സാമാന്യ നിര്ധാരം കാണാം. പ്രാരംഭവിലകള് തന്നിരുന്നാല് c1 , c2 നിശ്ചയിക്കുകയും ചെയ്യാം.
ലീഷാണ് (Legendre) സമവാക്യം
ഇതിന്റെ നിര്ധാരം ഘാതശ്രേണീരൂപത്തില് കാണാം. ലീഷാണ് ബഹുപദങ്ങള് എന്നറിയപ്പെടുന്ന ഈ ബഹുപദനിര്ധാരങ്ങള് പ്രസിദ്ധമാണ്. n-ാം ഡിഗ്രി ലീഷാണ് ബഹുപദത്തെ Pn (x) എന്നു കുറിച്ചാല്
എന്നീ ഫലങ്ങള് കിട്ടുന്നതാണ്. ലീഷാണ് ബഹുപദങ്ങള് എല്ലാം ചേര്ന്നാല് ഒരു ലംബികവ്യൂഹം (Orthogonal system) ആണെന്നു (2)-ല് നിന്നു മനസ്സിലാക്കാം. ഈ ലക്ഷണപ്രകാരം ഇവ ബഹുപദീയ ഏകദേശന (Polynomial approximation) സിദ്ധാന്തത്തില് പ്രമുഖസ്ഥാനം വഹിക്കുന്നു.
ബെസെല് (Bessel) സമവാക്യം
ഇതും ശ്രേണീരൂപത്തില് നിര്ധരിക്കാം. ബെസെല് ഫലനങ്ങള് എന്നറിയപ്പെടുന്ന ഇതിന്റെ നിര്ധാരങ്ങള് ഭൌതികശാസ്ത്രത്തില് പലയിടത്തും ഉപയോഗിക്കുന്നുണ്ട്. ഈ ഫലനങ്ങള്ക്കു പട്ടികകകള്തന്നെ പ്രസിദ്ധം ചെയ്തിട്ടുള്ളത് അവയുടെ പ്രയോഗ പ്രചാരം കാണിക്കുന്നു.
അതിഗുണോത്തര (Hyper Geometric) സമവാക്യം
ഇതും ശ്രേണീരൂപത്തിലാണു നിര്ധരിക്കുന്നത്. ഈ ശ്രേണീക്ക് അതിഗുണോത്തരശ്രേണി എന്നു പറയുന്നു. ഗണിതത്തിലെ ദ്വിപദീയം (binomial), ഘാതാങ്കീയം (exponential), ലോഗരിതീയം (logarithmic) മുതലായ ചില പ്രധാനപ്പെട്ട ശ്രേണികളും ഇതിന്റെ വിശേഷസ്ഥിതികളായി വരുത്താം.
ആംശിക (Partial) അവകലസമവാക്യങ്ങള്
സാധാരണ സമവാക്യങ്ങളുടെ നിര്ധാരത്തില് അനിയതസ്ഥിരങ്ങള് വരുന്നതിനു പകരം ആംശിക സമവാക്യങ്ങള്ക്ക് അനിയതഫലനങ്ങളാണ് വരുന്നത്. ഉദാ.x,y എന്നീ സ്വതന്ത്രചരങ്ങളും ux = 0 എന്നും തന്നിരുന്നാല്, u = φ(y) എന്നാകുന്നു. ഇവിടെ φ അനിയതഫലനം ആണ്.uxy = 0 എന്നായാല്,
എന്ന നിര്ധാരം ഉണ്ടാകുന്നു. ഇതില് എന്നിവ അനിയതഫലനങ്ങള് ആണ്. അതുപോലെതന്നെ പ്രാരംഭവ്യവസ്ഥകള് ചില പ്രത്യേക ബിന്ദുക്കളില് u ന്റെയോ അവകലജങ്ങളുടെയോ വില ആയിട്ടല്ല, ചില പ്രദേശങ്ങളുടെ അതിര്ത്തിയില് ഉടനീളം അവയുടെ വിലകള് നിജപ്പെടുത്തുന്ന നിശ്ചിത ഫലനങ്ങളായിട്ടാണു വരുന്നത്. ഉദാഹരണം (5) (i) ല് ചേര്ത്തിരിക്കുന്നു.
പ്രയോഗം-ഭൗതിക ധനതത്ത്വ ശാസ്ത്രങ്ങളില്
ഗണിതീയ ഭൗതികത്തില് അതിപ്രസിദ്ധങ്ങളായ മൂന്ന് അവകലസമവാക്യങ്ങള് താഴെ ചേര്ക്കുന്നു.
തരംഗ (Wave) സമവാക്യം
u tt = a2 uxxഇതിന്റെ ചില ഉപയോഗങ്ങളില് ഒന്ന്, രണ്ടറ്റം ഉറപ്പിച്ച് ഒരു തലത്തില് ചലിക്കാന് സ്വാതന്ത്ര്യമുള്ള ഒരു ചരടിന്റെ കമ്പനം പഠിക്കുന്നതിലാണ്. ചരടിന്റെ തലം (x,u) എന്ന സമതലവും t സമയവും ആണെന്നു സങ്കല്പിച്ചാല്,u = f (x,t ) (ചി. 2) എന്നു കണ്ടുപിടിക്കാം. എങ്കില് ഓരോ നിമിഷത്തിലും ചരട് ഏത് ആകൃതിയിലാണ് നില്ക്കുന്നത് എന്നറിയാം. അതിനുവേണ്ട പ്രാരംഭവ്യവസ്ഥകള് താഴെ പറയുന്നു.
(A)-ന്റെ അര്ഥം ചരടിന്റെ അറ്റങ്ങള് എപ്പോഴും ആ ബിന്ദുവിലും (1, o)-ത്തിലും നില്ക്കുന്നു എന്നാണ്. (B)ന്റെയാകട്ടെ ഒരു നിര്ദിഷ്ടനിമിഷത്തില് (ഇവിടെ t = 0) ചരടിന്റെ നിലയും അതിലെ ഓരോ ബിന്ദുവിന്റെയും പ്രവേഗവും നിജപ്പെടുത്തുന്നു.
ഊഷ്മചാലന (Heat Conduction) സമവാക്യം
ലപ്ളാസ് (Laplace) സമവാക്യം
ഇതിന്റെ നിര്ധാരങ്ങളെ ഹാര്മോണിക ഫലനങ്ങള് എന്നു പറയുന്നു.
(പ്രൊഫ. പി.സി. ജോസഫ്)