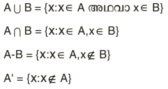This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗണസിദ്ധാന്തം(Set Theory)
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→Set Theory) |
(→Set Theory) |
||
| വരി 1: | വരി 1: | ||
==ഗണസിദ്ധാന്തം== | ==ഗണസിദ്ധാന്തം== | ||
| - | ==Set Theory== | + | ===Set Theory=== |
ആധുനിക ഗണിതശാസ്ത്രത്തിന്റെ മൗലികാധാരങ്ങളായി സ്വീകരിച്ചിട്ടുള്ള സംഘാതങ്ങളുടെ ബീജഗണിതം. പൊതുവേ ചില സവിശേഷതകളുള്ള ഏതാനും മൂലകാംഗങ്ങളുടെ കൂട്ടത്തെയാണ് ഗണിതീയമായി ഗണമെന്നു വ്യവച്ഛേദിക്കുന്നത്. ഗണങ്ങള്ക്ക് ആന്തരികമായും ബാഹ്യമായും പല സവിശേഷതകളുണ്ട്. യാദൃച്ഛികമായ മൂലകാംഗത്തിന്റെ സവിശേഷതകള് കണ്ടെത്താന് ശ്രമിച്ചിരുന്ന ക്ലാസ്സിക്കല് ഗണിതശാസ്ത്ര പ്രവര്ത്തനത്തില്നിന്നു ഭിന്നമായി ഗണങ്ങളുടെ സവിശേഷതകള് ആരായുന്ന രീതിയാണ് ആധുനിക ഗണിതശാസ്ത്രത്തില് കാണുന്നത്. സമൂഹത്തിന്റെ ഘടന, സമൂഹങ്ങള് തമ്മിലുള്ള ഗണിതീയബന്ധങ്ങള്, ഇവയില്നിന്ന് ഉരുത്തിരിഞ്ഞുവരുന്ന പ്രത്യേക ഘടനകള് എന്നിവയെല്ലാം ആധുനിക ഗണിതശാസ്ത്രത്തില് പ്രതിപാദിക്കുന്നു. | ആധുനിക ഗണിതശാസ്ത്രത്തിന്റെ മൗലികാധാരങ്ങളായി സ്വീകരിച്ചിട്ടുള്ള സംഘാതങ്ങളുടെ ബീജഗണിതം. പൊതുവേ ചില സവിശേഷതകളുള്ള ഏതാനും മൂലകാംഗങ്ങളുടെ കൂട്ടത്തെയാണ് ഗണിതീയമായി ഗണമെന്നു വ്യവച്ഛേദിക്കുന്നത്. ഗണങ്ങള്ക്ക് ആന്തരികമായും ബാഹ്യമായും പല സവിശേഷതകളുണ്ട്. യാദൃച്ഛികമായ മൂലകാംഗത്തിന്റെ സവിശേഷതകള് കണ്ടെത്താന് ശ്രമിച്ചിരുന്ന ക്ലാസ്സിക്കല് ഗണിതശാസ്ത്ര പ്രവര്ത്തനത്തില്നിന്നു ഭിന്നമായി ഗണങ്ങളുടെ സവിശേഷതകള് ആരായുന്ന രീതിയാണ് ആധുനിക ഗണിതശാസ്ത്രത്തില് കാണുന്നത്. സമൂഹത്തിന്റെ ഘടന, സമൂഹങ്ങള് തമ്മിലുള്ള ഗണിതീയബന്ധങ്ങള്, ഇവയില്നിന്ന് ഉരുത്തിരിഞ്ഞുവരുന്ന പ്രത്യേക ഘടനകള് എന്നിവയെല്ലാം ആധുനിക ഗണിതശാസ്ത്രത്തില് പ്രതിപാദിക്കുന്നു. | ||
Current revision as of 14:01, 18 ഏപ്രില് 2016
ഗണസിദ്ധാന്തം
Set Theory
ആധുനിക ഗണിതശാസ്ത്രത്തിന്റെ മൗലികാധാരങ്ങളായി സ്വീകരിച്ചിട്ടുള്ള സംഘാതങ്ങളുടെ ബീജഗണിതം. പൊതുവേ ചില സവിശേഷതകളുള്ള ഏതാനും മൂലകാംഗങ്ങളുടെ കൂട്ടത്തെയാണ് ഗണിതീയമായി ഗണമെന്നു വ്യവച്ഛേദിക്കുന്നത്. ഗണങ്ങള്ക്ക് ആന്തരികമായും ബാഹ്യമായും പല സവിശേഷതകളുണ്ട്. യാദൃച്ഛികമായ മൂലകാംഗത്തിന്റെ സവിശേഷതകള് കണ്ടെത്താന് ശ്രമിച്ചിരുന്ന ക്ലാസ്സിക്കല് ഗണിതശാസ്ത്ര പ്രവര്ത്തനത്തില്നിന്നു ഭിന്നമായി ഗണങ്ങളുടെ സവിശേഷതകള് ആരായുന്ന രീതിയാണ് ആധുനിക ഗണിതശാസ്ത്രത്തില് കാണുന്നത്. സമൂഹത്തിന്റെ ഘടന, സമൂഹങ്ങള് തമ്മിലുള്ള ഗണിതീയബന്ധങ്ങള്, ഇവയില്നിന്ന് ഉരുത്തിരിഞ്ഞുവരുന്ന പ്രത്യേക ഘടനകള് എന്നിവയെല്ലാം ആധുനിക ഗണിതശാസ്ത്രത്തില് പ്രതിപാദിക്കുന്നു.
ജര്മന് ഗണിതശാസ്ത്രജ്ഞനായ കാന്റോറാണ് ഗണസിദ്ധാന്തത്തിന്റെ ഉപജ്ഞാതാവ്. ക്ലിപ്തമായ അംഗസംഖ്യയുള്ള ഗണത്തെ സാന്തം(finite) എന്നും അല്ലാത്തതിനെ അനന്തം (infinite) എന്നും വിളിക്കുന്നു. സാന്തഗണങ്ങളെ സംബന്ധിച്ചിടത്തോളം സരളമായ പ്രശ്നങ്ങളേ ഗണിതത്തില് വരാറുള്ളൂ. എന്നാല് അനന്തമായവ അസംഖ്യം പ്രശ്നങ്ങളിലേക്കു ചൂണ്ടുന്നു.
കാര്ഡിനല്സംഖ്യ. അനന്തമായ ഗണങ്ങള് തമ്മില് സംഖ്യാബലത്തെ ആസ്പദമാക്കി താരതമ്യപ്പെടുത്തുമ്പോഴാണ് അനന്തത(infinity) എന്ന ആശയത്തിന്റെ ഗഹനതയെ നേരിടേണ്ടിവരിക. അതായത് അനന്തത എന്നത് ഒന്നല്ല, അതും അനന്തമാണ്. വലുപ്പച്ചെറുപ്പം വച്ചുനോക്കി അനന്തതകളെ ക്രമപ്പെടുത്തിയാല് ആ അനുക്രമം അനന്തമായിരിക്കും. ഈ രംഗത്താണ് കാന്റോര് ഏറെ സംഭാവന ചെയ്തിട്ടുള്ളത്.
ആദിവര്ഗക്കാരുടെ ജീവിതചര്യയില് നിന്നെടുത്ത ഒരു ആശയമാണ് ഒന്നിനൊന്ന് അനുയോഗം (one-to-one correspondence). എണ്ണാനറിയാത്ത അക്കാലത്ത് അവര് ആടുമാടുകളുടെ കണക്കെടുക്കുന്നത് ഒന്നിനുപകരം ഒരു കല്ലോ വടിക്കഷണമോ വച്ചായിരുന്നു. വൈകുന്നേരം തിരിച്ചെത്തുമ്പോള് ഒന്നിന് ഒന്ന് ഒത്തുനോക്കി ആടുമാടുകള് നഷ്ടപ്പെട്ടില്ലെന്നു ബോധ്യം വരുത്തുകയായിരുന്നു പതിവ്.
ഈ രീതി ഏതെങ്കിലും രണ്ടു ഗണത്തിലെ മൂലകാംഗങ്ങളെ താരതമ്യപ്പെടുത്താന് പ്രയോഗിച്ചാല് ഏതിലാണ് കൂടുതല് മൂലകാംഗങ്ങളുള്ളതെന്നും അതാണു വലിയ ഗണമെന്നും മനസ്സിലാക്കാം. ഈ രീതി അനന്തമായ ഗണങ്ങള്ക്ക് ആദ്യമായി പ്രയോഗിച്ചത് കാന്റോര് ആണ്. രണ്ടു ഗണങ്ങള്ക്ക് ഇപ്രകാരം തുല്യമായ മൂലകാംഗങ്ങളാണുള്ളതെങ്കില് ആ ഗണങ്ങളുടെ കാര്ഡിനല് സംഖ്യ സാന്തമോ അനന്തമോ ആകാം. 1, 2, 3, 4, 5 എന്നീ നിസര്ഗ സംഖ്യാഗണത്തിന്റെ കാര്ഡിനല്സംഖ്യ അനന്തതയാണ്. നിസര്ഗ സംഖ്യാഗണത്തിനോട് ഒന്നിനൊന്ന് അനുയോഗമുള്ള ഏതു ഗണത്തിന്റെയും കാര്ഡിനല്സംഖ്യ ഈ അനന്തത തന്നെയായിരിക്കും. No എന്നാണ് ഇതിന്റെ ചിഹ്നം. ഉദാ. 1, 4, 9..... എന്ന ഗണത്തിന്റെ കാര്ഡിനല് സംഖ്യ No തന്നെയാണ്. അടുത്ത അനന്തത 2No ആണെന്നു 1874-ല് കാന്റോര് ഗണിതീയമായി തെളിയിച്ചിട്ടുണ്ട്. അഥവാ No, 2No എന്നിവയുടെ ഇടയില് ഒരു അനന്തതപോലും ഇല്ലെന്നാണ് ഊഹം.
വലുപ്പച്ചെറുപ്പമനുസരിച്ച് ഗണങ്ങളെ ക്രമപ്പെടുത്താമെങ്കില്, ഒന്നു മറ്റൊന്നിനെക്കാള് വലുതാണെങ്കില്, അത് ഇതിന്റെ ഉപഗണമാണെന്നു പറയും. A,B-യെക്കാള് വലുതാണെങ്കില്, A ⊃ B എന്നും B,A-യെക്കാള് ചെറുതാണെങ്കില് B ⊂ A, എന്നും എഴുതുന്നു. A ⊃ B എ വലുത് ബി എന്നും B ⊂ A ബി ചെറുത് എ എന്നും വായിക്കാവുന്നതാണ്. ഇവിടെ B,A-യുടെ ഉപഗണം (subset) എന്നും പറയുന്നു. B,A-ക്കു തുല്യമാണെങ്കിലും ഗണിതീയമായി ആവശ്യാനുസരണം B,A-യുടെ ഉപഗണമാണെന്നു പറയാറുണ്ട് (ഇതില് B,A-യുടെ ഉപഗണവുമാണ്). വാസ്തവത്തില് തുല്യതയുടെ നിര്വചനം തന്നെ A വലുത് B, B വലുത് A എങ്കില് A=B എന്നോ; A ചെറുത് B, B ചെറുത് A എങ്കില് A=B എന്നോ ആണ്. കാര്ഡിനല് സംഖ്യകള് തുല്യമായിരിക്കുകയെന്നതാണ് ഗണങ്ങളുടെ സമത കാട്ടുന്ന സവിശേഷത.
സ്വാഭാവികമായ സന്ദര്ഭങ്ങളില് നിന്ന് അനവധി ഉദാഹരണങ്ങള് ഗണങ്ങളുടെ 'ഉള്പ്പെടല്' (inclusion) സ്വഭാവത്തെ ചിത്രീകരിക്കുന്നതായി കണ്ടെത്താന് കഴിയും. ഒരു കമ്മിറ്റിയില് ഉള്പ്പെടുത്താന് അധ്യാപകരില് ഗണിതശാസ്ത്രവും മലയാളവും അറിയാവുന്നവരായിരിക്കണമെന്നാണു നിയമമെങ്കില് ക്രമത്തില് ഇവരുടെ ഗണങ്ങള് A,B,C എന്നിങ്ങനെയാകുമ്പോള്, A⊇B, A⊇C എന്നിങ്ങനെ ഇക്കാര്യം കാണിക്കാവുന്നതാണ്. B യിലും C യിലും ഉള്ളവരാണല്ലോ കമ്മിറ്റി അംഗങ്ങള്. പൊതുവേ ഇതു B ∩ C(ബി സംഗമം സി) എന്നാണ് അത്തരക്കാരുടെ ഗണം സൂചിപ്പിക്കുക. അതുകൊണ്ട് A ⊇ B ∩ C എന്നുകൂടി ലഭ്യമാകുന്നു. ഗണിതശാസ്ത്രമോ മലയാളമോ ഏതെങ്കിലുമൊന്നോ രണ്ടുംകൂടിയേ അറിയാവുന്നവരുടെ ഗണത്തെ B U C(ബി യോഗം സി) എന്ന് എഴുതുന്നു. അപ്പോഴും A ⊇ B U C ആയിരിക്കും. എന്തായാലും ഇവരെല്ലാം അധ്യാപകര് എന്ന ഗണത്തില്പ്പെടുന്നതുകൊണ്ടാണിതു സംഭവിക്കുന്നത്.
സംഗമം, യോഗം, ഉള്പ്പെടല് എന്നിവ ചിത്രണം ചെയ്യാറുണ്ട്. വെന് ചിത്രണം (Venn diagram) എന്നാണിതിനു പേര്. U എന്ന സമ്പൂര്ണഗണം (Universe അഥവാ population) A എന്ന ഉപഗണം ഉള്ക്കൊള്ളുന്നു.
A,B എന്നീ ഗണങ്ങള്ക്കു പൊതുവായി ഒരു മൂലകാംഗം പോലുമില്ലെങ്കില് A സംഗമം B എന്നത് ശൂന്യമായിരിക്കും. അതായത് A ∩ B=ø(ഫൈ എന്നാണു ശൂന്യഗണം സൂചിപ്പിക്കുക). ഇതു ചിത്രരൂപത്തില് താഴെ കൊടുക്കുന്നു.
A,B എന്നീ ഗണങ്ങള്ക്കു പൊതുവായിരിക്കുന്ന മൂലകാംഗങ്ങള് A-യില്നിന്നു മാറ്റുകയാണെങ്കില് A-ല് ശേഷിക്കുന്ന മൂലകാംഗങ്ങളുടെ ഗണത്തെ A-B എന്നു സൂചിപ്പിക്കുന്നു. ചിത്രരൂപത്തിലാണെങ്കില് ഇപ്രകാരമായിരിക്കും. ബീജീയ രീതിയിലും ഗണം പ്രതിനിധാനം ചെയ്യാറുണ്ട്. ഒരു വ്യവസ്ഥയിലൂടെ മൂലകാംഗങ്ങളുടെ പൊതുസ്വഭാവം പ്രകടമാക്കുമ്പോള് അത് അവയുടെ ഗണത്തിന്റെ നിര്വചനമായിത്തീരുന്നു. 2x + 3y = 6 എന്ന സമവാക്യം സാധൂകരിക്കാവുന്ന x,y- യുടെയും x,y മൂല്യങ്ങളുള്ള ജോടികള് ചേര്ന്നാല് ഒരു ഗണമുണ്ടാകുന്നു.
A = {(x,y) : 2x + 3y = 6} ഇവിടെ മൂലകാംഗത്തിന്റെ രൂപം (x,y) എന്നിങ്ങനെയാണ്. B = {(x,y) : x-y= 1} എന്ന മറ്റൊരു ഗണംകൂടി നിര്വചിക്കപ്പെടുകയും A,B എന്നിവയില് പൊതുവായി കാണുന്ന മൂലകാംഗങ്ങളെ C എന്നു സൂചിപ്പിക്കുകയാണെങ്കില് C = A ∩ B എന്നത് C = {(x,y) : 2x + 3y = 6, x-y = 1) എന്നിങ്ങനെ ക്രോഡീകരിച്ചു പ്രകടിപ്പിക്കാവുന്നതാണ്.
ഗണം പ്രതിനിധാനം ചെയ്യുന്നതു സാധാരണ A = a,b,c...} എന്നിങ്ങനെയാണ്. ഈ രീതിയില് മൂലകാംഗങ്ങളെ വ്യക്തമായി കാണിച്ചിരിക്കും.
ഉള്പ്പെടല്, സംഗമം, യോഗം എന്നീ പ്രക്രിയകള് ചേര്ന്നുണ്ടാകുന്ന വിനിമേയ നിയമങ്ങളാണു താഴെ ചേര്ക്കുന്നത്.
![]() വിനിമേയ നിയമങ്ങള് ചിത്രീകരിക്കാവുന്നതാണ്.
വിനിമേയ നിയമങ്ങള് ചിത്രീകരിക്കാവുന്നതാണ്.
ആകെയുള്ള ബൃഹദ്ഗണത്തില് A ഗണത്തിലെ മൂലകാംഗങ്ങളെ മാറ്റിയാല് ശേഷിക്കുന്ന ഗണത്തെ A-യുടെ പൂരകം (complement) എന്നു പറയുന്നു; A' എന്നാണ് ചിഹ്നം.
X എന്ന മൂലകാംഗം A ഗണത്തില്പ്പെടുന്നു എന്നു കാണിക്കുന്നത് X ∈ A എന്നാണ്; പെടുന്നില്ലെങ്കില് ∉ എന്ന ചിഹ്നമാണുപയോഗിക്കുക. ഈ ചിഹ്നങ്ങള് ഉപയോഗിച്ച് A U B, A ∩ B,A-B, A' എന്നിവ നിര്വചിക്കാവുന്നതാണ്.
A യുടെ പൂരകത്തിന്റെ പൂരകം A തന്നെയായിരിക്കും; അതായത് (A')' = A ശൂന്യഗണത്തിന്റെ പൂരകം ബൃഹദ്ഗണം തന്നെ; അതായ് ø'= U ബൃഹദ് ഗണത്തിന്റേത് ശൂന്യഗണവും, U'=ø A-ഉം A'-ഉം യോഗം ചെയ്താല് ബൃഹദ്ഗണമാകുമെന്നത് അനുക്ത സിദ്ധമാണ്. A,B എന്നീ ഗണങ്ങളുടെ യൂണിയന്റെ പൂരകം രണ്ടിന്റെയും പൂരകങ്ങളുടെ സംഗമമായിരിക്കും; സംഗമത്തിന്റെ പൂരകം പൂരകങ്ങളുടെ സംഗമവും; (A U B)'= A'∩ B', (A ∩ B)'= A'U B' A,B-യുടെ ഉപഗണമാണെങ്കില് ആപൂരകം അപൂരകത്തിന്റെ ഉപഗണമാകും.
A1, A2, A3,....An എന്നിവയുടെ യോഗവും സംഗമവും സൂചകഗണ (Index set: 1 = {1,2,3.....n})ത്തിന്റെ സഹായത്തോടെ പ്രകടമാക്കാന് കഴിയും.
![]() ചുരുങ്ങിയത് ഒരു i എങ്കിലും I- ല്പ്പെടുന്നവിധം}
ചുരുങ്ങിയത് ഒരു i എങ്കിലും I- ല്പ്പെടുന്നവിധം}
= A1, A2,...} എന്ന അനുക്രമത്തിന്റെ യൂണിയനും ഛേദവുമാണ്.
ഗണങ്ങളുടെ ശൂന്യമല്ലാത്ത ഒരു വര്ഗ(class)ത്തിലെ ഏതെങ്കിലും രണ്ടു ഗണങ്ങളാണ് A,B എന്നിവ എങ്കില് താഴെ പറയുന്ന വ്യവസ്ഥകള്ക്കധീനമായി ആ ഗണവര്ഗം x ബൂളിയന് ആള്ജിബ്ര (Boolean algebra) എന്നറിയപ്പെടുന്നു; A-യും B-യും x-ല്പ്പെടുന്നെങ്കില് അവയുടെ യൂണിയനും ഛേദവും പൂര്ണകവും x-ല്പ്പെടുന്നു. അതായത് AU B∈ X, A∩B∈ X,A′∈ X ഈ വ്യവസ്ഥകള് പാലിക്കപ്പെടുമ്പോള് ശൂന്യഗണവും ബൃഹദ്ഗണവും x-ല്പ്പെടുമെന്ന് വ്യക്തമാണ്. ഗണങ്ങള് തമ്മില് ബന്ധപ്പെടുന്ന മറ്റൊരു രീതിയാണ് സമമിത വ്യത്യാസം (symmetric difference). ഇത് Δ എന്ന ചിഹ്നംകൊണ്ടു സൂചിപ്പിക്കുന്നു. A, B എന്നീ ഗണങ്ങളുടെ സമമിത വ്യത്യാസം അവ തമ്മില് ഈ ക്രമത്തിലുള്ള വ്യത്യാസത്തിന്റെയും ക്രമം തിരിച്ചുള്ള വ്യത്യാസത്തിന്റെയും യൂണിയനായി നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു. അതായത് A Δ B = (A− B)U (B− A) ഈ പ്രക്രിയയെ ആസ്പദമാക്കിയുള്ള വിനിമേയനിയമം(cummutative law), വിതരണ നിയമം(distributive law) എന്നിവ പാലിക്കപ്പെടുന്നതാണ്. അതായത്, A Δ B = B Δ A,A Δ (B Δ C) = (A Δ B)Δ C കൂടാതെ
AΔø = A,A Δ A = ø A (BΔ C) = (A ∩ B),Δ (A ∩ C). X എന്ന ഗണവര്ഗത്തില് A,B എന്നിവ ഏതെങ്കിലും മൂലകാംഗ ഗണമാണെങ്കില് A Δ B, A ∩ B എന്നിവയും x-ല്പ്പെടുന്നെങ്കില് x ഒരു റിങ്(Ring) ആണെന്നു പറയുന്നു.
ഗണങ്ങള് തമ്മില് ഗുണിക്കാന് കഴിയുമെന്നാണ് താഴെപ്പറയുന്ന നിര്വചനം കൊണ്ടു മനസ്സിലാക്കേണ്ടത്. X1, X2, X3........,Xn എന്നീ മൂലകാംഗങ്ങള് ക്രമത്തില് X1, X2, X3........,Xn എന്നീ ഗണങ്ങളിലെ അംഗങ്ങളെ പ്രതിനിധീകരിക്കുന്നതെങ്കില് ഈ ഗണങ്ങളുടെ ഗുണിതം (product) (X1, X2, ........,Xn) എന്ന പോലുള്ള അംഗങ്ങളുടെ ഗണമാണെന്ന് നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു. X= X1, X2, ........, Xn എന്ന ഗുണിതത്തിലെ ഏതൊരു അംഗവും X1, X2, ........,Xn എന്ന രൂപത്തിലുള്ളതായിരിക്കും. ഇതിലോരോന്നും ഓരോ ഘടകഗണത്തിലെ ഏതെങ്കിലുമൊരംഗമായിരിക്കും. ഘടകഗണങ്ങള് തുല്യമാണെങ്കില് ഗുണിതം X=Yn എന്ന് എഴുതാറുണ്ട്. സാധാരണയായി വാസ്തവിക സംഖ്യകളുടെ ഗണം R എന്നും സങ്കീര്ണസംഖ്യ (complex number)കളുടേത് C എന്നും സൂചിപ്പിക്കുകയാണെങ്കില്, R2 നിര്ദേശാങ്കതല (Co-ordinate plane)ത്തെയും R3 ഘടനജ്യാമതിതല (Solid geometrical space)ത്തെയും സൂചിപ്പിക്കുന്നു. ഇവ സാമാന്യവത്കരിച്ചാല് Rn, Cn എന്നിങ്ങനെ വാസ്തവികതലവും സങ്കീര്ണതലവും ചിഹ്നനം ചെയ്യുന്നു.
ഗണങ്ങളുടെ ഘടന മനസ്സിലാക്കാനുള്ള ആദ്യപടിയായി അവയുടെ മൂലകാംഗങ്ങളെ വിഭജിച്ചു പ്രത്യേക ഗണങ്ങളായി കണക്കാക്കുന്നു. പൊതുവായി ഒരു അംഗംപോലും ഇല്ലാത്തവിധം, എന്നാല് എല്ലാ അംഗങ്ങളും വിവിധ ഉപഗണങ്ങളിലായി വിന്യസിച്ചിരിക്കും വിധം, വിഭജിച്ചുണ്ടാകുന്ന ഗണങ്ങളുടെ സമുച്ചയത്തെ ഒരു വിഭജനം (Partition) എന്നു പറയുന്നു. വിവിധ രീതികളില് വിഭജിക്കാവുന്നതുകൊണ്ട് വിഭജനങ്ങള് നാനാവിധമുണ്ടെന്ന് സിദ്ധിക്കുന്നു. X എന്ന ഗണത്തിന്റെ ഒരു വിഭജനത്തെ {Ai} എന്നു സൂചിപ്പിക്കാം; ഇവിടെ Ai, i = 1,2.....എന്നത് X-ന്റെ വിഭിന്നവും ശൂന്യമല്ലാത്തതുമായ ഉപഗണങ്ങളായിരിക്കും; Ai-കളുടെ യൂണിയന് X തന്നെ. A1-കളെ വിഭജനഗണങ്ങള് എന്നു പറയുന്നു. ഉദാ. X = {a, b, c, d} എങ്കില് A1 = {a, c}, A2 = {b, d}; B1 = {a,b}, C1 = {c,d} എന്നിവ വ്യത്യസ്തമായ രണ്ടു വിഭജനങ്ങളാണ്.
ഒരു ഗണത്തിലെ ഏതെങ്കിലും രണ്ട് അംഗങ്ങള് തമ്മിലുള്ള ബന്ധം സൂചിപ്പിക്കാന് R എന്ന ചിഹ്നം ഉപയോഗിക്കുന്നു x,y, X-ലെ അംഗങ്ങളാണെങ്കില് xRy എന്ന ചിഹ്നം കൊണ്ടുദ്ദേശിക്കുന്നത് x-ന് y-നോട് R എന്ന ബന്ധമാണെന്നാണ്. ഇതിനു ദ്വയാംഗബന്ധം (binary relation) എന്നു പറയുന്നു. ഉദാ. x = y, x ≤ y; = ≤ എന്നിവ R എന്ന ബന്ധചിഹ്നത്തിന്റെ പ്രത്യേകമായ അര്ഥങ്ങളാണ്.
ദ്വയാംഗബന്ധത്തിന്റെ പ്രത്യേകതകള് പരിഗണിച്ച് അതിന് പ്രയോജനകരമായ ഒരു വ്യാഖ്യാനം നല്കി തുല്യമാനബന്ധം(equivalence relation) എന്ന പ്രത്യേക ഭാവം ഗണിതശാസ്ത്രത്തില് ഏര്പ്പെടുത്തിയിട്ടുണ്ട്. സ്വതുല്യത(reflexivity), സമമിതി (symmetry), സംക്രാമകത (Transitivity) എന്നീ മൂന്നു വ്യവസ്ഥകള്ക്കു വിധേയമായ ദ്വായാംഗബന്ധത്തെയാണ് തുല്യമാനബന്ധ (Equivalence relation)മെന്നു വ്യവഹരിക്കുന്നത്. R എന്ന ദ്വയാംഗബന്ധം സ്വതുല്യത പുലര്ത്തുന്നുവെങ്കില് xRx എല്ലാ അംഗങ്ങള്ക്കും ശരിയായിരിക്കും. സമമിതിയുണ്ടെങ്കില് xRy ഉള്ളപ്പോള് xRx ശരിയായിരിക്കും. ഉദാ x = y ആണെങ്കില് y = x സംക്രാമകത xRy, yRz ഉള്ളപ്പോള് xRz ശരിയായിരിക്കുമെന്നു സൂചിപ്പിക്കുന്നു. ഉദാ x = y, y = z ആണെങ്കില് x = z ആകുന്നു. ഈ വ്യവസ്ഥകള് ഒത്തുചേരുമ്പോള് സംജാതമാകുന്ന പ്രത്യേകതകള് ആധുനിക ഗണിതശാസ്ത്രത്തിനു ഗണ്യമായ പരിവര്ത്തനം വരുത്തിത്തീര്ന്നിട്ടുണ്ട്. ഒരു ഗണത്തിലെ x എന്ന അംഗത്തിനു തുല്യമാനബന്ധം പുലര്ത്തുന്ന അംഗങ്ങളുടെ സമാഹാരത്തെ {x} എന്ന ചിഹ്നംകൊണ്ടു സൂചിപ്പിക്കുന്നു: {x} = {y;y ∼} തുല്യമാനബന്ധത്തിന്റെ ചിഹ്നമാണ് ? എന്നത്. അതിനു തുല്യമാനഗണം എന്നു പറയുന്നു. ഏതു ഗണത്തിന്റെയും തുല്യമാനഗണങ്ങള് വ്യത്യസ്തങ്ങളായിരിക്കും; അവയ്ക്കു പൊതുവേ ഒരംഗംപോലുമുണ്ടാവില്ല. അപ്രകാരം തുല്യമാനഗണങ്ങളുടെ വര്ഗം ഒരു പ്രത്യേകയിനം വിഭജനമാണെന്നു സിദ്ധിക്കുന്നു.
തുല്യമാനബന്ധത്തിന്റെ മൂന്നു വ്യവസ്ഥകളില് സമമിതിക്കുമാത്രം ഭംഗം വരുത്തി പ്രതിസമമിതി (anti symmetry) എന്നൊരു വ്യവസ്ഥയായി മാറ്റുമെങ്കില് ഈ വ്യവസ്ഥകള്ക്കു വിധേയമായ സ്ഥിതിവിശേഷത്തെ ഭാഗികക്രമബന്ധം(partial order relation) എന്നു പറയുന്നു. അതായത് ഗണത്തിലെ ഏത് അംഗങ്ങളും സ്വതുല്യത, പ്രതിസമമിതി, സംക്രമാകത എന്നീ വ്യവസ്ഥകള്ക്കു വിധേയമാണെങ്കില് ആ ഗണം ഭാഗികക്രമീകൃതഗണം (partially ordered set) എന്നുപറയുന്നു. ഭാഗികക്രമബന്ധം '≤' (അഥവാ ≥)എന്ന ചിഹ്നം കൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്. x, y, z, ∈ X എങ്കില് x ≤ x എന്നത് ഓരോ അംഗവും അനുസരിക്കുന്നു; x ≤ y, y ≤ x എങ്കില് x = y എന്ന വ്യവസ്ഥയാണ് പ്രതിസമമിതി; x ≤ y, y ≤ z എങ്കില് x ≤ z എന്നത് സംക്രാമകതയും.
ഭാഗികക്രമം ഏതുജോടി അംഗങ്ങളെടുത്താലും ശരിയായിരിക്കുമെങ്കില് ആ ഗണത്തെ മുഴു ക്രമീകൃതഗണം (totally ordered set) അഥവാ രേഖീയക്രമീകൃതഗണം (linearly ordered set) എന്നുവിളിക്കുന്നു. ഇത്തരം ഗണത്തെ ചെയിന് (chain) എന്നും വിളിച്ചുവരുന്നു.
ആധുനികഗണിതശാസ്ത്രത്തില് സാര്വത്രികമായി ഉപയോഗിച്ചുവരുന്ന പ്രത്യേക ഗണങ്ങളാണ് ലാറ്റിസ്, ഗ്രൂപ്പ്, സെമിഗ്രൂപ്പ്, റിങ്, ഫീല്ഡ് എന്നീ ഗണിതീയഘടനകള്. മൂലകാംഗങ്ങള് അനുസരിക്കുന്ന പ്രത്യേക വ്യവസ്ഥകളെ ആധാരമാക്കിയാണ് ഗണത്തിനു ഘടനാപരമായ ഈ പേരുകള് ലഭിക്കുന്നത്. ജര്മന് ഗണിതശാസ്ത്രജ്ഞനായ കാന്റോര് വികസിപ്പിച്ചെടുത്ത ഈ ശാഖ അതിരറ്റ വിമര്ശനങ്ങള്ക്കു വിധേയമായിത്തീര്ന്നിട്ടുണ്ട്. 1900-ത്തിനുശേഷം ഈ വിമര്ശനങ്ങള് ക്രോഡീകരിച്ച് വൈരുധ്യങ്ങള് (Paradoxes) എന്ന പേരില് കുപ്രസിദ്ധമായി. വൈരുധ്യങ്ങളുടെ രണ്ടുദാഹരണങ്ങള് താഴെ ചേര്ക്കുന്നു.
എല്ലാ ഗണങ്ങളുടെയും ഗണമാണ് S എന്നിരിക്കട്ടെ, T,S -ന്റെ എല്ലാ ഉപഗണങ്ങളും ചേര്ന്ന ഗണവും. S-ന്റെ ഉപഗണമെന്ന നിലയ്ക്ക് T-യോടുതന്നെ ഒന്നിനൊന്ന് അനുയോഗ(one-to-one correspondence)ത്തിലായതിനാല് T-ക്ക് S-നെക്കാള് അംഗസംഖ്യ കൂടുതലാകാനിടയില്ല. ഇത് 1899-ല് പ്രസ്താവിക്കപ്പെട്ട 'കാന്റോര് വൈരുധ്യ'മാണ്. 1905-ല് ജെ.എ. റിച്ചാര്ഡ് കണ്ടെത്തിയ മറ്റൊരു വൈരുധ്യമാണ് ഇനിപ്പറയുന്നത്. ഇംഗ്ലീഷ് ഭാഷയിലെ വാക്യങ്ങളും (phrases) ഗണനീയം (countable) ആണ്. എന്നു വച്ചാല് അവ 1,2,3....} എന്ന ഗണവുമായി ഒന്നിനൊന്ന് അനുയോഗത്തിലാണെന്നര്ഥം. എല്ലാ വാക്യങ്ങളും ക്രമപ്പെടുത്തിയതിനുശേഷം സംഖ്യാസിദ്ധാന്തപരമായ വാക്യങ്ങളെല്ലാം മാറ്റിക്കളയുക. കാന്റോറുടെ ഒരു പ്രക്രിയ, ശേഷിക്കുന്ന ലിസ്റ്റില് പ്രയോജനപ്പെടുത്തിയാല് ഇംഗ്ലീഷ് ഭാഷയില് നിര്വചിക്കത്തക്ക ഏതു ഫങ്ഷനില് നിന്നും വ്യത്യസ്തമായ ഒരു ഫങ്ഷന് നിര്വചിക്കാന് കഴിയുമെന്നു മനസ്സിലാക്കാം. ഇതും ഒരു വൈരുധ്യമാണ്. ബി.സി. 6-ാം ശതകത്തില് എപിമെനിഡീസും (Epemnides) ബി.സി. 4-ാം ശതകത്തില് യൂബുലിഡീസും പ്രസ്താവിച്ചതായി പറയുന്ന വൈരുധ്യങ്ങള്ക്കു സമാനമാണ് ഈ ആധുനിക വൈരുധ്യങ്ങള്: ഒരാള് പറയുന്നു 'ഇപ്പോള് ഞാന് പറയുന്നതു നുണയാണ്'. ഈ പ്രസ്താവന ശരിയാണെങ്കില് ഇപ്പറഞ്ഞതും നുണയാണല്ലോ' ശരിയല്ലെങ്കില് പ്രസ്താവന തെറ്റാകുകയും ചെയ്യും. വൈരുധ്യങ്ങളെ നിഷ്പ്രഭമാക്കുന്ന ഒരു കുറവും ഇതുവരെ ഇതിനുണ്ടെന്നു കണ്ടെത്താന് കഴിഞ്ഞിട്ടില്ല. കാന്റോറുടെ വൈരുധ്യങ്ങള് അത്യധികം അനന്തമായ ഗണങ്ങളെ സംബന്ധിച്ചേ സാര്ഥകമാകൂ.
വൈരുധ്യങ്ങളെ മാറ്റിനിര്ത്തുന്ന തരത്തില് ഗണം നിര്വചിക്കപ്പെടുകയാണെങ്കില് ഗണത്തിനു സ്വാഭാവിക നിര്വചനം മാറ്റി ആക്സിയങ്ങളെ ആസ്പദമാക്കിയുള്ള പരിഗണന നല്കേണ്ടിവരും. 1908-ല് ഇറ്റലിയില് ഏണ്സ്റ്റ് സെര്മെലോ (Earnst Zermelo) ഇത്തരത്തില് ഗണസിദ്ധാന്തം പുനരാവിഷ്കരിക്കുകയുണ്ടായി. 1922-23 കാലത്ത് ജര്മനിയിലും സ്കാന്റിനേവിയയിലും എബ്രഹാം അഡോള്ഫ് ഫ്രേങ്കലും (Abraham Adolf Fraenkel) തൊറാള്ഫ് സ്കോലമും (Thoralf Skolem) ഇതു പരിഷ്കരിച്ചു. ആസ്ട്രിയന് താര്ക്കികനായ കുര്ട്ട് ഗെദല് (Kurt Godel). 'കാന്റോര് കണ്ടിന്വം' ഒരു ആക്സിയമായി ഇതില് ചേര്ത്താല് വൈരുധ്യാത്മകത സംഭവിക്കയില്ലെന്നു കണ്ടെത്തി. യു.എസ്സിലെ പോള് ജെ. കോഹന് 1963-ല് ഇതിന്റെ മറുവശം തെളിയിച്ചു. ഗണസിദ്ധാന്തത്തിനു വൈരുധ്യങ്ങളെ അടക്കിനിര്ത്തിക്കൊണ്ടുള്ള അസ്തിത്വമാണ് ഇവയിലൂടെ സ്ഥാപിതമായിട്ടുള്ളത്.