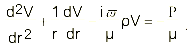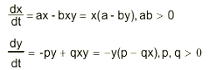This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ജൈവഗണിതം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→Biomathematics) |
(→Biomathematics) |
||
| വരി 65: | വരി 65: | ||
ഈ അവകല സമീകരണം നിര്ധാരണം ചെയ്താല് y=y<sub>0</sub> exp (-kt). ശരീരത്തില് ഔഷധം കുറയുന്ന നിരക്കിനെ സൂചിപ്പിക്കുന്ന മറ്റു നിയമങ്ങളും ഉണ്ട്. ചിലപ്പോള് ഒരു വലിയ മാത്ര ഔഷധം കൊടുത്തിട്ട് പിന്നീട് കൃത്യമായി ഇടവിട്ട് ചെറിയ മാത്ര കൊടുക്കാറുണ്ട്. അതനുസരിച്ച് ഔഷധം കുറയുന്ന നിരക്കിനെ സംബന്ധിച്ച നിയമങ്ങളിലും വ്യത്യാസം വരുന്നു. | ഈ അവകല സമീകരണം നിര്ധാരണം ചെയ്താല് y=y<sub>0</sub> exp (-kt). ശരീരത്തില് ഔഷധം കുറയുന്ന നിരക്കിനെ സൂചിപ്പിക്കുന്ന മറ്റു നിയമങ്ങളും ഉണ്ട്. ചിലപ്പോള് ഒരു വലിയ മാത്ര ഔഷധം കൊടുത്തിട്ട് പിന്നീട് കൃത്യമായി ഇടവിട്ട് ചെറിയ മാത്ര കൊടുക്കാറുണ്ട്. അതനുസരിച്ച് ഔഷധം കുറയുന്ന നിരക്കിനെ സംബന്ധിച്ച നിയമങ്ങളിലും വ്യത്യാസം വരുന്നു. | ||
| - | (ii)'''ഏക സ്പീഷീസിന്റെ ജനസംഖ്യാഗതികം''' (Population dynamics for single species). സമയത്തിന്റെ ഏതെങ്കിലും അളവിനെ കുറിക്കാന് എന്ന പ്രതീകമുപയോഗിക്കാം. സമയം ആകുമ്പോള് ഒരു സമൂഹത്തിന്റെ ജനസംഖ്യ x(t) ആയിരിക്കട്ടെ. ജനസംഖ്യ വര്ധിക്കുന്ന നിരക്കിനെ കുറിക്കുന്ന ഏറ്റവും ലഘുവായ സമവാക്യമാണ് [[ചിത്രം:Pg825screen.png|100px]] . ഇതാണ് ജനസംഖ്യാവര്ധനവിനെക്കുറിച്ചുള്ള മാള്ത്തൂസിയന് നിയമം(Malthusian law). ഈ സമീകരണം സമാകലിച്ചാല് x = x<sub>0</sub> exp(at).. അതായത് ജനസംഖ്യാവര്ധനവ് ചരഘാതാങ്കിയാണ് (exponential). വിഭവങ്ങള് അപരിമിതമാകുമ്പോള് മാത്രമേ ഇതു സാധ്യമാകുന്നുള്ളൂ. വിഭവങ്ങള് പരിമിതമായ ചുറ്റുപാടില് ആഭ്യന്തരമത്സരം കൂടി കണക്കിലെടുക്കേണ്ടതുണ്ട്. അതനുസരിച്ച് ജനസംഖ്യാ വര്ധനവിന്റെ നിരക്ക് [[ചിത്രം:Pg825 scree01.png| | + | (ii)'''ഏക സ്പീഷീസിന്റെ ജനസംഖ്യാഗതികം''' (Population dynamics for single species). സമയത്തിന്റെ ഏതെങ്കിലും അളവിനെ കുറിക്കാന് എന്ന പ്രതീകമുപയോഗിക്കാം. സമയം ആകുമ്പോള് ഒരു സമൂഹത്തിന്റെ ജനസംഖ്യ x(t) ആയിരിക്കട്ടെ. ജനസംഖ്യ വര്ധിക്കുന്ന നിരക്കിനെ കുറിക്കുന്ന ഏറ്റവും ലഘുവായ സമവാക്യമാണ് [[ചിത്രം:Pg825screen.png|100px]] . ഇതാണ് ജനസംഖ്യാവര്ധനവിനെക്കുറിച്ചുള്ള മാള്ത്തൂസിയന് നിയമം(Malthusian law). ഈ സമീകരണം സമാകലിച്ചാല് x = x<sub>0</sub> exp(at).. അതായത് ജനസംഖ്യാവര്ധനവ് ചരഘാതാങ്കിയാണ് (exponential). വിഭവങ്ങള് അപരിമിതമാകുമ്പോള് മാത്രമേ ഇതു സാധ്യമാകുന്നുള്ളൂ. വിഭവങ്ങള് പരിമിതമായ ചുറ്റുപാടില് ആഭ്യന്തരമത്സരം കൂടി കണക്കിലെടുക്കേണ്ടതുണ്ട്. അതനുസരിച്ച് ജനസംഖ്യാ വര്ധനവിന്റെ നിരക്ക് [[ചിത്രം:Pg825 scree01.png|100px]] ആണ് [[ചിത്രം:Pg 825 scree0002.png|30px]]. ആകുമ്പോള് [[ചിത്രം:Pg 825 screen0003.png|30px]] . അതായത് വര്ധനവില്ലാതെ ജനസംഖ്യ സുസ്ഥിരമാകുന്നത് [[ചിത്രം:Pg825 scre004.png|30px]] എന്ന മൂല്യത്തിലാണ്. പല രാജ്യങ്ങളിലെയും ജനസംഖ്യാവര്ധനവിന്റെ നിരക്ക് ഈ നിയമത്തെ സാധൂകരിക്കുന്നു. |
(പ്രൊഫ. കെ. ജയചന്ദ്രന്) | (പ്രൊഫ. കെ. ജയചന്ദ്രന്) | ||
15:12, 18 ഫെബ്രുവരി 2016-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ജൈവഗണിതം
Biomathematics
ജൈവശാസ്ത്രാപഗ്രഥനത്തിന് ഗണിത-സാംഖ്യിക പ്രവിധികള് ഉപയുക്തമാക്കുന്ന പ്രയുക്ത ഗണിതശാഖ. പ്രയുക്ത ഗണിത (applied mathematics)ത്തിന്റെ ഭാഗമായി അടുത്ത കാലത്ത് രൂപം കൊണ്ടു. ജീവശാസ്ത്രങ്ങളില് ഗണിതമോഡലുകളുടെ പ്രാധാന്യവും പ്രായോഗികരംഗത്ത് അവയുടെ ഉപയോഗവും ജൈവഗണിതപഠനങ്ങളില് ഉള്പ്പെടുന്നു. ജനിതകം, പരിസ്ഥിതിവിജ്ഞാനം, ന്യൂറോഫിസിയോളജി, ഹീമോഡൈനമിക്സ്, എപ്പിഡെമിയോളജി, ഫാര്മക്കോ കൈനറ്റിക്സ് തുടങ്ങിയ ശാസ്ത്രശാഖകളില് ഗണിതശാസ്ത്രസമീപനം ഉപയോഗപ്രദമാണ് എന്ന ആശയത്തില് നിന്നാണ് ജൈവഗണിതം രൂപംകൊണ്ടത്.
ദെക്കാര്ത്തെ (1596-1650), ഓയ്ലര് (1707-83) തുടങ്ങിയവരുടെ കാലംതൊട്ട് ജീവശാസ്ത്രത്തില് ഗണിതീയരീതികള് ഉപയോഗിച്ചുതുടങ്ങിയെങ്കിലും രണ്ടാംലോകയുദ്ധത്തിനു ശേഷമാണ് പ്രയുക്ത ഗണിതത്തിന്റെ സംഭാവനകള് ജീവശാസ്ത്രമേഖലയില് വ്യാപകമായി കണ്ടുതുടങ്ങിയത്. അതിനു മുമ്പ് പ്രയുക്ത ഗണിതപ്രശ്നങ്ങളുടെ നിര്ധാരണം x,y,z... തുടങ്ങിയ കുറച്ച് അജ്ഞാതരാശികളുടെ സംവൃതരൂപ നിര്ധാരണങ്ങളില് (closed form solutions) പരിമിതപ്പെട്ടിരുന്നു. ആയിരക്കണക്കിന് അജ്ഞാതരാശികളുള്ള ഗണിതമോഡലുകളുടെ നിര്ധാരണം കമ്പ്യൂട്ടറുകളുപയോഗിച്ച് ഇന്നു നടത്തുന്നു. ലോകയുദ്ധങ്ങള്ക്കുമുമ്പ് ഭൗതികശാസ്ത്രമേഖലകളിലാണ് ഗവേഷകര് വന്വിജയം കൈവരിച്ചതെങ്കില് ഇന്ന് ജീവശാസ്ത്രം, സാമൂഹ്യശാസ്ത്രം, മാനേജ്മെന്റ്, കമ്പ്യൂട്ടര് സയന്സ് തുടങ്ങിയ മേഖലകളിലെ ഗണിതശാസ്ത്രപരമായ സമീപനങ്ങള്ക്കാണ് അവര് ഊന്നല് കൊടുക്കുന്നത്.
ഭൗതികശാസ്ത്രങ്ങളിലും എന്ജിനീയറിങ്ങിലും താരതമ്യേന ലഘുവായ ഗണിതമോഡലുകളാണ് കൈകാര്യം ചെയ്യേണ്ടിവരുന്നത്. എന്നാല് ജീവശാസ്ത്രത്തിലും വൈദ്യശാസ്ത്രത്തിലുമുള്ള ഗണിതമോഡലുകള് വളരെ സങ്കീര്ണങ്ങളാണ്. അവ നിര്ധാരണം ചെയ്യാന് പലപ്പോഴും ഉയര്ന്ന ഗണിതശാഖകളുടെ പ്രയോഗം അത്യാവശ്യമാണ്. മാത്രമല്ല, ജൈവഗണിതത്തിലെ സങ്കീര്ണമായ പല പ്രശ്നങ്ങള്ക്കും ഉത്തരം ഇനിയും കണ്ടുപിടിക്കേണ്ടിയിരിക്കുന്ന ഗണിതവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു എന്ന് നിരീക്ഷിക്കപ്പെട്ടിട്ടുണ്ട്. സാധാരണ ജൈവഗണിതപ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യാന് അവകല സമീകരണങ്ങള് (differential equations), സമാകല സമീകരണങ്ങള് (integral equations) സമാകല-അവകല സമീകരണങ്ങള് (integral differential equations), സംഖ്യാത്മക വിശ്ലേഷണം, ഓപ്പറേഷന് റിസര്ച്ച് രീതികള് (O-R methods), ഗ്രാഫ് തിയറി, ടോപോളജി തുടങ്ങിയ ഉന്നത ഗണിതവിഭാഗങ്ങളാണ് ഉപയോഗിക്കുന്നത്.
1. ഗണിത മോഡലുകള് (Mathematical models). ബീജഗണിതത്തിലെ ഒരുദാഹണത്തിലൂടെ ഗണിത മോഡല് എന്താണെന്നു വ്യക്തമാക്കാം: അച്ഛന്റെ വയസ്സ് മകന്റെ വയസ്സിന്റെ ഏഴുമടങ്ങാണ്. അഞ്ചുവര്ഷം കഴിയുമ്പോള് അച്ഛന്റെ വയസ്സ് മകന്റെ വയസ്സിന്റെ നാലു മടങ്ങും. അച്ഛന്റെയും മകന്റെയും ഇപ്പോഴത്തെ വയസ്സ് കണ്ടുപിടിക്കണമെന്നിരിക്കട്ടെ. ബീജഗണിതരീതിയനുസരിച്ച് അച്ഛന്റെ വയസ്സ് x എന്നും മകന്റേത് y എന്നും സങ്കല്പിക്കുന്നു. അപ്പോള് x = 7y, x + 5 = 4 (y + 5) എന്നീ സമവാക്യങ്ങള് കിട്ടുന്നു. ഇവയെ നിര്ധാരണം ചെയ്താല് x = 35, y = 5. ആദ്യം കൊടുത്ത സമവാക്യങ്ങളാണ് ഈ പ്രശ്നത്തിന്റെ ജീവശാസ്ത്രപരമായ അവസ്ഥ(biological situation)യില് നിന്നു കിട്ടുന്ന ഗണിതമോഡല്. ഒരു സാധാരണ ഗണിതമോഡലിന്റെ ഏറ്റവും ലഘുവായ രൂപമാണിത്. ജീവശാസ്ത്രത്തിലെയോ വൈദ്യശാസ്ത്രത്തിലെയോ ഒരവസ്ഥയെ മനസ്സിലാക്കാന് അതിന് പല നിരീക്ഷണഫലങ്ങളെയും കൂട്ടിച്ചേര്ത്ത് ഒരു ഗണിത മോഡല് തയ്യാറാക്കുന്നു. ഈ മോഡലിലുള്ള അജ്ഞാത രാശികളുടെ മൂല്യം കണ്ടുപിടിച്ചാണ് പ്രശ്നപരിഹാരം തേടുന്നത്. ഗണിതമോഡലുകളുടെ ഘടന പലപ്പോഴും ബീജീയ(algebraic) സമവാക്യങ്ങളിലൊതുങ്ങുന്നില്ല. അവയില് അവകല സമീകരണങ്ങളും ആംശിക അവകല സമീകരണങ്ങളും (partial differential equations) സമാകല സമീകരണങ്ങളുമൊക്ക ധാരാളമായി പ്രത്യക്ഷപ്പെടാറുണ്ട്.
ഗണിത മോഡലുകള് രൂപപ്പെടുത്തുകയും അവയെ നിര്ധാരണം ചെയ്യുകയും ചെയ്യുന്ന പ്രക്രിയയാണ് ഗണിത മോഡലിങ് (mathematical modelling). ജീവശാസ്ത്രത്തിലെയും വൈദ്യശാസ്ത്രത്തിലെയും യാഥാര്ഥ്യങ്ങളെ ഗണിതവത്കരിച്ചു കിട്ടുന്ന ഗണിതരൂപങ്ങളെ (മോഡലുകളെ) നിര്ധാരണം ചെയ്ത് യാഥാര്ഥ്യവുമായി കൂട്ടിയിണക്കുകയാണ് ജൈവഗണിതത്തില് ചെയ്യുന്നത്. ഗണിത മോഡലുകളുടെയും ഗണിതരീതികളുടെയും സംയോജിതരൂപമാണ് ജൈവഗണിതം.
ഗണിത മോഡലുകള് ഉടനടി വസ്തുതകള് നേരില് ബോധ്യപ്പെടുത്തുന്നില്ലെങ്കിലും ജൈവപരിസരങ്ങളില് നടക്കുന്ന മാറ്റങ്ങള്ക്കു സൂചക(indicator)ങ്ങളായി വര്ത്തിക്കുന്നു. ഭൗതികശാസ്ത്രങ്ങളില് ഒരു മോഡല് നിര്മിക്കുമ്പോള് യഥാര്ഥ വസ്തുതയുടെ ഒരു ഏകദേശരൂപമാണ് കണക്കിലെടുക്കാറുള്ളത്. ഉദാ. ജ്യോതിശ്ശാസ്ത്രത്തില് സൂര്യന്റെയും ഗ്രഹങ്ങളുടെയും ചലനത്തെക്കുറിച്ചു മനസ്സിലാക്കാന് അവ ബിന്ദുക്കളായി (points) സങ്കല്പിക്കുന്നു. അതനുസരിച്ചു കിട്ടുന്ന ഫലങ്ങള് യാഥാര്ഥ്യവുമായി വളരെ പൊരുത്തപ്പെടുന്നതായാണ് കണ്ടുവരുന്നത്. ഇതുപോലെ ജൈവഗണിതത്തിലും മോഡലുകള് നിര്മിക്കാന് യഥാര്ഥാവസ്ഥയുടെ ഏകദേശസ്വഭാവം മാത്രമേ കണക്കിലെടുക്കാന് സാധ്യമാകുന്നുള്ളു. എങ്കിലും ഈ മോഡലുകളുടെ നിര്ധാരണ മൂല്യങ്ങള് യഥാര്ഥാവസ്ഥയെ വളരെ നേരിയ വ്യത്യാസത്തോടെ പ്രതിഫലിപ്പിക്കുന്നു.
ഭൗതികാവസ്ഥകളെക്കാള് വളരെ സങ്കീര്ണമാണ് ജൈവികാവസ്ഥകള് (biological situations). ഉദാ. മനുഷ്യശരീരത്തില് ധമനി(artery)കളിലൂടെയും കേശിക(capillary)ളിലൂടെയുമുള്ള രക്തപ്രവാഹത്തിന്റെ പഠനം പൈപ്പുകളിലൂടെയുള്ള ജലത്തിന്റെ ഒഴുക്കിനെക്കുറിച്ചുള്ളതിനെക്കാള് വിഷമം പിടിച്ചതാണ്. രക്തം ഒരു ന്യൂട്ടോണിയന് ദ്രാവകമല്ല; ശ്യാനതഗുണാങ്കം (Coefficient of viscosity) സ്ഥിരസംഖ്യയല്ലാത്ത ദ്രാവകമാണ്. അത് ഏകാത്മകം (homogeneous) പോലുമല്ല. വ്യത്യസ്ത വ്യാസങ്ങളുള്ള കുഴലുകളിലൂടെയാണ് രക്തം പ്രവഹിക്കുന്നത്. ശാഖോപശാഖകളായി വഴിപിരിയുന്ന രക്തക്കുഴലുകള് ഇലാസ്തികമാണ്. ഹൃദയം സദാനേരവും സ്പന്ദിക്കുന്നതുകൊണ്ട് പ്രവാഹം സ്പന്ദിതവുമാണ് (pulsatile). ഇത്തരം കാരണങ്ങള് ശരീരത്തില് രക്തമൊഴുകുന്നതിനെക്കുറിച്ചുള്ള പഠനങ്ങള് വളരെ ഗഹനമാക്കുന്നു. ഒരു പരിധിവരെ ജൈവശാസ്ത്രജ്ഞര് ഈ പ്രശ്നം ഗണിതമോഡലുകളിലൂടെ നിര്ധാരണം ചെയ്തിട്ടുണ്ട്. ഗണിതമോഡലുകള് രൂപീകരിക്കാന് ദ്രവഗതിക(Fluid dynamics) ത്തിലെ നേവിയര് - സ്റ്റോക്ക്സ് സമീകരണങ്ങള് (Navier - Stokes' equations) ഉപയോഗിക്കുന്നു. ദൃഢ ഇലാസ്തികക്കുഴലുകളില് സ്പന്ദിത രക്തപ്രവാഹത്തെ പ്രതിനിധീകരിക്കുന്ന സമീകരണം താഴെ കൊടുക്കുന്നു.
ഇതിന്റെ നിര്ധാരണം ബെസല് ഫലന(Bessel functions)ങ്ങളുപയോഗിച്ച് എഴുതാവുന്നതാണ്.
2. ജൈവഗണിത പശ്ചാത്തലം. ജീവശാസ്ത്രത്തിലും വൈദ്യശാസ്ത്രത്തിലുമുള്ള പ്രത്യേകാവസ്ഥകള് ഗണിതശാസ്ത്രസമീപനത്തിലൂടെ അപഗ്രഥിക്കാവുന്നതാണ്. ഗണിതരീതികളുപയോഗിച്ച് നിര്ധാരണം ചെയ്യാവുന്ന ചില പ്രശ്നാവസ്ഥകളാണ് ഇവിടെ കൊടുക്കുന്നത്.
(i) രാസചികിത്സ (Chemo therapy). ഔഷധങ്ങള് കൊണ്ട് കാന്സര് കോശങ്ങളെ ഉന്മൂലനം ചെയ്യുകയോ അവയുടെ വളര്ച്ചയെ പ്രതിരോധിക്കുകയോ ചെയ്യുക എന്നത് ഗവേഷണമേഖലയില് വളരെ പ്രാധാന്യമുള്ള വിഷയമാണ്. കാന്സര് കോശങ്ങളെ നശിപ്പിക്കുമ്പോള് സാധാരണകോശങ്ങള്ക്കു ഹാനി സംഭവിക്കാന് പാടില്ല. ഇതിന് രോഗിയുടെ ശരീരത്തില് പ്രയോഗിക്കുന്ന ഔഷധത്തിന്റെ സാന്ദ്രതയ്ക്ക് (concentration) ഒരു പരിധിയുണ്ട്. അതു നിശ്ചയിക്കാന് ഔഷധത്തിന്റെയോ അതിന്റെ ഉപോത്പന്ന (biproduct)ങ്ങളുടെയോ സാന്ദ്രത ശരീരഭാഗങ്ങളില് എങ്ങനെ പ്രവര്ത്തിക്കുന്നുവെന്നറിയണം. യു.എസ്സിലെ റാന്ഡ് കോര്പ്പറേഷന് ഇതറിയാന് ഒരു സൈദ്ധാന്തിക മാതൃക രൂപപ്പെടുത്തി. ബെല്മാന്, കോട്ട്സ്കിന് എന്നീ ശാസ്ത്രജ്ഞര് തയ്യാറാക്കിയ ഈ മാതൃകയില് വ്യത്യസ്ത സമയങ്ങളില് ശരീരത്തിന്റെ പരിസഞ്ചരണ വ്യവസ്ഥയില് (circulatory system) കുത്തിവയ്ക്കേണ്ട മരുന്നിന്റെ അളവ് രേഖപ്പെടുത്തിയിട്ടുണ്ട്. ധാരാളം അവകല-അന്തര സമീകരണങ്ങള് (differential-difference equations) ഉള്ക്കൊണ്ട ഈ മാതൃക നിര്ധാരണം ചെയ്യുവാന് ഗണിതശാസ്ത്രത്തിലെ ആധുനികരീതികള് ആവശ്യമായി വരുന്നു. ഈ വിധത്തില് കിട്ടുന്ന നിര്ധാരണമൂല്യങ്ങളും പരീക്ഷണശാലയില് മൃഗങ്ങളില് നടത്തിയ പരീക്ഷണഫലങ്ങളും വളരെ സൂക്ഷ്മമായ സാദൃശ്യം പുലര്ത്തുന്നു. അതുപോലെ രോഗിയുടെ ശരീരത്തില് പ്രയോഗിക്കുവാനുള്ള മരുന്നിന്റെ മാത്രയെ സംബന്ധിച്ച അനുകൂലതമ അളവിനെ (optimal measure) കുറിച്ചും ഗണിത മോഡലുകള് തയ്യാറാക്കാവുന്നതാണ്.
(ii) കീടനിയന്ത്രണ തന്ത്രം (Insect control strategy). കൃഷിയിടങ്ങളില് കീടങ്ങളെയും ക്ഷുദ്രജീവികളെയും നിയന്ത്രിക്കാനുള്ള പലതരം ഗണിതമോഡലുകള് തയ്യാറാക്കി കമ്പ്യൂട്ടറിന്റെ സഹായത്താല് അവയില് മെച്ചപ്പെട്ടത് തെരഞ്ഞെടുക്കുന്ന രീതി കൃഷിശാസ്ത്രജ്ഞര് സ്വീകരിച്ചിട്ടുണ്ട്.
(iiii) ഔഷധ വിതരണം (Drug distribution). വൈദ്യശാസ്ത്ര വിഭാഗമായ ഫാര്മക്കോളജിയില് നിഗമനങ്ങള്ക്കും തീരുമാനങ്ങള്ക്കും ഗണിതമോഡലുകള് ഉപയോഗിക്കുന്നുണ്ട്. ശരീരത്തില് ഏതു മരുന്നു കുത്തിവച്ചാലും ഗുളിക രൂപത്തില് കൊടുത്താലും ക്രമേണ അതിന്റെ ശക്തി കുറഞ്ഞുവരും. രോഗപ്രതിരോധത്തിനും രോഗമുക്തിക്കും ഒരു നിശ്ചിത അളവ് ഔഷധം ശരീരത്തില് എപ്പോഴും ആവശ്യവുമാണ്. കുറവിന്റ തോതനുസരിച്ച് യഥാസമയങ്ങളില് മരുന്ന് വീണ്ടും ശരീരത്തില് കുത്തിവയ്ക്കുന്നു. ഒരിക്കല് മരുന്നു പ്രയോഗിച്ചശേഷം വീണ്ടും മരുന്ന് ആവശ്യമായി വരുന്ന അനുകൂലതമ അന്തരാളം (optimum interval) ഒരു ഗണിത മോഡലിലൂടെ നിര്ണയിക്കാവുന്നതാണ്.
(iv) രോഗനിര്ണയം (medical diagnosis). രോഗത്തെ സംബന്ധിച്ച മുന്കാല അനുഭവങ്ങളും ഭിഷഗ്വരന്റെ പരിചയസമ്പത്തും രോഗചരിത്രത്തെക്കുറിച്ചുള്ള അവബോധവുമൊക്കെ പരിഗണിച്ചാണ് രോഗനിര്ണയത്തിന്റെ ഗണിത മോഡല് തയ്യാറാക്കുന്നത്. മുന്കൂട്ടി തീരുമാനിക്കപ്പെട്ട വ്യത്യസ്ത രോഗങ്ങളില് ഏതാണ് രോഗിയെ ബാധിച്ചിരിക്കുന്നത് എന്നറിയാന് രോഗിക്ക് ഓരോ രോഗവും പിടിപെടാനുള്ള സംഭാവ്യത (probability)യും അറിഞ്ഞിരിക്കണം. ഇതിന് സംഭാവ്യതാസിദ്ധാന്തത്തിലെ ബെയീസ് പ്രമേയമാണ് (Bayes' theorem) ഉപയോഗിക്കുന്നത്.
(v)ആഹാരക്രമം(Medical dieting). ഒരു വലിയ ആശുപത്രിയിലെ രോഗികള്ക്ക് ഒരേ തരത്തിലുള്ള ആഹാരമല്ല വേണ്ടത്. രോഗങ്ങളുടെ വ്യത്യാസമനുസരിച്ച് ആഹാരക്രമത്തില് വ്യത്യസ്തത പുലര്ത്തണം. എന്നാല് എല്ലാവര്ക്കും തികച്ചും വ്യത്യസ്തമായ ആഹാരപദാര്ഥങ്ങള് കൊടുക്കുക പ്രായോഗികമല്ല. അതുകൊണ്ട് പൊതുവായ ആഹാരപ്പട്ടിക (menu) തയ്യാറാക്കുമ്പോള് ഓരോ രോഗിക്കും ആവശ്യമുള്ളതില് പ്രധാനമായ ഒരിനമെങ്കിലും ഉള്ക്കൊള്ളിച്ച് ഇനങ്ങളുടെ എണ്ണം കുറയ്ക്കാന് ശ്രമിക്കുന്നു. മാട്രിക്സ് സിദ്ധാന്തമുപയോഗിച്ചു രൂപപ്പെടുത്തുന്ന ഒരു ഗണിത മോഡലാണിത്.
(vi)സാംക്രമിക രോഗവ്യാപനം(Spread of epidemics). പ്ലേഗ് തുടങ്ങിയ സാംക്രമിക രോഗ പഠനങ്ങളില് ഗണിത മോഡലുകള് ഉപയോഗിക്കാറുണ്ട്. രോഗബാധയുടെ കാലയളവില് ഒരു പ്രദേശത്ത് രോഗം ഉണ്ടെന്നു സംശയിക്കുന്നവര്, രോഗം ബാധിച്ചവര്, രോഗപ്രതിരക്ഷയുള്ളവര് (immune persons) എന്നിവരുടെ സംഖ്യ നിര്ണയിക്കുന്നത് ഏതാനും ആംശിക അവകലന സമീകരണങ്ങളുടെ നിര്ധാരണത്തിലൂടെയാണ്. സാംക്രമിക രോഗനിര്ണയത്തിനാവശ്യമായ ചെലവ് ഏറ്റവും കുറയ്ക്കുന്നതിനും ഡൈനാമിക് പ്രോഗ്രാമിങ്ങിന്റെ ഗണിതരീതികള് അവലംബിച്ച കണക്കുകൂട്ടലുകള് ആവശ്യമാണ്.
(vii) ജൈവബലതന്ത്രം (Biomechanics). ശരീരത്തിലെ പേശികളിലും എല്ലുകളിലും ഏല്ക്കുന്ന സമ്മര്ദം (stress), അവയുടെ താങ്ങുബലം (strain), തലയോട്ടിയില് മുറിവുകള്ക്കും ചതവുകള്ക്കും കാരണമായ ബലം (force) ഇവയൊക്കെ നിര്ണയിക്കുക സങ്കീര്ണമാണ്. ഈ ശരീരഭാഗങ്ങള് അസമമിതമായ (non-symmetric) ആകൃതിയോടുകൂടിയവയും സംയോജിത ഘടന(composite structure)യോടുകൂടിയവയും ആണ്. സാധാരണ ജ്യാമിതീയ രൂപങ്ങള്ക്കുള്ള ആകൃതിയല്ല ഈ ഭാഗങ്ങള്ക്ക്. ഇവയുമായി ബന്ധപ്പെട്ട ഗണിത മോഡലുകളെല്ലാം ആംശിക അവകലന സമീകരണങ്ങളാണ്.
(viii) ജൈവദ്രവഗതികം(Biofluid dynamics). ജൈവദ്രവങ്ങള് ന്യൂട്ടോണിയനോ ഏകാത്മകമോ അല്ല. ശരീരത്തിലുള്ള രക്തക്കുഴലുകള് ഇലാസ്തിക വസ്തുക്കള് കൊണ്ടാണ് നിര്മിച്ചിരിക്കുന്നത്. പൈപ്പുകളിലെ ജലപ്രവാഹപഠനത്തെക്കാള് സങ്കീര്ണമാണ് ശരീരത്തിലെ വലുതും ചെറുതുമായ കുഴലുകളിലൂടെ ഒഴുകുന്ന രക്തപ്രവാഹത്തെക്കുറിച്ചുള്ള പഠനം. പ്രാണവായുവിന്റെ ശ്വാസകോശങ്ങളിലൂടെയുള്ള സഞ്ചാരം, സന്ധികളിലൂടെയുള്ള സ്രവങ്ങളുടെ (sinovial fluid) ഒഴുക്ക് ഇവയൊക്കെ ഗണിത മോഡലുകളിലൂടെ അപഗ്രഥിക്കാം.
ജൈവദ്രവഗതികം രണ്ടു വിഭാഗങ്ങളായാണ് തരംതിരിച്ചിട്ടുള്ളത്. ബാഹ്യജൈവദ്രവഗതികത്തില് (External biofluid dynamics)പക്ഷികളുടെയും മൃഗങ്ങളുടെയും ദ്രവത്തിലൂടെയുള്ള ചലനം (ഉദാ. വായുവിലുള്ള പക്ഷികളുടെ പറക്കല്, വെള്ളത്തിലുള്ള മത്സ്യസഞ്ചാരം, ബീജാണു (spermatozoa), വൈറസ് തുടങ്ങിയ സൂക്ഷ്മ ജീവികളുടെ പ്ലവനഗതി തുടങ്ങിയവ) പരിഗണിക്കുന്നു. ആന്തരജൈവഗതികത്തില് (internal bio fluid dynamics) ദ്രവപ്രവാഹം, ശ്വാസകോശങ്ങളിലെ വായുസഞ്ചാരം, ശരീരത്തില് രക്തം, മസ്തിഷ്ക-മേരുദ്രവം (Cerebro-spinal fluid) എന്നിവയുടെ പ്രവാഹം തുടങ്ങിയവയാണ് പ്രതിപാദിക്കുന്നത്. ഹൃദയ സംവഹന വ്യവസ്ഥ(Cardio vascular system)യുടെ ഭൗതിക സാഹചര്യങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് ഹീമോഡൈനമിക്സ് (Hemodynamics). ഇതില് ഗണിതരീതികളും ഭൗതിക മോഡലുകളും ഉപയോഗിക്കുന്നു.
(ix) ജനസംഖ്യാഗതികം (Population dynamics). ജനസംഖ്യാഗതികത്തിലെ ഒരു പ്രധാന ഗണിത സങ്കല്പമാണ് 'ഇര-ഇരപിടിയന്' (Prey-predator model) മോഡല്. ഒരു വനപ്രദേശത്ത് കുറെ ചെറിയ പക്ഷികളും അവയെ ആഹരിക്കുന്ന കുറെ വലിയ പക്ഷികളും ഉണ്ടെന്നിരിക്കട്ടെ. അപ്പോള് ചെറിയ പക്ഷികള് ഇര വിഭാഗത്തിലും വലിയ പക്ഷികള് ഇരപിടിയന് വിഭാഗത്തിലും പെടുന്നു. ഒരു നിശ്ചിത സമയത്ത് ചെറിയ പക്ഷികളുടെ എണ്ണം x(t) യും വലിയ പക്ഷികളുടെ എണ്ണം y(t) യും ആണെന്നിരിക്കട്ടെ. വലിയ പക്ഷികള് ചെറിയവയെ ആക്രമിക്കുന്നില്ല എങ്കില് ചെറിയ പക്ഷികള് അവയുടെ സംഖ്യാബലമനുസരിച്ച് കൂടുകയും വലിയവ അവയുടെ സംഖ്യാബലമനുസരിച്ച് കുറയുകയും (ആഹാര ദൗര്ലഭ്യം മൂലം) ചെയ്യുന്നു. അതുകൊണ്ട് ![]() . എന്നാല് കാട്ടില് ഈ നിയമം ബാധകമല്ല. ചെറുതും വലുതുമായ പക്ഷികളുടെ സഹവാസം ചെറിയ പക്ഷികള്ക്കു വിനാശകരവും വലിയവയ്ക്കു ഗുണകരവുമാണ്. ചെറിയ പക്ഷികള്, ചെറുതും വലുതുമായ പക്ഷികളുടെ എണ്ണത്തിന്റെ ഗുണനഫലത്തിന് ആനുപാതികമായി കുറയുകയും വലിയ പക്ഷികള് ചെറുതും വലുതുമായ പക്ഷികളുടെ എണ്ണത്തിന്റെ ഗുണനഫലത്തിന് ആനുപാതികമായി കൂടുകയും ചെയ്യുന്നു എന്നു സങ്കല്പിക്കുക. അപ്പോള്,
. എന്നാല് കാട്ടില് ഈ നിയമം ബാധകമല്ല. ചെറുതും വലുതുമായ പക്ഷികളുടെ സഹവാസം ചെറിയ പക്ഷികള്ക്കു വിനാശകരവും വലിയവയ്ക്കു ഗുണകരവുമാണ്. ചെറിയ പക്ഷികള്, ചെറുതും വലുതുമായ പക്ഷികളുടെ എണ്ണത്തിന്റെ ഗുണനഫലത്തിന് ആനുപാതികമായി കുറയുകയും വലിയ പക്ഷികള് ചെറുതും വലുതുമായ പക്ഷികളുടെ എണ്ണത്തിന്റെ ഗുണനഫലത്തിന് ആനുപാതികമായി കൂടുകയും ചെയ്യുന്നു എന്നു സങ്കല്പിക്കുക. അപ്പോള്,
![]() യും
യും ![]() യും ഒന്നിച്ചു ശൂന്യമാകുമ്പോള്
യും ഒന്നിച്ചു ശൂന്യമാകുമ്പോള് ![]() ഇരയുടെയും (ചെറിയപക്ഷികള്) ഇരപിടിയന്മാരുടെയും (വലിയ പക്ഷികള്) എണ്ണം യഥാക്രമം യും യും ആകുമ്പോള് അവ യുടെ 'ജനസംഖ്യ' മാറ്റമില്ലാതെ സന്തുലിതാവസ്ഥയില് (equilibrium size) തുടരുന്നു. മുകളില് കൊടുത്ത സമീകരണങ്ങളില് നിന്ന്
ഇരയുടെയും (ചെറിയപക്ഷികള്) ഇരപിടിയന്മാരുടെയും (വലിയ പക്ഷികള്) എണ്ണം യഥാക്രമം യും യും ആകുമ്പോള് അവ യുടെ 'ജനസംഖ്യ' മാറ്റമില്ലാതെ സന്തുലിതാവസ്ഥയില് (equilibrium size) തുടരുന്നു. മുകളില് കൊടുത്ത സമീകരണങ്ങളില് നിന്ന്
പ്രാരംഭിക നിബന്ധനകള് x(0) = x0, y(0) = y0 ആയിരിക്കട്ടെ. ഈ അവകല സമീകരണം (Variable-separable equation)നിര്ധാരണം ചെയ്താല്, ![]() എന്നു കിട്ടുന്നു. x-y തലത്തിന്റെ ഒന്നാം ചതുര്ഥാംശത്തില് ഈ സമവാക്യം ഒരു അടഞ്ഞ പഥത്തെ (trajectory) പ്രതിനിധീകരിക്കുന്നു. പ്രാരംഭിക നിബന്ധനയനുസരിച്ച് ഈ പഥം (x0, y0) എന്ന ബിന്ദുവില്ക്കൂടി കടന്നുപോകും. അതുകൊണ്ട് x-y തലത്തിന്റെ ഒന്നാം ചതുര്ഥാംശത്തിലുള്ള ഏതു ബിന്ദുവില്ക്കൂടിയും ഇര-ഇരപിടിയന് മോഡലിനെ പ്രതിനിധീകരിക്കുന്ന ഒരു പഥമുണ്ട്. ഈ പഥങ്ങള് പരസ്പരം കൂട്ടിമുട്ടുന്നില്ല. എന്തുകൊണ്ടെന്നാല്, കൂട്ടിമുട്ടിയാല് ഒരേ ബിന്ദുവില് രണ്ടു വ്യത്യസ്ത ചരിവുകള് (slopes) വരും. ഇത് അസാധ്യമാണ്.
എന്നു കിട്ടുന്നു. x-y തലത്തിന്റെ ഒന്നാം ചതുര്ഥാംശത്തില് ഈ സമവാക്യം ഒരു അടഞ്ഞ പഥത്തെ (trajectory) പ്രതിനിധീകരിക്കുന്നു. പ്രാരംഭിക നിബന്ധനയനുസരിച്ച് ഈ പഥം (x0, y0) എന്ന ബിന്ദുവില്ക്കൂടി കടന്നുപോകും. അതുകൊണ്ട് x-y തലത്തിന്റെ ഒന്നാം ചതുര്ഥാംശത്തിലുള്ള ഏതു ബിന്ദുവില്ക്കൂടിയും ഇര-ഇരപിടിയന് മോഡലിനെ പ്രതിനിധീകരിക്കുന്ന ഒരു പഥമുണ്ട്. ഈ പഥങ്ങള് പരസ്പരം കൂട്ടിമുട്ടുന്നില്ല. എന്തുകൊണ്ടെന്നാല്, കൂട്ടിമുട്ടിയാല് ഒരേ ബിന്ദുവില് രണ്ടു വ്യത്യസ്ത ചരിവുകള് (slopes) വരും. ഇത് അസാധ്യമാണ്.
ഇരയുടെയും ഇരപിടിയന്മാരുടെയും സ്പീഷീസുകള് കുറഞ്ഞും കൂടിയും, കൂടിയും കുറഞ്ഞും വ്യത്യസ്ത അവസ്ഥകള് കടന്ന് ഒരു നിശ്ചിത കാലയളവിനുശേഷം തുടങ്ങിയയിടത്ത് എത്തുന്നു. ആവര്ത്തക(periodic) സ്വഭാവമുള്ള ഈ പ്രക്രിയ തുടര്ന്നുകൊണ്ടിരിക്കുന്നു.
3. ജൈവഗണിത മോഡലുകള്. വൈദ്യശാസ്ത്രത്തിലെയും ജനസംഖ്യാഗതികത്തിലെയും ചില ലഘുവായ ഗണിതമോഡലുകള് പരിശോധിക്കാം.
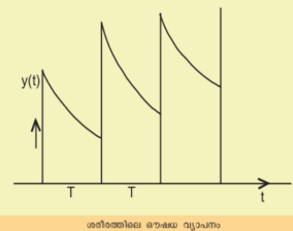
(i)മനുഷ്യശരീരത്തിലെ ഔഷധ വ്യാപനം (Drug distribution in the human body). രോഗബാധിതന് കൃത്യസമയങ്ങളില് ഔഷധം കഴിക്കുന്നതെന്തിന്? ഔഷധത്തിന്റെ അളവും അതു കഴിക്കുന്ന സമയാന്തരാളവും (time interval) തമ്മിലുള്ള ബന്ധമെന്ത്? ഇവയൊക്കെ ജൈവഗണിത പ്രശ്നങ്ങളാണ്. ആദ്യത്തെ മാത്ര ഔഷധം കഴിച്ചശേഷം ഔഷധം ശരീരത്തില് തീരുന്നതിനു മുമ്പ് അടുത്ത മാത്ര കഴിക്കുന്നു. ഈ അവസ്ഥയാണ് ചിത്രത്തില് ഉള്ളത്. സമയം t ആകുമ്പോള് ശരീരത്തിലുള്ള ഔഷധത്തിന്റെ അളവാണ് y(t). സമയം യില്, ഔഷധം ശരീരത്തില് കുറയുന്ന നിരക്കാണ്
![]()
ഈ അവകല സമീകരണം നിര്ധാരണം ചെയ്താല് y=y0 exp (-kt). ശരീരത്തില് ഔഷധം കുറയുന്ന നിരക്കിനെ സൂചിപ്പിക്കുന്ന മറ്റു നിയമങ്ങളും ഉണ്ട്. ചിലപ്പോള് ഒരു വലിയ മാത്ര ഔഷധം കൊടുത്തിട്ട് പിന്നീട് കൃത്യമായി ഇടവിട്ട് ചെറിയ മാത്ര കൊടുക്കാറുണ്ട്. അതനുസരിച്ച് ഔഷധം കുറയുന്ന നിരക്കിനെ സംബന്ധിച്ച നിയമങ്ങളിലും വ്യത്യാസം വരുന്നു.
(ii)ഏക സ്പീഷീസിന്റെ ജനസംഖ്യാഗതികം (Population dynamics for single species). സമയത്തിന്റെ ഏതെങ്കിലും അളവിനെ കുറിക്കാന് എന്ന പ്രതീകമുപയോഗിക്കാം. സമയം ആകുമ്പോള് ഒരു സമൂഹത്തിന്റെ ജനസംഖ്യ x(t) ആയിരിക്കട്ടെ. ജനസംഖ്യ വര്ധിക്കുന്ന നിരക്കിനെ കുറിക്കുന്ന ഏറ്റവും ലഘുവായ സമവാക്യമാണ് ![]() . ഇതാണ് ജനസംഖ്യാവര്ധനവിനെക്കുറിച്ചുള്ള മാള്ത്തൂസിയന് നിയമം(Malthusian law). ഈ സമീകരണം സമാകലിച്ചാല് x = x0 exp(at).. അതായത് ജനസംഖ്യാവര്ധനവ് ചരഘാതാങ്കിയാണ് (exponential). വിഭവങ്ങള് അപരിമിതമാകുമ്പോള് മാത്രമേ ഇതു സാധ്യമാകുന്നുള്ളൂ. വിഭവങ്ങള് പരിമിതമായ ചുറ്റുപാടില് ആഭ്യന്തരമത്സരം കൂടി കണക്കിലെടുക്കേണ്ടതുണ്ട്. അതനുസരിച്ച് ജനസംഖ്യാ വര്ധനവിന്റെ നിരക്ക്
. ഇതാണ് ജനസംഖ്യാവര്ധനവിനെക്കുറിച്ചുള്ള മാള്ത്തൂസിയന് നിയമം(Malthusian law). ഈ സമീകരണം സമാകലിച്ചാല് x = x0 exp(at).. അതായത് ജനസംഖ്യാവര്ധനവ് ചരഘാതാങ്കിയാണ് (exponential). വിഭവങ്ങള് അപരിമിതമാകുമ്പോള് മാത്രമേ ഇതു സാധ്യമാകുന്നുള്ളൂ. വിഭവങ്ങള് പരിമിതമായ ചുറ്റുപാടില് ആഭ്യന്തരമത്സരം കൂടി കണക്കിലെടുക്കേണ്ടതുണ്ട്. അതനുസരിച്ച് ജനസംഖ്യാ വര്ധനവിന്റെ നിരക്ക് ![]() ആണ്
ആണ് ![]() . ആകുമ്പോള്
. ആകുമ്പോള് ![]() . അതായത് വര്ധനവില്ലാതെ ജനസംഖ്യ സുസ്ഥിരമാകുന്നത്
. അതായത് വര്ധനവില്ലാതെ ജനസംഖ്യ സുസ്ഥിരമാകുന്നത് ![]() എന്ന മൂല്യത്തിലാണ്. പല രാജ്യങ്ങളിലെയും ജനസംഖ്യാവര്ധനവിന്റെ നിരക്ക് ഈ നിയമത്തെ സാധൂകരിക്കുന്നു.
എന്ന മൂല്യത്തിലാണ്. പല രാജ്യങ്ങളിലെയും ജനസംഖ്യാവര്ധനവിന്റെ നിരക്ക് ഈ നിയമത്തെ സാധൂകരിക്കുന്നു.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്)