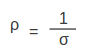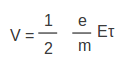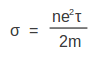This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ചാലകത
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(പുതിയ താള്‍: ==ചാലകത == ==Conductivity== പദാര്‍ഥങ്ങള്‍ക്ക് വൈദ്യുതി, താപം എന്നിവ വഹനം ...) |
(→Conductivity) |
||
| വരി 7: | വരി 7: | ||
വിദ്യുത്ചാലകതയുടെ പരിമാണം അടിസ്ഥാനമാക്കി പദാര്‍ഥങ്ങളെ സുചാലകം, അര്‍ധചാലകം, കുചാലകം, അതിചാലകം എന്നിങ്ങനെ നാലായി തിരിക്കാറുണ്ട്. സുചാലകങ്ങളെ സംബന്ധിച്ചുള്ള ഒരു പ്രധാന നിയമം ഓം എന്ന ശാസ്ത്രജ്ഞന്‍ ആവിഷ്കരിച്ചു. ഒരു വിദ്യുത്ക്ഷേത്രം (E) പ്രയോഗിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന ധാരാഘനത്വം (J) ഈ നിയമം അനുസരിച്ച് | വിദ്യുത്ചാലകതയുടെ പരിമാണം അടിസ്ഥാനമാക്കി പദാര്‍ഥങ്ങളെ സുചാലകം, അര്‍ധചാലകം, കുചാലകം, അതിചാലകം എന്നിങ്ങനെ നാലായി തിരിക്കാറുണ്ട്. സുചാലകങ്ങളെ സംബന്ധിച്ചുള്ള ഒരു പ്രധാന നിയമം ഓം എന്ന ശാസ്ത്രജ്ഞന്‍ ആവിഷ്കരിച്ചു. ഒരു വിദ്യുത്ക്ഷേത്രം (E) പ്രയോഗിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന ധാരാഘനത്വം (J) ഈ നിയമം അനുസരിച്ച് | ||
| - | J = | + | J = σ E (1) |
| + | |||
| + | എന്ന് എഴുതാവുന്നതാണ്. ധാരാഘനത്വം, വിദ്യുത്ക്ഷേത്രത്തിന് അനുലോമാനുപാതികമാണെന്ന് മേല്പറഞ്ഞ സമീകരണം സൂചിപ്പിക്കുന്നു. ധാരാഘനത്വവും വിദ്യുത്ക്ഷേത്രവും തമ്മിലുള്ള അനുപാതസംഖ്യയെ വിദ്യുത്ചാലകത എന്ന് നിര്‍വചിക്കാം. പദാര്‍ഥത്തിന്റെ രോധത്വവും (ρ) ചാലകതയും | ||
| + | |||
| + | [[ചിത്രം:Pg821 scrr001.png|100px]] | ||
| - | |||
| - | |||
| - | |||
എന്നു ബന്ധപ്പെടുത്താം. രോധത്വത്തിന്റെ മാത്ര ഓംമീറ്റര്‍ ആണ്. ഓമിന്റെ പ്രതിലോമത്തെ മോ എന്നു പറയാറുള്ളതുകൊണ്ടാണ് വിദ്യുത്ചാലകത മോ മീറ്റര്‍ <sup>-1</sup> എന്നെഴുതുന്നത്. | എന്നു ബന്ധപ്പെടുത്താം. രോധത്വത്തിന്റെ മാത്ര ഓംമീറ്റര്‍ ആണ്. ഓമിന്റെ പ്രതിലോമത്തെ മോ എന്നു പറയാറുള്ളതുകൊണ്ടാണ് വിദ്യുത്ചാലകത മോ മീറ്റര്‍ <sup>-1</sup> എന്നെഴുതുന്നത്. | ||
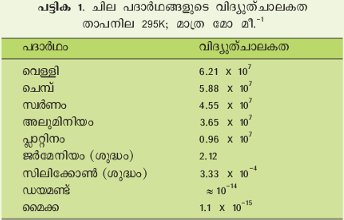
| - | ലോഹങ്ങളെല്ലാം സാമാന്യമായി സുചാലകവസ്തുക്കളാണ്. ജര്‍മേനിയം, സിലിക്കോണ്‍ തുടങ്ങിയവ അര്‍ധചാലകങ്ങള്‍. അവയുടെ ചാലകത ലോഹങ്ങളുടേതിനെക്കാള്‍ കുറവാണ്. ആംബര്‍, മൈക്ക, ഗ്ലാസ് തുടങ്ങിയവയുടെ ചാലകത ഏറ്റവും കുറവാകയാല്‍ അവ കുചാലകങ്ങള്‍ അഥവാ ഇന്‍സുലേറ്ററുകള്‍ എന്ന പേരില്‍ അറിയപ്പെടുന്നു. 295K യില്‍ ചില വസ്തുക്കളുടെ വിദ്യുത്ചാലകത | + | ലോഹങ്ങളെല്ലാം സാമാന്യമായി സുചാലകവസ്തുക്കളാണ്. ജര്‍മേനിയം, സിലിക്കോണ്‍ തുടങ്ങിയവ അര്‍ധചാലകങ്ങള്‍. അവയുടെ ചാലകത ലോഹങ്ങളുടേതിനെക്കാള്‍ കുറവാണ്. ആംബര്‍, മൈക്ക, ഗ്ലാസ് തുടങ്ങിയവയുടെ ചാലകത ഏറ്റവും കുറവാകയാല്‍ അവ കുചാലകങ്ങള്‍ അഥവാ ഇന്‍സുലേറ്ററുകള്‍ എന്ന പേരില്‍ അറിയപ്പെടുന്നു. 295K യില്‍ ചില വസ്തുക്കളുടെ വിദ്യുത്ചാലകത പട്ടിക 1-ല്‍ കൊടുത്തിരിക്കുന്നു. |
| + | |||
| + | [[ചിത്രം:Pg 821 scrt1.png]] (2) | ||
ലോഹങ്ങളുടെ വിദ്യുത്ചാലകതയെ വിശദീകരിക്കുന്നതിന് ഡ്രൂഡ്, ലോറന്‍സ് എന്ന രണ്ടു ശാസ്ത്രജ്ഞന്മാര്‍ സ്വതന്ത്ര ഇലക്ട്രോണ്‍ സിദ്ധാന്തം അവതരിപ്പിച്ചു. ത്രിവിമീയമായ അണുലാറ്റസില്‍ വളരെയേറെ സ്വതന്ത്ര ഇലക്ട്രോണുകള്‍ ഉള്ള ഘടനയാണ് ലോഹങ്ങള്‍ക്കുള്ളതെന്ന് അവര്‍ സങ്കല്പിച്ചു. ഇലക്ട്രോണുകള്‍ അനിയതമായ താപീയചലനങ്ങള്‍ക്കു വിധേയമാണ്. ഒരു വിദ്യുത്ക്ഷേത്രം പ്രയോഗിക്കുമ്പോള്‍ ഇലക്ട്രോണുകള്‍ക്കു ത്വരണം അനുഭവപ്പെടും. പക്ഷേ, ഇലക്ട്രോണുകള്‍ അണുലാറ്റിസുമായി നിരന്തരം സംഘട്ടനം നടത്തുകയും അവമന്ദനത്തിനു വിധേയമായിത്തീരുകയും ചെയ്യുന്നു. താപീയ ചലനത്തിനു പുറമേ, ഇലക്ട്രോണുകള്‍ക്ക് വിദ്യുത്ക്ഷേത്രത്തിന്റെ ദിശയില്‍ ഒരു അനുഗമനപ്രവേഗംകൂടി ഉണ്ടാകുമെന്നാണ് ഇതിന്റെ അനന്തരഫലം. രണ്ടു സംഘട്ടനങ്ങള്‍ക്കിടയിലുള്ള സമയാന്തരാളം ആണെങ്കില്‍ ഇപ്രകാരമുണ്ടാകുന്ന അനുഗമന പ്രവേഗം (v) താഴെപ്പറയുന്ന രീതിയില്‍ എഴുതാം. | ലോഹങ്ങളുടെ വിദ്യുത്ചാലകതയെ വിശദീകരിക്കുന്നതിന് ഡ്രൂഡ്, ലോറന്‍സ് എന്ന രണ്ടു ശാസ്ത്രജ്ഞന്മാര്‍ സ്വതന്ത്ര ഇലക്ട്രോണ്‍ സിദ്ധാന്തം അവതരിപ്പിച്ചു. ത്രിവിമീയമായ അണുലാറ്റസില്‍ വളരെയേറെ സ്വതന്ത്ര ഇലക്ട്രോണുകള്‍ ഉള്ള ഘടനയാണ് ലോഹങ്ങള്‍ക്കുള്ളതെന്ന് അവര്‍ സങ്കല്പിച്ചു. ഇലക്ട്രോണുകള്‍ അനിയതമായ താപീയചലനങ്ങള്‍ക്കു വിധേയമാണ്. ഒരു വിദ്യുത്ക്ഷേത്രം പ്രയോഗിക്കുമ്പോള്‍ ഇലക്ട്രോണുകള്‍ക്കു ത്വരണം അനുഭവപ്പെടും. പക്ഷേ, ഇലക്ട്രോണുകള്‍ അണുലാറ്റിസുമായി നിരന്തരം സംഘട്ടനം നടത്തുകയും അവമന്ദനത്തിനു വിധേയമായിത്തീരുകയും ചെയ്യുന്നു. താപീയ ചലനത്തിനു പുറമേ, ഇലക്ട്രോണുകള്‍ക്ക് വിദ്യുത്ക്ഷേത്രത്തിന്റെ ദിശയില്‍ ഒരു അനുഗമനപ്രവേഗംകൂടി ഉണ്ടാകുമെന്നാണ് ഇതിന്റെ അനന്തരഫലം. രണ്ടു സംഘട്ടനങ്ങള്‍ക്കിടയിലുള്ള സമയാന്തരാളം ആണെങ്കില്‍ ഇപ്രകാരമുണ്ടാകുന്ന അനുഗമന പ്രവേഗം (v) താഴെപ്പറയുന്ന രീതിയില്‍ എഴുതാം. | ||
| - | + | [[ചിത്രം:Pg 821 scree005.png]] (3) | |
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Pg821 scree1.png]] | |
| - | + | ||
| - | + | ||
പദാര്‍ഥത്തിന്റെ മാത്രാവ്യാപ്തിയിലുള്ള സ്വതന്ത്ര ഇലക്ട്രോണുകളുടെ എണ്ണം n ആണെങ്കില്‍ ധാരാഘനത്വം | പദാര്‍ഥത്തിന്റെ മാത്രാവ്യാപ്തിയിലുള്ള സ്വതന്ത്ര ഇലക്ട്രോണുകളുടെ എണ്ണം n ആണെങ്കില്‍ ധാരാഘനത്വം | ||
| - | J = ne v (4) | + | J = ne v (4) |
| - | + | υ യുടെ മൂല്യം പ്രതിസ്ഥാപിക്കുമ്പോള്‍ | |
| - | + | [[ചിത്രം:Pg821 scree006.png ]] (5) | |
ഈ സമീകരണത്തെ | ഈ സമീകരണത്തെ | ||
| വരി 39: | വരി 40: | ||
എന്ന ഓം നിയമവുമായി താരതമ്യം ചെയ്യുമ്പോള്‍ | എന്ന ഓം നിയമവുമായി താരതമ്യം ചെയ്യുമ്പോള്‍ | ||
| - | + | ||
| + | [[ചിത്രം:Pg821 scre007.png]] (6) | ||
| - | എന്നു ലഭിക്കുന്നു. ഇലക്ട്രോണുകളുടെ സംഘട്ടനങ്ങള്‍ക്കിടയിലെ മാധ്യമുക്തപഥം I-ഉം അനിയത ദിശകളിലേക്കുള്ള ശ.ശ.വേഗം u-ഉം ആണെങ്കില്‍ അതുകൊണ്ട് | + | എന്നു ലഭിക്കുന്നു. ഇലക്ട്രോണുകളുടെ സംഘട്ടനങ്ങള്‍ക്കിടയിലെ മാധ്യമുക്തപഥം I-ഉം അനിയത ദിശകളിലേക്കുള്ള ശ.ശ.വേഗം u-ഉം ആണെങ്കില്‍ [[ചിത്രം:Pg821 scree009.png]] അതുകൊണ്ട് |
| - | + | [[ചിത്രം:Pg 821 scree0010.png]] (7) | |
| - | I-ന് കാര്യമായ വ്യത്യാസം വരാത്ത അവസ്ഥകളി u കൂടുന്തോറും ചാലകത കുറഞ്ഞുവരുമെന്ന് ഈ സമീകരണം കാണിക്കുന്നു. താപഗതിക സിദ്ധാന്തമനുസരിച്ച് താപനില | + | I-ന് കാര്യമായ വ്യത്യാസം വരാത്ത അവസ്ഥകളി u കൂടുന്തോറും ചാലകത കുറഞ്ഞുവരുമെന്ന് ഈ സമീകരണം കാണിക്കുന്നു. താപഗതിക സിദ്ധാന്തമനുസരിച്ച് താപനില വര്‍ധിക്കുമ്പോ u കൂടേണ്ടതാണ്. അതുകൊണ്ട് വിദ്യുത്ചാലകത, താപനില വര്‍ധിക്കുന്തോറും കുറഞ്ഞുവരുമെന്നു കാണാം. ലോഹങ്ങളുടെ കാര്യത്തില്‍ σ, താപനിലയ്ക്കു പ്രതിലോമാനുപാതികമാണെന്ന് പരീക്ഷണങ്ങള്‍ വ്യക്തമാക്കുന്നു.n, l എന്നിവയ്ക്ക് താപനിലയനുസരിച്ച് വ്യത്യാസം ഉണ്ടാകുന്നില്ലെന്നു കരുതിക്കൊണ്ടാണ് നാം ഈ നിഗമനത്തിലെത്തിയത്. ഒരു അര്‍ധചാലകത്തിന്റെ കാര്യത്തില്‍ താപനിലയനുസരിച്ച് n മാറി വരുന്നതാണ്. ക്വാണ്ടം മെക്കാനിക സമീപനവും ഏതാണ്ട് ഇതേ രീതിയിലുള്ള നിഗമനങ്ങളിലേക്കു നയിക്കുമെന്ന് സാമാന്യമായി പറയാം. അര്‍ധചാലകവസ്തുക്കളില്‍ ഇലക്ട്രോണുകളും ഹോളുകളും ചാലകതയുണ്ടാക്കുന്നു. ഇവയെ യഥാക്രമം n ടൈപ്പ് ചാലകത, p ടൈപ്പ് ചാലകത എന്നു വിളിക്കുന്നു. അര്‍ധചാലകങ്ങളുടെ ചാലകത താപനില കൂടുന്തോറും എക്സ്പൊണന്‍ഷ്യല്‍ രീതിയില്‍ വര്‍ധിക്കുന്നു. |
കേവല പൂജ്യത്തോടടുത്ത താപനിലകളില്‍ മെര്‍ക്കുറിയുടെ ചാലകത അനന്തമാകുമെന്ന് 1911-ല്‍ കാമര്‍ലിങ് ഓണ്‍സ് എന്ന ശാസ്ത്രജ്ഞന്‍ കണ്ടുപിടിച്ചു. മോളിബ്ഡിനം, ലെഡ്, ടിന്‍ തുടങ്ങിയ മറ്റു പല വസ്തുക്കളും ഈ സ്വഭാവം പ്രദര്‍ശിപ്പിക്കുന്നുണ്ട്. ഇത്തരം വസ്തുക്കളെ അതിചാലകങ്ങള്‍ എന്നുപറയുന്നു. അതിചാലകങ്ങള്‍ അപകാന്തികവസ്തുക്കളെപ്പോലെ പെരുമാറുമെന്ന് മെയ്സ്നര്‍ കണ്ടെത്തി. രോധശൂന്യതയും അപകാന്തികത്വവുമാണ് അതിചാലകങ്ങളെ വേര്‍തിരിച്ചു കാണിക്കുന്ന ഗുണധര്‍മങ്ങള്‍. ഫോണോണ്‍ മുഖേന ഇലക്ട്രോണുകള്‍ പരസ്പരം ആകര്‍ഷിക്കപ്പെടുന്നതുകൊണ്ടാണ് അതിചാലകത ഉണ്ടാകുന്നതെന്ന് ബാര്‍ഡീന്‍, കൂപ്പര്‍, ഷ്റിഫര്‍ എന്നീ ശാസ്ത്രജ്ഞന്മാര്‍ വിശദമാക്കി (BCS സിദ്ധാന്തം). ഉയര്‍ന്ന താപനിലകളില്‍ ചില സെറാമിക് പദാര്‍ഥങ്ങള്‍ അതിചാലകത പ്രദര്‍ശിപ്പിക്കുന്നതായി അടുത്തകാലത്ത് കണ്ടുപിടിച്ചിട്ടുണ്ട്. ഇതിന്റെ കാരണം ആഇട സിദ്ധാന്തംകൊണ്ട് വിശദീകരിക്കാന്‍ കഴിയുകയില്ല. | കേവല പൂജ്യത്തോടടുത്ത താപനിലകളില്‍ മെര്‍ക്കുറിയുടെ ചാലകത അനന്തമാകുമെന്ന് 1911-ല്‍ കാമര്‍ലിങ് ഓണ്‍സ് എന്ന ശാസ്ത്രജ്ഞന്‍ കണ്ടുപിടിച്ചു. മോളിബ്ഡിനം, ലെഡ്, ടിന്‍ തുടങ്ങിയ മറ്റു പല വസ്തുക്കളും ഈ സ്വഭാവം പ്രദര്‍ശിപ്പിക്കുന്നുണ്ട്. ഇത്തരം വസ്തുക്കളെ അതിചാലകങ്ങള്‍ എന്നുപറയുന്നു. അതിചാലകങ്ങള്‍ അപകാന്തികവസ്തുക്കളെപ്പോലെ പെരുമാറുമെന്ന് മെയ്സ്നര്‍ കണ്ടെത്തി. രോധശൂന്യതയും അപകാന്തികത്വവുമാണ് അതിചാലകങ്ങളെ വേര്‍തിരിച്ചു കാണിക്കുന്ന ഗുണധര്‍മങ്ങള്‍. ഫോണോണ്‍ മുഖേന ഇലക്ട്രോണുകള്‍ പരസ്പരം ആകര്‍ഷിക്കപ്പെടുന്നതുകൊണ്ടാണ് അതിചാലകത ഉണ്ടാകുന്നതെന്ന് ബാര്‍ഡീന്‍, കൂപ്പര്‍, ഷ്റിഫര്‍ എന്നീ ശാസ്ത്രജ്ഞന്മാര്‍ വിശദമാക്കി (BCS സിദ്ധാന്തം). ഉയര്‍ന്ന താപനിലകളില്‍ ചില സെറാമിക് പദാര്‍ഥങ്ങള്‍ അതിചാലകത പ്രദര്‍ശിപ്പിക്കുന്നതായി അടുത്തകാലത്ത് കണ്ടുപിടിച്ചിട്ടുണ്ട്. ഇതിന്റെ കാരണം ആഇട സിദ്ധാന്തംകൊണ്ട് വിശദീകരിക്കാന്‍ കഴിയുകയില്ല. | ||
| - | താപചാലകത. ഏകസമാനമല്ലാതെ ചൂടാക്കപ്പെടുന്ന ഒരു വസ്തുവിന്റെ താപനില കൂടിയ ഭാഗത്തുനിന്ന് കുറഞ്ഞ സ്ഥലങ്ങളിലേക്കുള്ള താപപ്രേഷണമാണ് ചാലനം. ഖരവസ്തുക്കളില്‍ പ്രധാനമായും ഈ മാര്‍ഗത്തില്‍ക്കൂടിയാണ് താപപ്രേഷണം സംഭവിക്കുന്നത്. ഒരു പദാര്‍ഥത്തിലെ തന്മാത്രകള്‍ കേവലപൂജ്യത്തിനു മുകളിലുള്ള താപനിലകളില്‍ സ്പന്ദനം ചെയ്തുകൊണ്ടിരിക്കും. താപോര്‍ജം സ്വീകരിക്കുന്നതോടെ സ്പന്ദനം ശക്തിമത്താവുകയും സമീപസ്ഥങ്ങളും പതുക്കെ സ്പന്ദിക്കുന്നവയുമായ തന്മാത്രകള്‍ക്ക് ഊര്‍ജം കൈമാറുകയും ചെയ്യുന്നു. തന്മാത്രകള്‍ക്ക് സ്ഥാനാന്തരണം സംഭവിക്കാതെയാണ് ഇവിടെ ഊര്‍ജം പ്രേഷണം ചെയ്യപ്പെടുന്നത്. | + | '''താപചാലകത.''' ഏകസമാനമല്ലാതെ ചൂടാക്കപ്പെടുന്ന ഒരു വസ്തുവിന്റെ താപനില കൂടിയ ഭാഗത്തുനിന്ന് കുറഞ്ഞ സ്ഥലങ്ങളിലേക്കുള്ള താപപ്രേഷണമാണ് ചാലനം. ഖരവസ്തുക്കളില്‍ പ്രധാനമായും ഈ മാര്‍ഗത്തില്‍ക്കൂടിയാണ് താപപ്രേഷണം സംഭവിക്കുന്നത്. ഒരു പദാര്‍ഥത്തിലെ തന്മാത്രകള്‍ കേവലപൂജ്യത്തിനു മുകളിലുള്ള താപനിലകളില്‍ സ്പന്ദനം ചെയ്തുകൊണ്ടിരിക്കും. താപോര്‍ജം സ്വീകരിക്കുന്നതോടെ സ്പന്ദനം ശക്തിമത്താവുകയും സമീപസ്ഥങ്ങളും പതുക്കെ സ്പന്ദിക്കുന്നവയുമായ തന്മാത്രകള്‍ക്ക് ഊര്‍ജം കൈമാറുകയും ചെയ്യുന്നു. തന്മാത്രകള്‍ക്ക് സ്ഥാനാന്തരണം സംഭവിക്കാതെയാണ് ഇവിടെ ഊര്‍ജം പ്രേഷണം ചെയ്യപ്പെടുന്നത്. |
ഒരു വസ്തുവിന് ചാലനം വഴി താപം കൈമാറാനുള്ള കഴിവിന്റെ അളവാണ് താപചാലകത. | ഒരു വസ്തുവിന് ചാലനം വഴി താപം കൈമാറാനുള്ള കഴിവിന്റെ അളവാണ് താപചാലകത. | ||
| വരി 55: | വരി 57: | ||
കനമുള്ള ഒരു സ്ളാബിന്റെ ഛേദതല വിസ്തീര്‍ണം A ആണെന്നു കരുതുക. അതിന്റെ ഒരു വശത്തെ താപനില θയും എതിര്‍വശത്തേത് θ +Δθയും ആക്കി നിലനിര്‍ത്തുന്നുവെങ്കില്‍ വശങ്ങള്‍ക്കു ലംബമായി താപം പ്രവഹിക്കുന്ന നിരക്ക് ഛേദതലവിസ്തീര്‍ണത്തിനും താപനിലാവ്യത്യാസത്തിനും നേര്‍അനുപാതത്തിലും കനത്തിന് പ്രതിലോമാനുപാതത്തിലുമാണെന്ന് പരീക്ഷണങ്ങള്‍ കാണിക്കുന്നു. ഈ ഫലങ്ങളെ | കനമുള്ള ഒരു സ്ളാബിന്റെ ഛേദതല വിസ്തീര്‍ണം A ആണെന്നു കരുതുക. അതിന്റെ ഒരു വശത്തെ താപനില θയും എതിര്‍വശത്തേത് θ +Δθയും ആക്കി നിലനിര്‍ത്തുന്നുവെങ്കില്‍ വശങ്ങള്‍ക്കു ലംബമായി താപം പ്രവഹിക്കുന്ന നിരക്ക് ഛേദതലവിസ്തീര്‍ണത്തിനും താപനിലാവ്യത്യാസത്തിനും നേര്‍അനുപാതത്തിലും കനത്തിന് പ്രതിലോമാനുപാതത്തിലുമാണെന്ന് പരീക്ഷണങ്ങള്‍ കാണിക്കുന്നു. ഈ ഫലങ്ങളെ | ||
| - | + | [[ചിത്രം:Pg821 scree0011.png]] (8) | |
എന്ന് എഴുതാം. ഇവിടെ Q /t താപപ്രവാഹത്തിന്റെ നിരക്ക് ആണ്. Δxവളരെ ചെറുതാണെങ്കില്‍യും Δθചെറുതായിരിക്കും. അതുകൊണ്ട് സീമാന്തമൂല്യം എടുത്ത് സാമാന്യവത്കരണം നടത്തിയാല്‍ താപപ്രവാഹനിരക്ക് | എന്ന് എഴുതാം. ഇവിടെ Q /t താപപ്രവാഹത്തിന്റെ നിരക്ക് ആണ്. Δxവളരെ ചെറുതാണെങ്കില്‍യും Δθചെറുതായിരിക്കും. അതുകൊണ്ട് സീമാന്തമൂല്യം എടുത്ത് സാമാന്യവത്കരണം നടത്തിയാല്‍ താപപ്രവാഹനിരക്ക് | ||
| - | + | [[ചിത്രം:Pg821 scre0013.png ]] (9) | |
| - | എന്നാകുന്നു. ഇവിടെ | + | എന്നാകുന്നു. ഇവിടെ [[ചിത്രം:Pg822 scree05.png]] നെ താപനിലയുടെ ഗ്രേഡിയന്റ് അഥവാ ചരിവുമാനം എന്നുപറയാം. ചാലക പദാര്‍ഥത്തെമാത്രം ആശ്രയിക്കുന്ന സ്ഥിരാങ്കമാണ് K. ഇതിനെ താപചാലകത എന്നു നാമകരണം ചെയ്യാം. താപചാലനം സംബന്ധിച്ച നിരവധി ഗവേഷണങ്ങള്‍ നടത്തിയ ഫൂറിയര്‍ എന്ന ശാസ്ത്രജ്ഞന്റെ ബഹുമാനാര്‍ഥം മേല്‍ക്കൊടുത്ത സമീകരണത്തെ ഫൂറിയര്‍ സമീകരണം എന്നു പറയാറുണ്ട്. സ്ഥിരസ്ഥിതിയില്‍ താപനിലയുടെ മാത്രാഗ്രേഡിയന്റ് നിലവിലുള്ളപ്പോള്‍, മാത്രാവിസ്തീര്‍ണത്തിലൂടെ വശത്തിനു ലംബമായുള്ള താപധാരയാണ് പദാര്‍ഥത്തിന്റെ താപചാലകത എന്ന് നമുക്കു നിര്‍വചിക്കാം. എസ്.ഐ. പദ്ധതിയില്‍ വാട്ട് മീ.<sup>-1</sup> കെല്‍വിന്‍ <sup>-1</sup> എന്ന മാത്രയില്‍ ഇതു സൂചിപ്പിക്കപ്പെടുന്നു. |
വാതകങ്ങളുടെ താപചാലകതയെപ്പറ്റി പഠിക്കുവാന്‍ താപഗതികം ഒരു പരിധിവരെ സഹായിക്കും. ദ്രാവകങ്ങളിലെ ചാലനം ശബ്ദപ്രേഷണം നടക്കുന്നതുപോലെയാണ്. അണുലാറ്റിസുകളില്‍ക്കൂടി സഞ്ചരിക്കുന്ന തരംഗങ്ങള്‍ വഴിയാണ് ഡൈ ഇലക്ട്രിക് പദാര്‍ഥങ്ങളില്‍ ഊര്‍ജസംപ്രേഷണം ഉണ്ടാകുന്നത്. ലോഹങ്ങളിലാവട്ടെ, സ്വതന്ത്ര ഇലക്ട്രോണുകളാണ് താപചാലനത്തില്‍ പ്രധാനപങ്കുവഹിക്കുന്നത്. | വാതകങ്ങളുടെ താപചാലകതയെപ്പറ്റി പഠിക്കുവാന്‍ താപഗതികം ഒരു പരിധിവരെ സഹായിക്കും. ദ്രാവകങ്ങളിലെ ചാലനം ശബ്ദപ്രേഷണം നടക്കുന്നതുപോലെയാണ്. അണുലാറ്റിസുകളില്‍ക്കൂടി സഞ്ചരിക്കുന്ന തരംഗങ്ങള്‍ വഴിയാണ് ഡൈ ഇലക്ട്രിക് പദാര്‍ഥങ്ങളില്‍ ഊര്‍ജസംപ്രേഷണം ഉണ്ടാകുന്നത്. ലോഹങ്ങളിലാവട്ടെ, സ്വതന്ത്ര ഇലക്ട്രോണുകളാണ് താപചാലനത്തില്‍ പ്രധാനപങ്കുവഹിക്കുന്നത്. | ||
06:14, 21 ജനുവരി 2016-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ചാലകത
Conductivity
പദാര്‍ഥങ്ങള്‍ക്ക് വൈദ്യുതി, താപം എന്നിവ വഹനം ചെയ്യിക്കുന്നതിനുള്ള കഴിവിനെ സൂചിപ്പിക്കുന്ന പദം. വിദ്യുത്ചാലകത മോ മീറ്റര്‍-1 മാത്രയിലും താപചാലകത വാട്ട് മീറ്റര്‍ -1 കെല്‍വിന്‍ -1 മാത്രയിലും സൂചിപ്പിക്കുന്നു.
വിദ്യുത്ചാലകതയുടെ പരിമാണം അടിസ്ഥാനമാക്കി പദാര്‍ഥങ്ങളെ സുചാലകം, അര്‍ധചാലകം, കുചാലകം, അതിചാലകം എന്നിങ്ങനെ നാലായി തിരിക്കാറുണ്ട്. സുചാലകങ്ങളെ സംബന്ധിച്ചുള്ള ഒരു പ്രധാന നിയമം ഓം എന്ന ശാസ്ത്രജ്ഞന്‍ ആവിഷ്കരിച്ചു. ഒരു വിദ്യുത്ക്ഷേത്രം (E) പ്രയോഗിക്കുമ്പോള്‍ ഉണ്ടാകുന്ന ധാരാഘനത്വം (J) ഈ നിയമം അനുസരിച്ച്
J = σ E (1)
എന്ന് എഴുതാവുന്നതാണ്. ധാരാഘനത്വം, വിദ്യുത്ക്ഷേത്രത്തിന് അനുലോമാനുപാതികമാണെന്ന് മേല്പറഞ്ഞ സമീകരണം സൂചിപ്പിക്കുന്നു. ധാരാഘനത്വവും വിദ്യുത്ക്ഷേത്രവും തമ്മിലുള്ള അനുപാതസംഖ്യയെ വിദ്യുത്ചാലകത എന്ന് നിര്‍വചിക്കാം. പദാര്‍ഥത്തിന്റെ രോധത്വവും (ρ) ചാലകതയും
എന്നു ബന്ധപ്പെടുത്താം. രോധത്വത്തിന്റെ മാത്ര ഓംമീറ്റര്‍ ആണ്. ഓമിന്റെ പ്രതിലോമത്തെ മോ എന്നു പറയാറുള്ളതുകൊണ്ടാണ് വിദ്യുത്ചാലകത മോ മീറ്റര്‍ -1 എന്നെഴുതുന്നത്.
ലോഹങ്ങളെല്ലാം സാമാന്യമായി സുചാലകവസ്തുക്കളാണ്. ജര്‍മേനിയം, സിലിക്കോണ്‍ തുടങ്ങിയവ അര്‍ധചാലകങ്ങള്‍. അവയുടെ ചാലകത ലോഹങ്ങളുടേതിനെക്കാള്‍ കുറവാണ്. ആംബര്‍, മൈക്ക, ഗ്ലാസ് തുടങ്ങിയവയുടെ ചാലകത ഏറ്റവും കുറവാകയാല്‍ അവ കുചാലകങ്ങള്‍ അഥവാ ഇന്‍സുലേറ്ററുകള്‍ എന്ന പേരില്‍ അറിയപ്പെടുന്നു. 295K യില്‍ ചില വസ്തുക്കളുടെ വിദ്യുത്ചാലകത പട്ടിക 1-ല്‍ കൊടുത്തിരിക്കുന്നു.
(2)
ലോഹങ്ങളുടെ വിദ്യുത്ചാലകതയെ വിശദീകരിക്കുന്നതിന് ഡ്രൂഡ്, ലോറന്‍സ് എന്ന രണ്ടു ശാസ്ത്രജ്ഞന്മാര്‍ സ്വതന്ത്ര ഇലക്ട്രോണ്‍ സിദ്ധാന്തം അവതരിപ്പിച്ചു. ത്രിവിമീയമായ അണുലാറ്റസില്‍ വളരെയേറെ സ്വതന്ത്ര ഇലക്ട്രോണുകള്‍ ഉള്ള ഘടനയാണ് ലോഹങ്ങള്‍ക്കുള്ളതെന്ന് അവര്‍ സങ്കല്പിച്ചു. ഇലക്ട്രോണുകള്‍ അനിയതമായ താപീയചലനങ്ങള്‍ക്കു വിധേയമാണ്. ഒരു വിദ്യുത്ക്ഷേത്രം പ്രയോഗിക്കുമ്പോള്‍ ഇലക്ട്രോണുകള്‍ക്കു ത്വരണം അനുഭവപ്പെടും. പക്ഷേ, ഇലക്ട്രോണുകള്‍ അണുലാറ്റിസുമായി നിരന്തരം സംഘട്ടനം നടത്തുകയും അവമന്ദനത്തിനു വിധേയമായിത്തീരുകയും ചെയ്യുന്നു. താപീയ ചലനത്തിനു പുറമേ, ഇലക്ട്രോണുകള്‍ക്ക് വിദ്യുത്ക്ഷേത്രത്തിന്റെ ദിശയില്‍ ഒരു അനുഗമനപ്രവേഗംകൂടി ഉണ്ടാകുമെന്നാണ് ഇതിന്റെ അനന്തരഫലം. രണ്ടു സംഘട്ടനങ്ങള്‍ക്കിടയിലുള്ള സമയാന്തരാളം ആണെങ്കില്‍ ഇപ്രകാരമുണ്ടാകുന്ന അനുഗമന പ്രവേഗം (v) താഴെപ്പറയുന്ന രീതിയില്‍ എഴുതാം.
(3)
പദാര്‍ഥത്തിന്റെ മാത്രാവ്യാപ്തിയിലുള്ള സ്വതന്ത്ര ഇലക്ട്രോണുകളുടെ എണ്ണം n ആണെങ്കില്‍ ധാരാഘനത്വം
J = ne v (4)
υ യുടെ മൂല്യം പ്രതിസ്ഥാപിക്കുമ്പോള്‍
[[ചിത്രം:Pg821 scree006.png ]] (5)
ഈ സമീകരണത്തെ
J = σE
എന്ന ഓം നിയമവുമായി താരതമ്യം ചെയ്യുമ്പോള്‍
(6)
എന്നു ലഭിക്കുന്നു. ഇലക്ട്രോണുകളുടെ സംഘട്ടനങ്ങള്‍ക്കിടയിലെ മാധ്യമുക്തപഥം I-ഉം അനിയത ദിശകളിലേക്കുള്ള ശ.ശ.വേഗം u-ഉം ആണെങ്കില്‍ 
അതുകൊണ്ട്
(7)
I-ന് കാര്യമായ വ്യത്യാസം വരാത്ത അവസ്ഥകളി u കൂടുന്തോറും ചാലകത കുറഞ്ഞുവരുമെന്ന് ഈ സമീകരണം കാണിക്കുന്നു. താപഗതിക സിദ്ധാന്തമനുസരിച്ച് താപനില വര്‍ധിക്കുമ്പോ u കൂടേണ്ടതാണ്. അതുകൊണ്ട് വിദ്യുത്ചാലകത, താപനില വര്‍ധിക്കുന്തോറും കുറഞ്ഞുവരുമെന്നു കാണാം. ലോഹങ്ങളുടെ കാര്യത്തില്‍ σ, താപനിലയ്ക്കു പ്രതിലോമാനുപാതികമാണെന്ന് പരീക്ഷണങ്ങള്‍ വ്യക്തമാക്കുന്നു.n, l എന്നിവയ്ക്ക് താപനിലയനുസരിച്ച് വ്യത്യാസം ഉണ്ടാകുന്നില്ലെന്നു കരുതിക്കൊണ്ടാണ് നാം ഈ നിഗമനത്തിലെത്തിയത്. ഒരു അര്‍ധചാലകത്തിന്റെ കാര്യത്തില്‍ താപനിലയനുസരിച്ച് n മാറി വരുന്നതാണ്. ക്വാണ്ടം മെക്കാനിക സമീപനവും ഏതാണ്ട് ഇതേ രീതിയിലുള്ള നിഗമനങ്ങളിലേക്കു നയിക്കുമെന്ന് സാമാന്യമായി പറയാം. അര്‍ധചാലകവസ്തുക്കളില്‍ ഇലക്ട്രോണുകളും ഹോളുകളും ചാലകതയുണ്ടാക്കുന്നു. ഇവയെ യഥാക്രമം n ടൈപ്പ് ചാലകത, p ടൈപ്പ് ചാലകത എന്നു വിളിക്കുന്നു. അര്‍ധചാലകങ്ങളുടെ ചാലകത താപനില കൂടുന്തോറും എക്സ്പൊണന്‍ഷ്യല്‍ രീതിയില്‍ വര്‍ധിക്കുന്നു.
കേവല പൂജ്യത്തോടടുത്ത താപനിലകളില്‍ മെര്‍ക്കുറിയുടെ ചാലകത അനന്തമാകുമെന്ന് 1911-ല്‍ കാമര്‍ലിങ് ഓണ്‍സ് എന്ന ശാസ്ത്രജ്ഞന്‍ കണ്ടുപിടിച്ചു. മോളിബ്ഡിനം, ലെഡ്, ടിന്‍ തുടങ്ങിയ മറ്റു പല വസ്തുക്കളും ഈ സ്വഭാവം പ്രദര്‍ശിപ്പിക്കുന്നുണ്ട്. ഇത്തരം വസ്തുക്കളെ അതിചാലകങ്ങള്‍ എന്നുപറയുന്നു. അതിചാലകങ്ങള്‍ അപകാന്തികവസ്തുക്കളെപ്പോലെ പെരുമാറുമെന്ന് മെയ്സ്നര്‍ കണ്ടെത്തി. രോധശൂന്യതയും അപകാന്തികത്വവുമാണ് അതിചാലകങ്ങളെ വേര്‍തിരിച്ചു കാണിക്കുന്ന ഗുണധര്‍മങ്ങള്‍. ഫോണോണ്‍ മുഖേന ഇലക്ട്രോണുകള്‍ പരസ്പരം ആകര്‍ഷിക്കപ്പെടുന്നതുകൊണ്ടാണ് അതിചാലകത ഉണ്ടാകുന്നതെന്ന് ബാര്‍ഡീന്‍, കൂപ്പര്‍, ഷ്റിഫര്‍ എന്നീ ശാസ്ത്രജ്ഞന്മാര്‍ വിശദമാക്കി (BCS സിദ്ധാന്തം). ഉയര്‍ന്ന താപനിലകളില്‍ ചില സെറാമിക് പദാര്‍ഥങ്ങള്‍ അതിചാലകത പ്രദര്‍ശിപ്പിക്കുന്നതായി അടുത്തകാലത്ത് കണ്ടുപിടിച്ചിട്ടുണ്ട്. ഇതിന്റെ കാരണം ആഇട സിദ്ധാന്തംകൊണ്ട് വിശദീകരിക്കാന്‍ കഴിയുകയില്ല.
താപചാലകത. ഏകസമാനമല്ലാതെ ചൂടാക്കപ്പെടുന്ന ഒരു വസ്തുവിന്റെ താപനില കൂടിയ ഭാഗത്തുനിന്ന് കുറഞ്ഞ സ്ഥലങ്ങളിലേക്കുള്ള താപപ്രേഷണമാണ് ചാലനം. ഖരവസ്തുക്കളില്‍ പ്രധാനമായും ഈ മാര്‍ഗത്തില്‍ക്കൂടിയാണ് താപപ്രേഷണം സംഭവിക്കുന്നത്. ഒരു പദാര്‍ഥത്തിലെ തന്മാത്രകള്‍ കേവലപൂജ്യത്തിനു മുകളിലുള്ള താപനിലകളില്‍ സ്പന്ദനം ചെയ്തുകൊണ്ടിരിക്കും. താപോര്‍ജം സ്വീകരിക്കുന്നതോടെ സ്പന്ദനം ശക്തിമത്താവുകയും സമീപസ്ഥങ്ങളും പതുക്കെ സ്പന്ദിക്കുന്നവയുമായ തന്മാത്രകള്‍ക്ക് ഊര്‍ജം കൈമാറുകയും ചെയ്യുന്നു. തന്മാത്രകള്‍ക്ക് സ്ഥാനാന്തരണം സംഭവിക്കാതെയാണ് ഇവിടെ ഊര്‍ജം പ്രേഷണം ചെയ്യപ്പെടുന്നത്.
ഒരു വസ്തുവിന് ചാലനം വഴി താപം കൈമാറാനുള്ള കഴിവിന്റെ അളവാണ് താപചാലകത.
കനമുള്ള ഒരു സ്ളാബിന്റെ ഛേദതല വിസ്തീര്‍ണം A ആണെന്നു കരുതുക. അതിന്റെ ഒരു വശത്തെ താപനില θയും എതിര്‍വശത്തേത് θ +Δθയും ആക്കി നിലനിര്‍ത്തുന്നുവെങ്കില്‍ വശങ്ങള്‍ക്കു ലംബമായി താപം പ്രവഹിക്കുന്ന നിരക്ക് ഛേദതലവിസ്തീര്‍ണത്തിനും താപനിലാവ്യത്യാസത്തിനും നേര്‍അനുപാതത്തിലും കനത്തിന് പ്രതിലോമാനുപാതത്തിലുമാണെന്ന് പരീക്ഷണങ്ങള്‍ കാണിക്കുന്നു. ഈ ഫലങ്ങളെ
(8)
എന്ന് എഴുതാം. ഇവിടെ Q /t താപപ്രവാഹത്തിന്റെ നിരക്ക് ആണ്. Δxവളരെ ചെറുതാണെങ്കില്‍യും Δθചെറുതായിരിക്കും. അതുകൊണ്ട് സീമാന്തമൂല്യം എടുത്ത് സാമാന്യവത്കരണം നടത്തിയാല്‍ താപപ്രവാഹനിരക്ക്
[[ചിത്രം:Pg821 scre0013.png ]] (9)
എന്നാകുന്നു. ഇവിടെ 
നെ താപനിലയുടെ ഗ്രേഡിയന്റ് അഥവാ ചരിവുമാനം എന്നുപറയാം. ചാലക പദാര്‍ഥത്തെമാത്രം ആശ്രയിക്കുന്ന സ്ഥിരാങ്കമാണ് K. ഇതിനെ താപചാലകത എന്നു നാമകരണം ചെയ്യാം. താപചാലനം സംബന്ധിച്ച നിരവധി ഗവേഷണങ്ങള്‍ നടത്തിയ ഫൂറിയര്‍ എന്ന ശാസ്ത്രജ്ഞന്റെ ബഹുമാനാര്‍ഥം മേല്‍ക്കൊടുത്ത സമീകരണത്തെ ഫൂറിയര്‍ സമീകരണം എന്നു പറയാറുണ്ട്. സ്ഥിരസ്ഥിതിയില്‍ താപനിലയുടെ മാത്രാഗ്രേഡിയന്റ് നിലവിലുള്ളപ്പോള്‍, മാത്രാവിസ്തീര്‍ണത്തിലൂടെ വശത്തിനു ലംബമായുള്ള താപധാരയാണ് പദാര്‍ഥത്തിന്റെ താപചാലകത എന്ന് നമുക്കു നിര്‍വചിക്കാം. എസ്.ഐ. പദ്ധതിയില്‍ വാട്ട് മീ.-1 കെല്‍വിന്‍ -1 എന്ന മാത്രയില്‍ ഇതു സൂചിപ്പിക്കപ്പെടുന്നു.
വാതകങ്ങളുടെ താപചാലകതയെപ്പറ്റി പഠിക്കുവാന്‍ താപഗതികം ഒരു പരിധിവരെ സഹായിക്കും. ദ്രാവകങ്ങളിലെ ചാലനം ശബ്ദപ്രേഷണം നടക്കുന്നതുപോലെയാണ്. അണുലാറ്റിസുകളില്‍ക്കൂടി സഞ്ചരിക്കുന്ന തരംഗങ്ങള്‍ വഴിയാണ് ഡൈ ഇലക്ട്രിക് പദാര്‍ഥങ്ങളില്‍ ഊര്‍ജസംപ്രേഷണം ഉണ്ടാകുന്നത്. ലോഹങ്ങളിലാവട്ടെ, സ്വതന്ത്ര ഇലക്ട്രോണുകളാണ് താപചാലനത്തില്‍ പ്രധാനപങ്കുവഹിക്കുന്നത്.
ലോഹങ്ങളെ സംബന്ധിച്ച് താപചാലകതയും വിദ്യുത്ചാലകതയും തമ്മിലുള്ള ബന്ധം വീഡ്മാന്‍, ഫ്രാന്‍സ് എന്നിവര്‍ ആവിഷ്കരിച്ചു. ഒരു നിശ്ചിത താപനിലയില്‍ താപചാലകതയും വിദ്യുത്ചാലകതയും തമ്മിലുള്ള അനുപാതം സ്ഥിരമായിരിക്കും എന്നതാണ് വീഡ്മാന്‍-ഫ്രാന്‍സ് നിയമം. താപചാലകത, വിദ്യുത്ചാലകത, താപനില എന്നിവ യഥാക്രമം K,σ,Tഎന്നെഴുതിയാല്‍ K/σT ഒരു സ്ഥിരസംഖ്യയാണ്. ഇതിനെ ലോറന്‍സ് സംഖ്യയെന്നു വിളിക്കുന്നു. സ്വതന്ത്ര ഇലക്ട്രോണ്‍ സിദ്ധാന്തത്തില്‍ നിന്ന് ഇതിന്റെ മൂല്യം 2.45 x 108 വാട്ട് ഓം കെല്‍വിന്‍ -2 എന്ന് കിട്ടുന്നു.
മാലിന്യങ്ങളുണ്ടെങ്കില്‍ ലോഹങ്ങളുടെ താപചാലകതയ്ക്കു വലിയ മാറ്റം കാണാറുണ്ട്. ഒരു ഖരവസ്തു ദ്രാവകാവസ്ഥയിലേക്കു മാറിക്കഴിഞ്ഞാല്‍ താപചാലകത കുറയുന്നു. ദ്രാവകങ്ങളുടെ താപചാലകത താപനില വര്‍ധിക്കുമ്പോള്‍ കൂടുന്നതായി കാണാറുണ്ട്.
താപനിലയനുസരിച്ച് പദാര്‍ഥങ്ങളുടെ താപചാലകത വ്യത്യാസപ്പെടുമെങ്കിലും നിയതമായ ഒരു നിയമം മുഖേന ഈ വ്യതിയാനത്തെ സൂചിപ്പിക്കുവാന്‍ വിഷമമാണ്. ചില വസ്തുക്കള്‍ക്ക് താപനിലയും താപചാലകതയും തമ്മിലുള്ള ബന്ധം ചിത്രത്തില്‍ കാണിച്ചിരിക്കുന്നു.
(ഡോ. എം.കെ. രുദ്രവാരിയര്‍)
