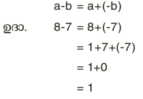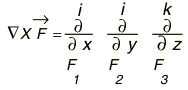This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗണിതശബ്ദാവലി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→ഗണിതശബ്ദാവലി) |
(→ഗണിതശബ്ദാവലി) |
||
| വരി 188: | വരി 188: | ||
'''ദശഭുജം''' (Decagon). പത്തു വശങ്ങളുള്ള ഒരു ബഹുഭുജം. | '''ദശഭുജം''' (Decagon). പത്തു വശങ്ങളുള്ള ഒരു ബഹുഭുജം. | ||
| - | '''ദശാംശം''' (Decimal). പത്ത് ആധാരമായുള്ള സംഖ്യാപദ്ധതി. ഉദാ. എണ്ണുവാനുപയോഗിക്കുന്ന സംഖ്യകള്, ഒറ്റ, പത്തിലൊന്ന്, നൂറിലൊന്ന് തുടങ്ങിയവയില് എഴുതുന്ന പരിമേയസംഖ്യ(rational number)യാണ് ദശാംശഭിന്നം (decimal fraction). ദശാംശ അങ്കനരീതിയനുസരിച്ച് നെ 0.125 എന്നെഴുതുന്നു. അക്കങ്ങള് ആവര്ത്തിക്കുന്ന ദശാംശഭിന്നത്തെ ആവര്ത്തി ദശാംശം (recurring decimal) എന്നു പറയുന്നു. ഉദാ. 1.666... | + | '''ദശാംശം''' (Decimal). പത്ത് ആധാരമായുള്ള സംഖ്യാപദ്ധതി. ഉദാ. എണ്ണുവാനുപയോഗിക്കുന്ന സംഖ്യകള്, ഒറ്റ, പത്തിലൊന്ന്, നൂറിലൊന്ന് തുടങ്ങിയവയില് എഴുതുന്ന പരിമേയസംഖ്യ(rational number)യാണ് ദശാംശഭിന്നം (decimal fraction). ദശാംശ അങ്കനരീതിയനുസരിച്ച് ⅛ നെ 0.125 എന്നെഴുതുന്നു. അക്കങ്ങള് ആവര്ത്തിക്കുന്ന ദശാംശഭിന്നത്തെ ആവര്ത്തി ദശാംശം (recurring decimal) എന്നു പറയുന്നു. ഉദാ. 1.666... |
'''ദശാംശസമ്പ്രദായം'''. 'പത്ത്' ആധാരമാക്കിയുള്ള സംഖ്യാസമ്പ്രദായം. | '''ദശാംശസമ്പ്രദായം'''. 'പത്ത്' ആധാരമാക്കിയുള്ള സംഖ്യാസമ്പ്രദായം. | ||
| വരി 194: | വരി 194: | ||
'''ദീര്ഘവൃത്തം'''. വിസ്ലേഷകജ്യാമിതിയില് ഉത്കേന്ദ്രത(e) ഒന്നില് കുറവായ കോണികം. അണ്ഡാകൃതിയായ വക്രമാണിത്. | '''ദീര്ഘവൃത്തം'''. വിസ്ലേഷകജ്യാമിതിയില് ഉത്കേന്ദ്രത(e) ഒന്നില് കുറവായ കോണികം. അണ്ഡാകൃതിയായ വക്രമാണിത്. | ||
| - | '''ദീര്ഘവൃത്തജം''' (Ellipsoid). ഓരോ സമതല പരിച്ഛേദവും ദീര്ഘവൃത്തമോ അല്ലെങ്കില് വൃത്തമോ ആയ ഘനരൂപം. ഇതിനു മൂന്നു സമമിത അക്ഷങ്ങള് (axes of symmetry) ഉണ്ട്. ഇതിന്റെ വിശേഷസ്ഥിതിയാണ് ഗോളം. നിര്ദേശാങ്കജ്യാമിതിയില് ദീര്ഘവൃത്തജത്തിന്റെ സമീകരണം ആണ്. | + | '''ദീര്ഘവൃത്തജം''' (Ellipsoid). ഓരോ സമതല പരിച്ഛേദവും ദീര്ഘവൃത്തമോ അല്ലെങ്കില് വൃത്തമോ ആയ ഘനരൂപം. ഇതിനു മൂന്നു സമമിത അക്ഷങ്ങള് (axes of symmetry) ഉണ്ട്. ഇതിന്റെ വിശേഷസ്ഥിതിയാണ് ഗോളം. നിര്ദേശാങ്കജ്യാമിതിയില് ദീര്ഘവൃത്തജത്തിന്റെ സമീകരണം [[ചിത്രം:Pg732_for_002.png]] ആണ്. |
'''ദൃഗ്ഗണിതം'''. ഒരു ജ്യോതിഷഗണിതപദ്ധതി. ആര്യഭടീയഗണിതത്തെ അടിസ്ഥാനമാക്കി അതിലെ ഗണനസംഖ്യകളെയും ഗണനക്രിയകളെയും ലഘുപ്പെടുത്തി, ഗണിച്ചുകിട്ടിയ ഫലങ്ങള്ക്ക് സൂക്ഷ്മതയുണ്ടാകാന് വേണ്ട സംകാരങ്ങളും ചെയ്ത് ദൃഷ്ടഫലംകൊണ്ട് കണ്ടുപിടിച്ച ഒരു പദ്ധതി. | '''ദൃഗ്ഗണിതം'''. ഒരു ജ്യോതിഷഗണിതപദ്ധതി. ആര്യഭടീയഗണിതത്തെ അടിസ്ഥാനമാക്കി അതിലെ ഗണനസംഖ്യകളെയും ഗണനക്രിയകളെയും ലഘുപ്പെടുത്തി, ഗണിച്ചുകിട്ടിയ ഫലങ്ങള്ക്ക് സൂക്ഷ്മതയുണ്ടാകാന് വേണ്ട സംകാരങ്ങളും ചെയ്ത് ദൃഷ്ടഫലംകൊണ്ട് കണ്ടുപിടിച്ച ഒരു പദ്ധതി. | ||
| വരി 200: | വരി 200: | ||
'''ദ്വയാംഗസമ്പ്രദായം'''. 0, 1 എന്നീ അക്കങ്ങള് മാത്രം ഉപയോഗിച്ചുള്ള സംഖ്യാസമ്പ്രദായം. ആധാരം '2' ആണ്. | '''ദ്വയാംഗസമ്പ്രദായം'''. 0, 1 എന്നീ അക്കങ്ങള് മാത്രം ഉപയോഗിച്ചുള്ള സംഖ്യാസമ്പ്രദായം. ആധാരം '2' ആണ്. | ||
| - | '''ദ്വിഘാതസമവാക്യം''' (Quadratic equation). രണ്ടാം ഘാതത്തിലുള്ള ബീജിയസമവാക്യം. ഉദാ. ax<sup>2</sup> + bx + c = 0 ഈ സമവാക്യത്തിന്റെ നിര്ധാരണമൂല്യങ്ങള് ആണ്. | + | '''ദ്വിഘാതസമവാക്യം''' (Quadratic equation). രണ്ടാം ഘാതത്തിലുള്ള ബീജിയസമവാക്യം. ഉദാ. ax<sup>2</sup> + bx + c = 0 ഈ സമവാക്യത്തിന്റെ നിര്ധാരണമൂല്യങ്ങള് [[ചിത്രം:Pag732for001.png]] ആണ്. |
'''ദ്വിപദ സിദ്ധാന്തം'''. ഒരു പ്രധാന ബീജീയസര്വസമവാക്യം. ഒരു ദ്വിപദ (binomial)ത്തിന്റെ ഏതു ഘാതത്തിന്റെയും വിപുലീകരണത്തിനുള്ള നിയമം. ദ്വിപദസൂത്രവാക്യം (binomial formula) എന്നു പറയാം. | '''ദ്വിപദ സിദ്ധാന്തം'''. ഒരു പ്രധാന ബീജീയസര്വസമവാക്യം. ഒരു ദ്വിപദ (binomial)ത്തിന്റെ ഏതു ഘാതത്തിന്റെയും വിപുലീകരണത്തിനുള്ള നിയമം. ദ്വിപദസൂത്രവാക്യം (binomial formula) എന്നു പറയാം. | ||
| വരി 212: | വരി 212: | ||
'''പരാബൊള''' (Parabola, '''പരാവലയം'''). ഒരു സ്ഥിരബിന്ദു (ഫോക്കസ്)വില് നിന്ന് ഒരു നിശ്ചിതരേഖ(ഡയറക്ട്രിക്സ്)യില് നിന്നുമുള്ള ദൂരം തുല്യമാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ സഞ്ചാരപഥമായ വക്രം. ഉത്കേന്ദ്രത (eccentricity) ഒന്ന് ആയ കോണികമാണ് പരാബൊള. ഇതിന്റെ മാനകസമീകരണം (standard equation) y<sup>2</sup> = 4ax ആണ്. | '''പരാബൊള''' (Parabola, '''പരാവലയം'''). ഒരു സ്ഥിരബിന്ദു (ഫോക്കസ്)വില് നിന്ന് ഒരു നിശ്ചിതരേഖ(ഡയറക്ട്രിക്സ്)യില് നിന്നുമുള്ള ദൂരം തുല്യമാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ സഞ്ചാരപഥമായ വക്രം. ഉത്കേന്ദ്രത (eccentricity) ഒന്ന് ആയ കോണികമാണ് പരാബൊള. ഇതിന്റെ മാനകസമീകരണം (standard equation) y<sup>2</sup> = 4ax ആണ്. | ||
| - | '''പരിമേയസംഖ്യ''' (Rational number). രണ്ടു പൂര്ണസംഖ്യകളുടെ അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ. pയും q-ഉം പൂര്ണസംഖ്യകളാണെങ്കില് എന്ന അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ പരിമേയസംഖ്യയാണ് (). ഉദാ. | + | '''പരിമേയസംഖ്യ''' (Rational number). രണ്ടു പൂര്ണസംഖ്യകളുടെ അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ. pയും q-ഉം പൂര്ണസംഖ്യകളാണെങ്കില് [[ചിത്രം:Pg733_for010.png]] എന്ന അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ പരിമേയസംഖ്യയാണ് (q ≠ 0). ഉദാ. [[ചിത്രം:Pg733_for_-_00.png]] |
'''പരിവൃത്തം''' (Circumcircle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു ശീര്ഷങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ഒരു ചക്രീയ ബഹുഭുജ (cyclic polygon)ത്തിന്റെ ശീര്ഷകങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ആയ വൃത്തം. വൃത്തകേന്ദ്രത്തെ പരികേന്ദ്ര(circumcentre)മെന്നു പറയുന്നു. | '''പരിവൃത്തം''' (Circumcircle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു ശീര്ഷങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ഒരു ചക്രീയ ബഹുഭുജ (cyclic polygon)ത്തിന്റെ ശീര്ഷകങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ആയ വൃത്തം. വൃത്തകേന്ദ്രത്തെ പരികേന്ദ്ര(circumcentre)മെന്നു പറയുന്നു. | ||
| വരി 218: | വരി 218: | ||
'''പിരമിഡ്''' (Pyramid). ആധാരം ബഹുഭുജവും പാര്ശ്വങ്ങള് പൊതുവായ ശീര്ഷമുള്ള ത്രികോണങ്ങളും ചേര്ന്ന ഘനരൂപം. ഒരു സമ-പിരമിഡില് (regular pyramid) പാര്ശ്വങ്ങള് ആധാരവുമായി തുല്യകോണങ്ങളുള്ള സര്വസമങ്ങളായ സമഭുജത്രികോണങ്ങളായിരിക്കും. | '''പിരമിഡ്''' (Pyramid). ആധാരം ബഹുഭുജവും പാര്ശ്വങ്ങള് പൊതുവായ ശീര്ഷമുള്ള ത്രികോണങ്ങളും ചേര്ന്ന ഘനരൂപം. ഒരു സമ-പിരമിഡില് (regular pyramid) പാര്ശ്വങ്ങള് ആധാരവുമായി തുല്യകോണങ്ങളുള്ള സര്വസമങ്ങളായ സമഭുജത്രികോണങ്ങളായിരിക്കും. | ||
| - | '''പൂജ്യം''' (Zero). ഒരു സംഖ്യയോടു മറ്റൊരു സംഖ്യ കൂട്ടിയാല് തുകയായി ആദ്യസംഖ്യതന്നെ കിട്ടുമെങ്കില് കൂട്ടിയ സംഖ്യ പൂജ്യമാണ്. പൂജ്യത്തെക്കുറിക്കാന് '0' എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. ശൂന്യഗണത്തിന്റെ കാര്ഡിനല്സംഖ്യ, സംഖ്യാരേഖയില് ധനസംഖ്യകളെയും ഋണസംഖ്യകളെയും വിഭജിക്കുന്ന ബിന്ദു, വാസ്തവിക സംഖ്യകളുടെ സങ്കലനത്തിലെ അനന്യകം(identity element)n-ന്റെ വില അനന്തതയെ സമീപിക്കുമ്പോള് -ന്റെ സീമ (limit) എന്നിങ്ങനെ പൂജ്യത്തെ പലവിധത്തില് വിശദീകരിക്കാം. | + | '''പൂജ്യം''' (Zero). ഒരു സംഖ്യയോടു മറ്റൊരു സംഖ്യ കൂട്ടിയാല് തുകയായി ആദ്യസംഖ്യതന്നെ കിട്ടുമെങ്കില് കൂട്ടിയ സംഖ്യ പൂജ്യമാണ്. പൂജ്യത്തെക്കുറിക്കാന് '0' എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. ശൂന്യഗണത്തിന്റെ കാര്ഡിനല്സംഖ്യ, സംഖ്യാരേഖയില് ധനസംഖ്യകളെയും ഋണസംഖ്യകളെയും വിഭജിക്കുന്ന ബിന്ദു, വാസ്തവിക സംഖ്യകളുടെ സങ്കലനത്തിലെ അനന്യകം(identity element)n-ന്റെ വില അനന്തതയെ സമീപിക്കുമ്പോള് [[ചിത്രം:Pg733for_-001.jpg]] -ന്റെ സീമ (limit) എന്നിങ്ങനെ പൂജ്യത്തെ പലവിധത്തില് വിശദീകരിക്കാം. |
'''പൂര്ണസംഖ്യ''' (integer). 1, 2, 3,..., 1, 2, 3, ...0 (പൂജ്യം) ഇവയില് ഏതെങ്കിലുമൊരു സംഖ്യ. | '''പൂര്ണസംഖ്യ''' (integer). 1, 2, 3,..., 1, 2, 3, ...0 (പൂജ്യം) ഇവയില് ഏതെങ്കിലുമൊരു സംഖ്യ. | ||
| വരി 228: | വരി 228: | ||
'''ബഹിര്വൃത്തം''' (Ex-circle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു വശങ്ങളില് ഒരു വശത്തെ ആന്തരികമായും രണ്ടു വശങ്ങളെ ബാഹ്യമായും സ്പര്ശിച്ചുവരയ്ക്കുന്ന വൃത്തം. ഇതിന്റെ കേന്ദ്രമാണ് ബഹിര്കേന്ദ്രം (ex-centre). ഒരു ത്രികോണത്തില് മൂന്നു ബഹിര്വൃത്തങ്ങള് വരയ്ക്കാം. | '''ബഹിര്വൃത്തം''' (Ex-circle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു വശങ്ങളില് ഒരു വശത്തെ ആന്തരികമായും രണ്ടു വശങ്ങളെ ബാഹ്യമായും സ്പര്ശിച്ചുവരയ്ക്കുന്ന വൃത്തം. ഇതിന്റെ കേന്ദ്രമാണ് ബഹിര്കേന്ദ്രം (ex-centre). ഒരു ത്രികോണത്തില് മൂന്നു ബഹിര്വൃത്തങ്ങള് വരയ്ക്കാം. | ||
| - | ബഹുപദം (Polynomial). എന്ന രൂപത്തിലുള്ള ബീജീയ വ്യഞ്ജകം (algebraic expression). ഇവിടെ | + | '''ബഹുപദം''' (Polynomial). [[ചിത്രം:Pg733formul002.jpg]] എന്ന രൂപത്തിലുള്ള ബീജീയ വ്യഞ്ജകം (algebraic expression). ഇവിടെ n ബഹുപദത്തിന്റെ ഡിഗ്രിയെ കുറിക്കുന്നു. n = 1 ആകുമ്പോള് ബഹുപദം രേഖീയ(linear)മാണ്. |
| - | ബഹുഫലകം (Polyhedron). ബഹുഭുജങ്ങള് വശങ്ങളായുള്ള (faces) ഘനരൂപം. മൂന്നോ അതിലധികമോ വശങ്ങള് (ഫലകങ്ങള്) സന്ധിക്കുന്ന ബിന്ദു ഇതിന്റെ ഒരു ശീര്ഷ(vertex)മാണ്. സമ(regular)ബഹുഫലകത്തിന്റെ എല്ലാ വശങ്ങളും സര്വസമങ്ങളായ സമബഹുഭുജങ്ങളായിരിക്കും. 4, 6, 8, 12, 20 എന്നിങ്ങനെ വശങ്ങളുള്ള അഞ്ചു സമബഹുഫലകങ്ങള് മാത്രമേയുള്ളൂ. നാലു സമത്രിഭുജങ്ങള് വശങ്ങളായ സമചതുഷ്ഫലകം (regular tetrahedron), ആറു സമചതുരങ്ങള് വശങ്ങളായ സമഷഡ്ഫലകം (regular hexahedron-cube), എട്ട് സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമ അഷ്ടഫലകം (regular Octahedron), പന്ത്രണ്ടു സമപഞ്ചഭുജങ്ങള് വശങ്ങളായുള്ള സമദ്വാദശ ഫലകം (regular dodecahedron), ഇരുപതു സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമവിംശഫലകം (regular icosahedron) ഇവയാണ് സമബഹുഫലകങ്ങള്. | + | '''ബഹുഫലകം''' (Polyhedron). ബഹുഭുജങ്ങള് വശങ്ങളായുള്ള (faces) ഘനരൂപം. മൂന്നോ അതിലധികമോ വശങ്ങള് (ഫലകങ്ങള്) സന്ധിക്കുന്ന ബിന്ദു ഇതിന്റെ ഒരു ശീര്ഷ(vertex)മാണ്. സമ(regular)ബഹുഫലകത്തിന്റെ എല്ലാ വശങ്ങളും സര്വസമങ്ങളായ സമബഹുഭുജങ്ങളായിരിക്കും. 4, 6, 8, 12, 20 എന്നിങ്ങനെ വശങ്ങളുള്ള അഞ്ചു സമബഹുഫലകങ്ങള് മാത്രമേയുള്ളൂ. നാലു സമത്രിഭുജങ്ങള് വശങ്ങളായ സമചതുഷ്ഫലകം (regular tetrahedron), ആറു സമചതുരങ്ങള് വശങ്ങളായ സമഷഡ്ഫലകം (regular hexahedron-cube), എട്ട് സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമ അഷ്ടഫലകം (regular Octahedron), പന്ത്രണ്ടു സമപഞ്ചഭുജങ്ങള് വശങ്ങളായുള്ള സമദ്വാദശ ഫലകം (regular dodecahedron), ഇരുപതു സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമവിംശഫലകം (regular icosahedron) ഇവയാണ് സമബഹുഫലകങ്ങള്. |
| - | ബാഹ്യഗണനം (Extrapolation). ഒരു രാശിയുടെ തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് ഫലനത്തിന്റെ വില ആകലനം ചെയ്യുന്ന സമ്പ്രദായം. സംഖ്യാത്മകരീതിയില്, ഗ്രാഫു വരച്ചോ ബാഹ്യഗണനം നടത്താം. ഗ്രാഫ്രീതിയില്, തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് വരച്ചു വികസിപ്പിച്ച ഗ്രാഫില്നിന്ന് ഫലനത്തിന്റെ വില കണ്ടുപിടിക്കുന്നു. ഗ്രാഫ് ഋജുരേഖയാണെങ്കില് ഈ രീതിയെ രേഖീയ ബാഹ്യഗണനം എന്നു പറയുന്നു. | + | '''ബാഹ്യഗണനം''' (Extrapolation). ഒരു രാശിയുടെ തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് ഫലനത്തിന്റെ വില ആകലനം ചെയ്യുന്ന സമ്പ്രദായം. സംഖ്യാത്മകരീതിയില്, ഗ്രാഫു വരച്ചോ ബാഹ്യഗണനം നടത്താം. ഗ്രാഫ്രീതിയില്, തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് വരച്ചു വികസിപ്പിച്ച ഗ്രാഫില്നിന്ന് ഫലനത്തിന്റെ വില കണ്ടുപിടിക്കുന്നു. ഗ്രാഫ് ഋജുരേഖയാണെങ്കില് ഈ രീതിയെ രേഖീയ ബാഹ്യഗണനം എന്നു പറയുന്നു. |
| - | + | '''ബൃഹദ് വൃത്തം''' (Great circle). കേന്ദ്രത്തില്ക്കൂടി പോകുന്ന സമതലം ഗോളത്തെ ഛേദിക്കുന്ന വൃത്തം. | |
| - | ഭാജ്യസംഖ്യ (Composite Number). ഒന്നോ സംഖ്യതന്നെയോ അല്ലാതെ മറ്റു പൂര്ണസംഖ്യകള് ഘടകങ്ങളുള്ള പൂര്ണസംഖ്യ ഉദാ. 6, 10, 12, 21, ... | + | '''ഭാജ്യസംഖ്യ''' (Composite Number). ഒന്നോ സംഖ്യതന്നെയോ അല്ലാതെ മറ്റു പൂര്ണസംഖ്യകള് ഘടകങ്ങളുള്ള പൂര്ണസംഖ്യ ഉദാ. 6, 10, 12, 21, ... |
| - | '''മാട്രിക്സ്''' (Matrix). വരികളായും (row) കോളങ്ങളായും (column) വിന്യസിക്കുന്ന സംഖ്യകളുടെ ദീര്ഘചതുര വ്യൂഹം. 'm' വരികളും 'n' കോളങ്ങളുമുള്ള മാട്രിക്സിന് m x n മാട്രിക്സ് എന്നു പറയുന്നു. 2 x 2 മാട്രിക്സിന് ഉദാ. . ഇവിടെ a,b,c,d ഇവ മാട്രിക്സിലെ അംഗങ്ങളാണ്. മാട്രിക്സിന് സംഖ്യാത്മക മൂല്യം (numerical value) ഇല്ല. തുല്യമായ വരികളും കോളങ്ങളും ഉള്ള മാട്രിക്സിനെ വര്ഗമാട്രിക്സ് (square matrix) എന്നു പറയുന്നു. അംഗങ്ങളെല്ലാം പൂജ്യമായ മാട്രിക്സാണ് ശൂന്യമാട്രിക്സ് (null matrix). കെയ്ലി (Cayley)യാണ് മാട്രിക്സുകളുടെ ബീജഗണിതത്തെക്കുറിച്ച് പഠനം നടത്തിയത്. | + | '''മാട്രിക്സ്''' (Matrix). വരികളായും (row) കോളങ്ങളായും (column) വിന്യസിക്കുന്ന സംഖ്യകളുടെ ദീര്ഘചതുര വ്യൂഹം. 'm' വരികളും 'n' കോളങ്ങളുമുള്ള മാട്രിക്സിന് m x n മാട്രിക്സ് എന്നു പറയുന്നു. 2 x 2 മാട്രിക്സിന് ഉദാ. [[ചിത്രം:Pg733screen003.jpg]] . ഇവിടെ a,b,c,d ഇവ മാട്രിക്സിലെ അംഗങ്ങളാണ്. മാട്രിക്സിന് സംഖ്യാത്മക മൂല്യം (numerical value) ഇല്ല. തുല്യമായ വരികളും കോളങ്ങളും ഉള്ള മാട്രിക്സിനെ വര്ഗമാട്രിക്സ് (square matrix) എന്നു പറയുന്നു. അംഗങ്ങളെല്ലാം പൂജ്യമായ മാട്രിക്സാണ് ശൂന്യമാട്രിക്സ് (null matrix). കെയ്ലി (Cayley)യാണ് മാട്രിക്സുകളുടെ ബീജഗണിതത്തെക്കുറിച്ച് പഠനം നടത്തിയത്. |
'''മാധ്യം''' (Mean). ഒരു കൂട്ടം സംഖ്യകളെ പ്രതിനിധീകരിക്കുന്ന സംഖ്യ.x<sub>1</sub>,x<sub>2</sub>, ... ...x<sub>n</sub> എന്നീ സംഖ്യകളുടെ സമാന്തരമാധ്യം (arithmetic mean)-ശരാശരി (average), [[ചിത്രം:733Screen001.jpg]] ആണ്. ഈ സംഖ്യകളുടെ ഗുണോത്തരമാധ്യം (geometric mean) [[ചിത്രം:Pg733scree02.jpg]] ഉം ഹരാത്മകമാധ്യം (harmonic mean) ഉം [[ചിത്രം:Pg_733_scree004.jpg]] ആണ്. | '''മാധ്യം''' (Mean). ഒരു കൂട്ടം സംഖ്യകളെ പ്രതിനിധീകരിക്കുന്ന സംഖ്യ.x<sub>1</sub>,x<sub>2</sub>, ... ...x<sub>n</sub> എന്നീ സംഖ്യകളുടെ സമാന്തരമാധ്യം (arithmetic mean)-ശരാശരി (average), [[ചിത്രം:733Screen001.jpg]] ആണ്. ഈ സംഖ്യകളുടെ ഗുണോത്തരമാധ്യം (geometric mean) [[ചിത്രം:Pg733scree02.jpg]] ഉം ഹരാത്മകമാധ്യം (harmonic mean) ഉം [[ചിത്രം:Pg_733_scree004.jpg]] ആണ്. | ||
| വരി 291: | വരി 291: | ||
'''സമരേഖീയം''' (Collinear). ഒരേ രേഖയിലുള്ള ബിന്ദുക്കളാണ് സമരേഖീയ ബിന്ദുക്കള്. | '''സമരേഖീയം''' (Collinear). ഒരേ രേഖയിലുള്ള ബിന്ദുക്കളാണ് സമരേഖീയ ബിന്ദുക്കള്. | ||
| - | '''സമാകലനം''' (Integration). സമാകലം (integral) കണ്ടുപിടിക്കുന്ന പ്രക്രിയ. അവകലനത്തിന്റെ വിപരീതക്രിയയാണ് സമാകലനം | + | '''സമാകലനം''' (Integration). സമാകലം (integral) കണ്ടുപിടിക്കുന്ന പ്രക്രിയ. അവകലനത്തിന്റെ വിപരീതക്രിയയാണ് സമാകലനം F(x)-ന്റെ അവകലം (ഡെറിവേറ്റീവ്) f(x) ആയാല് f(x)ന്റെ സമാകലമാണ് F(x). ഇതിനെ f(x)dx = F(x) എന്നെഴുതുന്നു. ഇവിടെ f(x) സമാകല്യവും (integrand) x സമാകലനത്തിലെ ചരവും (variable) ആണ്. നിശ്ചിത സമാകലത്തെ (definite integral) [[ചിത്രം:Pg_734_screen0003.jpg ]] എന്നെഴുതുന്നു. വക്രങ്ങള് പരിബദ്ധമാക്കുന്ന വിസ്തീര്ണം, പരിക്രമണ ഘനരൂപ (solid of revolution)ങ്ങളുടെ വ്യാപ്തം തുടങ്ങിയവ കണ്ടുപിടിക്കാന് നിശ്ചിത സമാകലങ്ങള് ഉപയോഗിക്കുന്നു. ഒരു ഫലനത്തെ സമാകലിക്കാന് പല രീതികളുണ്ട്. പ്രതിസ്ഥാപനം (substitution)കൊണ്ടും ഖണ്ഡങ്ങളാക്കിയും (by parts) ആംശികഭിന്ന (partial fraction)ങ്ങള് വഴിയും ഫലനങ്ങളെ സാധാരണയായി സമാകലിക്കാറുണ്ട്. |
'''സമാന്തരശ്രേഢി''' (Arithmetic Progression). തുടര്ച്ചയായ ഏതെങ്കിലും രണ്ടു പദങ്ങള് തമ്മിലുള്ള വ്യത്യാസം, സ്ഥിരസംഖ്യയാകുന്ന ശ്രേഢി. ഈ വ്യത്യാസത്തെ പൊതുവ്യത്യാസം (common difference) എന്നു പറയുന്നു. ആദ്യപദം a-യും പൊതുവ്യത്യാസം d-യും ആയ ശ്രേഢിയെ a, a + d, a + 2d....,a + (n-1) d.... എന്നെഴുതാം. ഉദാ. 5, 8, 11, 14, 17.... | '''സമാന്തരശ്രേഢി''' (Arithmetic Progression). തുടര്ച്ചയായ ഏതെങ്കിലും രണ്ടു പദങ്ങള് തമ്മിലുള്ള വ്യത്യാസം, സ്ഥിരസംഖ്യയാകുന്ന ശ്രേഢി. ഈ വ്യത്യാസത്തെ പൊതുവ്യത്യാസം (common difference) എന്നു പറയുന്നു. ആദ്യപദം a-യും പൊതുവ്യത്യാസം d-യും ആയ ശ്രേഢിയെ a, a + d, a + 2d....,a + (n-1) d.... എന്നെഴുതാം. ഉദാ. 5, 8, 11, 14, 17.... | ||
08:19, 7 സെപ്റ്റംബര് 2015-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ഗണിതശബ്ദാവലി
ഗണിതശാസ്ത്രത്തില് സാധാരണ ഉപയോഗിക്കുന്ന പ്രധാന സാങ്കേതിക സംജ്ഞകളുടെ ലഘുവിവരണം.
അങ്കഗണിതം (Arithmetic). ധനസംഖ്യകളുടെ ചതുഷ്ക്രിയകള് (കൂട്ടല്, കുറയ്ക്കല്, ഗുണിക്കല്, ഹരിക്കല്) ഉപയോഗിച്ചുള്ള കണക്കുകൂട്ടലുകളുടെ പഠനം. നിത്യജീവിതത്തില് ആവശ്യമായിവരുന്ന ഗണിതമാണ് അങ്കഗണിതം.
അനന്തത (infinity). സീമയില്ലാതെ വര്ധിക്കുന്ന ഒരു രാശിയുടെ വില. ഉദാ. ![]() ആയാല് x-ന്റെ വില പൂജ്യത്തോടടുക്കുമ്പോള്,y അനന്തതയോടടുക്കുന്നു. അനന്തത കുറിക്കാന് എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. സങ്കല്പിക്കാവുന്ന ഏതു വലിയ സംഖ്യയെക്കാളും വലുത് എന്ന് സാമാന്യമായി അനന്തതയെക്കുറിച്ചു പറയാം. അനന്തതയോളം വലിയ ഋണരാശിയെ എന്ന പ്രതീകംകൊണ്ടു കുറിക്കുന്നു.
ആയാല് x-ന്റെ വില പൂജ്യത്തോടടുക്കുമ്പോള്,y അനന്തതയോടടുക്കുന്നു. അനന്തത കുറിക്കാന് എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. സങ്കല്പിക്കാവുന്ന ഏതു വലിയ സംഖ്യയെക്കാളും വലുത് എന്ന് സാമാന്യമായി അനന്തതയെക്കുറിച്ചു പറയാം. അനന്തതയോളം വലിയ ഋണരാശിയെ എന്ന പ്രതീകംകൊണ്ടു കുറിക്കുന്നു.
അനന്തസ്പര്ശി (Asymptote). അനന്തദൂരത്തുള്ള ഒരു ബിന്ദുവില് വക്രത്തെ (curve) സ്പര്ശിക്കുന്ന രേഖ.
അനിര്ധാര്യ രൂപങ്ങള് (Indeterminate forms). സാധാരണരീതിയില് വില കണ്ടുപിടിക്കാന് സാധിക്കാത്ത ഗണിതരൂപങ്ങള് ![]() തുടങ്ങിയവ ഇതിലുള്പ്പെടുന്നു.
തുടങ്ങിയവ ഇതിലുള്പ്പെടുന്നു.
അന്തര്ഗണനം (Interpolation).y = f (x) എന്ന ഫലനത്തിന്റെ വില x = x1,x2...xn എന്നീ മൂല്യങ്ങള്ക്കൊത്ത് അറിയാമെങ്കില്,x-ന്റെ ഈ മൂല്യങ്ങള്ക്കിടയ്ക്കുവരുന്ന ഏതെങ്കിലും മൂല്യത്തിന് ഫലനത്തിന്റെ വില ആകലനം ചെയ്യുന്ന സമ്പ്രദായംx-ന്റെയുംy-യുടെയും വിലകള് ഗ്രാഫ് പേപ്പറില് അടയാളപ്പെടുത്തുകയാണെങ്കില് അടുത്തുവരുന്ന രണ്ടു ബിന്ദുക്കള്ക്കിടയിലെ ഫലനത്തിന്റെ വില കണ്ടുപിടിക്കാന് ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന നേര്രേഖ വരച്ചാല്മതി. ഇതിനെ രേഖീയ(linear) അന്തര്ഗണനം എന്നു പറയുന്നു.
അന്തര്വൃത്തം (Incircle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു വശങ്ങളെ സ്പര്ശിച്ചുകൊണ്ടു വരയ്ക്കുന്ന വൃത്തം. ഈ വൃത്തത്തിന്റെ കേന്ദ്രമാണ് അന്തഃകേന്ദ്രം (incentre).
അപകേന്ദ്രസരണം (Divergence). അനന്തശ്രേണിയുടെ ഒരു ഗുണധര്മം. ഈ ധര്മമുള്ള ശ്രേണിയെ അപകേന്ദ്രസാരി (divergent) എന്നു പറയുന്നു. ഈ ശ്രേണിയുടെ സങ്കലനഫലനം അപരിമിതമായിരിക്കും.
അപരിമേയ സംഖ്യ (Irrational number). രണ്ടു പൂര്ണസംഖ്യകളുടെ കൃത്യമായ അംശബന്ധമായി എഴുതാന് സാധിക്കാത്ത സംഖ്യ. ഉദാ. ![]()
അപസിദ്ധാന്തം (Fallacy). പ്രത്യക്ഷത്തില് ശരിയെന്നു തോന്നാവുന്ന അയുക്തികമായ പ്രസ്താവന. അടിസ്ഥാനതത്ത്വങ്ങളിലും രീതികളിലും തെറ്റുവരുമ്പോഴാണ് അപസിദ്ധാന്തപരമായ പ്രസ്താവന ഉണ്ടാകുന്നത്.
അബാക്കസ് (Abacus). ഏറ്റവും പഴക്കമുള്ളതും ലഘുവായതുമായ ഗണന ഉപകരണം. അബാക്കസിന്റെ ഫ്രെയിമില് നിരയായി ഘടിപ്പിച്ചിട്ടുള്ള കമ്പികളില് മുത്തുകള് കോര്ത്തിട്ടുണ്ട്. ഇവ ഉപയോഗിച്ചാണ് ഗണനം നടത്തുന്നത്. പൂര്ണസംഖ്യകളുടെ കണക്കുകൂട്ടലുകള്ക്ക് ഇതുപയോഗിക്കുന്നു.
അഭാജ്യസംഖ്യ (Prime number). ഒന്നിനെ(1)ക്കാള് വലുതും ഒന്നോ (1) അതുതന്നെയോ അല്ലാതെ മറ്റു പൂര്ണസംഖ്യാഘടകങ്ങള് ഇല്ലാത്തതുമായ പൂര്ണസംഖ്യ. 2 = 2 x 1 ആയതുകൊണ്ട് 2-ന്റെ ഒരു ഘടകം അതുതന്നെയാണ്; മറ്റേ ഘടകം 1-ഉം. അതുകൊണ്ട് 2 ഒരു അഭാജ്യസംഖ്യയാണ്. 3, 5, 7, 11, 13... ... ... തുടങ്ങിയവയും അഭാജ്യസംഖ്യകളാണ്. അനന്തം അഭാജ്യസംഖ്യകള് ഉണ്ടെന്ന് യൂക്ലിഡ് (Euclid) തെളിയിച്ചിട്ടുണ്ട്.
അഭികേന്ദ്രസരണം (Convergence). അനന്തശ്രേണിയുടെ ഒരു ഗുണധര്മം. ഈ ഗുണധര്മമുള്ള ശ്രേണി അഭികേന്ദ്രസാരി (convergent)യാണെന്നു പറയുന്നു. ഉദാ. ![]() എന്ന ശ്രേണി അഭികേന്ദ്രസാരിയാണ്. അഭികേന്ദ്രസാരിശ്രേണികളുടെ സങ്കലനഫലം (sum) പരിമിതസംഖ്യ(finite)യായിരിക്കും.
എന്ന ശ്രേണി അഭികേന്ദ്രസാരിയാണ്. അഭികേന്ദ്രസാരിശ്രേണികളുടെ സങ്കലനഫലം (sum) പരിമിതസംഖ്യ(finite)യായിരിക്കും.
അഭിഗൃഹീതം (Postulate). തെളിവ് ആവശ്യമില്ലാത്ത അഥവാ സ്വയം തെളിയുന്ന തത്ത്വം.
അംശബന്ധം (Ratio). ഒരേ തലത്തിലുള്ള രണ്ടു രാശികളുടെ വിലകള് (ഒരേ മാത്രയിലുള്ളത്) താരതമ്യപ്പെടുത്തുന്ന ഭിന്നം. രാശികളുടെ വിലകള് a-യും b-യും ആയാല് അംശബന്ധം ![]() എന്നോ a:b എന്നോ എഴുതുന്നു.
എന്നോ a:b എന്നോ എഴുതുന്നു.
അല്പതമം (Minimum).x രാശിയുടെ a മൂല്യത്തിന് ഇരുവശങ്ങളിലുടെ സമീപസ്ഥമായ മൂല്യങ്ങള്ക്കൊത്ത് f(x) ഫലനത്തിന് f(a)-യെക്കാള് കവിഞ്ഞ മൂല്യങ്ങള് ആണെങ്കില് ആ അന്തരാളത്തില് f(x)-ന്റെ അല്പതമം f(a) ആണെന്നു പറയും.
അവകലനം (Differentiation). ഒരു രാശിക്കുണ്ടാകുന്ന പരിവര്ത്തനമനുസരിച്ച് ബന്ധപ്പെട്ട മറ്റൊരു രാശിക്കുണ്ടാകുന്ന പരിവര്ത്തനത്തിന്റെ നിരക്കു കണ്ടുപിടിക്കുന്ന പ്രക്രിയ.y = f(x) എന്ന ഫലനത്തില്x-ന്റെ വര്ധനവ് (increment) Δx-ഉം അതനുസരിച്ച് y -യുടേത് Δy -യും ആയാല് ![]() എന്ന സീമയെ y-യുടെ അവകലം (derivative) അല്ലെങ്കില് അവകല ഗുണാങ്കം (differential coefficient) എന്നു പറയുന്നു. അവകലത്തെ കുറിക്കാന്
എന്ന സീമയെ y-യുടെ അവകലം (derivative) അല്ലെങ്കില് അവകല ഗുണാങ്കം (differential coefficient) എന്നു പറയുന്നു. അവകലത്തെ കുറിക്കാന് ![]() എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. അതുകൊണ്ട്
എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. അതുകൊണ്ട് ![]() . അവകലം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയാണ് അവകലനം. y = f(x) എന്ന ഫലനത്തിന്റെ ഗ്രാഫില് (x, y) എന്ന ബിന്ദുവിലെ സ്പര്ശരേഖയുടെ ചരിവ് (slope) ആണ്
. അവകലം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയാണ് അവകലനം. y = f(x) എന്ന ഫലനത്തിന്റെ ഗ്രാഫില് (x, y) എന്ന ബിന്ദുവിലെ സ്പര്ശരേഖയുടെ ചരിവ് (slope) ആണ് ![]() .
.
അഷ്ടഭുജം (Octagon). എട്ടു വശങ്ങളുള്ള സമതലബഹുഭുജം.
അസമത (Inequality). തുല്യമല്ലാത്ത രണ്ടു രാശികളെ തമ്മില് ബന്ധിപ്പിക്കുന്ന പ്രസ്താവന. a എന്നത് b-യെക്കാള് ചെറുതാണെങ്കില് a < b എന്നും a എന്നത് b-യെക്കാള് വലുതാണെങ്കില് a > b എന്നും എഴുതുന്നു. ഉദാ.x < 4 ആണെങ്കില് x2 < 16 എന്നു കിട്ടുന്നു.y2 > 25 ആയാല് y > 5 അല്ലെങ്കില് y < −5 .
അസ്ട്രോണമി (Astronomy). സൗരയൂഥത്തിലെ സൂര്യന്, ഗ്രഹങ്ങള്, ഉപഗ്രഹങ്ങള്, ഗാലക്സികളിലെ നക്ഷത്രങ്ങള് എന്നിവയുടെ സ്ഥാനത്തെക്കുറിച്ചും ചലനത്തെക്കുറിച്ചും പ്രതിപാദിക്കുന്ന ഗണിതശാസ്ത്രശാഖ.
അഹംസ്, പാപ്പിറസ് (Ahmes, Papyrus). ഈജിപ്തുകാരുടെ പുരാതന ഗണിതശാസ്ത്രഗ്രന്ഥം. ഏതാണ്ട് ബി.സി. 1700-ല് ആണ് ഇത് എഴുതപ്പെട്ടത്. ഗണിതസംബന്ധിയായി ഏറ്റവും പഴക്കമുള്ള ഈ പാപ്പിറസ് ചുരുളുകള് റൈന്ഡ് പാപ്പിറസ് (Rhind papyrus) എന്ന പേരിലും അറിയപ്പെടുന്നു. ബ്രിട്ടീഷ് മ്യൂസിയത്തിലാണ് ഇത് സൂക്ഷിക്കുന്നത്.
ആക്സിയം (Axiom). ഗണിതത്തിലെ ഓരോ തത്ത്വത്തിന്റെയും അടിസ്ഥാന സങ്കല്പനം.
ആധാരം (Base). ജ്യാമിതിയില്, ഒരു ഘനരൂപത്തിന്റെ ഏറ്റവും താഴെയുള്ള വശം (face). ഉദാ. പിരമിഡിന്റെ ആധാരം ഏറ്റവും താഴെയുള്ള മുഖമാണ്. ത്രികോണത്തിന്റെ ആധാരം അതിന്റെ ശീര്ഷലംബം പതിക്കുന്ന വശമാണ്. ലോഗരിതത്തില് N = a x ആയാല് logaN = x എന്നെഴുതുന്നു. ഇവിടെ a-യെ ലോഗരിതത്തിന്റെ ആധാരം എന്നു പറയും. സാധാരണ ലോഗരിതത്തില് ആധാരം 10 ആണ്. ഉദാ. 103=1000. അതുകൊണ്ട് log101000 = 3. ഇവിടെ ആധാരം 10 ആണ്.
ആരേഖം (Diagram). ഗണിതീയ ആശയങ്ങള് വിശദീകരിക്കാനുപയോഗിക്കുന്ന ചിത്രം. സാംഖ്യികീയ ദത്തങ്ങള് (statistical data) വിശദീകരിക്കുന്നതില് ബാര് ആരേഖം (Bar diagram), വൃത്താരേഖം (Pie diagram) മുതലായവയ്ക്കു വലിയ പ്രാധാന്യമുണ്ട്.
ആര്ഗന്ഡ് ഡയഗ്രം (Argand Diagram). സമ്മിശ്രസംഖ്യകള് ചിത്രണം ചെയ്യാന് ഉപയോഗിക്കുന്ന തലം.
ആല്ഗോള് (Algol). കംപ്യൂട്ടര് പ്രോഗ്രാമിങ്ങിന് ഉപയോഗിക്കുന്ന ഒരു ഭാഷ.
ആവൃത്തി (Frequency). ഒരു സാമ്പിളില് വിചരത്തിന്റെ (variate) ഒരു വില എത്രപ്രാവശ്യം ആവര്ത്തിക്കുന്നു എന്നു സൂചിപ്പിക്കുന്ന സംഖ്യ. ആവൃത്തിപ്പട്ടികയില് വിചരത്തിന്റെ വര്ഗംതിരിച്ചുള്ള ആവൃത്തി കൊടുത്തിരിക്കും.
ആള്ജിബ്ര (Algebra, ബീജഗണിതം). അങ്കഗണിതക്രിയകളില് സംഖ്യകള്ക്ക് പ്രതീകങ്ങള് ഉപയോഗിച്ചു സാമാന്യവത്കരിച്ചുണ്ടായ ഗണിതശാസ്ത്രശാഖ. അങ്കഗണിതത്തിലെ2 x ( 4 + 5 ) = 2 x 4 + 2 x 5 എന്ന പ്രസ്താവനയുടെ സാമാന്യവത്കരണമാണ് ബീജഗണിതത്തിലെ x (y+z) = xy + xz എന്ന വിതരണനിയമം (Distributive law).x,y,z എന്നിവയുടെ എല്ലാ വിലകള്ക്കും വിതരണനിയമം ബാധകമാണ്. xy = yx ആണെങ്കില് ഗുണനത്തെ സംബന്ധിച്ച് x,y വിനിമേയ നിയമം (Commutative law) അനുസരിക്കുന്നു.
ഇരട്ടസംഖ്യ (Even number). 2 ഘടകമായിട്ടുള്ള പൂര്ണസംഖ്യ. ഉദാ. 2, 4, 6, 8... ... ...
ഉച്ചതമം (Maximum, അധികതമം). ഒരു അന്തരാള (interval)ത്തില്x രാശിയുടെ മ മൂല്യത്തിന് ഇരുവശങ്ങളിലുള്ള സമീപസ്ഥമായ മൂല്യങ്ങള്ക്കൊത്ത് f(x) ഫലനത്തിന് f(a)യെക്കാള് കുറഞ്ഞ മൂല്യങ്ങള് ആണെങ്കില് f(x)-ന്റെ അധികതമം f(a) ആണെന്നു പറയും. x = മ ആകുമ്പോള് ഫലനം f(x)-ന്റെ മൂല്യം ഉച്ചതമമാണെങ്കില് f'(a) = 0, f(a) < 0. ഇവ ആവശ്യമായ നിബന്ധനകള് ആണ്.
ഉപപത്തി (Proof). ആക്സിയങ്ങളില്നിന്നു പ്രമേയത്തിന്റെ സാധുതയിലെത്തുന്ന യുക്തിയുക്തമായ വാദം.
ഉപപ്രമേയം (Corollary). ഒരു പ്രമേയത്തിന്റെ തെളിവില്നിന്നു കിട്ടുന്ന പ്രസ്താവന. പ്രമേയത്തിന്റെ വിശേഷസ്ഥിതിയെ (Particular case) ഉപപ്രമേയമെന്നു പറയാറുണ്ട്.
ഉത്കേന്ദ്രത (Eccentricity). ഒരു കോണിക (Conic)ത്തിലുള്ള ഏതെങ്കിലും ഒരു ബിന്ദുവിന് ഒരു നിശ്ചിത ബിന്ദു (ഫോക്കസ്), നിശ്ചിച നേര്വര (ഡയറക്ട്രിക്സ്) ഇവയില് നിന്നുള്ള ദൂരങ്ങളുടെ അനുപാതം. ഈ സ്ഥിരാങ്കത്തെ ല എന്നു കുറിക്കുന്നു. e <1 ആകുമ്പോള് കോണികം ദീര്ഘവൃത്തവും e >1 ആകുമ്പോള് ബഹിര്വലയവും e =1 ആകുമ്പോള് കോണികം പരാവലയവും ആയിരിക്കും.
ഏകവൃത്തീയ ബിന്ദുക്കള് (Concyclic points). ഒരേ വൃത്തത്തിന്റെ പരിധിയില് കിടക്കുന്ന ബിന്ദുക്കള്.
ഏകാന്തരശ്രേണി (Alternating series). പദങ്ങള് ഒന്നിടവിട്ട് (ഏകാന്തരക്രമത്തില്) ധനാത്മകവും ഋണാത്മകവുമായ അനന്തശ്രേണി. ഉദാ. ![]() .
.
ഒറ്റസംഖ്യ (Odd number). 2 ഘടകമല്ലാത്ത പൂര്ണസംഖ്യ. ഉദാ. 1, 3, 5, 7...
കംപ്യൂട്ടര് (Computer). ദത്തവും (data) നിര്ദേശങ്ങളും അനുസരിച്ച് ബൃഹത്തായ ഗണിതക്രിയകള് നിര്വഹിക്കുന്ന ഇലക്ട്രോണിക് ഉപകരണം. കംപ്യൂട്ടറില് പ്രയോഗിക്കുന്ന ദത്തവും നിര്ദേശങ്ങളും പ്രത്യേകരീതിയില് രൂപപ്പെടുത്തിയതായിരിക്കണം. നിലവിലുള്ള വ്യത്യസ്ത കംപ്യൂട്ടറുകള്-അനലോഗ് (analog), ഡിജിറ്റല് (digital), ഹൈബ്രിഡ് (hybrid).
കരണി (Surd). അപരിമേയസംഖ്യ ഉള്ക്കൊള്ളുന്ന ഒരു സംഖ്യാത്മകവ്യഞ്ജകം (numerical expression). ഉദാ. ![]() ദ്വിപദകരണി (quadratic surd). ഉദാ.
ദ്വിപദകരണി (quadratic surd). ഉദാ.![]()
കാര്ഡിനല് സംഖ്യ (Cardinal number). ഒരു ഗണത്തില് എത്ര അംഗങ്ങളുണ്ടെന്നു സൂചിപ്പിക്കുന്ന സംഖ്യ.
ക്യാറ്റെനറി (Catenary). ~ഒരു വടം രണ്ടു താങ്ങുകളില് ബന്ധിക്കുമ്പോഴുണ്ടാകുന്ന വക്രത്തിന്റെ ആകൃതി.y അക്ഷം സമമിതഅക്ഷ(axis of symmetry)മായി എടുത്താല് ക്യാറ്റെനറിയുടെ സമീകരണം ![]() ആണ്.
ആണ്.
കലനം (Calculus). ഫലനങ്ങളുടെ അവകലനം (differentiation), സമാകലനം (integration) ഇവയുമായി ബന്ധപ്പെട്ട ആശയങ്ങള്, ഇവയുടെ പ്രയോഗം എന്നിവയെക്കുറിച്ചു പ്രതിപാദിക്കുന്ന ഗണിതശാഖ.
കുറയ്ക്കല് (subtraction). വ്യവകലനം. a മാത്രയില് നിന്ന് b മാത്ര കുറയ്ക്കുകയെന്നാല് a മാത്രയും b യുടെ സങ്കലനവ്യുത്ക്രമവും (additive inverse) കൂട്ടുക എന്നര്ഥം.
കൂട്ടല് (Addition). സങ്കലനം. a മാത്രയും b മാത്രയും കൂടി കൂട്ടുകയെന്നാല് a+b. ഉദാ. 8+7 = 15.
കൊസൈന് (Cosine). ത്രികോണമിതിയിലെ ഒരു ഫലനം. ഒരു മട്ടത്രികോണത്തിന്റെ പാദകോണം θ ആയാല് പാദത്തിന്റെയും കര്ണത്തിന്റെയും അംശബന്ധത്തെ cosineθ (cos θ) എന്നെഴുതുന്നു.
കേള് (Curl). ഒരു അവകല സംകാരം (differential operator) സദിശഫലനത്തില് പ്രവര്ത്തിച്ചുണ്ടാകുന്ന സദിശഫലനം.
![]() എന്ന സദിശഫലനത്തിന്റെ കേളിനെ കുറിക്കാന്
എന്ന സദിശഫലനത്തിന്റെ കേളിനെ കുറിക്കാന് ![]() (അല്ലെങ്കില്
(അല്ലെങ്കില് ![]() ) എന്ന പ്രതീകമുപയോഗിക്കുന്നു.
) എന്ന പ്രതീകമുപയോഗിക്കുന്നു.
കോണ് (Cone). ഒരു മട്ടത്രികോണത്തിന്റെ ഏതെങ്കിലും ലഘുവശത്തെ അക്ഷമാക്കി ത്രികോണം ചുറ്റുമ്പോള് ഉളവാകുന്ന ഘനരൂപം.
കോണം (Angle). ഒരു നേര്രേഖ അതിലുള്ള ഒരു ബിന്ദുവിനെ ചുറ്റിത്തിരിയുമ്പോഴുള്ള തിരിയലിന്റെ അളവ്. അപ്രദക്ഷിണ(anticlock-wise) തിരിയല്കൊണ്ട് ധനകോണവും പ്രദക്ഷിണതിരിയല്കൊണ്ട് ഋണകോണവും ഉണ്ടാകുന്നു. രണ്ടു സമാന്തരരേഖകള് ഉള്ക്കൊള്ളുന്ന കോണം ശൂന്യമാണ്. ഡിഗ്രിയിലോ റേഡിയനിലോ കോണം അളക്കുന്നു.
1 പരിക്രമണം = 360 ഡിഗ്രി
1 ഡിഗ്രി = 60 മിനിറ്റ്
1 മിനിറ്റ് = 60 സെക്കന്ഡ്
കോണമാപകം (Protractor). കോണം (angle) നിര്മിക്കുവാനും അളക്കുവാനുമുള്ള ഉപകരണം.
കോണിജങ്ങള് (Conicoids). എല്ലാ സമതലഛേദങ്ങളും കോണികങ്ങളായുള്ള ത്രിമാനപ്രതലങ്ങള്.
കോണികസ്പര്ശങ്ങള് (Conics). കോണികങ്ങള് (Conics) പരസ്പരം സ്പര്ശിക്കുന്ന വാസ്തവിക ബിന്ദുക്കള്.
കോണികം (Conic). ഒരു സ്ഥിരബിന്ദു (ഫോക്കസ്)വില്നിന്നും ഒരു സ്ഥിരരേഖ (ഡയറക്ട്രിക്സ്)യില്നിന്നും ഉള്ള ദൂരങ്ങളുടെ അംശബന്ധം ഒരു സ്ഥിരാങ്കമാകത്തക്കവണ്ണം ചലിക്കുന്ന ബിന്ദുവിന്റെ സഞ്ചാരപഥമായ വക്രം.
കോബോള് (COBOL). കംപ്യൂട്ടര് പ്രോഗ്രാമിങ്ങിനുപയോഗിക്കുന്ന ഒരു പ്രതീകഭാഷ. Common Business-Oriented Language എന്നതിന്റെ ചുരുക്കരൂപമാണിത്.
കോമ്പസ് (Compass). വൃത്തം വരയ്ക്കാന് ഉപയോഗിക്കുന്ന ഒരു ഉപകരണം.
ക്രമഗുണിതം (Factorial). ഒരു പൂര്ണസംഖ്യയുടെയും അതിനെക്കാള് ചെറിയ 1 വരെയുള്ള എല്ലാ പൂര്ണ സംഖ്യകളുടെയും ഗുണനഫലം. ഉദാ. ക്രമഗുണിതം n-നെ n! എന്നോ ![]() എന്നോ എഴുതുന്നു.n! = 1 X 2 X 3...Xn. 6! = 1 X 2 X 3 X 4 X 5 X 6. ക്രമഗുണിത 0(0!) ത്തിന്റെ വില 1 എന്നു നിര്വചിച്ചിരിക്കുന്നു.
എന്നോ എഴുതുന്നു.n! = 1 X 2 X 3...Xn. 6! = 1 X 2 X 3 X 4 X 5 X 6. ക്രമഗുണിത 0(0!) ത്തിന്റെ വില 1 എന്നു നിര്വചിച്ചിരിക്കുന്നു.
ക്രമചയം (Permutation). സംഖ്യകളെയോ ചിഹ്നങ്ങളെയോ നിര്ദ്ദിഷ്ടക്രമത്തില് നിരത്തുകയും അപ്രകാരം നിരത്തുന്നത് എത്ര തരത്തിലാകാമെന്നു കണക്കാക്കുകയും ചെയ്യല്. ഉദാ. a, b, c എന്ന മൂന്ന് അക്ഷരങ്ങള്ക്ക് (a, b, c), (b, c, a), (c, a, b), (b, a, c), (c, b, a), (a, c, b) എന്നിങ്ങനെ ആറ് ക്രമചയങ്ങളുണ്ട്.
ക്രാന്തിവൃത്തം (Ecliptic). ഖഗോളത്തില് (celestial sphere) സൂര്യന്റെ സാങ്കല്പികസഞ്ചാരപഥമായ ബൃഹദ്വൃത്തം.
ക്ഷേത്രഫലം (Area). വിസ്തീര്ണം. സമതല ആകൃതിയുടെയോ പ്രതലത്തിന്റെയോ വിസ്താരം. ദീര്ഘചതുരത്തിന്റെ ക്ഷേത്രഫലം = നീളം x വീതി. ക്ഷേത്ര(ഫീല്ഡ്)ത്തിന്റെ ആകൃതിയനുസരിച്ച് ക്ഷേത്രഫലം കാണുവാനുള്ള വ്യത്യസ്ത ഫോര്മുലകള് ഉണ്ട്. ചതുരശ്ര ഏകകങ്ങളിലാണ് (squared units) ക്ഷേത്രഫലം അളക്കുന്നത്.
ഘനം (Cube), ഘനമൂലം (Cube root). എങ്കില് xന്റെ ഘനം x3 ഉം x3-ന്റെ ഘനമൂലം x-ഉം ആണ്. ഉദാ. 23= 8-ല് 2-ന്റെ ഘനം 8, 8-ന്റെ ഘനമൂലം 2.
ഗണിതപ്പട്ടിക (Mathematical table). സ്വതന്ത്ര ചരത്തിന്റെ വ്യത്യസ്ത വിലകള്ക്ക് ഫലനത്തിന്റെ മൂല്യം രേഖപ്പെടുത്തിയിട്ടുള്ള പട്ടിക. ഉദാ. log x, sin x, cos x, tan x തുടങ്ങിയ ഗണിതീയഫലനങ്ങളുടെ മൂല്യം x-ന്റെ വ്യത്യസ്ത വിലകള്ക്ക് ഗണനം ചെയ്ത പട്ടിക.
ഗണിതീയ ആഗമനം (Mathematical induction). ഒരു പ്രസ്താവനയോ ഫോര്മുലയോ എല്ലാ നിസര്ഗസംഖ്യകള്ക്കും ശരിയാണെന്നു തെളിയിക്കുന്ന ഗണിതരീതി.
ഗുണനം (Multiplication). രണ്ടോ അതിലധികമോ രാശികളുടെ ഗുണനഫലം കണ്ടുപിടിക്കാനുപയോഗിക്കുന്ന സംക്രിയ. ഗുണനത്തിന് അങ്കഗണിതത്തില് 'x' എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. b ധനപൂര്ണസംഖ്യയാണെങ്കില് a യെ അതിനോടു b പ്രാവശ്യം കൂട്ടുന്ന സംഖ്യയാണ് a x b. ഗുണനം ക്രമവിനിമേയ നിയമം (commutative law) അനുസരിക്കുന്നു. അതായത് a X b = b X a. സംഖ്യകളുടെ സാഹചര്യനിയമ(associative law)മാണ്. a X (b X c) = (a X b) X c. ഗുണനത്തില് a X 1 = a = 1 X a ആയതുകൊണ്ട് 1 എന്ന സംഖ്യ അനന്യക(identity element)മാണ്.
ഗുണാങ്കം (Coefficient). ഗുണനഘടകം. ഉദാ. 6x2-ല് x2-ന്റെ ഗുണാങ്കമാണ് 6 എന്ന സംഖ്യ. 3xy-ല് y-യുടെ ഗുണാങ്കമാണ് 3x.
ഗുണോത്തരശ്രേഢി (Geometric progression). ഒരു പദവും തൊട്ടുമുമ്പുള്ള പദവും തമ്മിലുള്ള അംശബന്ധം. ഈ അംശബന്ധത്തെ പൊതു അംശബന്ധം (common ratio) എന്നു പറയുന്നു. ആദ്യപദം a-യും പൊതു അനുപാതം r-ഉം ആയ ഗുണോത്തരശ്രേഢിയെ a, ar, ar2... arn-1... എന്നെഴുതാം ഉദാ 6, 12, 24, 48....
ഗോളജം (Spheroid). ഒരു ദീര്ഘവൃത്തത്തെ (ellipse) അതിന്റെ ദീര്ഘ അക്ഷമോ (major axis) ലഘു അക്ഷമോ (minor axis) അക്ഷമാക്കി പരിക്രമണം ചെയ്താല് കിട്ടുന്ന ഘനരൂപം. വലിച്ചുനീട്ടിയതോ രണ്ടറ്റവും പരത്തിയതോ ആയ ഗോളത്തെ ഗോളജമെന്നു സാമാന്യമായി പറയാം.
ഗോളം (Sphere). സ്പേസില് ഒരു നിശ്ചിബിന്ദു (fixed point)വില്നിന്നു തുല്യദൂരത്തിലുള്ള ബിന്ദുക്കള് ഉള്ക്കൊള്ളുന്ന സംവൃത പ്രതലം (closed surface). അര്ധവൃത്താകൃതിയിലുള്ള ഒരു തലത്തെ അതിന്റെ വ്യാസം അക്ഷമാക്കി പൂര്ണമായി പരിക്രമണം ചെയ്താല് കിട്ടുന്ന ഘനരൂപമാണ് ഗോളം. ഒരു ഗോളത്തിന്റെ വ്യാസാര്ധം r ആയാല് അതിന്റെ വ്യാപ്തം ![]() ഉം പ്രതലവിസ്തീര്ണം 4πr2 -ഉം ആണ്. നിര്ദേശാങ്കജ്യാമിതിയില് (0,0,0) എന്ന ബിന്ദു കേന്ദ്രവും r വ്യാസാര്ധവും ഉള്ള ഗോളത്തിന്റെ സമീകരണമാണ് x2 + y2 + z2 = r2.
ഉം പ്രതലവിസ്തീര്ണം 4πr2 -ഉം ആണ്. നിര്ദേശാങ്കജ്യാമിതിയില് (0,0,0) എന്ന ബിന്ദു കേന്ദ്രവും r വ്യാസാര്ധവും ഉള്ള ഗോളത്തിന്റെ സമീകരണമാണ് x2 + y2 + z2 = r2.
ഗ്രാഫ് (Graph). രണ്ടു ചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തെ സൂചിപ്പിക്കുന്ന ചിത്രം.
ഘടകം (Factor). ഒരു സംഖ്യ രണ്ടോ അതിലധികമോ പൂര്ണസംഖ്യകളുടെ ഗുണനഫലമാണെങ്കില്, ആ സംഖ്യകളെ ഗുണനഫലത്തിന്റെ ഘടകങ്ങളെന്നു പറയുന്നു. 15 = 3x 5 ആയതുകൊണ്ട് 15ന്റെ ഘടകമാണ് 3-ഉം 5-ഉം. ഇതുപോലെ (x 2 - y2) എന്ന ബീജീയവ്യഞ്ജകത്തിന്റെ ഘടകമാണ് (x + y), (x - y) എന്നിവ.
ഘനകോണം (Solid angle). സമതലകോണത്തിന്റെ ത്രിവിമീയസ്പേസിലുള്ള സമാനരൂപം. ഒരു ബിന്ദുവില് ഒരു പ്രതലം സമ്മുഖ(substend)മാക്കുന്ന കോണം, ഇതിന്റെ ഏകകമാണ് സ്റ്റെറേഡിയന്. ഏകക അകലത്തില് ഏകക വിസ്തീര്ണം സമ്മുഖമാക്കുന്ന ഘനകോണമാണ് ഒരു സ്റ്റെറേഡിയന്. ഉദാ. ഒരു ഗോളത്തിന്റെ പ്രതലം കേന്ദ്രത്തില് സ്റ്റെറേഡിയന് 4π സമ്മുഖമാക്കുന്നു.
ഘനരൂപം (Solid). സ്പേസിലെ ഏതെങ്കിലും ആകൃതി അല്ലെങ്കില് വസ്തു. ഉദാ. ഗോളം, വൃത്തസ്തംഭം, ക്യൂബ് മുതലായവ.
ചതുര്ഭുജം (Quadrilateral). നാലുവശങ്ങളുള്ള സമതല ആകൃതി. ട്രപ്പീസിയം, സമാന്തരികം, ദീര്ഘചതുരം (rectangle), സമചതുരം (square) മുതലായവ ചതുര്ഭുജത്തിന്റെ പ്രത്യേക രൂപങ്ങ(Particular cases)ളാണ്.
ചരം (Variable). വിലയ്ക്കു മാറ്റംവരുന്ന രാശി. ചരങ്ങളെ കുറിക്കാന് x, y അക്ഷരങ്ങള് ഉപയോഗിക്കുന്നു.
ഛിന്നകം (Frustum). ഒരു ഘനരൂപത്തെ മുറിക്കുമ്പോള് രണ്ട് സമാന്തരതലങ്ങള്ക്കുള്ളിലുള്ള ഭാഗം. ഒരു കോണിനെ ആധാരത്തിനു സമാന്തരമായി മുറിക്കുമ്പോള് ആധാരത്തിനും സമാന്തരതലത്തിനും ഇടയ്ക്കുള്ള ഭാഗമാണ് കോണിന്റെ ഛിന്നകം.
ഛേദകരേഖ (Secant). ജ്യാമിതിയില് ഒരു വക്രത്തെ ഒന്നോ അതിലധികമോ ബിന്ദുക്കളില് ഖണ്ഡിക്കുന്ന നേര്രേഖ.
ജ്യാമിതി (Geometry). സ്പേസിന്റെയും അതിലുള്ള വസ്തുക്കളുടെയും ഗുണധര്മങ്ങളെക്കുറിച്ചു പ്രതിപാദിക്കുന്ന ഗണിതശാസ്ത്രശാഖ. രേഖാഗണിതം, രേഖകള്, വക്രങ്ങള്, പ്രതലങ്ങള്, ഘനരൂപങ്ങള്, ബിന്ദുക്കള് ഇവയെക്കുറിച്ചു പഠനം നടത്തുന്നു. യൂക്ളിഡിയന് ജ്യാമിതിയില് രണ്ടു രേഖകളോ സമതലങ്ങളോ ഉള്ക്കൊള്ളുന്ന കോണം, വൃത്തം, ഗോളം, ഇവയുടെ ഗുണധര്മങ്ങള്, സമതലത്തിലുള്ള ബിന്ദുക്കള്, രേഖകള് മുതലായവയെക്കുറിച്ചു പ്രതിപാദിക്കുന്നു. ബീജഗണിതം ഉപയോഗിച്ചുള്ള ജ്യാമിതിയുടെ പഠനമാണ് നിര്ദേശങ്ക ജ്യാമിതി (Coordinate Geometry). അമൂര്ത്തങ്ങളായ ആശയങ്ങളും ചിന്താധാരകളും ഉള്ക്കൊള്ളുന്ന ടോപോളജി, ഫ്രക്ടല് ജ്യാമിതി പോലുള്ള ആധുനികവിഭാഗങ്ങള് ഇതിലുള്പ്പെടുന്നു.
ജ്യാമിതീയ മാധ്യം (Geometric mean). a, b എന്ന രണ്ടു ധനസംഖ്യകളുടെ ജ്യാമിതീയ മാധ്യമാണ് √ab സംഖ്യകള് a1,a2...an ആയാല് ജ്യാമിതീയമാധ്യം 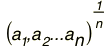 ആണ്.
ആണ്.
ജ്യാവ് (Chord). ഒരു വക്രത്തിലെ ഏതെങ്കിലും രണ്ടു ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന നേര്രേഖ.
ടോപോളജി (Topology). ആകൃതി, സ്പേസ് ഇവയുടെ സാമാന്യ ഗുണധര്മങ്ങളെക്കുറിച്ച് പ്രതിപാദിക്കുന്ന ആധുനിക ഗണിതശാസ്ത്രത്തിന്റെ വിശേഷിച്ചും ആധുനിക ജ്യാമിതിയുടെ ഒരു വിഭാഗം. വലിച്ചുനീട്ടല് (stretching), പിരിക്കല് (twisting) ഇവകൊണ്ടു മാറ്റംവരാത്ത ഗുണധര്മങ്ങളെക്കുറിച്ചുള്ള പഠനമാണ് ടോപോളജി. ഗോളവും ദീര്ഘവൃത്തജവും (ellipsoid) ജ്യാമിതിയില് വ്യത്യസ്ത രൂപങ്ങളാണ്. എന്നാല് ഇവയില് ഒന്നിനെ മറ്റേതായി രൂപാന്തരപ്പെടുത്താവുന്നതുകൊണ്ട് ടോപോളജിയില് ഇവ സമാനരൂപങ്ങളാണ്.
ഡിമോര്ഗന് നിയമങ്ങള് (De Morgan's Law). A,B,C ഏതെങ്കിലും മൂന്നു ഗണങ്ങളാണെങ്കില്
ഡെക്കാഹെഡ്രണ് (Decahedron). പത്തു പാര്ശ്വങ്ങളുള്ള ഘനരൂപം.
ഡൈവെര്ജന്സ് (Divergence). ഒരു അവകല സംകാരകം (differential operator) സദിശഫലനത്തില് പ്രവര്ത്തിച്ചുണ്ടാകുന്ന അദിശഫലനം (scalar function). ![]() എന്ന സദിശഫലനത്തിന്റെ ഡൈവെര്ജന്സ് കുറിക്കാന്
എന്ന സദിശഫലനത്തിന്റെ ഡൈവെര്ജന്സ് കുറിക്കാന് ![]() (അല്ലെങ്കില്
(അല്ലെങ്കില് ![]() ) എന്ന പ്രതീകമുപയോഗിക്കുന്നു.
) എന്ന പ്രതീകമുപയോഗിക്കുന്നു.
ത്രികോണ അസമത (Triangle inequality). ഒരു ത്രികോണത്തില് ഒരു വശം മറ്റു രണ്ടു വശങ്ങളുടെ തുകയെക്കാള് കുറവാണ് എന്ന ഗുണധര്മം.
ത്രികോണമിതി (Trigonometry). കോണങ്ങളുടെ ത്രികോണമിതീയ ഫലനങ്ങളുപയോഗിച്ച് ഒരു ത്രികോണത്തിലെ വശങ്ങളും കോണങ്ങളും തമ്മിലുള്ള ബന്ധങ്ങളുടെ പഠനം. ഒരു മട്ടത്രികോണത്തിലെ വശങ്ങളുടെ അംശബന്ധമായി ത്രികോണമിതീയഫലനങ്ങളെ നിര്വചിക്കാം. സൈന്, കോസൈന്, ടാന്ജെന്റ് എന്നിവയും അവയുടെ വ്യുത്ക്രമങ്ങളുമാണ് ത്രികോണമിതീയഫലനങ്ങള്.
ത്രികോണം. നേര്വരയിലല്ലാത്ത മൂന്ന് ബിന്ദുക്കളെ ഋജുരേഖാഖണ്ഡങ്ങളുപയോഗിച്ച് യോജിപ്പിക്കുമ്പോള് ലഭിക്കുന്ന ജ്യാമിതീയരൂപം.
ത്രൈരാശികം. അംശബന്ധത്തിന്റെ തുല്യമാനം അഥവാ അനുപാതമൂല്യം കണ്ടുപിടിക്കുന്നതിനുള്ള അടിസ്ഥാനനിയമം.
ദശഭുജം (Decagon). പത്തു വശങ്ങളുള്ള ഒരു ബഹുഭുജം.
ദശാംശം (Decimal). പത്ത് ആധാരമായുള്ള സംഖ്യാപദ്ധതി. ഉദാ. എണ്ണുവാനുപയോഗിക്കുന്ന സംഖ്യകള്, ഒറ്റ, പത്തിലൊന്ന്, നൂറിലൊന്ന് തുടങ്ങിയവയില് എഴുതുന്ന പരിമേയസംഖ്യ(rational number)യാണ് ദശാംശഭിന്നം (decimal fraction). ദശാംശ അങ്കനരീതിയനുസരിച്ച് ⅛ നെ 0.125 എന്നെഴുതുന്നു. അക്കങ്ങള് ആവര്ത്തിക്കുന്ന ദശാംശഭിന്നത്തെ ആവര്ത്തി ദശാംശം (recurring decimal) എന്നു പറയുന്നു. ഉദാ. 1.666...
ദശാംശസമ്പ്രദായം. 'പത്ത്' ആധാരമാക്കിയുള്ള സംഖ്യാസമ്പ്രദായം.
ദീര്ഘവൃത്തം. വിസ്ലേഷകജ്യാമിതിയില് ഉത്കേന്ദ്രത(e) ഒന്നില് കുറവായ കോണികം. അണ്ഡാകൃതിയായ വക്രമാണിത്.
ദീര്ഘവൃത്തജം (Ellipsoid). ഓരോ സമതല പരിച്ഛേദവും ദീര്ഘവൃത്തമോ അല്ലെങ്കില് വൃത്തമോ ആയ ഘനരൂപം. ഇതിനു മൂന്നു സമമിത അക്ഷങ്ങള് (axes of symmetry) ഉണ്ട്. ഇതിന്റെ വിശേഷസ്ഥിതിയാണ് ഗോളം. നിര്ദേശാങ്കജ്യാമിതിയില് ദീര്ഘവൃത്തജത്തിന്റെ സമീകരണം ![]() ആണ്.
ആണ്.
ദൃഗ്ഗണിതം. ഒരു ജ്യോതിഷഗണിതപദ്ധതി. ആര്യഭടീയഗണിതത്തെ അടിസ്ഥാനമാക്കി അതിലെ ഗണനസംഖ്യകളെയും ഗണനക്രിയകളെയും ലഘുപ്പെടുത്തി, ഗണിച്ചുകിട്ടിയ ഫലങ്ങള്ക്ക് സൂക്ഷ്മതയുണ്ടാകാന് വേണ്ട സംകാരങ്ങളും ചെയ്ത് ദൃഷ്ടഫലംകൊണ്ട് കണ്ടുപിടിച്ച ഒരു പദ്ധതി.
ദ്വയാംഗസമ്പ്രദായം. 0, 1 എന്നീ അക്കങ്ങള് മാത്രം ഉപയോഗിച്ചുള്ള സംഖ്യാസമ്പ്രദായം. ആധാരം '2' ആണ്.
ദ്വിഘാതസമവാക്യം (Quadratic equation). രണ്ടാം ഘാതത്തിലുള്ള ബീജിയസമവാക്യം. ഉദാ. ax2 + bx + c = 0 ഈ സമവാക്യത്തിന്റെ നിര്ധാരണമൂല്യങ്ങള് ![]() ആണ്.
ആണ്.
ദ്വിപദ സിദ്ധാന്തം. ഒരു പ്രധാന ബീജീയസര്വസമവാക്യം. ഒരു ദ്വിപദ (binomial)ത്തിന്റെ ഏതു ഘാതത്തിന്റെയും വിപുലീകരണത്തിനുള്ള നിയമം. ദ്വിപദസൂത്രവാക്യം (binomial formula) എന്നു പറയാം.
നിര്ദേശാങ്കങ്ങള്. സമതലത്തിലോ സ്പേസിലോ ഒരു ബിന്ദുവിന്റെ സ്ഥാനം ഉറപ്പിക്കുന്ന സംഖ്യകളുടെ ക്രമിതഗണം (ordered set). സമതലത്തില് ഏതെങ്കിലുമൊരു ബിന്ദുവാണ് P എങ്കില് ഈ ബിന്ദുവിനെ കുറിക്കാന് P(x,y) എന്നെഴുതുന്നു. ഇവിടെ x എന്ന സംഖ്യ ജ യുടെ x-നിര്ദേശാങ്കവും y എന്ന സംഖ്യ ജ യുടെ y-നിര്ദേശാങ്കവുമാണ്. ബിന്ദുവിന് y അക്ഷത്തില് നിന്നുള്ള ദൂരം x-ഉം x അക്ഷത്തില് നിന്നുള്ള ദൂരം y-ഉം ആണ്.
നിര്ദേശാങ്കജ്യാമിതി (Co-ordinate Geometry). സമതലത്തിലോ സ്പേസിലോ ഉള്ള ഒരു ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് ഉപയോഗിച്ചു നടത്തുന്ന ജ്യാമിതിയുടെ പഠനം. വിസ്ലേഷക-ജ്യാമിതി (Analytical Geometry) എന്നും കാര്ത്തീഷ്യന് ജ്യാമിതി എന്നും പറയുന്നു.
നിസര്ഗസംഖ്യ (Positive integer). സ്വാഭാവികസംഖ്യ, ധനാത്മക പൂര്ണസംഖ്യ. ഉദാ. 1, 2, 3,...
പരാബൊള (Parabola, പരാവലയം). ഒരു സ്ഥിരബിന്ദു (ഫോക്കസ്)വില് നിന്ന് ഒരു നിശ്ചിതരേഖ(ഡയറക്ട്രിക്സ്)യില് നിന്നുമുള്ള ദൂരം തുല്യമാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ സഞ്ചാരപഥമായ വക്രം. ഉത്കേന്ദ്രത (eccentricity) ഒന്ന് ആയ കോണികമാണ് പരാബൊള. ഇതിന്റെ മാനകസമീകരണം (standard equation) y2 = 4ax ആണ്.
പരിമേയസംഖ്യ (Rational number). രണ്ടു പൂര്ണസംഖ്യകളുടെ അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ. pയും q-ഉം പൂര്ണസംഖ്യകളാണെങ്കില് ![]() എന്ന അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ പരിമേയസംഖ്യയാണ് (q ≠ 0). ഉദാ.
എന്ന അംശബന്ധമായി എഴുതാവുന്ന സംഖ്യ പരിമേയസംഖ്യയാണ് (q ≠ 0). ഉദാ. ![]()
പരിവൃത്തം (Circumcircle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു ശീര്ഷങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ഒരു ചക്രീയ ബഹുഭുജ (cyclic polygon)ത്തിന്റെ ശീര്ഷകങ്ങളില്ക്കൂടി കടന്നുപോകുന്നതോ ആയ വൃത്തം. വൃത്തകേന്ദ്രത്തെ പരികേന്ദ്ര(circumcentre)മെന്നു പറയുന്നു.
പിരമിഡ് (Pyramid). ആധാരം ബഹുഭുജവും പാര്ശ്വങ്ങള് പൊതുവായ ശീര്ഷമുള്ള ത്രികോണങ്ങളും ചേര്ന്ന ഘനരൂപം. ഒരു സമ-പിരമിഡില് (regular pyramid) പാര്ശ്വങ്ങള് ആധാരവുമായി തുല്യകോണങ്ങളുള്ള സര്വസമങ്ങളായ സമഭുജത്രികോണങ്ങളായിരിക്കും.
പൂജ്യം (Zero). ഒരു സംഖ്യയോടു മറ്റൊരു സംഖ്യ കൂട്ടിയാല് തുകയായി ആദ്യസംഖ്യതന്നെ കിട്ടുമെങ്കില് കൂട്ടിയ സംഖ്യ പൂജ്യമാണ്. പൂജ്യത്തെക്കുറിക്കാന് '0' എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. ശൂന്യഗണത്തിന്റെ കാര്ഡിനല്സംഖ്യ, സംഖ്യാരേഖയില് ധനസംഖ്യകളെയും ഋണസംഖ്യകളെയും വിഭജിക്കുന്ന ബിന്ദു, വാസ്തവിക സംഖ്യകളുടെ സങ്കലനത്തിലെ അനന്യകം(identity element)n-ന്റെ വില അനന്തതയെ സമീപിക്കുമ്പോള് ![]() -ന്റെ സീമ (limit) എന്നിങ്ങനെ പൂജ്യത്തെ പലവിധത്തില് വിശദീകരിക്കാം.
-ന്റെ സീമ (limit) എന്നിങ്ങനെ പൂജ്യത്തെ പലവിധത്തില് വിശദീകരിക്കാം.
പൂര്ണസംഖ്യ (integer). 1, 2, 3,..., 1, 2, 3, ...0 (പൂജ്യം) ഇവയില് ഏതെങ്കിലുമൊരു സംഖ്യ.
ഫലനം (Function). ഒരു സംഖ്യയെയോ രാശിയെയോ മറ്റൊന്നിനോടു ബന്ധപ്പെടുത്തുന്ന നിര്വചിക്കപ്പെട്ട രീതി. ബീജഗണിതത്തില്x എന്ന ചരത്തിന്റെ ഫലനത്തെ f(x) എന്നു കുറിക്കുന്നു. ഉദാ.x,y എന്ന രണ്ടു ചരങ്ങളെy =x2 + 4 എന്ന സമീകരണംകൊണ്ടു ബന്ധപ്പെടുത്തിയാല്y എന്നത്x-ന്റെ ഒരു ഫലനമാണ്; അതായത് y = f(x) =x2 + 4. 'സംഖ്യയുടെ വര്ഗമെടുത്തു നാലു കൂട്ടുക' എന്നതാണ് ഇവിടെ ഫലനം.x-നെ സ്വതന്ത്രചര(independent variable)മെന്നുംy-യെ ആശ്രിതചര(dependent variable)മെന്നും പറയുന്നു. രണ്ടു ഗണങ്ങളിലെ അംഗങ്ങള് തമ്മിലുള്ള നിര്വചിക്കപ്പെട്ട ബന്ധമായും ഫലനത്തെ പരിഗണിക്കാവുന്നതാണ്. ആദ്യത്തെ ഗണത്തെ ഫലനത്തിന്റെ ഡൊമെയ്ന് (domain) എന്നും രണ്ടാമത്തെ ഗണത്തെ പരാസം (range) എന്നുംപറയുന്നു.
ഉദാ 1, 2, 3}, 2, 4, 6} എന്ന ഗണങ്ങള് തമ്മില് 'അംഗങ്ങളുടെ രണ്ടിരട്ടിയെടുക്കുക' എന്ന ഫലനം (f) നിര്വചിക്കാം. ഇവിടെ 1, 2, 3} ആണ് ഫലനത്തിന്റെ ഡൊമെയ്ന്.
ബഹിര്വൃത്തം (Ex-circle). ഒരു ത്രികോണത്തിന്റെ മൂന്നു വശങ്ങളില് ഒരു വശത്തെ ആന്തരികമായും രണ്ടു വശങ്ങളെ ബാഹ്യമായും സ്പര്ശിച്ചുവരയ്ക്കുന്ന വൃത്തം. ഇതിന്റെ കേന്ദ്രമാണ് ബഹിര്കേന്ദ്രം (ex-centre). ഒരു ത്രികോണത്തില് മൂന്നു ബഹിര്വൃത്തങ്ങള് വരയ്ക്കാം.
ബഹുപദം (Polynomial). ![]() എന്ന രൂപത്തിലുള്ള ബീജീയ വ്യഞ്ജകം (algebraic expression). ഇവിടെ n ബഹുപദത്തിന്റെ ഡിഗ്രിയെ കുറിക്കുന്നു. n = 1 ആകുമ്പോള് ബഹുപദം രേഖീയ(linear)മാണ്.
എന്ന രൂപത്തിലുള്ള ബീജീയ വ്യഞ്ജകം (algebraic expression). ഇവിടെ n ബഹുപദത്തിന്റെ ഡിഗ്രിയെ കുറിക്കുന്നു. n = 1 ആകുമ്പോള് ബഹുപദം രേഖീയ(linear)മാണ്.
ബഹുഫലകം (Polyhedron). ബഹുഭുജങ്ങള് വശങ്ങളായുള്ള (faces) ഘനരൂപം. മൂന്നോ അതിലധികമോ വശങ്ങള് (ഫലകങ്ങള്) സന്ധിക്കുന്ന ബിന്ദു ഇതിന്റെ ഒരു ശീര്ഷ(vertex)മാണ്. സമ(regular)ബഹുഫലകത്തിന്റെ എല്ലാ വശങ്ങളും സര്വസമങ്ങളായ സമബഹുഭുജങ്ങളായിരിക്കും. 4, 6, 8, 12, 20 എന്നിങ്ങനെ വശങ്ങളുള്ള അഞ്ചു സമബഹുഫലകങ്ങള് മാത്രമേയുള്ളൂ. നാലു സമത്രിഭുജങ്ങള് വശങ്ങളായ സമചതുഷ്ഫലകം (regular tetrahedron), ആറു സമചതുരങ്ങള് വശങ്ങളായ സമഷഡ്ഫലകം (regular hexahedron-cube), എട്ട് സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമ അഷ്ടഫലകം (regular Octahedron), പന്ത്രണ്ടു സമപഞ്ചഭുജങ്ങള് വശങ്ങളായുള്ള സമദ്വാദശ ഫലകം (regular dodecahedron), ഇരുപതു സമത്രിഭുജങ്ങള് വശങ്ങളായുള്ള സമവിംശഫലകം (regular icosahedron) ഇവയാണ് സമബഹുഫലകങ്ങള്.
ബാഹ്യഗണനം (Extrapolation). ഒരു രാശിയുടെ തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് ഫലനത്തിന്റെ വില ആകലനം ചെയ്യുന്ന സമ്പ്രദായം. സംഖ്യാത്മകരീതിയില്, ഗ്രാഫു വരച്ചോ ബാഹ്യഗണനം നടത്താം. ഗ്രാഫ്രീതിയില്, തന്നിട്ടുള്ള മൂല്യങ്ങളുടെ പരിധിക്കു പുറത്ത് വരച്ചു വികസിപ്പിച്ച ഗ്രാഫില്നിന്ന് ഫലനത്തിന്റെ വില കണ്ടുപിടിക്കുന്നു. ഗ്രാഫ് ഋജുരേഖയാണെങ്കില് ഈ രീതിയെ രേഖീയ ബാഹ്യഗണനം എന്നു പറയുന്നു.
ബൃഹദ് വൃത്തം (Great circle). കേന്ദ്രത്തില്ക്കൂടി പോകുന്ന സമതലം ഗോളത്തെ ഛേദിക്കുന്ന വൃത്തം.
ഭാജ്യസംഖ്യ (Composite Number). ഒന്നോ സംഖ്യതന്നെയോ അല്ലാതെ മറ്റു പൂര്ണസംഖ്യകള് ഘടകങ്ങളുള്ള പൂര്ണസംഖ്യ ഉദാ. 6, 10, 12, 21, ...
മാട്രിക്സ് (Matrix). വരികളായും (row) കോളങ്ങളായും (column) വിന്യസിക്കുന്ന സംഖ്യകളുടെ ദീര്ഘചതുര വ്യൂഹം. 'm' വരികളും 'n' കോളങ്ങളുമുള്ള മാട്രിക്സിന് m x n മാട്രിക്സ് എന്നു പറയുന്നു. 2 x 2 മാട്രിക്സിന് ഉദാ. ![]() . ഇവിടെ a,b,c,d ഇവ മാട്രിക്സിലെ അംഗങ്ങളാണ്. മാട്രിക്സിന് സംഖ്യാത്മക മൂല്യം (numerical value) ഇല്ല. തുല്യമായ വരികളും കോളങ്ങളും ഉള്ള മാട്രിക്സിനെ വര്ഗമാട്രിക്സ് (square matrix) എന്നു പറയുന്നു. അംഗങ്ങളെല്ലാം പൂജ്യമായ മാട്രിക്സാണ് ശൂന്യമാട്രിക്സ് (null matrix). കെയ്ലി (Cayley)യാണ് മാട്രിക്സുകളുടെ ബീജഗണിതത്തെക്കുറിച്ച് പഠനം നടത്തിയത്.
. ഇവിടെ a,b,c,d ഇവ മാട്രിക്സിലെ അംഗങ്ങളാണ്. മാട്രിക്സിന് സംഖ്യാത്മക മൂല്യം (numerical value) ഇല്ല. തുല്യമായ വരികളും കോളങ്ങളും ഉള്ള മാട്രിക്സിനെ വര്ഗമാട്രിക്സ് (square matrix) എന്നു പറയുന്നു. അംഗങ്ങളെല്ലാം പൂജ്യമായ മാട്രിക്സാണ് ശൂന്യമാട്രിക്സ് (null matrix). കെയ്ലി (Cayley)യാണ് മാട്രിക്സുകളുടെ ബീജഗണിതത്തെക്കുറിച്ച് പഠനം നടത്തിയത്.
മാധ്യം (Mean). ഒരു കൂട്ടം സംഖ്യകളെ പ്രതിനിധീകരിക്കുന്ന സംഖ്യ.x1,x2, ... ...xn എന്നീ സംഖ്യകളുടെ സമാന്തരമാധ്യം (arithmetic mean)-ശരാശരി (average), ![]() ആണ്. ഈ സംഖ്യകളുടെ ഗുണോത്തരമാധ്യം (geometric mean)
ആണ്. ഈ സംഖ്യകളുടെ ഗുണോത്തരമാധ്യം (geometric mean) ![]() ഉം ഹരാത്മകമാധ്യം (harmonic mean) ഉം
ഉം ഹരാത്മകമാധ്യം (harmonic mean) ഉം ![]() ആണ്.
ആണ്.
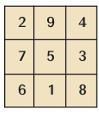
മാന്ത്രികചതുരം (Magic Square). നെടുകെയും കുറുകെയും കോണോടുകോണും കൂട്ടിയാല് ഒരേ സംഖ്യകിട്ടുന്ന വ്യത്യസ്ത സംഖ്യകളുടെ സമചതുരവ്യൂഹം (square array). മൂന്നാം ക്രമത്തിലുള്ള ഒരു മാന്ത്രിക ചതുരം കൊടുക്കുന്നു.
മീഡിയന് (Median). 1. ആരോഹണക്രമത്തിലോ അവരോഹണക്രമത്തിലോ ഉള്ള ഒരു കൂട്ടം സംഖ്യകളുടെ മധ്യസംഖ്യ. സംഖ്യകളുടെ എണ്ണം ഇരട്ടയാകുമ്പോള് മധ്യത്തിലുള്ള രണ്ടു സംഖ്യകളുടെ ശരാശരിയാണ് മീഡിയന്. ഉദാ. 1, 5, 7, 8, 8 എന്നീ സംഖ്യകളുടെ മീഡിയന് 7 ആണ്. 2, 3, 4, 8, 10, 12 എന്നീ സംഖ്യകളുടെ മീഡിയന് ½ (4+8), അതായത് 6 ആണ്. (2) ജ്യാമിതിയില് ത്രികോണത്തിന്റെ ഒരു ശീര്ഷത്തെ എതിര്വശത്തിന്റെ മധ്യബിന്ദുവുമായി യോജിപ്പിക്കുന്ന രേഖ. ഒരു ത്രികോണത്തിലെ മീഡിയനുകള് സംഗാമി (concurrent)യാണ്. സംഗമബിന്ദുവിനെ കേന്ദ്രകം (centroid) എന്നു പറയുന്നു.
മോഡ് (Mode). ഒരു കൂട്ടം സംഖ്യകളില് ഏററവും കൂടുതല് പ്രാവശ്യം ആവര്ത്തിച്ചുവരുന്ന സംഖ്യ. 1, 2, 3, 4, 2, 5, 2, 6 എന്നീ സംഖ്യകളുടെ മോഡ് 2 ആണ്.
മോഡുലസ് (Modulus). 1. ധനാത്മകമോ ഋണാത്മകമോ ആയ സംഖ്യയുടെ അളവിനെ ആ സംഖ്യയുടെ മോഡുലസ് എന്നു പറയുന്നു.x-ന്റെ മോഡുലസ് |x| എന്നു കാണിക്കുന്നു. ഉദാ. |+ 5| = 5,| −5| = 5
2. x സര്വസമം a (മോഡ് n) എന്നു പറഞ്ഞാല് n-ന്റെ പൂര്ണസംഖ്യാഗുണിതമാണ് x -a എന്നര്ഥം. x ≡ a (മോഡ് n). ഉദാ. 13 ≡ 1 (മോഡ് 3) എന്നത് 3-ന്റെ പെരുക്കമാണ് 13 - 1 (=12).
റേഡിയന് (Radian). ഒരു വൃത്തത്തില് വ്യാസാര്ധത്തിനു തുല്യദൈര്ഘ്യമുള്ള വൃത്തചാപം (arc) കേന്ദ്രത്തില് സമ്മുഖ(subtend)മാക്കുന്ന കോണം. π റേഡിയന് =180 ഡിഗ്രി.
റോംബസ് (Rhombus). തുല്യമായ നാലുവശങ്ങളുള്ള സമതല ആകൃതി (plane figure).
ലെമ്മ (Lemma). പ്രമേയിക. മുഖ്യപ്രമേയം തെളിയിക്കുന്നതിനാവശ്യമായ ലഘുപ്രമേയം. സാധാരണയായി പ്രമേയികയ്ക്ക് തെളിവു നല്കിയിട്ട് അതിനെ ആധാരമാക്കിയാണ് പ്രധാനപ്രമേയം തെളിയിക്കുന്നത്.
ലോഗരിതം (Logarithm). ഒരു സംഖ്യയെ മറ്റൊരു സംഖ്യയുടെ ഘാതരീതിയില് പ്രകടിപ്പിച്ചാല് സംഖ്യയുടെ ഘാതമായി വരുന്ന സംഖ്യ. 23 = 8 ആയതുകൊണ്ട് 3-നെ 8-ന്റെ ലോഗരിതം എന്നു പറയുന്നു. ഇവിടെ 2 ലോഗരിതത്തിന്റെ ആധാരമാണ്. പ്രതീകമുപയോഗിച്ച് log28 = 3 എന്നെഴുതുന്നു.
വര്ഗം (Square).x X x = x2 എങ്കില് x2 നെ xന്റെ വര്ഗം എന്നു പറയുന്നു. x,x2 ന്റെ വര്ഗമൂലവും ഉദാ. 3ന്റെ വര്ഗം 9. 9-ന്റെ വര്ഗമൂലം 3.
വികര്ണം ( Diagonal). ഒരു ബഹുഭുജത്തിന്റെ സമീപസ്ഥമല്ലാത്ത ഏതെങ്കിലും രണ്ടു ശീര്ഷകങ്ങളെ യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡം.
വിതതഭിന്നം ( Continued fraction). തുടര്ഭിന്നം. ഒരു പൂര്ണസംഖ്യയും ഭിന്നവും. ഭിന്നത്തിന്റെ ഹാരകം ( denominator) വീണ്ടുമൊരു പൂര്ണസംഖ്യയും ഭിന്നവും, ഇങ്ങനെ തുടര്ന്നെഴുതുന്ന ഭിന്നമാണ് വിതതഭിന്നം. ഉദാ. ![]() ഈ ഭിന്നത്തെ
ഈ ഭിന്നത്തെ ![]() എന്നെഴുതുന്നു.
എന്നെഴുതുന്നു.
വിതരണനിയമം (Distributive law). നോ. ആള്ജിബ്ര.
വിനിമേയനിയമം (Commutative law). നോ. ആള്ജിബ്ര.
വിലോപനം (Elimination). ബീജിയമോ (algebraic) ത്രികോണമിതീയമോ ആയ സമീകരണങ്ങളില്നിന്ന് ചില അജ്ഞാതരാശികളെ ഒഴിവാക്കുന്ന പ്രക്രിയ.
വിലോമം (Converse). ഒരു പ്രമേയം പ്രതിലോമക്രമത്തില് എഴുതിയ പ്രസ്താവന. പ്രമേയത്തിന്റെ വിലോമം എപ്പോഴും ശരിയായിരിക്കണമെന്നില്ല.
ശതമാനം (Percentage). നൂറ് (100) ഹാരകമായിവരുന്ന ഭിന്നമായി എഴുതാവുന്ന സംഖ്യ. ഉദാ. 6 ശതമാനം (6%), നു തുല്യമാണ്. ഭിന്നത്തെയോ ദശാംശത്തെയോ 100 കൊണ്ടു ഗുണിച്ചാല് ശതമാനമാകും. ഉദാ. 0.35 x 100 = 35%, ¼ x 100 = 25%
ശരാശരി (Average) മാധ്യം. ഒരു കൂട്ടം സംഖ്യകളെ പ്രതിനിധീകരിക്കുന്ന സംഖ്യ. a, b എന്ന രണ്ടു സംഖ്യകളുടെ ശരാശരി ![]() സംഖ്യകളുടെ തുകയെ അവയുടെ എണ്ണംകൊണ്ടു ഹരിച്ചാല് ശരാശരി കിട്ടും.
സംഖ്യകളുടെ തുകയെ അവയുടെ എണ്ണംകൊണ്ടു ഹരിച്ചാല് ശരാശരി കിട്ടും.
ഷഡ്ഭുജം (Hexagon). ആറുവശമുള്ള സമതല ബഹുഭുജം.
സംകാരം (Operator). (1) സങ്കലനം, വ്യവകലനം, ഗുണനം, വര്ഗമൂലമെടുക്കല്, ലോഗരിതമെടുക്കല് തുടങ്ങിയ ഗണിതഫലനങ്ങള് (2) ഒരു ഗണിതക്രിയയെയോ ഫലനത്തെയോ കുറിക്കുന്ന പ്രതീകം. ഉദാ.+,−,×,√, log (3) കലത്തിന്റെ (Calculus) ![]() എന്ന പ്രതീകം ഒരു അവകലന സംകാരമാണ്.
എന്ന പ്രതീകം ഒരു അവകലന സംകാരമാണ്.
സഞ്ചയം (Combination). സംഖ്യകളെയോ ചിഹ്നങ്ങളെയോ ക്രമം അവഗണിച്ച് കൂട്ടങ്ങളായി തിരിക്കുകയും ഇത് എത്ര തരത്തിലാകാമെന്ന് നിര്ണയിക്കുകയും ചെയ്യല്.
സദിശം (Vector). പരിമാണവും (magnitude) ദിശയും (direction) ഉള്ള ഭൌതികരാശി. ഉദാ. പ്രവേഗം (velocity), ബലം (force) മുതലായവ.
സമരൂപചിത്രങ്ങള് (Similar figures). ഒരേ ആകൃതിയിലുള്ള ചിത്രങ്ങള്.
സമരേഖീയം (Collinear). ഒരേ രേഖയിലുള്ള ബിന്ദുക്കളാണ് സമരേഖീയ ബിന്ദുക്കള്.
സമാകലനം (Integration). സമാകലം (integral) കണ്ടുപിടിക്കുന്ന പ്രക്രിയ. അവകലനത്തിന്റെ വിപരീതക്രിയയാണ് സമാകലനം F(x)-ന്റെ അവകലം (ഡെറിവേറ്റീവ്) f(x) ആയാല് f(x)ന്റെ സമാകലമാണ് F(x). ഇതിനെ f(x)dx = F(x) എന്നെഴുതുന്നു. ഇവിടെ f(x) സമാകല്യവും (integrand) x സമാകലനത്തിലെ ചരവും (variable) ആണ്. നിശ്ചിത സമാകലത്തെ (definite integral) ![]() എന്നെഴുതുന്നു. വക്രങ്ങള് പരിബദ്ധമാക്കുന്ന വിസ്തീര്ണം, പരിക്രമണ ഘനരൂപ (solid of revolution)ങ്ങളുടെ വ്യാപ്തം തുടങ്ങിയവ കണ്ടുപിടിക്കാന് നിശ്ചിത സമാകലങ്ങള് ഉപയോഗിക്കുന്നു. ഒരു ഫലനത്തെ സമാകലിക്കാന് പല രീതികളുണ്ട്. പ്രതിസ്ഥാപനം (substitution)കൊണ്ടും ഖണ്ഡങ്ങളാക്കിയും (by parts) ആംശികഭിന്ന (partial fraction)ങ്ങള് വഴിയും ഫലനങ്ങളെ സാധാരണയായി സമാകലിക്കാറുണ്ട്.
എന്നെഴുതുന്നു. വക്രങ്ങള് പരിബദ്ധമാക്കുന്ന വിസ്തീര്ണം, പരിക്രമണ ഘനരൂപ (solid of revolution)ങ്ങളുടെ വ്യാപ്തം തുടങ്ങിയവ കണ്ടുപിടിക്കാന് നിശ്ചിത സമാകലങ്ങള് ഉപയോഗിക്കുന്നു. ഒരു ഫലനത്തെ സമാകലിക്കാന് പല രീതികളുണ്ട്. പ്രതിസ്ഥാപനം (substitution)കൊണ്ടും ഖണ്ഡങ്ങളാക്കിയും (by parts) ആംശികഭിന്ന (partial fraction)ങ്ങള് വഴിയും ഫലനങ്ങളെ സാധാരണയായി സമാകലിക്കാറുണ്ട്.
സമാന്തരശ്രേഢി (Arithmetic Progression). തുടര്ച്ചയായ ഏതെങ്കിലും രണ്ടു പദങ്ങള് തമ്മിലുള്ള വ്യത്യാസം, സ്ഥിരസംഖ്യയാകുന്ന ശ്രേഢി. ഈ വ്യത്യാസത്തെ പൊതുവ്യത്യാസം (common difference) എന്നു പറയുന്നു. ആദ്യപദം a-യും പൊതുവ്യത്യാസം d-യും ആയ ശ്രേഢിയെ a, a + d, a + 2d....,a + (n-1) d.... എന്നെഴുതാം. ഉദാ. 5, 8, 11, 14, 17....
സംഭാവ്യത (Probability). സംഭവിക്കലിന്റെ സാധ്യതയുടെ സംഖ്യാത്മകമായ അളവ്. സമസംഭാവി(equally likely)-യും പരസ്പര അപവര്ജിയു (mututally exclusive)മായ n സ്ഥിതികളില് A എന്ന സംഭവം m തവണ സംഭവിക്കുന്നുവെങ്കില് A-യുടെ സംഭവിക്കലിന്റെ സംഭാവ്യത ![]() ആണ്. P(A) എപ്പോഴും 0-ത്തിനും 1-നും ഇടയ്ക്കായിരിക്കും. 0 ≤ P(A) ≤ 1 ; P(A) = 0
ആയാല് A സംഭവിക്കുന്നില്ല. P(A)=1 ആയാല് A-യ്ക്ക് നൂറുശതമാനവും സംഭവിക്കാന് സാധ്യതയുണ്ട് എന്നര്ഥം. ഉദാ. ഒരു നാണയം മുകളിലേക്ക് എറിയുകയാണെങ്കില് തലയോ (head) വാലോ (tail) കിട്ടാം. ഓരോന്നും കിട്ടാനുള്ള സഭാവ്യത ½ വീതമാണ്. അതുപോലെ ഒരു പകിട (dice) എറിയുമ്പോള് 1, 2 ,3, 4, 5, 6 ഈ സംഖ്യകളില് ഏതെങ്കിലും ഒന്നു കിട്ടാനുള്ള സംഭാവ്യത
ആണ്. P(A) എപ്പോഴും 0-ത്തിനും 1-നും ഇടയ്ക്കായിരിക്കും. 0 ≤ P(A) ≤ 1 ; P(A) = 0
ആയാല് A സംഭവിക്കുന്നില്ല. P(A)=1 ആയാല് A-യ്ക്ക് നൂറുശതമാനവും സംഭവിക്കാന് സാധ്യതയുണ്ട് എന്നര്ഥം. ഉദാ. ഒരു നാണയം മുകളിലേക്ക് എറിയുകയാണെങ്കില് തലയോ (head) വാലോ (tail) കിട്ടാം. ഓരോന്നും കിട്ടാനുള്ള സഭാവ്യത ½ വീതമാണ്. അതുപോലെ ഒരു പകിട (dice) എറിയുമ്പോള് 1, 2 ,3, 4, 5, 6 ഈ സംഖ്യകളില് ഏതെങ്കിലും ഒന്നു കിട്ടാനുള്ള സംഭാവ്യത ![]() ആണ്.
ആണ്.
സമവാക്യം (Equation). ഒരു സമീകരണത്തിലുള്ള രാശിക്കോ രാശികള്ക്കോ ചില പ്രത്യേക വിലകള് മാത്രമേ സ്വീകാര്യമായിരിക്കൂ എങ്കില് ആ സമീകരണം ഉദാ. 2x2 + x - 3 = 0 x-ന് ![]() എന്നീ വിലകള് മാത്രമേയുള്ളൂ.
എന്നീ വിലകള് മാത്രമേയുള്ളൂ.
സമ്മിശ്രസംഖ്യ (Complex number). x+iy എന്ന രൂപത്തിലുള്ള സംഖ്യ. ഇവിടെ xഉം yഉം വാസ്തവികസംഖ്യകളും (real numbers), i = √-1 ആണ്.
സര്വസമവാക്യം (Identity). ഒരു സമീകരണത്തിനുള്ള രാശിക്കോ രാശികള്ക്കോ ഏതു വിലകളും സ്വീകാര്യമാകുമെങ്കില് ആ സമീകരണം. ഉദാ. (a+b) (a-b) = a2-b2.
സാംഖ്യികം (Statistics). ദത്തം സംഭവിക്കുകയും വിസ്ലേഷിക്കുകയും ചെയ്യുക, അവയില് നിന്നു നിഗമനങ്ങളിലെത്തുക, വിസ്ലേഷണത്തെ ആധാരമാക്കി തീരുമാനങ്ങളെടുക്കുക എന്നിവയെക്കുറിച്ചുള്ള പഠനം, സാംഖ്യിക അനുമാനത്തില് (inference) സമഷ്ടിയെ (population) സംബന്ധിച്ച തീരുമാനങ്ങളെടുക്കുന്നത് സാമ്പിള് വിസ്ലേഷണത്തിന്റെ അടിസ്ഥാനത്തിലാണ്.
സാരണികം (Determinant). രാശികളുടെ സമചതുരവ്യൂഹം (square array). n2 രാശികളെ n വരികളും (rows) n കോളങ്ങളും (column) ഉള്ള സാരണികമായി എഴുതാം. n-നെ സാരണികത്തിന്റെ ക്രമം (order) എന്നു പറയുന്നു. ഉദാ. രണ്ടാം ക്രമത്തിലുള്ള ഒരു സാരണികമാണ് ![]() . ഇതിന്റെ വില = a1b2-a2b1. ബഹുസമവാക്യങ്ങളെ (simultaneous equation) നിര്ധാരണം ചെയ്യാന് സാരണികം ഉപയോഗിക്കുന്നു.
. ഇതിന്റെ വില = a1b2-a2b1. ബഹുസമവാക്യങ്ങളെ (simultaneous equation) നിര്ധാരണം ചെയ്യാന് സാരണികം ഉപയോഗിക്കുന്നു.
സെറ്റ് (Set). ഗണം നിര്വചിക്കാവുന്ന വസ്തുക്കളുടെയോ സംഖ്യകളുടെയോ കൂട്ടം. വസ്തുക്കളുടെയോ സംഖ്യകളുടെയോ സെറ്റിലെ അംഗങ്ങള് (elements) എന്നു പറയുന്നു. ഉദാ. 5,10 എന്ന രണ്ടു സംഖ്യകളുടെ ഗണത്തെ {5,10} എന്നെഴുതുന്നു. നിസര്ഗസംഖ്യകളുടെ ഗണമാണ് { 1,2,3... ...}. അംഗങ്ങള് ഒന്നും ഇല്ലാത്ത ഗണത്തെ ശൂന്യഗണം (null set) എന്നു പറയുന്നു.
സ്റ്റെറേഡിയന് (Steradian). ഒരു ഘനകോണം (solid angle) അളക്കുന്ന ഏകകം.
ഹരാത്മകശ്രേഢി (Harmonic progression). ഒരു സമാന്തരശ്രേഢിയിലെ പദങ്ങളുടെ വ്യുത്ക്രമ(reciprocal)മായ ശ്രേഢി. ഉദാ. ![]()
ഹരണം (Division). ഒരു സംഖ്യയില് മറ്റൊരു സംഖ്യ കൂട്ടല് രീതിയില് എത്ര തവണവരുന്നു എന്നും ശേഷിക്കുന്നതെന്തെന്നും കണ്ടെത്തുന്ന പ്രക്രിയ. ഹരിക്കപ്പെടുന്നതിനെ ഹാര്യം (dividend), ഹരിക്കുന്നതിനെ ഹാരകം (divisor), ഫലത്തെ ഹരണഫലം (quotient), ശേഷിക്കുന്നതിനെ ശിഷ്ടം (remainder) എന്നും പറയുന്നു. ഉദാ. 13 നെ 3 കൊണ്ട് ഹരിക്കുമ്പോള് 4 കിട്ടും; ബാക്കി 1. 13 ഹാര്യവും 3 ഹാരകവും 4 ഹരണഫലവും 1 ശിഷ്ടവും ആണ്.
ഹാരകം (Denominator). ഭിന്നത്തില്, താഴെയുള്ള സംഖ്യ. ഉദാ. ![]() എന്ന ഭിന്നകത്തില് ഹാരകം 5.
എന്ന ഭിന്നകത്തില് ഹാരകം 5.
ഹെലിക്സ് (Helix). സര്പ്പില(spiral) ആകൃതിയുള്ള സ്പേസ് വക്രം. സിലിണ്ടറിലുള്ള ഹെലിക്സിനെ സിലണ്ടറീയ ഹെലിക്സ് എന്നുപറയുന്നു. സ്ക്രൂ(screw)വിലുള്ള പിരിയുടെ ആകൃതി ഹെലിക്സാണ്.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്.,സപ)