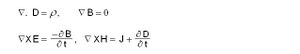This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഇലക്‌ട്രോമാഗ്നറ്റിസം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (പുതിയ താള്‍: == ഇലക്‌ട്രോമാഗ്നറ്റിസം == == Electromagnetism == വൈദ്യുതിയും കാന്തതയും തമ്മ...) |
Mksol (സംവാദം | സംഭാവനകള്) (→Electromagnetism) |
||
| വരി 2: | വരി 2: | ||
== Electromagnetism == | == Electromagnetism == | ||
| - | വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം പ്രതിപാദിക്കുന്ന ഭൗതികശാസ്‌ത്രശാഖ. വൈദ്യുതാധാനം (electric charge) ചലിക്കുമ്പോള്‍ ചാലകത്തിനുചുറ്റും ഉണ്ടാകുന്ന കാന്തികക്ഷേത്രവും (magnetic field), | + | വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം പ്രതിപാദിക്കുന്ന ഭൗതികശാസ്‌ത്രശാഖ. വൈദ്യുതാധാനം (electric charge) ചലിക്കുമ്പോള്‍ ചാലകത്തിനുചുറ്റും ഉണ്ടാകുന്ന കാന്തികക്ഷേത്രവും (magnetic field), കാന്തികക്ഷേത്രത്തില്‍ വൈദ്യുതാധാനം ചലിക്കുമ്പോള്‍ ആ ക്ഷേത്രത്തിലുണ്ടാകുന്ന വൈദ്യുതബലവും തമ്മിലുള്ള പ്രവര്‍ത്തന പ്രതിഭാസങ്ങള്‍ ഈ വിഭാഗത്തില്‍പ്പെടുന്നു. |
| - | + | ഓര്‍സ്റ്റഡിന്റെ പരീക്ഷണങ്ങളാണ്‌ (1820) ഇലക്‌ട്രോമാഗ്നറ്റിസത്തിലേക്ക്‌ ശാസ്‌ത്രലോകത്തിന്റെ ശ്രദ്ധ തിരിച്ചത്‌. ഒരു ചാലകത്തില്‍ക്കൂടി കടന്നുപോകുന്ന വൈദ്യുതകറണ്ട്‌ ഒരു കാന്തസൂചിയെ വ്യതിചലിപ്പിക്കും എന്ന്‌ അദ്ദേഹം കണ്ടുപിടിച്ചു. അതിനെത്തുടര്‍ന്ന്‌ ബയട്ട്‌, ഡവര്‍ട്ട്‌, ആമ്പിയര്‍, ഫാരഡെ, മാക്‌സ്‌വെല്‍ തുടങ്ങിയ പ്രമുഖ ശാസ്‌ത്രജ്ഞന്മാരും ഈ രംഗത്ത്‌ പരീക്ഷണങ്ങള്‍ നടത്തി. dl നീളമുള്ള ചാലകശകലത്തില്‍ക്കൂടി കടന്നുപോകുന്ന i വൈദ്യുതകറണ്ടിനാല്‍ ഒരു ബിന്ദുവില്‍ അനുഭവപ്പെടുന്ന കാന്തികസംവേശനം (dB) എത്രയാണെന്ന്‌ ബയട്ട്‌-സവര്‍ട്ട്‌ നിയമം പ്രസ്‌താവിക്കുന്നുണ്ട്‌. ആ നിയമപ്രകാരമുള്ള സമവാക്യം | |
[[ചിത്രം:Vol4_381_1.jpg|300px]] | [[ചിത്രം:Vol4_381_1.jpg|300px]] | ||
| - | ആണ്‌. ഇവിടെ r | + | ആണ്‌. ഇവിടെ r ചാലകത്തില്‍നിന്ന്‌ ആ ബിന്ദുവിന്റെ വിസ്ഥാപനസദിശവും (vector), θ ആ സദിശവും dl നീളവും തമ്മിലുള്ള കോണും, µഅന്തര്‍വേശനക്ഷമത(permeability)യും, B ആ ബിന്ദുവിലുള്ള പരിണത (resultant) കാന്തികക്ഷേത്രവും ആണ്‌. സമവാക്യത്തില്‍നിന്ന്‌ സമാകലനം (integration) വഴി കറണ്ട്‌ i കണ്ടുപിടിക്കാവുന്നതാണ്‌. |
| - | ആമ്പിയറുടെ പഠനങ്ങള്‍ വൈദ്യുത കറണ്ടിനെയും അതിനടുത്തുള്ള കാന്തികക്ഷേത്രത്തെയും ബന്ധപ്പെടുത്തുന്നു. ഒരു സംവൃതപഥത്തിനു (closed path) ചുറ്റുമാണ്‌ ഈ | + | ആമ്പിയറുടെ പഠനങ്ങള്‍ വൈദ്യുത കറണ്ടിനെയും അതിനടുത്തുള്ള കാന്തികക്ഷേത്രത്തെയും ബന്ധപ്പെടുത്തുന്നു. ഒരു സംവൃതപഥത്തിനു (closed path) ചുറ്റുമാണ്‌ ഈ ബന്ധത്തില്‍ രേഖാസമാകലനം (line integration) നടത്തിയിട്ടുള്ളത്‌. ഒരു കമ്പിക്കുചുറ്റുമുള്ള വൃത്താകാരസമാകലനപഥം ചിത്രത്തില്‍ കൊടുത്തിട്ടുണ്ട്‌. |
[[ചിത്രം:Vol4_381_2.jpg|thumb|]] | [[ചിത്രം:Vol4_381_2.jpg|thumb|]] | ||
| - | കറണ്ട്‌ പ്രവഹിക്കുന്ന കമ്പിക്കുചുറ്റും അനുഭവപ്പെടുന്ന കാന്തികക്ഷേത്രം ധാരാവാഹികളായ രണ്ടു ചാലകങ്ങള്‍ | + | കറണ്ട്‌ പ്രവഹിക്കുന്ന കമ്പിക്കുചുറ്റും അനുഭവപ്പെടുന്ന കാന്തികക്ഷേത്രം ധാരാവാഹികളായ രണ്ടു ചാലകങ്ങള്‍ തമ്മില്‍ അന്യോന്യപ്രവര്‍ത്തനത്തിനു വഴിതെളിക്കുന്നു, അതുമൂലം ധാരകള്‍ ഒരേ ദിശയില്‍ ആണെങ്കില്‍ കമ്പികള്‍ തമ്മില്‍ ആകര്‍ഷണവും എതിര്‍ദിശകളില്‍ ആണെങ്കില്‍ വികര്‍ഷണവും ഉണ്ടാകും. ഈ നിരീക്ഷണഫലങ്ങള്‍, ഒരു കാന്തികപദാര്‍ഥത്തില്‍ സ്ഥിരമായി ഭ്രമണം നടത്തുന്ന വൈദ്യുത കറണ്ടുകള്‍ അടങ്ങിയിരിക്കുന്നു എന്ന നിഗമനത്തിലേക്ക്‌ ആമ്പിയറെ നയിക്കുകയുണ്ടായി. മാക്‌സ്‌വെലിന്റെ സിദ്ധാന്തത്തോടെ വൈദ്യുതകറണ്ടില്‍ വൈദ്യുതാധാനങ്ങള്‍ പ്രവഹിക്കുന്നുവെന്നും അങ്ങനെ അവ ചലിക്കുമ്പോള്‍ കാന്തികക്ഷേത്രം ഉണ്ടാകുന്നു എന്നും ഉള്ള ധാരണ ഉറപ്പിക്കപ്പെട്ടു. |
| - | ഒരു വൈദ്യുത കറണ്ട്‌ കാന്തികക്ഷേത്രം ഉണ്ടാക്കുന്നു | + | ഒരു വൈദ്യുത കറണ്ട്‌ കാന്തികക്ഷേത്രം ഉണ്ടാക്കുന്നു എങ്കില്‍ കാന്തികക്ഷേത്രത്തില്‍നിന്ന്‌ വൈദ്യുതകറണ്ടും ലഭിക്കും എന്ന വിശ്വാസമാണ്‌ ഫാരഡെയെ വിദ്യുത്‌കാന്തികസംവേശനം കണ്ടുപിടിക്കുന്നതിലേക്കു നയിച്ചത്‌. കാന്തികക്ഷേത്രത്തിനു ലംബമായി ഒരു ആധാനം സഞ്ചരിക്കുകയാണെങ്കില്‍ ക്ഷേത്രദിശയ്‌ക്കും ചലനദിശയ്‌ക്കും ലംബമായി ഒരു വൈദ്യുതബലം അതിന്‌ അനുഭവപ്പെടുന്നു. അതുമൂലം ഒരു കമ്പിച്ചുരുളിനകത്തുകൂടി കടന്നുപോകുന്ന കാന്തികസംവേശനരേഖകള്‍ സമയത്തിനനുസരണമായി മാറുകയാണെങ്കില്‍ വിദ്യുത്‌-ചാലകബലം (electromotive force: EMF) ആ ചുരുളുകളില്‍ ഉണ്ടാകും. കമ്പിച്ചുരുളിനകത്തെ കാന്തികസംവേശനരേഖകള്‍, അതായത്‌ മാഗ്നറ്റിക്‌ഫ്‌ളക്‌സ്‌ ആണെങ്കില്‍ വിദ്യുത്‌ചാലകബലം e താഴെ ചേര്‍ക്കുന്നു. |
[[ചിത്രം:Vol4_381_3.jpg|300px]] | [[ചിത്രം:Vol4_381_3.jpg|300px]] | ||
| - | ഈ തത്ത്വത്തെ ഫാരഡെയുടെ വിദ്യുത്‌കാന്തികസംവേശന നിയമം എന്നുപറയുന്നു. | + | ഈ തത്ത്വത്തെ ഫാരഡെയുടെ വിദ്യുത്‌കാന്തികസംവേശന നിയമം എന്നുപറയുന്നു. പ്രരകകറണ്ടില്‍ (induced current) നിന്നുണ്ടാകുന്ന കാന്തികക്ഷേത്രം മാഗ്നറ്റിക്‌ ഫ്‌ളക്‌സിന്റെ പരിവര്‍ത്തനത്തിന്‌ എതിരാകത്തക്കവിധമായിരിക്കും പ്രരകവിദ്യുത്‌ചാലകബലത്തിന്റെ ദിശ (ലെന്‍സ്‌ നിയമം). അതുമൂലമാണ്‌ സമവാക്യത്തില്‍ ഋണചിഹ്നം (negative sign) കൊടുത്തിട്ടുള്ളത്‌. മാഗ്നറ്റിക്‌ ഫ്‌ളക്‌സ്‌ മാറുന്നത്‌ പലവിധത്തിലാകാം. കാന്തംതന്നെ ചലിക്കുകയോ ചാലകം ചലിക്കുകയോ അതല്ലെങ്കില്‍ ഇവയ്‌ക്കൊന്നിനും അനക്കമില്ലാത്തവിധത്തില്‍ കാന്തികക്ഷേത്രം മാറുകയോ ചെയ്‌താലും ചാലകത്തില്‍ വിദ്യുത്‌ചാലകബലം ഉണ്ടാകുകയും ആധാനങ്ങള്‍ പ്രവഹിച്ച്‌ കറണ്ട്‌ ലഭിക്കുകയും ചെയ്യും. ഇവിടെ പരിവര്‍ത്തി (varying) കാന്തികക്ഷേത്രം വൈദ്യുതക്ഷേത്രം ഉണ്ടാക്കുന്നു. ഈ വൈദ്യുതക്ഷേത്രം ആധാനങ്ങളെ ആകര്‍ഷിക്കുകയോ വികര്‍ഷിക്കുകയോ ചെയ്യുന്നതുമൂലം അവ ചലിക്കുകയും അങ്ങനെ പ്രരകകറണ്ട്‌ ലഭിക്കുകയും ചെയ്യുന്നു. കറണ്ട്‌ പ്രവഹിക്കുവാന്‍ ചാലകത്തോടുചേര്‍ന്ന്‌ ഒരു സംവൃതപഥം (closed circuit) ഉണ്ടായിരിക്കണം. അതില്ലെങ്കില്‍ വൈദ്യുതക്ഷേത്രം മാത്രമേ ഉണ്ടാകുകയുള്ളൂ. പ്രരകവൈദ്യുതക്ഷേത്രം ഋ ആണെ[[ചിത്രം:Vol4_381_4.jpg|300px]] |
| - | ഫാരഡെയുടെയും ആമ്പിയറുടെയും മറ്റും പഠനങ്ങള്‍ ഉപയോഗിച്ച്‌ വൈദ്യുതിയെ കാന്തശക്തിയുമായി ബന്ധപ്പെടുത്തുന്ന ഒരു സിദ്ധാന്തം ജയിംസ്‌ | + | ഫാരഡെയുടെയും ആമ്പിയറുടെയും മറ്റും പഠനങ്ങള്‍ ഉപയോഗിച്ച്‌ വൈദ്യുതിയെ കാന്തശക്തിയുമായി ബന്ധപ്പെടുത്തുന്ന ഒരു സിദ്ധാന്തം ജയിംസ്‌ ക്ലാര്‍ക്ക്‌ മാക്‌സ്‌വെല്‍ അവതരിപ്പിച്ചു. ആ സിദ്ധാന്തം മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ എന്ന്‌ അറിയപ്പെടുന്ന നാലു സമവാക്യങ്ങളില്‍ അടങ്ങിയിരിക്കുന്നു. |
[[ചിത്രം:Vol4_381_5.jpg|300px]] | [[ചിത്രം:Vol4_381_5.jpg|300px]] | ||
| - | ഇവിടെ ρ ആധാനത്തിന്റെ വ്യാപ്‌തസാന്ദ്രതയും (volume density of charge) D വൈദ്യുത വിസ്ഥാപനവും (displacement) ആകുന്നു. D എന്ന പദത്തിന്റെ പ്രവേശനം | + | ഇവിടെ ρ ആധാനത്തിന്റെ വ്യാപ്‌തസാന്ദ്രതയും (volume density of charge) D വൈദ്യുത വിസ്ഥാപനവും (displacement) ആകുന്നു. D എന്ന പദത്തിന്റെ പ്രവേശനം മാക്‌സ്‌വെല്‍ സിദ്ധാന്തത്തെ കരുത്തുറ്റതാക്കി എന്നു മനസ്സിലാക്കേണ്ടതാണ്‌. പരീക്ഷണഫലങ്ങള്‍ ഈ സമവാക്യങ്ങള്‍ക്കും സങ്കല്‌പത്തിനും സിദ്ധാന്തത്തിനും സാധുത്വം നല്‌കിയിരിക്കുന്നു. |
| - | വൈദ്യുതവിസ്ഥാപനമായ D-യുടെ പരിമാണം (dimension) ക്ഷേത്രഫലമാത്ര(unit area)യിലുള്ള ആധാനങ്ങളാണ്‌. K | + | വൈദ്യുതവിസ്ഥാപനമായ D-യുടെ പരിമാണം (dimension) ക്ഷേത്രഫലമാത്ര(unit area)യിലുള്ള ആധാനങ്ങളാണ്‌. K അന്തര്‍വേശകതയുള്ള ഒരു ഏകാത്മക മാധ്യമത്തില്‍ D-യുടെ മൂല്യം KE ആണ്‌. ഗൗസ്‌ സിദ്ധാന്തമനുസരിച്ച്‌ ഒരു സംവൃതപ്രതലത്തില്‍നിന്ന്‌ ബഹിര്‍ഗമിക്കുന്ന ഉ-യുടെ ഫ്‌ളക്‌സ്‌ ആ പ്രതലത്തിനകത്തുള്ള ആധാനങ്ങള്‍ക്കു തുല്യമായിരിക്കും. അതുകൊണ്ട്‌ [[ചിത്രം:Vol4_381_6.jpg|75px]] ആണ്‌. പ്രതലസമാകലനത്തെ വ്യാപ്‌തസമാകലനമാക്കിയാല്‍ മാക്‌സ്‌വെലിന്റെ ഒന്നാം സമവാക്യം ലഭിക്കും. ഇലക്‌ട്രിക ഫ്‌ളക്‌സ്‌ രേഖകള്‍ എവിടെയെങ്കിലും അവസാനിക്കുന്നുവെങ്കില്‍ അത്‌ വൈദ്യുതാധാനങ്ങളിലായിരിക്കും എന്നാണ്‌ ഇതുകൊണ്ട്‌ അര്‍ഥമാക്കുന്നത്‌. എന്നാല്‍ കാന്തികഫ്‌ളക്‌സ്‌ രേഖകളെ സംബന്ധിച്ച കാന്തികരേഖകള്‍ ~ഒരു സ്ഥലത്തും ചെന്നവസാനിക്കുന്നില്ല എന്നാണ്‌ രണ്ടാം സമവാക്യം ചൂണ്ടിക്കാണിക്കുന്നത്‌. ഫാരഡെയുടെ സംവേശനനിയമത്തില്‍ നിന്ന് ലഭിച്ചതാണ്‌ മൂന്നാം സമവാക്യം. നാലാമത്തെ സമവാക്യത്തില്‍ ഉ പദം ഇല്ലെങ്കില്‍ അത്‌ ആമ്പിയര്‍ നിയമമനുസരിച്ചുള്ള സമവാക്യം ആയിത്തീരും. ഈ പദം വന്നതെങ്ങനെയെന്നു താഴെ വിവരിക്കുന്നു. സാതത്യ (continuous) സമവാക്യം [[ചിത്രം:Vol4_382_1.jpg|75px]] എന്നാണ്‌. ആമ്പിയര്‍ നിയമത്തിലെ സമവാക്യത്തിന്റെ രണ്ടുവശത്തും വരുന്ന സദിശങ്ങളുടെ "ഡൈവേര്‍ജന്‍സ്‌' എടുത്താല്‍ [[ചിത്രം:Vol4_382_2.jpg|50px]]എന്നായിരിക്കും ലഭിക്കുക. അപ്പോള്‍ സമവാക്യത്തില്‍നിന്ന്‌ [[ചിത്രം:Vol4_382_3.jpg|50px]]എന്നു ലഭിക്കും. ആംപിയര്‍ നിയമത്തിന്റെ പരിമിതിയിലേക്കാണ്‌ ഇതു ചൂണ്ടുന്നത്‌. ആധാനസാന്ദ്രതയ്‌ക്ക്‌ കാലവ്യത്യാസം വരാത്ത സ്ഥിരമായ കറണ്ടുള്ള ക്ഷേത്രങ്ങള്‍ക്കു മാത്രമേ ആംപിയര്‍നിയമം ബാധകമാകുകയുള്ളൂ. ഏറ്റക്കുറച്ചിലുള്ള കറണ്ടുകളില്‍ സാതത്യസമവാക്യത്തിന്‌ അനുസരണമായി D പദം കൂട്ടിച്ചേര്‍ത്ത്‌ ആംപിയര്‍നിയമം പരിഷ്‌കരിക്കുകയാണ്‌ മാക്‌സ്‌വെല്‍ ചെയ്‌തത്‌. D-യെ വിസ്ഥാപന കറണ്ട്‌ എന്നു പറയുന്നു. |
| - | ഒരു ഡൈ-ഇലക്‌ട്രിക്കിലോ (dielectric) | + | ഒരു ഡൈ-ഇലക്‌ട്രിക്കിലോ (dielectric) അതല്ലെങ്കില്‍ ശൂന്യപ്രദേശത്തോ (vacuum) കറണ്ട്‌ സാന്ദ്രതയും ആധാനസാന്ദ്രതയും പൂജ്യമായിരിക്കും. അപ്പോള്‍ മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ ലഘൂകരണം വഴി |
[[ചിത്രം:Vol4_382_4.jpg|300px]] | [[ചിത്രം:Vol4_382_4.jpg|300px]] | ||
| - | എന്നായിത്തീരും. ഇവിടെ വിസ്ഥാപനകറണ്ട്‌ ഒരു പ്രധാന | + | എന്നായിത്തീരും. ഇവിടെ വിസ്ഥാപനകറണ്ട്‌ ഒരു പ്രധാന പങ്കുനിര്‍വഹിക്കുന്നു. ഈ സമവാക്യങ്ങളാണ്‌ വിദ്യുത്‌കാന്തികതരംഗങ്ങള്‍ സാധ്യമാണെന്ന്‌ വെളിപ്പെടുത്തുന്നത്‌. ഇതില്‍നിന്ന്‌ പ്രകാശത്തിന്റെ വിദ്യുത്‌കാന്തികസിദ്ധാന്തം മാക്‌സ്‌വെല്‍ ആവിഷ്‌കരിച്ചു. |
| - | വിദ്യുത്‌കാന്തിക ക്ഷേത്രത്തെയും | + | വിദ്യുത്‌കാന്തിക ക്ഷേത്രത്തെയും പദാര്‍ഥവുമായുള്ള അതിന്റെ അന്യോന്യപ്രക്രിയകളെയും വ്യക്തമായി പ്രതിപാദിക്കുവാന്‍ മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ക്കു സാധിച്ചു എന്നത്‌ ഒരു വസ്‌തുതയാണ്‌. ആപേക്ഷികതാസിദ്ധാന്തത്തിന്റെയും ക്വാണ്ടം മെക്കാനിക്‌സിന്റെയും വളര്‍ച്ച ഈ സമവാക്യങ്ങളുടെ പ്രാധാന്യം ഒട്ടും കുറച്ചിട്ടില്ല. ഇവിടെ രണ്ടു സദിശങ്ങള്‍ E-യും B-യും ഉപയോഗിച്ചാണ്‌ സിദ്ധാന്തം കെട്ടിപ്പടുത്തിട്ടുള്ളത്‌. എന്നാല്‍ ഈ സദിശങ്ങള്‍ സമമിതം (symmetric) ആയല്ല സിദ്ധാന്തത്തില്‍ പ്രത്യക്ഷപ്പെടുന്നത്‌. അവ സമമിതമായി പ്രത്യക്ഷപ്പെടുന്ന ഒരു സിദ്ധാന്തത്തിലേക്ക്‌ പല ശാസ്‌ത്രജ്ഞന്മാരുടെയും ശ്രദ്ധ തിരിഞ്ഞിട്ടുണ്ട്‌. കാന്തികാധാനങ്ങളും കാന്തികകറണ്ടുകളും ക്ഷേത്രസമവാക്യങ്ങളില്‍ പ്രത്യക്ഷെപ്പടാവുന്നതാണ്‌. 1931-ല്‍ പി.എ.എം. ഡിറാക്‌ ഏക കാന്തിക ധ്രുവങ്ങളും സാധ്യമാണെന്ന്‌ പ്രതിപാദിച്ചിരുന്നു. ഏകകാന്തികധ്രുവം കണ്ടുപിടിച്ചു എന്ന്‌ 1975-ല്‍ അവകാശപ്പെടുകയുമുണ്ടായിട്ടുണ്ട്‌. |
| - | (ഡോ. വി. ഉണ്ണിക്കൃഷ്‌ണന്‍ | + | (ഡോ. വി. ഉണ്ണിക്കൃഷ്‌ണന്‍ നായര്‍) |
Current revision as of 09:34, 11 സെപ്റ്റംബര്‍ 2014
ഇലക്‌ട്രോമാഗ്നറ്റിസം
Electromagnetism
വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം പ്രതിപാദിക്കുന്ന ഭൗതികശാസ്‌ത്രശാഖ. വൈദ്യുതാധാനം (electric charge) ചലിക്കുമ്പോള്‍ ചാലകത്തിനുചുറ്റും ഉണ്ടാകുന്ന കാന്തികക്ഷേത്രവും (magnetic field), കാന്തികക്ഷേത്രത്തില്‍ വൈദ്യുതാധാനം ചലിക്കുമ്പോള്‍ ആ ക്ഷേത്രത്തിലുണ്ടാകുന്ന വൈദ്യുതബലവും തമ്മിലുള്ള പ്രവര്‍ത്തന പ്രതിഭാസങ്ങള്‍ ഈ വിഭാഗത്തില്‍പ്പെടുന്നു. ഓര്‍സ്റ്റഡിന്റെ പരീക്ഷണങ്ങളാണ്‌ (1820) ഇലക്‌ട്രോമാഗ്നറ്റിസത്തിലേക്ക്‌ ശാസ്‌ത്രലോകത്തിന്റെ ശ്രദ്ധ തിരിച്ചത്‌. ഒരു ചാലകത്തില്‍ക്കൂടി കടന്നുപോകുന്ന വൈദ്യുതകറണ്ട്‌ ഒരു കാന്തസൂചിയെ വ്യതിചലിപ്പിക്കും എന്ന്‌ അദ്ദേഹം കണ്ടുപിടിച്ചു. അതിനെത്തുടര്‍ന്ന്‌ ബയട്ട്‌, ഡവര്‍ട്ട്‌, ആമ്പിയര്‍, ഫാരഡെ, മാക്‌സ്‌വെല്‍ തുടങ്ങിയ പ്രമുഖ ശാസ്‌ത്രജ്ഞന്മാരും ഈ രംഗത്ത്‌ പരീക്ഷണങ്ങള്‍ നടത്തി. dl നീളമുള്ള ചാലകശകലത്തില്‍ക്കൂടി കടന്നുപോകുന്ന i വൈദ്യുതകറണ്ടിനാല്‍ ഒരു ബിന്ദുവില്‍ അനുഭവപ്പെടുന്ന കാന്തികസംവേശനം (dB) എത്രയാണെന്ന്‌ ബയട്ട്‌-സവര്‍ട്ട്‌ നിയമം പ്രസ്‌താവിക്കുന്നുണ്ട്‌. ആ നിയമപ്രകാരമുള്ള സമവാക്യം
ആണ്‌. ഇവിടെ r ചാലകത്തില്‍നിന്ന്‌ ആ ബിന്ദുവിന്റെ വിസ്ഥാപനസദിശവും (vector), θ ആ സദിശവും dl നീളവും തമ്മിലുള്ള കോണും, µഅന്തര്‍വേശനക്ഷമത(permeability)യും, B ആ ബിന്ദുവിലുള്ള പരിണത (resultant) കാന്തികക്ഷേത്രവും ആണ്‌. സമവാക്യത്തില്‍നിന്ന്‌ സമാകലനം (integration) വഴി കറണ്ട്‌ i കണ്ടുപിടിക്കാവുന്നതാണ്‌.
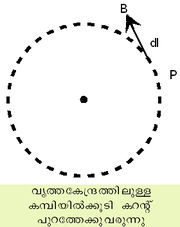
ആമ്പിയറുടെ പഠനങ്ങള്‍ വൈദ്യുത കറണ്ടിനെയും അതിനടുത്തുള്ള കാന്തികക്ഷേത്രത്തെയും ബന്ധപ്പെടുത്തുന്നു. ഒരു സംവൃതപഥത്തിനു (closed path) ചുറ്റുമാണ്‌ ഈ ബന്ധത്തില്‍ രേഖാസമാകലനം (line integration) നടത്തിയിട്ടുള്ളത്‌. ഒരു കമ്പിക്കുചുറ്റുമുള്ള വൃത്താകാരസമാകലനപഥം ചിത്രത്തില്‍ കൊടുത്തിട്ടുണ്ട്‌.
കറണ്ട്‌ പ്രവഹിക്കുന്ന കമ്പിക്കുചുറ്റും അനുഭവപ്പെടുന്ന കാന്തികക്ഷേത്രം ധാരാവാഹികളായ രണ്ടു ചാലകങ്ങള്‍ തമ്മില്‍ അന്യോന്യപ്രവര്‍ത്തനത്തിനു വഴിതെളിക്കുന്നു, അതുമൂലം ധാരകള്‍ ഒരേ ദിശയില്‍ ആണെങ്കില്‍ കമ്പികള്‍ തമ്മില്‍ ആകര്‍ഷണവും എതിര്‍ദിശകളില്‍ ആണെങ്കില്‍ വികര്‍ഷണവും ഉണ്ടാകും. ഈ നിരീക്ഷണഫലങ്ങള്‍, ഒരു കാന്തികപദാര്‍ഥത്തില്‍ സ്ഥിരമായി ഭ്രമണം നടത്തുന്ന വൈദ്യുത കറണ്ടുകള്‍ അടങ്ങിയിരിക്കുന്നു എന്ന നിഗമനത്തിലേക്ക്‌ ആമ്പിയറെ നയിക്കുകയുണ്ടായി. മാക്‌സ്‌വെലിന്റെ സിദ്ധാന്തത്തോടെ വൈദ്യുതകറണ്ടില്‍ വൈദ്യുതാധാനങ്ങള്‍ പ്രവഹിക്കുന്നുവെന്നും അങ്ങനെ അവ ചലിക്കുമ്പോള്‍ കാന്തികക്ഷേത്രം ഉണ്ടാകുന്നു എന്നും ഉള്ള ധാരണ ഉറപ്പിക്കപ്പെട്ടു. ഒരു വൈദ്യുത കറണ്ട്‌ കാന്തികക്ഷേത്രം ഉണ്ടാക്കുന്നു എങ്കില്‍ കാന്തികക്ഷേത്രത്തില്‍നിന്ന്‌ വൈദ്യുതകറണ്ടും ലഭിക്കും എന്ന വിശ്വാസമാണ്‌ ഫാരഡെയെ വിദ്യുത്‌കാന്തികസംവേശനം കണ്ടുപിടിക്കുന്നതിലേക്കു നയിച്ചത്‌. കാന്തികക്ഷേത്രത്തിനു ലംബമായി ഒരു ആധാനം സഞ്ചരിക്കുകയാണെങ്കില്‍ ക്ഷേത്രദിശയ്‌ക്കും ചലനദിശയ്‌ക്കും ലംബമായി ഒരു വൈദ്യുതബലം അതിന്‌ അനുഭവപ്പെടുന്നു. അതുമൂലം ഒരു കമ്പിച്ചുരുളിനകത്തുകൂടി കടന്നുപോകുന്ന കാന്തികസംവേശനരേഖകള്‍ സമയത്തിനനുസരണമായി മാറുകയാണെങ്കില്‍ വിദ്യുത്‌-ചാലകബലം (electromotive force: EMF) ആ ചുരുളുകളില്‍ ഉണ്ടാകും. കമ്പിച്ചുരുളിനകത്തെ കാന്തികസംവേശനരേഖകള്‍, അതായത്‌ മാഗ്നറ്റിക്‌ഫ്‌ളക്‌സ്‌ ആണെങ്കില്‍ വിദ്യുത്‌ചാലകബലം e താഴെ ചേര്‍ക്കുന്നു.
ഈ തത്ത്വത്തെ ഫാരഡെയുടെ വിദ്യുത്‌കാന്തികസംവേശന നിയമം എന്നുപറയുന്നു. പ്രരകകറണ്ടില്‍ (induced current) നിന്നുണ്ടാകുന്ന കാന്തികക്ഷേത്രം മാഗ്നറ്റിക്‌ ഫ്‌ളക്‌സിന്റെ പരിവര്‍ത്തനത്തിന്‌ എതിരാകത്തക്കവിധമായിരിക്കും പ്രരകവിദ്യുത്‌ചാലകബലത്തിന്റെ ദിശ (ലെന്‍സ്‌ നിയമം). അതുമൂലമാണ്‌ സമവാക്യത്തില്‍ ഋണചിഹ്നം (negative sign) കൊടുത്തിട്ടുള്ളത്‌. മാഗ്നറ്റിക്‌ ഫ്‌ളക്‌സ്‌ മാറുന്നത്‌ പലവിധത്തിലാകാം. കാന്തംതന്നെ ചലിക്കുകയോ ചാലകം ചലിക്കുകയോ അതല്ലെങ്കില്‍ ഇവയ്‌ക്കൊന്നിനും അനക്കമില്ലാത്തവിധത്തില്‍ കാന്തികക്ഷേത്രം മാറുകയോ ചെയ്‌താലും ചാലകത്തില്‍ വിദ്യുത്‌ചാലകബലം ഉണ്ടാകുകയും ആധാനങ്ങള്‍ പ്രവഹിച്ച്‌ കറണ്ട്‌ ലഭിക്കുകയും ചെയ്യും. ഇവിടെ പരിവര്‍ത്തി (varying) കാന്തികക്ഷേത്രം വൈദ്യുതക്ഷേത്രം ഉണ്ടാക്കുന്നു. ഈ വൈദ്യുതക്ഷേത്രം ആധാനങ്ങളെ ആകര്‍ഷിക്കുകയോ വികര്‍ഷിക്കുകയോ ചെയ്യുന്നതുമൂലം അവ ചലിക്കുകയും അങ്ങനെ പ്രരകകറണ്ട്‌ ലഭിക്കുകയും ചെയ്യുന്നു. കറണ്ട്‌ പ്രവഹിക്കുവാന്‍ ചാലകത്തോടുചേര്‍ന്ന്‌ ഒരു സംവൃതപഥം (closed circuit) ഉണ്ടായിരിക്കണം. അതില്ലെങ്കില്‍ വൈദ്യുതക്ഷേത്രം മാത്രമേ ഉണ്ടാകുകയുള്ളൂ. പ്രരകവൈദ്യുതക്ഷേത്രം ഋ ആണെ
ഫാരഡെയുടെയും ആമ്പിയറുടെയും മറ്റും പഠനങ്ങള്‍ ഉപയോഗിച്ച്‌ വൈദ്യുതിയെ കാന്തശക്തിയുമായി ബന്ധപ്പെടുത്തുന്ന ഒരു സിദ്ധാന്തം ജയിംസ്‌ ക്ലാര്‍ക്ക്‌ മാക്‌സ്‌വെല്‍ അവതരിപ്പിച്ചു. ആ സിദ്ധാന്തം മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ എന്ന്‌ അറിയപ്പെടുന്ന നാലു സമവാക്യങ്ങളില്‍ അടങ്ങിയിരിക്കുന്നു.
ഇവിടെ ρ ആധാനത്തിന്റെ വ്യാപ്‌തസാന്ദ്രതയും (volume density of charge) D വൈദ്യുത വിസ്ഥാപനവും (displacement) ആകുന്നു. D എന്ന പദത്തിന്റെ പ്രവേശനം മാക്‌സ്‌വെല്‍ സിദ്ധാന്തത്തെ കരുത്തുറ്റതാക്കി എന്നു മനസ്സിലാക്കേണ്ടതാണ്‌. പരീക്ഷണഫലങ്ങള്‍ ഈ സമവാക്യങ്ങള്‍ക്കും സങ്കല്‌പത്തിനും സിദ്ധാന്തത്തിനും സാധുത്വം നല്‌കിയിരിക്കുന്നു.
വൈദ്യുതവിസ്ഥാപനമായ D-യുടെ പരിമാണം (dimension) ക്ഷേത്രഫലമാത്ര(unit area)യിലുള്ള ആധാനങ്ങളാണ്‌. K അന്തര്‍വേശകതയുള്ള ഒരു ഏകാത്മക മാധ്യമത്തില്‍ D-യുടെ മൂല്യം KE ആണ്‌. ഗൗസ്‌ സിദ്ധാന്തമനുസരിച്ച്‌ ഒരു സംവൃതപ്രതലത്തില്‍നിന്ന്‌ ബഹിര്‍ഗമിക്കുന്ന ഉ-യുടെ ഫ്‌ളക്‌സ്‌ ആ പ്രതലത്തിനകത്തുള്ള ആധാനങ്ങള്‍ക്കു തുല്യമായിരിക്കും. അതുകൊണ്ട്‌ 
ആണ്‌. പ്രതലസമാകലനത്തെ വ്യാപ്‌തസമാകലനമാക്കിയാല്‍ മാക്‌സ്‌വെലിന്റെ ഒന്നാം സമവാക്യം ലഭിക്കും. ഇലക്‌ട്രിക ഫ്‌ളക്‌സ്‌ രേഖകള്‍ എവിടെയെങ്കിലും അവസാനിക്കുന്നുവെങ്കില്‍ അത്‌ വൈദ്യുതാധാനങ്ങളിലായിരിക്കും എന്നാണ്‌ ഇതുകൊണ്ട്‌ അര്‍ഥമാക്കുന്നത്‌. എന്നാല്‍ കാന്തികഫ്‌ളക്‌സ്‌ രേഖകളെ സംബന്ധിച്ച കാന്തികരേഖകള്‍ ~ഒരു സ്ഥലത്തും ചെന്നവസാനിക്കുന്നില്ല എന്നാണ്‌ രണ്ടാം സമവാക്യം ചൂണ്ടിക്കാണിക്കുന്നത്‌. ഫാരഡെയുടെ സംവേശനനിയമത്തില്‍ നിന്ന് ലഭിച്ചതാണ്‌ മൂന്നാം സമവാക്യം. നാലാമത്തെ സമവാക്യത്തില്‍ ഉ പദം ഇല്ലെങ്കില്‍ അത്‌ ആമ്പിയര്‍ നിയമമനുസരിച്ചുള്ള സമവാക്യം ആയിത്തീരും. ഈ പദം വന്നതെങ്ങനെയെന്നു താഴെ വിവരിക്കുന്നു. സാതത്യ (continuous) സമവാക്യം 
എന്നാണ്‌. ആമ്പിയര്‍ നിയമത്തിലെ സമവാക്യത്തിന്റെ രണ്ടുവശത്തും വരുന്ന സദിശങ്ങളുടെ "ഡൈവേര്‍ജന്‍സ്‌' എടുത്താല്‍ 
എന്നായിരിക്കും ലഭിക്കുക. അപ്പോള്‍ സമവാക്യത്തില്‍നിന്ന്‌ 
എന്നു ലഭിക്കും. ആംപിയര്‍ നിയമത്തിന്റെ പരിമിതിയിലേക്കാണ്‌ ഇതു ചൂണ്ടുന്നത്‌. ആധാനസാന്ദ്രതയ്‌ക്ക്‌ കാലവ്യത്യാസം വരാത്ത സ്ഥിരമായ കറണ്ടുള്ള ക്ഷേത്രങ്ങള്‍ക്കു മാത്രമേ ആംപിയര്‍നിയമം ബാധകമാകുകയുള്ളൂ. ഏറ്റക്കുറച്ചിലുള്ള കറണ്ടുകളില്‍ സാതത്യസമവാക്യത്തിന്‌ അനുസരണമായി D പദം കൂട്ടിച്ചേര്‍ത്ത്‌ ആംപിയര്‍നിയമം പരിഷ്‌കരിക്കുകയാണ്‌ മാക്‌സ്‌വെല്‍ ചെയ്‌തത്‌. D-യെ വിസ്ഥാപന കറണ്ട്‌ എന്നു പറയുന്നു.
ഒരു ഡൈ-ഇലക്‌ട്രിക്കിലോ (dielectric) അതല്ലെങ്കില്‍ ശൂന്യപ്രദേശത്തോ (vacuum) കറണ്ട്‌ സാന്ദ്രതയും ആധാനസാന്ദ്രതയും പൂജ്യമായിരിക്കും. അപ്പോള്‍ മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ ലഘൂകരണം വഴി
എന്നായിത്തീരും. ഇവിടെ വിസ്ഥാപനകറണ്ട്‌ ഒരു പ്രധാന പങ്കുനിര്‍വഹിക്കുന്നു. ഈ സമവാക്യങ്ങളാണ്‌ വിദ്യുത്‌കാന്തികതരംഗങ്ങള്‍ സാധ്യമാണെന്ന്‌ വെളിപ്പെടുത്തുന്നത്‌. ഇതില്‍നിന്ന്‌ പ്രകാശത്തിന്റെ വിദ്യുത്‌കാന്തികസിദ്ധാന്തം മാക്‌സ്‌വെല്‍ ആവിഷ്‌കരിച്ചു.
വിദ്യുത്‌കാന്തിക ക്ഷേത്രത്തെയും പദാര്‍ഥവുമായുള്ള അതിന്റെ അന്യോന്യപ്രക്രിയകളെയും വ്യക്തമായി പ്രതിപാദിക്കുവാന്‍ മാക്‌സ്‌വെല്‍ സമവാക്യങ്ങള്‍ക്കു സാധിച്ചു എന്നത്‌ ഒരു വസ്‌തുതയാണ്‌. ആപേക്ഷികതാസിദ്ധാന്തത്തിന്റെയും ക്വാണ്ടം മെക്കാനിക്‌സിന്റെയും വളര്‍ച്ച ഈ സമവാക്യങ്ങളുടെ പ്രാധാന്യം ഒട്ടും കുറച്ചിട്ടില്ല. ഇവിടെ രണ്ടു സദിശങ്ങള്‍ E-യും B-യും ഉപയോഗിച്ചാണ്‌ സിദ്ധാന്തം കെട്ടിപ്പടുത്തിട്ടുള്ളത്‌. എന്നാല്‍ ഈ സദിശങ്ങള്‍ സമമിതം (symmetric) ആയല്ല സിദ്ധാന്തത്തില്‍ പ്രത്യക്ഷപ്പെടുന്നത്‌. അവ സമമിതമായി പ്രത്യക്ഷപ്പെടുന്ന ഒരു സിദ്ധാന്തത്തിലേക്ക്‌ പല ശാസ്‌ത്രജ്ഞന്മാരുടെയും ശ്രദ്ധ തിരിഞ്ഞിട്ടുണ്ട്‌. കാന്തികാധാനങ്ങളും കാന്തികകറണ്ടുകളും ക്ഷേത്രസമവാക്യങ്ങളില്‍ പ്രത്യക്ഷെപ്പടാവുന്നതാണ്‌. 1931-ല്‍ പി.എ.എം. ഡിറാക്‌ ഏക കാന്തിക ധ്രുവങ്ങളും സാധ്യമാണെന്ന്‌ പ്രതിപാദിച്ചിരുന്നു. ഏകകാന്തികധ്രുവം കണ്ടുപിടിച്ചു എന്ന്‌ 1975-ല്‍ അവകാശപ്പെടുകയുമുണ്ടായിട്ടുണ്ട്‌.
(ഡോ. വി. ഉണ്ണിക്കൃഷ്‌ണന്‍ നായര്‍)
