This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കാര്ഡ്യോയ്ഡ്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Cardioid) |
Mksol (സംവാദം | സംഭാവനകള്) (→Cardioid) |
||
| വരി 1: | വരി 1: | ||
== കാര്ഡ്യോയ്ഡ് == | == കാര്ഡ്യോയ്ഡ് == | ||
== Cardioid == | == Cardioid == | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Vol7_278_image.jpg|thumb|കാർഡ്യോയ്ഡ്]] |
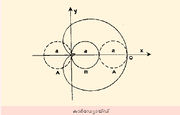
| - | ഹൃദയത്തിന്റെ ആകൃതിയിലുള്ള ഒരു ജ്യാമിതീയ വക്രം. ഒരു വൃത്തം അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തത്തിന്റെ ചുറ്റളവിലൂടെ ഒരേ സമതലത്തില് ഉരുളുമ്പോള് ആദ്യവൃത്തത്തിന്റെ ചുറ്റളവിലുള്ള ഒരു സ്ഥിരബിന്ദു സൃഷ്ടിക്കുന്ന വക്രം ആണ് കാര്ഡ്യോയ്ഡ്. ഇറ്റാലിയന് ഗണിതശാസ്ത്രജ്ഞനായ സാല്വെമിനി കാസ്റ്റിലോണ് (Johann Francesco Melchiore Salvemini Castillon, 1704-91) ആണ് വക്രത്തിന് ഈ പേര് നല്കിയത് (1741). A എന്നൊരു വൃത്തത്തിന്റെ ഒരു സ്ഥിരബിന്ദു Pഉം B അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തവുമാണെങ്കില് A Bയിന്മേല് ഉരുളുന്നതിന്റെ ആരംഭം P യിലായിരിക്കും. അതായത് P ആദ്യം A,B എന്നീ വൃത്തങ്ങളിലെ പൊതുബിന്ദുവാണ്. A ഉരുളുന്നതോടെ P, Bയില്നിന്ന് അകന്നുപോകുന്നു. Q എന്ന ബിന്ദുവില് P എത്തുമ്പോള് രണ്ടു വൃത്തങ്ങളുടെയും വ്യാസം ഒരേ നേര്വരയില് പ്രകടമാകുന്നു. തുടര്ന്ന് A ഉരുളുന്നതോടെ P വീണ്ടും B യോടടുക്കുന്നതു കാണാം. അവസാനം പൂര്വസ്ഥാനത്തെത്തി രണ്ടു വൃത്തങ്ങളുടെയും പൊതുബിന്ദു ആയിത്തീരുന്നു. P യുടെ സഞ്ചാരപഥത്തെയാണ് കാര്ഡ്യോയ്ഡ് എന്നു പറയുന്നത്. ഒരു സമതലത്തില് രണ്ടു ലംബീയ അക്ഷങ്ങളെ ആധാരമാക്കിയുള്ള കാര്ഡ്യോയ്ഡിന്റെ സമവാക്യം ( | + | ഹൃദയത്തിന്റെ ആകൃതിയിലുള്ള ഒരു ജ്യാമിതീയ വക്രം. ഒരു വൃത്തം അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തത്തിന്റെ ചുറ്റളവിലൂടെ ഒരേ സമതലത്തില് ഉരുളുമ്പോള് ആദ്യവൃത്തത്തിന്റെ ചുറ്റളവിലുള്ള ഒരു സ്ഥിരബിന്ദു സൃഷ്ടിക്കുന്ന വക്രം ആണ് കാര്ഡ്യോയ്ഡ്. ഇറ്റാലിയന് ഗണിതശാസ്ത്രജ്ഞനായ സാല്വെമിനി കാസ്റ്റിലോണ് (Johann Francesco Melchiore Salvemini Castillon, 1704-91) ആണ് വക്രത്തിന് ഈ പേര് നല്കിയത് (1741). A എന്നൊരു വൃത്തത്തിന്റെ ഒരു സ്ഥിരബിന്ദു Pഉം B അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തവുമാണെങ്കില് A Bയിന്മേല് ഉരുളുന്നതിന്റെ ആരംഭം P യിലായിരിക്കും. അതായത് P ആദ്യം A,B എന്നീ വൃത്തങ്ങളിലെ പൊതുബിന്ദുവാണ്. A ഉരുളുന്നതോടെ P, Bയില്നിന്ന് അകന്നുപോകുന്നു. Q എന്ന ബിന്ദുവില് P എത്തുമ്പോള് രണ്ടു വൃത്തങ്ങളുടെയും വ്യാസം ഒരേ നേര്വരയില് പ്രകടമാകുന്നു. തുടര്ന്ന് A ഉരുളുന്നതോടെ P വീണ്ടും B യോടടുക്കുന്നതു കാണാം. അവസാനം പൂര്വസ്ഥാനത്തെത്തി രണ്ടു വൃത്തങ്ങളുടെയും പൊതുബിന്ദു ആയിത്തീരുന്നു. P യുടെ സഞ്ചാരപഥത്തെയാണ് കാര്ഡ്യോയ്ഡ് എന്നു പറയുന്നത്. ഒരു സമതലത്തില് രണ്ടു ലംബീയ അക്ഷങ്ങളെ ആധാരമാക്കിയുള്ള കാര്ഡ്യോയ്ഡിന്റെ സമവാക്യം (x<sup>2</sup>+y<sup>2</sup>-ax)<sup>2</sup> = a<sup>2</sup>(x<sup>2</sup>+y<sup>2</sup>) എന്നായിരിക്കും. ധ്രുവീയാങ്കങ്ങളില് (polar coordinates) അത് P=a(1+Cosq) എന്നാണ് (a= വൃത്തവ്യാസം). |
06:11, 6 ജൂലൈ 2014-നു നിലവിലുണ്ടായിരുന്ന രൂപം
കാര്ഡ്യോയ്ഡ്
Cardioid
ഹൃദയത്തിന്റെ ആകൃതിയിലുള്ള ഒരു ജ്യാമിതീയ വക്രം. ഒരു വൃത്തം അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തത്തിന്റെ ചുറ്റളവിലൂടെ ഒരേ സമതലത്തില് ഉരുളുമ്പോള് ആദ്യവൃത്തത്തിന്റെ ചുറ്റളവിലുള്ള ഒരു സ്ഥിരബിന്ദു സൃഷ്ടിക്കുന്ന വക്രം ആണ് കാര്ഡ്യോയ്ഡ്. ഇറ്റാലിയന് ഗണിതശാസ്ത്രജ്ഞനായ സാല്വെമിനി കാസ്റ്റിലോണ് (Johann Francesco Melchiore Salvemini Castillon, 1704-91) ആണ് വക്രത്തിന് ഈ പേര് നല്കിയത് (1741). A എന്നൊരു വൃത്തത്തിന്റെ ഒരു സ്ഥിരബിന്ദു Pഉം B അതേ വ്യാസമുള്ള മറ്റൊരു വൃത്തവുമാണെങ്കില് A Bയിന്മേല് ഉരുളുന്നതിന്റെ ആരംഭം P യിലായിരിക്കും. അതായത് P ആദ്യം A,B എന്നീ വൃത്തങ്ങളിലെ പൊതുബിന്ദുവാണ്. A ഉരുളുന്നതോടെ P, Bയില്നിന്ന് അകന്നുപോകുന്നു. Q എന്ന ബിന്ദുവില് P എത്തുമ്പോള് രണ്ടു വൃത്തങ്ങളുടെയും വ്യാസം ഒരേ നേര്വരയില് പ്രകടമാകുന്നു. തുടര്ന്ന് A ഉരുളുന്നതോടെ P വീണ്ടും B യോടടുക്കുന്നതു കാണാം. അവസാനം പൂര്വസ്ഥാനത്തെത്തി രണ്ടു വൃത്തങ്ങളുടെയും പൊതുബിന്ദു ആയിത്തീരുന്നു. P യുടെ സഞ്ചാരപഥത്തെയാണ് കാര്ഡ്യോയ്ഡ് എന്നു പറയുന്നത്. ഒരു സമതലത്തില് രണ്ടു ലംബീയ അക്ഷങ്ങളെ ആധാരമാക്കിയുള്ള കാര്ഡ്യോയ്ഡിന്റെ സമവാക്യം (x2+y2-ax)2 = a2(x2+y2) എന്നായിരിക്കും. ധ്രുവീയാങ്കങ്ങളില് (polar coordinates) അത് P=a(1+Cosq) എന്നാണ് (a= വൃത്തവ്യാസം).