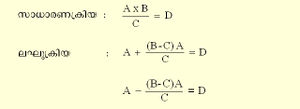This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കരണപദ്ധതി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→കരണപദ്ധതി) |
Mksol (സംവാദം | സംഭാവനകള്) (→കരണപദ്ധതി) |
||
| വരി 64: | വരി 64: | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Vol6_445_4.jpg|300px]] |
(ഫലം). ഈ ഫലത്തെ ഉപേക്ഷിച്ചിട്ട് ശിഷ്ടത്തെ 12 കൊണ്ടു ഗുണിച്ച് അതേ ഹാരകം (ഭൂദിനം) കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന ഫലം രാശി; ശിഷ്ടത്തെ 60 കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചു കിട്ടുന്നത് വികല. ഇതുപോലെ തന്നെ ശിഷ്ടങ്ങളില് നിന്നും തത്പരയും പ്രതത്പരയും വരുത്താന് സാധിക്കും. (60 പ്രതത്പര1 തത്പര; 60 തത്പര 1 വികല; 60 വികല 1 കല; 60 കല 1 ഭാഗ; 30 ഭാഗ 1 രാശി). കരണപദ്ധതി ഒന്നാമധ്യായത്തിലെ അതിപ്രധാനമായ മറ്റൊരു വിഷയം "ശകാബ്ദ സംസ്കാര'മാണ്. യുഗാരംഭത്തിലേക്ക് പഠിതാക്കളായ ഗ്രഹഭഗണങ്ങള്ക്കും മറ്റും നൂറ്റാണ്ടുകള് കഴിയുമ്പോള് വരാവുന്ന വ്യത്യാസങ്ങളെ കണക്കിലെടുത്തുകൊണ്ട് നിരീക്ഷണപടുക്കളായ ശാസ്ത്രജ്ഞന്മാര് ഗ്രഹമധ്യമങ്ങളുടെയും മറ്റും സൂക്ഷ്മതയ്ക്കു വേണ്ടി കാലാന്തരത്തില് നടപ്പില് വരുത്തിയ ഒരു പരിഷ്കാരമത്ര ശകാബ്ദസംസ്കാരം എന്ന പേരില് അറിയപ്പെടുന്നത്. ഈ വിശിഷ്ട ക്രിയാഭാഗം 12ഉം 13ഉം ശ്ലോകങ്ങളെക്കൊണ്ട് സവിസ്തരം പ്രതിപാദിക്കപ്പെട്ടിരിക്കുന്നു. | (ഫലം). ഈ ഫലത്തെ ഉപേക്ഷിച്ചിട്ട് ശിഷ്ടത്തെ 12 കൊണ്ടു ഗുണിച്ച് അതേ ഹാരകം (ഭൂദിനം) കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന ഫലം രാശി; ശിഷ്ടത്തെ 60 കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചു കിട്ടുന്നത് വികല. ഇതുപോലെ തന്നെ ശിഷ്ടങ്ങളില് നിന്നും തത്പരയും പ്രതത്പരയും വരുത്താന് സാധിക്കും. (60 പ്രതത്പര1 തത്പര; 60 തത്പര 1 വികല; 60 വികല 1 കല; 60 കല 1 ഭാഗ; 30 ഭാഗ 1 രാശി). കരണപദ്ധതി ഒന്നാമധ്യായത്തിലെ അതിപ്രധാനമായ മറ്റൊരു വിഷയം "ശകാബ്ദ സംസ്കാര'മാണ്. യുഗാരംഭത്തിലേക്ക് പഠിതാക്കളായ ഗ്രഹഭഗണങ്ങള്ക്കും മറ്റും നൂറ്റാണ്ടുകള് കഴിയുമ്പോള് വരാവുന്ന വ്യത്യാസങ്ങളെ കണക്കിലെടുത്തുകൊണ്ട് നിരീക്ഷണപടുക്കളായ ശാസ്ത്രജ്ഞന്മാര് ഗ്രഹമധ്യമങ്ങളുടെയും മറ്റും സൂക്ഷ്മതയ്ക്കു വേണ്ടി കാലാന്തരത്തില് നടപ്പില് വരുത്തിയ ഒരു പരിഷ്കാരമത്ര ശകാബ്ദസംസ്കാരം എന്ന പേരില് അറിയപ്പെടുന്നത്. ഈ വിശിഷ്ട ക്രിയാഭാഗം 12ഉം 13ഉം ശ്ലോകങ്ങളെക്കൊണ്ട് സവിസ്തരം പ്രതിപാദിക്കപ്പെട്ടിരിക്കുന്നു. | ||
| വരി 77: | വരി 77: | ||
കലിയുഗാരംഭദിനം മുതല് അഭീഷ്ടദിവസം വരെയുള്ള അഹര്ഗണത്തെ ഗ്രഹങ്ങളുടെ യുഗഭഗണങ്ങളെക്കൊണ്ടു ഗുണിച്ച് യുഗഭൂദിനങ്ങളെക്കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന രാശ്യാദി ഫലങ്ങളാണ് ഗ്രഹമധ്യമങ്ങളെന്ന് മുമ്പു പറഞ്ഞിട്ടുണ്ടല്ലോ. ഇത്തരം ക്രിയയ്ക്ക് ലാഘവം വരുത്താനുള്ള ഉപകരണവിശേഷങ്ങളാണ് ഖണ്ഡവും ധ്രുവവും. ഖണ്ഡം എന്നാല് വലിയ അഹര്ഗണത്തില് മുറിച്ചെടുത്ത ചെറിയ അഹര്ഗണമെന്നര്ഥം. ധ്രുവം എന്നാല് ഈ അഹര്ഗണഖണ്ഡത്തില് നിന്നും കണക്കാക്കി പ്രത്യേകം സൂക്ഷിക്കപ്പെടുന്ന മാറ്റമില്ലാത്ത മധ്യമങ്ങള് എന്ന് അര്ഥമാക്കാം. ഏതെങ്കിലും ഒരു കല്പിതദിനത്തിന് യുഗാദിമുതലുള്ള അഹര്ഗണവും ആഅഹര്ഗണത്തില് നിന്ന് മധ്യമങ്ങളും വരുത്തി സൂക്ഷിക്കുക. പിന്നീട് കല്പിതദിനം കഴിഞ്ഞുവരുന്ന ഏതെങ്കിലും അഭീഷ്ടദിവസത്തിലേക്ക് മധ്യമങ്ങള് വരുത്തേണ്ടിവന്നാല് ആ ദിവസത്തേക്ക് യുഗാദി മുതലുള്ള അഹര്ഗണം വരുത്തി കല്പിതദിനാഹര്ഗണത്തെ കുറയ്ക്കണം. അപ്പോള് വരുത്തുന്ന വലിയ അഹര്ഗണത്തില്നിന്നും മുമ്പു വരുത്തി സൂക്ഷിക്കപ്പെട്ടിട്ടുള്ള ചെറിയ അഹര്ഗണത്തെ കുറയ്ക്കണമെന്നും സാരം. ഇവിടെ, കുറയ്ക്കപ്പെടുന്ന ചെറിയ അഹര്ഗണം ഖണ്ഡം; ആ ഖണ്ഡത്തിനുള്ള മധ്യമങ്ങള് ധ്രുവങ്ങള്. ഇഷ്ടകാലാഹര്ഗണത്തില് നിന്നും ഖണ്ഡം കുറച്ചാല് ഖണ്ഡശേഷം. ഈ ഖണ്ഡശേഷത്തെ അതതു ഗ്രഹത്തിനു പറയപ്പെട്ടിട്ടുള്ള ഗുണകാരം കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചാല് വരുന്ന രാശ്യാദി ഫലങ്ങളില് ധ്രുവങ്ങള് കൂട്ടിയാല് അഭീഷ്ടകാലമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനു മാത്രം പ്രസ്തുത രാശ്യാദി ഫലങ്ങളെ ധ്രുവത്തില് നിന്നും കുറയ്ക്കണം. കാരണം രാഹു സദാ പിറകോട്ടാണല്ലോ സഞ്ചരിക്കുന്നത്. "സ്വധ്രുനശോധിതോളഹിഃ' എന്ന് പഞ്ചബോധത്തിലും പറയുന്നുണ്ട്. അഹര്ഗണം "ഖണ്ഡ'ത്തെക്കാള് കുറഞ്ഞിരുന്നാല് അവിടെ "ഖണ്ഡ'ത്തില് നിന്നും "അഹര്ഗണ'ത്തെ കുറച്ച് രാശ്യാദി ഫലങ്ങളെ വരുത്തി ധ്രുവങ്ങളില്നിന്നും കുറച്ചാല് ഗ്രഹമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനാകട്ടെ ധ്രുവത്തില് കൂട്ടുകയും വേണം. ഇപ്രകാരം കരണഗ്രന്ഥങ്ങളില് സ്വീകരിക്കപ്പെട്ടിട്ടുള്ള മധ്യമക്രിയയ്ക്ക് അടിസ്ഥാനമായ ഖണ്ഡങ്ങളെയും ധ്രുവങ്ങളെയും വരുത്താനുള്ള വിവിധമാര്ഗങ്ങള് ഈ പ്രകരത്തില് കാണാവുന്നതാണ്. | കലിയുഗാരംഭദിനം മുതല് അഭീഷ്ടദിവസം വരെയുള്ള അഹര്ഗണത്തെ ഗ്രഹങ്ങളുടെ യുഗഭഗണങ്ങളെക്കൊണ്ടു ഗുണിച്ച് യുഗഭൂദിനങ്ങളെക്കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന രാശ്യാദി ഫലങ്ങളാണ് ഗ്രഹമധ്യമങ്ങളെന്ന് മുമ്പു പറഞ്ഞിട്ടുണ്ടല്ലോ. ഇത്തരം ക്രിയയ്ക്ക് ലാഘവം വരുത്താനുള്ള ഉപകരണവിശേഷങ്ങളാണ് ഖണ്ഡവും ധ്രുവവും. ഖണ്ഡം എന്നാല് വലിയ അഹര്ഗണത്തില് മുറിച്ചെടുത്ത ചെറിയ അഹര്ഗണമെന്നര്ഥം. ധ്രുവം എന്നാല് ഈ അഹര്ഗണഖണ്ഡത്തില് നിന്നും കണക്കാക്കി പ്രത്യേകം സൂക്ഷിക്കപ്പെടുന്ന മാറ്റമില്ലാത്ത മധ്യമങ്ങള് എന്ന് അര്ഥമാക്കാം. ഏതെങ്കിലും ഒരു കല്പിതദിനത്തിന് യുഗാദിമുതലുള്ള അഹര്ഗണവും ആഅഹര്ഗണത്തില് നിന്ന് മധ്യമങ്ങളും വരുത്തി സൂക്ഷിക്കുക. പിന്നീട് കല്പിതദിനം കഴിഞ്ഞുവരുന്ന ഏതെങ്കിലും അഭീഷ്ടദിവസത്തിലേക്ക് മധ്യമങ്ങള് വരുത്തേണ്ടിവന്നാല് ആ ദിവസത്തേക്ക് യുഗാദി മുതലുള്ള അഹര്ഗണം വരുത്തി കല്പിതദിനാഹര്ഗണത്തെ കുറയ്ക്കണം. അപ്പോള് വരുത്തുന്ന വലിയ അഹര്ഗണത്തില്നിന്നും മുമ്പു വരുത്തി സൂക്ഷിക്കപ്പെട്ടിട്ടുള്ള ചെറിയ അഹര്ഗണത്തെ കുറയ്ക്കണമെന്നും സാരം. ഇവിടെ, കുറയ്ക്കപ്പെടുന്ന ചെറിയ അഹര്ഗണം ഖണ്ഡം; ആ ഖണ്ഡത്തിനുള്ള മധ്യമങ്ങള് ധ്രുവങ്ങള്. ഇഷ്ടകാലാഹര്ഗണത്തില് നിന്നും ഖണ്ഡം കുറച്ചാല് ഖണ്ഡശേഷം. ഈ ഖണ്ഡശേഷത്തെ അതതു ഗ്രഹത്തിനു പറയപ്പെട്ടിട്ടുള്ള ഗുണകാരം കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചാല് വരുന്ന രാശ്യാദി ഫലങ്ങളില് ധ്രുവങ്ങള് കൂട്ടിയാല് അഭീഷ്ടകാലമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനു മാത്രം പ്രസ്തുത രാശ്യാദി ഫലങ്ങളെ ധ്രുവത്തില് നിന്നും കുറയ്ക്കണം. കാരണം രാഹു സദാ പിറകോട്ടാണല്ലോ സഞ്ചരിക്കുന്നത്. "സ്വധ്രുനശോധിതോളഹിഃ' എന്ന് പഞ്ചബോധത്തിലും പറയുന്നുണ്ട്. അഹര്ഗണം "ഖണ്ഡ'ത്തെക്കാള് കുറഞ്ഞിരുന്നാല് അവിടെ "ഖണ്ഡ'ത്തില് നിന്നും "അഹര്ഗണ'ത്തെ കുറച്ച് രാശ്യാദി ഫലങ്ങളെ വരുത്തി ധ്രുവങ്ങളില്നിന്നും കുറച്ചാല് ഗ്രഹമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനാകട്ടെ ധ്രുവത്തില് കൂട്ടുകയും വേണം. ഇപ്രകാരം കരണഗ്രന്ഥങ്ങളില് സ്വീകരിക്കപ്പെട്ടിട്ടുള്ള മധ്യമക്രിയയ്ക്ക് അടിസ്ഥാനമായ ഖണ്ഡങ്ങളെയും ധ്രുവങ്ങളെയും വരുത്താനുള്ള വിവിധമാര്ഗങ്ങള് ഈ പ്രകരത്തില് കാണാവുന്നതാണ്. | ||
അടുത്തത് മധ്യഗതി വരുത്താനുള്ള മാര്ഗമാണ്. ഒരു ഗ്രഹത്തിന്റെ ഒരു ദിവസത്തെ ശരാശരി ഗതിയാണ് മധ്യഗതി. അതായത്, 60 നാഴിക കൊണ്ട് സ്വഭ്രമണവൃത്തത്തില് സഞ്ചരിക്കുന്ന ദൂരം. ഈ മധ്യഗതിക്രിയയില് "അനന്തപുരം' (21,600) ഗുണ്യം; ഭഗണം ഗുണകം; ഭൂദിനം ഹാരകം: | അടുത്തത് മധ്യഗതി വരുത്താനുള്ള മാര്ഗമാണ്. ഒരു ഗ്രഹത്തിന്റെ ഒരു ദിവസത്തെ ശരാശരി ഗതിയാണ് മധ്യഗതി. അതായത്, 60 നാഴിക കൊണ്ട് സ്വഭ്രമണവൃത്തത്തില് സഞ്ചരിക്കുന്ന ദൂരം. ഈ മധ്യഗതിക്രിയയില് "അനന്തപുരം' (21,600) ഗുണ്യം; ഭഗണം ഗുണകം; ഭൂദിനം ഹാരകം: | ||
| - | 21600 x ഭഗണം | + | (21600 x ഭഗണം )/ ഭൂദിനം = മധ്യഗതി (ഫലം) |
| - | + | ||
| - | + | ||
പഞ്ചബോധത്തില് പഠിതാക്കളായ മധ്യഗതികള് ധസൂര്യന് "ദാനധര്മ' (59 കല 8 വികല), ചന്ദ്രന് "മൃഗനിളസു' (790 കല 35 വികല) ഇത്യാദിപ ഇപ്രകാരം കണ്ടുപിടിക്കപ്പെട്ടിട്ടുള്ളവയാകുന്നു. | പഞ്ചബോധത്തില് പഠിതാക്കളായ മധ്യഗതികള് ധസൂര്യന് "ദാനധര്മ' (59 കല 8 വികല), ചന്ദ്രന് "മൃഗനിളസു' (790 കല 35 വികല) ഇത്യാദിപ ഇപ്രകാരം കണ്ടുപിടിക്കപ്പെട്ടിട്ടുള്ളവയാകുന്നു. | ||
അനന്തരം ചന്ദ്രഭഗണത്തില് നിന്നും ആകാശകക്ഷ്യയുടെ പരിധി നിര്ണയിക്കുന്നതിനും ഗ്രഹങ്ങളുടെ യോജനാത്മകമായ ദിനഗതിയും കക്ഷ്യാമണ്ഡലങ്ങളുടെ ചുറ്റളവുകളും ഗണിക്കുന്നതിനും ഉള്ള മാര്ഗങ്ങള് പ്രതിപാദിച്ചതിനുശേഷം ഒന്നാമധ്യായം അവസാനിപ്പിച്ചിരിക്കുന്നു. | അനന്തരം ചന്ദ്രഭഗണത്തില് നിന്നും ആകാശകക്ഷ്യയുടെ പരിധി നിര്ണയിക്കുന്നതിനും ഗ്രഹങ്ങളുടെ യോജനാത്മകമായ ദിനഗതിയും കക്ഷ്യാമണ്ഡലങ്ങളുടെ ചുറ്റളവുകളും ഗണിക്കുന്നതിനും ഉള്ള മാര്ഗങ്ങള് പ്രതിപാദിച്ചതിനുശേഷം ഒന്നാമധ്യായം അവസാനിപ്പിച്ചിരിക്കുന്നു. | ||
| വരി 98: | വരി 97: | ||
മഹാഹാരകംഭൂദിനം(അനൃശംസഃ കളാര്ഥീസമര്ത്യഃ) 1577917500 | മഹാഹാരകംഭൂദിനം(അനൃശംസഃ കളാര്ഥീസമര്ത്യഃ) 1577917500 | ||
ഈ സംഖ്യകളെ പരസ്പരം ഹരിച്ച് താഴെത്താഴെ 5 സ്ഥാനങ്ങളിലായി ഹരണഫലങ്ങളെയും, എല്ലാറ്റിനും അടിയില് (6-ാമത്തെ സ്ഥാനത്ത്) രൂപം (1) എന്ന സംഖ്യയെയും വയ്ക്കണം (എഴുതണം). | ഈ സംഖ്യകളെ പരസ്പരം ഹരിച്ച് താഴെത്താഴെ 5 സ്ഥാനങ്ങളിലായി ഹരണഫലങ്ങളെയും, എല്ലാറ്റിനും അടിയില് (6-ാമത്തെ സ്ഥാനത്ത്) രൂപം (1) എന്ന സംഖ്യയെയും വയ്ക്കണം (എഴുതണം). | ||
| + | |||
അപ്പോള് 27 (പ്രഥമവല്ലി) | അപ്പോള് 27 (പ്രഥമവല്ലി) | ||
3 | 3 | ||
| വരി 106: | വരി 106: | ||
</nowiki> | </nowiki> | ||
5-ാമത്തെ സംഖ്യയായ 1 ഉപാന്ത്യം; 4-ാമത്തെ സംഖ്യയായ | 5-ാമത്തെ സംഖ്യയായ 1 ഉപാന്ത്യം; 4-ാമത്തെ സംഖ്യയായ | ||
| - | 4 ഊര്ധ്വം. ആദ്യമായി അന്ത്യത്തെ ഉപാന്ത്യം കൊണ്ടു ഗുണിച്ച് ഊര്ധ്വം കൂട്ടണം: 1 | + | 4 ഊര്ധ്വം. ആദ്യമായി അന്ത്യത്തെ ഉപാന്ത്യം കൊണ്ടു ഗുണിച്ച് ഊര്ധ്വം കൂട്ടണം: 1 x 1 + 4 = 5. ഈ 5നെ അന്ത്യമായി കല്പിച്ചിട്ട് പ്രഥമവല്ലിയിലെ അന്ത്യത്തെ (രൂപത്തെ, 1 നെ) ഉപേക്ഷിക്കണം; അപ്പോള് 27, 3, 9,5, 1 (ദ്വിതീയവല്ലി). ഈ വല്ലിയില് അന്ത്യം 1; ഉപാന്ത്യം 5; ഊര്ധ്വം 9. മുമ്പത്തെപ്പോലെ ക്രിയചെയ്താല് 5x9+1 = 46. അന്ത്യത്തെ ത്യജിക്കുക; അപ്പോള് 27, 3, 46, 5 (തൃതീയവല്ലി). ഈ വല്ലിയില് അന്ത്യം 5, ഉപാന്ത്യം 46, ഊര്ധ്വം |
3. ക്രിയ ആവര്ത്തിച്ചാല് 3x 46 + 5 = 143. 5നെ ത്യജിക്കുക. 143നെ അന്ത്യമായി കല്പിച്ച് ക്രിയചെയ്താലുണ്ടാകുന്ന വല്ലി: 27, 143, 46 (ചതുര്ഥവല്ലി). ഈ വല്ലിയില് അന്ത്യം 46, ഉപാന്ത്യം 143, ഊര്ധ്വം 27. 143x 27 + 46 = 3907. അന്ത്യത്തെ (46) ഉപേക്ഷിക്കുക; അപ്പോള് 3907 (സന്നദ്ധാംഗം), 143 (ലാവണ്യം) എന്നിങ്ങനെ രണ്ടു സംഖ്യകള് സിദ്ധിക്കും. ഇവയില് ആദ്യത്തെ സംഖ്യ ഹാരകം; രണ്ടാമത്തേത് ഗുണകാരം. ഇപ്രകാരമാണ് ചന്ദ്രന്റെ മധ്യമക്രിയയില് "സന്നദ്ധാംഗം' എന്ന ഹാരകവും ലാവണ്യം എന്ന ഗുണകാരവും ലഭിക്കുന്നത്. | 3. ക്രിയ ആവര്ത്തിച്ചാല് 3x 46 + 5 = 143. 5നെ ത്യജിക്കുക. 143നെ അന്ത്യമായി കല്പിച്ച് ക്രിയചെയ്താലുണ്ടാകുന്ന വല്ലി: 27, 143, 46 (ചതുര്ഥവല്ലി). ഈ വല്ലിയില് അന്ത്യം 46, ഉപാന്ത്യം 143, ഊര്ധ്വം 27. 143x 27 + 46 = 3907. അന്ത്യത്തെ (46) ഉപേക്ഷിക്കുക; അപ്പോള് 3907 (സന്നദ്ധാംഗം), 143 (ലാവണ്യം) എന്നിങ്ങനെ രണ്ടു സംഖ്യകള് സിദ്ധിക്കും. ഇവയില് ആദ്യത്തെ സംഖ്യ ഹാരകം; രണ്ടാമത്തേത് ഗുണകാരം. ഇപ്രകാരമാണ് ചന്ദ്രന്റെ മധ്യമക്രിയയില് "സന്നദ്ധാംഗം' എന്ന ഹാരകവും ലാവണ്യം എന്ന ഗുണകാരവും ലഭിക്കുന്നത്. | ||
| വരി 140: | വരി 140: | ||
(ത്രിജ്യയെ അര്ധിച്ചാല് ഒരു രാശിയുടെ ജ്യാവ്; ത്രിജ്യാവര്ഗത്തെ അര്ധിച്ചു മൂലിച്ചാല്, 1മ്മ രാശിയുടെ ജ്യാവ് 12-ാം ജ്യാവ് ഈ രണ്ടു ജ്യാക്കളെക്കൊണ്ടു തന്നെ മറ്റുള്ള ജ്യാക്കളെയും വരുത്തിക്കൊള്ളേണ്ടതാകുന്നു) എന്ന പ്രസ്താവനയോടുകൂടി 24 മഹാജ്യാക്കളെയും വരുത്തിക്കാണിക്കുകയും ചെയ്യുന്നുണ്ട്. | (ത്രിജ്യയെ അര്ധിച്ചാല് ഒരു രാശിയുടെ ജ്യാവ്; ത്രിജ്യാവര്ഗത്തെ അര്ധിച്ചു മൂലിച്ചാല്, 1മ്മ രാശിയുടെ ജ്യാവ് 12-ാം ജ്യാവ് ഈ രണ്ടു ജ്യാക്കളെക്കൊണ്ടു തന്നെ മറ്റുള്ള ജ്യാക്കളെയും വരുത്തിക്കൊള്ളേണ്ടതാകുന്നു) എന്ന പ്രസ്താവനയോടുകൂടി 24 മഹാജ്യാക്കളെയും വരുത്തിക്കാണിക്കുകയും ചെയ്യുന്നുണ്ട്. | ||
പഞ്ചബോധത്തിലെ "ആത്മവിത് ശ്രഷ്ഠഃ' തുടങ്ങിയ വികലാദി മഹാജ്യാക്കളുടെയും, മാധവകൃതമായ "ശ്രഷ്ഠം നാമവരിഷ്ഠാനം' എന്നു തുടങ്ങുന്ന തത്പരാദിമഹാജ്യാക്കളുടെയും ഉത്പത്തിക്കു നിദാനം കരണപദ്ധതിയാണെന്ന് നിസ്സംശയം പറയാം. | പഞ്ചബോധത്തിലെ "ആത്മവിത് ശ്രഷ്ഠഃ' തുടങ്ങിയ വികലാദി മഹാജ്യാക്കളുടെയും, മാധവകൃതമായ "ശ്രഷ്ഠം നാമവരിഷ്ഠാനം' എന്നു തുടങ്ങുന്ന തത്പരാദിമഹാജ്യാക്കളുടെയും ഉത്പത്തിക്കു നിദാനം കരണപദ്ധതിയാണെന്ന് നിസ്സംശയം പറയാം. | ||
| + | |||
ചാപത്തില് നിന്ന് ജ്യാക്കളെ വരുത്തുന്നതുപോലെ തന്നെ ജ്യാക്കളില് നിന്ന് ചാപത്തെയും വരുത്താന് സാധിക്കും. അതാണ് ചാപീകരണം. ചാപീകരണക്രിയയ്ക്ക് ആവശ്യമായ ജ്യാക്കളാണ് പഞ്ചബോധത്തില് പറയപ്പെടുന്ന ("ഗൂഢാമേനകാ' 10543) 105 കല 43 വികല ഇത്യാദി ചാപജ്യാക്കള്. ആറാമധ്യായത്തിലെ അവസാന വിഷയം ചാപജ്യാനയനമത്ര. ഇപ്രകാരം വ്യാസവൃത്തങ്ങളെയും, മഹാജ്യാക്കളെയും, ചാപജ്യാക്കളെയും മറ്റും വരുത്താനുള്ള വഴി കാണിച്ചു തന്നതിനു ശേഷം ഏഴാമധ്യായത്തില് ഗ്രഹങ്ങളുടെ സ്ഫുടീകരണത്തിന് ആവശ്യമുള്ള ജ്യാക്കളുടെ ആഗമനത്തെപ്പറ്റി പ്രതിപാദിക്കുന്നു. | ചാപത്തില് നിന്ന് ജ്യാക്കളെ വരുത്തുന്നതുപോലെ തന്നെ ജ്യാക്കളില് നിന്ന് ചാപത്തെയും വരുത്താന് സാധിക്കും. അതാണ് ചാപീകരണം. ചാപീകരണക്രിയയ്ക്ക് ആവശ്യമായ ജ്യാക്കളാണ് പഞ്ചബോധത്തില് പറയപ്പെടുന്ന ("ഗൂഢാമേനകാ' 10543) 105 കല 43 വികല ഇത്യാദി ചാപജ്യാക്കള്. ആറാമധ്യായത്തിലെ അവസാന വിഷയം ചാപജ്യാനയനമത്ര. ഇപ്രകാരം വ്യാസവൃത്തങ്ങളെയും, മഹാജ്യാക്കളെയും, ചാപജ്യാക്കളെയും മറ്റും വരുത്താനുള്ള വഴി കാണിച്ചു തന്നതിനു ശേഷം ഏഴാമധ്യായത്തില് ഗ്രഹങ്ങളുടെ സ്ഫുടീകരണത്തിന് ആവശ്യമുള്ള ജ്യാക്കളുടെ ആഗമനത്തെപ്പറ്റി പ്രതിപാദിക്കുന്നു. | ||
ഗ്രഹങ്ങളുടെ സ്ഫുടക്രിയയില് രണ്ടുതരം ജ്യാക്കള് ഉള്പ്പെടുന്നുണ്ട്; മന്ദജ്യാക്കളും ശീഘ്രജ്യാക്കളും. ശീഘ്രജ്യാക്കളില്ത്തന്നെ മകരാദി എന്നും കര്ക്ക്യാദി എന്നും രണ്ടിനമുണ്ട്. രാശി, ഭാഗ, കലാദിസ്ഥാന നിര്ണയത്തിന് ആധാരമായ നക്ഷത്ര കക്ഷ്യയുടെയും ഗ്രഹങ്ങള് സഞ്ചരിക്കുന്ന വൃത്തങ്ങ(പ്രതിമണ്ഡലങ്ങ)ളുടെയും കേന്ദ്രബിന്ദുക്കള് ഒന്നല്ലാത്തതു കൊണ്ടു തന്നെയാണ് ഇത്തരം മൂന്നു വിധത്തിലുള്ള ജ്യാക്കളുപയോഗിച്ച് മന്ദഫലവും ശീഘ്രഫലവും വരുത്തി മധ്യമഗ്രഹങ്ങളെ സംസ്കരിച്ച് സ്ഫുടഗ്രഹങ്ങളാക്കി മാറ്റുന്നത്. മധ്യമസ്ഥാനത്ത് ഗ്രഹം ദൃശ്യമല്ല; സ്ഫുടസ്ഥാനത്തേ ദൃശ്യമാകയുള്ളു. | ഗ്രഹങ്ങളുടെ സ്ഫുടക്രിയയില് രണ്ടുതരം ജ്യാക്കള് ഉള്പ്പെടുന്നുണ്ട്; മന്ദജ്യാക്കളും ശീഘ്രജ്യാക്കളും. ശീഘ്രജ്യാക്കളില്ത്തന്നെ മകരാദി എന്നും കര്ക്ക്യാദി എന്നും രണ്ടിനമുണ്ട്. രാശി, ഭാഗ, കലാദിസ്ഥാന നിര്ണയത്തിന് ആധാരമായ നക്ഷത്ര കക്ഷ്യയുടെയും ഗ്രഹങ്ങള് സഞ്ചരിക്കുന്ന വൃത്തങ്ങ(പ്രതിമണ്ഡലങ്ങ)ളുടെയും കേന്ദ്രബിന്ദുക്കള് ഒന്നല്ലാത്തതു കൊണ്ടു തന്നെയാണ് ഇത്തരം മൂന്നു വിധത്തിലുള്ള ജ്യാക്കളുപയോഗിച്ച് മന്ദഫലവും ശീഘ്രഫലവും വരുത്തി മധ്യമഗ്രഹങ്ങളെ സംസ്കരിച്ച് സ്ഫുടഗ്രഹങ്ങളാക്കി മാറ്റുന്നത്. മധ്യമസ്ഥാനത്ത് ഗ്രഹം ദൃശ്യമല്ല; സ്ഫുടസ്ഥാനത്തേ ദൃശ്യമാകയുള്ളു. | ||
Current revision as of 13:07, 4 ജൂലൈ 2014
കരണപദ്ധതി
കേരളത്തില് നടപ്പിലിരിക്കുന്ന ഗ്രഹഗണിതപ്രക്രിയകളെ യുക്തിപൂര്വം പ്രതിപാദിച്ചുകൊണ്ട് പുതുമന സോമയാജി രചിച്ച ഒരു പ്രമാണ ഗ്രന്ഥം. ജ്യോതിശ്ശാസ്ത്രത്തിലെ ഗണിതസ്കന്ധത്തെ ഉപജീവിച്ചുകൊണ്ട് ഉണ്ടായിട്ടുള്ള ഗ്രന്ഥങ്ങളെ പൊതുവേ സിദ്ധാന്തം, തന്ത്രം, കരണം എന്നിങ്ങനെ മൂന്നായി വിഭജിക്കാവുന്നതാണ്. ജ്യോതിഷപ്രകാരം ഗ്രഹങ്ങള്ക്കെല്ലാം ഭൂമിക്കു ചുറ്റും പൂര്ണസംഖ്യാ പരിക്രമണങ്ങള് നടത്താന് വേണ്ട കാലയളവ് (സൂര്യന് 43,20,000 പരിക്രമണം, വ്യാഴം 3,64,220 പരിക്രമണം, ചന്ദ്രന് 5,77,53,336 പരിക്രമണം.. എന്നിങ്ങനെ) ആണ് ഒരു മഹായുഗം. മഹായുഗാരംഭം മുതല് അഭീഷ്ടകാലംവരെയുള്ള വര്ഷം, മാസം, ദിവസം, നാഴിക ഇവ അറിഞ്ഞ് ഗ്രഹസ്ഥാനങ്ങളെ ഗണിക്കുന്ന സമ്പ്രദായത്തിന് സിദ്ധാന്തം എന്നു പേര്. കൃതയുഗം, ത്രതായുഗം, ദ്വാപരയുഗം, കലിയുഗം എന്നീ നാലു യുഗങ്ങള് ഒരു മഹായുഗം. ഇപ്പോള് കലിയുഗമാണ്. കലിയുഗത്തിന്റെ ആരംഭം മുതല് വര്ഷാദികളെ കണക്കാക്കി ഗണിക്കുന്നതാണ് തന്ത്രം. കലിവര്ഷത്തിന്റെയോ ശകവര്ഷത്തിന്റെയോ മധ്യത്തിലുള്ള സൗകര്യപ്രദമായ ഏതെങ്കിലും സമയത്തെ ആരംഭബിന്ദുവായെടുത്ത് അതുമുതല് വര്ത്തമാന സമയപര്യന്തം ഗണിക്കുന്നത് കരണം. ഈ വിഭജനം അനുസരിച്ച് പ്രകൃതഗ്രന്ഥം തന്ത്രഗ്രന്ഥങ്ങളില് ഉള്പ്പെടുന്നു. പുതുമന ചോമാതിരി എന്നപേരില് അറിയപ്പെടുന്ന പുതുമന സോമയാജി ആണ് കരണപദ്ധതിയുടെ കര്ത്താവ്. ഗ്രന്ഥകാരന് ഗ്രന്ഥാവസാനത്തില് തന്നെപ്പറ്റി ഇപ്രകാരം പറയുന്നുണ്ട്:
"ഇതിശിവപുരനാമഗ്രാമജഃ കോപിയജ്വാ കിമപി കരണപദ്ധത്യാഹ്വയം തന്ത്രരൂപം വ്യധീത ഗണിതമേതത്............................'
ഇതില്നിന്ന് താന് സോമയാജിയാണെന്നും ജനിച്ചത് ശിവപുരം എന്നു പേരായ ഗ്രാമത്തിലാണെന്നും തെളിയുന്നു. കരണപദ്ധതിയുടെ വ്യാഖ്യാതാക്കളാണ് അദ്ദേഹത്തിന്റെ ഇല്ലപ്പേര് പറഞ്ഞുതരുന്നത്.
"നൂതനഗൃഹസോമസുതാ, രചിതായാഃ കരണപദ്ധതേര്വിദുഷാ ഭാഷാം വിലിഖതി കശ്ചിദ് ബാലാനാം ബോധനാര്ഥമല്പധിയാം'
"പുതുമന'യെ സംസ്കൃതീകരിച്ചതാണ് നൂതനഗൃഹം. കര്ത്താവ് ചൊവ്വരഗ്രാമത്തിലെ പുതുമന ഇല്ലത്തുള്ള ഒരു ചോമാതിരിയാണെന്നു വിചാരിക്കുന്നതാണ് യുക്തം. സോമയാജിയുടെ കാലം എ.ഡി. 1530നും 1700നും മധ്യേ ആകണമെന്നല്ലാതെ കൂടുതല് ക്ലിപ്തമായി പറയാന് നിവൃത്തിയില്ല. ഉള്ളടക്കം. കരണപദ്ധതിയിലെ ഉള്ളടക്കമെന്താണെന്ന് ഗ്രന്ഥാരംഭത്തില് ഗ്രന്ഥകാരന് തന്നെ പ്രസ്താവിക്കുന്നുണ്ട്:
"മാര്ത്താണ്ഡാദീന് ഗ്രഹാന് നത്വാ തത്പ്രസാദാദ് വിലിഖ്യതേ ഗുണഹാരഗുണാദീനാം
കരണേ, കാപി പദ്ധതിഃ' ഇതില്നിന്നു ഗുണഹാരഗുണാദിഗണിതമാണ് പ്രബന്ധ വിഷയമെന്ന് സിദ്ധിക്കുന്നു; കലിദിനം മുതല് ഗ്രഹണംവരെയുള്ള ഗണിതക്രിയകള്ക്ക് ആവശ്യമായ ഗുണകാരങ്ങള്, ഹാരകങ്ങള്, ജ്യാക്കള്, ഖണ്ഡങ്ങള്, ധ്രുവങ്ങള് തുടങ്ങിയ ഉപകരണങ്ങളുടെ സൂക്ഷ്മമായ വിജ്ഞാനമാണ് ഗ്രന്ഥത്തിന്റെ പ്രയോജനമെന്നും മനസ്സിലാക്കുവാന് സാധിക്കും. പ്രസ്തുത ഗണിതവിഷയങ്ങള് പത്തധ്യായങ്ങളിലായി ഈ ഗ്രന്ഥത്തില് പ്രതിപാദിക്കപ്പെടുന്നു. ഒന്നാമധ്യായത്തില് ഗുരുനമസ്കാരരൂപമായ മംഗളവും പ്രതിപാദ്യപ്രമേയത്തെക്കുറിച്ചുള്ള പ്രസ്താവനയും കഴിഞ്ഞ്, സൂര്യാദികളുടെ മധ്യമക്രിയയില് ഗുണകാരങ്ങളായ ഗ്രഹപര്യയങ്ങളെയും ഹാരകമായ ഭൂദിനത്തെയും "കടപയാദി' സംഖ്യയില് അവതരിപ്പിച്ചിരിക്കുന്നു (നോ: കടപയാദി സമ്പ്രദായം). നാനാജ്ഞാനപ്രഗല്ഭഃ (43,20,000 ഇത്യാദി സൂര്യാദിഗ്രഹപര്യയങ്ങളും അനൃശംസഃ കളാര്ഥീസമര്ത്യഃ (1,57,79,17,500) എന്നുള്ളത് ഭൂദിനങ്ങളും ആണ്. പര്യയങ്ങള് എന്നാല് സൂര്യാദികളായ ഗ്രഹങ്ങള് ഒരു യുഗത്തില് എത്ര പ്രാവശ്യം രാശിചക്രത്തെ ചുറ്റുന്നു എന്ന കണക്കാണ്. പര്യയങ്ങളെ ഭഗണങ്ങള് എന്നും പറയാറുണ്ട്. ഭൂദിനമെന്നാല് സാവനദിനം (സൂര്യോദയം മുതല് അടുത്ത സൂര്യോദയം വരെയുള്ള കാലം) എന്നര്ഥം. യുഗസാവനദിനങ്ങളാണ് യുഗഭൂദിനങ്ങള്. അനന്തരം ഒരു ചതുര്യുഗത്തില് സംഭവിക്കുന്ന "സൗരമാസ'ങ്ങളെയും "ചാന്ദ്ര'മാസങ്ങളെയും "അധിമാസ'ങ്ങളെയും മറ്റും അറിയുന്നതിനുള്ള മാര്ഗങ്ങള് വിവരിച്ചതിനു ശേഷം മുമ്പ് ഒരു യുഗത്തിലേക്കു പറയപ്പെട്ട ഭഗണാദികളെ കല്പത്തിലെ ഭഗണാദികളാക്കി മാറ്റുവാനുള്ള വഴി നിര്ദേശിക്കുന്നു. വളരെ പ്രാധാന്യമുള്ള ഈ ക്രിയാവിഭാഗം സോമയാജിയുടെ ഭാഷയില്ത്തന്നെ താഴെ ചേര്ക്കുന്നു:
"ഏവം യുഗോക്താ ഭഗണാദയസ്തേ "ദിനാനയ'ഘ്നാസ്തു ഭവന്തി കല്പേ ചതുര്ദശഃസ്യുര്മ നവോളത്ര, തേഷാം യുഗാനി രാസ (72) പ്രമിതാനി യസ്മാത്' (ക.1.6) "കൃതത്രതാദ്വാപരാഖ്യാഃ കലിശ്ചൈതേ യുഗാംഘ്രയഃ യുഗാം ഘ്രയസ്തു കല്പേളസ്മിന് ധിഗാദിത്യ (1839) മിതാ ഗതാഃ' (ക.1.7)
"യുഗഭഗണാദി'കളെ "ദിനാനയ' (1008) കൊണ്ടു ഗുണിച്ചാല് കല്പഭഗണാദികള് സിദ്ധിക്കും. പ്രപഞ്ചത്തിന്റെ ഉത്പത്തി മുതല് പ്രളയം വരെയുള്ള കാലമാണ് കല്പം. ഒരു കല്പത്തില് ആകെ 14 മന്വന്തരങ്ങള്; ഒരു മന്വന്തരത്തില് 72 ചതുര്യുഗങ്ങള്; ഒരു കല്പത്തില് മൊത്തം 1,008 ചതുര്യുഗങ്ങള് (72 x 14 = 1008: ദിനാനയ). വര്ത്തമാനകല്പത്തില് 6 മന്വന്തരങ്ങളും 7-ാമത്തെ മന്വന്തരത്തില് 27 ചതുര്യുഗങ്ങളും 28-ാമത്തെ ചതുര്യുഗത്തില് കൃത, ത്രതാ, ദ്വാപര എന്നിങ്ങനെ മൂന്ന് യുഗപാദങ്ങളും കഴിഞ്ഞിട്ട്, 4-ാമത്തെ പാദമായ കലിയുഗം നടന്നുകൊണ്ടിരിക്കുന്നു. ഈ കണക്കു കൂട്ടല് വച്ചുകൊണ്ടാണ് ഗ്രന്ഥകാരന്, വര്ത്തമാന കല്പത്തില്, ഇതു വരെ 1839 (ധിഗാദിത്യ) യുഗപാദങ്ങള് കഴിഞ്ഞിട്ടുണ്ടെന്ന് അസന്ദിഗ്ധമായി പ്രസ്താവിച്ചിരിക്കുന്നത്: (6x 72 + 27) 4 + 3 = 1839 (ധിഗാദിത്യ). അടുത്തത്, അഭീഷ്ടദിവസങ്ങളിലെ അഹര്ഗണം അഥവാ കലിദിനസംഖ്യ വരുത്താനുള്ള മാര്ഗനിദേശമാണ്. അഹര്ഗണത്തിലാണ് ഗ്രഹങ്ങളുടെ മധ്യമാദി ഗണിത മഹാസ്തംഭങ്ങള് പടുത്തുയര്ത്തിയിരിക്കുന്നത്. കലിദിനക്രിയകളുടെ സംഗ്രഹം തുടര്ന്നുചേര്ക്കുന്നു. തികഞ്ഞ കലിവര്ഷങ്ങളുടെ എണ്ണത്തെ 12 കൊണ്ടു ഗുണിച്ച് വര്ത്തമാന കലിവര്ഷത്തില് കഴിഞ്ഞ മേടം മുതലായ മാസങ്ങളുടെ സംഖ്യ കൂട്ടിയാല് കലിയുഗം തുടങ്ങിക്കഴിഞ്ഞിട്ടുള്ള സൗരമാസങ്ങളുടെ എണ്ണം കിട്ടും. ഇങ്ങനെ കിട്ടുന്ന ഗതസൗരമാസങ്ങളെ യുഗചാന്ദ്രമാസങ്ങളെക്കൊണ്ടു ഗുണിച്ച് യുഗസൗരമാസങ്ങളെക്കൊണ്ടു ഹരിച്ചാല്, ഗതചാന്ദ്രമാസങ്ങള്, അതായത് കലിയുഗാരംഭം മുതല് കഴിഞ്ഞിട്ടുള്ള ചാന്ദ്രമാസസംഖ്യ ലഭിക്കും (തൂലലോലോഗവാംഗണഃ 53433336, യുഗചാന്ദ്രമാസങ്ങള്, ജ്ഞാനീ നൂനം വേദകാമഃ 51840000 യുഗസൗരമാസങ്ങള്).
ഇങ്ങനെ ത്രരാശിക യുഗസൗരമാസം ക്രിയാരൂപം. ഇപ്രകാരം സിദ്ധിക്കുന്ന ഗതചാന്ദ്രമാസങ്ങളെ 30 കൊണ്ടു ഗുണിച്ച് നടപ്പു ചാന്ദ്രമാസത്തില് ചെന്ന തിഥികള് കൂട്ടിയാല് ഗതചാന്ദ്രദിനങ്ങള്, അതായത് കലിയുഗാരംഭം മുതല് അഭീഷ്ടദിവസം വരെ കഴിഞ്ഞിട്ടുള്ള ചാന്ദ്രദിനങ്ങളുടെ എണ്ണം കിട്ടും. പ്രസ്തുത ഗതചാന്ദ്ര ദിനങ്ങളെ യുഗഭൂദിനങ്ങളെക്കൊണ്ടു ഗുണിച്ച് യുഗചാന്ദ്രദിനങ്ങളെക്കൊണ്ടു ഹരിച്ചാല് അഹര്ഗണം ലഭിക്കും:
![]() (അഭീഷ്ടകലിദിനസംഖ്യ)
യുഗചാന്ദ്രദിനം: 6103000080 (അദീനജ്ഞാന നാഗോനപേക്ഷം). യുഗഭൂദിനം: 1577917500 (അനൃശംസഃ കളാര്ഥീ സമര്ത്യഃ).
ഈ കലിദിനക്രിയ വിവരിക്കുന്നതിനിടയില്, ദീര്ഘസംഖ്യകളുടെ ഗുണനഹരണങ്ങളിലുള്ള പ്രയാസങ്ങളെ ഒഴിവാക്കുന്നതിനുവേണ്ടി, ഗ്രന്ഥകാരന് സൂത്രരൂപേണ ഉപായങ്ങള് നിര്ദേശിച്ചിട്ടുണ്ട്:
(അഭീഷ്ടകലിദിനസംഖ്യ)
യുഗചാന്ദ്രദിനം: 6103000080 (അദീനജ്ഞാന നാഗോനപേക്ഷം). യുഗഭൂദിനം: 1577917500 (അനൃശംസഃ കളാര്ഥീ സമര്ത്യഃ).
ഈ കലിദിനക്രിയ വിവരിക്കുന്നതിനിടയില്, ദീര്ഘസംഖ്യകളുടെ ഗുണനഹരണങ്ങളിലുള്ള പ്രയാസങ്ങളെ ഒഴിവാക്കുന്നതിനുവേണ്ടി, ഗ്രന്ഥകാരന് സൂത്രരൂപേണ ഉപായങ്ങള് നിര്ദേശിച്ചിട്ടുണ്ട്:
ഗുണഹാരാന്തരഗുണിതം ഗുണ്യം ഹാരഹൃതം തു വാ ഗുണ്യേ ഗുണകാധിക, ല്പകത്വേ സ്വമൃണം കുര്യാത് ഫലസ്യ സംസിദ്ധ്യൈ.
ഗുണകത്തിന്റെയും ഹാരകത്തിന്റെയും വ്യത്യാസം കൊണ്ട് ഗുണ്യത്തെ ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചു കിട്ടുന്ന ഫലത്തെ, ഗണകം ഹാരകത്തെക്കാള് വലുതാണെങ്കില് ഗുണ്യത്തില് കൂട്ടണം; ചെറുതാണെങ്കില് കുറയ്ക്കണം; ഗുണ്യം അ; ഗുണകം ആ; ഹാരകം ഇ; ഫലം ഉ എന്നിരിക്കട്ടെ. ഇവിടെ
അടുത്തത് സൂര്യാദിഗ്രഹങ്ങുടെ മധ്യമങ്ങള് കണക്കാക്കുന്ന മാര്ഗമാണ്. മധ്യമങ്ങളെന്നാല് ഗ്രഹങ്ങള്ക്ക് അവരവരുടെ കക്ഷ്യാവൃത്തങ്ങളില് ശരാശരിക്കണക്കനുസരിച്ചുവരുന്ന സ്ഥൂലമായ സ്ഥാനങ്ങളാകുന്നു. മധ്യമക്രിയയില് അഹര്ഗണം ഗുണ്യവും യുഗഭഗണം ഗുണകവും ഭൂദിനം ഹാരകവും ആയി വരും. അതായത്
(ഫലം). ഈ ഫലത്തെ ഉപേക്ഷിച്ചിട്ട് ശിഷ്ടത്തെ 12 കൊണ്ടു ഗുണിച്ച് അതേ ഹാരകം (ഭൂദിനം) കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന ഫലം രാശി; ശിഷ്ടത്തെ 60 കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചു കിട്ടുന്നത് വികല. ഇതുപോലെ തന്നെ ശിഷ്ടങ്ങളില് നിന്നും തത്പരയും പ്രതത്പരയും വരുത്താന് സാധിക്കും. (60 പ്രതത്പര1 തത്പര; 60 തത്പര 1 വികല; 60 വികല 1 കല; 60 കല 1 ഭാഗ; 30 ഭാഗ 1 രാശി). കരണപദ്ധതി ഒന്നാമധ്യായത്തിലെ അതിപ്രധാനമായ മറ്റൊരു വിഷയം "ശകാബ്ദ സംസ്കാര'മാണ്. യുഗാരംഭത്തിലേക്ക് പഠിതാക്കളായ ഗ്രഹഭഗണങ്ങള്ക്കും മറ്റും നൂറ്റാണ്ടുകള് കഴിയുമ്പോള് വരാവുന്ന വ്യത്യാസങ്ങളെ കണക്കിലെടുത്തുകൊണ്ട് നിരീക്ഷണപടുക്കളായ ശാസ്ത്രജ്ഞന്മാര് ഗ്രഹമധ്യമങ്ങളുടെയും മറ്റും സൂക്ഷ്മതയ്ക്കു വേണ്ടി കാലാന്തരത്തില് നടപ്പില് വരുത്തിയ ഒരു പരിഷ്കാരമത്ര ശകാബ്ദസംസ്കാരം എന്ന പേരില് അറിയപ്പെടുന്നത്. ഈ വിശിഷ്ട ക്രിയാഭാഗം 12ഉം 13ഉം ശ്ലോകങ്ങളെക്കൊണ്ട് സവിസ്തരം പ്രതിപാദിക്കപ്പെട്ടിരിക്കുന്നു.
മാതൃകയ്ക്ക് ചന്ദ്രന്റെ ശകാബ്ദസംസ്കാരത്തെ ഇപ്രകാരം സംഗ്രഹിക്കാം:
കലിവര്ഷത്തില് നിന്നും "ധീസ്ഥയോഗം' (3179) കുറച്ചാല് ശകവര്ഷം. വര്ത്തമാന ശകവര്ഷത്തില് നിന്നും "വിഗ്ഭാവം' (444) കുറച്ചുകിട്ടുന്ന സംഖ്യയെ "ധനം' (9) കൊണ്ടു ഗുണിച്ച് "മന്ദം' (85) കൊണ്ടു ഹരിച്ചാല് ഫലം കല. ശിഷ്ടത്തെ 60 കൊണ്ടു ഗുണിച്ച് "മന്ദം' കൊണ്ടു തന്നെ ഹരിച്ചു കിട്ടുന്ന ഫലം വികല. ഈ കലാവികലകളെ അഹര്ഗണപ്രകാരം മുമ്പു വരുത്തിയ ചന്ദ്രമധ്യമത്തില് കുറച്ചാല് മധ്യമം സൂക്ഷ്മമായിത്തീരും. ഇതുപോലെതന്നെ ചന്ദ്രന്റെ മന്ദോച്ചമായ തുംഗമധ്യമത്തെയും കുജാദികളുടെ മധ്യമങ്ങളെയും പ്രത്യേകം നിര്ദിഷ്ടമായ ഗുണകങ്ങളും ഹാരകങ്ങളും ഉപയോഗിച്ച് സംസ്കരിക്കാവുന്നതാകുന്നു. ആദിത്യനുമാത്രം ശകാബ്ദ സംസ്കാരം ആവശ്യമില്ലെന്നും കാണിച്ചിട്ടുണ്ട്.
ഈ ക്രിയയില് 444 (വാഗ്ഭാവം) ശോധ്യ വര്ഷമായിക്കാണുന്നതുകൊണ്ട് ശകവര്ഷം 444ല് (എ.ഡി. 522) ആണ് ശകാബ്ദസംസ്കാരത്തിന്റെ ആവിര്ഭാവമെന്ന് ഊഹിക്കുന്നതില് തെറ്റില്ല. ആര്യഭടീയത്തിന്റെ കാലം എ.ഡി. 500 ആണ്. ആര്യഭടസിദ്ധാന്തത്തിലും നേരിയ പഴുതുകളുണ്ടെന്നു കാണുകയാലായിരിക്കണം ആ കാലം മുതല്ക്കുതന്നെയുള്ള വര്ഷങ്ങളെ ആസ്പദമാക്കി ശകാബ്ദ സംസ്കാരം വിധിക്കപ്പെട്ടിരിക്കുന്നത്. ഇനി ഈ അധ്യായത്തില് പ്രാധാന്യമര്ഹിക്കുന്ന മറ്റൊരു വിഷയം ഖണ്ഡവും ധ്രുവവും കണക്കാക്കാനുള്ള പദ്ധതിയാണ്.
കലിയുഗാരംഭദിനം മുതല് അഭീഷ്ടദിവസം വരെയുള്ള അഹര്ഗണത്തെ ഗ്രഹങ്ങളുടെ യുഗഭഗണങ്ങളെക്കൊണ്ടു ഗുണിച്ച് യുഗഭൂദിനങ്ങളെക്കൊണ്ടു ഹരിച്ചു കിട്ടുന്ന രാശ്യാദി ഫലങ്ങളാണ് ഗ്രഹമധ്യമങ്ങളെന്ന് മുമ്പു പറഞ്ഞിട്ടുണ്ടല്ലോ. ഇത്തരം ക്രിയയ്ക്ക് ലാഘവം വരുത്താനുള്ള ഉപകരണവിശേഷങ്ങളാണ് ഖണ്ഡവും ധ്രുവവും. ഖണ്ഡം എന്നാല് വലിയ അഹര്ഗണത്തില് മുറിച്ചെടുത്ത ചെറിയ അഹര്ഗണമെന്നര്ഥം. ധ്രുവം എന്നാല് ഈ അഹര്ഗണഖണ്ഡത്തില് നിന്നും കണക്കാക്കി പ്രത്യേകം സൂക്ഷിക്കപ്പെടുന്ന മാറ്റമില്ലാത്ത മധ്യമങ്ങള് എന്ന് അര്ഥമാക്കാം. ഏതെങ്കിലും ഒരു കല്പിതദിനത്തിന് യുഗാദിമുതലുള്ള അഹര്ഗണവും ആഅഹര്ഗണത്തില് നിന്ന് മധ്യമങ്ങളും വരുത്തി സൂക്ഷിക്കുക. പിന്നീട് കല്പിതദിനം കഴിഞ്ഞുവരുന്ന ഏതെങ്കിലും അഭീഷ്ടദിവസത്തിലേക്ക് മധ്യമങ്ങള് വരുത്തേണ്ടിവന്നാല് ആ ദിവസത്തേക്ക് യുഗാദി മുതലുള്ള അഹര്ഗണം വരുത്തി കല്പിതദിനാഹര്ഗണത്തെ കുറയ്ക്കണം. അപ്പോള് വരുത്തുന്ന വലിയ അഹര്ഗണത്തില്നിന്നും മുമ്പു വരുത്തി സൂക്ഷിക്കപ്പെട്ടിട്ടുള്ള ചെറിയ അഹര്ഗണത്തെ കുറയ്ക്കണമെന്നും സാരം. ഇവിടെ, കുറയ്ക്കപ്പെടുന്ന ചെറിയ അഹര്ഗണം ഖണ്ഡം; ആ ഖണ്ഡത്തിനുള്ള മധ്യമങ്ങള് ധ്രുവങ്ങള്. ഇഷ്ടകാലാഹര്ഗണത്തില് നിന്നും ഖണ്ഡം കുറച്ചാല് ഖണ്ഡശേഷം. ഈ ഖണ്ഡശേഷത്തെ അതതു ഗ്രഹത്തിനു പറയപ്പെട്ടിട്ടുള്ള ഗുണകാരം കൊണ്ടു ഗുണിച്ച് ഹാരകംകൊണ്ടു ഹരിച്ചാല് വരുന്ന രാശ്യാദി ഫലങ്ങളില് ധ്രുവങ്ങള് കൂട്ടിയാല് അഭീഷ്ടകാലമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനു മാത്രം പ്രസ്തുത രാശ്യാദി ഫലങ്ങളെ ധ്രുവത്തില് നിന്നും കുറയ്ക്കണം. കാരണം രാഹു സദാ പിറകോട്ടാണല്ലോ സഞ്ചരിക്കുന്നത്. "സ്വധ്രുനശോധിതോളഹിഃ' എന്ന് പഞ്ചബോധത്തിലും പറയുന്നുണ്ട്. അഹര്ഗണം "ഖണ്ഡ'ത്തെക്കാള് കുറഞ്ഞിരുന്നാല് അവിടെ "ഖണ്ഡ'ത്തില് നിന്നും "അഹര്ഗണ'ത്തെ കുറച്ച് രാശ്യാദി ഫലങ്ങളെ വരുത്തി ധ്രുവങ്ങളില്നിന്നും കുറച്ചാല് ഗ്രഹമധ്യമങ്ങള് സിദ്ധിക്കും. രാഹുവിനാകട്ടെ ധ്രുവത്തില് കൂട്ടുകയും വേണം. ഇപ്രകാരം കരണഗ്രന്ഥങ്ങളില് സ്വീകരിക്കപ്പെട്ടിട്ടുള്ള മധ്യമക്രിയയ്ക്ക് അടിസ്ഥാനമായ ഖണ്ഡങ്ങളെയും ധ്രുവങ്ങളെയും വരുത്താനുള്ള വിവിധമാര്ഗങ്ങള് ഈ പ്രകരത്തില് കാണാവുന്നതാണ്. അടുത്തത് മധ്യഗതി വരുത്താനുള്ള മാര്ഗമാണ്. ഒരു ഗ്രഹത്തിന്റെ ഒരു ദിവസത്തെ ശരാശരി ഗതിയാണ് മധ്യഗതി. അതായത്, 60 നാഴിക കൊണ്ട് സ്വഭ്രമണവൃത്തത്തില് സഞ്ചരിക്കുന്ന ദൂരം. ഈ മധ്യഗതിക്രിയയില് "അനന്തപുരം' (21,600) ഗുണ്യം; ഭഗണം ഗുണകം; ഭൂദിനം ഹാരകം:
(21600 x ഭഗണം )/ ഭൂദിനം = മധ്യഗതി (ഫലം)
പഞ്ചബോധത്തില് പഠിതാക്കളായ മധ്യഗതികള് ധസൂര്യന് "ദാനധര്മ' (59 കല 8 വികല), ചന്ദ്രന് "മൃഗനിളസു' (790 കല 35 വികല) ഇത്യാദിപ ഇപ്രകാരം കണ്ടുപിടിക്കപ്പെട്ടിട്ടുള്ളവയാകുന്നു. അനന്തരം ചന്ദ്രഭഗണത്തില് നിന്നും ആകാശകക്ഷ്യയുടെ പരിധി നിര്ണയിക്കുന്നതിനും ഗ്രഹങ്ങളുടെ യോജനാത്മകമായ ദിനഗതിയും കക്ഷ്യാമണ്ഡലങ്ങളുടെ ചുറ്റളവുകളും ഗണിക്കുന്നതിനും ഉള്ള മാര്ഗങ്ങള് പ്രതിപാദിച്ചതിനുശേഷം ഒന്നാമധ്യായം അവസാനിപ്പിച്ചിരിക്കുന്നു. രണ്ടാമധ്യായത്തില് ആദ്യമായി പറയുന്നത് ചന്ദ്രാദിഗ്രഹങ്ങളുടെ പര്യയങ്ങളെയും ഭൂദിനങ്ങളെയും സംസ്കരിക്കുന്നതിനുള്ള വഴിയാണ്. ഒന്നാമധ്യായത്തില് ശകാബ്ദ സംസ്കാരക്രിയയ്ക്ക് പറഞ്ഞതായ ഗുണകാരങ്ങളും ഹാരകങ്ങളും ഉപയോഗിച്ചുതന്നെയാണ് ഈ സംസ്കാരവും നിര്വഹിക്കപ്പെടുന്നത്. ഇപ്രകാരം സംസ്കരിച്ചെടുക്കുന്ന ഗ്രഹപര്യയങ്ങളെ മഹാഗുണകങ്ങളെന്നും ഭൂദിനങ്ങളെ മഹാഹാരകങ്ങളെന്നും പറയുന്നു. ഈ വലിയ സംഖ്യകളെ അപവര്ത്തനക്ക്രിയകൊണ്ടു ചെറുതാക്കാം. മഹാഗുണകത്തെ അപവര്ത്തിച്ചാല് ദൃഢഗുണകം. മഹാഹാരകത്തെ അപവര്ത്തിച്ചാല് ദൃഢഹാരകം. രണ്ടു സംഖ്യകളെ അന്യോന്യം ഹരിച്ചാല് ഒടുവില് ശേഷിക്കുന്ന ഹരണഫലത്തിന് അപവര്ത്തനം എന്നു പേര്. അപവര്ത്തനം കൊണ്ട് ആ രണ്ടു സംഖ്യകളെയും നിശ്ശേഷം ഹരിക്കാന് സാധിക്കും. അങ്ങനെ അപവര്ത്തിക്കപ്പെടുമ്പോള് അവ ദൃഢങ്ങളായും തീരും. ഈ തത്ത്വമാണ് ആചാര്യന് സൂത്രരൂപേണ അവതരിപ്പിച്ചിരിക്കുന്നത്:
"രാശ്യോരന്യോന്യഹാരേണ ശേഷഃസ്യാദപവര്ത്തനം തേന തൗ വിഹൃതൗ രാശീ ദൃഢാഖ്യാവപവര്ത്തിതൗ'
എന്ന് മഹാഗുണകങ്ങളും മഹാഹാരകങ്ങളും ഉപയോഗിച്ച് ക്രിയചെയ്താല് കിട്ടുന്ന ഫലങ്ങള്ക്കും ദൃഢഗുണകങ്ങളും ദൃഢഹാരകങ്ങളും ഉപയോഗിച്ചു ക്രിയചെയ്താല് കിട്ടുന്ന ഫലങ്ങള്ക്കും വ്യത്യാസം വരുന്നതല്ല. അഭീഷ്ടകാലത്തിനുള്ള അഹര്ഗണത്തെ മഹാഗുണകം കൊണ്ടോ ദൃഢഗുണകംകൊണ്ടോ ഗുണിച്ച് മഹാഹാരകം കൊണ്ടോ ദൃഢഹാരകം കൊണ്ടോ ഹരിച്ചാല് രാശി, ഭാഗ മുതലായ ഫലങ്ങള് സിദ്ധിക്കും. ഫലങ്ങളില് കലിയുഗാരംഭത്തിലുള്ള ഗ്രഹധ്രുവങ്ങള് കൂട്ടിയാല് ഗ്രഹമധ്യമങ്ങള് സിദ്ധിക്കും. ഇപ്രകാരം ഗ്രഹമധ്യമക്രിയയില് അപവര്ത്തനം കൊണ്ട് ക്രിയാലാഘവം വരുത്താനുള്ള മാര്ഗം ഉപദേശിച്ചു തന്നതിനുശേഷം ഗണിതശാസ്ത്ര പ്രസിദ്ധമായ "കുട്ടാകാരമാര്ഗ'മനുസരിച്ച് "വല്യുപസംഹാരം' ചെയ്ത് ഗുണകാരങ്ങളെയും ഹാരകങ്ങളെയും വരുത്താവുന്നതാണെന്ന് നിര്ദേശിക്കുന്നു.
പ്രസ്തുത വല്യുപസംഹാരക്രിയയുടെ ഒരു മാതൃക താഴെ കാണിക്കുന്നു:
മഹാഗുണകംചന്ദ്രപര്യയം (തിലബലമസുസൂക്ഷ്മം) 57753336 മഹാഹാരകംഭൂദിനം(അനൃശംസഃ കളാര്ഥീസമര്ത്യഃ) 1577917500 ഈ സംഖ്യകളെ പരസ്പരം ഹരിച്ച് താഴെത്താഴെ 5 സ്ഥാനങ്ങളിലായി ഹരണഫലങ്ങളെയും, എല്ലാറ്റിനും അടിയില് (6-ാമത്തെ സ്ഥാനത്ത്) രൂപം (1) എന്ന സംഖ്യയെയും വയ്ക്കണം (എഴുതണം). അപ്പോള് 27 (പ്രഥമവല്ലി) 3 9 4 1 1 (രൂപം) എന്നിങ്ങനെ വല്ലിയുണ്ടാകും. ഈ വല്ലിയില് 6-ാമത്തെ സംഖ്യയായ 1 (രൂപം) അന്ത്യം;
5-ാമത്തെ സംഖ്യയായ 1 ഉപാന്ത്യം; 4-ാമത്തെ സംഖ്യയായ 4 ഊര്ധ്വം. ആദ്യമായി അന്ത്യത്തെ ഉപാന്ത്യം കൊണ്ടു ഗുണിച്ച് ഊര്ധ്വം കൂട്ടണം: 1 x 1 + 4 = 5. ഈ 5നെ അന്ത്യമായി കല്പിച്ചിട്ട് പ്രഥമവല്ലിയിലെ അന്ത്യത്തെ (രൂപത്തെ, 1 നെ) ഉപേക്ഷിക്കണം; അപ്പോള് 27, 3, 9,5, 1 (ദ്വിതീയവല്ലി). ഈ വല്ലിയില് അന്ത്യം 1; ഉപാന്ത്യം 5; ഊര്ധ്വം 9. മുമ്പത്തെപ്പോലെ ക്രിയചെയ്താല് 5x9+1 = 46. അന്ത്യത്തെ ത്യജിക്കുക; അപ്പോള് 27, 3, 46, 5 (തൃതീയവല്ലി). ഈ വല്ലിയില് അന്ത്യം 5, ഉപാന്ത്യം 46, ഊര്ധ്വം 3. ക്രിയ ആവര്ത്തിച്ചാല് 3x 46 + 5 = 143. 5നെ ത്യജിക്കുക. 143നെ അന്ത്യമായി കല്പിച്ച് ക്രിയചെയ്താലുണ്ടാകുന്ന വല്ലി: 27, 143, 46 (ചതുര്ഥവല്ലി). ഈ വല്ലിയില് അന്ത്യം 46, ഉപാന്ത്യം 143, ഊര്ധ്വം 27. 143x 27 + 46 = 3907. അന്ത്യത്തെ (46) ഉപേക്ഷിക്കുക; അപ്പോള് 3907 (സന്നദ്ധാംഗം), 143 (ലാവണ്യം) എന്നിങ്ങനെ രണ്ടു സംഖ്യകള് സിദ്ധിക്കും. ഇവയില് ആദ്യത്തെ സംഖ്യ ഹാരകം; രണ്ടാമത്തേത് ഗുണകാരം. ഇപ്രകാരമാണ് ചന്ദ്രന്റെ മധ്യമക്രിയയില് "സന്നദ്ധാംഗം' എന്ന ഹാരകവും ലാവണ്യം എന്ന ഗുണകാരവും ലഭിക്കുന്നത്.
നക്ഷത്രഗണിതത്തിന് അടിസ്ഥാനമായ ചന്ദ്രസ്ഫുടം വരുത്തുന്നതിനുള്ള ഉപകരണങ്ങളായ ഖണ്ഡം, ധ്രുവം, വാക്യം ഇവയെക്കുറിച്ചുള്ള പ്രതിപാദനമാണ് മൂന്നാമധ്യായത്തിലുള്ളത്.
പഞ്ചാംഗങ്ങളില് ഓരോ ദിവസത്തെയും നക്ഷത്രങ്ങളില് ഗണിച്ചുചേര്ത്തിട്ടുണ്ട്. അശ്വതി മുതലായ പ്രസ്തുത നക്ഷത്രങ്ങളുടെ അടിസ്ഥാനം ചന്ദ്രന്റെ സ്ഫുടങ്ങളാണ്. കേരളത്തിലെ സുപ്രസിദ്ധ ഗണിതഗ്രന്ഥമായ പഞ്ചബോധത്തില് മധ്യമക്രിയ കൂടാതെ തന്നെ ചന്ദ്രനെ ഗണിക്കാനുള്ള ലഘുമാര്ഗം ഉപദേശിക്കപ്പെട്ടിട്ടുണ്ട്: "വാക്യധ്രുവൈക്യം ഹൃദയസ്ഫുടേന്ദുഃ' (വാക്യത്തില് ധ്രുവം കൂട്ടിയാല് ഉദയകാലചന്ദ്രസ്ഫുടം സിദ്ധിക്കും). ഇവിടെ ആദ്യമായി വാക്യം, ധ്രുവം ഇവ എന്താണെന്ന് അറിയേണ്ടിയിരിക്കുന്നു. പഞ്ചബോധത്തില്ത്തന്നെ "ഗീര്നഃ ശ്രയാ' എന്നു തുടങ്ങി "ഭവേത് സുഖം' എന്നവസാനിക്കുന്ന 248 ചന്ദ്രവാക്യങ്ങള് പഠിതങ്ങളായിട്ടുണ്ട്. "വരരുചി' കൃതവാക്യങ്ങളെന്നു വിശ്വസിക്കപ്പെട്ടുപോരുന്ന ഈ ചന്ദ്രവാക്യങ്ങള് കടപയാദിസംഖ്യയില് പറയപ്പെടുന്ന 248 ഭാഗികമായ ചന്ദ്രസ്ഫുടങ്ങള് തന്നെയാകുന്നു. അഭീഷ്ടദിനത്തിലേക്കുള്ള ചന്ദ്രവാക്യത്തില് ധ്രുവം കൂട്ടിയാല് ചന്ദ്രസ്ഫുടം സിദ്ധിക്കും. ഈ ക്രിയയില് അമിതയവോത്സുക(1741650) ഖണ്ഡം. ഈ ഖണ്ഡത്തെ കലിദിനത്തില് നിന്നും കുറച്ചു കിട്ടുന്നത് ഖണ്ഡശേഷം. ഈ ഖണ്ഡശേഷത്തില്നിന്നും ലഭിക്കുന്ന മധ്യമം ചന്ദ്രധ്രുവം. ചന്ദ്രവാക്യത്തില് ചന്ദ്രധ്രുവം കൂട്ടിയാല് ചന്ദ്രസ്ഫുടം കിട്ടുമെന്നു സാരം. ചന്ദ്രസ്ഫുട സാധനങ്ങളായ ഖണ്ഡങ്ങളെയും ധ്രുവങ്ങളെയും കണക്കാക്കുന്നതിനുള്ള വഴി മാത്രമല്ല; "ഗീര്നഃ ശ്രയാ' മുതലായ ചന്ദ്രവാക്യങ്ങളുടെ ഉത്പത്തിക്കു കാരണമായ വസ്തുതകളും ഈ അധ്യായത്തില്നിന്നും ഗ്രഹിക്കാന് സാധിക്കും.
നാലാമധ്യായത്തില് ആദ്യമായി നിര്ഗണിതം എന്ന ഗ്രന്ഥത്തെ പ്രമാണീകരിച്ചുകൊണ്ട് കുജാദിഗ്രഹങ്ങളുടെ (കുജന്, ബുധന്, ഗുരു, ശുക്രന്, ശനി) സ്ഫുടസാധനങ്ങളായ മന്ദഖണ്ഡങ്ങളെയും ശീഘ്രഖണ്ഡങ്ങളെയും വരുത്താനുള്ള വഴി കാണിക്കുന്നു. അതിനുശേഷം വാക്യകരണം എന്ന ഗ്രന്ഥത്തെ ആധാരമാക്കിക്കൊണ്ട് മണ്ഡലങ്ങളെയും ധ്രുവങ്ങളെയും വരുത്താനുള്ള വഴികാണിക്കുന്നു. ഈ മണ്ഡലങ്ങളുടെയും ധ്രുവങ്ങളുടെയും സഹായത്താലാണ് ശോധ്യദിനത്തെ കണ്ടുപിടിക്കുന്നത്. പഞ്ചബോധാദിഗ്രന്ഥങ്ങളില് പറയുന്ന അഹര്ഗണഖണ്ഡം തന്നെയാണ് വാക്യകരണത്തില് പറയുന്ന ശോധ്യദിനം. ശോധ്യദിനത്തില്നിന്നും ഗ്രഹധ്രുവങ്ങളും സിദ്ധിക്കുന്നതാണ്. അഭീഷ്ടകാലാഹര്ഗണത്തില് നിന്നും "ശോധ്യദിനം' കുറച്ച് ക്രിയചെയ്തുകിട്ടുന്ന ഫലങ്ങളില് ധ്രുവങ്ങളെക്കൂട്ടിയാല് കുജാദിഗ്രഹങ്ങളുടെ സ്ഫുടങ്ങള് സിദ്ധിക്കും. അടുത്തത് മൗഢ്യഖണ്ഡം വരുത്താനുള്ള മാര്ഗമാണ്. ഇതിന്റെ അടിത്തറ ശീഘ്രാച്ചത്തിന്െറയും മധ്യമഗ്രഹത്തിന്റെയും യോഗകാലമാണ്. മൗഢ്യഖണ്ഡത്തെ അഹര്ഗണത്തില്നിന്നും കുറച്ചുകിട്ടുന്ന ഖണ്ഡശേഷത്തില് നിന്നും ഗ്രന്ഥസ്ഫുടം വരുത്തി പ്രസ്തുത ഗ്രഹത്തിന്റെയും ആദിത്യന്റെയും പര്യയങ്ങളുടെ അന്തരമെടുത്ത് ആ അന്തരവും ഭൂദിനവും തമ്മില് ഹരിച്ചുകിട്ടുന്ന ഗുണകാരങ്ങളും ഹാരകങ്ങളും ഉപയോഗിച്ചു ക്രിയചെയ്താല് ഗ്രഹമൗഢ്യകാലം നിര്ണയിക്കുന്നതിന് സാധിക്കും. അനന്തരം ശോധ്യാബ്ദം വരുത്തി ശീഘ്രാച്ചഗ്രഹയോഗകാലം (ഇഷ്ടഗ്രഹസൂര്യസമാഗമകാലം) നിര്ണയിക്കുന്നതിനും, യുഗചാന്ദ്രമാസങ്ങളുടെയും, യുഗസൗരമാസങ്ങളുടെയും, യുഗസാവനദിനങ്ങളുടെയും അടിസ്ഥാനത്തില് അധിമാസഖണ്ഡങ്ങളെയും വരുത്താനുള്ള ഉപായങ്ങള് വിശദീകരിച്ചിരിക്കുന്നു.
ചതുര്ഥാധ്യായത്തെ മകുടം ചൂടിക്കുന്നത് അവസാനമായി പറയുന്ന ഗ്രഹണഖണ്ഡമാണ്. യുഗചന്ദ്രമാസസംഖ്യ യുഗസൂര്യപര്യയസംഖ്യ, യുഗരാഹുപര്യയസംഖ്യ ഇവയുടെ അടിസ്ഥാനത്തില് വിവരിക്കുന്ന ഹാരകങ്ങള് ഉപയോഗിച്ച് "പര്വാന്തകാലിക'മായ സൂര്യചന്ദ്രന്മാരുടെയും രാഹുവിന്റെയും മധ്യമങ്ങള് വരുത്തി ക്രിയചെയ്താല്, സൂര്യചന്ദ്രന്മാരുടെ ഗ്രഹണഖണ്ഡങ്ങള് സിദ്ധിക്കും എന്നതാണ് ഈ ക്രിയയുടെ രത്നച്ചുരുക്കം.
പ്രസ്തുത ക്രിയയെ പ്രതിപാദിക്കുന്ന "നീത്വാ മധ്യാര്ക്കചന്ദ്രൗ ഫണിനമപി ദൃശാ' ഇത്യാദി പദ്യത്തിലെ ദൃശാ എന്ന പ്രത്യേക നിര്ദേശം ശ്രദ്ധിക്കേണ്ട ഒന്നാണ്. ജാതകം, പ്രശ്നം, മുഹൂര്ത്തം മുതലായവയ്ക്ക് "പരഹിതഗണിതം' സമ്മതമാണെങ്കിലും ഗ്രഹണഗണിതത്തില് ദൃക്ക് അനുസരിച്ചു തന്നെ ഗ്രഹങ്ങളെ ഗണിക്കണം എന്നാണ് ആചാര്യന്റെ ആശയം. സര്വഥാ പ്രാധാന്യം വഹിക്കുന്ന ഗ്രഹണഖണ്ഡത്തോടു കൂടി ഈ അധ്യായം അവസാനിക്കുന്നു. ഗ്രഹങ്ങളുടെ കല്പ പര്യയങ്ങളെ സ്ഫുടീകരിക്കുന്നതിന്റെ ആവശ്യകതയും അതിനു വേണ്ടിയുള്ള ക്രിയകളുമാണ് അഞ്ചാമധ്യായത്തിലെ പ്രതിപാദ്യം.
"ഗ്രഹണഗ്രഹയോഗാദ്യൈര് യേഗ്രഹാസ്സുപരീക്ഷിതാഃ ദൃക്സമാസ്തത്സമാഃ കല്പേ കല്പ്യാ വാ ഭഗണാദയഃ'
(സൂര്യചന്ദ്രന്മാരുടെ ഗ്രഹണം, കുജാദിഗ്രഹങ്ങളുടെ പരസ്പരയോഗം മുതലായവ ഗണിക്കുമ്പോള് ഗണിക്കപ്പെടുന്ന സ്ഥാനവും, ആകാശത്തില് കാണപ്പെടുന്ന സ്ഥാനവും തുല്യമായി വരുന്നത്, ഏതു പദ്ധതി അനുസരിച്ചുള്ള ഗണിതത്തിലാണോ, ആപദ്ധതി അനുസരിച്ചു തന്നെ ഗ്രഹസ്ഫുടങ്ങള്ക്ക് ആധാരമായ കല്പഭഗണാദികളെയും സ്ഫുടീകരിക്കേണ്ടതാകുന്നു) എന്നിങ്ങനെ പര്യയപരിഷ്കരണത്തിന്റെ ആവശ്യകത വ്യക്തമാക്കിക്കൊണ്ട്, പ്രസ്തുത ക്രിയയ്ക്ക് ഉപയുക്തമായ മാര്ഗങ്ങളെ ഈ അധ്യായത്തില് പ്രതിപാദിച്ചിരിക്കുന്നു. ഇവിടെ രണ്ടു മാര്ഗങ്ങള് ഉപദേശിച്ചു തരുന്നുണ്ട്. ഒന്നാമത്തെ മാര്ഗത്തില് കല്പാരംഭത്തിലുള്ള സംക്രമധ്രുവങ്ങള് ആവശ്യമാണ്. പക്ഷേ പ്രളയത്തില് ഗ്രഹങ്ങള് ഇല്ലാത്തതുകൊണ്ട് ആ ധ്രുവങ്ങളുണ്ടാകാന് സാധ്യതയില്ല എന്നു കരുതി രണ്ടാമത്തെ മാര്ഗം നിര്ദേശിച്ചിരിക്കുന്നു. കല്പസംവത്സരങ്ങളെയും, കല്പസൂര്യഭഗണങ്ങളെയും പരസ്പരം ഹരിച്ച് വല്ലിഫലങ്ങളുണ്ടാക്കി ക്രിയ ചെയ്യുന്നതാണ് ശരിയെന്നും വിധിക്കുന്നുണ്ട്.
ഇപ്രകാരം അഞ്ചാമധ്യായത്തില് കല്പഭഗണങ്ങളെയും കല്പഭൂദിനങ്ങളെയും മറ്റും സ്ഫുടീകരിക്കുന്നതിനുള്ള ഉപായങ്ങളെ വിശദീകരിച്ചതിനുശേഷം ആറാമധ്യായത്തില്, വ്യാസംകൊണ്ട് വൃത്തപരിധിയെയും വൃത്തപരിധികൊണ്ട് വ്യാസത്തെയും വരുത്താനുള്ള മാര്ഗങ്ങളെ, പ്രാഥമികമായി നിര്ദേശിച്ചുകൊണ്ട്, തദ്വാരാ ഗ്രഹഗണിതത്തില് അതിപ്രധാനമായ ജ്യാഖണ്ഡങ്ങള് നിര്മിക്കാനുള്ള ബഹുവിധമായ ഉപായങ്ങള് പ്രദര്ശിപ്പിച്ചിരിക്കുന്നു.
രാശിചക്രത്തില് ഗ്രഹങ്ങളുടെ സ്ഥാനം നിര്ണയിക്കുന്നതിനുള്ള മുഖ്യമായ ഉപകരണങ്ങളാണ് ജ്യാക്കള്. ആകാശത്തില് വിഭിന്ന കേന്ദ്രങ്ങളോടുകൂടി വിഭിന്നവൃത്തങ്ങളിലായി സഞ്ചരിക്കുന്ന സൂര്യാദിഗ്രഹങ്ങളെ ഭൂമിക്കു സമാനാന്തരവും സര്വോപരി സ്ഥിതവും ആയ നക്ഷത്ര കക്ഷ്യയില്ക്കൂടി സഞ്ചരിക്കുന്നവയായി സങ്കല്പിച്ച് അവയുടെ സൂക്ഷ്മസ്ഥാനങ്ങള് നിര്ണയിക്കുന്നതിന് നിരീക്ഷണപടുക്കളായ ആചാര്യന്മാര് ചില മാനദണ്ഡങ്ങള് കണ്ടുപിടിച്ചു വച്ചിട്ടുണ്ട്. അത്തരം മാനസാധനങ്ങളില് പ്രധാനമാണ് ജ്യാക്കള്. നക്ഷത്ര കക്ഷ്യാരൂപമായ രാശിചക്രത്തിന് വൃത്തപരിധി 21,600 കലകളാണ് (രാശി ചക്രത്തില് 12 രാശികള്, 1 രാശിക്ക് 30 ഭാഗ, ഒരു ഭാഗയ്ക്ക് 60 കല). നക്ഷത്രകക്ഷ്യയുടെ കേന്ദ്രവും ഭൂമിയുടെ കേന്ദ്രവും ഒന്നുതന്നെയാണ്. നക്ഷത്രകക്ഷ്യയെ സമമായി വിഭജിച്ചുകൊണ്ട് കേന്ദ്രബിന്ദുവില്ക്കൂടി ഊര്ധ്വഗാമിയായി വൃത്തപരിധിയെ സ്പര്ശിക്കുന്ന രേഖയ്ക്ക് ഉച്ചരേഖ എന്നു പേര്. വ്യാസരേഖയ്ക്കു സമാനാന്തരമായി ഉച്ചരേഖയില്ക്കൂടി വിലങ്ങനെ, ഗ്രഹങ്ങളുടെ സ്ഥാനങ്ങളിലേക്കു പോകുന്ന രേഖകളാണ് ജ്യാക്കളെന്നു പറയുന്നത്. വൃത്തപരിധിഭാഗങ്ങള് ചാപരൂപ(വില്ലിന്റെ ആകൃതിയിലുള്ളവ)ങ്ങളും പരിധികളെ സ്പര്ശിക്കുന്ന സമരേഖകള് ജ്യാരൂപങ്ങളും (ഞാണിന്റെ സ്ഥാനം വഹിക്കുന്നവ) ആണ്. വക്രരേഖ ചാപം (വില്ല്); സമരേഖ ജ്യാവ് (ഞാണ്) എന്നര്ഥം. ഗ്രഹഗണിതത്തില് അര്ധജ്യാക്കളെക്കൊണ്ടാണ് വ്യവഹാരം. ഈ കണക്കില് മൂന്ന് രാശികളുടെ ജ്യാവ് വൃത്തവ്യാസാര്ധം (ത്രിജ്യ). ഇവിടെ അനന്തപുര (21,600), വൃത്തത്തിന്റെ വ്യാസാര്ധം "ജലേവലം' (3,438) എന്നു പ്രസിദ്ധം. ഒരു രാശിക്ക് എട്ട് ജ്യാക്കള് എന്ന കണക്കില് മൂന്നു രാശികളടങ്ങിയ ഗോളപാദത്തില് ആകെ 24 ജ്യാക്കള്. 3മ്ല ഭാഗയ്ക്ക് (225 കല) ഒരു ജ്യാവ്. ഈ കണക്കിന് 24-ാമത്തെ ജ്യാവിന് ത്രിജ്യ (ജലേവലം) ആണെന്നു സിദ്ധിക്കുന്നു. ഇപ്രകാരം നക്ഷത്രകക്ഷ്യാരൂപമായ മഹാവൃത്തത്തിന്െറ പരിധിയായ "അനന്തപുര'(21,600)ത്തില് നിന്നും അഭീഷ്ട ഗുണകാരങ്ങളും ഹാരകങ്ങളും ഉപയോഗിച്ച് വ്യാസാര്ധം വരുത്തി അര്ധിച്ചാല് ത്രിജ്യ കിട്ടുമെന്നും, ഈ ത്രിജ്യയില് നിന്നു തന്നെ ശേഷമുള്ള ജ്യാക്കളെയും കണ്ടു പിടിക്കാവുന്നതാണെന്നും ഗ്രന്ഥകാരന് തെളിയിച്ചിട്ടുണ്ട്.
"ത്രിജ്യാര്ധമേകാരാശിജ്യാ ത്രിജ്യാവര്ഗാര്ധതഃ പദം ഭവേദധ്യര്ധരാശിജ്യാ താഭ്യാമന്യഗുണാന്നയേത്'
(ത്രിജ്യയെ അര്ധിച്ചാല് ഒരു രാശിയുടെ ജ്യാവ്; ത്രിജ്യാവര്ഗത്തെ അര്ധിച്ചു മൂലിച്ചാല്, 1മ്മ രാശിയുടെ ജ്യാവ് 12-ാം ജ്യാവ് ഈ രണ്ടു ജ്യാക്കളെക്കൊണ്ടു തന്നെ മറ്റുള്ള ജ്യാക്കളെയും വരുത്തിക്കൊള്ളേണ്ടതാകുന്നു) എന്ന പ്രസ്താവനയോടുകൂടി 24 മഹാജ്യാക്കളെയും വരുത്തിക്കാണിക്കുകയും ചെയ്യുന്നുണ്ട്. പഞ്ചബോധത്തിലെ "ആത്മവിത് ശ്രഷ്ഠഃ' തുടങ്ങിയ വികലാദി മഹാജ്യാക്കളുടെയും, മാധവകൃതമായ "ശ്രഷ്ഠം നാമവരിഷ്ഠാനം' എന്നു തുടങ്ങുന്ന തത്പരാദിമഹാജ്യാക്കളുടെയും ഉത്പത്തിക്കു നിദാനം കരണപദ്ധതിയാണെന്ന് നിസ്സംശയം പറയാം.
ചാപത്തില് നിന്ന് ജ്യാക്കളെ വരുത്തുന്നതുപോലെ തന്നെ ജ്യാക്കളില് നിന്ന് ചാപത്തെയും വരുത്താന് സാധിക്കും. അതാണ് ചാപീകരണം. ചാപീകരണക്രിയയ്ക്ക് ആവശ്യമായ ജ്യാക്കളാണ് പഞ്ചബോധത്തില് പറയപ്പെടുന്ന ("ഗൂഢാമേനകാ' 10543) 105 കല 43 വികല ഇത്യാദി ചാപജ്യാക്കള്. ആറാമധ്യായത്തിലെ അവസാന വിഷയം ചാപജ്യാനയനമത്ര. ഇപ്രകാരം വ്യാസവൃത്തങ്ങളെയും, മഹാജ്യാക്കളെയും, ചാപജ്യാക്കളെയും മറ്റും വരുത്താനുള്ള വഴി കാണിച്ചു തന്നതിനു ശേഷം ഏഴാമധ്യായത്തില് ഗ്രഹങ്ങളുടെ സ്ഫുടീകരണത്തിന് ആവശ്യമുള്ള ജ്യാക്കളുടെ ആഗമനത്തെപ്പറ്റി പ്രതിപാദിക്കുന്നു. ഗ്രഹങ്ങളുടെ സ്ഫുടക്രിയയില് രണ്ടുതരം ജ്യാക്കള് ഉള്പ്പെടുന്നുണ്ട്; മന്ദജ്യാക്കളും ശീഘ്രജ്യാക്കളും. ശീഘ്രജ്യാക്കളില്ത്തന്നെ മകരാദി എന്നും കര്ക്ക്യാദി എന്നും രണ്ടിനമുണ്ട്. രാശി, ഭാഗ, കലാദിസ്ഥാന നിര്ണയത്തിന് ആധാരമായ നക്ഷത്ര കക്ഷ്യയുടെയും ഗ്രഹങ്ങള് സഞ്ചരിക്കുന്ന വൃത്തങ്ങ(പ്രതിമണ്ഡലങ്ങ)ളുടെയും കേന്ദ്രബിന്ദുക്കള് ഒന്നല്ലാത്തതു കൊണ്ടു തന്നെയാണ് ഇത്തരം മൂന്നു വിധത്തിലുള്ള ജ്യാക്കളുപയോഗിച്ച് മന്ദഫലവും ശീഘ്രഫലവും വരുത്തി മധ്യമഗ്രഹങ്ങളെ സംസ്കരിച്ച് സ്ഫുടഗ്രഹങ്ങളാക്കി മാറ്റുന്നത്. മധ്യമസ്ഥാനത്ത് ഗ്രഹം ദൃശ്യമല്ല; സ്ഫുടസ്ഥാനത്തേ ദൃശ്യമാകയുള്ളു.
പ്രതിമണ്ഡല പരിധിയില് ഗ്രഹസ്ഥാനത്തെ കേന്ദ്രമാക്കി മന്ദശീഘ്രഗതികളുടെ അടിസ്ഥാനത്തില് മന്ദവൃത്തം, ശീഘ്രവൃത്തം എന്നിങ്ങനെ രണ്ടുതരം വൃത്തങ്ങള് സ്ഫുടക്ക്രിയയ്ക്ക് വേണ്ടി കല്പിക്കപ്പെട്ടിരിക്കുന്നു. സൂര്യന് മുതല് ശനിവരെയുള്ള ഏഴ് ഗ്രഹങ്ങളുടെയും വൃത്തകലകള് പഠിതങ്ങളായിട്ടുണ്ട്. "ഭാനോര്ഗാനം' എന്നു തുടങ്ങി ഒന്ന് മുതല് മൂന്ന് വരെ ശ്ലോകങ്ങള് കൊണ്ടു പറഞ്ഞിരിക്കുന്നത് പ്രസ്തുത വൃത്തകലകളാണ്. സൂര്യനും ചന്ദ്രനും മന്ദവൃത്തങ്ങളേ ഉള്ളു; ശീഘ്രവൃത്തങ്ങളില്ല. കുജാദി ഗ്രഹങ്ങള്ക്ക് മന്ദവൃത്തങ്ങളും ശീഘ്രവൃത്തങ്ങളും ഉണ്ട്. ഗ്രഹങ്ങള്ക്ക് മന്ദവൃത്തത്തിലുള്ള ഉച്ചസ്ഥാനം മന്ദോച്ചം; ശീഘ്രവൃത്തത്തിലുള്ള ഉച്ചസ്ഥാനം ശീഘ്രാച്ചം. മധ്യമത്തില് മന്ദോച്ചം കുറച്ചാല് മന്ദകേന്ദ്രം; ശീഘ്രാച്ചം കുറച്ചാല് ശീഘ്രകേന്ദ്രം. ഈ കേന്ദ്രങ്ങളില് ഒന്നു മുതല് മൂന്നു വരെ രാശികള് ഓജപാദം. നാലു മുതല് ആറു വരെ രാശികള് യുഗ്മപാദം. ഏഴു മുതല് ഒന്പതു വരെ ഓജപാദം. 10 മുതല് 12 വരെ യുഗ്മപാദം. കുജാദികള്ക്ക് ഓജപാദത്തിലും യുഗ്മപാദത്തിലും പ്രത്യേകം പ്രത്യേകം മന്ദവൃത്തങ്ങളും ശീഘ്രവൃത്തങ്ങളും പറയപ്പെട്ടിട്ടുണ്ട്. പ്രസ്തുത വൃത്തങ്ങളെ സ്ഫുടീകരിച്ച് (സൂക്ഷ്മപ്പെടുത്തി) അവയില് നിന്നും മന്ദജ്യാക്കളെയും ശീഘ്രജ്യാക്കളെയും വരുത്താനുള്ള വിവിധ മാര്ഗങ്ങള് ഈ അധ്യായത്തില് ആചാര്യന് കാണിച്ചു തരുന്നുണ്ട്. ജ്യോതിശ്ചക്രത്തില് സൂര്യചന്ദ്രന്മാരുടെ സ്ഥാനനിര്ണയത്തേക്കാള് വളരെ പ്രയാസമുള്ളതാണ് കുജാദികളുടെ സ്ഥാനനിര്ണയം. "ജനേന' എന്നു തുടങ്ങുന്ന സൂര്യജ്യാക്കളും "നരോനു' എന്നു തുടങ്ങുന്ന ചന്ദ്രജ്യാക്കളും നാദിനം എന്നാരംഭിക്കുന്ന കുജാദികളുടെ ജ്യാക്കളും ഇപ്രകാരം സിദ്ധിച്ചിട്ടുള്ളവയാകുന്നു. ഈ ജ്യാക്കളുടെ ഉത്പാദനത്തിനു വേണ്ടിത്തന്നെയാണ് ഈ അധ്യായത്തിലെ സിംഹഭാഗവും വിനിയോഗിക്കപ്പെട്ടിട്ടുള്ളത്. കൂടാതെ കുലീന, രൂക്ഷജ്ഞ മുതലായ മാസവാക്യങ്ങളും; തിമിരേ, സുരരാട് മുതലായ സംക്രാന്തി വാക്യങ്ങളും; കവിഷ്, ഹാരിഷു തുടങ്ങിയ നക്ഷത്ര സംക്രാന്തി വാക്യങ്ങളും; പരഹിത സൂര്യസ്ഫുട ക്രിയയ്ക്ക് ആവശ്യമായ യോഗ്യാദി വാക്യങ്ങളും ഉണ്ടായിട്ടുള്ളത് എങ്ങനെയെന്ന് കാണിച്ചു തരികയും ചെയ്തിട്ടുണ്ട്.
അനന്തരം ഈ ജ്യാക്കളുപയോഗിച്ച്, മധ്യമഗ്രഹങ്ങളെ സ്ഫുടഗ്രഹങ്ങളാക്കി മാറ്റുന്നതിന് സഹായകമായ മന്ദകര്ണത്തെയും ശീഘ്രകര്ണത്തെയും വരുത്താനുള്ള ഉപായങ്ങളെ ഉപദേശിക്കുന്നു. മന്ദവൃത്തമനുസരിച്ചുള്ള ഗ്രഹസ്ഥാനത്തിനും ഭൂമധ്യത്തിനും തമ്മിലുള്ള അകലമാണ് മന്ദകര്ണം. ശീഘ്രവൃത്തമനുസരിച്ചുള്ള ഗ്രഹസ്ഥാനത്തിനും ഭൂമധ്യത്തിനും തമ്മിലുള്ള അകലമാണ് ശീഘ്രകര്ണം.
കര്ണാനയനത്തിനു ശേഷം, മൗഢ്യക്രിയയ്ക്ക് ആവശ്യമായ പരമവിക്ഷേപ കലകളെയും, സൂര്യചന്ദ്രന്മാരുടെയും ഭൂമിയുടെയും ബിംബവ്യാസയോജനകളെയും പ്രദര്ശിപ്പിച്ചുകൊണ്ട് സപ്തമാധ്യായം സമാപിച്ചിരിക്കുന്നു. സൂര്യബിംബത്തിനും ചന്ദ്രാദിബിംബങ്ങള്ക്കും ദക്ഷിണോത്തരമായി പരമാവധി വരാവുന്ന അകലമത്ര പരമവിക്ഷേപം. പകല് സൂര്യന്റെയും, രാത്രിയില് ചന്ദ്രന്റെയും ഛായയെ ആസ്പദമാക്കി സമയനിര്ണയം ചെയ്യുന്നതിനും, വിഷുവദ്വൃത്ത, ക്രാന്തിവൃത്തങ്ങളുടെയും അക്ഷാംശ, രേഖാംശങ്ങളുടെയും മറ്റും അടിസ്ഥാനത്തില് ഓരോ ദേശത്തിലും വ്യത്യസ്തമായി വരുന്ന രാശി പ്രമാണങ്ങള്, ദിനരാത്രപ്രമാണങ്ങള് മുതലായവ അറിയുന്നതിനും, ഗ്രഹങ്ങളുടെ മൗഢ്യാരംഭാവസാനകാലങ്ങളെ നിശ്ചയിക്കുന്നതിനും, സൂര്യചന്ദ്രന്മാരുടെ ഗ്രഹണകാലം സൂക്ഷ്മപ്പെടുത്തുന്നതിനും മറ്റുമായി കരണഗ്രന്ഥങ്ങളില് സ്വീകരിക്കപ്പെട്ടിട്ടുള്ള അക്ഷജ്യാവ്, ലംബജ്യാവ്, ക്രാന്തിജ്യാവ്, ദ്യുജ്യാവ്, കുജ്യാവ്, ചരജ്യാവ്, പ്രാണകാലാന്തരജ്യാവ് മുതലായ സുപ്രധാനങ്ങളും സങ്കീര്ണങ്ങളുമായ ബഹുവിധ ജ്യാക്കളുടെ നിര്മിതിയാണ് അഷ്ടമാധ്യായത്തിലെ പ്രതിപാദ്യം.
രാശിപ്രമാണങ്ങള് വരുത്താനുള്ള പദ്ധതിയും ഒരു നക്ഷത്രം ഉച്ചയാകുമ്പോള് ആരാശിയില് ചെന്ന നാഴികവിനാഴികകള് ഗണിക്കാനുള്ള ഉപായങ്ങളും ആണ് നവമാധ്യായത്തിലെ ഉള്ളടക്കം. മേടം മുതല് മീനം വരെയുള്ള 12 രാശികളുടെ പ്രമാണങ്ങള് (അളവുകള്) സ്ഥലഭേദമനുസരിച്ച് വ്യത്യസ്തങ്ങളായി വരും. ക്രാന്തിവൃത്തം (സൂര്യന്റെ ഭ്രമണവൃത്തം) വിഷുവദ്വൃത്തത്തില് നിന്നും ഉത്തര ദിക്കിലേക്കും ദക്ഷിണ ദിക്കിലേക്കും ചരിഞ്ഞു നില്ക്കുന്നതുകൊണ്ടും, ഭൂമധ്യരേഖയ്ക്കു തെക്കും വടക്കുമായി സ്ഥിതിചെയ്യുന്ന എല്ലാ ദേശങ്ങളിലെയും അക്ഷാംശങ്ങള് (ഹമശേൗേറല) വിഭിന്നങ്ങളായതുകൊണ്ടും ആണ് സ്ഥലഭേദമനുസരിച്ച് രാശിമാനങ്ങള്ക്കും വ്യത്യാസം സംഭവിച്ചിട്ടുള്ളത്.
360 ഭാഗ (ഡിഗ്രി) അടങ്ങിയ രാശിചക്രത്തില് 12 രാശികളും തുല്യങ്ങളാണ്. ഓരോ രാശിയിലും 30 ഭാഗ തന്നെ അടങ്ങിയിരിക്കുന്നു. എന്നാല് രാത്രിയും പകലും ഉള്പ്പെടെ മൊത്തം 60 നാഴികക്കണക്കിലുള്ള ഘടികാമണ്ഡലത്തില് എല്ലാ രാശികളുടെയും അളവ് അഞ്ച് നാഴികയല്ല. ചില രാശികള് അഞ്ച് നാഴികയില് കുറഞ്ഞിരിക്കും; ചിലതു കൂടിയും. എല്ലാ രാശികളും കൂടി കൂട്ടിയാല് 60 നാഴിക ഒത്തിരിക്കുകയും ചെയ്യും. ഈ രാശിമാനങ്ങള് നാഴികയും വിനാഴികയുമായിട്ടാണ് കിട്ടുന്നത്. ഇപ്രകാരമുള്ള രാശിമാനങ്ങള് കണ്ടുപിടിക്കുന്നതെങ്ങനെയെന്നാണ് ഇവിടെ പ്രതിപാദിക്കുന്നത്.
ഏതു രാശിയുടെ പ്രമാണമാണോ വരുത്തേണ്ടത്, ആ രാശിയുടെ അന്ത്യഭാഗയ്ക്ക് കാലലഗ്നത്തെ വരുത്തണം. രാശികളില് അയനം സംസ്കരിച്ച് അതതു ദേശത്തേക്കുള്ള ചരജ്യാവും പ്രാണകാലാന്തര ജ്യാവും വരുത്തി ആ രാശികളില് തന്നെ സംസ്കരിച്ചാല് രാശ്യന്തകാലലഗ്നം വരും. അതായത് ആ രാശിയുടെ അവസാനഭാഗയ്ക്കുള്ള ലഗ്നസ്ഫുടം സിദ്ധിക്കും.
അഭീഷ്ടരാശിയുടെ അന്ത്യകാല ലഗ്നസ്ഫുടത്തില് നിന്നും ആ രാശിയുടെ മുമ്പിലത്തെ രാശിയുടെ അന്ത്യകാല ലഗ്നസ്ഫുടത്തെ കുറച്ചാല് കിട്ടുന്ന തീയതികളെ 10ല് ഗുണിച്ചാല് അഭീഷ്ടരാശി പ്രമാണവിനാഴികകള് കിട്ടും. ഈ വിനാഴികകള് ആ രാശിയുടെ ഹാരകമായിരിക്കുകയും ചെയ്യും. വിനാഴികയെ 60 കൊണ്ടു ഹരിച്ചാല് ഫലം നാഴികയായും, ശിഷ്ടം വിനാഴികയായും വരുന്നതാണ്. ഈ രാശിപ്രമാണക്രിയയില് അയനാംശങ്ങള്, ചരജ്യാക്കള്, പ്രാണകാലാന്തരജ്യാക്കള് ഇവയാണ് മുഖ്യഘടകങ്ങള്. പ്രസ്തുത ക്രിയാപദ്ധതിയനുസരിച്ച് ഗണിച്ചു ചേര്ത്തിട്ടുള്ളവയാണ് വലിയ പഞ്ചാംഗങ്ങളിലും മറ്റും കാണപ്പെടുന്ന വിവിധ ദേശങ്ങളിലെ രാശിമാനങ്ങള്.
അശ്വതി മുതല് രേവതി വരെയുള്ള 27 നക്ഷത്രങ്ങളില് ഏതെങ്കിലും ഒരു നക്ഷത്രം ഉച്ചയാകുമ്പോള് (ആകാശമധ്യത്തെ പ്രാപിക്കുമ്പോള്) ലഗ്നം ഏതു രാശിയാണെന്നും, ആ രാശിയില് എത്ര നാഴിക കഴിഞ്ഞിട്ടുണ്ടെന്നും കണ്ടുപിടിക്കാനുള്ള വഴിയാണ് ഈ അധ്യായത്തിലെ മറ്റൊരു പ്രധാന വിഷയം. ഈ കിയയില് മധ്യാഹ്നകാലലഗ്നമാണ് ലക്ഷ്യം. അവിടെ എത്തിച്ചേരുന്നതിനു വേണ്ടിത്തന്നെയാണ്, ആദ്യമായി "തടജ്ഞ' (16) ഇത്യാദി നക്ഷത്രസ്ഫുടങ്ങളെയും, "നമ്യ' (10) ഇത്യാദി നക്ഷത്രവിക്ഷേപങ്ങളെയും അവതരിപ്പിച്ചിരിക്കുന്നത്. 360 അംശങ്ങള് (ഡിഗ്രികള്) അടങ്ങിയ രാശിചക്രത്തിലെ ഘടകങ്ങളായ 27 നക്ഷത്രങ്ങളുടെയും നിയതസ്ഥാനങ്ങളെയാണ് നക്ഷത്രസ്ഫുടാംശങ്ങള് കാണിക്കുന്നത്. അപക്രമമണ്ഡലത്തില് നിന്നു തെക്കോട്ടും വടക്കോട്ടും ഉള്ള മാറ്റത്തെയാണ് നക്ഷത്രങ്ങളുടെ വിക്ഷേപാംശങ്ങള് കുറിക്കുന്നത്. ചില നക്ഷത്രങ്ങള് അപക്രമമണ്ഡലത്തിന്റെ (ക്രാന്തിവൃത്തത്തിന്റെ) തെക്കുഭാഗത്തായും ചിലതു വടക്കുഭാഗത്തായും ആണ് സ്ഥിതി ചെയ്യുന്നത്. എത്ര ഡിഗ്രി മാറി നില്ക്കുന്നു എന്ന് ഈ വിക്ഷേപാംശങ്ങളില് നിന്നു ഗ്രഹിക്കാം. പ്രസ്തുത നക്ഷത്രസ്ഫുടങ്ങളെയും നക്ഷത്ര വിക്ഷേപങ്ങളെയും അവലംബിച്ചുകൊണ്ട് അയനാംശം (ക്രാന്തിജ്യാവ്, പ്രാണകാലാന്തരജ്യാവ്, ദ്യുജ്യാവ്ക്രാന്തിജ്യാവിന്റെ കോടിജ്യാവ്) ഇവയുടെ സഹായത്തോടു കൂടി മധ്യാഹ്നകാല ലഗ്നം നിര്ണയിക്കാന് സാധിക്കും. അഭീഷ്ട നക്ഷത്രത്തിന്റെ മധ്യാഹ്ന കാലലഗ്നത്തില് നിന്നും ആസന്നരാശ്യന്തത്തിലേക്കുള്ള കാലലഗ്നത്തെ കുറച്ചാല് ശേഷിക്കുന്ന അംശങ്ങളില് നിന്നു ലഗ്നരാശിയില് ചെന്ന നാഴികവിനാഴികകളും ലഭിക്കുന്നതാണ്. ദശമാധ്യായത്തിലാകട്ടെ, "നക്ഷത്രങ്ങളുടെ സ്ഫുടാംശങ്ങളും വിക്ഷേപാംശങ്ങളും പല ആചാര്യന്മാരാല് പലവിധത്തില് പറയപ്പെട്ടിട്ടുള്ളതായി കാണുന്നതുകൊണ്ട് യന്ത്രാപകരണങ്ങളുടെയും മറ്റും സഹായത്താല് ലഭ്യമാകുന്ന, അവയുടെ രൂപങ്ങളും ഛായകളും മനസ്സിലാക്കി നിര്ണയിക്കേണ്ടതാകുന്നു, എന്ന ഗവേഷണപരമായ മുഖവുരയോടുകൂടി മധ്യാഹ്നകാല ലഗ്നത്തില് നിന്നും വായുകാലം (നതകാലം) വരുത്തി തദ്വാരാ നക്ഷത്രസ്ഫുടങ്ങളെ നിര്ണയിക്കാന് സാധിക്കുമെന്ന് ഗ്രന്ഥകാരന് സമര്ഥിച്ചിരിക്കുന്നു. കാലലഗ്നത്തില് മൂന്ന് രാശി കുറച്ചാല് വരുന്നത് വായുകാലം. കാലലഗ്നത്തിനും ആകാശമധ്യത്തിനും ഇടയ്ക്കുള്ള ഘടികാമണ്ഡലപ്രദേശമാണ് വായുകാലം. ഈ വായുകാലത്തെത്തന്നെ നതകാലമെന്നും പറയാവുന്നതാണ്.
"ഘടികാമണ്ഡലേ യത്ര സ്പൃഷ്ടം തന്നതമണ്ഡലം തത്പ്രദേശോ വായുകാലോ, നതകാലഃ സ ചോച്യതേ'
(ഘടികാമണ്ഡലത്തില് യാതൊരിടത്ത് ആ ഘടികാമണ്ഡലത്തിന്റെ തന്നെ നതഭാഗമണ്ഡലം സ്പര്ശിക്കുന്നുവോ ആ പ്രദേശത്തിന് വായുകാലം എന്നു നാമം. വായുകാലവും നതകാലവും ഒന്നു തന്നെയാണ്. കാലലഗ്നത്തില് നിന്ന് പിമ്പോട്ട് എത്ര രാശി കഴിഞ്ഞാണ് നക്ഷത്രം നില്ക്കുന്നതെന്ന് നതകാലത്തില് നിന്നു മനസ്സിലാക്കുവാന് സാധിക്കും). കാലക്രിയകളെ പ്രതിപാദിക്കുന്ന 9-ും, 10-ും അധ്യായങ്ങള് പരസ്പരം ബന്ധപ്പെട്ടവയാണ്. പത്താമധ്യായത്തോടുകൂടി ഗ്രന്ഥം അവസാനിക്കുകയും ചെയ്യുന്നു. ഗ്രന്ഥസമാപ്തിയെക്കുറിക്കുന്നവയാണ് പത്താമധ്യായത്തിന്റെ അവസാനത്തില് കാണപ്പെടുന്ന രണ്ടു പദ്യങ്ങള്. അവയില് ആദ്യത്തെ പദ്യം ഫലശ്രുതിയാണ്. കലിദിനഗണിതം മുതല് ഗ്രഹണഗണിതം വരെ അനുക്രമമായി ഗണിതക്രിയകളെ മാത്രം പറഞ്ഞുകൊണ്ടു പോകുന്ന കരണഗ്രന്ഥങ്ങളില് നിന്നു തുലോം വ്യത്യസ്തമാണ് ഈ കരണപദ്ധതി എന്നുള്ളതില് സംശയമില്ല. അതുകൊണ്ടാണ്, ഗ്രന്ഥകര്ത്താവ് സ്വഗ്രന്ഥത്തെ
"കിമപികരണപദ്ധത്യാഹ്വയം തന്ത്രരൂപം വ്യധിത ഗണിതമേതത്'
എന്ന് തന്ത്രഗ്രന്ഥങ്ങളില് ഉള്പ്പെടുത്തിക്കാണിച്ചിരിക്കുന്നത്. നിലവിലിരിക്കുന്ന ഗണിതക്രിയകള്ക്കു വേണ്ടി കരണപദ്ധതി പഠിക്കണമെന്നില്ല. പക്ഷേ ഈ ഗണിതക്രിയകളുടെ യുക്തിമാര്ഗങ്ങളറിയണമെങ്കില് കരണപദ്ധതി പഠിക്കേണ്ടത് അത്യാവശ്യവുമാണ്. ഓരോ ക്രിയയും പ്രത്യേകം എടുത്ത് യുക്തി കാണിക്കുന്ന രീതിയല്ല ഇതില് ഗ്രന്ഥകാരന് അവലംബിച്ചിരിക്കുന്നത്. ഉദാഹരണമായി കലിദിനക്രിയ തന്നെ എടുക്കാം:
"അബ്ദാന് കലേരര്ധ ജഗന്നൃപേന്ദ്രര് ഹത്വാ തതോലാസഗിരീഢ്യഹീനാത് ഈഷച്ഛമാപ്തം ഗതമാസവാക്യ ഗതാഹയുക്തം ദൃഗണോളച്ഛവാതാത്.'
കലിദിനം വരുത്താന്, പഞ്ചബോധത്തില് പറഞ്ഞിട്ടുള്ള കരണസൂത്രമാണ് ഇത്. കലിവര്ഷത്തെ അര്ധജഗന്നൃപേന്ദ്ര (21,03,890) കൊണ്ടു ഗുണിച്ച് ലാസഗിരീഢ്യ (12,373) കുറച്ച്, ഈഷച്ഛമ (5,760) കൊണ്ടു ഹരിച്ചാല് കിട്ടുന്ന ഫലത്തില് ഗതമാസങ്ങളും ഗതദിനങ്ങളും കൂട്ടിയാല് കലിദിനം കിട്ടും. ഇവിടെ അര്ധ ജഗന്നൃപേന്ദ്ര കൊണ്ട് ഗുണിക്കുകയും ലാസഗിരീഢ്യ കുറയ്ക്കുകയും, ഈഷച്ഛമകൊണ്ട് ഹരിക്കുകയും ചെയ്യുന്നതിന്റെ യുക്തി കരണപദ്ധതിയില് കാണപ്പെടുന്നില്ല. അത്തരം യുക്തിമാര്ഗങ്ങളുടെ വെളിച്ചത്തിലേക്ക് വിദ്യാര്ഥികളെ നയിക്കുന്ന മട്ടിലല്ല ഗ്രന്ഥത്തിന്െറ രചന. പക്ഷേ ഗവേഷണ തത്പരരായ വിദ്യാര്ഥികള്ക്ക് സോമയാജിയുടെ ഈ പദ്ധതി ഉപരിപഠനത്തിനും ഗവേഷണപരമായ പരിശ്രമങ്ങള്ക്കും സഹായകമായിരിക്കും. നോ: സോമയാജി, പുതുമന
(പ്രാഫ. എസ്.കെ. പെരിനാട്)