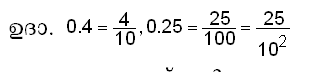This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

Current revision as of 11:15, 21 മാര്‍ച്ച് 2009

ദശാംശ സമ്പ്രദായം

Decimal system

'പത്ത്' ആധാരമാക്കിയുള്ള സംഖ്യാസമ്പ്രദായം. ദശാംശ സമ്പ്രദായമാണ് സംഖ്യാസമ്പ്രദായത്തില്‍ ഏറ്റവും സാര്‍വത്രികമായിട്ടുള്ളത്. എണ്ണുന്നതിനും സങ്കലനം, വ്യവകലനം, ഗുണനം, ഹരണം എന്നീ അങ്കഗണിത ക്രിയകള്‍ ചെയ്യുന്നതിനുമായി ഇന്ന് ലോകമെമ്പാടും അവലംബിച്ചുപോരുന്ന ഈ സമ്പ്രദായം സാധാരണക്കാര്‍ക്ക് സുപരിചിതമാണ്. വാണിജ്യം, വ്യവസായം, ശാസ്ത്രം തുടങ്ങി ജീവിതത്തിലെ മിക്ക വ്യാപാരങ്ങളിലും ദശാംശ സമ്പ്രദായം വളരെയേറെ പ്രാധാന്യമര്‍ഹിക്കുന്നു. സംസ്കൃത ഭാഷയില്‍ 'ദശം' എന്നാല്‍ പത്ത് എന്നാണര്‍ഥം. അതിനാലാണ് സംഖ്യകളുടെ ആധാരമായി പത്ത് സ്വീകരിച്ചിരിക്കുന്ന സമ്പ്രദായത്തിന് ദശാംശ സമ്പ്രദായം എന്ന പേര് വരാനിടയായത്.

ചരിത്ര പശ്ചാത്തലം. ദൈനംദിന ആവശ്യങ്ങള്‍ക്കായി സംഖ്യാ സമ്പ്രദായം വികസിപ്പിച്ച പല പ്രാചീന സമൂഹങ്ങളും തങ്ങള്‍ക്ക് അനുയോജ്യമായ ആധാര സംഖ്യകളും സ്വീകരിച്ചു പോന്നിരുന്നു. ഉദാഹരണമായി ഒന്ന്, രണ്ട്, രണ്ടിലധികം ഉള്ളതെല്ലാം അനേകം എന്ന് നാമകരണം ചെയ്തിരുന്ന പല സമ്പ്രദായങ്ങളും മധ്യ ആഫ്രിക്കന്‍ മേഖലയില്‍ പ്രചാരത്തിലുണ്ടായിരുന്നതായി കണ്ടെത്തിയിട്ടുണ്ട്. രണ്ട് ആധാരമായുള്ള സംഖ്യാ സമ്പ്രദായത്തിന്റെ തുടക്കമായി ഇത്തരം നാമകരണ രീതിയെ കണക്കാക്കാം. കൈവിരലുകള്‍ അടിസ്ഥാനമാക്കി അഞ്ച് ആധാരമായ സംഖ്യാ സമ്പ്രദായവും പല സമൂഹങ്ങളും ഉപയോഗപ്പെടുത്തിയിരുന്നു. മധ്യ അമേരിക്കയിലെ മായന്‍ സമൂഹം 20 അടിസ്ഥാനമാക്കിയുള്ള സംഖ്യാ സമ്പ്രദായം കൈകാര്യം ചെയ്തിരുന്നതായി കണ്ടെത്തിയിട്ടുണ്ട്. ഏകദേശം ബി.സി. 3000-ത്തില്‍ മെസപ്പൊട്ടേമിയയില്‍ 60 ആധാരമാക്കിയുള്ള സംഖ്യാ സമ്പ്രദായം വികസിപ്പിച്ചിരുന്നു. സമയം അളക്കുന്നതിനുള്ള ഏകകങ്ങളായി ഇപ്പോഴും നാം ഉപയോഗിക്കുന്ന മിനിറ്റ്, സെക്കന്‍ഡ് തുടങ്ങിയവ 60 അടിസ്ഥാനത്തിലുള്ളതാണ്. അതുപോലെ കോണ്‍ അളക്കുന്ന ഡിഗ്രിയും 60-ന്റെ അടിസ്ഥാനത്തിലുള്ള മിനിറ്റ്, സെക്കന്‍ഡ് എന്ന രീതിയിലാണ് വിഭജിച്ചിരിക്കുന്നത്. ഇവയെ 60 ആധാരമായ സംഖ്യാ സമ്പ്രദായത്തിന്റെ തുടര്‍ച്ചയായി കണക്കാക്കാം.

പത്ത് ആധാരമായുള്ള സംഖ്യാ സമ്പ്രദായം ഇന്ത്യയിലെ ഹാരപ്പന്‍ സംസ്കാരത്തിലും പ്രാചീന ഈജിപ്ഷ്യന്‍ സംസ്കാരത്തിലും പ്രചാരത്തിലിരുന്നതായി കണ്ടെത്തിയിട്ടുണ്ട്. ഏകദേശം ബി.സി. 3500-3000 കാലഘട്ടത്തില്‍ പ്രസ്തുത സംസ്കാരങ്ങള്‍ വികാസം പ്രാപിച്ചിരുന്നു എന്നാണ് കണക്കാക്കപ്പെടുന്നത്. സ്ഥാന വില അടിസ്ഥാനമാക്കി ഇന്നത്തെ നിലയില്‍ ദശാംശ സമ്പ്രദായം വികസിപ്പിച്ചെടുത്തത് ഇന്ത്യന്‍ ഗണിതശാസ്ത്രജ്ഞരാണ് എന്ന് അംഗീകരിക്കപ്പെട്ടിട്ടുണ്ട്.

പ്രാചീനകാലത്ത് ദശാംശ അക്കങ്ങളെ സൂചിപ്പിക്കുവാന്‍ പല തരത്തിലുള്ള ചിഹ്നങ്ങളും അക്ഷരങ്ങളും ഉപയോഗിച്ചിരുന്നു. ഈജിപ്തുകാരുടെ ഹൈറോഗ്ലിഫിക്സ് പദ്ധതി, സൈഫറിങ് പദ്ധതി, ബാബിലോണിയക്കാരുടെ ക്യൂനിഫോം സമ്പ്രദായം, ഇന്ത്യയിലെ കലിസംഖ്യ (പരല്പേര്), കടപയാദി സമ്പ്രദായം, പവഹസ്തലിഖിതങ്ങളിലെ അക്ഷരപല്ലി തുടങ്ങിയവയെല്ലാം ഇവയ്ക്ക് ഉദാഹരണങ്ങളാണ്.

പാശ്ചാത്യ രാജ്യങ്ങളില്‍ ദശാംശ സമ്പ്രദായം എത്തിയത് അറബികള്‍ വഴിയാണ്. അതിനാലാണ് ഭാരതീയ കണ്ടുപിടിത്തമായ ദശാംശ അക്കങ്ങളെ അറബിക് അക്കങ്ങള്‍ എന്നും പറയുന്നത്. പ്രാചീന ഭാരതീയ ഇതിഹാസങ്ങളില്‍ പത്തിന്റെ ഉയര്‍ന്ന ഘാതങ്ങള്‍ ആയി വരുന്ന വളരെ വലിയ സംഖ്യകള്‍ക്കുപോലും പ്രത്യേക പേരുകള്‍ ഉപയോഗിച്ചിരുന്നു. പത്ത്, നൂറ് (10²), ആയിരം (10³), എന്നിങ്ങനെ 10⁶² വരെ ഉള്ള സംഖ്യകളുടെ പേരുകള്‍ ഉപയോഗിച്ചിരുന്നു. ആര്യഭടീയ വ്യാഖ്യാനത്തില്‍ ഭാസ്കരാചാര്യര്‍ ദശാംശ ഗണിതം സവിസ്തരം പ്രതിപാദിച്ചിട്ടുണ്ട്.

ആധുനിക കാലത്ത് ദശാംശ അങ്കഗണിതത്തെക്കുറിച്ച് കൂടുതല്‍ വിവരങ്ങല്‍ നല്കിയത് ഡച്ച് ഗണിതശാസ്ത്രജ്ഞനായ സൈമണ്‍ സ്റ്റെവിന്‍ (1548-1620) ആണ്. സ്കോട്ടിഷ് ഗണിതശാസ്ത്രജ്ഞനായ ജോണ്‍ നേപ്പിയര്‍ (1550-1617) ഇന്നത്തെ ദശാംശ ബിന്ദുവിനു പകരം കോമ ഉപയോഗിച്ചു. ദശാംശചിഹ്നം ആദ്യമായി ഉപയോഗിച്ചത് സ്റ്റെവിന്‍ ആണ്. പക്ഷേ ഇന്നത്തെ രീതിയിലുളള ദശാംശബിന്ദു (.) ആദ്യമായി ഉപയോഗിച്ചത് 1617-ല്‍ ഇംഗ്ലീഷ് ഗണിതശാസ്ത്രജ്ഞനായ ഹെന്റി ബ്രിഗ്ഗ്സ് (1561-1639) ലോഗരിതത്തെക്കുറിച്ചുള്ള അദ്ദേഹത്തിന്റെ പഠനങ്ങളിലാണ്. ഇംഗ്ലീഷ് ഗണിതശാസ്ത്രജ്ഞനായ വില്യം ഓഗ്റ്റ്റെഡ് (1574-1660) ദശാംശഭിന്നത്തെപ്പറ്റി പഠനം നടത്തിയിട്ടുണ്ട്. ദശാംശ സമ്പ്രദായത്തെ കൂടുതല്‍ പ്രചരിപ്പിച്ചത് ഗണിതശാസ്ത്രജ്ഞനായ ഫിബൊനാച്ചിയാണ്.

സംഖ്യകളെ രേഖപ്പെടുത്തുന്നതിനുള്ള ചിഹ്നങ്ങളാണ് അക്കങ്ങള്‍ (digits). സ്ഥാനവില വ്യവസ്ഥയനുസരിച്ച് പത്ത് ചിഹ്നങ്ങളാണുള്ളത്. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 എന്നീ ചിഹ്നങ്ങളെ ദശാംശ അക്കങ്ങള്‍ എന്നു വിളിക്കുന്നു. ഒരു സംഖ്യയില്‍ ഒരക്കത്തിന്റെ വില നിര്‍ണയിക്കുന്നത് അതിന്റെ സ്ഥാനമനുസരിച്ചാണ്. വലത്തുനിന്ന് ഇടത്തോട്ടു പോകുന്തോറും, അക്കങ്ങളുടെ വില പത്തിന്റെ ഗുണിതങ്ങളാല്‍ വര്‍ധിച്ചുവരുന്നു. ഉദാഹരണമായി 25 എന്ന സംഖ്യയും 235 എന്ന സംഖ്യയും എടുക്കുക. 25 എന്നതില്‍ 5 എന്നത് ഒറ്റയുടെ സ്ഥാനത്തെ അക്കവും 2 എന്നത് പത്തിന്റെ സ്ഥാനത്തെ അക്കവുമാണ്. 235 എന്നതില്‍ 5 എന്നത് ഒറ്റയുടെ സ്ഥാനത്തും 3 എന്നത് പത്തിന്റെ സ്ഥാനത്തും 2 എന്നത് നൂറിന്റെ സ്ഥാനത്തും ഉള്ളവയാണ്. പൊതുവേ പറഞ്ഞാല്‍, സംഖ്യകളില്‍ വലത്തുനിന്ന് ഇടത്തോട്ടു പോകുന്തോറും ഒറ്റ, പത്ത്, നൂറ്, ആയിരം, പതിനായിരം എന്നിങ്ങനെയാണ് സ്ഥാനവില കണക്കാക്കുന്നത്. സംഖ്യകളില്‍, ശൂന്യസ്ഥലത്ത് പൂജ്യം കൊണ്ട് സ്ഥാനം കുറിക്കുന്നു. പൂജ്യത്തിന് സ്ഥാനക്രമമനുസരിച്ച് അതിന്റേതായ പ്രാധാന്യം ഉണ്ട്. ഒരു പൂര്‍ണസംഖ്യയുടെ ഒടുവില്‍ പൂജ്യം വന്നാല്‍ അതിന്റെ മൂല്യത്തെ ഇത് പത്തുമടങ്ങ് വര്‍ധിപ്പിക്കുന്നു. ഉദാഹരണത്തിന് 5-ന്റെ 10 മടങ്ങാണ് 50 എന്ന സംഖ്യ.

അതുപോലെ

56075 = 5x (10⁴) + 6x (10³) + 0x (10²) + 7x (10¹) + 5 എന്നാണ് അര്‍ഥം.

ദശാംശ അക്കങ്ങള്‍, സ്ഥാനവില വ്യവസ്ഥ ഇവ രണ്ടും കൂടിയുള്ള സംയോജനമാണ് ദശാംശ സമ്പ്രദായത്തിന്റെ ഉള്ളടക്കം.

ഒന്നില്‍ കുറവായ ഭിന്നസംഖ്യകളാണ് ദശാംശ ഭിന്നങ്ങള്‍. പത്തോ പത്തിന്റെ ഘാതങ്ങളോ (100, 1000, 10000 തുടങ്ങിയവ) ഛേദമായി വരുന്ന ഭിന്നമാണ് ദശാംശ ഭിന്നം.

ഏതു ധനവാസ്തവിക സംഖ്യയെയും താഴെപ്പറയുന്ന രൂപത്തില്‍ പ്രതിനിധാനം ചെയ്യാവുന്നതാണ്.

a_n(10ⁿ)+a_n-1 (10^n-1)+......+a, (10¹)+a₀+b₁ (10^-1)+b₂(10^-2) +...

ഇതില്‍ b₁, b₂...എന്നിവ അക്കങ്ങളാണ്. a_n(10ⁿ)+ a_n-1(10^n-1)+....+ a₀ എന്നത് പൂര്‍ണസംഖ്യാഭാഗവും b₁(10^-1)+b₂ (10^-2)എന്നത് ദശാംശ ഭിന്നഭാഗവും ആണ്.

പൂര്‍ണസംഖ്യയും ദശാംശ ഭിന്നവും ഉള്ള സംഖ്യകളെഴുതുമ്പോള്‍ a₀ന്റെയും b₁ന്റെയും ഇടയ്ക്ക് ഇടുന്ന ചിഹ്നമാണ് ദശാംശ ബിന്ദു (decimal point).

ഉദാ. 1.234 = 1+2 (10^-1) + 3 (10^-2) + 4 (10^-3). ഇവിടെ a₀ = 1 ഉം b₁ = 2 ഉം ആണ്. ദശാംശബിന്ദുവിന് വലതു ഭാഗത്തുള്ളവയാണ് സംഖ്യയിലെ ദശാംശഭിന്ന ഭാഗം.

1.234-ല്‍ ദശാംശഭിന്നം എന്നത് .234 ആണ്. ഇത് വായിക്കുന്നത് ഒന്ന് ദശാംശം രണ്ട് മൂന്ന് നാല് എന്നാണ്. ഇതില്‍ 2 എന്നത് പത്തിലൊന്ന് എന്ന സ്ഥാനത്തെയും 3 എന്നത് നൂറിലൊന്ന് എന്ന സ്ഥാനത്തെയും 4 എന്നത് ആയിരത്തിലൊന്ന് എന്ന സ്ഥാനത്തെയുമാണ് കുറിക്കുന്നത്.