This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഡി ബ്രോഗ്ളി തരംഗങ്ങള്‍
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(→ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍) |
(→ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍) |
||
| വരി 18: | വരി 18: | ||
ബൃഹത്തായ വസ്തുക്കള്‍ക്കും വളരെ ചെറിയ കണങ്ങള്‍ക്കും ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍ ഉണ്ടാകുമെങ്കിലും ഇലക്ട്രോണ്‍ പോലെയുള്ള അതിസൂക്ഷ്മ കണികകളുടെ ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യത്തിനു പ്രസക്തമായ മൂല്യമുണ്ടെന്നു കാണാം. ഉദാഹരണമായി 10<sup>-27</sup> ഗ്രാം പിണ്ഡമുള്ള ഒരു ഇലക്ട്രോണ്‍ 1 eV പൊട്ടന്‍ഷ്യല്‍ വ്യത്യാസത്തോടു കൂടിയ വിദ്യുത്മണ്ഡലത്തിലൂടെ സെ. മീ./സെ. പ്രവേഗത്തോടെ ചലിച്ചു തുടങ്ങിയാല്‍ | ബൃഹത്തായ വസ്തുക്കള്‍ക്കും വളരെ ചെറിയ കണങ്ങള്‍ക്കും ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍ ഉണ്ടാകുമെങ്കിലും ഇലക്ട്രോണ്‍ പോലെയുള്ള അതിസൂക്ഷ്മ കണികകളുടെ ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യത്തിനു പ്രസക്തമായ മൂല്യമുണ്ടെന്നു കാണാം. ഉദാഹരണമായി 10<sup>-27</sup> ഗ്രാം പിണ്ഡമുള്ള ഒരു ഇലക്ട്രോണ്‍ 1 eV പൊട്ടന്‍ഷ്യല്‍ വ്യത്യാസത്തോടു കൂടിയ വിദ്യുത്മണ്ഡലത്തിലൂടെ സെ. മീ./സെ. പ്രവേഗത്തോടെ ചലിച്ചു തുടങ്ങിയാല്‍ | ||
| + | |||
ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യം | ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യം | ||
<math>\lambda =\frac{h}{mv}</math> | <math>\lambda =\frac{h}{mv}</math> | ||
| - | =\frac{6.63\times10^-27}{10^-27\times6\time | + | <math>=\frac{6.63\times10^-27}{10^-27\times6\time |
10^27 =10^-7cm</math> | 10^27 =10^-7cm</math> | ||
ആയിരിക്കും. എക്സ് റേ-യുടെ തരംഗദൈര്‍ഘ്യത്തോട് ഏകദേശം തുല്യമായ 10-7 സെ. മീ. എന്നത് തീരെ നിസ്സാരമായ മൂല്യമല്ല; ഇതു കുപിടിക്കാന്‍ സാധിക്കുന്നതുമാണ്. സൈദ്ധാന്തികമായി ഡി ബ്രോഗ്ളി തരംഗങ്ങളെ കുപിടിക്കാന്‍ കഴിഞ്ഞതും ഇങ്ങനെയാണ്. | ആയിരിക്കും. എക്സ് റേ-യുടെ തരംഗദൈര്‍ഘ്യത്തോട് ഏകദേശം തുല്യമായ 10-7 സെ. മീ. എന്നത് തീരെ നിസ്സാരമായ മൂല്യമല്ല; ഇതു കുപിടിക്കാന്‍ സാധിക്കുന്നതുമാണ്. സൈദ്ധാന്തികമായി ഡി ബ്രോഗ്ളി തരംഗങ്ങളെ കുപിടിക്കാന്‍ കഴിഞ്ഞതും ഇങ്ങനെയാണ്. | ||
10:08, 15 ഡിസംബര്‍ 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍
De Broglie waves
ഭൗതികശാസ്ത്രത്തിലെ ക്വാണ്ടം സിദ്ധാന്തപ്രകാരം, ചലിക്കുന്ന ഏതൊരു വസ്തുവിനോടും അനുബന്ധിച്ചുള്ള ദ്രവ്യതരംഗങ്ങള്‍. 1924-ല്‍ ഫ്രഞ്ചു ഭൗതികശാസ്ത്രജ്ഞനായ ലൂയി ഡി ബ്രോഗ്ലിയാണ് ഈ തരംഗസിദ്ധാന്ത പരികല്പനയ്ക്കു തുടക്കമിട്ടത്. ഈ തരംഗങ്ങള്‍ ഇദ്ദേഹത്തിന്റെ പേരില്‍ത്തന്നെ പില്ക്കാലത്ത് അറിയപ്പെട്ടുതുടങ്ങി.
തരംഗ ഗതിക സിദ്ധാന്തമനുസരിച്ച് ചലനാവസ്ഥയിലുള്ള ഏതൊരു വസ്തുവിനോടും ബന്ധപ്പെട്ട് അതിന്റെ ദ്രവ്യ തരംഗവും ഉണ്ടായിരിക്കും. വസ്തുവിന്റെ വലുപ്പത്തിനു നിരപേക്ഷമാണ് ഈ തരംഗങ്ങള്‍.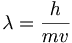
എന്ന സമവാക്യം വഴി ഡി ബ്രോഗ്ലി തരംഗങ്ങളുടെ തരംഗദൈര്‍ഘ്യം(wave length ) കണ്ടുപിടിക്കാം. ഇവിടെ
തരംഗദൈര്‍ഘ്യത്തേയും
λ അവ പുറപ്പെടുവിക്കുന്ന വസ്തുവിന്റെ ദ്രവ്യമാനത്തേയും
m പ്രവേഗത്തേയും പ്രതിനിധാനം ചെയ്യുന്നു.
v എന്നത് പ്ലാങ്ക് സ്ഥിരാങ്കം (Planck's constant) ആണ്;
h=6.63×10-27എര്‍ഗ്. സെക്കന്‍ഡ്.
ഹാര്യമായ h-ന്റെ മൂല്യം വളരെ ചെറുതായതിനാല്‍ സാധാരണ വസ്തുക്കളെ സംബന്ധിച്ച് ഇത്തരം ദൈര്‍ഘ്യങ്ങളും വളരെ ചെറുതായിരിക്കും. ഇത്രയും അതിസൂക്ഷ്മമായ തരംഗങ്ങളെ ഇന്ദ്രിയങ്ങള്‍ വഴി തിരിച്ചറിയുവാന്‍ നമുക്കു കഴിയുന്നില്ല. സൂക്ഷ്മോപകരണങ്ങള്‍ക്കുപോലും അളക്കാന്‍ വയ്യാത്തത്ര നിസ്സാരമാണവ.
ബൃഹത്തായ വസ്തുക്കള്‍ക്കും വളരെ ചെറിയ കണങ്ങള്‍ക്കും ഡി ബ്രോഗ്ലി തരംഗങ്ങള്‍ ഉണ്ടാകുമെങ്കിലും ഇലക്ട്രോണ്‍ പോലെയുള്ള അതിസൂക്ഷ്മ കണികകളുടെ ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യത്തിനു പ്രസക്തമായ മൂല്യമുണ്ടെന്നു കാണാം. ഉദാഹരണമായി 10-27 ഗ്രാം പിണ്ഡമുള്ള ഒരു ഇലക്ട്രോണ്‍ 1 eV പൊട്ടന്‍ഷ്യല്‍ വ്യത്യാസത്തോടു കൂടിയ വിദ്യുത്മണ്ഡലത്തിലൂടെ സെ. മീ./സെ. പ്രവേഗത്തോടെ ചലിച്ചു തുടങ്ങിയാല്‍
ഡി ബ്രോഗ്ലി തരംഗദൈര്‍ഘ്യം
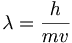
parse ചെയ്യുവാന്‍ പരാജയപ്പെട്ടു (Missing texvc executable; please see math/README to configure.): =\frac{6.63\times10^-27}{10^-27\times6\time 10^27 =10^-7cm
ആയിരിക്കും. എക്സ് റേ-യുടെ തരംഗദൈര്‍ഘ്യത്തോട് ഏകദേശം തുല്യമായ 10-7 സെ. മീ. എന്നത് തീരെ നിസ്സാരമായ മൂല്യമല്ല; ഇതു കുപിടിക്കാന്‍ സാധിക്കുന്നതുമാണ്. സൈദ്ധാന്തികമായി ഡി ബ്രോഗ്ളി തരംഗങ്ങളെ കുപിടിക്കാന്‍ കഴിഞ്ഞതും ഇങ്ങനെയാണ്.
