This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ചതുര്ഭുജം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(പുതിയ താള്: ==ചതുര്ഭുജം== നാലു നേര്രേഖകള് വശങ്ങളായുള്ള സമതല ചിത്രം. വശങ...) |
(→ചതുര്ഭുജം) |
||
| വരി 1: | വരി 1: | ||
==ചതുര്ഭുജം== | ==ചതുര്ഭുജം== | ||
| - | നാലു നേര്രേഖകള് വശങ്ങളായുള്ള സമതല ചിത്രം. വശങ്ങള് സന്ധിക്കുന്ന ബിന്ദുക്കളാണ് ചതുര്ഭുജത്തിന്റെ ശീര്ഷങ്ങള് (vertices). എതിര് ശീര്ഷങ്ങളെ യോജിപ്പിക്കുന്ന രേഖയെ വികര്ണം (diagonal) എന്നുപറയുന്നു. ചതുര്ഭുജത്തിന് പല രൂപങ്ങളുണ്ട്. സമചതുരം (square), ദീര്ഘചതുരം (rectangle), സമാന്തര ചതുര്ഭുജം (parallelogram), സമചതുര്ഭുജം (rhombus) | + | നാലു നേര്രേഖകള് വശങ്ങളായുള്ള സമതല ചിത്രം. വശങ്ങള് സന്ധിക്കുന്ന ബിന്ദുക്കളാണ് ചതുര്ഭുജത്തിന്റെ ശീര്ഷങ്ങള് (vertices). എതിര് ശീര്ഷങ്ങളെ യോജിപ്പിക്കുന്ന രേഖയെ വികര്ണം (diagonal) എന്നുപറയുന്നു. ചതുര്ഭുജത്തിന് പല രൂപങ്ങളുണ്ട്. സമചതുരം (square), ദീര്ഘചതുരം (rectangle), സമാന്തര ചതുര്ഭുജം (parallelogram), സമചതുര്ഭുജം (rhombus), ലംബകം (trapedium) ഇവയാണ് വ്യത്യസ്ത രൂപങ്ങള്. |
| - | , ലംബകം (trapedium) ഇവയാണ് വ്യത്യസ്ത രൂപങ്ങള്. | + | |
| - | 1. സമചതുരം. വശങ്ങള് തുല്യവും കോണുകള് 90<sup>o</sup> വീതവുമുള്ള ചതുര്ഭുജം. | + | 1.'''സമചതുരം.''' വശങ്ങള് തുല്യവും കോണുകള് 90<sup>o</sup> വീതവുമുള്ള ചതുര്ഭുജം. |
| - | 2. ദീര്ഘചതുരം. നാലുകോണുകളും 90<sup>o</sup> വീതമുള്ള ചതുര്ഭുജം. | + | 2.'''ദീര്ഘചതുരം.''' നാലുകോണുകളും 90<sup>o</sup> വീതമുള്ള ചതുര്ഭുജം. |
| - | 3.സമാന്തരചതുര്ഭുജം. രണ്ടുജോടി സമാന്തര വശങ്ങളുള്ളത്. | + | 3.'''സമാന്തരചതുര്ഭുജം.''' രണ്ടുജോടി സമാന്തര വശങ്ങളുള്ളത്. |
| - | 4.സമചതുര്ഭുജം. നാലുവശങ്ങളും തുല്യമായത്. | + | 4.'''സമചതുര്ഭുജം.''' നാലുവശങ്ങളും തുല്യമായത്. |
| - | 5.ലംബകം. രണ്ടു വശങ്ങള് സമാന്തരമായത്. | + | 5.'''ലംബകം.''' രണ്ടു വശങ്ങള് സമാന്തരമായത്. |
| - | + | ||
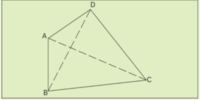
| - | സമതലത്തിലെ നാലു നേര്രേഖകളും അവ രണ്ടു വീതം തുടര്ച്ചയായി സന്ധിക്കുന്ന നാലു ബിന്ദുക്കളും ചേര്ന്നതാണ് സാധാരണ ചതുര്ഭുജം (simple quadrilateral). ചതുര്ഭുജം ABCD-യില് A, B, C, D ഇവ ശീര്ഷങ്ങള്. | + | [[ചിത്രം:Vol 10 Scre640.png|200px]] |
| + | |||
| + | സമതലത്തിലെ നാലു നേര്രേഖകളും അവ രണ്ടു വീതം തുടര്ച്ചയായി സന്ധിക്കുന്ന നാലു ബിന്ദുക്കളും ചേര്ന്നതാണ് സാധാരണ ചതുര്ഭുജം (simple quadrilateral). ചതുര്ഭുജം ABCD-യില് A, B, C, D ഇവ ശീര്ഷങ്ങള്. [[ചിത്രം:Vol 10 Pg640 scr03.png]] ഇവ വികര്ണങ്ങള്. [[ചിത്രം:Vol 10 pg 640 Scre04.png]] | ||
ചതുര്ഭുജത്തിലെ നാലു ശീര്ഷങ്ങളും ഒരു വൃത്തപരിധിയിലായാല്, അതിനെ ചക്രീയ ചതുര്ഭുജം (cyclic quadrilateral) എന്നു പറയുന്നു. ടോളമിയുടെ സിദ്ധാന്തമനുസരിച്ച് ഒരു ചക്രീയ ചതുര്ഭുജത്തിലെ രണ്ടുജോടി എതിര്വശങ്ങളുടെ ഗുണനഫലങ്ങളുടെ തുക വികര്ണങ്ങളുടെ ഗുണനഫലത്തിനു തുല്യമാണ്. ഒരു ചക്രീയ ചതുര്ഭുജത്തിന്റെ വശങ്ങള് a, b, c, d bpw 2S = a + | ചതുര്ഭുജത്തിലെ നാലു ശീര്ഷങ്ങളും ഒരു വൃത്തപരിധിയിലായാല്, അതിനെ ചക്രീയ ചതുര്ഭുജം (cyclic quadrilateral) എന്നു പറയുന്നു. ടോളമിയുടെ സിദ്ധാന്തമനുസരിച്ച് ഒരു ചക്രീയ ചതുര്ഭുജത്തിലെ രണ്ടുജോടി എതിര്വശങ്ങളുടെ ഗുണനഫലങ്ങളുടെ തുക വികര്ണങ്ങളുടെ ഗുണനഫലത്തിനു തുല്യമാണ്. ഒരു ചക്രീയ ചതുര്ഭുജത്തിന്റെ വശങ്ങള് a, b, c, d bpw 2S = a + | ||
b + c + d യും ആയാല് അതിന്റെ വിസ്തീര്ണം | b + c + d യും ആയാല് അതിന്റെ വിസ്തീര്ണം | ||
| - | + | [[ചിത്രം:Vol10 pg 640 scre02.png]] | |
എ.ഡി. 7-ാം ശ.-ത്തില് ജീവിച്ചിരുന്ന ഭാരതീയ ഗണിതജ്ഞനായ ബ്രഹ്മഗുപ്തന്റെ കൃതിയില് ഈ പ്രമേയത്തെക്കുറിച്ചുള്ള പ്രസ്താവമുണ്ട്. | എ.ഡി. 7-ാം ശ.-ത്തില് ജീവിച്ചിരുന്ന ഭാരതീയ ഗണിതജ്ഞനായ ബ്രഹ്മഗുപ്തന്റെ കൃതിയില് ഈ പ്രമേയത്തെക്കുറിച്ചുള്ള പ്രസ്താവമുണ്ട്. | ||
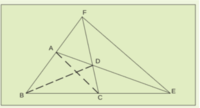
സമതലത്തിലുള്ള നാലു നേര്രേഖകളും അവയുടെ ആറു സംഗമബിന്ദുക്കളും ചേര്ന്ന രൂപമാണ് പൂര്ണ ചതുര്ഭുജം (complete quadrilateral). ഇതിന് മൂന്നു വികര്ണങ്ങളുണ്ട്. | സമതലത്തിലുള്ള നാലു നേര്രേഖകളും അവയുടെ ആറു സംഗമബിന്ദുക്കളും ചേര്ന്ന രൂപമാണ് പൂര്ണ ചതുര്ഭുജം (complete quadrilateral). ഇതിന് മൂന്നു വികര്ണങ്ങളുണ്ട്. | ||
| + | |||
| + | [[ചിത്രം:Vol 10 pg 640 Scre05.png|200px]] | ||
വികര്ണങ്ങള് വശങ്ങളായുള്ള ത്രികോണത്തിനെ വികര്ണ രേഖാത്രികോണം (diagonal line triangle) എന്നു പറയുന്നു. ക്ഷേത്ര ഗണിതപരമായി പല സവിശേഷതകളും പൂര്ണ ചതുര്ഭുജത്തിന്റെ വികര്ണ രേഖകള്ക്കുണ്ട്. | വികര്ണങ്ങള് വശങ്ങളായുള്ള ത്രികോണത്തിനെ വികര്ണ രേഖാത്രികോണം (diagonal line triangle) എന്നു പറയുന്നു. ക്ഷേത്ര ഗണിതപരമായി പല സവിശേഷതകളും പൂര്ണ ചതുര്ഭുജത്തിന്റെ വികര്ണ രേഖകള്ക്കുണ്ട്. | ||
(പ്രൊഫ. കെ. ജയചന്ദ്രന്) | (പ്രൊഫ. കെ. ജയചന്ദ്രന്) | ||
15:39, 13 ജനുവരി 2016-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ചതുര്ഭുജം
നാലു നേര്രേഖകള് വശങ്ങളായുള്ള സമതല ചിത്രം. വശങ്ങള് സന്ധിക്കുന്ന ബിന്ദുക്കളാണ് ചതുര്ഭുജത്തിന്റെ ശീര്ഷങ്ങള് (vertices). എതിര് ശീര്ഷങ്ങളെ യോജിപ്പിക്കുന്ന രേഖയെ വികര്ണം (diagonal) എന്നുപറയുന്നു. ചതുര്ഭുജത്തിന് പല രൂപങ്ങളുണ്ട്. സമചതുരം (square), ദീര്ഘചതുരം (rectangle), സമാന്തര ചതുര്ഭുജം (parallelogram), സമചതുര്ഭുജം (rhombus), ലംബകം (trapedium) ഇവയാണ് വ്യത്യസ്ത രൂപങ്ങള്.
1.സമചതുരം. വശങ്ങള് തുല്യവും കോണുകള് 90o വീതവുമുള്ള ചതുര്ഭുജം.
2.ദീര്ഘചതുരം. നാലുകോണുകളും 90o വീതമുള്ള ചതുര്ഭുജം.
3.സമാന്തരചതുര്ഭുജം. രണ്ടുജോടി സമാന്തര വശങ്ങളുള്ളത്.
4.സമചതുര്ഭുജം. നാലുവശങ്ങളും തുല്യമായത്.
5.ലംബകം. രണ്ടു വശങ്ങള് സമാന്തരമായത്.
സമതലത്തിലെ നാലു നേര്രേഖകളും അവ രണ്ടു വീതം തുടര്ച്ചയായി സന്ധിക്കുന്ന നാലു ബിന്ദുക്കളും ചേര്ന്നതാണ് സാധാരണ ചതുര്ഭുജം (simple quadrilateral). ചതുര്ഭുജം ABCD-യില് A, B, C, D ഇവ ശീര്ഷങ്ങള്. ![]() ഇവ വികര്ണങ്ങള്.
ഇവ വികര്ണങ്ങള്. ![]()
ചതുര്ഭുജത്തിലെ നാലു ശീര്ഷങ്ങളും ഒരു വൃത്തപരിധിയിലായാല്, അതിനെ ചക്രീയ ചതുര്ഭുജം (cyclic quadrilateral) എന്നു പറയുന്നു. ടോളമിയുടെ സിദ്ധാന്തമനുസരിച്ച് ഒരു ചക്രീയ ചതുര്ഭുജത്തിലെ രണ്ടുജോടി എതിര്വശങ്ങളുടെ ഗുണനഫലങ്ങളുടെ തുക വികര്ണങ്ങളുടെ ഗുണനഫലത്തിനു തുല്യമാണ്. ഒരു ചക്രീയ ചതുര്ഭുജത്തിന്റെ വശങ്ങള് a, b, c, d bpw 2S = a + b + c + d യും ആയാല് അതിന്റെ വിസ്തീര്ണം
എ.ഡി. 7-ാം ശ.-ത്തില് ജീവിച്ചിരുന്ന ഭാരതീയ ഗണിതജ്ഞനായ ബ്രഹ്മഗുപ്തന്റെ കൃതിയില് ഈ പ്രമേയത്തെക്കുറിച്ചുള്ള പ്രസ്താവമുണ്ട്.
സമതലത്തിലുള്ള നാലു നേര്രേഖകളും അവയുടെ ആറു സംഗമബിന്ദുക്കളും ചേര്ന്ന രൂപമാണ് പൂര്ണ ചതുര്ഭുജം (complete quadrilateral). ഇതിന് മൂന്നു വികര്ണങ്ങളുണ്ട്.
വികര്ണങ്ങള് വശങ്ങളായുള്ള ത്രികോണത്തിനെ വികര്ണ രേഖാത്രികോണം (diagonal line triangle) എന്നു പറയുന്നു. ക്ഷേത്ര ഗണിതപരമായി പല സവിശേഷതകളും പൂര്ണ ചതുര്ഭുജത്തിന്റെ വികര്ണ രേഖകള്ക്കുണ്ട്.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്)