This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോണം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Angle) |
Mksol (സംവാദം | സംഭാവനകള്) (→Angle) |
||
| വരി 4: | വരി 4: | ||
== Angle == | == Angle == | ||
| - | [[ചിത്രം:Vol9_17_cone2.jpg|thumb|]] | + | [[ചിത്രം:Vol9_17_cone2.jpg|thumb|കോണം]] |
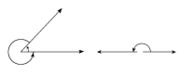
സമതല ജ്യാമിതിയില് ഒരു ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്വരകളുടെ ജോടി. രേഖകളെ കോണത്തിന്റെ വശങ്ങളെന്നും ബിന്ദുവിനെ ശീര്ഷം (vertex) എന്നും പറയുന്നു. a,b എന്നിവ O എന്ന ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്രേഖകളാണെങ്കില് ഇവ ഉള്ക്കൊള്ളുന്ന കോണം (a.b) എന്നുരേഖപ്പെടുത്താം. (a,b) -ഉം (b,a) -ഉം വ്യത്യസ്ത കോണങ്ങളാണ്. ചിത്രത്തില് അവയെ ക്രമത്തില് എന്നിവകൊണ്ട് സൂചിപ്പിച്ചിരിക്കുന്നു. ഈ സൂചനയനുസരിച്ചും കോണം നിര്വചിക്കപ്പെടാറുണ്ട്. Oa, Ob എന്നീ രേഖകളുടെ സമതലത്തില് O എന്ന ബിന്ദുവിനെ ആധാരമാക്കി b യിലെത്താന് a യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണമാണ് (a,b) എന്ന കോണം; അതുപോലെ a യിലെത്താന് b യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണം (b.a). ഈ പരിമാണങ്ങളെ ക്രമത്തില് എന്നിങ്ങനെ ഇവിടെ കണക്കാക്കിയിരിക്കുന്നു. ശീര്ഷത്തിലൂടെ കടന്നുപോകുന്ന ഒരു നേര്വരയുടെ ഒരു ഭാഗം a എന്നാണെങ്കില് മറുവശം 'a' എന്നുകണക്കാക്കപ്പെടുന്നു; ഈ രണ്ടുവശങ്ങളുടെ ജോടി സൂചിപ്പിക്കുന്ന കോണത്തെ (a,-a) എന്നും. കോണം ഡിഗ്രിയായും റേഡിയന് ആയും അളക്കാറുണ്ട്. ഡിഗ്രി 'º' എന്നും റേഡിയന് 'c' എന്നും അടയാളപ്പെടുത്തുന്നു. ശീര്ഷത്തിനു ചുറ്റുമുള്ള കോണം 360 ഡിഗ്രിയായി കണക്കാക്കുന്നതുകൊണ്ട്, (a,a) പൂജ്യമോ 3600 യോ ആകാം; (a,-a) എന്നത് 180º. ശീര്ഷത്തിന്റെ ചുറ്റുമുള്ള കോണം റേഡിയന് ആയി കണക്കാക്കുമ്പോള് (a,a) പൂജ്യം റേഡിയനോ റേഡിയനോ ആകുന്നു; (a,-a) റേഡിയനും. അതായത് 360º ക്കു തുല്യമാണ് റേഡിയന്; x റേഡിയന് ഡിഗ്രിക്കും, അഥവാ y ഡിഗ്രി റേഡിയനും തുല്യം. 90º-യില് കുറഞ്ഞ കോണത്തെ ന്യൂനകോണം (acute angle) എന്നും 90º-യില് കൂടിയതിനെ ബൃഹത്കോണം (obtuse angle) എന്നും 90º ആണെങ്കില് മട്ടകോണം (right angle) എന്നും വിളിക്കുന്നു. | സമതല ജ്യാമിതിയില് ഒരു ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്വരകളുടെ ജോടി. രേഖകളെ കോണത്തിന്റെ വശങ്ങളെന്നും ബിന്ദുവിനെ ശീര്ഷം (vertex) എന്നും പറയുന്നു. a,b എന്നിവ O എന്ന ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്രേഖകളാണെങ്കില് ഇവ ഉള്ക്കൊള്ളുന്ന കോണം (a.b) എന്നുരേഖപ്പെടുത്താം. (a,b) -ഉം (b,a) -ഉം വ്യത്യസ്ത കോണങ്ങളാണ്. ചിത്രത്തില് അവയെ ക്രമത്തില് എന്നിവകൊണ്ട് സൂചിപ്പിച്ചിരിക്കുന്നു. ഈ സൂചനയനുസരിച്ചും കോണം നിര്വചിക്കപ്പെടാറുണ്ട്. Oa, Ob എന്നീ രേഖകളുടെ സമതലത്തില് O എന്ന ബിന്ദുവിനെ ആധാരമാക്കി b യിലെത്താന് a യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണമാണ് (a,b) എന്ന കോണം; അതുപോലെ a യിലെത്താന് b യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണം (b.a). ഈ പരിമാണങ്ങളെ ക്രമത്തില് എന്നിങ്ങനെ ഇവിടെ കണക്കാക്കിയിരിക്കുന്നു. ശീര്ഷത്തിലൂടെ കടന്നുപോകുന്ന ഒരു നേര്വരയുടെ ഒരു ഭാഗം a എന്നാണെങ്കില് മറുവശം 'a' എന്നുകണക്കാക്കപ്പെടുന്നു; ഈ രണ്ടുവശങ്ങളുടെ ജോടി സൂചിപ്പിക്കുന്ന കോണത്തെ (a,-a) എന്നും. കോണം ഡിഗ്രിയായും റേഡിയന് ആയും അളക്കാറുണ്ട്. ഡിഗ്രി 'º' എന്നും റേഡിയന് 'c' എന്നും അടയാളപ്പെടുത്തുന്നു. ശീര്ഷത്തിനു ചുറ്റുമുള്ള കോണം 360 ഡിഗ്രിയായി കണക്കാക്കുന്നതുകൊണ്ട്, (a,a) പൂജ്യമോ 3600 യോ ആകാം; (a,-a) എന്നത് 180º. ശീര്ഷത്തിന്റെ ചുറ്റുമുള്ള കോണം റേഡിയന് ആയി കണക്കാക്കുമ്പോള് (a,a) പൂജ്യം റേഡിയനോ റേഡിയനോ ആകുന്നു; (a,-a) റേഡിയനും. അതായത് 360º ക്കു തുല്യമാണ് റേഡിയന്; x റേഡിയന് ഡിഗ്രിക്കും, അഥവാ y ഡിഗ്രി റേഡിയനും തുല്യം. 90º-യില് കുറഞ്ഞ കോണത്തെ ന്യൂനകോണം (acute angle) എന്നും 90º-യില് കൂടിയതിനെ ബൃഹത്കോണം (obtuse angle) എന്നും 90º ആണെങ്കില് മട്ടകോണം (right angle) എന്നും വിളിക്കുന്നു. | ||
06:41, 7 ജനുവരി 2015-നു നിലവിലുണ്ടായിരുന്ന രൂപം
കോണം
Angle
സമതല ജ്യാമിതിയില് ഒരു ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്വരകളുടെ ജോടി. രേഖകളെ കോണത്തിന്റെ വശങ്ങളെന്നും ബിന്ദുവിനെ ശീര്ഷം (vertex) എന്നും പറയുന്നു. a,b എന്നിവ O എന്ന ബിന്ദുവിലൂടെ കടന്നുപോകുന്ന നേര്രേഖകളാണെങ്കില് ഇവ ഉള്ക്കൊള്ളുന്ന കോണം (a.b) എന്നുരേഖപ്പെടുത്താം. (a,b) -ഉം (b,a) -ഉം വ്യത്യസ്ത കോണങ്ങളാണ്. ചിത്രത്തില് അവയെ ക്രമത്തില് എന്നിവകൊണ്ട് സൂചിപ്പിച്ചിരിക്കുന്നു. ഈ സൂചനയനുസരിച്ചും കോണം നിര്വചിക്കപ്പെടാറുണ്ട്. Oa, Ob എന്നീ രേഖകളുടെ സമതലത്തില് O എന്ന ബിന്ദുവിനെ ആധാരമാക്കി b യിലെത്താന് a യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണമാണ് (a,b) എന്ന കോണം; അതുപോലെ a യിലെത്താന് b യ്ക്കു തിരിയേണ്ടിവരുന്ന പരിമാണം (b.a). ഈ പരിമാണങ്ങളെ ക്രമത്തില് എന്നിങ്ങനെ ഇവിടെ കണക്കാക്കിയിരിക്കുന്നു. ശീര്ഷത്തിലൂടെ കടന്നുപോകുന്ന ഒരു നേര്വരയുടെ ഒരു ഭാഗം a എന്നാണെങ്കില് മറുവശം 'a' എന്നുകണക്കാക്കപ്പെടുന്നു; ഈ രണ്ടുവശങ്ങളുടെ ജോടി സൂചിപ്പിക്കുന്ന കോണത്തെ (a,-a) എന്നും. കോണം ഡിഗ്രിയായും റേഡിയന് ആയും അളക്കാറുണ്ട്. ഡിഗ്രി 'º' എന്നും റേഡിയന് 'c' എന്നും അടയാളപ്പെടുത്തുന്നു. ശീര്ഷത്തിനു ചുറ്റുമുള്ള കോണം 360 ഡിഗ്രിയായി കണക്കാക്കുന്നതുകൊണ്ട്, (a,a) പൂജ്യമോ 3600 യോ ആകാം; (a,-a) എന്നത് 180º. ശീര്ഷത്തിന്റെ ചുറ്റുമുള്ള കോണം റേഡിയന് ആയി കണക്കാക്കുമ്പോള് (a,a) പൂജ്യം റേഡിയനോ റേഡിയനോ ആകുന്നു; (a,-a) റേഡിയനും. അതായത് 360º ക്കു തുല്യമാണ് റേഡിയന്; x റേഡിയന് ഡിഗ്രിക്കും, അഥവാ y ഡിഗ്രി റേഡിയനും തുല്യം. 90º-യില് കുറഞ്ഞ കോണത്തെ ന്യൂനകോണം (acute angle) എന്നും 90º-യില് കൂടിയതിനെ ബൃഹത്കോണം (obtuse angle) എന്നും 90º ആണെങ്കില് മട്ടകോണം (right angle) എന്നും വിളിക്കുന്നു.