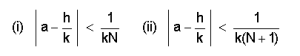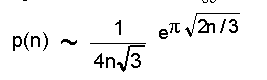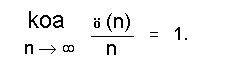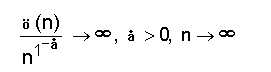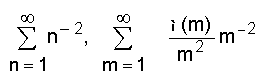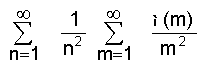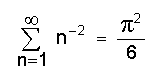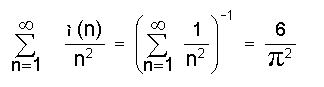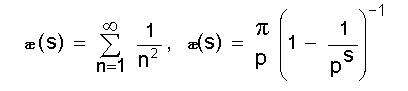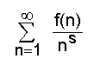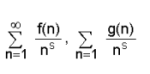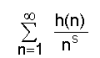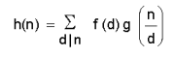This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

06:16, 20 മാര്‍ച്ച് 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം

അനലിറ്റിക് നമ്പര്‍ തിയറി

Analytic number theory

പൂര്‍ണസംഖ്യകളുടെ ബഹുമുഖമായ സവിശേഷതകളെ അടിസ്ഥാനപരമായി വിശകലനം ചെയ്യുന്ന ഗണിതശാസ്ത്രശാഖ. വിശ്ളേഷകസംഖ്യാസിദ്ധാന്തം എന്നും ഇത് അറിയപ്പെടുന്നു. പ്രാചീന ഗ്രീക് ഗണിതശാസ്ത്രജ്ഞനായ യൂക്ളിഡും ഭാരതീയാചാര്യന്‍മാരായ ബ്രഹ്മഗുപ്തനും ഭാസ്കരാചാര്യനും സംഖ്യാസിദ്ധാന്തം (Number theory) വികസിപ്പിച്ചവരാണ്. എന്നാല്‍ അടുത്ത കാലത്താണ് ഈ ശാഖയ്ക്ക് ഏറെ വളര്‍ച്ചയുണ്ടായിട്ടുള്ളത്. ലീഷാണ്‍, ഗോസ്, വോണ്‍ മങ്കോള്‍ട്, ബെര്‍ട്രന്റ്, ഷെബിഷെഫ്, മെര്‍ടണ്‍സ്, ലാന്റോ, മിങ്കൌസ്കീ, ഡിറീക്ലെ, റീമാന്‍, ഇങ്ഹാം, ഉസ്പെന്‍സ്കി, സീഗല്‍, ഹഡമാര്‍ഡ്, ഡെലാവാലി പൂസ്സിന്‍, ലിന്നിക്ക്, സെല്‍ബര്‍ഗ്, വിനഗ്രഡോഫ്, ഹാര്‍ഡി, രാമാനുജന്‍, എസ്.എസ്.പിള്ള എന്നീ ഗണിതശാസ്ത്രജ്ഞന്‍മാര്‍ വിശ്ളേഷകസംഖ്യാസിദ്ധാന്തത്തെ പരിപോഷിപ്പിച്ചിട്ടുണ്ട്.

അനാലിസിസ്' (Analysis) അഥവാ വിശ്ളേഷണം എന്ന ഗണിതശാഖയുടെ തത്ത്വങ്ങള്‍ ഉപയോഗിച്ച്, പൂര്‍ണസംഖ്യകള്‍ ഉള്‍ക്കൊള്ളുന്ന അനന്തശ്രേണികളുടേയും അനന്തമായി തുടരുന്ന അഭാജ്യസംഖ്യകളുടേയും (prime numbers) ഗുണധര്‍മ വിചിന്തനം സാധിക്കുന്നു. വിശ്ളേഷണത്തിലെ ഒരു പ്രധാനതത്ത്വമായ സീമ (limit) ഇതില്‍ സാര്‍വത്രികമായി പ്രയോഗിച്ചുവരുന്നു. സംഖ്യാസിദ്ധാന്തത്തിലെ പ്രാഥമികമായ തത്ത്വങ്ങളും അതിലുപരി അങ്കഗണിതഫലനങ്ങളുടെ മൌലികമായ ഗുണധര്‍മങ്ങളും വിശ്ളേഷകസംഖ്യാസിദ്ധാന്തത്തിന്റെ അവശ്യഘടകങ്ങളാണ്. ഈ തത്ത്വങ്ങളില്‍ പടുത്തുയര്‍ത്തിയിട്ടുള്ള ഈ ഗണിതശാഖ ഗവേഷണരംഗത്തെ സജീവപ്രശ്നമായി തുടരുന്നു. ആധുനിക ഗണിതശാഖകളായ ഗണസിദ്ധാന്തം (Set Theory), കേവല ബീജഗണിതം (Abstract Algebra), ടോപോളജി (Topology) എന്നിവയുടെ പ്രേരണകൊണ്ട് ബഹുമുഖമായ വളര്‍ച്ചയ്ക്കു വിധേയമായിക്കൊണ്ടിരിക്കുകയാണ് അനലിറ്റിക് നമ്പര്‍ തിയറി.

മൗലിക തത്ത്വങ്ങള്‍

പൂര്‍ണസംഖ്യകളുടെ ലളിതമായ സവിശേഷതകള്‍ ഏകദേശമായ സ്വയംസമ്പൂര്‍ണതയ്ക്കായി താഴെചേര്‍ക്കുന്നു.

1-ഉം അതേ സംഖ്യയുമൊഴികെ മറ്റൊരു ഘടകവുമില്ലാത്ത പൂര്‍ണസംഖ്യയാണ് അഭാജ്യസംഖ്യ (prime number); ഇത്തരത്തിലല്ലാത്തവ സങ്കീര്‍ണസംഖ്യയും (composite number). ഏതു പൂര്‍ണസംഖ്യയും അഭാജ്യസംഖ്യകളുടെ ഗുണിതമായി കണക്കാക്കാന്‍ കഴിയും. ഒരു പൂര്‍ണസംഖ്യയ്ക്ക് ഒന്നില്‍ കൂടുതല്‍ രൂപത്തില്‍ ഈ അഭാജ്യഘടകസംവിധാനം ഉണ്ടായിരിക്കയില്ല. പൂര്‍ണസംഖ്യകളുടെ ഈ സവിശേഷതയ്ക്ക് ഐകഘടകീകരണതത്ത്വം (Unique Factorisation Theorem) എന്നു പറയുന്നു. ഇതനുസരിച്ചാണ് പൂര്‍ണസംഖ്യയെ n = pa qb ......rc അഥവാ IIpa എന്നിങ്ങനെ ഘടകരൂപത്തില്‍ എഴുതുന്നത്.

അനന്തത

Infinity

ഒരു പൂര്‍ണസംഖ്യയെ തുടര്‍ന്നു വരുന്ന മറ്റൊരു പൂര്‍ണസംഖ്യയുണ്ട്. ഈ ദര്‍ശനം തുടര്‍ന്നു പോയാല്‍ സ്വാഭാവികമായി തോന്നുന്ന ഒരു ആശയമാണ് അനന്തത. പൂര്‍ണസംഖ്യകള്‍ അനന്തമായി അനുസ്യൂതം തുടരുന്നുവെന്നൂഹിക്കാം. എന്നാല്‍ അഭാജ്യസംഖ്യകളും ഇതുപോലെ അനന്തമായി തുടരുന്നുണ്ടോയെന്ന് അല്പം ചിന്തിക്കേണ്ടിവരും. അഭാജ്യസംഖ്യകളും അപ്രകാരം തന്നെ തുടരുന്നുണ്ട്. 2, 3, 5, 7, 11, 13, 17, 19 എന്നു തുടങ്ങിയ അഭാജ്യസംഖ്യകളുടെ അനുക്രമം അനന്തമാണ്. യൂക്ളിഡ് എന്ന ഗണിതശാസ്ത്രാചാര്യന്‍ ഈ വസ്തുത തെളിയിച്ചിട്ടുണ്ട്. അഭാജ്യസംഖ്യകളുടെ അനുക്രമം ഒന്നും വിടാതെ p എന്ന അഭാജ്യസംഖ്യവരെ, തമ്മില്‍ ഗുണിച്ചാല്‍, ഈ ഗുണിതത്തെ p വരെയുള്ള എല്ലാ അഭാജ്യസംഖ്യകള്‍കൊണ്ടും കൃത്യമായി ഹരിക്കാന്‍ കഴിയുന്നു. എന്നാല്‍ ഈ ഗുണിതത്തിനോട് 1 ചേര്‍ത്തുണ്ടാകുന്ന സംഖ്യയെ p വരെയുള്ള ഏതൊരു അഭാജ്യസംഖ്യകൊണ്ടും ഹരിക്കാന്‍ കഴിയില്ലെന്നതിനാല്‍ത്തന്നെ ആ സംഖ്യ ഒരു അഭാജ്യസംഖ്യ ആണന്നോ, അല്ലാത്തപക്ഷം അതിന് p യേക്കാള്‍ വലിയ ഒരു അഭാജ്യസംഖ്യാഘടകം ഉണ്ടന്നോ മനസ്സിലാക്കാം. ഈ വാദം തുടരുന്നതായാല്‍ ഒരു അഭാജ്യസംഖ്യയ്ക്കപ്പുറത്ത് മറ്റൊന്നുണ്ടെന്നും അങ്ങനെ ആ അനുക്രമം അനന്തമായി തുടരുന്നുവെന്നും സിദ്ധിക്കുന്നു.

അനന്തതയുമായുള്ള ഈ ബന്ധം യഥാര്‍ഥമായ ചില പ്രശ്നങ്ങള്‍ക്കു വഴിതെളിച്ചു. ഏതെങ്കിലുമൊരു പൂര്‍ണസംഖ്യക്ക് താഴെ ആ സംഖ്യയോട് ആപേക്ഷിക അഭാജ്യതയുള്ള (relative prime), അതായത് ആ സംഖ്യയുമായി 1 ഒഴികെ പൊതുഘടകമില്ലാത്ത, സംഖ്യകളുടെ എണ്ണം, ഒരു സംഖ്യയുടെ അഭാജ്യഘടകങ്ങളുടെ എണ്ണം, അവയുടെ ആകെത്തുക എന്നീ പ്രശ്നങ്ങള്‍ അങ്കഗണിതഫലനംവഴി മനസ്സിലാക്കി. (n), d(n), (n) എന്നിവ ക്രമത്തില്‍ ഈ ഫലനങ്ങളാണ്.

= വിഗണസംഖ്യകള്‍ -ഗണസംഖ്യകള്‍-ഏകദേശനം

Irrationals -Rationals-Approximation

√2 ഒരു വിഗണസംഖ്യയാണ്. √2 വിന് 1.414 എന്നൊരു മൂല്യം ആരോപിക്കുന്നതായി കാണാം. ഇതില്‍ അടങ്ങിയിട്ടുള്ള തത്ത്വമാണ് ഏകദേശനം എന്ന ആശയത്തിലുള്ളത്. ഏതൊരു വിഗണസംഖ്യയ്ക്കും ഒരു ഗണസംഖ്യയെ ഏകദേശ മൂല്യമായി അംഗീകരിക്കാമെന്നു തെളിയിച്ചിട്ടുണ്ട്. ഈ പ്രമേയങ്ങള്‍ ഇതിനുപോദ്ബലകമായി എടുക്കാം.

a ഒരു വിഗണസംഖ്യയും, N ധനാത്മക പൂര്‍ണസംഖ്യയും ആണെങ്കില്‍ താഴെപറയുന്ന വ്യവസ്ഥകളിലേതെങ്കിലും ഒന്നനുസരിച്ച്, a-യോട് അടുപ്പമുള്ള h/k എന്ന ഒരു ഗണസംഖ്യയുണ്ടായിരിക്കും. ഇവിടെ (k<= N)

ഇതിലെ രണ്ടാമത്തെ വ്യവസ്ഥ വാസ്തവത്തില്‍ ആദ്യത്തേതിനേക്കാള്‍ കണിശമാണ്; രണ്ടാമത്തേതില്‍ ഒന്നാമത്തേതും ഉള്‍പ്പെടുന്നു. ഇത്തരം മെച്ചപ്പെടുത്തലുകളാണ് ഇമ്മാതിരി പ്രക്രിയയിലുള്ള ഗവേഷണത്തിന്റെ ലക്ഷ്യം.

അങ്കഗണിത ഫലനങ്ങളും ജാലിക ബിന്ദുക്കളും

Arithmetical Functions and Lattice Points

അങ്കഗണിതഫലനങ്ങളുടെ മൂല്യത്തില്‍ ആധാരസംഖ്യയുടെ വലുപ്പച്ചെറുപ്പമനുസരിച്ചുണ്ടാകുന്ന മാറ്റങ്ങളെപ്പറ്റിയുള്ള പഠനം ഈ ശാഖയിലെ പ്രധാന വശമാണ്. n-നേക്കാള്‍ കുറഞ്ഞതും n-നോട് ആപേക്ഷിക അഭാജ്യവുമായ പൂര്‍ണ സംഖ്യകളുടെ എണ്ണം, അതായത് ø (n), n-നേക്കാള്‍ കുറവായിരിക്കുമെന്നത് വളരെ എളുപ്പം മനസ്സിലാക്കാം: ø(n) < n ഈ അസമതാവാക്യത്തെ മെച്ചപ്പെടുത്തിയിട്ടുണ്ട്. അതുപോലെ d(n) എന്ന ഘടകഫലന (divisor function) ത്തിന്റെ മൂല്യം, n ഒരു അഭാജ്യസംഖ്യയായിരിക്കുമ്പോള്‍, 2 ആണ്; അതായത് d(n)-ന്റെ അല്പതമ സീമ 2. σ(n), μ(n),&gama; (n) എന്നീ അങ്കഗണിതഫലനങ്ങളും ഇവയുടെ സാമാന്യവത്കരണങ്ങളും പഠനവിധേയമായിട്ടുണ്ട്. അനലിറ്റിക് നമ്പര്‍ തിയറിയിലെ ഏറ്റവും മൌലികമായ പ്രശ്നം അഭാജ്യ സംഖ്യാപ്രമിതി (Prime Number Theorem) എന്നതാണ്. ഓയിലര്‍, സീഗല്‍, ഷെബിഷെഫ്, ലാന്റോ, സെല്‍ബര്‍ഗ്, വിനഗ്രഡോഫ് എന്നിവരെല്ലാം ഈ പ്രമേയത്തിനു ഭേദഗതികള്‍ നല്കിയിട്ടുണ്ട്. അഭാജ്യസംഖ്യാ ശ്രേണി അനന്തമായി തുടരുന്നു. അതിനാല്‍ ഏതെങ്കിലും ഒരു ക്ളിപ്തസംഖ്യയ്ക്കു താഴെ എത്ര അഭാജ്യസംഖ്യകളുണ്ടായിരിക്കുമെന്നു മനസ്സിലാക്കേണ്ടതാവശ്യമായി വരുന്നു. ഇതിനൊരു ഫോര്‍മുല തീര്‍ക്കാന്‍ കഴിയാത്തതിനാല്‍ ഏകദേശനിലയില്‍ തിട്ടപ്പടുത്താന്‍ ശ്രമം നടന്നു. ഇതിന്റെ ഫലമായിട്ടാണ് ഈ പ്രസിദ്ധമായ പ്രമിതി രൂപപ്പെട്ടത്. f(n) ഒരു അങ്കഗണിതഫലനം ആണെങ്കില്‍ താഴെയുള്ള

F(N)=Σ^N_n=1f(n)

എന്ന ആകെത്തുകയ്ക്ക് ആകലനഫലനം (summatory function) എന്നു പറയാം. അങ്കഗണിതഫലനത്തിന്റെ ഗതിവിഗതികള്‍ പഠിക്കാന്‍ ആകലനഫലനവും അതിന്റെ ശരാശരി ഫലനവും (average function) ഉപയോഗിക്കാറുണ്ട്.

ചില അങ്കഗണിത ഫലനങ്ങള്‍ക്കു ജ്യാമിതീയ വ്യാഖ്യാനങ്ങളുണ്ട്. എളുപ്പത്തില്‍ ഗ്രഹിക്കാവുന്ന ജ്യാമിതീയ മാര്‍ഗങ്ങള്‍ ഉപയോഗിച്ച്, സംഖ്യാസിദ്ധാന്തത്തിലെ വിശ്ളേഷണ പ്രശ്നങ്ങള്‍ക്കു പരിഹാരം കാണാന്‍ കഴിയും. n-മാന യുക്ളീഡിയ പ്രതലത്തിലെ (n-Dimensional Euclidean Space) പൂര്‍ണ സംഖ്യാനിര്‍ദേശാങ്കങ്ങളുള്ള (Integer co-ordinates) ബിന്ദുവാണ് ജാലികബിന്ദു. ഒരു പ്രത്യേക തലത്തിലെ ജാലികബിന്ദുക്കളുടെ എണ്ണവുമായി ബന്ധപ്പെടുത്തി അങ്കഗണിതഫലനങ്ങളുടെ ഗതിവിഗതികള്‍ തിട്ടപ്പെടുത്താന്‍ കഴിയും.

വിഭജന പ്രശ്നം

Partition Problem

n എന്ന ധനപരമായ ഒരു പൂര്‍ണസംഖ്യയെ ധനപരമായ മറ്റു പൂര്‍ണസംഖ്യകളുടെ തുകയായി എത്രവിധത്തില്‍ എഴുതാമെന്നൊരു പ്രശ്നമുണ്ട്. വിഭജനപ്രശ്നം എന്നാണിതിനു പേര്. p(n) എന്നാണ് ഈ ഫലനത്തെ സൂചിപ്പിച്ചുപോരുന്നത്. ഉദാ.

5 = 4+1 = 3+2 = 3+1+1 = 2+2+1

= 2+1+1+1 = 1+1+1+1+1

അങ്ങനെ 5 എന്ന സംഖ്യയെ ഏഴു തരത്തില്‍ സംഖ്യകളുടെ തുകകളായി പ്രകടിപ്പിക്കാം. അതായത് p(5) = 7. p(n)-ന്റെ മൂല്യം കണിശമായി കണ്ടുപിടിക്കുവാന്‍ കഴിഞ്ഞിട്ടില്ല :

രാമാനുജനും ഹാര്‍ഡിയും കൂടി കണ്ടെത്തിയ ഒരു വ്യഞ്ജകം ആണിത് (1917).

വെയറിങ് പ്രശ്നം

Waring Problem

നിസര്‍ഗസംഖ്യകളെ പ്രതിനിധാനം ചെയ്യാവുന്ന രൂപങ്ങളെ (forms) കുറിച്ചുള്ള പഠനമാണ് വെയറിങ് പ്രശ്നം ഉള്‍ക്കൊള്ളുന്നത്. അതായത്, ഏത് ഒറ്റ സംഖ്യയും രണ്ടു നിസര്‍ഗ സംഖ്യകളുടെ വര്‍ഗവ്യത്യാസത്തിനു തുല്യമായിരിക്കും: 7 = 4²-3²; 2n+1 = (n+1)²-n². ഇതില്‍ 7-നെ 4²-3² എന്ന രൂപത്തില്‍ പ്രകടിപ്പിച്ചിരിക്കുന്നു. ഇത്തരം പ്രശ്നങ്ങളുടെ ഉപജ്ഞാതാവ് എ.ഡി. മൂന്നാം ശ.-ത്തില്‍ ജീവിച്ചിരുന്ന ഡയോഫാന്റസ് എന്ന ഗണിതശാസ്ത്രജ്ഞനാണ്.

1 + 2 + 3 + ....... + n = n (n+1) / 2

എന്ന സമവാക്യത്തിന്റെ വലതുഭാഗത്തുനിന്ന് n എന്നതിന് 1, 2, 3, 4, .... എന്നീ മൂല്യങ്ങള്‍ ഉപയോഗിച്ചുകിട്ടുന്ന സംഖ്യകള്‍ ക്രമത്തില്‍ 1, 3, 6, 10, ... എന്നിവയാണ്. ഈ സംഖ്യകളെ ത്രിഭുജസംഖ്യകളെന്നു പറയുന്നു. ഇതുപോലെ ബഹുഭുജസംഖ്യകളെ n + 1/2(x-2)(n²-n) എന്നു സൂചിപ്പിക്കാം. ഇതില്‍ n = 0, 1, 2,... എന്നെടുത്താല്‍ വിവിധതരം ബഹുഭുജസംഖ്യകള്‍ കിട്ടുന്നു; x ന്റെ മൂല്യം 4 ആണെങ്കില്‍ വര്‍ഗസംഖ്യകളായിരിക്കും കിട്ടുക. ഏതു വര്‍ഗസംഖ്യയും ത്രിഭുജസംഖ്യയോ അല്ലെങ്കില്‍ രണ്ടോ മൂന്നോ അത്തരം സംഖ്യകളുടെ ആകെത്തുകയോ ആയിരിക്കുമെന്ന് ഫെര്‍മെ (1636) എന്ന ഗണിതശാസ്ത്രജ്ഞന്‍ പ്രസ്താവിക്കുകയുണ്ടായി. അതില്‍ കവിഞ്ഞ്, ഏതു നിസര്‍ഗസംഖ്യയും x രാശിയിലുള്ള x ബഹുഭുജസംഖ്യകളുടെ ആകെത്തുകയായിരിക്കും എന്നുകൂടി ഫെര്‍മെയുടെ പ്രമേയം സൂചിപ്പിക്കുന്നു. ഏതു നിസര്‍ഗസംഖ്യയും 4 വര്‍ഗസംഖ്യകളുടെ ആകെത്തുകയായിരിക്കുമെന്ന് ലഗ്രാഞ്ചെ (1772) തെളിയിക്കുകയുണ്ടായി; ത്രിഭുജസംഖ്യകള്‍ക്കു ലീഷാണും (1798) മറ്റുള്ളവയ്ക്കു കോഷിയും (1813-15). ഏതു നിസര്‍ഗസംഖ്യയും കവിഞ്ഞത് 9 ഘനമാനങ്ങളുടെ ആകെത്തുകയായിരിക്കും; അഥവാ കവിഞ്ഞത് 19 ചതുര്‍മാനങ്ങളുടെ ആകെത്തുക; കവിഞ്ഞത്, 37 പഞ്ചമാനങ്ങളുടെ ആകെത്തുക. 1770-ല്‍ ഇ.വെയറിങ് അഭിപ്രായപ്പെട്ടതാണിത്. ചുരുങ്ങിയത് എത്ര പദങ്ങള്‍ (terms) ഓരോ പ്രതിനിധാനത്തിലുമുണ്ടായിരിക്കുമെന്ന പ്രശ്നം അവശേഷിച്ചു. ജി.എച്ച്. ഹാര്‍ഡി, ലിറ്റില്‍വൂഡ്, രാമാനുജന്‍ എന്നീ ഗണിതശാസ്ത്രജ്ഞന്മാരാണ് വെയറിങ് പ്രശ്നം പിന്നീട് (1917) ഗഹനമായി പഠിച്ചത്. ഓരോ പ്രതിനിധാനത്തിലും ഉണ്ടാകാവുന്ന k-രാശിയിലുള്ള സംഖ്യകളുടെ എണ്ണം ചുരുങ്ങിയത് g(k) ആണെങ്കില്‍, g(k)-യെ വെയറിങ് സ്ഥിരാങ്കമെന്നു പറയുന്നു. g(6)-ന്റെ മൂല്യം 184-ല്‍ താഴെയും g(7)-ന്റേത് 323-ല്‍ താഴെയും g(8)-ന്റേത് 596-ല്‍ താഴെയും ആയിരിക്കുമെന്ന് 1934-ല്‍ ആര്‍.ഡി. ജെയിംസ് തെളിയിച്ചു. ഐ.എം. വിനഗ്രഡോഫ് ചില ഗവേഷണഫലങ്ങള്‍ പ്രസിദ്ധീകരിച്ചതിനെത്തുടര്‍ന്ന് യു.എസ്സിലെ എല്‍.ഇ. ഡിക്സണും ഇന്ത്യയിലെ എസ്.എസ്. പിള്ളയും കുറെ പരീക്ഷണങ്ങള്‍ നടത്തി. 1936-ല്‍ അവര്‍ സ്വതന്ത്രമായി ഈ പ്രശ്നം മിക്കവാറും പരിഹരിച്ചു. q=(3/2)^kഎന്നിരിക്കട്ടെ. അവര്‍ തെളിയിച്ചത് ഇതാണ്:

g^(k)=2^k + q-2; k≥7

(3/2)^k - q ≤ 1 -(1/2)^k (q+3)

400-ല്‍ താഴെയാണ് k-യുടെ മൂല്യമെങ്കില്‍ ഇത് ശരിയായിരിക്കും. മറ്റുള്ള മൂല്യങ്ങളെ സംബന്ധിച്ച വ്യവസ്ഥയാണ് താഴെ കാണുന്നത്:

(3/2)^k - q =1-(1/2)^k (q+2)

1944-ല്‍ ഐ. നിവന്‍ ഈ വ്യവസ്ഥയിലും പ്രശ്നം പരിഹരിച്ചു. 1940-ല്‍ എസ്.എസ്.പിള്ള തന്നെ g(6) = 73 എന്നു തെളിയിച്ചു. 1944 ആയപ്പോഴേക്കും k = 4, 5 എന്നീ വ്യവസ്ഥകളൊഴികെ മറ്റെല്ലാം വെയറിങ് പ്രശ്നത്തില്‍ പരിഹൃതങ്ങളായി.

ജാലികബിന്ദു ഫലനം

Lattice Point Function

ഒരു പൂര്‍ണസംഖ്യ(n)യെ രണ്ടു പൂര്‍ണസംഖ്യകളുടെ വര്‍ഗങ്ങളുടെ ആകെത്തുകയായി ഏതേതുവിധത്തിലെല്ലാം പ്രതിനിധാനം ചെയ്യാന്‍ കഴിയുമെന്നതിന്റെ എണ്ണം സൂചിപ്പിക്കുന്നതാണ് ഈ ഫലനം. γ(n) എന്നാണിതിന്റെ ചിഹ്നം. അതായത്, x²+y² = n എന്ന സമവാക്യം x, y, n എന്നിവ പൂര്‍ണസംഖ്യകളാകുന്നവിധം നിര്‍ധാരണം ചെയ്യാവുന്നതിന്റെ എണ്ണം γ(n). ഉദാ. 1 = (+_-1)² + 0² =0² + (+-1)². അതുകൊണ്ട് γ(1) = 4. γ(n) ഗുണനാത്മകഫലനം (multiplicative function) അല്ല. നോ: അങ്കഗണിതഫലനം

ചില സംഖ്യകളെ (n), n = x² + y² എന്ന രൂപത്തില്‍ n, x, y പൂര്‍ണസംഖ്യകളാകുന്നവിധം പ്രതിനിധാനം ചെയ്യാന്‍ കഴികയില്ല. അതുകൊണ്ട് γ(n) ചുരുങ്ങിയത് പൂജ്യം ആകാം. അതായത്

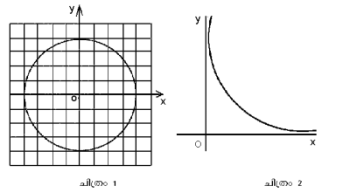
k n-നെ ആശ്രയിക്കാത്ത ഒരു സ്ഥിരസംഖ്യ. γ(n)-ന്റെ ഈ അളവുമാനത്തെക്കാള്‍ (order of magnitude) പഠനവിധേയത്വമുള്ളത് R(N)എന്നൊരു ഫലനമാണ്. x² + y² = N എന്ന വൃത്തത്തിന്റെ പരിധിയിന്‍മേലും അകത്തും ഉള്‍ക്കൊള്ളുന്ന ജാലികബിന്ദുക്കളുടെ എണ്ണമാണ് R(N) സൂചിപ്പിക്കുന്നതെന്ന് ജ്യാമിതീയ പരിഗണനകള്‍ വഴി മനസ്സിലാക്കാം. ഏകദേശം ആ വൃത്തത്തിന്റെ വിസ്തീര്‍ണം ആയിരിക്കും R(N).

ഗോസ് തിയറം

Gauss Theorem

ചിത്രം (1)-ല്‍ ഏകക വിസ്തീര്‍ണം (unit area) ഉള്ള ചതുരങ്ങളുടെ ശീര്‍ഷങ്ങളാണ് വൃത്തത്തിന്റെ സമതലത്തിലുള്ള ജാലികബിന്ദുക്കള്‍. വൃത്തത്തിനകത്തും പരിധിയിന്‍മേലും ഉള്ള ജാലികബിന്ദുക്കള്‍ക്ക് അനുയോഗത്തിലുള്ള ചതുരങ്ങള്‍ കണക്കാക്കിയാല്‍ R(N) ഈ ചതുരങ്ങളുടെ ആകെ വിസ്തീര്‍ണമാണെന്നു മനസ്സിലാക്കാം. കണക്കാക്കേണ്ടതായ എല്ലാ ചതുരങ്ങളും വൃത്തത്തിനകത്തല്ല. ഏതായാലും x²+y² = (√N + √2)² എന്ന വൃത്തത്തിനകത്തായിരിക്കും. അതുകൊണ്ട് R(N) < π(√N + √2)2. അതുപോലെതന്നെ ആ ചതുരങ്ങള്‍ (√N - √2) വ്യാസാര്‍ധമുള്ള വൃത്തത്തിനു പുറത്തായിരിക്കും. R(N)> π(√N - √2)² ,N≥2 അതുകൊണ്ട് π(N-2√2N + 2) < R(N)<π (N+2√2N + 2) അതുകൊണ്ട്,R(N)=πN + O(√N) .

ഘടക ഫലനത്തിന്റെ അളവുമാനം

d(n)-ന്റെ ഏറ്റവും കുറഞ്ഞ മൂല്യം 2 ആണ്. കൂടിയത് എത്രയുമാകാം. xy = n എന്ന സമവാക്യം x, y, n എന്നിവ പൂര്‍ണ സംഖ്യകളാകുന്നവിധം നിര്‍ധാരണം ചെയ്യാവുന്ന എണ്ണമാണ് d(n). ചിത്രം 2-ലെ, xy = n എന്ന ബഹിര്‍വളയത്തിന്‍മേലും, അതിനും OX-, OY- അക്ഷങ്ങള്‍ക്കുമിടയിലുള്ളതുമായ ജാലികബിന്ദുക്കളുടെ എണ്ണമാണ് d(n). d(n) = O(n^ε),ε > 0 എന്നു തെളിയിച്ചിട്ടുണ്ട്.

ഓയിലര്‍ ഫലനത്തിന്റെ അളവുമാനം

ø(n)<n എന്നത് എളുപ്പം മനസ്സിലാക്കാം. ,ø(n) = n(1-1/p), n=p^m, 1/p =ε എന്നെടുത്താല്‍ (ø(n)> n (1 -ø) എന്നു സിദ്ധിക്കുന്നു. ഇതില്‍നിന്നു

ø(n)-ന്റെ അളവുമാനത്തിന്റെ മറ്റൊരു സീമയാണ്.

മോബയസ് ഫലനത്തിന്റെ അളവുമാനം

മോബയസ് ഫലനത്തിന്റെ അളവുമാനമെടുക്കാന്‍ Σ^∞_n=1 μ(n)/n² എന്ന വാക്യമാണുപയോഗിക്കുന്നത്.

എന്നീ അനന്തശ്രേണികള്‍ രണ്ടും നിരപേക്ഷ-അഭികേന്ദ്രസരണം (absolutely convergent) ആണ്.

ഈ ഗുണിതത്തില്‍ ആദ്യത്തെപദം ഒന്നും മറ്റെല്ലാം പൂജ്യവുമായിരിക്കും.

എന്നു തെളിയിക്കാന്‍ കഴിയും. ഇതില്‍ നിന്നു മനസ്സിലാക്കുന്നത്.

എന്നാണ്.

റീമാന്‍ സീറ്റാഫലനം

(s)ഡിറീക്ലെ ശ്രേണികള്‍. s > 1 ആണെങ്കില്‍, താഴെ പറയുന്ന അനന്തശ്രേണികള്‍ അഭികേന്ദ്രസരണങ്ങളാണ്. അനലിറ്റിക് നമ്പര്‍ തിയറിയില്‍ ഈ ഫലനത്തിന് വളരെ പ്രാധാന്യമുണ്ട്.

ഇതിനു റീമാന്‍ സീറ്റാ ഫലനമെന്നു പറയുന്നു. സീറ്റാ ഫലനമുപയോഗിച്ച് അങ്കഗണിതഫലനങ്ങള്‍ ഉള്‍ക്കൊള്ളുന്ന ശ്രേണികളുടെ പഠനം നടത്താവുന്നതാണ്. f(n) ഒരു അങ്കഗണിതഫലനമാണെങ്കില്‍,

ഒരു ഡിറീക്ലെ ശ്രേണിയാണ്. അഭികേന്ദ്രസരണവ്യവസ്ഥകള്‍ക്ക് വിധേയമായി

എന്നിവ ഗുണിച്ചാല്‍ ഫലം

എന്നൊരു ഡിറീക്ലെ ശ്രേണിതന്നെയായിരിക്കും. ഇവിടെ h(n) എന്ന അങ്കഗണിതഫലനം,

എന്ന ഡിറീക്ലെ സംയോഗമാണ്. റീമാന്‍ സീറ്റാഫലനവുമായി ഇതിനെ ബന്ധപ്പെടുത്താന്‍ കഴിഞ്ഞിട്ടുണ്ട്.

ഈ ആശയങ്ങളെല്ലാം ആധുനിക ബീജഗണിതത്തിന്റെ തത്ത്വങ്ങള്‍ ഉപയോഗിച്ച് സാമാന്യവത്കരിക്കാനും പുതിയ രൂപങ്ങളില്‍ പ്രകടിപ്പിക്കാനും കഴിയുന്നതാണ്.

അഭാജ്യ സംഖ്യാപ്രമിതി

Prime Number Theorem

x സാമാന്യമായ ഒരു അഭാജ്യസംഖ്യയെ കുറിക്കുന്നു. x ഉള്‍പ്പെടെ x വരെയുള്ള എല്ലാ അഭാജ്യസംഖ്യകളുടെയും എണ്ണം π(x). π(x)-ന്റെ 'ഏകദേശമൂല്യം' (approximate value) x / log_e x ആണെന്ന് ക്രിസ്ത്വബ്ദം 1800-നടുപ്പിച്ച് ലീഷാണ്‍ (ലജന്റര്‍: Legendre,1752-1833) എന്ന ഫ്രഞ്ചുഗണിതശാസ്ത്രജ്ഞനും ഗോസ് (Gauss,1777-1855) എന്ന ജര്‍മന്‍ ഗണിതശാസ്ത്രജ്ഞനും അന്യോന്യമറിയാതെ കണ്ടെത്തി.

എന്ന അംശബന്ധത്തിന്റെ വില ഒന്നിനോടടുക്കുന്നു. ഇതാണ് അഭാജ്യസംഖ്യാപ്രമിതി. ഗണിതശാസ്ത്രമണ്ഡലത്തില്‍ മികച്ച ഒരു സ്ഥാനമാണ് ഈ തിയറത്തിനുള്ളത്. ജെ. ഹഡമാര്‍ഡ് (J.Hadamard, 1865-1963) എന്ന ഫ്രഞ്ചു ഗണിതശാസ്ത്രജ്ഞനും ബല്‍ജിയക്കാരനായ ഡെ ല വാലി പൂസ്സിന്‍ (De la Vallee Poussin, 1866-1962) എന്ന ഗണിതശാസ്ത്രജ്ഞനും അന്യോന്യമറിയാതെ അഭാജ്യസംഖ്യാ പ്രമിതിക്ക് 1896-ല്‍ ഉപപത്തി (proof) കണ്ടുപിടിച്ചു. പിന്നീടു പല ഉപപത്തികളും ആവിഷ്കൃതങ്ങളായിട്ടുണ്ടെങ്കിലും 1949-ല്‍ എര്‍ഡോ, സെല്‍ബര്‍ഗ് (Erdoo and Selberg) എന്നിവര്‍ ചേര്‍ന്ന് പ്രൊസീഡിങ്സ് ഒഫ് നാഷണല്‍ അക്കാദമി ഒഫ് സയന്‍സസ് എന്ന പ്രസിദ്ധീകരണത്തിലും അതേകൊല്ലം സെല്‍ബര്‍ഗ് തനിച്ച് ആനല്‍സ് ഒഫ് മാത്തമാറ്റിക്സ് എന്ന പ്രസിദ്ധീകരണത്തിലും ഇതിനു സരളമായ ഉപപത്തികള്‍ പ്രസിദ്ധം ചെയ്തു. നോ: അനാലിസിസ്, അങ്കഗണിതഫലനം, സംഖ്യാസിദ്ധാന്തം