This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കാറ്റ്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Wind) |
Mksol (സംവാദം | സംഭാവനകള്) (→Wind) |
||
| വരി 9: | വരി 9: | ||
= 2.237 മൈല്/മണി. = 1.944 നോട്ട്. | = 2.237 മൈല്/മണി. = 1.944 നോട്ട്. | ||
കാറ്റിന്റെ വേഗത അളക്കുന്നതിനുള്ള ഉപകരണമാണ് അനീമോമീറ്റര്. | കാറ്റിന്റെ വേഗത അളക്കുന്നതിനുള്ള ഉപകരണമാണ് അനീമോമീറ്റര്. | ||
| - | + | ||
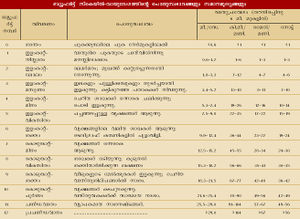
അന്തരീക്ഷവിജ്ഞാനികള് കാറ്റിന്റെ സാമാന-്യമായ വേഗത നിര്ണയിക്കുന്നതിന് ഒരു പ്രതേ-്യകതരം വര്ഗീകരണ സംവിധാനമാണ് ഉപയോഗിക്കുന്നത്. വേഗത അടിസ്ഥാനമാക്കി കാറ്റിനെ ഇനം തിരിക്കുന്ന ഈ മാപനവ-്യവസ്ഥയെ ബ്യൂഫര്ട്ട് സ്കെയില് (Beaufort scale) എന്നു പറയുന്നു. | അന്തരീക്ഷവിജ്ഞാനികള് കാറ്റിന്റെ സാമാന-്യമായ വേഗത നിര്ണയിക്കുന്നതിന് ഒരു പ്രതേ-്യകതരം വര്ഗീകരണ സംവിധാനമാണ് ഉപയോഗിക്കുന്നത്. വേഗത അടിസ്ഥാനമാക്കി കാറ്റിനെ ഇനം തിരിക്കുന്ന ഈ മാപനവ-്യവസ്ഥയെ ബ്യൂഫര്ട്ട് സ്കെയില് (Beaufort scale) എന്നു പറയുന്നു. | ||
| - | കാറ്റുകളുടെ വര്ഗീകരണം. ഉത്പത്തി, സഞ്ചാരദിശ, വേഗത, പരിസഞ്ചാരണം എന്നീ ഘടകങ്ങളെ ആശ്രയിച്ചും കാറ്റുകളെ ഇനം തിരിക്കാവുന്നതാണ്. ഇവയില് പരിസഞ്ചാരണത്തിന്റെ വ്യാപ്തി അടിസ്ഥാനമാക്കിയുള്ള വര്ഗീകരണത്തിനാണ് ആഗോളതല പ്രാധാന്യം.മൂന്ന് വാതവ്യവസ്ഥകളാണ് പൊതുവേ അംഗീകരിക്കപ്പെട്ടിട്ടുള്ളത്: ഭൂമണ്ഡലീയം (planetary), ദ്വിതീയം (secondary), സ്ഥാനീയം (tertiary). ഭൂമിയുടെ ഗോളാകൃതി, ഭൗമാന്തരീക്ഷത്തിന്റെ ചായ്വ്, ഭ്രമണം, പ്രദക്ഷിണം എന്നീ രീതികളില് ഭൂമിക്കുള്ള ചലനം എന്നിവയുടെ ഫലമായി ഉണ്ടാകുന്ന കാറ്റുകളാണ് ഭൂമണ്ഡലീയ വാതങ്ങളായി പരിഗണിക്കപ്പെടുന്നത്. വാണിജ്യവാതങ്ങള് (Trade winds), പെശ്ചിമവാതങ്ങള് (Westerlies), ധ്രുവവാതങ്ങള് (Polar winds)എന്നിവ ഈ വിഭാഗത്തില്പ്പെടുന്നു. | + | ''' |
| - | [[ചിത്രം: | + | കാറ്റുകളുടെ വര്ഗീകരണം'''. ഉത്പത്തി, സഞ്ചാരദിശ, വേഗത, പരിസഞ്ചാരണം എന്നീ ഘടകങ്ങളെ ആശ്രയിച്ചും കാറ്റുകളെ ഇനം തിരിക്കാവുന്നതാണ്. ഇവയില് പരിസഞ്ചാരണത്തിന്റെ വ്യാപ്തി അടിസ്ഥാനമാക്കിയുള്ള വര്ഗീകരണത്തിനാണ് ആഗോളതല പ്രാധാന്യം.മൂന്ന് വാതവ്യവസ്ഥകളാണ് പൊതുവേ അംഗീകരിക്കപ്പെട്ടിട്ടുള്ളത്: ഭൂമണ്ഡലീയം (planetary), ദ്വിതീയം (secondary), സ്ഥാനീയം (tertiary). ഭൂമിയുടെ ഗോളാകൃതി, ഭൗമാന്തരീക്ഷത്തിന്റെ ചായ്വ്, ഭ്രമണം, പ്രദക്ഷിണം എന്നീ രീതികളില് ഭൂമിക്കുള്ള ചലനം എന്നിവയുടെ ഫലമായി ഉണ്ടാകുന്ന കാറ്റുകളാണ് ഭൂമണ്ഡലീയ വാതങ്ങളായി പരിഗണിക്കപ്പെടുന്നത്. വാണിജ്യവാതങ്ങള് (Trade winds), പെശ്ചിമവാതങ്ങള് (Westerlies), ധ്രുവവാതങ്ങള് (Polar winds)എന്നിവ ഈ വിഭാഗത്തില്പ്പെടുന്നു. |
| + | |||
| + | [[ചിത്രം:Vol7_365_chart.jpg|300px]] | ||
| + | |||
| + | |||
| + | |||
വായുപിണ്ഡങ്ങള് കൂട്ടിമുട്ടുന്നതിനെത്തുടര്ന്ന് ഉരുത്തിയിരിയുന്ന ചക്രവാതങ്ങള് (Cyclones); പ്രതിചക്രവാതങ്ങള് (Anticyclones); കെടല്, കര എന്നിവയുടെ ആപേക്ഷികസ്ഥാനങ്ങളെ ആശ്രയിച്ച് പ്രത്യേകഋതുക്കളില് വീശുന്ന മണ്സൂണ് കാറ്റുകള് തുടങ്ങിയവ ദ്വിതീയ വാതങ്ങളുടെ കൂട്ടത്തില്പ്പെടുന്നു. അന്തരീക്ഷാവസ്ഥയില് ദൈനികമോ താത്കാലികമോ ആയി ഏര്പ്പെടുന്ന ഏറ്റക്കുറവുകളുടെ ഫലമായി തികച്ചും സ്ഥാനീയമായി താരതമ്യേന ചെറിയ മേഖലകളില് മാത്രം അനുഭവപ്പെടുന്നയിനം കാറ്റുകളാണ് മൂന്നാമത്തെ വിഭാഗത്തില്പ്പെടുന്നത്. ഇവയില്ത്തന്നെ അന്തരീക്ഷ താപനിലയിലെ ഏറ്റക്കുറവുകളിലൂടെ ഉരുത്തിരിയുന്ന കരകടല്ക്കാറ്റുകള്, ഘനത്വ വാതങ്ങള് (Gravity winds)എന്ന ഉപവിഭാഗത്തില്പ്പെടുത്താറുണ്ട്. | വായുപിണ്ഡങ്ങള് കൂട്ടിമുട്ടുന്നതിനെത്തുടര്ന്ന് ഉരുത്തിയിരിയുന്ന ചക്രവാതങ്ങള് (Cyclones); പ്രതിചക്രവാതങ്ങള് (Anticyclones); കെടല്, കര എന്നിവയുടെ ആപേക്ഷികസ്ഥാനങ്ങളെ ആശ്രയിച്ച് പ്രത്യേകഋതുക്കളില് വീശുന്ന മണ്സൂണ് കാറ്റുകള് തുടങ്ങിയവ ദ്വിതീയ വാതങ്ങളുടെ കൂട്ടത്തില്പ്പെടുന്നു. അന്തരീക്ഷാവസ്ഥയില് ദൈനികമോ താത്കാലികമോ ആയി ഏര്പ്പെടുന്ന ഏറ്റക്കുറവുകളുടെ ഫലമായി തികച്ചും സ്ഥാനീയമായി താരതമ്യേന ചെറിയ മേഖലകളില് മാത്രം അനുഭവപ്പെടുന്നയിനം കാറ്റുകളാണ് മൂന്നാമത്തെ വിഭാഗത്തില്പ്പെടുന്നത്. ഇവയില്ത്തന്നെ അന്തരീക്ഷ താപനിലയിലെ ഏറ്റക്കുറവുകളിലൂടെ ഉരുത്തിരിയുന്ന കരകടല്ക്കാറ്റുകള്, ഘനത്വ വാതങ്ങള് (Gravity winds)എന്ന ഉപവിഭാഗത്തില്പ്പെടുത്താറുണ്ട്. | ||
കാറ്റുകള് നിരന്തരമായി വീശുന്നവയോ പ്രത്യേക കാലങ്ങളിലോ ദിവസങ്ങളിലോ അപൂര്വമായോ മാത്രം വീശുന്നവയോ ആവാം. സഞ്ചാരദിശയെ നേര്വിപരീതമായി വ്യതിചലിപ്പിക്കുന്ന ഉഭയദിശാ (amphidromic) വാതങ്ങളും ഉണ്ട്; കരകടല്ക്കാറ്റുകള് ഇതിനുദാഹരണങ്ങളാണ്. | കാറ്റുകള് നിരന്തരമായി വീശുന്നവയോ പ്രത്യേക കാലങ്ങളിലോ ദിവസങ്ങളിലോ അപൂര്വമായോ മാത്രം വീശുന്നവയോ ആവാം. സഞ്ചാരദിശയെ നേര്വിപരീതമായി വ്യതിചലിപ്പിക്കുന്ന ഉഭയദിശാ (amphidromic) വാതങ്ങളും ഉണ്ട്; കരകടല്ക്കാറ്റുകള് ഇതിനുദാഹരണങ്ങളാണ്. | ||
| - | വായുസഞ്ചലന സവിശേഷതകള്. ഭൗമോപരിതലത്തിലൂടെ സഞ്ചരിക്കുമ്പോള് വായുവിന് ദിശയിലും വേഗതയിലും അനുക്രമമായ ഏറ്റക്കുറവുകള് ഉണ്ടാകുന്നത് സാധാരണമാണ്. ഇതിന്റെ ഫലമായി നിശ്ചിതപഥത്തിലൂടെ സഞ്ചരിക്കുന്ന വായുപിണ്ഡത്തിന്റെ പ്രവേഗ(velocity)ത്തില് വ്യതിയാനം വരുന്നു. പ്രവേഗത്തിലെ ഏറ്റക്കുറവാണ് ത്വരണം (acceleration). ന്യൂട്ടന്റെ രണ്ടാമത്തെ ചലനനിയമപ്രകാരം വായുപിണ്ഡത്തിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുത്തുന്നതിന് പര്യാപ്തമായി ഏതെങ്കിലും ഒരു ബലം പ്രവര്ത്തിക്കേണ്ടതുണ്ട്. ഇതില്നിന്ന് വായുപിണ്ഡത്തിന്റെ സഞ്ചാരത്തിന്കാറ്റിന്ഹേതുകമായി എന്തൊക്കെയോ ബലങ്ങള് പ്രവര്ത്തിക്കുന്നുണ്ടെന്ന് അനുമാനിക്കാവുന്നതാണ്. ഈ ബലങ്ങളുടെ അനേ-്യാന്യ പ്രവര്ത്തനം ഏറെക്കുറെ സന്തുലിതമാകുമ്പോള് കാറ്റിന് ത്വരണം സംഭവിക്കുകയില്ല; സ്ഥിരമായ പ്രവേഗത്തോടെ കാറ്റ് വീശുകയും ചെയ്യും. നേരെമറിച്ച് മേല്പറഞ്ഞ ബലങ്ങള് അസന്തുലിതമായിരിക്കുമ്പോള് കാറ്റിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുന്നു. സാധാരണ അനുഭവത്തില്നിന്ന് കാറ്റിന്റെ പ്രവേഗത്തില് രണ്ടു രീതിയില് വ്യത്യാസം ഏര്പ്പെടുന്നതായിക്കാണാം: (i) ക്രമരഹിതമായ പിശറുകള്; നിമിഷങ്ങളോളം മാത്രം നീണ്ടുനില്ക്കുന്നവ; (ii) അനുക്രമമായി ഉണ്ടായി മണിക്കൂറുകളോ, ദിവസങ്ങളോളമോ നീണ്ടുനില്ക്കുന്നവ. | + | |
| + | '''വായുസഞ്ചലന സവിശേഷതകള്.''' ഭൗമോപരിതലത്തിലൂടെ സഞ്ചരിക്കുമ്പോള് വായുവിന് ദിശയിലും വേഗതയിലും അനുക്രമമായ ഏറ്റക്കുറവുകള് ഉണ്ടാകുന്നത് സാധാരണമാണ്. ഇതിന്റെ ഫലമായി നിശ്ചിതപഥത്തിലൂടെ സഞ്ചരിക്കുന്ന വായുപിണ്ഡത്തിന്റെ പ്രവേഗ(velocity)ത്തില് വ്യതിയാനം വരുന്നു. പ്രവേഗത്തിലെ ഏറ്റക്കുറവാണ് ത്വരണം (acceleration). ന്യൂട്ടന്റെ രണ്ടാമത്തെ ചലനനിയമപ്രകാരം വായുപിണ്ഡത്തിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുത്തുന്നതിന് പര്യാപ്തമായി ഏതെങ്കിലും ഒരു ബലം പ്രവര്ത്തിക്കേണ്ടതുണ്ട്. ഇതില്നിന്ന് വായുപിണ്ഡത്തിന്റെ സഞ്ചാരത്തിന്കാറ്റിന്ഹേതുകമായി എന്തൊക്കെയോ ബലങ്ങള് പ്രവര്ത്തിക്കുന്നുണ്ടെന്ന് അനുമാനിക്കാവുന്നതാണ്. ഈ ബലങ്ങളുടെ അനേ-്യാന്യ പ്രവര്ത്തനം ഏറെക്കുറെ സന്തുലിതമാകുമ്പോള് കാറ്റിന് ത്വരണം സംഭവിക്കുകയില്ല; സ്ഥിരമായ പ്രവേഗത്തോടെ കാറ്റ് വീശുകയും ചെയ്യും. നേരെമറിച്ച് മേല്പറഞ്ഞ ബലങ്ങള് അസന്തുലിതമായിരിക്കുമ്പോള് കാറ്റിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുന്നു. സാധാരണ അനുഭവത്തില്നിന്ന് കാറ്റിന്റെ പ്രവേഗത്തില് രണ്ടു രീതിയില് വ്യത്യാസം ഏര്പ്പെടുന്നതായിക്കാണാം: (i) ക്രമരഹിതമായ പിശറുകള്; നിമിഷങ്ങളോളം മാത്രം നീണ്ടുനില്ക്കുന്നവ; (ii) അനുക്രമമായി ഉണ്ടായി മണിക്കൂറുകളോ, ദിവസങ്ങളോളമോ നീണ്ടുനില്ക്കുന്നവ. | ||
| + | |||
| + | [[ചിത്രം:Vol7_366_image1.jpg|300px]] | ||
കാറ്റിന്റെ സാമാന്യ സ്വഭാവം പരിഗണിക്കുമ്പോള് ആദ-്യത്തെമാതിരി വേഗവ്യത്യാസങ്ങള് അവഗണിക്കാവുന്നതേ ഉള്ളൂ. എന്നാല് ഏറെ സമയം നീണ്ടുനില്ക്കുന്ന രണ്ടാമത്തെയിനം ഏറ്റക്കുറവുകളില് നന്നേ താണതായ ത്വരണം മൂലം കാറ്റ് തുടര്ച്ചയായും നിയതമായും വീശുന്നതായി അനുഭവപ്പെടുന്നു. | കാറ്റിന്റെ സാമാന്യ സ്വഭാവം പരിഗണിക്കുമ്പോള് ആദ-്യത്തെമാതിരി വേഗവ്യത്യാസങ്ങള് അവഗണിക്കാവുന്നതേ ഉള്ളൂ. എന്നാല് ഏറെ സമയം നീണ്ടുനില്ക്കുന്ന രണ്ടാമത്തെയിനം ഏറ്റക്കുറവുകളില് നന്നേ താണതായ ത്വരണം മൂലം കാറ്റ് തുടര്ച്ചയായും നിയതമായും വീശുന്നതായി അനുഭവപ്പെടുന്നു. | ||
| വരി 23: | വരി 31: | ||
വായുപ്രവേഗവും മര്ദവിതരണവും തമ്മിലുള്ള ഈ ബന്ധം ഒരു പൊതുനിയമമെന്ന നിലയില് പ്രചരിപ്പിച്ചത് (1857) ബൈസ്ബാലട്ട് എന്ന ശാസ്ത്രജ്ഞന് ആയിരുന്നു. "കാറ്റിന് പുറം തിരിഞ്ഞുനില്ക്കുന്ന ഒരു നിരീക്ഷകനെ സംബന്ധിച്ചിടത്തോളം നിമ്നമര്ദം ഉത്തരാര്ധഗോളത്തില് ഇടതു പുറത്തും ദക്ഷിണാര്ധഗോളത്തില് വലതുപുറത്തുമായിരിക്കും' എന്ന ഈ വസ്തുത ബൈസ്ബാലട്ട് നിയമം എന്ന് അറിയപ്പെടുന്നു. തികച്ചും വസ്തുനിഷ്ഠമല്ലെന്നിരിക്കിലും നാവികര്ക്കും മറ്റ് അന്തരീക്ഷ നിരീക്ഷകര്ക്കും മാര്ഗദര്ശനം നല്കുവാന് ഈ നിയമത്തിനുകഴിഞ്ഞു. ബൈസ്ബാലട്ട് നിയമം വ്യവച്ഛേദിച്ചുപരിശോധിച്ചാല് ഉത്തരാര്ധഗോളത്തെ സംബന്ധിച്ചിടത്തോളം ഉച്ചമര്ധത്തിനു ചുറ്റും പ്രദക്ഷിണദിശയിലും നിമ്നമര്ദത്തിനു ചുറ്റും അപ്രദക്ഷിണദിശയിലും കാറ്റുവീശുന്നതിനുള്ള സാധ്യത വ്യക്തമാവുന്നു. | വായുപ്രവേഗവും മര്ദവിതരണവും തമ്മിലുള്ള ഈ ബന്ധം ഒരു പൊതുനിയമമെന്ന നിലയില് പ്രചരിപ്പിച്ചത് (1857) ബൈസ്ബാലട്ട് എന്ന ശാസ്ത്രജ്ഞന് ആയിരുന്നു. "കാറ്റിന് പുറം തിരിഞ്ഞുനില്ക്കുന്ന ഒരു നിരീക്ഷകനെ സംബന്ധിച്ചിടത്തോളം നിമ്നമര്ദം ഉത്തരാര്ധഗോളത്തില് ഇടതു പുറത്തും ദക്ഷിണാര്ധഗോളത്തില് വലതുപുറത്തുമായിരിക്കും' എന്ന ഈ വസ്തുത ബൈസ്ബാലട്ട് നിയമം എന്ന് അറിയപ്പെടുന്നു. തികച്ചും വസ്തുനിഷ്ഠമല്ലെന്നിരിക്കിലും നാവികര്ക്കും മറ്റ് അന്തരീക്ഷ നിരീക്ഷകര്ക്കും മാര്ഗദര്ശനം നല്കുവാന് ഈ നിയമത്തിനുകഴിഞ്ഞു. ബൈസ്ബാലട്ട് നിയമം വ്യവച്ഛേദിച്ചുപരിശോധിച്ചാല് ഉത്തരാര്ധഗോളത്തെ സംബന്ധിച്ചിടത്തോളം ഉച്ചമര്ധത്തിനു ചുറ്റും പ്രദക്ഷിണദിശയിലും നിമ്നമര്ദത്തിനു ചുറ്റും അപ്രദക്ഷിണദിശയിലും കാറ്റുവീശുന്നതിനുള്ള സാധ്യത വ്യക്തമാവുന്നു. | ||
| - | + | ||
| - | ഭൂവിക്ഷേപവാതം (Geostrophic wind). സാമാന്യേന സന്തുലിതമായി വീശുന്ന കാറ്റുകളുടെ ഉദ്ഭവത്തിന് നിദാനവും അവയുടെ ഗതിയെ സ്വാധീനിക്കുന്നതുമായ ബല (force) ങ്ങളെ ഇനി പരിഗണിക്കാം. തികച്ചും സന്തുലിതമായ ഒരു വായുധാര ഉണ്ടെന്നിരിക്കട്ടെ. തിരശ്ചീനമായ ഗതി കണക്കാക്കുന്നതിനാല് വായുവിന്റെ ഭാരം ഉള്പ്പെടെ ഉര്ധ്വാധര ദിശയില് പ്രവര്ത്തിക്കുന്ന ബലങ്ങളെ തത്കാലം വിഗണിക്കാം. ക്ഷൈതിജ ദിശയില് പ്രവര്ത്തിക്കുന്ന രണ്ടു ബലങ്ങളുടെ പരിണത (resulrant) ദേിശയിലാണ് കാറ്റ് ഒഴുകുന്നതെന്നു വരുന്നു. ഈ രണ്ടു ബലങ്ങളില് ഒന്ന് മര്ദവിതരണത്തിലെ ഉച്ചനീചത്വങ്ങളെ അടിസ്ഥാനമാക്കി ഉണ്ടാവുന്ന ഘനത്വബലം (gradient force) ആണെന്ന് നേരത്തെ സൂചിപ്പിച്ചു. ഉച്ചമര്ദ (high) ത്തില്നിന്നും നിമ്നമര്ദ (low) ത്തിലേക്കു വായു ഒഴുകിനീങ്ങുന്നു. ഇടതൂര്ന്ന സമമര്ദരേഖകള് തീവ്രമായ മര്ദവ്യത്യാസം സൂചിപ്പിക്കുന്നു. ഈ രേഖകള്ക്കു കുറുകെ ലംബികദിശയില് ശക്തമായ ഘനത്വബലം (G) അനുഭവപ്പെടുന്നു. സാധാരണയായി G യുടെ തോത് കിലോമീറ്ററിന് 0.01 മില്ലിബാര് ആണ്. G യുടെ പരിമാണം സമമര്ദരേഖകള് ഇടതിങ്ങിയിരിക്കുമ്പോള് കൂടുതലായും അവ നന്നെ അകലത്തിലാകുമ്പോള് വളരെ കുറവായും കാണപ്പെടുന്നു. മര്ദവ്യതിയാനങ്ങളുടെ ഫലമായി ഉത്തേജിതമാകുന്ന മര്ദപ്രവണതാബലം (pressure gradient force) X, മര്ദഘനത്വം G യുമായി സമാനുപാതബന്ധം പുലര്ത്തുന്നു. ഈ ബന്ധത്തെ K1 എന്ന സ്ഥിരാങ്കത്തിന്റെ സഹായത്തോടെ | + | '''ഭൂവിക്ഷേപവാതം''' (Geostrophic wind). സാമാന്യേന സന്തുലിതമായി വീശുന്ന കാറ്റുകളുടെ ഉദ്ഭവത്തിന് നിദാനവും അവയുടെ ഗതിയെ സ്വാധീനിക്കുന്നതുമായ ബല (force) ങ്ങളെ ഇനി പരിഗണിക്കാം. തികച്ചും സന്തുലിതമായ ഒരു വായുധാര ഉണ്ടെന്നിരിക്കട്ടെ. തിരശ്ചീനമായ ഗതി കണക്കാക്കുന്നതിനാല് വായുവിന്റെ ഭാരം ഉള്പ്പെടെ ഉര്ധ്വാധര ദിശയില് പ്രവര്ത്തിക്കുന്ന ബലങ്ങളെ തത്കാലം വിഗണിക്കാം. ക്ഷൈതിജ ദിശയില് പ്രവര്ത്തിക്കുന്ന രണ്ടു ബലങ്ങളുടെ പരിണത (resulrant) ദേിശയിലാണ് കാറ്റ് ഒഴുകുന്നതെന്നു വരുന്നു. ഈ രണ്ടു ബലങ്ങളില് ഒന്ന് മര്ദവിതരണത്തിലെ ഉച്ചനീചത്വങ്ങളെ അടിസ്ഥാനമാക്കി ഉണ്ടാവുന്ന ഘനത്വബലം (gradient force) ആണെന്ന് നേരത്തെ സൂചിപ്പിച്ചു. ഉച്ചമര്ദ (high) ത്തില്നിന്നും നിമ്നമര്ദ (low) ത്തിലേക്കു വായു ഒഴുകിനീങ്ങുന്നു. ഇടതൂര്ന്ന സമമര്ദരേഖകള് തീവ്രമായ മര്ദവ്യത്യാസം സൂചിപ്പിക്കുന്നു. ഈ രേഖകള്ക്കു കുറുകെ ലംബികദിശയില് ശക്തമായ ഘനത്വബലം (G) അനുഭവപ്പെടുന്നു. സാധാരണയായി G യുടെ തോത് കിലോമീറ്ററിന് 0.01 മില്ലിബാര് ആണ്. G യുടെ പരിമാണം സമമര്ദരേഖകള് ഇടതിങ്ങിയിരിക്കുമ്പോള് കൂടുതലായും അവ നന്നെ അകലത്തിലാകുമ്പോള് വളരെ കുറവായും കാണപ്പെടുന്നു. മര്ദവ്യതിയാനങ്ങളുടെ ഫലമായി ഉത്തേജിതമാകുന്ന മര്ദപ്രവണതാബലം (pressure gradient force) X, മര്ദഘനത്വം G യുമായി സമാനുപാതബന്ധം പുലര്ത്തുന്നു. ഈ ബന്ധത്തെ K1 എന്ന സ്ഥിരാങ്കത്തിന്റെ സഹായത്തോടെ |
X = K1. G ........(i) | X = K1. G ........(i) | ||
എന്ന് വാക്യരൂപേണ സൂചിപ്പിക്കാം. സമ മര്ദരേഖകളുടെ വിന്യാസക്രമത്തെ ഘി എന്ന സംജ്ഞയാല് വ്യഞ്ജിപ്പിച്ചാല് അത് ത മായി വിപരീതാനുപാതത്തിലായിരിക്കുമെന്നും മേല്പറഞ്ഞ വാക്യത്തില് നിന്ന് സിദ്ധിക്കുന്നു. | എന്ന് വാക്യരൂപേണ സൂചിപ്പിക്കാം. സമ മര്ദരേഖകളുടെ വിന്യാസക്രമത്തെ ഘി എന്ന സംജ്ഞയാല് വ്യഞ്ജിപ്പിച്ചാല് അത് ത മായി വിപരീതാനുപാതത്തിലായിരിക്കുമെന്നും മേല്പറഞ്ഞ വാക്യത്തില് നിന്ന് സിദ്ധിക്കുന്നു. | ||
| + | |||
മര്ദപ്രവണതാബലത്തിനുമാത്രം വിധേയമായി ഒഴുകുന്ന വായുധാര അസന്തുലിതമായി നിമ്നമര്ദ കേന്ദ്രങ്ങളുടെ ഉള്ളിലേക്കു വീശുകയും അവ വായു തിങ്ങിക്കൂടുന്നതു നിമിത്തം ഗുരുമര്ദകേന്ദ്രങ്ങളായി മാറുകയും ചെയ്യേണ്ടതാണ്. എന്നാല് സാധാരണയായി ഇത്തരം പ്രക്രിയകള് പ്രാവര്ത്തികമായിക്കാണുന്നില്ല. ഇതില്നിന്ന് മര്ദപ്രവണതാബലത്തെ സമീകരിക്കുവാന് പോന്ന ഒരു ബലം കൂടിയെങ്കിലും കാറ്റിന്റെ ഗതിയെ സ്വാധീനിക്കുന്നുവെന്ന് അനുമാനിക്കേണ്ടിവരുന്നു. ഭൂഭ്രമണഫലമായി ഉരുത്തിരിയുന്ന ഒരു ബലമാണ് ഈ രീതിയിലുള്ള സ്വാധീനത ചെലുത്തുന്നതെന്ന് നിരീക്ഷണങ്ങളിലൂടെ ബോധ്യമായിട്ടുണ്ട്. സ്വന്തം അച്ചുതണ്ടിനെ ആധാരമാക്കി ഭ്രമണം ചെയ്യുന്ന ഭൂമിയുടെ ഗോളാകാരമായ പ്രതലത്തില് വര്ത്തിക്കുന്ന ഏതൊരുവസ്തുവും പ്രസ്തുത ചലനത്താല് പ്രരിപ്പിക്കപ്പെട്ട്, ഉത്തരാര്ധഗോളത്തില് വലത്തോട്ടും ദക്ഷിണാര്ധഗോളത്തില് ഇടത്തോട്ടും വ്യതിചലിക്കുന്നു. അനുസ്യൂതമായ ഈ സ്ഥാനചലനം വിവിധ അക്ഷാംശീയ മണ്ഡലങ്ങളില് അനുഭവപ്പെടുന്ന വ്യത്യസ്ത പ്രവേഗങ്ങളുടെ ഫലമായി വസ്തുവിന്റെ ഗതിയില് ത്വരണം (acceleration) ഏര്പ്പെടുത്തുന്നു. ഈ ത്വരണം അനുഭവപ്പെടുന്നത് വസ്തുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബമായ ദിശയിലാണ്. ഇത്തരം വ്യതിചലനത്തിന് നിദാനമായ ബലത്തിന് ഭൂവിക്ഷേപബലം (Geostrophic force) എന്നു പറയുന്നു. ഭൂവിക്ഷേപബലത്തിന്റെ മൂല്യം നിര്ണയിച്ചത് കൊരിയോലി (1792-1843) എന്ന ശാസ്ത്രജ്ഞനായിരുന്നു. ഇക്കാരണത്താല് ഭൂവിക്ഷേപബലത്തിനെ കൊരിയോലി ബലം എന്നും വിശേഷിപ്പിക്കാറുണ്ട്. ഭൂവിക്ഷേപബലം ഥ ചലിതവസ്തുവിന്റെ പ്രവേഗം ഢയുമായി സമാനുപാതത്തിലായിരിക്കും. | മര്ദപ്രവണതാബലത്തിനുമാത്രം വിധേയമായി ഒഴുകുന്ന വായുധാര അസന്തുലിതമായി നിമ്നമര്ദ കേന്ദ്രങ്ങളുടെ ഉള്ളിലേക്കു വീശുകയും അവ വായു തിങ്ങിക്കൂടുന്നതു നിമിത്തം ഗുരുമര്ദകേന്ദ്രങ്ങളായി മാറുകയും ചെയ്യേണ്ടതാണ്. എന്നാല് സാധാരണയായി ഇത്തരം പ്രക്രിയകള് പ്രാവര്ത്തികമായിക്കാണുന്നില്ല. ഇതില്നിന്ന് മര്ദപ്രവണതാബലത്തെ സമീകരിക്കുവാന് പോന്ന ഒരു ബലം കൂടിയെങ്കിലും കാറ്റിന്റെ ഗതിയെ സ്വാധീനിക്കുന്നുവെന്ന് അനുമാനിക്കേണ്ടിവരുന്നു. ഭൂഭ്രമണഫലമായി ഉരുത്തിരിയുന്ന ഒരു ബലമാണ് ഈ രീതിയിലുള്ള സ്വാധീനത ചെലുത്തുന്നതെന്ന് നിരീക്ഷണങ്ങളിലൂടെ ബോധ്യമായിട്ടുണ്ട്. സ്വന്തം അച്ചുതണ്ടിനെ ആധാരമാക്കി ഭ്രമണം ചെയ്യുന്ന ഭൂമിയുടെ ഗോളാകാരമായ പ്രതലത്തില് വര്ത്തിക്കുന്ന ഏതൊരുവസ്തുവും പ്രസ്തുത ചലനത്താല് പ്രരിപ്പിക്കപ്പെട്ട്, ഉത്തരാര്ധഗോളത്തില് വലത്തോട്ടും ദക്ഷിണാര്ധഗോളത്തില് ഇടത്തോട്ടും വ്യതിചലിക്കുന്നു. അനുസ്യൂതമായ ഈ സ്ഥാനചലനം വിവിധ അക്ഷാംശീയ മണ്ഡലങ്ങളില് അനുഭവപ്പെടുന്ന വ്യത്യസ്ത പ്രവേഗങ്ങളുടെ ഫലമായി വസ്തുവിന്റെ ഗതിയില് ത്വരണം (acceleration) ഏര്പ്പെടുത്തുന്നു. ഈ ത്വരണം അനുഭവപ്പെടുന്നത് വസ്തുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബമായ ദിശയിലാണ്. ഇത്തരം വ്യതിചലനത്തിന് നിദാനമായ ബലത്തിന് ഭൂവിക്ഷേപബലം (Geostrophic force) എന്നു പറയുന്നു. ഭൂവിക്ഷേപബലത്തിന്റെ മൂല്യം നിര്ണയിച്ചത് കൊരിയോലി (1792-1843) എന്ന ശാസ്ത്രജ്ഞനായിരുന്നു. ഇക്കാരണത്താല് ഭൂവിക്ഷേപബലത്തിനെ കൊരിയോലി ബലം എന്നും വിശേഷിപ്പിക്കാറുണ്ട്. ഭൂവിക്ഷേപബലം ഥ ചലിതവസ്തുവിന്റെ പ്രവേഗം ഢയുമായി സമാനുപാതത്തിലായിരിക്കും. | ||
| വരി 34: | വരി 43: | ||
ഉത്തരാര്ധഗോളത്തില് ഈ ബലം പ്രവര്ത്തിക്കുന്നത് വായുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബികമായി അതിന്റെ വലതു പാര്ശ്വത്തിലേക്കായിരിക്കും. ചലിക്കാത്ത വായുപിണ്ഡങ്ങളെ സംബന്ധിച്ചിടത്തോളം ഭൂവിക്ഷേപബലം അനുഭവയോഗ്യമല്ല. | ഉത്തരാര്ധഗോളത്തില് ഈ ബലം പ്രവര്ത്തിക്കുന്നത് വായുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബികമായി അതിന്റെ വലതു പാര്ശ്വത്തിലേക്കായിരിക്കും. ചലിക്കാത്ത വായുപിണ്ഡങ്ങളെ സംബന്ധിച്ചിടത്തോളം ഭൂവിക്ഷേപബലം അനുഭവയോഗ്യമല്ല. | ||
| + | |||
| + | [[ചിത്രം:Vol7_366_image2.jpg|300px]] | ||
| + | |||
മേല്പറഞ്ഞ രണ്ടുബലങ്ങളുടെ മാത്രം സ്വാധീനതയില് വീശുന്ന കാറ്റുകളെ ഭൂവിക്ഷേപവാതം എന്നു വിശേഷിപ്പിക്കുന്നു. മര്ദപ്രവണതയെയും ഭൂവിക്ഷേപബലത്തെയും ആധാരമാക്കി ഒരു വായുപിണ്ഡത്തിന് ഇരുപുറവുമായി വരച്ചിട്ടുള്ള സമമര്ദരേഖകളുടെ മാതൃകാആരേഖമാണ് ചിത്രം 2ല് കാണുന്നത്. ഇതിന്റെ അടിസ്ഥാനത്തില് കാറ്റിന്റെ പരിണതദിശ എന്തായിരിക്കുമെന്നു നോക്കാം. സമമര്ദരേഖകളുടെ പ്രത്യേകമായ വിന്യാസക്രമത്തില് മര്ദപ്രവണതാബലത്തിന്റെ ദിശ ചിത്രത്തില് കാണിച്ചിരിക്കുന്നു. കാറ്റിന്റെ ഒഴുക്ക് സന്തുലിതമാകുമ്പോള് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാബലത്തിനു തുല്യവും നേര്വിപരീതവും ആവണം: ഇത് കാറ്റിന്റെ സഞ്ചാരദിശയുടെ വലതുപുറമാവുകയും വേണം. ഇക്കാരണത്താല് നിമ്നമര്ദത്തിനു വലത്തു സമമര്ദരേഖകള്ക്കു സമാന്തരമായാണ് വായുപിണ്ഡം ചലിക്കേണ്ടതെന്നു വരുന്നു. | മേല്പറഞ്ഞ രണ്ടുബലങ്ങളുടെ മാത്രം സ്വാധീനതയില് വീശുന്ന കാറ്റുകളെ ഭൂവിക്ഷേപവാതം എന്നു വിശേഷിപ്പിക്കുന്നു. മര്ദപ്രവണതയെയും ഭൂവിക്ഷേപബലത്തെയും ആധാരമാക്കി ഒരു വായുപിണ്ഡത്തിന് ഇരുപുറവുമായി വരച്ചിട്ടുള്ള സമമര്ദരേഖകളുടെ മാതൃകാആരേഖമാണ് ചിത്രം 2ല് കാണുന്നത്. ഇതിന്റെ അടിസ്ഥാനത്തില് കാറ്റിന്റെ പരിണതദിശ എന്തായിരിക്കുമെന്നു നോക്കാം. സമമര്ദരേഖകളുടെ പ്രത്യേകമായ വിന്യാസക്രമത്തില് മര്ദപ്രവണതാബലത്തിന്റെ ദിശ ചിത്രത്തില് കാണിച്ചിരിക്കുന്നു. കാറ്റിന്റെ ഒഴുക്ക് സന്തുലിതമാകുമ്പോള് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാബലത്തിനു തുല്യവും നേര്വിപരീതവും ആവണം: ഇത് കാറ്റിന്റെ സഞ്ചാരദിശയുടെ വലതുപുറമാവുകയും വേണം. ഇക്കാരണത്താല് നിമ്നമര്ദത്തിനു വലത്തു സമമര്ദരേഖകള്ക്കു സമാന്തരമായാണ് വായുപിണ്ഡം ചലിക്കേണ്ടതെന്നു വരുന്നു. | ||
മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തിനു തുല്യമായിരിക്കുമ്പോള് (i), (ii) എന്നീ വാക്യങ്ങളില് നിന്ന് | മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തിനു തുല്യമായിരിക്കുമ്പോള് (i), (ii) എന്നീ വാക്യങ്ങളില് നിന്ന് | ||
K1G = K2V V = K3G. (K3 എന്നത് മറ്റൊരു സ്ഥിരാങ്കം)......(iii) എന്നു സിദ്ധിക്കുന്നു. അതായത് കാറ്റിന്റെ ഗതിവേഗം ഢ മര്ദപ്രവണതയ്ക്ക് ആനുപാതികവും സമമര്ദരേഖകള് തമ്മിലുള്ള അകലത്തിന് വിപരീതാനുപാതികവുമായിരിക്കും. | K1G = K2V V = K3G. (K3 എന്നത് മറ്റൊരു സ്ഥിരാങ്കം)......(iii) എന്നു സിദ്ധിക്കുന്നു. അതായത് കാറ്റിന്റെ ഗതിവേഗം ഢ മര്ദപ്രവണതയ്ക്ക് ആനുപാതികവും സമമര്ദരേഖകള് തമ്മിലുള്ള അകലത്തിന് വിപരീതാനുപാതികവുമായിരിക്കും. | ||
| + | |||
പ്രായോഗികതലത്തില് ഭൂവിക്ഷേപവാതം ഒരു സങ്കല്പം മാത്രമാണെന്നു കാണാവുന്നതാണ്. എങ്കില്പ്പോലും സമമര്ദരേഖകളുടെ വിന്യാസം അടിസ്ഥാനമാക്കി ഇതിന്റെ മൂല്യനിര്ണയം സാധിക്കാവുന്നതാണ്. വാക്യം (ii) ലെ കൊരിയോലിസ് സമഷ്ടിജം ഗ2ന്റെ മൂല്യം പരിഗണിച്ചാല് മറ്റൊരു വസ്തുതകൂടി വ്യക്തമാകും. ഭൂഭ്രമണത്തിന്റെ കോണികപ്രവേഗം w, അക്ഷാംശം f എന്നിവയെ ആധാരമാക്കി M പിണ്ഡമായുള്ള വായുപിണ്ഡത്തിന്റെ കൊരിയോലിസ് സമഷ്ടിജം K2, | പ്രായോഗികതലത്തില് ഭൂവിക്ഷേപവാതം ഒരു സങ്കല്പം മാത്രമാണെന്നു കാണാവുന്നതാണ്. എങ്കില്പ്പോലും സമമര്ദരേഖകളുടെ വിന്യാസം അടിസ്ഥാനമാക്കി ഇതിന്റെ മൂല്യനിര്ണയം സാധിക്കാവുന്നതാണ്. വാക്യം (ii) ലെ കൊരിയോലിസ് സമഷ്ടിജം ഗ2ന്റെ മൂല്യം പരിഗണിച്ചാല് മറ്റൊരു വസ്തുതകൂടി വ്യക്തമാകും. ഭൂഭ്രമണത്തിന്റെ കോണികപ്രവേഗം w, അക്ഷാംശം f എന്നിവയെ ആധാരമാക്കി M പിണ്ഡമായുള്ള വായുപിണ്ഡത്തിന്റെ കൊരിയോലിസ് സമഷ്ടിജം K2, | ||
K2 = 2. M. w Sinf | K2 = 2. M. w Sinf | ||
എന്ന് വാക്യരൂപേണ ലഭിക്കുന്നു. Oo അക്ഷാംശത്തില് കൊരിയോലിസ് സമഷ്ടിജത്തിന്റെ മൂല്യവും പൂജ്യമായിത്തീരുന്നു. മധ്യരേഖാമേഖലയില് ഭൂവിക്ഷേപബലം അനുഭവപ്പെടുന്നില്ലെന്നും കാറ്റിന്റെ ഗതി തികച്ചും മര്ദപ്രവണതയെ അടിസ്ഥാനമാക്കി ആയിരിക്കുമെന്നുമാണ് ഇതു സൂചിപ്പിക്കുന്നത്. | എന്ന് വാക്യരൂപേണ ലഭിക്കുന്നു. Oo അക്ഷാംശത്തില് കൊരിയോലിസ് സമഷ്ടിജത്തിന്റെ മൂല്യവും പൂജ്യമായിത്തീരുന്നു. മധ്യരേഖാമേഖലയില് ഭൂവിക്ഷേപബലം അനുഭവപ്പെടുന്നില്ലെന്നും കാറ്റിന്റെ ഗതി തികച്ചും മര്ദപ്രവണതയെ അടിസ്ഥാനമാക്കി ആയിരിക്കുമെന്നുമാണ് ഇതു സൂചിപ്പിക്കുന്നത്. | ||
| - | ഘര്ഷണവും കാറ്റിന്റെ ഗതിയും. കാറ്റിന്റെ ശരാശരി വേഗത കണക്കാക്കുന്നത് ഭൂനിരപ്പില്നിന്ന് 10 മീ. ഉയരത്തിലുള്ള പ്രവേഗം അളന്നിട്ടാണ്. ഇങ്ങനെ നിര്ണയിക്കപ്പെടുന്ന വേഗതയും തറനിരപ്പിലെ സമമര്ദരേഖകളുടെ അടിസ്ഥാനത്തില് നിര്ണയിക്കപ്പെടുന്ന ഭൂവിക്ഷേപമൂല്യവും പല കാര്യത്തിലും സാദൃശ്യം പുലര്ത്തുമെങ്കിലും രണ്ടു പ്രധാന വ്യതിരേകങ്ങള് ശ്രദ്ധിക്കാവുന്നതാണ്: | + | |
| + | '''ഘര്ഷണവും കാറ്റിന്റെ ഗതിയും'''. കാറ്റിന്റെ ശരാശരി വേഗത കണക്കാക്കുന്നത് ഭൂനിരപ്പില്നിന്ന് 10 മീ. ഉയരത്തിലുള്ള പ്രവേഗം അളന്നിട്ടാണ്. ഇങ്ങനെ നിര്ണയിക്കപ്പെടുന്ന വേഗതയും തറനിരപ്പിലെ സമമര്ദരേഖകളുടെ അടിസ്ഥാനത്തില് നിര്ണയിക്കപ്പെടുന്ന ഭൂവിക്ഷേപമൂല്യവും പല കാര്യത്തിലും സാദൃശ്യം പുലര്ത്തുമെങ്കിലും രണ്ടു പ്രധാന വ്യതിരേകങ്ങള് ശ്രദ്ധിക്കാവുന്നതാണ്: | ||
[[ചിത്രം:Vol5p338_katrina-u s -2005.jpg|thumb|2005-ൽ യു.എസ്. തീരത്തു വീശിയ കത്രീന കൊടുങ്കാറ്റിന്റെ ഉപഗ്രഹചിത്രം]] | [[ചിത്രം:Vol5p338_katrina-u s -2005.jpg|thumb|2005-ൽ യു.എസ്. തീരത്തു വീശിയ കത്രീന കൊടുങ്കാറ്റിന്റെ ഉപഗ്രഹചിത്രം]] | ||
(i) ഭൂവിക്ഷേപദിശയില് നിന്ന് പിന്നാക്കംമാറിയ ഒരു ദിശയിലാണ് കാറ്റ് യഥാര്ഥത്തില് വീശുന്നത്; ഈ ചായ്വ് കടലിനുമുകളില് 10o യും കരയില് 30o യോളവുമായി കാണപ്പെടുന്നു. | (i) ഭൂവിക്ഷേപദിശയില് നിന്ന് പിന്നാക്കംമാറിയ ഒരു ദിശയിലാണ് കാറ്റ് യഥാര്ഥത്തില് വീശുന്നത്; ഈ ചായ്വ് കടലിനുമുകളില് 10o യും കരയില് 30o യോളവുമായി കാണപ്പെടുന്നു. | ||
(ii) യഥാര്ഥപ്രവേഗം ഭൂവിക്ഷേപമൂല്യത്തെ അപേക്ഷിച്ച് കുറവായിരിക്കും; കടലില് ഭാഗമായും കരയില് ആയും കുറഞ്ഞുകാണുന്നു. | (ii) യഥാര്ഥപ്രവേഗം ഭൂവിക്ഷേപമൂല്യത്തെ അപേക്ഷിച്ച് കുറവായിരിക്കും; കടലില് ഭാഗമായും കരയില് ആയും കുറഞ്ഞുകാണുന്നു. | ||
| + | |||
| + | [[ചിത്രം:Vol7_366_image3.jpg|300px]] | ||
| + | |||
മേല്പറഞ്ഞ വ്യതിരേകങ്ങള്ക്ക് ആസ്പദം ഘര്ഷണബല (frictional force)ത്തിന്റെ സ്വാധീനതയാണെന്നു കാണാം. ഘര്ഷണം ഭൂപ്രതലത്തിനും വായുപിണ്ഡത്തിനും ഇടയിലോ, വായുപിണ്ഡത്തിലെ തന്മാത്രകള്ക്കിടയിലോ പ്രാവര്ത്തികമാവാം. മര്ദപ്രവണത, ഭൂവിക്ഷേപം, ഘര്ഷണം എന്നീ ബലങ്ങള് പരസ്പരം സമതുലിതമായി വര്ത്തിച്ചാല്, കാറ്റിന്റെ ഗതി ചിത്രം 3ല് കാണിച്ചിരിക്കുന്നതുപോലെ ആയിരിക്കും. ഘര്ഷണത്തിന്റെ പ്രഭാവം ശക്തമായി അനുഭവപ്പെടുന്നത് തറനിരപ്പിന് അടുത്തായിരിക്കും; ഉയരം ചെല്ലുന്തോറും ഈ പ്രഭാവം പെട്ടെന്നു കുറഞ്ഞുകാണുന്നു. ശരാശരി 500 മീ.ന് ഉയരെ ഘര്ഷണത്തിന്റെ ശക്തി തികച്ചും വിഗണനീയമാണ്. അന്തരീക്ഷവായുവില് ഭൂപ്രതലത്തോടടുത്ത് ഉണ്ടായിക്കാണുന്ന വിക്ഷോഭങ്ങളുടെ പരിസീമയും 500 മീ. തന്നെയാണ്. ഇതിനുമുകളിലുള്ള ഉപര്യന്തരീക്ഷത്തില് ഭൂവിക്ഷേപവാതങ്ങള് ഉണ്ടായിരിക്കാവുന്നതാണെന്ന സൂചനയാണ് ഇത്നല്കുന്നത്. | മേല്പറഞ്ഞ വ്യതിരേകങ്ങള്ക്ക് ആസ്പദം ഘര്ഷണബല (frictional force)ത്തിന്റെ സ്വാധീനതയാണെന്നു കാണാം. ഘര്ഷണം ഭൂപ്രതലത്തിനും വായുപിണ്ഡത്തിനും ഇടയിലോ, വായുപിണ്ഡത്തിലെ തന്മാത്രകള്ക്കിടയിലോ പ്രാവര്ത്തികമാവാം. മര്ദപ്രവണത, ഭൂവിക്ഷേപം, ഘര്ഷണം എന്നീ ബലങ്ങള് പരസ്പരം സമതുലിതമായി വര്ത്തിച്ചാല്, കാറ്റിന്റെ ഗതി ചിത്രം 3ല് കാണിച്ചിരിക്കുന്നതുപോലെ ആയിരിക്കും. ഘര്ഷണത്തിന്റെ പ്രഭാവം ശക്തമായി അനുഭവപ്പെടുന്നത് തറനിരപ്പിന് അടുത്തായിരിക്കും; ഉയരം ചെല്ലുന്തോറും ഈ പ്രഭാവം പെട്ടെന്നു കുറഞ്ഞുകാണുന്നു. ശരാശരി 500 മീ.ന് ഉയരെ ഘര്ഷണത്തിന്റെ ശക്തി തികച്ചും വിഗണനീയമാണ്. അന്തരീക്ഷവായുവില് ഭൂപ്രതലത്തോടടുത്ത് ഉണ്ടായിക്കാണുന്ന വിക്ഷോഭങ്ങളുടെ പരിസീമയും 500 മീ. തന്നെയാണ്. ഇതിനുമുകളിലുള്ള ഉപര്യന്തരീക്ഷത്തില് ഭൂവിക്ഷേപവാതങ്ങള് ഉണ്ടായിരിക്കാവുന്നതാണെന്ന സൂചനയാണ് ഇത്നല്കുന്നത്. | ||
| - | കാറ്റിനെ സ്വാധീനിക്കുന്ന മറ്റു ഘടകങ്ങള്. കാറ്റിന്റെ ഗതിയെ മാറ്റിമറിക്കുന്നതില് ഘര്ഷണത്തിന് അതിപ്രധാനമായ പങ്കുണ്ട്. പ്രാദേശികമായി നോക്കുമ്പോള് ഇക്കാര്യത്തില് ഘര്ഷണത്തോടൊപ്പം പ്രഭാവം പുലര്ത്തുന്ന മറ്റുചില ഘടകങ്ങള് കൂടി ഉള്ളതായിക്കാണാം. ഈ ഘടകങ്ങള് ഭൂവിക്ഷേപഘടകവുമായി വിദൂരബന്ധംപോലുമില്ലാത്ത നിലയില് അനിയമിതമായ ദിശകളിലേക്ക് കാറ്റിന്റെ ഗതി മാറ്റിക്കുവാനുള്ള ശക്തിപോലും പുലര്ത്തിക്കാണുന്നു. | + | '''കാറ്റിനെ സ്വാധീനിക്കുന്ന മറ്റു ഘടകങ്ങള്'''. കാറ്റിന്റെ ഗതിയെ മാറ്റിമറിക്കുന്നതില് ഘര്ഷണത്തിന് അതിപ്രധാനമായ പങ്കുണ്ട്. പ്രാദേശികമായി നോക്കുമ്പോള് ഇക്കാര്യത്തില് ഘര്ഷണത്തോടൊപ്പം പ്രഭാവം പുലര്ത്തുന്ന മറ്റുചില ഘടകങ്ങള് കൂടി ഉള്ളതായിക്കാണാം. ഈ ഘടകങ്ങള് ഭൂവിക്ഷേപഘടകവുമായി വിദൂരബന്ധംപോലുമില്ലാത്ത നിലയില് അനിയമിതമായ ദിശകളിലേക്ക് കാറ്റിന്റെ ഗതി മാറ്റിക്കുവാനുള്ള ശക്തിപോലും പുലര്ത്തിക്കാണുന്നു. |
| + | |||
(i) വാസ്തുശില്പങ്ങള്, വന്മരങ്ങള്, കുന്നുകള് തുടങ്ങിയ എല്ലാ തടസ്സങ്ങളും കാറ്റിന്റെ ഒഴുക്കില് വരുത്തുന്ന പരിവര്ത്തനങ്ങള് സാരമായ വിക്ഷോഭ (turbelence) ങ്ങള്ക്കു കാരണമായിത്തീരാം. വ്യാപകമായ അളവില്, ഒരു താഴ്വര ഒട്ടാകെത്തന്നെ മര്ദവിന്യാസം സമാന്തരദിശയിലായിത്തീരുവാന് ഇത് കാരണമായിത്തീരുന്നു. പ്രത്യേക സാഹചര്യങ്ങളില് മര്ദപ്രവണത തീക്ഷ്ണമാവുകയും സമമര്ദവിതാനങ്ങള് ഇടതിങ്ങി വരികയും ചെയ്യുമ്പോള് വാതപിണ്ഡങ്ങള് ഊര്ന്നിറങ്ങി ശക്തമായ കാറ്റുവീശുവാനുള്ള സാധ്യതയുണ്ടാകുന്നു. "ഫോയന്മിസ്ട്രല്' തുടങ്ങിയ പ്രചണ്ഡങ്ങളായ സ്ഥാനീയവാതങ്ങള് ഇങ്ങനെ ഉണ്ടാകുന്നവയാണ്. | (i) വാസ്തുശില്പങ്ങള്, വന്മരങ്ങള്, കുന്നുകള് തുടങ്ങിയ എല്ലാ തടസ്സങ്ങളും കാറ്റിന്റെ ഒഴുക്കില് വരുത്തുന്ന പരിവര്ത്തനങ്ങള് സാരമായ വിക്ഷോഭ (turbelence) ങ്ങള്ക്കു കാരണമായിത്തീരാം. വ്യാപകമായ അളവില്, ഒരു താഴ്വര ഒട്ടാകെത്തന്നെ മര്ദവിന്യാസം സമാന്തരദിശയിലായിത്തീരുവാന് ഇത് കാരണമായിത്തീരുന്നു. പ്രത്യേക സാഹചര്യങ്ങളില് മര്ദപ്രവണത തീക്ഷ്ണമാവുകയും സമമര്ദവിതാനങ്ങള് ഇടതിങ്ങി വരികയും ചെയ്യുമ്പോള് വാതപിണ്ഡങ്ങള് ഊര്ന്നിറങ്ങി ശക്തമായ കാറ്റുവീശുവാനുള്ള സാധ്യതയുണ്ടാകുന്നു. "ഫോയന്മിസ്ട്രല്' തുടങ്ങിയ പ്രചണ്ഡങ്ങളായ സ്ഥാനീയവാതങ്ങള് ഇങ്ങനെ ഉണ്ടാകുന്നവയാണ്. | ||
(ii) ഒരു വായുപിണ്ഡത്തിന്റെ സഞ്ചാരപഥ (trajectory)ത്തില് ഉച്ചനിമ്നമര്ദകേന്ദ്രങ്ങളെ ആധാരമാക്കി ഉണ്ടാകാവുന്ന വക്രത മറ്റൊരു ഘടകമാണ്. വക്രദിശയില് ചലനം തുടരുന്നതിന് അഭികേന്ദ്രകം (centripetal) ആയ ഒരു ത്വരണം ഉണ്ടായിരിക്കണം. ഇതിന് കേന്ദ്രത്തിന്റെ നേര്ക്ക് പ്രവര്ത്തിക്കുന്ന ഒരു പരിണതബലവും ആവശ്യമാണ്. അതായത് മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തെക്കാള് കൂടുതലായിരിക്കണം. ഇതുപോലെ ഒരു ഗുരുമര്ദകേന്ദ്രത്തിനു ചുറ്റുമുള്ള വക്രഗതിക്ക് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാ ബലത്തെക്കാള് കൂടുതലായിരിക്കേണ്ടതുണ്ട്. ഇവയുടെ സ്വാധീനതയില് ഏതെങ്കിലും വക്രപഥത്തിലൂടെ സന്തുലിതമായി സഞ്ചരിക്കുന്ന കാറ്റിനെ മര്ദപ്രവണതാവാതം (Gradient wind) എന്നു വിശേഷിപ്പിക്കുന്നു. | (ii) ഒരു വായുപിണ്ഡത്തിന്റെ സഞ്ചാരപഥ (trajectory)ത്തില് ഉച്ചനിമ്നമര്ദകേന്ദ്രങ്ങളെ ആധാരമാക്കി ഉണ്ടാകാവുന്ന വക്രത മറ്റൊരു ഘടകമാണ്. വക്രദിശയില് ചലനം തുടരുന്നതിന് അഭികേന്ദ്രകം (centripetal) ആയ ഒരു ത്വരണം ഉണ്ടായിരിക്കണം. ഇതിന് കേന്ദ്രത്തിന്റെ നേര്ക്ക് പ്രവര്ത്തിക്കുന്ന ഒരു പരിണതബലവും ആവശ്യമാണ്. അതായത് മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തെക്കാള് കൂടുതലായിരിക്കണം. ഇതുപോലെ ഒരു ഗുരുമര്ദകേന്ദ്രത്തിനു ചുറ്റുമുള്ള വക്രഗതിക്ക് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാ ബലത്തെക്കാള് കൂടുതലായിരിക്കേണ്ടതുണ്ട്. ഇവയുടെ സ്വാധീനതയില് ഏതെങ്കിലും വക്രപഥത്തിലൂടെ സന്തുലിതമായി സഞ്ചരിക്കുന്ന കാറ്റിനെ മര്ദപ്രവണതാവാതം (Gradient wind) എന്നു വിശേഷിപ്പിക്കുന്നു. | ||
(iii) ഭൂവിക്ഷേപവാതം താരതമ്യേന ദുര്ബലമായിരിക്കുമ്പോള് കടല്ത്തീരങ്ങളില് കടല്കരക്കാറ്റുകള് ഉണ്ടാവുക സാധാരണമാണ്. ഇതിന് വായുപിണ്ഡങ്ങള്ക്കുള്ളില് ഊര്ധ്വാധരമായുണ്ടാകുന്ന വികാസസങ്കോചങ്ങള് ആവശ്യമാണ്. | (iii) ഭൂവിക്ഷേപവാതം താരതമ്യേന ദുര്ബലമായിരിക്കുമ്പോള് കടല്ത്തീരങ്ങളില് കടല്കരക്കാറ്റുകള് ഉണ്ടാവുക സാധാരണമാണ്. ഇതിന് വായുപിണ്ഡങ്ങള്ക്കുള്ളില് ഊര്ധ്വാധരമായുണ്ടാകുന്ന വികാസസങ്കോചങ്ങള് ആവശ്യമാണ്. | ||
| + | [[ചിത്രം:Vol5p338_katrina-u s -2005.jpg|thumb|2005-ൽ യു.എസ്. തീരത്തു വീശിയ കത്രീന കൊടുങ്കാറ്റിന്റെ ഉപഗ്രഹചിത്രം]] | ||
കാറ്റിന്റെ ഗതിയിലും സ്വഭാവത്തിലും ദിനംപ്രതി ഉണ്ടാകുന്ന വ്യതിയാനങ്ങള് ഭൂനിരപ്പുതൊട്ട് 500 മീ. വരെ ഉയരത്തിലുള്ള വിക്ഷോഭമണ്ഡലത്തിലെ സ്ഥായിത്വ(stability)ത്തെ ആശ്രയിച്ചിരിക്കും. സ്ഥായിയായ അന്തരീക്ഷത്തില് ഘര്ഷണബലത്തിന്റെ പ്രഭാവം കൂടുതല് ശക്തമാണ്. എന്നാല് അന്തരീക്ഷത്തിലെ അസ്ഥായിത്വം വായുപിണ്ഡത്തിനുള്ളിലെ ഇളക്കങ്ങള്ക്കും പിശറിനും സഹായകമാവുന്നതുമൂലം ഘര്ഷണത്തിന്റെ സ്വാധീനത കുറയ്ക്കുന്നു. ഇക്കാരണത്താല് കാറ്റിന്റെ വേഗത ഏറ്റവും കൂടുന്നത് മധ്യാഹ്നം കഴിഞ്ഞുള്ള സമയത്തായിരിക്കും. പ്രഭാതവേളയില് മന്ദമാരുതന് വീശുന്നതിന്റെ കാരണവും വേറൊന്നല്ല. നോ: ആഗോളവാതസഞ്ചരണം; പശ്ചിമവാതങ്ങള്; വാണിജ്യവാതങ്ങള് | കാറ്റിന്റെ ഗതിയിലും സ്വഭാവത്തിലും ദിനംപ്രതി ഉണ്ടാകുന്ന വ്യതിയാനങ്ങള് ഭൂനിരപ്പുതൊട്ട് 500 മീ. വരെ ഉയരത്തിലുള്ള വിക്ഷോഭമണ്ഡലത്തിലെ സ്ഥായിത്വ(stability)ത്തെ ആശ്രയിച്ചിരിക്കും. സ്ഥായിയായ അന്തരീക്ഷത്തില് ഘര്ഷണബലത്തിന്റെ പ്രഭാവം കൂടുതല് ശക്തമാണ്. എന്നാല് അന്തരീക്ഷത്തിലെ അസ്ഥായിത്വം വായുപിണ്ഡത്തിനുള്ളിലെ ഇളക്കങ്ങള്ക്കും പിശറിനും സഹായകമാവുന്നതുമൂലം ഘര്ഷണത്തിന്റെ സ്വാധീനത കുറയ്ക്കുന്നു. ഇക്കാരണത്താല് കാറ്റിന്റെ വേഗത ഏറ്റവും കൂടുന്നത് മധ്യാഹ്നം കഴിഞ്ഞുള്ള സമയത്തായിരിക്കും. പ്രഭാതവേളയില് മന്ദമാരുതന് വീശുന്നതിന്റെ കാരണവും വേറൊന്നല്ല. നോ: ആഗോളവാതസഞ്ചരണം; പശ്ചിമവാതങ്ങള്; വാണിജ്യവാതങ്ങള് | ||
(എന്.ജെ.കെ. നായര്) | (എന്.ജെ.കെ. നായര്) | ||
15:41, 7 ജൂലൈ 2014-നു നിലവിലുണ്ടായിരുന്ന രൂപം
കാറ്റ്
Wind
തിരശ്ചീനദിശയില് ചലിക്കുന്ന വായു, പ്രതലസ്വഭാവത്തിന് ആപേക്ഷികമായി ഭൂനിരപ്പിന് ഏറെക്കുറെ സമാന്തരമായി ചലിക്കുന്ന വായുധാരയാണ് കാറ്റ് അഥവാ വാതം. ഭൂപ്രതലത്തിലെ വിവിധഭാഗങ്ങള് വ്യത-്യസ്തതോതുകളില് ചൂടാകുകയും തണുക്കുകയും ചെയ്യുന്നതിന്റെ ഫലമായാണ് കാറ്റ് ഉണ്ടാകുന്നത്. അന്തരീക്ഷത്തിലെ താപനിലയിലും ജലാംശത്തിന്റെ തോതിലും ഉണ്ടാകുന്ന ഏറ്റക്കുറവുകളെ സമീകരിക്കുന്നതിന് ഒരിടത്തുനിന്നു മറ്റൊരിടത്തേക്ക് നീരാവിയെയും ഊര്ജഘടകങ്ങളെയും പരിവഹിച്ചെത്തിക്കുന്ന പ്രക്രിയയെ ആഗോളതലത്തില് പൂര്ത്തീകരിക്കുന്നത് നാനാദിശകളിലായി അനുസ-്യൂതം വീശിക്കൊണ്ടിരിക്കുന്ന കാറ്റുകളാണ്. താപോര്ജം സംക്രമിപ്പിച്ചും അന്തരീക്ഷത്തിലേക്കുയരുന്ന നീരാവിയെ നിര്ഗമിപ്പിച്ചും ബാഷ്പീകരണപ്രക്രിയയെ ത്വരിപ്പിക്കുന്നതില് കാറ്റുകള്ക്ക് വലുതായ പങ്കുണ്ട്. വര്ഷണത്തിനും അതിനു ഹേതുവായിത്തീരുന്ന മേഘജാലങ്ങളുടെ രൂപവത്കരണത്തിനും കാറ്റുകള് സഹായകങ്ങളാണ്. കടലുകളിലും ഇതര ജലാശയങ്ങളിലും അനന്തമായ തിരമാലകള് സൃഷ്ടിച്ചും അവയെ ശോഷിപ്പിച്ചും ഊര്ജസഞ്ചലനം സാധിക്കുന്നതും കാറ്റുകള് തന്നെയാണ്.
നിര്വചനപ്രകാരം പ്രത്യേകദിശയില് ഏതു വേഗതയിലും ചലിക്കുന്ന വായുവിനെ കാറ്റ് എന്നു പറയാം. കാറ്റിന്റെ ദിശ നിര്ണയിക്കുന്നത് ഏതു ഭാഗത്തുനിന്നു വീശുന്നു എന്നതിനെ ആശ്രയിച്ചാണ്. തെക്കുനിന്നു വരുന്ന കാറ്റിനെ തെക്കന് കാറ്റായും തെക്കുപടിഞ്ഞാറുനിന്നു വീശുന്നതിനെ തെക്കു പടിഞ്ഞാറന് കാറ്റായും വ്യവഹരിക്കുന്നു. കാറ്റിന്റെ വേഗത സൂചിപ്പിക്കുന്നതിന് നോട്ട് (knot)എന്ന മാനമാണ് സാധാരണ സ്വീകരിക്കുന്നത്. ഒരു നോട്ട് എന്നത് മണിക്കൂറില് 1.15 മൈല് (1.85 കി.മീ.) എന്ന ക്രമത്തിലുള്ള വേഗതയെക്കുറിക്കുന്നു. വായുവേഗം ശരാശരി സെക്കന്ഡില് ഇത്ര മീറ്ററെന്നോ, മണിക്കൂറില് ഇത്ര മൈല് അല്ലെങ്കില് ഇത്ര കിലോമീറ്റര് എന്നോ രേഖപ്പെടുത്താറുണ്ട്.
1 മീ./സെ. = 3.6 കി.മീ./മണി. = 2.237 മൈല്/മണി. = 1.944 നോട്ട്. കാറ്റിന്റെ വേഗത അളക്കുന്നതിനുള്ള ഉപകരണമാണ് അനീമോമീറ്റര്.
അന്തരീക്ഷവിജ്ഞാനികള് കാറ്റിന്റെ സാമാന-്യമായ വേഗത നിര്ണയിക്കുന്നതിന് ഒരു പ്രതേ-്യകതരം വര്ഗീകരണ സംവിധാനമാണ് ഉപയോഗിക്കുന്നത്. വേഗത അടിസ്ഥാനമാക്കി കാറ്റിനെ ഇനം തിരിക്കുന്ന ഈ മാപനവ-്യവസ്ഥയെ ബ്യൂഫര്ട്ട് സ്കെയില് (Beaufort scale) എന്നു പറയുന്നു. കാറ്റുകളുടെ വര്ഗീകരണം. ഉത്പത്തി, സഞ്ചാരദിശ, വേഗത, പരിസഞ്ചാരണം എന്നീ ഘടകങ്ങളെ ആശ്രയിച്ചും കാറ്റുകളെ ഇനം തിരിക്കാവുന്നതാണ്. ഇവയില് പരിസഞ്ചാരണത്തിന്റെ വ്യാപ്തി അടിസ്ഥാനമാക്കിയുള്ള വര്ഗീകരണത്തിനാണ് ആഗോളതല പ്രാധാന്യം.മൂന്ന് വാതവ്യവസ്ഥകളാണ് പൊതുവേ അംഗീകരിക്കപ്പെട്ടിട്ടുള്ളത്: ഭൂമണ്ഡലീയം (planetary), ദ്വിതീയം (secondary), സ്ഥാനീയം (tertiary). ഭൂമിയുടെ ഗോളാകൃതി, ഭൗമാന്തരീക്ഷത്തിന്റെ ചായ്വ്, ഭ്രമണം, പ്രദക്ഷിണം എന്നീ രീതികളില് ഭൂമിക്കുള്ള ചലനം എന്നിവയുടെ ഫലമായി ഉണ്ടാകുന്ന കാറ്റുകളാണ് ഭൂമണ്ഡലീയ വാതങ്ങളായി പരിഗണിക്കപ്പെടുന്നത്. വാണിജ്യവാതങ്ങള് (Trade winds), പെശ്ചിമവാതങ്ങള് (Westerlies), ധ്രുവവാതങ്ങള് (Polar winds)എന്നിവ ഈ വിഭാഗത്തില്പ്പെടുന്നു.
വായുപിണ്ഡങ്ങള് കൂട്ടിമുട്ടുന്നതിനെത്തുടര്ന്ന് ഉരുത്തിയിരിയുന്ന ചക്രവാതങ്ങള് (Cyclones); പ്രതിചക്രവാതങ്ങള് (Anticyclones); കെടല്, കര എന്നിവയുടെ ആപേക്ഷികസ്ഥാനങ്ങളെ ആശ്രയിച്ച് പ്രത്യേകഋതുക്കളില് വീശുന്ന മണ്സൂണ് കാറ്റുകള് തുടങ്ങിയവ ദ്വിതീയ വാതങ്ങളുടെ കൂട്ടത്തില്പ്പെടുന്നു. അന്തരീക്ഷാവസ്ഥയില് ദൈനികമോ താത്കാലികമോ ആയി ഏര്പ്പെടുന്ന ഏറ്റക്കുറവുകളുടെ ഫലമായി തികച്ചും സ്ഥാനീയമായി താരതമ്യേന ചെറിയ മേഖലകളില് മാത്രം അനുഭവപ്പെടുന്നയിനം കാറ്റുകളാണ് മൂന്നാമത്തെ വിഭാഗത്തില്പ്പെടുന്നത്. ഇവയില്ത്തന്നെ അന്തരീക്ഷ താപനിലയിലെ ഏറ്റക്കുറവുകളിലൂടെ ഉരുത്തിരിയുന്ന കരകടല്ക്കാറ്റുകള്, ഘനത്വ വാതങ്ങള് (Gravity winds)എന്ന ഉപവിഭാഗത്തില്പ്പെടുത്താറുണ്ട്.
കാറ്റുകള് നിരന്തരമായി വീശുന്നവയോ പ്രത്യേക കാലങ്ങളിലോ ദിവസങ്ങളിലോ അപൂര്വമായോ മാത്രം വീശുന്നവയോ ആവാം. സഞ്ചാരദിശയെ നേര്വിപരീതമായി വ്യതിചലിപ്പിക്കുന്ന ഉഭയദിശാ (amphidromic) വാതങ്ങളും ഉണ്ട്; കരകടല്ക്കാറ്റുകള് ഇതിനുദാഹരണങ്ങളാണ്.
വായുസഞ്ചലന സവിശേഷതകള്. ഭൗമോപരിതലത്തിലൂടെ സഞ്ചരിക്കുമ്പോള് വായുവിന് ദിശയിലും വേഗതയിലും അനുക്രമമായ ഏറ്റക്കുറവുകള് ഉണ്ടാകുന്നത് സാധാരണമാണ്. ഇതിന്റെ ഫലമായി നിശ്ചിതപഥത്തിലൂടെ സഞ്ചരിക്കുന്ന വായുപിണ്ഡത്തിന്റെ പ്രവേഗ(velocity)ത്തില് വ്യതിയാനം വരുന്നു. പ്രവേഗത്തിലെ ഏറ്റക്കുറവാണ് ത്വരണം (acceleration). ന്യൂട്ടന്റെ രണ്ടാമത്തെ ചലനനിയമപ്രകാരം വായുപിണ്ഡത്തിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുത്തുന്നതിന് പര്യാപ്തമായി ഏതെങ്കിലും ഒരു ബലം പ്രവര്ത്തിക്കേണ്ടതുണ്ട്. ഇതില്നിന്ന് വായുപിണ്ഡത്തിന്റെ സഞ്ചാരത്തിന്കാറ്റിന്ഹേതുകമായി എന്തൊക്കെയോ ബലങ്ങള് പ്രവര്ത്തിക്കുന്നുണ്ടെന്ന് അനുമാനിക്കാവുന്നതാണ്. ഈ ബലങ്ങളുടെ അനേ-്യാന്യ പ്രവര്ത്തനം ഏറെക്കുറെ സന്തുലിതമാകുമ്പോള് കാറ്റിന് ത്വരണം സംഭവിക്കുകയില്ല; സ്ഥിരമായ പ്രവേഗത്തോടെ കാറ്റ് വീശുകയും ചെയ്യും. നേരെമറിച്ച് മേല്പറഞ്ഞ ബലങ്ങള് അസന്തുലിതമായിരിക്കുമ്പോള് കാറ്റിന്റെ ഗതിയില് ത്വരണം ഏര്പ്പെടുന്നു. സാധാരണ അനുഭവത്തില്നിന്ന് കാറ്റിന്റെ പ്രവേഗത്തില് രണ്ടു രീതിയില് വ്യത്യാസം ഏര്പ്പെടുന്നതായിക്കാണാം: (i) ക്രമരഹിതമായ പിശറുകള്; നിമിഷങ്ങളോളം മാത്രം നീണ്ടുനില്ക്കുന്നവ; (ii) അനുക്രമമായി ഉണ്ടായി മണിക്കൂറുകളോ, ദിവസങ്ങളോളമോ നീണ്ടുനില്ക്കുന്നവ.
കാറ്റിന്റെ സാമാന്യ സ്വഭാവം പരിഗണിക്കുമ്പോള് ആദ-്യത്തെമാതിരി വേഗവ്യത്യാസങ്ങള് അവഗണിക്കാവുന്നതേ ഉള്ളൂ. എന്നാല് ഏറെ സമയം നീണ്ടുനില്ക്കുന്ന രണ്ടാമത്തെയിനം ഏറ്റക്കുറവുകളില് നന്നേ താണതായ ത്വരണം മൂലം കാറ്റ് തുടര്ച്ചയായും നിയതമായും വീശുന്നതായി അനുഭവപ്പെടുന്നു.
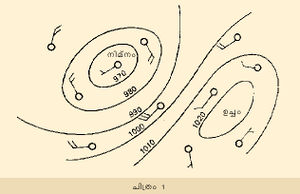
ഒരു പ്രത്യേക സ്ഥാനത്തെ കാറ്റിന്റെ വേഗതയും നിലവിലുള്ള മര്ദവ്യവസ്ഥയും നിരീക്ഷിച്ചാല് ഇവയ്ക്കിടയിലെ സവിശേഷബന്ധം ബോധ്യമാവുന്നതാണ്. ഉത്തരാര്ധഗോളത്തിലെ ഒരു നിശ്ചിത സ്ഥാനത്ത് നിരീക്ഷണത്തെത്തുടര്ന്ന് രേഖപ്പെടുത്തിയ സമ മര്ദരേഖകളും കാറ്റിന്റെ ഗതിയും ഉള്ക്കൊള്ളുന്ന ആരേഖമാണ് ചിത്രം 1. വായുദിശ രേഖപ്പെടുത്തുന്ന ശരങ്ങളിലെ തൂവലുകളില് ഓരോന്നും മണിക്കൂറില് 10 നോട്ട് എന്ന തോതിലും പകുതിത്തൂവല് മണിക്കൂറില് 5 നോട്ട് എന്ന തോതിലുമുള്ള വേഗത സൂചിപ്പിക്കുന്നു. ചിത്രം നിരീക്ഷിച്ചാല് രണ്ടു കാര്യങ്ങള് വ്യക്തമാകും: (i) കാറ്റുവീശുന്നത് സമ മര്ദരേഖകള്ക്ക് ഏതാണ്ട് സമാന്തരമായാണ്: ഏറ്റവും താണമര്ദം പ്രവേഗദിശയുടെ ഇടതുഭാഗത്തായിക്കാണുന്നു. (ii) സമ മര്ദരേഖകള് താരതമ്യേന തിങ്ങിക്കാണുന്ന ഇടങ്ങളില് വായുവേഗം ഏറ്റവും കൂടുതലായിരിക്കും.
വായുപ്രവേഗവും മര്ദവിതരണവും തമ്മിലുള്ള ഈ ബന്ധം ഒരു പൊതുനിയമമെന്ന നിലയില് പ്രചരിപ്പിച്ചത് (1857) ബൈസ്ബാലട്ട് എന്ന ശാസ്ത്രജ്ഞന് ആയിരുന്നു. "കാറ്റിന് പുറം തിരിഞ്ഞുനില്ക്കുന്ന ഒരു നിരീക്ഷകനെ സംബന്ധിച്ചിടത്തോളം നിമ്നമര്ദം ഉത്തരാര്ധഗോളത്തില് ഇടതു പുറത്തും ദക്ഷിണാര്ധഗോളത്തില് വലതുപുറത്തുമായിരിക്കും' എന്ന ഈ വസ്തുത ബൈസ്ബാലട്ട് നിയമം എന്ന് അറിയപ്പെടുന്നു. തികച്ചും വസ്തുനിഷ്ഠമല്ലെന്നിരിക്കിലും നാവികര്ക്കും മറ്റ് അന്തരീക്ഷ നിരീക്ഷകര്ക്കും മാര്ഗദര്ശനം നല്കുവാന് ഈ നിയമത്തിനുകഴിഞ്ഞു. ബൈസ്ബാലട്ട് നിയമം വ്യവച്ഛേദിച്ചുപരിശോധിച്ചാല് ഉത്തരാര്ധഗോളത്തെ സംബന്ധിച്ചിടത്തോളം ഉച്ചമര്ധത്തിനു ചുറ്റും പ്രദക്ഷിണദിശയിലും നിമ്നമര്ദത്തിനു ചുറ്റും അപ്രദക്ഷിണദിശയിലും കാറ്റുവീശുന്നതിനുള്ള സാധ്യത വ്യക്തമാവുന്നു.
ഭൂവിക്ഷേപവാതം (Geostrophic wind). സാമാന്യേന സന്തുലിതമായി വീശുന്ന കാറ്റുകളുടെ ഉദ്ഭവത്തിന് നിദാനവും അവയുടെ ഗതിയെ സ്വാധീനിക്കുന്നതുമായ ബല (force) ങ്ങളെ ഇനി പരിഗണിക്കാം. തികച്ചും സന്തുലിതമായ ഒരു വായുധാര ഉണ്ടെന്നിരിക്കട്ടെ. തിരശ്ചീനമായ ഗതി കണക്കാക്കുന്നതിനാല് വായുവിന്റെ ഭാരം ഉള്പ്പെടെ ഉര്ധ്വാധര ദിശയില് പ്രവര്ത്തിക്കുന്ന ബലങ്ങളെ തത്കാലം വിഗണിക്കാം. ക്ഷൈതിജ ദിശയില് പ്രവര്ത്തിക്കുന്ന രണ്ടു ബലങ്ങളുടെ പരിണത (resulrant) ദേിശയിലാണ് കാറ്റ് ഒഴുകുന്നതെന്നു വരുന്നു. ഈ രണ്ടു ബലങ്ങളില് ഒന്ന് മര്ദവിതരണത്തിലെ ഉച്ചനീചത്വങ്ങളെ അടിസ്ഥാനമാക്കി ഉണ്ടാവുന്ന ഘനത്വബലം (gradient force) ആണെന്ന് നേരത്തെ സൂചിപ്പിച്ചു. ഉച്ചമര്ദ (high) ത്തില്നിന്നും നിമ്നമര്ദ (low) ത്തിലേക്കു വായു ഒഴുകിനീങ്ങുന്നു. ഇടതൂര്ന്ന സമമര്ദരേഖകള് തീവ്രമായ മര്ദവ്യത്യാസം സൂചിപ്പിക്കുന്നു. ഈ രേഖകള്ക്കു കുറുകെ ലംബികദിശയില് ശക്തമായ ഘനത്വബലം (G) അനുഭവപ്പെടുന്നു. സാധാരണയായി G യുടെ തോത് കിലോമീറ്ററിന് 0.01 മില്ലിബാര് ആണ്. G യുടെ പരിമാണം സമമര്ദരേഖകള് ഇടതിങ്ങിയിരിക്കുമ്പോള് കൂടുതലായും അവ നന്നെ അകലത്തിലാകുമ്പോള് വളരെ കുറവായും കാണപ്പെടുന്നു. മര്ദവ്യതിയാനങ്ങളുടെ ഫലമായി ഉത്തേജിതമാകുന്ന മര്ദപ്രവണതാബലം (pressure gradient force) X, മര്ദഘനത്വം G യുമായി സമാനുപാതബന്ധം പുലര്ത്തുന്നു. ഈ ബന്ധത്തെ K1 എന്ന സ്ഥിരാങ്കത്തിന്റെ സഹായത്തോടെ
X = K1. G ........(i)
എന്ന് വാക്യരൂപേണ സൂചിപ്പിക്കാം. സമ മര്ദരേഖകളുടെ വിന്യാസക്രമത്തെ ഘി എന്ന സംജ്ഞയാല് വ്യഞ്ജിപ്പിച്ചാല് അത് ത മായി വിപരീതാനുപാതത്തിലായിരിക്കുമെന്നും മേല്പറഞ്ഞ വാക്യത്തില് നിന്ന് സിദ്ധിക്കുന്നു.
മര്ദപ്രവണതാബലത്തിനുമാത്രം വിധേയമായി ഒഴുകുന്ന വായുധാര അസന്തുലിതമായി നിമ്നമര്ദ കേന്ദ്രങ്ങളുടെ ഉള്ളിലേക്കു വീശുകയും അവ വായു തിങ്ങിക്കൂടുന്നതു നിമിത്തം ഗുരുമര്ദകേന്ദ്രങ്ങളായി മാറുകയും ചെയ്യേണ്ടതാണ്. എന്നാല് സാധാരണയായി ഇത്തരം പ്രക്രിയകള് പ്രാവര്ത്തികമായിക്കാണുന്നില്ല. ഇതില്നിന്ന് മര്ദപ്രവണതാബലത്തെ സമീകരിക്കുവാന് പോന്ന ഒരു ബലം കൂടിയെങ്കിലും കാറ്റിന്റെ ഗതിയെ സ്വാധീനിക്കുന്നുവെന്ന് അനുമാനിക്കേണ്ടിവരുന്നു. ഭൂഭ്രമണഫലമായി ഉരുത്തിരിയുന്ന ഒരു ബലമാണ് ഈ രീതിയിലുള്ള സ്വാധീനത ചെലുത്തുന്നതെന്ന് നിരീക്ഷണങ്ങളിലൂടെ ബോധ്യമായിട്ടുണ്ട്. സ്വന്തം അച്ചുതണ്ടിനെ ആധാരമാക്കി ഭ്രമണം ചെയ്യുന്ന ഭൂമിയുടെ ഗോളാകാരമായ പ്രതലത്തില് വര്ത്തിക്കുന്ന ഏതൊരുവസ്തുവും പ്രസ്തുത ചലനത്താല് പ്രരിപ്പിക്കപ്പെട്ട്, ഉത്തരാര്ധഗോളത്തില് വലത്തോട്ടും ദക്ഷിണാര്ധഗോളത്തില് ഇടത്തോട്ടും വ്യതിചലിക്കുന്നു. അനുസ്യൂതമായ ഈ സ്ഥാനചലനം വിവിധ അക്ഷാംശീയ മണ്ഡലങ്ങളില് അനുഭവപ്പെടുന്ന വ്യത്യസ്ത പ്രവേഗങ്ങളുടെ ഫലമായി വസ്തുവിന്റെ ഗതിയില് ത്വരണം (acceleration) ഏര്പ്പെടുത്തുന്നു. ഈ ത്വരണം അനുഭവപ്പെടുന്നത് വസ്തുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബമായ ദിശയിലാണ്. ഇത്തരം വ്യതിചലനത്തിന് നിദാനമായ ബലത്തിന് ഭൂവിക്ഷേപബലം (Geostrophic force) എന്നു പറയുന്നു. ഭൂവിക്ഷേപബലത്തിന്റെ മൂല്യം നിര്ണയിച്ചത് കൊരിയോലി (1792-1843) എന്ന ശാസ്ത്രജ്ഞനായിരുന്നു. ഇക്കാരണത്താല് ഭൂവിക്ഷേപബലത്തിനെ കൊരിയോലി ബലം എന്നും വിശേഷിപ്പിക്കാറുണ്ട്. ഭൂവിക്ഷേപബലം ഥ ചലിതവസ്തുവിന്റെ പ്രവേഗം ഢയുമായി സമാനുപാതത്തിലായിരിക്കും.
Y = K2. V..........(ii)
ഉത്തരാര്ധഗോളത്തില് ഈ ബലം പ്രവര്ത്തിക്കുന്നത് വായുവിന്റെ സഞ്ചാരപഥത്തിന് ലംബികമായി അതിന്റെ വലതു പാര്ശ്വത്തിലേക്കായിരിക്കും. ചലിക്കാത്ത വായുപിണ്ഡങ്ങളെ സംബന്ധിച്ചിടത്തോളം ഭൂവിക്ഷേപബലം അനുഭവയോഗ്യമല്ല.
മേല്പറഞ്ഞ രണ്ടുബലങ്ങളുടെ മാത്രം സ്വാധീനതയില് വീശുന്ന കാറ്റുകളെ ഭൂവിക്ഷേപവാതം എന്നു വിശേഷിപ്പിക്കുന്നു. മര്ദപ്രവണതയെയും ഭൂവിക്ഷേപബലത്തെയും ആധാരമാക്കി ഒരു വായുപിണ്ഡത്തിന് ഇരുപുറവുമായി വരച്ചിട്ടുള്ള സമമര്ദരേഖകളുടെ മാതൃകാആരേഖമാണ് ചിത്രം 2ല് കാണുന്നത്. ഇതിന്റെ അടിസ്ഥാനത്തില് കാറ്റിന്റെ പരിണതദിശ എന്തായിരിക്കുമെന്നു നോക്കാം. സമമര്ദരേഖകളുടെ പ്രത്യേകമായ വിന്യാസക്രമത്തില് മര്ദപ്രവണതാബലത്തിന്റെ ദിശ ചിത്രത്തില് കാണിച്ചിരിക്കുന്നു. കാറ്റിന്റെ ഒഴുക്ക് സന്തുലിതമാകുമ്പോള് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാബലത്തിനു തുല്യവും നേര്വിപരീതവും ആവണം: ഇത് കാറ്റിന്റെ സഞ്ചാരദിശയുടെ വലതുപുറമാവുകയും വേണം. ഇക്കാരണത്താല് നിമ്നമര്ദത്തിനു വലത്തു സമമര്ദരേഖകള്ക്കു സമാന്തരമായാണ് വായുപിണ്ഡം ചലിക്കേണ്ടതെന്നു വരുന്നു. മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തിനു തുല്യമായിരിക്കുമ്പോള് (i), (ii) എന്നീ വാക്യങ്ങളില് നിന്ന് K1G = K2V V = K3G. (K3 എന്നത് മറ്റൊരു സ്ഥിരാങ്കം)......(iii) എന്നു സിദ്ധിക്കുന്നു. അതായത് കാറ്റിന്റെ ഗതിവേഗം ഢ മര്ദപ്രവണതയ്ക്ക് ആനുപാതികവും സമമര്ദരേഖകള് തമ്മിലുള്ള അകലത്തിന് വിപരീതാനുപാതികവുമായിരിക്കും.
പ്രായോഗികതലത്തില് ഭൂവിക്ഷേപവാതം ഒരു സങ്കല്പം മാത്രമാണെന്നു കാണാവുന്നതാണ്. എങ്കില്പ്പോലും സമമര്ദരേഖകളുടെ വിന്യാസം അടിസ്ഥാനമാക്കി ഇതിന്റെ മൂല്യനിര്ണയം സാധിക്കാവുന്നതാണ്. വാക്യം (ii) ലെ കൊരിയോലിസ് സമഷ്ടിജം ഗ2ന്റെ മൂല്യം പരിഗണിച്ചാല് മറ്റൊരു വസ്തുതകൂടി വ്യക്തമാകും. ഭൂഭ്രമണത്തിന്റെ കോണികപ്രവേഗം w, അക്ഷാംശം f എന്നിവയെ ആധാരമാക്കി M പിണ്ഡമായുള്ള വായുപിണ്ഡത്തിന്റെ കൊരിയോലിസ് സമഷ്ടിജം K2, K2 = 2. M. w Sinf
എന്ന് വാക്യരൂപേണ ലഭിക്കുന്നു. Oo അക്ഷാംശത്തില് കൊരിയോലിസ് സമഷ്ടിജത്തിന്റെ മൂല്യവും പൂജ്യമായിത്തീരുന്നു. മധ്യരേഖാമേഖലയില് ഭൂവിക്ഷേപബലം അനുഭവപ്പെടുന്നില്ലെന്നും കാറ്റിന്റെ ഗതി തികച്ചും മര്ദപ്രവണതയെ അടിസ്ഥാനമാക്കി ആയിരിക്കുമെന്നുമാണ് ഇതു സൂചിപ്പിക്കുന്നത്.
ഘര്ഷണവും കാറ്റിന്റെ ഗതിയും. കാറ്റിന്റെ ശരാശരി വേഗത കണക്കാക്കുന്നത് ഭൂനിരപ്പില്നിന്ന് 10 മീ. ഉയരത്തിലുള്ള പ്രവേഗം അളന്നിട്ടാണ്. ഇങ്ങനെ നിര്ണയിക്കപ്പെടുന്ന വേഗതയും തറനിരപ്പിലെ സമമര്ദരേഖകളുടെ അടിസ്ഥാനത്തില് നിര്ണയിക്കപ്പെടുന്ന ഭൂവിക്ഷേപമൂല്യവും പല കാര്യത്തിലും സാദൃശ്യം പുലര്ത്തുമെങ്കിലും രണ്ടു പ്രധാന വ്യതിരേകങ്ങള് ശ്രദ്ധിക്കാവുന്നതാണ്:
(i) ഭൂവിക്ഷേപദിശയില് നിന്ന് പിന്നാക്കംമാറിയ ഒരു ദിശയിലാണ് കാറ്റ് യഥാര്ഥത്തില് വീശുന്നത്; ഈ ചായ്വ് കടലിനുമുകളില് 10o യും കരയില് 30o യോളവുമായി കാണപ്പെടുന്നു. (ii) യഥാര്ഥപ്രവേഗം ഭൂവിക്ഷേപമൂല്യത്തെ അപേക്ഷിച്ച് കുറവായിരിക്കും; കടലില് ഭാഗമായും കരയില് ആയും കുറഞ്ഞുകാണുന്നു.
മേല്പറഞ്ഞ വ്യതിരേകങ്ങള്ക്ക് ആസ്പദം ഘര്ഷണബല (frictional force)ത്തിന്റെ സ്വാധീനതയാണെന്നു കാണാം. ഘര്ഷണം ഭൂപ്രതലത്തിനും വായുപിണ്ഡത്തിനും ഇടയിലോ, വായുപിണ്ഡത്തിലെ തന്മാത്രകള്ക്കിടയിലോ പ്രാവര്ത്തികമാവാം. മര്ദപ്രവണത, ഭൂവിക്ഷേപം, ഘര്ഷണം എന്നീ ബലങ്ങള് പരസ്പരം സമതുലിതമായി വര്ത്തിച്ചാല്, കാറ്റിന്റെ ഗതി ചിത്രം 3ല് കാണിച്ചിരിക്കുന്നതുപോലെ ആയിരിക്കും. ഘര്ഷണത്തിന്റെ പ്രഭാവം ശക്തമായി അനുഭവപ്പെടുന്നത് തറനിരപ്പിന് അടുത്തായിരിക്കും; ഉയരം ചെല്ലുന്തോറും ഈ പ്രഭാവം പെട്ടെന്നു കുറഞ്ഞുകാണുന്നു. ശരാശരി 500 മീ.ന് ഉയരെ ഘര്ഷണത്തിന്റെ ശക്തി തികച്ചും വിഗണനീയമാണ്. അന്തരീക്ഷവായുവില് ഭൂപ്രതലത്തോടടുത്ത് ഉണ്ടായിക്കാണുന്ന വിക്ഷോഭങ്ങളുടെ പരിസീമയും 500 മീ. തന്നെയാണ്. ഇതിനുമുകളിലുള്ള ഉപര്യന്തരീക്ഷത്തില് ഭൂവിക്ഷേപവാതങ്ങള് ഉണ്ടായിരിക്കാവുന്നതാണെന്ന സൂചനയാണ് ഇത്നല്കുന്നത്.
കാറ്റിനെ സ്വാധീനിക്കുന്ന മറ്റു ഘടകങ്ങള്. കാറ്റിന്റെ ഗതിയെ മാറ്റിമറിക്കുന്നതില് ഘര്ഷണത്തിന് അതിപ്രധാനമായ പങ്കുണ്ട്. പ്രാദേശികമായി നോക്കുമ്പോള് ഇക്കാര്യത്തില് ഘര്ഷണത്തോടൊപ്പം പ്രഭാവം പുലര്ത്തുന്ന മറ്റുചില ഘടകങ്ങള് കൂടി ഉള്ളതായിക്കാണാം. ഈ ഘടകങ്ങള് ഭൂവിക്ഷേപഘടകവുമായി വിദൂരബന്ധംപോലുമില്ലാത്ത നിലയില് അനിയമിതമായ ദിശകളിലേക്ക് കാറ്റിന്റെ ഗതി മാറ്റിക്കുവാനുള്ള ശക്തിപോലും പുലര്ത്തിക്കാണുന്നു.
(i) വാസ്തുശില്പങ്ങള്, വന്മരങ്ങള്, കുന്നുകള് തുടങ്ങിയ എല്ലാ തടസ്സങ്ങളും കാറ്റിന്റെ ഒഴുക്കില് വരുത്തുന്ന പരിവര്ത്തനങ്ങള് സാരമായ വിക്ഷോഭ (turbelence) ങ്ങള്ക്കു കാരണമായിത്തീരാം. വ്യാപകമായ അളവില്, ഒരു താഴ്വര ഒട്ടാകെത്തന്നെ മര്ദവിന്യാസം സമാന്തരദിശയിലായിത്തീരുവാന് ഇത് കാരണമായിത്തീരുന്നു. പ്രത്യേക സാഹചര്യങ്ങളില് മര്ദപ്രവണത തീക്ഷ്ണമാവുകയും സമമര്ദവിതാനങ്ങള് ഇടതിങ്ങി വരികയും ചെയ്യുമ്പോള് വാതപിണ്ഡങ്ങള് ഊര്ന്നിറങ്ങി ശക്തമായ കാറ്റുവീശുവാനുള്ള സാധ്യതയുണ്ടാകുന്നു. "ഫോയന്മിസ്ട്രല്' തുടങ്ങിയ പ്രചണ്ഡങ്ങളായ സ്ഥാനീയവാതങ്ങള് ഇങ്ങനെ ഉണ്ടാകുന്നവയാണ്.
(ii) ഒരു വായുപിണ്ഡത്തിന്റെ സഞ്ചാരപഥ (trajectory)ത്തില് ഉച്ചനിമ്നമര്ദകേന്ദ്രങ്ങളെ ആധാരമാക്കി ഉണ്ടാകാവുന്ന വക്രത മറ്റൊരു ഘടകമാണ്. വക്രദിശയില് ചലനം തുടരുന്നതിന് അഭികേന്ദ്രകം (centripetal) ആയ ഒരു ത്വരണം ഉണ്ടായിരിക്കണം. ഇതിന് കേന്ദ്രത്തിന്റെ നേര്ക്ക് പ്രവര്ത്തിക്കുന്ന ഒരു പരിണതബലവും ആവശ്യമാണ്. അതായത് മര്ദപ്രവണതാബലം ഭൂവിക്ഷേപബലത്തെക്കാള് കൂടുതലായിരിക്കണം. ഇതുപോലെ ഒരു ഗുരുമര്ദകേന്ദ്രത്തിനു ചുറ്റുമുള്ള വക്രഗതിക്ക് ഭൂവിക്ഷേപബലം മര്ദപ്രവണതാ ബലത്തെക്കാള് കൂടുതലായിരിക്കേണ്ടതുണ്ട്. ഇവയുടെ സ്വാധീനതയില് ഏതെങ്കിലും വക്രപഥത്തിലൂടെ സന്തുലിതമായി സഞ്ചരിക്കുന്ന കാറ്റിനെ മര്ദപ്രവണതാവാതം (Gradient wind) എന്നു വിശേഷിപ്പിക്കുന്നു. (iii) ഭൂവിക്ഷേപവാതം താരതമ്യേന ദുര്ബലമായിരിക്കുമ്പോള് കടല്ത്തീരങ്ങളില് കടല്കരക്കാറ്റുകള് ഉണ്ടാവുക സാധാരണമാണ്. ഇതിന് വായുപിണ്ഡങ്ങള്ക്കുള്ളില് ഊര്ധ്വാധരമായുണ്ടാകുന്ന വികാസസങ്കോചങ്ങള് ആവശ്യമാണ്.
കാറ്റിന്റെ ഗതിയിലും സ്വഭാവത്തിലും ദിനംപ്രതി ഉണ്ടാകുന്ന വ്യതിയാനങ്ങള് ഭൂനിരപ്പുതൊട്ട് 500 മീ. വരെ ഉയരത്തിലുള്ള വിക്ഷോഭമണ്ഡലത്തിലെ സ്ഥായിത്വ(stability)ത്തെ ആശ്രയിച്ചിരിക്കും. സ്ഥായിയായ അന്തരീക്ഷത്തില് ഘര്ഷണബലത്തിന്റെ പ്രഭാവം കൂടുതല് ശക്തമാണ്. എന്നാല് അന്തരീക്ഷത്തിലെ അസ്ഥായിത്വം വായുപിണ്ഡത്തിനുള്ളിലെ ഇളക്കങ്ങള്ക്കും പിശറിനും സഹായകമാവുന്നതുമൂലം ഘര്ഷണത്തിന്റെ സ്വാധീനത കുറയ്ക്കുന്നു. ഇക്കാരണത്താല് കാറ്റിന്റെ വേഗത ഏറ്റവും കൂടുന്നത് മധ്യാഹ്നം കഴിഞ്ഞുള്ള സമയത്തായിരിക്കും. പ്രഭാതവേളയില് മന്ദമാരുതന് വീശുന്നതിന്റെ കാരണവും വേറൊന്നല്ല. നോ: ആഗോളവാതസഞ്ചരണം; പശ്ചിമവാതങ്ങള്; വാണിജ്യവാതങ്ങള്
(എന്.ജെ.കെ. നായര്)