This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ടൂറിങ് മെഷീന്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→ഭാഗങ്ങള്) |
(→ടേപ്പ്) |
||
| വരി 24: | വരി 24: | ||
===ടേപ്പ്=== | ===ടേപ്പ്=== | ||
| - | ചെറിയ സമചതുരങ്ങള് ഉള്ള അനന്തമായൊരു ടേപ്പാണിത്. ഓരോ ചതുരത്തിലും ഒരു ചിഹ്നം രേഖപ്പെടുത്തുകയും സൂക്ഷിച്ചു വയ്ക്കുകയും ചെയ്യാം. എന്നാല് തിരഞ്ഞെടുക്കാവുന്ന ചിഹ്നങ്ങളുടെ എണ്ണം ഇവിടെയും സാന്തമാണ്. ഈ ചിഹ്നങ്ങള് ഏത് അക്ഷരമാലയിലേതുമാകാം. ഉദാഹരണമായി | + | ചെറിയ സമചതുരങ്ങള് ഉള്ള അനന്തമായൊരു ടേപ്പാണിത്. ഓരോ ചതുരത്തിലും ഒരു ചിഹ്നം രേഖപ്പെടുത്തുകയും സൂക്ഷിച്ചു വയ്ക്കുകയും ചെയ്യാം. എന്നാല് തിരഞ്ഞെടുക്കാവുന്ന ചിഹ്നങ്ങളുടെ എണ്ണം ഇവിടെയും സാന്തമാണ്. ഈ ചിഹ്നങ്ങള് ഏത് അക്ഷരമാലയിലേതുമാകാം. ഉദാഹരണമായി {A,B,C...,Z,a,b,c,.....z}, {0, 1, 2, ..., n}{ 0, 1} എന്നീ ഗണങ്ങള് ചിഹ്ന ഗണത്തെ സൂചിപ്പിക്കുന്നവയാകാം. ഇത്തരത്തിലുള്ള ഗണങ്ങളില്നിന്ന് ആവശ്യാനുസരണം ഒരു ഗണം സ്വീകരിക്കാം. |
| - | + | ===റീഡ്-റൈറ്റ് ഹെഡ്=== | |
| - | + | ടേപ്പില് നിന്ന് കണ്ട്രോള് യൂണിറ്റിലേക്കും മറിച്ചും വിവരങ്ങള് കൈമാറുന്നത് റീഡ്-റൈറ്റ് ഹെഡ്ഡിലൂടെയാണ്. ടേപ്പിലെ സമചതുരത്തില് നിലവിലുള്ള വിവരം വായിച്ചശേഷം അതിന്റേയും മെഷീനിന്റെ അവസ്ഥയുടേയും അടിസ്ഥാനത്തില് പുതിയൊരു ചിഹ്നം രേഖപ്പെടുത്തുന്നു. തുടര്ന്ന് ടേപ്പിലൂടെ മുന്-പിന്-ഇടതു-വലത് ദിശകളില് ഏതെങ്കിലും ഒന്നിലേക്ക് ഒരു സമചതുര ദൂരം റീഡ്-റൈറ്റ് ഹെഡ് നീങ്ങുന്നു. തത്ഫലമായി മെഷീന് പുതിയൊരു അവസ്ഥയിലേക്ക് പ്രവേശിക്കുകയും ചെയ്യും. | |
| - | + | ==പ്രവര്ത്തന രീതി== | |
| - | + | പടിപടിയായിട്ടുള്ള നിരവധി വിവിക്ത പ്രക്രിയകളിലൂടെയാണ് (discrete steps) ടൂറിങ് മെഷീന് ഗണിത ക്രിയകള് ചെയ്യുന്നത്. ഏതു സമയത്തും മെഷീനിന്റെ പ്രവര്ത്തന രീതി പൂര്ണമായി നിശ്ചയിക്കുന്നത് അതിന്റെ റീഡ്-റൈറ്റ് ഹെഡ് വായിക്കുന്ന ചിഹ്നവും കണ്ട്രോള് യൂണിറ്റിന്റെ നിലവിലുള്ള ആന്തരിക അവസ്ഥയും ചേര്ന്നാണ്. മെഷീന്, ഏതു സമയത്തും, അതിന് അനുവദിച്ചിട്ടുള്ള സാന്ത അവസ്ഥകളിലേതെങ്കിലുമൊന്നിലായിരിക്കും. ഓരോ അവസ്ഥയിലും മെഷീനിന് നടപ്പാക്കേണ്ട ധാരാളം നിര്ദേശങ്ങള് കാണും. ഒരു നിശ്ചിത ചിഹ്നത്തെയാണ് മെഷീന് വായിക്കുന്നതെങ്കില് അത് വായിച്ചശേഷം എന്ത് ക്രിയ ചെയ്യണമെന്നും തുടര്ന്ന് മെഷീന് ഏത് അവസ്ഥയിലേക്ക് പോകണമെന്നും തീരുമാനിക്കുന്നത് ഈ നിര്ദേശങ്ങളാണ്. | |
| - | പ്രാപിക്കുന്നു. പുതിയതായി എഴുതുന്ന ചിഹ്നം ഇപ്പോള് വായിക്കുന്നതു തന്നെയാകാം; അതുപോലെ ടേപ്പില് റീഡ് - റൈറ്റ് ഹെഡ്ഡിനു കീഴിലുള്ള ചതുരത്തിനു മുകളില്ത്തന്നെ മുന്നോട്ടോ, | + | ടേപ്പിലെ ഒരു ചിഹ്നം സ്കാന് ചെയ്ത ശേഷം റീഡ്-റൈറ്റ് ഹെഡ് ടേപ്പില് ഒരു പുതിയ ചിഹ്നം എഴുതുന്നു. പിന്നീട് നിശ്ചിത നിര്ദേശ പ്രകാരം ഒരു ചതുര ദൂരം വലത്തോട്ടോ ഇടത്തോട്ടോ ഹെഡിനെ നീക്കി മെഷീന് പുതിയ ആന്തരിക അവസ്ഥയെ പ്രാപിക്കുന്നു. പുതിയതായി എഴുതുന്ന ചിഹ്നം ഇപ്പോള് വായിക്കുന്നതു തന്നെയാകാം; അതുപോലെ ടേപ്പില് റീഡ് - റൈറ്റ് ഹെഡ്ഡിനു കീഴിലുള്ള ചതുരത്തിനു മുകളില്ത്തന്നെ മുന്നോട്ടോ, പിന്നോട്ടോ പോകാതെ നില്ക്കുകയുമാവാം. പഴയ അവസ്ഥയിലേക്കു തന്നെ പുനപ്രവേശനവും നടത്താം; എന്നാല് ചില നിശ്ചിത 'ചിഹ്ന-അവസ്ഥാ' സാഹചര്യങ്ങളില് മെഷീന് നിശ്ചലമാവുകയും ചെയ്യും. |
| - | + | '''ടൂറിങ് - കംപ്യൂട്ടബിള് ഫലനം:''' വാസ്തവിക സംഖ്യകളുടെ (real numbers) ദശാംശ വിപുലീകരണത്തിലെ (decimal expansions) അക്കങ്ങളെ കണ്ടുപിടിക്കാനാണ് ടൂറിങ് മുഖ്യമായും തന്റെ മെഷീന് പ്രയോജനപ്പെടുത്തിയിരുന്നത്. എന്നാല് ടൂറിങ് മെഷീനുപയോഗിച്ച് ഏതു സംഖ്യാ-സിദ്ധാന്ത ഫലനത്തിന്റേയും മൂല്യം കണക്കാക്കാനും അനുയോജ്യമായ രീതിയില് അവയെ മാറ്റിയെടുക്കാനുമാവും. 'x' എന്ന ഓരോ ധനപൂര്ണ സംഖ്യയ്ക്കും (natural number) മെഷീന് ഏതെങ്കിലുമൊരു 'f' ഫലനത്തിന്റെ മൂല്യം y=f(x) എന്ന് കൃത്യമായി കണക്കാക്കുകയും, 'x' ആര്ഗുമെന്റ് നല്കിയാല് മെഷീന് 'f' ഫലനം ഗണിക്കുകയും ചെയ്താല്, 'f' നെ ടൂറിങ് - കംപ്യൂട്ടബിള് ഫലനമെന്ന് വിശേഷിപ്പിക്കാം. പില്ക്കാലത്ത് α- ഡിഫൈനബിള് ഫലനവും', പൊതു 'റിക്കേഴ്സീവ് ഫലനവും', 'ടൂറിങ്-കംപ്യൂട്ടബിള് - ഫലനവും', ഒന്നുതന്നെയെന്നു തെളിയിക്കപ്പെട്ടു. | |
| - | + | ==പ്രോഗ്രാം== | |
| - | + | ഓരോ ചിഹ്നം-അവസ്ഥാ കൂട്ടുകെട്ടിനും ടൂറിങ് മെഷീന് എന്തു ചെയ്യണം എന്ന് നിര്വചിച്ചിരിക്കുന്നത് അതിലെ പ്രോഗ്രാമിലാണ്. സ്റ്റേറ്റ് ട്രാന്സിഷന് ഡയഗ്രാം,' ഫ്ളോ ഡയഗ്രാം,' അസെംബ്ളി-ലൈക്ക് ലാങ്ഗ്വേജ്, പട്ടിക, നാലംഗ ഗണം (ലെ ീള ൂൌശിുൌഹല) എന്നിങ്ങനെ വ്യത്യസ്ത രീതിയില് ഈ പ്രോഗ്രാം രേഖപ്പെടുത്താം. | |
| - | + | ||
| - | + | ||
ഢ വിവിധ മാതൃകകള്. അമൂര്ത്ത കംപ്യൂട്ടിങ് ഉപകരണങ്ങളില്' വച്ച് ഏറ്റവും കൂടുതല് സൈദ്ധാന്തിക പഠനത്തിന് വിധേയമായിട്ടുള്ളത് ടൂറിങ് മെഷീനുകളാണ്. വിവിധ ഗണിത ശാസ്ത്രജ്ഞര് ടൂറിങ് മെഷീനിന്റെ ആദ്യ മാതൃകയ്ക്ക് പല രൂപമാറ്റങ്ങളും വരുത്തിയിട്ടുണ്ട്. എന്നാല് ഏതു ഫലന വര്ഗത്തേയും (ളൌിരശീിേ രഹമ) ആദ്യത്തെ ടൂറിങ് മെഷീനും അതിന്റെ പുതിയ മാതൃകകളും ഒരേ രീതിയില് തന്നെയാണ് കൈകാര്യം ചെയ്യുന്നത്. ഒരു വിഭാഗത്തില്പ്പെട്ട ഏതു മോഡലിന്റെ പ്രവര്ത്തനത്തേയും അനുകരിക്കുന്ന (ശാൌെഹമലേ) ഒരു സ്റ്റാന്ഡേഡ് ടൂറിങ് മെഷീന് ഉണ്ടായിരിക്കും; എന്നാല് വിവിധ മോഡലുകളുടെ ഗണന ദക്ഷത വ്യത്യസ്തമായിരിക്കാം. പോസ്റ്റ്-ഡേവിസ്, ഒണ്-എന്ഡഡ് ടേപ്പ്, പേപ്പര് ടേപ്പ്, ടു-സിംബല്, ടു-സ്റ്റേറ്റ്്, മള്ട്ടിടേപ്പ്, മള്ട്ടിഹെഡ്, മള്ട്ടിഡൈമെന്ഷെനെല്, ഫൈനൈറ്റ്-സ്റ്റേറ്റ്് നോണ്ഡിറ്റര്മിനിസ്റ്റിക്, റാന്ഡം അക്സെസ്, ഇട്രേറ്റീവ്-അരെ, മെഷീനുകള് ഇത്തരം മാതൃകകളില് പ്രധാനപ്പെട്ടവയാണ്. | ഢ വിവിധ മാതൃകകള്. അമൂര്ത്ത കംപ്യൂട്ടിങ് ഉപകരണങ്ങളില്' വച്ച് ഏറ്റവും കൂടുതല് സൈദ്ധാന്തിക പഠനത്തിന് വിധേയമായിട്ടുള്ളത് ടൂറിങ് മെഷീനുകളാണ്. വിവിധ ഗണിത ശാസ്ത്രജ്ഞര് ടൂറിങ് മെഷീനിന്റെ ആദ്യ മാതൃകയ്ക്ക് പല രൂപമാറ്റങ്ങളും വരുത്തിയിട്ടുണ്ട്. എന്നാല് ഏതു ഫലന വര്ഗത്തേയും (ളൌിരശീിേ രഹമ) ആദ്യത്തെ ടൂറിങ് മെഷീനും അതിന്റെ പുതിയ മാതൃകകളും ഒരേ രീതിയില് തന്നെയാണ് കൈകാര്യം ചെയ്യുന്നത്. ഒരു വിഭാഗത്തില്പ്പെട്ട ഏതു മോഡലിന്റെ പ്രവര്ത്തനത്തേയും അനുകരിക്കുന്ന (ശാൌെഹമലേ) ഒരു സ്റ്റാന്ഡേഡ് ടൂറിങ് മെഷീന് ഉണ്ടായിരിക്കും; എന്നാല് വിവിധ മോഡലുകളുടെ ഗണന ദക്ഷത വ്യത്യസ്തമായിരിക്കാം. പോസ്റ്റ്-ഡേവിസ്, ഒണ്-എന്ഡഡ് ടേപ്പ്, പേപ്പര് ടേപ്പ്, ടു-സിംബല്, ടു-സ്റ്റേറ്റ്്, മള്ട്ടിടേപ്പ്, മള്ട്ടിഹെഡ്, മള്ട്ടിഡൈമെന്ഷെനെല്, ഫൈനൈറ്റ്-സ്റ്റേറ്റ്് നോണ്ഡിറ്റര്മിനിസ്റ്റിക്, റാന്ഡം അക്സെസ്, ഇട്രേറ്റീവ്-അരെ, മെഷീനുകള് ഇത്തരം മാതൃകകളില് പ്രധാനപ്പെട്ടവയാണ്. | ||
09:45, 3 നവംബര് 2008-നു നിലവിലുണ്ടായിരുന്ന രൂപം
ഉള്ളടക്കം |
ടൂറിങ് മെഷീന്
Turing Machine
അലന് എം. ടൂറിങ് 1936-ല് കണ്ടുപിടിച്ച ഒരു സൈദ്ധാന്തിക അമൂര്ത്ത (abstract) കംപ്യൂട്ടിങ് ഉപകരണം. ഒരിക്കലും തെറ്റായ പ്രവര്ത്തനം കാണിക്കാത്ത ഇതിന്റെ വിവര സംഭരണ ശേഷി സീമാതീതമാണ്.
ആമുഖം
ടൂറിങ് എന്ന ബ്രിട്ടീഷ് ഗണിത ശാസ്ത്രജ്ഞന് 1936-ല് പ്രസിദ്ധീകരിച്ച 'ഓണ് കംപ്യൂട്ടബിള് നംബേഴ്സ് വിത്ത് ആന് ആപ്ലിക്കേഷന് ടു ദി എന്റ്ചെയ്ഡുന്ഗ്സ്പ്രോബ്ളെം എന്ന ഗവേഷണ പ്രബന്ധത്തിലാണ് ടൂറിങ് മെഷീനിനെപ്പറ്റി ആദ്യമായി സൂചന നല്കിയിട്ടുള്ളത്.
കംപ്യൂട്ടര് സയന്സ്, കംപ്യൂട്ടബിലിറ്റി, കംപ്യൂട്ടേഷന് എന്നീ ശാസ്ത്ര ശാഖകളുമായി ബന്ധപ്പെട്ട ആധുനിക സിദ്ധാന്തങ്ങളുടെ മൗലിക സങ്കല്പനമാണ് ടൂറിങ് മെഷീന്. ടൂറിങ് മെഷീന് ഉപയോഗിച്ച് ഏതു ഗണിത ക്രിയയും, അത് എത്ര സങ്കീര്ണമായതാണെങ്കില്ക്കൂടിയും, പരിഹരിക്കാനാവുമെന്ന് ടൂറിങ് തെളിയിച്ചു.
ആധുനിക കംപ്യൂട്ടറിന്റെ സൈദ്ധാന്തിക മുന്ഗാമിയായ ടൂറിങ് മെഷീന് കംപ്യൂട്ടറുകള്ക്ക് എന്ത് സാധ്യം, എന്ത് അസാധ്യം, എന്നു സൂചിപ്പിക്കുന്നു. വിവരങ്ങള് ശേഖരിച്ചു വയ്ക്കാന് ടൂറിങ് മെഷീനിനുള്ള ശേഷി അപരിമിതമായതിനാല് ഒരു കംപ്യൂട്ടിങ് യന്ത്രത്തിന്റെ കഴിവിന്റെ ഉപരി സീമ (upper limit) നിര്വചിക്കാനും ടൂറിങ് മെഷീനിന് സാധിക്കും. മാത്രമല്ല, ക്ലീന് (Kleene), ചര്ച് (Church), റോസെര് (Rosser), മാര്കോവ് (Markov)തുടങ്ങിയവരുടെ ഫോര്മല് സിസ്റ്റം ഉപയോഗിച്ച് നിര്വചിക്കാവുന്ന എല്ലാ ഫലന വിഭാഗങ്ങളേയും (function classes) ടൂറിങ് മെഷീനുകളുപയോഗിച്ചും നിര്വചിക്കാനാവുമെന്ന് തെളിയിക്കപ്പെട്ടിട്ടുണ്ട്.
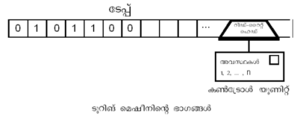
ഭാഗങ്ങള്
ടൂറിങ് മെഷീനിന് കണ്ട്രോള് യൂണിറ്റ് അഥവാ നിയന്ത്രണ ഘടകം, ടേപ്പ്, റീഡ്-റൈറ്റ് ഹെഡ് എന്നീ മൂന്നു ഭാഗങ്ങളുണ്ട്
കണ്ട്രോള് യൂണിറ്റ്
ഇതിന് വിവിധ അവസ്ഥകള് (states) സ്വീകരിക്കാമെങ്കിലും അനുവദനീയ അവസ്ഥകളുടെ എണ്ണം സാന്തം (finite) ആണ്. എല്ലാ അവസ്ഥയിലും ഇതിന് റീഡ്-റൈറ്റ്' ഹെഡ് ഉപയോഗിച്ച് ടേപ്പിലെ ഒരു സമചതുരത്തില് നിന്ന് ഒരു ചിഹ്നം വായിക്കാനാകും. യൂണിറ്റിന്റെ നിലവിലുള്ള അവസ്ഥയേയും വായിച്ച ചിഹ്നത്തേയും അടിസ്ഥാനമാക്കി യൂണിറ്റ് അതിന്റെ നിലവിലുള്ള അവസ്ഥയില് നിന്ന് മറ്റൊന്നിലേക്ക് പ്രവേശിക്കുന്നു.
ടേപ്പ്
ചെറിയ സമചതുരങ്ങള് ഉള്ള അനന്തമായൊരു ടേപ്പാണിത്. ഓരോ ചതുരത്തിലും ഒരു ചിഹ്നം രേഖപ്പെടുത്തുകയും സൂക്ഷിച്ചു വയ്ക്കുകയും ചെയ്യാം. എന്നാല് തിരഞ്ഞെടുക്കാവുന്ന ചിഹ്നങ്ങളുടെ എണ്ണം ഇവിടെയും സാന്തമാണ്. ഈ ചിഹ്നങ്ങള് ഏത് അക്ഷരമാലയിലേതുമാകാം. ഉദാഹരണമായി {A,B,C...,Z,a,b,c,.....z}, {0, 1, 2, ..., n}{ 0, 1} എന്നീ ഗണങ്ങള് ചിഹ്ന ഗണത്തെ സൂചിപ്പിക്കുന്നവയാകാം. ഇത്തരത്തിലുള്ള ഗണങ്ങളില്നിന്ന് ആവശ്യാനുസരണം ഒരു ഗണം സ്വീകരിക്കാം.
റീഡ്-റൈറ്റ് ഹെഡ്
ടേപ്പില് നിന്ന് കണ്ട്രോള് യൂണിറ്റിലേക്കും മറിച്ചും വിവരങ്ങള് കൈമാറുന്നത് റീഡ്-റൈറ്റ് ഹെഡ്ഡിലൂടെയാണ്. ടേപ്പിലെ സമചതുരത്തില് നിലവിലുള്ള വിവരം വായിച്ചശേഷം അതിന്റേയും മെഷീനിന്റെ അവസ്ഥയുടേയും അടിസ്ഥാനത്തില് പുതിയൊരു ചിഹ്നം രേഖപ്പെടുത്തുന്നു. തുടര്ന്ന് ടേപ്പിലൂടെ മുന്-പിന്-ഇടതു-വലത് ദിശകളില് ഏതെങ്കിലും ഒന്നിലേക്ക് ഒരു സമചതുര ദൂരം റീഡ്-റൈറ്റ് ഹെഡ് നീങ്ങുന്നു. തത്ഫലമായി മെഷീന് പുതിയൊരു അവസ്ഥയിലേക്ക് പ്രവേശിക്കുകയും ചെയ്യും.
പ്രവര്ത്തന രീതി
പടിപടിയായിട്ടുള്ള നിരവധി വിവിക്ത പ്രക്രിയകളിലൂടെയാണ് (discrete steps) ടൂറിങ് മെഷീന് ഗണിത ക്രിയകള് ചെയ്യുന്നത്. ഏതു സമയത്തും മെഷീനിന്റെ പ്രവര്ത്തന രീതി പൂര്ണമായി നിശ്ചയിക്കുന്നത് അതിന്റെ റീഡ്-റൈറ്റ് ഹെഡ് വായിക്കുന്ന ചിഹ്നവും കണ്ട്രോള് യൂണിറ്റിന്റെ നിലവിലുള്ള ആന്തരിക അവസ്ഥയും ചേര്ന്നാണ്. മെഷീന്, ഏതു സമയത്തും, അതിന് അനുവദിച്ചിട്ടുള്ള സാന്ത അവസ്ഥകളിലേതെങ്കിലുമൊന്നിലായിരിക്കും. ഓരോ അവസ്ഥയിലും മെഷീനിന് നടപ്പാക്കേണ്ട ധാരാളം നിര്ദേശങ്ങള് കാണും. ഒരു നിശ്ചിത ചിഹ്നത്തെയാണ് മെഷീന് വായിക്കുന്നതെങ്കില് അത് വായിച്ചശേഷം എന്ത് ക്രിയ ചെയ്യണമെന്നും തുടര്ന്ന് മെഷീന് ഏത് അവസ്ഥയിലേക്ക് പോകണമെന്നും തീരുമാനിക്കുന്നത് ഈ നിര്ദേശങ്ങളാണ്.
ടേപ്പിലെ ഒരു ചിഹ്നം സ്കാന് ചെയ്ത ശേഷം റീഡ്-റൈറ്റ് ഹെഡ് ടേപ്പില് ഒരു പുതിയ ചിഹ്നം എഴുതുന്നു. പിന്നീട് നിശ്ചിത നിര്ദേശ പ്രകാരം ഒരു ചതുര ദൂരം വലത്തോട്ടോ ഇടത്തോട്ടോ ഹെഡിനെ നീക്കി മെഷീന് പുതിയ ആന്തരിക അവസ്ഥയെ പ്രാപിക്കുന്നു. പുതിയതായി എഴുതുന്ന ചിഹ്നം ഇപ്പോള് വായിക്കുന്നതു തന്നെയാകാം; അതുപോലെ ടേപ്പില് റീഡ് - റൈറ്റ് ഹെഡ്ഡിനു കീഴിലുള്ള ചതുരത്തിനു മുകളില്ത്തന്നെ മുന്നോട്ടോ, പിന്നോട്ടോ പോകാതെ നില്ക്കുകയുമാവാം. പഴയ അവസ്ഥയിലേക്കു തന്നെ പുനപ്രവേശനവും നടത്താം; എന്നാല് ചില നിശ്ചിത 'ചിഹ്ന-അവസ്ഥാ' സാഹചര്യങ്ങളില് മെഷീന് നിശ്ചലമാവുകയും ചെയ്യും.
ടൂറിങ് - കംപ്യൂട്ടബിള് ഫലനം: വാസ്തവിക സംഖ്യകളുടെ (real numbers) ദശാംശ വിപുലീകരണത്തിലെ (decimal expansions) അക്കങ്ങളെ കണ്ടുപിടിക്കാനാണ് ടൂറിങ് മുഖ്യമായും തന്റെ മെഷീന് പ്രയോജനപ്പെടുത്തിയിരുന്നത്. എന്നാല് ടൂറിങ് മെഷീനുപയോഗിച്ച് ഏതു സംഖ്യാ-സിദ്ധാന്ത ഫലനത്തിന്റേയും മൂല്യം കണക്കാക്കാനും അനുയോജ്യമായ രീതിയില് അവയെ മാറ്റിയെടുക്കാനുമാവും. 'x' എന്ന ഓരോ ധനപൂര്ണ സംഖ്യയ്ക്കും (natural number) മെഷീന് ഏതെങ്കിലുമൊരു 'f' ഫലനത്തിന്റെ മൂല്യം y=f(x) എന്ന് കൃത്യമായി കണക്കാക്കുകയും, 'x' ആര്ഗുമെന്റ് നല്കിയാല് മെഷീന് 'f' ഫലനം ഗണിക്കുകയും ചെയ്താല്, 'f' നെ ടൂറിങ് - കംപ്യൂട്ടബിള് ഫലനമെന്ന് വിശേഷിപ്പിക്കാം. പില്ക്കാലത്ത് α- ഡിഫൈനബിള് ഫലനവും', പൊതു 'റിക്കേഴ്സീവ് ഫലനവും', 'ടൂറിങ്-കംപ്യൂട്ടബിള് - ഫലനവും', ഒന്നുതന്നെയെന്നു തെളിയിക്കപ്പെട്ടു.
പ്രോഗ്രാം
ഓരോ ചിഹ്നം-അവസ്ഥാ കൂട്ടുകെട്ടിനും ടൂറിങ് മെഷീന് എന്തു ചെയ്യണം എന്ന് നിര്വചിച്ചിരിക്കുന്നത് അതിലെ പ്രോഗ്രാമിലാണ്. സ്റ്റേറ്റ് ട്രാന്സിഷന് ഡയഗ്രാം,' ഫ്ളോ ഡയഗ്രാം,' അസെംബ്ളി-ലൈക്ക് ലാങ്ഗ്വേജ്, പട്ടിക, നാലംഗ ഗണം (ലെ ീള ൂൌശിുൌഹല) എന്നിങ്ങനെ വ്യത്യസ്ത രീതിയില് ഈ പ്രോഗ്രാം രേഖപ്പെടുത്താം.
ഢ വിവിധ മാതൃകകള്. അമൂര്ത്ത കംപ്യൂട്ടിങ് ഉപകരണങ്ങളില്' വച്ച് ഏറ്റവും കൂടുതല് സൈദ്ധാന്തിക പഠനത്തിന് വിധേയമായിട്ടുള്ളത് ടൂറിങ് മെഷീനുകളാണ്. വിവിധ ഗണിത ശാസ്ത്രജ്ഞര് ടൂറിങ് മെഷീനിന്റെ ആദ്യ മാതൃകയ്ക്ക് പല രൂപമാറ്റങ്ങളും വരുത്തിയിട്ടുണ്ട്. എന്നാല് ഏതു ഫലന വര്ഗത്തേയും (ളൌിരശീിേ രഹമ) ആദ്യത്തെ ടൂറിങ് മെഷീനും അതിന്റെ പുതിയ മാതൃകകളും ഒരേ രീതിയില് തന്നെയാണ് കൈകാര്യം ചെയ്യുന്നത്. ഒരു വിഭാഗത്തില്പ്പെട്ട ഏതു മോഡലിന്റെ പ്രവര്ത്തനത്തേയും അനുകരിക്കുന്ന (ശാൌെഹമലേ) ഒരു സ്റ്റാന്ഡേഡ് ടൂറിങ് മെഷീന് ഉണ്ടായിരിക്കും; എന്നാല് വിവിധ മോഡലുകളുടെ ഗണന ദക്ഷത വ്യത്യസ്തമായിരിക്കാം. പോസ്റ്റ്-ഡേവിസ്, ഒണ്-എന്ഡഡ് ടേപ്പ്, പേപ്പര് ടേപ്പ്, ടു-സിംബല്, ടു-സ്റ്റേറ്റ്്, മള്ട്ടിടേപ്പ്, മള്ട്ടിഹെഡ്, മള്ട്ടിഡൈമെന്ഷെനെല്, ഫൈനൈറ്റ്-സ്റ്റേറ്റ്് നോണ്ഡിറ്റര്മിനിസ്റ്റിക്, റാന്ഡം അക്സെസ്, ഇട്രേറ്റീവ്-അരെ, മെഷീനുകള് ഇത്തരം മാതൃകകളില് പ്രധാനപ്പെട്ടവയാണ്.
ഢക മേന്മകള്. സരളതയാണ് ടൂറിങ് മെഷീനിന്റെ ഏറ്റവും വലിയ ഗുണമേന്മയായി കണക്കാക്കപ്പെടുന്നത്. കൂടാതെ ഏതൊരു കംപ്യൂട്ടിങ് സിസ്റ്റത്തിനും വേണ്ട മൌലിക സ്വഭാവ വിശേഷങ്ങളായ ഫൈനൈറ്റ് പ്രോഗ്രാം, ബൃഹത്തായ ഡേറ്റ സ്റ്റോര്, പടിപടിയായുള്ളതും നിര്ധാരണാത്മകവുമായ ഗണന രീതി എന്നിവയും ഇതിനുണ്ട്. ഏതു കംപ്യൂട്ടറിന്റേയും പ്രവര്ത്തനത്തെ ഒരു ടൂറിങ് മെഷീനുപയോഗിച്ച് സിമുലേറ്റു ചെയ്യാന് കഴിയും; ചിലപ്പോള് മെഷീനിന്റെ പ്രവര്ത്തന വേഗത കുറവായിരിക്കുമെന്നു മാത്രം. അതുപോലെ ഏതു ടൂറിങ് മെഷീനിന്റെ പ്രവര്ത്തനത്തെ സിമുലേറ്റു ചെയ്യാനും കംപ്യൂട്ടറിനും സാധ്യമാണ്; പക്ഷേ, വലിയ അളവ് ഡേറ്റ കൈകാര്യം ചെയ്യാനുള്ള കഴിവ് കംപ്യൂട്ടറിന് ഉണ്ടായിരിക്കണം.
ഒരു അക്യുമുലേറ്ററും' വേണ്ടത്ര മെമ്മറി' അഥവാ സ്റ്റോറേജ്' ശേഷിയുമുള്ള ഒരു മിനി കംപ്യൂട്ടറില് സിംഗില് അഡ്രസ് 'വോണ് ന്യൂമാന്' മെഷീനിലെ ടഡആടഠഞഅഇഠ, ടഠഛഞഋ, ഠഞഅചടഎഋഞ ഛച ങകചഡട, എന്നീ മൂന്നു നിര്ദേശങ്ങളുപയോഗിച്ച്, ഏതു ഗണന ക്രിയയും ചെയ്യാനാകും. വ്യാഖ്യാനാത്മക (ശിലൃുൃേലശ്േല) നടപടിക്രമങ്ങള് ഉപയോഗിച്ച് ടൂറിങ് മെഷീനുകള്ക്ക് പരസ്പരം സിമുലേറ്റു ചെയ്യാനുമാകും. ഒരു ടൂറിങ് മെഷീനിന്റെ പ്രോഗ്രാം, ഇന്പുട്ട് ഡേറ്റ, എന്നിവ സ്വീകരിച്ച് പ്രസ്തുത ഗണന രീതി സിമുലേറ്റു ചെയ്യാവുന്ന തരത്തില് മറ്റൊരു ടൂറിങ് മെഷീനിന്റെ പ്രോഗ്രാം ചിട്ടപ്പെടുത്താനാകും. ഇത്തരത്തിലുള്ള ടൂറിങ് മെഷീനിനെ യൂണിവേഴ്സല് ടൂറിങ് മെഷീന്' എന്നു പറയുന്നു.
ഢകക ഗണന ക്രിയകളുടെ 'സമയ സങ്കീര്ണത'. ടൂറിങ് മെഷീന് ഗണന ക്രിയകളുടെ സമയ സങ്കീര്ണതയെക്കുറിച്ചുള്ള പഠനം യഥാര്ഥ ഹാര്ഡ്വെയെറുകളുപയോഗിച്ചുള്ള ഗണനത്തിന്റെ ദക്ഷതയെക്കുറിച്ചറിയാന് സഹായകമാണ്.
പ്രോസസ്സറുകളുടെ എണ്ണം സാന്തമായ ഏതൊരു മെഷീനും ഉപയോഗിച്ച് ചെയ്യുന്ന ഗണന ക്രിയകളുടെ മൂല്യത്തിന്റെ ബഹുപദ ഫലനമായി കണക്കാക്കാവുന്നതാണ്, പ്രസ്തുത ക്രിയയ്ക്ക് ഒരു ടൂറിങ് മെഷീനില് വേണ്ടിവരുന്ന ഗണന ക്രിയകളുടെ എണ്ണം. അതുപോലെ ഏറ്റവും കുറഞ്ഞത് രണ്ട് ടേപ്പെങ്കിലും ടൂറിങ് മെഷീനില് ഉണ്ടെങ്കില് അതിന്റെ പ്രവര്ത്തനത്തിനുള്ള ചെലവും യഥാര്ഥ മെഷീനിന്റെ പ്രവര്ത്തന ചെലവും തമ്മിലുള്ള ബന്ധം മിക്കപ്പോഴും രേഖീയമായിരിക്കും.
ടേപ്പിലെ ഒരു സമചതുരത്തില് ഏറ്റവും കുറഞ്ഞത് രണ്ട് ചിഹ്നമെങ്കിലും ഉള്ക്കൊള്ളിക്കാവുന്ന തരത്തില് ചിഹ്ന ഗണത്തെ വിപുലീകരിച്ചാല് (ചിലപ്പോള് ഇതിനായി കൂടുതല് പ്രോഗ്രാമിങ് ആവശ്യമായെന്നിരിക്കും.) ടൂറിങ് മെഷീനിന്റെ പ്രവര്ത്തന വേഗതയെ ആദ്യത്തേതിനെ അപേക്ഷിച്ച് രണ്ട് മടങ്ങോളമെങ്കിലും വര്ധിപ്പിക്കാവുന്നതാണ്. അതായത്, ഒരു മണിക്കൂര്, മെഷീന് പ്രവര്ത്തിപ്പിക്കുന്നതില് വരുന്ന ചെലവില് (മെഷീന് മണിക്കൂറിന്റെ മൂല്യം), മാറ്റമുണ്ടാകുന്നില്ല. മറിച്ച്, ഒരു യഥാര്ഥ മെഷീനിന്റെ വേഗത ഇരട്ടിയാക്കണമെങ്കില് ഒന്നുകില് വിലകൂടിയ ഹാര്ഡ്വെയെറുപയോഗിക്കേണ്ടിവരും; അല്ലെങ്കില് അതിലെ സാങ്കേതിക രീതിയില് വലിയൊരു മാറ്റമുണ്ടാക്കണം. ഇതിലേതു സംഭവിച്ചാലും മെഷീനിന്റെ മെഷീന് മണിക്കൂറിന്റെ' മൂല്യം വര്ധിക്കുകയേയുള്ളു.
പോസ്റ്റ്-ഡേവിഡ്, ഒണ് എന്ഡഡ് ടേപ്പ്, ടു-ടേപ്പ്, എന്നീ രൂപഭേദങ്ങള്ക്ക് സാധാരണയുള്ള ഒണ്-ടേപ്പ് ടൂറിങ് മെഷീ നിന്റെയത്ര വേഗതയില് പ്രവര്ത്തിക്കാനാകും. എന്നാല്, പരിമിത ചിഹ്നങ്ങളുള്ള ഒരു ടു-സിംബല് മെഷീനിന്റെ വേഗത ഒണ്-ടേപ്പിന്റേതിനെക്കാള് കുറവായിരിക്കും.
ഒണ്-ടേപ്പ് ടൂറിങ് മെഷീനുകള്ക്ക്, സമയ നഷ്ടം കൂടാതെ മള്ട്ടിടേപ്പ് ഇനങ്ങളെ എല്ലായ്പ്പോഴും സിമുലേറ്റു ചെയ്യാനാവില്ല. ഉദാഹരണത്തിന് പ്രോസസറുകളുടെ എണ്ണം സാന്തമായ ഏതൊരു ടൂറിങ് മെഷീനും ' സമയം കൊണ്ടു ചെയ്തു തീര്ക്കുന്ന ഒരു ഗണന ക്രിയയെ ഒരു ഒണ്-ടേപ്പ് മെഷീനില് സിമുലേറ്റു ചെയ്താല് അതില് പ്രസ്തുത ക്രിയ പൂര്ത്തിയാക്കാന് വേണ്ടിവരുന്ന പരമാവധി സമയം 2 ആയിരിക്കും; അതില് കൂടില്ല. തന്മൂലം ഒണ്-ടേപ്പ് ഇനത്തെ അപേക്ഷിച്ച് ദക്ഷത കൂടിയവയാണ് മള്ട്ടിടേപ്പ്, മള്ട്ടിഹെഡ്ഡ്, മള്ട്ടിഡൈമെന്ഷെനെല് ഇനങ്ങള്. അതിനാല് ദക്ഷതാ പഠനങ്ങള്ക്ക് ഏറ്റവും ഉത്തമം മള്ട്ടിടേപ്പ് മോഡലാണ്. എന്നാല് കംപ്യൂട്ടബിലിറ്റി - നോണ്കംപ്യൂട്ടബിലിറ്റി പഠനത്തിന് അനുയോജ്യം സരള പ്രവര്ത്തനമുള്ള ഒണ്-ടേപ്പ് ഇനം തന്നെ.
ഢകകക ഡിസൈന് പ്രോഗ്രാമുകള്. ഇന്ന് വിവിധ വെബ്സൈറ്റുകളില് ടൂറിങ് മെഷീന് ഡിസൈന് പ്രോഗ്രാമുകളും അവയുടെ വിന്ഡൊ' വേര്ഷനും ലഭ്യമാണ്. ഇതുപയോഗിച്ച് വിദ്യാര്ഥികള്ക്ക് ടൂറിങ് മെഷീന് രൂപകല്പനയും ഡീബഗ്ഗിങ്ങും നിര്വഹിക്കാനാവും. സാധാരണ വേഡ് പ്രോസസ്സറുകളില് കാണപ്പെടുന്ന കട്ട്-കോപ്പി-പെയിസ്റ്റ് സൌകര്യം ഇതിലും ലഭ്യമാണ്.