Current revision as of 04:47, 29 നവംബര്‍ 2014

അങ്കഗണിതഫലനം

Arithmetic function

ഗണിതശാസ്ത്രത്തില്‍, ഒരു ധനപൂര്‍ണസംഖ്യയെ (positive integer) മറ്റൊന്നായി രൂപാന്തരപ്പെടുത്തുമ്പോള്‍ അത് ഉള്‍ക്കൊള്ളുന്ന ക്രിയ. വിപുലമായ അര്‍ഥത്തില്‍, ഒരു വസ്തു മറ്റൊന്നായി മാറുമ്പോള്‍ ആ പ്രക്രിയയില്‍ ഉള്‍ക്കൊള്ളുന്ന ക്രിയയെ സൂചിപ്പിക്കുന്നതാണ് ഫലനം. ഒരു സംഖ്യയുടെ മൂന്നിരട്ടിയോട് അഞ്ച് ചേര്‍ത്താല്‍ മറ്റൊരു സംഖ്യയുണ്ടാകുന്നു. ഇതില്‍ സാമാന്യമായി സംഖ്യയെ n എന്നു സൂചിപ്പിച്ചാല്‍ പുതിയ സംഖ്യ 3n + 5 എന്നായിരിക്കും. 3n + 5 എന്ന സംഖ്യ രൂപപ്പെടാന്‍ n എന്ന സംഖ്യയില്‍ ഏല്പിക്കുന്ന ക്രിയയ്ക്കാണ് ഇവിടെ n-ന്റെ ഫലനമെന്നു പറയുന്നത്: f(n)= 3n + 5. n ഒരു ധനപൂര്‍ണസംഖ്യയാകുമ്പോള്‍ 3n+ 5-ഉം ധനപൂര്‍ണസംഖ്യയാകുന്നു. അതുകൊണ്ട് ഇവിടെ f ഒരു അങ്കഗണിതഫലനമാണ്.

സംഖ്യകളുടെ സവിശേഷതകള്‍ സംഖ്യാസിദ്ധാന്ത(Theory of numbers)ത്തിലൂടെ ഫലനങ്ങളുപയോഗിച്ച് പഠിക്കുന്ന ഒരു ഗണിതശാഖയാണ് ഇത് ഉള്‍ക്കൊള്ളുന്നത്. ധനപൂര്‍ണസംഖ്യകള്‍ തമ്മിലുള്ള ബന്ധമാണ് ഇതിലെ പ്രധാന പ്രമേയം. ഉദാഹരണമായി ഏതു സംഖ്യയുടെയും രണ്ടിരട്ടി എന്ന ആശയം ഫലനംവഴി സൂചിപ്പിക്കാം.f(n) = 2n എന്ന നിര്‍വചനംകൊണ്ട് മേല്‍പറഞ്ഞ അര്‍ഥം വ്യക്തമാക്കാവുന്നതാണ്. ഇവിടെ n എന്നത് ഏതു ധനപൂര്‍ണസംഖ്യയുമാകാം. n = 3 ആണെങ്കില്‍, f(3) = 6 എന്നു ലഭിക്കുന്നു. ഇതിന്നര്‍ഥം : 3-ന്റെ രണ്ടിരട്ടി സമം 6. ഇതില്‍ f ഒരു അങ്കഗണിതഫലനമാണ്. മിശ്രസംഖ്യാഗണത്തിന്റെ, ധനപൂര്‍ണസംഖ്യാഗണത്തിലേക്കുള്ള ഒരു രൂപാന്തരമാണ് അങ്കഗണിതഫലനം അഥവാ സംഖ്യാഫലനം എന്നു നിര്‍വചിക്കാം. അതായത് ഒരു മിശ്രസംഖ്യ ഒരു ധനപൂര്‍ണസംഖ്യയായി രൂപാന്തരപ്പെടുന്നു. ഇതിലുള്‍പ്പെടുന്ന നിയമമാണ് സംഖ്യാഫലനം. ധനപൂര്‍ണസംഖ്യകളുടെ സവിശേഷതകള്‍ പരിഗണിച്ച് അങ്കഗണിതഫലനങ്ങള്‍, സംഖ്യാസിദ്ധാന്തചരിത്രം (History of Number Theory) എഴുതിയ എല്‍.ഇ. ഡിക്സണ്‍ രേഖപ്പെടുത്തിയിട്ടുണ്ട്. I(n), E(n), d(n), μ(n), E₀(n) എന്നിവ ഉദാഹരണങ്ങളാണ്. അവിഭാജ്യഘടകങ്ങളായി n പിരിച്ചെഴുതിയാല്‍ n=p₁^a₁p₂^a₂......p_r^a_rഎന്നൊരു രൂപമുണ്ടാകുന്നു. P₁, P₂........ എന്നിവ വ്യത്യസ്തമായ അവിഭാജ്യഘടകങ്ങളാണ്. എങ്കില്‍ I(n) =n,E(n) = 1. n-ന്റെ ആകെയുള്ള ഘടകങ്ങളുടെ എണ്ണം സൂചിപ്പിക്കുന്നതാണ് d(n); μ(1) = 1, μ (p₁, ...........p_r) = (-1)^r, μ(p²) = 0. അതായത് n-ന് ഏതെങ്കിലുമൊരു വര്‍ഗസംഖ്യ (square) ഘടകമായുണ്ടെങ്കില്‍ ആ സംഖ്യയെ സംബന്ധിച്ച് μ എന്ന അങ്കഗണിതഫലനത്തിന്റെ മൂല്യം 0 ആണ്; E₀(1) = 1, മറ്റെല്ലാ പൂര്‍ണസംഖ്യകള്‍ക്കും E₀(n)=0. കുറെക്കൂടി ഉയര്‍ന്നതരം ഫലനങ്ങളാണ് φ(n), σ(n) എന്നിവ. ഓയിലര്‍ എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ പേരിലറിയപ്പെടുന്ന φ(n) (ഓയിലര്‍ ഫലനം) അങ്കഗണിതഫലനത്തില്‍ വളരെ പ്രാധാന്യമര്‍ഹിക്കുന്നു. ടോഷന്റ് ഫലനം (Totient function) എന്ന വര്‍ഗത്തില്‍പ്പെടുന്നു ഇത്. n = 12 എങ്കില്‍, 12-ല്‍ താഴെ 12-നോടു പൊതുഘടകമില്ലാത്ത ധനപൂര്‍ണസംഖ്യകളുടെ എണ്ണമാണ് φ(12) സൂചിപ്പിക്കുന്നത്, ഘടകങ്ങള്‍ പരിഗണിക്കുമ്പോള്‍ 1, 5, 7, 11 എന്നിവയുടെ എണ്ണം. അതായത്, φ(12) = 4. 1, 2, 3, 4, 6, 12 ആണ് 12-ന്റെ ഘടകങ്ങള്‍. അതുകൊണ്ട് d(12) = 6, σ(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28. അതായത് ഘടകങ്ങളുടെ ആകെത്തുക.

കോണ്‍വല്യൂഷനുകള്‍ (Convolutions). രണ്ട് അങ്കഗണിതഫലനങ്ങള്‍ തമ്മില്‍ ഗുണനാടിസ്ഥാനത്തില്‍ ബന്ധപ്പെടുന്ന സമ്പ്രദായമാണ് കോണ്‍വല്യൂഷന്‍. മൂലസംഖ്യയുടെ (argument) ഗുണനഘടകങ്ങളുടേയും സങ്കലനപദങ്ങളു(addition terms)ടേയും അടിസ്ഥാനങ്ങള്‍ അനുസരിച്ച് രണ്ടുതരത്തില്‍ കോണ്‍വല്യൂഷന്‍ ഉണ്ടാകുന്നു. ഇതില്‍ ആദ്യത്തേതിന് ഡിറീക്ലെ സംയോഗം (Dirchlet Composition ) എന്നും രണ്ടാമത്തേതിന് കോഷി സംയോഗം (Cauchy Composition ) എന്നും ആദ്യമായി പറഞ്ഞത് ഇ.ടി. ബെല്‍ ആണ്. f, g, h എന്നീ സംഖ്യാഫലനങ്ങള്‍ താഴെ കൊടുക്കുന്ന തരത്തില്‍ ബന്ധപ്പെട്ടിരുന്നാല്‍, അതായത് h (n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ ഒരു (ഡിറീക്ലെ) സംയോഗം ആണ് h എന്നു പറയപ്പെടുന്നു. h(n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ കോഷി സംയോഗവും. nന്റെ ഘടകങ്ങളെയാണ് d സൂചിപ്പിക്കു ന്നത്. ഘടകങ്ങളില്‍ n-ഉം ഉള്‍പ്പെടുന്നു. പഠനവിധേയമായിക്കൊണ്ടിരിക്കുന്ന സംയോഗമാണ് ആദ്യത്തേത്.

1930-തിനോടടുത്ത് ആര്‍. വൈദ്യനാഥസ്വാമി (മദ്രാസ് യൂണിവേഴ്സിറ്റിയില്‍ ഗണിതശാസ്ത്രവിഭാഗം പ്രൊഫസര്‍ ആയിരുന്നു) തന്റെ മെമോയര്‍ ഓണ്‍ മള്‍ട്ടിപ്ളിക്കേറ്റീവ് ഫങ്ഷന്‍സ് (Memoir on Multiplicative Functions) എന്ന ഗവേഷണപ്രബന്ധം പ്രസിദ്ധീകരിച്ചു. അതില്‍ നാലുതരം യോഗങ്ങളെപ്പറ്റി പറയുന്നു: സംയോഗം (കോമ്പോസിഷന്‍), കോണ്‍വല്യൂഷന്‍, ഫലനഗുണനം (മള്‍ട്ടിപ്ളിക്കേഷന്‍), ബ്ളോക് കോണ്‍വല്യൂഷന്‍.

ആദ്യം ഉദാഹരണമായി കാണിച്ച ഡിറിക്ലെ സംയോഗത്തെയാണ് സാധാരണയായി സംയോഗം എന്നു പറയുന്നത്; n എന്നതിന്റെ എല്ലാ ഘടകങ്ങളും ഉപയോഗപ്പെടുത്തി എഴുതാവുന്ന എല്ലാ പദങ്ങളുടെയും ആകെത്തുക. ഉദാ.

ഇതില്‍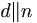 ${d} \Vert {n}$ എന്ന അങ്കനംകൊണ്ട് ഉദ്ദേശിക്കുന്നത്: n-ന്റെ ബ്ളോക്ക് ഘടകം, ഏകകഘടകം അഥവാ യൂണിറ്ററി ഘടകം ആണ് dഎന്ന ധനപൂര്‍ണസംഖ്യ. രണ്ടു പൂരക ഘടകങ്ങള്‍ക്കു തമ്മില്‍ പൊതുഘടകം 1 (ഒന്ന്) ഒഴികെ മറ്റൊന്നും ഇല്ലെങ്കില്‍ അവയെ ബ്ളോക്ക് ഘടകങ്ങള്‍ എന്നു പറയുന്നു. ഉദാ. 1, 3, 4, 12 എന്നിവ 12-ന്റെ ബ്ളോക്ക് ഘടകങ്ങളാണ്.

h (12) = f(1) g(12) + f(3) g(4) + f(4) g(3) + f(12) g(1).

ഇത്തരം കോണ്‍വല്യൂഷനുകള്‍ വേറെയുമുണ്ട്. സാധാരണ കോണ്‍വല്യൂഷനായ സംയോഗത്തിന്റെ സാമാന്യരൂപങ്ങളാണ് a-ഗുണനം, k-ഗുണനം എന്നിവ.

(1) a-ഗുണനം. a(m,n) ഒരു അങ്കഗണിതഫലനമാണെന്നു കരുതുക; m, n എന്നീ രണ്ടു പൂര്‍ണസംഖ്യകളെ ആസ്പദമാക്കിയുള്ള ഫലനം. എങ്കില്‍, h (n) = d/n-w എന്നത് f,g എന്നിവയുടെ a-ഗുണനമാണ്. a-ഫലനത്തെ കെര്‍ണല്‍ (കാതല്‍ = Kernel) എന്നു പറയുന്നു.

(ii) k-ഗുണനം. k(n) ഒരു അങ്കഗണിതഫലനമാണെന്നു കരുതുക. h (n) =(a) g(b). ഇതിന് f, g എന്നിവയുടെ k-ഗുണനമെന്നുപറയുന്നു. ഇവിടെ a,bസാമാന്യമായത്. a-ഗുണനത്തില്‍ സ-ഗുണനവും സാധാരണ സംയോഗവും ഇത്തരം മറ്റനവധി കോണ്‍വല്യൂഷനുകളും അടങ്ങിയിട്ടുണ്ട്. a-ഫലനത്തിന്റെ പ്രത്യേകതയനുസരിച്ച് a-ഗുണനത്തിന്റെ സ്വഭാവം മാറുന്നു.

പ്രതിലോമഫലനം (Inverse function ). f,g ഫലനങ്ങളുടെ സംയോഗത്തിന്റെ ഫലമായി ലഭിക്കുന്ന ഫലനം E₀ ആണെങ്കില്‍, അതായത് = E₀ (n) എങ്കില്‍ f-ഉം g-ഉം പരസ്പരം പ്രതിലോമഫലനങ്ങളാണെന്നു പറയുന്നു. f-ന്റെ പ്രതിലോമഫലനത്തെ f ^-1 (എഫ് പ്രതിലോമം) എന്നു രേഖപ്പെടുത്താറുണ്ട്. ഓരോ കോണ്‍വല്യൂഷനെയും അടിസ്ഥാനമാക്കി f-ന് പ്രതിലോമമുണ്ടായിരിക്കും. അഥവാ പ്രതിലോമഫലനം ഉണ്ടാക്കുന്ന പ്രക്രിയയ്ക്കു മാത്രമേ കോണ്‍വല്യൂഷന്‍ എന്നു പറയാവൂ. ഗ്രൂപ്പ് സിദ്ധാന്തത്തില്‍ കാണുന്ന പ്രതിലോമതത്ത്വം തന്നെയാണിവിടെയും (നോ: ഗ്രൂപ്പ് സിദ്ധാന്തം). അതായത് കോണ്‍വല്യൂഷന്‍ എന്നത് ഒരു ഗ്രൂപ്പ് ക്രിയയാണ്. അപ്പോള്‍ രണ്ട് അങ്കഗണിതഫലനങ്ങള്‍ കോണ്‍വല്യൂഷന്‍ വഴി കൂടിച്ചേരുമ്പോള്‍ മൂന്നാമതൊരു അങ്കഫലനമുണ്ടാകുന്നു; ഏത് അങ്കഫലനത്തിനും കോണ്‍വല്യൂഷന്‍ ക്രിയയിലൂടെ ഒരു പ്രതിലോമഫലനമുണ്ടാകുന്നു; ഈ ക്രിയയുടെതന്നെ അടിസ്ഥാനത്തില്‍ ഒരു ഏകകഫലനമുണ്ടാകുന്നു. ഇത്രയുമായാല്‍ അങ്കഗണിതഫലനഗണം തന്നെ സാങ്കേതികാര്‍ഥത്തില്‍ കോണ്‍വല്യൂഷന്‍ ക്രിയ ഉള്‍ക്കൊള്ളുന്ന ഒരു ഗ്രൂപ്പ് ആണെന്നു പറയാം.

ഗുണനാത്മക അങ്കഗണിതഫലനം (Multiplicative functions). അങ്കഗണിതഫലനങ്ങള്‍ പൊതുവേ അനവധി മൂലകാങ്കങ്ങളെ ആധാരമാക്കിയാകാം:

f(m₁,m₂, .........., m_r). (m₁n₁, m₂n₂) = 1 ആകുമ്പോള്‍, f(m₁,m₂) f(n₁,n₂) = f(m₁n₁, m₂n₂) ആണെങ്കില്‍, f(m₁,m₂) ഒരു ഗുണനാത്മക അങ്കഗണിതഫലനമാണെന്നു പറയുന്നു. ഒരു വ്യവസ്ഥയുമില്ലാതെ തന്നെ f(m₁,m₂) f(n₁,n₂) = f(m₁n₁, m₂n₂) ആണെങ്കില്‍, f(m₁,m₂) ഒരു ലീനിയര്‍ അഥവാ മുഴുഗുണനാത്മകഫലനമാണെന്നു പറയുന്നു. മൌലിക-അങ്കഗണിതഫലനങ്ങള്‍ എല്ലാംതന്നെ ആദ്യത്തേതിനുദാഹരണമാണ്. I (n) ഒരു ലീനിയര്‍ ഫലനമാണ്. μ(n), d(n),σ(n), ø(n), എന്നീ ഫലനങ്ങള്‍ ഗുണനാത്മകമാണ്. n-നു പകരം ഒരു അവിഭാജ്യസംഖ്യയുടെ ഘാതം (p^a) ഉപയോഗിച്ച് ഫലനത്തിന്റെ മൂല്യവാക്യം നിര്‍ണയിക്കാന്‍ എളുപ്പമാണ്. ഇങ്ങനെ മൂല്യവാക്യങ്ങള്‍ നിര്‍ണയിച്ചാല്‍ n = πp^a ആണെങ്കില്‍,

d(n) = π(a+1),φ(n) = nπ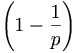 $\left (1-\frac{1}{p}\right)$

σ(n) = π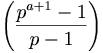 $\left(\frac{p^{a+1}-1}{p-1}\right)$ ആയിരിക്കും

ഉദാ: n = 12 = 2² x 3¹; d(12) = (2+1) (1+1) = 6

σ(12)= 12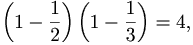 $\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) = 4,$

σ(12) = 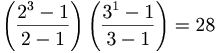$\left(\frac{2^3-1}{2-1}\right)\left(\frac{3^1-1}{3-1}\right) = 28$

ഈ സംഖ്യാഫലനങ്ങള്‍ക്കു വളരെ സാമാന്യവത്കരണങ്ങള്‍ ഉണ്ടായിട്ടുണ്ട്. ഉദാ. I_k(n),ø_k(n),d_k(n),σ_k(n). അങ്കഗണിതഫലനങ്ങളുടെ വൈശ്ളേഷികവശത്തെപ്പറ്റി പ്രതിപാദിക്കുന്നത് അനലിറ്റിക് നമ്പര്‍ തിയറിയിലാണ്. അനാലിസിസ് എന്ന മൗലികഗണിതശാഖയിലെ തത്ത്വങ്ങള്‍ ഉപയോഗിച്ചാണ് ഈ പഠനം സാധിക്കുന്നത്.

ആധുനിക ബീജഗണിതത്തിന്റെ സ്വാധീനം അങ്കഗണിതഫലനവിജ്ഞാനത്തെ വളര്‍ത്തിയിട്ടുണ്ട്. വളരെക്കാലത്തെ വളര്‍ച്ചയുടെ അടിസ്ഥാനത്തില്‍ എല്‍.ഇ. ഡിക്സണ്‍ ഇതിന്റെ ചരിത്രം എഴുതി. അടുത്തകാലത്താണ് ഇ.ടി.ബെല്‍ ഈ ശാഖയെ ഒരു സിദ്ധാന്തമായി വളര്‍ത്തിയത് (1927). സംഖ്യാഫലനസിദ്ധാന്തത്തില്‍, ആധുനിക ബീജഗണിതത്തിന്റെ പ്രേരണയോടെ അങ്കഗണിതഫലനത്തിന് ഒരു താത്വികാടിസ്ഥാനം ഉണ്ടായി. സംഖ്യാഫലനഗണിതം എന്നൊരു ശാഖതന്നെ വളര്‍ത്തിയത് ബെല്‍ ആണ്. പിന്നീട് ആര്‍. വൈദ്യനാഥസ്വാമി, കാര്‍ലിറ്റ്സ്, എക്ഫോര്‍ഡ് കോഹന്‍, ലെഹ്‍മര്‍ എന്നിവര്‍ അത് കുറെക്കൂടി താത്ത്വികമായി വികസിപ്പിച്ചു.

സംഖ്യാഫലനങ്ങള്‍ക്കു കൂടുതല്‍ വ്യാപകമായ സാമാന്യവത്കരണങ്ങള്‍ സാധിച്ചിട്ടുണ്ട്. ജി.സി. റോട്ട എന്ന ഗണിതശാസ്ത്രജ്ഞനാണ് ഈ വഴിക്കു മൗലികപ്രാധാന്യമുള്ള ഗവേഷണങ്ങള്‍ ആരംഭിച്ചത്. ഇന്‍സിഡന്‍സ് ആള്‍ജിബ്ര (Incidence Algebra) എന്നൊരു ശാഖ വളര്‍ത്തി. മിശ്രസംഖ്യ (complex numbers)കളുടെ സ്ഥാനത്ത് ഭാഗികമായി ക്രമപ്പെടുത്തിയ ജാലികാന്തരാളങ്ങള്‍ (Lattice inrervals) ഉപയോഗിച്ചുകൊണ്ട് സംഖ്യാഫലനങ്ങളുടെ അര്‍ഥവ്യാപ്തി വര്‍ധിപ്പിച്ചത് റോട്ടയാണ്. മോബയസ്മ്യൂ-(μ) ഫലനത്തിന്റെ സാമാന്യവത്കരണത്തിലാണ് റോട്ട കൂടുതല്‍ ശ്രദ്ധിച്ചത്. എന്നാല്‍ ഡേവിഡ് എ. സ്മിത്ത് ഇന്‍സിഡന്‍സ് ഫലനങ്ങളെന്ന പേരില്‍ അങ്കഗണിതഫലനത്തിന്റെ ഏറ്റവും വിപുലമായ സാമാന്യവത്കരണം സാധിച്ചു (1967). ക്ളാസിക്കല്‍ അങ്കഗണിതഫലനങ്ങള്‍ ഉള്‍പ്പെടുന്ന അനവധി സര്‍വസമീകരണങ്ങ(Identities)ളുടെ ക്ളിഷ്ടത ഒഴിവാക്കുന്ന രീതിയിലാണ് ഇന്‍സിഡന്‍സ് ഫലനങ്ങളുപയോഗിച്ച് സമാന്തരമായ സര്‍വസമീകരണങ്ങള്‍ കണ്ടെത്തിയത്. ഈ ഗവേഷണം കോമ്പിനറ്റോറിയല്‍ അനാലിസിസ് എന്ന ശാഖയിലുള്‍പ്പെടുന്നു. അങ്കഗണിതഫലനങ്ങള്‍ കൈകാര്യം ചെയ്യുമ്പോഴുള്ള ക്ളിഷ്ടത ഒഴിവാക്കുകയും കൂടുതല്‍ സാമാന്യമായ ഫലനത്തിലെത്തുകയും ചെയ്യുന്നതരത്തിലാണ് ഇന്‍സിഡന്‍സ് ഗവേഷണം എത്തിയിരിക്കുന്നത്. നോ: അനലിറ്റിക് നമ്പര്‍ തിയറി; ആള്‍ജിബ്ര; മോഡേണ്‍ ആള്‍ജിബ്ര; സംഖ്യാസിദ്ധാന്തം; ലാറ്റിസ്തിയറി

@@ വരി 2: / വരി 2: @@
 Arithmetic function
-ഗണിതശാസ്ത്രത്തില്‍, ഒരു ധനപൂര്‍ണസംഖ്യയെ (positive integer) മറ്റൊന്നായി രൂപാന്തരപ്പെടുത്തുമ്പോള്‍ അത് ഉള്‍ക്കൊള്ളുന്ന ക്രിയ. വിപുലമായ അര്‍ഥത്തില്‍, ഒരു വസ്തു മറ്റൊന്നായി മാറുമ്പോള്‍ ആ പ്രക്രിയയില്‍ ഉള്‍ക്കൊള്ളുന്ന ക്രിയയെ സൂചിപ്പിക്കുന്നതാണ് ഫലനം. ഒരു സംഖ്യയുടെ മൂന്നിരട്ടിയോട് അഞ്ച് ചേര്‍ത്താല്‍ മറ്റൊരു സംഖ്യയുണ്ടാകുന്നു. ഇതില്‍ സാമാന്യമായി സംഖ്യയെ n എന്നു സൂചിപ്പിച്ചാല്‍ പുതിയ സംഖ്യ  3n + 5  എന്നായിരിക്കും. 3n + 5 എന്ന സംഖ്യ രൂപപ്പെടാന്‍ n എന്ന സംഖ്യയില്‍ ഏല്പിക്കുന്ന ക്രിയയ്ക്കാണ് ഇവിടെ n-ന്റെ ഫലനമെന്നു പറയുന്നത്: f(n)= 3n + 5. n ഒരു ധനപൂര്‍ണസംഖ്യയാകുമ്പോള്‍ 3n+ 5-ഉം ധനപൂര്‍ണസംഖ്യയാകുന്നു. അതുകൊണ്ട് ഇവിടെ ള ഒരു അങ്കഗണിതഫലനമാണ്.
+ഗണിതശാസ്ത്രത്തില്‍, ഒരു ധനപൂര്‍ണസംഖ്യയെ (positive integer) മറ്റൊന്നായി രൂപാന്തരപ്പെടുത്തുമ്പോള്‍ അത് ഉള്‍ക്കൊള്ളുന്ന ക്രിയ. വിപുലമായ അര്‍ഥത്തില്‍, ഒരു വസ്തു മറ്റൊന്നായി മാറുമ്പോള്‍ ആ പ്രക്രിയയില്‍ ഉള്‍ക്കൊള്ളുന്ന ക്രിയയെ സൂചിപ്പിക്കുന്നതാണ് ഫലനം. ഒരു സംഖ്യയുടെ മൂന്നിരട്ടിയോട് അഞ്ച് ചേര്‍ത്താല്‍ മറ്റൊരു സംഖ്യയുണ്ടാകുന്നു. ഇതില്‍ സാമാന്യമായി സംഖ്യയെ n എന്നു സൂചിപ്പിച്ചാല്‍ പുതിയ സംഖ്യ  3n + 5  എന്നായിരിക്കും. 3n + 5 എന്ന സംഖ്യ രൂപപ്പെടാന്‍ n എന്ന സംഖ്യയില്‍ ഏല്പിക്കുന്ന ക്രിയയ്ക്കാണ് ഇവിടെ n-ന്റെ ഫലനമെന്നു പറയുന്നത്: f(n)= 3n + 5. n ഒരു ധനപൂര്‍ണസംഖ്യയാകുമ്പോള്‍ 3n+ 5-ഉം ധനപൂര്‍ണസംഖ്യയാകുന്നു. അതുകൊണ്ട് ഇവിടെ f ഒരു അങ്കഗണിതഫലനമാണ്.
-സംഖ്യകളുടെ സവിശേഷതകള്‍ സംഖ്യാസിദ്ധാന്ത(Theory of numbers)ത്തിലൂടെ ഫലനങ്ങളുപയോഗിച്ച് പഠിക്കുന്ന ഒരു ഗണിതശാഖയാണ് ഇത് ഉള്‍ക്കൊള്ളുന്നത്. ധനപൂര്‍ണസംഖ്യകള്‍ തമ്മിലുള്ള ബന്ധമാണ് ഇതിലെ പ്രധാന പ്രമേയം. ഉദാഹരണമായി ഏതു സംഖ്യയുടെയും രണ്ടിരട്ടി എന്ന ആശയം ഫലനംവഴി സൂചിപ്പിക്കാം.f(n) = 2n എന്ന നിര്‍വചനംകൊണ്ട് മേല്‍പറഞ്ഞ അര്‍ഥം വ്യക്തമാക്കാവുന്നതാണ്. ഇവിടെ n എന്നത് ഏതു ധനപൂര്‍ണസംഖ്യയുമാകാം. n = 3 ആണെങ്കില്‍, f(3) = 6 എന്നു ലഭിക്കുന്നു. ഇതിന്നര്‍ഥം : 3-ന്റെ രണ്ടിരട്ടി സമം 6. ഇതില്‍ ള ഒരു അങ്കഗണിതഫലനമാണ്. മിശ്രസംഖ്യാഗണത്തിന്റെ, ധനപൂര്‍ണസംഖ്യാഗണത്തിലേക്കുള്ള ഒരു രൂപാന്തരമാണ് അങ്കഗണിതഫലനം അഥവാ സംഖ്യാഫലനം എന്നു നിര്‍വചിക്കാം. അതായത് ഒരു മിശ്രസംഖ്യ ഒരു ധനപൂര്‍ണസംഖ്യയായി രൂപാന്തരപ്പെടുന്നു. ഇതിലുള്‍പ്പെടുന്ന നിയമമാണ് സംഖ്യാഫലനം. ധനപൂര്‍ണസംഖ്യകളുടെ സവിശേഷതകള്‍ പരിഗണിച്ച് അങ്കഗണിതഫലനങ്ങള്‍, സംഖ്യാസിദ്ധാന്തചരിത്രം (History of Number Theory) എഴുതിയ എല്‍.ഇ. ഡിക്സണ്‍ രേഖപ്പെടുത്തിയിട്ടുണ്ട്. I(n), E(n), d(n), &mu;(n), E<sub>0</sub>(n) എന്നിവ ഉദാഹരണങ്ങളാണ്. അവിഭാജ്യഘടകങ്ങളായി n പിരിച്ചെഴുതിയാല്‍ n=p<sub>1</sub><sup>a<sub>1</sub></sup>p<sub>2</sub><sup>a<sub>2</sub></sup>......p<sub>r</sub><sup>a<sub>r</sub></sup>എന്നൊരു രൂപമുണ്ടാകുന്നു. P<sub>1</sub>, P<sub>2</sub>........ എന്നിവ വ്യത്യസ്തമായ അവിഭാജ്യഘടകങ്ങളാണ്. എങ്കില്‍ I(n) =n,E(n) = 1. n-ന്റെ ആകെയുള്ള ഘടകങ്ങളുടെ എണ്ണം സൂചിപ്പിക്കുന്നതാണ് d(n); &mu;(1) = 1, &mu; (p<sub>1</sub>, ...........p<sub>r</sub>) = (-1)<sup>r</sup>, &mu;(p<sup>2</sup>) = 0. അതായത് n-ന് ഏതെങ്കിലുമൊരു വര്‍ഗസംഖ്യ (square) ഘടകമായുണ്ടെങ്കില്‍ ആ സംഖ്യയെ സംബന്ധിച്ച് &mu; എന്ന അങ്കഗണിതഫലനത്തിന്റെ മൂല്യം 0 ആണ്; E<sub>0</sub>(1) = 1, മറ്റെല്ലാ പൂര്‍ണസംഖ്യകള്‍ക്കും E<sub>0</sub>(n)=0. കുറെക്കൂടി ഉയര്‍ന്നതരം ഫലനങ്ങളാണ് &phi;(n), &sigma;(n) എന്നിവ. ഓയിലര്‍ എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ പേരിലറിയപ്പെടുന്ന &phi;(n) (ഓയിലര്‍ ഫലനം) അങ്കഗണിതഫലനത്തില്‍ വളരെ പ്രാധാന്യമര്‍ഹിക്കുന്നു. ടോഷന്റ് ഫലനം (Totient function) എന്ന വര്‍ഗത്തില്‍പ്പെടുന്നു ഇത്. n = 12 എങ്കില്‍, 12-ല്‍ താഴെ 12-നോടു പൊതുഘടകമില്ലാത്ത ധനപൂര്‍ണസംഖ്യകളുടെ എണ്ണമാണ് &phi;(12) സൂചിപ്പിക്കുന്നത്, ഘടകങ്ങള്‍ പരിഗണിക്കുമ്പോള്‍ 1, 5, 7, 11 എന്നിവയുടെ എണ്ണം. അതായത്, &phi;(12) = 4. 1, 2, 3, 4, 6, 12 ആണ് 12-ന്റെ ഘടകങ്ങള്‍. അതുകൊണ്ട് d(12) = 6, &sigma;(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28. അതായത് ഘടകങ്ങളുടെ ആകെത്തുക.
+സംഖ്യകളുടെ സവിശേഷതകള്‍ സംഖ്യാസിദ്ധാന്ത(Theory of numbers)ത്തിലൂടെ ഫലനങ്ങളുപയോഗിച്ച് പഠിക്കുന്ന ഒരു ഗണിതശാഖയാണ് ഇത് ഉള്‍ക്കൊള്ളുന്നത്. ധനപൂര്‍ണസംഖ്യകള്‍ തമ്മിലുള്ള ബന്ധമാണ് ഇതിലെ പ്രധാന പ്രമേയം. ഉദാഹരണമായി ഏതു സംഖ്യയുടെയും രണ്ടിരട്ടി എന്ന ആശയം ഫലനംവഴി സൂചിപ്പിക്കാം.f(n) = 2n എന്ന നിര്‍വചനംകൊണ്ട് മേല്‍പറഞ്ഞ അര്‍ഥം വ്യക്തമാക്കാവുന്നതാണ്. ഇവിടെ n എന്നത് ഏതു ധനപൂര്‍ണസംഖ്യയുമാകാം. n = 3 ആണെങ്കില്‍, f(3) = 6 എന്നു ലഭിക്കുന്നു. ഇതിന്നര്‍ഥം : 3-ന്റെ രണ്ടിരട്ടി സമം 6. ഇതില്‍ f ഒരു അങ്കഗണിതഫലനമാണ്. മിശ്രസംഖ്യാഗണത്തിന്റെ, ധനപൂര്‍ണസംഖ്യാഗണത്തിലേക്കുള്ള ഒരു രൂപാന്തരമാണ് അങ്കഗണിതഫലനം അഥവാ സംഖ്യാഫലനം എന്നു നിര്‍വചിക്കാം. അതായത് ഒരു മിശ്രസംഖ്യ ഒരു ധനപൂര്‍ണസംഖ്യയായി രൂപാന്തരപ്പെടുന്നു. ഇതിലുള്‍പ്പെടുന്ന നിയമമാണ് സംഖ്യാഫലനം. ധനപൂര്‍ണസംഖ്യകളുടെ സവിശേഷതകള്‍ പരിഗണിച്ച് അങ്കഗണിതഫലനങ്ങള്‍, സംഖ്യാസിദ്ധാന്തചരിത്രം (History of Number Theory) എഴുതിയ എല്‍.ഇ. ഡിക്സണ്‍ രേഖപ്പെടുത്തിയിട്ടുണ്ട്. I(n), E(n), d(n), &mu;(n), E<sub>0</sub>(n) എന്നിവ ഉദാഹരണങ്ങളാണ്. അവിഭാജ്യഘടകങ്ങളായി n പിരിച്ചെഴുതിയാല്‍ n=p<sub>1</sub><sup>a<sub>1</sub></sup>p<sub>2</sub><sup>a<sub>2</sub></sup>......p<sub>r</sub><sup>a<sub>r</sub></sup>എന്നൊരു രൂപമുണ്ടാകുന്നു. P<sub>1</sub>, P<sub>2</sub>........ എന്നിവ വ്യത്യസ്തമായ അവിഭാജ്യഘടകങ്ങളാണ്. എങ്കില്‍ I(n) =n,E(n) = 1. n-ന്റെ ആകെയുള്ള ഘടകങ്ങളുടെ എണ്ണം സൂചിപ്പിക്കുന്നതാണ് d(n); &mu;(1) = 1, &mu; (p<sub>1</sub>, ...........p<sub>r</sub>) = (-1)<sup>r</sup>, &mu;(p<sup>2</sup>) = 0. അതായത് n-ന് ഏതെങ്കിലുമൊരു വര്‍ഗസംഖ്യ (square) ഘടകമായുണ്ടെങ്കില്‍ ആ സംഖ്യയെ സംബന്ധിച്ച് &mu; എന്ന അങ്കഗണിതഫലനത്തിന്റെ മൂല്യം 0 ആണ്; E<sub>0</sub>(1) = 1, മറ്റെല്ലാ പൂര്‍ണസംഖ്യകള്‍ക്കും E<sub>0</sub>(n)=0. കുറെക്കൂടി ഉയര്‍ന്നതരം ഫലനങ്ങളാണ് &phi;(n), &sigma;(n) എന്നിവ. ഓയിലര്‍ എന്ന ഗണിതശാസ്ത്രജ്ഞന്റെ പേരിലറിയപ്പെടുന്ന &phi;(n) (ഓയിലര്‍ ഫലനം) അങ്കഗണിതഫലനത്തില്‍ വളരെ പ്രാധാന്യമര്‍ഹിക്കുന്നു. ടോഷന്റ് ഫലനം (Totient function) എന്ന വര്‍ഗത്തില്‍പ്പെടുന്നു ഇത്. n = 12 എങ്കില്‍, 12-ല്‍ താഴെ 12-നോടു പൊതുഘടകമില്ലാത്ത ധനപൂര്‍ണസംഖ്യകളുടെ എണ്ണമാണ് &phi;(12) സൂചിപ്പിക്കുന്നത്, ഘടകങ്ങള്‍ പരിഗണിക്കുമ്പോള്‍ 1, 5, 7, 11 എന്നിവയുടെ എണ്ണം. അതായത്, &phi;(12) = 4. 1, 2, 3, 4, 6, 12 ആണ് 12-ന്റെ ഘടകങ്ങള്‍. അതുകൊണ്ട് d(12) = 6, &sigma;(12) = 1 + 2 + 3 + 4 + 6 + 12 = 28. അതായത് ഘടകങ്ങളുടെ ആകെത്തുക.
-'''കോണ്‍വല്യൂഷനുകള്‍''' (Convolutions). രണ്ട് അങ്കഗണിതഫലനങ്ങള്‍ തമ്മില്‍ ഗുണനാടിസ്ഥാനത്തില്‍ ബന്ധപ്പെടുന്ന സമ്പ്രദായമാണ് കോണ്‍വല്യൂഷന്‍. മൂലസംഖ്യയുടെ (argument) ഗുണനഘടകങ്ങളുടേയും സങ്കലനപദങ്ങളു(addition bterms)ടേയും അടിസ്ഥാനങ്ങള്‍ അനുസരിച്ച് രണ്ടുതരത്തില്‍ കോണ്‍വല്യൂഷന്‍ ഉണ്ടാകുന്നു. ഇതില്‍ ആദ്യത്തേതിന് ഡിറീക്ലെ സംയോഗം (Dirchlet Composition ) എന്നും രണ്ടാമത്തേതിന് കോഷി സംയോഗം (Cauchy Composition ) എന്നും ആദ്യമായി പറഞ്ഞത് ഇ.ടി. ബെല്‍ ആണ്. ള, ഴ, വ എന്നീ സംഖ്യാഫലനങ്ങള്‍ താഴെ കൊടുക്കുന്ന തരത്തില്‍ ബന്ധപ്പെട്ടിരുന്നാല്‍, അതായത് h (n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ ഒരു (ഡിറീക്ലെ) സംയോഗം ആണ് h എന്നു പറയപ്പെടുന്നു.   h(n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ കോഷി സംയോഗവും. nന്റെ ഘടകങ്ങളെയാണ് d സൂചിപ്പിക്കു ന്നത്. ഘടകങ്ങളില്‍ n-ഉം ഉള്‍പ്പെടുന്നു. പഠനവിധേയമായിക്കൊണ്ടിരിക്കുന്ന സംയോഗമാണ് ആദ്യത്തേത്.
+'''കോണ്‍വല്യൂഷനുകള്‍''' (Convolutions). രണ്ട് അങ്കഗണിതഫലനങ്ങള്‍ തമ്മില്‍ ഗുണനാടിസ്ഥാനത്തില്‍ ബന്ധപ്പെടുന്ന സമ്പ്രദായമാണ് കോണ്‍വല്യൂഷന്‍. മൂലസംഖ്യയുടെ (argument) ഗുണനഘടകങ്ങളുടേയും സങ്കലനപദങ്ങളു(addition terms)ടേയും അടിസ്ഥാനങ്ങള്‍ അനുസരിച്ച് രണ്ടുതരത്തില്‍ കോണ്‍വല്യൂഷന്‍ ഉണ്ടാകുന്നു. ഇതില്‍ ആദ്യത്തേതിന് ഡിറീക്ലെ സംയോഗം (Dirchlet Composition ) എന്നും രണ്ടാമത്തേതിന് കോഷി സംയോഗം (Cauchy Composition ) എന്നും ആദ്യമായി പറഞ്ഞത് ഇ.ടി. ബെല്‍ ആണ്. f, g, h എന്നീ സംഖ്യാഫലനങ്ങള്‍ താഴെ കൊടുക്കുന്ന തരത്തില്‍ ബന്ധപ്പെട്ടിരുന്നാല്‍, അതായത് h (n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ ഒരു (ഡിറീക്ലെ) സംയോഗം ആണ് h എന്നു പറയപ്പെടുന്നു.   h(n) = എന്നാണെങ്കില്‍ f,g എന്നിവയുടെ കോഷി സംയോഗവും. nന്റെ ഘടകങ്ങളെയാണ് d സൂചിപ്പിക്കു ന്നത്. ഘടകങ്ങളില്‍ n-ഉം ഉള്‍പ്പെടുന്നു. പഠനവിധേയമായിക്കൊണ്ടിരിക്കുന്ന സംയോഗമാണ് ആദ്യത്തേത്.
--തിനോടടുത്ത് (മദ്രാസ് യൂണിവേഴ്സിറ്റിയില്‍ ഗണിതശാസ്ത്രവിഭാഗം പ്രൊഫസര്‍ ആയിരുന്നു) ആര്‍. വൈദ്യനാഥസ്വാമി തന്റെ മെമോയര്‍ ഓണ്‍ മള്‍ട്ടിപ്ളിക്കേറ്റീവ് ഫങ്ഷന്‍സ് (Memoir on Multiplicative Functions) എന്ന ഗവേഷണപ്രബന്ധം പ്രസിദ്ധീകരിച്ചു. അതില്‍ നാലുതരം യോഗങ്ങളെപ്പറ്റി പറയുന്നു: സംയോഗം (കോമ്പോസിഷന്‍), കോണ്‍വല്യൂഷന്‍, ഫലനഗുണനം (മള്‍ട്ടിപ്ളിക്കേഷന്‍), ബ്ളോക് കോണ്‍വല്യൂഷന്‍.
+-തിനോടടുത്ത്  ആര്‍. വൈദ്യനാഥസ്വാമി (മദ്രാസ് യൂണിവേഴ്സിറ്റിയില്‍ ഗണിതശാസ്ത്രവിഭാഗം പ്രൊഫസര്‍ ആയിരുന്നു) തന്റെ മെമോയര്‍ ഓണ്‍ മള്‍ട്ടിപ്ളിക്കേറ്റീവ് ഫങ്ഷന്‍സ് (Memoir on Multiplicative Functions) എന്ന ഗവേഷണപ്രബന്ധം പ്രസിദ്ധീകരിച്ചു. അതില്‍ നാലുതരം യോഗങ്ങളെപ്പറ്റി പറയുന്നു: സംയോഗം (കോമ്പോസിഷന്‍), കോണ്‍വല്യൂഷന്‍, ഫലനഗുണനം (മള്‍ട്ടിപ്ളിക്കേഷന്‍), ബ്ളോക് കോണ്‍വല്യൂഷന്‍.
 ആദ്യം ഉദാഹരണമായി കാണിച്ച ഡിറിക്ലെ സംയോഗത്തെയാണ് സാധാരണയായി സംയോഗം എന്നു പറയുന്നത്; n എന്നതിന്റെ എല്ലാ ഘടകങ്ങളും ഉപയോഗപ്പെടുത്തി എഴുതാവുന്ന എല്ലാ പദങ്ങളുടെയും ആകെത്തുക. ഉദാ.
@@ വരി 14: / വരി 14: @@
 [[Image:p158a.png]]
-ഇതില്‍ d/n എന്ന അങ്കനംകൊണ്ട് ഉദ്ദേശിക്കുന്നത്: n-ന്റെ ബ്ളോക്ക് ഘടകം, ഏകകഘടകം അഥവാ യൂണിറ്ററി ഘടകം ആണ് dഎന്ന ധനപൂര്‍ണസംഖ്യ. രണ്ടു പൂരക ഘടകങ്ങള്‍ക്കു തമ്മില്‍  പൊതുഘടകം 1 (ഒന്ന്) ഒഴികെ മറ്റൊന്നും ഇല്ലെങ്കില്‍ അവയെ ബ്ളോക്ക് ഘടകങ്ങള്‍ എന്നു പറയുന്നു. ഉദാ. 1, 3, 4, 12 എന്നിവ 12-ന്റെ ബ്ളോക്ക് ഘടകങ്ങളാണ്.
+ഇതില്‍  <math> {d} \Vert {n} </math>
+എന്ന അങ്കനംകൊണ്ട് ഉദ്ദേശിക്കുന്നത്: n-ന്റെ ബ്ളോക്ക് ഘടകം, ഏകകഘടകം അഥവാ യൂണിറ്ററി ഘടകം ആണ് dഎന്ന ധനപൂര്‍ണസംഖ്യ. രണ്ടു പൂരക ഘടകങ്ങള്‍ക്കു തമ്മില്‍  പൊതുഘടകം 1 (ഒന്ന്) ഒഴികെ മറ്റൊന്നും ഇല്ലെങ്കില്‍ അവയെ ബ്ളോക്ക് ഘടകങ്ങള്‍ എന്നു പറയുന്നു. ഉദാ. 1, 3, 4, 12 എന്നിവ 12-ന്റെ ബ്ളോക്ക് ഘടകങ്ങളാണ്.
 h (12) = f(1) g(12) + f(3) g(4) + f(4) g(3) + f(12) g(1).
@@ വരി 28: / വരി 29: @@
 '''ഗുണനാത്മക അങ്കഗണിതഫലനം''' (Multiplicative functions). അങ്കഗണിതഫലനങ്ങള്‍ പൊതുവേ അനവധി മൂലകാങ്കങ്ങളെ ആധാരമാക്കിയാകാം:
-f(m<sub>1</sub>,m<sub>2</sub>, .........., m<sub>r</sub>). (m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) = 1 ആകുമ്പോള്‍, f(m<sub>1</sub>,m<sub>2</sub>) f(n<sub>1</sub>,n<sub>2</sub>) = f(m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) ആണെങ്കില്‍, f(m<sub>1</sub>,m<sub>2</sub>) ഒരു ഗുണനാത്മക അങ്കഗണിതഫലനമാണെന്നു പറയുന്നു. ഒരു വ്യവസ്ഥയുമില്ലാതെ തന്നെ f(m<sub>1</sub>,m<sub>2</sub>) f(n<sub>1</sub>,n<sub>2</sub>) = f(m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) ആണെങ്കില്‍, f(m<sub>1</sub>,m<sub></sub> ഒരു ലീനിയര്‍ അഥവാ മുഴുഗുണനാത്മകഫലനമാണെന്നു പറയുന്നു. മൌലിക-അങ്കഗണിതഫലനങ്ങള്‍ എല്ലാംതന്നെ ആദ്യത്തേതിനുദാഹരണമാണ്. I (n) ഒരു ലീനിയര്‍ ഫലനമാണ്. &mu;(n), d(n),&sigma;(n), &oslash;(n), എന്നീ ഫലനങ്ങള്‍ ഗുണനാത്മകമാണ്. n-നു പകരം ഒരു അവിഭാജ്യസംഖ്യയുടെ ഘാതം (p<sup>a</sup>) ഉപയോഗിച്ച് ഫലനത്തിന്റെ മൂല്യവാക്യം നിര്‍ണയിക്കാന്‍ എളുപ്പമാണ്. ഇങ്ങനെ മൂല്യവാക്യങ്ങള്‍ നിര്‍ണയിച്ചാല്‍ n = &pi;p<sup>a</sup> ആണെങ്കില്‍,
+f(m<sub>1</sub>,m<sub>2</sub>, .........., m<sub>r</sub>). (m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) = 1 ആകുമ്പോള്‍, f(m<sub>1</sub>,m<sub>2</sub>) f(n<sub>1</sub>,n<sub>2</sub>) = f(m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) ആണെങ്കില്‍, f(m<sub>1</sub>,m<sub>2</sub>) ഒരു ഗുണനാത്മക അങ്കഗണിതഫലനമാണെന്നു പറയുന്നു. ഒരു വ്യവസ്ഥയുമില്ലാതെ തന്നെ f(m<sub>1</sub>,m<sub>2</sub>) f(n<sub>1</sub>,n<sub>2</sub>) = f(m<sub>1</sub>n<sub>1</sub>, m<sub>2</sub>n<sub>2</sub>) ആണെങ്കില്‍, f(m<sub>1</sub>,m<sub>2</sub>) ഒരു ലീനിയര്‍ അഥവാ മുഴുഗുണനാത്മകഫലനമാണെന്നു പറയുന്നു. മൌലിക-അങ്കഗണിതഫലനങ്ങള്‍ എല്ലാംതന്നെ ആദ്യത്തേതിനുദാഹരണമാണ്. I (n) ഒരു ലീനിയര്‍ ഫലനമാണ്. &mu;(n), d(n),&sigma;(n), &oslash;(n), എന്നീ ഫലനങ്ങള്‍ ഗുണനാത്മകമാണ്. n-നു പകരം ഒരു അവിഭാജ്യസംഖ്യയുടെ ഘാതം (p<sup>a</sup>) ഉപയോഗിച്ച് ഫലനത്തിന്റെ മൂല്യവാക്യം നിര്‍ണയിക്കാന്‍ എളുപ്പമാണ്. ഇങ്ങനെ മൂല്യവാക്യങ്ങള്‍ നിര്‍ണയിച്ചാല്‍ n = &pi;p<sup>a</sup> ആണെങ്കില്‍,
 '''d(n)      =  &pi;(a+1),&phi;(n) = n&pi;'''<math>\left (1-\frac{1}{p}\right)</math>
-'''&sigma;(n)  = &pi;'''<math>\left(\frac{p^{a+1}-1}{p-1}\right)</math>ആയിരിക്കും
+'''&sigma;(n)  = &pi;'''<math>\left(\frac{p^{a+1}-1}{p-1}\right)</math>'''ആയിരിക്കും'''
 '''ഉദാ:  n  = 12  = 2<sup>2</sup> x 3<sup>1</sup>; d(12) = (2+1) (1+1) = 6'''
@@ വരി 38: / വരി 39: @@
 '''&sigma;(12)= 12'''<math>\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right) = 4,</math>
-&sigma;(12) = <math>\begin{pmatrix}2<sup>3</sup>-1\\2-1\end{pmatrix}</math>
+'''&sigma;(12)''' = <math>\left(\frac{2^3-1}{2-1}\right)\left(\frac{3^1-1}{3-1}\right) = 28 </math>
 ഈ സംഖ്യാഫലനങ്ങള്‍ക്കു വളരെ സാമാന്യവത്കരണങ്ങള്‍ ഉണ്ടായിട്ടുണ്ട്. ഉദാ. I<sub>k</sub>(n),&oslash;<sub>k</sub>(n),d<sub>k</sub>(n),&sigma;<sub>k</sub>(n). അങ്കഗണിതഫലനങ്ങളുടെ വൈശ്ളേഷികവശത്തെപ്പറ്റി പ്രതിപാദിക്കുന്നത് അനലിറ്റിക് നമ്പര്‍ തിയറിയിലാണ്. അനാലിസിസ് എന്ന മൗലികഗണിതശാഖയിലെ തത്ത്വങ്ങള്‍ ഉപയോഗിച്ചാണ് ഈ പഠനം സാധിക്കുന്നത്.
-ആധുനിക ബീജഗണിതത്തിന്റെ സ്വാധീനം അങ്കഗണിതഫലനവിജ്ഞാനത്തെ വളര്‍ത്തിയിട്ടുണ്ട്. വളരെക്കാലത്തെ വളര്‍ച്ചയുടെ അടിസ്ഥാനത്തില്‍ എല്‍.ഇ. ഡിക്സണ്‍ ഇതിന്റെ ചരിത്രം എഴുതി. അടുത്തകാലത്താണ് ഇ.ടി.ബെല്‍ ഈ ശാഖയെ ഒരു സിദ്ധാന്തമായി വളര്‍ത്തിയത് (1927). സംഖ്യാഫലനസിദ്ധാന്തത്തില്‍, ആധുനിക ബീജഗണിതത്തിന്റെ പ്രേരണയോടെ അങ്കഗണിതഫലനത്തിന് ഒരു താത്വികാടിസ്ഥാനം ഉണ്ടായി. സംഖ്യാഫലനഗണിതം എന്നൊരു ശാഖതന്നെ വളര്‍ത്തിയത് ബെല്‍ ആണ്. പിന്നീട് ആര്‍. വൈദ്യനാഥസ്വാമി, കാര്‍ലിറ്റ്സ്, എക്ഫോര്‍ഡ് കോഹന്‍, ലെഹ്മര്‍ എന്നിവര്‍ അത് കുറെക്കൂടി താത്ത്വികമായി വികസിപ്പിച്ചു.
+ആധുനിക ബീജഗണിതത്തിന്റെ സ്വാധീനം അങ്കഗണിതഫലനവിജ്ഞാനത്തെ വളര്‍ത്തിയിട്ടുണ്ട്. വളരെക്കാലത്തെ വളര്‍ച്ചയുടെ അടിസ്ഥാനത്തില്‍ എല്‍.ഇ. ഡിക്സണ്‍ ഇതിന്റെ ചരിത്രം എഴുതി. അടുത്തകാലത്താണ് ഇ.ടി.ബെല്‍ ഈ ശാഖയെ ഒരു സിദ്ധാന്തമായി വളര്‍ത്തിയത് (1927). സംഖ്യാഫലനസിദ്ധാന്തത്തില്‍, ആധുനിക ബീജഗണിതത്തിന്റെ പ്രേരണയോടെ അങ്കഗണിതഫലനത്തിന് ഒരു താത്വികാടിസ്ഥാനം ഉണ്ടായി. സംഖ്യാഫലനഗണിതം എന്നൊരു ശാഖതന്നെ വളര്‍ത്തിയത് ബെല്‍ ആണ്. പിന്നീട് ആര്‍. വൈദ്യനാഥസ്വാമി, കാര്‍ലിറ്റ്സ്, എക്ഫോര്‍ഡ് കോഹന്‍, ലെഹ്‍മര്‍ എന്നിവര്‍ അത് കുറെക്കൂടി താത്ത്വികമായി വികസിപ്പിച്ചു.
 സംഖ്യാഫലനങ്ങള്‍ക്കു കൂടുതല്‍ വ്യാപകമായ സാമാന്യവത്കരണങ്ങള്‍ സാധിച്ചിട്ടുണ്ട്. ജി.സി. റോട്ട എന്ന ഗണിതശാസ്ത്രജ്ഞനാണ് ഈ വഴിക്കു മൗലികപ്രാധാന്യമുള്ള ഗവേഷണങ്ങള്‍ ആരംഭിച്ചത്. ഇന്‍സിഡന്‍സ് ആള്‍ജിബ്ര (Incidence Algebra) എന്നൊരു ശാഖ വളര്‍ത്തി. മിശ്രസംഖ്യ (complex numbers)കളുടെ സ്ഥാനത്ത് ഭാഗികമായി ക്രമപ്പെടുത്തിയ ജാലികാന്തരാളങ്ങള്‍ (Lattice inrervals) ഉപയോഗിച്ചുകൊണ്ട് സംഖ്യാഫലനങ്ങളുടെ അര്‍ഥവ്യാപ്തി വര്‍ധിപ്പിച്ചത് റോട്ടയാണ്. മോബയസ്മ്യൂ-(&mu;) ഫലനത്തിന്റെ സാമാന്യവത്കരണത്തിലാണ് റോട്ട കൂടുതല്‍ ശ്രദ്ധിച്ചത്. എന്നാല്‍ ഡേവിഡ് എ. സ്മിത്ത് ഇന്‍സിഡന്‍സ് ഫലനങ്ങളെന്ന പേരില്‍ അങ്കഗണിതഫലനത്തിന്റെ ഏറ്റവും വിപുലമായ സാമാന്യവത്കരണം സാധിച്ചു (1967). ക്ളാസിക്കല്‍ അങ്കഗണിതഫലനങ്ങള്‍ ഉള്‍പ്പെടുന്ന അനവധി സര്‍വസമീകരണങ്ങ(Identities)ളുടെ ക്ളിഷ്ടത ഒഴിവാക്കുന്ന രീതിയിലാണ് ഇന്‍സിഡന്‍സ് ഫലനങ്ങളുപയോഗിച്ച് സമാന്തരമായ സര്‍വസമീകരണങ്ങള്‍ കണ്ടെത്തിയത്. ഈ ഗവേഷണം കോമ്പിനറ്റോറിയല്‍ അനാലിസിസ് എന്ന ശാഖയിലുള്‍പ്പെടുന്നു. അങ്കഗണിതഫലനങ്ങള്‍ കൈകാര്യം ചെയ്യുമ്പോഴുള്ള ക്ളിഷ്ടത ഒഴിവാക്കുകയും കൂടുതല്‍ സാമാന്യമായ ഫലനത്തിലെത്തുകയും ചെയ്യുന്നതരത്തിലാണ് ഇന്‍സിഡന്‍സ് ഗവേഷണം എത്തിയിരിക്കുന്നത്. നോ: അനലിറ്റിക് നമ്പര്‍ തിയറി; ആള്‍ജിബ്ര; മോഡേണ്‍ ആള്‍ജിബ്ര; സംഖ്യാസിദ്ധാന്തം; ലാറ്റിസ്തിയറി
 [[Category:ഗണിതം]]

അങ്കഗണിതഫലനം

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

Current revision as of 04:47, 29 നവംബര്‍ 2014

അങ്കഗണിതഫലനം

താളിന്റെ അനുബന്ധങ്ങള്‍

സ്വകാര്യതാളുകള്‍

ഉള്ളടക്കം

തിരയൂ

പണിസഞ്ചി