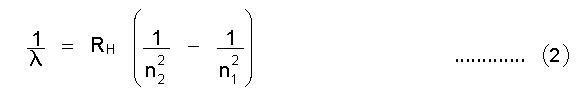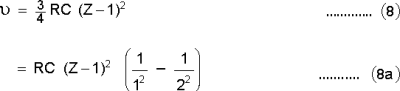This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അണു
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→ബോര് അണു) |
Mksol (സംവാദം | സംഭാവനകള്) (→അണുസംരചനയും ആവര്ത്തനപ്പട്ടികയും) |
||
| (ഇടക്കുള്ള 19 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 17: | വരി 17: | ||
സ്പെയ്സും, ദ്രവ്യവും സാന്തം ആണെന്ന് ഉദ്ഘോഷിച്ചിരുന്ന അരിസ്റ്റോട്ടലിന്റെ സിദ്ധാന്തമായിരുന്നു മധ്യകാലഘട്ടത്തില് പദാര്ഥഘടനയെക്കുറിച്ച് നിലവിലിരുന്നത്. ഏതു വസ്തുവിന്റെയും മൗലിക ഘടകങ്ങളായ ചൂട്, തണുപ്പ്, വരള്ച്ച, ഈര്പ്പം എന്നിവയുടെ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തി പുതിയ വസ്തുക്കള് ഉണ്ടാക്കാനുള്ള ശ്രമത്തിലാണ് അക്കാലത്ത് രസതന്ത്രജ്ഞര് ഏര്പ്പെട്ടിരുന്നത്. ഈ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തലായിരുന്നു രസവാദിക(Alchemists)ളുടെ ലക്ഷ്യം. പരിമാണാത്മക രസതന്ത്രത്തിന്റെ വളര്ച്ചയോടെയാണ് പദാര്ഥഘടനയെക്കുറിച്ചുള്ള പരസ്പരവിരുദ്ധചിന്താഗതികളെ വിലയിരുത്താന്വേണ്ട പരീക്ഷണത്തെളിവുകള് ലഭിച്ചത്. | സ്പെയ്സും, ദ്രവ്യവും സാന്തം ആണെന്ന് ഉദ്ഘോഷിച്ചിരുന്ന അരിസ്റ്റോട്ടലിന്റെ സിദ്ധാന്തമായിരുന്നു മധ്യകാലഘട്ടത്തില് പദാര്ഥഘടനയെക്കുറിച്ച് നിലവിലിരുന്നത്. ഏതു വസ്തുവിന്റെയും മൗലിക ഘടകങ്ങളായ ചൂട്, തണുപ്പ്, വരള്ച്ച, ഈര്പ്പം എന്നിവയുടെ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തി പുതിയ വസ്തുക്കള് ഉണ്ടാക്കാനുള്ള ശ്രമത്തിലാണ് അക്കാലത്ത് രസതന്ത്രജ്ഞര് ഏര്പ്പെട്ടിരുന്നത്. ഈ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തലായിരുന്നു രസവാദിക(Alchemists)ളുടെ ലക്ഷ്യം. പരിമാണാത്മക രസതന്ത്രത്തിന്റെ വളര്ച്ചയോടെയാണ് പദാര്ഥഘടനയെക്കുറിച്ചുള്ള പരസ്പരവിരുദ്ധചിന്താഗതികളെ വിലയിരുത്താന്വേണ്ട പരീക്ഷണത്തെളിവുകള് ലഭിച്ചത്. | ||
| - | ആധുനിക അണുസിദ്ധാന്തത്തിന്റെ പ്രണേതാവ് ജോണ് ഡാള്ട്ടന് (1766-1844) ആണ്. മീഥേന്, എഥിലീന്, കാര്ബണ് മോണോക്സൈഡ്, കാര്ബണ്ഡൈഓക്സൈഡ് തുടങ്ങിയ വാതകങ്ങളുടെ സമന്വിത-ബഹുഗുണിതാംശബന്ധനിയമം (Multiproduct ratio rule) നിര്ദേശിക്കാന് ഈ സിദ്ധാന്തം ഡാള്ട്ടനെ സഹായിച്ചു. A എന്ന മൂലകം | + | ആധുനിക അണുസിദ്ധാന്തത്തിന്റെ പ്രണേതാവ് ജോണ് ഡാള്ട്ടന് (1766-1844) ആണ്. മീഥേന്, എഥിലീന്, കാര്ബണ് മോണോക്സൈഡ്, കാര്ബണ്ഡൈഓക്സൈഡ് തുടങ്ങിയ വാതകങ്ങളുടെ സമന്വിത-ബഹുഗുണിതാംശബന്ധനിയമം (Multiproduct ratio rule) നിര്ദേശിക്കാന് ഈ സിദ്ധാന്തം ഡാള്ട്ടനെ സഹായിച്ചു. A എന്ന മൂലകം B എന്ന മൂലകവുമായി സംയോജിച്ച് രണ്ടോ അതിലധികമോ യൗഗികങ്ങള് ഉണ്ടാകുമ്പോള്, ഒരു നിശ്ചിത ഭാരത്തിലുള്ള A-യുമായി സംയോജിക്കുന്ന B-യുടെ ഭാരങ്ങള് ലഘുപൂര്ണസംഖ്യകളുടെ അംശബന്ധത്തിലായിരിക്കുമെന്നതാണ് (ratio of integers) ബഹുഗുണിതാനുപാത നിയമം. രാസപ്രതിപ്രവര്ത്തനത്തില് പങ്കെടുക്കുന്ന മൂലകങ്ങളുടെ പരിമാണങ്ങളെപ്പറ്റിയുള്ള പഠനം നാലാമത്തെ രാസസംയോഗനിയമത്തിനു വഴിതെളിച്ചു. ഒരു മൂലകത്തിന്റെ ഒരേ ഭാരവുമായി പ്രതിപ്രവര്ത്തിക്കുന്ന രണ്ടു മൂലകങ്ങളുടെ ഭാരങ്ങള് തമ്മിലുള്ള അനുപാതം, ഇവ തമ്മില് പ്രതിപ്രവര്ത്തിക്കുമ്പോഴുള്ള ഭാരാനുപാതത്തിന് സമമോ അല്ലെങ്കില് അതിന്റ വേറെ ഗുണിതമോ ആയിരിക്കും. |
==ഡാള്ട്ടന് സിദ്ധാന്തം== | ==ഡാള്ട്ടന് സിദ്ധാന്തം== | ||
| വരി 60: | വരി 60: | ||
(surface tension model) | (surface tension model) | ||
| - | തന്മാത്രയുടെ വലുപ്പം ഏകദേശം കൃത്യമായി കണക്കു കൂട്ടിയത് തോമസ് യങ് എന്ന ഇംഗ്ളീഷ് ഭൌതികശാസ്ത്രജ്ഞനാണ്. ദ്രാവകങ്ങളുടെ പ്രതലബലവും വലിവുബലവും (tensil strength) ആധാരമാക്കിയാണ് യങ് തന്റെ നിഗമനങ്ങളിലെത്തിയത്. തന്മാത്രകളുടെ വലുപ്പം നിര്ണയിക്കാന് പ്രതലബലവും ദ്രാവകങ്ങളുടെ ബാഷ്പലീന താപവും (latent heat of vapourisation) ആണ് ജെ.ജെ. വാട്ടേഴ്സണ് ഉപയോഗപ്പെടുത്തിയത് (1845). അദ്ദേഹം കണക്കു കൂട്ടിയത് ഇങ്ങനെയാണ്: ഒരു ദ്രാവകപ്രതലത്തില് 1 ച.സെ.മീ. വിസ്താരം ഉണ്ടാക്കാന് വേണ്ട ഊര്ജമാണ് പ്രതലബലം; ഒരു ഗ്രാം ദ്രാവകത്തെ പൂര്ണമായി അതിന്റെ തിളനിലയില് ബാഷ്പമാക്കാന്, അതായത് തന്മാത്രകളെ വേര്തിരിക്കാന് വേണ്ട ഊര്ജം ബാഷ്പലീനതാപവും. തന്മാത്രകളെ d വശമുള്ള ക്യൂബുകളായി സങ്കല്പിച്ചാല് V വ്യാപ്തം ദ്രാവകത്തില് V/d<sup>3</sup> തന്മാത്രകള് ഉണ്ടായിരിക്കും. ഒരു തന്മാത്രയുടെ പാര്ശ്വതല വിസ്തീര്ണം 6d<sup>2</sup> ആയതിനാല് ആകെ തന്മാത്രകളുടെ വിസ്താരം V/d<sup>3</sup>x6d<sup>2</sup>=6V/d ആണ്. അതിനാല് തന്മാത്രകളുടെ വിസ്താരം വര്ധിപ്പിക്കാന് ചെലവായ ഊര്ജം = പ്രതലബലം | + | തന്മാത്രയുടെ വലുപ്പം ഏകദേശം കൃത്യമായി കണക്കു കൂട്ടിയത് തോമസ് യങ് എന്ന ഇംഗ്ളീഷ് ഭൌതികശാസ്ത്രജ്ഞനാണ്. ദ്രാവകങ്ങളുടെ പ്രതലബലവും വലിവുബലവും (tensil strength) ആധാരമാക്കിയാണ് യങ് തന്റെ നിഗമനങ്ങളിലെത്തിയത്. തന്മാത്രകളുടെ വലുപ്പം നിര്ണയിക്കാന് പ്രതലബലവും ദ്രാവകങ്ങളുടെ ബാഷ്പലീന താപവും (latent heat of vapourisation) ആണ് ജെ.ജെ. വാട്ടേഴ്സണ് ഉപയോഗപ്പെടുത്തിയത് (1845). അദ്ദേഹം കണക്കു കൂട്ടിയത് ഇങ്ങനെയാണ്: ഒരു ദ്രാവകപ്രതലത്തില് 1 ച.സെ.മീ. വിസ്താരം ഉണ്ടാക്കാന് വേണ്ട ഊര്ജമാണ് പ്രതലബലം; ഒരു ഗ്രാം ദ്രാവകത്തെ പൂര്ണമായി അതിന്റെ തിളനിലയില് ബാഷ്പമാക്കാന്, അതായത് തന്മാത്രകളെ വേര്തിരിക്കാന് വേണ്ട ഊര്ജം ബാഷ്പലീനതാപവും. തന്മാത്രകളെ d വശമുള്ള ക്യൂബുകളായി സങ്കല്പിച്ചാല് V വ്യാപ്തം ദ്രാവകത്തില് V/d<sup>3</sup> തന്മാത്രകള് ഉണ്ടായിരിക്കും. ഒരു തന്മാത്രയുടെ പാര്ശ്വതല വിസ്തീര്ണം 6d<sup>2</sup> ആയതിനാല് ആകെ തന്മാത്രകളുടെ വിസ്താരം V/d<sup>3</sup>x6d<sup>2</sup>=6V/d ആണ്. അതിനാല് തന്മാത്രകളുടെ വിസ്താരം വര്ധിപ്പിക്കാന് ചെലവായ ഊര്ജം = പ്രതലബലം x വിസ്താരം=Sx6V/d=6SV/d . ബാഷ്പ ലീനതാപം L എങ്കില് V വ്യാപ്തം ദ്രാവകം ബാഷ്പീകരിക്കാന് ചെലവഴിച്ച ഊര്ജം = VL. ഇവ രണ്ടും തുല്യമായതിനാല്,6SV/d=VL . അതായത്, d=6S/L. വെള്ളത്തിന് S = 70 ഡൈന്/സെ.മീ. എന്നും H=Z<sup>2</sup>e<sup>4</sup>M/8∈<sup>2</sup><sub>0</sub> |
h<sup>3</sup>C എര്ഗ്/ഘ. സെ.മീ. എന്നും സ്വീകരിച്ചാല് d = 2 x 10<sup>-10</sup> മീ. അതായത് ജലതന്മാത്രയുടെ വലുപ്പം 0.20 നാനോ മീ. എന്നു വരുന്നു (1 നാനോ മീ. = 10<sup>-9</sup> മീ.) | h<sup>3</sup>C എര്ഗ്/ഘ. സെ.മീ. എന്നും സ്വീകരിച്ചാല് d = 2 x 10<sup>-10</sup> മീ. അതായത് ജലതന്മാത്രയുടെ വലുപ്പം 0.20 നാനോ മീ. എന്നു വരുന്നു (1 നാനോ മീ. = 10<sup>-9</sup> മീ.) | ||
| വരി 67: | വരി 67: | ||
(Mean free path model) | (Mean free path model) | ||
| - | ഗതികസിദ്ധാന്ത നിഗമനങ്ങള് തന്മാത്രകളുടെ വേഗത്തെപ്പറ്റിയുള്ള പഠനത്തില് ഏറെ പ്രാധാന്യം അര്ഹിക്കുന്നു. മിക്ക തന്മാത്രകളുടെയും വേഗം 25<u>°</u>c-ല് 300 മീറ്ററിലധികമാണ്. എങ്കിലും ഘനത്വംകൂടിയ കാര്ബണ് ഡൈഓക്സൈഡ് പോലുള്ള ഒരു വാതകം അന്തരീക്ഷത്തിലേക്കു തുറന്നുവച്ചിരുന്നാല് വായുവുമായുള്ള അതിന്റെ മിശ്രണം വളരെവേഗം നടക്കുന്നില്ലെന്നു പരീക്ഷണങ്ങള് തെളിയിച്ചിട്ടുണ്ട്. വളരെ കുറച്ചു ദൂരം മാത്രം സഞ്ചരിക്കുമ്പോഴേക്കും തന്മാത്രകള് തമ്മില് സംഘട്ടനം നടക്കുന്നതായിരിക്കണം അതിനു കാരണം. രണ്ടു അനുക്രമസംഘട്ടനങ്ങള്ക്കിടയില് ഒരു തന്മാത്ര സഞ്ചരിക്കുന്ന ശ.ശ. ദൂരമാണ് അതിന്റെ മാധ്യമുക്തപഥം. ഗതികസിദ്ധാന്തത്തില് തന്മാത്രകളെ കട്ടിയുള്ള ഗോളങ്ങളായി കല്പിച്ചിരിക്കുന്നു. ഒരു വ്യാപ്തമാത്ര(unit volume)യില് d വ്യാസമുള്ള n വാതക തന്മാത്രകളുണ്ടെങ്കില്, തന്മാത്രയുടെ മാധ്യമുക്തപഥം λ_യ്ക്കുള്ള സമീകരണം ഇങ്ങനെയാണ് & | + | ഗതികസിദ്ധാന്ത നിഗമനങ്ങള് തന്മാത്രകളുടെ വേഗത്തെപ്പറ്റിയുള്ള പഠനത്തില് ഏറെ പ്രാധാന്യം അര്ഹിക്കുന്നു. മിക്ക തന്മാത്രകളുടെയും വേഗം 25<u>°</u>c-ല് 300 മീറ്ററിലധികമാണ്. എങ്കിലും ഘനത്വംകൂടിയ കാര്ബണ് ഡൈഓക്സൈഡ് പോലുള്ള ഒരു വാതകം അന്തരീക്ഷത്തിലേക്കു തുറന്നുവച്ചിരുന്നാല് വായുവുമായുള്ള അതിന്റെ മിശ്രണം വളരെവേഗം നടക്കുന്നില്ലെന്നു പരീക്ഷണങ്ങള് തെളിയിച്ചിട്ടുണ്ട്. വളരെ കുറച്ചു ദൂരം മാത്രം സഞ്ചരിക്കുമ്പോഴേക്കും തന്മാത്രകള് തമ്മില് സംഘട്ടനം നടക്കുന്നതായിരിക്കണം അതിനു കാരണം. രണ്ടു അനുക്രമസംഘട്ടനങ്ങള്ക്കിടയില് ഒരു തന്മാത്ര സഞ്ചരിക്കുന്ന ശ.ശ. ദൂരമാണ് അതിന്റെ മാധ്യമുക്തപഥം. ഗതികസിദ്ധാന്തത്തില് തന്മാത്രകളെ കട്ടിയുള്ള ഗോളങ്ങളായി കല്പിച്ചിരിക്കുന്നു. ഒരു വ്യാപ്തമാത്ര(unit volume)യില് d വ്യാസമുള്ള n വാതക തന്മാത്രകളുണ്ടെങ്കില്, തന്മാത്രയുടെ മാധ്യമുക്തപഥം λ_യ്ക്കുള്ള സമീകരണം ഇങ്ങനെയാണ് λ=1/√2πnd<sup>2</sup>.V വ്യാപ്തം വാതകത്തില് V<sub>n</sub> തന്മാത്രകള് ഉണ്ടായിരിക്കും. വാതകം ദ്രാവകമായി സംഘനിക്കുമ്പോള് വ്യാപ്തം V ആണെങ്കില് തുല്യ ഗോളങ്ങളുടെ സങ്കുലന രീതി (packing nature) കണക്കിലെടുത്താല് v = Vnd<sup>3</sup> എന്നു തെളിയിക്കാം. അപ്പോള്,Vλ=Vd/√2π എന്നു കിട്ടുന്നു. മിക്ക വാതകങ്ങള്ക്കും V = 0.005V, λ= 2 x 10<sup>-8</sup> മീ. ആയതിനാല് d = 0.20 നാനോമീറ്റര് (നോ: അന്താരാഷ്ട്രമാത്രാ സമ്പ്രദായം) എന്നു കിട്ടുന്നു. തന്മാത്രകളുടെ വലുപ്പം ഏകദേശം 0.20 നാനോമീറ്റര് വരും. 1 ഘ.സെ.മീ. തന്മാത്രയില് ഏകദേശം 4.5 x 10<sup>19</sup> തന്മാത്രകള് ഉണ്ടെന്ന് ഈ തന്മാത്രാ വലുപ്പം ഉപയോഗിച്ച് 1865-ല് ജെ. ലോഷ്മിഡ്റ്റ് നിര്ണയിച്ചു. രസതന്ത്രജ്ഞരെ സംബന്ധിച്ചിടത്തോളം ഒരു ഗ്രാം വാതകത്തില്, അതായത് 22415 ഘ.സെ.മീ. വാതകത്തില് എത്ര തന്മാത്രകളുണ്ടെന്നുള്ള അറിവ് പ്രധാനമാണ്. ഈ അറിവ് ഓരോ മൂലക അണുവിന്റെയും കേവലഭാരം നിര്ണയിക്കാന് സഹായിക്കുന്നു. ഒരു ഗ്രാം തന്മാത്രയിലുള്ള അണുക്കളുടെ സംഖ്യയെ അവോഗാഡ്രോസംഖ്യ N<sub>0</sub> എന്നു പറയുന്നു. ഏറ്റവും പുതിയ വിധികളനുസരിച്ചുള്ള നിര്ണയപ്രകാരം അവോഗാഡ്രോസംഖ്യ 6.02252 x 10<sup>23</sup> ആണ്. ഇതില്നിന്ന് ഹൈഡ്രജന് അണുവിന്റെ ഭാരം = 1.673 x 10<sup>-27</sup> കി.ഗ്രാം എന്നു കിട്ടുന്നു. ഏതു മൂലകത്തിലെ അണുവിന്റെയും കേവലഭാരം കാണാന് അതിന്റെ അണുഭാരത്തെ ഹൈഡ്രജന്-അണുഭാരം കൊണ്ട് ഗുണിച്ചാല് മതി. |
===എണ്ണഫിലിം രീതി=== | ===എണ്ണഫിലിം രീതി=== | ||
| വരി 79: | വരി 79: | ||
(X-ray diffraction) | (X-ray diffraction) | ||
| - | ക്രിസ്റ്റലീയ ഖരങ്ങള്ക്ക് നിശ്ചിത ജ്യാമിതീയ രൂപമുണ്ട്. അവയില് നിശ്ചിത ജ്യാമിതീയ മാതൃകകളിലാണ് അണുക്കള് വിന്യസിച്ചിരിക്കുന്നത്. ക്രിസ്റ്റലിലെ മാത്രാസെല്ലിന്റെ വ്യാപ്തം (v) കാണാനുള്ള സമീകരണം V=ZM/N<sub>0</sub> | + | ക്രിസ്റ്റലീയ ഖരങ്ങള്ക്ക് നിശ്ചിത ജ്യാമിതീയ രൂപമുണ്ട്. അവയില് നിശ്ചിത ജ്യാമിതീയ മാതൃകകളിലാണ് അണുക്കള് വിന്യസിച്ചിരിക്കുന്നത്. ക്രിസ്റ്റലിലെ മാത്രാസെല്ലിന്റെ വ്യാപ്തം (v) കാണാനുള്ള സമീകരണം V=ZM/N<sub>0</sub>ρ ആണ്. ഇവിടെ Z മാത്രാസെല്ലിലുള്ള അണുക്കളുടെ എണ്ണം, M അണുഭാരം, N<sub>0</sub> അവോഗാഡ്രോസംഖ്യ,ρ ഘനത്വം എന്നിവയെ പ്രതിനിധാനം ചെയ്യുന്നു. അലുമിനിയം ലോഹത്തിന്റെ ക്രിസ്റ്റലില് മാത്രാസെല്ലിന്റെ വ്യാപ്തം പരിശോധിക്കുമ്പോള് ഇത് വ്യക്തമാകും. അലൂമിനിയത്തിന് Z = 4, M= 26.98,ρ = 2.7 ഗ്രാം/ഘ.സെ.മീ. ആയതിനാല്,V=4 x 26.98/2.7 x 6.023 x 10<sup>23</sup> = 64.86 x 10<sup>-21</sup> ഘ.സെ.മീ. മാത്രാസെല്ലിന് ക്യൂബ് ആകൃതി ആയതിനാല്, ക്യൂബിന്റെ വശം = 4.049 x 10<sup>-8</sup> സെ.മീ. = 0.4049 നാനോമീറ്റര്. ഗോളങ്ങളുടെ ജ്യാമിതീയ സങ്കുലനം കണക്കിലെടുക്കുമ്പോള്, അലുമിനിയം അണുവിന്റെ വ്യാസം 0.286 നാനോമീറ്റര് എന്നുവരുന്നു. ഇപ്രകാരം പല അണുക്കളുടെയും വ്യാസം നിര്ണയിച്ചിട്ടുണ്ട്. |
അണുഭാരം കൂടുന്ന മുറയ്ക്ക് അണുക്കളുടെ വലുപ്പം കൂടുന്നുണ്ടെങ്കിലും ഈ വസ്തുത ഒരു നിയമമായി ഗണിക്കവയ്യ. ഏറ്റവും കൂടുതല് വലുപ്പമുള്ള അണുക്കളുടെ കൂട്ടത്തില്പെടുന്നു ക്ഷാരലോഹങ്ങള്. അണുക്കളുടെ വലുപ്പം സാമാന്യമായി 0.1 മുതല് 0.5 വരെ നാനോമീറ്റര് ആണെന്നു പറയാം. | അണുഭാരം കൂടുന്ന മുറയ്ക്ക് അണുക്കളുടെ വലുപ്പം കൂടുന്നുണ്ടെങ്കിലും ഈ വസ്തുത ഒരു നിയമമായി ഗണിക്കവയ്യ. ഏറ്റവും കൂടുതല് വലുപ്പമുള്ള അണുക്കളുടെ കൂട്ടത്തില്പെടുന്നു ക്ഷാരലോഹങ്ങള്. അണുക്കളുടെ വലുപ്പം സാമാന്യമായി 0.1 മുതല് 0.5 വരെ നാനോമീറ്റര് ആണെന്നു പറയാം. | ||
| വരി 91: | വരി 91: | ||
പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങുന്നവയായിരുന്നു ഫാരഡെയുടെ ഗവേഷണങ്ങള്. ഒരേ പരിമാണം വൈദ്യുതി, വിവിധ ഇലക്ട്രോളൈറ്റുക(electrolytes)ളില്കൂടി പ്രവഹിപ്പിച്ചാല്, നിക്ഷേപിക്കപ്പെടുന്ന പദാര്ഥങ്ങളുടെ ഭാരം അവയുടെ രാസതുല്യാങ്കഭാരങ്ങള്ക്ക് ആനുപാതികമായിരിക്കുമെന്നു മൈക്കേല്ഫാരഡെ 1833-ല് കണ്ടുപിടിച്ചു. ഒരു കി.ഗ്രാം. തുല്യാങ്കം പദാര്ഥം നിക്ഷേപിക്കപ്പെടാന് 9.6522 x10<sup>7</sup> കൂളും വൈദ്യുതി വേണമെന്ന് ഫാരഡെ കണ്ടെത്തി. ഈ വസ്തുത പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങാന് പര്യാപ്തമായിരുന്നു. | പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങുന്നവയായിരുന്നു ഫാരഡെയുടെ ഗവേഷണങ്ങള്. ഒരേ പരിമാണം വൈദ്യുതി, വിവിധ ഇലക്ട്രോളൈറ്റുക(electrolytes)ളില്കൂടി പ്രവഹിപ്പിച്ചാല്, നിക്ഷേപിക്കപ്പെടുന്ന പദാര്ഥങ്ങളുടെ ഭാരം അവയുടെ രാസതുല്യാങ്കഭാരങ്ങള്ക്ക് ആനുപാതികമായിരിക്കുമെന്നു മൈക്കേല്ഫാരഡെ 1833-ല് കണ്ടുപിടിച്ചു. ഒരു കി.ഗ്രാം. തുല്യാങ്കം പദാര്ഥം നിക്ഷേപിക്കപ്പെടാന് 9.6522 x10<sup>7</sup> കൂളും വൈദ്യുതി വേണമെന്ന് ഫാരഡെ കണ്ടെത്തി. ഈ വസ്തുത പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങാന് പര്യാപ്തമായിരുന്നു. | ||
| - | സാധാരണ പരിതഃസ്ഥിതികളില് വാതകങ്ങള് നല്ല ഇന്സുലേറ്ററുകളാണ്. ഉയര്ന്ന പൊട്ടന്ഷ്യല് പ്രയോഗിച്ചാല് ഒരു ഡിസ്ചാര്ജ് മാത്രമേ ഉണ്ടാകയുള്ളു. പക്ഷേ, മര്ദം കുറയും തോറും അതിലെ വാതകം ചാലകത പ്രദര്ശിപ്പിക്കുകയും പല ദീപ്തിപ്രവാഹങ്ങള് അതില് ഉണ്ടാക്കുകയും ചെയ്യും. ഡിസ്ചാര്ജ് ട്യൂബുകളില് ഉണ്ടാകുന്ന ഇത്തരം പ്രതിഭാസങ്ങളെപ്പറ്റി ജെ. പ്ളക്കര് (1858), ഡബ്ള്യു. ഹിറ്റോര്ഫ് (1869), വില്യം ക്രൂക്സ് (1879) തുടങ്ങി പലരും പഠനം നടത്തി. മര്ദം 1- 0.1 ന്യൂട്ടണ് മീ<sup>-2</sup> ആയിരിക്കുമ്പോള് കാഥോഡില്നിന്നു പുറപ്പെടുന്ന കിരണങ്ങളെ ഇ. ഗോള്ഡ്സ്റ്റൈന് എന്ന ശാസ്ത്രജ്ഞന് കാഥോഡ്കിരണങ്ങള് ( | + | സാധാരണ പരിതഃസ്ഥിതികളില് വാതകങ്ങള് നല്ല ഇന്സുലേറ്ററുകളാണ്. ഉയര്ന്ന പൊട്ടന്ഷ്യല് പ്രയോഗിച്ചാല് ഒരു ഡിസ്ചാര്ജ് മാത്രമേ ഉണ്ടാകയുള്ളു. പക്ഷേ, മര്ദം കുറയും തോറും അതിലെ വാതകം ചാലകത പ്രദര്ശിപ്പിക്കുകയും പല ദീപ്തിപ്രവാഹങ്ങള് അതില് ഉണ്ടാക്കുകയും ചെയ്യും. ഡിസ്ചാര്ജ് ട്യൂബുകളില് ഉണ്ടാകുന്ന ഇത്തരം പ്രതിഭാസങ്ങളെപ്പറ്റി ജെ. പ്ളക്കര് (1858), ഡബ്ള്യു. ഹിറ്റോര്ഫ് (1869), വില്യം ക്രൂക്സ് (1879) തുടങ്ങി പലരും പഠനം നടത്തി. മര്ദം 1- 0.1 ന്യൂട്ടണ് മീ<sup>-2</sup> ആയിരിക്കുമ്പോള് കാഥോഡില്നിന്നു പുറപ്പെടുന്ന കിരണങ്ങളെ ഇ. ഗോള്ഡ്സ്റ്റൈന് എന്ന ശാസ്ത്രജ്ഞന് കാഥോഡ്കിരണങ്ങള് (cathoderays) എന്നു വിളിച്ചു. കാഥോഡ്കിരണങ്ങള് കണങ്ങളാണ്; കാഥോഡിനു ലംബമായി നേര്രേഖയില് സഞ്ചരിക്കുന്നു; കാന്തികമണ്ഡലത്തിലും വിദ്യുത്മണ്ഡലത്തിലും അവ വ്യതിചലിക്കുന്നു എന്നെല്ലാം തെളിയിക്കപ്പെട്ടു. കാഥോഡ്കണങ്ങള്ക്ക് ഋണചാര്ജ് ഉണ്ടെന്ന് സര് ജെ.ജെ. തോംപ്സണ് തെളിയിച്ചു. പല വാതകങ്ങളും ഉപയോഗിച്ച് പരീക്ഷണങ്ങള് ആവര്ത്തിച്ചതിന്റെ ഫലമായി എല്ലാ വസ്തുക്കളിലും ഋണവൈദ്യുതിമാത്ര, അതായത് ഇലക്ട്രോണ്, ഒരു മൌലികഘടകമാണെന്നു സ്ഥാപിക്കപ്പെട്ടു. ഇലക്ട്രോണിന്റെ ചാര്ജ് e-ഉം ദ്രവ്യമാനം m-ഉം ആണെങ്കില്, e/m ന്റെ മൂല്യം 1.76 x 10<sup>11</sup> കൂളും കി.ഗ്രാം<sup>-1</sup> ആകുന്നു. |
ദ്വാരങ്ങളുള്ള ഒരു കാഥോഡ് ഉപയോഗിക്കുകയും മര്ദം വളരെ കുറയാതിരിക്കയും ചെയ്യുന്നെങ്കില്, ആനോഡില് (anode) നിന്ന്, അതായത് ധന ഇലക്ട്രോഡില്നിന്ന് വര്ണ രശ്മികള് പുറപ്പെടുന്നുണ്ടെന്ന് ഇ. ഗോള്ഡ്സ്റ്റൈന് (1886) തെളിയിച്ചു. ഇവയെ ധനകിരണങ്ങള് എന്നു വിളിക്കുന്നു. ഈ കണങ്ങളെക്കുറിച്ചുള്ള ഗവേഷണങ്ങളുടെ ഫലമായി ഏറ്റവും ഭാരം കുറഞ്ഞ ധനകണത്തിന് ഹൈഡ്രജന് അണുവിന്റെ ഭാരമുണ്ടെന്ന് തെളിയിക്കപ്പെട്ടു. റഥര്ഫോര്ഡ് ഈ കണത്തെ പ്രോട്ടോണ് (proton) എന്നു വിളിച്ചു. | ദ്വാരങ്ങളുള്ള ഒരു കാഥോഡ് ഉപയോഗിക്കുകയും മര്ദം വളരെ കുറയാതിരിക്കയും ചെയ്യുന്നെങ്കില്, ആനോഡില് (anode) നിന്ന്, അതായത് ധന ഇലക്ട്രോഡില്നിന്ന് വര്ണ രശ്മികള് പുറപ്പെടുന്നുണ്ടെന്ന് ഇ. ഗോള്ഡ്സ്റ്റൈന് (1886) തെളിയിച്ചു. ഇവയെ ധനകിരണങ്ങള് എന്നു വിളിക്കുന്നു. ഈ കണങ്ങളെക്കുറിച്ചുള്ള ഗവേഷണങ്ങളുടെ ഫലമായി ഏറ്റവും ഭാരം കുറഞ്ഞ ധനകണത്തിന് ഹൈഡ്രജന് അണുവിന്റെ ഭാരമുണ്ടെന്ന് തെളിയിക്കപ്പെട്ടു. റഥര്ഫോര്ഡ് ഈ കണത്തെ പ്രോട്ടോണ് (proton) എന്നു വിളിച്ചു. | ||
| വരി 129: | വരി 129: | ||
[[Image:pno327.rather.png|left]] | [[Image:pno327.rather.png|left]] | ||
| - | സ്വര്ണത്തകിടിന്റെ പിന്നില് സിങ്ക്സള്ഫൈഡ് സ്ക്രീന് സ്ഥാപിച്ചു. α-കണങ്ങള് ഈ സ്ക്രീനില് പതിച്ചാല് പ്രകാശസ്ഫുരണങ്ങള് ഉണ്ടാകും. മിക്കവാറും എല്ലാ α-കണങ്ങളും തകിടില്ക്കൂടി കടന്നുപോകുമെന്നും ചിലതിനു മാത്രം വ്യതിചലനം ഉണ്ടാകുമെന്നും ആയിരുന്നു പ്രതീക്ഷ. തോംപ്സന്റെ അണുമാതൃകയില് ചാര്ജുകള് ഏകസമാനമായതിനാല് പ്രതീക്ഷിക്കാവുന്നതാണ് ഇത്. പക്ഷേ ഗൈഗറും മാര്സ്ഡനും കണ്ടത് ഇതാണ്: മിക്ക α-കണങ്ങളും തകിടിലൂടെ കടന്നുപോയി; പക്ഷേ ചിലത് വലിയ കോണങ്ങളില് പ്രകീര്ണനം ചെയ്യപ്പെട്ടു. ചിലതു പിറകോട്ടു പ്രകീര്ണനം | + | സ്വര്ണത്തകിടിന്റെ പിന്നില് സിങ്ക്സള്ഫൈഡ് സ്ക്രീന് സ്ഥാപിച്ചു. α-കണങ്ങള് ഈ സ്ക്രീനില് പതിച്ചാല് പ്രകാശസ്ഫുരണങ്ങള് ഉണ്ടാകും. മിക്കവാറും എല്ലാ α-കണങ്ങളും തകിടില്ക്കൂടി കടന്നുപോകുമെന്നും ചിലതിനു മാത്രം വ്യതിചലനം ഉണ്ടാകുമെന്നും ആയിരുന്നു പ്രതീക്ഷ. തോംപ്സന്റെ അണുമാതൃകയില് ചാര്ജുകള് ഏകസമാനമായതിനാല് പ്രതീക്ഷിക്കാവുന്നതാണ് ഇത്. പക്ഷേ ഗൈഗറും മാര്സ്ഡനും കണ്ടത് ഇതാണ്: മിക്ക α-കണങ്ങളും തകിടിലൂടെ കടന്നുപോയി; പക്ഷേ ചിലത് വലിയ കോണങ്ങളില് പ്രകീര്ണനം ചെയ്യപ്പെട്ടു. ചിലതു പിറകോട്ടു പ്രകീര്ണനം ചെയ്യപ്പെട്ട α-കണങ്ങള്ക്ക് ഇലക്ട്രോണിന്റെ 7,000 മടങ്ങ് ഭാരം ഉണ്ടായിരുന്നതിനാലും, അവ നല്ല വേഗത്തില് പാഞ്ഞിരുന്നതിനാലും തീവ്രബലം പ്രവര്ത്തിച്ചെങ്കില് മാത്രമേ അവ പിന്തിരിയുകയുള്ളു എന്ന നിഗമനത്തില് അവര് എത്തി. |
===റഥര്ഫോര്ഡ് മാതൃക=== | ===റഥര്ഫോര്ഡ് മാതൃക=== | ||
| വരി 171: | വരി 171: | ||
ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കിയാണ് ബോര്, ഹൈഡ്രജന് അണുവിന്റെ വ്യാസാര്ധം (radius), അനുവദനീയ പരിപഥ ഊര്ജം (circuit energy) എന്നിവ പരികലനം നടത്തിയതും നിരീക്ഷ്യസ്പെക്ട്രരേഖകള് (visible spectral lines) സൈദ്ധാന്തികമായി പ്രവചിക്കാമെന്നു തെളിയിച്ചതും. | ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കിയാണ് ബോര്, ഹൈഡ്രജന് അണുവിന്റെ വ്യാസാര്ധം (radius), അനുവദനീയ പരിപഥ ഊര്ജം (circuit energy) എന്നിവ പരികലനം നടത്തിയതും നിരീക്ഷ്യസ്പെക്ട്രരേഖകള് (visible spectral lines) സൈദ്ധാന്തികമായി പ്രവചിക്കാമെന്നു തെളിയിച്ചതും. | ||
| - | m,v,r എന്നിവ യഥാക്രമം ഇലക്ട്രോണിന്റെ ദ്രവ്യമാനം, ഭ്രമണവേഗം, ഭ്രമണപഥത്രിജ്യ (radius) എന്നിവ ആണെങ്കില് ബോര് സ്ഥിരാവസ്ഥ ഇങ്ങനെ കുറിക്കാം: 2π mvr =nh. ഇവിടെ n പ്ളാങ്ക് സ്ഥിരാങ്കവും ആണ്. ഈ സമീകരണത്തെ mvr =n h/2 എന്നെഴുതിയാല് ബോറിന്റെ രണ്ടാമത്തെ സങ്കല്പനമായി. ഇവിടെ mvr | + | m,v,r എന്നിവ യഥാക്രമം ഇലക്ട്രോണിന്റെ ദ്രവ്യമാനം, ഭ്രമണവേഗം, ഭ്രമണപഥത്രിജ്യ (radius) എന്നിവ ആണെങ്കില് ബോര് സ്ഥിരാവസ്ഥ ഇങ്ങനെ കുറിക്കാം: 2π mvr =nh. ഇവിടെ n പ്ളാങ്ക് സ്ഥിരാങ്കവും ആണ്. ഈ സമീകരണത്തെ mvr =n h/2π എന്നെഴുതിയാല് ബോറിന്റെ രണ്ടാമത്തെ സങ്കല്പനമായി. ഇവിടെ mvr കോണീയസംവേഗവും n ക്വാണ്ടംസംഖ്യയും ആണ്. രേഖാസ്പെക്ട്രത്തില് അണു ഊര്ജവികിരണം നടത്തുന്നുണ്ട്. ഇതിന് ബോര് നല്കിയ വിശദീകരണം ഇതാണ്: സാധാരണ അണു നിമ്നതലത്തില് (ground state) ആണ്; അത് ഉത്സര്ജിതമാകുമ്പോള് ക്വാണ്ടീകരിച്ച ഊര്ജം (quantized energy) അവശോഷണം ചെയ്കയും ഇലക്ട്രോണ് താത്കാലികമായി ഉത്തേജിതാവസ്ഥയില് ആകുകയും ചെയ്യുന്നു. ക്ഷണികമായ ഈ ഉത്തേജിതാവസ്ഥയില് നിന്ന് (ഊര്ജം: En<sub>2</sub>) ആദ്യാവസ്ഥയിലേക്ക് (ഊര്ജം: En<sub>1</sub>) ഇലക്ട്രോണ് വരുമ്പോള് ഊര്ജവികിരണം നടത്തുന്നു. അതായത്, |
[[Image:p328b1.png]] | [[Image:p328b1.png]] | ||
| - | (3), (4), (5), (6) എന്നീ സമീകരണങ്ങളില്, Ze = അണുകേന്ദ്രചാര്ജ്, e = ഇലക്ട്രോണ്ചാര്ജ്, m = ഇലക്ട്രോണ് ദ്രവ്യമാനം, (സ്വതന്ത്ര സ്പെയ്സിന്റെ വിദ്യുത്ശീലത) = 8.854 x10 <sup>-12</sup> ഫാരഡ് മീ.<sup>-1 | + | (3), (4), (5), (6) എന്നീ സമീകരണങ്ങളില്, Ze = അണുകേന്ദ്രചാര്ജ്, e = ഇലക്ട്രോണ്ചാര്ജ്, m = ഇലക്ട്രോണ് ദ്രവ്യമാനം, (സ്വതന്ത്ര സ്പെയ്സിന്റെ വിദ്യുത്ശീലത) = 8.854 x10 <sup>-12</sup> ഫാരഡ് മീ.<sup>-1</sup> n= ക്വാണ്ടം സംഖ്യ എന്നിവ ആണ്. ബോര് സിദ്ധാന്തത്തിന്റെ സാധുത്വം പരിശോധിക്കാന് റിഡ്ബര്ഗ് സ്ഥിരാങ്കത്തിന്റെ എംപിരികസമീകരണമൂല്യവും സമീകരണം (6)-ന്റെ മൂല്യവും തമ്മിലുള്ള പൊരുത്തം പ്രയോജനപ്പെടുത്താം. ഹൈഡ്രജന് അണുവിന് z = 1, e = 1.60 x 10<sup>-19</sup> |
കൂളും m = 9.11 x 10<sup>-31</sup> കി.ഗ്രാം, c = 3 x 10<sup>8</sup> മീ. സെ.<sup>-1</sup>, h = 6.62 x 10<sup>-34</sup> ജൂള് സെ. എന്നീ മൂല്യങ്ങള് സമീകരണം (6)-ല് പ്രതിസ്ഥാപിച്ചാല്, R<sub>H</sub> = 1.099 x 10<sup>7</sup> മീ.<sup>-1</sup> എന്നുകിട്ടുന്നു. R<sub>H</sub>-ന്റെ മൂല്യങ്ങള് ഏകദേശം തുല്യമായതിനാല് ബോര് സിദ്ധാന്തം വിജയമായിരുന്നു എന്നു പറയാം; ഹൈഡ്രജന് അണുവിന്റെ ത്രിജ്യ 0.053 നാനോമീറ്ററും. | കൂളും m = 9.11 x 10<sup>-31</sup> കി.ഗ്രാം, c = 3 x 10<sup>8</sup> മീ. സെ.<sup>-1</sup>, h = 6.62 x 10<sup>-34</sup> ജൂള് സെ. എന്നീ മൂല്യങ്ങള് സമീകരണം (6)-ല് പ്രതിസ്ഥാപിച്ചാല്, R<sub>H</sub> = 1.099 x 10<sup>7</sup> മീ.<sup>-1</sup> എന്നുകിട്ടുന്നു. R<sub>H</sub>-ന്റെ മൂല്യങ്ങള് ഏകദേശം തുല്യമായതിനാല് ബോര് സിദ്ധാന്തം വിജയമായിരുന്നു എന്നു പറയാം; ഹൈഡ്രജന് അണുവിന്റെ ത്രിജ്യ 0.053 നാനോമീറ്ററും. | ||
| വരി 181: | വരി 181: | ||
പക്ഷേ, ബോര് സിദ്ധാന്തത്തിന്റെ വിജയം താത്കാലികം മാത്രം ആയിരുന്നു. ഒന്നിലധികം ഇലക്ട്രോണുകള് ഉള്ള അണുക്കളുടെ കാര്യത്തില് ബോര് സിദ്ധാന്തം പരാജയപ്പെട്ടു. | പക്ഷേ, ബോര് സിദ്ധാന്തത്തിന്റെ വിജയം താത്കാലികം മാത്രം ആയിരുന്നു. ഒന്നിലധികം ഇലക്ട്രോണുകള് ഉള്ള അണുക്കളുടെ കാര്യത്തില് ബോര് സിദ്ധാന്തം പരാജയപ്പെട്ടു. | ||
| - | |||
===ദീര്ഘവൃത്ത ഭ്രമണപഥ ഇലക്ട്രോണ്=== | ===ദീര്ഘവൃത്ത ഭ്രമണപഥ ഇലക്ട്രോണ്=== | ||
| വരി 195: | വരി 194: | ||
(Magnetic Quantum number). | (Magnetic Quantum number). | ||
| - | സ്പെക്ട്രരേഖകളുടെ സൂക്ഷ്മഘടന വിശദീകരിക്കാന് ദീര്ഘവൃത്തഭ്രമണപഥങ്ങള് സഹായകമായി. എങ്കിലും ക്ഷാരലോഹങ്ങളുടെ സ്പെക്ട്രങ്ങളിലെ ദ്വന്ദ്വ(pair)ത്തെ വിശദീകരിക്കാന് ഇത് പര്യാപ്തമായില്ല. ഗൂഡ്സ്മിത്ത്, ഉള്ളന്ബെക്ക് എന്നിവര് 1925-ല് ഇലക്ട്രോണ് ചക്രണം എന്ന സങ്കല്പം ഉന്നയിച്ചു. ഭൂമി സ്വന്തം അച്ചുതണ്ടില് കറങ്ങുന്നതുപോലെ ഇലക്ട്രോണും കറങ്ങുന്നുണ്ട്. ഭൂമി, സൂര്യനെ | + | സ്പെക്ട്രരേഖകളുടെ സൂക്ഷ്മഘടന വിശദീകരിക്കാന് ദീര്ഘവൃത്തഭ്രമണപഥങ്ങള് സഹായകമായി. എങ്കിലും ക്ഷാരലോഹങ്ങളുടെ സ്പെക്ട്രങ്ങളിലെ ദ്വന്ദ്വ(pair)ത്തെ വിശദീകരിക്കാന് ഇത് പര്യാപ്തമായില്ല. ഗൂഡ്സ്മിത്ത്, ഉള്ളന്ബെക്ക് എന്നിവര് 1925-ല് ഇലക്ട്രോണ് ചക്രണം എന്ന സങ്കല്പം ഉന്നയിച്ചു. ഭൂമി സ്വന്തം അച്ചുതണ്ടില് കറങ്ങുന്നതുപോലെ ഇലക്ട്രോണും കറങ്ങുന്നുണ്ട്. ഭൂമി, സൂര്യനെ 365¼ ദിവസംകൊണ്ട് പ്രദക്ഷിണം വയ്ക്കുന്നു; പക്ഷേ സ്വന്തം അച്ചുതണ്ടില് 24 മണിക്കൂര് കൊണ്ട് കറങ്ങുന്നു. ഇലക്ട്രോണാകട്ടെ ദീര്ഘവൃത്തഭ്രമണപഥത്തില് അണുകേന്ദ്രത്തെ പ്രദക്ഷിണം വയ്ക്കുന്നു. സ്വന്തം അച്ചുതണ്ടില് 1/2(h/2π)കോണിയ സംവേഗ(angular momentum)ത്തോടെ കറങ്ങുന്നു. ഇതില്നിന്ന് ഇലക്ട്രോണിന് ചക്രണ ക്വാണ്ടംസംഖ്യ s ഉണ്ടെന്നും S = 1/2എന്നും കിട്ടുന്നു. ഇലക്ട്രോണ് അതിന്റെ ഭ്രമണപഥദിശയില് കറങ്ങുമ്പോള് സമാന്തര ചക്രണവും(S=+1/2) എതിര്ദിശകളിലാകുമ്പോള് പ്രതിസമാന്തരചക്രണവും (S=-1/2) നടത്തുന്നുവെന്ന് പറയുന്നു. |
ഈ പശ്ചാത്തലത്തില്, അണുവിലെ ഒരു ഇലക്ട്രോണിന്റെ അവസ്ഥ രേഖപ്പെടുത്താന് n,l,s എന്നീ മൂന്നു ക്വാണ്ടംസംഖ്യകള് ആവശ്യമെന്നു വരുന്നു. | ഈ പശ്ചാത്തലത്തില്, അണുവിലെ ഒരു ഇലക്ട്രോണിന്റെ അവസ്ഥ രേഖപ്പെടുത്താന് n,l,s എന്നീ മൂന്നു ക്വാണ്ടംസംഖ്യകള് ആവശ്യമെന്നു വരുന്നു. | ||
| വരി 209: | വരി 208: | ||
(Pauli Principle). | (Pauli Principle). | ||
| - | ദൂരവ്യാപകഫലങ്ങള് ഉളവാക്കിയ പൌളിതത്ത്വം, അതായത് പൌളി അപവര്ജനതത്ത്വം (Pauil | + | ദൂരവ്യാപകഫലങ്ങള് ഉളവാക്കിയ പൌളിതത്ത്വം, അതായത് പൌളി അപവര്ജനതത്ത്വം (Pauil's Exclusion Principle) 1925-ല് വൂള്ഫ് ഗാങ് പൌളി എന്ന ശാസ്ത്രജ്ഞന് പ്രസ്താവിച്ചതാണ്. ആ തത്ത്വം ഇതാണ്: ഒരു അണുവില് n,l,s,ml എന്നീ 4 ക്വാണ്ടംസംഖ്യകള്ക്ക് തുല്യമായിട്ട് രണ്ട് ഇലക്ട്രോണുകള് ഉണ്ടാകയില്ല. z അണുസംഖ്യയുള്ള ഒരു അണുവില് z ഇലക്ട്രോണുകള് ഉണ്ടായിരിക്കും. ഈ ഇലക്ട്രോണുകളെ വ്യത്യസ്തഭ്രമണപഥങ്ങളിലാണ് ക്രമപ്പെടുത്തിയിരിക്കുന്നത്. ഈ ഇലക്ട്രോണുകള് ഓരോന്നിനും തനതായ 4 ക്വാണ്ടംസംഖ്യകള് ഉണ്ട്; ഇവയാണ് ഇലക്ട്രോണിന്റെ അവസ്ഥ നിര്ണയിക്കുന്നത്. |
| - | ഒരേ മുഖ്യക്വാണ്ടംസംഖ്യ n ഉള്ള ഇലക്ട്രോണുകള് ഒരേ ഷെല്ലില് ഉള്ളവയെന്നു പറയുന്നു. അണുകേന്ദ്രത്തോട് ഏറ്റവും അടുത്ത ഭ്രമണപഥത്തിന് (n = 1), ഇത് K-ഷെല്; (n = 2), L-ഷെല്; (n = 3), | + | ഒരേ മുഖ്യക്വാണ്ടംസംഖ്യ n ഉള്ള ഇലക്ട്രോണുകള് ഒരേ ഷെല്ലില് ഉള്ളവയെന്നു പറയുന്നു. അണുകേന്ദ്രത്തോട് ഏറ്റവും അടുത്ത ഭ്രമണപഥത്തിന് (n = 1), ഇത് K-ഷെല്; (n = 2), L-ഷെല്; (n = 3), M ഷെല് ഇത്യാദി. ഒരു ഷെല്ലില് ഉണ്ടാകാവുന്ന പരാമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം 2n<sup>2</sup> ആണ്. ഇവിടെ n മുഖ്യക്വാണ്ടം സംഖ്യയാണ്. nനും lനും ഒരേ മൂല്യമുള്ള ഇലക്ട്രോണുകളെ സബ്ഷെല് ഇലക്ട്രോണുകള് എന്നു പറയുന്നു. ഒരു ഷെല്ലില് ആകാവുന്നത്ര ഇലക്ട്രോണുകള് ഉണ്ടെങ്കില് ആ ഷെല് പൂര്ണമായി എന്നു പറയുന്നു. |
===മോസ്ലി നിയമം=== | ===മോസ്ലി നിയമം=== | ||
| - | 1913-ല് ആണ് ഹെന്റി ജി. മോസ്ലി എന്ന ബ്രിട്ടിഷ് ഭൌതികശാസ്ത്രജ്ഞന് പല ലോഹമൂലകങ്ങളുടെയും സ്വാഭാവിക എക്സ്റേസ്പെക്ട്രത്തെക്കുറിച്ച് ക്രമവത്കൃതമായ പഠനം നടത്തിയത്. ഇതിന്റെ ഫലമായി, മൂലകത്തിന്റെ അണുസംഖ്യ z കൂടുന്നതനുസരിച്ച് എക്സ്റേയുടെ ആവൃത്തി കുറയുന്നതായി കണ്ടു. | + | 1913-ല് ആണ് ഹെന്റി ജി. മോസ്ലി എന്ന ബ്രിട്ടിഷ് ഭൌതികശാസ്ത്രജ്ഞന് പല ലോഹമൂലകങ്ങളുടെയും സ്വാഭാവിക എക്സ്റേസ്പെക്ട്രത്തെക്കുറിച്ച് ക്രമവത്കൃതമായ പഠനം നടത്തിയത്. ഇതിന്റെ ഫലമായി, മൂലകത്തിന്റെ അണുസംഖ്യ z കൂടുന്നതനുസരിച്ച് എക്സ്റേയുടെ ആവൃത്തി കുറയുന്നതായി കണ്ടു. ν ആവൃത്തിയും c, b എന്നിവ സ്ഥിരാങ്കങ്ങളുമായ മോസ്ലി നിയമം ഇങ്ങനെ കുറിക്കാം: |
[[Image:pno.330Fa1.png]] | [[Image:pno.330Fa1.png]] | ||
| വരി 237: | വരി 236: | ||
(Proton,Neutron). | (Proton,Neutron). | ||
| - | അണുസംരചനയില് ധനചാര്ജിതമാത്രയാണ് പ്രോട്ടോണ്. ധനകിരണവിശ്ളേഷണത്തില് ഇവയെ കണ്ടെത്തിയെന്നു നേരത്തെ സൂചിപ്പിച്ചു. ഇലക്ട്രോണ് നഷ്ടപ്പെട്ട ഹൈഡ്രജന് അണുവാണ് പ്രോട്ടോണ്; അതായത് ഹൈഡ്രജന്റെ അണുകേന്ദ്രം. ഇതിന് ഇലക്ട്രോണിന്റെ 1,837 മടങ്ങ് ഭാരമുണ്ട്. ഹൈഡ്രജന് അണുക്കള് ആണ് മൂലകങ്ങളുടെ അടിസ്ഥാനം എന്ന് പ്രൌട്ട്, 1815-ല് പ്രസ്താവിച്ചിട്ടുണ്ട്. അണുസംഖ്യയും അണുഭാരവും തമ്മിലുള്ള അനുപാതം പകുതിയിലധികം മൂലകങ്ങള്ക്കും 1-ല് കുറവായതിനാല് രണ്ടു പ്രശ്നങ്ങള് ഉണ്ടായി: (1) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുഭാരത്തെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു; ചാര്ജ് തുലനപ്പെടുത്താന് ആവശ്യമായ ഇലക്ട്രോണുകള് ഉണ്ടായിരിക്കുകയും ചെയ്യും; (2) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുസംഖ്യയെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു. ബാക്കിഭാരം ഉദാസീനവും പ്രോട്ടോണിന്റെ അത്രഭാരമുള്ളതുമായ ആവശ്യമുള്ളിടത്തോളം ഉദാസീനകണങ്ങളുടേതാണ്. 1932-ല് ജെ. | + | അണുസംരചനയില് ധനചാര്ജിതമാത്രയാണ് പ്രോട്ടോണ്. ധനകിരണവിശ്ളേഷണത്തില് ഇവയെ കണ്ടെത്തിയെന്നു നേരത്തെ സൂചിപ്പിച്ചു. ഇലക്ട്രോണ് നഷ്ടപ്പെട്ട ഹൈഡ്രജന് അണുവാണ് പ്രോട്ടോണ്; അതായത് ഹൈഡ്രജന്റെ അണുകേന്ദ്രം. ഇതിന് ഇലക്ട്രോണിന്റെ 1,837 മടങ്ങ് ഭാരമുണ്ട്. ഹൈഡ്രജന് അണുക്കള് ആണ് മൂലകങ്ങളുടെ അടിസ്ഥാനം എന്ന് പ്രൌട്ട്, 1815-ല് പ്രസ്താവിച്ചിട്ടുണ്ട്. അണുസംഖ്യയും അണുഭാരവും തമ്മിലുള്ള അനുപാതം പകുതിയിലധികം മൂലകങ്ങള്ക്കും 1-ല് കുറവായതിനാല് രണ്ടു പ്രശ്നങ്ങള് ഉണ്ടായി: (1) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുഭാരത്തെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു; ചാര്ജ് തുലനപ്പെടുത്താന് ആവശ്യമായ ഇലക്ട്രോണുകള് ഉണ്ടായിരിക്കുകയും ചെയ്യും; (2) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുസംഖ്യയെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു. ബാക്കിഭാരം ഉദാസീനവും പ്രോട്ടോണിന്റെ അത്രഭാരമുള്ളതുമായ ആവശ്യമുള്ളിടത്തോളം ഉദാസീനകണങ്ങളുടേതാണ്. 1932-ല് ജെ. ചാഡ്വിക്, അത്തരം കണങ്ങള് കണ്ടുപിടിച്ചു. വിദ്യുത്-ചാര്ജില്ലാത്ത പ്രോട്ടോണിനോളം തന്നെ ഭാരമുള്ള ഈ കണങ്ങളാണ് ന്യൂട്രോണുകള് എന്നറിയപ്പെടുന്നത്. |
===ദ്രവ്യമാനസംഖ്യ=== | ===ദ്രവ്യമാനസംഖ്യ=== | ||
| വരി 264: | വരി 263: | ||
(Uncertainty Principle). | (Uncertainty Principle). | ||
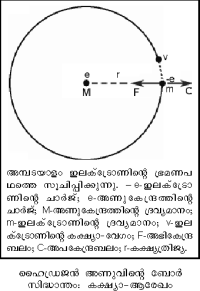
| - | അണുസംരചനയിലെ ഇലക്ട്രോണിന് തരംഗഗുണധര്മങ്ങള് ആരോപിക്കുമ്പോള് ഇലക്ട്രോണിനെ ഒരു ബിന്ദുവായല്ല പ്രത്യുത, സ്പെയ്സില് നിശ്ചിത തരംഗനീളമുള്ള തരംഗസമൂഹം ആയിവേണം പരിഗണിക്കുവാന്. ഇതിന്റെ ഫലമോ? ഒരണുവില് ഇലക്ട്രോണിന്റെ കൃത്യസ്ഥാനം നിര്ണയിക്കാന് സാധിക്കാതെവരുന്നു. മറ്റൊരുവിധത്തില് പറഞ്ഞാല് ഇലക്ട്രോണ്, അണുകേന്ദ്രത്തില് നിന്ന് r ദൂരത്തില് സ്ഥിതിചെയ്യുന്നു എന്നു പറയുന്നതിന്നുപകരം ഇലക്ട്രോണ്, r-നും (r + dr)നും ഇടയില് ഉണ്ടെന്നു പറയേണ്ടിവരുന്നു. അതായത്, ഇലക്ട്രോണിന്റെ സ്ഥാനനിര്ണയത്തില് അനിശ്ചിതത്വം dr ഉണ്ടാകുന്നു, dr എന്നത് ദെ ബ്രോയെ തരംഗനീളത്തെയും തദ്വാരാ ഇലക്ട്രോണിന്റെ സംവേഗത്തെയും ആശ്രയിച്ചിരിക്കുന്നതിനാല്, ഈ ആശയങ്ങള് ഹൈസന്ബര്ഗിന്റെ അനിശ്ചിതത്വ തത്ത്വത്തിനു വഴിതെളിച്ചു. സ്ഥാനാന്തരണത്തിലുള്ള അനിശ്ചിതത്വം | + | അണുസംരചനയിലെ ഇലക്ട്രോണിന് തരംഗഗുണധര്മങ്ങള് ആരോപിക്കുമ്പോള് ഇലക്ട്രോണിനെ ഒരു ബിന്ദുവായല്ല പ്രത്യുത, സ്പെയ്സില് നിശ്ചിത തരംഗനീളമുള്ള തരംഗസമൂഹം ആയിവേണം പരിഗണിക്കുവാന്. ഇതിന്റെ ഫലമോ? ഒരണുവില് ഇലക്ട്രോണിന്റെ കൃത്യസ്ഥാനം നിര്ണയിക്കാന് സാധിക്കാതെവരുന്നു. മറ്റൊരുവിധത്തില് പറഞ്ഞാല് ഇലക്ട്രോണ്, അണുകേന്ദ്രത്തില് നിന്ന് r ദൂരത്തില് സ്ഥിതിചെയ്യുന്നു എന്നു പറയുന്നതിന്നുപകരം ഇലക്ട്രോണ്, r-നും (r + dr)നും ഇടയില് ഉണ്ടെന്നു പറയേണ്ടിവരുന്നു. അതായത്, ഇലക്ട്രോണിന്റെ സ്ഥാനനിര്ണയത്തില് അനിശ്ചിതത്വം dr ഉണ്ടാകുന്നു, dr എന്നത് ദെ ബ്രോയെ തരംഗനീളത്തെയും തദ്വാരാ ഇലക്ട്രോണിന്റെ സംവേഗത്തെയും ആശ്രയിച്ചിരിക്കുന്നതിനാല്, ഈ ആശയങ്ങള് ഹൈസന്ബര്ഗിന്റെ അനിശ്ചിതത്വ തത്ത്വത്തിനു വഴിതെളിച്ചു. സ്ഥാനാന്തരണത്തിലുള്ള അനിശ്ചിതത്വം Δx-ഉം (x-അക്ഷദിശയില്) സംവേഗത്തിലുള്ള അനിശ്ചിതത്വം Δpx-ഉം ആണെങ്കില് (x-ദിശയിലുള്ള സംവേഗം), ഇവയുടെ ഗുണിതം h-നെക്കാള് വലുതോ h-നു തുല്യമോ ആകാം എന്ന് ഹൈസന്ബര്ഗ് തെളിയിച്ചു. മേല്പറഞ്ഞ പുതിയ തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തില് ഹൈഡ്രജന് അണുവിന്റെ ഘടന ഇപ്രകാരമാണ്. ബോര്സിദ്ധാന്തത്തില് അവ്യവസ്ഥിതമായാണ് ഇലക്ട്രോണിന്റെ ഭ്രമണപഥത്രിജ്യയും വേഗവും പ്രതിപാദിച്ചിട്ടുള്ളത്. ബോര് ക്വാണ്ടീകരണതത്ത്വം mvr = n h/2π ആണ്; n = 1 എങ്കില്, ഹൈഡ്രജന് അണു സാധാരണ അവസ്ഥയിലാണ്; ത്രിജ്യ r = h/2πmv -ഉം. ഡി ബ്രോഗ്ളി സിദ്ധാന്തമനുസരിച്ച് mv സംവേഗമുള്ള തരംഗത്തിന്റെ തരംഗനീളം: λ = h/mv-ഉം: അതായത് ഈ ബന്ധം ബോര്ത്രിജ്യയ്ക്കുള്ള സമീകരണത്തില് എഴുതിയാല് λ = 2 πrഎന്നു കിട്ടുന്നു. ഇതില്നിന്ന്, ഇലക്ട്രോണ് തരംഗനീളത്തിന്റെ ഗുണിതത്തോളം വൃത്തപരിധിയുള്ള ഭ്രമണപഥങ്ങളിലാണ് ഇലക്ട്രോണ് ഉണ്ടായിരിക്കുക എന്നു വരുന്നു. സ്ഥിരമായ ഭ്രമണപഥങ്ങളുണ്ടെന്നതിന് വ്യക്തമായ തെളിവാണ് ഇത്. |
| - | ആധുനിക സങ്കല്പത്തില്, ഇലക്ട്രോണ് നിശ്ചിത ഭ്രമണപഥത്തില് അണുകേന്ദ്രത്തെ ചുറ്റുന്നു എന്നല്ല പറയുന്നത്. പകരം അണുകേന്ദ്രത്തിനു ചുറ്റും സ്പെയ്സില് ഒരു സാന്ത-ഋണചാര്ജ് (finite negative | + | ആധുനിക സങ്കല്പത്തില്, ഇലക്ട്രോണ് നിശ്ചിത ഭ്രമണപഥത്തില് അണുകേന്ദ്രത്തെ ചുറ്റുന്നു എന്നല്ല പറയുന്നത്. പകരം അണുകേന്ദ്രത്തിനു ചുറ്റും സ്പെയ്സില് ഒരു സാന്ത-ഋണചാര്ജ് (finite negative charge) ഉണ്ടെന്നു സങ്കല്പിച്ചിരിക്കുന്നു. അണുകേന്ദ്രത്തിനു ചുറ്റുമുള്ള ഈ ചാര്ജ്-പടലത്തില്, അണുകേന്ദ്രത്തില്നിന്ന് ഏതു ദൂരത്തില് വേണമെങ്കിലും ഇലക്ട്രോണ് സ്ഥിതി ചെയ്യാം.ശൂന്യതാസാന്ദ്രപ്രദേശങ്ങളാല് വേര്തിരിഞ്ഞുകിടക്കുന്ന അതിസാന്ദ്രതയുടെ സ്ഥാനീകൃതമേഖലകള് എന്നതാണ് അണുവിന്റെ ആധുനിക നിര്വചനം. |
==അണുസംരചനയും ആവര്ത്തനപ്പട്ടികയും== | ==അണുസംരചനയും ആവര്ത്തനപ്പട്ടികയും== | ||
| - | |||
| - | |||
[[Image:p331.png|thumb|200x300px|left|ബോര്-സോമര്ഫെല്ഡ് അണു കക്ഷ്യകള്]] | [[Image:p331.png|thumb|200x300px|left|ബോര്-സോമര്ഫെല്ഡ് അണു കക്ഷ്യകള്]] | ||
| + | |||
| + | മൂലകങ്ങളെ അണുസംഖ്യയുടെ ക്രമത്തില് പട്ടികയാക്കിയാല് സദൃശ ഭൌതികഗുണധര്മങ്ങളും രാസഗുണധര്മങ്ങളും ഉള്ള മൂലകങ്ങള് ക്രമാനുഗതമായ അന്തരാളങ്ങളില് ആവര്ത്തിതമാകുന്നതായി കാണാം. റഷ്യന് രസതന്ത്രജ്ഞനായ ദിമ്ത്രി മെന്ദെല്യേഫ് ഈ എംപിരികനിരീക്ഷണം 1869-ല് ആവര്ത്തനനിയമം എന്നപേരില് പ്രസിദ്ധപ്പെടുത്തി. മൂലകങ്ങളുടെ ആവര്ത്തനഗുണധര്മങ്ങളെ പ്രദര്ശിപ്പിക്കുന്ന പട്ടികയാണ് ആവര്ത്തനപ്പട്ടിക. മെന്ദെല്യേഫ്, സദൃശഗുണധര്മങ്ങളുള്ള മൂലകങ്ങളെ ഗ്രൂപ്പുകളായി തിരിച്ചു. നോ: ആവര്ത്തനപ്പട്ടിക | ||
മെന്ദെല്യേഫിന്റെ ആശയങ്ങള്ക്ക് ആധുനിക-അണുസംരചനയുടെ വെളിച്ചത്തില് മൌലികമായ സ്ഥാനമുണ്ട്. z അണുസംഖ്യയുള്ള ഒരു അണുവിന്റെ അണുകേന്ദ്രത്തിനുചുറ്റും z ഇലക്ട്രോണുകള് ഭ്രമണം ചെയ്തുകൊണ്ടിരിക്കും. ഈ ഇലക്ട്രോണുകള് വിവിധ ഷെല്ലുകളിലും സബ്ഷെല്ലുകളിലും ആണ് ക്രമപ്പെടുത്തിയിരിക്കുന്നത്. ക്വാണ്ടം സംഖ്യ n ഉള്ള ഒരു ഷെല്ലില് ക്രമപ്പെടുത്താവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം 2n<sup>2</sup> ആണെന്നു നേരത്തെ സൂചിപ്പിച്ചു. പരമാവധി ഇലക്ട്രോണുകളുള്ള ഒരു ഷെല്ലിനെ പൂര്ണ ഷെല് എന്നു പറയുന്നു. ഈ പൂര്ണത മൂലകത്തിന്റെ രാസസ്ഥിരതയെ കാണിക്കുന്നു. നിഷ്ക്രിയവാതകങ്ങളായ (inert gases) ഹീലിയം, നിയോണ് തുടങ്ങിയവയ്ക്ക് പൂര്ണ ഇലക്ട്രോണ് ഷെല്ലുകളാണ് ഉള്ളത്. സാമാന്യമായി ഈ മൂലകങ്ങള് രാസപ്രവര്ത്തനവ്യഗ്രത പ്രദര്ശിപ്പിക്കുന്നില്ല. ഓരോ ഷെല്ലിലും സബ്ഷെല്ലിലും ഉണ്ടാകാവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം താഴെ കൊടുക്കുന്നു: | മെന്ദെല്യേഫിന്റെ ആശയങ്ങള്ക്ക് ആധുനിക-അണുസംരചനയുടെ വെളിച്ചത്തില് മൌലികമായ സ്ഥാനമുണ്ട്. z അണുസംഖ്യയുള്ള ഒരു അണുവിന്റെ അണുകേന്ദ്രത്തിനുചുറ്റും z ഇലക്ട്രോണുകള് ഭ്രമണം ചെയ്തുകൊണ്ടിരിക്കും. ഈ ഇലക്ട്രോണുകള് വിവിധ ഷെല്ലുകളിലും സബ്ഷെല്ലുകളിലും ആണ് ക്രമപ്പെടുത്തിയിരിക്കുന്നത്. ക്വാണ്ടം സംഖ്യ n ഉള്ള ഒരു ഷെല്ലില് ക്രമപ്പെടുത്താവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം 2n<sup>2</sup> ആണെന്നു നേരത്തെ സൂചിപ്പിച്ചു. പരമാവധി ഇലക്ട്രോണുകളുള്ള ഒരു ഷെല്ലിനെ പൂര്ണ ഷെല് എന്നു പറയുന്നു. ഈ പൂര്ണത മൂലകത്തിന്റെ രാസസ്ഥിരതയെ കാണിക്കുന്നു. നിഷ്ക്രിയവാതകങ്ങളായ (inert gases) ഹീലിയം, നിയോണ് തുടങ്ങിയവയ്ക്ക് പൂര്ണ ഇലക്ട്രോണ് ഷെല്ലുകളാണ് ഉള്ളത്. സാമാന്യമായി ഈ മൂലകങ്ങള് രാസപ്രവര്ത്തനവ്യഗ്രത പ്രദര്ശിപ്പിക്കുന്നില്ല. ഓരോ ഷെല്ലിലും സബ്ഷെല്ലിലും ഉണ്ടാകാവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം താഴെ കൊടുക്കുന്നു: | ||
| - | അണുസംഖ്യ z = 11 ഉള്ള മൂലകം സോഡിയം ആണ്. സോഡിയത്തില് 11 ഇലക്ട്രോണുകള് ഉണ്ട്. മേല്കൊടുത്ത പട്ടികയില്നിന്ന് സോഡിയത്തിന് K-ഷെല്ലില് 2 ഇലക്ട്രോണും L-ഷെല്ലില് 8 ഇലക്ട്രോണും M-ഷെല്ലില് 1 ഇലക്ട്രോണും ഉണ്ടെന്ന് (11 = 2 + 8 + 1) കാണാം. സോഡിയത്തിന്റെ ബാഹ്യതമ ഷെല് | + | അണുസംഖ്യ z = 11 ഉള്ള മൂലകം സോഡിയം ആണ്. സോഡിയത്തില് 11 ഇലക്ട്രോണുകള് ഉണ്ട്. മേല്കൊടുത്ത പട്ടികയില്നിന്ന് സോഡിയത്തിന് K-ഷെല്ലില് 2 ഇലക്ട്രോണും L-ഷെല്ലില് 8 ഇലക്ട്രോണും M-ഷെല്ലില് 1 ഇലക്ട്രോണും ഉണ്ടെന്ന് (11 = 2 + 8 + 1) കാണാം. സോഡിയത്തിന്റെ ബാഹ്യതമ ഷെല് M-ഷെല്ലാണ്. ഇതിലെ ഇലക്ട്രോണിനെ സംയോജക-ഇലക്ട്രോണ് (Valence electron) എന്നു പറയുന്നു. രാസസംയോഗങ്ങളില് സോഡിയത്തിന് നഷ്ടമാകുന്ന ഇലക്ട്രോണ് ഇതാണ്. |
മൂലകങ്ങള് അവയുടെ ബാഹ്യതമ ഷെല്ലില് 8 ഇലക്ട്രോണുകള് നേടി ഷെല് പൂര്ത്തിയാക്കാന് ശ്രമിക്കുന്നു. ഈ ശ്രമമാണ് രാസപ്രവര്ത്തനത്തിനുള്ള പല കാരണങ്ങളില് ഒന്ന്. ബാഹ്യതമ ഷെല്ലില് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകളേ ഉള്ളുവെങ്കില് ആ ഇലക്ട്രോണുകളെ നഷ്ടപ്പെടുത്തിയും ഷെല് പൂര്ത്തിയാക്കാന് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകള് മാത്രമേ ആവശ്യമുള്ളുവെങ്കില് ഇലക്ട്രോണ് സ്വീകരിച്ചുമാണ് ബാഹ്യതമ ഷെല് പൂര്ത്തിയാക്കുന്നത് എന്ന് സാമാന്യമായി പറയാം. ഇതാണ് രാസസംയോജകതയുടെ അടിസ്ഥാനം. | മൂലകങ്ങള് അവയുടെ ബാഹ്യതമ ഷെല്ലില് 8 ഇലക്ട്രോണുകള് നേടി ഷെല് പൂര്ത്തിയാക്കാന് ശ്രമിക്കുന്നു. ഈ ശ്രമമാണ് രാസപ്രവര്ത്തനത്തിനുള്ള പല കാരണങ്ങളില് ഒന്ന്. ബാഹ്യതമ ഷെല്ലില് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകളേ ഉള്ളുവെങ്കില് ആ ഇലക്ട്രോണുകളെ നഷ്ടപ്പെടുത്തിയും ഷെല് പൂര്ത്തിയാക്കാന് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകള് മാത്രമേ ആവശ്യമുള്ളുവെങ്കില് ഇലക്ട്രോണ് സ്വീകരിച്ചുമാണ് ബാഹ്യതമ ഷെല് പൂര്ത്തിയാക്കുന്നത് എന്ന് സാമാന്യമായി പറയാം. ഇതാണ് രാസസംയോജകതയുടെ അടിസ്ഥാനം. | ||
| വരി 284: | വരി 283: | ||
(Muon, Meson-Atoms). | (Muon, Meson-Atoms). | ||
| - | |||
[[Image:pno.332Electron.png|right]] | [[Image:pno.332Electron.png|right]] | ||
| - | മെസോണുകള്) ഉള്ള അണുക്കള് ഉണ്ടെന്ന് കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. ഇലക്ട്രോണിന്റെ തന്നെ ചാര്ജുള്ള ഈ ഋണചാര്ജിതകണങ്ങള്ക്ക് ഇലക്ട്രോണിന്റെ പലമടങ്ങ് ഭാരമുണ്ട്. ഈ അണുക്കള്ക്ക് ഒരു അണുകേന്ദ്രവും ഭ്രമണപഥത്തില് ഒരു മ്യുവോണും (ഈ അണുവാണ് മ്യുവോണ് അണു) അല്ലെങ്കില് ഒരു മെസോണും (ഇതാണ് മെസോണ് അണു) അധികം ഉണ്ടായിരിക്കും. ഘടന ഏകദേശം ഹൈഡ്രജന് അണുവിന്റേതുപോലെയാണെങ്കിലും ഒരു പ്രധാന വ്യത്യാസം ഉണ്ട്. മ്യുവോണ് അണുവിനും മെസോണ് അണുവിനും അണുകേന്ദ്രം ഏതു വേണമെങ്കിലും ആകാം. മെസോണ് അല്ലെങ്കില് മ്യുവോണ്-ഭ്രമണപഥത്തിനുപുറമേ അണു ഉദാസീനമാകാന് വേണ്ടത്ര ഇലക്ട്രോണുകള് വിവിധ ഭ്രമണപഥങ്ങളില് ചലിക്കുന്നുണ്ടായിരിക്കും; ഈ അണുക്കള് അല്പായുസ്സുകളാണ്. അണുകേന്ദ്രം, മെസോണിനെ (അല്ലെങ്കില് മ്യുവോണിനെ) പിടിച്ചെടുക്കുന്നതോ അഥവാ മെസോണിന് (മ്യുവോണിന്) സ്വയം ക്ഷയം സംഭവിക്കുന്നതോ ആണ് ഇതിനു കാരണം. ഒരു പോസിട്രോണും ഇലക്ട്രോണും ഉള്ള പോസിട്രോണിയം അണുവും കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. പക്ഷേ, ക്ഷണിക-അസ്തിത്വമുള്ള ഈ അണു പോസിട്രോണ്-ഇലക്ട്രോണ് സംഘട്ടനം മൂലം ഊര്ജമായി മാറുന്നു. നോ: അണുകേന്ദ്രം, അണുകേന്ദ്ര ആഘൂര്ണം, അണുകേന്ദ്രവിജ്ഞാനീയം, അണുശക്തിതേജോവശിഷ്ടങ്ങള്, റേഡിയോ ആക്റ്റിവത | + | |
| + | ഭ്രമണപഥത്തില് ഇലക്ട്രോണിനുപകരം മറ്റു ചില ഋണചാര്ജിതകണങ്ങള് (മ്യുവോണുകള്, മെസോണുകള്) ഉള്ള അണുക്കള് ഉണ്ടെന്ന് കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. ഇലക്ട്രോണിന്റെ തന്നെ ചാര്ജുള്ള ഈ ഋണചാര്ജിതകണങ്ങള്ക്ക് ഇലക്ട്രോണിന്റെ പലമടങ്ങ് ഭാരമുണ്ട്. ഈ അണുക്കള്ക്ക് ഒരു അണുകേന്ദ്രവും ഭ്രമണപഥത്തില് ഒരു മ്യുവോണും (ഈ അണുവാണ് മ്യുവോണ് അണു) അല്ലെങ്കില് ഒരു മെസോണും (ഇതാണ് മെസോണ് അണു) അധികം ഉണ്ടായിരിക്കും. ഘടന ഏകദേശം ഹൈഡ്രജന് അണുവിന്റേതുപോലെയാണെങ്കിലും ഒരു പ്രധാന വ്യത്യാസം ഉണ്ട്. മ്യുവോണ് അണുവിനും മെസോണ് അണുവിനും അണുകേന്ദ്രം ഏതു വേണമെങ്കിലും ആകാം. മെസോണ് അല്ലെങ്കില് മ്യുവോണ്-ഭ്രമണപഥത്തിനുപുറമേ അണു ഉദാസീനമാകാന് വേണ്ടത്ര ഇലക്ട്രോണുകള് വിവിധ ഭ്രമണപഥങ്ങളില് ചലിക്കുന്നുണ്ടായിരിക്കും; ഈ അണുക്കള് അല്പായുസ്സുകളാണ്. അണുകേന്ദ്രം, മെസോണിനെ (അല്ലെങ്കില് മ്യുവോണിനെ) പിടിച്ചെടുക്കുന്നതോ അഥവാ മെസോണിന് (മ്യുവോണിന്) സ്വയം ക്ഷയം സംഭവിക്കുന്നതോ ആണ് ഇതിനു കാരണം. ഒരു പോസിട്രോണും ഇലക്ട്രോണും ഉള്ള പോസിട്രോണിയം അണുവും കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. പക്ഷേ, ക്ഷണിക-അസ്തിത്വമുള്ള ഈ അണു പോസിട്രോണ്-ഇലക്ട്രോണ് സംഘട്ടനം മൂലം ഊര്ജമായി മാറുന്നു. നോ: അണുകേന്ദ്രം, അണുകേന്ദ്ര ആഘൂര്ണം, അണുകേന്ദ്രവിജ്ഞാനീയം, അണുശക്തിതേജോവശിഷ്ടങ്ങള്, റേഡിയോ ആക്റ്റിവത | ||
(പി.എം. മധുസൂദനന്) | (പി.എം. മധുസൂദനന്) | ||
[[Category:ഭൗതികം-ന്യൂക്ളിയര്]] | [[Category:ഭൗതികം-ന്യൂക്ളിയര്]] | ||
Current revision as of 07:57, 21 നവംബര് 2014
അണു
Atom
ഭൗതികപദാര്ഥങ്ങളുടെ അവിഭാജ്യാംശമെന്നു കരുതപ്പെട്ടിരുന്ന കണിക.
പ്രാചീനസങ്കല്പങ്ങള്
പദാര്ഥഘടനയെക്കുറിച്ചുള്ള സങ്കല്പത്തിന് ഇരുപത്തഞ്ച് നൂറ്റാണ്ടിലധികം പഴക്കമുണ്ട്. പൗരാണിക ഭാരതീയരും ഗ്രീക്കുകാരും ഇതിനെപ്പറ്റി പ്രതിപാദിച്ചിട്ടുണ്ട്. ഭാരതീയ ചിന്തകരില് പ്രമുഖന് ആയിരുന്ന 'കണാദന്' (ബി.സി. 6-5 ശ.) പദാര്ഥത്തിന്റെ ഏറ്റവും ചെറിയ അംശത്തെ 'അണു' എന്ന് വിളിച്ചു. ബി.സി. 5-ാം ശ.-ത്തിലാണ് ഗ്രീസില് 'അണുവാദികള്' ഉണ്ടായത്. ഈ കാലഘട്ടത്തില് ജീവിച്ചിരുന്ന ലൂസിപ്പസും അദ്ദേഹത്തിന്റെ ശിഷ്യനായ ഡമോക്രിറ്റസും ആയിരുന്നു ഇവരില് പ്രമുഖര്. പദാര്ഥങ്ങളെല്ലാം അവിഭാജ്യങ്ങളായ ചെറിയ കണങ്ങളെക്കൊണ്ടാണ് നിര്മിച്ചിരിക്കുന്നതെന്ന് ഡമോക്രിറ്റസ് അഭിപ്രായപ്പെട്ടു. ഈ അവിഭാജ്യ കണങ്ങളെ 'അത്തോമ' (വിഭജിക്കാന് കഴിയാത്തത്) എന്നു വിളിച്ചു. ഇതില്നിന്നാണ് ഇംഗ്ളീഷില് ആറ്റം (Atom) എന്ന പദം ഉണ്ടായത്. ഡമോക്രിറ്റസിന്റെ അണുസിദ്ധാന്തത്തെ എപ്പിക്ക്യൂറസ് എന്ന ഗ്രീക്കു ചിന്തകനും പിന്താങ്ങിയിരുന്നു. 'വസ്തുക്കളുടെ പ്രകൃതം' എന്ന ലുക്രീഷ്യസിന്റെ കവിതയിലും ഈ അഭിപ്രായം നിഴലിച്ചു കാണാം.
അണുസിദ്ധാന്തം വളര്ച്ച പ്രാപിച്ചുകൊണ്ടിരുന്നകാലത്തുതന്നെയാണ് (ബി.സി. 5-ാം ശ.) എംപെഡോക്ള്സ് തന്റെ ചതുര്ഭൂതസിദ്ധാന്തം മുന്നോട്ടുവച്ചത്: ഈ പ്രപഞ്ചം മുഴുവനും അഗ്നി, വായു, പൃഥ്വി, ജലം എന്നീ നാലു ഭൂതങ്ങള്കൊണ്ടാണ് നിര്മിച്ചിരിക്കുന്നത്. സുപ്രസിദ്ധ ഗ്രീക്കുചിന്തകനായ അരിസ്റ്റോട്ടല് ഈ സിദ്ധാന്തത്തെ ശക്തമായി പിന്താങ്ങി. സര്വ വസ്തുക്കളിലും ഒരേ ബീജഭൂതം (hyle) ആണ് ഉള്ളത്. ഈ വസ്തുവിന് മൗലിക ഘടകങ്ങളായി നാലു ഗുണങ്ങള് ഉണ്ട്: ചൂട്, തണുപ്പ്, വരള്ച്ച, ഈര്പ്പം. ഈ ഘടകങ്ങളുടെ ഉള്ളടക്ക വ്യത്യാസമാണ് പദാര്ഥങ്ങളുടെ വൈവിധ്യത്തിനു കാരണം. അരിസ്റ്റോട്ടലിന്റെ ഈ സിദ്ധാന്തം 2,000 വര്ഷത്തോളം നിലനിന്നു. ഇതിനു സമാനമാണ് ഭാരതീയരുടെ പഞ്ചഭൂതസിദ്ധാന്തം. ഇതനുസരിച്ച് പ്രപഞ്ചത്തിലുള്ള എല്ലാ പദാര്ഥങ്ങളും അഗ്നി, വായു, ജലം, പൃഥ്വി, ആകാശം എന്നീ അഞ്ചു ഭൂതങ്ങള്കൊണ്ടാണ് നിര്മിച്ചിരിക്കുന്നത്.
അരിസ്റ്റോട്ടലിന്റെ എതിര്പ്പുകളെ അതിജീവിക്കാന് ഡമോക്രിറ്റസിന്റെ അണുസിദ്ധാന്തത്തിനു കഴിഞ്ഞില്ല. അങ്ങനെ പല ശതകങ്ങളോളം സുഷുപ്തിയിലാണ്ട അണുസങ്കല്പം നവോത്ഥാനകാലത്തിനുശേഷമാണ് യൂറോപ്പില് പുനരുജ്ജീവിച്ചത്. 16-ഉം 17-ഉം ശ.-ങ്ങളില് ഗലീലിയോ ഗലീലി, റെനേ ദെകാര്ത്തെ, ഫ്രാന്സിസ് ബേക്കണ്, റോബര്ട്ട് ബോയ് ല് , ഐസക് ന്യൂട്ടണ് തുടങ്ങിയ ശാസ്ത്രജ്ഞന്മാരും ദാര്ശനികരും പദാര്ഥം സാന്തം (finite) അല്ലെന്നും പ്രത്യുത അണു എന്ന പരമകണങ്ങള്കൊണ്ട് ഉണ്ടാക്കപ്പെട്ടതാണെന്നും ഉള്ള അഭിപ്രായക്കാരായിരുന്നു.
അണുസങ്കല്പത്തിനുള്ള രസതന്ത്ര തെളിവുകള്
സ്പെയ്സും, ദ്രവ്യവും സാന്തം ആണെന്ന് ഉദ്ഘോഷിച്ചിരുന്ന അരിസ്റ്റോട്ടലിന്റെ സിദ്ധാന്തമായിരുന്നു മധ്യകാലഘട്ടത്തില് പദാര്ഥഘടനയെക്കുറിച്ച് നിലവിലിരുന്നത്. ഏതു വസ്തുവിന്റെയും മൗലിക ഘടകങ്ങളായ ചൂട്, തണുപ്പ്, വരള്ച്ച, ഈര്പ്പം എന്നിവയുടെ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തി പുതിയ വസ്തുക്കള് ഉണ്ടാക്കാനുള്ള ശ്രമത്തിലാണ് അക്കാലത്ത് രസതന്ത്രജ്ഞര് ഏര്പ്പെട്ടിരുന്നത്. ഈ ഉള്ളടക്കം വ്യത്യാസപ്പെടുത്തലായിരുന്നു രസവാദിക(Alchemists)ളുടെ ലക്ഷ്യം. പരിമാണാത്മക രസതന്ത്രത്തിന്റെ വളര്ച്ചയോടെയാണ് പദാര്ഥഘടനയെക്കുറിച്ചുള്ള പരസ്പരവിരുദ്ധചിന്താഗതികളെ വിലയിരുത്താന്വേണ്ട പരീക്ഷണത്തെളിവുകള് ലഭിച്ചത്.
ആധുനിക അണുസിദ്ധാന്തത്തിന്റെ പ്രണേതാവ് ജോണ് ഡാള്ട്ടന് (1766-1844) ആണ്. മീഥേന്, എഥിലീന്, കാര്ബണ് മോണോക്സൈഡ്, കാര്ബണ്ഡൈഓക്സൈഡ് തുടങ്ങിയ വാതകങ്ങളുടെ സമന്വിത-ബഹുഗുണിതാംശബന്ധനിയമം (Multiproduct ratio rule) നിര്ദേശിക്കാന് ഈ സിദ്ധാന്തം ഡാള്ട്ടനെ സഹായിച്ചു. A എന്ന മൂലകം B എന്ന മൂലകവുമായി സംയോജിച്ച് രണ്ടോ അതിലധികമോ യൗഗികങ്ങള് ഉണ്ടാകുമ്പോള്, ഒരു നിശ്ചിത ഭാരത്തിലുള്ള A-യുമായി സംയോജിക്കുന്ന B-യുടെ ഭാരങ്ങള് ലഘുപൂര്ണസംഖ്യകളുടെ അംശബന്ധത്തിലായിരിക്കുമെന്നതാണ് (ratio of integers) ബഹുഗുണിതാനുപാത നിയമം. രാസപ്രതിപ്രവര്ത്തനത്തില് പങ്കെടുക്കുന്ന മൂലകങ്ങളുടെ പരിമാണങ്ങളെപ്പറ്റിയുള്ള പഠനം നാലാമത്തെ രാസസംയോഗനിയമത്തിനു വഴിതെളിച്ചു. ഒരു മൂലകത്തിന്റെ ഒരേ ഭാരവുമായി പ്രതിപ്രവര്ത്തിക്കുന്ന രണ്ടു മൂലകങ്ങളുടെ ഭാരങ്ങള് തമ്മിലുള്ള അനുപാതം, ഇവ തമ്മില് പ്രതിപ്രവര്ത്തിക്കുമ്പോഴുള്ള ഭാരാനുപാതത്തിന് സമമോ അല്ലെങ്കില് അതിന്റ വേറെ ഗുണിതമോ ആയിരിക്കും.
ഡാള്ട്ടന് സിദ്ധാന്തം
രാസസംയോഗ നിയമങ്ങള് വിശദീകരിക്കാനായി ജോണ് ഡാള്ട്ടന് 1803-ല് നിര്ദേശിച്ച അണുസിദ്ധാന്തത്തിന്റെ അഭിഗൃഹീതങ്ങള് (postulates) താഴെ ചേര്ക്കുന്നു: (1) പദാര്ഥം അവിഭാജ്യങ്ങളായ അണുക്കള് അടങ്ങിയതാണ്; (2) ഒരു മൂലകത്തിന്റെ എല്ലാ അണുക്കളും ഭാരത്തിലും ഗുണധര്മങ്ങളിലും സര്വസമമാണ്; (3) വിവിധ മൂലകങ്ങള്ക്ക് വിവിധതരം അണുക്കളാണ് ഉള്ളത്; വിവിധ മൂലകങ്ങളുടെ അണുക്കള് ഭാരത്തില് വ്യത്യസ്തമാണ്; (4) അണുക്കള് അവിനശ്യമാണ്; രാസപ്രവര്ത്തനം അണുക്കളുടെ പുനഃക്രമീകരണം മാത്രമാണ്; (5) ലഘു അംശബന്ധത്തില് വിവിധമൂലകങ്ങള് സംയോജിച്ചാണ് രാസയൌഗികങ്ങള് ഉണ്ടാകുന്നത്. ഈ അഭിഗൃഹീതങ്ങളില്നിന്ന് രാസസംയോഗനിയമങ്ങള് വ്യുത്പാദിപ്പിക്കാവുന്നതാണ്.
ഡാള്ട്ടന്റെ അണുസിദ്ധാന്തം അപൂര്ണമായിരുന്നു. അണുക്കളുടെ ആ.ഭാ. നിര്ണയിക്കാനുള്ള മാര്ഗത്തിനുപോലും ഡാള്ട്ടന്റെ അഭിഗൃഹീതങ്ങള് പ്രയോജകീഭവിക്കുന്നില്ല. ഘടകമൂലകങ്ങളുടെ എത്ര അണുക്കള് വീതം ചേര്ന്നാണ് യൗഗികം ഉണ്ടാകുന്നതെന്ന് കണ്ടുപിടിക്കാന് ഡാള്ട്ടന് മാര്ഗമൊന്നുമില്ലായിരുന്നു. ഒരു യൌഗികം ഉണ്ടാകുമ്പോള് രണ്ടു മൂലകങ്ങള് W1, W2 ഗ്രാം വീതം ചേരുന്നുവെങ്കില് . w1/w2=n1A1 / n2A2.ഇവിടെ A1, A2 മൂലകങ്ങളുടെ അണുഭാരവും n1, n2 സംയോജനത്തില് പങ്കെടുക്കുന്ന മൂലകഅണുക്കളുടെ എണ്ണവും ആണ്.n1 : n2 എന്ന അനുപാതം അറിഞ്ഞാല്ത്തന്നെ, അണുക്കളുടെ ആപേക്ഷികഭാരമേ നിര്ണയിക്കാനാവൂ. അതിനാല് അണുസിദ്ധാന്തം പ്രയോഗിക്കാന്വേണ്ടി ഡാള്ട്ടന് ചില സ്വേച്ഛാസങ്കല്പങ്ങള് ഉപയോഗിച്ചു: രണ്ടു മൂലകങ്ങള് സംയോജിച്ച് ഒരേയൊരു യൌഗികമേ ഉണ്ടാകുന്നുള്ളുവെങ്കില് ആ യൗഗികത്തില് രണ്ടു മൂലകങ്ങളുടെയും ഓരോ അണുക്കള് മാത്രമേ ഉണ്ടായിരിക്കുകയുള്ളു എന്ന്. ഹൈഡ്രജന് പെറോക്സൈഡ് അന്ന് അറിയപ്പെടാതിരുന്നതിനാല്, വെള്ളത്തെ ഒരു ഹൈഡ്രജന് അണുവും ഒരു ഓക്സിജന് അണുവും ചേര്ന്നുള്ള യൗഗികമായാണ് ഡാള്ട്ടന് കണക്കാക്കിയത്. ഡാള്ട്ടന്റെ തത്ത്വം ലളിതമെങ്കിലും തെറ്റായിരുന്നു. വികസിച്ചുകൊണ്ടിരുന്ന രസതന്ത്രത്തില് പല ബുദ്ധിമുട്ടുകള്ക്കും അത് വഴിവച്ചു.
വാതകങ്ങള് രാസപരമായി സംയോജിക്കുന്ന പ്രതിപ്രവര്ത്തനങ്ങളെപ്പറ്റി പഠനം നടത്തുന്നതിനിടയിലാണ് ഡാള്ട്ടന്റെ അണുസിദ്ധാന്തം ബുദ്ധിമുട്ടുകളെ നേരിട്ടത്. വാതകങ്ങള് തമ്മിലുള്ള സംയോജനത്തെ സംബന്ധിച്ച ഒരു നിയമം 1808-ല് ഗേലൂസാക് എന്ന ശാസ്ത്രജ്ഞന് കണ്ടുപിടിച്ചു. ഒരേ താപനിലയിലും മര്ദത്തിലും വാതകം A, വാതകം B യുമായി പ്രതിപ്രവര്ത്തിച്ച് വാതകം C ഉണ്ടാകുമ്പോള് A, B,C എന്നീ വാതകങ്ങളുടെ വ്യാപ്തപരമായ അംശബന്ധം (volumetric ratio) ലഘുപൂര്ണ സംഖ്യകള് ആയിരിക്കും. രണ്ട് ഉദാഹരണങ്ങള് താഴെ കൊടുക്കുന്നു: 1 വ്യാപ്തം ഹൈഡ്രജന് + 1 വ്യാപ്തം ക്ളോറിന് = 2 വ്യാപ്തം ഹൈഡ്രജന്ക്ളോറൈഡ്; 2 വ്യാപ്തം ഹൈഡ്രജന് + 1 വ്യാപ്തം ഓക്സിജന് = 2 വ്യാപ്തം നീരാവി. ഇതില്നിന്ന് സുപ്രധാനമായ ഒരു നിഗമനത്തിലെത്താന് കഴിയും. വാതകാവസ്ഥയിലുള്ള മൂലകങ്ങള് ലളിതമായ വ്യാപ്താനുപാതത്തിലും അണുക്കള് ലളിതാനുപാതത്തിലും സംയോജിക്കുകയാണെങ്കില്, ഒരേ വ്യാപ്തം പ്രതിപ്രവര്ത്തകവാതകങ്ങളിലുള്ള അണുക്കളുടെ എണ്ണങ്ങള് പരസ്പരം ബന്ധപ്പെട്ടിരിക്കണം. ഒരേ താപനിലയിലും ഒരേ മര്ദത്തിലും വിവിധ വാതകങ്ങളുടെ തുല്യവ്യാപ്തത്തിലുള്ള അണുക്കളുടെ എണ്ണം തുല്യമായിരിക്കുമെന്ന ആശയം ഡാള്ട്ടന് സ്വീകരിച്ചിരുന്നു. അതുപ്രകാരം 1 വ്യാപ്തം ഹൈഡ്രജന് (n)+1 വ്യാപ്തം ക്ലോറിന് (n) = 2 വ്യാപ്തം ഹൈഡ്രജന്ക്ളോറൈഡ് (2n യൗഗിക അണുക്കള്). അതായത്, 1 ഹൈഡ്രജന് അണു + 1 ക്ലോറിന് അണു = 2 ഹൈഡ്രജന്ക്ളോറൈഡ് യൗഗിക അണുക്കള്. അല്ലെങ്കില് ഒരു ഹൈഡ്രജന്ക്ളോറൈഡ് യൗഗിക അണുവില് 1/2 ഹൈഡ്രജന് അണുവും 1/2 ക്ലോറിന് അണുവും ഉണ്ട്. അണുവിനെ വിഭജിക്കാമെന്ന ഈ നിഗമനം, അണു അവിഭാജ്യമാണെന്ന ഡാള്ട്ടന് സിദ്ധാന്തത്തിനു വിരുദ്ധമാകുന്നു.
അവോഗാഡ്രോ പരികല്പന
ഈ പ്രതിസന്ധി പരിഹരിക്കാന് 1811-ല് ഇറ്റാലിയന് ഭൗതികശാസ്ത്രജ്ഞനായ അവോഗാഡ്രോ, മൗലിക അണുക്കളും വാതകങ്ങളിലെ ഏറ്റവും ചെറിയ കണികകളും തമ്മില് വ്യവഛേദിച്ചാല് മതിയെന്ന് നിര്ദേശിച്ചു. അണുക്കള് ചേര്ന്നുണ്ടാകുന്ന ഈ വാതകകണങ്ങളെ അദ്ദേഹം തന്മാത്രകള് (molecules) എന്നു വിളിച്ചു. മൂലകങ്ങളുടെ ഗുണധര്മങ്ങളും സ്വതന്ത്ര-അസ്തിത്വവുമുള്ള കണം അണുവല്ല, അണുക്കള് ഘടകങ്ങളായുള്ള തന്മാത്രകളാണ്. അങ്ങനെ ഗേലൂസാക്, ഡാള്ട്ടന് എന്നിവരുടെ ഗവേഷണഫലങ്ങളെ അവോഗാഡ്രോ കോര്ത്തിണക്കി. ഒരേ താപനിലയിലും മര്ദത്തിലും തുല്യവ്യാപ്തം വാതകങ്ങളില് തുല്യ എണ്ണം തന്മാത്രകള് ഉണ്ടെന്ന് അദ്ദേഹം നിര്ദേശിച്ചു. ഹൈഡ്രജന്, നൈട്രജന് തുടങ്ങിയ സാധാരണ വാതകങ്ങളുടെ തന്മാത്രകള് ദ്വിഅണുക (diatomic)മാണെന്നും വെള്ളത്തിന്റെ തന്മാത്രയില് രണ്ടു ഹൈഡ്രജന് അണുക്കളും ഒരു ഓക്സിജന് അണുവും ആണ് ഉള്ളതെന്നും ഇതുമൂലം തെളിഞ്ഞു (നോ: അവോഗാഡ്രോ). അവോഗാഡ്രോനിര്ദേശത്തെ രൂക്ഷമായി വിമര്ശിച്ചത് ഡാള്ട്ടന് തന്നെയായിരുന്നു. ഒരേജാതി അണുക്കള് സംയോജിച്ച് തന്മാത്രകള് ഉണ്ടാകുന്നുവെന്ന സങ്കല്പം അദ്ദേഹത്തിനു സ്വീകാര്യമായിരുന്നില്ല. രണ്ടു ഹൈഡ്രജന് അണുക്കള് ചേര്ന്ന് തന്മാത്രയുണ്ടാകുന്നെങ്കില് എന്തുകൊണ്ട് ഹൈഡ്രജന് അണുക്കള് കൂടുതല് ചേര്ന്ന് ദ്രാവകമാകുന്നില്ല? വളരെ പ്രസക്തമായ ഈ ചോദ്യത്തിന് ഉത്തരം കിട്ടാന് ഒരു നൂറ്റാണ്ടോളം വീണ്ടും കാത്തിരിക്കേണ്ടിവന്നു.
തന്മാത്രാഭാരം
(Molecular weight).
മൂലകങ്ങളുടെയും യൗഗികങ്ങളുടെയും തന്മാത്രാഭാരം നിര്ണയിക്കാന് അവോഗാഡ്രോസിദ്ധാന്തം വഴിയൊരുക്കി. ഒരേ താപനിലയിലും മര്ദത്തിലും 1 ലി. വാതകത്തിന്റെ ഭാരവും അത്രയും വ്യാപ്തം മാനകവാതകത്തിന്റെ ഭാരവും തമ്മിലുള്ള അനുപാതമാണ് വാതകത്തിന്റെ ആപേക്ഷികഘനത്വം. അതിനാല്, അവോഗാഡ്രോ പരികല്പനയനുസരിച്ച് രണ്ടു വാതകങ്ങളും ഒരേ മര്ദത്തിലും ഒരേ താപനിലയിലും ആണെങ്കില് താഴെ പറയുന്നതു ശരിയായിരിക്കും.
ഹൈഡ്രജന്, ഓക്സിജന് എന്നീ വാതകങ്ങളെ മാനകവാതകങ്ങള് ആയി കണക്കാക്കാം. ഇവ ദ്വിഅണുകങ്ങളാണ്. ഹൈഡ്രജന്റെ അണുഭാരം സ്വേച്ഛാകല്പിതമായി 1 എന്ന് സ്വീകരിച്ചാല് തന്മാത്രാഭാരം = 2x ആപേക്ഷികഘനത്വം എന്നു ലഭിക്കുന്നു. ഒരു വാതകമൂലകത്തിന്റെ തന്മാത്രാഭാരം ഇപ്രകാരം നിര്ണയിക്കുമ്പോള് അതില്നിന്ന് ഒരു തന്മാത്രയിലുള്ള അണുക്കളുടെ എണ്ണം അറിയാന് കഴിയുന്നു. അതില്നിന്ന് മൂലകത്തിന്റെ ആപേക്ഷിക അണുഭാരം നിര്ണയിക്കാം.
അണുഭാരം
(Atomic weight)
1860-ലെ അന്താരാഷ്ട്ര അണുഭാര സമ്മേളനം ഡാള്ട്ടന്-അവോഗാഡ്രോ പദ്ധതി അംഗീകരിച്ചു. അതിനുശേഷം നിരവധി യൌഗികങ്ങളുടെ അതിസൂക്ഷ്മവിശ്ളേഷണഫലമായി അണുഭാരങ്ങളുടെ പട്ടിക തയ്യാറാക്കി.
അണുഭാരം ആപേക്ഷികഭാരമാണ്. അതിനാല് മൂലകങ്ങളില്വച്ച് ഏറ്റവും കനം കുറഞ്ഞ ഹൈഡ്രജന് ആണ് ആദ്യം മാനകവാതകമായി സ്വീകരിച്ചത്. പക്ഷേ, ഹൈഡ്രജന് യൌഗികങ്ങള് പരിമിതങ്ങളായതിനാലും ഓക്സിജനുമായി ചേര്ന്ന് മിക്ക മൂലകങ്ങളും യൌഗികങ്ങള് ഉണ്ടാക്കുമെന്നതിനാലും 1902-ല് ഓക്സിജന് (O) മാനകവാതകമായി സ്വീകരിക്കുകയും ഓക്സിജന്റെ അണുഭാരം 16.000 എന്ന് നിശ്ചയിക്കുകയും ചെയ്തു. അതുവരെ ഓക്സിജന്റെ അണുഭാരം ഇതില്നിന്ന് അല്പം വ്യത്യസ്തമായിരുന്നു. തുടര്ന്ന് O = 16.000 അടിസ്ഥാനമാക്കി അണുഭാരപ്പട്ടിക പരിഷ്കരിക്കപ്പെട്ടു.
ഡാള്ട്ടന് സങ്കല്പിച്ചതുപോലെ ഒരേ മൂലകത്തിന്റെ എല്ലാ അണുക്കളും സമഭാരികങ്ങള് അല്ലാത്തതിനാല് (നോ: ഐസോടോപ്പുകള്) രാസ-അണുഭാരം ശ.ശ. ഭാരം മാത്രമേ ആകുന്നുള്ളു. പ്രകൃതിയില് ഓക്സിജന്റെ സ്ഥാനീയങ്ങളുടെ സംഘടനം, വളരെ കൃത്യമായി പറഞ്ഞാല്, സ്ഥിരമല്ല. എങ്കിലും O = 16.000 എന്ന തോതാണ് 1961 വരെ സ്വീകരിച്ചിരുന്നത്. ഓരോ അണുവിന്റെയും പെരുമാറ്റത്തിനാണ് ഭൌതികശാസ്ത്രത്തില് പ്രാധാന്യം. അതിനാല് ഏതെങ്കിലും ഒരു അണുവിന്റെ ഒരു പ്രത്യേകസ്ഥാനീയത്തിന്റെ ദ്രവ്യമാനത്തെ അടിസ്ഥാനമാക്കിവേണം അണുഭാരപ്പട്ടിക തയ്യാറാക്കുവാന്. കാര്ബണ് അണുവിന്റെ C = 12.000 എന്ന സ്ഥാനീയമാണ് ഇതിന് മാനകം ആയി 1961-ല് സ്വീകരിച്ചത്. ഈ തോതിനെ കാര്ബണ്മാനകം എന്നു പറയുന്നു.
അണു-തന്മാത്രകളുടെ വലുപ്പം
അണുക്കള് യഥാര്ഥത്തില് ഉണ്ടെന്നതിന് വ്യക്തവും ഭൌതികവും ആയ തെളിവുകള് നല്കാതെ അണുസിദ്ധാന്തത്തെ ഒരു പ്രവര്ത്തന പ്രക്രിയയായി മാത്രമേ ഇതുവരെ അവതരിപ്പിച്ചിട്ടുള്ളു. അണുവിന്റെ ശരിയായ വലുപ്പത്തെക്കുറിച്ചും ഭാരത്തെക്കുറിച്ചും വേണ്ടത്ര തെളിവുകള്കൂടി ലഭിച്ചാല് മാത്രമേ അണുസിദ്ധാന്തത്തിന് നിരാക്ഷേപമായ യുക്തിസഹത ലഭിക്കയുള്ളു. അണുക്കളുടെ സംയോഗംമൂലം തന്മാത്രകള് ഉണ്ടാകുന്നുവെന്ന് സങ്കല്പിക്കുകയാണെങ്കില്, രണ്ടോ മൂന്നോ അണുക്കള് ചേര്ന്ന് ഉണ്ടാകുന്ന തന്മാത്രയുടെ വലുപ്പം അണുവിന്റേതിനേക്കാള് വളരെയേറെ ആകാന് ഇടയില്ല.
പ്രതലവലിവുരീതി
(surface tension model)
തന്മാത്രയുടെ വലുപ്പം ഏകദേശം കൃത്യമായി കണക്കു കൂട്ടിയത് തോമസ് യങ് എന്ന ഇംഗ്ളീഷ് ഭൌതികശാസ്ത്രജ്ഞനാണ്. ദ്രാവകങ്ങളുടെ പ്രതലബലവും വലിവുബലവും (tensil strength) ആധാരമാക്കിയാണ് യങ് തന്റെ നിഗമനങ്ങളിലെത്തിയത്. തന്മാത്രകളുടെ വലുപ്പം നിര്ണയിക്കാന് പ്രതലബലവും ദ്രാവകങ്ങളുടെ ബാഷ്പലീന താപവും (latent heat of vapourisation) ആണ് ജെ.ജെ. വാട്ടേഴ്സണ് ഉപയോഗപ്പെടുത്തിയത് (1845). അദ്ദേഹം കണക്കു കൂട്ടിയത് ഇങ്ങനെയാണ്: ഒരു ദ്രാവകപ്രതലത്തില് 1 ച.സെ.മീ. വിസ്താരം ഉണ്ടാക്കാന് വേണ്ട ഊര്ജമാണ് പ്രതലബലം; ഒരു ഗ്രാം ദ്രാവകത്തെ പൂര്ണമായി അതിന്റെ തിളനിലയില് ബാഷ്പമാക്കാന്, അതായത് തന്മാത്രകളെ വേര്തിരിക്കാന് വേണ്ട ഊര്ജം ബാഷ്പലീനതാപവും. തന്മാത്രകളെ d വശമുള്ള ക്യൂബുകളായി സങ്കല്പിച്ചാല് V വ്യാപ്തം ദ്രാവകത്തില് V/d3 തന്മാത്രകള് ഉണ്ടായിരിക്കും. ഒരു തന്മാത്രയുടെ പാര്ശ്വതല വിസ്തീര്ണം 6d2 ആയതിനാല് ആകെ തന്മാത്രകളുടെ വിസ്താരം V/d3x6d2=6V/d ആണ്. അതിനാല് തന്മാത്രകളുടെ വിസ്താരം വര്ധിപ്പിക്കാന് ചെലവായ ഊര്ജം = പ്രതലബലം x വിസ്താരം=Sx6V/d=6SV/d . ബാഷ്പ ലീനതാപം L എങ്കില് V വ്യാപ്തം ദ്രാവകം ബാഷ്പീകരിക്കാന് ചെലവഴിച്ച ഊര്ജം = VL. ഇവ രണ്ടും തുല്യമായതിനാല്,6SV/d=VL . അതായത്, d=6S/L. വെള്ളത്തിന് S = 70 ഡൈന്/സെ.മീ. എന്നും H=Z2e4M/8∈20 h3C എര്ഗ്/ഘ. സെ.മീ. എന്നും സ്വീകരിച്ചാല് d = 2 x 10-10 മീ. അതായത് ജലതന്മാത്രയുടെ വലുപ്പം 0.20 നാനോ മീ. എന്നു വരുന്നു (1 നാനോ മീ. = 10-9 മീ.)
മാധ്യമുക്തപഥരീതി
(Mean free path model)
ഗതികസിദ്ധാന്ത നിഗമനങ്ങള് തന്മാത്രകളുടെ വേഗത്തെപ്പറ്റിയുള്ള പഠനത്തില് ഏറെ പ്രാധാന്യം അര്ഹിക്കുന്നു. മിക്ക തന്മാത്രകളുടെയും വേഗം 25°c-ല് 300 മീറ്ററിലധികമാണ്. എങ്കിലും ഘനത്വംകൂടിയ കാര്ബണ് ഡൈഓക്സൈഡ് പോലുള്ള ഒരു വാതകം അന്തരീക്ഷത്തിലേക്കു തുറന്നുവച്ചിരുന്നാല് വായുവുമായുള്ള അതിന്റെ മിശ്രണം വളരെവേഗം നടക്കുന്നില്ലെന്നു പരീക്ഷണങ്ങള് തെളിയിച്ചിട്ടുണ്ട്. വളരെ കുറച്ചു ദൂരം മാത്രം സഞ്ചരിക്കുമ്പോഴേക്കും തന്മാത്രകള് തമ്മില് സംഘട്ടനം നടക്കുന്നതായിരിക്കണം അതിനു കാരണം. രണ്ടു അനുക്രമസംഘട്ടനങ്ങള്ക്കിടയില് ഒരു തന്മാത്ര സഞ്ചരിക്കുന്ന ശ.ശ. ദൂരമാണ് അതിന്റെ മാധ്യമുക്തപഥം. ഗതികസിദ്ധാന്തത്തില് തന്മാത്രകളെ കട്ടിയുള്ള ഗോളങ്ങളായി കല്പിച്ചിരിക്കുന്നു. ഒരു വ്യാപ്തമാത്ര(unit volume)യില് d വ്യാസമുള്ള n വാതക തന്മാത്രകളുണ്ടെങ്കില്, തന്മാത്രയുടെ മാധ്യമുക്തപഥം λ_യ്ക്കുള്ള സമീകരണം ഇങ്ങനെയാണ് λ=1/√2πnd2.V വ്യാപ്തം വാതകത്തില് Vn തന്മാത്രകള് ഉണ്ടായിരിക്കും. വാതകം ദ്രാവകമായി സംഘനിക്കുമ്പോള് വ്യാപ്തം V ആണെങ്കില് തുല്യ ഗോളങ്ങളുടെ സങ്കുലന രീതി (packing nature) കണക്കിലെടുത്താല് v = Vnd3 എന്നു തെളിയിക്കാം. അപ്പോള്,Vλ=Vd/√2π എന്നു കിട്ടുന്നു. മിക്ക വാതകങ്ങള്ക്കും V = 0.005V, λ= 2 x 10-8 മീ. ആയതിനാല് d = 0.20 നാനോമീറ്റര് (നോ: അന്താരാഷ്ട്രമാത്രാ സമ്പ്രദായം) എന്നു കിട്ടുന്നു. തന്മാത്രകളുടെ വലുപ്പം ഏകദേശം 0.20 നാനോമീറ്റര് വരും. 1 ഘ.സെ.മീ. തന്മാത്രയില് ഏകദേശം 4.5 x 1019 തന്മാത്രകള് ഉണ്ടെന്ന് ഈ തന്മാത്രാ വലുപ്പം ഉപയോഗിച്ച് 1865-ല് ജെ. ലോഷ്മിഡ്റ്റ് നിര്ണയിച്ചു. രസതന്ത്രജ്ഞരെ സംബന്ധിച്ചിടത്തോളം ഒരു ഗ്രാം വാതകത്തില്, അതായത് 22415 ഘ.സെ.മീ. വാതകത്തില് എത്ര തന്മാത്രകളുണ്ടെന്നുള്ള അറിവ് പ്രധാനമാണ്. ഈ അറിവ് ഓരോ മൂലക അണുവിന്റെയും കേവലഭാരം നിര്ണയിക്കാന് സഹായിക്കുന്നു. ഒരു ഗ്രാം തന്മാത്രയിലുള്ള അണുക്കളുടെ സംഖ്യയെ അവോഗാഡ്രോസംഖ്യ N0 എന്നു പറയുന്നു. ഏറ്റവും പുതിയ വിധികളനുസരിച്ചുള്ള നിര്ണയപ്രകാരം അവോഗാഡ്രോസംഖ്യ 6.02252 x 1023 ആണ്. ഇതില്നിന്ന് ഹൈഡ്രജന് അണുവിന്റെ ഭാരം = 1.673 x 10-27 കി.ഗ്രാം എന്നു കിട്ടുന്നു. ഏതു മൂലകത്തിലെ അണുവിന്റെയും കേവലഭാരം കാണാന് അതിന്റെ അണുഭാരത്തെ ഹൈഡ്രജന്-അണുഭാരം കൊണ്ട് ഗുണിച്ചാല് മതി.
എണ്ണഫിലിം രീതി
(Oil film model).
വെള്ളത്തില് ലയിക്കാത്തതും ധ്രുവീയ-അന്ത്യ ഗ്രൂപ്പുകള് (polar terminal groups) ഉള്ളതുമായ ഒലിയിക് അമ്ളം (Oleic acid) പോലുള്ള ചില കാര്ബണികയൌഗികങ്ങള് ശുദ്ധജല പ്രതലത്തില് പരക്കുമെന്ന് 1891-ല് ഫ്രൌളിന് പോക്കല്സ് തെളിയിച്ചു. റാലിപ്രഭു, ഈ പരീക്ഷണം തുടര്ന്നു. ജലപ്രതലത്തിലേക്ക് ഒഴിക്കുന്ന ഒലിയിക് അമ്ളത്തിന്റെ അളവ് ഒരു പരിമാണത്തില് കുറവാണെങ്കില് വെള്ളത്തിന്റെ പ്രതലബലത്തില് കുറവുണ്ടാകുന്നില്ലെന്ന് 1899-ല് അദ്ദേഹം കണ്ടുപിടിച്ചു. ഈ പരിമാണത്തിന് ക്രാന്തികപരിമാണം (critical measure) എന്നു പറയുന്നു. ക്രാന്തികപരിമാണത്തില് കൂടുതലായാല് പ്രതലബലം കുറയുന്നതായും തെളിയിക്കപ്പെട്ടു. ജലപ്രതലത്തില് ഒലിയിക് അമ്ളത്തിന്റെ ഒരു സാന്ത ഏകതന്മാത്രാഫിലിം (finite single molecule film) ഉണ്ടാകുമ്പോഴാണ് പ്രതലബലത്തില് മാറ്റംവരുന്നതെന്ന് അദ്ദേഹം അനുമാനിച്ചു. 1 ഘ.സെ.മീ. ഏകതന്മാത്രാഫിലിം ഉണ്ടാകാന് എത്ര ഒലിയിക് അമ്ളം വേണമെന്ന് പരീക്ഷണത്തിലൂടെ റാലിപ്രഭു നിര്ണയിച്ചു. ശുദ്ധ അമ്ളത്തിലും ഏകതന്മാത്രാഫിലിമിലും അമ്ളത്തിന്റെ ഘനത്വം തുല്യമാണെന്ന സങ്കല്പത്തില് അദ്ദേഹം അമ്ളതന്മാത്രയുടെ വലുപ്പം 1.00 നാനോമീറ്റര് ആണെന്നു കണ്ടു
എക്സ്റേ വിഭംഗനം
(X-ray diffraction)
ക്രിസ്റ്റലീയ ഖരങ്ങള്ക്ക് നിശ്ചിത ജ്യാമിതീയ രൂപമുണ്ട്. അവയില് നിശ്ചിത ജ്യാമിതീയ മാതൃകകളിലാണ് അണുക്കള് വിന്യസിച്ചിരിക്കുന്നത്. ക്രിസ്റ്റലിലെ മാത്രാസെല്ലിന്റെ വ്യാപ്തം (v) കാണാനുള്ള സമീകരണം V=ZM/N0ρ ആണ്. ഇവിടെ Z മാത്രാസെല്ലിലുള്ള അണുക്കളുടെ എണ്ണം, M അണുഭാരം, N0 അവോഗാഡ്രോസംഖ്യ,ρ ഘനത്വം എന്നിവയെ പ്രതിനിധാനം ചെയ്യുന്നു. അലുമിനിയം ലോഹത്തിന്റെ ക്രിസ്റ്റലില് മാത്രാസെല്ലിന്റെ വ്യാപ്തം പരിശോധിക്കുമ്പോള് ഇത് വ്യക്തമാകും. അലൂമിനിയത്തിന് Z = 4, M= 26.98,ρ = 2.7 ഗ്രാം/ഘ.സെ.മീ. ആയതിനാല്,V=4 x 26.98/2.7 x 6.023 x 1023 = 64.86 x 10-21 ഘ.സെ.മീ. മാത്രാസെല്ലിന് ക്യൂബ് ആകൃതി ആയതിനാല്, ക്യൂബിന്റെ വശം = 4.049 x 10-8 സെ.മീ. = 0.4049 നാനോമീറ്റര്. ഗോളങ്ങളുടെ ജ്യാമിതീയ സങ്കുലനം കണക്കിലെടുക്കുമ്പോള്, അലുമിനിയം അണുവിന്റെ വ്യാസം 0.286 നാനോമീറ്റര് എന്നുവരുന്നു. ഇപ്രകാരം പല അണുക്കളുടെയും വ്യാസം നിര്ണയിച്ചിട്ടുണ്ട്.
അണുഭാരം കൂടുന്ന മുറയ്ക്ക് അണുക്കളുടെ വലുപ്പം കൂടുന്നുണ്ടെങ്കിലും ഈ വസ്തുത ഒരു നിയമമായി ഗണിക്കവയ്യ. ഏറ്റവും കൂടുതല് വലുപ്പമുള്ള അണുക്കളുടെ കൂട്ടത്തില്പെടുന്നു ക്ഷാരലോഹങ്ങള്. അണുക്കളുടെ വലുപ്പം സാമാന്യമായി 0.1 മുതല് 0.5 വരെ നാനോമീറ്റര് ആണെന്നു പറയാം.
അണുവിന്റെ അസ്തിത്വത്തിന് മറ്റു തെളിവുകള്
അണുവെന്ന സങ്കല്പത്തിന് 20-ാം ശ.-ത്തിന്റെ ആരംഭംവരെ നിഗമനാത്മകമായ തെളിവുകള് അല്ലാതെ യഥാര്ഥ തെളിവുകള് ലഭിച്ചിരുന്നില്ല. ഇലക്ട്രോണ്, റേഡിയോ ആക്റ്റിവത തുടങ്ങിയവയുടെ കണ്ടുപിടിത്തത്തോടെയാണ് പദാര്ഥത്തിന്റെ അണുഘടനയെ സംബന്ധിച്ച യാഥാര്ഥ്യങ്ങള് വെളിച്ചം കണ്ടത്.
ഇലക്ട്രോണ്
പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങുന്നവയായിരുന്നു ഫാരഡെയുടെ ഗവേഷണങ്ങള്. ഒരേ പരിമാണം വൈദ്യുതി, വിവിധ ഇലക്ട്രോളൈറ്റുക(electrolytes)ളില്കൂടി പ്രവഹിപ്പിച്ചാല്, നിക്ഷേപിക്കപ്പെടുന്ന പദാര്ഥങ്ങളുടെ ഭാരം അവയുടെ രാസതുല്യാങ്കഭാരങ്ങള്ക്ക് ആനുപാതികമായിരിക്കുമെന്നു മൈക്കേല്ഫാരഡെ 1833-ല് കണ്ടുപിടിച്ചു. ഒരു കി.ഗ്രാം. തുല്യാങ്കം പദാര്ഥം നിക്ഷേപിക്കപ്പെടാന് 9.6522 x107 കൂളും വൈദ്യുതി വേണമെന്ന് ഫാരഡെ കണ്ടെത്തി. ഈ വസ്തുത പദാര്ഥത്തിന്റെ അണുസിദ്ധാന്തത്തെ പിന്താങ്ങാന് പര്യാപ്തമായിരുന്നു.
സാധാരണ പരിതഃസ്ഥിതികളില് വാതകങ്ങള് നല്ല ഇന്സുലേറ്ററുകളാണ്. ഉയര്ന്ന പൊട്ടന്ഷ്യല് പ്രയോഗിച്ചാല് ഒരു ഡിസ്ചാര്ജ് മാത്രമേ ഉണ്ടാകയുള്ളു. പക്ഷേ, മര്ദം കുറയും തോറും അതിലെ വാതകം ചാലകത പ്രദര്ശിപ്പിക്കുകയും പല ദീപ്തിപ്രവാഹങ്ങള് അതില് ഉണ്ടാക്കുകയും ചെയ്യും. ഡിസ്ചാര്ജ് ട്യൂബുകളില് ഉണ്ടാകുന്ന ഇത്തരം പ്രതിഭാസങ്ങളെപ്പറ്റി ജെ. പ്ളക്കര് (1858), ഡബ്ള്യു. ഹിറ്റോര്ഫ് (1869), വില്യം ക്രൂക്സ് (1879) തുടങ്ങി പലരും പഠനം നടത്തി. മര്ദം 1- 0.1 ന്യൂട്ടണ് മീ-2 ആയിരിക്കുമ്പോള് കാഥോഡില്നിന്നു പുറപ്പെടുന്ന കിരണങ്ങളെ ഇ. ഗോള്ഡ്സ്റ്റൈന് എന്ന ശാസ്ത്രജ്ഞന് കാഥോഡ്കിരണങ്ങള് (cathoderays) എന്നു വിളിച്ചു. കാഥോഡ്കിരണങ്ങള് കണങ്ങളാണ്; കാഥോഡിനു ലംബമായി നേര്രേഖയില് സഞ്ചരിക്കുന്നു; കാന്തികമണ്ഡലത്തിലും വിദ്യുത്മണ്ഡലത്തിലും അവ വ്യതിചലിക്കുന്നു എന്നെല്ലാം തെളിയിക്കപ്പെട്ടു. കാഥോഡ്കണങ്ങള്ക്ക് ഋണചാര്ജ് ഉണ്ടെന്ന് സര് ജെ.ജെ. തോംപ്സണ് തെളിയിച്ചു. പല വാതകങ്ങളും ഉപയോഗിച്ച് പരീക്ഷണങ്ങള് ആവര്ത്തിച്ചതിന്റെ ഫലമായി എല്ലാ വസ്തുക്കളിലും ഋണവൈദ്യുതിമാത്ര, അതായത് ഇലക്ട്രോണ്, ഒരു മൌലികഘടകമാണെന്നു സ്ഥാപിക്കപ്പെട്ടു. ഇലക്ട്രോണിന്റെ ചാര്ജ് e-ഉം ദ്രവ്യമാനം m-ഉം ആണെങ്കില്, e/m ന്റെ മൂല്യം 1.76 x 1011 കൂളും കി.ഗ്രാം-1 ആകുന്നു.
ദ്വാരങ്ങളുള്ള ഒരു കാഥോഡ് ഉപയോഗിക്കുകയും മര്ദം വളരെ കുറയാതിരിക്കയും ചെയ്യുന്നെങ്കില്, ആനോഡില് (anode) നിന്ന്, അതായത് ധന ഇലക്ട്രോഡില്നിന്ന് വര്ണ രശ്മികള് പുറപ്പെടുന്നുണ്ടെന്ന് ഇ. ഗോള്ഡ്സ്റ്റൈന് (1886) തെളിയിച്ചു. ഇവയെ ധനകിരണങ്ങള് എന്നു വിളിക്കുന്നു. ഈ കണങ്ങളെക്കുറിച്ചുള്ള ഗവേഷണങ്ങളുടെ ഫലമായി ഏറ്റവും ഭാരം കുറഞ്ഞ ധനകണത്തിന് ഹൈഡ്രജന് അണുവിന്റെ ഭാരമുണ്ടെന്ന് തെളിയിക്കപ്പെട്ടു. റഥര്ഫോര്ഡ് ഈ കണത്തെ പ്രോട്ടോണ് (proton) എന്നു വിളിച്ചു.
റേഡിയോ ആക്റ്റിവത
(Radio activity)
റേഡിയോ ആക്റ്റിവ് മൂലകങ്ങളെക്കുറിച്ചുള്ള പഠനം അണുവിന്റെ അസ്തിത്വത്തിനു നേരിട്ടുള്ള തെളിവു നല്കുന്നു. ഉദാഹരണത്തിന്, റേഡിയോ ആക്റ്റിവ് മൂലകങ്ങളില്നിന്ന് α(ആല്ഫാ), β(ബീറ്റാ) γ(ഗാമാ)-രശ്മികള് ഉത്സര്ജിക്കപ്പെടുന്നു. α-കണം സിങ്ക്സള്ഫൈഡ് സ്ക്രീനില് പതിക്കുമ്പോള് ഉണ്ടാകുന്ന സ്പന്ദങ്ങള് നിരീക്ഷിക്കാവുന്നതാണ്.
ബ്രൌണിയന് ചലനം
(Brownian motion).
ഇംഗ്ളീഷ് സസ്യശാസ്ത്രജ്ഞനായ റോബര്ട്ട് ബ്രൌണ് 1827-ല് ദ്രാവകത്തില് നിലംബിതമായ പൂമ്പൊടി ഇടതടവില്ലാതെ ചലിക്കുന്നതായി കണ്ടു. ഈ ചലനത്തെ ബ്രൌണിയന് ചലനമെന്നു വിളിക്കുന്നു. 1906-ല് ഐന്സ്റ്റൈന് ഈ ചലനത്തെ വിശകലനം ചെയ്ത് ഒരു സമീകരണം കണ്ടെത്തി. ജെ. പെരിന്, ബ്രൌണിയന് ചലനപഠനംവഴി അവോഗാഡ്രോ സംഖ്യയുടെ മൂല്യം നിര്ണയിച്ചു. ക്രിസ്റ്റലുകളുടെ എക്സ്റേകള് ഉപയോഗിച്ചുള്ള പഠനങ്ങളും അണുക്കളുടെ വലുപ്പം അളക്കാന് സഹായിച്ചിട്ടുണ്ട്.
അണുവിനെ നേരിട്ടു കാണാനുള്ള ശ്രമം വിജയിച്ചിട്ടുണ്ട്. ഇ. ഡബ്ളിയു. മുള്ളര്ഫീല്ഡ് അയോണ്മൈക്രോസ്കോപ് ഉപയോഗിച്ച് അണുവിന്റെ പത്തുലക്ഷം ഇരട്ടി വലുപ്പമുള്ള ചിത്രങ്ങള് എടുത്തിട്ടുണ്ട്.
ന്യൂക്ളിയര് അണു
(Nuclear atom).
റേഡിയോ ആക്റ്റിവത, ഇലക്ട്രോണ് എന്നിവയുടെ കണ്ടുപിടിത്തം അണുസംരചന മനസ്സിലാക്കാന് സഹായിച്ചു. റേഡിയോ ആക്റ്റിവ് മൂലകങ്ങളില്നിന്ന് ധനകണങ്ങളും ഋണകണങ്ങളും ഉത്സര്ജിക്കുന്നുണ്ടെന്ന അറിവ്, അണു നിര്മിച്ചിരിക്കുന്നത് ധനചാര്ജും ഋണചാര്ജും ചേര്ന്നാണെന്ന നിഗമനത്തിന് വഴി തെളിച്ചു. ഈ അഭിപ്രായം സാധുവാണെങ്കില്, അണു ഉദാസീനമായതിനാല് ധനചാര്ജുകളുടെയും ഋണചാര്ജുകളുടെയും എണ്ണം തുല്യമായിരിക്കണം. ഇലക്ട്രോണുകളുടെ ഭാരം നിസ്സാരമായതിനാല് അണുവിന്റെ ഭാരം മുഴുവന് കേന്ദ്രീകരിച്ചിരിക്കുന്നത് ധനചാര്ജിലായിരിക്കുകയും വേണം.
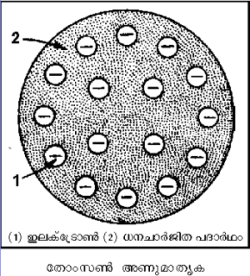
തോംപ്സണ് മാതൃക
മേല്പറഞ്ഞ കാര്യങ്ങള് കണക്കിലെടുത്ത് 1898-ല് സര്. ജെ.ജെ. തോംപ്സണ് അണുവിന് ഒരു മാതൃക ഉണ്ടാക്കി. ഏകസമാന ഘനത്വമുള്ള (uniform density) ധനചാര്ജിതഗോളത്തില് തുല്യ ഋണചാര്ജ് ഉണ്ടാകാന് വേണ്ടത്ര ഇലക്ട്രോണുകള് വിതറിയിട്ടുള്ള ഒരു മാതൃകയാണ് തോംപ്സണ് വിവക്ഷിച്ച അണു. തോംപ്സണ്-ന്റെ മാതൃക തികച്ചും യുക്തിസഹമെന്ന് അന്ന് അംഗീകരിച്ചിരുന്നു.
1904-ല് ജപ്പാന്കാരനായ എച്ച്. നഗയോക്ക അണുവിന് 'ശനിമാതൃക' (Saturn model) നിര്ദേശിച്ചു. ശനിഗ്രഹത്തിനു ചുറ്റും വലയങ്ങള് ഉള്ളതുപോലെ, ധനചാര്ജ് അണുവിന്റെ കേന്ദ്രത്തിലും അതിനുചുറ്റും വലയത്തില് ഇലക്ട്രോണുകളും എന്ന ഈ മാതൃക യഥാര്ഥത്തില് ശ്രദ്ധിക്കപ്പെട്ടില്ല.
ആല്ഫാ-കണ പ്രകീര്ണനം
(α-particle scattering).
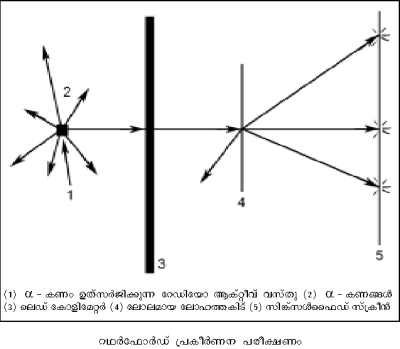
1911-ല് ഗൈഗറും മാര്സ്ഡനും അണുവിന്നുള്ളില് എന്താണെന്നറിയാനുള്ള ശ്രദ്ധേയമായ ഒരു പരീക്ഷണം നടത്തി. റഥര്ഫോര്ഡിന്റെ നിര്ദേശാനുസരണം നടത്തിയ ഈ പരീക്ഷണത്തില് റേഡിയോ ആക്റ്റിവ് മൂലകങ്ങളില്നിന്ന് ഉത്സര്ജിക്കുന്ന വേഗമേറിയ α-കണങ്ങളാണ് അന്വേഷണമാധ്യമം (probe) ആയി ഉപയോഗിച്ചത്. അവ α-കണം ഉത്സര്ജിക്കുന്ന വസ്തു, ചിത്രത്തില് കാണിച്ചിരിക്കുന്നതുപോലെ സൂക്ഷ്മസുഷിരമുള്ള ഒരു ലെഡ്സ്ക്രീനിന്റെ പിന്നില്വച്ചു. അങ്ങനെ α-കണങ്ങളുടെ ഒരു നേരിയ വ്യൂഹം ഉണ്ടാക്കി. ഈ വ്യൂഹം കനം കുറഞ്ഞ സ്വര്ണത്തകിടില് പതിപ്പിച്ചു.
സ്വര്ണത്തകിടിന്റെ പിന്നില് സിങ്ക്സള്ഫൈഡ് സ്ക്രീന് സ്ഥാപിച്ചു. α-കണങ്ങള് ഈ സ്ക്രീനില് പതിച്ചാല് പ്രകാശസ്ഫുരണങ്ങള് ഉണ്ടാകും. മിക്കവാറും എല്ലാ α-കണങ്ങളും തകിടില്ക്കൂടി കടന്നുപോകുമെന്നും ചിലതിനു മാത്രം വ്യതിചലനം ഉണ്ടാകുമെന്നും ആയിരുന്നു പ്രതീക്ഷ. തോംപ്സന്റെ അണുമാതൃകയില് ചാര്ജുകള് ഏകസമാനമായതിനാല് പ്രതീക്ഷിക്കാവുന്നതാണ് ഇത്. പക്ഷേ ഗൈഗറും മാര്സ്ഡനും കണ്ടത് ഇതാണ്: മിക്ക α-കണങ്ങളും തകിടിലൂടെ കടന്നുപോയി; പക്ഷേ ചിലത് വലിയ കോണങ്ങളില് പ്രകീര്ണനം ചെയ്യപ്പെട്ടു. ചിലതു പിറകോട്ടു പ്രകീര്ണനം ചെയ്യപ്പെട്ട α-കണങ്ങള്ക്ക് ഇലക്ട്രോണിന്റെ 7,000 മടങ്ങ് ഭാരം ഉണ്ടായിരുന്നതിനാലും, അവ നല്ല വേഗത്തില് പാഞ്ഞിരുന്നതിനാലും തീവ്രബലം പ്രവര്ത്തിച്ചെങ്കില് മാത്രമേ അവ പിന്തിരിയുകയുള്ളു എന്ന നിഗമനത്തില് അവര് എത്തി.
റഥര്ഫോര്ഡ് മാതൃക
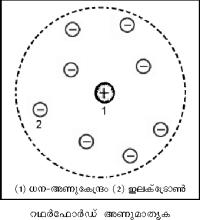
(Rutherford model).
ഈ പരീക്ഷണഫലങ്ങള്ക്ക് വിശദീകരണം നല്കാന് റഥര്ഫോര്ഡ് 'കേന്ദ്രീയ അണുമാതൃക' നിര്ദേശിച്ചു. അണുവിന്റെ ധനചാര്ജും ഭാരവും സാന്ദ്രീകരിച്ചിരിക്കുന്നത് അതിലെ വളരെ ചെറിയ അണുകേന്ദ്രത്തിലാണ്. ഇലക്ട്രോണുകള് നിശ്ചിത അകലത്തില് സൂര്യനു ചുറ്റും ഗ്രഹങ്ങളെന്നപോലെ കറങ്ങിക്കൊണ്ടിരിക്കുന്നു. α-കണങ്ങള് സ്വര്ണത്തകിടിലൂടെ നേരെ കടന്നുപോകാന് കാരണം അണു മൊത്തത്തില് പൊള്ളയായതാണ്. മാത്രമല്ല, റഥര്ഫോര്ഡ് മാതൃകയില് അണുകേന്ദ്രത്തിലെ വിദ്യുത്ബലം തോംപ്സണ് മാതൃകയിലെക്കാള് 108 മടങ്ങ് അധികമുണ്ടെന്ന് പരികലനംവഴി കാണിക്കാന് കഴിയും. അതാണ് α-കണങ്ങള് വലിയ കോണങ്ങളില് പ്രകീര്ണനവിധേയമാകാന് കാരണം.
ഇലക്ട്രോണുകള് ഭ്രമണപഥത്തില് ചലിച്ചുകൊണ്ടിരുന്നാല് മാത്രമേ റഥര്ഫോര്ഡ് അണുവിന് സ്ഥിരതയുള്ളു. പക്ഷേ, ക്ളാസ്സിക്കല് വിദ്യുത്-ഗതികം (Electro-Dynamics) അനുസരിച്ച് ചലിച്ചുകൊണ്ടിരിക്കുന്ന ഒരു ചാര്ജ് ത്വരണവിധേയമാകുന്നതിനാല് ഊര്ജവികിരണം നടത്തും. അങ്ങനെയാവുമ്പോള് കുറെ കഴിഞ്ഞാല്, ഇലക്ട്രോണ് ഊര്ജം ക്ഷയിച്ച് ഒരു സര്പ്പിളപഥത്തിലൂടെ ചലിച്ച് അണുകേന്ദ്രത്തില് പതിക്കും. പക്ഷേ, അണു നശിക്കാത്തതിനാല് ഇപ്രകാരം സംഭവിക്കയില്ലെന്ന് തീര്ച്ചയാണ്. ഈ പരസ്പരവൈരുധ്യത്തില്നിന്ന് സ്ഥൂലവസ്തുക്കള്ക്ക് ബാധകമായ ഭൌതികനിയമങ്ങള് സൂക്ഷ്മവസ്തുക്കളായ അണുക്കള്ക്ക് ബാധകമല്ലെന്ന് മനസ്സിലാക്കാവുന്നതാണ്.
ബോര് അണുമാതൃക
(Bohr atom model).
അണുവിന്റെ പെരുമാറ്റവുമായി പൊരുത്തപ്പെടുന്ന ആദ്യത്തെ അണുസിദ്ധാന്തം-ഹൈഡ്രജന് അണുവിന്റെ സംരചന-നിര്ദേശിച്ചത് 1913-ല്, നീല്സ്ബോര് ആണ്. പല പോരായ്മകളും ഉണ്ടെങ്കിലും ബോര് സിദ്ധാന്തം നല്ലൊരു കാല്വയ്പ് ആയിരുന്നു. 1900-ല് തപ്തവസ്തുക്കളുടെ സ്പെക്ട്രം വിശദീകരിക്കാനാണ് മാക്സ്-പ്ളാങ്ക് ക്വാണ്ടം സിദ്ധാന്തം ആവിഷ്കരിച്ചത്. വികിരണങ്ങള് ക്വാണ്ടങ്ങളായി, അതായത് പാക്കറ്റുകളായി, ആണ് ഉത്സര്ജിക്കപ്പെടുന്നതെന്നും ക്വാണ്ടത്തിന്റെ മിനിമം ഊര്ജം E=hv ആണെന്നും അദ്ദേഹം പ്രസ്താവിച്ചു. ഇവിടെ h പ്ളാങ്ക് സ്ഥിരാങ്കവും vവികിരണത്തിന്റെ ആവൃത്തിയും ആണ്. ഇലക്ട്രോണിന്റെ ചലനത്തിന് ക്ളാസ്സിക്കല് വിദ്യുത്ഗതികത്തിനുപകരം ക്വാണ്ടം സിദ്ധാന്തം ബോര് പ്രയോഗിച്ചു.
അണുസ്പെക്ട്രം
(Atomic Spectrum).
മൂലകങ്ങളുടെ സ്പെക്ട്രരേഖകള്, പ്രത്യേകിച്ചും സുസ്ഥാപിതമായ ഹൈഡ്രജന് സ്പെക്ട്രരേഖകള് ആണ് തന്റെ അണുസിദ്ധാന്തത്തില് ബോറിനെ എത്തിച്ചത്. ഹൈഡ്രജന്റെ സ്പെക്ട്രത്തില് നാലു പ്രധാന രേഖകള് - ചുവപ്പ്, പച്ച, നീല, വയലറ്റ് - ഉണ്ട്. 1885-ല് ജെ.ജെ. ബാമര് ഈ രേഖകളുടെ തരംഗനീളം അളന്നു. അതിനെ വളരെ കൃത്യമായി
എന്ന സൂത്രം പ്രതിനിധാനം ചെയ്യുന്നു. ഇവിടെ λ= തരംഗനീളം; RH = ഹൈഡ്രജനുള്ള റിഡ്ബര്ഗ് സ്ഥിരാങ്കം = 109677 സെ.മീ.-1; n= 3, 4, 5 ..... ഇത്യാദി പൂര്ണ സംഖ്യകള്
സമീകരണം (1)-ന്റെ സാമാന്യരൂപം റിറ്റ്സ് (Ritz) നിര്ദേശിച്ചു.
ഇത്തരം ബന്ധങ്ങളെ ക്വാണ്ടം സിദ്ധാന്തത്തിന്റെ വെളിച്ചത്തില് വിശദീകരിക്കാനാണ് ബോര് ശ്രമിച്ചത്.
ബോര് അണു
(Bohr atom).
സ്വേച്ഛാകല്പിത രീതിയിലാണ് ബോര് തന്റെ അണുസിദ്ധാന്തം നിര്ദേശിച്ചത്. ഹൈഡ്രജന് അണുമാതൃകയ്ക്കും ബോര് സ്വീകരിച്ച സങ്കല്പനങ്ങള് (assumptions) താഴെ കൊടുക്കുന്നു : (1) അണുകേന്ദ്രത്തിനു ചുറ്റും വൃത്താകാരമായ ഭ്രമണപഥത്തില് ഇലക്ട്രോണ് സഞ്ചരിക്കുന്നു; (2) കോണീയസംവേഗം h/2λ യുടെ ഗുണിതങ്ങളായിട്ടുള്ള ഭ്രമണപഥങ്ങള് മാത്രമേ അനുവദനീയമായുള്ളു; (3) അനുവദനീയ ഭ്രമണപഥത്തില് ആയിരിക്കുമ്പോള് ഇലക്ട്രോണ് ഊര്ജവികിരണം നടത്തുന്നില്ല. ഒരു അനുവദനീയ ഭ്രമണപഥത്തില് നിന്ന് മറ്റൊന്നിലേക്ക് ഇലക്ട്രോണ് ചാടുമ്പോള് ഊര്ജവികിരണം ഉണ്ടാകുന്നു.
ഈ സങ്കല്പനങ്ങളെ അടിസ്ഥാനമാക്കിയാണ് ബോര്, ഹൈഡ്രജന് അണുവിന്റെ വ്യാസാര്ധം (radius), അനുവദനീയ പരിപഥ ഊര്ജം (circuit energy) എന്നിവ പരികലനം നടത്തിയതും നിരീക്ഷ്യസ്പെക്ട്രരേഖകള് (visible spectral lines) സൈദ്ധാന്തികമായി പ്രവചിക്കാമെന്നു തെളിയിച്ചതും.
m,v,r എന്നിവ യഥാക്രമം ഇലക്ട്രോണിന്റെ ദ്രവ്യമാനം, ഭ്രമണവേഗം, ഭ്രമണപഥത്രിജ്യ (radius) എന്നിവ ആണെങ്കില് ബോര് സ്ഥിരാവസ്ഥ ഇങ്ങനെ കുറിക്കാം: 2π mvr =nh. ഇവിടെ n പ്ളാങ്ക് സ്ഥിരാങ്കവും ആണ്. ഈ സമീകരണത്തെ mvr =n h/2π എന്നെഴുതിയാല് ബോറിന്റെ രണ്ടാമത്തെ സങ്കല്പനമായി. ഇവിടെ mvr കോണീയസംവേഗവും n ക്വാണ്ടംസംഖ്യയും ആണ്. രേഖാസ്പെക്ട്രത്തില് അണു ഊര്ജവികിരണം നടത്തുന്നുണ്ട്. ഇതിന് ബോര് നല്കിയ വിശദീകരണം ഇതാണ്: സാധാരണ അണു നിമ്നതലത്തില് (ground state) ആണ്; അത് ഉത്സര്ജിതമാകുമ്പോള് ക്വാണ്ടീകരിച്ച ഊര്ജം (quantized energy) അവശോഷണം ചെയ്കയും ഇലക്ട്രോണ് താത്കാലികമായി ഉത്തേജിതാവസ്ഥയില് ആകുകയും ചെയ്യുന്നു. ക്ഷണികമായ ഈ ഉത്തേജിതാവസ്ഥയില് നിന്ന് (ഊര്ജം: En2) ആദ്യാവസ്ഥയിലേക്ക് (ഊര്ജം: En1) ഇലക്ട്രോണ് വരുമ്പോള് ഊര്ജവികിരണം നടത്തുന്നു. അതായത്,
(3), (4), (5), (6) എന്നീ സമീകരണങ്ങളില്, Ze = അണുകേന്ദ്രചാര്ജ്, e = ഇലക്ട്രോണ്ചാര്ജ്, m = ഇലക്ട്രോണ് ദ്രവ്യമാനം, (സ്വതന്ത്ര സ്പെയ്സിന്റെ വിദ്യുത്ശീലത) = 8.854 x10 -12 ഫാരഡ് മീ.-1 n= ക്വാണ്ടം സംഖ്യ എന്നിവ ആണ്. ബോര് സിദ്ധാന്തത്തിന്റെ സാധുത്വം പരിശോധിക്കാന് റിഡ്ബര്ഗ് സ്ഥിരാങ്കത്തിന്റെ എംപിരികസമീകരണമൂല്യവും സമീകരണം (6)-ന്റെ മൂല്യവും തമ്മിലുള്ള പൊരുത്തം പ്രയോജനപ്പെടുത്താം. ഹൈഡ്രജന് അണുവിന് z = 1, e = 1.60 x 10-19 കൂളും m = 9.11 x 10-31 കി.ഗ്രാം, c = 3 x 108 മീ. സെ.-1, h = 6.62 x 10-34 ജൂള് സെ. എന്നീ മൂല്യങ്ങള് സമീകരണം (6)-ല് പ്രതിസ്ഥാപിച്ചാല്, RH = 1.099 x 107 മീ.-1 എന്നുകിട്ടുന്നു. RH-ന്റെ മൂല്യങ്ങള് ഏകദേശം തുല്യമായതിനാല് ബോര് സിദ്ധാന്തം വിജയമായിരുന്നു എന്നു പറയാം; ഹൈഡ്രജന് അണുവിന്റെ ത്രിജ്യ 0.053 നാനോമീറ്ററും.
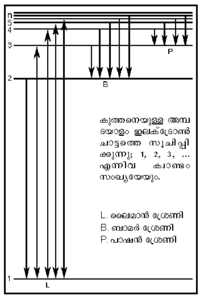
ബോര് സമീകരണം (4)-ല് n1,n2 എന്നിവയെ മുഖ്യക്വാണ്ടംസംഖ്യകളെന്നു പറയുന്നു. ഹൈഡ്രജന് അണുവിന്റെ ഊര്ജം ഇലക്ട്രോണ് ചലനംമൂലമുള്ളതാണ്. ഇത് സമീകരണം (3)-ല് നിന്നു കിട്ടുന്നു. E-യുടെ മൂല്യം മൌലിക സ്ഥിരാങ്കങ്ങള്ക്കുപുറമേ n2-നെക്കൂടി ആശ്രയിച്ചിരിക്കുന്നു; അതായത് n വലുതാകുംതോറും Eയുടെ സംഖ്യാമൂല്യം കുറയുന്നു. നിമ്നതമാവസ്ഥയില്, അതായത്,n = 1 ആകുമ്പോള്, ഇലക്ട്രോണ്, അണുകേന്ദ്രത്തിന് ഏറ്റവും അടുത്തായിരിക്കും; ഊര്ജത്തിന്റെതാകട്ടെ ഋണമൂല്യ-ഉച്ചതമവും. അണു ഉത്തേജിക്കപ്പെടുമ്പോള്, ഭ്രമണപഥത്തിന്റെ ത്രിജ്യ കൂടുതലുള്ള n = 2, 3, 4 തുടങ്ങിയ തലങ്ങളിലേക്ക് അതായത് ഋണ-ഊര്ജം കുറയുന്ന ഭ്രമണപഥങ്ങളിലേക്ക് ഇലക്ട്രോണ് ചാടുന്നു. ഈ അവസ്ഥയില്നിന്ന് നിമ്നതലത്തിലേക്ക് ഇലക്ട്രോണ് വരുമ്പോള്, അവശോഷണം ചെയ്ത ധന-ഊര്ജം വികിരിണമായി പ്രത്യക്ഷപ്പെടുന്നു. ഇങ്ങനെ സ്പെക്ട്രരേഖകള് ഉണ്ടാകുന്നു.പക്ഷേ, ബോര് സിദ്ധാന്തത്തിന്റെ വിജയം താത്കാലികം മാത്രം ആയിരുന്നു. ഒന്നിലധികം ഇലക്ട്രോണുകള് ഉള്ള അണുക്കളുടെ കാര്യത്തില് ബോര് സിദ്ധാന്തം പരാജയപ്പെട്ടു.
ദീര്ഘവൃത്ത ഭ്രമണപഥ ഇലക്ട്രോണ്
(Elliptical orbit electron).
പ്രതിലോമാനുപാത (inversely propotional) ആകര്ഷണത്തിനു വിധേയമായി ഇലക്ട്രോണ് അണുകേന്ദ്രത്തിനു ചുറ്റും ഭ്രമണം ചെയ്യുന്നതിനാല്, ഇലക്ട്രോണിന്റെ ഭ്രമണപഥം ദീര്ഘവൃത്തമായിരിക്കണം. സൂര്യനു ചുറ്റും ഭൂമി ഭ്രമണം ചെയ്യുന്നത് ഇത്തരം ഭ്രമണപഥത്തിലാണ്. ഹൈഡ്രജനെക്കാള് സങ്കീര്ണങ്ങളായ അണുക്കള്ക്കു ബോര് സിദ്ധാന്തത്തിന്റെ സാമാന്യവത്കരണവും ഇലക്ട്രോണിന്റെ ദീര്ഘവൃത്തഭ്രമണപഥങ്ങളും ബ്രിട്ടിഷ് ഭൌതികശാസ്ത്രജ്ഞനായ ഡബ്ളിയു. വില്സനും (1915) ജര്മന് ശാസ്ത്രജ്ഞനായ എ. സോമര്ഫെല്ഡും (1916) സ്വതന്ത്രമായിത്തന്നെ നിര്ദേശിച്ചു. ദീര്ഘവൃത്തഭ്രമണപഥങ്ങളെ നിര്ദേശിക്കാന് അവര് രണ്ടാമതൊരു ക്വാണ്ടംസംഖ്യ-ദിഗംശീയക്വാണ്ടംസംഖ്യ (azimuthal quantum number)-കൂടി നിര്ദേശിച്ചു. പിന്നീട് ദീര്ഘവൃത്തത്തിന്റെ അര്ധമുഖ്യാക്ഷം a-ഉം അര്ധലഘ്വക്ഷം b-ഉം ആണെങ്കില് ![]() ആണെന്നു തെളിയിച്ചു. ഇവിടെ lപൂര്ണസംഖ്യയും nമുഖ്യക്വാണ്ടംസംഖ്യയുമാണ്. കൂടാതെ l- ന് 0, 1, 2, 3 ഇത്യാദി (n- 1) വരെ മൂല്യങ്ങളുണ്ടാകാം; അതനുസരിച്ച് ഇലക്ട്രോണിന് ഭ്രമണപഥങ്ങളും n = 1,n = 2,n = 3 ഉള്ള ഇലക്ട്രോണുകളുടെ ഭ്രമണപഥങ്ങളാണ് ചിത്രത്തില് കാണിച്ചിരിക്കുന്നത്.
ആണെന്നു തെളിയിച്ചു. ഇവിടെ lപൂര്ണസംഖ്യയും nമുഖ്യക്വാണ്ടംസംഖ്യയുമാണ്. കൂടാതെ l- ന് 0, 1, 2, 3 ഇത്യാദി (n- 1) വരെ മൂല്യങ്ങളുണ്ടാകാം; അതനുസരിച്ച് ഇലക്ട്രോണിന് ഭ്രമണപഥങ്ങളും n = 1,n = 2,n = 3 ഉള്ള ഇലക്ട്രോണുകളുടെ ഭ്രമണപഥങ്ങളാണ് ചിത്രത്തില് കാണിച്ചിരിക്കുന്നത്.
മുഖ്യക്വാണ്ടം സംഖ്യ n = 3 ആകുമ്പോള് l = 0, 1, 2 ആണ്. സാധാരണ l= 0-നെ sഎന്നും l= 1-നെ p എന്നുംl = 2-നെ dഎന്നുംl = 3-നെ f എന്നും പറയാറുണ്ട്. n = 3 ഉള്ള ഭ്രമണപഥങ്ങളെ 3s,3p, 3d എന്നും വിളിക്കാറുണ്ട്. ഇതില്നിന്ന് n = 3 ഉള്ള ഭ്രമണപഥത്തിലെ ഇലക്ട്രോണിന് മൂന്നു വ്യത്യസ്ത ഊര്ജതലങ്ങളുണ്ടെന്നു വരുന്നു. ഐന്സ്റ്റൈന്റെ വിശേഷ ആപേക്ഷികതാസിദ്ധാന്തത്തില് നിന്ന് കാണിക്കാവുന്നതാണിത്. സ്പെക്ട്രരേഖകളുടെ സൂക്ഷ്മഘടനയിലേക്കും ഇത് വെളിച്ചം വീശുന്നു.
ചക്രണ ക്വാണ്ടംസംഖ്യ
(Magnetic Quantum number).
സ്പെക്ട്രരേഖകളുടെ സൂക്ഷ്മഘടന വിശദീകരിക്കാന് ദീര്ഘവൃത്തഭ്രമണപഥങ്ങള് സഹായകമായി. എങ്കിലും ക്ഷാരലോഹങ്ങളുടെ സ്പെക്ട്രങ്ങളിലെ ദ്വന്ദ്വ(pair)ത്തെ വിശദീകരിക്കാന് ഇത് പര്യാപ്തമായില്ല. ഗൂഡ്സ്മിത്ത്, ഉള്ളന്ബെക്ക് എന്നിവര് 1925-ല് ഇലക്ട്രോണ് ചക്രണം എന്ന സങ്കല്പം ഉന്നയിച്ചു. ഭൂമി സ്വന്തം അച്ചുതണ്ടില് കറങ്ങുന്നതുപോലെ ഇലക്ട്രോണും കറങ്ങുന്നുണ്ട്. ഭൂമി, സൂര്യനെ 365¼ ദിവസംകൊണ്ട് പ്രദക്ഷിണം വയ്ക്കുന്നു; പക്ഷേ സ്വന്തം അച്ചുതണ്ടില് 24 മണിക്കൂര് കൊണ്ട് കറങ്ങുന്നു. ഇലക്ട്രോണാകട്ടെ ദീര്ഘവൃത്തഭ്രമണപഥത്തില് അണുകേന്ദ്രത്തെ പ്രദക്ഷിണം വയ്ക്കുന്നു. സ്വന്തം അച്ചുതണ്ടില് 1/2(h/2π)കോണിയ സംവേഗ(angular momentum)ത്തോടെ കറങ്ങുന്നു. ഇതില്നിന്ന് ഇലക്ട്രോണിന് ചക്രണ ക്വാണ്ടംസംഖ്യ s ഉണ്ടെന്നും S = 1/2എന്നും കിട്ടുന്നു. ഇലക്ട്രോണ് അതിന്റെ ഭ്രമണപഥദിശയില് കറങ്ങുമ്പോള് സമാന്തര ചക്രണവും(S=+1/2) എതിര്ദിശകളിലാകുമ്പോള് പ്രതിസമാന്തരചക്രണവും (S=-1/2) നടത്തുന്നുവെന്ന് പറയുന്നു.
ഈ പശ്ചാത്തലത്തില്, അണുവിലെ ഒരു ഇലക്ട്രോണിന്റെ അവസ്ഥ രേഖപ്പെടുത്താന് n,l,s എന്നീ മൂന്നു ക്വാണ്ടംസംഖ്യകള് ആവശ്യമെന്നു വരുന്നു.
കാന്തിക ക്വാണ്ടംസംഖ്യ
(Magnetic Quantum number).
സ്പെക്ട്രരേഖകള് തീവ്രകാന്തികമണ്ഡലത്തില് ഘടകങ്ങളായി വേര്തിരിയുന്നുണ്ടെന്ന് സീമാന് (Zeeman) കണ്ടുപിടിച്ചിരുന്നു. ഈ പ്രതിഭാസമാണ് സീമാന് പ്രഭാവം. കാന്തികമണ്ഡലത്തിന്റെ അഭാവത്തില് ഒറ്റയെന്നു തോന്നുന്ന രേഖകള് കാന്തികമണ്ഡലത്തില് രണ്ടോ അതിലധികമോ ആയി വേര്തിരിയുന്നു. നിസ്സാരമായ ഈ സ്ഥാനാന്തരങ്ങളെ, അതായത് പുതിയ രേഖകളെ വിശദീകരിക്കാന് അണുവിനു സ്വീകരിക്കാവുന്ന പുതിയ ഊര്ജതലങ്ങളെ നിര്ദേശിക്കേണ്ടിവന്നു. ഈ പുതിയ ക്വാണ്ടംസംഖ്യയെ ദിഗംശീയകാന്തിക ക്വാണ്ടംസംഖ്യ ml എന്നു വിളിച്ചു. ഈ പ്രഭാവത്തിന്റെ പൂര്ണ വിശകലനത്തില്നിന്ന് mlന് (2l+1) മൂല്യങ്ങള് ഉണ്ടാകാമെന്നു വരുന്നു. അതായത് l= 2 എങ്കില് ml=-2, -1, 0, + 1, + 2 എന്നീ 5 മൂല്യങ്ങള് ഉണ്ട്. കാന്തിക ക്വാണ്ടം സംഖ്യയുടെ ആവിര്ഭാവത്തോടെ അണുവിലെ ഒരു ഇലക്ട്രോണിനെ പൂര്ണമായി നിര്ദേശിക്കാന് 4 ക്വാണ്ടംസംഖ്യകള് n,l,s വേണമെന്നു തീര്ച്ചയായി.
പൌളി തത്ത്വം
(Pauli Principle).
ദൂരവ്യാപകഫലങ്ങള് ഉളവാക്കിയ പൌളിതത്ത്വം, അതായത് പൌളി അപവര്ജനതത്ത്വം (Pauil's Exclusion Principle) 1925-ല് വൂള്ഫ് ഗാങ് പൌളി എന്ന ശാസ്ത്രജ്ഞന് പ്രസ്താവിച്ചതാണ്. ആ തത്ത്വം ഇതാണ്: ഒരു അണുവില് n,l,s,ml എന്നീ 4 ക്വാണ്ടംസംഖ്യകള്ക്ക് തുല്യമായിട്ട് രണ്ട് ഇലക്ട്രോണുകള് ഉണ്ടാകയില്ല. z അണുസംഖ്യയുള്ള ഒരു അണുവില് z ഇലക്ട്രോണുകള് ഉണ്ടായിരിക്കും. ഈ ഇലക്ട്രോണുകളെ വ്യത്യസ്തഭ്രമണപഥങ്ങളിലാണ് ക്രമപ്പെടുത്തിയിരിക്കുന്നത്. ഈ ഇലക്ട്രോണുകള് ഓരോന്നിനും തനതായ 4 ക്വാണ്ടംസംഖ്യകള് ഉണ്ട്; ഇവയാണ് ഇലക്ട്രോണിന്റെ അവസ്ഥ നിര്ണയിക്കുന്നത്.
ഒരേ മുഖ്യക്വാണ്ടംസംഖ്യ n ഉള്ള ഇലക്ട്രോണുകള് ഒരേ ഷെല്ലില് ഉള്ളവയെന്നു പറയുന്നു. അണുകേന്ദ്രത്തോട് ഏറ്റവും അടുത്ത ഭ്രമണപഥത്തിന് (n = 1), ഇത് K-ഷെല്; (n = 2), L-ഷെല്; (n = 3), M ഷെല് ഇത്യാദി. ഒരു ഷെല്ലില് ഉണ്ടാകാവുന്ന പരാമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം 2n2 ആണ്. ഇവിടെ n മുഖ്യക്വാണ്ടം സംഖ്യയാണ്. nനും lനും ഒരേ മൂല്യമുള്ള ഇലക്ട്രോണുകളെ സബ്ഷെല് ഇലക്ട്രോണുകള് എന്നു പറയുന്നു. ഒരു ഷെല്ലില് ആകാവുന്നത്ര ഇലക്ട്രോണുകള് ഉണ്ടെങ്കില് ആ ഷെല് പൂര്ണമായി എന്നു പറയുന്നു.
മോസ്ലി നിയമം
1913-ല് ആണ് ഹെന്റി ജി. മോസ്ലി എന്ന ബ്രിട്ടിഷ് ഭൌതികശാസ്ത്രജ്ഞന് പല ലോഹമൂലകങ്ങളുടെയും സ്വാഭാവിക എക്സ്റേസ്പെക്ട്രത്തെക്കുറിച്ച് ക്രമവത്കൃതമായ പഠനം നടത്തിയത്. ഇതിന്റെ ഫലമായി, മൂലകത്തിന്റെ അണുസംഖ്യ z കൂടുന്നതനുസരിച്ച് എക്സ്റേയുടെ ആവൃത്തി കുറയുന്നതായി കണ്ടു. ν ആവൃത്തിയും c, b എന്നിവ സ്ഥിരാങ്കങ്ങളുമായ മോസ്ലി നിയമം ഇങ്ങനെ കുറിക്കാം:
സ്വാഭാവിക എക്സ്റേ സ്പെക്ട്രം നിര്ണയിക്കുന്നതില് അണുസംഖ്യ മൌലികപ്രാധാന്യമുള്ളതാണെന്ന് അദ്ദേഹം സമര്ഥിച്ചു.
റഥര്ഫോര്ഡ്-ബോര് ഹൈഡ്രജന് അണുസിദ്ധാന്തം പുറത്തുവന്ന കാലത്തുതന്നെയാണ് മോസ്ലിയുടെ ഗവേഷണങ്ങളും നടന്നത്. സമീകരണം (7)-ല് c -യുടെ മൂല്യം Kα രേഖയനുസരിച്ച് 3/4RCആണെന്നു കണ്ടു. R റിഡ്ബര്ഗ് സ്ഥിരാംഗവും c പ്രകാശവേഗവും ആകുന്നു. b-യുടെ വില ഏകദേശം 1 ആണെന്നു കണ്ടു. ഈ മൂല്യങ്ങള് (7)-ല് എഴുതിയാല്
ഈ സമീകരണം ഹൈഡ്രജന് സ്പെക്ട്രത്തിന് ബോര് സിദ്ധാന്തം നല്കുന്ന സമീകരണത്തിന് തുല്യമാണ് [(4), (6) എന്നീ സമീകരണങ്ങള് നോക്കുകപ. പക്ഷേ, ഒരു വ്യത്യാസം മാത്രം: z-നുപകരം (z - 1)-ഉം n2 = 2-ഉം n = 1-ഉം n1-1-ഉം ആണ്. ഇതില്നിന്ന് എക്സ്റേ സ്പെക്ട്രത്തിന്റെ ഉദ്ഭവവും ഹൈഡ്രജന് സ്പെക്ട്രത്തിന്റേതുപോലെതന്നെയാണെന്നു കിട്ടുന്നു. മോസ്ലി-ഗവേഷണങ്ങളുടെ പ്രാധാന്യം അണുവിന്റെ സംരചനയെ മൂലകങ്ങളുടെ സ്വാഭാവിക എക്സ്റേ സ്പെക്ട്രവുമായി ബന്ധപ്പെടുത്തിയതുമാത്രമല്ല; അണുവിനെ സംബന്ധിച്ചിടത്തോളം മൌലികപ്രാധാന്യമുള്ള അണുസംഖ്യ എന്ന വസ്തുത, അണുസംഖ്യ നിര്ണയിക്കുന്നതില് എക്സ്റേ സ്പെക്ട്രത്തിന്റെ പ്രയോജനം എന്നിവയും ആ ഗവേഷണഫലങ്ങളാണ്.
ഐസോടോപ്പ്
(Isotope)
ഒരു മൂലകത്തെ നിര്വചിക്കാന് അതിന്റെ അണുസംഖ്യ z പ്രസ്താവിച്ചാല് മതി; പക്ഷേ, ഈ നിര്വചനം അതിലെ അണുവിനെ കൃത്യമായി സൂചിപ്പിക്കാന് സഹായിക്കണമെന്നില്ല. ഇതിനു കാരണം ഒരേ മൂലകംതന്നെ വ്യത്യസ്ത അണുഭാരങ്ങളുള്ള അണുക്കളുടെ മിശ്രിതമായതാണ്. ഉദാഹരണത്തിന് ഓക്സിജനില് 16-ഉം 17-ഉം 18-ഉം വീതം അണുഭാരമുള്ള അണുക്കളുണ്ട്. ഒരേമൂലകത്തിന്റെ വ്യത്യസ്ത-അണുഭാരങ്ങളുള്ള അണുക്കളെ ആ മൂലകത്തിന്റെ സ്ഥാനീയങ്ങള് അഥവാ ഐസോടോപ്പുകള് എന്നു പറയുന്നു. ഇന്ന് ഭൂമിയില് ഏകദേശം 284 ഐസോടോപ്പുകള് എല്ലാ മൂലകങ്ങള്ക്കുമായി ഉണ്ട്.
പ്രോട്ടോണ്, ന്യൂട്രോണ്
(Proton,Neutron).
അണുസംരചനയില് ധനചാര്ജിതമാത്രയാണ് പ്രോട്ടോണ്. ധനകിരണവിശ്ളേഷണത്തില് ഇവയെ കണ്ടെത്തിയെന്നു നേരത്തെ സൂചിപ്പിച്ചു. ഇലക്ട്രോണ് നഷ്ടപ്പെട്ട ഹൈഡ്രജന് അണുവാണ് പ്രോട്ടോണ്; അതായത് ഹൈഡ്രജന്റെ അണുകേന്ദ്രം. ഇതിന് ഇലക്ട്രോണിന്റെ 1,837 മടങ്ങ് ഭാരമുണ്ട്. ഹൈഡ്രജന് അണുക്കള് ആണ് മൂലകങ്ങളുടെ അടിസ്ഥാനം എന്ന് പ്രൌട്ട്, 1815-ല് പ്രസ്താവിച്ചിട്ടുണ്ട്. അണുസംഖ്യയും അണുഭാരവും തമ്മിലുള്ള അനുപാതം പകുതിയിലധികം മൂലകങ്ങള്ക്കും 1-ല് കുറവായതിനാല് രണ്ടു പ്രശ്നങ്ങള് ഉണ്ടായി: (1) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുഭാരത്തെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു; ചാര്ജ് തുലനപ്പെടുത്താന് ആവശ്യമായ ഇലക്ട്രോണുകള് ഉണ്ടായിരിക്കുകയും ചെയ്യും; (2) അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണം അണുസംഖ്യയെ അടിസ്ഥാനമാക്കിയിരിക്കുന്നു. ബാക്കിഭാരം ഉദാസീനവും പ്രോട്ടോണിന്റെ അത്രഭാരമുള്ളതുമായ ആവശ്യമുള്ളിടത്തോളം ഉദാസീനകണങ്ങളുടേതാണ്. 1932-ല് ജെ. ചാഡ്വിക്, അത്തരം കണങ്ങള് കണ്ടുപിടിച്ചു. വിദ്യുത്-ചാര്ജില്ലാത്ത പ്രോട്ടോണിനോളം തന്നെ ഭാരമുള്ള ഈ കണങ്ങളാണ് ന്യൂട്രോണുകള് എന്നറിയപ്പെടുന്നത്.
ദ്രവ്യമാനസംഖ്യ
(Mass Number).
ഒരു മൂലകത്തിന്റെ അണുസംഖ്യ Z-ഉം അതിന്റെ അണുകേന്ദ്രത്തില് ന്യൂട്രോണുകളുടെ എണ്ണം N-ഉം ആണെങ്കില് Z + N = A എന്ന സമീകരണത്തില് A, അണുവിന്റെ ദ്രവ്യമാനസംഖ്യയെന്നു പറയുന്നു. അണുസംഖ്യയെന്നാല് ഒരണുവിന്റെ അണുകേന്ദ്രത്തിലുള്ള പ്രോട്ടോണുകളുടെ എണ്ണമാണ്. അണുകേന്ദ്രത്തില് പ്രോട്ടോണും ന്യൂട്രോണും ഉണ്ട്. അണുകേന്ദ്രത്തിന്റെ ത്രിജ്യ 10-12 - 10-14 മീറ്ററിനുള്ളിലാണ്.
ക്വാണ്ടം സിദ്ധാന്തം
(Quantum Theory).
അണുവിനെയും അതിലെ സൂക്ഷ്മകണങ്ങളെയും പ്രതിപാദിക്കുന്ന ശാസ്ത്രശാഖയാണ് ക്വാണ്ടം ബലതന്ത്രം അഥവാ തരംഗബലതന്ത്രം (Quantum Mechanics). നിത്യജീവിതത്തില് അനുഭവമില്ലാത്ത പല പുതിയ സങ്കല്പങ്ങളും ഇതില് അടങ്ങിയിട്ടുണ്ട്.
ക്വാണ്ടം സിദ്ധാന്തത്തിന്റെ (ഇന്ന് പഴയ ക്വാണ്ടം സിദ്ധാന്തം എന്നാണ് ഇതിനെ വിളിക്കുന്നത്.) സൂത്രധാരന്മാര് പ്ളാങ്ക്, ഐന്സ്റ്റൈന്, ബോര് തുടങ്ങിയവരാണ്. 1924-ഓടുകൂടിയാണ് മൌലികപ്രാധാന്യമുള്ള പല ഭൌതികസത്യങ്ങളെയും വിശദീകരിക്കാന് ഇത് പര്യാപ്തമല്ലെന്നു കണ്ടത്. ബോര് ഇലക്ട്രോണിന്റെ സ്ഥിരഭ്രമണപഥം, സ്പെക്ട്രരേഖകളുടെ ആപേക്ഷിക തീവ്രത തുടങ്ങിയവയെപ്പറ്റിയൊന്നും പഴയ ക്വാണ്ടം സിദ്ധാന്തത്തില് പ്രതിപാദിക്കുന്നില്ല.
ദെ ബ്രോയെ (ഡി ബ്രോഗ്ളി) നിയമം
ചലിക്കുന്ന കണങ്ങള്ക്ക് തരംഗങ്ങളുടെ സ്വാഭാവികഗുണധര്മങ്ങളുണ്ടെന്ന് 1924-ല് ഡി ബ്രോഗ്ളിയെ ചൂണ്ടിക്കാട്ടി. m ദ്രവ്യമാനവും v വേഗവും (അതായത്, സംവേഗം P =mv) ഉള്ള ഒരു കണത്തിന്റെ തരംഗനീളം λ സൂചിപ്പിക്കുന്നെങ്കില്, λ-യുടെ മൂല്യം ഈ സമീകരണം കൊണ്ട് കണക്കാക്കാം: (h: പ്ളാങ്ക് സ്ഥിരാങ്കം) λ=h/mv=h/p ആണെന്ന് അദ്ദേഹം തെളിയിച്ചു. ഇതില്നിന്ന് ഇലക്ട്രോണ്, പ്രോട്ടോണ്, ന്യൂട്രോണ്, അണു, തന്മാത്ര തുടങ്ങിയവയ്ക്കെല്ലാം തരംഗഗുണധര്മങ്ങളുണ്ടെന്നുവരുന്നു - അതായത്, സൂക്ഷ്മകണങ്ങള്ക്ക് തരംഗ-കണദ്വന്ദ്വഭാവം ഉണ്ടെന്നുസാരം. ദെ ബ്രോയെയുടെ ഈ സിദ്ധാന്തം 1927-ല് ഡേവിസണ്, ജെര്മന് എന്നിവരും സര് ജി.പി. തോംപ്സണും ഇലക്ട്രോണ് വിഭംഗനംവഴി തെളിയിച്ചു.
പല സന്ദര്ഭങ്ങളിലും ഇലക്ട്രോണിന്റെ തരംഗസ്വഭാവം പ്രസക്തമല്ല; പക്ഷേ, ചില സന്ദര്ഭങ്ങളില് തരംഗസ്വഭാവം അതിപ്രധാനമാണുതാനും. ഒരു ട്രയോഡ് വാല്വിലെ (Triode valve) ആനോഡ് വിദ്യുത്ധാരയെപ്പറ്റി പ്രതിപാദിക്കുന്നിടത്ത് ഇലക്ട്രോണിനെ കണമായി പരിഗണിക്കണം; ഇലക്ട്രോണ് മൈക്രോസ്കോപ്പിലും ഇലക്ട്രോണ് വിഭംഗനത്തിലും അതിനെ തരംഗമായും.
അനിശ്ചിതത്വ തത്ത്വം
(Uncertainty Principle).
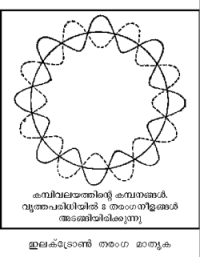
അണുസംരചനയിലെ ഇലക്ട്രോണിന് തരംഗഗുണധര്മങ്ങള് ആരോപിക്കുമ്പോള് ഇലക്ട്രോണിനെ ഒരു ബിന്ദുവായല്ല പ്രത്യുത, സ്പെയ്സില് നിശ്ചിത തരംഗനീളമുള്ള തരംഗസമൂഹം ആയിവേണം പരിഗണിക്കുവാന്. ഇതിന്റെ ഫലമോ? ഒരണുവില് ഇലക്ട്രോണിന്റെ കൃത്യസ്ഥാനം നിര്ണയിക്കാന് സാധിക്കാതെവരുന്നു. മറ്റൊരുവിധത്തില് പറഞ്ഞാല് ഇലക്ട്രോണ്, അണുകേന്ദ്രത്തില് നിന്ന് r ദൂരത്തില് സ്ഥിതിചെയ്യുന്നു എന്നു പറയുന്നതിന്നുപകരം ഇലക്ട്രോണ്, r-നും (r + dr)നും ഇടയില് ഉണ്ടെന്നു പറയേണ്ടിവരുന്നു. അതായത്, ഇലക്ട്രോണിന്റെ സ്ഥാനനിര്ണയത്തില് അനിശ്ചിതത്വം dr ഉണ്ടാകുന്നു, dr എന്നത് ദെ ബ്രോയെ തരംഗനീളത്തെയും തദ്വാരാ ഇലക്ട്രോണിന്റെ സംവേഗത്തെയും ആശ്രയിച്ചിരിക്കുന്നതിനാല്, ഈ ആശയങ്ങള് ഹൈസന്ബര്ഗിന്റെ അനിശ്ചിതത്വ തത്ത്വത്തിനു വഴിതെളിച്ചു. സ്ഥാനാന്തരണത്തിലുള്ള അനിശ്ചിതത്വം Δx-ഉം (x-അക്ഷദിശയില്) സംവേഗത്തിലുള്ള അനിശ്ചിതത്വം Δpx-ഉം ആണെങ്കില് (x-ദിശയിലുള്ള സംവേഗം), ഇവയുടെ ഗുണിതം h-നെക്കാള് വലുതോ h-നു തുല്യമോ ആകാം എന്ന് ഹൈസന്ബര്ഗ് തെളിയിച്ചു. മേല്പറഞ്ഞ പുതിയ തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തില് ഹൈഡ്രജന് അണുവിന്റെ ഘടന ഇപ്രകാരമാണ്. ബോര്സിദ്ധാന്തത്തില് അവ്യവസ്ഥിതമായാണ് ഇലക്ട്രോണിന്റെ ഭ്രമണപഥത്രിജ്യയും വേഗവും പ്രതിപാദിച്ചിട്ടുള്ളത്. ബോര് ക്വാണ്ടീകരണതത്ത്വം mvr = n h/2π ആണ്; n = 1 എങ്കില്, ഹൈഡ്രജന് അണു സാധാരണ അവസ്ഥയിലാണ്; ത്രിജ്യ r = h/2πmv -ഉം. ഡി ബ്രോഗ്ളി സിദ്ധാന്തമനുസരിച്ച് mv സംവേഗമുള്ള തരംഗത്തിന്റെ തരംഗനീളം: λ = h/mv-ഉം: അതായത് ഈ ബന്ധം ബോര്ത്രിജ്യയ്ക്കുള്ള സമീകരണത്തില് എഴുതിയാല് λ = 2 πrഎന്നു കിട്ടുന്നു. ഇതില്നിന്ന്, ഇലക്ട്രോണ് തരംഗനീളത്തിന്റെ ഗുണിതത്തോളം വൃത്തപരിധിയുള്ള ഭ്രമണപഥങ്ങളിലാണ് ഇലക്ട്രോണ് ഉണ്ടായിരിക്കുക എന്നു വരുന്നു. സ്ഥിരമായ ഭ്രമണപഥങ്ങളുണ്ടെന്നതിന് വ്യക്തമായ തെളിവാണ് ഇത്.
ആധുനിക സങ്കല്പത്തില്, ഇലക്ട്രോണ് നിശ്ചിത ഭ്രമണപഥത്തില് അണുകേന്ദ്രത്തെ ചുറ്റുന്നു എന്നല്ല പറയുന്നത്. പകരം അണുകേന്ദ്രത്തിനു ചുറ്റും സ്പെയ്സില് ഒരു സാന്ത-ഋണചാര്ജ് (finite negative charge) ഉണ്ടെന്നു സങ്കല്പിച്ചിരിക്കുന്നു. അണുകേന്ദ്രത്തിനു ചുറ്റുമുള്ള ഈ ചാര്ജ്-പടലത്തില്, അണുകേന്ദ്രത്തില്നിന്ന് ഏതു ദൂരത്തില് വേണമെങ്കിലും ഇലക്ട്രോണ് സ്ഥിതി ചെയ്യാം.ശൂന്യതാസാന്ദ്രപ്രദേശങ്ങളാല് വേര്തിരിഞ്ഞുകിടക്കുന്ന അതിസാന്ദ്രതയുടെ സ്ഥാനീകൃതമേഖലകള് എന്നതാണ് അണുവിന്റെ ആധുനിക നിര്വചനം.
അണുസംരചനയും ആവര്ത്തനപ്പട്ടികയും
മൂലകങ്ങളെ അണുസംഖ്യയുടെ ക്രമത്തില് പട്ടികയാക്കിയാല് സദൃശ ഭൌതികഗുണധര്മങ്ങളും രാസഗുണധര്മങ്ങളും ഉള്ള മൂലകങ്ങള് ക്രമാനുഗതമായ അന്തരാളങ്ങളില് ആവര്ത്തിതമാകുന്നതായി കാണാം. റഷ്യന് രസതന്ത്രജ്ഞനായ ദിമ്ത്രി മെന്ദെല്യേഫ് ഈ എംപിരികനിരീക്ഷണം 1869-ല് ആവര്ത്തനനിയമം എന്നപേരില് പ്രസിദ്ധപ്പെടുത്തി. മൂലകങ്ങളുടെ ആവര്ത്തനഗുണധര്മങ്ങളെ പ്രദര്ശിപ്പിക്കുന്ന പട്ടികയാണ് ആവര്ത്തനപ്പട്ടിക. മെന്ദെല്യേഫ്, സദൃശഗുണധര്മങ്ങളുള്ള മൂലകങ്ങളെ ഗ്രൂപ്പുകളായി തിരിച്ചു. നോ: ആവര്ത്തനപ്പട്ടിക
മെന്ദെല്യേഫിന്റെ ആശയങ്ങള്ക്ക് ആധുനിക-അണുസംരചനയുടെ വെളിച്ചത്തില് മൌലികമായ സ്ഥാനമുണ്ട്. z അണുസംഖ്യയുള്ള ഒരു അണുവിന്റെ അണുകേന്ദ്രത്തിനുചുറ്റും z ഇലക്ട്രോണുകള് ഭ്രമണം ചെയ്തുകൊണ്ടിരിക്കും. ഈ ഇലക്ട്രോണുകള് വിവിധ ഷെല്ലുകളിലും സബ്ഷെല്ലുകളിലും ആണ് ക്രമപ്പെടുത്തിയിരിക്കുന്നത്. ക്വാണ്ടം സംഖ്യ n ഉള്ള ഒരു ഷെല്ലില് ക്രമപ്പെടുത്താവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം 2n2 ആണെന്നു നേരത്തെ സൂചിപ്പിച്ചു. പരമാവധി ഇലക്ട്രോണുകളുള്ള ഒരു ഷെല്ലിനെ പൂര്ണ ഷെല് എന്നു പറയുന്നു. ഈ പൂര്ണത മൂലകത്തിന്റെ രാസസ്ഥിരതയെ കാണിക്കുന്നു. നിഷ്ക്രിയവാതകങ്ങളായ (inert gases) ഹീലിയം, നിയോണ് തുടങ്ങിയവയ്ക്ക് പൂര്ണ ഇലക്ട്രോണ് ഷെല്ലുകളാണ് ഉള്ളത്. സാമാന്യമായി ഈ മൂലകങ്ങള് രാസപ്രവര്ത്തനവ്യഗ്രത പ്രദര്ശിപ്പിക്കുന്നില്ല. ഓരോ ഷെല്ലിലും സബ്ഷെല്ലിലും ഉണ്ടാകാവുന്ന പരമാവധി ഇലക്ട്രോണുകളുടെ എണ്ണം താഴെ കൊടുക്കുന്നു:
അണുസംഖ്യ z = 11 ഉള്ള മൂലകം സോഡിയം ആണ്. സോഡിയത്തില് 11 ഇലക്ട്രോണുകള് ഉണ്ട്. മേല്കൊടുത്ത പട്ടികയില്നിന്ന് സോഡിയത്തിന് K-ഷെല്ലില് 2 ഇലക്ട്രോണും L-ഷെല്ലില് 8 ഇലക്ട്രോണും M-ഷെല്ലില് 1 ഇലക്ട്രോണും ഉണ്ടെന്ന് (11 = 2 + 8 + 1) കാണാം. സോഡിയത്തിന്റെ ബാഹ്യതമ ഷെല് M-ഷെല്ലാണ്. ഇതിലെ ഇലക്ട്രോണിനെ സംയോജക-ഇലക്ട്രോണ് (Valence electron) എന്നു പറയുന്നു. രാസസംയോഗങ്ങളില് സോഡിയത്തിന് നഷ്ടമാകുന്ന ഇലക്ട്രോണ് ഇതാണ്.
മൂലകങ്ങള് അവയുടെ ബാഹ്യതമ ഷെല്ലില് 8 ഇലക്ട്രോണുകള് നേടി ഷെല് പൂര്ത്തിയാക്കാന് ശ്രമിക്കുന്നു. ഈ ശ്രമമാണ് രാസപ്രവര്ത്തനത്തിനുള്ള പല കാരണങ്ങളില് ഒന്ന്. ബാഹ്യതമ ഷെല്ലില് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകളേ ഉള്ളുവെങ്കില് ആ ഇലക്ട്രോണുകളെ നഷ്ടപ്പെടുത്തിയും ഷെല് പൂര്ത്തിയാക്കാന് ഒന്നോ രണ്ടോ ഇലക്ട്രോണുകള് മാത്രമേ ആവശ്യമുള്ളുവെങ്കില് ഇലക്ട്രോണ് സ്വീകരിച്ചുമാണ് ബാഹ്യതമ ഷെല് പൂര്ത്തിയാക്കുന്നത് എന്ന് സാമാന്യമായി പറയാം. ഇതാണ് രാസസംയോജകതയുടെ അടിസ്ഥാനം.
മ്യുവോണ്, മെസോണ് അണുക്കള്
(Muon, Meson-Atoms).
ഭ്രമണപഥത്തില് ഇലക്ട്രോണിനുപകരം മറ്റു ചില ഋണചാര്ജിതകണങ്ങള് (മ്യുവോണുകള്, മെസോണുകള്) ഉള്ള അണുക്കള് ഉണ്ടെന്ന് കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. ഇലക്ട്രോണിന്റെ തന്നെ ചാര്ജുള്ള ഈ ഋണചാര്ജിതകണങ്ങള്ക്ക് ഇലക്ട്രോണിന്റെ പലമടങ്ങ് ഭാരമുണ്ട്. ഈ അണുക്കള്ക്ക് ഒരു അണുകേന്ദ്രവും ഭ്രമണപഥത്തില് ഒരു മ്യുവോണും (ഈ അണുവാണ് മ്യുവോണ് അണു) അല്ലെങ്കില് ഒരു മെസോണും (ഇതാണ് മെസോണ് അണു) അധികം ഉണ്ടായിരിക്കും. ഘടന ഏകദേശം ഹൈഡ്രജന് അണുവിന്റേതുപോലെയാണെങ്കിലും ഒരു പ്രധാന വ്യത്യാസം ഉണ്ട്. മ്യുവോണ് അണുവിനും മെസോണ് അണുവിനും അണുകേന്ദ്രം ഏതു വേണമെങ്കിലും ആകാം. മെസോണ് അല്ലെങ്കില് മ്യുവോണ്-ഭ്രമണപഥത്തിനുപുറമേ അണു ഉദാസീനമാകാന് വേണ്ടത്ര ഇലക്ട്രോണുകള് വിവിധ ഭ്രമണപഥങ്ങളില് ചലിക്കുന്നുണ്ടായിരിക്കും; ഈ അണുക്കള് അല്പായുസ്സുകളാണ്. അണുകേന്ദ്രം, മെസോണിനെ (അല്ലെങ്കില് മ്യുവോണിനെ) പിടിച്ചെടുക്കുന്നതോ അഥവാ മെസോണിന് (മ്യുവോണിന്) സ്വയം ക്ഷയം സംഭവിക്കുന്നതോ ആണ് ഇതിനു കാരണം. ഒരു പോസിട്രോണും ഇലക്ട്രോണും ഉള്ള പോസിട്രോണിയം അണുവും കണ്ടുപിടിക്കപ്പെട്ടിട്ടുണ്ട്. പക്ഷേ, ക്ഷണിക-അസ്തിത്വമുള്ള ഈ അണു പോസിട്രോണ്-ഇലക്ട്രോണ് സംഘട്ടനം മൂലം ഊര്ജമായി മാറുന്നു. നോ: അണുകേന്ദ്രം, അണുകേന്ദ്ര ആഘൂര്ണം, അണുകേന്ദ്രവിജ്ഞാനീയം, അണുശക്തിതേജോവശിഷ്ടങ്ങള്, റേഡിയോ ആക്റ്റിവത
(പി.എം. മധുസൂദനന്)