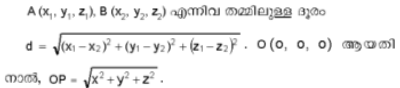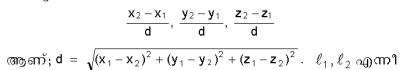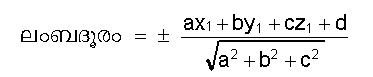This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനലിറ്റിക്കല് ജ്യോമട്രി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(New page: = അനലിറ്റിക്കല് ജ്യോമട്രി = അിമഹ്യശേരമഹ ഴലീാലൃ്യ ബീജീയസമ്പ്രദായങ്ങ...) |
|||
| (ഇടക്കുള്ള 31 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | = അനലിറ്റിക്കല് ജ്യോമട്രി = | + | = അനലിറ്റിക്കല് ജ്യോമട്രി = |
| - | + | Analytical geometry | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | ബീജീയസമ്പ്രദായങ്ങള് ഉപയോഗിച്ച് ക്ഷേത്രഗണിതത്തിലെ പ്രശ്നങ്ങള്ക്കു പരിഹാരം കണ്ടെത്തുന്ന ഗണിതശാസ്ത്ര ശാഖ. വിശ്ളേഷകജ്യാമിതി (Analytic Geometry), നിര്ദേശാങ്കജ്യാമിതി (Co-ordinate Geometry), കാര്ത്തീയജ്യാമിതി (Cartesian Geometry) എന്നീ പേരുകളിലും ഇതറിയപ്പെടുന്നു. | ||
സിറാക്കൂസിലെ ആര്ക്കിമിഡീസിന്റെയും പെര്ഗയിലെ അപ്പോളോണിയസിന്റെയും കാലഘട്ടം മുതല് ഈ ഗണിത ശാഖയെപ്പറ്റിയുള്ള ചില പരിജ്ഞാനശകലങ്ങള് പ്രചരിച്ചിരുന്നു. ഈജിപ്തുകാര്ക്ക് ഇതേപ്പറ്റി സ്ഥൂലമായ ജ്ഞാനം ഉണ്ടായിരുന്നതായി കരുതപ്പെടുന്നു. എങ്കിലും ഈ ശാസ്ത്രശാഖയ്ക്കു വികാസം സിദ്ധിച്ചത് പിയേര് ദെ ഫെര്മെ (1601-65), റെനെ ദെക്കാര്ത്ത് (1596-1650) എന്നീ ഫ്രഞ്ചു ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ കാലത്തായിരുന്നു. ഐസക് ന്യൂട്ടന് (1642-1727), ലൈബ്നിറ്റ്സ് (1646-1716) എന്നിവരും മികച്ച സംഭാവനകള് ഈ ശാഖയ്ക്കു നല്കിയിട്ടുണ്ട്. | സിറാക്കൂസിലെ ആര്ക്കിമിഡീസിന്റെയും പെര്ഗയിലെ അപ്പോളോണിയസിന്റെയും കാലഘട്ടം മുതല് ഈ ഗണിത ശാഖയെപ്പറ്റിയുള്ള ചില പരിജ്ഞാനശകലങ്ങള് പ്രചരിച്ചിരുന്നു. ഈജിപ്തുകാര്ക്ക് ഇതേപ്പറ്റി സ്ഥൂലമായ ജ്ഞാനം ഉണ്ടായിരുന്നതായി കരുതപ്പെടുന്നു. എങ്കിലും ഈ ശാസ്ത്രശാഖയ്ക്കു വികാസം സിദ്ധിച്ചത് പിയേര് ദെ ഫെര്മെ (1601-65), റെനെ ദെക്കാര്ത്ത് (1596-1650) എന്നീ ഫ്രഞ്ചു ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ കാലത്തായിരുന്നു. ഐസക് ന്യൂട്ടന് (1642-1727), ലൈബ്നിറ്റ്സ് (1646-1716) എന്നിവരും മികച്ച സംഭാവനകള് ഈ ശാഖയ്ക്കു നല്കിയിട്ടുണ്ട്. | ||
| - | + | == അക്ഷങ്ങളും നിര്ദേശാങ്കങ്ങളും == | |
| + | Axes and Co-ordinates | ||
| - | + | ഒരു സമതലത്തില് ഛ എന്നൊരു സ്ഥിരബിന്ദുവില്കൂടി രണ്ടു ലംബരേഖകള് വരയ്ക്കുക. ഈ രേഖകളെ ആധാരമാക്കി ആ സമതലത്തിലെ ഏതു ബിന്ദുവും അടയാളപ്പെടുത്താവുന്നതാണ്. ചിത്രം 1-ല് o കേന്ദ്രവും XOY', YOY' എന്നീ പരസ്പരലംബങ്ങളായ രേഖകള് നിര്ദേശാക്ഷങ്ങ(Co-ordinates axes)ളും ആണ്. 1, II, III, IV എന്ന് അടയാളപ്പെടുത്തിയിരിക്കുന്ന നാലു പ്രദേശങ്ങളായി സമതലത്തെ വിഭജിച്ചിരിക്കുന്നു. ഈ ഓരോ ഖണ്ഡത്തിനും പാദഖണ്ഡം (quadrant) എന്നു പറയുന്നു. p ഒരു സാമാന്യബിന്ദു ആണെന്നു കരുതുക; PL, X-അക്ഷത്തിലേക്കുള്ള ലംബമാണെങ്കില് OL, LP എന്നിവയുടെ നീളം X,Y, എന്നു സൂചിപ്പിക്കാം.X,Y എന്നിവ ക്രമത്തില് P-യുടെ X-നിര്ദേശാങ്കവും Y-നിര്ദേശാങ്കവുമാണ്. O-ല് നിന്നു OX ദിശയില് അളക്കുന്നതെല്ലാം ധനാത്മകവും, OX എന്ന ദിശയിലുള്ളത് ഋണാത്മകവുമായി പരിഗണിക്കപ്പെടുന്നു. അതുപോലെ OY ധനാത്മകവും, OY' ഋണാത്മകവും. ഈ സങ്കല്പങ്ങളനുസരിച്ച് ചിത്രം(1) OL,LP, എന്നിവ ധനാത്മകമാണ്. ഒന്നാം പാദഖണ്ഡത്തിലെ ബിന്ദുക്കളുടെ നിര്ദേശാങ്കങ്ങള് രണ്ടും ധനാത്മകമാണ്; രണ്ടാം പാദത്തില് X ഋണാത്മകവും Y ധനാത്മകവും; മൂന്നില് രണ്ടും ഋണാത്മകം; നാലില് X ധനാത്മകവും Y ഋണാത്മകവും. ഒരു ബിന്ദുവിന്റെ x-നിര്ദേശാങ്കത്തെ 'ആബ്സിസ' എന്നും y-നിര്ദേശാങ്കത്തെ 'ഓര്ഡിനേറ്റ്' എന്നും പറയാറുണ്ട്. p എന്ന ബിന്ദുവിനെ (x, y) എന്ന് സൂചിപ്പിക്കുന്നു. | |
| + | [[Image:p.no.453.jpg|thumb|250x250px|left|ചിത്രം1.]] | ||
| - | + | === തിര്യഗക്ഷങ്ങള് === | |
| + | Oblique axes | ||
| - | + | ലംബമല്ലാത്ത രണ്ടു നേര്വരകള് അവയുടെ സമതലത്തിലെ ബിന്ദുക്കളെ പ്രതിനിധാനം ചെയ്യാനുള്ള അക്ഷങ്ങളായി ഉപയോഗിക്കാവുന്നതാണ് (ചിത്രം 2). ഇതില് o കേന്ദ്രവും xox', yoy' അക്ഷരേഖകളുമാണ്; pഏതെങ്കിലുമൊരു സാമാന്യബിന്ദുവും. p-ല് നിന്നു yoy'നു സമാന്തരമായി ഒരു രേഖ വരച്ചാല് അത് xox' നെ L എന്ന ബിന്ദുവില് ഛേദിക്കുന്നു എന്നിരിക്കട്ടെ. എങ്കില് OL ആബ്സിസയും LP ഓര്ഡിനേറ്റുമാണ്. | |
| - | |||
| - | + | XOX എന്ന X-അക്ഷരേഖയിലുള്ള ഏതു ബിന്ദുവിന്റെയും Y-നിര്ദേശാങ്കം (y-കോടി അഥവാ ഓര്ഡിനേറ്റ്) പൂജ്യവും YOY'ലുള്ള ബിന്ദുവിന്റെ x-നിര്ദേശാങ്കം (x-കോടി അഥവാ ആബ്സിസ) പൂജ്യവുമാണ്. അതുകൊണ്ട് x-അക്ഷത്തിലെ ഏതു ബിന്ദുവും (x,o) എന്നും y-അക്ഷത്തിലെ ഏതു ബിന്ദുവും (o,y) എന്നും സൂചിപ്പിക്കാം. ഈ രണ്ടു രേഖകളുടെയും സംഗമസ്ഥാനത്തെ പ്രഭവസ്ഥാനം (initial point) എന്നു വിളിച്ചുപോരുന്നു. ആ ബിന്ദുവിനെ (o,o) എന്ന നിര്ദേശാങ്കങ്ങള്കൊണ്ടു സൂചിപ്പിക്കാം. | |
| - | + | == ബിന്ദുപഥങ്ങള് == | |
| + | Locus | ||
| - | + | അനലിറ്റിക്കല് ജ്യോമട്രി അനുസരിച്ച്, നിയതമായ ഏതു വക്രരേഖയും (ordered curve) ചില പ്രത്യേകനിയമപ്രകാരം നീങ്ങുന്ന ബിന്ദുക്കളുടെ സഞ്ചാരപഥമാണ്. നിര്ദിഷ്ടമായ നിയമങ്ങളനുസരിച്ച് തുടര്ന്നുവരുമ്പോള് ഒരു പഥം സംജാതമാകുന്നു. ഇതാണ്, സഞ്ചാരപഥമെന്നതുകൊണ്ട് ഉദ്ദേശിക്കുന്നത്. ഇവിടെ ജ്യാമിതീയ നിയമങ്ങളെ ബീജീയ വാക്യങ്ങളായി മാറ്റുന്നു. x-അക്ഷത്തില്നിന്ന് ഇരുവശത്തേക്കും നീങ്ങാത്ത ബിന്ദുക്കളുടെ പഥം XOX' എന്ന നേര്വരതന്നെ. അതുകൊണ്ട് XOX'-ന്റെ സമവാക്യം y = 0. x-അക്ഷത്തിലെ എല്ലാ ബിന്ദുക്കള്ക്കും അനുയോജ്യമായ നിയമമാണിത്. അതുപോലെ yoy'-ന്റെ സമവാക്യം X = 0. ഒരു സ്ഥിരബിന്ദു(fixed point)വില്നിന്ന് എപ്പോഴും r ദൂരത്തില് കിടക്കുന്ന ബിന്ദുക്കളുടെ ബിന്ദുപഥം ആ സ്ഥിരബിന്ദു കേന്ദ്രമാക്കിക്കൊണ്ടും, r വ്യാസാര്ധമാക്കിക്കൊണ്ടുമുള്ള വൃത്ത പരിധിയാണ്. ബിന്ദുപഥത്തിനു കൂടുതല് ഉദാഹരണങ്ങള് തുടര്ന്നു കാണാവുന്നതാണ്. | |
| - | + | [[Image:p.no.454A.jpg|thumb|250x250px|left|ചിത്രം3.]] | |
| + | [[Image:p.no.454a.jpg|thumb|250x150px|none|ചിത്രം4.]] | ||
| + | === നേര്വരകള് === | ||
| - | + | നേര്വരയെ പൊതുവായി പ്രതിനിധാനം ചെയ്യുന്നത് ഏകഘാത സമവാക്യ(first degree equation)ത്തിലൂടെയാണ്: ax + by + c = 0. ഒരു നേര്വര ഉറപ്പിക്കാന് അത്യാവശ്യമായ വ്യവസ്ഥകളെ ആധാരമാക്കിയാണ് അതിന്റെ സമവാക്യം രൂപപ്പെടുന്നത്. (1) രണ്ടു ബിന്ദുക്കള് യോജിപ്പിച്ചാല് ഒരു നേര്വരയുണ്ടാകുന്നു. (II) ഒരു ബിന്ദുവും നേര്വര X-അക്ഷവുമായുണ്ടാക്കുന്ന ചരിവുമാനവും (slope) അറിഞ്ഞാല് ഒരു നേര്വരയുണ്ടാക്കാം. (III) ചരിവുമാനവും y-അക്ഷരേഖയിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡവും (intercept) അറിഞ്ഞാല് ഒരു നേര്വരയുണ്ടാക്കാം. (iv) രേഖ x, y അക്ഷങ്ങളിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡങ്ങള് അറിഞ്ഞാല് ഒരു രേഖ വരയ്ക്കാം. സാധാരണയായി ഇത്തരത്തിലുള്ള വ്യവസ്ഥകളനുസരിച്ചാണ് നേര്വരയുണ്ടാകുന്നത്. | |
| - | + | (1) ചിത്രം 3-ല് A,B ആ എന്നീ ബിന്ദുക്കള് (x<sub>1</sub>, y<sub>1</sub>), (x<sub>2</sub>,y<sub>2</sub>) ആണ്. ഇവ യോജിപ്പിച്ചുണ്ടാവുന്ന നേര്വര(AB)യുടെ സമവാക്യം നിര്ണയിക്കാം. p(x,y) രേഖയിലുള്ള ഒരു സാമാന്യ ബിന്ദുവാണെങ്കില് AP,AB എന്നീ രേഖകള് ഒരേ നേര്വരയിലായതിനാല് ചരിവുമാനങ്ങള് തുല്യമായിരിക്കും. അതായത് . AC/PC = AD/BD ഇതില്നിന്നു | |
| - | + | y-y<sub>1</sub> / x- x<sub>1</sub> = y<sub>1</sub> - y | |
| + | <sub>2</sub>/x<sub>1</sub> - x<sub>2</sub> | ||
| + | എന്നു സിദ്ധിക്കുന്നു. അതായത്, | ||
| - | + | [[Image:p478.png]] | |
| - | + | (ii) A(x<sub>1</sub>,y<sub>1</sub>) എന്ന ബിന്ദുവിലൂടെ കടക്കുന്നതും mചരിവുമാനം ഉള്ളതുമായ നേര്വരയുടെ സമവാക്യം എന്നു സിദ്ധിക്കുന്നു. (1)-ല് ചരിവുമാനമാണ്. ചരിവുകോണ് ø ആണെങ്കില് tanø ആണ് ചരിവുമാനം. | |
| - | + | (iii) ചരിവുമാനം m-ഉം രേഖ y-അക്ഷത്തില് ഉണ്ടാക്കുന്ന ഖണ്ഡം കേന്ദ്രത്തില്നിന്ന് അളക്കുമ്പോള് c-യുമാണെങ്കില്, രേഖ വരയ്ക്കാന് കഴിയും. ചിത്രം 5 നോക്കിയാല് p(x,y) രേഖയിലെ ഒരു സാമാന്യബിന്ദുവും OQ = c ഛേദഖണ്ഡവും øചരിവുകോണുമാണെന്നും കാണാം. എങ്കില് m = tanø = PN/QN; അതായത് | |
| - | + | PN =m.QN. ഇതില്നിന്നു y =mx + c എന്നു സിദ്ധിക്കുന്നു. PQ എന്ന രേഖയുടെ സമവാക്യമാണിത്. | |
| - | + | (iv) ചിത്രം 6 പരിശോധിച്ചാല് a, b എന്നിവ, അക്ഷങ്ങളിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡങ്ങളും p(x,y) ഒരു സാമാന്യബിന്ദുവുമാണെന്നു മനസ്സിലാക്കാം. ത്രികോണങ്ങളുടെ ജ്യാമിതീയ സവിശേഷതയനുസരിച്ച് AM/AO = MP/OB ആണ്. ഇതില്നിന്നു a-x/a = y/b എന്നു സിദ്ധിക്കുന്നു. അതായത് x/a + y/b = 1 | |
| - | |||
| - | + | (V) (ചിത്രം 7). കേന്ദ്രത്തില്നിന്നു AB എന്ന ഋജുരേഖയിലേക്കുള്ള ലംബത്തി(OM)ന്റെ നീളം p-ഉം OM x-അക്ഷവുമായുണ്ടാക്കുന്ന കോണം α-യുമാണ്. എങ്കില് AB-യുടെ സമവാക്യം | |
| - | + | x cosα + y sinα = p ആയിരിക്കും. | |
| - | |||
| - | + | മേല്പറഞ്ഞ സമവാക്യരൂപങ്ങളില്നിന്നു മനസ്സിലാക്കാവുന്നത്, നേര്വരയുടെ സമവാക്യം ഏകഘാതസമവാക്യമായിരിക്കുമെന്നതാണ്. അതായത്, ax + by + c = 0 രണ്ടു നേര്വരകള്ക്കിടയിലുള്ള കോണം ø ആണെങ്കില് താഴെ കാണുന്നവിധം കണക്കാക്കാന് കഴിയും: (m1 > m2) | |
| - | + | tan ø = m<sub>1</sub> - m<sub>2</sub> / 1+m<sub>1</sub> | |
| + | m<sub>2</sub> | ||
| - | + | ഇവിടെ m<sub>1</sub>,m<sub>2</sub> എന്നിവ, രേഖകളുടെ ചരിവുമാനമാണ്. രേഖകള് സമാന്തരമാണെങ്കില്,m<sub>1</sub>= m<sub>2</sub>; ലംബമാണെങ്കില് | |
| + | m<sub>1</sub>m<sub>2</sub> = -1. | ||
| - | + | [[Image:p478b.png]] | |
| + | == ദ്വിഘാത സമവാക്യങ്ങള് == | ||
| + | Second degree equations in x,y | ||
| - | + | പൊതുവായ ദ്വിഘാതസമവാക്യമാണ് ax<sup>2</sup> + 2hxy + by<sup>2</sup> + 2gx + 2fy + c = 0 ചില വ്യവസ്ഥകളനുസരിച്ച് ഈ വാക്യം ഒരു ജോടി നേര്രേഖകളെയോ ഒരു വൃത്തത്തെയോ മറ്റു കോണികഖണ്ഡങ്ങ(conic sections)ളെയോ പ്രതിനിധാനം ചെയ്യുന്നതാണ്. രണ്ടു ഏകഘാതവാക്യങ്ങളുടെ ഗുണിതമാണ് ഇതിലെ വാക്യമെങ്കില് ആ വാക്യം രണ്ടു നേര്വരകളെ കുറിക്കുന്നു. ഈ വ്യവസ്ഥ നിര്ണയിക്കാന് കഴിയും. abc + 2fgh- af<sup> | |
| + | 2</sup>- bg<sup>2</sup>- ch<sup>2</sup> = 0 എന്നതാണ് ഈ വ്യവസ്ഥ. x<sup>2</sup>,y<sup>2</sup> എന്നിവയുടെ ഗുണനാങ്കങ്ങള് തുല്യമായിരിക്കയും, xyയുടെ ഗുണനാങ്കം പൂജ്യമായിരിക്കുകയുമാണെങ്കില്, അതായത് ax<sup>2</sup> + ay<sup>2</sup> + 2gx + 2fy + c = 0, ഒരു വൃത്തത്തിന്റെ സമവാക്യമുണ്ടാകുന്നു. | ||
| + | x<sup>2</sup>+y<sup>2</sup>+2gx+2fy+c=0, | ||
| - | + | x<sup>2</sup>/a<sup>2</sup> + y<sup>2</sup> / b<sup>2</sup> = 1 | |
| + | y<sup>2</sup> = 4ax,x<sup>2</sup>/a<sup>2</sup> - y<sup>2</sup> | ||
| + | /b<sup>2</sup> =1 | ||
| - | + | എന്നീ പ്രത്യേക സമവാക്യ രൂപങ്ങള് വൃത്തം, ദീര്ഘവൃത്തം (ellipse), പരവളയം (parabola), ബഹിര്വളയം (hyperbola) എന്നിവയെ സൂചിപ്പിക്കുന്നു. നിര്ദിഷ്ടാങ്കrപദ്ധതിയിലെ കേന്ദ്രം വൃത്തകേന്ദ്രമായും r വ്യാസാര്ധമായും ഉള്ള വൃത്തത്തിന്റെ സമവാക്യം ചിത്രം 8-ല് നിന്നു കണക്കാക്കാം: x<sup>2</sup> + y<sup>2</sup> = | |
| + | r<sup>2</sup>. | ||
| - | + | === ദൂരം === | |
| + | Distance | ||
| - | + | A (x<sub>1</sub>,y<sub>1</sub>), B (x<sub>2</sub>, y<sub>2</sub>) എന്നീ രണ്ടു ബിന്ദുക്കള് തമ്മിലുള്ള ദൂരം പിത്തഗറസ്തത്ത്വം ഉപയോഗിച്ച് കണ്ടെത്താന് കഴിയും. ചിത്രം 9-ല് ACB ഒരു മട്ടത്രികോണമാണ്. BC<sup>2</sup> + AC<sup>2</sup> = AB | |
| + | <sup>2</sup>. ഇതില്നിന്നു, AB=√(x<sub>1</sub> - x<sub> | ||
| + | 2</sub>)<sup>2</sup>+(y<sub>1</sub>-y<sub>2</sub>)<sup>2</sup> എന്നു നിര്ണയിക്കാം. ഇതില് B കേന്ദ്രത്തില് തന്നെയാണെങ്കില് BA, അതായത് OA=√x<sub>1</sub><sup>2</sup>+y<sub>1</sub><sup>2</sup>എന്നു കാണാം. (x<sub>1</sub>,y<sub>1</sub>)ല് നിന്നു ax + by + c = 0 എന്ന നേര്വരയിലേക്കു വരയ്ക്കുന്ന ലംബത്തിന്റെ നീളം, | ||
| - | + | x cos α+y sin α=p എന്ന സമവാക്യത്തോട് ax + by + c = 0 താരതമ്യപ്പെടുത്തിയാല് കിട്ടുന്നതാണ്: | |
| + | [[Image:p479bb.png]] | ||
| + | കേന്ദ്രത്തില്നിന്നുള്ള ദൂരം താഴെ കാണുന്നവിധം ആണ് എന്നു മനസ്സിലാക്കാം. (കേന്ദ്രം:x1 = 0, y1 = 0) | ||
| - | + | p=+- ax<sub>1</sub>+by<sub>1</sub>+c/√a<sup>2</sup> | |
| + | +b<sup>2</sup> | ||
| - | + | === വിസ്തീര്ണം === | |
| + | Area | ||
| - | + | A (x<sub>1</sub>,y<sub>1</sub>), B (x<sub>2</sub>, y<sub>2</sub>), C (x<sub>3</sub>,y<sub>3</sub>) എന്നീ ബിന്ദുക്കള് ശീര്ഷ(vertices)ങ്ങളായുള്ള ത്രികോണത്തിന്റെ വിസ്തീര്ണം കാണുന്നത്, ഈ ബിന്ദുക്കളില് നിന്നും X-അക്ഷത്തിലേക്ക് ലംബം വരച്ച് ദ്വിവശസമാന്തര ചതുര്ഭുജങ്ങളുടെ (trapezium) വിസ്തീര്ണങ്ങള് നിര്ണയിച്ചാണ് (ചിത്രം 10); വിസ്തീര്ണത്തിനു Δഎന്ന ചിഹ്നമാണ് ഉപയോഗിക്കുന്നത്. | |
| - | |||
| - | + | മൂന്നു ബിന്ദുക്കള് ഈരണ്ടെണ്ണം നേര്വരകൊണ്ടു യോജിപ്പിച്ചുണ്ടാകുന്ന ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യം ആണെങ്കില് ആ മൂന്നു ബിന്ദുക്കളും ഒരേ നേര്വരയിലാണെന്ന് അതില് നിന്നു മനസ്സിലാക്കാം. | |
| - | |||
| + | == ധ്രുവാങ്ക പദ്ധതി == | ||
| + | Pollar Co-ordinate System | ||
| - | + | ഇതുവരെ പ്രതിപാദിച്ച കാര്ത്തീയ നിര്ദേശാങ്കപദ്ധതി പോലെ തന്നെ പ്രയോജനകരമായ മറ്റൊരു പദ്ധതിയാണിത്. ഒരു സ്ഥിരബിന്ദുവും അതില് നിന്നുള്ള ഒരു സ്ഥിര നേര്വരയും അടിസ്ഥാനപ്പെടുത്തി പ്രതലത്തിലെ ബിന്ദുക്കള് നിര്ണയിക്കുന്ന സമ്പ്രദായമാണിത്. ചിത്രം 11-ല് o സ്ഥിരബിന്ദുവും ox സ്ഥിരരേഖയും ആണ്. p എന്ന ഒരു ബിന്ദുവിന്റെ ധ്രുവാങ്കങ്ങള് നിര്ണയിക്കുന്നത് op എന്ന ത്രിജ്യരേഖ(radius vector)യുടെ നീളം r-ഉം OX-ല് നിന്ന് സമതലത്തിലൂടെ O കേന്ദ്രമാക്കി അപ്രദക്ഷിണമായി (anticlock-wise) തിരിയുമ്പോള് op ഉണ്ടാക്കുന്ന e എന്ന കോണവും ഉപയോഗിച്ചാണ്. ഇവിടെ r ,ø ഇവ ആണ് p-യുടെ ധ്രുവാങ്കങ്ങള്. p എന്ന ബിന്ദുവിനെ (r,ø) എന്നു രേഖപ്പെടുത്താം. | |
| + | [[Image:p480a.png]] | ||
| + | സമ്മിശ്ര സംഖ്യകളെ (Complex numbers) വിശ്ളേഷകജ്യാമിതിയില് അവതരിപ്പിക്കാന് ധ്രുവാങ്കങ്ങള് ഉപയോഗപ്പെടുത്തുന്നു. x + iy-യുടെ ആംപ്ളിറ്റ്യൂഡ് ø,r=+√x<sup>2</sup>+y<sup>2</sup> മോഡുലസ് എന്നിവ (r,ø) എന്ന ബിന്ദുവായി അങ്കനം ചെയ്യുന്നു. (r,ø) എന്നതു (r,ø+2nπ + 2nII ആയും എഴുതാം. നോ: സമ്മിശ്ര സംഖ്യ | ||
| - | |||
| - | + | === അക്ഷ രൂപാന്തരണം === | |
| + | Transformation of axes | ||
| + | (i) കേന്ദ്രം o-യില്നിന്നു o'-യിലേക്കും ആധാരരേഖകള് x, oy എന്നിവയ്ക്കു സമാന്തരമായി o'x, o'y (ലംബം) എന്നിവയിലേക്കും മാറ്റിയാല്, പുതിയ ആധാരരേഖകളെ അപേക്ഷിച്ച് നിര്ദിഷ്ടാങ്കങ്ങള് നിര്ണയിക്കാം. p എന്ന ബിന്ദു x-,y- അക്ഷങ്ങളെ ആധാരമാക്കി (x,y) x -, y- എന്നിവയെ ആസ്പദമാക്കി (x,y) യും ആണെങ്കില്, ചിത്രം 12-ല് നിന്ന്, x = X + h, y = Y + K എന്നു സിദ്ധിക്കുന്നു. അതായത് X = x-h, Y =y-k. ഇവിടെx-, y- അക്ഷങ്ങളെ അപേക്ഷിച്ചുള്ള കോടികളാണ് (h, k). | ||
| - | + | (ii) O കേന്ദ്രമാക്കി അക്ഷങ്ങളെ αകോണിലൂടെ തിരിച്ചും അക്ഷങ്ങളുടെ രൂപാന്തരണം സാധിക്കാം (ചിത്രം 13). p-യുടെ ധ്രുവാങ്കങ്ങള് (r,ø) ആയിരുന്നെങ്കില് ഇതനുസരിച്ച് (r,ø+α) ആയിത്തീരും. അങ്ങനെx =r cos ø,y=r sin ø എന്നിവയുപയോഗിച്ച് X= r cos(ø+α),Y=r sin (ø+α) എന്നു സിദ്ധിക്കുന്നു. അതായത്, X = r cosøcos | |
| + | α -ysinα | ||
| - | + | Y = r sinøcos α + r cosø sin α =x sinα +y cos α | |
| + | == വിസ്തീര്ണ കോടികള് == | ||
| + | Arieal Co-ordinates | ||
| + | ഒരു ത്രികോണത്തെ ആധാരമാക്കി കോടികള് നിര്ണയിക്കുന്ന സമ്പ്രദായമാണിത്. p എന്ന സാമാന്യബിന്ദുവിന്റെ കോടികള് ΔBPC,ΔCPA,ΔAPB എന്നീ വിസ്തീര്ണങ്ങളുടെ അനുപാതത്തിലായിരിക്കും. അതായത് t1, t2, t3 ആണ് കോടികളെങ്കില് | ||
| + | t<sub>1</sub>: t<sub>2</sub> :t<sub>3</sub> = ΔBPC :ΔCPA :ΔAPB ഇവയ്ക്ക് p-യുടെ ബേരികേന്ദ്രീയ കോടികളെന്നും (Bary-centric co-ordinates) പറയുന്നു. ഇവിടെ t<sub>1</sub> + t<sub>2</sub> + t<sub>3</sub> = 1 എന്നാകുന്ന വിധത്തിലാണെങ്കില് ഇവയെ വിസ്തീര്ണ കോടികള് എന്നു പറയാം. | ||
| - | |||
| + | == കോണിക ഖണ്ഡങ്ങള് == | ||
| + | Conic Sections | ||
| - | + | ഇരുഭാഗത്തേക്കും നീണ്ടുകിടക്കുന്ന (ചിത്രം 14) കോണിന്റെ (Cone) പ്രത്യേക ഖണ്ഡങ്ങളുടെ പഠനം വിശ്ളേഷകജ്യാമിതിയില് സുപ്രധാനമാണ്. കോണിന്റെ അക്ഷത്തോടു ചേര്ത്ത് കോണിനെ ഒരു സമതലംകൊണ്ടു ഛേദിക്കുകയാണെങ്കില് ബാഹ്യമായി കാണുന്ന പരിച്ഛേദം (cross section) രണ്ടു ഋജുരേഖകളായിരിക്കും. അക്ഷത്തിനു ലംബമായി ഖണ്ഡിക്കുമ്പോള് പരിച്ഛേദം വൃത്താകാരവും ചരിവു വശത്തിനു സമാന്തരമായിട്ടാണെങ്കില് പരവളയവും സമാന്തരമല്ലാതെയാണെങ്കില് ദീര്ഘവൃത്തവും രണ്ടു ഭാഗത്തെ അക്ഷത്തിനു സമാന്തരമായി ഖണ്ഡിക്കുമ്പോള് ബഹിര്വളയവും ഉണ്ടാകുന്നു. | |
| - | |||
| - | + | കോണിക(conic)ത്തെ സാമാന്യമായി ഇങ്ങനെയാണ് നിര്വചിച്ചിരിക്കുന്നത്: s ഒരു സ്ഥിരബിന്ദുവും d ഒരു സ്ഥിര ഋജുരേഖയുമാണെന്നു സങ്കല്പിക്കുക; p കോണികത്തിലെ ഏതെങ്കിലുമൊരു സാമാന്യബിന്ദുവും; p-ല് നിന്നു d-യിലേക്കുള്ള ദൂരം PM . എങ്കില് SP/PM =e (e ഏതെങ്കിലുമൊരു സംഖ്യയാകാം). e ക്ളിപ്തമായിരിക്കുന്നവിധം p ചലിക്കുമ്പോഴുണ്ടാകുന്ന ബിന്ദുപദമാണ് കോണികം; e കോണികത്തിന്റെ ഉത്കേന്ദ്രതയും (eccentricity). eയുടെ മൂല്യം 1 ആകുമ്പോള് കോണികം ഒരു പരവളയവും e യുടെ മൂല്യം 1-ല് കുറവാകുമ്പോള് ദീര്ഘവൃത്തവും e യുടെ മൂല്യം 1-ല് കൂടുതല് ആകുമ്പോള് ബഹിര്വളയവും ആയിരിക്കും (ചിത്രം 15). | |
| - | + | === വൃത്തം === | |
| + | Circle | ||
| - | + | x<sup>2</sup> + y<sup>2</sup> + 2gx + 2fy + c = 0 ആണ് ഒരു സാധാരണ വൃത്തത്തിന്റെ സമവാക്യം. ഈ വൃത്തത്തിന്റെ കേന്ദ്രവും വ്യാസാര്ധവും കാണാന് സമവാക്യത്തെ (x + g)<sup>2</sup> +(y + f)<sup>2</sup>= √g<sup>2</sup>+f<sup>2</sup>-c)<sup>2</sup> എന്നാക്കിയാല് മതി. കേന്ദ്രം (-g,-f)-ഉം വ്യാസാര്ധം √g<sup>2</sup> | |
| + | +f<sup>2</sup>-cയുമാണ്. വൃത്തത്തിന്മേലുള്ള ഏതു ബിന്ദുവിനേയും പ്രാചല(parameter)ത്തിലൂടെ കാണിക്കാന് കഴിയും. x<sup>2</sup> + y<sup>2</sup> = r<sup>2</sup> എന്ന വൃത്തത്തിന്മേലുള്ള ഏതു ബിന്ദു | ||
| + | വും x = r cos ø, y= r sin ø എന്ന പ്രാചലപ്രതിനിധാനം വഴി സൂചിപ്പിക്കാം. | ||
| - | + | === പരവളയം === | |
| + | Parabola | ||
| + | കോണികത്തിന്റെ പൊതു തത്ത്വമനുസരിച്ച്, ചിത്രം (16)-ല് നിന്നു SP = PM. p(x,y) ഇവിടെ പരവളയത്തിന്മേലുള്ള സാമാന്യ ബിന്ദുവാണ്. s-ല് കൂടി d-ക്കു ലംബം വരച്ച് അത് x-അക്ഷമായി എടുക്കുകയും SZ (= 2a)-ന്റെ മധ്യബിന്ദു o കേന്ദ്രമായും o-ല് കൂടി ox-നു വരയ്ക്കുന്ന ലംബം y-അക്ഷമായും എടുക്കുകയാണെങ്കില്, s (a, o)-ഉം PM = x+a യുമാണെന്നുകാണാം. SP = PM-ല് നിന്നു Y2 = 4 ax എന്നു സിദ്ധിക്കുന്നു. S-ല് കൂടി അക്ഷത്തിനുള്ള ലംബഖണ്ഡമാണ് LSL' . LSL' = 4a. S പരവളയത്തിന്റെ അഭികേന്ദ്ര(focus)വും d നിയന്ത്രണരേഖ(directrix)യുമാണ്. | ||
| + | === ദീര്ഘവൃത്തം === | ||
| + | Ellipse | ||
| - | + | CA, CB എന്നിവയാണ് അക്ഷങ്ങള്; C കേന്ദ്രവും. (ചിത്രം 17) CA = a എന്നെടുത്താല് CS = ae, CZ = a/e എന്നിവ നിര്ണയിക്കാം. ഇവിടെ e ദീര്ഘവൃത്തത്തിന്റെ ഉത്കേന്ദ്രതയാണ്. ഒന്നിനെക്കാള് ചെറുതായിരിക്കും e. SP = e PM ഉപയോഗിച്ചാല് | |
| + | x<sup>2</sup>/a<sup>2</sup> + y<sup>2</sup>/b<sup>2</sup> =1, | ||
| + | b<sup>2</sup>=a<sup>2</sup>(1-e<sup>2</sup>) | ||
| - | + | എന്നു ദീര്ഘവൃത്തത്തിന്റെ സമവാക്യം ഉണ്ടാകുന്നു. b = a ആയാല് ദീര്ഘവൃത്തം വൃത്തമായി മാറും. | |
| + | === ബഹിര്വളയം === | ||
| + | Hyperbola | ||
| - | + | ചിത്രം 18-ല് ചിത്രം (17)-ലെ നിര്ദിഷ്ടാങ്കപദ്ധതിതന്നെ. A, A' എന്നീ ബിന്ദുക്കള് ബഹിര്വളയത്തിലെ ബിന്ദുക്കളാണെന്നു കരുതുക. AA' = 2a എന്നെടുത്ത് അതിന്റെ മധ്യബിന്ദു C കേന്ദ്രമായും C യിലൂടെയുള്ള ലംബം CY എന്നത് Y-അക്ഷമായും സ്വീകരിക്കുക. CA = a, CZ = a/e, CS = ae. ഇവിടെ ഉത്കേന്ദ്രത e ഒന്നിനേക്കാള് വലുതായിരിക്കും. P(x,y) ബഹിര്വളയത്തിലെ ഒരു സാമാന്യ ബിന്ദുവാണ് SP = e PM ഉപയോഗിച്ചാല് | |
| + | x<sup>2</sup>/a<sup>2</sup> - y<sup>2</sup>/b<sup>2</sup> = 1 | ||
| + | b<sup>2</sup> = a<sup>2</sup>(e<sup>2</sup>-1) | ||
| + | |||
| + | എന്ന സമവാക്യങ്ങള് സിദ്ധിക്കുന്നു. | ||
| - | + | x = at<sup>2</sup>, y = 2 at പരവളയത്തിന്റെയും x = a cos ø, y= b sin ø ദീീര്ഘവൃത്തത്തിന്റെയും x = a sec ø, y = b tan ø, ബഹിര്വളയത്തിന്റേയും പ്രാചലപ്രതിനിധാനങ്ങളാണ്. | |
| - | + | ജ്യാവ് (chord), സ്പര്ശകം (tangent) എന്നിങ്ങനെയുള്ള മറ്റു പ്രമേയങ്ങളും വിശ്ളേഷക ജ്യാമിതിയില് പ്രതിപാദിക്കപ്പെടുന്നു. | |
| - | + | == ത്രിമാന പദ്ധതി == | |
| - | + | Three Dimensional System | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ഭൌതിക സ്വഭാവമുള്ള ഏതു വസ്തുവിനും മൂന്നു അളവുകളുണ്ട്: നീളം, വീതി, കനം. ഇവയെ ആസ്പദമാക്കിയുള്ള പദ്ധതിയാണിത്. ദ്വിമാനപദ്ധതിയുടെ ഒരു വിപുലീകരണം മാത്രമാണിത്. | |
| - | + | പരസ്പരം ലംബങ്ങളായ മൂന്നു ഋജുരേഖകള് O എന്ന ബിന്ദുവില് കൂട്ടിമുട്ടുന്നു (ചിത്രം 19). XOX', YOY', ZOZ' എന്നിവയാണ് അക്ഷങ്ങള്; O കേന്ദ്രവും. XOY, YOZ, ZOX എന്നീ മൂന്നു സമതലങ്ങള് ഈരണ്ടെണ്ണം യോജിക്കുന്ന രേഖകളാണ് OX, OY, OZ എന്നീ അക്ഷങ്ങള്. p എന്നൊരു സാമാന്യ ബിന്ദുവിന്റെ നിര്ദിഷ്ടാങ്കങ്ങള് കണ്ടുപിടിക്കാന് p-ല് നിന്നു XOY തലത്തിലേക്കു ലംബം വരയ്ക്കുന്നു. M ലംബത്തിന്റെ പാദമാണ്. M-ല് നിന്നു XOX' ലേക്കു ലംബം MN വരയ്ക്കുക. എങ്കില് ON, NM, MP എന്നിവ, ദിശകള് കൂടി കണക്കിലെടുത്തുകൊണ്ട് x, y, z എന്ന ക്രമത്തില് p-യുടെ അങ്കങ്ങളാണെന്നു പറയുന്നു. | |
| - | + | [[Image:p481A.png]] | |
| - | + | === ദിശാകോണുകളും ദിശാകൊസൈനുകളും === | |
| + | Direction angles and Direction cosines | ||
| - | + | === ദിശാകോണുകളും ദിശാകൊസൈനുകളും === | |
| + | Direction angles and Direction cosines | ||
| - | + | lഒരു സാമാന്യ ഋജുരേഖയും l<sup>1</sup>ഈരേഖയ്ക്കു സമാന്തരമായി കേന്ദ്രത്തിലൂടെയുള്ള രേഖയും αβγഎന്നിവ OX, OY, OZ എന്നീ അക്ഷരേഖകളുമായി l<sup>1</sup>ഉണ്ടാക്കുന്ന കോണുകളുമാണെന്നു സങ്കല്പിക്കുക.എങ്കില്αβ&gama;എന്നിവ l-ന്റെ ദിശാകോണുകളും cosα, cosβcos&gama;ദിശാകൊസൈനുകളുമാണ്.cos<sup>2</sup>α, cos<sup>2</sup>βB,cos<sup>2</sup>γ=1എന്നു തെളിയിക്കാന് കഴിയും.y2+u2=1 ആയിരിക്കുന്ന വിധത്തിലുള്ള ഏതു സംഖ്യകളും ^,u,yക്ലുപ്തദിശയിലുള്ള ഏതു ഋജുരേഖയുടേയും ദിശാകൊസൈനുകളായിരിക്കും. ദിശാകൊസൈനുകള്ക്ക് ആനുപാതികമായിട്ടുള്ള a, b, c സംഖ്യകളെ ദിശാസംഖ്യകളെന്നു പറയുന്നു. x<sub>2</sub>-x<sub>1</sub>, y<sub>2</sub>-y<sub>1</sub>, z<sub>2</sub>-z<sub>1</sub> എന്നിവ AB ഋജുരേഖയുടെ ദിശാസംഖ്യകളാണ്. AB യിലെ ഒരു ബിന്ദുവാണ് p(x,y) എങ്കില് AP-ക്കും PB-ക്കും ദിശാസംഖ്യകള് ഒരേ അനുപാതത്തിലായിരിക്കും. അതായത് x<sub>1</sub>-x = k (x<sub>2</sub>-x<sub>1</sub>),y<sub>1</sub>-y = k (y<sub>2</sub>-y<sub>1</sub>), z<sub>1</sub>-z = k (z<sub>2</sub> - z<sub>1</sub>). ഇതില് k ഒരു വാസ്തവിക സംഖ്യയാണ്. AB യുടെ ദിശാസംഖ്യകള് | |
| - | + | [[Image:p481B.png]] | |
| + | ആണ്;d = √(x<sub>1</sub>-x<sub>2</sub>)2+(y<sub>1</sub>-y<sub>2</sub> | ||
| + | )<sup>2</sup>+(z<sub>1</sub>-z<sub>2</sub>)<sup>2</sup> | ||
| + | .l<sub>1</sub>,l<sub>2</sub> എന്നീ ഋജുരേഖകള് തമ്മിലുള്ള കോണ്യും അവയുടെ ദിശാകൊസൈനുകള് cos α<sub>1</sub> cosβ<sub>1</sub> | ||
| + | cosγ<sub>1</sub> cos α<sub>2</sub> cosβ<sub>2</sub>cosγ<sub>2</sub>എന്നിവയുമാണെങ്കില് | ||
| + | cosø=cosα<sub>1</sub>cosα<sub>2</sub>+ | ||
| + | cosβ<sub>1</sub>cosβ<sub>2</sub>+cosγ<sub>1</sub> | ||
| + | cosγ<sub>2</sub>ആയിരിക്കും. ക്രമത്തില് a<sub>1</sub>, b<sub>1</sub>, c<sub>1</sub>; a<sub>2</sub>, b<sub>2</sub>, c | ||
| + | <sub>2</sub> എന്നിവ രണ്ടു ലംബരേഖകളുടെ ദിശാസംഖ്യകളെങ്കില്, a<sub>1</sub> | ||
| + | a<sub>2</sub> + b<sub>1</sub> b<sub>2</sub> + c<sub>1</sub> | ||
| + | c<sub>2</sub> = 0 ആകുന്നു. | ||
| + | ''' | ||
| + | === തലങ്ങളും സമവാക്യങ്ങളും === | ||
| + | Surfaces and Equations | ||
| - | + | ചിത്രം 20-ല്, π ഒരു സമതലം; l π-ക്കു ലംബരേഖ; a, b, c l-ന്റെ ദിശാസംഖ്യകള്; A(x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>) l ന്റെ പാദം;B(x,y,z) π -ലുള്ള മറ്റൊരു ബിന്ദു. ഇതില് BAയും l രേഖയും ലംബമാണ്. അതുകൊണ്ട് | |
| - | |||
| - | + | a(x<sub>1</sub>-x) + b(y<sub>1</sub>-y) + c(z<sub>1</sub>-z) = 0. ഏതെങ്കിലുമൊരു സമതലവുമായി ഇങ്ങനെ ബന്ധപ്പെട്ട ഒരു ഏകഘാത സമവാക്യമുണ്ടായിരിക്കും. അതായത് ax + by + cz + d = 0 എന്ന ഏകഘാതസമവാക്യത്തെ A(x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>) എന്നൊരു ബിന്ദു 'തൃപ്തിപ്പെടുത്തു'മെങ്കില്, ഈ ബിന്ദുവിലൂടെ കടന്നുപോകുന്നതും a, b, c എന്നിവ ദിശാസംഖ്യകളുള്ള ഋജുരേഖയ്ക്കു ലംബവുമായ സമതലത്തിന്റെ സമവാക്യം. a(x-x<sub>1</sub>) + b(y-y<sub>1</sub>) + c(z-z<sub>1</sub>) = 0 ആയിരിക്കും. yoz,zox,xoyഛദ, ദഛത, തഛഥ എന്നീ സമതലങ്ങളുടെ സമവാക്യങ്ങള് ക്രമത്തില് x=o,z=o = 0, എന്നിവയാണ്. | |
| - | + | === ലംബീയ ദൂരം === | |
| + | Perpendicular Distance | ||
| - | + | A(x<sub>1</sub>,y<sub>1</sub>,z<sub>1</sub>)-ല് നിന്നു ax + by + cz + d = 0 എന്ന സമതലത്തിലേക്കുള്ള | |
| - | + | [[Image:p481C.png]] | |
| + | |||
| + | a<sub>1</sub>x+ b<sub>1</sub>y +c<sub>1</sub>z + d<sub>1</sub> = 0, a<sub>2</sub>x + b<sub>2</sub> + y<sub>2</sub> + d<sub>2</sub> = 0 എന്നീ സമതലങ്ങള് സമാന്തരമാണെങ്കില്, | ||
| + | a<sub>1</sub>, b<sub>1</sub>, c<sub>1</sub>; a<sub>2</sub>, | ||
| + | b<sub>2</sub>, c<sub>2</sub> എന്നിവ ക്രമത്തില് അനുപാതത്തിലായിരിക്കും. ലംബമാണെങ്കില്, a<sub>1</sub>a<sub>2</sub> + b<sub>1</sub>b<sub>2</sub> + c<sub>1</sub>c<sub>2</sub>= 0. ഒരേ രേഖയിലല്ലാത്ത മൂന്നു ബിന്ദുക്കള് A(x<sub>i</sub>,y<sub>i</sub>,z<sub>i</sub>), | ||
| - | + | i = 1,2,3 ഒരു സമതലം സൃഷ്ടിക്കുന്നു. ആ സമതലത്തിന്റെ സമവാക്യം: | |
| - | + | [[Image:p481d.png]] | |
| + | a<sub>i</sub> x + b<sub>i</sub>,y + c<sub>i</sub>z + d = 0, i = 1, 2, 3; എന്നീ 3 സമതലങ്ങള് ഒരേ ബിന്ദുവിലൂടെ കടന്നുപോകുന്നുവെന്നതിനുള്ള വ്യവസ്ഥ. | ||
| + | [[Image:p481e.png]] | ||
| - | |||
| + | f(x, y, z) = 0 എന്നൊരു സമവാക്യത്തെ തൃപ്തിപ്പെടുത്തുന്ന ബിന്ദുക്കളുടെ ബിന്ദുപഥത്തെ പ്രതലം (surface) എന്നു പറയുന്നു. വക്രരേഖകളുണ്ടാകുന്നതു രണ്ടു തലങ്ങള് കൂട്ടിമുട്ടുമ്പോഴാണ്. അതുകൊണ്ട് f<sub>1</sub>(x1, y1 z) = 0, f<sub>2</sub> (x, y, z) = 0 എന്നിവ ചേര്ന്ന് ആ വക്രരേഖകളെ പ്രതിനിധാനം ചെയ്യുന്നു; പ്രാചലം (t) ഉപയോഗിച്ചും വക്രരേഖകളെ പ്രതിനിധാനം ചെയ്യാം: | ||
| + | x = f(t), y = g(t), z = h(t). | ||
| - | + | === ഗോള പ്രതലം === | |
| + | Spherical Surface | ||
| - | + | r വ്യാസാര്ധവും (x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>) കേന്ദ്രവുമുള്ള ഗോളപ്രതലത്തിന്റെ സമവാക്യം | |
| - | + | (x-x<sub>1</sub>)<sup>2</sup> + (y-y<sub>1</sub>)<sup>2</sup> + (z-z<sub>1</sub>)<sup>2</sup> = r<sup>2</sup> ആണ്. അതായത്, | |
| - | + | x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup> + 2 dx + 2 ey + 2 fz + g = 0. | |
| - | + | === വൃത്തസ്തംഭ പ്രതലം === | |
| + | Cylindrical Surface | ||
| - | + | zഅക്ഷത്തിനു സമാന്തരമായ വൃത്തസ്തംഭത്തിന്റെ സമവാക്യം | |
| - | + | x2+y2 = r2, z = 0; വൃത്താകാരമായ പരിച്ഛേദത്തിന്റെ വ്യാസാര്ധം r | |
| - | + | ചക്രണതലം (surface of rotation ) ഉണ്ടാകുന്നത് സമതലവക്രം (c: plane curve) ഏതെങ്കിലുമൊരു നേര്രേഖ(l)യ്ക്കു ചുറ്റും കറങ്ങുമ്പോഴാണ്. f(x,y) = 0, z = 0 എന്നിവ c എന്ന വക്രത്തിന്റെ സമവാക്യങ്ങളും l രേഖ x-അക്ഷവുമാണെങ്കില് ചക്രണതലസമവാക്യം | |
| + | f(x,√y<sup>2</sup>+z<sup>2</sup> ആയിരിക്കും. | ||
| - | + | == n-മാന പദ്ധതി == | |
| - | + | ത്രിമാനപദ്ധതിയുടെ മാതൃകയെ സാമാന്യവത്കരിക്കുമ്പോള് n-മാനപദ്ധതിയുണ്ടാകുന്നു. താത്ത്വിക ഗണിതശാസ്ത്രത്തിലെന്നല്ല ഭൌതികശാസ്ത്രം, സ്ഥിതിവിവരശാസ്ത്രം എന്നിവയിലും n-മാനപദ്ധതി ഫലപ്രദമായി ഉപയോഗിച്ചുവരുന്നു. നോ: ആള്ജിബ്ര, ത്രികോണമിതി, ജ്യാമിതി | |
| + | [[Category:ഗണിതം]] | ||
Current revision as of 11:57, 8 ഏപ്രില് 2008
ഉള്ളടക്കം |
അനലിറ്റിക്കല് ജ്യോമട്രി
Analytical geometry
ബീജീയസമ്പ്രദായങ്ങള് ഉപയോഗിച്ച് ക്ഷേത്രഗണിതത്തിലെ പ്രശ്നങ്ങള്ക്കു പരിഹാരം കണ്ടെത്തുന്ന ഗണിതശാസ്ത്ര ശാഖ. വിശ്ളേഷകജ്യാമിതി (Analytic Geometry), നിര്ദേശാങ്കജ്യാമിതി (Co-ordinate Geometry), കാര്ത്തീയജ്യാമിതി (Cartesian Geometry) എന്നീ പേരുകളിലും ഇതറിയപ്പെടുന്നു.
സിറാക്കൂസിലെ ആര്ക്കിമിഡീസിന്റെയും പെര്ഗയിലെ അപ്പോളോണിയസിന്റെയും കാലഘട്ടം മുതല് ഈ ഗണിത ശാഖയെപ്പറ്റിയുള്ള ചില പരിജ്ഞാനശകലങ്ങള് പ്രചരിച്ചിരുന്നു. ഈജിപ്തുകാര്ക്ക് ഇതേപ്പറ്റി സ്ഥൂലമായ ജ്ഞാനം ഉണ്ടായിരുന്നതായി കരുതപ്പെടുന്നു. എങ്കിലും ഈ ശാസ്ത്രശാഖയ്ക്കു വികാസം സിദ്ധിച്ചത് പിയേര് ദെ ഫെര്മെ (1601-65), റെനെ ദെക്കാര്ത്ത് (1596-1650) എന്നീ ഫ്രഞ്ചു ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ കാലത്തായിരുന്നു. ഐസക് ന്യൂട്ടന് (1642-1727), ലൈബ്നിറ്റ്സ് (1646-1716) എന്നിവരും മികച്ച സംഭാവനകള് ഈ ശാഖയ്ക്കു നല്കിയിട്ടുണ്ട്.
അക്ഷങ്ങളും നിര്ദേശാങ്കങ്ങളും
Axes and Co-ordinates
ഒരു സമതലത്തില് ഛ എന്നൊരു സ്ഥിരബിന്ദുവില്കൂടി രണ്ടു ലംബരേഖകള് വരയ്ക്കുക. ഈ രേഖകളെ ആധാരമാക്കി ആ സമതലത്തിലെ ഏതു ബിന്ദുവും അടയാളപ്പെടുത്താവുന്നതാണ്. ചിത്രം 1-ല് o കേന്ദ്രവും XOY', YOY' എന്നീ പരസ്പരലംബങ്ങളായ രേഖകള് നിര്ദേശാക്ഷങ്ങ(Co-ordinates axes)ളും ആണ്. 1, II, III, IV എന്ന് അടയാളപ്പെടുത്തിയിരിക്കുന്ന നാലു പ്രദേശങ്ങളായി സമതലത്തെ വിഭജിച്ചിരിക്കുന്നു. ഈ ഓരോ ഖണ്ഡത്തിനും പാദഖണ്ഡം (quadrant) എന്നു പറയുന്നു. p ഒരു സാമാന്യബിന്ദു ആണെന്നു കരുതുക; PL, X-അക്ഷത്തിലേക്കുള്ള ലംബമാണെങ്കില് OL, LP എന്നിവയുടെ നീളം X,Y, എന്നു സൂചിപ്പിക്കാം.X,Y എന്നിവ ക്രമത്തില് P-യുടെ X-നിര്ദേശാങ്കവും Y-നിര്ദേശാങ്കവുമാണ്. O-ല് നിന്നു OX ദിശയില് അളക്കുന്നതെല്ലാം ധനാത്മകവും, OX എന്ന ദിശയിലുള്ളത് ഋണാത്മകവുമായി പരിഗണിക്കപ്പെടുന്നു. അതുപോലെ OY ധനാത്മകവും, OY' ഋണാത്മകവും. ഈ സങ്കല്പങ്ങളനുസരിച്ച് ചിത്രം(1) OL,LP, എന്നിവ ധനാത്മകമാണ്. ഒന്നാം പാദഖണ്ഡത്തിലെ ബിന്ദുക്കളുടെ നിര്ദേശാങ്കങ്ങള് രണ്ടും ധനാത്മകമാണ്; രണ്ടാം പാദത്തില് X ഋണാത്മകവും Y ധനാത്മകവും; മൂന്നില് രണ്ടും ഋണാത്മകം; നാലില് X ധനാത്മകവും Y ഋണാത്മകവും. ഒരു ബിന്ദുവിന്റെ x-നിര്ദേശാങ്കത്തെ 'ആബ്സിസ' എന്നും y-നിര്ദേശാങ്കത്തെ 'ഓര്ഡിനേറ്റ്' എന്നും പറയാറുണ്ട്. p എന്ന ബിന്ദുവിനെ (x, y) എന്ന് സൂചിപ്പിക്കുന്നു.
തിര്യഗക്ഷങ്ങള്
Oblique axes
ലംബമല്ലാത്ത രണ്ടു നേര്വരകള് അവയുടെ സമതലത്തിലെ ബിന്ദുക്കളെ പ്രതിനിധാനം ചെയ്യാനുള്ള അക്ഷങ്ങളായി ഉപയോഗിക്കാവുന്നതാണ് (ചിത്രം 2). ഇതില് o കേന്ദ്രവും xox', yoy' അക്ഷരേഖകളുമാണ്; pഏതെങ്കിലുമൊരു സാമാന്യബിന്ദുവും. p-ല് നിന്നു yoy'നു സമാന്തരമായി ഒരു രേഖ വരച്ചാല് അത് xox' നെ L എന്ന ബിന്ദുവില് ഛേദിക്കുന്നു എന്നിരിക്കട്ടെ. എങ്കില് OL ആബ്സിസയും LP ഓര്ഡിനേറ്റുമാണ്.
XOX എന്ന X-അക്ഷരേഖയിലുള്ള ഏതു ബിന്ദുവിന്റെയും Y-നിര്ദേശാങ്കം (y-കോടി അഥവാ ഓര്ഡിനേറ്റ്) പൂജ്യവും YOY'ലുള്ള ബിന്ദുവിന്റെ x-നിര്ദേശാങ്കം (x-കോടി അഥവാ ആബ്സിസ) പൂജ്യവുമാണ്. അതുകൊണ്ട് x-അക്ഷത്തിലെ ഏതു ബിന്ദുവും (x,o) എന്നും y-അക്ഷത്തിലെ ഏതു ബിന്ദുവും (o,y) എന്നും സൂചിപ്പിക്കാം. ഈ രണ്ടു രേഖകളുടെയും സംഗമസ്ഥാനത്തെ പ്രഭവസ്ഥാനം (initial point) എന്നു വിളിച്ചുപോരുന്നു. ആ ബിന്ദുവിനെ (o,o) എന്ന നിര്ദേശാങ്കങ്ങള്കൊണ്ടു സൂചിപ്പിക്കാം.
ബിന്ദുപഥങ്ങള്
Locus
അനലിറ്റിക്കല് ജ്യോമട്രി അനുസരിച്ച്, നിയതമായ ഏതു വക്രരേഖയും (ordered curve) ചില പ്രത്യേകനിയമപ്രകാരം നീങ്ങുന്ന ബിന്ദുക്കളുടെ സഞ്ചാരപഥമാണ്. നിര്ദിഷ്ടമായ നിയമങ്ങളനുസരിച്ച് തുടര്ന്നുവരുമ്പോള് ഒരു പഥം സംജാതമാകുന്നു. ഇതാണ്, സഞ്ചാരപഥമെന്നതുകൊണ്ട് ഉദ്ദേശിക്കുന്നത്. ഇവിടെ ജ്യാമിതീയ നിയമങ്ങളെ ബീജീയ വാക്യങ്ങളായി മാറ്റുന്നു. x-അക്ഷത്തില്നിന്ന് ഇരുവശത്തേക്കും നീങ്ങാത്ത ബിന്ദുക്കളുടെ പഥം XOX' എന്ന നേര്വരതന്നെ. അതുകൊണ്ട് XOX'-ന്റെ സമവാക്യം y = 0. x-അക്ഷത്തിലെ എല്ലാ ബിന്ദുക്കള്ക്കും അനുയോജ്യമായ നിയമമാണിത്. അതുപോലെ yoy'-ന്റെ സമവാക്യം X = 0. ഒരു സ്ഥിരബിന്ദു(fixed point)വില്നിന്ന് എപ്പോഴും r ദൂരത്തില് കിടക്കുന്ന ബിന്ദുക്കളുടെ ബിന്ദുപഥം ആ സ്ഥിരബിന്ദു കേന്ദ്രമാക്കിക്കൊണ്ടും, r വ്യാസാര്ധമാക്കിക്കൊണ്ടുമുള്ള വൃത്ത പരിധിയാണ്. ബിന്ദുപഥത്തിനു കൂടുതല് ഉദാഹരണങ്ങള് തുടര്ന്നു കാണാവുന്നതാണ്.
നേര്വരകള്
നേര്വരയെ പൊതുവായി പ്രതിനിധാനം ചെയ്യുന്നത് ഏകഘാത സമവാക്യ(first degree equation)ത്തിലൂടെയാണ്: ax + by + c = 0. ഒരു നേര്വര ഉറപ്പിക്കാന് അത്യാവശ്യമായ വ്യവസ്ഥകളെ ആധാരമാക്കിയാണ് അതിന്റെ സമവാക്യം രൂപപ്പെടുന്നത്. (1) രണ്ടു ബിന്ദുക്കള് യോജിപ്പിച്ചാല് ഒരു നേര്വരയുണ്ടാകുന്നു. (II) ഒരു ബിന്ദുവും നേര്വര X-അക്ഷവുമായുണ്ടാക്കുന്ന ചരിവുമാനവും (slope) അറിഞ്ഞാല് ഒരു നേര്വരയുണ്ടാക്കാം. (III) ചരിവുമാനവും y-അക്ഷരേഖയിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡവും (intercept) അറിഞ്ഞാല് ഒരു നേര്വരയുണ്ടാക്കാം. (iv) രേഖ x, y അക്ഷങ്ങളിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡങ്ങള് അറിഞ്ഞാല് ഒരു രേഖ വരയ്ക്കാം. സാധാരണയായി ഇത്തരത്തിലുള്ള വ്യവസ്ഥകളനുസരിച്ചാണ് നേര്വരയുണ്ടാകുന്നത്.
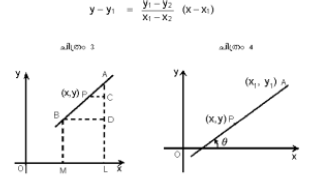
(1) ചിത്രം 3-ല് A,B ആ എന്നീ ബിന്ദുക്കള് (x1, y1), (x2,y2) ആണ്. ഇവ യോജിപ്പിച്ചുണ്ടാവുന്ന നേര്വര(AB)യുടെ സമവാക്യം നിര്ണയിക്കാം. p(x,y) രേഖയിലുള്ള ഒരു സാമാന്യ ബിന്ദുവാണെങ്കില് AP,AB എന്നീ രേഖകള് ഒരേ നേര്വരയിലായതിനാല് ചരിവുമാനങ്ങള് തുല്യമായിരിക്കും. അതായത് . AC/PC = AD/BD ഇതില്നിന്നു
y-y1 / x- x1 = y1 - y 2/x1 - x2 എന്നു സിദ്ധിക്കുന്നു. അതായത്,
(ii) A(x1,y1) എന്ന ബിന്ദുവിലൂടെ കടക്കുന്നതും mചരിവുമാനം ഉള്ളതുമായ നേര്വരയുടെ സമവാക്യം എന്നു സിദ്ധിക്കുന്നു. (1)-ല് ചരിവുമാനമാണ്. ചരിവുകോണ് ø ആണെങ്കില് tanø ആണ് ചരിവുമാനം.
(iii) ചരിവുമാനം m-ഉം രേഖ y-അക്ഷത്തില് ഉണ്ടാക്കുന്ന ഖണ്ഡം കേന്ദ്രത്തില്നിന്ന് അളക്കുമ്പോള് c-യുമാണെങ്കില്, രേഖ വരയ്ക്കാന് കഴിയും. ചിത്രം 5 നോക്കിയാല് p(x,y) രേഖയിലെ ഒരു സാമാന്യബിന്ദുവും OQ = c ഛേദഖണ്ഡവും øചരിവുകോണുമാണെന്നും കാണാം. എങ്കില് m = tanø = PN/QN; അതായത്
PN =m.QN. ഇതില്നിന്നു y =mx + c എന്നു സിദ്ധിക്കുന്നു. PQ എന്ന രേഖയുടെ സമവാക്യമാണിത്.
(iv) ചിത്രം 6 പരിശോധിച്ചാല് a, b എന്നിവ, അക്ഷങ്ങളിലുണ്ടാക്കുന്ന ഛേദഖണ്ഡങ്ങളും p(x,y) ഒരു സാമാന്യബിന്ദുവുമാണെന്നു മനസ്സിലാക്കാം. ത്രികോണങ്ങളുടെ ജ്യാമിതീയ സവിശേഷതയനുസരിച്ച് AM/AO = MP/OB ആണ്. ഇതില്നിന്നു a-x/a = y/b എന്നു സിദ്ധിക്കുന്നു. അതായത് x/a + y/b = 1
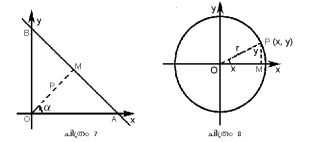
(V) (ചിത്രം 7). കേന്ദ്രത്തില്നിന്നു AB എന്ന ഋജുരേഖയിലേക്കുള്ള ലംബത്തി(OM)ന്റെ നീളം p-ഉം OM x-അക്ഷവുമായുണ്ടാക്കുന്ന കോണം α-യുമാണ്. എങ്കില് AB-യുടെ സമവാക്യം
x cosα + y sinα = p ആയിരിക്കും.
മേല്പറഞ്ഞ സമവാക്യരൂപങ്ങളില്നിന്നു മനസ്സിലാക്കാവുന്നത്, നേര്വരയുടെ സമവാക്യം ഏകഘാതസമവാക്യമായിരിക്കുമെന്നതാണ്. അതായത്, ax + by + c = 0 രണ്ടു നേര്വരകള്ക്കിടയിലുള്ള കോണം ø ആണെങ്കില് താഴെ കാണുന്നവിധം കണക്കാക്കാന് കഴിയും: (m1 > m2)
tan ø = m1 - m2 / 1+m1 m2
ഇവിടെ m1,m2 എന്നിവ, രേഖകളുടെ ചരിവുമാനമാണ്. രേഖകള് സമാന്തരമാണെങ്കില്,m1= m2; ലംബമാണെങ്കില്
m1m2 = -1.
ദ്വിഘാത സമവാക്യങ്ങള്
Second degree equations in x,y
പൊതുവായ ദ്വിഘാതസമവാക്യമാണ് ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 ചില വ്യവസ്ഥകളനുസരിച്ച് ഈ വാക്യം ഒരു ജോടി നേര്രേഖകളെയോ ഒരു വൃത്തത്തെയോ മറ്റു കോണികഖണ്ഡങ്ങ(conic sections)ളെയോ പ്രതിനിധാനം ചെയ്യുന്നതാണ്. രണ്ടു ഏകഘാതവാക്യങ്ങളുടെ ഗുണിതമാണ് ഇതിലെ വാക്യമെങ്കില് ആ വാക്യം രണ്ടു നേര്വരകളെ കുറിക്കുന്നു. ഈ വ്യവസ്ഥ നിര്ണയിക്കാന് കഴിയും. abc + 2fgh- af 2- bg2- ch2 = 0 എന്നതാണ് ഈ വ്യവസ്ഥ. x2,y2 എന്നിവയുടെ ഗുണനാങ്കങ്ങള് തുല്യമായിരിക്കയും, xyയുടെ ഗുണനാങ്കം പൂജ്യമായിരിക്കുകയുമാണെങ്കില്, അതായത് ax2 + ay2 + 2gx + 2fy + c = 0, ഒരു വൃത്തത്തിന്റെ സമവാക്യമുണ്ടാകുന്നു.
x2+y2+2gx+2fy+c=0,
x2/a2 + y2 / b2 = 1
y2 = 4ax,x2/a2 - y2 /b2 =1
എന്നീ പ്രത്യേക സമവാക്യ രൂപങ്ങള് വൃത്തം, ദീര്ഘവൃത്തം (ellipse), പരവളയം (parabola), ബഹിര്വളയം (hyperbola) എന്നിവയെ സൂചിപ്പിക്കുന്നു. നിര്ദിഷ്ടാങ്കrപദ്ധതിയിലെ കേന്ദ്രം വൃത്തകേന്ദ്രമായും r വ്യാസാര്ധമായും ഉള്ള വൃത്തത്തിന്റെ സമവാക്യം ചിത്രം 8-ല് നിന്നു കണക്കാക്കാം: x2 + y2 = r2.
ദൂരം
Distance
A (x1,y1), B (x2, y2) എന്നീ രണ്ടു ബിന്ദുക്കള് തമ്മിലുള്ള ദൂരം പിത്തഗറസ്തത്ത്വം ഉപയോഗിച്ച് കണ്ടെത്താന് കഴിയും. ചിത്രം 9-ല് ACB ഒരു മട്ടത്രികോണമാണ്. BC2 + AC2 = AB 2. ഇതില്നിന്നു, AB=√(x1 - x 2)2+(y1-y2)2 എന്നു നിര്ണയിക്കാം. ഇതില് B കേന്ദ്രത്തില് തന്നെയാണെങ്കില് BA, അതായത് OA=√x12+y12എന്നു കാണാം. (x1,y1)ല് നിന്നു ax + by + c = 0 എന്ന നേര്വരയിലേക്കു വരയ്ക്കുന്ന ലംബത്തിന്റെ നീളം,
x cos α+y sin α=p എന്ന സമവാക്യത്തോട് ax + by + c = 0 താരതമ്യപ്പെടുത്തിയാല് കിട്ടുന്നതാണ്:
കേന്ദ്രത്തില്നിന്നുള്ള ദൂരം താഴെ കാണുന്നവിധം ആണ് എന്നു മനസ്സിലാക്കാം. (കേന്ദ്രം:x1 = 0, y1 = 0)
p=+- ax1+by1+c/√a2 +b2
വിസ്തീര്ണം
Area
A (x1,y1), B (x2, y2), C (x3,y3) എന്നീ ബിന്ദുക്കള് ശീര്ഷ(vertices)ങ്ങളായുള്ള ത്രികോണത്തിന്റെ വിസ്തീര്ണം കാണുന്നത്, ഈ ബിന്ദുക്കളില് നിന്നും X-അക്ഷത്തിലേക്ക് ലംബം വരച്ച് ദ്വിവശസമാന്തര ചതുര്ഭുജങ്ങളുടെ (trapezium) വിസ്തീര്ണങ്ങള് നിര്ണയിച്ചാണ് (ചിത്രം 10); വിസ്തീര്ണത്തിനു Δഎന്ന ചിഹ്നമാണ് ഉപയോഗിക്കുന്നത്.
മൂന്നു ബിന്ദുക്കള് ഈരണ്ടെണ്ണം നേര്വരകൊണ്ടു യോജിപ്പിച്ചുണ്ടാകുന്ന ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യം ആണെങ്കില് ആ മൂന്നു ബിന്ദുക്കളും ഒരേ നേര്വരയിലാണെന്ന് അതില് നിന്നു മനസ്സിലാക്കാം.
ധ്രുവാങ്ക പദ്ധതി
Pollar Co-ordinate System
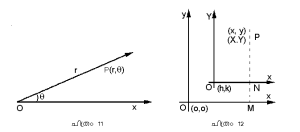
ഇതുവരെ പ്രതിപാദിച്ച കാര്ത്തീയ നിര്ദേശാങ്കപദ്ധതി പോലെ തന്നെ പ്രയോജനകരമായ മറ്റൊരു പദ്ധതിയാണിത്. ഒരു സ്ഥിരബിന്ദുവും അതില് നിന്നുള്ള ഒരു സ്ഥിര നേര്വരയും അടിസ്ഥാനപ്പെടുത്തി പ്രതലത്തിലെ ബിന്ദുക്കള് നിര്ണയിക്കുന്ന സമ്പ്രദായമാണിത്. ചിത്രം 11-ല് o സ്ഥിരബിന്ദുവും ox സ്ഥിരരേഖയും ആണ്. p എന്ന ഒരു ബിന്ദുവിന്റെ ധ്രുവാങ്കങ്ങള് നിര്ണയിക്കുന്നത് op എന്ന ത്രിജ്യരേഖ(radius vector)യുടെ നീളം r-ഉം OX-ല് നിന്ന് സമതലത്തിലൂടെ O കേന്ദ്രമാക്കി അപ്രദക്ഷിണമായി (anticlock-wise) തിരിയുമ്പോള് op ഉണ്ടാക്കുന്ന e എന്ന കോണവും ഉപയോഗിച്ചാണ്. ഇവിടെ r ,ø ഇവ ആണ് p-യുടെ ധ്രുവാങ്കങ്ങള്. p എന്ന ബിന്ദുവിനെ (r,ø) എന്നു രേഖപ്പെടുത്താം.
സമ്മിശ്ര സംഖ്യകളെ (Complex numbers) വിശ്ളേഷകജ്യാമിതിയില് അവതരിപ്പിക്കാന് ധ്രുവാങ്കങ്ങള് ഉപയോഗപ്പെടുത്തുന്നു. x + iy-യുടെ ആംപ്ളിറ്റ്യൂഡ് ø,r=+√x2+y2 മോഡുലസ് എന്നിവ (r,ø) എന്ന ബിന്ദുവായി അങ്കനം ചെയ്യുന്നു. (r,ø) എന്നതു (r,ø+2nπ + 2nII ആയും എഴുതാം. നോ: സമ്മിശ്ര സംഖ്യ
അക്ഷ രൂപാന്തരണം
Transformation of axes
(i) കേന്ദ്രം o-യില്നിന്നു o'-യിലേക്കും ആധാരരേഖകള് x, oy എന്നിവയ്ക്കു സമാന്തരമായി o'x, o'y (ലംബം) എന്നിവയിലേക്കും മാറ്റിയാല്, പുതിയ ആധാരരേഖകളെ അപേക്ഷിച്ച് നിര്ദിഷ്ടാങ്കങ്ങള് നിര്ണയിക്കാം. p എന്ന ബിന്ദു x-,y- അക്ഷങ്ങളെ ആധാരമാക്കി (x,y) x -, y- എന്നിവയെ ആസ്പദമാക്കി (x,y) യും ആണെങ്കില്, ചിത്രം 12-ല് നിന്ന്, x = X + h, y = Y + K എന്നു സിദ്ധിക്കുന്നു. അതായത് X = x-h, Y =y-k. ഇവിടെx-, y- അക്ഷങ്ങളെ അപേക്ഷിച്ചുള്ള കോടികളാണ് (h, k).
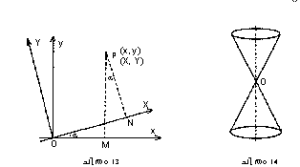
(ii) O കേന്ദ്രമാക്കി അക്ഷങ്ങളെ αകോണിലൂടെ തിരിച്ചും അക്ഷങ്ങളുടെ രൂപാന്തരണം സാധിക്കാം (ചിത്രം 13). p-യുടെ ധ്രുവാങ്കങ്ങള് (r,ø) ആയിരുന്നെങ്കില് ഇതനുസരിച്ച് (r,ø+α) ആയിത്തീരും. അങ്ങനെx =r cos ø,y=r sin ø എന്നിവയുപയോഗിച്ച് X= r cos(ø+α),Y=r sin (ø+α) എന്നു സിദ്ധിക്കുന്നു. അതായത്, X = r cosøcos α -ysinα
Y = r sinøcos α + r cosø sin α =x sinα +y cos α
വിസ്തീര്ണ കോടികള്
Arieal Co-ordinates
ഒരു ത്രികോണത്തെ ആധാരമാക്കി കോടികള് നിര്ണയിക്കുന്ന സമ്പ്രദായമാണിത്. p എന്ന സാമാന്യബിന്ദുവിന്റെ കോടികള് ΔBPC,ΔCPA,ΔAPB എന്നീ വിസ്തീര്ണങ്ങളുടെ അനുപാതത്തിലായിരിക്കും. അതായത് t1, t2, t3 ആണ് കോടികളെങ്കില് t1: t2 :t3 = ΔBPC :ΔCPA :ΔAPB ഇവയ്ക്ക് p-യുടെ ബേരികേന്ദ്രീയ കോടികളെന്നും (Bary-centric co-ordinates) പറയുന്നു. ഇവിടെ t1 + t2 + t3 = 1 എന്നാകുന്ന വിധത്തിലാണെങ്കില് ഇവയെ വിസ്തീര്ണ കോടികള് എന്നു പറയാം.
കോണിക ഖണ്ഡങ്ങള്
Conic Sections
ഇരുഭാഗത്തേക്കും നീണ്ടുകിടക്കുന്ന (ചിത്രം 14) കോണിന്റെ (Cone) പ്രത്യേക ഖണ്ഡങ്ങളുടെ പഠനം വിശ്ളേഷകജ്യാമിതിയില് സുപ്രധാനമാണ്. കോണിന്റെ അക്ഷത്തോടു ചേര്ത്ത് കോണിനെ ഒരു സമതലംകൊണ്ടു ഛേദിക്കുകയാണെങ്കില് ബാഹ്യമായി കാണുന്ന പരിച്ഛേദം (cross section) രണ്ടു ഋജുരേഖകളായിരിക്കും. അക്ഷത്തിനു ലംബമായി ഖണ്ഡിക്കുമ്പോള് പരിച്ഛേദം വൃത്താകാരവും ചരിവു വശത്തിനു സമാന്തരമായിട്ടാണെങ്കില് പരവളയവും സമാന്തരമല്ലാതെയാണെങ്കില് ദീര്ഘവൃത്തവും രണ്ടു ഭാഗത്തെ അക്ഷത്തിനു സമാന്തരമായി ഖണ്ഡിക്കുമ്പോള് ബഹിര്വളയവും ഉണ്ടാകുന്നു.
കോണിക(conic)ത്തെ സാമാന്യമായി ഇങ്ങനെയാണ് നിര്വചിച്ചിരിക്കുന്നത്: s ഒരു സ്ഥിരബിന്ദുവും d ഒരു സ്ഥിര ഋജുരേഖയുമാണെന്നു സങ്കല്പിക്കുക; p കോണികത്തിലെ ഏതെങ്കിലുമൊരു സാമാന്യബിന്ദുവും; p-ല് നിന്നു d-യിലേക്കുള്ള ദൂരം PM . എങ്കില് SP/PM =e (e ഏതെങ്കിലുമൊരു സംഖ്യയാകാം). e ക്ളിപ്തമായിരിക്കുന്നവിധം p ചലിക്കുമ്പോഴുണ്ടാകുന്ന ബിന്ദുപദമാണ് കോണികം; e കോണികത്തിന്റെ ഉത്കേന്ദ്രതയും (eccentricity). eയുടെ മൂല്യം 1 ആകുമ്പോള് കോണികം ഒരു പരവളയവും e യുടെ മൂല്യം 1-ല് കുറവാകുമ്പോള് ദീര്ഘവൃത്തവും e യുടെ മൂല്യം 1-ല് കൂടുതല് ആകുമ്പോള് ബഹിര്വളയവും ആയിരിക്കും (ചിത്രം 15).
വൃത്തം
Circle
x2 + y2 + 2gx + 2fy + c = 0 ആണ് ഒരു സാധാരണ വൃത്തത്തിന്റെ സമവാക്യം. ഈ വൃത്തത്തിന്റെ കേന്ദ്രവും വ്യാസാര്ധവും കാണാന് സമവാക്യത്തെ (x + g)2 +(y + f)2= √g2+f2-c)2 എന്നാക്കിയാല് മതി. കേന്ദ്രം (-g,-f)-ഉം വ്യാസാര്ധം √g2 +f2-cയുമാണ്. വൃത്തത്തിന്മേലുള്ള ഏതു ബിന്ദുവിനേയും പ്രാചല(parameter)ത്തിലൂടെ കാണിക്കാന് കഴിയും. x2 + y2 = r2 എന്ന വൃത്തത്തിന്മേലുള്ള ഏതു ബിന്ദു വും x = r cos ø, y= r sin ø എന്ന പ്രാചലപ്രതിനിധാനം വഴി സൂചിപ്പിക്കാം.
പരവളയം
Parabola
കോണികത്തിന്റെ പൊതു തത്ത്വമനുസരിച്ച്, ചിത്രം (16)-ല് നിന്നു SP = PM. p(x,y) ഇവിടെ പരവളയത്തിന്മേലുള്ള സാമാന്യ ബിന്ദുവാണ്. s-ല് കൂടി d-ക്കു ലംബം വരച്ച് അത് x-അക്ഷമായി എടുക്കുകയും SZ (= 2a)-ന്റെ മധ്യബിന്ദു o കേന്ദ്രമായും o-ല് കൂടി ox-നു വരയ്ക്കുന്ന ലംബം y-അക്ഷമായും എടുക്കുകയാണെങ്കില്, s (a, o)-ഉം PM = x+a യുമാണെന്നുകാണാം. SP = PM-ല് നിന്നു Y2 = 4 ax എന്നു സിദ്ധിക്കുന്നു. S-ല് കൂടി അക്ഷത്തിനുള്ള ലംബഖണ്ഡമാണ് LSL' . LSL' = 4a. S പരവളയത്തിന്റെ അഭികേന്ദ്ര(focus)വും d നിയന്ത്രണരേഖ(directrix)യുമാണ്.
ദീര്ഘവൃത്തം
Ellipse
CA, CB എന്നിവയാണ് അക്ഷങ്ങള്; C കേന്ദ്രവും. (ചിത്രം 17) CA = a എന്നെടുത്താല് CS = ae, CZ = a/e എന്നിവ നിര്ണയിക്കാം. ഇവിടെ e ദീര്ഘവൃത്തത്തിന്റെ ഉത്കേന്ദ്രതയാണ്. ഒന്നിനെക്കാള് ചെറുതായിരിക്കും e. SP = e PM ഉപയോഗിച്ചാല്
x2/a2 + y2/b2 =1, b2=a2(1-e2)
എന്നു ദീര്ഘവൃത്തത്തിന്റെ സമവാക്യം ഉണ്ടാകുന്നു. b = a ആയാല് ദീര്ഘവൃത്തം വൃത്തമായി മാറും.
ബഹിര്വളയം
Hyperbola
ചിത്രം 18-ല് ചിത്രം (17)-ലെ നിര്ദിഷ്ടാങ്കപദ്ധതിതന്നെ. A, A' എന്നീ ബിന്ദുക്കള് ബഹിര്വളയത്തിലെ ബിന്ദുക്കളാണെന്നു കരുതുക. AA' = 2a എന്നെടുത്ത് അതിന്റെ മധ്യബിന്ദു C കേന്ദ്രമായും C യിലൂടെയുള്ള ലംബം CY എന്നത് Y-അക്ഷമായും സ്വീകരിക്കുക. CA = a, CZ = a/e, CS = ae. ഇവിടെ ഉത്കേന്ദ്രത e ഒന്നിനേക്കാള് വലുതായിരിക്കും. P(x,y) ബഹിര്വളയത്തിലെ ഒരു സാമാന്യ ബിന്ദുവാണ് SP = e PM ഉപയോഗിച്ചാല്
x2/a2 - y2/b2 = 1 b2 = a2(e2-1)
എന്ന സമവാക്യങ്ങള് സിദ്ധിക്കുന്നു.
x = at2, y = 2 at പരവളയത്തിന്റെയും x = a cos ø, y= b sin ø ദീീര്ഘവൃത്തത്തിന്റെയും x = a sec ø, y = b tan ø, ബഹിര്വളയത്തിന്റേയും പ്രാചലപ്രതിനിധാനങ്ങളാണ്.
ജ്യാവ് (chord), സ്പര്ശകം (tangent) എന്നിങ്ങനെയുള്ള മറ്റു പ്രമേയങ്ങളും വിശ്ളേഷക ജ്യാമിതിയില് പ്രതിപാദിക്കപ്പെടുന്നു.
ത്രിമാന പദ്ധതി
Three Dimensional System
ഭൌതിക സ്വഭാവമുള്ള ഏതു വസ്തുവിനും മൂന്നു അളവുകളുണ്ട്: നീളം, വീതി, കനം. ഇവയെ ആസ്പദമാക്കിയുള്ള പദ്ധതിയാണിത്. ദ്വിമാനപദ്ധതിയുടെ ഒരു വിപുലീകരണം മാത്രമാണിത്.
പരസ്പരം ലംബങ്ങളായ മൂന്നു ഋജുരേഖകള് O എന്ന ബിന്ദുവില് കൂട്ടിമുട്ടുന്നു (ചിത്രം 19). XOX', YOY', ZOZ' എന്നിവയാണ് അക്ഷങ്ങള്; O കേന്ദ്രവും. XOY, YOZ, ZOX എന്നീ മൂന്നു സമതലങ്ങള് ഈരണ്ടെണ്ണം യോജിക്കുന്ന രേഖകളാണ് OX, OY, OZ എന്നീ അക്ഷങ്ങള്. p എന്നൊരു സാമാന്യ ബിന്ദുവിന്റെ നിര്ദിഷ്ടാങ്കങ്ങള് കണ്ടുപിടിക്കാന് p-ല് നിന്നു XOY തലത്തിലേക്കു ലംബം വരയ്ക്കുന്നു. M ലംബത്തിന്റെ പാദമാണ്. M-ല് നിന്നു XOX' ലേക്കു ലംബം MN വരയ്ക്കുക. എങ്കില് ON, NM, MP എന്നിവ, ദിശകള് കൂടി കണക്കിലെടുത്തുകൊണ്ട് x, y, z എന്ന ക്രമത്തില് p-യുടെ അങ്കങ്ങളാണെന്നു പറയുന്നു.
ദിശാകോണുകളും ദിശാകൊസൈനുകളും
Direction angles and Direction cosines
ദിശാകോണുകളും ദിശാകൊസൈനുകളും
Direction angles and Direction cosines
lഒരു സാമാന്യ ഋജുരേഖയും l1ഈരേഖയ്ക്കു സമാന്തരമായി കേന്ദ്രത്തിലൂടെയുള്ള രേഖയും αβγഎന്നിവ OX, OY, OZ എന്നീ അക്ഷരേഖകളുമായി l1ഉണ്ടാക്കുന്ന കോണുകളുമാണെന്നു സങ്കല്പിക്കുക.എങ്കില്αβ&gama;എന്നിവ l-ന്റെ ദിശാകോണുകളും cosα, cosβcos&gama;ദിശാകൊസൈനുകളുമാണ്.cos2α, cos2βB,cos2γ=1എന്നു തെളിയിക്കാന് കഴിയും.y2+u2=1 ആയിരിക്കുന്ന വിധത്തിലുള്ള ഏതു സംഖ്യകളും ^,u,yക്ലുപ്തദിശയിലുള്ള ഏതു ഋജുരേഖയുടേയും ദിശാകൊസൈനുകളായിരിക്കും. ദിശാകൊസൈനുകള്ക്ക് ആനുപാതികമായിട്ടുള്ള a, b, c സംഖ്യകളെ ദിശാസംഖ്യകളെന്നു പറയുന്നു. x2-x1, y2-y1, z2-z1 എന്നിവ AB ഋജുരേഖയുടെ ദിശാസംഖ്യകളാണ്. AB യിലെ ഒരു ബിന്ദുവാണ് p(x,y) എങ്കില് AP-ക്കും PB-ക്കും ദിശാസംഖ്യകള് ഒരേ അനുപാതത്തിലായിരിക്കും. അതായത് x1-x = k (x2-x1),y1-y = k (y2-y1), z1-z = k (z2 - z1). ഇതില് k ഒരു വാസ്തവിക സംഖ്യയാണ്. AB യുടെ ദിശാസംഖ്യകള്
ആണ്;d = √(x1-x2)2+(y1-y2 )2+(z1-z2)2 .l1,l2 എന്നീ ഋജുരേഖകള് തമ്മിലുള്ള കോണ്യും അവയുടെ ദിശാകൊസൈനുകള് cos α1 cosβ1 cosγ1 cos α2 cosβ2cosγ2എന്നിവയുമാണെങ്കില് cosø=cosα1cosα2+ cosβ1cosβ2+cosγ1 cosγ2ആയിരിക്കും. ക്രമത്തില് a1, b1, c1; a2, b2, c 2 എന്നിവ രണ്ടു ലംബരേഖകളുടെ ദിശാസംഖ്യകളെങ്കില്, a1 a2 + b1 b2 + c1 c2 = 0 ആകുന്നു.
തലങ്ങളും സമവാക്യങ്ങളും
Surfaces and Equations
ചിത്രം 20-ല്, π ഒരു സമതലം; l π-ക്കു ലംബരേഖ; a, b, c l-ന്റെ ദിശാസംഖ്യകള്; A(x1, y1, z1) l ന്റെ പാദം;B(x,y,z) π -ലുള്ള മറ്റൊരു ബിന്ദു. ഇതില് BAയും l രേഖയും ലംബമാണ്. അതുകൊണ്ട്
a(x1-x) + b(y1-y) + c(z1-z) = 0. ഏതെങ്കിലുമൊരു സമതലവുമായി ഇങ്ങനെ ബന്ധപ്പെട്ട ഒരു ഏകഘാത സമവാക്യമുണ്ടായിരിക്കും. അതായത് ax + by + cz + d = 0 എന്ന ഏകഘാതസമവാക്യത്തെ A(x1, y1, z1) എന്നൊരു ബിന്ദു 'തൃപ്തിപ്പെടുത്തു'മെങ്കില്, ഈ ബിന്ദുവിലൂടെ കടന്നുപോകുന്നതും a, b, c എന്നിവ ദിശാസംഖ്യകളുള്ള ഋജുരേഖയ്ക്കു ലംബവുമായ സമതലത്തിന്റെ സമവാക്യം. a(x-x1) + b(y-y1) + c(z-z1) = 0 ആയിരിക്കും. yoz,zox,xoyഛദ, ദഛത, തഛഥ എന്നീ സമതലങ്ങളുടെ സമവാക്യങ്ങള് ക്രമത്തില് x=o,z=o = 0, എന്നിവയാണ്.
ലംബീയ ദൂരം
Perpendicular Distance
A(x1,y1,z1)-ല് നിന്നു ax + by + cz + d = 0 എന്ന സമതലത്തിലേക്കുള്ള
a1x+ b1y +c1z + d1 = 0, a2x + b2 + y2 + d2 = 0 എന്നീ സമതലങ്ങള് സമാന്തരമാണെങ്കില്, a1, b1, c1; a2, b2, c2 എന്നിവ ക്രമത്തില് അനുപാതത്തിലായിരിക്കും. ലംബമാണെങ്കില്, a1a2 + b1b2 + c1c2= 0. ഒരേ രേഖയിലല്ലാത്ത മൂന്നു ബിന്ദുക്കള് A(xi,yi,zi),
i = 1,2,3 ഒരു സമതലം സൃഷ്ടിക്കുന്നു. ആ സമതലത്തിന്റെ സമവാക്യം:
ai x + bi,y + ciz + d = 0, i = 1, 2, 3; എന്നീ 3 സമതലങ്ങള് ഒരേ ബിന്ദുവിലൂടെ കടന്നുപോകുന്നുവെന്നതിനുള്ള വ്യവസ്ഥ.
f(x, y, z) = 0 എന്നൊരു സമവാക്യത്തെ തൃപ്തിപ്പെടുത്തുന്ന ബിന്ദുക്കളുടെ ബിന്ദുപഥത്തെ പ്രതലം (surface) എന്നു പറയുന്നു. വക്രരേഖകളുണ്ടാകുന്നതു രണ്ടു തലങ്ങള് കൂട്ടിമുട്ടുമ്പോഴാണ്. അതുകൊണ്ട് f1(x1, y1 z) = 0, f2 (x, y, z) = 0 എന്നിവ ചേര്ന്ന് ആ വക്രരേഖകളെ പ്രതിനിധാനം ചെയ്യുന്നു; പ്രാചലം (t) ഉപയോഗിച്ചും വക്രരേഖകളെ പ്രതിനിധാനം ചെയ്യാം:
x = f(t), y = g(t), z = h(t).
ഗോള പ്രതലം
Spherical Surface
r വ്യാസാര്ധവും (x1, y1, z1) കേന്ദ്രവുമുള്ള ഗോളപ്രതലത്തിന്റെ സമവാക്യം
(x-x1)2 + (y-y1)2 + (z-z1)2 = r2 ആണ്. അതായത്,
x2 + y2 + z2 + 2 dx + 2 ey + 2 fz + g = 0.
വൃത്തസ്തംഭ പ്രതലം
Cylindrical Surface
zഅക്ഷത്തിനു സമാന്തരമായ വൃത്തസ്തംഭത്തിന്റെ സമവാക്യം
x2+y2 = r2, z = 0; വൃത്താകാരമായ പരിച്ഛേദത്തിന്റെ വ്യാസാര്ധം r
ചക്രണതലം (surface of rotation ) ഉണ്ടാകുന്നത് സമതലവക്രം (c: plane curve) ഏതെങ്കിലുമൊരു നേര്രേഖ(l)യ്ക്കു ചുറ്റും കറങ്ങുമ്പോഴാണ്. f(x,y) = 0, z = 0 എന്നിവ c എന്ന വക്രത്തിന്റെ സമവാക്യങ്ങളും l രേഖ x-അക്ഷവുമാണെങ്കില് ചക്രണതലസമവാക്യം f(x,√y2+z2 ആയിരിക്കും.
n-മാന പദ്ധതി
ത്രിമാനപദ്ധതിയുടെ മാതൃകയെ സാമാന്യവത്കരിക്കുമ്പോള് n-മാനപദ്ധതിയുണ്ടാകുന്നു. താത്ത്വിക ഗണിതശാസ്ത്രത്തിലെന്നല്ല ഭൌതികശാസ്ത്രം, സ്ഥിതിവിവരശാസ്ത്രം എന്നിവയിലും n-മാനപദ്ധതി ഫലപ്രദമായി ഉപയോഗിച്ചുവരുന്നു. നോ: ആള്ജിബ്ര, ത്രികോണമിതി, ജ്യാമിതി