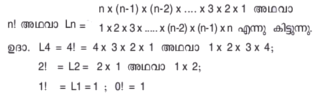This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ക്രമഗുണിതം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(പുതിയ താള്‍: ==ക്രമഗുണിതം== ==Factorial== ഒന്നില്‍ ആരംഭിക്കുകയോ അവസാനിക്കുകയോ ചെയ്...) |
(→Factorial) |
||
| വരി 5: | വരി 5: | ||
ഒന്നില്‍ ആരംഭിക്കുകയോ അവസാനിക്കുകയോ ചെയ്യുന്ന ക്രമാനുസാരിയായ ധനപൂര്‍ണസംഖ്യകളുടെ ശൃംഖലാഗുണനഫലം. ഒരു ധനപൂര്‍ണസംഖ്യ ആണെന്നിരിക്കട്ടെ. n-നെ (n-1) കൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലത്തെകൊണ്ട് (n - 2) ഗുണിക്കുക. ഇങ്ങനെ ഓരോ ഗുണനഫലത്തെയും അവരോഹണക്രമത്തില്‍ അടുത്തുവരുന്ന പൂര്‍ണസംഖ്യകൊണ്ട് 1 എന്ന സംഖ്യ ഗുണകമായി വരുന്നതുവരെ തുടര്‍ന്നു ഗുണിക്കുക. അപ്പോള്‍ കിട്ടുന്നn x (n-1) x (n-2) x ..... x 3 x 2x 1 എന്ന ഗുണനഫലത്തെ n! അഥവാ Ln എന്നു രേഖപ്പെടുത്തുകയും n ക്രമഗുണിതം' അഥവാ 'ക്രമഗുണിതം n' എന്ന് ഉച്ചരിക്കുകയും ചെയ്തുവരുന്നു. 'n' ല്‍ നിന്നാരംഭിച്ച് 1 -ല്‍ എത്തുന്നതിനു പകരം 1-ല്‍ നിന്നാരംഭിച്ച് n-ല്‍ എത്തുകയാണെങ്കിലും കിട്ടുന്നത് n! അഥവാ Ln ആണ്. അതുകൊണ്ട് | ഒന്നില്‍ ആരംഭിക്കുകയോ അവസാനിക്കുകയോ ചെയ്യുന്ന ക്രമാനുസാരിയായ ധനപൂര്‍ണസംഖ്യകളുടെ ശൃംഖലാഗുണനഫലം. ഒരു ധനപൂര്‍ണസംഖ്യ ആണെന്നിരിക്കട്ടെ. n-നെ (n-1) കൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലത്തെകൊണ്ട് (n - 2) ഗുണിക്കുക. ഇങ്ങനെ ഓരോ ഗുണനഫലത്തെയും അവരോഹണക്രമത്തില്‍ അടുത്തുവരുന്ന പൂര്‍ണസംഖ്യകൊണ്ട് 1 എന്ന സംഖ്യ ഗുണകമായി വരുന്നതുവരെ തുടര്‍ന്നു ഗുണിക്കുക. അപ്പോള്‍ കിട്ടുന്നn x (n-1) x (n-2) x ..... x 3 x 2x 1 എന്ന ഗുണനഫലത്തെ n! അഥവാ Ln എന്നു രേഖപ്പെടുത്തുകയും n ക്രമഗുണിതം' അഥവാ 'ക്രമഗുണിതം n' എന്ന് ഉച്ചരിക്കുകയും ചെയ്തുവരുന്നു. 'n' ല്‍ നിന്നാരംഭിച്ച് 1 -ല്‍ എത്തുന്നതിനു പകരം 1-ല്‍ നിന്നാരംഭിച്ച് n-ല്‍ എത്തുകയാണെങ്കിലും കിട്ടുന്നത് n! അഥവാ Ln ആണ്. അതുകൊണ്ട് | ||
| - | സഞ്ചയ(combination)ത്തില്‍ എന്നൊരു ഫലമുണ്ട്. ഇവിടെ 'r'ന് 'n' എന്ന മൂല്യം കല്പിക്കുകയാണെങ്കില്‍ എന്നു കിട്ടുന്നു. നോ. ക്രമചയം, സഞ്ചയം | + | [[ചിത്രം:Pg343_scree01.png]] |
| + | |||
| + | സഞ്ചയ(combination)ത്തില്‍ [[ചിത്രം:Pg343_scree009.png]] എന്നൊരു ഫലമുണ്ട്. ഇവിടെ 'r'ന് 'n' എന്ന മൂല്യം കല്പിക്കുകയാണെങ്കില്‍ [[ചിത്രം:Pg343_scree03.png]] എന്നു കിട്ടുന്നു. നോ. ക്രമചയം, സഞ്ചയം | ||
(ഡോ. എസ്. പരമേശ്വരന്‍) | (ഡോ. എസ്. പരമേശ്വരന്‍) | ||
Current revision as of 16:39, 14 സെപ്റ്റംബര്‍ 2015
ക്രമഗുണിതം
Factorial
ഒന്നില്‍ ആരംഭിക്കുകയോ അവസാനിക്കുകയോ ചെയ്യുന്ന ക്രമാനുസാരിയായ ധനപൂര്‍ണസംഖ്യകളുടെ ശൃംഖലാഗുണനഫലം. ഒരു ധനപൂര്‍ണസംഖ്യ ആണെന്നിരിക്കട്ടെ. n-നെ (n-1) കൊണ്ടു ഗുണിച്ചുകിട്ടുന്ന ഫലത്തെകൊണ്ട് (n - 2) ഗുണിക്കുക. ഇങ്ങനെ ഓരോ ഗുണനഫലത്തെയും അവരോഹണക്രമത്തില്‍ അടുത്തുവരുന്ന പൂര്‍ണസംഖ്യകൊണ്ട് 1 എന്ന സംഖ്യ ഗുണകമായി വരുന്നതുവരെ തുടര്‍ന്നു ഗുണിക്കുക. അപ്പോള്‍ കിട്ടുന്നn x (n-1) x (n-2) x ..... x 3 x 2x 1 എന്ന ഗുണനഫലത്തെ n! അഥവാ Ln എന്നു രേഖപ്പെടുത്തുകയും n ക്രമഗുണിതം' അഥവാ 'ക്രമഗുണിതം n' എന്ന് ഉച്ചരിക്കുകയും ചെയ്തുവരുന്നു. 'n' ല്‍ നിന്നാരംഭിച്ച് 1 -ല്‍ എത്തുന്നതിനു പകരം 1-ല്‍ നിന്നാരംഭിച്ച് n-ല്‍ എത്തുകയാണെങ്കിലും കിട്ടുന്നത് n! അഥവാ Ln ആണ്. അതുകൊണ്ട്
സഞ്ചയ(combination)ത്തില്‍ 
എന്നൊരു ഫലമുണ്ട്. ഇവിടെ 'r'ന് 'n' എന്ന മൂല്യം കല്പിക്കുകയാണെങ്കില്‍ 
എന്നു കിട്ടുന്നു. നോ. ക്രമചയം, സഞ്ചയം
(ഡോ. എസ്. പരമേശ്വരന്‍)
