This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോംപ്‌ടണ്‍ പ്രഭാവം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Compton Effect) |
(→Compton Effect) |
||
| (ഇടക്കുള്ള 5 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 4: | വരി 4: | ||
== Compton Effect == | == Compton Effect == | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Screenshot-4.png|300px|thumb|]] |
| - | പ്ലാന്നിന്റെ ക്വാണ്ടം സിദ്ധാന്തം ശരിയാണെന്നു സ്ഥാപിച്ച ആദ്യത്തെ പരീക്ഷണം. പ്ലാന്നിന്റെ സിദ്ധാന്തവും അതിന്‌ ഐന്‍സ്റ്റൈന്‍ നല്‍കിയ വ്യാഖ്യാനവും അനുസരിച്ച്‌ പ്രകാശം ഉത്സര്‍ജിക്കുന്നതും സഞ്ചരിക്കുന്നതും ആഗിരണം ചെയ്യപ്പെടുന്നതും ഊര്‍ജക്വാണ്ടങ്ങള്‍ ആയിട്ടാണ്‌. ആവൃത്തിയും | + | പ്ലാന്നിന്റെ ക്വാണ്ടം സിദ്ധാന്തം ശരിയാണെന്നു സ്ഥാപിച്ച ആദ്യത്തെ പരീക്ഷണം. പ്ലാന്നിന്റെ സിദ്ധാന്തവും അതിന്‌ ഐന്‍സ്റ്റൈന്‍ നല്‍കിയ വ്യാഖ്യാനവും അനുസരിച്ച്‌ പ്രകാശം ഉത്സര്‍ജിക്കുന്നതും സഞ്ചരിക്കുന്നതും ആഗിരണം ചെയ്യപ്പെടുന്നതും ഊര്‍ജക്വാണ്ടങ്ങള്‍ ആയിട്ടാണ്‌. ν ആവൃത്തിയും 𝜆 തരംഗദൈര്‍ഘ്യവുമുള്ള പ്രകാശത്തിന്റെ ക്വാണ്ടത്തിന്‌ (ഫോട്ടോണ്‍) [[ചിത്രം:Pag_159screen.png]] ഊര്‍ജമുണ്ടായിരിക്കും (C-പ്രകാശപ്രവേഗം). ഇതിനെ സാധൂകരിക്കുന്ന പരീക്ഷണമാണ്‌ 1923-ല്‍ ആര്‍തര്‍ ഹോളി കോംപ്‌ടണ്‍ (1892-1962) നടത്തിയത്‌. ഈ പഠനത്തിന്‌ 1927-ല്‍ ബ്രിട്ടീഷ്‌ ശാസ്‌ത്രജ്ഞനായ ബി.ടി.ആര്‍.വില്‍സണുമായി ഇദ്ദേഹം നോബല്‍സമ്മാനം പങ്കിട്ടു. |
| - | ഒരു നിശ്ചിത തരംഗദൈര്‍ഘ്യം മാത്രമുള്ള എക്‌സ്‌-റേ ഇദ്ദേഹം ഒരു ഗ്രാഫൈറ്റ്‌ തകിടില്‍ പതിപ്പിച്ചു. തകിടില്‍നിന്നു വിവിധ കോണങ്ങളിലായി പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയുടെ തീവ്രത ഇദ്ദേഹം അളന്നു. പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയില്‍തരംഗദൈര്‍ഘ്യമുള്ള എക്‌സ്‌-റേ യോടൊപ്പം, അതില്‍ക്കൂടുതല്‍ തരംഗദൈര്‍ഘ്യം ഉള്ള എക്‌സ്‌-റേയും കാണപ്പെട്ടു. പ്രകീര്‍ണനകോണം | + | |
| - | [[ചിത്രം: | + | ഒരു നിശ്ചിത തരംഗദൈര്‍ഘ്യം മാത്രമുള്ള (𝜆) എക്‌സ്‌-റേ ഇദ്ദേഹം ഒരു ഗ്രാഫൈറ്റ്‌ തകിടില്‍ പതിപ്പിച്ചു. തകിടില്‍നിന്നു വിവിധ കോണങ്ങളിലായി പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയുടെ തീവ്രത ഇദ്ദേഹം അളന്നു. പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയില്‍തരംഗദൈര്‍ഘ്യമുള്ള എക്‌സ്‌-റേ യോടൊപ്പം, അതില്‍ക്കൂടുതല്‍ തരംഗദൈര്‍ഘ്യം 𝜆 ഉള്ള എക്‌സ്‌-റേയും കാണപ്പെട്ടു. പ്രകീര്‍ണനകോണം (φ) കൂടുന്നതനുസരിച്ച്‌ ഈ രണ്ടു തരംഗദൈര്‍ഘ്യങ്ങള്‍ തമ്മിലുള്ള വ്യത്യാസവും കൂടിവന്നു. ഇവിടെ പ്രകീര്‍ണനകോണം എന്നു പറയുന്നതു തകിടില്‍ പതിച്ച എക്‌സ്‌-റേയുടെയും പ്രകീര്‍ണിത എക്‌സ്‌-റേയുടെയും ദിശകള്‍ക്കിടയിലുള്ള കോണമാണ്‌ (ചിത്രം1) എക്‌സ്‌-റേയ്‌ക്ക്‌ ഒരു വിദ്യുത്‌ കാന്തികതരംഗത്തിന്റെ സ്വഭാവം മാത്രമാണ്‌ ഉണ്ടായിരുന്നതെങ്കില്‍ പ്രകീര്‍ണനംമൂലം പുതിയ തരംഗദൈര്‍ഘ്യമുള്ള എക്‌സ്‌-റേ ഉണ്ടാവുക അസാധ്യമായിരുന്നു. |
| + | |||
| + | [[ചിത്രം:160.png]] | ||
| + | |||
കോംപ്‌ടന്റെ പരീക്ഷണഫലത്തെ ക്വാണ്ടംസിദ്ധാന്തമനുസരിച്ചു വിജയകരമായി വ്യാഖ്യാനിക്കുന്നതിന്‌ അദ്ദേഹത്തിനു കഴിഞ്ഞു. തരംഗദൈര്‍ഘ്യവ്യത്യാസവും പ്രകീര്‍ണനകോണവും തമ്മിലുള്ള ബന്ധം ഒരു സമീകരണംവഴി താഴെ വിവരിക്കുന്ന പ്രകാരം അദ്ദേഹം സ്ഥാപിച്ചു. | കോംപ്‌ടന്റെ പരീക്ഷണഫലത്തെ ക്വാണ്ടംസിദ്ധാന്തമനുസരിച്ചു വിജയകരമായി വ്യാഖ്യാനിക്കുന്നതിന്‌ അദ്ദേഹത്തിനു കഴിഞ്ഞു. തരംഗദൈര്‍ഘ്യവ്യത്യാസവും പ്രകീര്‍ണനകോണവും തമ്മിലുള്ള ബന്ധം ഒരു സമീകരണംവഴി താഴെ വിവരിക്കുന്ന പ്രകാരം അദ്ദേഹം സ്ഥാപിച്ചു. | ||
| - | തരംഗദൈര്‍ഘ്യവും ആവൃത്തിയുമുള്ള എക്‌സ്‌-റേയുടെ ഒരു ഫോട്ടോണില്‍ | + | 𝜆 തരംഗദൈര്‍ഘ്യവും ν ആവൃത്തിയുമുള്ള എക്‌സ്‌-റേയുടെ ഒരു ഫോട്ടോണില്‍ h ν ഊര്‍ജം ഉണ്ടായിരിക്കും. ഇവിടെ h പ്ലാന്ന്‌ സ്ഥിരാന്നത്തെ കുറിക്കുന്നു. ഈ ഫോട്ടോണിനെ h/𝜆 സംവേഗമുള്ള ഒരു കണമായി ക്വാണ്ടംസിദ്ധാന്തം കണക്കാക്കുന്നു. ഈ ഫോട്ടോണ്‍ ഗ്രാഫൈറ്റിലെ മിക്കവാറും സ്വതന്ത്രവും, വിരാമാവസ്ഥയിലുള്ളതുമായ ഒരു ഇലക്‌ട്രാണുമായി കൂട്ടിമുട്ടുമ്പോള്‍, ഫോട്ടോണിലെ ഊര്‍ജത്തിന്റെ ഒരു ഭാഗം ഗതികോര്‍ജമായി ഇലക്‌ട്രോണ്‍ സ്വീകരിച്ചു θകോണത്തില്‍ക്കൂടെ ഒരു വശത്തേക്കു തെറിക്കുന്നു. ഫോട്ടോണിലെ ബാക്കി ഊര്‍ജം മറ്റൊരു കുറഞ്ഞ (ν) ആവൃത്തിയും കൂടിയ തരംഗദൈര്‍ഘ്യം 𝜆 ഉം ഉള്ള ഒരു ഫോട്ടോണായി ø കോണത്തില്‍ കൂടെ പോകുന്നു. സംഘട്ടനത്തിനു മുമ്പും പിമ്പുമുള്ള അവസ്ഥ ചിത്രം 1-ല്‍ കാണിച്ചിരിക്കുന്നു. ആപേക്ഷികതാ സിദ്ധാന്തമനുസരിച്ച്‌ ഇലക്‌ട്രാണിന്റെ ഗതികോര്‍ജം (m – m<sub>0</sub>)C<sup>2</sup> ആയിരിക്കും. ഇവിടെ m എന്നത്‌ പ്രവേഗമുള്ള ഇലക്‌ട്രാണിന്റെ ദ്രവ്യമാനവും m<sub>0</sub> അതിന്റെ വിരാമസ്ഥിതിയിലുള്ള ദ്രവ്യമാനവുമാണ്‌. ആപേക്ഷികതാസിദ്ധാന്തപ്രകാരം [[ചിത്രം:160sce1.png]] ഊര്‍ജസംരക്ഷണനിയമമനുസരിച്ച്‌ |
| - | + (m – | + | hν = hν '+ (m – m<sub>O</sub>)C<sup>2</sup> ...... (1) ഫോട്ടോണും ഇലക്‌ട്രാണും തമ്മിലുള്ള സംഘട്ടനം രണ്ടു കണങ്ങളുടെ ഇലാസ്‌തിക സംഘട്ടനമായി കരുതാവുന്നതാണ്‌. അപ്പോള്‍ സംഘട്ടനം സംവേഗസംരക്ഷണനിയമം പാലിക്കുന്നതായി കണക്കാക്കാം. x - ദിശയിലെയും y - ദിശയിലെയും സംവേഗം പരിഗണിക്കുമ്പോള്‍ |
| - | + | ||
| - | + | [[ചിത്രം:160_formula3.png]] | |
| - | മേല്‍ വിവരിച്ച സമീകരണങ്ങളില്‍നിന്നു -ഉം -ഉം ഒഴിവാക്കുമ്പോള്‍ | + | |
| + | മേല്‍ വിവരിച്ച സമീകരണങ്ങളില്‍നിന്നു ν -ഉം - θ ഉം ഒഴിവാക്കുമ്പോള്‍ | ||
| + | |||
| + | [[ചിത്രം:Scree01.png]] | ||
എന്ന സമീകരണം ലഭിക്കുന്നു. | എന്ന സമീകരണം ലഭിക്കുന്നു. | ||
| + | |||
പ്രകീര്‍ണനകോണം 150º വരെ ആക്കിക്കൊണ്ടു ചെയ്‌ത പരീക്ഷണങ്ങള്‍ ഈ സമീകരണത്തെ സ്ഥിരീകരിക്കുന്നു. | പ്രകീര്‍ണനകോണം 150º വരെ ആക്കിക്കൊണ്ടു ചെയ്‌ത പരീക്ഷണങ്ങള്‍ ഈ സമീകരണത്തെ സ്ഥിരീകരിക്കുന്നു. | ||
| - | സമീകരണം(4)-ലെ "കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം' എന്നറിയപ്പെടുന്നു. ആകുമ്പോള്‍ ലഭിക്കുന്ന - ആണ്‌ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം. ഇതിന്റെ അളവ്‌ 0.024 A അഥവാ 2. | + | |
| - | പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേ ഊര്‍ജത്തില്‍ പ്രകീര്‍ണനത്തിനുപയോഗിച്ച എക്‌സ്‌-റേയുടെ തരംഗങ്ങള്‍ തന്നെ ഭാവവ്യത്യാസം കൂടാതെ കാണപ്പെടുന്നത്‌ എന്തുകൊണ്ടാണെന്നുള്ള ചോദ്യം ഇവിടെ അവശേഷിക്കുന്നു. ഫോട്ടോണ്‍ കൂട്ടിമുട്ടുന്നതു ഗ്രഫൈറ്റിലെ കാര്‍ബണ്‍ അണുവില്‍ പ്രബലമായി ബന്ധിക്കപ്പെട്ടിരിക്കുന്ന ഒരു ഇലക്‌ട്രാണുമായിട്ട്‌ ആകാം. ആ ഇലക്‌ട്രാണിനു പരമാണുവോടുകൂടെയല്ലാതെ വേര്‍പെട്ടു സ്വതന്ത്രമായി തെറിക്കാന്‍ കഴിയുന്നില്ല. അപ്പോള്‍ കോംപ്‌ടണ്‍ സമീകരണത്തില്‍ | + | |
| + | സമീകരണം(4)-ലെ [[ചിത്രം:Page_160for_3.png ]] "കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം' എന്നറിയപ്പെടുന്നു. φ = 90º ആകുമ്പോള്‍ ലഭിക്കുന്ന 𝜆'- 𝜆 ആണ്‌ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം. ഇതിന്റെ അളവ്‌ 0.024 A അഥവാ 2.4X10<sup>–12</sup> മീ. ആണ്‌. φ = 180º ആകുമ്പോള്‍ ആണ്‌ ഏറ്റവും കൂടിയ തരംഗദൈര്‍ഘ്യവ്യത്യാസം (𝜆'-𝜆 = 2 X 0.024 A) ഉണ്ടാകുന്നത്‌. | ||
| + | |||
| + | പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേ ഊര്‍ജത്തില്‍ പ്രകീര്‍ണനത്തിനുപയോഗിച്ച എക്‌സ്‌-റേയുടെ തരംഗങ്ങള്‍ തന്നെ ഭാവവ്യത്യാസം കൂടാതെ കാണപ്പെടുന്നത്‌ എന്തുകൊണ്ടാണെന്നുള്ള ചോദ്യം ഇവിടെ അവശേഷിക്കുന്നു. ഫോട്ടോണ്‍ കൂട്ടിമുട്ടുന്നതു ഗ്രഫൈറ്റിലെ കാര്‍ബണ്‍ അണുവില്‍ പ്രബലമായി ബന്ധിക്കപ്പെട്ടിരിക്കുന്ന ഒരു ഇലക്‌ട്രാണുമായിട്ട്‌ ആകാം. ആ ഇലക്‌ട്രാണിനു പരമാണുവോടുകൂടെയല്ലാതെ വേര്‍പെട്ടു സ്വതന്ത്രമായി തെറിക്കാന്‍ കഴിയുന്നില്ല. അപ്പോള്‍ കോംപ്‌ടണ്‍ സമീകരണത്തില്‍ m<sub>0</sub>-യ്‌ക്കു പകരം ഒരു കാര്‍ബണ്‍ പരമാണുവിന്റെ ദ്രവ്യമാനമായിരിക്കണം ചേര്‍ക്കേണ്ടത്‌. ഇത്‌ ഒരു ഇലക്‌ട്രാണിന്റെ ദ്രവ്യമാനത്തെക്കാള്‍ ഏറെ മടങ്ങ്‌ വലുതാണ്‌. അപ്പോള്‍ 𝜆'- 𝜆 യുടെ അളവു 𝜆 - യോടു താരതമ്യപ്പെടുത്തുമ്പോള്‍ നിസ്സാരമായിരിക്കും. അതായത്‌ 𝜆' മിക്കവാറും 𝜆-ക്കു സമമായിരിക്കും; അഥവാ, ഈ പ്രകീര്‍ണനം തരംഗദൈര്‍ഘ്യവ്യത്യാസം ഉണ്ടാക്കുന്നില്ല. | ||
ഗ്രാഫൈറ്റിനു പകരം അണുദ്രവ്യമാനം കുറവായിട്ടുള്ള മറ്റു മൂലകങ്ങളും കോംപ്‌ടണ്‍ പരീക്ഷണത്തിനുപയോഗിക്കാവുന്നതാണ്‌. പരീക്ഷണത്തിനുപയോഗിക്കുന്ന എക്‌സ്‌-റേ യുടെ തരംഗദൈര്‍ഘ്യമോ പ്രകീര്‍ണനഹേതുവായ പദാര്‍ഥത്തിന്റെ സ്വഭാവമോ പ്രകീര്‍ണനഫലമായി ഉണ്ടാകുന്ന തരംഗദൈര്‍ഘ്യവ്യതിയാനത്തെ ബാധിക്കുന്നില്ല. എന്നാല്‍, ഇവ രണ്ടും പ്രകീര്‍ണിത എക്‌സ്‌-റേ വിഭാഗങ്ങളുടെ താരതമ്യതീവ്രതയെ ബാധിക്കും. | ഗ്രാഫൈറ്റിനു പകരം അണുദ്രവ്യമാനം കുറവായിട്ടുള്ള മറ്റു മൂലകങ്ങളും കോംപ്‌ടണ്‍ പരീക്ഷണത്തിനുപയോഗിക്കാവുന്നതാണ്‌. പരീക്ഷണത്തിനുപയോഗിക്കുന്ന എക്‌സ്‌-റേ യുടെ തരംഗദൈര്‍ഘ്യമോ പ്രകീര്‍ണനഹേതുവായ പദാര്‍ഥത്തിന്റെ സ്വഭാവമോ പ്രകീര്‍ണനഫലമായി ഉണ്ടാകുന്ന തരംഗദൈര്‍ഘ്യവ്യതിയാനത്തെ ബാധിക്കുന്നില്ല. എന്നാല്‍, ഇവ രണ്ടും പ്രകീര്‍ണിത എക്‌സ്‌-റേ വിഭാഗങ്ങളുടെ താരതമ്യതീവ്രതയെ ബാധിക്കും. | ||
| - | ദൃശ്യപ്രകാശം ഉപയോഗിച്ചുള്ള കോംപ്‌ടണ്‍ പരീക്ഷണം വിജയകരമല്ല. ഏറ്റവും കൂടുതലായ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യവ്യത്യാസം 0.048 | + | ദൃശ്യപ്രകാശം ഉപയോഗിച്ചുള്ള കോംപ്‌ടണ്‍ പരീക്ഷണം വിജയകരമല്ല. ഏറ്റവും കൂടുതലായ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യവ്യത്യാസം 0.048 A മാത്രമാണ്‌. ദൃശ്യമായ പ്രകാശത്തിന്റെ തരംഗദൈര്‍ഘ്യത്തോടു താരതമ്യപ്പെടുത്തുമ്പോള്‍ ഇത്‌ തുച്ഛമാണ്‌. |
കോംപ്‌ടണ്‍ പ്രഭാവത്തിനു "രാമന്‍ പ്രഭാവ'വുമായി ചില സാമ്യങ്ങളുണ്ട്‌. രാമന്‍ പ്രഭാവവും ഒരു പ്രകീര്‍ണനം ആണ്‌. ഇവിടെ, ഫോട്ടോണുകള്‍ പതിക്കുന്ന പദാര്‍ഥത്തിലെ തന്മാത്രകളുടെ അവസ്ഥ (ഉത്തേജിതമോ അല്ലയോ എന്നത്‌) അനുസരിച്ച്‌ പ്രകീര്‍ണിത പ്രകാശത്തിന്റെ തരംഗദൈര്‍ഘ്യം കുറയുകയും കൂടുകയും ചെയ്യാം എന്നതാണ്‌ വ്യത്യാസം. | കോംപ്‌ടണ്‍ പ്രഭാവത്തിനു "രാമന്‍ പ്രഭാവ'വുമായി ചില സാമ്യങ്ങളുണ്ട്‌. രാമന്‍ പ്രഭാവവും ഒരു പ്രകീര്‍ണനം ആണ്‌. ഇവിടെ, ഫോട്ടോണുകള്‍ പതിക്കുന്ന പദാര്‍ഥത്തിലെ തന്മാത്രകളുടെ അവസ്ഥ (ഉത്തേജിതമോ അല്ലയോ എന്നത്‌) അനുസരിച്ച്‌ പ്രകീര്‍ണിത പ്രകാശത്തിന്റെ തരംഗദൈര്‍ഘ്യം കുറയുകയും കൂടുകയും ചെയ്യാം എന്നതാണ്‌ വ്യത്യാസം. | ||
(പ്രൊഫ. ടി.ബി. തോമസ്‌) | (പ്രൊഫ. ടി.ബി. തോമസ്‌) | ||
Current revision as of 16:17, 6 ഓഗസ്റ്റ്‌ 2015
കോംപ്‌ടണ്‍ പ്രഭാവം
Compton Effect
പ്ലാന്നിന്റെ ക്വാണ്ടം സിദ്ധാന്തം ശരിയാണെന്നു സ്ഥാപിച്ച ആദ്യത്തെ പരീക്ഷണം. പ്ലാന്നിന്റെ സിദ്ധാന്തവും അതിന്‌ ഐന്‍സ്റ്റൈന്‍ നല്‍കിയ വ്യാഖ്യാനവും അനുസരിച്ച്‌ പ്രകാശം ഉത്സര്‍ജിക്കുന്നതും സഞ്ചരിക്കുന്നതും ആഗിരണം ചെയ്യപ്പെടുന്നതും ഊര്‍ജക്വാണ്ടങ്ങള്‍ ആയിട്ടാണ്‌. ν ആവൃത്തിയും 𝜆 തരംഗദൈര്‍ഘ്യവുമുള്ള പ്രകാശത്തിന്റെ ക്വാണ്ടത്തിന്‌ (ഫോട്ടോണ്‍) 
ഊര്‍ജമുണ്ടായിരിക്കും (C-പ്രകാശപ്രവേഗം). ഇതിനെ സാധൂകരിക്കുന്ന പരീക്ഷണമാണ്‌ 1923-ല്‍ ആര്‍തര്‍ ഹോളി കോംപ്‌ടണ്‍ (1892-1962) നടത്തിയത്‌. ഈ പഠനത്തിന്‌ 1927-ല്‍ ബ്രിട്ടീഷ്‌ ശാസ്‌ത്രജ്ഞനായ ബി.ടി.ആര്‍.വില്‍സണുമായി ഇദ്ദേഹം നോബല്‍സമ്മാനം പങ്കിട്ടു.
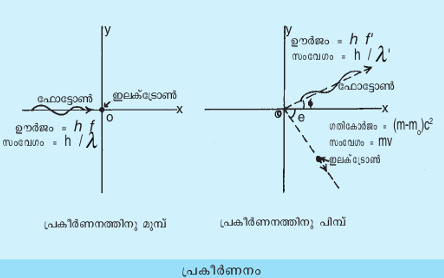
ഒരു നിശ്ചിത തരംഗദൈര്‍ഘ്യം മാത്രമുള്ള (𝜆) എക്‌സ്‌-റേ ഇദ്ദേഹം ഒരു ഗ്രാഫൈറ്റ്‌ തകിടില്‍ പതിപ്പിച്ചു. തകിടില്‍നിന്നു വിവിധ കോണങ്ങളിലായി പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയുടെ തീവ്രത ഇദ്ദേഹം അളന്നു. പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേയില്‍തരംഗദൈര്‍ഘ്യമുള്ള എക്‌സ്‌-റേ യോടൊപ്പം, അതില്‍ക്കൂടുതല്‍ തരംഗദൈര്‍ഘ്യം 𝜆 ഉള്ള എക്‌സ്‌-റേയും കാണപ്പെട്ടു. പ്രകീര്‍ണനകോണം (φ) കൂടുന്നതനുസരിച്ച്‌ ഈ രണ്ടു തരംഗദൈര്‍ഘ്യങ്ങള്‍ തമ്മിലുള്ള വ്യത്യാസവും കൂടിവന്നു. ഇവിടെ പ്രകീര്‍ണനകോണം എന്നു പറയുന്നതു തകിടില്‍ പതിച്ച എക്‌സ്‌-റേയുടെയും പ്രകീര്‍ണിത എക്‌സ്‌-റേയുടെയും ദിശകള്‍ക്കിടയിലുള്ള കോണമാണ്‌ (ചിത്രം1) എക്‌സ്‌-റേയ്‌ക്ക്‌ ഒരു വിദ്യുത്‌ കാന്തികതരംഗത്തിന്റെ സ്വഭാവം മാത്രമാണ്‌ ഉണ്ടായിരുന്നതെങ്കില്‍ പ്രകീര്‍ണനംമൂലം പുതിയ തരംഗദൈര്‍ഘ്യമുള്ള എക്‌സ്‌-റേ ഉണ്ടാവുക അസാധ്യമായിരുന്നു.
കോംപ്‌ടന്റെ പരീക്ഷണഫലത്തെ ക്വാണ്ടംസിദ്ധാന്തമനുസരിച്ചു വിജയകരമായി വ്യാഖ്യാനിക്കുന്നതിന്‌ അദ്ദേഹത്തിനു കഴിഞ്ഞു. തരംഗദൈര്‍ഘ്യവ്യത്യാസവും പ്രകീര്‍ണനകോണവും തമ്മിലുള്ള ബന്ധം ഒരു സമീകരണംവഴി താഴെ വിവരിക്കുന്ന പ്രകാരം അദ്ദേഹം സ്ഥാപിച്ചു.
𝜆 തരംഗദൈര്‍ഘ്യവും ν ആവൃത്തിയുമുള്ള എക്‌സ്‌-റേയുടെ ഒരു ഫോട്ടോണില്‍ h ν ഊര്‍ജം ഉണ്ടായിരിക്കും. ഇവിടെ h പ്ലാന്ന്‌ സ്ഥിരാന്നത്തെ കുറിക്കുന്നു. ഈ ഫോട്ടോണിനെ h/𝜆 സംവേഗമുള്ള ഒരു കണമായി ക്വാണ്ടംസിദ്ധാന്തം കണക്കാക്കുന്നു. ഈ ഫോട്ടോണ്‍ ഗ്രാഫൈറ്റിലെ മിക്കവാറും സ്വതന്ത്രവും, വിരാമാവസ്ഥയിലുള്ളതുമായ ഒരു ഇലക്‌ട്രാണുമായി കൂട്ടിമുട്ടുമ്പോള്‍, ഫോട്ടോണിലെ ഊര്‍ജത്തിന്റെ ഒരു ഭാഗം ഗതികോര്‍ജമായി ഇലക്‌ട്രോണ്‍ സ്വീകരിച്ചു θകോണത്തില്‍ക്കൂടെ ഒരു വശത്തേക്കു തെറിക്കുന്നു. ഫോട്ടോണിലെ ബാക്കി ഊര്‍ജം മറ്റൊരു കുറഞ്ഞ (ν) ആവൃത്തിയും കൂടിയ തരംഗദൈര്‍ഘ്യം 𝜆 ഉം ഉള്ള ഒരു ഫോട്ടോണായി ø കോണത്തില്‍ കൂടെ പോകുന്നു. സംഘട്ടനത്തിനു മുമ്പും പിമ്പുമുള്ള അവസ്ഥ ചിത്രം 1-ല്‍ കാണിച്ചിരിക്കുന്നു. ആപേക്ഷികതാ സിദ്ധാന്തമനുസരിച്ച്‌ ഇലക്‌ട്രാണിന്റെ ഗതികോര്‍ജം (m – m0)C2 ആയിരിക്കും. ഇവിടെ m എന്നത്‌ പ്രവേഗമുള്ള ഇലക്‌ട്രാണിന്റെ ദ്രവ്യമാനവും m0 അതിന്റെ വിരാമസ്ഥിതിയിലുള്ള ദ്രവ്യമാനവുമാണ്‌. ആപേക്ഷികതാസിദ്ധാന്തപ്രകാരം 
ഊര്‍ജസംരക്ഷണനിയമമനുസരിച്ച്‌
hν = hν '+ (m – mO)C2 ...... (1) ഫോട്ടോണും ഇലക്‌ട്രാണും തമ്മിലുള്ള സംഘട്ടനം രണ്ടു കണങ്ങളുടെ ഇലാസ്‌തിക സംഘട്ടനമായി കരുതാവുന്നതാണ്‌. അപ്പോള്‍ സംഘട്ടനം സംവേഗസംരക്ഷണനിയമം പാലിക്കുന്നതായി കണക്കാക്കാം. x - ദിശയിലെയും y - ദിശയിലെയും സംവേഗം പരിഗണിക്കുമ്പോള്‍
മേല്‍ വിവരിച്ച സമീകരണങ്ങളില്‍നിന്നു ν -ഉം - θ ഉം ഒഴിവാക്കുമ്പോള്‍
എന്ന സമീകരണം ലഭിക്കുന്നു.
പ്രകീര്‍ണനകോണം 150º വരെ ആക്കിക്കൊണ്ടു ചെയ്‌ത പരീക്ഷണങ്ങള്‍ ഈ സമീകരണത്തെ സ്ഥിരീകരിക്കുന്നു.
സമീകരണം(4)-ലെ 
"കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം' എന്നറിയപ്പെടുന്നു. φ = 90º ആകുമ്പോള്‍ ലഭിക്കുന്ന 𝜆'- 𝜆 ആണ്‌ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യം. ഇതിന്റെ അളവ്‌ 0.024 A അഥവാ 2.4X10–12 മീ. ആണ്‌. φ = 180º ആകുമ്പോള്‍ ആണ്‌ ഏറ്റവും കൂടിയ തരംഗദൈര്‍ഘ്യവ്യത്യാസം (𝜆'-𝜆 = 2 X 0.024 A) ഉണ്ടാകുന്നത്‌.
പ്രകീര്‍ണനം സംഭവിച്ച എക്‌സ്‌-റേ ഊര്‍ജത്തില്‍ പ്രകീര്‍ണനത്തിനുപയോഗിച്ച എക്‌സ്‌-റേയുടെ തരംഗങ്ങള്‍ തന്നെ ഭാവവ്യത്യാസം കൂടാതെ കാണപ്പെടുന്നത്‌ എന്തുകൊണ്ടാണെന്നുള്ള ചോദ്യം ഇവിടെ അവശേഷിക്കുന്നു. ഫോട്ടോണ്‍ കൂട്ടിമുട്ടുന്നതു ഗ്രഫൈറ്റിലെ കാര്‍ബണ്‍ അണുവില്‍ പ്രബലമായി ബന്ധിക്കപ്പെട്ടിരിക്കുന്ന ഒരു ഇലക്‌ട്രാണുമായിട്ട്‌ ആകാം. ആ ഇലക്‌ട്രാണിനു പരമാണുവോടുകൂടെയല്ലാതെ വേര്‍പെട്ടു സ്വതന്ത്രമായി തെറിക്കാന്‍ കഴിയുന്നില്ല. അപ്പോള്‍ കോംപ്‌ടണ്‍ സമീകരണത്തില്‍ m0-യ്‌ക്കു പകരം ഒരു കാര്‍ബണ്‍ പരമാണുവിന്റെ ദ്രവ്യമാനമായിരിക്കണം ചേര്‍ക്കേണ്ടത്‌. ഇത്‌ ഒരു ഇലക്‌ട്രാണിന്റെ ദ്രവ്യമാനത്തെക്കാള്‍ ഏറെ മടങ്ങ്‌ വലുതാണ്‌. അപ്പോള്‍ 𝜆'- 𝜆 യുടെ അളവു 𝜆 - യോടു താരതമ്യപ്പെടുത്തുമ്പോള്‍ നിസ്സാരമായിരിക്കും. അതായത്‌ 𝜆' മിക്കവാറും 𝜆-ക്കു സമമായിരിക്കും; അഥവാ, ഈ പ്രകീര്‍ണനം തരംഗദൈര്‍ഘ്യവ്യത്യാസം ഉണ്ടാക്കുന്നില്ല.
ഗ്രാഫൈറ്റിനു പകരം അണുദ്രവ്യമാനം കുറവായിട്ടുള്ള മറ്റു മൂലകങ്ങളും കോംപ്‌ടണ്‍ പരീക്ഷണത്തിനുപയോഗിക്കാവുന്നതാണ്‌. പരീക്ഷണത്തിനുപയോഗിക്കുന്ന എക്‌സ്‌-റേ യുടെ തരംഗദൈര്‍ഘ്യമോ പ്രകീര്‍ണനഹേതുവായ പദാര്‍ഥത്തിന്റെ സ്വഭാവമോ പ്രകീര്‍ണനഫലമായി ഉണ്ടാകുന്ന തരംഗദൈര്‍ഘ്യവ്യതിയാനത്തെ ബാധിക്കുന്നില്ല. എന്നാല്‍, ഇവ രണ്ടും പ്രകീര്‍ണിത എക്‌സ്‌-റേ വിഭാഗങ്ങളുടെ താരതമ്യതീവ്രതയെ ബാധിക്കും.
ദൃശ്യപ്രകാശം ഉപയോഗിച്ചുള്ള കോംപ്‌ടണ്‍ പരീക്ഷണം വിജയകരമല്ല. ഏറ്റവും കൂടുതലായ കോംപ്‌ടണ്‍ തരംഗദൈര്‍ഘ്യവ്യത്യാസം 0.048 A മാത്രമാണ്‌. ദൃശ്യമായ പ്രകാശത്തിന്റെ തരംഗദൈര്‍ഘ്യത്തോടു താരതമ്യപ്പെടുത്തുമ്പോള്‍ ഇത്‌ തുച്ഛമാണ്‌.
കോംപ്‌ടണ്‍ പ്രഭാവത്തിനു "രാമന്‍ പ്രഭാവ'വുമായി ചില സാമ്യങ്ങളുണ്ട്‌. രാമന്‍ പ്രഭാവവും ഒരു പ്രകീര്‍ണനം ആണ്‌. ഇവിടെ, ഫോട്ടോണുകള്‍ പതിക്കുന്ന പദാര്‍ഥത്തിലെ തന്മാത്രകളുടെ അവസ്ഥ (ഉത്തേജിതമോ അല്ലയോ എന്നത്‌) അനുസരിച്ച്‌ പ്രകീര്‍ണിത പ്രകാശത്തിന്റെ തരംഗദൈര്‍ഘ്യം കുറയുകയും കൂടുകയും ചെയ്യാം എന്നതാണ്‌ വ്യത്യാസം.
(പ്രൊഫ. ടി.ബി. തോമസ്‌)
