This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോണികങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Conics) |
(→Conics) |
||
| (ഇടക്കുള്ള 4 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 4: | വരി 4: | ||
== Conics == | == Conics == | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Page_76_screen.png|300px|right|thumb]] |
| - | + | ||
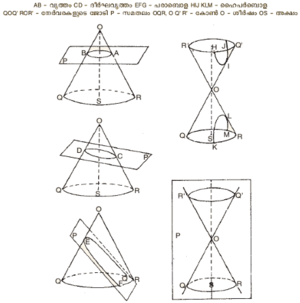
ഒരു സമതലം ഏതെങ്കിലും കോണിനെ വിവിധ രീതികളില് ഛേദിക്കുമ്പോള് കോണിന്റെ വക്രതലത്തില് ഉളവാകുന്ന വക്രങ്ങള്. ഛേദരീതിയുടെ മാറ്റംകൊണ്ട് ഫലത്തിലും മാറ്റം വരുന്നു. ഒരു ത്രികോണം ഒരു വശത്തെ അക്ഷമാക്കി ചുറ്റുമ്പോള് ഉണ്ടാകുന്ന ഘനരൂപമായി കോണ് നിര്വചിക്കപ്പെടുന്നപക്ഷം ആ കോണിന്റെ അക്ഷത്തിനു ലംബമായിട്ടാണ് സമതലം കോണിനെ ഛേദിക്കുന്നതെങ്കില് ഛേദവക്രം വൃത്തമായിരിക്കും; ചരിഞ്ഞാണെങ്കില് ദീര്ഘവൃത്തവും. കോണിന്റെ ജനക(generator)ത്തിനു സമാന്തരമായിട്ടാണെങ്കില് ഛേദവക്രം പരാവലയവും (parabola): കോണ് ശീര്ഷത്തിന്റെ ഇരുവശങ്ങളിലും വ്യാപിച്ചു കിടക്കുന്നതായിട്ടാണ് ഗണിതശാസ്ത്രജ്ഞന്മാര് സങ്കല്പിക്കുന്നത്. അതായത് ജനകം ശീര്ഷത്തിലൂടെ രണ്ടുവശത്തേക്കും അനന്തദൂരം നീട്ടിയതിനു ശേഷം അക്ഷത്തെ ആധാരമാക്കി ചുറ്റുമ്പോള് രണ്ടു ഖണ്ഡങ്ങള് ഉണ്ടാകുന്നു. സമതലം ശീര്ഷത്തില്നിന്നു മാറ്റി കോണിന്റെ അക്ഷത്തിനു സമാന്തരമായി ഈ രണ്ടു ഖണ്ഡങ്ങളെയും ഛേദിക്കുമ്പോള് ഉണ്ടാകുന്ന വക്രമാണ് (hyperbola) ബഹിര്വലയം. സമതലം അക്ഷത്തിലൂടെ കടന്നുപോകുമ്പോള് ഉണ്ടാകുന്ന ഛേദവക്രം പരസ്പരം ഖണ്ഡിക്കുന്ന ഒരു ജോടി നേര്വരകളായിത്തീരുന്നു. ഈ വിവിധ വക്രങ്ങളെ സാമാന്യമായി കോണികങ്ങള് എന്നു വിളിക്കുന്നു. | ഒരു സമതലം ഏതെങ്കിലും കോണിനെ വിവിധ രീതികളില് ഛേദിക്കുമ്പോള് കോണിന്റെ വക്രതലത്തില് ഉളവാകുന്ന വക്രങ്ങള്. ഛേദരീതിയുടെ മാറ്റംകൊണ്ട് ഫലത്തിലും മാറ്റം വരുന്നു. ഒരു ത്രികോണം ഒരു വശത്തെ അക്ഷമാക്കി ചുറ്റുമ്പോള് ഉണ്ടാകുന്ന ഘനരൂപമായി കോണ് നിര്വചിക്കപ്പെടുന്നപക്ഷം ആ കോണിന്റെ അക്ഷത്തിനു ലംബമായിട്ടാണ് സമതലം കോണിനെ ഛേദിക്കുന്നതെങ്കില് ഛേദവക്രം വൃത്തമായിരിക്കും; ചരിഞ്ഞാണെങ്കില് ദീര്ഘവൃത്തവും. കോണിന്റെ ജനക(generator)ത്തിനു സമാന്തരമായിട്ടാണെങ്കില് ഛേദവക്രം പരാവലയവും (parabola): കോണ് ശീര്ഷത്തിന്റെ ഇരുവശങ്ങളിലും വ്യാപിച്ചു കിടക്കുന്നതായിട്ടാണ് ഗണിതശാസ്ത്രജ്ഞന്മാര് സങ്കല്പിക്കുന്നത്. അതായത് ജനകം ശീര്ഷത്തിലൂടെ രണ്ടുവശത്തേക്കും അനന്തദൂരം നീട്ടിയതിനു ശേഷം അക്ഷത്തെ ആധാരമാക്കി ചുറ്റുമ്പോള് രണ്ടു ഖണ്ഡങ്ങള് ഉണ്ടാകുന്നു. സമതലം ശീര്ഷത്തില്നിന്നു മാറ്റി കോണിന്റെ അക്ഷത്തിനു സമാന്തരമായി ഈ രണ്ടു ഖണ്ഡങ്ങളെയും ഛേദിക്കുമ്പോള് ഉണ്ടാകുന്ന വക്രമാണ് (hyperbola) ബഹിര്വലയം. സമതലം അക്ഷത്തിലൂടെ കടന്നുപോകുമ്പോള് ഉണ്ടാകുന്ന ഛേദവക്രം പരസ്പരം ഖണ്ഡിക്കുന്ന ഒരു ജോടി നേര്വരകളായിത്തീരുന്നു. ഈ വിവിധ വക്രങ്ങളെ സാമാന്യമായി കോണികങ്ങള് എന്നു വിളിക്കുന്നു. | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Page_screen76.png|250px]] |
| + | |||
ഗ്രീക്കുകാരാണ് കോണികങ്ങളെക്കുറിച്ചു കൂടുതല് പഠനം നടത്തിയിട്ടുള്ളത്. അവരുടെ സമീപനം ജ്യാമിതീയവീക്ഷണത്തില്നിന്ന് ബീജീയസമീപനത്തിലേക്ക് വളര്ന്നു. കോണിന്റെ ഖണ്ഡങ്ങളെന്ന നിലയിലല്ല പിന്നീട് കോണികങ്ങളെക്കുറിച്ചുള്ള പഠനം പുരോഗതി പ്രാപിച്ചത്; വിശ്ലേഷകജ്യാമിതി (Analytical geometry) എന്ന ഗണിതശാഖയായിട്ടാണ് ഈ പഠനം വളര്ന്നുവന്നത്. ബീജഗണിത തത്ത്വങ്ങളെ ഉപജീവിച്ച് കോണികങ്ങളുടെ നിര്വചനത്തിനുതന്നെ മാറ്റം വരുത്തി. വൃത്തം, ദീര്ഘവൃത്തം, പരാവലയം, ബഹിര്വലയം, നേര്വരകളുടെ ജോടി എന്നീ കോണികവക്രങ്ങളെ ദ്വിഘാതസമവാക്യങ്ങളില്ക്കൂടി നിര്വചിക്കാനും ബീജീയപരിഗണനകള് വഴി അവയുടെ സവിശേഷതകള് കണ്ടെത്താനും തുടങ്ങി. ഈ വക്രങ്ങളെ കോണികങ്ങള് എന്നു വിളിക്കുന്നതുതന്നെ അര്ഥശൂന്യമാകുംവണ്ണം പുതിയ നിര്വചനങ്ങള് പഴയതില് നിന്ന് ഏറെ വ്യത്യസ്തമായിത്തീര്ന്നു. കാര്ത്തീയ നിര്ദേശാന്ന (Co-ordinate system) പദ്ധതിയില് ദ്വിഘാത സമവാക്യങ്ങളുടെ ആരേഖങ്ങളായി ആ വക്രങ്ങളെ പരിഗണിച്ചു. ചില കോണികങ്ങള്ക്ക് "ദീര്ഘവൃത്തം' എന്നും മറ്റുചിലതിന് ബഹിര്വലയം എന്നും പേരുകള് നല്കിയത് പ്രാചീന ഗ്രീക്ക് ഗണിത ശാസ്ത്രജ്ഞനായ അപ്പളോണിയസ് (ബി.സി. 260-200) ആണ്, അതിനു മുമ്പുതന്നെ ഇവയില്നിന്നു വ്യത്യസ്തമായ ഒരുതരം കോണികങ്ങള്ക്ക് പരാവലയം എന്ന പേര് ആര്ക്കിമിഡിസ് (ബി.സി. 287-212) ഉപയോഗിച്ചിരുന്നു. ഇതിനു പ്രചോദനമായത് പ്രാചീന ഗ്രീക്ക് ഗണിതജ്ഞനായ സാമോസിലെ കോനനിന്റെ ആശയങ്ങളാണ് (ബി.സി. 3-ാം ശ.). | ഗ്രീക്കുകാരാണ് കോണികങ്ങളെക്കുറിച്ചു കൂടുതല് പഠനം നടത്തിയിട്ടുള്ളത്. അവരുടെ സമീപനം ജ്യാമിതീയവീക്ഷണത്തില്നിന്ന് ബീജീയസമീപനത്തിലേക്ക് വളര്ന്നു. കോണിന്റെ ഖണ്ഡങ്ങളെന്ന നിലയിലല്ല പിന്നീട് കോണികങ്ങളെക്കുറിച്ചുള്ള പഠനം പുരോഗതി പ്രാപിച്ചത്; വിശ്ലേഷകജ്യാമിതി (Analytical geometry) എന്ന ഗണിതശാഖയായിട്ടാണ് ഈ പഠനം വളര്ന്നുവന്നത്. ബീജഗണിത തത്ത്വങ്ങളെ ഉപജീവിച്ച് കോണികങ്ങളുടെ നിര്വചനത്തിനുതന്നെ മാറ്റം വരുത്തി. വൃത്തം, ദീര്ഘവൃത്തം, പരാവലയം, ബഹിര്വലയം, നേര്വരകളുടെ ജോടി എന്നീ കോണികവക്രങ്ങളെ ദ്വിഘാതസമവാക്യങ്ങളില്ക്കൂടി നിര്വചിക്കാനും ബീജീയപരിഗണനകള് വഴി അവയുടെ സവിശേഷതകള് കണ്ടെത്താനും തുടങ്ങി. ഈ വക്രങ്ങളെ കോണികങ്ങള് എന്നു വിളിക്കുന്നതുതന്നെ അര്ഥശൂന്യമാകുംവണ്ണം പുതിയ നിര്വചനങ്ങള് പഴയതില് നിന്ന് ഏറെ വ്യത്യസ്തമായിത്തീര്ന്നു. കാര്ത്തീയ നിര്ദേശാന്ന (Co-ordinate system) പദ്ധതിയില് ദ്വിഘാത സമവാക്യങ്ങളുടെ ആരേഖങ്ങളായി ആ വക്രങ്ങളെ പരിഗണിച്ചു. ചില കോണികങ്ങള്ക്ക് "ദീര്ഘവൃത്തം' എന്നും മറ്റുചിലതിന് ബഹിര്വലയം എന്നും പേരുകള് നല്കിയത് പ്രാചീന ഗ്രീക്ക് ഗണിത ശാസ്ത്രജ്ഞനായ അപ്പളോണിയസ് (ബി.സി. 260-200) ആണ്, അതിനു മുമ്പുതന്നെ ഇവയില്നിന്നു വ്യത്യസ്തമായ ഒരുതരം കോണികങ്ങള്ക്ക് പരാവലയം എന്ന പേര് ആര്ക്കിമിഡിസ് (ബി.സി. 287-212) ഉപയോഗിച്ചിരുന്നു. ഇതിനു പ്രചോദനമായത് പ്രാചീന ഗ്രീക്ക് ഗണിതജ്ഞനായ സാമോസിലെ കോനനിന്റെ ആശയങ്ങളാണ് (ബി.സി. 3-ാം ശ.). | ||
ജ്യോതിശ്ശാസ്ത്രത്തില് കോണികങ്ങള് ഏറെ പ്രാധാന്യമര്ഹിക്കുന്നു. ന്യൂട്ടന്റെ ഗുരുത്വാകര്ഷണതത്ത്വത്തിലെ വ്യുത്ക്രമവര്ഗനിയമമനുസരിച്ച് ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം ദീര്ഘവൃത്തമാണ്; മറ്റു ചില ജ്യോതിര്ഗോളങ്ങളുടേത് പരാവലയവും ബഹിര്വലയവും. പ്രക്ഷേപീയ ജ്യാമിതി (projective geometry)യുടെ വികാസത്തോടെ കോണികങ്ങള്ക്ക് നൂതനമായ വ്യാഖ്യാനമുണ്ടായിട്ടുണ്ട്. നോ. പ്രക്ഷേപീയ ജ്യാമിതി | ജ്യോതിശ്ശാസ്ത്രത്തില് കോണികങ്ങള് ഏറെ പ്രാധാന്യമര്ഹിക്കുന്നു. ന്യൂട്ടന്റെ ഗുരുത്വാകര്ഷണതത്ത്വത്തിലെ വ്യുത്ക്രമവര്ഗനിയമമനുസരിച്ച് ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം ദീര്ഘവൃത്തമാണ്; മറ്റു ചില ജ്യോതിര്ഗോളങ്ങളുടേത് പരാവലയവും ബഹിര്വലയവും. പ്രക്ഷേപീയ ജ്യാമിതി (projective geometry)യുടെ വികാസത്തോടെ കോണികങ്ങള്ക്ക് നൂതനമായ വ്യാഖ്യാനമുണ്ടായിട്ടുണ്ട്. നോ. പ്രക്ഷേപീയ ജ്യാമിതി | ||
Current revision as of 17:03, 2 ഓഗസ്റ്റ് 2015
കോണികങ്ങള്
Conics
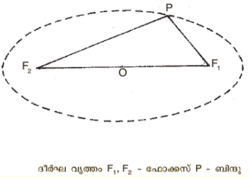
ഒരു സമതലം ഏതെങ്കിലും കോണിനെ വിവിധ രീതികളില് ഛേദിക്കുമ്പോള് കോണിന്റെ വക്രതലത്തില് ഉളവാകുന്ന വക്രങ്ങള്. ഛേദരീതിയുടെ മാറ്റംകൊണ്ട് ഫലത്തിലും മാറ്റം വരുന്നു. ഒരു ത്രികോണം ഒരു വശത്തെ അക്ഷമാക്കി ചുറ്റുമ്പോള് ഉണ്ടാകുന്ന ഘനരൂപമായി കോണ് നിര്വചിക്കപ്പെടുന്നപക്ഷം ആ കോണിന്റെ അക്ഷത്തിനു ലംബമായിട്ടാണ് സമതലം കോണിനെ ഛേദിക്കുന്നതെങ്കില് ഛേദവക്രം വൃത്തമായിരിക്കും; ചരിഞ്ഞാണെങ്കില് ദീര്ഘവൃത്തവും. കോണിന്റെ ജനക(generator)ത്തിനു സമാന്തരമായിട്ടാണെങ്കില് ഛേദവക്രം പരാവലയവും (parabola): കോണ് ശീര്ഷത്തിന്റെ ഇരുവശങ്ങളിലും വ്യാപിച്ചു കിടക്കുന്നതായിട്ടാണ് ഗണിതശാസ്ത്രജ്ഞന്മാര് സങ്കല്പിക്കുന്നത്. അതായത് ജനകം ശീര്ഷത്തിലൂടെ രണ്ടുവശത്തേക്കും അനന്തദൂരം നീട്ടിയതിനു ശേഷം അക്ഷത്തെ ആധാരമാക്കി ചുറ്റുമ്പോള് രണ്ടു ഖണ്ഡങ്ങള് ഉണ്ടാകുന്നു. സമതലം ശീര്ഷത്തില്നിന്നു മാറ്റി കോണിന്റെ അക്ഷത്തിനു സമാന്തരമായി ഈ രണ്ടു ഖണ്ഡങ്ങളെയും ഛേദിക്കുമ്പോള് ഉണ്ടാകുന്ന വക്രമാണ് (hyperbola) ബഹിര്വലയം. സമതലം അക്ഷത്തിലൂടെ കടന്നുപോകുമ്പോള് ഉണ്ടാകുന്ന ഛേദവക്രം പരസ്പരം ഖണ്ഡിക്കുന്ന ഒരു ജോടി നേര്വരകളായിത്തീരുന്നു. ഈ വിവിധ വക്രങ്ങളെ സാമാന്യമായി കോണികങ്ങള് എന്നു വിളിക്കുന്നു.
ഗ്രീക്കുകാരാണ് കോണികങ്ങളെക്കുറിച്ചു കൂടുതല് പഠനം നടത്തിയിട്ടുള്ളത്. അവരുടെ സമീപനം ജ്യാമിതീയവീക്ഷണത്തില്നിന്ന് ബീജീയസമീപനത്തിലേക്ക് വളര്ന്നു. കോണിന്റെ ഖണ്ഡങ്ങളെന്ന നിലയിലല്ല പിന്നീട് കോണികങ്ങളെക്കുറിച്ചുള്ള പഠനം പുരോഗതി പ്രാപിച്ചത്; വിശ്ലേഷകജ്യാമിതി (Analytical geometry) എന്ന ഗണിതശാഖയായിട്ടാണ് ഈ പഠനം വളര്ന്നുവന്നത്. ബീജഗണിത തത്ത്വങ്ങളെ ഉപജീവിച്ച് കോണികങ്ങളുടെ നിര്വചനത്തിനുതന്നെ മാറ്റം വരുത്തി. വൃത്തം, ദീര്ഘവൃത്തം, പരാവലയം, ബഹിര്വലയം, നേര്വരകളുടെ ജോടി എന്നീ കോണികവക്രങ്ങളെ ദ്വിഘാതസമവാക്യങ്ങളില്ക്കൂടി നിര്വചിക്കാനും ബീജീയപരിഗണനകള് വഴി അവയുടെ സവിശേഷതകള് കണ്ടെത്താനും തുടങ്ങി. ഈ വക്രങ്ങളെ കോണികങ്ങള് എന്നു വിളിക്കുന്നതുതന്നെ അര്ഥശൂന്യമാകുംവണ്ണം പുതിയ നിര്വചനങ്ങള് പഴയതില് നിന്ന് ഏറെ വ്യത്യസ്തമായിത്തീര്ന്നു. കാര്ത്തീയ നിര്ദേശാന്ന (Co-ordinate system) പദ്ധതിയില് ദ്വിഘാത സമവാക്യങ്ങളുടെ ആരേഖങ്ങളായി ആ വക്രങ്ങളെ പരിഗണിച്ചു. ചില കോണികങ്ങള്ക്ക് "ദീര്ഘവൃത്തം' എന്നും മറ്റുചിലതിന് ബഹിര്വലയം എന്നും പേരുകള് നല്കിയത് പ്രാചീന ഗ്രീക്ക് ഗണിത ശാസ്ത്രജ്ഞനായ അപ്പളോണിയസ് (ബി.സി. 260-200) ആണ്, അതിനു മുമ്പുതന്നെ ഇവയില്നിന്നു വ്യത്യസ്തമായ ഒരുതരം കോണികങ്ങള്ക്ക് പരാവലയം എന്ന പേര് ആര്ക്കിമിഡിസ് (ബി.സി. 287-212) ഉപയോഗിച്ചിരുന്നു. ഇതിനു പ്രചോദനമായത് പ്രാചീന ഗ്രീക്ക് ഗണിതജ്ഞനായ സാമോസിലെ കോനനിന്റെ ആശയങ്ങളാണ് (ബി.സി. 3-ാം ശ.).
ജ്യോതിശ്ശാസ്ത്രത്തില് കോണികങ്ങള് ഏറെ പ്രാധാന്യമര്ഹിക്കുന്നു. ന്യൂട്ടന്റെ ഗുരുത്വാകര്ഷണതത്ത്വത്തിലെ വ്യുത്ക്രമവര്ഗനിയമമനുസരിച്ച് ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം ദീര്ഘവൃത്തമാണ്; മറ്റു ചില ജ്യോതിര്ഗോളങ്ങളുടേത് പരാവലയവും ബഹിര്വലയവും. പ്രക്ഷേപീയ ജ്യാമിതി (projective geometry)യുടെ വികാസത്തോടെ കോണികങ്ങള്ക്ക് നൂതനമായ വ്യാഖ്യാനമുണ്ടായിട്ടുണ്ട്. നോ. പ്രക്ഷേപീയ ജ്യാമിതി