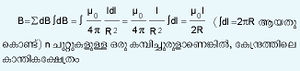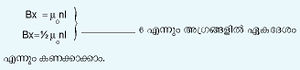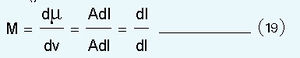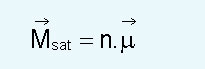This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കാന്തത
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Magnetism) |
Mksol (സംവാദം | സംഭാവനകള്) (→Magnetism) |
||
| (ഇടക്കുള്ള ഒരു പതിപ്പിലെ മാറ്റം ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 2: | വരി 2: | ||
== Magnetism == | == Magnetism == | ||
<gallery Caption=" "> | <gallery Caption=" "> | ||
| - | Image:Vol7p62_William_Gilbert.jpg|വില്യം | + | Image:Vol7p62_William_Gilbert.jpg|വില്യം ഗില്ബെര്ട് |
| - | Image:Vol7p62_Hans_Christian_orsted_daguerreotype.jpg|ഹാന്സ് ക്രിസ്റ്റ്യന് | + | Image:Vol7p62_Hans_Christian_orsted_daguerreotype.jpg|ഹാന്സ് ക്രിസ്റ്റ്യന് ഓര്സ്റ്റഡ് |
| - | Image:Vol7p62_Faraday.jpg| | + | Image:Vol7p62_Faraday.jpg|മൈക്കേല് ഫാരഡെ |
| - | Image:Vol7p62_James_Clerk_Maxwell.jpg|ജെയിംസ് | + | Image:Vol7p62_James_Clerk_Maxwell.jpg|ജെയിംസ് ക്ലാര്ക്ക് മാക്സ്വെല് |
</gallery> | </gallery> | ||
ചാര്ജിതകണങ്ങളുടെ ആപേക്ഷികചലനം, ചക്രണം (spin) ഇവ, കണങ്ങള് തമ്മിലുള്ള അന്യോന്യ പ്രവര്ത്തനത്തില് സൃഷ്ടിക്കുന്ന ഒരു പ്രഭാവം. ഇതിന്റെ സ്ഥൂലഫലം പലരൂപത്തില് പ്രത്യക്ഷപ്പെടാം; സ്ഥിരകാന്തങ്ങള് തമ്മിലും വൈദ്യുതപ്രവാഹവും കാന്തവും തമ്മിലും വൈദ്യുത പ്രവാഹങ്ങള് തമ്മിലുമുള്ള ആകര്ഷണവികര്ഷണങ്ങള് ഇതില്പ്പെടും. വൈദ്യുതബലത്തിന്റെ ( electrical force) തന്നെ ഒരു സവിശേഷ ആപേക്ഷികതാ പ്രഭാവം ( Relatiarstic effect) മാത്രമാണ് കാന്തത എന്ന് ഐന്സ്റ്റൈന്റെ സിദ്ധാന്തം ഉപയോഗിച്ച് തെളിയിക്കാന് കഴിയും. | ചാര്ജിതകണങ്ങളുടെ ആപേക്ഷികചലനം, ചക്രണം (spin) ഇവ, കണങ്ങള് തമ്മിലുള്ള അന്യോന്യ പ്രവര്ത്തനത്തില് സൃഷ്ടിക്കുന്ന ഒരു പ്രഭാവം. ഇതിന്റെ സ്ഥൂലഫലം പലരൂപത്തില് പ്രത്യക്ഷപ്പെടാം; സ്ഥിരകാന്തങ്ങള് തമ്മിലും വൈദ്യുതപ്രവാഹവും കാന്തവും തമ്മിലും വൈദ്യുത പ്രവാഹങ്ങള് തമ്മിലുമുള്ള ആകര്ഷണവികര്ഷണങ്ങള് ഇതില്പ്പെടും. വൈദ്യുതബലത്തിന്റെ ( electrical force) തന്നെ ഒരു സവിശേഷ ആപേക്ഷികതാ പ്രഭാവം ( Relatiarstic effect) മാത്രമാണ് കാന്തത എന്ന് ഐന്സ്റ്റൈന്റെ സിദ്ധാന്തം ഉപയോഗിച്ച് തെളിയിക്കാന് കഴിയും. | ||
| വരി 15: | വരി 15: | ||
'''ചരിത്രം'''. കാന്തതയുടെ ചരിത്രം ബി.സി. എട്ടാം ശതകത്തില് തുടങ്ങുന്നു. അക്കാലത്തെ ഗ്രീക്കു രേഖകളില് മാഗ്നറ്റൈറ്റ് എന്നു വിളിച്ചിരുന്ന, കാന്തതയുള്ള ഇരുമ്പുധാതുവിനെപ്പറ്റി പരാമര്ശമുണ്ട്. പ്രകൃതിയില് സുലഭമായിക്കാണുന്ന ഈ ധാതു ഇരുമ്പിനെ ശക്തമായി ആകര്ഷിക്കുന്നുവെന്ന് ഗ്രീക്കുകാര് മനസ്സിലാക്കി. പില്ക്കാലത്ത് റോമന് ദാര്ശനികനായ ലുക്രീഷ്യസ് (എ.ഡി. 1-ാം ശ.), ഗ്രീസിലെ മഗ്നീഷ്യ ( Magnesia) എന്ന സ്ഥലത്ത് ഈ ധാതു ധാരാളമായി കണ്ടെത്തിയതുകൊണ്ടാണ് ഇതിന് മാഗ്നറ്റ് എന്നു പേരുണ്ടായത് എന്നഭിപ്രായപ്പെട്ടിട്ടുണ്ട്. എന്നാല് മറ്റൊരു ദാര്ശനികനായ പ്ലിനി ദി എല്ഡര് അഭിപ്രായപ്പെട്ടത് ഏഷ്യാമൈനറിലുള്ള ആട്ടിടയരാണ് ഈ പ്രതിഭാസം കണ്ടെത്തിയത് എന്നാണ്.കാന്തതയെ സംബന്ധിച്ച ശാസ്ത്രീയമായ നിഗമനങ്ങള് പ്രത്യക്ഷമാകുന്നത് പ്രസിദ്ധ ഗ്രീക്കു തത്ത്വചിന്തകരായ അരിസ്റ്റോട്ടിലും ഥെയ്ല്സും (ബി.സി. 6255-45) തമ്മിലുള്ള ചര്ച്ചകളിലൂടെയാണ്. ഏതാണ്ട് ഇതേ കാലയളവില്ത്തന്നെ, പ്രാചീന ഇന്ത്യയിലെ ആദ്യ ശസ്ത്രക്രിയാ വിദഗ്ധനായ സുശ്രുതന് തന്റെ ശസ്ത്രക്രിയകളില് കാന്തം ഉപയോഗിച്ചിരുന്നതായി സൂചനയുണ്ട്. പ്രാചീന ചൈനയില് ബി.സി. 4-ാം നൂറ്റാണ്ടില് പുറത്തിറങ്ങിയ "ബുക്ക് ഒഫ് ദ് ഡെവിള് പാലീമാസ്റ്റര്സ്' എന്ന കൃതിയില് കാന്തതയെ സംബന്ധിച്ച പരാമര്ശം കാണുന്നുണ്ട്. "ലോഡ് സ്റ്റോണ്' (Lodestone) ഇരുമ്പിനെ ആകര്ഷിക്കുന്നു' എന്നാണതില് പറയുന്നത് (ലോഡ്സ്റ്റോണ് അയണ് ഓക്സൈഡ് അടങ്ങിയ പദാര്ഥമാണ്. തെക്കുവടക്കു ദിശ സൂചിപ്പിക്കാനുള്ള അതിനെ ഗ്രീക്കുകാര് മുമ്പേ തിരിച്ചറിഞ്ഞിരുന്നു). 12-ാം നൂറ്റാണ്ടില് ചൈനക്കാര് ദിശാനിര്ണയത്തിന് ലോഡ്സ്റ്റോണ് വടക്കുനോക്കി( compass) ആയി വ്യാപകമായുപയോഗിച്ചു തുടങ്ങി. യൂറോപ്പില് അലക്സാണ്ടര് നെക്കാം (1157-1217) എന്ന ഇംഗ്ലീഷുകാരന് 1187ല് പുറത്തിറക്കിയ ഒരു കൃതിയില് ദിശാനിര്ണയത്തിനായി വടക്കുനോക്കി ഉപയോഗിക്കുന്നതായി പറയുന്നുണ്ട്. | '''ചരിത്രം'''. കാന്തതയുടെ ചരിത്രം ബി.സി. എട്ടാം ശതകത്തില് തുടങ്ങുന്നു. അക്കാലത്തെ ഗ്രീക്കു രേഖകളില് മാഗ്നറ്റൈറ്റ് എന്നു വിളിച്ചിരുന്ന, കാന്തതയുള്ള ഇരുമ്പുധാതുവിനെപ്പറ്റി പരാമര്ശമുണ്ട്. പ്രകൃതിയില് സുലഭമായിക്കാണുന്ന ഈ ധാതു ഇരുമ്പിനെ ശക്തമായി ആകര്ഷിക്കുന്നുവെന്ന് ഗ്രീക്കുകാര് മനസ്സിലാക്കി. പില്ക്കാലത്ത് റോമന് ദാര്ശനികനായ ലുക്രീഷ്യസ് (എ.ഡി. 1-ാം ശ.), ഗ്രീസിലെ മഗ്നീഷ്യ ( Magnesia) എന്ന സ്ഥലത്ത് ഈ ധാതു ധാരാളമായി കണ്ടെത്തിയതുകൊണ്ടാണ് ഇതിന് മാഗ്നറ്റ് എന്നു പേരുണ്ടായത് എന്നഭിപ്രായപ്പെട്ടിട്ടുണ്ട്. എന്നാല് മറ്റൊരു ദാര്ശനികനായ പ്ലിനി ദി എല്ഡര് അഭിപ്രായപ്പെട്ടത് ഏഷ്യാമൈനറിലുള്ള ആട്ടിടയരാണ് ഈ പ്രതിഭാസം കണ്ടെത്തിയത് എന്നാണ്.കാന്തതയെ സംബന്ധിച്ച ശാസ്ത്രീയമായ നിഗമനങ്ങള് പ്രത്യക്ഷമാകുന്നത് പ്രസിദ്ധ ഗ്രീക്കു തത്ത്വചിന്തകരായ അരിസ്റ്റോട്ടിലും ഥെയ്ല്സും (ബി.സി. 6255-45) തമ്മിലുള്ള ചര്ച്ചകളിലൂടെയാണ്. ഏതാണ്ട് ഇതേ കാലയളവില്ത്തന്നെ, പ്രാചീന ഇന്ത്യയിലെ ആദ്യ ശസ്ത്രക്രിയാ വിദഗ്ധനായ സുശ്രുതന് തന്റെ ശസ്ത്രക്രിയകളില് കാന്തം ഉപയോഗിച്ചിരുന്നതായി സൂചനയുണ്ട്. പ്രാചീന ചൈനയില് ബി.സി. 4-ാം നൂറ്റാണ്ടില് പുറത്തിറങ്ങിയ "ബുക്ക് ഒഫ് ദ് ഡെവിള് പാലീമാസ്റ്റര്സ്' എന്ന കൃതിയില് കാന്തതയെ സംബന്ധിച്ച പരാമര്ശം കാണുന്നുണ്ട്. "ലോഡ് സ്റ്റോണ്' (Lodestone) ഇരുമ്പിനെ ആകര്ഷിക്കുന്നു' എന്നാണതില് പറയുന്നത് (ലോഡ്സ്റ്റോണ് അയണ് ഓക്സൈഡ് അടങ്ങിയ പദാര്ഥമാണ്. തെക്കുവടക്കു ദിശ സൂചിപ്പിക്കാനുള്ള അതിനെ ഗ്രീക്കുകാര് മുമ്പേ തിരിച്ചറിഞ്ഞിരുന്നു). 12-ാം നൂറ്റാണ്ടില് ചൈനക്കാര് ദിശാനിര്ണയത്തിന് ലോഡ്സ്റ്റോണ് വടക്കുനോക്കി( compass) ആയി വ്യാപകമായുപയോഗിച്ചു തുടങ്ങി. യൂറോപ്പില് അലക്സാണ്ടര് നെക്കാം (1157-1217) എന്ന ഇംഗ്ലീഷുകാരന് 1187ല് പുറത്തിറക്കിയ ഒരു കൃതിയില് ദിശാനിര്ണയത്തിനായി വടക്കുനോക്കി ഉപയോഗിക്കുന്നതായി പറയുന്നുണ്ട്. | ||
| - | ഇംഗ്ലീഷ് | + | ഇംഗ്ലീഷ് ഭിഷഗ്വരനും തത്ത്വജ്ഞാനിയുമായ വില്യം ഗില്ബര്ട്ട് (1540-1605) ആണ് ഇംഗ്ലണ്ടില് കാന്തതയെ സംബന്ധിച്ച് ആദ്യമായി ശാസ്ത്രീയ പഠനങ്ങള്ക്ക് തുടക്കംകുറിച്ചത്. ഭൂമി ഒരു വലിയ കാന്തമാണെന്ന് ആദ്യമായി പ്രസ്താവിച്ചതും അദ്ദേഹമാണ്. ചുട്ടുപഴുപ്പിച്ച കാന്തക്കല്ലിന് കാന്തത നഷ്ടപ്പെടുമെന്നും വൈദ്യുതിയെ കാന്തതയില് നിന്ന് വേര്തിരിക്കാമെന്നും അദ്ദേഹം മനസ്സിലാക്കി. കാന്തതയെക്കുറിച്ച് അക്കാലത്ത് നിലവിലുണ്ടായിരുന്ന ഒട്ടുമിക്ക അറിവുകളും സമാഹരിച്ച് 1600ല് അദ്ദേഹം പ്രസിദ്ധീകരിച്ച ദെ മാഗ്നറ്റെ മാഗ്നറ്റിസിസ്കേ കോര്പ്പോറിബസ്, എറ്റ് ദേ മാഗ്നോ മാഗ്നറ്റേ ദെല്ലുറേ (ഭൂമിയെന്ന മഹത്തായ കാന്തത്തെയും കാന്തിക വസ്തുക്കളെയും മറ്റു കാന്തങ്ങളെയും കുറിച്ച്) എന്ന പുസ്തകത്തില് ടെറല്ല (terella) എന്ന പേരിലാണ് ഭൂമിയെന്ന ഭീമന് കാന്തതയെപ്പറ്റി പരാമര്ശിച്ചിട്ടുള്ളത്. വടക്കുനോക്കി വടക്കുദിശയിലേക്ക് ചൂണ്ടിനില്ക്കുന്നത് ഭൂമിയെന്ന കാന്തത്തിന്റെ സ്വാധീനത്താലാണെന്നായിരുന്നു അദ്ദേഹം വാദിച്ചത്. അതിനുമുന്പ് ധ്രുവനക്ഷത്ര(polaris)ത്തിന്റെ സ്വാധീനമാണ് അതിനുപിന്നില് എന്നായിരുന്നു പരക്കെയുള്ള ധാരണ. |
| - | ഭൂകാന്തികതയുടെ സ്വഭാവത്തെപ്പറ്റി പഠിച്ച മറ്റൊരാള് ജര്മന് ഗണിതജ്ഞനായ കാള് ഫ്രീദ്റിഷ് ഗോസസ് (1777-1855) ആണ്. കാന്തികതയെപ്പറ്റിയുള്ള പരിമാണാത്മകമായ പഠനം നടത്തിയത് ചാള്സ് അഗസ്റ്റിന് കൂളംബ് (1736-1806) ആണ്. വൈദ്യുത ചാര്ജുകളിലെന്നപോലെ കാന്തികധ്രുവങ്ങള് തമ്മിലും ഉള്ള ആകര്ഷണവികര്ഷണ ബലങ്ങള്ക്ക് വ്യുത്ക്രമവര്ഗനിയമം (diverse square law) ബാധകമാണെന്ന് അദ്ദേഹം വ്യക്തമാക്കി. 1785ലായിരുന്നു ഇത്. 1819ല് കോപ്പന്ഹേഗന് സര്വകലാശാലയിലെ പ്രാഫസറായിരുന്ന ഡച്ച് ഭൗതികജ്ഞന് ഹാന്സ് ക്രിസ്റ്റ്യന് ഓര്സ്റ്റഡ് (1777-1851) വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം കണ്ടെത്തി. വൈദ്യുതി പ്രവഹിക്കുന്ന ഒരു ചാലകം സമീപത്തുള്ള കാന്തസൂചിയെ സ്വാധീനിക്കുന്നതായി തന്റെ പരീക്ഷണങ്ങള്ക്കിടയില് അദ്ദേഹം യാദൃച്ഛികമായി കണ്ടെത്തുകയായിരുന്നു. ആന്ദ്രമേരി ആമ്പിയര് (1775-1836) എന്ന ഫ്രഞ്ച് | + | ഭൂകാന്തികതയുടെ സ്വഭാവത്തെപ്പറ്റി പഠിച്ച മറ്റൊരാള് ജര്മന് ഗണിതജ്ഞനായ കാള് ഫ്രീദ്റിഷ് ഗോസസ് (1777-1855) ആണ്. കാന്തികതയെപ്പറ്റിയുള്ള പരിമാണാത്മകമായ പഠനം നടത്തിയത് ചാള്സ് അഗസ്റ്റിന് കൂളംബ് (1736-1806) ആണ്. വൈദ്യുത ചാര്ജുകളിലെന്നപോലെ കാന്തികധ്രുവങ്ങള് തമ്മിലും ഉള്ള ആകര്ഷണവികര്ഷണ ബലങ്ങള്ക്ക് വ്യുത്ക്രമവര്ഗനിയമം (diverse square law) ബാധകമാണെന്ന് അദ്ദേഹം വ്യക്തമാക്കി. 1785ലായിരുന്നു ഇത്. 1819ല് കോപ്പന്ഹേഗന് സര്വകലാശാലയിലെ പ്രാഫസറായിരുന്ന ഡച്ച് ഭൗതികജ്ഞന് ഹാന്സ് ക്രിസ്റ്റ്യന് ഓര്സ്റ്റഡ് (1777-1851) വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം കണ്ടെത്തി. വൈദ്യുതി പ്രവഹിക്കുന്ന ഒരു ചാലകം സമീപത്തുള്ള കാന്തസൂചിയെ സ്വാധീനിക്കുന്നതായി തന്റെ പരീക്ഷണങ്ങള്ക്കിടയില് അദ്ദേഹം യാദൃച്ഛികമായി കണ്ടെത്തുകയായിരുന്നു. ആന്ദ്രമേരി ആമ്പിയര് (1775-1836) എന്ന ഫ്രഞ്ച് ശാസ്ത്രജ്ഞനും സമാനമായ പരീക്ഷണങ്ങള് നടത്തുകയുണ്ടായി. |
കാന്തികബലം പ്രയോഗിച്ച് മറ്റു വസ്തുക്കളിലും, ഏറിയോ കുറഞ്ഞോ, കാന്തത സൃഷ്ടിക്കാന് കഴിയുമെന്ന് ഫാരഡെ 1845ല് കണ്ടെത്തി. യു.എസ്സിലെ ജോസഫ് ഹെന്റിയും വിദ്യുത്കാന്തികവേശനം എന്ന ഈ പ്രതിഭാസം സ്വതന്ത്രമായി കണ്ടെത്തിയിരുന്നു. ഫാരഡേയാണ് കാന്തികക്ഷേത്രം (magnatic field) എന്ന ആശയത്തിന് ജന്മം നല്കിയത്. ഫാരഡെയുടെ തത്ത്വങ്ങള്ക്ക് ജെയിംസ് ക്ലാര്ക്ക് മാക്സ്വെല് (James Clerk Maxwell) എക്സ്പെരിമെന്റല് റിസര്ച്ചസ് ഇന് ഇലക്ട്രിസിറ്റി എന്ന ഗ്രന്ഥത്തിലൂടെ ഗണിതരൂപം നല്കി. വിദ്യുത്കാന്തത (electromagnetism)എന്ന ശാസ്ത്രശാഖയ്ക്ക് അതോടെ തുടക്കമായി. അദ്ദേഹത്തിന്റെ ട്രീറ്റിസ് ഓണ് ഇലക്ട്രിസിറ്റി ആന്ഡ് മാഗ്നറ്റിസം എന്ന ഗ്രന്ഥം (1873) ആണ് അതിനു തുടക്കം കുറിച്ചത്. വിദ്യുത്കാന്തിക തരംഗങ്ങള് ത്വരണം ചെയ്യുന്ന ചാര്ജുകളില്നിന്ന് ഉദ്ഭവിക്കുകയും പ്രകാശവേഗത്തില് പ്രക്ഷണം ചെയ്യപ്പെടുകയും ചെയ്യുന്നു എന്ന് ഗണിതപരമായി മാക്സ്വെല് തെളിയിച്ചു. പ്രകാശം ഒരു വിദ്യുത്കാന്തിക തരംഗമാണെന്ന് അദ്ദേഹം സമര്ഥിക്കുകയും ചെയ്തു. ഹൈന്റിഷ് ഹെര്ട്സ് (Heinrich Hertz) എന്ന ജര്മന് ഭൗതികശാസ്ത്രജ്ഞന് വിദ്യുത്കാന്തിക തരംഗങ്ങളുടെ നിലനില്പ് പരീക്ഷണത്തിലൂടെ തെളിയിച്ചു. | കാന്തികബലം പ്രയോഗിച്ച് മറ്റു വസ്തുക്കളിലും, ഏറിയോ കുറഞ്ഞോ, കാന്തത സൃഷ്ടിക്കാന് കഴിയുമെന്ന് ഫാരഡെ 1845ല് കണ്ടെത്തി. യു.എസ്സിലെ ജോസഫ് ഹെന്റിയും വിദ്യുത്കാന്തികവേശനം എന്ന ഈ പ്രതിഭാസം സ്വതന്ത്രമായി കണ്ടെത്തിയിരുന്നു. ഫാരഡേയാണ് കാന്തികക്ഷേത്രം (magnatic field) എന്ന ആശയത്തിന് ജന്മം നല്കിയത്. ഫാരഡെയുടെ തത്ത്വങ്ങള്ക്ക് ജെയിംസ് ക്ലാര്ക്ക് മാക്സ്വെല് (James Clerk Maxwell) എക്സ്പെരിമെന്റല് റിസര്ച്ചസ് ഇന് ഇലക്ട്രിസിറ്റി എന്ന ഗ്രന്ഥത്തിലൂടെ ഗണിതരൂപം നല്കി. വിദ്യുത്കാന്തത (electromagnetism)എന്ന ശാസ്ത്രശാഖയ്ക്ക് അതോടെ തുടക്കമായി. അദ്ദേഹത്തിന്റെ ട്രീറ്റിസ് ഓണ് ഇലക്ട്രിസിറ്റി ആന്ഡ് മാഗ്നറ്റിസം എന്ന ഗ്രന്ഥം (1873) ആണ് അതിനു തുടക്കം കുറിച്ചത്. വിദ്യുത്കാന്തിക തരംഗങ്ങള് ത്വരണം ചെയ്യുന്ന ചാര്ജുകളില്നിന്ന് ഉദ്ഭവിക്കുകയും പ്രകാശവേഗത്തില് പ്രക്ഷണം ചെയ്യപ്പെടുകയും ചെയ്യുന്നു എന്ന് ഗണിതപരമായി മാക്സ്വെല് തെളിയിച്ചു. പ്രകാശം ഒരു വിദ്യുത്കാന്തിക തരംഗമാണെന്ന് അദ്ദേഹം സമര്ഥിക്കുകയും ചെയ്തു. ഹൈന്റിഷ് ഹെര്ട്സ് (Heinrich Hertz) എന്ന ജര്മന് ഭൗതികശാസ്ത്രജ്ഞന് വിദ്യുത്കാന്തിക തരംഗങ്ങളുടെ നിലനില്പ് പരീക്ഷണത്തിലൂടെ തെളിയിച്ചു. | ||
| വരി 29: | വരി 29: | ||
[[ചിത്രം:Vol7_93_image1.jpg|300px]] | [[ചിത്രം:Vol7_93_image1.jpg|300px]] | ||
| - | ഒരു വൈദ്യുത സര്ക്കീറ്റ് ഒരു ബിന്ദുവില് സൃഷ്ടിക്കുന്ന ആകെ കാന്തികക്ഷേത്രം കാണണമെങ്കില് അതിലെ ഓരോ പ്രവാഹശകലം dl ഉം സൃഷ്ടിക്കുന്ന ക്ഷേത്രശകലങ്ങളുടെ തുക അഥവാ സമാകലം കണ്ടാല് മതി. | + | ഒരു വൈദ്യുത സര്ക്കീറ്റ് ഒരു ബിന്ദുവില് സൃഷ്ടിക്കുന്ന ആകെ കാന്തികക്ഷേത്രം കാണണമെങ്കില് അതിലെ ഓരോ പ്രവാഹശകലം dl ഉം സൃഷ്ടിക്കുന്ന ക്ഷേത്രശകലങ്ങളുടെ തുക അഥവാ സമാകലം കണ്ടാല് മതി. ഏതാനും സമമിത സര്ക്കീറ്റ് രൂപങ്ങളിലൊഴികെ മറ്റിടങ്ങളില് ഇതു കാണുക എളുപ്പമല്ല. അത്തരം ചില സമമിത സര്ക്കീറ്റുകള് ഇവയാണ് |
(a) '''വൃത്താകാര വൈദ്യുത വലയം''' (current loop). R വ്യാസാര്ധമുള്ള ഒരു വൃത്താകാര വൈദ്യുതവലയം പരിഗണിച്ചാല്, അതിന്റെ കേന്ദ്രം Pയെ സംബന്ധിച്ചിടത്തോളം ഓരോ പ്രവാഹശകലം ldlന്റെയും ദൂരസദിശം R, ld lന് ലംബമായിരിക്കും. അത് P യില് സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രം dB അക്ഷത്തിന്റെ ദിശയില് ആയിരിക്കും. അതുകൊണ്ട് ആ വലയം വൃത്തകേന്ദ്രത്തില് സൃഷ്ടിക്കുന്ന മൊത്തം കാന്തികക്ഷേത്രം | (a) '''വൃത്താകാര വൈദ്യുത വലയം''' (current loop). R വ്യാസാര്ധമുള്ള ഒരു വൃത്താകാര വൈദ്യുതവലയം പരിഗണിച്ചാല്, അതിന്റെ കേന്ദ്രം Pയെ സംബന്ധിച്ചിടത്തോളം ഓരോ പ്രവാഹശകലം ldlന്റെയും ദൂരസദിശം R, ld lന് ലംബമായിരിക്കും. അത് P യില് സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രം dB അക്ഷത്തിന്റെ ദിശയില് ആയിരിക്കും. അതുകൊണ്ട് ആ വലയം വൃത്തകേന്ദ്രത്തില് സൃഷ്ടിക്കുന്ന മൊത്തം കാന്തികക്ഷേത്രം | ||
| വരി 83: | വരി 83: | ||
[[ചിത്രം:Vol7_95_formula2.jpg|300px]] | [[ചിത്രം:Vol7_95_formula2.jpg|300px]] | ||
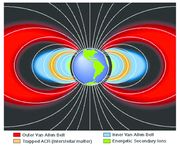
| - | പരിക്രമണ ആവൃത്തിയെ സൈക്ലോട്രാണ് ആവൃത്തി എന്നുവിളിക്കും. കണികത്വരിത്രങ്ങള് (സൈക്ലോട്രാണ്, സിങ്ക്രാട്രാണ് മുതല-ായവ), മാസ്സ് സ്പെക്ട്രാമീറ്റര് തുടങ്ങിയവയുടെ നിര്മിതിയില് ഈ സമവാക്യങ്ങള് നിര്ണായകമാണ്.[[ചിത്രം:Vol7p62_pic1_radiation_belts.jpg|thumb|വാലന് അലന് | + | പരിക്രമണ ആവൃത്തിയെ സൈക്ലോട്രാണ് ആവൃത്തി എന്നുവിളിക്കും. കണികത്വരിത്രങ്ങള് (സൈക്ലോട്രാണ്, സിങ്ക്രാട്രാണ് മുതല-ായവ), മാസ്സ് സ്പെക്ട്രാമീറ്റര് തുടങ്ങിയവയുടെ നിര്മിതിയില് ഈ സമവാക്യങ്ങള് നിര്ണായകമാണ്.[[ചിത്രം:Vol7p62_pic1_radiation_belts.jpg|thumb|വാലന് അലന് ബെല്റ്റ്]] |
കണത്തിന്റെ പ്രാരംഭ ചലനദിശ കാന്തികക്ഷേത്രരേഖകള്ക്കു ചരിഞ്ഞ ദിശയിലാണെങ്കില് അതിന്റെ തുടര്ന്നുള്ള ചലനം രണ്ടു ഘടകങ്ങള് ചേര്ന്നതായിരിക്കും. കണത്തിന്റെ പ്രവേഗത്തിലെ ക്ഷേത്രത്തിനു ലംബമായ ഘടകം അതിനെ ബലരേഖകള്ക്കു ചുറ്റും വൃത്തപഥത്തില് ചലിപ്പിക്കുമ്പോള്, സമാന്തരഘടകം അതിനെ ക്ഷേത്രദിശയില് ചലിപ്പിക്കുന്നു. കണത്തിന്റെ പരിണതചലനം ഒരു ഹെലിക്സിന്റെ രൂപത്തിലായിരിക്കും. | കണത്തിന്റെ പ്രാരംഭ ചലനദിശ കാന്തികക്ഷേത്രരേഖകള്ക്കു ചരിഞ്ഞ ദിശയിലാണെങ്കില് അതിന്റെ തുടര്ന്നുള്ള ചലനം രണ്ടു ഘടകങ്ങള് ചേര്ന്നതായിരിക്കും. കണത്തിന്റെ പ്രവേഗത്തിലെ ക്ഷേത്രത്തിനു ലംബമായ ഘടകം അതിനെ ബലരേഖകള്ക്കു ചുറ്റും വൃത്തപഥത്തില് ചലിപ്പിക്കുമ്പോള്, സമാന്തരഘടകം അതിനെ ക്ഷേത്രദിശയില് ചലിപ്പിക്കുന്നു. കണത്തിന്റെ പരിണതചലനം ഒരു ഹെലിക്സിന്റെ രൂപത്തിലായിരിക്കും. | ||
ഭൂമിക്കുചുറ്റും വാന് അലന് ബെല്റ്റ് എന്നറിയപ്പെടുന്ന കാന്തികമേഖലയുണ്ട്. സൗരവാതത്തില് (solar wind) ഉള്പ്പെട്ട പ്രാട്ടോണുകളും ആല്ഫാകണങ്ങളും മറ്റും ഈ കാന്തികബലരേഖകളെ മുറിച്ചുകടക്കുമ്പോള് അവയുടെ പഥം ഹെലിക്കല് ആവുകയും അവ ബലരേഖകളുടെ ദിശയില് സഞ്ചരിച്ച് ധ്രുവങ്ങളില് എത്തിച്ചേരുകയും ചെയ്യുന്നു. ധ്രുവമേഖലയില് ഇവ ഭൂമിയോട് അടുക്കുന്നതുകൊണ്ട് അന്തരീക്ഷ തന്മാത്രകളുമായി കൂട്ടിയിടിക്കാന് ഇടയാവുകയും പ്രകാശം ചൊരിയാന് ഇടയാവുകയും ചെയ്യും. ഇതാണ് ധ്രുവദീപ്തി എന്നറിയപ്പെടുന്നത്. | ഭൂമിക്കുചുറ്റും വാന് അലന് ബെല്റ്റ് എന്നറിയപ്പെടുന്ന കാന്തികമേഖലയുണ്ട്. സൗരവാതത്തില് (solar wind) ഉള്പ്പെട്ട പ്രാട്ടോണുകളും ആല്ഫാകണങ്ങളും മറ്റും ഈ കാന്തികബലരേഖകളെ മുറിച്ചുകടക്കുമ്പോള് അവയുടെ പഥം ഹെലിക്കല് ആവുകയും അവ ബലരേഖകളുടെ ദിശയില് സഞ്ചരിച്ച് ധ്രുവങ്ങളില് എത്തിച്ചേരുകയും ചെയ്യുന്നു. ധ്രുവമേഖലയില് ഇവ ഭൂമിയോട് അടുക്കുന്നതുകൊണ്ട് അന്തരീക്ഷ തന്മാത്രകളുമായി കൂട്ടിയിടിക്കാന് ഇടയാവുകയും പ്രകാശം ചൊരിയാന് ഇടയാവുകയും ചെയ്യും. ഇതാണ് ധ്രുവദീപ്തി എന്നറിയപ്പെടുന്നത്. | ||
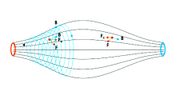
| - | '''കാന്തികക്കുപ്പി'''. ചാര്ജിതകണങ്ങള് ചലിക്കുന്നത് ഏകസമാനമല്ലാത്ത (non uniform) കാന്തിക ക്ഷേത്രത്തിലാണെങ്കില് അവയുടെ ചലനം സങ്കീര്ണമായിരിക്കും. ക്ഷേത്രതീവ്രത മധ്യഭാഗത്തു കുറവും അഗ്രങ്ങളില് കൂടുതലും ഉള്ള ഒരു സംവിധാനമാണ് ഈ കാന്തികക്കുപ്പി. ഇതില് ചലിക്കുന്ന ചാര്ജിതകണങ്ങള് അഗ്രങ്ങളില്വച്ച് വിപരീതദിശ | + | '''കാന്തികക്കുപ്പി'''. ചാര്ജിതകണങ്ങള് ചലിക്കുന്നത് ഏകസമാനമല്ലാത്ത (non uniform) കാന്തിക ക്ഷേത്രത്തിലാണെങ്കില് അവയുടെ ചലനം സങ്കീര്ണമായിരിക്കും. ക്ഷേത്രതീവ്രത മധ്യഭാഗത്തു കുറവും അഗ്രങ്ങളില് കൂടുതലും ഉള്ള ഒരു സംവിധാനമാണ് ഈ കാന്തികക്കുപ്പി. ഇതില് ചലിക്കുന്ന ചാര്ജിതകണങ്ങള് അഗ്രങ്ങളില്വച്ച് വിപരീതദിശ കൈവരിക്കാനും അങ്ങനെ മുന്നോട്ടും പിന്നോട്ടും പലവട്ടം സഞ്ചരിക്കാന് ഇടയാവുകയും ചെയ്യും. ഇതിനിടയ്ക്ക് അവയിലേക്ക് ഊര്ജം പകര്ന്നു നല്കാന് കഴിഞ്ഞാല് (ഉദാ. വിദ്യുത്കാന്തിക ഊര്ജരൂപത്തില്) അവ അതിശക്തിയോടെ അന്യോന്യം കൂട്ടിയിടിക്കും. ഈ വിധം ആണവ ഫ്യൂഷന് കൈവരിക്കാന് കഴിയുമോ എന്ന പരീക്ഷണങ്ങള് ധാരാളം നടന്നുവരുന്നു. |
[[ചിത്രം:Vol7p62_magnetic bottle.jpg|thumb|കാന്തികക്കുപ്പി]] | [[ചിത്രം:Vol7p62_magnetic bottle.jpg|thumb|കാന്തികക്കുപ്പി]] | ||
| വരി 97: | വരി 97: | ||
[[ചിത്രം:Vol7_96_formula4.jpg|300px]] | [[ചിത്രം:Vol7_96_formula4.jpg|300px]] | ||
| - | കാന്തികാഘൂര്ണത്തിന്റെ SI യൂണിറ്റ് A.m<sup>2</sup> ആണ്; ടോര്ക്കിന്റേത് A.m<sup>2</sup> .T അഥവാ N.m ടോര്ക്ക് ഇവിടെ നിര്ണയിച്ചത് ഒരു ദീര്ഘചതുരവലയത്തിനാണെങ്കിലും വൈദ്യുതി പ്രവഹിക്കുന്ന ഏതു രൂപത്തിലുള്ള | + | കാന്തികാഘൂര്ണത്തിന്റെ SI യൂണിറ്റ് A.m<sup>2</sup> ആണ്; ടോര്ക്കിന്റേത് A.m<sup>2</sup> .T അഥവാ N.m ടോര്ക്ക് ഇവിടെ നിര്ണയിച്ചത് ഒരു ദീര്ഘചതുരവലയത്തിനാണെങ്കിലും വൈദ്യുതി പ്രവഹിക്കുന്ന ഏതു രൂപത്തിലുള്ള വലയത്തിനും സമവാക്യം (12), (13) ഇവ ബാധകമാണ്. |
[[ചിത്രം:Vol7_96_formula5.jpg|300px]] | [[ചിത്രം:Vol7_96_formula5.jpg|300px]] | ||
| വരി 166: | വരി 166: | ||
[[ചിത്രം:Vol7_98_formula11.jpg|300px]] | [[ചിത്രം:Vol7_98_formula11.jpg|300px]] | ||
| - | '''അനുകാന്തത'''. സ്ഥിരകാന്തികാഘൂര്ണമുള്ള ആറ്റങ്ങള് അടങ്ങിയ പദാര്ഥങ്ങളിലാണ് അനുകാന്തത ദൃശ്യമാകുന്നത്. അവ തമ്മില് ദുര്ബലമായി പ്രതിപ്രവര്ത്തിക്കുന്നതുമൂലം ചെറിയ കാന്തശീലത (X<sub>m</sub>) സൃഷ്ടിക്കപ്പെടുന്നു. ബാഹ്യക്ഷേത്രമൊന്നും പ്രയോഗിക്കാത്തപ്പോള് ഈ ആറ്റമിക കാന്തികാഘൂര്ണങ്ങളെല്ലാം അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കും. ബാഹ്യക്ഷേത്രം പ്രയോഗിക്കുമ്പോള് ഇവ ക്ഷേത്രദിശയില് സംരേഖിതമാകുന്നു. ഒപ്പം, താപീയചലനങ്ങള് അവയെ | + | '''അനുകാന്തത'''. സ്ഥിരകാന്തികാഘൂര്ണമുള്ള ആറ്റങ്ങള് അടങ്ങിയ പദാര്ഥങ്ങളിലാണ് അനുകാന്തത ദൃശ്യമാകുന്നത്. അവ തമ്മില് ദുര്ബലമായി പ്രതിപ്രവര്ത്തിക്കുന്നതുമൂലം ചെറിയ കാന്തശീലത (X<sub>m</sub>) സൃഷ്ടിക്കപ്പെടുന്നു. ബാഹ്യക്ഷേത്രമൊന്നും പ്രയോഗിക്കാത്തപ്പോള് ഈ ആറ്റമിക കാന്തികാഘൂര്ണങ്ങളെല്ലാം അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കും. ബാഹ്യക്ഷേത്രം പ്രയോഗിക്കുമ്പോള് ഇവ ക്ഷേത്രദിശയില് സംരേഖിതമാകുന്നു. ഒപ്പം, താപീയചലനങ്ങള് അവയെ അനിയതമാക്കാനും ശ്രമിക്കുന്നു. ബാഹ്യക്ഷേത്രത്തിന്റെ ശക്തിയെയും താപനിലയെയും ആശ്രയിച്ചിരിക്കും ഒരു പദാര്ഥത്തില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തശീലത. |
[[ചിത്രം:Vol7_99_formula1.jpg|300px]] | [[ചിത്രം:Vol7_99_formula1.jpg|300px]] | ||
| വരി 176: | വരി 176: | ||
ഇതാണ് ക്യൂറി നിയമം. ഒരു അനുകാന്തികവസ്തുവിലെ കാന്തീകരണം അതിന്റെ കേവലതാപനിലയ്ക്ക് വിപരീതാനുപാതത്തിലായിരിക്കും എന്നാണ് പിയറി ക്യൂറി കണ്ടെത്തിയത്. | ഇതാണ് ക്യൂറി നിയമം. ഒരു അനുകാന്തികവസ്തുവിലെ കാന്തീകരണം അതിന്റെ കേവലതാപനിലയ്ക്ക് വിപരീതാനുപാതത്തിലായിരിക്കും എന്നാണ് പിയറി ക്യൂറി കണ്ടെത്തിയത്. | ||
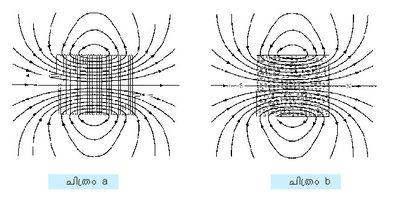
| - | '''അയസ്കാന്തത'''. ഇരുമ്പ്, കൊബാള്ട്ട്, നിക്കല് എന്നീ ലോഹങ്ങളിലും അവയുടെ കൂട്ടുലോഹങ്ങളിലും ഗഡോലിനിയം, ഡിസ്പ്രാസിയം തുടങ്ങിയ | + | '''അയസ്കാന്തത'''. ഇരുമ്പ്, കൊബാള്ട്ട്, നിക്കല് എന്നീ ലോഹങ്ങളിലും അവയുടെ കൂട്ടുലോഹങ്ങളിലും ഗഡോലിനിയം, ഡിസ്പ്രാസിയം തുടങ്ങിയ ഏതാനും സംയുക്തങ്ങളിലും കാണപ്പെടുന്ന പ്രതിഭാസമാണ് അയസ്കാന്തത. അയസ്കാന്തിക പദാര്ഥങ്ങള്ക്ക് വളരെ ഉയര്ന്ന കാന്തശീലത (Xm) ഉണ്ട്. ഒരു ചെറിയ ബാഹ്യക്ഷേത്രം മതി ഇത്തരം വസ്തുക്കളില് വലിയതോതില് ആറ്റമിക കാന്തികാഘൂര്ണങ്ങളുടെ സംരേഖനം സാധ്യമാക്കാന്. ചില സാഹചര്യങ്ങളില്, ബാഹ്യക്ഷേത്രം പിന്നീട് നീക്കിയാലും സംരേഖനം നിലനില്ക്കുന്നു. ഇതിനുകാരണം പ്രാദേശികമായി ദ്വിധ്രുവങ്ങള് തമ്മില് നിലവില്വരുന്ന അതിശക്തമായ പ്രതിപ്രവര്ത്തനമാണ്. കാന്തികധ്രുവങ്ങള് സംരേഖിതമായി സ്ഥിതിചെയ്യുന്ന ഇത്തരം മേഖലകളെ കാന്തിക ഡൊമെയ്നുകള് (magnetic domains)എന്നു വിളിക്കുന്നു. സാധാരണയായി ഈ ഡൊമെയ്നുകള് സൂക്ഷ്മരൂപങ്ങളായിരിക്കും. ഇവ അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കുന്നതുകൊണ്ട് സ്ഥൂലവസ്തുവിന് കാന്തികത ഉണ്ടാവില്ല. ബാഹ്യക്ഷേത്രം പ്രയോഗിക്കുമ്പോള് ഈ ഡൊമെയ്നുകള് ക്ഷേത്രദിശയില് സംരേഖിതമാകുക മാത്രമല്ല ക്ഷേത്രദിശയിലുള്ള ഡൊമെയ്നുകള് കൂടുതല് വിസ്തൃതമാവുകയും മറ്റു ദിശയിലുള്ളവയുടെ വിസ്തൃതി കുറയുകയും ചെയ്യാം. (ചിത്രം a, b കാണുക) എല്ലാ അയസ്കാന്തിക വസ്തുക്കള്ക്കും ക്യൂറി താപനില (Curi Temperature θ)എന്നറിയപ്പെടുന്ന ഒരു താപനില ഉണ്ടായിരിക്കും. അതിനുമുകളില് പദാര്ഥത്തിലെ താപീയചലനങ്ങള് ശക്തമായതുകൊണ്ട് സംരേഖനം അസാധ്യമായിത്തീരുകയും അയസ്കാന്തിക വസ്തു ഒരു അനുകാന്തിക വസ്തുവായി മാറുകയും ചെയ്യും. ആ അവസ്ഥയില് പദാര്ഥത്തിന്റെ കാന്തശീലത |
[[ചിത്രം:Vol7_99_image1.jpg|300px]] | [[ചിത്രം:Vol7_99_image1.jpg|300px]] | ||
| വരി 191: | വരി 191: | ||
അയസ്കാന്തികവസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തികക്ഷേത്രതീവ്രതയും (B) പ്രയുക്തകാന്തികക്ഷേത്രവും (Bapp) ചേര്ത്ത് ഒരു ഗ്രാഫ് വരച്ചാല് ചിത്രത്തിലേതുപോലെ കാണപ്പെടും. പോളിനോയിഡിലെ വൈദ്യുതപ്രവാഹം പൂജ്യത്തില്നിന്ന് ക്രമേണ വര്ധിച്ചാല് ആയുടെ മൂല്യം പൂജ്യത്തില്നിന്ന് ലേക്ക് ഉയര്ന്ന് പൂരിത കാന്തീകൃതാവസ്ഥയില് എത്തുന്നു. അപ്പോള് എല്ലാ കാന്തിക ഡൊമെയ്നുകളും സംരേഖിതമായതായി കണക്കാക്കാം. പിന്നീടങ്ങോട്ട് പ്രവാഹം (I)വര്ധിപ്പിച്ചാല് B യിലുണ്ടാകുന്ന വര്ധന [[ചിത്രം:Vol7_99_formula6.jpg|50px]] ലുണ്ടാക്കുന്ന വര്ധനയുടെ മാത്രം ഫലമായിരിക്കും. P<sub>1</sup>ല് നിന്ന് B<sub>app</sup>ക്രമേണ കുറച്ചുകൊണ്ടുവന്നാല് മുന്ചക്രത്തിലൂടെ തിരിച്ചുപോകുന്നില്ല എന്നു കാണാം. ഡൊമെയ്നുകളുടെ സംരേഖനം... (reversible) അല്ല എന്ന് ഇതു സൂചിപ്പിക്കുന്നു. B<sub>app</sup> പൂജ്യമായാലും കാന്തികവസ്തുവിലെ കാന്തീകരണം കുറച്ച് അവശേഷിക്കുന്നു (P<sub>4</sup>). ഇത് അവശിഷ്ടക്ഷേത്രം (Remant field, Brem) എന്നറിയപ്പെടുന്നു. ഈ പ്രതിഭാസത്തെ ഹിസ്റ്ററിസിസ് (ഗ്രീക്കില് Hysteros=പിന്നില്) എന്നു വിളിക്കുന്നു. ഈ അവസ്ഥയിലുള്ള ഇരുമ്പ്ദണ്ഡ് ഒരു സ്ഥിരകാന്തമാണ്. സോളിനോയിഡിലെ വൈദ്യുതിയുടെ ദിശമാറ്റി ക്രമേണ വര്ധിപ്പിച്ചാല് 'C'യില് കാന്തികക്ഷേത്രം പൂജ്യമാകും. തുടര്ന്നും ഈ ദിശയില് വര്ധിപ്പിച്ചാല്, P<sub>2</sup> എന്ന ബിന്ദുവില് എതിര്ദിശയിലെ പൂരിതക്ഷേത്രം ലഭിക്കുന്നു. തുടര്ന്ന് കുറച്ചുകൊണ്ടുവന്ന് പൂജ്യത്തിലെത്തിച്ച് വീണ്ടും ദിശമാറ്റി വര്ധിപ്പിച്ചാല് P<sub>2</sup>P<sub>3</sup>P<sub>1</sup>വക്രം ലഭിക്കുന്നു. ഒരു അയസ്കാന്തിക വസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തീകരണം (M) അതിന്റെ മുന്ചരിത്രത്തെ (അത് മുമ്പ് കാന്തീകരിക്കപ്പെട്ടിട്ടുണ്ടോ എന്നതിനെ) ആശ്രയിച്ചിരിക്കുന്നുവെന്ന് ഹിസ്റ്ററിസിസ് വക്രം സൂചിപ്പിക്കുന്നു. | അയസ്കാന്തികവസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തികക്ഷേത്രതീവ്രതയും (B) പ്രയുക്തകാന്തികക്ഷേത്രവും (Bapp) ചേര്ത്ത് ഒരു ഗ്രാഫ് വരച്ചാല് ചിത്രത്തിലേതുപോലെ കാണപ്പെടും. പോളിനോയിഡിലെ വൈദ്യുതപ്രവാഹം പൂജ്യത്തില്നിന്ന് ക്രമേണ വര്ധിച്ചാല് ആയുടെ മൂല്യം പൂജ്യത്തില്നിന്ന് ലേക്ക് ഉയര്ന്ന് പൂരിത കാന്തീകൃതാവസ്ഥയില് എത്തുന്നു. അപ്പോള് എല്ലാ കാന്തിക ഡൊമെയ്നുകളും സംരേഖിതമായതായി കണക്കാക്കാം. പിന്നീടങ്ങോട്ട് പ്രവാഹം (I)വര്ധിപ്പിച്ചാല് B യിലുണ്ടാകുന്ന വര്ധന [[ചിത്രം:Vol7_99_formula6.jpg|50px]] ലുണ്ടാക്കുന്ന വര്ധനയുടെ മാത്രം ഫലമായിരിക്കും. P<sub>1</sup>ല് നിന്ന് B<sub>app</sup>ക്രമേണ കുറച്ചുകൊണ്ടുവന്നാല് മുന്ചക്രത്തിലൂടെ തിരിച്ചുപോകുന്നില്ല എന്നു കാണാം. ഡൊമെയ്നുകളുടെ സംരേഖനം... (reversible) അല്ല എന്ന് ഇതു സൂചിപ്പിക്കുന്നു. B<sub>app</sup> പൂജ്യമായാലും കാന്തികവസ്തുവിലെ കാന്തീകരണം കുറച്ച് അവശേഷിക്കുന്നു (P<sub>4</sup>). ഇത് അവശിഷ്ടക്ഷേത്രം (Remant field, Brem) എന്നറിയപ്പെടുന്നു. ഈ പ്രതിഭാസത്തെ ഹിസ്റ്ററിസിസ് (ഗ്രീക്കില് Hysteros=പിന്നില്) എന്നു വിളിക്കുന്നു. ഈ അവസ്ഥയിലുള്ള ഇരുമ്പ്ദണ്ഡ് ഒരു സ്ഥിരകാന്തമാണ്. സോളിനോയിഡിലെ വൈദ്യുതിയുടെ ദിശമാറ്റി ക്രമേണ വര്ധിപ്പിച്ചാല് 'C'യില് കാന്തികക്ഷേത്രം പൂജ്യമാകും. തുടര്ന്നും ഈ ദിശയില് വര്ധിപ്പിച്ചാല്, P<sub>2</sup> എന്ന ബിന്ദുവില് എതിര്ദിശയിലെ പൂരിതക്ഷേത്രം ലഭിക്കുന്നു. തുടര്ന്ന് കുറച്ചുകൊണ്ടുവന്ന് പൂജ്യത്തിലെത്തിച്ച് വീണ്ടും ദിശമാറ്റി വര്ധിപ്പിച്ചാല് P<sub>2</sup>P<sub>3</sup>P<sub>1</sup>വക്രം ലഭിക്കുന്നു. ഒരു അയസ്കാന്തിക വസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തീകരണം (M) അതിന്റെ മുന്ചരിത്രത്തെ (അത് മുമ്പ് കാന്തീകരിക്കപ്പെട്ടിട്ടുണ്ടോ എന്നതിനെ) ആശ്രയിച്ചിരിക്കുന്നുവെന്ന് ഹിസ്റ്ററിസിസ് വക്രം സൂചിപ്പിക്കുന്നു. | ||
| - | + | ഏതാനും അയസ്കാന്തിക വസ്തുക്കളിലെ പൂരിത കാന്തികക്ഷേത്രം μ<sub>o</sub>M<sub>s</sub>(ടെസ് ലയില്), ആപേക്ഷിക പാരഗമ്യത μ<sub>r</sub> ഇവ ചുവടെ കൊടുക്കുന്നു. | |
[[ചിത്രം:Vol7_100_chart.jpg|300px]] | [[ചിത്രം:Vol7_100_chart.jpg|300px]] | ||
| + | |||
| + | [[ചിത്രം:Vol7_100_image1.jpg|300px]] | ||
കാന്തീകരണവും വികാന്തീകരണവും നടക്കുമ്പോള് സംഭവിക്കുന്ന താപനംമൂലം ഊര്ജനഷ്ടം സംഭവിക്കുന്നുണ്ട്. ഹിസ്റ്ററിസിസ് വക്രത്തിന്റെ ഉള്വിസ്തൃതി ഈ നഷ്ടത്തിന് ആനുപാതികമാണ്. ഉള്വിസ്തൃതി (ഊര്ജനഷ്ടം) കുറഞ്ഞ ഹിസ്റ്ററിസിസ് വക്രമുള്ള പദാര്ഥത്തെ മൃദുകാന്തികവസ്തു (soft magnetic material) എന്നുപറയും. ഉദാ. പച്ചിരുമ്പ്. ഇതിന്റെ ആൃലാ പൂജ്യത്തോട് അടുത്താണ്. ട്രാന്സ്ഫോര്മര് കോറുകളിലും മറ്റും ഇത്തരം പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കുക. മറിച്ച്, സ്ഥിരകാന്തങ്ങള് നിര്മിക്കാന് കഠിന(hard) പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കാറ്. ഉദാ. അല്നികോ, കാര്ബണ് സ്റ്റീല്. | കാന്തീകരണവും വികാന്തീകരണവും നടക്കുമ്പോള് സംഭവിക്കുന്ന താപനംമൂലം ഊര്ജനഷ്ടം സംഭവിക്കുന്നുണ്ട്. ഹിസ്റ്ററിസിസ് വക്രത്തിന്റെ ഉള്വിസ്തൃതി ഈ നഷ്ടത്തിന് ആനുപാതികമാണ്. ഉള്വിസ്തൃതി (ഊര്ജനഷ്ടം) കുറഞ്ഞ ഹിസ്റ്ററിസിസ് വക്രമുള്ള പദാര്ഥത്തെ മൃദുകാന്തികവസ്തു (soft magnetic material) എന്നുപറയും. ഉദാ. പച്ചിരുമ്പ്. ഇതിന്റെ ആൃലാ പൂജ്യത്തോട് അടുത്താണ്. ട്രാന്സ്ഫോര്മര് കോറുകളിലും മറ്റും ഇത്തരം പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കുക. മറിച്ച്, സ്ഥിരകാന്തങ്ങള് നിര്മിക്കാന് കഠിന(hard) പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കാറ്. ഉദാ. അല്നികോ, കാര്ബണ് സ്റ്റീല്. | ||
Current revision as of 06:48, 5 ഓഗസ്റ്റ് 2014
കാന്തത
Magnetism
ചാര്ജിതകണങ്ങളുടെ ആപേക്ഷികചലനം, ചക്രണം (spin) ഇവ, കണങ്ങള് തമ്മിലുള്ള അന്യോന്യ പ്രവര്ത്തനത്തില് സൃഷ്ടിക്കുന്ന ഒരു പ്രഭാവം. ഇതിന്റെ സ്ഥൂലഫലം പലരൂപത്തില് പ്രത്യക്ഷപ്പെടാം; സ്ഥിരകാന്തങ്ങള് തമ്മിലും വൈദ്യുതപ്രവാഹവും കാന്തവും തമ്മിലും വൈദ്യുത പ്രവാഹങ്ങള് തമ്മിലുമുള്ള ആകര്ഷണവികര്ഷണങ്ങള് ഇതില്പ്പെടും. വൈദ്യുതബലത്തിന്റെ ( electrical force) തന്നെ ഒരു സവിശേഷ ആപേക്ഷികതാ പ്രഭാവം ( Relatiarstic effect) മാത്രമാണ് കാന്തത എന്ന് ഐന്സ്റ്റൈന്റെ സിദ്ധാന്തം ഉപയോഗിച്ച് തെളിയിക്കാന് കഴിയും.
ഒരു നിശ്ചല ചാര്ജിനു ചുറ്റും സ്ഥിതവൈദ്യുതക്ഷേത്രം (static electric force) മാത്രമേ ഉണ്ടായിരിക്കൂ. ചാര്ജ് സമവേഗത്തില് ചലിക്കുമ്പോള് അതിനുചുറ്റും സ്ഥിത വൈദ്യുതക്ഷേത്രത്തോടൊപ്പം ഒരു സ്ഥിതകാന്തിക ക്ഷേത്രംകൂടി സൃഷ്ടിക്കപ്പെടുന്നു. ചാര്ജിന്റെ ചലനം ത്വരണത്തോടെയാണെങ്കില് വൈദ്യുതകാന്തികക്ഷേത്രങ്ങള് സംയോജിച്ച്, ഊര്ജപ്പൊതികളുടെ (energy packets or quanta) അഥവാ ഫോട്ടോണുകളുടെ രൂപത്തില് സ്വതന്ത്രമാക്കപ്പെടുകയും പ്രകാശവേഗത്തില് ചുറ്റും പ്രസരിക്കപ്പെടുകയും ചെയ്യുന്നു.
കാന്തികബലം അനുഭവപ്പെടുന്ന മേഖലയെ കാന്തികക്ഷേത്രം അഥവാ കാന്തികമണ്ഡലം എന്നു വിളിക്കും. വൈദ്യുതി ഉപയോഗിച്ചുള്ള എല്ലാ യന്ത്രസംവിധാനങ്ങളും പ്രവര്ത്തിക്കുന്നത് വൈദ്യുതിയുടെ കാന്തികപ്രഭാവത്തെ അടിസ്ഥാനമാക്കിയാണ്.
ചരിത്രം. കാന്തതയുടെ ചരിത്രം ബി.സി. എട്ടാം ശതകത്തില് തുടങ്ങുന്നു. അക്കാലത്തെ ഗ്രീക്കു രേഖകളില് മാഗ്നറ്റൈറ്റ് എന്നു വിളിച്ചിരുന്ന, കാന്തതയുള്ള ഇരുമ്പുധാതുവിനെപ്പറ്റി പരാമര്ശമുണ്ട്. പ്രകൃതിയില് സുലഭമായിക്കാണുന്ന ഈ ധാതു ഇരുമ്പിനെ ശക്തമായി ആകര്ഷിക്കുന്നുവെന്ന് ഗ്രീക്കുകാര് മനസ്സിലാക്കി. പില്ക്കാലത്ത് റോമന് ദാര്ശനികനായ ലുക്രീഷ്യസ് (എ.ഡി. 1-ാം ശ.), ഗ്രീസിലെ മഗ്നീഷ്യ ( Magnesia) എന്ന സ്ഥലത്ത് ഈ ധാതു ധാരാളമായി കണ്ടെത്തിയതുകൊണ്ടാണ് ഇതിന് മാഗ്നറ്റ് എന്നു പേരുണ്ടായത് എന്നഭിപ്രായപ്പെട്ടിട്ടുണ്ട്. എന്നാല് മറ്റൊരു ദാര്ശനികനായ പ്ലിനി ദി എല്ഡര് അഭിപ്രായപ്പെട്ടത് ഏഷ്യാമൈനറിലുള്ള ആട്ടിടയരാണ് ഈ പ്രതിഭാസം കണ്ടെത്തിയത് എന്നാണ്.കാന്തതയെ സംബന്ധിച്ച ശാസ്ത്രീയമായ നിഗമനങ്ങള് പ്രത്യക്ഷമാകുന്നത് പ്രസിദ്ധ ഗ്രീക്കു തത്ത്വചിന്തകരായ അരിസ്റ്റോട്ടിലും ഥെയ്ല്സും (ബി.സി. 6255-45) തമ്മിലുള്ള ചര്ച്ചകളിലൂടെയാണ്. ഏതാണ്ട് ഇതേ കാലയളവില്ത്തന്നെ, പ്രാചീന ഇന്ത്യയിലെ ആദ്യ ശസ്ത്രക്രിയാ വിദഗ്ധനായ സുശ്രുതന് തന്റെ ശസ്ത്രക്രിയകളില് കാന്തം ഉപയോഗിച്ചിരുന്നതായി സൂചനയുണ്ട്. പ്രാചീന ചൈനയില് ബി.സി. 4-ാം നൂറ്റാണ്ടില് പുറത്തിറങ്ങിയ "ബുക്ക് ഒഫ് ദ് ഡെവിള് പാലീമാസ്റ്റര്സ്' എന്ന കൃതിയില് കാന്തതയെ സംബന്ധിച്ച പരാമര്ശം കാണുന്നുണ്ട്. "ലോഡ് സ്റ്റോണ്' (Lodestone) ഇരുമ്പിനെ ആകര്ഷിക്കുന്നു' എന്നാണതില് പറയുന്നത് (ലോഡ്സ്റ്റോണ് അയണ് ഓക്സൈഡ് അടങ്ങിയ പദാര്ഥമാണ്. തെക്കുവടക്കു ദിശ സൂചിപ്പിക്കാനുള്ള അതിനെ ഗ്രീക്കുകാര് മുമ്പേ തിരിച്ചറിഞ്ഞിരുന്നു). 12-ാം നൂറ്റാണ്ടില് ചൈനക്കാര് ദിശാനിര്ണയത്തിന് ലോഡ്സ്റ്റോണ് വടക്കുനോക്കി( compass) ആയി വ്യാപകമായുപയോഗിച്ചു തുടങ്ങി. യൂറോപ്പില് അലക്സാണ്ടര് നെക്കാം (1157-1217) എന്ന ഇംഗ്ലീഷുകാരന് 1187ല് പുറത്തിറക്കിയ ഒരു കൃതിയില് ദിശാനിര്ണയത്തിനായി വടക്കുനോക്കി ഉപയോഗിക്കുന്നതായി പറയുന്നുണ്ട്.
ഇംഗ്ലീഷ് ഭിഷഗ്വരനും തത്ത്വജ്ഞാനിയുമായ വില്യം ഗില്ബര്ട്ട് (1540-1605) ആണ് ഇംഗ്ലണ്ടില് കാന്തതയെ സംബന്ധിച്ച് ആദ്യമായി ശാസ്ത്രീയ പഠനങ്ങള്ക്ക് തുടക്കംകുറിച്ചത്. ഭൂമി ഒരു വലിയ കാന്തമാണെന്ന് ആദ്യമായി പ്രസ്താവിച്ചതും അദ്ദേഹമാണ്. ചുട്ടുപഴുപ്പിച്ച കാന്തക്കല്ലിന് കാന്തത നഷ്ടപ്പെടുമെന്നും വൈദ്യുതിയെ കാന്തതയില് നിന്ന് വേര്തിരിക്കാമെന്നും അദ്ദേഹം മനസ്സിലാക്കി. കാന്തതയെക്കുറിച്ച് അക്കാലത്ത് നിലവിലുണ്ടായിരുന്ന ഒട്ടുമിക്ക അറിവുകളും സമാഹരിച്ച് 1600ല് അദ്ദേഹം പ്രസിദ്ധീകരിച്ച ദെ മാഗ്നറ്റെ മാഗ്നറ്റിസിസ്കേ കോര്പ്പോറിബസ്, എറ്റ് ദേ മാഗ്നോ മാഗ്നറ്റേ ദെല്ലുറേ (ഭൂമിയെന്ന മഹത്തായ കാന്തത്തെയും കാന്തിക വസ്തുക്കളെയും മറ്റു കാന്തങ്ങളെയും കുറിച്ച്) എന്ന പുസ്തകത്തില് ടെറല്ല (terella) എന്ന പേരിലാണ് ഭൂമിയെന്ന ഭീമന് കാന്തതയെപ്പറ്റി പരാമര്ശിച്ചിട്ടുള്ളത്. വടക്കുനോക്കി വടക്കുദിശയിലേക്ക് ചൂണ്ടിനില്ക്കുന്നത് ഭൂമിയെന്ന കാന്തത്തിന്റെ സ്വാധീനത്താലാണെന്നായിരുന്നു അദ്ദേഹം വാദിച്ചത്. അതിനുമുന്പ് ധ്രുവനക്ഷത്ര(polaris)ത്തിന്റെ സ്വാധീനമാണ് അതിനുപിന്നില് എന്നായിരുന്നു പരക്കെയുള്ള ധാരണ.
ഭൂകാന്തികതയുടെ സ്വഭാവത്തെപ്പറ്റി പഠിച്ച മറ്റൊരാള് ജര്മന് ഗണിതജ്ഞനായ കാള് ഫ്രീദ്റിഷ് ഗോസസ് (1777-1855) ആണ്. കാന്തികതയെപ്പറ്റിയുള്ള പരിമാണാത്മകമായ പഠനം നടത്തിയത് ചാള്സ് അഗസ്റ്റിന് കൂളംബ് (1736-1806) ആണ്. വൈദ്യുത ചാര്ജുകളിലെന്നപോലെ കാന്തികധ്രുവങ്ങള് തമ്മിലും ഉള്ള ആകര്ഷണവികര്ഷണ ബലങ്ങള്ക്ക് വ്യുത്ക്രമവര്ഗനിയമം (diverse square law) ബാധകമാണെന്ന് അദ്ദേഹം വ്യക്തമാക്കി. 1785ലായിരുന്നു ഇത്. 1819ല് കോപ്പന്ഹേഗന് സര്വകലാശാലയിലെ പ്രാഫസറായിരുന്ന ഡച്ച് ഭൗതികജ്ഞന് ഹാന്സ് ക്രിസ്റ്റ്യന് ഓര്സ്റ്റഡ് (1777-1851) വൈദ്യുതിയും കാന്തതയും തമ്മിലുള്ള ബന്ധം കണ്ടെത്തി. വൈദ്യുതി പ്രവഹിക്കുന്ന ഒരു ചാലകം സമീപത്തുള്ള കാന്തസൂചിയെ സ്വാധീനിക്കുന്നതായി തന്റെ പരീക്ഷണങ്ങള്ക്കിടയില് അദ്ദേഹം യാദൃച്ഛികമായി കണ്ടെത്തുകയായിരുന്നു. ആന്ദ്രമേരി ആമ്പിയര് (1775-1836) എന്ന ഫ്രഞ്ച് ശാസ്ത്രജ്ഞനും സമാനമായ പരീക്ഷണങ്ങള് നടത്തുകയുണ്ടായി.
കാന്തികബലം പ്രയോഗിച്ച് മറ്റു വസ്തുക്കളിലും, ഏറിയോ കുറഞ്ഞോ, കാന്തത സൃഷ്ടിക്കാന് കഴിയുമെന്ന് ഫാരഡെ 1845ല് കണ്ടെത്തി. യു.എസ്സിലെ ജോസഫ് ഹെന്റിയും വിദ്യുത്കാന്തികവേശനം എന്ന ഈ പ്രതിഭാസം സ്വതന്ത്രമായി കണ്ടെത്തിയിരുന്നു. ഫാരഡേയാണ് കാന്തികക്ഷേത്രം (magnatic field) എന്ന ആശയത്തിന് ജന്മം നല്കിയത്. ഫാരഡെയുടെ തത്ത്വങ്ങള്ക്ക് ജെയിംസ് ക്ലാര്ക്ക് മാക്സ്വെല് (James Clerk Maxwell) എക്സ്പെരിമെന്റല് റിസര്ച്ചസ് ഇന് ഇലക്ട്രിസിറ്റി എന്ന ഗ്രന്ഥത്തിലൂടെ ഗണിതരൂപം നല്കി. വിദ്യുത്കാന്തത (electromagnetism)എന്ന ശാസ്ത്രശാഖയ്ക്ക് അതോടെ തുടക്കമായി. അദ്ദേഹത്തിന്റെ ട്രീറ്റിസ് ഓണ് ഇലക്ട്രിസിറ്റി ആന്ഡ് മാഗ്നറ്റിസം എന്ന ഗ്രന്ഥം (1873) ആണ് അതിനു തുടക്കം കുറിച്ചത്. വിദ്യുത്കാന്തിക തരംഗങ്ങള് ത്വരണം ചെയ്യുന്ന ചാര്ജുകളില്നിന്ന് ഉദ്ഭവിക്കുകയും പ്രകാശവേഗത്തില് പ്രക്ഷണം ചെയ്യപ്പെടുകയും ചെയ്യുന്നു എന്ന് ഗണിതപരമായി മാക്സ്വെല് തെളിയിച്ചു. പ്രകാശം ഒരു വിദ്യുത്കാന്തിക തരംഗമാണെന്ന് അദ്ദേഹം സമര്ഥിക്കുകയും ചെയ്തു. ഹൈന്റിഷ് ഹെര്ട്സ് (Heinrich Hertz) എന്ന ജര്മന് ഭൗതികശാസ്ത്രജ്ഞന് വിദ്യുത്കാന്തിക തരംഗങ്ങളുടെ നിലനില്പ് പരീക്ഷണത്തിലൂടെ തെളിയിച്ചു.
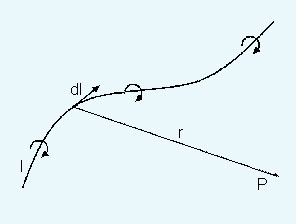
ഇത് ബയോര്ട്സവാര്ട് നിയമം എന്നറിയപ്പെടുന്നു. ആംപിയര് നിയമമെന്നും അറിയപ്പെടുന്നുണ്ട്. ജയിലെ കാന്തികക്ഷേത്രദിശ ദൂരസദിശം വൈദ്യുതപ്രവാഹ ശകലം dl ഇവയ്ക്ക് ലംബമായിരിക്കും. ഇതുകാണാന് പ്രദക്ഷിണ സ്ക്രൂ നിയമം (right handed screw rule) ഉപയോഗിക്കാം. ഒരു പ്രദക്ഷിണ സ്ക്രൂ വൈദ്യുതപ്രവാഹ ദിശയില് ചലിക്കുംവിധം കറക്കിയാല്, അതിന്റെ കറക്കത്തിന്റെ ദിശയായിരിക്കും ചാലകത്തിനു ചുറ്റുമുള്ള കാന്തികക്ഷേത്രത്തിന്റെ ദിശ. dl,r ഇവ ഒരേ ദിശയിലോ എതിര്ദിശയിലോ ആയിട്ടുള്ള സ്ഥാനങ്ങളില് ആയിരിക്കും.
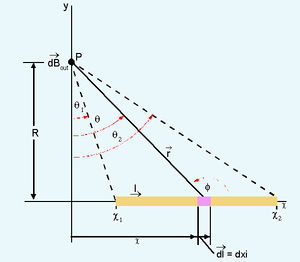
ഒരു വൈദ്യുത സര്ക്കീറ്റ് ഒരു ബിന്ദുവില് സൃഷ്ടിക്കുന്ന ആകെ കാന്തികക്ഷേത്രം കാണണമെങ്കില് അതിലെ ഓരോ പ്രവാഹശകലം dl ഉം സൃഷ്ടിക്കുന്ന ക്ഷേത്രശകലങ്ങളുടെ തുക അഥവാ സമാകലം കണ്ടാല് മതി. ഏതാനും സമമിത സര്ക്കീറ്റ് രൂപങ്ങളിലൊഴികെ മറ്റിടങ്ങളില് ഇതു കാണുക എളുപ്പമല്ല. അത്തരം ചില സമമിത സര്ക്കീറ്റുകള് ഇവയാണ്
(a) വൃത്താകാര വൈദ്യുത വലയം (current loop). R വ്യാസാര്ധമുള്ള ഒരു വൃത്താകാര വൈദ്യുതവലയം പരിഗണിച്ചാല്, അതിന്റെ കേന്ദ്രം Pയെ സംബന്ധിച്ചിടത്തോളം ഓരോ പ്രവാഹശകലം ldlന്റെയും ദൂരസദിശം R, ld lന് ലംബമായിരിക്കും. അത് P യില് സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രം dB അക്ഷത്തിന്റെ ദിശയില് ആയിരിക്കും. അതുകൊണ്ട് ആ വലയം വൃത്തകേന്ദ്രത്തില് സൃഷ്ടിക്കുന്ന മൊത്തം കാന്തികക്ഷേത്രം
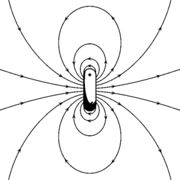
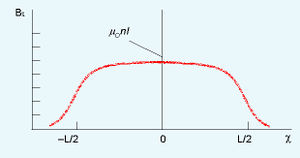
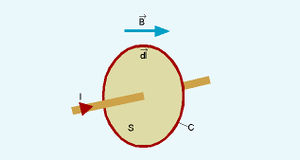
b. സോളിനോയ്ഡ്. ഒന്നിനോടൊന്നു ചേര്ത്തുവച്ച വൈദ്യുതവലയങ്ങളായി ഒരു സോളിനോയ്ഡിനെ പരിഗണിക്കാം. അതിന്റെ അക്ഷത്തിലും സമീപത്തും പ്രബലവും ഏകസമാനവും (uniform) ആയ കാന്തികക്ഷേത്രം സൃഷ്ടിക്കാന് കഴിയും. ചുരുളിന്റെ നീളം L ഉം ചുറ്റുകളുടെ എണ്ണം N ഉം ആണെങ്കില്, N പ്രവാഹവലയങ്ങള് തൊട്ടുതൊട്ടുവയ്ക്കുന്നതിനു തുല്യമാണ് ഇതിന്റെ കാന്തികക്ഷേത്രം. ഒരു സോളിനോയ്ഡ് സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രരേഖകളും ഒരു ബാര് മാഗ്നറ്റ് സൃഷ്ടിക്കുന്ന ക്ഷേത്രരേഖകളും തമ്മിലുള്ള സമാനത ശ്രദ്ധിക്കുക ധചിത്രം (a), (b)പ. ഇരുമ്പ് രാക്കുപൊടി ഉപയോഗിച്ച് ഇത് ദൃശ്യവത്കരിച്ചിരിക്കുന്നു. (ചിത്രം c)
സോളിനോയ്ഡില് dx നീളം പരിഗണിച്ചാല് അതിലെ ചുറ്റുകളുടെ എണ്ണം dN=ndx, n= ഏകകനീളത്തിലടങ്ങിയ ചുറ്റുകള് (n=NL). അക്ഷത്തിലെ ഏതൊരു ബിന്ദുവിലും അക്ഷദിശയില് ഈ dN ചുറ്റുകള് സൃഷ്ടിക്കുന്ന ക്ഷേത്രം
നീളമേറിയ (L>>R) ഒരു സോളിനോയിഡിന്റെ ഉള്ളില്, അഗ്രങ്ങളില് നിന്നകലെ,
c. നേര്ചാലകം. ഒരു നേര്ചാലകം P എന്ന ബിന്ദുവില് സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രം കാണാന് അതിലെ ഓരോ വൈദ്യുതശകലം dx ഉം ജയില് സൃഷ്ടിക്കുന്ന ക്ഷേത്രങ്ങളുടെ തുക കണ്ടാല്
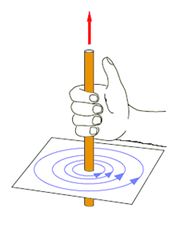
ക്ഷേത്രദിശ വലതുകൈ നിയമം ഉപയോഗിച്ച് നിര്ണയിക്കാം. വൈദ്യുത പ്രവാഹദിശയില് പെരുവിരല് വരുംവിധം ചാലകത്തെ വലതുകൈകൊണ്ടുപിടിച്ചാല്, വിരലുകള് ചാലകത്തെ ചുറ്റിയ ദിശ കാന്തികക്ഷേത്രദിശയായിരിക്കും.
ഒരു കാന്തികക്ഷേത്രത്തില് 1 കൂളംബ് ചാര്ജ് 1 മീ./സെക്കന്ഡ് വേഗത്തില് സഞ്ചരിക്കുമ്പോള് അതില് അനുഭവപ്പെടുന്ന ബലം 1 ന്യൂട്ടണ് ആണെങ്കില് ആ ക്ഷേത്രത്തിന്റെ തീവ്രത 1 ടെസ്ല (T) ആണെന്നു പറയും. IT=IN/(C.m/s)=1N/(A.m) ഇത് ഒരു വലിയ യൂണിറ്റാണ്. ഒരു സാധാരണ സ്ഥിരകാന്തത്തിന്റെ സമീപത്ത് അനുഭവപ്പെടുന്ന കാന്തികക്ഷേത്രം 0.0010.D1 T ആണ്. ഭൂകാന്തികക്ഷേത്രം ഏകദേശം 4x10-4Tആണ്. ശക്തിയേറിയ വിദ്യുത്കാന്തങ്ങള്ക്ക് 1-2 T വരെയും അതിചാലക കാന്തങ്ങള്ക്ക് 10T വരെയും ക്ഷേത്ര തീവ്രത നേടാന് കഴിഞ്ഞിട്ടുണ്ട്. ടെസ്ല ഒരു വലിയ യൂണിറ്റ് ആയതുകൊണ്ട് 10-4യ്ക്കു തുല്യമായ ഗൗസ് എന്ന CGS യൂണിറ്റ് പലപ്പോഴും ഉപയോഗിക്കാറുണ്ട്. ഒരു കാന്തികക്ഷേത്രത്തില് വച്ചിരിക്കുന്ന ചാലകത്തിലൂടെ വൈദ്യുതിപ്രവഹിക്കുമ്പോള് ചാലകത്തില് അനുഭവപ്പെടുന്ന ബലം അതിലെ ഓരോ ചാര്ജിലും അനുഭവപ്പെടുന്ന ബലങ്ങളുടെ തുകയ്ക്ക് തുല്യമായിരിക്കും. dl നീളവും A ഛേദവിസ്തൃതിയും ഉള്ള ഒരു ചാലകശകലം സങ്കല്പിച്ചാല്, അതില് അനുഭവപ്പെടുന്ന ബലം F=υVdxB.Adl ആയിരിക്കും. വൈദ്യുതപ്രവാഹദിശയിലുള്ള ചാര്ജിന്റെ ശരാശരി പ്രവേഗവും (drift velocity),Adl പ്രസ്തുത ചാലകത്തിലെ ചാര്ജുകളുടെ എണ്ണവുമാണ്.
L നീളമുള്ള ഒരു ചാലകത്തിന്മേലുള്ള ആകെ ബലം കാണാന് ഇതിന്റെ സമാകലം കണ്ടാല്മതി.
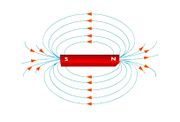
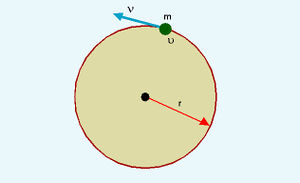
ക്ഷേത്രബലരേഖകള്. കാന്തികക്ഷേത്രത്തിന്റെ തീവ്രതയും ദിശയും ക്ഷേത്രബലരേഖകള്കൊണ്ട് പ്രതിനിധീകരിക്കാമെന്ന ആശയം അവതരിപ്പിച്ചത് ഫാരഡേ (Michael Faraday) ആണ്. ക്ഷേത്രത്തിനു ലംബമായി ഏകക വിസ്തൃതിയുള്ള ഛേദതലത്തിലൂടെ കടന്നുപോകുന്ന രേഖകളുടെ എണ്ണമാണ് തീവ്രതയെ പ്രതിനിധീകരിക്കുന്നത്. ഓരോ സ്ഥാനത്തെയും ക്ഷേത്രദിശ അതിലേ കടന്നുപോകുന്ന ബലരേഖയ്ക്കു പരക്കുന്ന സ്പര്ശരേഖയും (Tangent) സൂചിപ്പിക്കും. ഒരു വൈദ്യുതപ്രവാഹം സൃഷ്ടിക്കുന്ന കാന്തികബലരേഖകള് പ്രവാഹദിശയ്ക്കു ചുറ്റും ഏകകേന്ദ്രവൃത്തങ്ങളായി ചിത്രീകരിക്കാം. ഒരു കാന്തം സൃഷ്ടിക്കുന്ന ക്ഷേത്രരേഖകള് കാന്തത്തിനു പുറത്ത് ഉത്തരധ്രുവത്തില്നിന്ന് ദക്ഷിണധ്രുവത്തിലേക്കും കാന്തത്തിനുള്ളില് ദക്ഷിണധ്രുവത്തില് നിന്ന് ഉത്തരധ്രുവത്തിലേക്കുമാണ് സങ്കല്പിക്കുന്നത്. കാന്തികക്ഷേത്രരേഖകള് പൂര്ണപരിപഥങ്ങള് സൃഷ്ടിക്കുന്നു എന്നര്ഥം.ഒരു ചാര്ജിതകണത്തിന്റെ കാന്തികക്ഷേത്രത്തിലെ പഥം. ഒരു ചാര്ജിതകണം കാന്തികക്ഷേത്രത്തിലൂടെ ചലിച്ചാല് അതില് അനുഭവപ്പെടുന്ന ബലം എപ്പോഴും ചലനദിശയ്ക്ക് ലംബമായതുകൊണ്ട് അതൊരു വക്രപഥത്തില് ചലിക്കാന് നിര്ബന്ധിതമാകുന്നു. എന്നാല്, അതിന്റെ വേഗതയിലോ ഗതികോര്ജത്തിലോ മാറ്റമുണ്ടാകുന്നില്ല. കണത്തിന്റെ ചലനദിശ കാന്തികക്ഷേത്രത്തിനു ലംബമായാല് പഥം വൃത്തമായിരിക്കും. ഇവിടെ ബലം,
കണത്തിന്റെ ആക്കം (momentum) mvകൂടുമ്പോള് r കൂടും. ഒപ്പം ആ യും വര്ധിപ്പിച്ചാല് r സ്ഥിരമാക്കിനിര്ത്താം. കണം സ്ഥിരവൃത്തപഥത്തിലായിരിക്കുമ്പോള് അതിന്റെ ആവര്ത്തനകാലവും ആവൃത്തിയും ഇപ്രകാരമായിരിക്കും.
പരിക്രമണ ആവൃത്തിയെ സൈക്ലോട്രാണ് ആവൃത്തി എന്നുവിളിക്കും. കണികത്വരിത്രങ്ങള് (സൈക്ലോട്രാണ്, സിങ്ക്രാട്രാണ് മുതല-ായവ), മാസ്സ് സ്പെക്ട്രാമീറ്റര് തുടങ്ങിയവയുടെ നിര്മിതിയില് ഈ സമവാക്യങ്ങള് നിര്ണായകമാണ്.കണത്തിന്റെ പ്രാരംഭ ചലനദിശ കാന്തികക്ഷേത്രരേഖകള്ക്കു ചരിഞ്ഞ ദിശയിലാണെങ്കില് അതിന്റെ തുടര്ന്നുള്ള ചലനം രണ്ടു ഘടകങ്ങള് ചേര്ന്നതായിരിക്കും. കണത്തിന്റെ പ്രവേഗത്തിലെ ക്ഷേത്രത്തിനു ലംബമായ ഘടകം അതിനെ ബലരേഖകള്ക്കു ചുറ്റും വൃത്തപഥത്തില് ചലിപ്പിക്കുമ്പോള്, സമാന്തരഘടകം അതിനെ ക്ഷേത്രദിശയില് ചലിപ്പിക്കുന്നു. കണത്തിന്റെ പരിണതചലനം ഒരു ഹെലിക്സിന്റെ രൂപത്തിലായിരിക്കും. ഭൂമിക്കുചുറ്റും വാന് അലന് ബെല്റ്റ് എന്നറിയപ്പെടുന്ന കാന്തികമേഖലയുണ്ട്. സൗരവാതത്തില് (solar wind) ഉള്പ്പെട്ട പ്രാട്ടോണുകളും ആല്ഫാകണങ്ങളും മറ്റും ഈ കാന്തികബലരേഖകളെ മുറിച്ചുകടക്കുമ്പോള് അവയുടെ പഥം ഹെലിക്കല് ആവുകയും അവ ബലരേഖകളുടെ ദിശയില് സഞ്ചരിച്ച് ധ്രുവങ്ങളില് എത്തിച്ചേരുകയും ചെയ്യുന്നു. ധ്രുവമേഖലയില് ഇവ ഭൂമിയോട് അടുക്കുന്നതുകൊണ്ട് അന്തരീക്ഷ തന്മാത്രകളുമായി കൂട്ടിയിടിക്കാന് ഇടയാവുകയും പ്രകാശം ചൊരിയാന് ഇടയാവുകയും ചെയ്യും. ഇതാണ് ധ്രുവദീപ്തി എന്നറിയപ്പെടുന്നത്.
കാന്തികക്കുപ്പി. ചാര്ജിതകണങ്ങള് ചലിക്കുന്നത് ഏകസമാനമല്ലാത്ത (non uniform) കാന്തിക ക്ഷേത്രത്തിലാണെങ്കില് അവയുടെ ചലനം സങ്കീര്ണമായിരിക്കും. ക്ഷേത്രതീവ്രത മധ്യഭാഗത്തു കുറവും അഗ്രങ്ങളില് കൂടുതലും ഉള്ള ഒരു സംവിധാനമാണ് ഈ കാന്തികക്കുപ്പി. ഇതില് ചലിക്കുന്ന ചാര്ജിതകണങ്ങള് അഗ്രങ്ങളില്വച്ച് വിപരീതദിശ കൈവരിക്കാനും അങ്ങനെ മുന്നോട്ടും പിന്നോട്ടും പലവട്ടം സഞ്ചരിക്കാന് ഇടയാവുകയും ചെയ്യും. ഇതിനിടയ്ക്ക് അവയിലേക്ക് ഊര്ജം പകര്ന്നു നല്കാന് കഴിഞ്ഞാല് (ഉദാ. വിദ്യുത്കാന്തിക ഊര്ജരൂപത്തില്) അവ അതിശക്തിയോടെ അന്യോന്യം കൂട്ടിയിടിക്കും. ഈ വിധം ആണവ ഫ്യൂഷന് കൈവരിക്കാന് കഴിയുമോ എന്ന പരീക്ഷണങ്ങള് ധാരാളം നടന്നുവരുന്നു.
ഒരു വൈദ്യുതവലയത്തിലനുഭവപ്പെടുന്ന ടോര്ക്ക്. വൈദ്യുതി പ്രവഹിക്കുന്ന ഒരു വലയം ഒരു കാന്തികക്ഷേത്രത്തില് വച്ചാല് അതില് തുല്യവും വീപരീതവുമായ രണ്ടുബലങ്ങള് 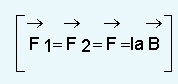 പ്രവര്ത്തിക്കുന്നു. അതു സൃഷ്ടിക്കുന്ന ടോര്ക്ക്
പ്രവര്ത്തിക്കുന്നു. അതു സൃഷ്ടിക്കുന്ന ടോര്ക്ക് ![]() ഇവിടെ A=ab=വലയത്തിന്റെ വിസ്തൃതിയാണ് θ, വലയവിസ്തൃതിക്ക് ലംബമായ ഏകക സദിശവും കാന്തികക്ഷേത്രം Bയും തമ്മിലുള്ള കോണളവാണ്. വലയത്തിന് N ചുറ്റുകളുണ്ടെങ്കില്,
ഇവിടെ A=ab=വലയത്തിന്റെ വിസ്തൃതിയാണ് θ, വലയവിസ്തൃതിക്ക് ലംബമായ ഏകക സദിശവും കാന്തികക്ഷേത്രം Bയും തമ്മിലുള്ള കോണളവാണ്. വലയത്തിന് N ചുറ്റുകളുണ്ടെങ്കില്, ![]()
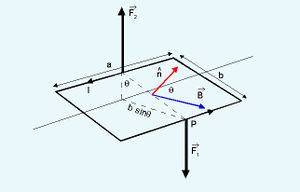
കാന്തികാഘൂര്ണത്തിന്റെ SI യൂണിറ്റ് A.m2 ആണ്; ടോര്ക്കിന്റേത് A.m2 .T അഥവാ N.m ടോര്ക്ക് ഇവിടെ നിര്ണയിച്ചത് ഒരു ദീര്ഘചതുരവലയത്തിനാണെങ്കിലും വൈദ്യുതി പ്രവഹിക്കുന്ന ഏതു രൂപത്തിലുള്ള വലയത്തിനും സമവാക്യം (12), (13) ഇവ ബാധകമാണ്.
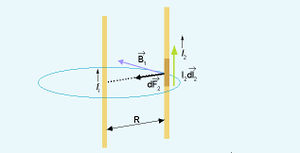
രണ്ടു സമാന്തര ചാലകക്കമ്പികള് തമ്മിലുള്ള ബലം. ദീര്ഘവും സമാന്തരവുമായ രണ്ടു ചാലകങ്ങള് സങ്കല്പിക്കുക. അവയിലൂടെ I, I1 വീതം വൈദ്യുതി ഒരേ ദിശയില് പ്രവഹിക്കുന്നു എന്നും കരുതുക. ആദ്യത്തെ കമ്പിയിലെ ഒരു പ്രവാഹശകലം ldlല് രണ്ടാമത്തെ കമ്പിയിലെ പ്രവാഹം സൃഷ്ടിക്കുന്ന കാന്തികക്ഷേത്രം B1 പ്രയോഗിക്കുന്ന ബലം ![]() ആയിരിക്കും. ഇത് ldl നു ലംബമായി രണ്ടാമത്തെ ചാലകത്തിന്റെ ദിശയില് ആയിരിക്കും. തിരിച്ച് രണ്ടാമത്തെ കമ്പിയിലെ
ആയിരിക്കും. ഇത് ldl നു ലംബമായി രണ്ടാമത്തെ ചാലകത്തിന്റെ ദിശയില് ആയിരിക്കും. തിരിച്ച് രണ്ടാമത്തെ കമ്പിയിലെ 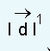 പ്രവാഹശകലത്തില് ഒന്നാമത്തെ കമ്പിസൃഷ്ടിക്കുന്ന ബലം
പ്രവാഹശകലത്തില് ഒന്നാമത്തെ കമ്പിസൃഷ്ടിക്കുന്ന ബലം ![]() , ഒന്നാമത്തെ ചാലകത്തിനു നേര്ക്കും ആയിരിക്കും. അതായത്, രണ്ടു സമാന്തര പ്രവാഹങ്ങള് പരസ്പരം ആകര്ഷിക്കുന്നു. ഒന്നിന്റെ പ്രവാഹദിശ തിരിച്ചായാല് വികര്ഷണമാവും ഫലം. ഇവ ആദ്യമായി അളന്നു തിട്ടപ്പെടുത്തിയത് ആമ്പിയറാണ്.
, ഒന്നാമത്തെ ചാലകത്തിനു നേര്ക്കും ആയിരിക്കും. അതായത്, രണ്ടു സമാന്തര പ്രവാഹങ്ങള് പരസ്പരം ആകര്ഷിക്കുന്നു. ഒന്നിന്റെ പ്രവാഹദിശ തിരിച്ചായാല് വികര്ഷണമാവും ഫലം. ഇവ ആദ്യമായി അളന്നു തിട്ടപ്പെടുത്തിയത് ആമ്പിയറാണ്.
ചാലകങ്ങളുടെ നീളം (L), അവ തമ്മിലുള്ള അകല (R)വുമായി താരതമ്യം ചെയ്യുമ്പോള് വളരെ വലുതാണെങ്കില് (L>>R),
അനന്ത ദൈര്ഘ്യമുള്ളതും സമാന്തരവുമായ രണ്ടു നേര്ത്ത ചാലകങ്ങള് ശൂന്യതയില് അന്യോന്യം 1 മീ. അകലത്തില്വച്ച് അവയിലൂടെ തുല്യഅളവില് വൈദ്യുതികടത്തിവിടുമ്പോള് അവയ്ക്കിടയില് ന്യൂട്ടണ് ബലം അനുഭവപ്പെടുന്നുവെങ്കില്, പ്രവഹിക്കുന്ന വൈദ്യുതി 1 ആമ്പിയര് ആണെന്നു പറയാം.
ഗോസ്സ് നിയമം. വൈദ്യുതക്ഷേത്രവും കാന്തികക്ഷേത്രവും തമ്മിലുള്ള പ്രധാനവ്യത്യാസം, വൈദ്യുതക്ഷേത്രരേഖകള് ഒരു ചാര്ജില് തുടങ്ങി മറ്റൊന്നില് അവസാനിക്കുമ്പോള് കാന്തികക്ഷേത്രരേഖകള് സംവൃതവക്രങ്ങളാണ്. അതുകൊണ്ട്, ഒരു കാന്തധ്രുവത്തിനുചുറ്റും ഒരു സംവൃതപ്രതലം (closed surface) സങ്കല്പിച്ചാല് (ഇതിനെ ഗോസ്സ് പ്രതലം എന്നുവിളിക്കുന്നു) അതിലൂടെ പുറത്തേക്കു പോകുന്ന ബലരേഖകളും അകത്തേക്കുവരുന്ന ബലരേഖകളും എണ്ണത്തില് തുല്യമായിരിക്കും, അഥവാ, ആ പ്രതലത്തിലൂടെയുള്ള ആകെ ഫ്ളക്സ് പൂജ്യമായിരിക്കും.
ഇതാണ് കാന്തികക്ഷേത്രത്തെ സംബന്ധിച്ച ഗോസ്സ് നിയമം. കാന്തിക ഏകധ്രുവം (monopole) പി.എ.എം. ഡിറാക്കിന്റെ സിദ്ധാന്തം പ്രവചിക്കുന്നുണ്ടെങ്കിലും അവയെ ഇതുവരെ കണ്ടെത്തിയിട്ടില്ല. കാന്തികതയുടെ അടിസ്ഥാനം ഇപ്പോഴും കാന്തികദ്വിധ്രുവങ്ങള് തന്നെ.
ആമ്പിയര് നിയമം. I വൈദ്യുതപ്രവാഹത്തിനുചുറ്റും ലംബദിശയില് ട എന്ന പ്രതലവും അതിന്റെ പരിധി ഇയും പരിഗണിക്കുക. കാന്തികക്ഷേത്രം ക്ക് ഏതൊരു ദൈര്ഘ്യശകലം ന്റെയും ദിശയിലുള്ള ഘടകം ആണെങ്കില്, ആമ്പിയര് ![]()
![]() പരിവൃത്തി സമാകലം (circulation integral) എന്നറിയപ്പെടുന്നു. ടോകാമാക് (Tokamak) ഫ്യൂഷന് ടെസ്റ്റ് റിയാക്ടര് പോലുള്ള സംവിധാനങ്ങളിലെ ടോറോയിഡല് കുഴലുകള്ക്കുള്ളിലെ കാന്തികക്ഷേത്രതീവ്രത, ക്ഷേത്രവിതരണം ഇവ കണക്കാക്കാന് ആമ്പിയര് നിയമം പ്രയോജനപ്പെടുന്നു.
പരിവൃത്തി സമാകലം (circulation integral) എന്നറിയപ്പെടുന്നു. ടോകാമാക് (Tokamak) ഫ്യൂഷന് ടെസ്റ്റ് റിയാക്ടര് പോലുള്ള സംവിധാനങ്ങളിലെ ടോറോയിഡല് കുഴലുകള്ക്കുള്ളിലെ കാന്തികക്ഷേത്രതീവ്രത, ക്ഷേത്രവിതരണം ഇവ കണക്കാക്കാന് ആമ്പിയര് നിയമം പ്രയോജനപ്പെടുന്നു.
പദാര്ഥങ്ങളുടെ കാന്തത. പദാര്ഥങ്ങളിലെ ആറ്റങ്ങള്ക്ക് അവയുടെ അണുകേന്ദ്രങ്ങള്ക്കു ചുറ്റുമുള്ള ഇലക്ട്രാണുകളുടെ പരിക്രമണം കാരണം കാന്തിക ഡൈപോള് മുമന്റ് ഉണ്ടായിരിക്കും. കൂടാതെ ഇലക്ട്രാണുകളുടെ ചക്രണം (spin) കാരണം തനത് (intrinsic) കാന്തിക മൂമന്റും ഉണ്ടായിരിക്കും. ഇവ അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കുന്നതുകൊണ്ട് പദാര്ഥങ്ങള്ക്ക് മൊത്തത്തില് കാന്തതദൃശ്യമായിരിക്കില്ല. എന്നാല് ഒരു ബാഹ്യകാന്തിക ക്ഷേത്രത്തില് ആറ്റമിക കാന്തങ്ങള് സംരേഖിത (aligned)മാകുന്നതുമൂലം പദാര്ഥം കാന്തികത കൈവരിക്കും. വസ്തുവിനുള്ളില് നടക്കുന്ന കാന്തികധ്രുവീകരണം ബാഹ്യക്ഷേത്രത്തിന് സമാന്തരദിശയിലോ എതിര്ദിശയിലോ ആകാം. ആറ്റമിക ഡൈപോളുകളുടെ ദിശയും അളവും അനുസരിച്ച് വസ്തുക്കളെ അനുകാന്തികം (paramagnatic), പ്രതികാന്തികം (diamagnetic), അയസ്കാന്തികം (ferromagnetic), ഫെറികാന്തികം (ferrimagnetic) എന്നിങ്ങനെ വിഭജിക്കാം. അനുകാന്തികവസ്തുക്കളിലെ ഡൈപോളുകള് താരതമ്യേന ദുര്ബലമായി മാത്രം അന്യോന്യം പ്രതിപ്രവര്ത്തിക്കുന്നവയാണ്. ബാഹ്യക്ഷേത്രത്തിന്റെ സാമീപ്യത്തില് മാത്രം അവ ചെറിയതോതില് സംരേഖിതമാകുന്നതുകൊണ്ട് (ആറ്റങ്ങളുടെ/തന്മാത്രകളുടെ താപീയചലനം ഇവയെ എപ്പോഴും അനിയതമാക്കിക്കൊണ്ടിരിക്കും.) ചെറിയ അളവില് ഇവ കാന്തികത കൈവരിക്കും. പ്രതികാന്തികത ഉണ്ടാകുന്നത് ബാഹ്യക്ഷേത്രത്തിന്റെ സ്വാധീനംമൂലം ഇലക്ട്രാണുകളുടെ പരിക്രമണപഥത്തിലുണ്ടാകുന്ന ചെറിയ വ്യതിയാനംമൂലമാണ്. ഇതു സൃഷ്ടിക്കുന്ന കാന്തികാഘൂര്ണം എപ്പോഴും ബാഹ്യക്ഷേത്രത്തിനു വിപരീതദിശയില് (ലെന്സ് നിയമം അനുസരിക്കുന്ന ദിശയില്) ആയിരിക്കും. മൊത്തം ക്ഷേത്രതീവ്രതയില് കുറവുവരുത്താനാണ് ഇത് ശ്രമിക്കുക. എല്ലാ പദാര്ഥങ്ങളിലും പ്രതികാന്തത സൃഷ്ടിക്കപ്പെടുന്നുണ്ട്. എന്നാല് അനുകാന്തികതയും അയസ്കാന്തികതയുമായി താരതമ്യം ചെയ്താല് ഇവ നന്നേ ചെറുതായതുകൊണ്ട് അത്തരം വസ്തുക്കളില് ഇവ ദൃശ്യമായിരിക്കില്ല. അതില്ലാത്ത വസ്തുക്കളില് മാത്രമേ പ്രതികാന്തത ദൃശ്യമാകൂ.
സമീപസ്ഥങ്ങളായ കാന്തികഡൈപോളുകള് (ഇവ ഇലക്ട്രാണ് ചക്രണംമൂലം സൃഷ്ടിക്കപ്പെടുന്നവയാണ്) അന്യോന്യം വലിയ അളവിലും വിസ്തൃതിയിലും പ്രതിപ്രവര്ത്തിക്കാന് കഴിയുന്ന പദാര്ഥങ്ങളാണ് അയസ്കാന്തിക വസ്തുക്കള്. ചെറിയ ബാഹ്യക്ഷേത്രത്തില്പ്പോലും ഇവ വലിയതോതില് സംരേഖിതമാവുകയും ക്ഷേത്രതീവ്രത വളരെ വര്ധിക്കുകയും ചെയ്യുന്നു. ബാഹ്യക്ഷേത്രം നീക്കിയാലും ഈ അവസ്ഥ തുടര്ന്നെന്നുവരാം.
കാന്തീകരണവും കാന്തശീലതയും. ഒരു പദാര്ഥത്തെ ശക്തിയേറിയ ഒരു കാന്തികക്ഷേത്രത്തില് (ഉദാ. വൈദ്യുതിപ്രവഹിക്കുന്ന ഒരു സോളിനോയ്ഡില്) വച്ചാല് അതിലെ കാന്തിക ഡൈപോളുകള് (അവസ്ഥിരമോ പ്രരിതമോ ആകാം) ക്ഷേത്രദിശയില് സംരേഖിതമാകും. പദാര്ഥം നേടിയ കാന്തതയുടെ സൂചകമാണ് കാന്തീകരണം (Magnetisation, M).
 അണുഘടനയെക്കുറിച്ച് ഒരു ധാരണയുമില്ലാതിരുന്ന കാലത്ത് കാന്തീകരണത്തെ സംബന്ധിച്ച് ആമ്പിയര് സൃഷ്ടിച്ചെടുത്ത ചില ധാരണകള് ഇന്നും പ്രയോജനകരമായി തുടരുന്നു. കാന്തീകരിക്കപ്പെട്ട ഒരു സിലിണ്ടര് പരിഗണിക്കുക. സിലിണ്ടറിനുള്ളില് ഒരേ ദിശയില് കാന്തികഘൂര്ണമുള്ള അനേകം വൈദ്യുതപ്രവാഹ വലയങ്ങള് സങ്കല്പിക്കാം. പദാര്ഥത്തിനുള്ഭാഗത്ത് സമീപസ്ഥ വലയങ്ങളിലെ പ്രവാഹദിശകള് വിപരീതങ്ങളായതിനാല് പരിണതപ്രവാഹം ശൂന്യമാക്കപ്പെടുന്നു. എന്നാല് സിലിണ്ടറിന്റെ പ്രതലത്തില് പരിണതപ്രവാഹം ശൂന്യമാക്കപ്പെടുന്നില്ല. പ്രതലത്തിലെ പരിണത പ്രവാഹം ആമ്പീരിയന് പ്രവാഹം (amperean current)എന്നറിയപ്പെടുന്നു. ഇത് ഒരു സോളിനോയിഡുപോലെ പ്രവര്ത്തിക്കും.
അണുഘടനയെക്കുറിച്ച് ഒരു ധാരണയുമില്ലാതിരുന്ന കാലത്ത് കാന്തീകരണത്തെ സംബന്ധിച്ച് ആമ്പിയര് സൃഷ്ടിച്ചെടുത്ത ചില ധാരണകള് ഇന്നും പ്രയോജനകരമായി തുടരുന്നു. കാന്തീകരിക്കപ്പെട്ട ഒരു സിലിണ്ടര് പരിഗണിക്കുക. സിലിണ്ടറിനുള്ളില് ഒരേ ദിശയില് കാന്തികഘൂര്ണമുള്ള അനേകം വൈദ്യുതപ്രവാഹ വലയങ്ങള് സങ്കല്പിക്കാം. പദാര്ഥത്തിനുള്ഭാഗത്ത് സമീപസ്ഥ വലയങ്ങളിലെ പ്രവാഹദിശകള് വിപരീതങ്ങളായതിനാല് പരിണതപ്രവാഹം ശൂന്യമാക്കപ്പെടുന്നു. എന്നാല് സിലിണ്ടറിന്റെ പ്രതലത്തില് പരിണതപ്രവാഹം ശൂന്യമാക്കപ്പെടുന്നില്ല. പ്രതലത്തിലെ പരിണത പ്രവാഹം ആമ്പീരിയന് പ്രവാഹം (amperean current)എന്നറിയപ്പെടുന്നു. ഇത് ഒരു സോളിനോയിഡുപോലെ പ്രവര്ത്തിക്കും.
സിലിണ്ടറില് dl കനവും A ഛേദതല വിസ്തൃതിയുമുള്ള ഒരു തകിട് സങ്കല്പിച്ചാല്, അതിന്റെ വ്യാപ്തം dv=Adl; ആമ്പീരിയന് പ്രവാഹം dl ആണെങ്കില് തകിടിന്റെ കാന്തികാഘൂര്ണം dμ=Adl. അപ്പോള് ആ തകിടിന്റെ കാന്തീകരണം (ഏകക വ്യാപ്തത്തിന്റെ കാന്തികാഘൂര്ണം
Mന്റെ യൂണിറ്റ് ആമ്പിയര്/മീറ്റര് (Am-1) ആണ്. സമീകരണം (18) സൂചിപ്പിക്കുന്നത് ഒരു സിലിണ്ടറില് അക്ഷദിശയ്ക്കു സമാന്തരമായി സൃഷ്ടിക്കപ്പെടുന്ന കാന്തീകരണം ങ, സിലിണ്ടറിന്റെ പ്രതലത്തിലെ 1 മീ. ദൈര്ഘ്യത്തില് (dl-1) M ആമ്പിയര് വൈദ്യുതി പ്രവഹിച്ചാലുള്ള കാന്തികക്ഷേത്രത്തിനു തുല്യമാണ് എന്നാണ്. സിലിണ്ടറിനെ ഒരു സോളിനോയിഡായി പരിഗണിച്ചാല്, സമവാക്യം (6) ലെ ![]() യ്ക്കു പകരം
യ്ക്കു പകരം
എന്നെഴുതാം. സിലിണ്ടറിനെ ![]() ഉള്ള ഒരു വൈദ്യുത സോളിനോയിഡിനുള്ളില് വച്ചാല്, മൊത്തം കാന്തികക്ഷേത്രം,
ഉള്ള ഒരു വൈദ്യുത സോളിനോയിഡിനുള്ളില് വച്ചാല്, മൊത്തം കാന്തികക്ഷേത്രം,
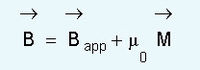
അനുകാന്തിക, അയസ്കാന്തിക വസ്തുക്കളില് രണ്ടുഘടകങ്ങളും ഒരേ ദിശയില് ആയിരിക്കും; പ്രതികാന്തിക വസ്തുക്കളില് എതിര്ദിശയിലും, അനുകാന്തിക, പ്രതികാന്തിക വസ്തുക്കളില് കാന്തീകരണം പ്രയുക്ത ക്ഷേത്രത്തിന് Bappനേര്അനുപാതത്തിലായിരിക്കും. അതായത്,
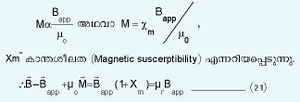
μrനെ ആപേക്ഷിക പാരഗമ്യത (relative permeability) എന്നും വിളിക്കുന്നു. ഒരു പദാര്ഥത്തിന്റെ പാരഗമ്യതμ=μo.μr എന്നെഴുതാം. അനുകാന്തിക വസ്തുക്കള്ക്ക്വളരെ ചെറുതും പോസിറ്റീവും ആയിരിക്കും. അതിന്റെ മൂല്യം താപനിലയനുസരിച്ച് മാറും. പ്രതികാന്തിക വസ്തുക്കള്ക്ക് Xmനന്നേച്ചെറുതും നെഗറ്റീവും താപനിലയെ ആശ്രയിക്കാത്തതുമാണ്. മിക്ക വസ്തുക്കള്ക്കും χm~10-5 μr ~1 ഉം ആണ്. എന്നാല് അയസ്കാന്തിക വസ്തുക്കളുടെ μr ~ 5,000-1,00,000 എന്ന തോതില് വ്യത്യസ്തമായി കാണപ്പെടുന്നു. സ്ഥിരകാന്തങ്ങളിലാകട്ടെ μrനിര്വചിക്കാനേ കഴിയില്ല; കാരണം,Bapp ന്റെ അഭാവത്തിലും അവ കാന്തത പ്രദര്ശിപ്പിക്കുന്നു (ചിത്രം 1, 2, 3 കാണുക).
ആറ്റമിക കാന്തികാഘൂര്ണം. അയസ്കാന്തികതയ്ക്കും അനുകാന്തികതയ്ക്കും കാരണം ആറ്റങ്ങളുടെയോ തന്മാത്രകളുടെയോ സ്ഥിരകാന്തികാഘൂര്ണങ്ങളെയാണ്. ആറ്റമിക ഇലക്ട്രാണുകളുടെ കാന്തികാഘൂര്ണം ഒരു ക്വാണ്ടം പ്രതിഭാസമാണെങ്കിലും അതിന്റെ പൊതുസ്വഭാവം മനസ്സിലാക്കാന് ക്ലാസ്സിക്കല് ഭൗതികം മതിയാകും.m പിണ്ഡവും ചാര്ജും ഉള്ള ഒരു കണം r വ്യാസാര്ധമുള്ള ഒരു വൃത്തത്തില് കറങ്ങിയാല് അതിന്റെ കോണീയ സംവേഗം (angular momentum)
ഇലക്ട്രാണ് പരിക്രമണത്തിന്റെ കോണീയസംവേഗവും കാന്തികാഘൂര്ണവും തമ്മിലുള്ള ഈ ബന്ധം ക്വാണ്ടം സിദ്ധാന്തമനുസരിച്ചും ശരിയാണ്. ഒരുപാധിയുണ്ടെന്നു മാത്രംകോണീയ സംവേഗം 'L' ന്റെ മൂല്യം h(=h/2π, h പ്ലാങ്ക് സ്ഥിരാങ്കം) പൂര്ണസംഖ്യാഗുണിതങ്ങളായിരിക്കണം.
ഒരു ആറ്റത്തിന്റെ കാന്തികാഘൂര്ണം അതിലെ എല്ലാ ഇലക്ട്രാണുകളുടെയും കാന്തികാഘൂര്ണങ്ങളുടെ ആകെത്തുകയാണ്. പരിണതാഘൂര്ണം ചില ആറ്റങ്ങളിലും പൂജ്യമായിരിക്കും. പദാര്ഥങ്ങളിലെ ആറ്റങ്ങളുടെ/തന്മാത്രകളുടെ എല്ലാം കാന്തികാഘൂര്ണങ്ങള് സംരേഖിതമായാല് ആ പദാര്ഥത്തിലെ ഏകകവ്യാപ്തത്തിന്റെ കാന്തികാഘൂര്ണം അതിലടങ്ങിയ ആറ്റങ്ങളുടെ/തന്മാത്രകളുടെ എണ്ണവും (n) ഓരോന്നിന്റെയും കാന്തികാഘൂര്ണവും തമ്മിലുള്ള ഗുണനഫലത്തിനു തുല്യമാകും. ഇതാണ് പൂരിതകാന്തീകരണം (saturation magnatisation).
അനുകാന്തത. സ്ഥിരകാന്തികാഘൂര്ണമുള്ള ആറ്റങ്ങള് അടങ്ങിയ പദാര്ഥങ്ങളിലാണ് അനുകാന്തത ദൃശ്യമാകുന്നത്. അവ തമ്മില് ദുര്ബലമായി പ്രതിപ്രവര്ത്തിക്കുന്നതുമൂലം ചെറിയ കാന്തശീലത (Xm) സൃഷ്ടിക്കപ്പെടുന്നു. ബാഹ്യക്ഷേത്രമൊന്നും പ്രയോഗിക്കാത്തപ്പോള് ഈ ആറ്റമിക കാന്തികാഘൂര്ണങ്ങളെല്ലാം അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കും. ബാഹ്യക്ഷേത്രം പ്രയോഗിക്കുമ്പോള് ഇവ ക്ഷേത്രദിശയില് സംരേഖിതമാകുന്നു. ഒപ്പം, താപീയചലനങ്ങള് അവയെ അനിയതമാക്കാനും ശ്രമിക്കുന്നു. ബാഹ്യക്ഷേത്രത്തിന്റെ ശക്തിയെയും താപനിലയെയും ആശ്രയിച്ചിരിക്കും ഒരു പദാര്ഥത്തില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തശീലത.
ഇത് സാധാരണ താപനിലയില് ആറ്റങ്ങളുടെ താപീയ ഊര്ജ (KT)ത്തെക്കാള് വളരെ (സു. 200ല് 1) കുറവായിരിക്കുമെന്നതിനാല്, ഭൂരിഭാഗം ആറ്റങ്ങളും അനിയതമായിരിക്കും. ഒരു ദുര്ബലക്ഷേത്രത്തില് കാന്തവത്കരണം ക്ഷേത്രതീവ്രതയ്ക്ക് ഏതാണ്ട് ആനുപാതികമായിരിക്കും.
ഇതാണ് ക്യൂറി നിയമം. ഒരു അനുകാന്തികവസ്തുവിലെ കാന്തീകരണം അതിന്റെ കേവലതാപനിലയ്ക്ക് വിപരീതാനുപാതത്തിലായിരിക്കും എന്നാണ് പിയറി ക്യൂറി കണ്ടെത്തിയത്.
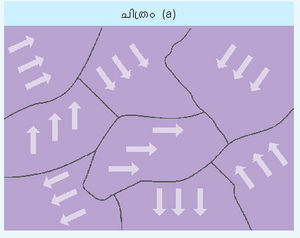
അയസ്കാന്തത. ഇരുമ്പ്, കൊബാള്ട്ട്, നിക്കല് എന്നീ ലോഹങ്ങളിലും അവയുടെ കൂട്ടുലോഹങ്ങളിലും ഗഡോലിനിയം, ഡിസ്പ്രാസിയം തുടങ്ങിയ ഏതാനും സംയുക്തങ്ങളിലും കാണപ്പെടുന്ന പ്രതിഭാസമാണ് അയസ്കാന്തത. അയസ്കാന്തിക പദാര്ഥങ്ങള്ക്ക് വളരെ ഉയര്ന്ന കാന്തശീലത (Xm) ഉണ്ട്. ഒരു ചെറിയ ബാഹ്യക്ഷേത്രം മതി ഇത്തരം വസ്തുക്കളില് വലിയതോതില് ആറ്റമിക കാന്തികാഘൂര്ണങ്ങളുടെ സംരേഖനം സാധ്യമാക്കാന്. ചില സാഹചര്യങ്ങളില്, ബാഹ്യക്ഷേത്രം പിന്നീട് നീക്കിയാലും സംരേഖനം നിലനില്ക്കുന്നു. ഇതിനുകാരണം പ്രാദേശികമായി ദ്വിധ്രുവങ്ങള് തമ്മില് നിലവില്വരുന്ന അതിശക്തമായ പ്രതിപ്രവര്ത്തനമാണ്. കാന്തികധ്രുവങ്ങള് സംരേഖിതമായി സ്ഥിതിചെയ്യുന്ന ഇത്തരം മേഖലകളെ കാന്തിക ഡൊമെയ്നുകള് (magnetic domains)എന്നു വിളിക്കുന്നു. സാധാരണയായി ഈ ഡൊമെയ്നുകള് സൂക്ഷ്മരൂപങ്ങളായിരിക്കും. ഇവ അനിയതമായി വിതരണം ചെയ്യപ്പെട്ടിരിക്കുന്നതുകൊണ്ട് സ്ഥൂലവസ്തുവിന് കാന്തികത ഉണ്ടാവില്ല. ബാഹ്യക്ഷേത്രം പ്രയോഗിക്കുമ്പോള് ഈ ഡൊമെയ്നുകള് ക്ഷേത്രദിശയില് സംരേഖിതമാകുക മാത്രമല്ല ക്ഷേത്രദിശയിലുള്ള ഡൊമെയ്നുകള് കൂടുതല് വിസ്തൃതമാവുകയും മറ്റു ദിശയിലുള്ളവയുടെ വിസ്തൃതി കുറയുകയും ചെയ്യാം. (ചിത്രം a, b കാണുക) എല്ലാ അയസ്കാന്തിക വസ്തുക്കള്ക്കും ക്യൂറി താപനില (Curi Temperature θ)എന്നറിയപ്പെടുന്ന ഒരു താപനില ഉണ്ടായിരിക്കും. അതിനുമുകളില് പദാര്ഥത്തിലെ താപീയചലനങ്ങള് ശക്തമായതുകൊണ്ട് സംരേഖനം അസാധ്യമായിത്തീരുകയും അയസ്കാന്തിക വസ്തു ഒരു അനുകാന്തിക വസ്തുവായി മാറുകയും ചെയ്യും. ആ അവസ്ഥയില് പദാര്ഥത്തിന്റെ കാന്തശീലത
എന്നെഴുതണം. ഇതാണ് ക്യൂറിവെയ്സ് നിയമം (Curi-weiss law)
ഒരു നീണ്ട ഇരുമ്പ്ദണ്ഡ് ഒരു സോളിനോയിഡിനുള്ളില്വച്ച് വൈദ്യുതപ്രവാഹം ക്രമേണ കൂട്ടിയാല് സൃഷ്ടിക്കപ്പെടുന്ന പരിണത കാന്തികക്ഷേത്രം.
അയസ്കാന്തികവസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തികക്ഷേത്രതീവ്രതയും (B) പ്രയുക്തകാന്തികക്ഷേത്രവും (Bapp) ചേര്ത്ത് ഒരു ഗ്രാഫ് വരച്ചാല് ചിത്രത്തിലേതുപോലെ കാണപ്പെടും. പോളിനോയിഡിലെ വൈദ്യുതപ്രവാഹം പൂജ്യത്തില്നിന്ന് ക്രമേണ വര്ധിച്ചാല് ആയുടെ മൂല്യം പൂജ്യത്തില്നിന്ന് ലേക്ക് ഉയര്ന്ന് പൂരിത കാന്തീകൃതാവസ്ഥയില് എത്തുന്നു. അപ്പോള് എല്ലാ കാന്തിക ഡൊമെയ്നുകളും സംരേഖിതമായതായി കണക്കാക്കാം. പിന്നീടങ്ങോട്ട് പ്രവാഹം (I)വര്ധിപ്പിച്ചാല് B യിലുണ്ടാകുന്ന വര്ധന ![]() ലുണ്ടാക്കുന്ന വര്ധനയുടെ മാത്രം ഫലമായിരിക്കും. P1</sup>ല് നിന്ന് Bapp</sup>ക്രമേണ കുറച്ചുകൊണ്ടുവന്നാല് മുന്ചക്രത്തിലൂടെ തിരിച്ചുപോകുന്നില്ല എന്നു കാണാം. ഡൊമെയ്നുകളുടെ സംരേഖനം... (reversible) അല്ല എന്ന് ഇതു സൂചിപ്പിക്കുന്നു. Bapp</sup> പൂജ്യമായാലും കാന്തികവസ്തുവിലെ കാന്തീകരണം കുറച്ച് അവശേഷിക്കുന്നു (P4</sup>). ഇത് അവശിഷ്ടക്ഷേത്രം (Remant field, Brem) എന്നറിയപ്പെടുന്നു. ഈ പ്രതിഭാസത്തെ ഹിസ്റ്ററിസിസ് (ഗ്രീക്കില് Hysteros=പിന്നില്) എന്നു വിളിക്കുന്നു. ഈ അവസ്ഥയിലുള്ള ഇരുമ്പ്ദണ്ഡ് ഒരു സ്ഥിരകാന്തമാണ്. സോളിനോയിഡിലെ വൈദ്യുതിയുടെ ദിശമാറ്റി ക്രമേണ വര്ധിപ്പിച്ചാല് 'C'യില് കാന്തികക്ഷേത്രം പൂജ്യമാകും. തുടര്ന്നും ഈ ദിശയില് വര്ധിപ്പിച്ചാല്, P2</sup> എന്ന ബിന്ദുവില് എതിര്ദിശയിലെ പൂരിതക്ഷേത്രം ലഭിക്കുന്നു. തുടര്ന്ന് കുറച്ചുകൊണ്ടുവന്ന് പൂജ്യത്തിലെത്തിച്ച് വീണ്ടും ദിശമാറ്റി വര്ധിപ്പിച്ചാല് P2</sup>P3</sup>P1</sup>വക്രം ലഭിക്കുന്നു. ഒരു അയസ്കാന്തിക വസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തീകരണം (M) അതിന്റെ മുന്ചരിത്രത്തെ (അത് മുമ്പ് കാന്തീകരിക്കപ്പെട്ടിട്ടുണ്ടോ എന്നതിനെ) ആശ്രയിച്ചിരിക്കുന്നുവെന്ന് ഹിസ്റ്ററിസിസ് വക്രം സൂചിപ്പിക്കുന്നു.
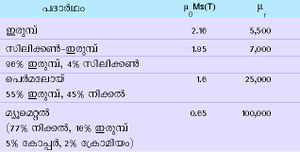
ഏതാനും അയസ്കാന്തിക വസ്തുക്കളിലെ പൂരിത കാന്തികക്ഷേത്രം μoMs(ടെസ് ലയില്), ആപേക്ഷിക പാരഗമ്യത μr ഇവ ചുവടെ കൊടുക്കുന്നു.
ലുണ്ടാക്കുന്ന വര്ധനയുടെ മാത്രം ഫലമായിരിക്കും. P1</sup>ല് നിന്ന് Bapp</sup>ക്രമേണ കുറച്ചുകൊണ്ടുവന്നാല് മുന്ചക്രത്തിലൂടെ തിരിച്ചുപോകുന്നില്ല എന്നു കാണാം. ഡൊമെയ്നുകളുടെ സംരേഖനം... (reversible) അല്ല എന്ന് ഇതു സൂചിപ്പിക്കുന്നു. Bapp</sup> പൂജ്യമായാലും കാന്തികവസ്തുവിലെ കാന്തീകരണം കുറച്ച് അവശേഷിക്കുന്നു (P4</sup>). ഇത് അവശിഷ്ടക്ഷേത്രം (Remant field, Brem) എന്നറിയപ്പെടുന്നു. ഈ പ്രതിഭാസത്തെ ഹിസ്റ്ററിസിസ് (ഗ്രീക്കില് Hysteros=പിന്നില്) എന്നു വിളിക്കുന്നു. ഈ അവസ്ഥയിലുള്ള ഇരുമ്പ്ദണ്ഡ് ഒരു സ്ഥിരകാന്തമാണ്. സോളിനോയിഡിലെ വൈദ്യുതിയുടെ ദിശമാറ്റി ക്രമേണ വര്ധിപ്പിച്ചാല് 'C'യില് കാന്തികക്ഷേത്രം പൂജ്യമാകും. തുടര്ന്നും ഈ ദിശയില് വര്ധിപ്പിച്ചാല്, P2</sup> എന്ന ബിന്ദുവില് എതിര്ദിശയിലെ പൂരിതക്ഷേത്രം ലഭിക്കുന്നു. തുടര്ന്ന് കുറച്ചുകൊണ്ടുവന്ന് പൂജ്യത്തിലെത്തിച്ച് വീണ്ടും ദിശമാറ്റി വര്ധിപ്പിച്ചാല് P2</sup>P3</sup>P1</sup>വക്രം ലഭിക്കുന്നു. ഒരു അയസ്കാന്തിക വസ്തുവില് സൃഷ്ടിക്കപ്പെടുന്ന കാന്തീകരണം (M) അതിന്റെ മുന്ചരിത്രത്തെ (അത് മുമ്പ് കാന്തീകരിക്കപ്പെട്ടിട്ടുണ്ടോ എന്നതിനെ) ആശ്രയിച്ചിരിക്കുന്നുവെന്ന് ഹിസ്റ്ററിസിസ് വക്രം സൂചിപ്പിക്കുന്നു.
ഏതാനും അയസ്കാന്തിക വസ്തുക്കളിലെ പൂരിത കാന്തികക്ഷേത്രം μoMs(ടെസ് ലയില്), ആപേക്ഷിക പാരഗമ്യത μr ഇവ ചുവടെ കൊടുക്കുന്നു.
കാന്തീകരണവും വികാന്തീകരണവും നടക്കുമ്പോള് സംഭവിക്കുന്ന താപനംമൂലം ഊര്ജനഷ്ടം സംഭവിക്കുന്നുണ്ട്. ഹിസ്റ്ററിസിസ് വക്രത്തിന്റെ ഉള്വിസ്തൃതി ഈ നഷ്ടത്തിന് ആനുപാതികമാണ്. ഉള്വിസ്തൃതി (ഊര്ജനഷ്ടം) കുറഞ്ഞ ഹിസ്റ്ററിസിസ് വക്രമുള്ള പദാര്ഥത്തെ മൃദുകാന്തികവസ്തു (soft magnetic material) എന്നുപറയും. ഉദാ. പച്ചിരുമ്പ്. ഇതിന്റെ ആൃലാ പൂജ്യത്തോട് അടുത്താണ്. ട്രാന്സ്ഫോര്മര് കോറുകളിലും മറ്റും ഇത്തരം പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കുക. മറിച്ച്, സ്ഥിരകാന്തങ്ങള് നിര്മിക്കാന് കഠിന(hard) പദാര്ഥങ്ങളാണ് ഉപയോഗിക്കാറ്. ഉദാ. അല്നികോ, കാര്ബണ് സ്റ്റീല്.
പ്രതികാന്തത. കാന്തശീലത (Xm) നെഗറ്റീവ് ആയിട്ടുള്ള പദാര്ഥങ്ങളാണ് പ്രതികാന്തിക വസ്തുക്കള്. 1845ല് മൈക്കല് ഫാരഡേയാണ് പ്രതികാന്തത ആദ്യമായി കണ്ടെത്തിയത്. ബിസ്മത്ത് കാന്തത്തിന്റെ രണ്ടുധ്രുവങ്ങളാലും വികര്ഷിക്കപ്പെടുന്നു എന്നദ്ദേഹം കണ്ടെത്തി. കാന്തികക്ഷേത്രത്തില് വസ്തുവിനുണ്ടാകുന്ന പ്രരിതകാന്തതയാണിതിനുകാരണം. പ്രരിതകാന്തികാഘൂര്ണം എല്ലായ്പ്പോഴും പ്രയുക്തക്ഷേത്രത്തിനു വിപരീതദിശയിലായിരിക്കും എന്നതാണ് പ്രതികാന്തതയുടെ സവിശേഷത. മിക്കപ്പോഴും പ്രതികാന്തത അനുകാന്തതയുടെ 100-1000ത്തില് ഒരംശമേ വരൂ. എന്നാല്, അനുകാന്തതയില്നിന്ന് വ്യത്യസ്തമായി, ഇത് പദാര്ഥ താപനിലയെ ആശ്രയിക്കുന്നില്ല.
പ്രതികാന്തശീലത ആശ്രയിച്ചിരിക്കുന്നത് പദാര്ഥത്തിന്റെ ആറ്റത്തിലെ ഇലക്ട്രാണ് വിതരണത്തെയും അവയുടെ ഊര്ജനിലകളെയും ആണ്. ബാഹ്യകാന്തികക്ഷേത്രം പ്രയോഗിക്കപ്പെടുമ്പോള് ഇലക്ട്രാണ് കക്ഷ്യ(orbit)യില് ചെറിയമാറ്റം സംഭവിക്കുന്നു. ഓരോ ഇലക്ട്രാണും ഒരു അധികകാന്തികാഘൂര്ണം കൈവരിക്കുന്നു. ഒരു സാമ്പിളിലെ ആറ്റങ്ങളുടെ എണ്ണം N ഉം ബാഹ്യക്ഷേത്രം ആയും ഓരോ ആറ്റത്തിലെയും ഇലക്ട്രാണുകളുടെ ആരവര്ഗത്തിന്റെ മാധ്യം (mean square radius)![]() ഉം ആണെങ്കില് കാന്തീകരണം
ഉം ആണെങ്കില് കാന്തീകരണം ![]() ആയിരിക്കും. (m=ഇലക്ട്രാണിന്റെ പിണ്ഡം) ഇതില് നിന്ന്,
ആയിരിക്കും. (m=ഇലക്ട്രാണിന്റെ പിണ്ഡം) ഇതില് നിന്ന്,
ഫെറികാന്തത. ലോഡ്സ്റ്റോണ് അഥവാ മാഗ്നറ്റൈറ്റ് (Fe3O4) ഫെറൈറ്റ് വിഭാഗത്തില്പ്പെടുന്ന ഒരു പദാര്ഥമാണ്. ഇവയ്ക്ക് അയസ്കാന്തങ്ങളെപ്പോലെ തനത് കാന്തത (Spontaneous magnetism), കാന്തികാവശേഷണം (remanance) തുടങ്ങിയ സവിശേഷതകള് ഉണ്ടെങ്കിലും അവയില് നിന്ന് വ്യത്യസ്തമായി വളരെകുറഞ്ഞ വൈദ്യുതചാലകതയേയുള്ളൂ. ഇതുമൂലം എ.സി. കാന്തികക്ഷേത്രങ്ങളില് പ്രവര്ത്തിക്കുമ്പോള് എഡ്ഡി കറന്റ് (eddy current) മൂലമുള്ള ഊര്ജനഷ്ടവും താപസൃഷ്ടിയും നന്നേ കുറവായിരിക്കും. എഡ്ഡി കറണ്ടുമൂലമുള്ള ഊര്ജനഷ്ടം ആവൃത്തിക്കൊത്ത് വര്ധിക്കുന്ന ഒന്നായതുകൊണ്ട് ഇലക്ട്രാണിക്സിലും കംപ്യൂട്ടര്, റേഡിയോ, മ്യൂസിക് റിക്കാര്ഡുകള് തുടങ്ങിയ സംവിധാനങ്ങളിലും ഇവയ്ക്ക് വ്യാപകമായ ഉപയോഗമാണുള്ളത്.