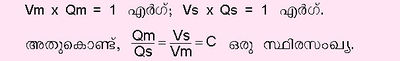This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഏകകങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Units) |
Mksol (സംവാദം | സംഭാവനകള്) (→Units) |
||
| (ഇടക്കുള്ള 4 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 5: | വരി 5: | ||
== Units == | == Units == | ||
| - | അളവിന്റെ മാനദണ്ഡങ്ങള്. ഏതൊരു ഭൗതികപരിമാണത്തെയും | + | അളവിന്റെ മാനദണ്ഡങ്ങള്. ഏതൊരു ഭൗതികപരിമാണത്തെയും പൂര്ണമായി വിശദീകരിക്കണമെങ്കില് അത് അളക്കുവാന് ഉപയോഗിച്ച മാത്രയും ആ പരിമാണത്തില് ആ മാത്ര എത്ര പ്രാവശ്യം ഉള്ക്കൊണ്ടിട്ടുണ്ടെന്നും അറിയേണ്ടതുണ്ട്. ഏതു പരിമാണത്തെ അളക്കുവാനും അതിന്റേതായ ഒരു മാത്ര വേണം. വ്യത്യസ്ത ഭൗതിക പരിമാണങ്ങളെ അളക്കുവാന് അനേകം മാത്രകള് ഉണ്ടെങ്കിലും അവയെല്ലാംതന്നെ നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൂന്ന് അടിസ്ഥാനമാത്രകളില്നിന്ന് വ്യുത്പാദിപ്പിക്കാവുന്നതാണ്. അതിനാല്, നീളം, ദ്രവ്യമാനം, സമയം എന്നീ പരിമാണങ്ങളുടെ മാത്രകളെ അടിസ്ഥാനമാത്രകള് അഥവാ മൗലിക മാത്രകള് എന്നും ബലം, വ്യാപ്തം, വിസ്തീര്ണം, പ്രവേഗം മുതലായ മറ്റു അളവുകളുടെ മാത്രകള് മൗലിക അളവുകളില്നിന്നും വ്യുത്പാദിപ്പിക്കാവുന്നതുകൊണ്ട് അവയുടെ മാത്രകളെ വ്യുത്പന്നമാത്രകള് (derived units)എന്നും പറയുന്നു. |
| - | മാപനരംഗത്തു നിലവിലുള്ള വ്യത്യസ്ത സമ്പ്രദായങ്ങളെ പൊതുവേ രണ്ടായി തരംതിരിക്കാം; മെട്രിക് പദ്ധതി, ബ്രിട്ടീഷ് പദ്ധതി. മെട്രിക് | + | മാപനരംഗത്തു നിലവിലുള്ള വ്യത്യസ്ത സമ്പ്രദായങ്ങളെ പൊതുവേ രണ്ടായി തരംതിരിക്കാം; മെട്രിക് പദ്ധതി, ബ്രിട്ടീഷ് പദ്ധതി. മെട്രിക് പദ്ധതിയില്ത്തന്നെ രണ്ട് ഉപഭാഗങ്ങളുണ്ട്. സി.ജി.എസ്. പദ്ധതി, എം.കെ.എസ്. പദ്ധതി. |
സി.ജി.എസ്. പദ്ധതി. ഓരോ പദ്ധതിയിലെയും മൗലിക മാത്രകളുടെ ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ച് ആ പദ്ധതിക്ക് പേരിട്ടിരിക്കുന്നു. | സി.ജി.എസ്. പദ്ധതി. ഓരോ പദ്ധതിയിലെയും മൗലിക മാത്രകളുടെ ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ച് ആ പദ്ധതിക്ക് പേരിട്ടിരിക്കുന്നു. | ||
| - | + | ഇതില് നീളത്തിന്റെ മൗലികമാത്ര മീറ്ററിന്റെ നൂറില് ഒരംശമായി സെ.മീ. ആകുന്നു. ക്രിപ്റ്റോണ്-86 അണുവിന്റെ 2P<sub>10</sub>, 5d<sub>5</sub> എന്നീ ഊര്ജനിലകള് തമ്മില് നടക്കുന്ന ഊര്ജ സംക്രമണത്തിന്റെ ഫലമായി ഉണ്ടാകുന്ന ഏകവര്ണവികിരണത്തിന്റെ ശൂന്യത(vaccum state)യിലുള്ള തരംഗദൈര്ഘ്യത്തിന്റെ 16,50,763.73 മടങ്ങായി മീറ്റര് നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു. | |
| - | ദ്രവ്യമാനത്തിന്റെ മാത്രയായ ഗ്രാം ഒരു കിലോഗ്രാമിന്റെ | + | ദ്രവ്യമാനത്തിന്റെ മാത്രയായ ഗ്രാം ഒരു കിലോഗ്രാമിന്റെ ആയിരത്തില് ഒരു ഭാഗമാണ്. പാരിസിനടുത്ത് സെവര് എന്ന സ്ഥലത്ത് സൂക്ഷിച്ചിട്ടുള്ള പ്ലാറ്റിനം-ഇറിഡിയം സംയുക്തലോഹത്തില് ചെയ്ത വൃത്തസ്തംഭ(cylinder)ത്തിന്റെ ദ്രവ്യമാനത്തെ ഒരു കിലോഗ്രാം ആയി സ്വീകരിച്ചിരിക്കുന്നു. |
| - | സീസിയം-133 അണുവിന്റെ രണ്ടു പ്രതേ്യക | + | സീസിയം-133 അണുവിന്റെ രണ്ടു പ്രതേ്യക ഊര്ജനിലകള് തമ്മിലുള്ള ഊര്ജസംക്രമണത്തിന്റെ ഫലമായുണ്ടാകുന്ന വികിരണത്തിന്റെ സ്പന്ദനകാലത്തെ 9, 19, 26, 31, 770 കൊണ്ടു ഗുണിച്ചാല് കിട്ടുന്നത് സമയത്തിന്റെ മാത്രയായി (സെക്കന്ഡ്) നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു. |
| - | എം.കെ.എസ്. പദ്ധതി. നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൗലികപരിമാണങ്ങളുടെ മാത്രകള് യഥാക്രമം | + | എം.കെ.എസ്. പദ്ധതി. നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൗലികപരിമാണങ്ങളുടെ മാത്രകള് യഥാക്രമം മീറ്റര്, കിലോഗ്രാം, സെക്കന്ഡ് ആയിരക്കണമെന്ന് 1935-ല് ഇന്റര്നാഷണല് ഇലക്ട്രാ കമ്മിഷന് ചെയ്ത ശിപാര്ശയനുസരിച്ച് ഈ പദ്ധതി നിലവില്വന്നു. തത്ഫലമായി പ്രവേഗത്തിന്റെ മാത്ര മീറ്റര്/സെക്കന്ഡും ത്വരണത്തിന്റേത് മീറ്റര്/സെക്കന്ഡ്<sup>2</sup>-ഉം ബലത്തിന്റേത് ന്യൂട്ടണും ആയി. ഒരു കിലോഗ്രാം ദ്രവ്യമാനത്തിന് ഒരു മീറ്റര്/സെക്കന്ഡ്<sup>2</sup> ത്വരണം നല്കുവാന് ആവശ്യമായ ബലമാണ് ഒരു ന്യൂട്ടണ്. അതുപോലെ പ്രവൃത്തിയുടെയും ശക്തിയുടെയും മാത്രകള് യഥാക്രമം ജൂളും (Joule), വാട്ടും (watt) ആയി. അതായത്, |
| + | |||
| + | [[ചിത്രം:Vol5_434_formula1.jpg|400px]] | ||
| + | |||
| + | വ്യുത്പന്ന ഏകകങ്ങളും വിമകളും (Derived units and Dimensions). ഭൗതികത്തില് മിക്ക പരിമാണവും നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൂന്ന് മൗലിക ഏകകങ്ങളെ അടിസ്ഥാനമാക്കി അളക്കാവുന്നതാണ്. അഥവാ അത്തരം പരിമാണങ്ങളുടെ ഏകകങ്ങള് മൗലിക ഏകകങ്ങളില്നിന്നും വ്യുത്പാദിപ്പിക്കാവുന്നവയാണ്. അതിനാല് മൗലിക ഏകകങ്ങള് ഉപയോഗിച്ച് വ്യുത്പാദിപ്പിക്കുന്നവയെ വ്യുത്പന്ന ഏകകങ്ങള് എന്നുപറയുന്നു. ഉദാ. പ്രവേഗത്തിന്റെ ഏകകം. | ||
| + | ഒന്നോ അതിലധികമോ മൗലിക ഏകകങ്ങളെ ആശ്രയിക്കുന്ന വ്യുത്പന്ന ഏകകങ്ങളെ അനുയോജ്യമായ ഘാത(power)ങ്ങളിലേക്ക് ഉയര്ത്തി വിമീയസൂത്രം (dimentional formula) ലഭ്യമാക്കാം. വ്യുത്പന്ന ഏകകങ്ങള് ലഭിക്കുവാനായി മൗലിക ഏകകങ്ങളെ ഏത് ഘാതത്തിലേക്ക് ഉയര്ത്തണമോ അതിനെ വ്യുത്പന്ന ഏകകത്തിന്റെ വിമയെന്നുപറയുന്നു. ഉദാ. | ||
<nowiki> | <nowiki> | ||
| - | + | വിസ്തീര്ണം = നീളം x വീതി | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
A = L x L | A = L x L | ||
</nowiki> | </nowiki> | ||
| - | ഇതുതന്നെ M<sup>0</sup> L<sup>2</sup> T<sup>0</sup> എന്ന് എഴുതാം; ഇവിടെ M, L, T എന്നിവ ദ്രവ്യമാനം നീളം, സമയം എന്നീ മൗലിക ഏകകങ്ങളെ കുറിക്കുന്നു. ഇവിടെ | + | ഇതുതന്നെ M<sup>0</sup> L<sup>2</sup> T<sup>0</sup> എന്ന് എഴുതാം; ഇവിടെ M, L, T എന്നിവ ദ്രവ്യമാനം നീളം, സമയം എന്നീ മൗലിക ഏകകങ്ങളെ കുറിക്കുന്നു. ഇവിടെ വിസ്തീര്ണത്തിന് ദ്രവ്യമാനത്തില് പൂജ്യവും നീളത്തില് രണ്ടും സമയത്തില് പൂജ്യവും വിമകളാണ് ഉള്ളത്. അതായത് വിസ്തീര്ണത്തിന്റെ വിമീയസൂത്രം L<sup>2</sup> ആകുന്നു. അതുപോലെ |
| - | + | ||
| - | + | [[ചിത്രം:Vol5_434_formula2.jpg|400px]] | |
| - | + | ||
| - | + | ഇതുപോലെ ഏതു ഭൗതികപരിമാണത്തിന്റെയും വിമകളും വിമീയസൂത്രങ്ങളും നിര്ണയിക്കാം (പട്ടിക 1). | |
| - | + | ||
| - | + | Vm, Vs എന്നിവ യഥാക്രമം ഇ.എം.യുയിലെയും ഇ.എസ്.യുയിലെയും പൊട്ടന്ഷ്യല് അന്തരത്തിന്റെ കേവലമാത്രകളും Qm, Qs എന്നിവ യഥാക്രമം ചാര്ജിന്റെ കേവല മാത്രകളും ആണെങ്കില് | |
| - | + | ||
| - | + | [[ചിത്രം:Vol5_434_formula3.jpg|400px]] | |
| - | + | ||
| - | + | [[ചിത്രം:Vol5_435_chart.jpg|600px]] | |
| - | + | ||
| - | + | പരീക്ഷണങ്ങളില്നിന്നും C-യുടെ മൂല്യം 3x10<sup>10</sup> ആണെന്നു കണ്ടെത്തി. ഇത് പ്രകാശത്തിന്റെ ശൂന്യതയിലുള്ള വേഗത്തിനു തുല്യമാണ്. Cm, Cs ഇവ രണ്ടു ക്രമങ്ങളിലെയും വൈദ്യുതധാരിതയുടെ ഏകകങ്ങളാണെങ്കില്. | |
| - | + | ||
| - | + | [[ചിത്രം:Vol5_435_formula1.jpg|400px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol5_435_chart2.jpg|400px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
Current revision as of 08:20, 14 ഓഗസ്റ്റ് 2014
ഏകകങ്ങള്
Units
അളവിന്റെ മാനദണ്ഡങ്ങള്. ഏതൊരു ഭൗതികപരിമാണത്തെയും പൂര്ണമായി വിശദീകരിക്കണമെങ്കില് അത് അളക്കുവാന് ഉപയോഗിച്ച മാത്രയും ആ പരിമാണത്തില് ആ മാത്ര എത്ര പ്രാവശ്യം ഉള്ക്കൊണ്ടിട്ടുണ്ടെന്നും അറിയേണ്ടതുണ്ട്. ഏതു പരിമാണത്തെ അളക്കുവാനും അതിന്റേതായ ഒരു മാത്ര വേണം. വ്യത്യസ്ത ഭൗതിക പരിമാണങ്ങളെ അളക്കുവാന് അനേകം മാത്രകള് ഉണ്ടെങ്കിലും അവയെല്ലാംതന്നെ നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൂന്ന് അടിസ്ഥാനമാത്രകളില്നിന്ന് വ്യുത്പാദിപ്പിക്കാവുന്നതാണ്. അതിനാല്, നീളം, ദ്രവ്യമാനം, സമയം എന്നീ പരിമാണങ്ങളുടെ മാത്രകളെ അടിസ്ഥാനമാത്രകള് അഥവാ മൗലിക മാത്രകള് എന്നും ബലം, വ്യാപ്തം, വിസ്തീര്ണം, പ്രവേഗം മുതലായ മറ്റു അളവുകളുടെ മാത്രകള് മൗലിക അളവുകളില്നിന്നും വ്യുത്പാദിപ്പിക്കാവുന്നതുകൊണ്ട് അവയുടെ മാത്രകളെ വ്യുത്പന്നമാത്രകള് (derived units)എന്നും പറയുന്നു.
മാപനരംഗത്തു നിലവിലുള്ള വ്യത്യസ്ത സമ്പ്രദായങ്ങളെ പൊതുവേ രണ്ടായി തരംതിരിക്കാം; മെട്രിക് പദ്ധതി, ബ്രിട്ടീഷ് പദ്ധതി. മെട്രിക് പദ്ധതിയില്ത്തന്നെ രണ്ട് ഉപഭാഗങ്ങളുണ്ട്. സി.ജി.എസ്. പദ്ധതി, എം.കെ.എസ്. പദ്ധതി. സി.ജി.എസ്. പദ്ധതി. ഓരോ പദ്ധതിയിലെയും മൗലിക മാത്രകളുടെ ആദ്യക്ഷരങ്ങള് ഉപയോഗിച്ച് ആ പദ്ധതിക്ക് പേരിട്ടിരിക്കുന്നു.
ഇതില് നീളത്തിന്റെ മൗലികമാത്ര മീറ്ററിന്റെ നൂറില് ഒരംശമായി സെ.മീ. ആകുന്നു. ക്രിപ്റ്റോണ്-86 അണുവിന്റെ 2P10, 5d5 എന്നീ ഊര്ജനിലകള് തമ്മില് നടക്കുന്ന ഊര്ജ സംക്രമണത്തിന്റെ ഫലമായി ഉണ്ടാകുന്ന ഏകവര്ണവികിരണത്തിന്റെ ശൂന്യത(vaccum state)യിലുള്ള തരംഗദൈര്ഘ്യത്തിന്റെ 16,50,763.73 മടങ്ങായി മീറ്റര് നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു.
ദ്രവ്യമാനത്തിന്റെ മാത്രയായ ഗ്രാം ഒരു കിലോഗ്രാമിന്റെ ആയിരത്തില് ഒരു ഭാഗമാണ്. പാരിസിനടുത്ത് സെവര് എന്ന സ്ഥലത്ത് സൂക്ഷിച്ചിട്ടുള്ള പ്ലാറ്റിനം-ഇറിഡിയം സംയുക്തലോഹത്തില് ചെയ്ത വൃത്തസ്തംഭ(cylinder)ത്തിന്റെ ദ്രവ്യമാനത്തെ ഒരു കിലോഗ്രാം ആയി സ്വീകരിച്ചിരിക്കുന്നു.
സീസിയം-133 അണുവിന്റെ രണ്ടു പ്രതേ്യക ഊര്ജനിലകള് തമ്മിലുള്ള ഊര്ജസംക്രമണത്തിന്റെ ഫലമായുണ്ടാകുന്ന വികിരണത്തിന്റെ സ്പന്ദനകാലത്തെ 9, 19, 26, 31, 770 കൊണ്ടു ഗുണിച്ചാല് കിട്ടുന്നത് സമയത്തിന്റെ മാത്രയായി (സെക്കന്ഡ്) നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു.
എം.കെ.എസ്. പദ്ധതി. നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൗലികപരിമാണങ്ങളുടെ മാത്രകള് യഥാക്രമം മീറ്റര്, കിലോഗ്രാം, സെക്കന്ഡ് ആയിരക്കണമെന്ന് 1935-ല് ഇന്റര്നാഷണല് ഇലക്ട്രാ കമ്മിഷന് ചെയ്ത ശിപാര്ശയനുസരിച്ച് ഈ പദ്ധതി നിലവില്വന്നു. തത്ഫലമായി പ്രവേഗത്തിന്റെ മാത്ര മീറ്റര്/സെക്കന്ഡും ത്വരണത്തിന്റേത് മീറ്റര്/സെക്കന്ഡ്2-ഉം ബലത്തിന്റേത് ന്യൂട്ടണും ആയി. ഒരു കിലോഗ്രാം ദ്രവ്യമാനത്തിന് ഒരു മീറ്റര്/സെക്കന്ഡ്2 ത്വരണം നല്കുവാന് ആവശ്യമായ ബലമാണ് ഒരു ന്യൂട്ടണ്. അതുപോലെ പ്രവൃത്തിയുടെയും ശക്തിയുടെയും മാത്രകള് യഥാക്രമം ജൂളും (Joule), വാട്ടും (watt) ആയി. അതായത്,
വ്യുത്പന്ന ഏകകങ്ങളും വിമകളും (Derived units and Dimensions). ഭൗതികത്തില് മിക്ക പരിമാണവും നീളം, ദ്രവ്യമാനം, സമയം എന്നീ മൂന്ന് മൗലിക ഏകകങ്ങളെ അടിസ്ഥാനമാക്കി അളക്കാവുന്നതാണ്. അഥവാ അത്തരം പരിമാണങ്ങളുടെ ഏകകങ്ങള് മൗലിക ഏകകങ്ങളില്നിന്നും വ്യുത്പാദിപ്പിക്കാവുന്നവയാണ്. അതിനാല് മൗലിക ഏകകങ്ങള് ഉപയോഗിച്ച് വ്യുത്പാദിപ്പിക്കുന്നവയെ വ്യുത്പന്ന ഏകകങ്ങള് എന്നുപറയുന്നു. ഉദാ. പ്രവേഗത്തിന്റെ ഏകകം. ഒന്നോ അതിലധികമോ മൗലിക ഏകകങ്ങളെ ആശ്രയിക്കുന്ന വ്യുത്പന്ന ഏകകങ്ങളെ അനുയോജ്യമായ ഘാത(power)ങ്ങളിലേക്ക് ഉയര്ത്തി വിമീയസൂത്രം (dimentional formula) ലഭ്യമാക്കാം. വ്യുത്പന്ന ഏകകങ്ങള് ലഭിക്കുവാനായി മൗലിക ഏകകങ്ങളെ ഏത് ഘാതത്തിലേക്ക് ഉയര്ത്തണമോ അതിനെ വ്യുത്പന്ന ഏകകത്തിന്റെ വിമയെന്നുപറയുന്നു. ഉദാ.
വിസ്തീര്ണം = നീളം x വീതി A = L x L
ഇതുതന്നെ M0 L2 T0 എന്ന് എഴുതാം; ഇവിടെ M, L, T എന്നിവ ദ്രവ്യമാനം നീളം, സമയം എന്നീ മൗലിക ഏകകങ്ങളെ കുറിക്കുന്നു. ഇവിടെ വിസ്തീര്ണത്തിന് ദ്രവ്യമാനത്തില് പൂജ്യവും നീളത്തില് രണ്ടും സമയത്തില് പൂജ്യവും വിമകളാണ് ഉള്ളത്. അതായത് വിസ്തീര്ണത്തിന്റെ വിമീയസൂത്രം L2 ആകുന്നു. അതുപോലെ
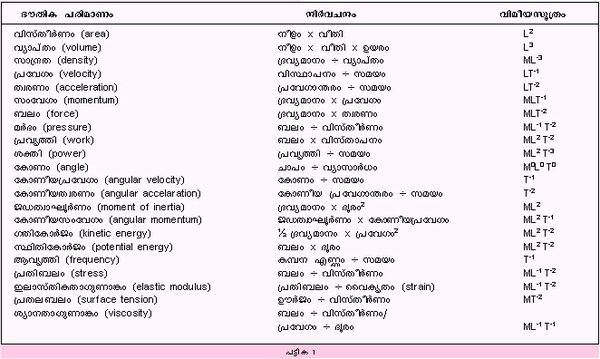
ഇതുപോലെ ഏതു ഭൗതികപരിമാണത്തിന്റെയും വിമകളും വിമീയസൂത്രങ്ങളും നിര്ണയിക്കാം (പട്ടിക 1).
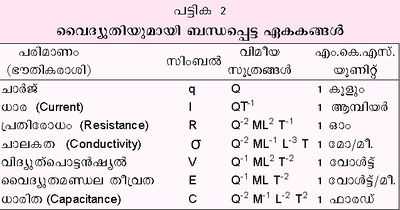
Vm, Vs എന്നിവ യഥാക്രമം ഇ.എം.യുയിലെയും ഇ.എസ്.യുയിലെയും പൊട്ടന്ഷ്യല് അന്തരത്തിന്റെ കേവലമാത്രകളും Qm, Qs എന്നിവ യഥാക്രമം ചാര്ജിന്റെ കേവല മാത്രകളും ആണെങ്കില്
പരീക്ഷണങ്ങളില്നിന്നും C-യുടെ മൂല്യം 3x1010 ആണെന്നു കണ്ടെത്തി. ഇത് പ്രകാശത്തിന്റെ ശൂന്യതയിലുള്ള വേഗത്തിനു തുല്യമാണ്. Cm, Cs ഇവ രണ്ടു ക്രമങ്ങളിലെയും വൈദ്യുതധാരിതയുടെ ഏകകങ്ങളാണെങ്കില്.