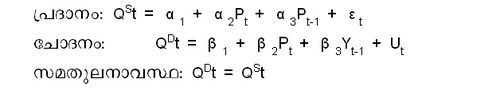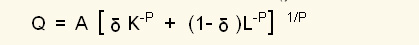This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
എ(ഇ)ക്കണോമെട്രിക്സ്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→പ്രവചനം (Forecasting)) |
Mksol (സംവാദം | സംഭാവനകള്) (→പ്രവചനം (Forecasting)) |
||
| (ഇടക്കുള്ള 5 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 5: | വരി 5: | ||
== Econometrics == | == Econometrics == | ||
| - | ഗണിതശാസ്ത്രം, സ്ഥിതിവിവരശാസ്ത്രം എന്നീ മേഖലകളിലെ ചരങ്ങളുടെ | + | ഗണിതശാസ്ത്രം, സ്ഥിതിവിവരശാസ്ത്രം എന്നീ മേഖലകളിലെ ചരങ്ങളുടെ അടിസ്ഥാനത്തില് സാമ്പത്തികശാസ്ത്രതത്ത്വങ്ങളും നിയമങ്ങളും കൂടുതല് കൃത്യതയോടെ പുനരാവിഷ്കരിക്കുന്ന സാമ്പത്തികശാസ്ത്രരേഖ. "എക്കണോമെട്രിക്സ്' എന്ന പദത്തിന് നോര്വേക്കാരനായ സാമ്പത്തികസംഖ്യാശാസ്ത്രകാരന് റാഗ്നര് ഫ്രിഷിനോട് കടപ്പെട്ടിരിക്കുന്നു. 1926-ല് ഇദ്ദേഹമാണ് ഈ പദം ആദ്യമായി ഉപയോഗിച്ചത്. |
എക്കണോമെട്രിക്സ് താഴെപ്പറയുന്ന മൂന്നുകാര്യങ്ങളാണ് ഉന്നംവയ്ക്കുന്നത്. | എക്കണോമെട്രിക്സ് താഴെപ്പറയുന്ന മൂന്നുകാര്യങ്ങളാണ് ഉന്നംവയ്ക്കുന്നത്. | ||
| വരി 11: | വരി 11: | ||
1. സാമ്പത്തികശാസ്ത്ര സിദ്ധാന്തങ്ങളുടെ സാധൂകരണം വിലയിരുത്തുക. | 1. സാമ്പത്തികശാസ്ത്ര സിദ്ധാന്തങ്ങളുടെ സാധൂകരണം വിലയിരുത്തുക. | ||
| - | 2. സാമ്പത്തിക നയരൂപീകരണത്തിനുവേണ്ടി സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തിന്റെ ഗുണോത്തരമൂല്യം ആകലനം ചെയ്തു | + | 2. സാമ്പത്തിക നയരൂപീകരണത്തിനുവേണ്ടി സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തിന്റെ ഗുണോത്തരമൂല്യം ആകലനം ചെയ്തു നല്കുക. |
| - | 3. സംഭവ്യതയുടെ | + | 3. സംഭവ്യതയുടെ അടിസ്ഥാനത്തില് സാമ്പത്തികചരങ്ങളുടെ വ്യാപ്തിയുടെ മൂല്യം പ്രവചിക്കുക. |
| - | എക്കണോമെട്രിക്സ് പഠനങ്ങളെ താത്ത്വികവും (theoretical) പ്രായോഗികവുമായി (applied) രണ്ടായി തരംതിരിക്കാം. എക്കണോമെട്രിക്സ് പഠന മാതൃകയിലൂടെ സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തെ അളന്നു തിട്ടപ്പെടുത്തുവാനുള്ള അനുയോജ്യമായ സമ്പ്രദായം വികസിപ്പിക്കുകയാണ് താത്ത്വിക എക്കണോമെട്രിക്സ് ശാഖ ചെയ്യുന്നത്. രണ്ടാമത്തെ | + | എക്കണോമെട്രിക്സ് പഠനങ്ങളെ താത്ത്വികവും (theoretical) പ്രായോഗികവുമായി (applied) രണ്ടായി തരംതിരിക്കാം. എക്കണോമെട്രിക്സ് പഠന മാതൃകയിലൂടെ സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തെ അളന്നു തിട്ടപ്പെടുത്തുവാനുള്ള അനുയോജ്യമായ സമ്പ്രദായം വികസിപ്പിക്കുകയാണ് താത്ത്വിക എക്കണോമെട്രിക്സ് ശാഖ ചെയ്യുന്നത്. രണ്ടാമത്തെ ശാഖയില് സാമ്പത്തിക ശാസ്ത്രസിദ്ധാന്തങ്ങളുടെ വിലയിരുത്തലിനും അതിലൂടെ ഭാവിപ്രവചനത്തിനുമായി സാമ്പത്തിക ശാസ്ത്ര സിദ്ധാന്തങ്ങളിലെ വിവിധ മേഖലകളില് എക്കണോമെട്രിക്സിന്റെ പ്രായോഗികത കൈവരുത്തുന്നു. |
എക്കണോമെട്രിക്സിന്റെ രീതിശാസ്ത്രം (Methodology). എക്കണോമെട്രിക്സ് രീതിശാസ്ത്രത്തെ നാലു ഘട്ടങ്ങളായി തരംതിരിക്കാം. | എക്കണോമെട്രിക്സിന്റെ രീതിശാസ്ത്രം (Methodology). എക്കണോമെട്രിക്സ് രീതിശാസ്ത്രത്തെ നാലു ഘട്ടങ്ങളായി തരംതിരിക്കാം. | ||
| - | == | + | == നിര്ദേശം (Specification) == |
| - | എക്കണോമെട്രിക്സ് പഠനത്തിന്റെ ആദ്യഘട്ടം പഠിക്കേണ്ടുന്ന വസ്തുതയുടെ സ്വഭാവം എന്തെന്നു മനസ്സിലാക്കുന്നു. ഉദാഹരണത്തിന് രാജ്യത്തിന്റെ ഇറക്കുമതി | + | എക്കണോമെട്രിക്സ് പഠനത്തിന്റെ ആദ്യഘട്ടം പഠിക്കേണ്ടുന്ന വസ്തുതയുടെ സ്വഭാവം എന്തെന്നു മനസ്സിലാക്കുന്നു. ഉദാഹരണത്തിന് രാജ്യത്തിന്റെ ഇറക്കുമതി നിര്ണയിക്കുന്ന ഘടകങ്ങളെക്കുറിച്ച് പഠിക്കണമെന്നിരിക്കട്ടെ. ഇതിനുവേണ്ടി, ഇറക്കുമതി ചോദന സമവാക്യം രൂപപ്പെടുത്തുന്നു. ഈ ചോദന സമവാക്യത്തില് ഉള്ക്കൊള്ളിക്കേണ്ട പ്രധാനഘടകങ്ങള് ഇറക്കുമതി ചെയ്യുന്ന സാധനങ്ങള് വാങ്ങുന്നവരുടെ വരുമാനം, സാധനത്തിന്റെ വില, സാധനത്തിനു പകരം വയ്ക്കാവുന്ന സാധനത്തിന്റെ വില എന്നിവയാണ്. ഇപ്രകാരം ഇറക്കുമതി ചോദനത്തെ താഴെപ്പറയുന്ന സമവാക്യത്തില് കാണിക്കാം. |
M = F (Y, P<sub>m</sub>, P<sub>D</sub>) | M = F (Y, P<sub>m</sub>, P<sub>D</sub>) | ||
| വരി 32: | വരി 32: | ||
PD= ഇറക്കുമതിസാധനത്തിന് പകരംവയ്ക്കാവുന്ന സാധനത്തിന്റെ വില. | PD= ഇറക്കുമതിസാധനത്തിന് പകരംവയ്ക്കാവുന്ന സാധനത്തിന്റെ വില. | ||
| - | പ്രസ്തുത | + | പ്രസ്തുത ഫലനബന്ധത്തില് (functional relation) M-ഉം Yഉം തമ്മില് ഒരേ ദിശാബന്ധവും, M-ഉം PDയും തമ്മില് വിപരീതദിശാബന്ധവുമാണുള്ളത്. ചോദനത്തെയും അതിനെ സ്വാധീനിക്കുന്ന ചരങ്ങളെയും ഒരു ലളിതമായ രേഖീയ സമവാക്യത്തില് ഇപ്രകാരം മാറ്റിയെഴുതാം. |
M = b<sub>0</sub> + b<sub>1</sub>Y + b<sub>2</sub>P<sub>m</sub> + b<sub>3</sub>P<sub>D</sub> | M = b<sub>0</sub> + b<sub>1</sub>Y + b<sub>2</sub>P<sub>m</sub> + b<sub>3</sub>P<sub>D</sub> | ||
| - | + | ഇതില് b<sub>0</sub>, b<sub>1</sub>, b<sub>2</sub>, b<sub>3</sub> എന്നിവയെ "പരാമീറ്റേഴ്സ്' എന്നു വിളിക്കുന്നു. ഈ സമവാക്യത്തില് b0-യുടെ മൂല്യം സ്ഥിരമായിരിക്കും. സമവാക്യത്തില് ഉള്ക്കൊള്ളിച്ചിരിക്കുന്ന എല്ലാ ഘടകങ്ങളുടെയും മൂല്യം പൂജ്യമാകുന്ന സാഹചര്യത്തില് വരാവുന്ന ഇറക്കുമതി ചോദനമൂല്യമാണ് യ0അര്ഥമാക്കുന്നത്. എന്നാല് b1, b2, b3 എന്നിവ അതാത് വിവരണചരങ്ങളുടെ (explanatory variable) ഗുണോത്തരങ്ങളെ (Co-efficient)സൂചിപ്പിക്കുന്നു. ഉദാഹരണത്തിന് b1അര്ഥമാക്കുന്നത Y-ല് ഉണ്ടാകുന്ന ഒരു ഏകക മാറ്റത്തിന് ഫലമായി M-നുണ്ടാകുന്ന വ്യതിയാനത്തെ സൂചിപ്പിക്കുന്നു. | |
| - | + | മുകളില് ഉപയോഗിച്ച സമവാക്യത്തിന്റെ പ്രാവര്ത്തിക രൂപം വിവരങ്ങളുടെ ലഭ്യതയുടെയും അവയുടെ വിശ്വാസ്യതയുടെയും അടിസ്ഥാനത്തില് മാറ്റത്തിന് വിധേയമാണ്. സാധാരണ സാഹചര്യങ്ങളില് പ്രത്യേകിച്ചും സാമ്പത്തിക സാമൂഹിക ചരങ്ങള് തമ്മിലുള്ള പ്രാവര്ത്തികബന്ധം കൃത്യമായി പ്രവചിക്കാന് അസാധ്യമാണ്. ഈ സാഹചര്യത്തില് പ്രവചിക്കാന് പറ്റാത്ത ഘടകങ്ങളുടെ സ്വാധീനം ഗണിത സമവാക്യത്തില് ഉള്പ്പെടുത്താനായി 'U' എന്ന സംജ്ഞ ഉപയോഗിക്കുന്നു. വ്യാഖ്യാനിക്കാന് കഴിയാത്ത ഘടകങ്ങളുടെ സ്വാധീനവും അനിശ്ചിതാവസ്ഥയും 'U'-ല് ഉള്ക്കൊണ്ടിരിക്കുന്നു. | |
M = b<sub>0</sub> + b<sub>1</sub>Y + b<sub>2</sub>P<sub>m</sub> + b<sub>3</sub>P<sub>D</sub> + U | M = b<sub>0</sub> + b<sub>1</sub>Y + b<sub>2</sub>P<sub>m</sub> + b<sub>3</sub>P<sub>D</sub> + U | ||
| - | ഇപ്രകാരമുള്ള സമവാക്യങ്ങളെ | + | ഇപ്രകാരമുള്ള സമവാക്യങ്ങളെ പ്രവര്ത്തനരീതി സമവാക്യങ്ങള് (Behavioural equations)എന്നുവിളിക്കുന്നു. പ്രവര്ത്തനരീതി സമവാക്യങ്ങളില് അനിശ്ചിതഘടകങ്ങളാല് (Stochastic Element) തീരുമാനിക്കുന്ന 'U' എന്ന ഒരു ഘടകം കൂടിയുണ്ടാകും. സമവാക്യത്തില് ഉള്പ്പെട്ട എല്ലാ ഘടകങ്ങളുടെയും സ്വാധീനം നിര്വചിച്ചശേഷം വരുന്ന ശിഷ്ടമായാണ് (Residual) 'U' നെ കണക്കാക്കുന്നത്. സാമ്പിള് വിവരങ്ങള് ഉപയോഗിച്ച് എക്കണോമെട്രിക്സ് മാതൃകയും അതിനുവേണ്ട ഗണിതസമവാക്യങ്ങളും രൂപപ്പെടുത്തുകയാണെങ്കില് 'U' എന്ന സംജ്ഞയ്ക്കു പകരം 'e' ആണുപയോഗിക്കുന്നത്. 'e' എന്ന സംജ്ഞ അര്ഥമാക്കുന്നത് എക്കണോമെട്രിക്സ് പഠനമാതൃകാനിര്ണയത്തില് വരുന്ന പിശകുകളുടെ ആകെത്തുകയാണ് (error term). |
==ആകലനം (Estimation)== | ==ആകലനം (Estimation)== | ||
| - | എക്കണോമെട്രിക്സ് പഠനമാതൃകയുടെ | + | എക്കണോമെട്രിക്സ് പഠനമാതൃകയുടെ നിര്ദേശമനുസരിച്ച് ആകലനപ്രക്രിയയെ ആശ്രയിച്ചിരിക്കുന്നു. പഠനമാതൃകയുടെ പ്രാചനത്തിന്റെ ഏറ്റവും ശരിയെന്നു ബോധ്യമുള്ള മൂല്യം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയാണ് പൊതുവേ ആകലനപ്രക്രിയകൊണ്ടുദ്ദേശിക്കുന്നത്. ഇങ്ങനെ ലഭിക്കുന്ന മൂല്യത്തെ എസ്റ്റിമേറ്റര് (Estimator) എന്നു വിളിക്കുന്നു. മുന്വിധിരാഹിത്യം (Unbiasedness), കുറഞ്ഞ വ്യതിയാനം (minimum variance) സ്ഥിരത (Consistency) എന്നിവയാണ് എസ്റ്റിമേറ്ററിന്റെ സവിശേഷതകള്. |
| - | + | മൂല്യനിര്ണയത്തിനുവേണ്ടി വ്യാപകമായി ഉപയോഗിക്കുന്ന ഒരു സങ്കേതമാണ് സാധാരണ ന്യൂനതമവര്ഗരീതി (Ordinary Least Squares- OLS). കൂടാതെ ദ്വിഘട്ട ന്യൂനതമവര്ഗരീതി (two stage least square method), ത്രിഘട്ട ന്യൂനതമവര്ഗരീതി (three stage least square method) അപൂര്ണ പരിജ്ഞാന ഉച്ചതമസാധ്യതാരീതി (Limited information maximum likelihood method) പൂര്ണ പരിജ്ഞാന ഉച്ചതമസാധ്യതാരീതി (full information maximum likelihood method) എന്നിവയും ഉപയോഗിക്കാറുണ്ട്. | |
==സിദ്ധാന്തപരിശോധന (Hypothesis Testing)== | ==സിദ്ധാന്തപരിശോധന (Hypothesis Testing)== | ||
| - | ആകലനം കഴിഞ്ഞ എക്കണോമെട്രിക്സ് മാതൃകയുടെ ആകലനമൂല്യം (estimates) വിശ്വസനീയമാണോ എന്നു ചില മാനദണ്ഡങ്ങളുടെ | + | ആകലനം കഴിഞ്ഞ എക്കണോമെട്രിക്സ് മാതൃകയുടെ ആകലനമൂല്യം (estimates) വിശ്വസനീയമാണോ എന്നു ചില മാനദണ്ഡങ്ങളുടെ വെളിച്ചത്തില് വിലയിരുത്തുന്നു. ഈ വിലയിരുത്തലുകളില്ക്കൂടി പ്രാചനങ്ങളുടെ മൂല്യം സൈദ്ധാന്തികമായി അര്ഥവത്താണോയെന്നും സംഖ്യാവ്യാപനപരമായി സാധ്യതയുള്ളതാണോയെന്നും വിലയിരുത്തുന്നു. പ്രധാനമായും താഴെപ്പറയുന്ന മൂന്നു മാനദണ്ഡങ്ങളാണ് പ്രാചനങ്ങളുടെ കണക്കാക്കപ്പെട്ട മൂല്യം വിലയിരുത്താന് അടിസ്ഥാനമാക്കുന്നത്. |
| - | (1) | + | (1) കാരണങ്ങളില് നിന്നും കാര്യങ്ങളെ തെളിയിക്കുന്ന മാനദണ്ഡം (Economic 'a priori') സാമ്പത്തികശാസ്ത്ര സിദ്ധാന്തങ്ങള് വിലയിരുത്താനുപയോഗിക്കുന്നു. |
(2) സംഖ്യാശാസ്ത്രമാനദണ്ഡം (statistical crieteria) ഇവിടെ സംഖ്യാശാസ്ത്ര സിദ്ധാന്തങ്ങളെ വിലയിരുത്താനുപയോഗിക്കുന്നു. | (2) സംഖ്യാശാസ്ത്രമാനദണ്ഡം (statistical crieteria) ഇവിടെ സംഖ്യാശാസ്ത്ര സിദ്ധാന്തങ്ങളെ വിലയിരുത്താനുപയോഗിക്കുന്നു. | ||
| - | (3) എക്കണോമെട്രിക്സ് മാനദണ്ഡം എക്കണോമെട്രിക്സ് തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തിലുള്ളതാണ് ഇവിടത്തെ | + | (3) എക്കണോമെട്രിക്സ് മാനദണ്ഡം എക്കണോമെട്രിക്സ് തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തിലുള്ളതാണ് ഇവിടത്തെ പരിശോധനാമാര്ഗങ്ങള്. ഇത്തരത്തിലുള്ള പരിശോധനാമാര്ഗങ്ങളില്ക്കൂടി ആകലനമൂല്യത്തില് അത്യാവശ്യം വേണ്ട സവിശേഷതകളായ മുന്വിധിരാഹിത്യം (unbiasedness), സ്ഥിരത (consistency), പര്യാപ്തത (sufficiency) എന്നിവയുണ്ടോ എന്നു സ്ഥാപിക്കുന്നു. |
| - | വ്യക്തിഗത പരാമീറ്റേഴ്സിനെ സംബന്ധിച്ച സംഖ്യാശാസ്ത്ര | + | വ്യക്തിഗത പരാമീറ്റേഴ്സിനെ സംബന്ധിച്ച സംഖ്യാശാസ്ത്ര പരിശോധനാമാര്ഗത്തില് പ്രധാനപ്പെട്ട ഒന്നാണ് ടി-ടെസ്റ്റ് (t-test). അതുപോലെ സാധാരണ ഉപയോഗിക്കുന്ന സങ്കേതമായ പ്രതിപരീതി (regression) ആശ്രിതചരങ്ങളുടെ (dependent variable) വ്യതിയാനത്തെ എത്രത്തോളം വ്യാഖ്യാനിക്കുന്നുവെന്നും കണക്കാക്കാം. ഇതിനുവേണ്ടി ഉപയോഗിക്കുന്ന ഒന്നാണ് കോ-എഫിഷ്യന്റ് ഒഫ് ഡിറ്റര്മിനേഷന് (co-efficient of determination അഥവാ R<sup>2</sup>). |
R<sup>2</sup>= വ്യാഖ്യാനിക്കപ്പെടുന്ന ആശ്രയചരത്തിലുണ്ടാകുന്ന വ്യതിയാനം / ആശ്രയചരത്തിലുണ്ടായ മൊത്തം വ്യതിയാനം | R<sup>2</sup>= വ്യാഖ്യാനിക്കപ്പെടുന്ന ആശ്രയചരത്തിലുണ്ടാകുന്ന വ്യതിയാനം / ആശ്രയചരത്തിലുണ്ടായ മൊത്തം വ്യതിയാനം | ||
| വരി 68: | വരി 68: | ||
== പ്രവചനം (Forecasting)== | == പ്രവചനം (Forecasting)== | ||
| - | ലഭ്യമായ സാമ്പിള് വിവരങ്ങളുടെ പരിധിക്കപ്പുറത്ത് ചില ചരങ്ങളുടെ മൂല്യം പ്രവചിക്കാനായി എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിക്കുന്നു. വ്യത്യസ്ത സാമ്പത്തികനയങ്ങളുടെ തെരഞ്ഞെടുപ്പും വിലയിരുത്തലുമായി പ്രവചനം ബന്ധപ്പെട്ടിരിക്കുന്നു. ഉചിതമായ ആശ്രിതചരത്തിന്റെ | + | ലഭ്യമായ സാമ്പിള് വിവരങ്ങളുടെ പരിധിക്കപ്പുറത്ത് ചില ചരങ്ങളുടെ മൂല്യം പ്രവചിക്കാനായി എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിക്കുന്നു. വ്യത്യസ്ത സാമ്പത്തികനയങ്ങളുടെ തെരഞ്ഞെടുപ്പും വിലയിരുത്തലുമായി പ്രവചനം ബന്ധപ്പെട്ടിരിക്കുന്നു. ഉചിതമായ ആശ്രിതചരത്തിന്റെ യഥാര്ഥമൂല്യവും എക്കണോമെട്രിക്സ് മാതൃകയിലൂടെ ലഭിച്ച മൂല്യവും തമ്മിലുള്ള അന്തരം താരതമ്യം ചെയ്യുകയും സംഖ്യാശാസ്ത്ര പരിശോധനയ്ക്ക് വിധേയമാക്കുകയും ചെയ്യുന്നു. ഇവ തമ്മിലുള്ള അന്തരം ഗണ്യമാണെങ്കില് ഉപയോഗിച്ച പഠനമാതൃകയ്ക്ക് പ്രവചനശേഷിയില്ലെന്ന നിഗമനത്തിലെത്തുന്നു. |
| - | മുമ്പ് പ്രതിപാദിച്ച | + | മുമ്പ് പ്രതിപാദിച്ച രേഖീയപ്രാവര്ത്തിക രൂപത്തിലുള്ള എക്കണോമെട്രിക്സ് പഠനമാതൃക കൂടാതെ മറ്റു തരത്തിലുള്ള പ്രാവര്ത്തിക രൂപങ്ങളുമുണ്ട്. ഇതില് പ്രധാനപ്പെട്ടവ |
| - | (1) ഡബിള് ലോഗ്/ലോഗ് | + | (1) ഡബിള് ലോഗ്/ലോഗ് ലീനിയര്/കോണ്സ്റ്റന്റ് ഇലാസ്റ്റിസിറ്റി മാതൃകകള് (Double log/log linear/constant elasticity). |
(2) സെമിലോഗ് (Semilog) മാതൃകകള് | (2) സെമിലോഗ് (Semilog) മാതൃകകള് | ||
| - | (3) | + | (3) റെസിപ്രാക്കല് ട്രാന്സ്ഫോര്മേഷഷന് അഥവാ ഹൈപ്പര്ബോളിക് (Reciprocal transformation or hyperbolic) മാതൃകകള്. |
| - | കാലം (time) ഒരു പ്രവണതാചരമായി ഉപയോഗിക്കുമ്പോള് ഉപയുക്തമാക്കാവുന്ന | + | കാലം (time) ഒരു പ്രവണതാചരമായി ഉപയോഗിക്കുമ്പോള് ഉപയുക്തമാക്കാവുന്ന പ്രാവര്ത്തിക മാതൃകകളില് പ്രധാനപ്പെട്ടവ (1) രേഖീയ പ്രവണതാ സമവാക്യം (linear trend equation), (2) എക്സ്പൊണെന്ഷ്യല് പ്രവണതാ സമവാക്യം (exponential trend equation) (3) ലോജിസ്റ്റിക് പ്രവണത സമവാക്യം (Logistic trend equation) എന്നിവയാണ്. |
എക്കണോമെട്രിക്സ് പഠനമാതൃകകള്. എക്കണോമെട്രിക്സ് പഠനമാതൃകകളെ ഏകസമവാക്യ മാതൃകകള് എന്നും ബഹുസമവാക്യ മാതൃകകള് എന്നും തരംതിരിക്കാം. | എക്കണോമെട്രിക്സ് പഠനമാതൃകകള്. എക്കണോമെട്രിക്സ് പഠനമാതൃകകളെ ഏകസമവാക്യ മാതൃകകള് എന്നും ബഹുസമവാക്യ മാതൃകകള് എന്നും തരംതിരിക്കാം. | ||
| - | ഏകസമവാക്യ മാതൃകകള്. പ്രസ്തുത | + | ഏകസമവാക്യ മാതൃകകള്. പ്രസ്തുത മാതൃകകളില് ഒരു ആശ്രിതചരവും (dependent variables)ഒന്നോ അതിലധികമോ സ്വതന്ത്ര വിവരണ ചരങ്ങളും കാണാം. ഒറ്റ വിവരണ |
| - | ചരമുള്ള പ്രതിപരീതി (regression) മാതൃകകളെ ലളിത പ്രതിപരീതി മാതൃകകളെന്നും | + | ചരമുള്ള പ്രതിപരീതി (regression) മാതൃകകളെ ലളിത പ്രതിപരീതി മാതൃകകളെന്നും ഒന്നില്ക്കൂടുതല് വിവരണാത്മക ചരങ്ങളുള്ള പ്രതിപരീതി മാതൃകകളെ ബഹു പ്രതിപരീതി മാതൃകകളെന്നും വിളിക്കുന്നു. സാധാരണ ഉപയോഗിക്കുന്ന പ്രതിപരീതി സങ്കേതം ക്ലാസ്സിക്കല് ന്യൂനതമവര്ഗ (Classical least square) രീതിയാണ്. ഈ സങ്കേതം വഴി വിവരണ ചരങ്ങളുടെ യഥാര്ഥമൂല്യവും ആകലനമൂല്യവും തമ്മിലുള്ള അന്തരം ഏറ്റവുമധികം ലഘൂകരിക്കുന്നു. മറ്റൊരു സങ്കേതമായ ഉച്ചതമസാധ്യതാരീതിയും (Maximum likelihood estimation) ഉപയോഗിച്ചുവരുന്നു. |
| - | ഏകസമവാക്യ പ്രതിപരീതി (Single Equation regression) മാതൃകകള് പ്രധാനമായും സാമ്പത്തിക ചരങ്ങളുടെ പ്രവണതയെ പ്രവചിക്കാന് ഉപയോഗിക്കുന്നു. ചരങ്ങളുടെ മൂല്യപ്രവചനം ഏകസംഖ്യാപ്രവചനമെന്നും (Point forecast) പരിധിപ്രവചനമെന്നും (Interval forecast) രണ്ടായി തരംതിരിക്കാം. | + | ഏകസമവാക്യ പ്രതിപരീതി (Single Equation regression) മാതൃകകള് പ്രധാനമായും സാമ്പത്തിക ചരങ്ങളുടെ പ്രവണതയെ പ്രവചിക്കാന് ഉപയോഗിക്കുന്നു. ചരങ്ങളുടെ മൂല്യപ്രവചനം ഏകസംഖ്യാപ്രവചനമെന്നും (Point forecast) പരിധിപ്രവചനമെന്നും (Interval forecast) രണ്ടായി തരംതിരിക്കാം. ഇതില് രണ്ടാമത്തെ രീതിയില് പ്രവചനമൂല്യം ഒരു പരിധിക്കുള്ളിലായിരിക്കും. മൂല്യപ്രവചനത്തെ സോപാധിക(conditional)മെന്നും നിരുപാധിക(unconditional)മെന്നും തരംതിരിക്കാം. സോപാധിക മൂല്യപ്രവചനത്തില് ചില വിവരണ ചരങ്ങളുടെ മൂല്യം ലഭ്യമല്ലാത്തിനാല് ആശ്രിതചരങ്ങളുടെ മൂല്യം ഊഹിച്ചെടുക്കണം. എന്നാല് നിരുപാധിക മൂല്യപ്രവചനത്തില് എല്ലാ വിവരണചരങ്ങളുടെയും മൂല്യം കൃത്യമായും ലഭ്യമായതില് മൂല്യപ്രവചനം സുനിശ്ചിതമായി നടത്താം. നിര്വചനപിഴ (Forecast error) എറ്റവും കുറഞ്ഞിരിക്കുന്നതാണ് നല്ല പ്രവചനസങ്കേതത്തിന്റെ സവിശേഷത. ഏകസമവാക്യ മാതൃകകളില് സാധാരണ ന്യൂനതമവര്ഗരീതി (Ordinary least square-OLS) സങ്കേതം നിര്വചനപിഴ ഏറ്റവുമധികം കുറച്ചുകൊണ്ട് ചരങ്ങളുടെ മൂല്യം കണക്കാക്കുന്നു. ഇതുകൂടാതെ വിതരണവിളംബ(Distributed log) മാതൃകകളും അവ ഉപയോഗിച്ചുകൊണ്ടുള്ള ആകലനവും ഏകസമവാക്യ മാതൃകയില് ഉള്പ്പെടുന്നു. രണ്ട് പ്രധാനപ്പെട്ട വിളംബ(lag) മാതൃകകളായ ജ്യാമിതീയവിളംബവും (Geomatric lag) ബഹുപദവിളംബ (Polynomial lag) മാതൃകകളുമാണ് സാധാരണ ഉപയോഗിക്കുന്നത്. ജ്യാമിതീയവിളംബ മാതൃകകളില് വിളംബ വിവരണചരങ്ങള്ക്ക് (lagged explanatory variables) കൊടുക്കുന്ന മൂല്യം (weights) ധനസംഖ്യ (positive number) ആയിരിക്കും. അത് സമയാനുബന്ധമായി ജ്യാമിതീയ അളവില് കുറയുമെന്നും അനുമാനിക്കുന്നു. |
| - | ഏകസമവാക്യമാതൃകകളുടെ | + | ഏകസമവാക്യമാതൃകകളുടെ പരിധിയില് വരുന്ന വേറൊരു വിഷയമാണ് കാരണ പരിശോധന (casuality test). സാമ്പത്തികശാസ്ത്രത്തില് പൊതുവെയുള്ള ഒരു പ്രശ്നം ഒരു ചരത്തിലുണ്ടാകുന്ന വ്യതിയാനം മറ്റൊരു ചരത്തിന്റെ മാറ്റത്തിന് ഹേതുവാകുന്നുണ്ടോയെന്ന് നിര്ണയിക്കുന്നതാണ്. സാമ്പത്തിക ശാസ്ത്രജ്ഞന്മാരായ ഗ്രാന്ജറും (Granger) സിംസും (Sims) രൂപപ്പെടുത്തിയ കാരണപരിശോധന (casuality test) ഉപയോഗിച്ച് ഇതു പരിഹരിക്കാവുന്നതാണ്. |
| - | + | പാനല് ഡേറ്റ ഉപയോഗിച്ചുള്ള ഏകസമവാക്യമാതൃകകള്. ഒരുകൂട്ടം സ്ഥിരമായ വ്യക്തിഗത സാമ്പിളുകള് ഒരു ദീര്ഘകാലത്തേക്ക് ശേഖരിക്കുന്ന ദത്തങ്ങള്ക്കാണ് പാനല്ഡേറ്റയെന്നു പറയുന്നത്. ഇതിന്റെ ഫലമായി വ്യക്തിഗത സാമ്പിളുകളെ സംബന്ധിച്ച് പലതരത്തിലുള്ള നിരീക്ഷണവിവരങ്ങള് ശേഖരിക്കാന് സാധിക്കുന്നു. ഇത്തരത്തില് കാലാനുസരണശ്രണി വിവരങ്ങളും (time series data) പരിച്ഛേദവിവരങ്ങളും (cross section data) സമന്വയിപ്പിച്ചാണ് പാനല്ഡേറ്റ ഉണ്ടാക്കുന്നത്. | |
| - | + | പാനല്ഡേറ്റ ഉപയോഗിച്ചുകൊണ്ട് എക്കണോമെട്രിക്സ് പഠനങ്ങള്ക്ക് താഴെപ്പറയുന്ന സങ്കേതങ്ങളാണ് ഉപയോഗിക്കുന്നത്. | |
| - | (1) കാലശ്രണി (time series) ദത്തങ്ങളും പരിച്ഛേദ(cross section)ദത്തങ്ങളും സംയോജിപ്പിച്ച് സാധാരണ | + | (1) കാലശ്രണി (time series) ദത്തങ്ങളും പരിച്ഛേദ(cross section)ദത്തങ്ങളും സംയോജിപ്പിച്ച് സാധാരണ ന്യൂനതമവര്ഗ(ordinary leas square) സങ്കേതം. |
(2) പകരത്തിനുള്ള ചരങ്ങള് (dummy variables). | (2) പകരത്തിനുള്ള ചരങ്ങള് (dummy variables). | ||
| വരി 98: | വരി 98: | ||
(3) പരിച്ഛേദ ദത്തങ്ങളുടെയും കാലശ്രണി ദത്തങ്ങളുടെയും വ്യതിയാനം ഉള്ക്കൊള്ളിച്ചുകൊണ്ടുള്ള യാദൃച്ഛിക സ്വാധീനമാതൃക (Random effect model) ഉപയോഗിച്ച്. | (3) പരിച്ഛേദ ദത്തങ്ങളുടെയും കാലശ്രണി ദത്തങ്ങളുടെയും വ്യതിയാനം ഉള്ക്കൊള്ളിച്ചുകൊണ്ടുള്ള യാദൃച്ഛിക സ്വാധീനമാതൃക (Random effect model) ഉപയോഗിച്ച്. | ||
| - | അരേഖീയ ഏകസമവാക്യ | + | അരേഖീയ ഏകസമവാക്യ മൂല്യനിര്ണയം (Non-linear single equation estimation). |
[[ചിത്രം:Vol5_21_formula.jpg|500px]] | [[ചിത്രം:Vol5_21_formula.jpg|500px]] | ||
| വരി 104: | വരി 104: | ||
ഇത്തരത്തിലുള്ള അരേഖീയ സമവാക്യങ്ങളെ രേഖാസമവാക്യമാക്കാന് സാധിക്കുകയില്ല. ഈ സമവാക്യങ്ങളുടെ ഉത്തരം കണ്ടുപിടിക്കാന് വിവിധതരത്തിലുള്ള എക്കണോമെട്രിക്സ് സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നു. | ഇത്തരത്തിലുള്ള അരേഖീയ സമവാക്യങ്ങളെ രേഖാസമവാക്യമാക്കാന് സാധിക്കുകയില്ല. ഈ സമവാക്യങ്ങളുടെ ഉത്തരം കണ്ടുപിടിക്കാന് വിവിധതരത്തിലുള്ള എക്കണോമെട്രിക്സ് സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നു. | ||
| - | ഏകസമവാക്യഗുണാത്മക | + | ഏകസമവാക്യഗുണാത്മക തെരഞ്ഞെടുക്കല് മാതൃക (Single Equatgion Qualitative Choice Model). ഇവിടെ ആശ്രിതചരങ്ങള് രണ്ടോ അതിലധികമോ ഗുണാത്മക തെരഞ്ഞെടുക്കല് (Qualitative Choice) ഉള്ക്കൊള്ളുന്നതായിരിക്കും. ഇപ്രകാരമുള്ള മാതൃകകളുടെ ലക്ഷ്യം ഒരു പ്രത്യേകസാഹചര്യത്തില് ഒരു വ്യക്തി കൈക്കൊണ്ടേക്കാവുന്ന തെരഞ്ഞെടുക്കലിന്റെ സംഭവ്യത(probability) മനസ്സിലാക്കുകയാണ്. ഗുണാത്മക തെരഞ്ഞെടുക്കല് മാതൃകയുടെ ഗുണോത്തരമൂല്യം (coefficient) കണക്കാക്കാനായി പ്രധാനമായും ഉപയോഗിക്കുന്ന മാതൃകകള് രേഖീയസംഭവ്യത (Linear Probability) പ്രാബിത് (Probit) ലോജിത് (logit)എന്നിവയാണ്. |
ബഹുസമവാക്യ മാതൃകകള് (Multi equation Models).ഒരു കൂട്ടം ചരങ്ങളുടെ പരസ്പരബന്ധം പഠിക്കുന്നതിന് ബഹുസമവാക്യ മാതൃകകള് സഹായിക്കുന്നു. പലപ്പോഴും ഒരു കൂട്ടം ബഹുസമ പരസ്പരബന്ധവാക്യങ്ങളുടെ (simultaneous interdependent equation)ശ്രണിയിലൂടെയാണ് മിക്ക വ്യാപാര സാമ്പത്തിക മാതൃകകളുടെയും പ്രക്രിയ പ്രതിനിധാനം ചെയ്യപ്പെടുന്നത്. | ബഹുസമവാക്യ മാതൃകകള് (Multi equation Models).ഒരു കൂട്ടം ചരങ്ങളുടെ പരസ്പരബന്ധം പഠിക്കുന്നതിന് ബഹുസമവാക്യ മാതൃകകള് സഹായിക്കുന്നു. പലപ്പോഴും ഒരു കൂട്ടം ബഹുസമ പരസ്പരബന്ധവാക്യങ്ങളുടെ (simultaneous interdependent equation)ശ്രണിയിലൂടെയാണ് മിക്ക വ്യാപാര സാമ്പത്തിക മാതൃകകളുടെയും പ്രക്രിയ പ്രതിനിധാനം ചെയ്യപ്പെടുന്നത്. | ||
| - | ബഹുസമവാക്യ ശ്രണി (Miscelleneous Equation System). പ്രസ്തുത മാതൃകകള് ഒരുകൂട്ടം സമവാക്യങ്ങള് ഉള്ക്കൊണ്ടിരിക്കും. ഓരോ സമവാക്യവും ഓരോ ചരങ്ങളെ വിശദീകരിക്കാന് ഉപയുക്തമായിരിക്കും. ഉദാഹരണത്തിന് മൂന്നു സമവാക്യങ്ങള് ഉള്ക്കൊള്ളുന്ന പ്രദാന-ചോദന (supply-demand)മാതൃക താഴെപ്പറയുന്ന | + | ബഹുസമവാക്യ ശ്രണി (Miscelleneous Equation System). പ്രസ്തുത മാതൃകകള് ഒരുകൂട്ടം സമവാക്യങ്ങള് ഉള്ക്കൊണ്ടിരിക്കും. ഓരോ സമവാക്യവും ഓരോ ചരങ്ങളെ വിശദീകരിക്കാന് ഉപയുക്തമായിരിക്കും. ഉദാഹരണത്തിന് മൂന്നു സമവാക്യങ്ങള് ഉള്ക്കൊള്ളുന്ന പ്രദാന-ചോദന (supply-demand)മാതൃക താഴെപ്പറയുന്ന രീതിയില് വിശദീകരിക്കാം. |
[[ചിത്രം:Vol5_21_formula2.jpg|500px]] | [[ചിത്രം:Vol5_21_formula2.jpg|500px]] | ||
| - | ഈ മൂന്ന് സമവാക്യങ്ങളും | + | ഈ മൂന്ന് സമവാക്യങ്ങളും ചേര്ന്ന് വിപണിവില, ചോദനത്തിന്റെയും പ്രദാനത്തിന്റെയും അളവ് എന്നിവ നിര്ണയിക്കുന്നു. മേല്പറഞ്ഞ മാതൃകയില് QDt , QSt, Pt എന്നിവയുടെ മൂല്യം സമവാക്യങ്ങളുടെ സംവിധാനത്തില് ഉള്ളില്വച്ചുതന്നെ നിര്ണയിക്കപ്പെടുന്നതിനാല് അവ ആന്തരോദ്ഭവ (Endogenous) ചരങ്ങളെന്ന് അറിയപ്പെടുന്നു. എന്നാല് Pt-1, Yt എന്നീ ചരങ്ങളുടെ മൂല്യം സമവാക്യങ്ങളുടെ സംവിധാനത്തിനകത്ത് നിര്ണയിക്കാത്ത മുന്നിര്ണയ (Pre-determined) ചരങ്ങളാണ്. അവ സംവിധാനത്തിലുള്ളിലെ ആന്തരോദ്ഭവചരങ്ങളുടെ ചലനം നിര്ണയിക്കുന്നു. മുകളില് പ്രതിപാദിച്ച മാതൃകയില് Yt എന്ന ചരത്തിന്റെ മൂല്യം പൂര്ണമായും സമവാക്യശ്രണിക്ക് പുറത്ത് നിര്ണയിക്കപ്പെടുന്നതിനാല് അവയെ ബഹുജന്യ ചരങ്ങള് (Exogeneous Variables)എന്നു വിളിക്കുന്നു. |
| - | + | ഒന്നില്ക്കൂടുതല് സമവാക്യങ്ങള് ഒരു മാതൃകയില് നിര്ദേശിക്കുമ്പോള് (യുഗവത് സമവാക്യമാതൃകകള്) സമവാക്യങ്ങളെ തമ്മില് വ്യക്തമായി വേര്തിരിച്ചു മനസ്സിലാക്കത്തക്കവണ്ണം നിര്ദേശിക്കപ്പെടേണ്ടതാണ്. ഉദാ. ചോദന സമവാക്യത്തിലും (demand equation) പ്രദാനസമവാക്യത്തിലും (supply equation) പ്രത്യക്ഷപ്പെടുന്ന ചരങ്ങള് കമ്പോളവിലയും കമ്പോളത്തില് വിറ്റഴിയുന്ന ചരക്കിന്റെ അളവുമാണ്. ഈ രണ്ടു സമവാക്യങ്ങളിലും ഒരേ സെറ്റ് ചരങ്ങള് ഒരുപോലെ പ്രത്യക്ഷപ്പെടുന്നതിനാല് കമ്പോളദത്തം ഉപയോഗിച്ച് ആകലനം ചെയ്യപ്പെടുന്ന അത്തരം ഒരു സമവാക്യം യഥാര്ഥത്തില് ചോദനഫലത്തെയാണോ പ്രദാനഫലത്തെയാണോ പ്രതിനിധാനം ചെയ്യുന്നത് എന്ന് സംശയമുണ്ടാകുന്നു. രണ്ട് സമവാക്യങ്ങളും തമ്മില് വേര്തിരിച്ചറിയുവാന് തക്കവണ്ണം അവ നിര്ദേശിക്കപ്പെടാത്തതിന്റെ തകരാറാണ് ഈ സംശയത്തിന് കാരണം. ഇങ്ങനെയുള്ള സന്ദര്ഭങ്ങള് എക്കണോമെട്രിക്സ് പഠനങ്ങളില് സാധാരണമാണ്. അഭിജ്ഞാനപ്രശ്നം (identification problem) എന്ന് ഇതറിയപ്പെടുന്നു. ബഹുസമവാക്യമാതൃകയുടെ ഒരു പ്രധാനപ്രശ്നം സമവാക്യങ്ങളുടെ തിരിച്ചറിയലാണ്. ചില സമവാക്യങ്ങള് കൃത്യമായി തിരിച്ചറിയാം ചിലവ കുറച്ചുമാത്രം തിരിച്ചറിയാം ചിലത് ആവശ്യത്തിലധികം തിരിച്ചറിയാം. സമവാക്യത്തില് പ്രതിപാദിച്ചിരിക്കുന്ന ഓരോ ചരത്തിന്റെയും അദ്വീതമൂല്യം കണക്കാക്കണമെങ്കില് ആ സമവാക്യത്തെ കൃത്യമായി തിരിച്ചറിയാം എന്നു പറയാം. അതേസമയം ഒരേ ചരത്തിന് ഒന്നിലധികം മൂല്യം ലഭിക്കുകയാണെങ്കില് ആ സമവാക്യം ആവശ്യത്തിലധികം തിരിച്ചറിയപ്പെട്ടവയെന്നു പറയാം. എന്നാല് ചരങ്ങളുടെ മൂല്യം കണ്ടുപിടിക്കാന് സാധിക്കാത്ത സമവാക്യങ്ങളെ തിരിച്ചറിയാന് സാധിക്കാത്ത (unidentified) സമവാക്യങ്ങളെന്നു പറയുന്നു. | |
| - | അനുകരണമാതൃക (Simulation Models). പൊതുനയരൂപീകരണ രൂപകല്പനയ്ക്കായി പൊതുവേ ഉപയോഗിക്കുന്ന അനുകരണ മാതൃക ആണ് ബഹു സമവാക്യമാതൃകകള് ഉപയോഗിക്കുന്ന വേറൊരു മേഖല. പ്രായോഗിക | + | അനുകരണമാതൃക (Simulation Models). പൊതുനയരൂപീകരണ രൂപകല്പനയ്ക്കായി പൊതുവേ ഉപയോഗിക്കുന്ന അനുകരണ മാതൃക ആണ് ബഹു സമവാക്യമാതൃകകള് ഉപയോഗിക്കുന്ന വേറൊരു മേഖല. പ്രായോഗിക ജീവിതത്തില് അനുഭവവേദ്യമായവയും അല്ലാത്തവയുമായ സംഗതിയെ പ്രതിനിധാനം ചെയ്യുന്ന ഒരു കൂട്ടം ബഹുസമവാക്യത്തിന് ഗണിതപരമായ മൂല്യനിര്ണയം നടത്തുന്ന പ്രക്രിയയാണ് അനുകരണം എന്നര്ഥമാക്കുന്നത്. ഉദാഹരണത്തിന് അതീവ ലളിതമായ ഒരു സ്ഥൂലസാമ്പത്തിക ശാസ്ത്ര സമവാക്യം നോക്കുക. |
[[ചിത്രം:Vol5_22_formula1.jpg|500px]] | [[ചിത്രം:Vol5_22_formula1.jpg|500px]] | ||
| - | + | ഇതില് Ct, It,Y എന്നിവ ആന്തരോദ്ഭവചരങ്ങളും Gt ബഹുജന്യചരവുമാണ് a1, a2, a3, b1, b2, b3 എന്നീ പരാമീറ്റേഴ്സിന്റെ മൂല്യം നല്കിയിരിക്കുകയും ഇയേുടെയും It യുടെയും തുടക്കത്തിലുള്ള മൂല്യം നിര്ദേശിക്കുകയും യുടെ ഒരു സമയപാത നിര്ണയിക്കുകയും ചെയ്താല് Ct, It, Yt എന്നിവയുടെ മൂല്യം ഒരുമിച്ച് കണ്ടെത്താന് കഴിയും. | |
| - | കാലശ്രണി (Time series) മാതൃകകള്. ഇവിടെ ഒരു ചരത്തിന്റെ മൂല്യം അതിന്റെ തന്നെ ഭൂതകാലമൂല്യവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. | + | കാലശ്രണി (Time series) മാതൃകകള്. ഇവിടെ ഒരു ചരത്തിന്റെ മൂല്യം അതിന്റെ തന്നെ ഭൂതകാലമൂല്യവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ഭൂതകാലമൂല്യങ്ങളില്ക്കൂടി ചരങ്ങളുടെ ഭാവികാലമൂല്യങ്ങള് കണക്കാക്കാന് സാധിക്കുന്നു. എല്ലാ കാലശ്രണി മാതൃകകളും ഏകസമവാക്യ പ്രതിപരീതി (single equation regression) മാതൃകളാണ്. ഇവയെ പക്ഷേ നമുക്ക് നിര്ണയനകാലശ്രണി മാതൃക(deterministic time series models) എന്നും അനിശ്ചിതകാലശ്രണി(stochastic time series) മാതൃകകളെന്നും രണ്ടായി തിരിക്കാം. ഇതില് ആദ്യത്തേത് ഏകസംഖ്യാപ്രവചനവും (Point estimate) രണ്ടാമത്തേത് പ്രവചനമൂല്യവും ഒരു വിശ്വസനീയ പരിധിക്കുള്ളില് നടത്തുന്നു. |
| - | അനിശ്ചിതകാലശ്രണി | + | അനിശ്ചിതകാലശ്രണി മാതൃകകളില് പ്രധാനപ്പെട്ട ഒന്നാണ് രേഖീയ അനിശ്ചിതകാലശ്രണി മാതൃക (Linear Stochastic Time Series). അനിശ്ചിതാവസ്ഥയെ ഉള്ക്കൊണ്ട് പഠനവിധേയമാക്കുന്ന സംഗതിയെപ്പറ്റി പഠിക്കാനായി പ്രധാനമായും രണ്ടു സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നു. അവ ഓട്ടോ റിഗ്രഷന് (Auto Regression) രീതിയും മൂവിങ് ആവറേജ് (Moving average) രീതിയുമാണ്. ഈ രണ്ടുരീതികളും യോജിപ്പിച്ചുള്ള മിശ്രണരീതിയും അവലംബിച്ചു കാണുന്നുണ്ട്. ഏതു സങ്കേതത്തിലും മൂന്നുഘട്ടങ്ങളുണ്ട്. |
| - | ഘട്ടം 1: | + | ഘട്ടം 1: തിരിച്ചറിയല് (identification). ഇവിടെ ഉപയോഗിക്കുന്ന കാലശ്രണി രൂപത്തിലുള്ള വിവരങ്ങളുടെ സ്വഭാവസമത്വം അളക്കുന്നു. |
| - | ഘട്ടം 2: ആകലനം. ഈ | + | ഘട്ടം 2: ആകലനം. ഈ ഘട്ടത്തില് മാതൃകകളിലെ പരാമീറ്റേഴ്സിന്റെ മൂല്യം കണക്കാക്കുന്നു. |
| - | ഘട്ടം 3: പ്രശ്നനിദാനമായ പരിശോധന (diagnostic checking) | + | ഘട്ടം 3: പ്രശ്നനിദാനമായ പരിശോധന (diagnostic checking) ഇതില്ക്കൂടി ഇതുവരെ ആവര്ത്തിച്ചത് ശരിയാണോയെന്നു സ്വീകരിച്ച് മാതൃക ഉപയോഗമുള്ളതാക്കാന് യോഗ്യമാണോ എന്നും പഠിക്കുന്നു. ഉപയോഗിക്കുന്ന മാതൃകകളുടെ പരാമീറ്റര് കാര്യക്ഷമത വര്ധിപ്പിക്കാനാണിതു ചെയ്യുന്നത്. |
| - | എക്കണോമെട്രിക്സ് മാതൃകകളുടെ പ്രായോഗികത. സാമ്പത്തികശാസ്ത്രത്തിന്റെ പല മേഖലകളിലും വിഷയങ്ങളിലും വളരെ വിപുലമായി ഇത്തരം മാതൃകകള് ഉപയോഗിച്ചുവരുന്നു. | + | എക്കണോമെട്രിക്സ് മാതൃകകളുടെ പ്രായോഗികത. സാമ്പത്തികശാസ്ത്രത്തിന്റെ പല മേഖലകളിലും വിഷയങ്ങളിലും വളരെ വിപുലമായി ഇത്തരം മാതൃകകള് ഉപയോഗിച്ചുവരുന്നു. ഇവയില് ചില പ്രധാനപ്പെട്ട മേഖലകള് ഉപഭോഗം, നിക്ഷേപം, ചോദനവിശകലനം, ഉത്പാദനവിശകലനം, ധനകാര്യം, അന്താരാഷ്ട്ര വാണിജ്യം എന്നിവയാണ്. |
| - | ഉപഭോഗസിദ്ധാന്തങ്ങളും എക്കണോമെട്രിക്സ് മാതൃകകളും. ഉപഭോഗസിദ്ധാന്തങ്ങളുടെ | + | ഉപഭോഗസിദ്ധാന്തങ്ങളും എക്കണോമെട്രിക്സ് മാതൃകകളും. ഉപഭോഗസിദ്ധാന്തങ്ങളുടെ നിര്ദേശത്തെ വിശദീകരിക്കാനും വിവിധതരം ഉപഭോഗസിദ്ധാന്തങ്ങള് പൂര്ണരൂപത്തില് വെളിപ്പെടുത്താനും എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിക്കുന്നു. കെയിന്സ്, മില്റ്റണ് ഫ്രിഡ്മാന്, മോഡിഗ്ലാനി, ഡ്യൂസന്ബെറി എന്നിവരുടെ ഉപഭോഗസിദ്ധാന്തങ്ങള് വിശദീകരിക്കുന്നത് എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചാണ്. ലളിതരൂപത്തില് ഉപഭോഗത്തെ പ്രാവര്ത്തികരീതിയില് ഇങ്ങനെ വിശേഷിപ്പിക്കാം. |
C=f(Y) | C=f(Y) | ||
| വരി 141: | വരി 141: | ||
Y = ഉപയോഗിക്കാന് കഴിയുന്ന വരുമാനം (disposable income) | Y = ഉപയോഗിക്കാന് കഴിയുന്ന വരുമാനം (disposable income) | ||
| - | മുകളിലത്തെ | + | മുകളിലത്തെ പൊതുസമവാക്യത്തില്നിന്നും കെയിന്സിന്റെ ഉപഭോഗമനഃശാസ്ത്ര സിദ്ധാന്തത്തിന്റെ ഉപഭോഗസമവാക്യം ഇങ്ങനെ എഴുതാം. |
C=a+bY+U | C=a+bY+U | ||
| - | ഇവിടെ 'a' | + | ഇവിടെ 'a' എന്നാല് ഏറ്റവും കുറഞ്ഞ വരുമാനമില്ലാത്ത അവസ്ഥയില്പ്പോലും ജീവിക്കാന് ആവശ്യമായ ഉപഭോഗം. 'b' സീമാന്ത ഉപഭോഗപ്രവണതയെ (marginal propensity to consume) സൂചിപ്പിക്കുന്നു. |
| - | 'u' | + | 'u' എന്നാല് അനിശ്ചിതഘടകങ്ങളുടെ സ്വാധീനം |
ജെയിംസ് ന്യൂസന്ബറിയുടെ ആപേക്ഷിക ഉപഭോഗസിദ്ധാന്തം ഇപ്രകാരം എഴുതാം. | ജെയിംസ് ന്യൂസന്ബറിയുടെ ആപേക്ഷിക ഉപഭോഗസിദ്ധാന്തം ഇപ്രകാരം എഴുതാം. | ||
| വരി 152: | വരി 152: | ||
C = a + bY<sub>t</sub> + cY<sub>max</sub> + U<sub>t</sub> | C = a + bY<sub>t</sub> + cY<sub>max</sub> + U<sub>t</sub> | ||
| - | + | ഇതില് Yt= നിലവിലുള്ള വരുമാന അളവ് | |
| - | Ymax= ഭൂതകാലത്തെ ഏറ്റവും കൂടിയ വരുമാനം 'b', 'c', Yt യോടും Ymax-നോടും | + | Ymax= ഭൂതകാലത്തെ ഏറ്റവും കൂടിയ വരുമാനം 'b', 'c', Yt യോടും Ymax-നോടും ചേര്ന്ന ഗുണോത്തരങ്ങളുടെ മൂല്യം. |
| - | + | മില്റ്റണ് ഫ്രീഡ്മാന്റെ സ്ഥിരവരുമാന ഉപഭോഗസിദ്ധാന്തത്തെ ഇപ്രകാരം ലളിതവത്കരിക്കാം. | |
Ct* = α Y<sub>pt</sub> | Ct* = α Y<sub>pt</sub> | ||
| - | + | ഇതില് Ypt എന്നാല് സ്ഥിരമായി പ്രതീക്ഷിക്കപ്പെടുന്ന വരുമാനയളവ്. ഈ തത്ത്വം അനുസരിച്ച് ഒരു വ്യക്തിയുടെ ഉപഭോഗം അയാള് പ്രതീക്ഷിക്കുന്ന സ്ഥിരവരുമാനത്തിന്റെ അളവിനെ ആശ്രയിച്ചിരിക്കും. | |
| - | ഇതുപോലെ മോഡിഗ്ലാനി, | + | ഇതുപോലെ മോഡിഗ്ലാനി, സ്രംബര്ഗ്, ആന്റോ എന്നിവര് വികസിപ്പിച്ചെടുത്ത ജീവിതചക്ര ഉപഭോഗസിദ്ധാന്തത്തെ ഇങ്ങനെയെഴുതാം. |
[[ചിത്രം:Vol5_22_formula2.jpg|500px]] | [[ചിത്രം:Vol5_22_formula2.jpg|500px]] | ||
| - | + | മുകളില്പ്പറഞ്ഞ സമവാക്യത്തില് 'A' ആസ്തിയെയും 'Yet' ഭോവിയില് വരാവുന്ന വരുമാനത്തിന്റെ വര്ത്തമാനമൂല്യത്തെയും സൂചിപ്പിക്കുന്നു. ഈ സൂത്രവാക്യമനുസരിച്ച് വര്ത്തമാനകാലത്തെ ഒരു വ്യക്തിയുടെ ഉപഭോഗ അളവ് അയാളുടെ ആസ്തിയും വരുമാനവും ശിഷ്ടജീവിതത്തില് അയാള്ക്ക് വന്നുചേരുമെന്ന് പ്രതീക്ഷിക്കുന്ന വരുമാനത്തെയും ആശ്രയിച്ചിരിക്കും. | |
| - | ഉത്പാദനഫലനവും എക്കണോമെട്രിക്സും. ഉത്പാദനപ്രകിയ വിശദീകരിക്കാന് ഉപയോഗിക്കുന്ന ഉത്പാദന-ഉത്പാദനഘടകബന്ധത്തിനാണ് ഉത്പാദനഫലനം (production function) എന്നു പറയുന്നത്. ഉത്പാദനം അതിനുപയോഗിക്കുന്ന വിവിധവിഭവങ്ങളുമായി പ്രധാനമായും മൂലധനം (Capital) | + | ഉത്പാദനഫലനവും എക്കണോമെട്രിക്സും. ഉത്പാദനപ്രകിയ വിശദീകരിക്കാന് ഉപയോഗിക്കുന്ന ഉത്പാദന-ഉത്പാദനഘടകബന്ധത്തിനാണ് ഉത്പാദനഫലനം (production function) എന്നു പറയുന്നത്. ഉത്പാദനം അതിനുപയോഗിക്കുന്ന വിവിധവിഭവങ്ങളുമായി പ്രധാനമായും മൂലധനം (Capital) തൊഴില് (labour) ഒരു നിശ്ചിതസാങ്കേതികവിദ്യയുടെ അടിസ്ഥാനത്തില് എങ്ങനെ ഏതു രീതിയില് സന്നിവേശിക്കപ്പെട്ടിരിക്കുന്നു എന്നാണ് ഉത്പാദനഫലനങ്ങള് കാണിക്കുന്നത്. |
ഉത്പാദനഫലനത്തിന്റെ പൊതുരൂപം ഇങ്ങനെ കാണിക്കാം. | ഉത്പാദനഫലനത്തിന്റെ പൊതുരൂപം ഇങ്ങനെ കാണിക്കാം. | ||
Q = f(X1, X2, X3) | Q = f(X1, X2, X3) | ||
| - | + | ഇതില് Q = ഉത്പാദനം | |
X1, X2, X3 .....Xn= ഉത്പാദനത്തിനുപയോഗിക്കുന്ന വിവിധതരം ഉത്പാദനഘടകങ്ങള്. | X1, X2, X3 .....Xn= ഉത്പാദനത്തിനുപയോഗിക്കുന്ന വിവിധതരം ഉത്പാദനഘടകങ്ങള്. | ||
| വരി 185: | വരി 185: | ||
ഇവിടെ Q = ഉത്പാദന അളവ് | ഇവിടെ Q = ഉത്പാദന അളവ് | ||
| - | L = | + | L = തൊഴില്ശക്തിയുടെ അളവ് |
K= മൂലധനം | K= മൂലധനം | ||
| - | a<sub>1</sub>,a<sub>2</sub> എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും ഗുണാത്മകങ്ങളാണ്, ഇവിടെ a1,a2 എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും സീമാന്ത ഉത്പാദനക്ഷമതയാണ്. a0 എന്ന പദം | + | a<sub>1</sub>,a<sub>2</sub> എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും ഗുണാത്മകങ്ങളാണ്, ഇവിടെ a1,a2 എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും സീമാന്ത ഉത്പാദനക്ഷമതയാണ്. a0 എന്ന പദം കൊണ്ടര്ഥമാക്കുന്നത് തൊഴിലും മൂലധനവും ഇല്ലെങ്കില്പ്പോലും മറ്റു ഘടകങ്ങളുടെ പ്രവര്ത്തനഫലമായി ഉണ്ടാകാവുന്ന ഏറ്റവും കുറഞ്ഞ അളവിലുള്ള ഉത്പാദനം. ഈ സമവാക്യത്തില് ഉത്പാദനത്തിന്റെ അളവ് തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും അളവിനനുസരിച്ച് രേഖീയമാതൃകയില് മാറിക്കൊണ്ടിരിക്കും. |
ആദ്യമായി ഏറ്റവും പ്രചുരപ്രചാരം നേടിയ ഉത്പാദനഫലനം സൃഷ്ടിച്ചത് കോബ്, ഡഗ്ലസ് എന്നീ രണ്ടു സാമ്പത്തികശാസ്ത്രജ്ഞന്മാരാണ്. ഇന്നത് കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനം എന്നറിയപ്പെടുന്നു. താഴെപ്പറയുന്നതാണ് ഈ ഉത്പാദനഫലനത്തിന്റെ ഗണിതാത്മകരൂപം. | ആദ്യമായി ഏറ്റവും പ്രചുരപ്രചാരം നേടിയ ഉത്പാദനഫലനം സൃഷ്ടിച്ചത് കോബ്, ഡഗ്ലസ് എന്നീ രണ്ടു സാമ്പത്തികശാസ്ത്രജ്ഞന്മാരാണ്. ഇന്നത് കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനം എന്നറിയപ്പെടുന്നു. താഴെപ്പറയുന്നതാണ് ഈ ഉത്പാദനഫലനത്തിന്റെ ഗണിതാത്മകരൂപം. | ||
| വരി 195: | വരി 195: | ||
[[ചിത്രം:Vol5_23_formula1.jpg|500px]] | [[ചിത്രം:Vol5_23_formula1.jpg|500px]] | ||
| - | + | ഇതില് Q ഉത്പാദനത്തെയും L തൊഴിലിനെയും K മൂലധനത്തെയും സൂചിപ്പിക്കുന്നു. ഉത്പാദനഫലനത്തിന്റെ പ്രാചനങ്ങളാണ്. ഇതില് യും യും തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും സീമാന്തഉത്പാദനക്ഷമതയാണ്. "' അര്ഥമാക്കുന്നത് സാങ്കേതികവിദ്യയുടെ മാറ്റം ഉത്പാദനത്തില് ഉണ്ടാക്കുന്ന മാറ്റത്തിന്റെ അളവിനെയാണ്. | |
| - | അതുകൂടാതെ ഉത്പാദനപ്രക്രിയയിലെ പ്രത്യായനിരക്കിനെയാണ് സൂചിപ്പിക്കുന്നത്. | + | അതുകൂടാതെ ഉത്പാദനപ്രക്രിയയിലെ പ്രത്യായനിരക്കിനെയാണ് സൂചിപ്പിക്കുന്നത്. ഒന്നില്ക്കൂടുതലെങ്കില് ഉത്പാദനത്തില് ആരോഹണപ്രത്യായവും ഒന്നില് കുറവാണെങ്കില് അവരോഹണ പ്രത്യായവും ഒന്നായിരുന്നാല് സ്ഥിരപ്രത്യായവും ആണെന്ന് അനുമാനിക്കാം. |
| - | കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനത്തിന്റെ കുറവു പരിഹരിക്കുന്നതിന്റെ ഭാഗമായി ആരോ (arrow) തുടങ്ങിയ സാമ്പത്തിക | + | കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനത്തിന്റെ കുറവു പരിഹരിക്കുന്നതിന്റെ ഭാഗമായി ആരോ (arrow) തുടങ്ങിയ സാമ്പത്തിക ശാസ്ത്രജ്ഞന്മാര് വികസിപ്പിച്ചെടുത്ത് ഉത്പാദനഫലനമാണ് സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തിക മാതൃക (Constant Elasticity of Substitution-CES) ഇതിന്റെ ഗണനാത്മക പ്രാവൃത്തികരൂപം. |
[[ചിത്രം:Vol5_23_formula2.jpg|500px]] | [[ചിത്രം:Vol5_23_formula2.jpg|500px]] | ||
| - | + | ഇതില് = ഉത്പാദനവും E = തൊഴിലും = മൂലധനവും എന്നിവ പരാമീറ്റേഴ്സാണ്പ്രാചനങ്ങളുമാണ് "'യും ഉത്പാദനഫലനത്തില് മൂലധനത്തിനും തൊഴിലിനുമുള്ള ആനുപാതിക പ്രാധാന്യമൂല്യങ്ങളും എന്നത് പ്രതിസ്ഥാപനപ്രാചനവുമാണ്. | |
| - | കോബ്-ഡഗ്ലസിന്റെയും, സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (CES) ഉത്പാദനഫലനത്തിന്റെ ചുവടുപിടിച്ചുകൊണ്ട് ക്രിസ്റ്റിന്സണ് | + | കോബ്-ഡഗ്ലസിന്റെയും, സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (CES) ഉത്പാദനഫലനത്തിന്റെ ചുവടുപിടിച്ചുകൊണ്ട് ക്രിസ്റ്റിന്സണ് തുടങ്ങിയവര് വികസിപ്പിച്ചെടുത്ത ഉത്പാദനഫലനമാണ് ട്രാന്സ് ലോഗ് (translog) അഥവാ ട്രാന്സിഡന്ഷ്യല് ലോഗ 'Transidential Logarithmic' ഉത്പാദനഫലനം. ഇതിന്റെ ഗണനാത്മകപ്രാവര്ത്തിക രൂപം താഴെ പറയുന്നവയാണ്. |
[[ചിത്രം:Vol5_23_formula3.jpg|500px]] | [[ചിത്രം:Vol5_23_formula3.jpg|500px]] | ||
| - | + | ഇതില് log Q, ഉത്പാദനത്തിന്റെ ലോഗരിതമൂല്യവും log K, log L എന്നിവ മൂലധനത്തിന്റെയും തൊഴിലിന്റെയും ലോഗരിത മൂല്യങ്ങളുമാണ്. | |
| - | + | മുകളില്പ്പറഞ്ഞ ഉത്പാദനഫലനങ്ങളുടെ ഒരു പ്രധാനപ്പെട്ട കുറവായ സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത മാറ്റി അസ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (Variable Elasticity of Substitution-VES) ഉത്പാദനഫലനത്തിനായി ശ്രമങ്ങള് ഏറെ നടന്നു. VES ഉത്പാദനഫലനത്തിന്റെ പ്രധാനമാതൃകകള് വികസിപ്പിച്ചത് ലുവും ഫ്ളെറ്റ്ച്ചറും (Lu and Fletcher, 1968) സാറ്റോയും ഹോഫ്മാനും (Sato and Hofman, 1968), റവാന്കര് (Ravankar, 1971) എന്നിവരാണ്. | |
| - | ഉത്പാദനഫലനത്തിന്റെ ഒരു ഗണനാത്മക | + | ഉത്പാദനഫലനത്തിന്റെ ഒരു ഗണനാത്മക പ്രാവര്ത്തികരൂപമിതാണ്. |
[[ചിത്രം:Vol5_23_formula4.jpg|500px]] | [[ചിത്രം:Vol5_23_formula4.jpg|500px]] | ||
| - | നിക്ഷേപവും എക്കണോമെട്രിക്സ് ഉപയോഗവും. മൂലധനശേഖരം | + | നിക്ഷേപവും എക്കണോമെട്രിക്സ് ഉപയോഗവും. മൂലധനശേഖരം വര്ധിക്കുന്നത് ശിഷ്ടനിക്ഷേപം (Net investment) വഴിയാണ്. ശിഷ്ടനിക്ഷേപത്തെ ഗണനാത്മക സമവാക്യത്തില് ഇങ്ങനെ എഴുതാം. |
[[ചിത്രം:Vol5_23_formula5.jpg|500px]] | [[ചിത്രം:Vol5_23_formula5.jpg|500px]] | ||
| - | ഇവിടെ Qt എന്നത് കോലഘട്ടത്തെ ഉത്പാദനവും Qt-1,(t-1) കാലഘട്ടത്തെ ഉത്പാദനവുമാണ്. ഈ സമവാക്യം | + | ഇവിടെ Qt എന്നത് കോലഘട്ടത്തെ ഉത്പാദനവും Qt-1,(t-1) കാലഘട്ടത്തെ ഉത്പാദനവുമാണ്. ഈ സമവാക്യം സൂചിപ്പിക്കുന്നതെന്തെന്നാല് അതത് കാലഘട്ടത്തിലെ മൊത്ത നിക്ഷേപം ആ വര്ഷങ്ങളിലെ ഉത്പാദന അളവിനെയും അതിനു തൊട്ടുമുമ്പുള്ള വര്ഷത്തിലെ ഉത്പാദനത്തെയും നിര്ണയിക്കുന്നു. ഈ സമവാക്യത്തിലെ 'b' ആക്സിലറൈസേഷന് (accelerisation) ഗുണാത്മകതയെന്നും 'c' എന്നത് മൊത്തം മൂലധനത്തിനുണ്ടാകുന്ന തേയ്മാനശതമാനവുമാണ്. സാമ്പത്തികശാസ്ത്രത്തില് പ്രത്യേകിച്ചും സ്ഥൂലസാമ്പത്തിക ശാസ്ത്ര പഠനത്തില് വളരെ വിപുലമായ രീതിയില് നിക്ഷേപപഠനങ്ങളില് എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചു വരുന്നു. കെയ്ന്സിന്റെയും ക്ലാസ്സിക്കല്, നവക്ലാസ്സിക്കല് തുടങ്ങിയ ശാഖകളുടെ എക്കണോമെട്രിക്സ് മാതൃകകള് നിക്ഷേപപഠനങ്ങളില് ഉപയോഗിച്ചുവരുന്നു. |
| - | നിക്ഷേപമാതൃകകള് പലപ്പോഴും കാലവിളംബ(time lag) | + | നിക്ഷേപമാതൃകകള് പലപ്പോഴും കാലവിളംബ(time lag) ത്തില് നിര്ദേശിക്കുന്നുണ്ട്. നിക്ഷേപഫലനത്തില് വിതരണവിളംബ(റdistribution lag)മുപയോഗിച്ചുകൊണ്ട് സാമ്പത്തികശാസ്ത്രജ്ഞര് സ്വീകരിച്ച കോയെക്(Koyeck)ന്റെ മാതൃക വളരെ പ്രശസ്തമാണ്. ഈ ഫലനം കോയെക് വിളംബം (Koyeck lag) എന്ന് അറിയപ്പെടുന്നു. ഇതില് മൂലധനശേഖരം ജ്യാമതീയവിളംബത്തില് (geomatric lag) ഉത്പാദനവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നതായി തെളിയിക്കുന്നു. |
| - | പണം സംബന്ധിച്ച പഠനവും എക്കണോമെട്രിക്സും. പണം സംബന്ധിയായ സാമ്പത്തികശാസ്ത്ര | + | പണം സംബന്ധിച്ച പഠനവും എക്കണോമെട്രിക്സും. പണം സംബന്ധിയായ സാമ്പത്തികശാസ്ത്ര പഠനത്തില് എക്കണോമെട്രിക്സ് മാതൃക ഉപയോഗിക്കുന്ന ഒരു പ്രധാന മേഖലയാണ് പണത്തിന്റെ ചോദനനിര്ദേശം. പണചോദനത്തിന്റെ പൊതുനിര്ദേശം ഗണനാത്മകരൂപത്തില് |
M<sub>d</sub> = aYP + b(R)WP | M<sub>d</sub> = aYP + b(R)WP | ||
| - | + | ഇതില് Md എന്നത് പണത്തിന്റെ ചോദനയളവും Y എന്നത് യഥാര്ഥ വരുമാനവും P കമ്പോള പൊതുവിലയും W യഥാര്ഥ ധനത്തിന്റെ അളവും R പ്രതീക്ഷിത പലിശനിരക്കുമാണ്. പണത്തിന്റെ ചോദനം പ്രധാനമായും ദൈനംദിന ക്രയവിക്രയത്തിനും അനിശ്ചിതാവസ്ഥയെ മറികടക്കാനുള്ള കരുതലായും, ഊഹക്കച്ചവടത്തിനുമായിരിക്കും. അതുപോലെ ഇവിടെ ധനം പണരൂപത്തിലും മറ്റു സ്വത്തായിട്ടും കൈവശം വയ്ക്കുന്നു. | |
| - | പണചോദനത്തിന്റെ ഫലനത്തിന്റെ ഘടനയെക്കുറിച്ച് പല സാമ്പത്തികശാസ്ത്ര ചിന്താവിഭാഗങ്ങളും വ്യക്തികളും വിശദമായി പ്രതിപാദിച്ചിട്ടുണ്ടെങ്കിലും | + | പണചോദനത്തിന്റെ ഫലനത്തിന്റെ ഘടനയെക്കുറിച്ച് പല സാമ്പത്തികശാസ്ത്ര ചിന്താവിഭാഗങ്ങളും വ്യക്തികളും വിശദമായി പ്രതിപാദിച്ചിട്ടുണ്ടെങ്കിലും മില്ട്ടണ് ഫ്രഡ്മാന്റെ പണചോദനത്തിന്റെ സിദ്ധാന്തം പ്രശസ്തമാണ്. മില്ട്ടണ് ഫ്രഡ്മാന് താഴെക്കൊടുത്തിരിക്കുന്ന സമവാക്യത്തിലൂടെ പണചോദനത്തെ വിശകലനം ചെയ്യുന്നു. |
[[ചിത്രം:Vol5_24_formula1.jpg|500px]] | [[ചിത്രം:Vol5_24_formula1.jpg|500px]] | ||
| - | ഇവിടെ ദൈനംദിനാവശ്യത്തിലധികം വരുന്ന പണത്തിനെ | + | ഇവിടെ ദൈനംദിനാവശ്യത്തിലധികം വരുന്ന പണത്തിനെ ഒന്നുകില് സര്ക്കാരിന്റെ കടപ്പത്രത്തിലോ അല്ലെങ്കില് ഓഹരികളിലോ നിക്ഷേപിക്കുമെന്ന് അനുമാനിക്കുന്നു. |
| - | ചോദനപഠനവും എക്കണോമെട്രിക്സും. ആദ്യകാല എക്കണോമെട്രിക്സ് | + | ചോദനപഠനവും എക്കണോമെട്രിക്സും. ആദ്യകാല എക്കണോമെട്രിക്സ് പഠനങ്ങളില് ഏറിയകൂറും ഈ വിഭാഗത്തില്പ്പെടുന്നവയാണ്. ചോദനപഠനത്തിന്റെ പ്രധാനവിഷയം ഒരു ഉപഭോക്താവിന് ഒരു വസ്തുവിനുണ്ടാകുന്ന ചോദനം ഏതൊക്കെ ചരങ്ങളുടെ മാറ്റവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു എന്നതാണ്. ഏറ്റവും ലളിതമായ സങ്കല്പത്തില് ഒരു സാധനത്തിന്റെ ചോദനം ആ സാധനത്തിന്റെ വിലയും വ്യക്തിയുടെ വരുമാനവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ചോദനമെന്ന ആശ്രിതചരത്തെയും അതിനെ നിര്ണയിക്കുന്ന സ്വതന്ത്രചരങ്ങളായ സാധനവിലയെയും വ്യക്തിവരുമാനത്തെയും ചോദനസമവാക്യത്തിലൂടെ വ്യക്തമാക്കാം. ചോദന സമവാക്യത്തിന്റെ വികസനം പ്രധാനമായും സ്റ്റോണ് (stone, 1954) വികസിപ്പിച്ചെടുത്ത രേഖീയ ചെലവ് വ്യവസ്ഥ (Linear expenditure system)യിലും ഹൊതാക്കര് (Hothakker, 1965) വികസിപ്പിച്ചെടുത്ത ലോഗരിത രേഖാ (log-linear) അഥവാ സ്ഥിര ഇലാസ്തികത ചോദനവ്യവസ്ഥ(Constant Elasticity of Demand system)യുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. |
[[ചിത്രം:Vol5_24_formula2.jpg|500px]] | [[ചിത്രം:Vol5_24_formula2.jpg|500px]] | ||
| - | + | മുകളില് സൂചിപ്പിച്ച രണ്ടു സമവാക്യങ്ങളും ന്യൂനതമവര്ഗനിയമം (Least Square Method)അനുസരിച്ച് ആകലനം ചെയ്യപ്പെടാം. ഒന്നാമത്തെ സമവാക്യമനുസരിച്ച് വരുമാനം ഒരു ഏകകം കൂടുമ്പോള് ചോദനം 'b'ഏകകം കൂടുമെന്നും വില ഒരു ഏകകം കൂടുമ്പോള് ചോദനം 'c' ഏകകം കുറയുമെന്നും കാണാം. ഇവിടെ ചോദനവും വരുമാനവും തമ്മില് ധനബന്ധവും(Positive relation), ചോദനവും വിലയും തമ്മില് ഋണബന്ധവും(Negative relation) ഉണ്ടെന്നു സങ്കല്പിക്കുന്നു. | |
| - | + | എന്നാല് രണ്ടാമത്തെ ലോഗരിത രേഖീയ സമവാക്യമനുസരിച്ച് വരുമാനം ഒരു ശതമാനം വര്ധിച്ചാല് ചോദനം 'b' ഏകകം കൂടുമെന്നും വില ഒരു ശതമാനം കൂടുമ്പോള് ചോദനം 'c' ഏകകം കുറയുമെന്നും അനുമാനിക്കുന്നു. രണ്ടാമത്തെ സമവാക്യം ഉപയോഗിക്കുകയാണെങ്കില് 'b' വരുമാന ഇലാസ്തികതയും (Income Elasticity) 'c' വില ഇലാസ്തികതയും(Price Elasticity) ആണ്. എന്നാല് ആദ്യത്തെ ഫലനമായ രേഖീയ സമവാക്യമാണ് ഉപയോഗിക്കുന്നതെങ്കില് വരുമാന ഇലാസ്തികത Yb/D എന്നും വില ഇലാസ്തികത Pc/D എന്നും കണക്കാക്കാം. സാധാരണ ചരങ്ങളെ സംബന്ധിച്ചിടത്തോളം വില ഇലാസ്തികത ഋണസംഖ്യയും(Negative Number) വരുമാന ഇലാസ്തികത ധനസംഖ്യയും(Positive Number) ആയിരിക്കും. | |
| - | ഇന്ത്യന് | + | ഇന്ത്യന് പഠനങ്ങളില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. ഇന്ത്യയില് എക്കണോമെട്രിക്സ് പഠനങ്ങള് കൃഷി, വ്യവസായം, ധനസാമ്പത്തികവ്യവസ്ഥ, ചോദനവിശകലനം, അന്താരാഷ്ട്ര വാണിജ്യം തുടങ്ങി അനേകം മേഖലകളില് വ്യാപകമായി ഉപയോഗിച്ചുവരുന്നു. |
| - | + | കാര്ഷികസമ്പദ്ശാസ്ത്രത്തില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. കാര്ഷികമേഖല ഇന്ത്യയില് വളരെ ആഴത്തില് പ്രായോഗിക ഗവേഷണപഠനം നടന്ന ഒരു മേഖലയാണ്. പല പഠനങ്ങളും കാലശ്രണിദത്തവും (Time series data) പരിച്ഛേദദത്തവും (Cross section data) ഉപയോഗിച്ച് പല തരത്തിലുള്ള എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചിരുന്നു. എന്നിരുന്നാലും മിക്ക പഠനങ്ങളിലും ഇത്തരത്തിലുള്ള എക്കണോമെട്രിക്സ് മാതൃകയുടെ ഉപയോഗത്തിന് ചില പരിമിതികള് ഉണ്ടായിരുന്നു. പല എക്കണോമെട്രിക്സ് സങ്കേതങ്ങള് ഉപയോഗിക്കുമ്പോള് സാധാരണ അനുമാനങ്ങളായ കമ്പോളമത്സരം, ലാഭേച്ഛ എന്ന ലക്ഷ്യം, മാതൃകാനിര്ദേശത്തില് സ്ഥാപനങ്ങളെയും സര്ക്കാര് നയങ്ങളുടെയും അവഗണന, യോജിക്കാത്ത സംഖ്യാസങ്കേതങ്ങളുടെ ഉപയോഗം, കാര്ഷിക സാങ്കേതിക വിദ്യയെ പ്രതിനിധാനം ചെയ്യാന്വേണ്ടി അനിയന്ത്രിതമായി കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനം ഉപയോഗിക്കല് എന്നിവ ചിലതുമാത്രമാണ്. മേല്പറഞ്ഞ പരിമിതികള് കാര്ഷികമേഖലയില് ഇന്ത്യയില് നടക്കുന്ന എക്കണോമെട്രിക്സ് പഠനങ്ങളുടെ പ്രായോഗികത കുറയ്ക്കുന്നു. | |
| - | പ്രായോഗിക | + | പ്രായോഗിക ഉത്പാദനഫലനത്തില് വളരെയധികം ബഹുനിവേശ(Multi-input) ഉത്പാദകഫലനങ്ങള് ഉപയോഗിച്ചിരുന്നു. പഠനങ്ങളില്ക്കൂടി പല ആകലനങ്ങള് നടത്തിയിരുന്നു. സാമ്പത്തിക വിവേചന പരിശോധന(Economic Rationality test) അതിര് ഉത്പാദകഫലന(Frontier Production Function)ത്തില് കൂടി കൃഷിയിടത്തെ സാങ്കേതികമേന്മ അളന്നു തിട്ടപ്പെടുത്തല്, കൃഷിയിടത്തെ വ്യാപ്തിയും ഉത്പാദനക്ഷമതയും തമ്മിലുള്ള ബന്ധം, ചെലവിന്റെയും ലാഭത്തിന്റെയും ഫലനങ്ങളുട ആകലനം എന്നിവ അവയില് ചിലതാണ്. |
| - | വ്യവസായപഠനത്തിന് എക്കണോമെട്രിക്സിന്റെ പ്രായോഗികത | + | വ്യവസായപഠനത്തിന് എക്കണോമെട്രിക്സിന്റെ പ്രായോഗികത ഇന്ത്യയില്. ഇന്ത്യന് വ്യവസായത്തെപ്പറ്റി എക്കണോമെട്രിക്സ് പഠനങ്ങള് കഴിഞ്ഞ 40 വര്ഷത്തിനുള്ളില് വളരെ നടന്നിരിക്കുന്നു. വ്യവസായ ഗവേഷണത്തിന്റെ പ്രധാനവിഷയങ്ങള് ഉത്പാദനഫലനം, നിക്ഷേപഫലനം, തൊഴില് ചോദനഫലനം, ചെലവ് ഫലനം എന്നിവയാണ്. അടുത്തകാലത്തായി പുതിയ മേഖലകളായ ഗവേഷണവും വികസനവും, ഉത്പാദനശേഷി വിനിയോഗം, വളര്ച്ച, ലാഭം എന്നീ മേഖലകളും പഠനവിധേയമാകുന്നു. ഇന്ത്യന് വ്യവസായപഠനത്തില് ഏറ്റവും പ്രചാരമുള്ള മേഖല ഉത്പാദനഫലനത്തെക്കുറിച്ചാണ്. അതിനുവേണ്ടി ഉപയോഗിക്കുന്ന ദത്തം പ്രധാനമായി കണ്സസ് ഒഫ് മാനുഫാക്ചേര്ഡ് ഇന്ഡസ്ട്രീസ് (Consus of Manufacturing Industries)ഉം ആന്വല് സര്വേ ഒഫ് ഇന്ഡസ്ട്രീസ് (Annual Survey of Industries)മാണ്. മിക്ക പഠനത്തിലും തൊഴിലും മൂലധനവും ഉത്പാദനഘടകമാക്കിയ മൂല്യവര്ധിത ഉത്പാദിതഫലനമാണ് ഉപയോഗിച്ചിട്ടുള്ളത്. പഠനത്തില് ഉപയോഗിക്കപ്പെട്ട പ്രധാന ഉത്പാദനഫലനങ്ങള് കോബ്-ഡഗ്ലസ് (Cobb-Douglas), സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (Constant Elasticity of Substitution), ട്രാന്സ്ലോഗ് ഉത്പാദനഫലനങ്ങള് എന്നിവയാണ്. മിക്ക പഠനത്തിലും ന്യൂനതമവര്ഗരീതി (Least Square Method) ഉപയോഗിച്ചാണ് ആകലനം നടത്തിയിരുന്നത്. ഇതുകൂടാതെ മറ്റു ആകലന സങ്കേതങ്ങളായ ജനറലൈസ്ഡ് മെത്തേഡ് ഒഫ് മൊമെന്റ്സ് (Generalised Method of moments), ഇന്സ്ട്രുമെന്റല് വേരിയബ്ള് (Instrumental variable) രീതികളും ഉപയോഗിച്ചിരുന്നു. |
| - | + | പണസമ്പദ്ശാത്രത്തില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. പണസമ്പദ്ശാസ്ത്രത്തില് (Monetary Economics)എക്കണോമെട്രിക്സിന്റെ പ്രധാന ഉപയോഗം പണഫലനത്തിന്റെ (Money Function) ചോദനഫലനവും പ്രദാന ഫലനവും ആകലനം ചെയ്യുന്നതിലാണ്. പണത്തിന്റെ ചോദനത്തില് പ്രധാനപ്പെട്ട ആകലനം യഥാര്ഥ വരുമാനത്തെയും യഥാര്ഥ പലിശനിരക്കിനെയും ബന്ധപ്പെടുത്തി യഥാര്ഥ പണചോദനത്തിന്റെ ഹ്രസ്വദീര്ഘകാല ഇലാസ്തികത കണ്ടെത്താനാണ്. അതു കൂടാതെ പണചോദന ഫലനത്തിന്റെ സ്ഥിരത പണമിഥ്യാബോധം (Money illusion), ഇലാസ്തികതയുടെ ചലനാത്മകക്രമം എന്നിവയും പഠനത്തിന് ആധാരമായിട്ടുണ്ട്. | |
| - | ചോദനസമ്പ്രദായവും എക്കണോമെട്രിക്സും. എക്കണോമെട്രിക്സിന്റെ ഏറ്റവും പ്രധാനപ്പെട്ട ആദ്യകാല ഉപയോഗം ഉപഭോക്തചോദന ഫലനത്തിന്റെ പ്രയോഗത്തിലാണ്. ചോദനസമവാക്യ | + | ചോദനസമ്പ്രദായവും എക്കണോമെട്രിക്സും. എക്കണോമെട്രിക്സിന്റെ ഏറ്റവും പ്രധാനപ്പെട്ട ആദ്യകാല ഉപയോഗം ഉപഭോക്തചോദന ഫലനത്തിന്റെ പ്രയോഗത്തിലാണ്. ചോദനസമവാക്യ ആകലനത്തില് രണ്ട് പ്രധാന സമീപനങ്ങളാണ് സ്വീകരിച്ചിരുന്നത്. ഒരു പ്രത്യേക വസ്തുവിന്റെയോ ഒരു കൂട്ടം വസ്തുവിന്റെയോ ചോദന സമവാക്യം ആകലനം ചെയ്യുകയാണ് ആദ്യകാല സമീപനത്തിലൂടെ ചെയ്തിരുന്നത്. രണ്ടാമത്തെ, ഈ അടുത്തകാലത്തായി വികസിപ്പിച്ച സമീപനത്തില് ഓരോ കൂട്ടം സാധനങ്ങളുടെയും ചോദനസമവാക്യങ്ങള് ഒരുമിച്ച് മൊത്തചോദന സമ്പ്രദായ (Complete demand system) ആകലനം ചെയ്യുന്നു. രണ്ടാമത്തെ സമീപനം താത്ത്വികമായി മുന്ഗണന അര്ഹിക്കുന്നുണ്ടെങ്കിലും ഇതിന്റെ ആകലനത്തില് അതിനൂതനമായ എക്കണോമെട്രിക്സ് സങ്കേതങ്ങളായ പ്രത്യക്ഷത്തില് ബന്ധമില്ലാത്ത പ്രതിപരിതി ആകലനം (Semingly unrelated regression estimation, SURE) അല്ലെങ്കില് ഉച്ചതമസാധ്യതാരീതി (Maximum likelihood method) ഉപയോഗം അനിവാര്യമാക്കിത്തീര്ക്കുന്നു. ഇത്തരം സങ്കേതങ്ങള് രേഖീയമല്ലാത്ത ശുഭപ്രതീക്ഷാ അല്ഗോരിഥം (Nonlinear Optimistics Algorithm) ഉപയോഗിക്കേണ്ടതായി വരികയും ആകലനം സങ്കീര്ണമാകാന് ഇടയാകുകയും ചെയ്യുന്നു. |
| - | അന്താരാഷ്ട്രവാണിജ്യവും എക്കണോമെട്രിക്സും. അന്താരാഷ്ട്രവാണിജ്യവുമായി ബന്ധപ്പെട്ട് ധാരാളം എക്കണോമെട്രിക്സ് പഠനങ്ങള് | + | അന്താരാഷ്ട്രവാണിജ്യവും എക്കണോമെട്രിക്സും. അന്താരാഷ്ട്രവാണിജ്യവുമായി ബന്ധപ്പെട്ട് ധാരാളം എക്കണോമെട്രിക്സ് പഠനങ്ങള് ഇന്ത്യയില് നടത്തിയിരിക്കുന്നു. ഉത്പാദനഘടക സമ്പന്നതാസിദ്ധാന്ത(factor endowment theory)ത്തിന്റെ വിലയിരുത്തല്, വെളിപ്പെടുത്തപ്പെട്ട താരതമ്യ നേട്ടവും (Revealed comparative advantage) അവയെ നിര്ണയിക്കുന്ന ഘടകങ്ങളും മറ്റും അന്താരാഷ്ട്രവാണിജ്യവുമായി ബന്ധപ്പെട്ട പ്രധാന പഠനവിഷയങ്ങളാണ്. അടുത്ത കാലത്തായി വികസിത-വികസ്വര രാജ്യങ്ങളില് പ്രത്യേകിച്ചും ഇന്ത്യയില് വ്യവസായ വാണിജ്യനയങ്ങളില് ഉദാരവത്കരണം വഴിയുള്ള സ്വാധീനം വിപുലമായ രീതിയില് പഠനവിധേയമായിട്ടുണ്ട്. |
| - | + | മേല്സൂചിപ്പിച്ച മേഖലകള് കൂടാതെ സ്ഥൂലസമ്പദ്ഘടന,ദേശീയസംസ്ഥാന ആസൂത്രണ പ്രക്രിയയെപ്പറ്റിയും യുക്തിസഹമായ തിരഞ്ഞെടുപ്പ് സിദ്ധാന്തം, ജനസംഖ്യാ സമ്പദ്ശാസ്ത്രം, വികസന സമ്പദ്ശാസ്ത്രം, സാമ്പത്തികചരിത്രം തുടങ്ങിയ മേഖലകളിലെല്ലാം എക്കണോമെട്രിക്സിന്റെ രീതിശാസ്ത്രം ഉപയോഗിച്ചുവരുന്നു. സ്ഥൂല-സൂക്ഷ്മ സാമ്പത്തിക പ്രക്രിയകളെക്കുറിച്ച് ഏക്കണോമെട്രിക്സ് അപഗ്രഥനത്തിലൂടെ ലഭ്യമാകുന്ന പ്രവചനങ്ങളും പ്രവണതാ സൂചനകളും ഗവണ്മെന്റുകളുടെ സാമ്പത്തിക നയരൂപീകരണത്തില് ഗണ്യമായ സ്വാധീനം ചെലുത്തുന്നുണ്ട്. | |
(ഡോ. വി. നാഗരാജന് നായിഡു) | (ഡോ. വി. നാഗരാജന് നായിഡു) | ||
Current revision as of 08:45, 13 ഓഗസ്റ്റ് 2014
ഉള്ളടക്കം |
എ(ഇ)ക്കണോമെട്രിക്സ്
Econometrics
ഗണിതശാസ്ത്രം, സ്ഥിതിവിവരശാസ്ത്രം എന്നീ മേഖലകളിലെ ചരങ്ങളുടെ അടിസ്ഥാനത്തില് സാമ്പത്തികശാസ്ത്രതത്ത്വങ്ങളും നിയമങ്ങളും കൂടുതല് കൃത്യതയോടെ പുനരാവിഷ്കരിക്കുന്ന സാമ്പത്തികശാസ്ത്രരേഖ. "എക്കണോമെട്രിക്സ്' എന്ന പദത്തിന് നോര്വേക്കാരനായ സാമ്പത്തികസംഖ്യാശാസ്ത്രകാരന് റാഗ്നര് ഫ്രിഷിനോട് കടപ്പെട്ടിരിക്കുന്നു. 1926-ല് ഇദ്ദേഹമാണ് ഈ പദം ആദ്യമായി ഉപയോഗിച്ചത്.
എക്കണോമെട്രിക്സ് താഴെപ്പറയുന്ന മൂന്നുകാര്യങ്ങളാണ് ഉന്നംവയ്ക്കുന്നത്.
1. സാമ്പത്തികശാസ്ത്ര സിദ്ധാന്തങ്ങളുടെ സാധൂകരണം വിലയിരുത്തുക.
2. സാമ്പത്തിക നയരൂപീകരണത്തിനുവേണ്ടി സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തിന്റെ ഗുണോത്തരമൂല്യം ആകലനം ചെയ്തു നല്കുക.
3. സംഭവ്യതയുടെ അടിസ്ഥാനത്തില് സാമ്പത്തികചരങ്ങളുടെ വ്യാപ്തിയുടെ മൂല്യം പ്രവചിക്കുക.
എക്കണോമെട്രിക്സ് പഠനങ്ങളെ താത്ത്വികവും (theoretical) പ്രായോഗികവുമായി (applied) രണ്ടായി തരംതിരിക്കാം. എക്കണോമെട്രിക്സ് പഠന മാതൃകയിലൂടെ സാമ്പത്തികചരങ്ങള് തമ്മിലുള്ള ബന്ധത്തെ അളന്നു തിട്ടപ്പെടുത്തുവാനുള്ള അനുയോജ്യമായ സമ്പ്രദായം വികസിപ്പിക്കുകയാണ് താത്ത്വിക എക്കണോമെട്രിക്സ് ശാഖ ചെയ്യുന്നത്. രണ്ടാമത്തെ ശാഖയില് സാമ്പത്തിക ശാസ്ത്രസിദ്ധാന്തങ്ങളുടെ വിലയിരുത്തലിനും അതിലൂടെ ഭാവിപ്രവചനത്തിനുമായി സാമ്പത്തിക ശാസ്ത്ര സിദ്ധാന്തങ്ങളിലെ വിവിധ മേഖലകളില് എക്കണോമെട്രിക്സിന്റെ പ്രായോഗികത കൈവരുത്തുന്നു.
എക്കണോമെട്രിക്സിന്റെ രീതിശാസ്ത്രം (Methodology). എക്കണോമെട്രിക്സ് രീതിശാസ്ത്രത്തെ നാലു ഘട്ടങ്ങളായി തരംതിരിക്കാം.
നിര്ദേശം (Specification)
എക്കണോമെട്രിക്സ് പഠനത്തിന്റെ ആദ്യഘട്ടം പഠിക്കേണ്ടുന്ന വസ്തുതയുടെ സ്വഭാവം എന്തെന്നു മനസ്സിലാക്കുന്നു. ഉദാഹരണത്തിന് രാജ്യത്തിന്റെ ഇറക്കുമതി നിര്ണയിക്കുന്ന ഘടകങ്ങളെക്കുറിച്ച് പഠിക്കണമെന്നിരിക്കട്ടെ. ഇതിനുവേണ്ടി, ഇറക്കുമതി ചോദന സമവാക്യം രൂപപ്പെടുത്തുന്നു. ഈ ചോദന സമവാക്യത്തില് ഉള്ക്കൊള്ളിക്കേണ്ട പ്രധാനഘടകങ്ങള് ഇറക്കുമതി ചെയ്യുന്ന സാധനങ്ങള് വാങ്ങുന്നവരുടെ വരുമാനം, സാധനത്തിന്റെ വില, സാധനത്തിനു പകരം വയ്ക്കാവുന്ന സാധനത്തിന്റെ വില എന്നിവയാണ്. ഇപ്രകാരം ഇറക്കുമതി ചോദനത്തെ താഴെപ്പറയുന്ന സമവാക്യത്തില് കാണിക്കാം.
M = F (Y, Pm, PD)
M= ഇറക്കുമതിചെയ്യേണ്ടുന്ന വസ്തുവിന്റെ അളവ്
Y= വാങ്ങുന്നയാളിന്റെ വരുമാനം
Pm= ഇറക്കുമതിസാധനത്തിന്റെ വില
PD= ഇറക്കുമതിസാധനത്തിന് പകരംവയ്ക്കാവുന്ന സാധനത്തിന്റെ വില.
പ്രസ്തുത ഫലനബന്ധത്തില് (functional relation) M-ഉം Yഉം തമ്മില് ഒരേ ദിശാബന്ധവും, M-ഉം PDയും തമ്മില് വിപരീതദിശാബന്ധവുമാണുള്ളത്. ചോദനത്തെയും അതിനെ സ്വാധീനിക്കുന്ന ചരങ്ങളെയും ഒരു ലളിതമായ രേഖീയ സമവാക്യത്തില് ഇപ്രകാരം മാറ്റിയെഴുതാം.
M = b0 + b1Y + b2Pm + b3PD
ഇതില് b0, b1, b2, b3 എന്നിവയെ "പരാമീറ്റേഴ്സ്' എന്നു വിളിക്കുന്നു. ഈ സമവാക്യത്തില് b0-യുടെ മൂല്യം സ്ഥിരമായിരിക്കും. സമവാക്യത്തില് ഉള്ക്കൊള്ളിച്ചിരിക്കുന്ന എല്ലാ ഘടകങ്ങളുടെയും മൂല്യം പൂജ്യമാകുന്ന സാഹചര്യത്തില് വരാവുന്ന ഇറക്കുമതി ചോദനമൂല്യമാണ് യ0അര്ഥമാക്കുന്നത്. എന്നാല് b1, b2, b3 എന്നിവ അതാത് വിവരണചരങ്ങളുടെ (explanatory variable) ഗുണോത്തരങ്ങളെ (Co-efficient)സൂചിപ്പിക്കുന്നു. ഉദാഹരണത്തിന് b1അര്ഥമാക്കുന്നത Y-ല് ഉണ്ടാകുന്ന ഒരു ഏകക മാറ്റത്തിന് ഫലമായി M-നുണ്ടാകുന്ന വ്യതിയാനത്തെ സൂചിപ്പിക്കുന്നു.
മുകളില് ഉപയോഗിച്ച സമവാക്യത്തിന്റെ പ്രാവര്ത്തിക രൂപം വിവരങ്ങളുടെ ലഭ്യതയുടെയും അവയുടെ വിശ്വാസ്യതയുടെയും അടിസ്ഥാനത്തില് മാറ്റത്തിന് വിധേയമാണ്. സാധാരണ സാഹചര്യങ്ങളില് പ്രത്യേകിച്ചും സാമ്പത്തിക സാമൂഹിക ചരങ്ങള് തമ്മിലുള്ള പ്രാവര്ത്തികബന്ധം കൃത്യമായി പ്രവചിക്കാന് അസാധ്യമാണ്. ഈ സാഹചര്യത്തില് പ്രവചിക്കാന് പറ്റാത്ത ഘടകങ്ങളുടെ സ്വാധീനം ഗണിത സമവാക്യത്തില് ഉള്പ്പെടുത്താനായി 'U' എന്ന സംജ്ഞ ഉപയോഗിക്കുന്നു. വ്യാഖ്യാനിക്കാന് കഴിയാത്ത ഘടകങ്ങളുടെ സ്വാധീനവും അനിശ്ചിതാവസ്ഥയും 'U'-ല് ഉള്ക്കൊണ്ടിരിക്കുന്നു.
M = b0 + b1Y + b2Pm + b3PD + U
ഇപ്രകാരമുള്ള സമവാക്യങ്ങളെ പ്രവര്ത്തനരീതി സമവാക്യങ്ങള് (Behavioural equations)എന്നുവിളിക്കുന്നു. പ്രവര്ത്തനരീതി സമവാക്യങ്ങളില് അനിശ്ചിതഘടകങ്ങളാല് (Stochastic Element) തീരുമാനിക്കുന്ന 'U' എന്ന ഒരു ഘടകം കൂടിയുണ്ടാകും. സമവാക്യത്തില് ഉള്പ്പെട്ട എല്ലാ ഘടകങ്ങളുടെയും സ്വാധീനം നിര്വചിച്ചശേഷം വരുന്ന ശിഷ്ടമായാണ് (Residual) 'U' നെ കണക്കാക്കുന്നത്. സാമ്പിള് വിവരങ്ങള് ഉപയോഗിച്ച് എക്കണോമെട്രിക്സ് മാതൃകയും അതിനുവേണ്ട ഗണിതസമവാക്യങ്ങളും രൂപപ്പെടുത്തുകയാണെങ്കില് 'U' എന്ന സംജ്ഞയ്ക്കു പകരം 'e' ആണുപയോഗിക്കുന്നത്. 'e' എന്ന സംജ്ഞ അര്ഥമാക്കുന്നത് എക്കണോമെട്രിക്സ് പഠനമാതൃകാനിര്ണയത്തില് വരുന്ന പിശകുകളുടെ ആകെത്തുകയാണ് (error term).
ആകലനം (Estimation)
എക്കണോമെട്രിക്സ് പഠനമാതൃകയുടെ നിര്ദേശമനുസരിച്ച് ആകലനപ്രക്രിയയെ ആശ്രയിച്ചിരിക്കുന്നു. പഠനമാതൃകയുടെ പ്രാചനത്തിന്റെ ഏറ്റവും ശരിയെന്നു ബോധ്യമുള്ള മൂല്യം കണ്ടുപിടിക്കുന്ന പ്രക്രിയയാണ് പൊതുവേ ആകലനപ്രക്രിയകൊണ്ടുദ്ദേശിക്കുന്നത്. ഇങ്ങനെ ലഭിക്കുന്ന മൂല്യത്തെ എസ്റ്റിമേറ്റര് (Estimator) എന്നു വിളിക്കുന്നു. മുന്വിധിരാഹിത്യം (Unbiasedness), കുറഞ്ഞ വ്യതിയാനം (minimum variance) സ്ഥിരത (Consistency) എന്നിവയാണ് എസ്റ്റിമേറ്ററിന്റെ സവിശേഷതകള്.
മൂല്യനിര്ണയത്തിനുവേണ്ടി വ്യാപകമായി ഉപയോഗിക്കുന്ന ഒരു സങ്കേതമാണ് സാധാരണ ന്യൂനതമവര്ഗരീതി (Ordinary Least Squares- OLS). കൂടാതെ ദ്വിഘട്ട ന്യൂനതമവര്ഗരീതി (two stage least square method), ത്രിഘട്ട ന്യൂനതമവര്ഗരീതി (three stage least square method) അപൂര്ണ പരിജ്ഞാന ഉച്ചതമസാധ്യതാരീതി (Limited information maximum likelihood method) പൂര്ണ പരിജ്ഞാന ഉച്ചതമസാധ്യതാരീതി (full information maximum likelihood method) എന്നിവയും ഉപയോഗിക്കാറുണ്ട്.
സിദ്ധാന്തപരിശോധന (Hypothesis Testing)
ആകലനം കഴിഞ്ഞ എക്കണോമെട്രിക്സ് മാതൃകയുടെ ആകലനമൂല്യം (estimates) വിശ്വസനീയമാണോ എന്നു ചില മാനദണ്ഡങ്ങളുടെ വെളിച്ചത്തില് വിലയിരുത്തുന്നു. ഈ വിലയിരുത്തലുകളില്ക്കൂടി പ്രാചനങ്ങളുടെ മൂല്യം സൈദ്ധാന്തികമായി അര്ഥവത്താണോയെന്നും സംഖ്യാവ്യാപനപരമായി സാധ്യതയുള്ളതാണോയെന്നും വിലയിരുത്തുന്നു. പ്രധാനമായും താഴെപ്പറയുന്ന മൂന്നു മാനദണ്ഡങ്ങളാണ് പ്രാചനങ്ങളുടെ കണക്കാക്കപ്പെട്ട മൂല്യം വിലയിരുത്താന് അടിസ്ഥാനമാക്കുന്നത്.
(1) കാരണങ്ങളില് നിന്നും കാര്യങ്ങളെ തെളിയിക്കുന്ന മാനദണ്ഡം (Economic 'a priori') സാമ്പത്തികശാസ്ത്ര സിദ്ധാന്തങ്ങള് വിലയിരുത്താനുപയോഗിക്കുന്നു.
(2) സംഖ്യാശാസ്ത്രമാനദണ്ഡം (statistical crieteria) ഇവിടെ സംഖ്യാശാസ്ത്ര സിദ്ധാന്തങ്ങളെ വിലയിരുത്താനുപയോഗിക്കുന്നു.
(3) എക്കണോമെട്രിക്സ് മാനദണ്ഡം എക്കണോമെട്രിക്സ് തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തിലുള്ളതാണ് ഇവിടത്തെ പരിശോധനാമാര്ഗങ്ങള്. ഇത്തരത്തിലുള്ള പരിശോധനാമാര്ഗങ്ങളില്ക്കൂടി ആകലനമൂല്യത്തില് അത്യാവശ്യം വേണ്ട സവിശേഷതകളായ മുന്വിധിരാഹിത്യം (unbiasedness), സ്ഥിരത (consistency), പര്യാപ്തത (sufficiency) എന്നിവയുണ്ടോ എന്നു സ്ഥാപിക്കുന്നു.
വ്യക്തിഗത പരാമീറ്റേഴ്സിനെ സംബന്ധിച്ച സംഖ്യാശാസ്ത്ര പരിശോധനാമാര്ഗത്തില് പ്രധാനപ്പെട്ട ഒന്നാണ് ടി-ടെസ്റ്റ് (t-test). അതുപോലെ സാധാരണ ഉപയോഗിക്കുന്ന സങ്കേതമായ പ്രതിപരീതി (regression) ആശ്രിതചരങ്ങളുടെ (dependent variable) വ്യതിയാനത്തെ എത്രത്തോളം വ്യാഖ്യാനിക്കുന്നുവെന്നും കണക്കാക്കാം. ഇതിനുവേണ്ടി ഉപയോഗിക്കുന്ന ഒന്നാണ് കോ-എഫിഷ്യന്റ് ഒഫ് ഡിറ്റര്മിനേഷന് (co-efficient of determination അഥവാ R2).
R2= വ്യാഖ്യാനിക്കപ്പെടുന്ന ആശ്രയചരത്തിലുണ്ടാകുന്ന വ്യതിയാനം / ആശ്രയചരത്തിലുണ്ടായ മൊത്തം വ്യതിയാനം
R2-ന്റെ മൂല്യം എപ്പോഴും പൂജ്യത്തിനും ഒന്നിനും ഇടയ്ക്കായിരിക്കും.
പ്രവചനം (Forecasting)
ലഭ്യമായ സാമ്പിള് വിവരങ്ങളുടെ പരിധിക്കപ്പുറത്ത് ചില ചരങ്ങളുടെ മൂല്യം പ്രവചിക്കാനായി എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിക്കുന്നു. വ്യത്യസ്ത സാമ്പത്തികനയങ്ങളുടെ തെരഞ്ഞെടുപ്പും വിലയിരുത്തലുമായി പ്രവചനം ബന്ധപ്പെട്ടിരിക്കുന്നു. ഉചിതമായ ആശ്രിതചരത്തിന്റെ യഥാര്ഥമൂല്യവും എക്കണോമെട്രിക്സ് മാതൃകയിലൂടെ ലഭിച്ച മൂല്യവും തമ്മിലുള്ള അന്തരം താരതമ്യം ചെയ്യുകയും സംഖ്യാശാസ്ത്ര പരിശോധനയ്ക്ക് വിധേയമാക്കുകയും ചെയ്യുന്നു. ഇവ തമ്മിലുള്ള അന്തരം ഗണ്യമാണെങ്കില് ഉപയോഗിച്ച പഠനമാതൃകയ്ക്ക് പ്രവചനശേഷിയില്ലെന്ന നിഗമനത്തിലെത്തുന്നു.
മുമ്പ് പ്രതിപാദിച്ച രേഖീയപ്രാവര്ത്തിക രൂപത്തിലുള്ള എക്കണോമെട്രിക്സ് പഠനമാതൃക കൂടാതെ മറ്റു തരത്തിലുള്ള പ്രാവര്ത്തിക രൂപങ്ങളുമുണ്ട്. ഇതില് പ്രധാനപ്പെട്ടവ
(1) ഡബിള് ലോഗ്/ലോഗ് ലീനിയര്/കോണ്സ്റ്റന്റ് ഇലാസ്റ്റിസിറ്റി മാതൃകകള് (Double log/log linear/constant elasticity).
(2) സെമിലോഗ് (Semilog) മാതൃകകള്
(3) റെസിപ്രാക്കല് ട്രാന്സ്ഫോര്മേഷഷന് അഥവാ ഹൈപ്പര്ബോളിക് (Reciprocal transformation or hyperbolic) മാതൃകകള്.
കാലം (time) ഒരു പ്രവണതാചരമായി ഉപയോഗിക്കുമ്പോള് ഉപയുക്തമാക്കാവുന്ന പ്രാവര്ത്തിക മാതൃകകളില് പ്രധാനപ്പെട്ടവ (1) രേഖീയ പ്രവണതാ സമവാക്യം (linear trend equation), (2) എക്സ്പൊണെന്ഷ്യല് പ്രവണതാ സമവാക്യം (exponential trend equation) (3) ലോജിസ്റ്റിക് പ്രവണത സമവാക്യം (Logistic trend equation) എന്നിവയാണ്.
എക്കണോമെട്രിക്സ് പഠനമാതൃകകള്. എക്കണോമെട്രിക്സ് പഠനമാതൃകകളെ ഏകസമവാക്യ മാതൃകകള് എന്നും ബഹുസമവാക്യ മാതൃകകള് എന്നും തരംതിരിക്കാം.
ഏകസമവാക്യ മാതൃകകള്. പ്രസ്തുത മാതൃകകളില് ഒരു ആശ്രിതചരവും (dependent variables)ഒന്നോ അതിലധികമോ സ്വതന്ത്ര വിവരണ ചരങ്ങളും കാണാം. ഒറ്റ വിവരണ ചരമുള്ള പ്രതിപരീതി (regression) മാതൃകകളെ ലളിത പ്രതിപരീതി മാതൃകകളെന്നും ഒന്നില്ക്കൂടുതല് വിവരണാത്മക ചരങ്ങളുള്ള പ്രതിപരീതി മാതൃകകളെ ബഹു പ്രതിപരീതി മാതൃകകളെന്നും വിളിക്കുന്നു. സാധാരണ ഉപയോഗിക്കുന്ന പ്രതിപരീതി സങ്കേതം ക്ലാസ്സിക്കല് ന്യൂനതമവര്ഗ (Classical least square) രീതിയാണ്. ഈ സങ്കേതം വഴി വിവരണ ചരങ്ങളുടെ യഥാര്ഥമൂല്യവും ആകലനമൂല്യവും തമ്മിലുള്ള അന്തരം ഏറ്റവുമധികം ലഘൂകരിക്കുന്നു. മറ്റൊരു സങ്കേതമായ ഉച്ചതമസാധ്യതാരീതിയും (Maximum likelihood estimation) ഉപയോഗിച്ചുവരുന്നു.
ഏകസമവാക്യ പ്രതിപരീതി (Single Equation regression) മാതൃകകള് പ്രധാനമായും സാമ്പത്തിക ചരങ്ങളുടെ പ്രവണതയെ പ്രവചിക്കാന് ഉപയോഗിക്കുന്നു. ചരങ്ങളുടെ മൂല്യപ്രവചനം ഏകസംഖ്യാപ്രവചനമെന്നും (Point forecast) പരിധിപ്രവചനമെന്നും (Interval forecast) രണ്ടായി തരംതിരിക്കാം. ഇതില് രണ്ടാമത്തെ രീതിയില് പ്രവചനമൂല്യം ഒരു പരിധിക്കുള്ളിലായിരിക്കും. മൂല്യപ്രവചനത്തെ സോപാധിക(conditional)മെന്നും നിരുപാധിക(unconditional)മെന്നും തരംതിരിക്കാം. സോപാധിക മൂല്യപ്രവചനത്തില് ചില വിവരണ ചരങ്ങളുടെ മൂല്യം ലഭ്യമല്ലാത്തിനാല് ആശ്രിതചരങ്ങളുടെ മൂല്യം ഊഹിച്ചെടുക്കണം. എന്നാല് നിരുപാധിക മൂല്യപ്രവചനത്തില് എല്ലാ വിവരണചരങ്ങളുടെയും മൂല്യം കൃത്യമായും ലഭ്യമായതില് മൂല്യപ്രവചനം സുനിശ്ചിതമായി നടത്താം. നിര്വചനപിഴ (Forecast error) എറ്റവും കുറഞ്ഞിരിക്കുന്നതാണ് നല്ല പ്രവചനസങ്കേതത്തിന്റെ സവിശേഷത. ഏകസമവാക്യ മാതൃകകളില് സാധാരണ ന്യൂനതമവര്ഗരീതി (Ordinary least square-OLS) സങ്കേതം നിര്വചനപിഴ ഏറ്റവുമധികം കുറച്ചുകൊണ്ട് ചരങ്ങളുടെ മൂല്യം കണക്കാക്കുന്നു. ഇതുകൂടാതെ വിതരണവിളംബ(Distributed log) മാതൃകകളും അവ ഉപയോഗിച്ചുകൊണ്ടുള്ള ആകലനവും ഏകസമവാക്യ മാതൃകയില് ഉള്പ്പെടുന്നു. രണ്ട് പ്രധാനപ്പെട്ട വിളംബ(lag) മാതൃകകളായ ജ്യാമിതീയവിളംബവും (Geomatric lag) ബഹുപദവിളംബ (Polynomial lag) മാതൃകകളുമാണ് സാധാരണ ഉപയോഗിക്കുന്നത്. ജ്യാമിതീയവിളംബ മാതൃകകളില് വിളംബ വിവരണചരങ്ങള്ക്ക് (lagged explanatory variables) കൊടുക്കുന്ന മൂല്യം (weights) ധനസംഖ്യ (positive number) ആയിരിക്കും. അത് സമയാനുബന്ധമായി ജ്യാമിതീയ അളവില് കുറയുമെന്നും അനുമാനിക്കുന്നു.
ഏകസമവാക്യമാതൃകകളുടെ പരിധിയില് വരുന്ന വേറൊരു വിഷയമാണ് കാരണ പരിശോധന (casuality test). സാമ്പത്തികശാസ്ത്രത്തില് പൊതുവെയുള്ള ഒരു പ്രശ്നം ഒരു ചരത്തിലുണ്ടാകുന്ന വ്യതിയാനം മറ്റൊരു ചരത്തിന്റെ മാറ്റത്തിന് ഹേതുവാകുന്നുണ്ടോയെന്ന് നിര്ണയിക്കുന്നതാണ്. സാമ്പത്തിക ശാസ്ത്രജ്ഞന്മാരായ ഗ്രാന്ജറും (Granger) സിംസും (Sims) രൂപപ്പെടുത്തിയ കാരണപരിശോധന (casuality test) ഉപയോഗിച്ച് ഇതു പരിഹരിക്കാവുന്നതാണ്. പാനല് ഡേറ്റ ഉപയോഗിച്ചുള്ള ഏകസമവാക്യമാതൃകകള്. ഒരുകൂട്ടം സ്ഥിരമായ വ്യക്തിഗത സാമ്പിളുകള് ഒരു ദീര്ഘകാലത്തേക്ക് ശേഖരിക്കുന്ന ദത്തങ്ങള്ക്കാണ് പാനല്ഡേറ്റയെന്നു പറയുന്നത്. ഇതിന്റെ ഫലമായി വ്യക്തിഗത സാമ്പിളുകളെ സംബന്ധിച്ച് പലതരത്തിലുള്ള നിരീക്ഷണവിവരങ്ങള് ശേഖരിക്കാന് സാധിക്കുന്നു. ഇത്തരത്തില് കാലാനുസരണശ്രണി വിവരങ്ങളും (time series data) പരിച്ഛേദവിവരങ്ങളും (cross section data) സമന്വയിപ്പിച്ചാണ് പാനല്ഡേറ്റ ഉണ്ടാക്കുന്നത്.
പാനല്ഡേറ്റ ഉപയോഗിച്ചുകൊണ്ട് എക്കണോമെട്രിക്സ് പഠനങ്ങള്ക്ക് താഴെപ്പറയുന്ന സങ്കേതങ്ങളാണ് ഉപയോഗിക്കുന്നത്.
(1) കാലശ്രണി (time series) ദത്തങ്ങളും പരിച്ഛേദ(cross section)ദത്തങ്ങളും സംയോജിപ്പിച്ച് സാധാരണ ന്യൂനതമവര്ഗ(ordinary leas square) സങ്കേതം.
(2) പകരത്തിനുള്ള ചരങ്ങള് (dummy variables).
(3) പരിച്ഛേദ ദത്തങ്ങളുടെയും കാലശ്രണി ദത്തങ്ങളുടെയും വ്യതിയാനം ഉള്ക്കൊള്ളിച്ചുകൊണ്ടുള്ള യാദൃച്ഛിക സ്വാധീനമാതൃക (Random effect model) ഉപയോഗിച്ച്.
അരേഖീയ ഏകസമവാക്യ മൂല്യനിര്ണയം (Non-linear single equation estimation).
ഇത്തരത്തിലുള്ള അരേഖീയ സമവാക്യങ്ങളെ രേഖാസമവാക്യമാക്കാന് സാധിക്കുകയില്ല. ഈ സമവാക്യങ്ങളുടെ ഉത്തരം കണ്ടുപിടിക്കാന് വിവിധതരത്തിലുള്ള എക്കണോമെട്രിക്സ് സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നു.
ഏകസമവാക്യഗുണാത്മക തെരഞ്ഞെടുക്കല് മാതൃക (Single Equatgion Qualitative Choice Model). ഇവിടെ ആശ്രിതചരങ്ങള് രണ്ടോ അതിലധികമോ ഗുണാത്മക തെരഞ്ഞെടുക്കല് (Qualitative Choice) ഉള്ക്കൊള്ളുന്നതായിരിക്കും. ഇപ്രകാരമുള്ള മാതൃകകളുടെ ലക്ഷ്യം ഒരു പ്രത്യേകസാഹചര്യത്തില് ഒരു വ്യക്തി കൈക്കൊണ്ടേക്കാവുന്ന തെരഞ്ഞെടുക്കലിന്റെ സംഭവ്യത(probability) മനസ്സിലാക്കുകയാണ്. ഗുണാത്മക തെരഞ്ഞെടുക്കല് മാതൃകയുടെ ഗുണോത്തരമൂല്യം (coefficient) കണക്കാക്കാനായി പ്രധാനമായും ഉപയോഗിക്കുന്ന മാതൃകകള് രേഖീയസംഭവ്യത (Linear Probability) പ്രാബിത് (Probit) ലോജിത് (logit)എന്നിവയാണ്.
ബഹുസമവാക്യ മാതൃകകള് (Multi equation Models).ഒരു കൂട്ടം ചരങ്ങളുടെ പരസ്പരബന്ധം പഠിക്കുന്നതിന് ബഹുസമവാക്യ മാതൃകകള് സഹായിക്കുന്നു. പലപ്പോഴും ഒരു കൂട്ടം ബഹുസമ പരസ്പരബന്ധവാക്യങ്ങളുടെ (simultaneous interdependent equation)ശ്രണിയിലൂടെയാണ് മിക്ക വ്യാപാര സാമ്പത്തിക മാതൃകകളുടെയും പ്രക്രിയ പ്രതിനിധാനം ചെയ്യപ്പെടുന്നത്.
ബഹുസമവാക്യ ശ്രണി (Miscelleneous Equation System). പ്രസ്തുത മാതൃകകള് ഒരുകൂട്ടം സമവാക്യങ്ങള് ഉള്ക്കൊണ്ടിരിക്കും. ഓരോ സമവാക്യവും ഓരോ ചരങ്ങളെ വിശദീകരിക്കാന് ഉപയുക്തമായിരിക്കും. ഉദാഹരണത്തിന് മൂന്നു സമവാക്യങ്ങള് ഉള്ക്കൊള്ളുന്ന പ്രദാന-ചോദന (supply-demand)മാതൃക താഴെപ്പറയുന്ന രീതിയില് വിശദീകരിക്കാം.
ഈ മൂന്ന് സമവാക്യങ്ങളും ചേര്ന്ന് വിപണിവില, ചോദനത്തിന്റെയും പ്രദാനത്തിന്റെയും അളവ് എന്നിവ നിര്ണയിക്കുന്നു. മേല്പറഞ്ഞ മാതൃകയില് QDt , QSt, Pt എന്നിവയുടെ മൂല്യം സമവാക്യങ്ങളുടെ സംവിധാനത്തില് ഉള്ളില്വച്ചുതന്നെ നിര്ണയിക്കപ്പെടുന്നതിനാല് അവ ആന്തരോദ്ഭവ (Endogenous) ചരങ്ങളെന്ന് അറിയപ്പെടുന്നു. എന്നാല് Pt-1, Yt എന്നീ ചരങ്ങളുടെ മൂല്യം സമവാക്യങ്ങളുടെ സംവിധാനത്തിനകത്ത് നിര്ണയിക്കാത്ത മുന്നിര്ണയ (Pre-determined) ചരങ്ങളാണ്. അവ സംവിധാനത്തിലുള്ളിലെ ആന്തരോദ്ഭവചരങ്ങളുടെ ചലനം നിര്ണയിക്കുന്നു. മുകളില് പ്രതിപാദിച്ച മാതൃകയില് Yt എന്ന ചരത്തിന്റെ മൂല്യം പൂര്ണമായും സമവാക്യശ്രണിക്ക് പുറത്ത് നിര്ണയിക്കപ്പെടുന്നതിനാല് അവയെ ബഹുജന്യ ചരങ്ങള് (Exogeneous Variables)എന്നു വിളിക്കുന്നു.
ഒന്നില്ക്കൂടുതല് സമവാക്യങ്ങള് ഒരു മാതൃകയില് നിര്ദേശിക്കുമ്പോള് (യുഗവത് സമവാക്യമാതൃകകള്) സമവാക്യങ്ങളെ തമ്മില് വ്യക്തമായി വേര്തിരിച്ചു മനസ്സിലാക്കത്തക്കവണ്ണം നിര്ദേശിക്കപ്പെടേണ്ടതാണ്. ഉദാ. ചോദന സമവാക്യത്തിലും (demand equation) പ്രദാനസമവാക്യത്തിലും (supply equation) പ്രത്യക്ഷപ്പെടുന്ന ചരങ്ങള് കമ്പോളവിലയും കമ്പോളത്തില് വിറ്റഴിയുന്ന ചരക്കിന്റെ അളവുമാണ്. ഈ രണ്ടു സമവാക്യങ്ങളിലും ഒരേ സെറ്റ് ചരങ്ങള് ഒരുപോലെ പ്രത്യക്ഷപ്പെടുന്നതിനാല് കമ്പോളദത്തം ഉപയോഗിച്ച് ആകലനം ചെയ്യപ്പെടുന്ന അത്തരം ഒരു സമവാക്യം യഥാര്ഥത്തില് ചോദനഫലത്തെയാണോ പ്രദാനഫലത്തെയാണോ പ്രതിനിധാനം ചെയ്യുന്നത് എന്ന് സംശയമുണ്ടാകുന്നു. രണ്ട് സമവാക്യങ്ങളും തമ്മില് വേര്തിരിച്ചറിയുവാന് തക്കവണ്ണം അവ നിര്ദേശിക്കപ്പെടാത്തതിന്റെ തകരാറാണ് ഈ സംശയത്തിന് കാരണം. ഇങ്ങനെയുള്ള സന്ദര്ഭങ്ങള് എക്കണോമെട്രിക്സ് പഠനങ്ങളില് സാധാരണമാണ്. അഭിജ്ഞാനപ്രശ്നം (identification problem) എന്ന് ഇതറിയപ്പെടുന്നു. ബഹുസമവാക്യമാതൃകയുടെ ഒരു പ്രധാനപ്രശ്നം സമവാക്യങ്ങളുടെ തിരിച്ചറിയലാണ്. ചില സമവാക്യങ്ങള് കൃത്യമായി തിരിച്ചറിയാം ചിലവ കുറച്ചുമാത്രം തിരിച്ചറിയാം ചിലത് ആവശ്യത്തിലധികം തിരിച്ചറിയാം. സമവാക്യത്തില് പ്രതിപാദിച്ചിരിക്കുന്ന ഓരോ ചരത്തിന്റെയും അദ്വീതമൂല്യം കണക്കാക്കണമെങ്കില് ആ സമവാക്യത്തെ കൃത്യമായി തിരിച്ചറിയാം എന്നു പറയാം. അതേസമയം ഒരേ ചരത്തിന് ഒന്നിലധികം മൂല്യം ലഭിക്കുകയാണെങ്കില് ആ സമവാക്യം ആവശ്യത്തിലധികം തിരിച്ചറിയപ്പെട്ടവയെന്നു പറയാം. എന്നാല് ചരങ്ങളുടെ മൂല്യം കണ്ടുപിടിക്കാന് സാധിക്കാത്ത സമവാക്യങ്ങളെ തിരിച്ചറിയാന് സാധിക്കാത്ത (unidentified) സമവാക്യങ്ങളെന്നു പറയുന്നു. അനുകരണമാതൃക (Simulation Models). പൊതുനയരൂപീകരണ രൂപകല്പനയ്ക്കായി പൊതുവേ ഉപയോഗിക്കുന്ന അനുകരണ മാതൃക ആണ് ബഹു സമവാക്യമാതൃകകള് ഉപയോഗിക്കുന്ന വേറൊരു മേഖല. പ്രായോഗിക ജീവിതത്തില് അനുഭവവേദ്യമായവയും അല്ലാത്തവയുമായ സംഗതിയെ പ്രതിനിധാനം ചെയ്യുന്ന ഒരു കൂട്ടം ബഹുസമവാക്യത്തിന് ഗണിതപരമായ മൂല്യനിര്ണയം നടത്തുന്ന പ്രക്രിയയാണ് അനുകരണം എന്നര്ഥമാക്കുന്നത്. ഉദാഹരണത്തിന് അതീവ ലളിതമായ ഒരു സ്ഥൂലസാമ്പത്തിക ശാസ്ത്ര സമവാക്യം നോക്കുക.
ഇതില് Ct, It,Y എന്നിവ ആന്തരോദ്ഭവചരങ്ങളും Gt ബഹുജന്യചരവുമാണ് a1, a2, a3, b1, b2, b3 എന്നീ പരാമീറ്റേഴ്സിന്റെ മൂല്യം നല്കിയിരിക്കുകയും ഇയേുടെയും It യുടെയും തുടക്കത്തിലുള്ള മൂല്യം നിര്ദേശിക്കുകയും യുടെ ഒരു സമയപാത നിര്ണയിക്കുകയും ചെയ്താല് Ct, It, Yt എന്നിവയുടെ മൂല്യം ഒരുമിച്ച് കണ്ടെത്താന് കഴിയും.
കാലശ്രണി (Time series) മാതൃകകള്. ഇവിടെ ഒരു ചരത്തിന്റെ മൂല്യം അതിന്റെ തന്നെ ഭൂതകാലമൂല്യവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ഭൂതകാലമൂല്യങ്ങളില്ക്കൂടി ചരങ്ങളുടെ ഭാവികാലമൂല്യങ്ങള് കണക്കാക്കാന് സാധിക്കുന്നു. എല്ലാ കാലശ്രണി മാതൃകകളും ഏകസമവാക്യ പ്രതിപരീതി (single equation regression) മാതൃകളാണ്. ഇവയെ പക്ഷേ നമുക്ക് നിര്ണയനകാലശ്രണി മാതൃക(deterministic time series models) എന്നും അനിശ്ചിതകാലശ്രണി(stochastic time series) മാതൃകകളെന്നും രണ്ടായി തിരിക്കാം. ഇതില് ആദ്യത്തേത് ഏകസംഖ്യാപ്രവചനവും (Point estimate) രണ്ടാമത്തേത് പ്രവചനമൂല്യവും ഒരു വിശ്വസനീയ പരിധിക്കുള്ളില് നടത്തുന്നു.
അനിശ്ചിതകാലശ്രണി മാതൃകകളില് പ്രധാനപ്പെട്ട ഒന്നാണ് രേഖീയ അനിശ്ചിതകാലശ്രണി മാതൃക (Linear Stochastic Time Series). അനിശ്ചിതാവസ്ഥയെ ഉള്ക്കൊണ്ട് പഠനവിധേയമാക്കുന്ന സംഗതിയെപ്പറ്റി പഠിക്കാനായി പ്രധാനമായും രണ്ടു സങ്കേതങ്ങള് ഉപയോഗിക്കുന്നു. അവ ഓട്ടോ റിഗ്രഷന് (Auto Regression) രീതിയും മൂവിങ് ആവറേജ് (Moving average) രീതിയുമാണ്. ഈ രണ്ടുരീതികളും യോജിപ്പിച്ചുള്ള മിശ്രണരീതിയും അവലംബിച്ചു കാണുന്നുണ്ട്. ഏതു സങ്കേതത്തിലും മൂന്നുഘട്ടങ്ങളുണ്ട്.
ഘട്ടം 1: തിരിച്ചറിയല് (identification). ഇവിടെ ഉപയോഗിക്കുന്ന കാലശ്രണി രൂപത്തിലുള്ള വിവരങ്ങളുടെ സ്വഭാവസമത്വം അളക്കുന്നു.
ഘട്ടം 2: ആകലനം. ഈ ഘട്ടത്തില് മാതൃകകളിലെ പരാമീറ്റേഴ്സിന്റെ മൂല്യം കണക്കാക്കുന്നു.
ഘട്ടം 3: പ്രശ്നനിദാനമായ പരിശോധന (diagnostic checking) ഇതില്ക്കൂടി ഇതുവരെ ആവര്ത്തിച്ചത് ശരിയാണോയെന്നു സ്വീകരിച്ച് മാതൃക ഉപയോഗമുള്ളതാക്കാന് യോഗ്യമാണോ എന്നും പഠിക്കുന്നു. ഉപയോഗിക്കുന്ന മാതൃകകളുടെ പരാമീറ്റര് കാര്യക്ഷമത വര്ധിപ്പിക്കാനാണിതു ചെയ്യുന്നത്.
എക്കണോമെട്രിക്സ് മാതൃകകളുടെ പ്രായോഗികത. സാമ്പത്തികശാസ്ത്രത്തിന്റെ പല മേഖലകളിലും വിഷയങ്ങളിലും വളരെ വിപുലമായി ഇത്തരം മാതൃകകള് ഉപയോഗിച്ചുവരുന്നു. ഇവയില് ചില പ്രധാനപ്പെട്ട മേഖലകള് ഉപഭോഗം, നിക്ഷേപം, ചോദനവിശകലനം, ഉത്പാദനവിശകലനം, ധനകാര്യം, അന്താരാഷ്ട്ര വാണിജ്യം എന്നിവയാണ്.
ഉപഭോഗസിദ്ധാന്തങ്ങളും എക്കണോമെട്രിക്സ് മാതൃകകളും. ഉപഭോഗസിദ്ധാന്തങ്ങളുടെ നിര്ദേശത്തെ വിശദീകരിക്കാനും വിവിധതരം ഉപഭോഗസിദ്ധാന്തങ്ങള് പൂര്ണരൂപത്തില് വെളിപ്പെടുത്താനും എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിക്കുന്നു. കെയിന്സ്, മില്റ്റണ് ഫ്രിഡ്മാന്, മോഡിഗ്ലാനി, ഡ്യൂസന്ബെറി എന്നിവരുടെ ഉപഭോഗസിദ്ധാന്തങ്ങള് വിശദീകരിക്കുന്നത് എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചാണ്. ലളിതരൂപത്തില് ഉപഭോഗത്തെ പ്രാവര്ത്തികരീതിയില് ഇങ്ങനെ വിശേഷിപ്പിക്കാം.
C=f(Y)
ഇവിടെ C= ഉപഭോഗവസ്തുവിന്റെ അളവ്
Y = ഉപയോഗിക്കാന് കഴിയുന്ന വരുമാനം (disposable income)
മുകളിലത്തെ പൊതുസമവാക്യത്തില്നിന്നും കെയിന്സിന്റെ ഉപഭോഗമനഃശാസ്ത്ര സിദ്ധാന്തത്തിന്റെ ഉപഭോഗസമവാക്യം ഇങ്ങനെ എഴുതാം.
C=a+bY+U
ഇവിടെ 'a' എന്നാല് ഏറ്റവും കുറഞ്ഞ വരുമാനമില്ലാത്ത അവസ്ഥയില്പ്പോലും ജീവിക്കാന് ആവശ്യമായ ഉപഭോഗം. 'b' സീമാന്ത ഉപഭോഗപ്രവണതയെ (marginal propensity to consume) സൂചിപ്പിക്കുന്നു. 'u' എന്നാല് അനിശ്ചിതഘടകങ്ങളുടെ സ്വാധീനം
ജെയിംസ് ന്യൂസന്ബറിയുടെ ആപേക്ഷിക ഉപഭോഗസിദ്ധാന്തം ഇപ്രകാരം എഴുതാം.
C = a + bYt + cYmax + Ut
ഇതില് Yt= നിലവിലുള്ള വരുമാന അളവ്
Ymax= ഭൂതകാലത്തെ ഏറ്റവും കൂടിയ വരുമാനം 'b', 'c', Yt യോടും Ymax-നോടും ചേര്ന്ന ഗുണോത്തരങ്ങളുടെ മൂല്യം.
മില്റ്റണ് ഫ്രീഡ്മാന്റെ സ്ഥിരവരുമാന ഉപഭോഗസിദ്ധാന്തത്തെ ഇപ്രകാരം ലളിതവത്കരിക്കാം.
Ct* = α Ypt
ഇതില് Ypt എന്നാല് സ്ഥിരമായി പ്രതീക്ഷിക്കപ്പെടുന്ന വരുമാനയളവ്. ഈ തത്ത്വം അനുസരിച്ച് ഒരു വ്യക്തിയുടെ ഉപഭോഗം അയാള് പ്രതീക്ഷിക്കുന്ന സ്ഥിരവരുമാനത്തിന്റെ അളവിനെ ആശ്രയിച്ചിരിക്കും.
ഇതുപോലെ മോഡിഗ്ലാനി, സ്രംബര്ഗ്, ആന്റോ എന്നിവര് വികസിപ്പിച്ചെടുത്ത ജീവിതചക്ര ഉപഭോഗസിദ്ധാന്തത്തെ ഇങ്ങനെയെഴുതാം.
മുകളില്പ്പറഞ്ഞ സമവാക്യത്തില് 'A' ആസ്തിയെയും 'Yet' ഭോവിയില് വരാവുന്ന വരുമാനത്തിന്റെ വര്ത്തമാനമൂല്യത്തെയും സൂചിപ്പിക്കുന്നു. ഈ സൂത്രവാക്യമനുസരിച്ച് വര്ത്തമാനകാലത്തെ ഒരു വ്യക്തിയുടെ ഉപഭോഗ അളവ് അയാളുടെ ആസ്തിയും വരുമാനവും ശിഷ്ടജീവിതത്തില് അയാള്ക്ക് വന്നുചേരുമെന്ന് പ്രതീക്ഷിക്കുന്ന വരുമാനത്തെയും ആശ്രയിച്ചിരിക്കും.
ഉത്പാദനഫലനവും എക്കണോമെട്രിക്സും. ഉത്പാദനപ്രകിയ വിശദീകരിക്കാന് ഉപയോഗിക്കുന്ന ഉത്പാദന-ഉത്പാദനഘടകബന്ധത്തിനാണ് ഉത്പാദനഫലനം (production function) എന്നു പറയുന്നത്. ഉത്പാദനം അതിനുപയോഗിക്കുന്ന വിവിധവിഭവങ്ങളുമായി പ്രധാനമായും മൂലധനം (Capital) തൊഴില് (labour) ഒരു നിശ്ചിതസാങ്കേതികവിദ്യയുടെ അടിസ്ഥാനത്തില് എങ്ങനെ ഏതു രീതിയില് സന്നിവേശിക്കപ്പെട്ടിരിക്കുന്നു എന്നാണ് ഉത്പാദനഫലനങ്ങള് കാണിക്കുന്നത്. ഉത്പാദനഫലനത്തിന്റെ പൊതുരൂപം ഇങ്ങനെ കാണിക്കാം.
Q = f(X1, X2, X3)
ഇതില് Q = ഉത്പാദനം
X1, X2, X3 .....Xn= ഉത്പാദനത്തിനുപയോഗിക്കുന്ന വിവിധതരം ഉത്പാദനഘടകങ്ങള്.
പ്രധാനപ്പെട്ട ഉത്പാദനഫലനരൂപങ്ങള് രേഖീയ(linear), കോബ്-ഡഗ്ലാസ്(Cobb-Douglas) ഉത്പാദനഫലനം, സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത(Constant Elasticity of Sustitution) അസ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (variable elasticity of substitution), ട്രാന്സ് ലോഗ് (Trans log) ഉത്പാദനഫലനം എന്നിവയാണ്.
രേഖീയ ഉത്പാദനഫലനത്തെ ഗണിതാത്മകമായി ഇങ്ങനെ വിവരിക്കാം.
Q = a0 + a1L + a2K
ഇവിടെ Q = ഉത്പാദന അളവ്
L = തൊഴില്ശക്തിയുടെ അളവ്
K= മൂലധനം
a1,a2 എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും ഗുണാത്മകങ്ങളാണ്, ഇവിടെ a1,a2 എന്നിവ തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും സീമാന്ത ഉത്പാദനക്ഷമതയാണ്. a0 എന്ന പദം കൊണ്ടര്ഥമാക്കുന്നത് തൊഴിലും മൂലധനവും ഇല്ലെങ്കില്പ്പോലും മറ്റു ഘടകങ്ങളുടെ പ്രവര്ത്തനഫലമായി ഉണ്ടാകാവുന്ന ഏറ്റവും കുറഞ്ഞ അളവിലുള്ള ഉത്പാദനം. ഈ സമവാക്യത്തില് ഉത്പാദനത്തിന്റെ അളവ് തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും അളവിനനുസരിച്ച് രേഖീയമാതൃകയില് മാറിക്കൊണ്ടിരിക്കും.
ആദ്യമായി ഏറ്റവും പ്രചുരപ്രചാരം നേടിയ ഉത്പാദനഫലനം സൃഷ്ടിച്ചത് കോബ്, ഡഗ്ലസ് എന്നീ രണ്ടു സാമ്പത്തികശാസ്ത്രജ്ഞന്മാരാണ്. ഇന്നത് കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനം എന്നറിയപ്പെടുന്നു. താഴെപ്പറയുന്നതാണ് ഈ ഉത്പാദനഫലനത്തിന്റെ ഗണിതാത്മകരൂപം.
ഇതില് Q ഉത്പാദനത്തെയും L തൊഴിലിനെയും K മൂലധനത്തെയും സൂചിപ്പിക്കുന്നു. ഉത്പാദനഫലനത്തിന്റെ പ്രാചനങ്ങളാണ്. ഇതില് യും യും തൊഴിലിന്റെയും മൂലധനത്തിന്റെയും സീമാന്തഉത്പാദനക്ഷമതയാണ്. "' അര്ഥമാക്കുന്നത് സാങ്കേതികവിദ്യയുടെ മാറ്റം ഉത്പാദനത്തില് ഉണ്ടാക്കുന്ന മാറ്റത്തിന്റെ അളവിനെയാണ്.
അതുകൂടാതെ ഉത്പാദനപ്രക്രിയയിലെ പ്രത്യായനിരക്കിനെയാണ് സൂചിപ്പിക്കുന്നത്. ഒന്നില്ക്കൂടുതലെങ്കില് ഉത്പാദനത്തില് ആരോഹണപ്രത്യായവും ഒന്നില് കുറവാണെങ്കില് അവരോഹണ പ്രത്യായവും ഒന്നായിരുന്നാല് സ്ഥിരപ്രത്യായവും ആണെന്ന് അനുമാനിക്കാം.
കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനത്തിന്റെ കുറവു പരിഹരിക്കുന്നതിന്റെ ഭാഗമായി ആരോ (arrow) തുടങ്ങിയ സാമ്പത്തിക ശാസ്ത്രജ്ഞന്മാര് വികസിപ്പിച്ചെടുത്ത് ഉത്പാദനഫലനമാണ് സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തിക മാതൃക (Constant Elasticity of Substitution-CES) ഇതിന്റെ ഗണനാത്മക പ്രാവൃത്തികരൂപം.
ഇതില് = ഉത്പാദനവും E = തൊഴിലും = മൂലധനവും എന്നിവ പരാമീറ്റേഴ്സാണ്പ്രാചനങ്ങളുമാണ് "'യും ഉത്പാദനഫലനത്തില് മൂലധനത്തിനും തൊഴിലിനുമുള്ള ആനുപാതിക പ്രാധാന്യമൂല്യങ്ങളും എന്നത് പ്രതിസ്ഥാപനപ്രാചനവുമാണ്. കോബ്-ഡഗ്ലസിന്റെയും, സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (CES) ഉത്പാദനഫലനത്തിന്റെ ചുവടുപിടിച്ചുകൊണ്ട് ക്രിസ്റ്റിന്സണ് തുടങ്ങിയവര് വികസിപ്പിച്ചെടുത്ത ഉത്പാദനഫലനമാണ് ട്രാന്സ് ലോഗ് (translog) അഥവാ ട്രാന്സിഡന്ഷ്യല് ലോഗ 'Transidential Logarithmic' ഉത്പാദനഫലനം. ഇതിന്റെ ഗണനാത്മകപ്രാവര്ത്തിക രൂപം താഴെ പറയുന്നവയാണ്.
ഇതില് log Q, ഉത്പാദനത്തിന്റെ ലോഗരിതമൂല്യവും log K, log L എന്നിവ മൂലധനത്തിന്റെയും തൊഴിലിന്റെയും ലോഗരിത മൂല്യങ്ങളുമാണ്.
മുകളില്പ്പറഞ്ഞ ഉത്പാദനഫലനങ്ങളുടെ ഒരു പ്രധാനപ്പെട്ട കുറവായ സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത മാറ്റി അസ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (Variable Elasticity of Substitution-VES) ഉത്പാദനഫലനത്തിനായി ശ്രമങ്ങള് ഏറെ നടന്നു. VES ഉത്പാദനഫലനത്തിന്റെ പ്രധാനമാതൃകകള് വികസിപ്പിച്ചത് ലുവും ഫ്ളെറ്റ്ച്ചറും (Lu and Fletcher, 1968) സാറ്റോയും ഹോഫ്മാനും (Sato and Hofman, 1968), റവാന്കര് (Ravankar, 1971) എന്നിവരാണ്.
ഉത്പാദനഫലനത്തിന്റെ ഒരു ഗണനാത്മക പ്രാവര്ത്തികരൂപമിതാണ്.
നിക്ഷേപവും എക്കണോമെട്രിക്സ് ഉപയോഗവും. മൂലധനശേഖരം വര്ധിക്കുന്നത് ശിഷ്ടനിക്ഷേപം (Net investment) വഴിയാണ്. ശിഷ്ടനിക്ഷേപത്തെ ഗണനാത്മക സമവാക്യത്തില് ഇങ്ങനെ എഴുതാം.
ഇവിടെ Qt എന്നത് കോലഘട്ടത്തെ ഉത്പാദനവും Qt-1,(t-1) കാലഘട്ടത്തെ ഉത്പാദനവുമാണ്. ഈ സമവാക്യം സൂചിപ്പിക്കുന്നതെന്തെന്നാല് അതത് കാലഘട്ടത്തിലെ മൊത്ത നിക്ഷേപം ആ വര്ഷങ്ങളിലെ ഉത്പാദന അളവിനെയും അതിനു തൊട്ടുമുമ്പുള്ള വര്ഷത്തിലെ ഉത്പാദനത്തെയും നിര്ണയിക്കുന്നു. ഈ സമവാക്യത്തിലെ 'b' ആക്സിലറൈസേഷന് (accelerisation) ഗുണാത്മകതയെന്നും 'c' എന്നത് മൊത്തം മൂലധനത്തിനുണ്ടാകുന്ന തേയ്മാനശതമാനവുമാണ്. സാമ്പത്തികശാസ്ത്രത്തില് പ്രത്യേകിച്ചും സ്ഥൂലസാമ്പത്തിക ശാസ്ത്ര പഠനത്തില് വളരെ വിപുലമായ രീതിയില് നിക്ഷേപപഠനങ്ങളില് എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചു വരുന്നു. കെയ്ന്സിന്റെയും ക്ലാസ്സിക്കല്, നവക്ലാസ്സിക്കല് തുടങ്ങിയ ശാഖകളുടെ എക്കണോമെട്രിക്സ് മാതൃകകള് നിക്ഷേപപഠനങ്ങളില് ഉപയോഗിച്ചുവരുന്നു.
നിക്ഷേപമാതൃകകള് പലപ്പോഴും കാലവിളംബ(time lag) ത്തില് നിര്ദേശിക്കുന്നുണ്ട്. നിക്ഷേപഫലനത്തില് വിതരണവിളംബ(റdistribution lag)മുപയോഗിച്ചുകൊണ്ട് സാമ്പത്തികശാസ്ത്രജ്ഞര് സ്വീകരിച്ച കോയെക്(Koyeck)ന്റെ മാതൃക വളരെ പ്രശസ്തമാണ്. ഈ ഫലനം കോയെക് വിളംബം (Koyeck lag) എന്ന് അറിയപ്പെടുന്നു. ഇതില് മൂലധനശേഖരം ജ്യാമതീയവിളംബത്തില് (geomatric lag) ഉത്പാദനവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നതായി തെളിയിക്കുന്നു.
പണം സംബന്ധിച്ച പഠനവും എക്കണോമെട്രിക്സും. പണം സംബന്ധിയായ സാമ്പത്തികശാസ്ത്ര പഠനത്തില് എക്കണോമെട്രിക്സ് മാതൃക ഉപയോഗിക്കുന്ന ഒരു പ്രധാന മേഖലയാണ് പണത്തിന്റെ ചോദനനിര്ദേശം. പണചോദനത്തിന്റെ പൊതുനിര്ദേശം ഗണനാത്മകരൂപത്തില്
Md = aYP + b(R)WP
ഇതില് Md എന്നത് പണത്തിന്റെ ചോദനയളവും Y എന്നത് യഥാര്ഥ വരുമാനവും P കമ്പോള പൊതുവിലയും W യഥാര്ഥ ധനത്തിന്റെ അളവും R പ്രതീക്ഷിത പലിശനിരക്കുമാണ്. പണത്തിന്റെ ചോദനം പ്രധാനമായും ദൈനംദിന ക്രയവിക്രയത്തിനും അനിശ്ചിതാവസ്ഥയെ മറികടക്കാനുള്ള കരുതലായും, ഊഹക്കച്ചവടത്തിനുമായിരിക്കും. അതുപോലെ ഇവിടെ ധനം പണരൂപത്തിലും മറ്റു സ്വത്തായിട്ടും കൈവശം വയ്ക്കുന്നു.
പണചോദനത്തിന്റെ ഫലനത്തിന്റെ ഘടനയെക്കുറിച്ച് പല സാമ്പത്തികശാസ്ത്ര ചിന്താവിഭാഗങ്ങളും വ്യക്തികളും വിശദമായി പ്രതിപാദിച്ചിട്ടുണ്ടെങ്കിലും മില്ട്ടണ് ഫ്രഡ്മാന്റെ പണചോദനത്തിന്റെ സിദ്ധാന്തം പ്രശസ്തമാണ്. മില്ട്ടണ് ഫ്രഡ്മാന് താഴെക്കൊടുത്തിരിക്കുന്ന സമവാക്യത്തിലൂടെ പണചോദനത്തെ വിശകലനം ചെയ്യുന്നു.
ഇവിടെ ദൈനംദിനാവശ്യത്തിലധികം വരുന്ന പണത്തിനെ ഒന്നുകില് സര്ക്കാരിന്റെ കടപ്പത്രത്തിലോ അല്ലെങ്കില് ഓഹരികളിലോ നിക്ഷേപിക്കുമെന്ന് അനുമാനിക്കുന്നു.
ചോദനപഠനവും എക്കണോമെട്രിക്സും. ആദ്യകാല എക്കണോമെട്രിക്സ് പഠനങ്ങളില് ഏറിയകൂറും ഈ വിഭാഗത്തില്പ്പെടുന്നവയാണ്. ചോദനപഠനത്തിന്റെ പ്രധാനവിഷയം ഒരു ഉപഭോക്താവിന് ഒരു വസ്തുവിനുണ്ടാകുന്ന ചോദനം ഏതൊക്കെ ചരങ്ങളുടെ മാറ്റവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു എന്നതാണ്. ഏറ്റവും ലളിതമായ സങ്കല്പത്തില് ഒരു സാധനത്തിന്റെ ചോദനം ആ സാധനത്തിന്റെ വിലയും വ്യക്തിയുടെ വരുമാനവുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. ചോദനമെന്ന ആശ്രിതചരത്തെയും അതിനെ നിര്ണയിക്കുന്ന സ്വതന്ത്രചരങ്ങളായ സാധനവിലയെയും വ്യക്തിവരുമാനത്തെയും ചോദനസമവാക്യത്തിലൂടെ വ്യക്തമാക്കാം. ചോദന സമവാക്യത്തിന്റെ വികസനം പ്രധാനമായും സ്റ്റോണ് (stone, 1954) വികസിപ്പിച്ചെടുത്ത രേഖീയ ചെലവ് വ്യവസ്ഥ (Linear expenditure system)യിലും ഹൊതാക്കര് (Hothakker, 1965) വികസിപ്പിച്ചെടുത്ത ലോഗരിത രേഖാ (log-linear) അഥവാ സ്ഥിര ഇലാസ്തികത ചോദനവ്യവസ്ഥ(Constant Elasticity of Demand system)യുമായി ബന്ധപ്പെട്ടിരിക്കുന്നു.
മുകളില് സൂചിപ്പിച്ച രണ്ടു സമവാക്യങ്ങളും ന്യൂനതമവര്ഗനിയമം (Least Square Method)അനുസരിച്ച് ആകലനം ചെയ്യപ്പെടാം. ഒന്നാമത്തെ സമവാക്യമനുസരിച്ച് വരുമാനം ഒരു ഏകകം കൂടുമ്പോള് ചോദനം 'b'ഏകകം കൂടുമെന്നും വില ഒരു ഏകകം കൂടുമ്പോള് ചോദനം 'c' ഏകകം കുറയുമെന്നും കാണാം. ഇവിടെ ചോദനവും വരുമാനവും തമ്മില് ധനബന്ധവും(Positive relation), ചോദനവും വിലയും തമ്മില് ഋണബന്ധവും(Negative relation) ഉണ്ടെന്നു സങ്കല്പിക്കുന്നു. എന്നാല് രണ്ടാമത്തെ ലോഗരിത രേഖീയ സമവാക്യമനുസരിച്ച് വരുമാനം ഒരു ശതമാനം വര്ധിച്ചാല് ചോദനം 'b' ഏകകം കൂടുമെന്നും വില ഒരു ശതമാനം കൂടുമ്പോള് ചോദനം 'c' ഏകകം കുറയുമെന്നും അനുമാനിക്കുന്നു. രണ്ടാമത്തെ സമവാക്യം ഉപയോഗിക്കുകയാണെങ്കില് 'b' വരുമാന ഇലാസ്തികതയും (Income Elasticity) 'c' വില ഇലാസ്തികതയും(Price Elasticity) ആണ്. എന്നാല് ആദ്യത്തെ ഫലനമായ രേഖീയ സമവാക്യമാണ് ഉപയോഗിക്കുന്നതെങ്കില് വരുമാന ഇലാസ്തികത Yb/D എന്നും വില ഇലാസ്തികത Pc/D എന്നും കണക്കാക്കാം. സാധാരണ ചരങ്ങളെ സംബന്ധിച്ചിടത്തോളം വില ഇലാസ്തികത ഋണസംഖ്യയും(Negative Number) വരുമാന ഇലാസ്തികത ധനസംഖ്യയും(Positive Number) ആയിരിക്കും.
ഇന്ത്യന് പഠനങ്ങളില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. ഇന്ത്യയില് എക്കണോമെട്രിക്സ് പഠനങ്ങള് കൃഷി, വ്യവസായം, ധനസാമ്പത്തികവ്യവസ്ഥ, ചോദനവിശകലനം, അന്താരാഷ്ട്ര വാണിജ്യം തുടങ്ങി അനേകം മേഖലകളില് വ്യാപകമായി ഉപയോഗിച്ചുവരുന്നു.
കാര്ഷികസമ്പദ്ശാസ്ത്രത്തില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. കാര്ഷികമേഖല ഇന്ത്യയില് വളരെ ആഴത്തില് പ്രായോഗിക ഗവേഷണപഠനം നടന്ന ഒരു മേഖലയാണ്. പല പഠനങ്ങളും കാലശ്രണിദത്തവും (Time series data) പരിച്ഛേദദത്തവും (Cross section data) ഉപയോഗിച്ച് പല തരത്തിലുള്ള എക്കണോമെട്രിക്സ് മാതൃകകള് ഉപയോഗിച്ചിരുന്നു. എന്നിരുന്നാലും മിക്ക പഠനങ്ങളിലും ഇത്തരത്തിലുള്ള എക്കണോമെട്രിക്സ് മാതൃകയുടെ ഉപയോഗത്തിന് ചില പരിമിതികള് ഉണ്ടായിരുന്നു. പല എക്കണോമെട്രിക്സ് സങ്കേതങ്ങള് ഉപയോഗിക്കുമ്പോള് സാധാരണ അനുമാനങ്ങളായ കമ്പോളമത്സരം, ലാഭേച്ഛ എന്ന ലക്ഷ്യം, മാതൃകാനിര്ദേശത്തില് സ്ഥാപനങ്ങളെയും സര്ക്കാര് നയങ്ങളുടെയും അവഗണന, യോജിക്കാത്ത സംഖ്യാസങ്കേതങ്ങളുടെ ഉപയോഗം, കാര്ഷിക സാങ്കേതിക വിദ്യയെ പ്രതിനിധാനം ചെയ്യാന്വേണ്ടി അനിയന്ത്രിതമായി കോബ്-ഡഗ്ലസ് ഉത്പാദനഫലനം ഉപയോഗിക്കല് എന്നിവ ചിലതുമാത്രമാണ്. മേല്പറഞ്ഞ പരിമിതികള് കാര്ഷികമേഖലയില് ഇന്ത്യയില് നടക്കുന്ന എക്കണോമെട്രിക്സ് പഠനങ്ങളുടെ പ്രായോഗികത കുറയ്ക്കുന്നു.
പ്രായോഗിക ഉത്പാദനഫലനത്തില് വളരെയധികം ബഹുനിവേശ(Multi-input) ഉത്പാദകഫലനങ്ങള് ഉപയോഗിച്ചിരുന്നു. പഠനങ്ങളില്ക്കൂടി പല ആകലനങ്ങള് നടത്തിയിരുന്നു. സാമ്പത്തിക വിവേചന പരിശോധന(Economic Rationality test) അതിര് ഉത്പാദകഫലന(Frontier Production Function)ത്തില് കൂടി കൃഷിയിടത്തെ സാങ്കേതികമേന്മ അളന്നു തിട്ടപ്പെടുത്തല്, കൃഷിയിടത്തെ വ്യാപ്തിയും ഉത്പാദനക്ഷമതയും തമ്മിലുള്ള ബന്ധം, ചെലവിന്റെയും ലാഭത്തിന്റെയും ഫലനങ്ങളുട ആകലനം എന്നിവ അവയില് ചിലതാണ്.
വ്യവസായപഠനത്തിന് എക്കണോമെട്രിക്സിന്റെ പ്രായോഗികത ഇന്ത്യയില്. ഇന്ത്യന് വ്യവസായത്തെപ്പറ്റി എക്കണോമെട്രിക്സ് പഠനങ്ങള് കഴിഞ്ഞ 40 വര്ഷത്തിനുള്ളില് വളരെ നടന്നിരിക്കുന്നു. വ്യവസായ ഗവേഷണത്തിന്റെ പ്രധാനവിഷയങ്ങള് ഉത്പാദനഫലനം, നിക്ഷേപഫലനം, തൊഴില് ചോദനഫലനം, ചെലവ് ഫലനം എന്നിവയാണ്. അടുത്തകാലത്തായി പുതിയ മേഖലകളായ ഗവേഷണവും വികസനവും, ഉത്പാദനശേഷി വിനിയോഗം, വളര്ച്ച, ലാഭം എന്നീ മേഖലകളും പഠനവിധേയമാകുന്നു. ഇന്ത്യന് വ്യവസായപഠനത്തില് ഏറ്റവും പ്രചാരമുള്ള മേഖല ഉത്പാദനഫലനത്തെക്കുറിച്ചാണ്. അതിനുവേണ്ടി ഉപയോഗിക്കുന്ന ദത്തം പ്രധാനമായി കണ്സസ് ഒഫ് മാനുഫാക്ചേര്ഡ് ഇന്ഡസ്ട്രീസ് (Consus of Manufacturing Industries)ഉം ആന്വല് സര്വേ ഒഫ് ഇന്ഡസ്ട്രീസ് (Annual Survey of Industries)മാണ്. മിക്ക പഠനത്തിലും തൊഴിലും മൂലധനവും ഉത്പാദനഘടകമാക്കിയ മൂല്യവര്ധിത ഉത്പാദിതഫലനമാണ് ഉപയോഗിച്ചിട്ടുള്ളത്. പഠനത്തില് ഉപയോഗിക്കപ്പെട്ട പ്രധാന ഉത്പാദനഫലനങ്ങള് കോബ്-ഡഗ്ലസ് (Cobb-Douglas), സ്ഥിരപ്രതിസ്ഥാപന ഇലാസ്തികത (Constant Elasticity of Substitution), ട്രാന്സ്ലോഗ് ഉത്പാദനഫലനങ്ങള് എന്നിവയാണ്. മിക്ക പഠനത്തിലും ന്യൂനതമവര്ഗരീതി (Least Square Method) ഉപയോഗിച്ചാണ് ആകലനം നടത്തിയിരുന്നത്. ഇതുകൂടാതെ മറ്റു ആകലന സങ്കേതങ്ങളായ ജനറലൈസ്ഡ് മെത്തേഡ് ഒഫ് മൊമെന്റ്സ് (Generalised Method of moments), ഇന്സ്ട്രുമെന്റല് വേരിയബ്ള് (Instrumental variable) രീതികളും ഉപയോഗിച്ചിരുന്നു.
പണസമ്പദ്ശാത്രത്തില് എക്കണോമെട്രിക്സിന്റെ ഉപയോഗം. പണസമ്പദ്ശാസ്ത്രത്തില് (Monetary Economics)എക്കണോമെട്രിക്സിന്റെ പ്രധാന ഉപയോഗം പണഫലനത്തിന്റെ (Money Function) ചോദനഫലനവും പ്രദാന ഫലനവും ആകലനം ചെയ്യുന്നതിലാണ്. പണത്തിന്റെ ചോദനത്തില് പ്രധാനപ്പെട്ട ആകലനം യഥാര്ഥ വരുമാനത്തെയും യഥാര്ഥ പലിശനിരക്കിനെയും ബന്ധപ്പെടുത്തി യഥാര്ഥ പണചോദനത്തിന്റെ ഹ്രസ്വദീര്ഘകാല ഇലാസ്തികത കണ്ടെത്താനാണ്. അതു കൂടാതെ പണചോദന ഫലനത്തിന്റെ സ്ഥിരത പണമിഥ്യാബോധം (Money illusion), ഇലാസ്തികതയുടെ ചലനാത്മകക്രമം എന്നിവയും പഠനത്തിന് ആധാരമായിട്ടുണ്ട്.
ചോദനസമ്പ്രദായവും എക്കണോമെട്രിക്സും. എക്കണോമെട്രിക്സിന്റെ ഏറ്റവും പ്രധാനപ്പെട്ട ആദ്യകാല ഉപയോഗം ഉപഭോക്തചോദന ഫലനത്തിന്റെ പ്രയോഗത്തിലാണ്. ചോദനസമവാക്യ ആകലനത്തില് രണ്ട് പ്രധാന സമീപനങ്ങളാണ് സ്വീകരിച്ചിരുന്നത്. ഒരു പ്രത്യേക വസ്തുവിന്റെയോ ഒരു കൂട്ടം വസ്തുവിന്റെയോ ചോദന സമവാക്യം ആകലനം ചെയ്യുകയാണ് ആദ്യകാല സമീപനത്തിലൂടെ ചെയ്തിരുന്നത്. രണ്ടാമത്തെ, ഈ അടുത്തകാലത്തായി വികസിപ്പിച്ച സമീപനത്തില് ഓരോ കൂട്ടം സാധനങ്ങളുടെയും ചോദനസമവാക്യങ്ങള് ഒരുമിച്ച് മൊത്തചോദന സമ്പ്രദായ (Complete demand system) ആകലനം ചെയ്യുന്നു. രണ്ടാമത്തെ സമീപനം താത്ത്വികമായി മുന്ഗണന അര്ഹിക്കുന്നുണ്ടെങ്കിലും ഇതിന്റെ ആകലനത്തില് അതിനൂതനമായ എക്കണോമെട്രിക്സ് സങ്കേതങ്ങളായ പ്രത്യക്ഷത്തില് ബന്ധമില്ലാത്ത പ്രതിപരിതി ആകലനം (Semingly unrelated regression estimation, SURE) അല്ലെങ്കില് ഉച്ചതമസാധ്യതാരീതി (Maximum likelihood method) ഉപയോഗം അനിവാര്യമാക്കിത്തീര്ക്കുന്നു. ഇത്തരം സങ്കേതങ്ങള് രേഖീയമല്ലാത്ത ശുഭപ്രതീക്ഷാ അല്ഗോരിഥം (Nonlinear Optimistics Algorithm) ഉപയോഗിക്കേണ്ടതായി വരികയും ആകലനം സങ്കീര്ണമാകാന് ഇടയാകുകയും ചെയ്യുന്നു.
അന്താരാഷ്ട്രവാണിജ്യവും എക്കണോമെട്രിക്സും. അന്താരാഷ്ട്രവാണിജ്യവുമായി ബന്ധപ്പെട്ട് ധാരാളം എക്കണോമെട്രിക്സ് പഠനങ്ങള് ഇന്ത്യയില് നടത്തിയിരിക്കുന്നു. ഉത്പാദനഘടക സമ്പന്നതാസിദ്ധാന്ത(factor endowment theory)ത്തിന്റെ വിലയിരുത്തല്, വെളിപ്പെടുത്തപ്പെട്ട താരതമ്യ നേട്ടവും (Revealed comparative advantage) അവയെ നിര്ണയിക്കുന്ന ഘടകങ്ങളും മറ്റും അന്താരാഷ്ട്രവാണിജ്യവുമായി ബന്ധപ്പെട്ട പ്രധാന പഠനവിഷയങ്ങളാണ്. അടുത്ത കാലത്തായി വികസിത-വികസ്വര രാജ്യങ്ങളില് പ്രത്യേകിച്ചും ഇന്ത്യയില് വ്യവസായ വാണിജ്യനയങ്ങളില് ഉദാരവത്കരണം വഴിയുള്ള സ്വാധീനം വിപുലമായ രീതിയില് പഠനവിധേയമായിട്ടുണ്ട്.
മേല്സൂചിപ്പിച്ച മേഖലകള് കൂടാതെ സ്ഥൂലസമ്പദ്ഘടന,ദേശീയസംസ്ഥാന ആസൂത്രണ പ്രക്രിയയെപ്പറ്റിയും യുക്തിസഹമായ തിരഞ്ഞെടുപ്പ് സിദ്ധാന്തം, ജനസംഖ്യാ സമ്പദ്ശാസ്ത്രം, വികസന സമ്പദ്ശാസ്ത്രം, സാമ്പത്തികചരിത്രം തുടങ്ങിയ മേഖലകളിലെല്ലാം എക്കണോമെട്രിക്സിന്റെ രീതിശാസ്ത്രം ഉപയോഗിച്ചുവരുന്നു. സ്ഥൂല-സൂക്ഷ്മ സാമ്പത്തിക പ്രക്രിയകളെക്കുറിച്ച് ഏക്കണോമെട്രിക്സ് അപഗ്രഥനത്തിലൂടെ ലഭ്യമാകുന്ന പ്രവചനങ്ങളും പ്രവണതാ സൂചനകളും ഗവണ്മെന്റുകളുടെ സാമ്പത്തിക നയരൂപീകരണത്തില് ഗണ്യമായ സ്വാധീനം ചെലുത്തുന്നുണ്ട്.
(ഡോ. വി. നാഗരാജന് നായിഡു)