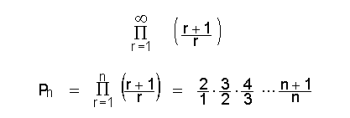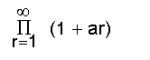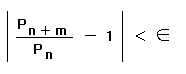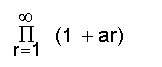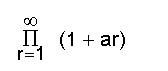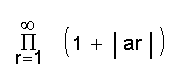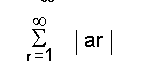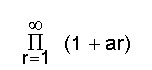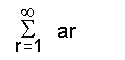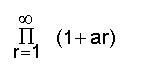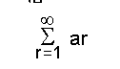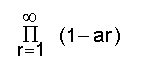This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനന്ത ഗുണിതങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→അനന്ത ഗുണിതങ്ങള്) |
Mksol (സംവാദം | സംഭാവനകള്) (→അനന്ത ഗുണിതങ്ങള്) |
||
| (ഇടക്കുള്ള 4 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 2: | വരി 2: | ||
Infinite products | Infinite products | ||
| - | ഗണിതത്തില് ഘടകങ്ങള് അവസാനമില്ലാതെ തുടര്ച്ചയായി ചേര്ത്ത് ഗുണിച്ചുണ്ടാകുന്ന ഫലം. | + | ഗണിതത്തില് ഘടകങ്ങള് അവസാനമില്ലാതെ തുടര്ച്ചയായി ചേര്ത്ത് ഗുണിച്ചുണ്ടാകുന്ന ഫലം. ∏എന്ന ചിഹ്നം ഉപയോഗിച്ച് അനന്തഗുണിതത്തെ സംക്ഷിപ്തരൂപത്തില് എഴുതാം. ഉദാ.2/1.3/2.4/3........... എന്ന അനന്തഗുണിതം തന്നെയാണ്: |
[[Image:p465.png]] | [[Image:p465.png]] | ||
| - | എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ | + | എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന |
| + | സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ | ||
| + | [[Image:466f.png]] | ||
| - | എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് | + | |
| + | എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് P<sub>n</sub> എന്ന ആംശികഗുണിതം | ||
| + | |||
| + | [[Image:466f.png]] | ||
എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന | എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന | ||
| + | [[Image:466f.png]] | ||
| - | |||
| + | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമാകാമെങ്കില് അവശ്യം വേണ്ടതും (necessary) മതിയായതുമായ (sufficient) ഒരു വ്യവസ്ഥ ഇതാണ്: ∈ എന്ന ധനരാശി എത്ര ചെറുതായിരുന്നാലും, n≥N<sub>0</sub> ആണെങ്കില്, m = 1, 2, 3... എന്ന മൂല്യങ്ങള്ക്കെല്ലാം | ||
| - | + | [[Image:p466d.png]] | |
| - | എന്ന | + | എന്ന അസമത (inequality) ഒത്തുവരത്തക്കവണ്ണം N<sub>0</sub> എന്നൊരു പൂര്ണസംഖ്യ കണ്ടെത്തുവാന് കഴിയണം. ഈ പ്രസ്താവനയിലെ m-ന് 1 എന്ന മൂല്യം കല്പിക്കുന്നതായാല് |
| - | + | [[Image:p466e.png]] | |
| + | എന്ന അഭികേന്ദ്രസരണ-അനന്തഗുണിതത്തില് a<sub>n+1</sub> പൂജ്യത്തെ സമീപിച്ചുകൊണ്ടിരിക്കുമെന്നു സിദ്ധിക്കുന്നു. ഈ നിബന്ധന അഭികേന്ദ്രസരണത്തിനു വേണ്ടതാണ്; പക്ഷേ മതിയാകുന്നതല്ല.അനന്തഗുണിതങ്ങളെ സംബന്ധിച്ചുള്ള ചില പ്രമേയങ്ങള് (theorems) ചുവടെ ചേര്ക്കുന്നു. ഇവിടെ എല്ലാ a<sub>r</sub>-ഉം വാസ്തവികസംഖ്യകള് (real numbers) ആണെന്നു സങ്കല്പിച്ചിരിക്കുകയാണ്. | ||
| + | |||
| + | '''പ്രമേയം-1'''. എല്ലാ ar-ഉം ധനാത്മകമാണെന്നിരിക്കട്ടെ. അപ്പോള് a<sub>1</sub> + a<sub>2</sub> + a<sub>3</sub> + ...എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | |||
| + | [[Image:p466c.png]] | ||
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ. | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ. | ||
| വരി 31: | വരി 42: | ||
'''പ്രമേയം-2.''' | '''പ്രമേയം-2.''' | ||
| - | + | [[Image:p466g.png]] | |
എന്ന അനന്തഗുണിതം അല്ലെങ്കില് | എന്ന അനന്തഗുണിതം അല്ലെങ്കില് | ||
| - | + | [[Image:p466h.png]] | |
എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും | എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും | ||
| + | [[Image:p466i.png]] | ||
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ | എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ | ||
| + | |||
| + | [[Image:p466j.png]] | ||
എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ | എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | |||
| + | [[Image:p466k.png]] | ||
| വരി 51: | വരി 67: | ||
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു. | എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു. | ||
| - | '''പ്രമേയം-3'''. എല്ലാ ar-ഉം 0 ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള് | + | '''പ്രമേയം-3'''. എല്ലാ ar-ഉം 0≤ ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള് |
| + | |||
| + | [[Image:p466l.png]] | ||
അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ | ||
| + | |||
| + | [[Image:p466m.png]] | ||
| വരി 62: | വരി 82: | ||
(ഡോ. എസ്. പരമേശ്വരന്) | (ഡോ. എസ്. പരമേശ്വരന്) | ||
| + | [[Category:ഗണിതം]] | ||
Current revision as of 11:10, 23 നവംബര് 2014
അനന്ത ഗുണിതങ്ങള്
Infinite products
ഗണിതത്തില് ഘടകങ്ങള് അവസാനമില്ലാതെ തുടര്ച്ചയായി ചേര്ത്ത് ഗുണിച്ചുണ്ടാകുന്ന ഫലം. ∏എന്ന ചിഹ്നം ഉപയോഗിച്ച് അനന്തഗുണിതത്തെ സംക്ഷിപ്തരൂപത്തില് എഴുതാം. ഉദാ.2/1.3/2.4/3........... എന്ന അനന്തഗുണിതം തന്നെയാണ്:
എന്നത് മുന് ഉദാഹരണത്തിലെ ആംശികഗുണിതം (partial product) എന്നു പറയപ്പെടുന്നു. (ഒരു അനന്തഗുണിതത്തിന്റെ) ആംശിക ഗുണിതത്തിലുള്ള ഘടകങ്ങളുടെ എണ്ണം വര്ധിച്ചുകൊണ്ടിരിക്കുമ്പോള്, അതിന്റെ മൂല്യങ്ങള് പൂജ്യത്തില്നിന്നു ഭിന്നമായ ഒരു പരിമിത സംഖ്യയോട് അടുത്തുകൊണ്ടിരിക്കുകയാണെങ്കില്, ആ അനന്തഗുണിതത്തെ അഭികേന്ദ്രസരണം (convergent) എന്നും; ആ ആംശികഗുണിതത്തിന്റെ മൂല്യങ്ങള് ഘടകങ്ങളുടെ എണ്ണം വര്ധിക്കുന്നതോടൊത്ത്, അനന്തതയെയോ പൂജ്യത്തെയോ സമീപിച്ചു കൊണ്ടിരിക്കുകയാണെങ്കില്,ആ അനന്തഗുണിതത്തെ അപകേന്ദ്രസരണം (divergent) എന്നും പറയുന്നു. അനന്തഗുണിതത്തിലെ ഏതെങ്കിലും ഒരു ഘടകത്തിന്റെ മൂല്യം പൂജ്യമാണെങ്കില് ആ അനന്തഗുണിതത്തിന്റെ തന്നെ മൂല്യം പൂജ്യമാണ്. ഒരു ആംശികഗുണിതത്തിന്റെ മൂല്യം പൂജ്യത്തെ സമീപിക്കുന്നു എന്നു പറയുമ്പോള് ഘടകങ്ങള്ക്കൊന്നിനും പൂജ്യം മൂല്യമായിരിക്കുകയില്ലെന്ന് ഓര്ക്കേണ്ടതുണ്ട്. പ്രതിപാദന സൌകര്യത്തെ ഉദ്ദേശിച്ച് അനന്തഗുണിതങ്ങളെ
എന്ന തരത്തിലാണ് എഴുതിപ്പോരുന്നത്. അപ്പോള് Pn എന്ന ആംശികഗുണിതം
എന്നാകും. ഘടകങ്ങളെല്ലാം പൂജ്യത്തില്നിന്നു ഭിന്നമായിരിക്കുന്ന
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമാകാമെങ്കില് അവശ്യം വേണ്ടതും (necessary) മതിയായതുമായ (sufficient) ഒരു വ്യവസ്ഥ ഇതാണ്: ∈ എന്ന ധനരാശി എത്ര ചെറുതായിരുന്നാലും, n≥N0 ആണെങ്കില്, m = 1, 2, 3... എന്ന മൂല്യങ്ങള്ക്കെല്ലാം
എന്ന അസമത (inequality) ഒത്തുവരത്തക്കവണ്ണം N0 എന്നൊരു പൂര്ണസംഖ്യ കണ്ടെത്തുവാന് കഴിയണം. ഈ പ്രസ്താവനയിലെ m-ന് 1 എന്ന മൂല്യം കല്പിക്കുന്നതായാല്
എന്ന അഭികേന്ദ്രസരണ-അനന്തഗുണിതത്തില് an+1 പൂജ്യത്തെ സമീപിച്ചുകൊണ്ടിരിക്കുമെന്നു സിദ്ധിക്കുന്നു. ഈ നിബന്ധന അഭികേന്ദ്രസരണത്തിനു വേണ്ടതാണ്; പക്ഷേ മതിയാകുന്നതല്ല.അനന്തഗുണിതങ്ങളെ സംബന്ധിച്ചുള്ള ചില പ്രമേയങ്ങള് (theorems) ചുവടെ ചേര്ക്കുന്നു. ഇവിടെ എല്ലാ ar-ഉം വാസ്തവികസംഖ്യകള് (real numbers) ആണെന്നു സങ്കല്പിച്ചിരിക്കുകയാണ്.
പ്രമേയം-1. എല്ലാ ar-ഉം ധനാത്മകമാണെന്നിരിക്കട്ടെ. അപ്പോള് a1 + a2 + a3 + ...എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കൂ.
പ്രമേയം-2.
എന്ന അനന്തഗുണിതം അല്ലെങ്കില്
എന്ന അനന്തശ്രേണി അഭികേന്ദ്രസരണമാണെങ്കില്, തീര്ച്ചയായും
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കും. അഥവാ
എന്ന അനന്തശ്രേണി നിരപേക്ഷ അഭികേന്ദ്രസരണം (absolutely convergent) ആണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതം അഭികേന്ദ്രസരണമായിരിക്കുകയുള്ളു.
പ്രമേയം-3. എല്ലാ ar-ഉം 0≤ ar < 1 എന്ന നിബന്ധന പാലിക്കുന്നുണ്ടെന്നിരിക്കട്ടെ. അപ്പോള്
അഭികേന്ദ്രസരണമാണെങ്കില്, എങ്കില് മാത്രമേ
എന്ന അനന്തഗുണിതവും അഭികേന്ദ്രസരണമായിരിക്കൂ. നോ: അനാലിസിസ്; അഭികേന്ദ്രസരണം, അപകേന്ദ്രസരണം
(ഡോ. എസ്. പരമേശ്വരന്)