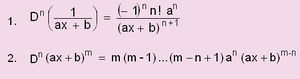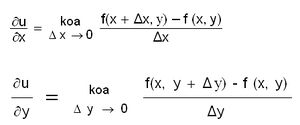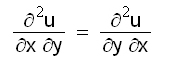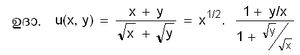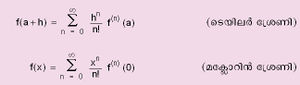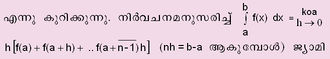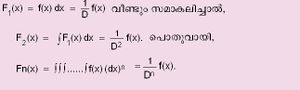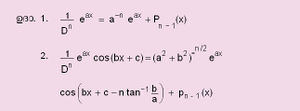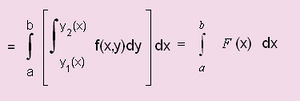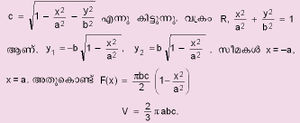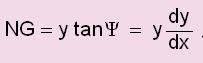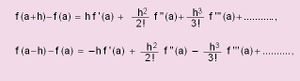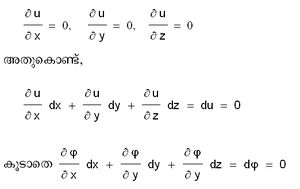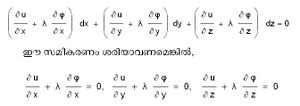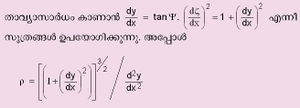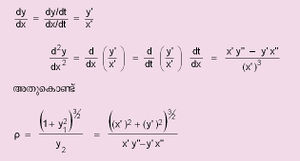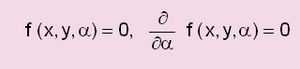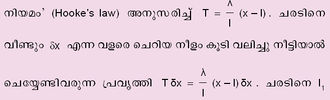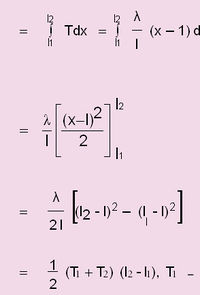This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കലനം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (പുതിയ താള്: == കലനം == == Calculus == ഫലനത്തിലെ അടിസ്ഥാന ക്രിയകളായ അവകലനം (Differentiation), സമാ...) |
Mksol (സംവാദം | സംഭാവനകള്) (→അവകലനം) |
||
| (ഇടക്കുള്ള 52 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 6: | വരി 6: | ||
അവകലനത്തിനും സമാകലനത്തിനും ഉപയോഗിക്കുന്ന സാങ്കേതിക രീതികളനുസരിച്ച് അവകലനം നിഗമനാത്മകവും (deductive) സമാകലനം ആഗമനാത്മകവും (inductive) ആണ്. ഈ രണ്ടു വിഭാഗങ്ങളില് ആഗമനാത്മക സ്വഭാവമുള്ള സമാകലനമാണ് ആദ്യം ആവിഷ്കരിക്കപ്പെട്ടത്. വക്രത്തിനു സ്പര്ശകം വരയ്ക്കുക, വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കുക തുടങ്ങിയ ചില ഒറ്റതിരിഞ്ഞ പ്രശ്നങ്ങളുടെ നിര്ധാരണം സംബന്ധിച്ച ഗണിതശാസ്ത്രാന്വേഷണങ്ങളില്നിന്നാണ് കലനം രൂപംകൊണ്ടത്. എന്നാല് പില്ക്കാലത്ത് ഇതിന്റെ അടിസ്ഥാന സങ്കല്പങ്ങളും രീതിയും പ്രായോഗികതലത്തിലുള്ള ഉപയോഗങ്ങളും വളരെ വികാസം പ്രാപിച്ചതിനാല് കലനം ഗണിതത്തിലെ വളരെ പ്രാധാന്യമുള്ള വിഷയമായി മാറിയിരിക്കുന്നു. | അവകലനത്തിനും സമാകലനത്തിനും ഉപയോഗിക്കുന്ന സാങ്കേതിക രീതികളനുസരിച്ച് അവകലനം നിഗമനാത്മകവും (deductive) സമാകലനം ആഗമനാത്മകവും (inductive) ആണ്. ഈ രണ്ടു വിഭാഗങ്ങളില് ആഗമനാത്മക സ്വഭാവമുള്ള സമാകലനമാണ് ആദ്യം ആവിഷ്കരിക്കപ്പെട്ടത്. വക്രത്തിനു സ്പര്ശകം വരയ്ക്കുക, വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കുക തുടങ്ങിയ ചില ഒറ്റതിരിഞ്ഞ പ്രശ്നങ്ങളുടെ നിര്ധാരണം സംബന്ധിച്ച ഗണിതശാസ്ത്രാന്വേഷണങ്ങളില്നിന്നാണ് കലനം രൂപംകൊണ്ടത്. എന്നാല് പില്ക്കാലത്ത് ഇതിന്റെ അടിസ്ഥാന സങ്കല്പങ്ങളും രീതിയും പ്രായോഗികതലത്തിലുള്ള ഉപയോഗങ്ങളും വളരെ വികാസം പ്രാപിച്ചതിനാല് കലനം ഗണിതത്തിലെ വളരെ പ്രാധാന്യമുള്ള വിഷയമായി മാറിയിരിക്കുന്നു. | ||
== ചരിത്രം== | == ചരിത്രം== | ||
| - | എ.ഡി. 10-ാം നൂറ്റാണ്ടില്ത്തന്നെ അവകലനത്തിലെ ചില പ്രമേയങ്ങള് ഇന്ത്യന് ഗണിതശാസ്ത്രജ്ഞന്മാര്ക്ക് അറിയാമായിരുന്നു. മഞ്ജുളാചാര്യനും (932) അദ്ദേഹത്തിന്റെ കൃതിയുടെ വ്യാഖ്യാതാവായ പ്രശസ്തിധരനും (958), എന്ന സൂത്രവാക്യം അറിയാമായിരുന്നു എന്ന് പ്രാഫ. ബി.ബി. ദത്ത ചൂണ്ടിക്കാണിക്കുന്നു. അതുപോലെ f(x) മഹത്തമമാകുമ്പോള് ആണെന്ന് ഭാസ്കരാചാര്യനും (1150) ഗ്രഹിച്ചിരുന്നു. ഇന്നത്തെ രീതിയിലല്ലെങ്കിലും അവകലജം എന്ന ആശയത്തെപ്പറ്റി ആദ്യമായി ചിന്തിച്ച | + | എ.ഡി. 10-ാം നൂറ്റാണ്ടില്ത്തന്നെ അവകലനത്തിലെ ചില പ്രമേയങ്ങള് ഇന്ത്യന് ഗണിതശാസ്ത്രജ്ഞന്മാര്ക്ക് അറിയാമായിരുന്നു. മഞ്ജുളാചാര്യനും (932) അദ്ദേഹത്തിന്റെ കൃതിയുടെ വ്യാഖ്യാതാവായ പ്രശസ്തിധരനും (958), δ(sin θ) = cos θ δθ എന്ന സൂത്രവാക്യം അറിയാമായിരുന്നു എന്ന് പ്രാഫ. ബി.ബി. ദത്ത ചൂണ്ടിക്കാണിക്കുന്നു. അതുപോലെ f(x) മഹത്തമമാകുമ്പോള് ആണെന്ന് ഭാസ്കരാചാര്യനും (1150) ഗ്രഹിച്ചിരുന്നു. ഇന്നത്തെ രീതിയിലല്ലെങ്കിലും അവകലജം എന്ന ആശയത്തെപ്പറ്റി ആദ്യമായി ചിന്തിച്ച ഗണിതശാസ്ത്രജ്ഞന് ഭാസ്കരാചാര്യനാണ്. കലനം ഒരു ഗണിതശാസ്ത്രശാഖയായി രൂപം പ്രാപിച്ചത് അഞ്ചു നൂറ്റാണ്ടുകള്ക്കുശേഷമാണ്. |
| - | + | ||
| - | 1612ല് ജ്യോതിശ്ശാസ്ത്രജ്ഞനായ കെപ്ലര് ദീര്ഘ വൃത്ത(ellipse)ത്തിന്റെ വിസ്തീര്ണം കണക്കുകൂട്ടി കണ്ടുപിടിച്ചു. യൂക്ലിഡ് ഉപയോഗിച്ചതില് നിന്നു വ്യത്യസ്തമായ രീതിയിലായിരുന്നു കെപ്ലര് വിസ്തീര്ണം കണ്ടുപിടിച്ചത്. ഒരു നിശ്ചിത വിസ്തീര്ണത്തെയോ വ്യാപ്തത്തെയോ അനന്തസൂക്ഷ്മങ്ങളായ ദീര്ഘചതുരങ്ങളായോ ഡിസ്ക്കുകളായോ ഭാഗിച്ചാണ് കെപ്ലര് മൊത്തം വിസ്തീര്ണവും വ്യാപ്തവും കണക്കാക്കിയത്. കെപ്ലറുടെ രീതി സ്വീകരിച്ച് 1635ല് ഗലീലിയോ, ഗലീലിയുടെ ശിഷ്യനായിരുന്ന ബൊണാവെന്റ്യുറ കാവലിറി "അഭാജ്യങ്ങളുടെ ജ്യാമിതി' എഴുതി. ഏകസമാനമല്ലാത്ത വ്യാപ്തങ്ങളുടെ ഗുരുത്വകേന്ദ്രം കണ്ടുപിടിക്കാന് അദ്ദേഹത്തിനു സാധിച്ചു. ഫെര്മ (1601-65) യുടെ ഗവേഷണം വിപരീത ദിശയിലായിരുന്നു. സ്പര്ശകങ്ങള് വരയ്ക്കുക, വക്രങ്ങളുടെ (ഫലനങ്ങളുടെ) മഹത്തമന്യൂനതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കുക തുടങ്ങിയ പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യാന് ഫെര്മയ്ക്കു കഴിഞ്ഞു (1629). 40 വര്ഷങ്ങള്ക്കുശേഷം ഐസക് ബറോ (Lectiones Opticae et Geometricae, 1669) ഒരു സീമാപ്രക്രിയയിലൂടെ അവകലജത്തെ നിര്വചിച്ചു. രണ്ടാംതര രാശികളെ ഉപേക്ഷിച്ചും a, e(ഇന്നത്തെ രീതിയില് ഇവ ഉള്ക്കൊള്ളാത്ത പദങ്ങളെ വിട്ടുകളഞ്ഞും അദ്ദേഹം yലും xലും ഉള്ള വ്യതിയാനങ്ങളുടെ അനുപാതം a/e കണ്ടുപിടിച്ചു. അങ്ങനെ അവകലനത്തിന്റെ ആധുനിക രീതിയോടടുത്തെത്താന് ഐസക് ബറോവിനു സാധിച്ചു. സ്പര്ശകങ്ങളെ സംബന്ധിച്ചും വിസ്തീര്ണത്തെ സംബന്ധിച്ചുമുള്ള പ്രതിലോമബന്ധം ആദ്യമായി മനസ്സിലാക്കിയത് അദ്ദേഹമായിരുന്നു. | + | 1612ല് ജ്യോതിശ്ശാസ്ത്രജ്ഞനായ കെപ്ലര് ദീര്ഘ വൃത്ത(ellipse)ത്തിന്റെ വിസ്തീര്ണം കണക്കുകൂട്ടി കണ്ടുപിടിച്ചു. യൂക്ലിഡ് ഉപയോഗിച്ചതില് നിന്നു വ്യത്യസ്തമായ രീതിയിലായിരുന്നു കെപ്ലര് വിസ്തീര്ണം കണ്ടുപിടിച്ചത്. ഒരു നിശ്ചിത വിസ്തീര്ണത്തെയോ വ്യാപ്തത്തെയോ അനന്തസൂക്ഷ്മങ്ങളായ ദീര്ഘചതുരങ്ങളായോ ഡിസ്ക്കുകളായോ ഭാഗിച്ചാണ് കെപ്ലര് മൊത്തം വിസ്തീര്ണവും വ്യാപ്തവും കണക്കാക്കിയത്. കെപ്ലറുടെ രീതി സ്വീകരിച്ച് 1635ല് ഗലീലിയോ, ഗലീലിയുടെ ശിഷ്യനായിരുന്ന ബൊണാവെന്റ്യുറ കാവലിറി "അഭാജ്യങ്ങളുടെ ജ്യാമിതി' എഴുതി. ഏകസമാനമല്ലാത്ത വ്യാപ്തങ്ങളുടെ ഗുരുത്വകേന്ദ്രം കണ്ടുപിടിക്കാന് അദ്ദേഹത്തിനു സാധിച്ചു. ഫെര്മ (1601-65) യുടെ ഗവേഷണം വിപരീത ദിശയിലായിരുന്നു. സ്പര്ശകങ്ങള് വരയ്ക്കുക, വക്രങ്ങളുടെ (ഫലനങ്ങളുടെ) മഹത്തമന്യൂനതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കുക തുടങ്ങിയ പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യാന് ഫെര്മയ്ക്കു കഴിഞ്ഞു (1629). 40 വര്ഷങ്ങള്ക്കുശേഷം ഐസക് ബറോ (Lectiones Opticae et Geometricae, 1669) ഒരു സീമാപ്രക്രിയയിലൂടെ അവകലജത്തെ നിര്വചിച്ചു. രണ്ടാംതര രാശികളെ ഉപേക്ഷിച്ചും a, e(ഇന്നത്തെ രീതിയില് δy, δx) ഇവ ഉള്ക്കൊള്ളാത്ത പദങ്ങളെ വിട്ടുകളഞ്ഞും അദ്ദേഹം yലും xലും ഉള്ള വ്യതിയാനങ്ങളുടെ അനുപാതം a/e കണ്ടുപിടിച്ചു. അങ്ങനെ അവകലനത്തിന്റെ ആധുനിക രീതിയോടടുത്തെത്താന് ഐസക് ബറോവിനു സാധിച്ചു. സ്പര്ശകങ്ങളെ സംബന്ധിച്ചും വിസ്തീര്ണത്തെ സംബന്ധിച്ചുമുള്ള പ്രതിലോമബന്ധം ആദ്യമായി മനസ്സിലാക്കിയത് അദ്ദേഹമായിരുന്നു. |
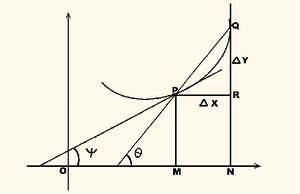
| - | ഈ പശ്ചാത്തലത്തിലാണ് ഐസക് ന്യൂട്ടനും (1642-1727) ഗോഡ്ഫ്രീദ് ഫൊണ് ലൈബ്നിറ്റ്സും (1646-1716) രംഗത്തെത്തുന്നത്. കലനത്തിന്റെ ക്രമാനുസൃതമായ ആവിഷ്കാരത്തില് പങ്കാളികളാവാന് അവര്ക്ക് സാധിച്ചു. ന്യൂട്ടന് സീമാപ്രക്രിയയിലൂടെ സമാകലനത്തെ കണക്കാക്കുന്ന പഴയരീതി ഉപേക്ഷിക്കുകയും സമാകലനത്തെ പ്രതി അവകലജമായി പരിഗണിക്കുകയും ചെയ്തു. 1666 മുതല് പ്രസിദ്ധീകരിക്കപ്പെട്ട മൂന്നു പ്രബന്ധങ്ങളില് കലനത്തിലുള്ള ന്യൂട്ടന്റെ സംഭാവനകള് ഉള്ക്കൊള്ളുന്നു. അദ്ദേഹം കാലത്തെ (time) അന്തിമമായ സ്വതന്ത്രചരമായി പരിഗണിക്കുകയും xന്റെ വര്ധമാനവേഗതയെ (ന്യൂട്ടന് ഇതിനെ "ഫ്ളക്ഷന്' എന്നു വിളിക്കുന്നു) | + | ഈ പശ്ചാത്തലത്തിലാണ് ഐസക് ന്യൂട്ടനും (1642-1727) ഗോഡ്ഫ്രീദ് ഫൊണ് ലൈബ്നിറ്റ്സും (1646-1716) രംഗത്തെത്തുന്നത്. കലനത്തിന്റെ ക്രമാനുസൃതമായ ആവിഷ്കാരത്തില് പങ്കാളികളാവാന് അവര്ക്ക് സാധിച്ചു. ന്യൂട്ടന് സീമാപ്രക്രിയയിലൂടെ സമാകലനത്തെ കണക്കാക്കുന്ന പഴയരീതി ഉപേക്ഷിക്കുകയും സമാകലനത്തെ പ്രതി അവകലജമായി പരിഗണിക്കുകയും ചെയ്തു. 1666 മുതല് പ്രസിദ്ധീകരിക്കപ്പെട്ട മൂന്നു പ്രബന്ധങ്ങളില് കലനത്തിലുള്ള ന്യൂട്ടന്റെ സംഭാവനകള് ഉള്ക്കൊള്ളുന്നു. അദ്ദേഹം കാലത്തെ (time) അന്തിമമായ സ്വതന്ത്രചരമായി പരിഗണിക്കുകയും xന്റെ വര്ധമാനവേഗതയെ (ന്യൂട്ടന് ഇതിനെ "ഫ്ളക്ഷന്' എന്നു വിളിക്കുന്നു) x (=x ഡോട്ട്) എന്ന പ്രതീകം കൊണ്ടു കുറിക്കുകയും ചെയ്തു. xന്റെയും yന്റെയും അനുപാതമാണ് അവകലജ ഗുണാങ്കം (differential coefficient). തേന്റെ ആചാര്യനായ ഐസക് ബറോ ഉപയോഗിച്ച e, a എന്നീ അക്ഷരങ്ങള്ക്കുപകരം ന്യൂട്ടന് x<sub>0</sub>, y<sub>0</sub> എന്നീ പ്രതീകങ്ങളാണ് ഉപയോഗി ച്ചത്. അദ്ദേഹം രണ്ടു ഫലനങ്ങളുടെ തുകയെയും ഫലനങ്ങളുടെ ഫലനത്തെയും അവകലിക്കാനുള്ള നിയമങ്ങള് കണ്ടുപിടിച്ചു. "n, ധന പൂര്ണസംഖ്യയാകുമ്പോള്, d/dx (x<sup>n</sup>) = nx<sup>n-1</sup>എന്ന സൂത്രവാക്യവും ന്യൂട്ടനാണ് കണ്ടുപിടിച്ചത്. |
| - | ലൈബ്നിറ്റ്സ് (Leibnitz), കലനത്തിന്റെ അടിസ്ഥാനതത്ത്വങ്ങള് സ്വതന്ത്രമായി കണ്ടുപിടിച്ച ഗണിതജ്ഞനാണ്. രണ്ടു ഫലനങ്ങളുടെ തുക, വ്യത്യാസം, ഗുണനഫലം, അനുപാതം എന്നിവയുടെ അവകലജങ്ങള് കണ്ടുപിടിച്ച അദ്ദേഹം അവകലന നിയമങ്ങളെ ക്രാഡീകരിച്ചു.m ധനപൂര്ണ സംഖ്യയാകുമ്പോള്, എന്ന നിയമം ലൈബ്നിറ്റ്സ് സ്വതന്ത്രമായി ആവിഷ്കരിച്ചു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ "m-ാമത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള "ലൈബ്നിറ്റ്സ് നിയമം' പ്രസിദ്ധമാണ്. ആധുനിക പ്രതീകങ്ങളായ എന്നിവയോടൊപ്പം കാല്കുലസ് ഡിഫറന്ഷ്യാലിസ് (calculus differentialis),കാല്ക്കുലസ് ഇന്റഗ്രാലിസ് (calculus integralis) തുടങ്ങിയ പേരുകളും ലൈബ്നിറ്റ്സ് കൊടുത്തിട്ടുള്ളവയാണ്. 1684ലാണ് ലൈബ്നിറ്റ്സിന്റെ കലനത്തെ സംബന്ധിച്ച ലേഖനം പ്രസിദ്ധീകരിക്കപ്പെട്ടത്. തുടര്ന്ന് 1686ല് സമാകലനത്തിലെ പ്രമേയങ്ങള് ഉള്ക്കൊള്ളുന്ന മറ്റൊരു ഗവേഷണപ്രബന്ധവും ലൈബ്നിറ്റ്സ് പ്രസിദ്ധീകരിച്ചു. ഐസക് ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നീ ശാസ്ത്രജ്ഞരെയാണ് അവകലനത്തിന്റെ ഉപജ്ഞാതാക്കളായി പാശ്ചാത്യ പണ്ഡിതന്മാര് കണക്കാക്കുന്നത്. | + | |
| + | ലൈബ്നിറ്റ്സ് (Leibnitz), കലനത്തിന്റെ അടിസ്ഥാനതത്ത്വങ്ങള് സ്വതന്ത്രമായി കണ്ടുപിടിച്ച ഗണിതജ്ഞനാണ്. രണ്ടു ഫലനങ്ങളുടെ തുക, വ്യത്യാസം, ഗുണനഫലം, അനുപാതം എന്നിവയുടെ അവകലജങ്ങള് കണ്ടുപിടിച്ച അദ്ദേഹം അവകലന നിയമങ്ങളെ ക്രാഡീകരിച്ചു.m ധനപൂര്ണ സംഖ്യയാകുമ്പോള്, dx<sup>m</sup>=mx<sup>m-1</sup>dx എന്ന നിയമം ലൈബ്നിറ്റ്സ് സ്വതന്ത്രമായി ആവിഷ്കരിച്ചു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ "m-ാമത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള "ലൈബ്നിറ്റ്സ് നിയമം' പ്രസിദ്ധമാണ്. ആധുനിക പ്രതീകങ്ങളായ d/dx, ∫ എന്നിവയോടൊപ്പം കാല്കുലസ് ഡിഫറന്ഷ്യാലിസ് (calculus differentialis),കാല്ക്കുലസ് ഇന്റഗ്രാലിസ് (calculus integralis) തുടങ്ങിയ പേരുകളും ലൈബ്നിറ്റ്സ് കൊടുത്തിട്ടുള്ളവയാണ്. 1684ലാണ് ലൈബ്നിറ്റ്സിന്റെ കലനത്തെ സംബന്ധിച്ച ലേഖനം പ്രസിദ്ധീകരിക്കപ്പെട്ടത്. തുടര്ന്ന് 1686ല് സമാകലനത്തിലെ പ്രമേയങ്ങള് ഉള്ക്കൊള്ളുന്ന മറ്റൊരു ഗവേഷണപ്രബന്ധവും ലൈബ്നിറ്റ്സ് പ്രസിദ്ധീകരിച്ചു. ഐസക് ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നീ ശാസ്ത്രജ്ഞരെയാണ് അവകലനത്തിന്റെ ഉപജ്ഞാതാക്കളായി പാശ്ചാത്യ പണ്ഡിതന്മാര് കണക്കാക്കുന്നത്. | ||
ലൈബ്നിറ്റ്സിന്റെ ഗവേഷണം മുന്നോട്ടു കൊണ്ടുപോയത് ബെര്ണൂലി സഹോദരന്മാരായിരുന്നു. ശ്രദ്ധേയമായ "ഹോസ്പിറ്റല് നിയമം' ഉള്ക്കൊള്ളിച്ചുകൊണ്ടും 1696ല് ബെര്ണൂലിയുടെ ഗവേഷണ വിദ്യാര്ഥിയായ എല് ഹോസ്പിറ്റല് (Marquisde I'Hospital) കലനത്തെ സംബന്ധിച്ച ആദ്യത്തെ "ടെക്സ്റ്റ് ബുക്ക്' പ്രസിദ്ധീകരിച്ചു. | ലൈബ്നിറ്റ്സിന്റെ ഗവേഷണം മുന്നോട്ടു കൊണ്ടുപോയത് ബെര്ണൂലി സഹോദരന്മാരായിരുന്നു. ശ്രദ്ധേയമായ "ഹോസ്പിറ്റല് നിയമം' ഉള്ക്കൊള്ളിച്ചുകൊണ്ടും 1696ല് ബെര്ണൂലിയുടെ ഗവേഷണ വിദ്യാര്ഥിയായ എല് ഹോസ്പിറ്റല് (Marquisde I'Hospital) കലനത്തെ സംബന്ധിച്ച ആദ്യത്തെ "ടെക്സ്റ്റ് ബുക്ക്' പ്രസിദ്ധീകരിച്ചു. | ||
18-ാം ശ.ത്തിലെ ഗണിതശാസ്ത്ര പുരോഗതി കലനത്തെയും ബലതന്ത്രത്തില് (Mechanics)അതു ചെലുത്തിയ സ്വാധീനത്തെയും കേന്ദ്രീകരിച്ചായിരുന്നു. ഈ നൂറ്റാണ്ടില് കലനത്തിന്റെ ഉപജ്ഞാതാവായി ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നിവരില് ആരെ അംഗീകരിക്കണം എന്ന തര്ക്കത്തില് വ്യാപൃതരായിരുന്ന ബ്രിട്ടീഷ് ഗണിത ശാസ്ത്രജ്ഞര്ക്ക് ലൈബ്നിറ്റ്സിന്റെ രീതികളോടും പ്രതീകങ്ങളോടും താത്പര്യം തോന്നിയില്ല. ഇക്കാരണത്താല് അവരുടെ ഗവേഷണഫലങ്ങള് ടെയിലര്, മെക്ലാറിന് എന്നിവരുടെ പ്രമേയങ്ങളില് മാത്രം ഒതുങ്ങിനിന്നു. എന്നാല് യൂറോപ്പില് ഓയ്ലര്, ക്ലെയറാട്ട് തുടങ്ങിയവരുടെ ശ്രമങ്ങളുടെ ഫലമായി കലനതത്ത്വങ്ങളില് വളരെയേറെ പുരോഗതിയുണ്ടായി. ആംശിക അവകലജ(Partial derivative)ത്തെക്കുറിച്ചു മനസ്സിലാക്കാനും ഉച്ചതര വിമകളിലുള്ള സമഷ്ടി(space)യെക്കുറിച്ച് പഠിക്കുവാനും അവര്ക്കു സാധിച്ചു. അവകലന സമീകരണങ്ങളെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങള് രൂപം കൊണ്ടത് അക്കാലത്താണ്. | 18-ാം ശ.ത്തിലെ ഗണിതശാസ്ത്ര പുരോഗതി കലനത്തെയും ബലതന്ത്രത്തില് (Mechanics)അതു ചെലുത്തിയ സ്വാധീനത്തെയും കേന്ദ്രീകരിച്ചായിരുന്നു. ഈ നൂറ്റാണ്ടില് കലനത്തിന്റെ ഉപജ്ഞാതാവായി ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നിവരില് ആരെ അംഗീകരിക്കണം എന്ന തര്ക്കത്തില് വ്യാപൃതരായിരുന്ന ബ്രിട്ടീഷ് ഗണിത ശാസ്ത്രജ്ഞര്ക്ക് ലൈബ്നിറ്റ്സിന്റെ രീതികളോടും പ്രതീകങ്ങളോടും താത്പര്യം തോന്നിയില്ല. ഇക്കാരണത്താല് അവരുടെ ഗവേഷണഫലങ്ങള് ടെയിലര്, മെക്ലാറിന് എന്നിവരുടെ പ്രമേയങ്ങളില് മാത്രം ഒതുങ്ങിനിന്നു. എന്നാല് യൂറോപ്പില് ഓയ്ലര്, ക്ലെയറാട്ട് തുടങ്ങിയവരുടെ ശ്രമങ്ങളുടെ ഫലമായി കലനതത്ത്വങ്ങളില് വളരെയേറെ പുരോഗതിയുണ്ടായി. ആംശിക അവകലജ(Partial derivative)ത്തെക്കുറിച്ചു മനസ്സിലാക്കാനും ഉച്ചതര വിമകളിലുള്ള സമഷ്ടി(space)യെക്കുറിച്ച് പഠിക്കുവാനും അവര്ക്കു സാധിച്ചു. അവകലന സമീകരണങ്ങളെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങള് രൂപം കൊണ്ടത് അക്കാലത്താണ്. | ||
| + | |||
== നൂതന വികാസങ്ങള്== | == നൂതന വികാസങ്ങള്== | ||
| - | കലനത്തില് ആധുനികതയുടെ തുടക്കം കുറിച്ചത് 19-ാം ശ.ത്തിലാണ്. 1823ല് പ്രസിദ്ധീകൃതമായ പ്രാമാണിക ഗ്രന്ഥത്തിലൂടെ (Resume Des Lecons Sur le Calcul Infinitesimal) ഫ്രഞ്ച് ഗണിതജ്ഞനായ അഗസ്തിന് എല്. കോഷി ഈ തുടക്കത്തിനു അടിസ്ഥാനമിട്ടു. അതോടെ ഗണിത വിശ്ലേഷണം ഒരു പ്രത്യേകശാഖയായി ഉരുത്തിരിഞ്ഞു. കൂടാതെ എന്ന അവകല സംകാരക(differential operator)ത്തിന്റെ ഉപയോഗത്തിലൂടെ കലനത്തിലെ പല പ്രശ്നങ്ങളും ബീജഗണിതരീതിയില് നിര്ധാരണം ചെയ്യുവാനും കോഷിക്കു കഴിഞ്ഞു. കാള് വെയര് സ്റ്റ്രാസ് (1815-97) ഈ ശാഖ വികസിപ്പിച്ചു. | + | കലനത്തില് ആധുനികതയുടെ തുടക്കം കുറിച്ചത് 19-ാം ശ.ത്തിലാണ്. 1823ല് പ്രസിദ്ധീകൃതമായ പ്രാമാണിക ഗ്രന്ഥത്തിലൂടെ (Resume Des Lecons Sur le Calcul Infinitesimal) ഫ്രഞ്ച് ഗണിതജ്ഞനായ അഗസ്തിന് എല്. കോഷി ഈ തുടക്കത്തിനു അടിസ്ഥാനമിട്ടു. അതോടെ ഗണിത വിശ്ലേഷണം ഒരു പ്രത്യേകശാഖയായി ഉരുത്തിരിഞ്ഞു. കൂടാതെ D(=d/dx) എന്ന അവകല സംകാരക(differential operator)ത്തിന്റെ ഉപയോഗത്തിലൂടെ കലനത്തിലെ പല പ്രശ്നങ്ങളും ബീജഗണിതരീതിയില് നിര്ധാരണം ചെയ്യുവാനും കോഷിക്കു കഴിഞ്ഞു. കാള് വെയര് സ്റ്റ്രാസ് (1815-97) ഈ ശാഖ വികസിപ്പിച്ചു. |
ഈ നൂറ്റാണ്ടില് ഗണിതഗവേഷണത്തിന്റെ പല മേഖലകളിലൂടെ കലനം വികാസം പ്രാപിച്ചുകൊണ്ടിരിക്കുന്നു. റീമാന് സമാകലനത്തിനു ലെബേഗും സ്റ്റീല്ജീസും കൊടുത്ത പുതിയ വ്യാഖ്യാനം ഗണിതചരിത്രത്തില് ഒരപൂര്വ സംഭവമാണ്. സൂക്ഷ്മങ്ങളായ പണിയായുധങ്ങളെ സ്വരൂപിക്കുവാനും ശാസ്ത്രവികാസത്തെ അപ്രതീക്ഷിത ദിശകളിലേക്കു നയിക്കുവാനും സഹായിക്കുന്ന ഏറ്റവും ശക്തമായ ഒരു മാധ്യമമായി മാറിയിരിക്കുകയാണ് കലനസിദ്ധാന്തം. | ഈ നൂറ്റാണ്ടില് ഗണിതഗവേഷണത്തിന്റെ പല മേഖലകളിലൂടെ കലനം വികാസം പ്രാപിച്ചുകൊണ്ടിരിക്കുന്നു. റീമാന് സമാകലനത്തിനു ലെബേഗും സ്റ്റീല്ജീസും കൊടുത്ത പുതിയ വ്യാഖ്യാനം ഗണിതചരിത്രത്തില് ഒരപൂര്വ സംഭവമാണ്. സൂക്ഷ്മങ്ങളായ പണിയായുധങ്ങളെ സ്വരൂപിക്കുവാനും ശാസ്ത്രവികാസത്തെ അപ്രതീക്ഷിത ദിശകളിലേക്കു നയിക്കുവാനും സഹായിക്കുന്ന ഏറ്റവും ശക്തമായ ഒരു മാധ്യമമായി മാറിയിരിക്കുകയാണ് കലനസിദ്ധാന്തം. | ||
പ്രാരംഭിക കലനത്തിലെ പ്രധാനപ്പെട്ട ആശയങ്ങളും പ്രക്രിയകളും പ്രയോഗവും മാത്രമേ ഈ ലേഖനത്തില് ഉള്ക്കൊള്ളിച്ചിട്ടുള്ളു. വികസിത കലന(advanced calculus)ത്തെിലെ പ്രധാന ആശയങ്ങളും പ്രയോഗങ്ങളും ഉപവിഭാഗങ്ങളും (ഫലനവിശ്ലേഷണം (Functional Analysis), സമ്മിശ്രവിശ്ലേഷണം (omplex Analysis), ടെന്സര് വിശ്ലേഷണം (Tensor Analysis), വിശ്ലേഷക ജ്യാമിതി (Analytic Geometry) തുടങ്ങിയവ.) വിശ്ലേഷണം (Analysis)എന്ന ഗണിതശാഖയുടെ ഭാഗമാണ്. | പ്രാരംഭിക കലനത്തിലെ പ്രധാനപ്പെട്ട ആശയങ്ങളും പ്രക്രിയകളും പ്രയോഗവും മാത്രമേ ഈ ലേഖനത്തില് ഉള്ക്കൊള്ളിച്ചിട്ടുള്ളു. വികസിത കലന(advanced calculus)ത്തെിലെ പ്രധാന ആശയങ്ങളും പ്രയോഗങ്ങളും ഉപവിഭാഗങ്ങളും (ഫലനവിശ്ലേഷണം (Functional Analysis), സമ്മിശ്രവിശ്ലേഷണം (omplex Analysis), ടെന്സര് വിശ്ലേഷണം (Tensor Analysis), വിശ്ലേഷക ജ്യാമിതി (Analytic Geometry) തുടങ്ങിയവ.) വിശ്ലേഷണം (Analysis)എന്ന ഗണിതശാഖയുടെ ഭാഗമാണ്. | ||
| + | |||
== ഫലനത്തിന്റെ സീമയും സാതത്യവും== | == ഫലനത്തിന്റെ സീമയും സാതത്യവും== | ||
ഫലനത്തിന്റെ സീമയും സാതത്യവും (Limit and continuity of function). y = f (x) എന്ന ഫലനം സങ്കല്പിക്കുക. ഇവിടെ x എന്ന ചരം a എന്ന സംഖ്യയോട് ഏതെങ്കിലും വിധത്തില് അടുക്കുമ്പോള്, f (x) അടുക്കുന്നത് A യോടാണെങ്കില്, | ഫലനത്തിന്റെ സീമയും സാതത്യവും (Limit and continuity of function). y = f (x) എന്ന ഫലനം സങ്കല്പിക്കുക. ഇവിടെ x എന്ന ചരം a എന്ന സംഖ്യയോട് ഏതെങ്കിലും വിധത്തില് അടുക്കുമ്പോള്, f (x) അടുക്കുന്നത് A യോടാണെങ്കില്, | ||
A യെxഎന്ന ചരം a യോടടുക്കുമ്പോഴുള്ള f (x) ന്റെ സീമ എന്നു പറയുന്നു. പ്രതീകാത്മകമായി സീമ f (x) = A എന്ന് എഴുതുന്നു. x, a യോടടുക്കുന്നത് രണ്ടുവിധത്തിലാകാം. സംഖ്യാരേഖയില് (Number line) a0 യുടെ വലതുവശത്തുള്ള വലിയ സംഖ്യകളില് നിന്നോ ഇടതുവശത്തുള്ള ചെറിയ സംഖ്യകളില് നിന്നോ x, a യോടടുക്കാം. | A യെxഎന്ന ചരം a യോടടുക്കുമ്പോഴുള്ള f (x) ന്റെ സീമ എന്നു പറയുന്നു. പ്രതീകാത്മകമായി സീമ f (x) = A എന്ന് എഴുതുന്നു. x, a യോടടുക്കുന്നത് രണ്ടുവിധത്തിലാകാം. സംഖ്യാരേഖയില് (Number line) a0 യുടെ വലതുവശത്തുള്ള വലിയ സംഖ്യകളില് നിന്നോ ഇടതുവശത്തുള്ള ചെറിയ സംഖ്യകളില് നിന്നോ x, a യോടടുക്കാം. | ||
| - | സീമയുടെ നിര്വചനം കൂടുതല് വ്യക്തമായി ഇങ്ങനെ പറയാം. x, a യോടടുക്കുമ്പോള് f(x) ന്റെ സീമ അ ആകണമെങ്കില്, തന്നിട്ടുള്ള ഏതെങ്കിലും ചെറിയ ധനസംഖ്യയായ | + | സീമയുടെ നിര്വചനം കൂടുതല് വ്യക്തമായി ഇങ്ങനെ പറയാം. x, a യോടടുക്കുമ്പോള് f(x) ന്റെ സീമ അ ആകണമെങ്കില്, തന്നിട്ടുള്ള ഏതെങ്കിലും ചെറിയ ധനസംഖ്യയായ ε (എപ്പ്സിലോണ്) സംഗതമായിx ന്റെ എല്ലാ വിലകള്ക്കും (x ≠ a), |f(x)-A|<ε ആകുമ്പോള് |x-a|<δആകത്തക്കവണ്ണം δ (ഡെല്റ്റ) എന്ന ചെറിയ ധനസംഖ്യ ഉണ്ടായിരിക്കണം. "x ന്റെ എല്ലാ വിലകള്ക്കും' എന്നതുകൊണ്ടും വലതു സീമയും ഇടതു സീമയും ഉണ്ടായിരിക്കണമെന്ന് അവ തുല്യമായിരിക്കണമെന്നും അര്ഥമാക്കുന്നു. അതായത് x→<sup>സീമ</sup>a+ f(x)=A=x→<sup>സീമ</sup>a- f(x) സീമാപ്രക്രിയയില് ഫലനത്തിന് x = a ആകുമ്പോഴുള്ള വില കണക്കിലെടുക്കുന്നില്ല. അതുകൊണ്ടാണ് x≠a എന്നു പറഞ്ഞത്.x=a ആകുമ്പോള് ഫലനത്തിനു മൂല്യം ഉണ്ടാകുകയോ ഉണ്ടാകാതിരിക്കുകയോ ചെയ്യാം. മൂല്യം ഉണ്ടെങ്കില്ത്തന്നെ അത് സീമയുടെ വിലയ്ക്ക് തുല്യമാകണമെന്നും ഇല്ല; ഫലനത്തിന്റെ മൂല്യവും ഫലനത്തിന്റെ സീമയും വ്യത്യസ്തങ്ങളായ സങ്കല്പങ്ങളാണ്. അതുപോലെ x,a യോടടുക്കുമ്പോള് (x→a)xന്റെ വില a യോടും ശരിക്കും "അടുത്തുവരുന്നു'. എന്നാല് x ഒരിക്കലും a യോടു തുല്യമാകുന്നില്ല. |
| - | ഒരു ഫലനത്തിന്റെ മൂല്യവും സീമയും തുല്യമാകുമ്പോള് ഫലനം സതതമാണെന്നു (continuous)പറയുന്നു. അതുകൊണ്ട് ഫലനസാതത്യത്തിന്റെ നിബന്ധനകള് | + | ഒരു ഫലനത്തിന്റെ മൂല്യവും സീമയും തുല്യമാകുമ്പോള് ഫലനം സതതമാണെന്നു (continuous)പറയുന്നു. അതുകൊണ്ട് ഫലനസാതത്യത്തിന്റെ നിബന്ധനകള് x→<sup>സീമ</sup>a+ f(x)=f(a)= x→<sup>സീമ</sup>a- എന്നെഴുതുന്നു. ഇവയില് ഏതെങ്കിലും ഒരു നിബന്ധന ശരിയായില്ലെങ്കില് ഫലനം x=a യില് സതതമല്ല. ഒരു അന്തരാള(interval) ത്തിലെ എല്ലാ ബിന്ദുക്കളിലും സതതമായിരിക്കുന്ന ഫലനം ആ അന്തരാളത്തില് സതതമാണെന്നു പറയുന്നു. |
| + | |||
| + | '''അനന്തസൂക്ഷ്മങ്ങള്''' (Infinitesimals). സീമയുടെ (മുകളില് കൊടുത്ത) നിര്വചനത്തില്ഒരു സ്വേച്ഛാസ്ഥിരസംഖ്യ (arbitrary constant)യോണ്. അത് ഏതെങ്കിലും ചെറിയ സംഖ്യയാകാം. f(x)→A ആകുമ്പോള്, ε പൂജ്യത്തോടടുക്കുന്നു. അതുപോലെ δ യും ε നെ ആശ്രയിക്കുന്ന ഒരു സ്വേച്ഛാസ്ഥിര സംഖ്യയാണ്. x→a ആകുമ്പോള് δ യും പൂജ്യത്തോടടുക്കുന്നു. ഇങ്ങനെയുള്ള രാശികളെ (ε-ഉം δ-ഉം) അനന്ത സൂക്ഷ്മങ്ങളെന്നോ സീമാപൂജ്യങ്ങളെന്നോ (limiting zeros) പറയുന്നു. സീമാപൂജ്യങ്ങള് കേവല പൂജ്യ(absolute zeros)ങ്ങളല്ലാത്തതുകൊണ്ടും അവകൊണ്ടുള്ള ഹരണം അനുവദനീയമാണ്. മുകളില് കൊടുത്ത പ്രത്യേകസ്ഥിതിയില് ε,δ→0 ആകുമ്പോള്, ε/a' ഒരു നിശ്ചിത സംഖ്യ(fixed number)യോടടുക്കുകയാണെങ്കില്, ഈ സീമയെ അവകലജഗുണാങ്കം (differential coefficient)എന്നു പറയുന്നു. | ||
| - | |||
== അവകലനം== | == അവകലനം== | ||
| - | അനന്തസൂക്ഷ്മമായ അളവുകള് ക്രാഡീകരിക്കാനുള്ള മാര്ഗമാണ് സീമാതത്ത്വം ഉപയോഗിച്ച് കലനത്തില് പ്രതിപാദിക്കപ്പെടുന്നത്. അനന്തസൂക്ഷ്മങ്ങളായ | + | അനന്തസൂക്ഷ്മമായ അളവുകള് ക്രാഡീകരിക്കാനുള്ള മാര്ഗമാണ് സീമാതത്ത്വം ഉപയോഗിച്ച് കലനത്തില് പ്രതിപാദിക്കപ്പെടുന്നത്. അനന്തസൂക്ഷ്മങ്ങളായ δഉം εഉം യഥാക്രമം x ലും y = f(x) ഉള്ള സംഗത വ്യത്യാസങ്ങളാണ്. ഇവയെ Δx എന്നും Δy(ഡെല്റ്റ x, ഡെല്റ്റ y) എന്നും സാധാരണ കുറിക്കുന്നു. Δy/Δxനെ ഈ രാശികളുടെ വ്യത്യാസ ഭാഗഫലമെന്നു (difference quotient) വിളിക്കുന്നു. xന്റെ Δx എന്ന അന്തരാളത്തില് y ക്കുണ്ടാകുന്ന ശരാശരി വര്ധനവാണ് Δy/Δx. ഇവിടെ [[ചിത്രം:Vol6_610 full_1 a.jpg|75px]] Δy/Δx ഉണ്ടെങ്കില് അതിനെ y യുടെ x കൊണ്ടുള്ള അവകലജ ഗുണാങ്കം അഥവാ അവകലജം എന്നു പറയുന്നു (differential coefficient of y with respect to x). ഈ സീമയെ കുറിക്കാന് dy/dx എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_610 full_1 b.jpg|300px]] | |
| - | + | ||
| - | u,x ന്റെ ഫലനവും ആയാല് (ശൃംഖലാനിയമം).y = | + | |
| + | |||
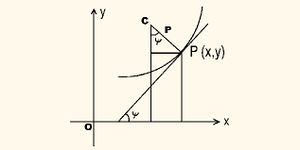
| + | അവകലജത്തിന് ജ്യാമിതീയ വ്യാഖ്യാനം നല്കാവുന്നതാണ്. വിശ്ലേഷക ജ്യാമിതിയില് P(x,y), Q(x+Δy, y+Δx) എന്നീ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന രേഖയായ PQ വിന്റെ ചരിവുമാനം (slope) Δy/Δx ആണ്. ഇവിടെ കൊടുത്തിട്ടുള്ള ഗ്രാഫില് നിന്ന് Δy/Δx = tanθ. Q എന്ന ബിന്ദു, വക്രത്തിലൂടെ സഞ്ചരിച്ച് P യോടടുക്കുമ്പോള് Δx → 0, θ → Ψ . അതുകൊണ്ട് [[ചിത്രം:Vol6_610 full_2 d.jpg|200px]] അതായത്, dy/dx=tanΨ. | ||
| + | |||
| + | അങ്ങനെ y = f(x) എന്ന വക്രത്തിന്റെ (x, y) എന്ന ബിന്ദുവിലുള്ള ചരിവുമാനമാണ് dy/dx. | ||
| + | |||
| + | അതായത് സ്പര്ശക(tangent)ത്തേിന്റെ ചരിവുമാനമാണ് അവകലജം. അവകലജഗുണാങ്കത്തെ മറ്റൊരു വിധത്തിലും വ്യാഖ്യാനിക്കാം. മാറ്റത്തിന്റെ ക്ഷണികനിരക്ക് എന്നു അവകലജത്തെ നിര്വചിക്കാവുന്നതാണ്. xനുണ്ടാകുന്ന | ||
| + | |||
| + | [[ചിത്രം:Vol6_610 full_3 a.jpg|300px]] | ||
| + | |||
| + | മാറ്റമനുസരിച് yക്കുണ്ടാകുന്ന മാറ്റത്തിന്റെ തോതാണ് (rate of change)y യുടെ x കൊണ്ടുള്ള അവകലജഗുണാങ്കം. സെക്കന്ഡില് ദൂരം സെഞ്ചരിക്കുന്ന ഒരു കണത്തിന്റെ (particle) പ്രവേഗം (velocity), ത്വരണം (acceleration) എന്നിവയുടെ പരിമാണം കണ്ടുപിടിക്കാന് v=ds/dt, a=d<sup>2</sup>s/dt<sup>2</sup> എന്നീ സൂത്രവാക്യങ്ങള് ഉപയോഗിക്കുന്നു. കൂടാതെ ചലിക്കുന്ന ഒരു കണത്തിന്റെ സെക്കന്ഡിലുള്ള കാര്ത്തീയ നിര്ദേശാങ്കങ്ങള് (x,y,z) ആയാല് അതിന്റെ പ്രവേഗ ഘടകങ്ങള് (velocity components) dx/dt, dy/dt, dz/dt ആണ്. | ||
| + | |||
| + | x = a എന്ന വിലയ്ക്കും y = f(x) എന്ന ഫലനം വര്ധിക്കുകയാണെങ്കില്,xന്റെ ഈ വിലയ്ക്ക് dy/dx ധനാത്മകമായിരിക്കും. അതുപോലെ ഫലനം കുറയുകയാണെങ്കില് dy/dx ഋണാത്മകമായിരിക്കും. x=a യ്ക്ക് dy/dxന്റെ വിലയെ കുറിക്കാന് (dy/dx)<sub>a</sub> എന്നെഴുതാം. (dy/dx)<sub>a</sub>=0 ആകുമ്പോള് x=a യ്ക്ക് y കൂടുകയോ കുറയുകയോ ചെയ്യുന്നില്ല. അപ്പോള് y യെ അചലബിന്ദു (stationary point)എന്നു വിളിക്കുന്നു. അചലബിന്ദുവില് വക്രത്തിനു വരയ്ക്കുന്ന സ്പര്ശകം x അക്ഷത്തിനു സമാന്തരമായിരിക്കും. ഫലനത്തിന്റെ മഹത്തമന്യൂനതമമൂല്യങ്ങള് കണ്ടുപിടിക്കാന് ഈ വസ്തുത ഉപയോഗിക്കുന്നു. | ||
| + | |||
| + | അവകലജ ഗുണാങ്കത്തിന്റെ നിര്വചനത്തില് നിന്ന് പ്രാരംഭികഫലനങ്ങളുടെ അവകലജങ്ങള് കണ്ടുപിടിക്കാം. x<sup>n</sup>, sin x, cos x, e<sup>x</sup>, log x, 1/x എന്നീ ഫലനങ്ങളുടെ അവകലജങ്ങള് യഥാക്രമം nx<sup>n-1</sup>, cos x, -sin x, e<sup>x</sup>, 1/x ആണ്. രണ്ടു ഫലനങ്ങളുടെ തുക, വ്യത്യാസം, ഗുണനഫലം, ഭാഗഫലം ഇവയുടെ അവകലജങ്ങള് കണ്ടുപിടിക്കാന് പ്രത്യേക നിയമങ്ങളുണ്ട്. ഗുണനഫലംu,vയുടെ അവകലജം, [[ചിത്രം:Vol6_611_2 a.jpg|150px]]ഉം u/vയുടെ അവകലജം [[ചിത്രം:Vol6_611_2 b.jpg|150px]]ഉം ആണ്. xഉം yഉം t എന്ന പ്രാചല (parameter) ത്തിന്റെ ഫലനങ്ങളാണെങ്കില് [[ചിത്രം:Vol6_611_2 c.jpg|75px]] അതുപോലെ yഉം zഉം xന്റെ ഫലനങ്ങളാണെങ്കില് y യുടെ z കൊണ്ടുള്ള അവകലജം [[ചിത്രം:Vol6_611_2 d.jpg|75px]] ആണ്.y, u ന്റെ ഫലനവും, u,x ന്റെ ഫലനവും ആയാല് [[ചിത്രം:Vol6_611_2 e.jpg|75px]] (ശൃംഖലാനിയമം).y = u<sup>v</sup> ആയാല് ലോഗരിതീയ അവകലന രീതിയുപയോഗിച്ച് കണ്ടുപിടിക്കാവുന്നതാണ്. | ||
=== ഉത്തരോത്തര അവകലനം=== | === ഉത്തരോത്തര അവകലനം=== | ||
| - | ഒരു ഫലനത്തിന്റെ അവകലജങ്ങളെ തുടര്ച്ചയായി അവകലിച്ചാല് ഉയര്ന്ന ക്രമത്തിലുള്ള അവകലജങ്ങള് കിട്ടും. ഈ പ്രക്രിയയെ ഉത്തരോത്തര അവകലനം എന്നു പറയുന്നു. | + | |
| + | ഒരു ഫലനത്തിന്റെ അവകലജങ്ങളെ തുടര്ച്ചയായി അവകലിച്ചാല് ഉയര്ന്ന ക്രമത്തിലുള്ള അവകലജങ്ങള് കിട്ടും. ഈ പ്രക്രിയയെ ഉത്തരോത്തര അവകലനം എന്നു പറയുന്നു. n മത്തെ അവകലജത്തെ കുറിക്കാന് [[ചിത്രം:Vol6_611_2 f.jpg|200px]] തുടങ്ങിയ പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ n മത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള സൂത്രവാക്യമാണ് "ലൈബ്നിറ്റ്സ് പ്രമേയം'. അതായത്, u, vഇവ | ||
x ന്റെ ഫലനങ്ങളാണെങ്കില്, | x ന്റെ ഫലനങ്ങളാണെങ്കില്, | ||
| + | |||
| + | [[ചിത്രം:Vol6_611_3 a.jpg|300px]] | ||
ചില സാധാരണ ഫലനങ്ങളുടെ n-ാമത്തെ അവകലജത്തിന്റെ സൂത്രവാക്യങ്ങള് താഴെ കൊടുക്കുന്നു: | ചില സാധാരണ ഫലനങ്ങളുടെ n-ാമത്തെ അവകലജത്തിന്റെ സൂത്രവാക്യങ്ങള് താഴെ കൊടുക്കുന്നു: | ||
| + | |||
| + | [[ചിത്രം:Vol6_611_3 b.jpg|300px]] | ||
| + | |||
| + | [[ചിത്രം:Vol6_611_1c.jpg|300px]] | ||
=== ആംശിക അവകലനം=== | === ആംശിക അവകലനം=== | ||
| - | ഒന്നില് ക്കൂടുതല് സ്വതന്ത്രചരങ്ങളുള്ള ഫലനങ്ങള്ക്ക് ആംശിക അവകലജങ്ങള് നിര്വചിക്കാവുന്നതാണ്. സ്വതന്ത്രചരങ്ങളില് ഏതെങ്കിലും ഒന്നുമാത്രം വ്യത്യാസപ്പെടുകയും മറ്റെല്ലാം സ്ഥിരമായിരിക്കുകയും ചെയ്യുമ്പോഴുള്ള വ്യത്യാസ ഭാഗഫലത്തിന്റെ (difference quotient) സീമയാണ് ആ ചരം കൊണ്ടുള്ള ആംശിക അവകലജം.u = f(x,y) രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ ഫലനമായിരിക്കട്ടെ. അപ്പോള് | + | ഒന്നില് ക്കൂടുതല് സ്വതന്ത്രചരങ്ങളുള്ള ഫലനങ്ങള്ക്ക് ആംശിക അവകലജങ്ങള് നിര്വചിക്കാവുന്നതാണ്. സ്വതന്ത്രചരങ്ങളില് ഏതെങ്കിലും ഒന്നുമാത്രം വ്യത്യാസപ്പെടുകയും മറ്റെല്ലാം സ്ഥിരമായിരിക്കുകയും ചെയ്യുമ്പോഴുള്ള വ്യത്യാസ ഭാഗഫലത്തിന്റെ (difference quotient) സീമയാണ് ആ ചരം കൊണ്ടുള്ള ആംശിക അവകലജം.u = f(x,y) രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ ഫലനമായിരിക്കട്ടെ. അപ്പോള് ∂u/∂x, ∂u/∂y എന്നീ ആംശിക അവകലജങ്ങളെ |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_611_1d.jpg|300px]]ചിക്കാം. | |
| - | + | ഉത്തരോത്തര അവകലനംകൊണ്ട് ഉയര്ന്ന ക്രമങ്ങളിലുള്ള ആംശിക അവകലജങ്ങള് കിട്ടുന്നു. [[ചിത്രം:Vol6_611_2 g.jpg|100px]] ഉം x, y എന്നിവയുടെ ഫലനങ്ങളാകയാല് അവയെ വീണ്ടും അവകലിക്കാം. അങ്ങനെ, | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_611_2 h.jpg|200px]]എന്നീ ഉയര്ന്ന ക്രമങ്ങളിലുള്ള അവകലജങ്ങള് കിട്ടുന്നു. സാധാരണ സ്ഥിതികളില്, | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_611_2 i.jpg|200px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | ഒരു ബീജീയ വ്യഞ്ജകത്തിലെ (algebraic expression) എല്ലാ പദങ്ങളുടെയും ഘാതം (degree) തുല്യമായിരുന്നാല് അതിനെ സമഘാതഫലനം (homogeneous function) എന്നു പറയുന്നു. x,y ചരങ്ങളുടെ 'n'-ാം ഘാതത്തിലുള്ള | ||
| + | സമഘാത ഫലനം u (x,y) ആയാല് അതിനെu(x,y) = x<sup>n</sup> f(y/x)എന്നെഴുതാം. | ||
| + | |||
| + | [[ചിത്രം:Vol6_611_2 j.jpg|300px]] | ||
| + | |||
| + | x, yചരങ്ങളുടെ n-ാം ഘാതത്തിലുള്ള സമഘാത ഫലനം u(x,y) ആയാല് [[ചിത്രം:Vol6_611_3 c.jpg|200px]] (ഓയ്ലര് പ്രമേയം). ഓയ്ലര് പ്രമേയത്തിന്റെ പൊതുരൂപം താഴെ കൊടുക്കുന്നു: | ||
| + | |||
| + | |||
| + | x1, x2, x3 ... ചരങ്ങളുടെ n-ാം ഘാതത്തിലുള്ള സമഘാതഫലനം u(x1, x2, x3 ...) ആയാല് [[ചിത്രം:Vol6_611_3 d.jpg|200px]] | ||
| + | |||
| + | u(x, y) എന്ന ഫലനത്തില് xഉം yഉം എന്ന ചരത്തിന്റെ ഫലനങ്ങളാണെങ്കില് പൂര്ണ അവകലജം (total derivative) കണ്ടുപിടിക്കാന് [[ചിത്രം:Vol6_612_1.jpg|100px]] എന്ന സൂത്രവാക്യം ഉപയോഗിക്കുന്നു. | ||
| + | |||
| + | === മാധ്യമൂല്യ പ്രമേയങ്ങള് (Mean Value Theorems)=== | ||
| + | |||
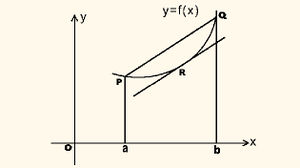
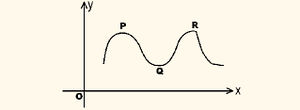
| + | അവിച്ഛിന്നമായി വര്ധിച്ചുകൊണ്ടിരിക്കുന്ന വേഗതയോടെ പാഞ്ഞുപോകുന്ന ഒരു തീവണ്ടി അതിന്റെ യാത്രയ്ക്കിടയില് ഒരിടത്തെങ്കിലും ശരാശരി വേഗതയില് സഞ്ചരിക്കുമെന്നു വ്യക്തമാണ്. അതുപോലെ P, Q എന്നീ ബിന്ദുക്കളില്ക്കൂടി കടന്നുപോകുന്ന ഒരു വക്രത്തിന് ഈ ബിന്ദുക്കള്ക്കുള്ളില് എല്ലായിടത്തും നിയതമായ സ്പര്ശകങ്ങളുണ്ടെങ്കില്, ചാപം PQ വിനു സമാന്തരമായി സ്പര്ശകമുള്ള R എന്ന ഒരു ബിന്ദുവെങ്കിലും വക്രത്തിലുണ്ടായിരിക്കും. ഇതാണ് മാധ്യമൂല്യപ്രമേയത്തിന്റെ ജ്യാമിതീയ സ്വഭാവം. അവകലനത്തിലെ ഏറ്റവും പ്രധാനപ്പെട്ട പ്രമേയമാണിത്. വിശ്ലേഷണരീതിയില് പ്രമേയത്തെ ഇങ്ങനെ പ്രസ്താവിക്കാം: [a, b] എന്ന സംവൃത അന്തരാള(closed interval)ത്തില് f(x) സതതവും, (a, b) എന്ന വിവൃത അന്തരാളത്തില് f(x) അവകലനീയവുമായാല്, [[ചിത്രം:Vol6_612_3.jpg|100px]] ആകത്തക്കവണ്ണം (a, b) യില് xന് c എന്ന ഒരു വിലയെങ്കിലും ഉണ്ടായിരിക്കും. "ലാഗ്രഞ്ചിന്റെ മാധ്യമൂല്യപ്രമേയം' എന്ന പേരില് ഇത് അറിയപ്പെടുന്നു. b - a = h ആയാല് c = a + θh (0 < θ < 1) എന്നെഴുതാം. അപ്പോള്, f(a+h) = f(a) + hf (a + θh). മാധ്യമൂല്യപ്രമേയത്തിന്റെ മറ്റൊരു രൂപമാണിത്. | ||
| + | |||
| + | [[ചിത്രം:Vol6_612_2.jpg|300px]] | ||
| + | |||
| + | മാധ്യമൂല്യപ്രമേയത്തിന്റെ വ്യാപകരൂപമാണ് "ടെയിലര് പ്രമേയം' (Taylor's Theorem). ഈ പ്രമേയത്തെ ഇങ്ങനെ പ്രസ്താവിക്കാം: (a, a+h) എന്ന അന്തരാളത്തില് f (x)ഉം അതിന്റെ ആദ്യത്തെ (n 1) അവകലജങ്ങളും സതതമായിരിക്കുകയും, (a, a+h) അന്തരാളത്തില് x ന്റെ എല്ലാ വിലകള്ക്കും f <sup>(n)</sup>(x) ഉണ്ടായിരിക്കുകയും ചെയ്യുമ്പോള്, | ||
| + | |||
| + | [[ചിത്രം:Vol6_612_4.jpg|300px]] | ||
| + | |||
| + | മുകളില് കൊടുത്ത പ്രമേയങ്ങളില് f(x) ന്റെ എല്ലാ അവകലജങ്ങളും സതതവും n →∞,n പദങ്ങള് കഴിഞ്ഞുള്ള ശിഷ്ടം പൂജ്യത്തോടടുക്കുകയും ചെയ്യുന്നു എങ്കില് ടെയിലര് ശ്രണിയും മക്ലോറിന് ശ്രണിയും കിട്ടുന്നു: | ||
| + | |||
| + | [[ചിത്രം:Vol6_612_5.jpg|300px]] | ||
| + | |||
| + | മക്ലോറിന് ശ്രണിയുപയോഗിച്ച് sin x, cos x, tan x, e<sup>x</sup> തുടങ്ങിയ പല ഫലനങ്ങളെയും ഘാതശ്രണികളായി വികസിപ്പിക്കാനും അവയുടെ ഏകദേശവില കണ്ടുപിടിക്കാനും സാധിക്കുന്നു. | ||
| + | |||
| + | |||
| + | [[ചിത്രം:Vol6_612_6.jpg|300px]] | ||
| + | |||
| + | |||
| + | Δx വളരെ ചെറുതായതുകൊണ്ട് അതിന്റെ ഉയര്ന്ന ഘാതങ്ങള് അവഗണിക്കാവുന്നതാണ്. അപ്പോള് Δy=f'(x).Δx (ഏകദേശം) x ന്റെ മാപനത്തിലുള്ള പിശക് Δx ആയാല് y ന്റെ മാപനത്തിലുള്ള പിശക് Δy ആണ്. അതുകൊണ്ടും മുകളില് കൊടുത്തത് x, y എന്നിവയുടെ പിശകുകളുടെ ഏകദേശമാണ് (approximate error relation). | ||
| + | |||
| + | ഇതുവരെ അവകലജ ഗുണാങ്കമായ dy/dxനെ ഒരു പ്രതീകമായിട്ടാണ് ഗണിച്ചത്. എന്നാല് ചിലപ്പോള് dy ക്കും dx നും പ്രത്യേക അര്ഥ കല്പനകള് നടത്തി ഉപയോഗിക്കാറുണ്ട്. ഏതെങ്കിലും രണ്ടു ചെറിയ രാശികളായ dy, dx എന്നിവയുടെ അനുപാതം -dy/dx എന്ന അവകലജ ഗുണാങ്കമാണെങ്കില് dy, dx എന്നിവയെ യഥാക്രമം y യുടെയും x ന്റെയും അവകലങ്ങള് (differentials)എന്നു പറയുന്നു. | ||
| - | |||
| - | |||
== സമാകലനം== | == സമാകലനം== | ||
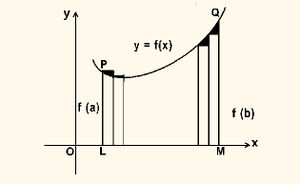
ഒരു തലത്തിലെ വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കാനാണ് സമാകലനം ആദ്യകാലത്ത് ഉപയോഗിച്ചിരുന്നത്. അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമയായി റീമാന് (182666) സമാകലത്തെ (Integration) നിര്വചിച്ചു. പില്ക്കാലത്ത് ലെബേഗ് സമാകലനത്തിനു പുതിയ നിര്വചനം കൊടുത്തിട്ടുണ്ടെങ്കിലും റീമാന്റെ നിര്വചനം പ്രായോഗികതലത്തില് സുപ്രധാനമാണ്. | ഒരു തലത്തിലെ വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കാനാണ് സമാകലനം ആദ്യകാലത്ത് ഉപയോഗിച്ചിരുന്നത്. അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമയായി റീമാന് (182666) സമാകലത്തെ (Integration) നിര്വചിച്ചു. പില്ക്കാലത്ത് ലെബേഗ് സമാകലനത്തിനു പുതിയ നിര്വചനം കൊടുത്തിട്ടുണ്ടെങ്കിലും റീമാന്റെ നിര്വചനം പ്രായോഗികതലത്തില് സുപ്രധാനമാണ്. | ||
| - | f(x) എന്ന ഫലനത്തിന്റെ x = a, x = b എന്നീ സീമകള്ക്കുള്ളിലുള്ള നിശ്ചിത സമാകലത്തെ (definite integral) | + | |
| - | + | f(x) എന്ന ഫലനത്തിന്റെ x = a, x = b എന്നീ സീമകള്ക്കുള്ളിലുള്ള നിശ്ചിത സമാകലത്തെ (definite integral) [[ചിത്രം:Vol6_612_7.jpg|100px]] | |
| - | മുകളില് കൊടുത്ത നിശ്ചിത സമാകലനത്തിന്റെ നിര്വചനം ഒരു സാമാന്യനിര്വചനത്തിന്റെ വിശേഷ രൂപമാണ്. നിശ്ചിതസമാകലത്തെ സംബന്ധിച്ച സാമാന്യ നിര്വചനം താഴെ കൊടുക്കുന്നു: (a, b) അന്തരാളത്തിലുള്ള ഫലനം f(x) എടുക്കുക, അന്തരാളം (a,b) യെ ( | + | |
| - | + | [[ചിത്രം:Vol6_613_1.jpg|330px]] | |
| - | + | ||
| - | + | തീയ രീതിയില്, ഈ നിര്വചനമനുസരിച്ചുള്ള നിശ്ചിതസമാകലം വിസ്തീര്ണത്തെ (LMQP) കുറിക്കുന്നു. ഇവിടെ ചിത്രത്തില് ചെറിയ ദീര്ഘചതുരങ്ങളുടെ വീതി h→0, ദീര്ഘചതുരങ്ങളുടെ എണ്ണം (n) അനന്തത്തോടടുക്കുകയും ദീര്ഘചതുരങ്ങളുടെ മുകളിലുള്ള വക്രീയ ത്രികോണങ്ങളുടെ വിസ്തീര്ണങ്ങളുടെ തുക പൂജ്യത്തോടടുക്കുകയും ചെയ്യുന്നു. | |
| - | + | ||
| - | + | ||
| + | |||
| + | മുകളില് കൊടുത്ത നിശ്ചിത സമാകലനത്തിന്റെ നിര്വചനം ഒരു സാമാന്യനിര്വചനത്തിന്റെ വിശേഷ രൂപമാണ്. നിശ്ചിതസമാകലത്തെ സംബന്ധിച്ച സാമാന്യ നിര്വചനം താഴെ കൊടുക്കുന്നു: (a, b) അന്തരാളത്തിലുള്ള | ||
| + | |||
| + | [[ചിത്രം:Vol6_613_2.jpg|300px]] | ||
| + | |||
| + | ഫലനം f(x) എടുക്കുക, അന്തരാളം (a,b) യെ (x<sub>r-1</sub>, x<sub>r</sub>) r = 1, 2, ... nഎന്ന n ഭാഗങ്ങളാക്കുക. ഈ ഉപഅന്തരാളങ്ങള് (sub-intervals) തുല്യമാകണമെന്നില്ല.r-ാമത്തെ | ||
| + | |||
| + | [[ചിത്രം:Vol6_613_3.jpg|300px]] | ||
| + | |||
| + | |||
| + | ത്തിലെ മൗലിക പ്രമേയമാണ്. ഇതില് നിന്ന്, സങ്കലനവും വ്യവകലനവുംപോലെ അവകലനവും സമാകലനവും പ്രതിലോമ ക്രിയകളാണെന്ന് വ്യക്തമാണ്. ഗ്രാഫികമായി ഈ പ്രമേയം പരിശോധിക്കാവുന്നതാണ്. | ||
| + | |||
| + | [[ചിത്രം:Vol6_613_4.jpg|300px]] | ||
| - | + | [[ചിത്രം:Vol6_613_5.jpg|300px]] | |
F(x) നെ f (x) ന്റെ പൂര്വഗം എന്നു പറയുന്നു. | F(x) നെ f (x) ന്റെ പൂര്വഗം എന്നു പറയുന്നു. | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_613_6.jpg|300px]] | |
| - | + | ||
| - | + | ഒരു ഫലനത്തിന്റെ പ്രതിഅവകലജത്തിലെ രണ്ട് അംഗങ്ങള് തമ്മിലുള്ള വ്യത്യാസം ഒരു സ്വേച്ഛാ സ്ഥിരാങ്കമായിരിക്കും. | |
| - | + | ||
| + | |||
| + | [[ചിത്രം:Vol6_613_7.jpg|300px]] | ||
| + | |||
=== നിശ്ചിത സമാകലംപ്രാരംഭിക പ്രമേയങ്ങള്=== | === നിശ്ചിത സമാകലംപ്രാരംഭിക പ്രമേയങ്ങള്=== | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_614_1.jpg|300px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
f (x) യുഗ്മഫലനമാകുമ്പോള്, = 0, f (x) ഒറ്റഫലനമാകുമ്പോള്. | f (x) യുഗ്മഫലനമാകുമ്പോള്, = 0, f (x) ഒറ്റഫലനമാകുമ്പോള്. | ||
| - | + | ||
| - | + | [[ചിത്രം:Vol6_614_2.jpg|300px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
=== ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള്=== | === ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള്=== | ||
ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള് രണ്ടുവിധത്തിലാവാം. ഉത്തരോത്തര അവകലനത്തിനു സദൃശമായി ഒരു ഫലനത്തെ ഉത്തരോത്തരമായി n പ്രാവശ്യം സമാകലിച്ചാല് ഫലനത്തിന്റെ n-ാമത്തെ സമാകലം കിട്ടുന്നു. കൂടാതെ സാധാരണ സമാകലത്തിന്റെ പരിധി ഉയര്ന്ന വിമകളിലേക്കു വ്യാപിപ്പിച്ചാല് മറ്റൊരു തരത്തിലുള്ള സമാകലം കിട്ടുന്നു. | ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള് രണ്ടുവിധത്തിലാവാം. ഉത്തരോത്തര അവകലനത്തിനു സദൃശമായി ഒരു ഫലനത്തെ ഉത്തരോത്തരമായി n പ്രാവശ്യം സമാകലിച്ചാല് ഫലനത്തിന്റെ n-ാമത്തെ സമാകലം കിട്ടുന്നു. കൂടാതെ സാധാരണ സമാകലത്തിന്റെ പരിധി ഉയര്ന്ന വിമകളിലേക്കു വ്യാപിപ്പിച്ചാല് മറ്റൊരു തരത്തിലുള്ള സമാകലം കിട്ടുന്നു. | ||
| - | ==== പുനരാവൃത്ത സമാകലം==== | + | ==== പുനരാവൃത്ത സമാകലം(Iterated integral)==== |
| - | f(x) എന്ന ഫലനത്തിന്റെ സമാകലനം F1(x) ആയിരിക്കട്ടെ. അതായത് | + | f(x) എന്ന ഫലനത്തിന്റെ സമാകലനം F1(x) ആയിരിക്കട്ടെ. അതായത് |
| - | + | ||
| + | [[ചിത്രം:Vol6_614_3.jpg|300px]] | ||
| - | സമാകലനത്തിന്റെ ഓരോ ഘട്ടത്തിലുമുണ്ടാകുന്ന സമാകലന അചരം (constant of integration) അടുത്തഘട്ടത്തില് സമാകലിക്കപ്പെടുന്നു. അതുകൊണ്- | + | സമാകലനത്തിന്റെ ഓരോ ഘട്ടത്തിലുമുണ്ടാകുന്ന സമാകലന അചരം (constant of integration) അടുത്തഘട്ടത്തില് സമാകലിക്കപ്പെടുന്നു. അതുകൊണ് n-ആമത്തെ സമാകലത്തില്, P<sub>n-1</sub>(x) = |
| - | + | A<sub>1</sub>x<sup>n-1</sup>+ A<sub>2</sub> x<sup>n-2</sup> + ......... + A<sub>1</sub> എന്ന ബഹുപദം കൂടി കിട്ടുന്നു. | |
| - | + | ||
| - | + | [[ചിത്രം:Vol6_614_4.jpg|300px]] | |
==== ബഹുസമാകലം==== | ==== ബഹുസമാകലം==== | ||
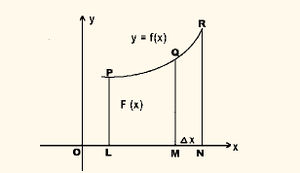
| - | (x, y) തലത്തിലുള്ള | + | (x, y) തലത്തിലുള്ള ഒരു വക്രം y = f(x) ആയിരിക്കട്ടെ. അപ്പോള് xന്റെ (a,b) എന്ന അന്തരാളത്തില് വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണമാണ് ∫<sub>a</sub><sup>b</sup>f(x) dx ഈ സമാകലത്തിനു ഭൗതികമായ ഒരു അര്ഥകല്പന നടത്താവുന്നതാണ്.x അക്ഷത്തില് x = a, x = b എന്നീ ബിന്ദുക്കള്ക്കിടയിലുള്ളതും സാന്ദ്രത ρ=f(x) ആയതുമായ ഒരു ദണ്ഡിന്റെ ദ്രവ്യമാനമാണ് ഈ സമാകലം കുറിക്കുന്നത്. വിസ്തീര്ണത്തെ സംബന്ധിച്ച അര്ഥകല്പനയ്ക്കു സമാനമായ മറ്റൊരാശയമുപയോഗിച്ച് Z= f(x,y) എന്ന ഫലനത്തിന്റെ യുഗ്മസമാകലം (double integral) നിര്വചിക്കാവുന്നതാണ്. Z= f(x,y) എന്ന പ്രതലത്തിന്റെ (x,y) തലത്തിലുള്ള വിക്ഷേപം (projection), ഞ എന്ന വക്രമുള്ക്കൊള്ളുന്ന പ്രദേശമായിരിക്കട്ടെ. അപ്പോള് ഈ പ്രതലം ഉള്ക്കൊള്ളുന്ന സ്തംഭത്തിന്റെ വ്യാപ്തത്തെ കുറിക്കുന്ന സമാകലമാണ് ∫∫<sub>R</sub> f(x,y)dydx ചിത്രീകരിക്കാവുന്ന പ്രതലത്തെ പ്രതിനിധീകരിക്കുന്ന പ്രതലം Z = f(x,y) യും സമാകലനപരിധി, വിസ്തീര്ണവുമാണ്. ഞ ഒറ്റവക്രമോ (ഉദാ. ദീര്ഘവൃത്തം) രണ്ടോ അതിലധികമോ വക്രങ്ങള് ചേര്ന്നതോ ആകാം. സാന്ദ്രതാഫലനം ρ=f(x,y) ആകുമ്പോള് വക്രം R ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണത്തിന്റെ ദ്രവ്യമാനമായും ഈ സമാകലത്തെ കണക്കാക്കാം. യുഗ്മസമാകലത്തെ ഇരട്ട അനന്തശ്രണിയുടെ സീമയായും മറ്റൊരു വിധത്തില് വ്യാഖ്യാനിക്കാവുന്നതാണ്. |
| - | ഒരു വക്രം y = f(x) ആയിരിക്കട്ടെ. അപ്പോള് xന്റെ (a,b) എന്ന അന്തരാളത്തില് വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണമാണ് ഈ സമാകലത്തിനു ഭൗതികമായ ഒരു അര്ഥകല്പന നടത്താവുന്നതാണ്.x അക്ഷത്തില് x = a, x = b എന്നീ ബിന്ദുക്കള്ക്കിടയിലുള്ളതും സാന്ദ്രത ആയതുമായ ഒരു ദണ്ഡിന്റെ ദ്രവ്യമാനമാണ് ഈ സമാകലം കുറിക്കുന്നത്. വിസ്തീര്ണത്തെ സംബന്ധിച്ച അര്ഥകല്പനയ്ക്കു സമാനമായ മറ്റൊരാശയമുപയോഗിച്ച് Z= f(x,y) എന്ന ഫലനത്തിന്റെ യുഗ്മസമാകലം (double integral) നിര്വചിക്കാവുന്നതാണ്. Z= f(x,y) എന്ന പ്രതലത്തിന്റെ (x,y) തലത്തിലുള്ള വിക്ഷേപം (projection), ഞ എന്ന വക്രമുള്ക്കൊള്ളുന്ന പ്രദേശമായിരിക്കട്ടെ. അപ്പോള് ഈ പ്രതലം ഉള്ക്കൊള്ളുന്ന സ്തംഭത്തിന്റെ വ്യാപ്തത്തെ കുറിക്കുന്ന സമാകലമാണ് | + | |
=== യുഗ്മസമാകലത്തിന്റെ മുല്യനിര്ണയനം=== | === യുഗ്മസമാകലത്തിന്റെ മുല്യനിര്ണയനം=== | ||
| - | ഒരു യുഗ്മസമാകലത്തിന്റെ മൂല്യം നിര്ണയിക്കുവാന് ആദ്യം അതിനെ ഒരു ലഘുസമാകലമായി മാറ്റുന്നു. എന്നിട്ട് ലഘുസമാകലത്തെ സമാകലിക്കുന്നു. പ്രതീകാത്മകമായി ഈ പ്രക്രിയകളെ ഇങ്ങനെ എഴുതാം: യുടെയും x ന്റെയും നിശ്ചിതസീമകള്ക്കിടയി x നെ സ്ഥിരമായി സങ്കല്പിച്ചു | + | ഒരു യുഗ്മസമാകലത്തിന്റെ മൂല്യം നിര്ണയിക്കുവാന് ആദ്യം അതിനെ ഒരു ലഘുസമാകലമായി മാറ്റുന്നു. എന്നിട്ട് ലഘുസമാകലത്തെ സമാകലിക്കുന്നു. പ്രതീകാത്മകമായി ഈ പ്രക്രിയകളെ ഇങ്ങനെ എഴുതാം: ∫∫f(x,y)dy dx = [∫f(x,y)dy]dx,y യുടെയും x ന്റെയും നിശ്ചിതസീമകള്ക്കിടയി x നെ സ്ഥിരമായി സങ്കല്പിച്ചു (x ന്റെ വില x<sub>0</sub> ആയിരിക്കട്ടെ. ചിത്രത്തില് x<sub>0</sub> = OL) യുടെ മൂല്യം നിര്ണയിക്കുന്നു.x = x<sub>0</sub> ആകുമ്പോള് y യുടെ സീമകള് വക്രം R ന്റെ സമീകരണത്തില് നിന്നു കിട്ടുന്നു (ചിത്രത്തില് x = x<sub>0</sub> = OL ആകുമ്പോള്,y യുടെ വില y<sub>1</sub>ല് നിന്ന് y<sub>2</sub>ലേക്കു മാറുന്നു). |
| - | (x ന്റെ വില | + | |
| - | ഖരരൂപത്തെ x = | + | ഖരരൂപത്തെ x = x<sub>0</sub> എന്ന തലം ഛേദിക്കുന്ന ലംബപരിച്ഛേദത്തെ F(x0) എന്ന ഫലനം പ്രതിനിധാനം ചെയ്യുന്നു. |
| - | + | ||
| - | x = x0, x = x0 + dx0 എന്നീ തലങ്ങള് ഉള്ക്കൊള്ളുന്ന നേര്ത്ത ലംബഖണ്ഡമാണ് F(x0) dx0. x0 നെ വര്ത്തമാന നിര്ദേശാങ്ക (current co-ordinate) ത്തിലേക്ക് മാറ്റി F(x) നെ യുക്തമായ സീമകള്ക്കുള്ളില് സമാകലിച്ചാല് എന്ന ലഘു സമാകലം കിട്ടുന്നു. | + | [[ചിത്രം:Vol6_614_5.jpg|300px]] |
| - | അങ്ങനെ | + | |
| - | === വിഷമ സമാകലങ്ങള്=== | + | x = x0, x = x0 + dx0 എന്നീ തലങ്ങള് ഉള്ക്കൊള്ളുന്ന നേര്ത്ത ലംബഖണ്ഡമാണ് F(x0) dx0. x0 നെ വര്ത്തമാന നിര്ദേശാങ്ക (current co-ordinate) ത്തിലേക്ക് മാറ്റി F(x) നെ യുക്തമായ സീമകള്ക്കുള്ളില് സമാകലിച്ചാല് |
| - | റെീമാന്റെ നിര്വചനമനുസരിച്ച് സമാകലം ല് സമാകലന അന്തരാളം (a, b) പരിമിതവും (finite) ഈ അന്തരാളത്തില് ഫലനം f(x) പരിബദ്ധവും (bounded) ആയിരിക്കണം. എന്നാല് ഇങ്ങനെ അല്ലാതെയും പ്രത്യേക സ്ഥിതികളെക്കൂടി ചേര്ത്ത് കോഷി, റീമാന്റെ നിര്വചനത്തെ പുതുക്കിയിട്ടുണ്ട്. പ്രത്യേക സ്ഥിതികള് താഴെപ്പറയുന്നവയാണ്: | + | [[ചിത്രം:Vol6_615_2.jpg|200px]] എന്ന ലഘു സമാകലം കിട്ടുന്നു. |
| + | |||
| + | അങ്ങനെ ∫ ∫ f(x,y)dydx | ||
| + | |||
| + | |||
| + | [[ചിത്രം:Vol6_615_2.jpg|300px]] | ||
| + | |||
| + | ഉദാ: [[ചിത്രം:Vol6_615_3.jpg|200px]] എന്ന ദീർഘവൃതജത്തിന്റെ (ellipsoid) (x,y) - തലത്തിലുള്ള വ്യാപ്തം കണക്കാക്കാം പ്രതലത്തിന്റെ സമീകരണത്തിൽ നിന്ന് z=f(x,y)= | ||
| + | |||
| + | [[ചിത്രം:Vol6_615_4.jpg|300px]] | ||
| + | |||
| + | === വിഷമ സമാകലങ്ങള്(Improper integrals)=== | ||
| + | റെീമാന്റെ നിര്വചനമനുസരിച്ച് സമാകലം [[ചിത്രം:Vol6_615_6.jpg|200px]] ല് സമാകലന അന്തരാളം (a, b) പരിമിതവും (finite) ഈ അന്തരാളത്തില് ഫലനം f(x) പരിബദ്ധവും (bounded) ആയിരിക്കണം. എന്നാല് ഇങ്ങനെ അല്ലാതെയും പ്രത്യേക സ്ഥിതികളെക്കൂടി ചേര്ത്ത് കോഷി, റീമാന്റെ നിര്വചനത്തെ പുതുക്കിയിട്ടുണ്ട്. പ്രത്യേക സ്ഥിതികള് താഴെപ്പറയുന്നവയാണ്: | ||
| + | |||
1. സമാകലന പരിധി അനന്തമായിരിക്കുന്ന അവസ്ഥ. അതായത് മ,യ ഇവയില് ഏതെങ്കിലും ഒന്നോ, രണ്ടും വെവ്വേറെയോ അനന്തമായിരിക്കും. | 1. സമാകലന പരിധി അനന്തമായിരിക്കുന്ന അവസ്ഥ. അതായത് മ,യ ഇവയില് ഏതെങ്കിലും ഒന്നോ, രണ്ടും വെവ്വേറെയോ അനന്തമായിരിക്കും. | ||
| - | + | ||
| + | [[ചിത്രം:Vol6_615_6.jpg|300px]] | ||
| + | |||
2. സീമകള് പരിമിതമാണെങ്കിലും ഫലനം f (x) പരിബദ്ധമായിരിക്കുകയില്ല; അതായത് f (x) ന് പരിമിതമായ അനന്ത അസാതത്യങ്ങള് (infinite discontinuities) ഉണ്ടായിരിക്കും. | 2. സീമകള് പരിമിതമാണെങ്കിലും ഫലനം f (x) പരിബദ്ധമായിരിക്കുകയില്ല; അതായത് f (x) ന് പരിമിതമായ അനന്ത അസാതത്യങ്ങള് (infinite discontinuities) ഉണ്ടായിരിക്കും. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | + | [[ചിത്രം:Vol6_615_7.jpg|300px]] | |
| + | ഇത്തരം സമാകലങ്ങളെ വിഷമ സമാകലങ്ങള് എന്നു പറയുന്നു. സമാകലന അന്തരാളത്തില് (a,b)ല് ഫലനം f(x) ന് x = c എന്ന ബിന്ദുവില് മാത്രം അനന്ത അസാതത്യം ഉണ്ടെന്നു സങ്കല്പിക്കുക. മറ്റെല്ലാ ബിന്ദുക്കളിലും ഫലനം പരിബദ്ധമാണ്. അപ്പോള് x = c എന്ന ബിന്ദുവിനെ (c-ε<sub>1</sub>,c+ε<sub>2</sub>) എന്ന ചെറിയ ഇടവേളയില് (ε<sub>1</sub>,ε<sub>2</sub> സ്വേച്ഛാപരങ്ങളായ ചെറിയ സംഖ്യകളാണ്) ഒതുക്കിയാല് അന്തരാളം (a,b) യുടെ മറ്റു ഭാഗങ്ങളില് f(x) പരിബദ്ധമാണ്. അപ്പോള് , [[ചിത്രം:Vol6_615_8.jpg|100px]] എന്നീ സമാകലങ്ങള്ക്ക് അസ്തിത്വമുണ്ട്. അവ ε<sub>1</sub>,ε<sub>2</sub> എന്നിവയുടെഫലനങ്ങളാണ്. വലതുവശത്തെ സീമകള് ഉണ്ടെങ്കില്, [[ചിത്രം:Vol6_615_9.jpg|100px]][[ചിത്രം:Vol6_615_11.jpg|100px]] ഈ മൂല്യത്തെ സമാകലത്തിന്റെ പൊതുമൂല്യം എന്നു പറയുന്നു. പൊതു മൂല്യമുണ്ടെങ്കില് സമാകലം അഭികേന്ദ്രസാരി (convergent) ആണ്. | ||
| + | |||
| + | ε<sub>1</sub>=ε<sub>2</sub>ആകുമ്പോള് സമാകലത്തിന്റെ മുഖ്യമൂല്യം (principal value) കിട്ടുന്നു. മുഖ്യമൂല്യത്തെ കുറിക്കാന് കോഷി [[ചിത്രം:Vol6_615_11.jpg|100px]] എന്ന പ്രതീകമുപയോഗിക്കുന്നു. സമാകലങ്ങള്ക്ക് പൊതുമൂല്യം എപ്പോഴും ഉണ്ടായിരിക്കണമെന്നില്ല. എന്നാല് പൊതുമൂല്യം ഉള്ളപ്പോള് അതു മുഖ്യമൂല്യം തന്നെയായിരിക്കും. | ||
| + | |||
| + | [[ചിത്രം:Vol6_615_13.jpg|300px]] | ||
| + | |||
| + | അസ്തിത്വമില്ലാത്തതിനാല് സമാകലത്തിനു പൊതുമൂല്യമില്ല. എന്നാല് ഈ സമാകലത്തിന്റെ മുഖ്യമൂല്യം പൂജ്യമാണ്. | ||
| + | |||
| + | [[ചിത്രം:Vol6_615_14.jpg|300px]] | ||
| + | |||
| + | |||
| + | വലതുവശത്തെ സീമകള് ഉണ്ടെങ്കില് സമാകലങ്ങള് അഭികേന്ദ്രസാരിയാണെന്നു പറയുന്നു. മൂന്നാമത്തെ സമാകലത്തിന്റെ മുഖ്യമൂല്യം [[ചിത്രം:Vol6_615_15.jpg|200px]] ആണ്. | ||
| - | |||
| - | |||
=== സവിശേഷതയുള്ള സമാകലങ്ങള്=== | === സവിശേഷതയുള്ള സമാകലങ്ങള്=== | ||
സമാകലനംകൊണ്ട് ബീജീയം, ത്രികോണമിതീയം, ലോഗരിതീയം, ഹൈപ്പര് ജ്യാമിതീയം തുടങ്ങിയ ഫലനങ്ങള് ഉണ്ടാവുന്നു. എന്നാല് ഇത്തരത്തിലല്ലാത്ത സവിശേഷ സ്വഭാവമുള്ള പല ഫലനങ്ങളും സമാകലനം കൊണ്ടും കിട്ടാറുണ്ട്. അവയില് ചില ഫലനങ്ങളാണ് താഴെ പറയുന്നത്: | സമാകലനംകൊണ്ട് ബീജീയം, ത്രികോണമിതീയം, ലോഗരിതീയം, ഹൈപ്പര് ജ്യാമിതീയം തുടങ്ങിയ ഫലനങ്ങള് ഉണ്ടാവുന്നു. എന്നാല് ഇത്തരത്തിലല്ലാത്ത സവിശേഷ സ്വഭാവമുള്ള പല ഫലനങ്ങളും സമാകലനം കൊണ്ടും കിട്ടാറുണ്ട്. അവയില് ചില ഫലനങ്ങളാണ് താഴെ പറയുന്നത്: | ||
| - | |||
| - | |||
| - | |||
| - | + | [[ചിത്രം:Vol6_616_1.jpg|300px]] | |
| - | + | ||
| - | + | [[ചിത്രം:Vol6_616_2.jpg|300px]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
== കലനം പ്രായോഗിക തലത്തില്== | == കലനം പ്രായോഗിക തലത്തില്== | ||
പ്രായോഗിക തലത്തില് കലനത്തിന്റെ ഉപയോഗം വ്യക്തമാക്കുന്ന ചില ഉദാഹരണങ്ങള് താഴെ കൊടുക്കുന്നു: | പ്രായോഗിക തലത്തില് കലനത്തിന്റെ ഉപയോഗം വ്യക്തമാക്കുന്ന ചില ഉദാഹരണങ്ങള് താഴെ കൊടുക്കുന്നു: | ||
=== സ്പര്ശകങ്ങളും അഭിലംബങ്ങളും=== | === സ്പര്ശകങ്ങളും അഭിലംബങ്ങളും=== | ||
| - | |||
| - | |||
| - | + | [[ചിത്രം:Vol6_616_3.jpg|300px]] | |
| + | |||
| + | [[ചിത്രം:Vol6_616_4.jpg|300px]] | ||
| + | |||
| + | (x1, y1) എന്ന ബിന്ദുവില് പ്രതിച്ഛേദിക്കുന്നy = f(x), y = g(x) എന്നീ വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം ഈ ബിന്ദുവില് വക്രങ്ങള്ക്കു വരയ്ക്കുന്ന സ്പര്ശകങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണമായി നിര്വചിച്ചിരിക്കുന്നു. അതുകൊണ്ടും വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം, [[ചിത്രം:Vol6_616_5.jpg|100px]] ആണ്. പ്രതിച്ഛേദബിന്ദുവില് വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം 90° ആണെങ്കില് അവ, ലംബികമായി പ്രതിച്ഛേദിക്കുന്നു എന്നു പറയുന്നു. അപ്പോള് | ||
| + | |||
| + | 1+f '(x1) g'(x1) = 0. വക്രങ്ങള് പരസ്പരം സ്പര്ശിക്കുമ്പോള് f '(x1) = g'(x1) എന്നു കിട്ടുന്നു. | ||
| + | |||
| + | [[ചിത്രം:Vol6_616_6.jpg|300px]] | ||
| + | |||
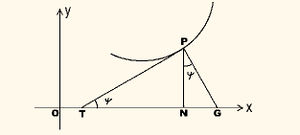
| + | വക്രത്തിനു P എന്ന ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകം PTഉം അഭിലംബം PGഉം x അക്ഷത്തെ T,G എന്നീ ബിന്ദുക്കളില് പ്രതിച്ഛേദിക്കുന്നു എന്നിരിക്കട്ടെ. കൂടാതെ Pല്ക്കൂടി x അക്ഷത്തിനു വരയ്ക്കുന്ന ലംബം PN ആയിരിക്കട്ടെ. അപ്പോള് PT, PG, TN, NG എന്നിവയെ യഥാക്രമം സ്പര്ശകം, അഭിലംബം, ഉപസ്പര്ശകം (subtangent), ഉപലംബം (subnormal) എന്നിവയുടെ ദൈര്ഘ്യമായി നിര്വചിച്ചിരിക്കുന്നു. ചിത്രത്തില് നിന്ന് ഇവ കണ്ടുപിടിക്കാവുന്നതാണ്. ഉദാ. ഉപലംബത്തിന്റെ ദൈര്ഘ്യം, . | ||
| + | |||
| + | [[ചിത്രം:Vol6_616_7.jpg|300px]] | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
=== അനന്ത സ്പര്ശകം=== | === അനന്ത സ്പര്ശകം=== | ||
| - | ഒരു വക്രത്തെ അനന്തത്തില് സ്പര്ശിക്കുന്നതും എന്നാല് അനന്തത്തിലല്ലാത്തതുമായ വാസ്തവിക രേഖയാണ് അനന്തസ്പര്ശകം. ഉദാ.xy = | + | ഒരു വക്രത്തെ അനന്തത്തില് സ്പര്ശിക്കുന്നതും എന്നാല് അനന്തത്തിലല്ലാത്തതുമായ വാസ്തവിക രേഖയാണ് അനന്തസ്പര്ശകം. ഉദാ.xy = c<sup>2</sup> (സമകോണീയ ഹൈപ്പര്ബോള) എന്ന വക്രത്തെ x അക്ഷവും |
| - | y അക്ഷവും അനന്തത്തില് സ്പര്ശിക്കുന്നു. അതുകൊണ്ട് x,y അക്ഷങ്ങളാണ് xy = | + | y അക്ഷവും അനന്തത്തില് സ്പര്ശിക്കുന്നു. അതുകൊണ്ട് x,y അക്ഷങ്ങളാണ് xy = c<sup>2</sup> എന്ന വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള്. |
| - | n-ാമത്തെ ഡിഗ്രിയിലുള്ള ഒരു ബീജീയവക്രത്തെ എന്ന് എഴുതാവുന്നതാണ്. ഈ വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാം.y = mx + | + | |
| + | n-ാമത്തെ ഡിഗ്രിയിലുള്ള ഒരു ബീജീയവക്രത്തെ [[ചിത്രം:Vol6_616_8.jpg|200px]] എന്ന് എഴുതാവുന്നതാണ്. ഈ വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാം.y = mx + δഎന്ന രേഖ ഈ വക്രത്തെ പ്രതിച്ഛേദിക്കുന്ന ബിന്ദുക്കളുടെ x നിര്ദേശാങ്കങ്ങള് കിട്ടുവാന് ഈ സമീകരണങ്ങളില്നിന്ന് y യെ ഒഴിവാക്കുന്നു. അപ്പോള് | ||
| + | |||
| + | [[ചിത്രം:Vol6_617_1.jpg|300px]] | ||
| + | |||
| + | ഓരോ പദത്തെയും ടെയിലര് പ്രമേയമുപയോഗിച്ച് വികസിപ്പിച്ചാല്, x<sup>n</sup>Φ<sub>2</sub>(m) +x<sup>(n-1)</sup>[c Φ<sub>2</sub>(m)+ Φ<sub>n-1</sub>(m)]+.. =0 . y = mx + c അനന്തസ്പര്ശിയാകുമ്പോള് മുകളില്ക്കൊടുത്ത സമീകരണത്തിന് രണ്ട് അനന്തമൂല്യങ്ങള് (inifinite roots) വേണ്ടിയിരിക്കുന്നു. അതുകൊണ്ട്, φ<sub>n</sub>(m) =0, cφ<sub>n'</sub>(m)+φ<sub>n-1</sub>(m)=0 ആദ്യത്തെ സമീകരണത്തില് നിന്ന് m ന് n വിലകള് കിട്ടുന്നു. അവ m1, m2, ..., mn ആയിരിക്കട്ടെ. രണ്ടാമത്തെ സമീകരണത്തില് നിന്ന് ര യുടെ വിലകള് കിട്ടുന്നു. അതുകൊണ്ടും അനന്തസ്പര്ശകങ്ങളുടെ സമീകരണങ്ങള്, y = m<sub>1</sub> x + c<sub>1</sub>, y = m<sub>2</sub> x + c<sub>2</sub>, ..., y = m<sub>n</sub> x + c<sub>n</sub> ആണ്. | ||
| + | |||
| + | x,y അക്ഷങ്ങള്ക്കു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാന് താഴെ കൊടുക്കുന്ന പ്രവര്ത്തനസൂത്രങ്ങള് ഉപയോഗിക്കുന്നു. വക്രത്തിന്റെ സമീകരണത്തില് x ന്റെ ഏറ്റവും ഉയര്ന്ന ഡിഗ്രിയിലുള്ള പദത്തിന്റെ ഗുണാങ്കത്തെ പൂജ്യത്തോടു സമീകരിച്ചാല് x അക്ഷത്തിനു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കിട്ടും. അതുപോലെ y യുടെ ഏറ്റവും ഉയര്ന്ന ഡിഗ്രിയിലുള്ള പദത്തിന്റെ ഗുണാങ്കത്തെ പൂജ്യത്തോടു സമീകരിച്ചാല് y അക്ഷത്തിനു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കിട്ടും. | ||
| - | |||
| - | |||
=== ഉച്ചതമങ്ങളും നിമ്നതമങ്ങളും=== | === ഉച്ചതമങ്ങളും നിമ്നതമങ്ങളും=== | ||
ഒരു വക്രത്തിന്റെ ഒരു ഖണ്ഡം പരിഗണിക്കുക. ആ വക്രഖണ്ഡത്തിന്റെ ഉച്ചതമവും നിമ്നതമവും കണ്ടുപിടിക്കാന് അവകലജങ്ങള് പ്രയോജനപ്പെടുന്നു. നിമ്നോന്നത ബിന്ദുക്കളില് y' എന്നത് പൂജ്യമായിരിക്കും.y" ന്റെ വില ഋണസംഖ്യയാണെങ്കില് ആ ബിന്ദു ഉച്ചതമത്തിന്റെയും ധനസംഖ്യയാണെങ്കില് നിമ്നതമത്തിന്റെയും ആയിരിക്കും. | ഒരു വക്രത്തിന്റെ ഒരു ഖണ്ഡം പരിഗണിക്കുക. ആ വക്രഖണ്ഡത്തിന്റെ ഉച്ചതമവും നിമ്നതമവും കണ്ടുപിടിക്കാന് അവകലജങ്ങള് പ്രയോജനപ്പെടുന്നു. നിമ്നോന്നത ബിന്ദുക്കളില് y' എന്നത് പൂജ്യമായിരിക്കും.y" ന്റെ വില ഋണസംഖ്യയാണെങ്കില് ആ ബിന്ദു ഉച്ചതമത്തിന്റെയും ധനസംഖ്യയാണെങ്കില് നിമ്നതമത്തിന്റെയും ആയിരിക്കും. | ||
| - | ഉച്ചതമമൂല്യത്തില് വര്ധിച്ചുകൊണ്ടിരിക്കുന്ന ഒരു ഫലനത്തിന്റെ വര്ധനവ് നില്ക്കുകയും ഫലനം ക്രമേണ കുറയുകയും ചെയ്യുന്നു (ചിത്രത്തില് P എന്ന സ്ഥാനം). ഫലനം കുറയുന്നത് ചിലപ്പോള് പെട്ടെന്നാവുകയും ചെയ്യാം (ചിത്രത്തില് R എന്ന സ്ഥാനം). അതുപോലെ നിമ്നതമത്തില് കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന ഫലനം വര്ധിക്കുവാന് ആരംഭിക്കുന്നു. രണ്ടിടത്തും ചരിവ് f '(x) ന്റെ ചിഹ്നം മാറുന്നു (ഫലനം വര്ധിക്കുമ്പോള് f '(x) ധനാത്മകവും കുറയുമ്പോള് ഋണാത്മകവും ആണ്). ഒരു ഫലനത്തിന്റെ ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കാന് പ്രായോഗികമായി ഉപയോഗമുള്ള വസ്തുതയാണിത്. ഫലനം f(x), x = a യില് ഉച്ചതമമാകുമ്പോള് f ' (a) = 0, f " (a) < 0; അതുപോലെ നിമ്നതമമാകുമ്പോള് f '(a) = 0, f " (a) > 0. | + | ഉച്ചതമമൂല്യത്തില് വര്ധിച്ചുകൊണ്ടിരിക്കുന്ന ഒരു ഫലനത്തിന്റെ വര്ധനവ് നില്ക്കുകയും ഫലനം ക്രമേണ കുറയുകയും ചെയ്യുന്നു (ചിത്രത്തില് P എന്ന സ്ഥാനം). ഫലനം കുറയുന്നത് ചിലപ്പോള് പെട്ടെന്നാവുകയും ചെയ്യാം (ചിത്രത്തില് R എന്ന സ്ഥാനം). അതുപോലെ നിമ്നതമത്തില് കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന ഫലനം വര്ധിക്കുവാന് ആരംഭിക്കുന്നു. രണ്ടിടത്തും ചരിവ് f '(x) ന്റെ ചിഹ്നം മാറുന്നു (ഫലനം വര്ധിക്കുമ്പോള് f '(x) ധനാത്മകവും കുറയുമ്പോള് |
| + | |||
| + | [[ചിത്രം:Vol6_617_2.jpg|300px]] | ||
| + | |||
| + | ഋണാത്മകവും ആണ്). ഒരു ഫലനത്തിന്റെ ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കാന് പ്രായോഗികമായി ഉപയോഗമുള്ള വസ്തുതയാണിത്. ഫലനം f(x), x = a യില് ഉച്ചതമമാകുമ്പോള് f ' (a) = 0, f " (a) < 0; അതുപോലെ നിമ്നതമമാകുമ്പോള് f '(a) = 0, f " (a) > 0. | ||
| + | |||
| + | |||
ടെയിലര് പ്രമേയമുപയോഗിച്ച് ഒരു ഫലനം ഉച്ചതമവും നിമ്നതമവുമാകാനുള്ള ആവശ്യകവും പര്യാപ്തവുമായ നിബന്ധനകള് കണ്ടുപിടിക്കാവുന്നതാണ്.x = a യില് ഫലനം f(x) ഉച്ചതമമോ നിമ്നതമമോ ആകുമ്പോള്, വ ന്റെ ചെറിയ വിലകള്ക്ക്, | ടെയിലര് പ്രമേയമുപയോഗിച്ച് ഒരു ഫലനം ഉച്ചതമവും നിമ്നതമവുമാകാനുള്ള ആവശ്യകവും പര്യാപ്തവുമായ നിബന്ധനകള് കണ്ടുപിടിക്കാവുന്നതാണ്.x = a യില് ഫലനം f(x) ഉച്ചതമമോ നിമ്നതമമോ ആകുമ്പോള്, വ ന്റെ ചെറിയ വിലകള്ക്ക്, | ||
| + | |||
| + | [[ചിത്രം:Vol6_617_3.jpg|300px]] | ||
എന്നിവ ഒരേ ചിഹ്നത്തോടുകൂടിയതായിരിക്കും. ഇതില് നിന്ന് ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്കുള്ള പൊതുപ്രമേയം കിട്ടുന്നു: | എന്നിവ ഒരേ ചിഹ്നത്തോടുകൂടിയതായിരിക്കും. ഇതില് നിന്ന് ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്കുള്ള പൊതുപ്രമേയം കിട്ടുന്നു: | ||
| - | f ' (a) = f " (a) = f | + | |
| + | f ' (a) = f " (a) = f '' (a) = ... = f <sup>n-1</sup> (a) = 0, f <sup>(n)</sup> (a) ≠ 0 ആകുമ്പോള്, f(a) ഉച്ചതമമോ നിമ്നതമോ ആകണമെങ്കില് പൂജ്യമാകാത്ത ആദ്യത്തെ അവകലജം, അതായത് f(n)(a) ഇരട്ടക്രമത്തോടുകൂടിയതായിരിക്കണം. കൂടാതെ ഉച്ചതമമൂല്യത്തിന് f(n)(a) ഋണാത്മകവും നിമ്നതമ മൂല്യത്തിന് f(n)(a) ധനാത്മകവും ആകണം. | ||
| + | |||
ഇവിടെ n = 2 ആകുമ്പോഴുള്ള പ്രത്യേക സ്ഥിതിയാണ് ഗ്രാഫിക് പരിഗണനയില് നിന്ന് മുന്പു ലഭിച്ച നിബന്ധനകള്. അതായത് ഉച്ചതമ മൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) < 0; നിമ്നതമമൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) > 0. | ഇവിടെ n = 2 ആകുമ്പോഴുള്ള പ്രത്യേക സ്ഥിതിയാണ് ഗ്രാഫിക് പരിഗണനയില് നിന്ന് മുന്പു ലഭിച്ച നിബന്ധനകള്. അതായത് ഉച്ചതമ മൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) < 0; നിമ്നതമമൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) > 0. | ||
| - | ഉദാ. തരംഗദൈര്ഘ്യം | + | ഉദാ. തരംഗദൈര്ഘ്യം λ ഉള്ള തരംഗങ്ങള്ക്ക് ആഴത്തില് വെള്ളമുള്ളിടത്ത് വേഗത [[ചിത്രം:Vol6_617_4.jpg|100px]] യോട് ആനുപാതികമാണ് (a സ്ഥിരരാശി). എന്നാല് λ = a ആകുമ്പോള് വേഗത ന്യൂനതമമാകും. |
| + | |||
=== പ്രതിബന്ധിത ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് === | === പ്രതിബന്ധിത ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് === | ||
| - | + | (Constrained extrema). ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കേണ്ട ഫലനത്തിലെ രാശികള് എപ്പോഴും സ്വതന്ത്രമായിരിക്കണമെന്നില്ല. അവ തമ്മില് ഒരു ബന്ധം ഉണ്ടായിരിക്കും. അങ്ങനെയുള്ള അവസരങ്ങളില് ഉച്ചതമനിമ്നതമമൂല്യങ്ങള് കണ്ടുപിക്കാന് ലാഗ്രഞ്ചിന്റെ "അനിര്ധാരിത ഗുണനരീതി' (method of undetermined multipliers). ഉപയോഗിക്കാവുന്നതാണ്. | |
| - | u = f (x,y,z) എന്ന ഫലനത്തിലെ രാശികള് തമ്മിലുള്ള ബന്ധം (x,y,z) = 0 ആയിരിക്കട്ടെ. ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്ക് | + | u = f (x,y,z) എന്ന ഫലനത്തിലെ രാശികള് തമ്മിലുള്ള ബന്ധം φ(x,y,z) = 0 ആയിരിക്കട്ടെ. ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്ക് |
| - | + | [[ചിത്രം:Vol6_617_5.jpg|300px]] | |
| - | |||
അതുകൊണ്ട് രണ്ടാമത്തെ സമീകരണത്തെ കൊണ്ട് ഗുണിച്ചു ആദ്യത്തേതിനോട് കൂട്ടിയാല്, | അതുകൊണ്ട് രണ്ടാമത്തെ സമീകരണത്തെ കൊണ്ട് ഗുണിച്ചു ആദ്യത്തേതിനോട് കൂട്ടിയാല്, | ||
| - | |||
| - | കൂടാതെ (x,y,z) = 0. | + | |
| - | ഈ നാലു സമീകരണങ്ങളും നിര്ധാരണം ചെയ്താല് | + | [[ചിത്രം:Vol6_617_6.jpg|300px]] |
| - | ഫലനം u = f(x,y,z) യഥാര്ഥത്തില് x,y,z മുകളില് കണ്ടുപിടിക്കുന്ന വിലകള്ക്ക് ഉച്ചതമമാകുമോ നിമ്നതമമാകുമോ എന്നറിയാന്, പരിഗണിക്കുന്ന പ്രശ്നത്തിന്റെ ഭൗതിക സാഹചര്യങ്ങള്കൂടി ഉപയോഗിക്കേണ്ടതാണ്. | + | |
| + | കൂടാതെ φ(x,y,z) = 0. | ||
| + | ഈ നാലു സമീകരണങ്ങളും നിര്ധാരണം ചെയ്താല് u അചലമായിരിക്കുമ്പോഴുള്ള (ഉച്ചതമോ നിമ്നതമമോ ആയിരിക്കുമ്പോഴുള്ളx, y, z ന്റെ മൂല്യങ്ങള് കിട്ടുന്നു. | ||
| + | ഫലനം u = f(x,y,z) യഥാര്ഥത്തില് x,y,z മുകളില് കണ്ടുപിടിക്കുന്ന വിലകള്ക്ക് ഉച്ചതമമാകുമോ നിമ്നതമമാകുമോ എന്നറിയാന്, പരിഗണിക്കുന്ന പ്രശ്നത്തിന്റെ ഭൗതിക സാഹചര്യങ്ങള്കൂടി ഉപയോഗിക്കേണ്ടതാണ്. | ||
=== വക്രത=== | === വക്രത=== | ||
| - | വക്രങ്ങളുടെ ഒരു അവകല ഗുണധര്മമാണ് വക്രത. വക്രത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകത്തിന്റെ ദിശ, ചാപ (arc) ത്തിനനുസരണമായി വ്യത്യാസപ്പെടുന്നതിന്റെ തോതാണ് വക്രത. സ്പര്ശകത്തിന്റെ ദിശയെ കുറിക്കുന്ന കോണം | + | വക്രങ്ങളുടെ ഒരു അവകല ഗുണധര്മമാണ് വക്രത. വക്രത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകത്തിന്റെ ദിശ, ചാപ (arc) ത്തിനനുസരണമായി വ്യത്യാസപ്പെടുന്നതിന്റെ തോതാണ് വക്രത. സ്പര്ശകത്തിന്റെ ദിശയെ കുറിക്കുന്ന കോണം Ψ ഉം ചാപദൈര്ഘ്യം ξഉം ആയാല് വക്രത n=dΨ/dξആണ്. വക്രതയുടെ വ്യുത്ക്രമത്തെ 1/ρ വക്രതാവ്യാസാര്ധം(radius of curvature) എന്നു പറയുന്നു. ഒരു വൃത്തത്തിന്റെ വക്രതാവ്യാസാര്ധം അതിന്റെ വ്യാസാര്ധത്തോടു തുല്യമാണ്. |
| - | കാര്ത്തീയ സമീകരണംy = f(x) ഉള്ള ഒരു വക്രത്തിന്റെ | + | |
| + | കാര്ത്തീയ സമീകരണംy = f(x) ഉള്ള ഒരു വക്രത്തിന്റെ വക്ര | ||
| + | |||
| + | [[ചിത്രം:Vol6_618_1.jpg|300px]] | ||
| - | = 0 ആകുമ്പോള് വക്രം ശൂന്യവൃത്തമാകുകയും ((point circle), | + | ρ= 0 ആകുമ്പോള് വക്രം ശൂന്യവൃത്തമാകുകയും ((point circle), ρ= ∞ ആകുമ്പോള് വക്രം ഋജുരേഖയായി "അപഭ്രംശിക്കുക'യും (degenerate) ചെയ്യുന്നു. ചരിവുകോണം Ψ കൂടുമ്പോള്, ചാപദൈര്ഘ്യം ξ കൂടുകയോ കുറയുകയോ ചെയ്യുന്നതനുസരിച്ച് ρ<>0; അതായത് x വിലകള് കൂടുമ്പോള്, വക്രം ഇടത്തോട്ടോ വലത്തോട്ടോ തിരിയുന്നതനുസരിച്ച് fn മുകളിലോട്ടോ താഴോട്ടോ അവതലം (concave) ആകുന്നതനുസരിച്ച് ρ<>0 ആകുന്നു. ഉദാ. ഒരു വക്രത്തിന്റെ പ്രാചലികസമീകരണം (parametric equation) x = f(t), y =Φ (t) ആയിരിക്കട്ടെ. |
| + | [[ചിത്രം:Vol6_618_2.jpg|300px]] | ||
| - | |||
| - | + | [[ചിത്രം:Vol6_618_3.jpg|300px]] | |
| - | + | ||
| - | + | ||
| - | = | + | വക്രത്തിലെ P(x,y) എന്ന ബിന്ദുവിലെ അഭിലംബത്തില് (വക്രത്തിന്റെ അവതല വശത്തുള്ള അഭിലംബത്തില്) PC = ρആകത്തക്കവണ്ണം C(x,y) എടുക്കുക. Cയെ വക്രതാകേന്ദ്രം (centre of curvature) എന്നു പറയുന്നു. വക്രതാകേന്ദ്രത്തിന്റെ നിര്ദേശാങ്കങ്ങള്,ആണ്. |
| - | ഒരു ഋജുരേഖയുടെ സമവാക്യമാണ്. ക്ക് പല വിലകള് കൊടുത്താല് വ്യത്യസ്തങ്ങളായ രേഖകള് കിട്ടുന്നു. അങ്ങനെ ക്കു പല വിലകള് കൊടുത്തുണ്ടാകുന്ന രേഖകളെല്ലാംകൂടി ഒരു രേഖാകുലം (family of | + | [[ചിത്രം:Vol6_618_4.jpg|300px]] |
| - | ഒരു വക്രം, തന്നിട്ടുള്ള വക്രകുലത്തിലെ എല്ലാ അംഗങ്ങളെയും സ്പര്ശിക്കുകയും അതിലെ ഓരോ ബിന്ദുവിനെയും വക്രകുലത്തിലെ ഏതെങ്കിലും ഒരംഗം സ്പര്ശിക്കപ്പെടുകയും ചെയ്യുന്നു എങ്കില് ആ വക്രത്തെ വക്രകുലത്തിന്റെ എന്വെലപ് എന്നു പറയുന്നു. ഉദാഹരണമായി, വിശ്ലേഷകജ്യാമിതിയില് നിന്ന് | + | |
| - | + | വക്രതാകേന്ദ്രം (x,y) ന്റെ ബിന്ദുപഥത്തെ (locus) കേന്ദ്രജം (evolute) എന്നു പറയുന്നു. വക്രത്തിലെ ഏതെങ്കിലും രണ്ടുബിന്ദുക്കള് തമ്മിലുള്ള ചാപദൈര്ഘ്യം, ആ ബിന്ദുക്കളിലെ വക്രതാവ്യാസാര്ധങ്ങള് തമ്മിലുള്ള വ്യത്യാസമാണെന്നു തെളിയിക്കാവുന്നതാണ്. | |
| - | ചിത്രത്തില് കാണുന്ന രേഖാകുലത്തിലെ തുടര്ച്ചയായ രണ്ടു അംഗങ്ങളുടെ അന്തിമമായ പ്രതിച്ഛേദ ബിന്ദുവിന്റെ (സീമാന്ത പ്രതിച്ഛേദ ബിന്ദു) ബിന്ദുപഥമാണ് എന്വെലപ്. ഈ ആശയമുപയോഗിച്ച് എന്വെലപ്പിനെ മറ്റൊരുവിധത്തില് നിര്വചിക്കാം: എന്ന വക്രകുലത്തിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് യെ | + | |
| + | === എന്വെലപ് (Envelope)=== | ||
| + | |||
| + | xcosα+ysinα=1 ഒരു ഋജുരേഖയുടെ സമവാക്യമാണ്. α ക്ക് പല വിലകള് കൊടുത്താല് വ്യത്യസ്തങ്ങളായ രേഖകള് കിട്ടുന്നു. അങ്ങനെ α ക്കു പല വിലകള് കൊടുത്തുണ്ടാകുന്ന രേഖകളെല്ലാംകൂടി ഒരു രേഖാകുലം (family of straight lines) ആകുന്നു. ഇവിടെ αയെ പ്രാചലം (parameter) എന്നു പറയുന്നു. ഒരു പ്രാചലം മാത്രമുള്ള വക്രകുലത്തെ കുറിക്കാന് f(x,y,α)എന്നെഴുതാം.x<sup>2</sup> + y<sup>2</sup> = a<sup>2</sup> ഒരു ഏകപ്രാചലവൃത്തകുലമാണ് (a പ്രാചലം). | ||
| + | ഒരു വക്രം, തന്നിട്ടുള്ള വക്രകുലത്തിലെ എല്ലാ അംഗങ്ങളെയും സ്പര്ശിക്കുകയും അതിലെ ഓരോ ബിന്ദുവിനെയും വക്രകുലത്തിലെ ഏതെങ്കിലും ഒരംഗം സ്പര്ശിക്കപ്പെടുകയും ചെയ്യുന്നു എങ്കില് ആ വക്രത്തെ വക്രകുലത്തിന്റെ എന്വെലപ് എന്നു പറയുന്നു. ഉദാഹരണമായി, വിശ്ലേഷകജ്യാമിതിയില് നിന്ന് xcosα+ysinα=1 എന്ന രേഖാകുലം, വൃത്തം x<sup>2</sup>+y<sup>2</sup> = 1 നെ സ്പര്ശിക്കുന്നു. കൂടാതെ ഈ വൃത്തത്തിലെ ഏതു ബിന്ദുവിലെയും സ്പര്ശകത്തിന്റെ സാമാന്യരൂപം ആണ്. അതുകൊണ്ട് ഈ രേഖാകുലത്തിന്റെ എന്വെലപ് | ||
| + | x<sup>2</sup> + y<sup>2</sup> = 1 എന്ന വൃത്തമാണെന്ന് അനുമാനിക്കാം. | ||
| + | ചിത്രത്തില് കാണുന്ന രേഖാകുലത്തിലെ തുടര്ച്ചയായ രണ്ടു അംഗങ്ങളുടെ അന്തിമമായ പ്രതിച്ഛേദ ബിന്ദുവിന്റെ (സീമാന്ത പ്രതിച്ഛേദ ബിന്ദു) ബിന്ദുപഥമാണ് എന്വെലപ്. ഈ ആശയമുപയോഗിച്ച് എന്വെലപ്പിനെ മറ്റൊരുവിധത്തില് | ||
| + | |||
| + | [[ചിത്രം:Vol6_618_5.jpg|300px]] | ||
| + | |||
| + | നിര്വചിക്കാം: f(x,y,α)എന്ന വക്രകുലത്തിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് α യെ | ||
| + | |||
| + | [[ചിത്രം:Vol6_618_6.jpg|300px]] | ||
| + | |||
| + | എന്നീ സമീകരണങ്ങളില് നിന്ന് വിലുപ്തമാക്കുന്നു (eliminate). ഉദാ. [[ചിത്രം:Vol6_618_7.jpg|100px]] (m പ്രാചലം) ഒരു രേഖാകുലമാണ്. ഇതിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് പ്രാചലം m നെ, [[ചിത്രം:Vol6_618_7.jpg|100px]], [[ചിത്രം:Vol6_618_9.jpg|100px]] എന്നീ സമവാക്യങ്ങളില് നിന്നു വിലുപ്തമാക്കുന്നു. അപ്പോള്, കിട്ടുന്ന y<sup>2</sup> = 4ax എന്ന പരാവളയം (parabola) ആണ് മുകളില് കൊടുത്ത രേഖാകുലത്തിന്റെ എന്വെലപ്. | ||
| + | ഒരു വക്രത്തിലെ വ്യത്യസ്ത ബിന്ദുക്കളിലെ വക്രതാ കേന്ദ്രങ്ങളുടെ ബിന്ദുപഥമാണ് കേന്ദ്രജം. ഈ ബിന്ദുക്കളിലെ അഭിലംബങ്ങളുടെ എന്വെലപ്പായും കേന്ദ്രജത്തെ പരിഗണിക്കാവുന്നതാണ്. പരാവളയം y<sup>2</sup> = 4ax ന്റെ കേന്ദ്രജം "ബിന്ദുപഥ' കല്പന ഉപയോഗിച്ചും 'എന്വെലപ്' ഉപയോഗിച്ചും കണ്ടുപിടിക്കുന്നത് ഇപ്രകാരമാണ്. | ||
| + | |||
| + | 1.y<sup>2</sup> = 4ax ലെ ഒരു ബിന്ദു (at<sup>2</sup>, 2at)എന്നെടുക്കാം. അപ്പോള് വക്രതാ കേന്ദ്രത്തിന്റെ നിര്ദേശാങ്കങ്ങള് x=2a+3at<sup>2</sup>, y=2at<sup>3</sup> ആണ്. യെ വിലുപ്തമാക്കിയാല് കേന്ദ്രജത്തിന്റെ സമവാക്യം 27ay<sup>2</sup> = 4(x-2a)<sup>3</sup> എന്ന അര്ധ ത്രിഘാത പരാവളയം (semi cubical parabola) ആണെന്നു കാണാം. | ||
| + | |||
| + | 2. പരാവളയത്തിലെ (at<sup>2</sup>, 2at)എന്ന ബിന്ദുവിലെ അഭിലംബംy + xt = 2at + at<sup>3</sup> ആേണ്. കൊണ്ട് ആംശികമായി അവകലിച്ചാല്,x = 2a + 3at<sup>2</sup>. | ||
| + | പ്രാചലം യെ വിലുപ്തമാക്കിയാല്, എന്വെലപ് 27 ay<sup>2</sup> = 4 (x-2a)<sup>3</sup> എന്നു കിട്ടുന്നു. ഇതാണ് മുകളില് കൊടുത്തപോലെ കേന്ദ്രജത്തിന്റെ സമവാക്യം. | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
=== അനിര്ധാര്യ രൂപങ്ങള്=== | === അനിര്ധാര്യ രൂപങ്ങള്=== | ||
| - | ഫലനം f(x), xന്റെ പ്രത്യേക വിലകള്ക്ക് അനിര്ധാര്യരൂപം | + | ഫലനം f(x), xന്റെ പ്രത്യേക വിലകള്ക്ക് അനിര്ധാര്യരൂപം 0/0 ആകുമ്പോള്, സീമ എന്ന ആശയമുപയോഗിച്ച് ഫലനത്തിന് "സീമാന്തമൂല്യങ്ങള്' (limiting values) കൊടുക്കാവുന്നതാണ്. അനിര്ധാര്യ രൂപങ്ങള് മറ്റുവിധത്തിലുമാകാം. ∞/∞, ∞-∞, 0<sup>0</sup>, 1<sup>∞</sup>, ∞<sup>0</sup>ഇവയൊക്കെ അനിര്ധാര്യ രൂപങ്ങളാണ്. |
| - | "ഹോസ്പിറ്റല് നിയമ'മനുസരിച്ച്, f(a) = 0, | + | |
| + | "ഹോസ്പിറ്റല് നിയമ'മനുസരിച്ച്, f(a) = 0, Φ(a)=0 ആകു | ||
| + | |||
| + | [[ചിത്രം:Vol6_619_1.jpg|300px]] | ||
| + | |||
ഉദാ. . | ഉദാ. . | ||
| - | ബീജീയ ലഘുകരണം കൊണ്ട് തുടങ്ങിയ അനിര്ധാര്യരൂപങ്ങളെ എന്ന രൂപത്തിലേക്ക് മാറ്റാവുന്നതാണ് | + | ബീജീയ ലഘുകരണം കൊണ്ട് ∞/∞, ∞x0, ∞-∞ തുടങ്ങിയ അനിര്ധാര്യരൂപങ്ങളെ എന്ന രൂപത്തിലേക്ക് മാറ്റാവുന്നതാണ്. |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | [[ചിത്രം:Vol6_619_2.jpg|100px]] എന്ന സര്വ സമവാക്യം (identity)∞-∞ എന്ന അനിര്ധാര്യരൂപത്തെ 0/0 ലേക്ക് മാറ്റുന്നതാണ്. അതുകൊണ്ട് ഇത്തരം സന്ദര്ഭങ്ങളില് ഹോസ്പിറ്റല് നിയമമുപയോഗിച്ച് ഫലനങ്ങളുടെ സീമകള് കണ്ടുപിടിക്കാം. | ||
| + | |||
| + | [[ചിത്രം:Vol6_619_3.jpg|300px]] | ||
| - | + | [[ചിത്രം:Vol6_619_4.jpg|300px]] | |
അതുകൊണ്ട്, k = eº = 1. | അതുകൊണ്ട്, k = eº = 1. | ||
=== സമീകരണങ്ങളുടെ ഏകദേശ മൂല്യങ്ങള്ന്യൂട്ടന്റെ രീതി=== | === സമീകരണങ്ങളുടെ ഏകദേശ മൂല്യങ്ങള്ന്യൂട്ടന്റെ രീതി=== | ||
| - | സമീകരണം f(x) = 0 ന് 'a' എന്ന സംഖ്യയ്ക്കടുത്ത് മൂല്യമുണ്ടെങ്കില് മൂല്യത്തിന്റെ ഏകദേശവില കണ്ടുപിടിക്കാവുന്നതാണ്. മൂല്യം a+h ആയാല് f(a+h) = 0; f(a) + hf '(a) = 0 (ഏകദേശം). ഇതില് നിന്ന് | + | സമീകരണം f(x) = 0 ന് 'a' എന്ന സംഖ്യയ്ക്കടുത്ത് മൂല്യമുണ്ടെങ്കില് മൂല്യത്തിന്റെ ഏകദേശവില കണ്ടുപിടിക്കാവുന്നതാണ്. മൂല്യം a+h ആയാല് f(a+h) = 0; f(a) + hf '(a) = 0 (ഏകദേശം). ഇതില് നിന്ന് |
| + | |||
| + | [[ചിത്രം:Vol6_619_5.jpg|300px]] | ||
| + | |||
| + | പിടിക്കാവുന്നതാണ്. ഇങ്ങനെ തുടര്ന്നാല് ആവശ്യമുള്ള സൂക്ഷ്മതയോടെ ഏതു സമവാക്യത്തിന്റെയും ഏകദേശവില കിട്ടുന്നു. സമീകരണം x<sup>3</sup> + 2x - 5 = 0 ന്റെ ഒരു മൂല്യത്തിന്റെ ഏകദേശവില 1.3 ആണ്. ന്യൂട്ടന്റെ രീതി ഉപയോഗിച്ചാല് അടുത്ത ഏകദേശവില 1.33 എന്നും കുറച്ചുകൂടി സൂക്ഷ്മമായ ഏകദേശവില 1.3283 എന്നും കിട്ടുന്നു. | ||
=== ഫലനങ്ങളുടെ ശ്രണീ വികസനം=== | === ഫലനങ്ങളുടെ ശ്രണീ വികസനം=== | ||
മെക്ലോറില് ശ്രണിയുപയോഗിച്ച് പല ഫലനങ്ങളെയും അഭികേന്ദ്രസരണ നിബന്ധനകള്ക്കു വിധേയമായി ഘാതശ്രണികളായി വികസിപ്പിക്കാവുന്നതാണ്. ഫലനം f(x) ന്റെ മക്ലോറിന് ശ്രണി: | മെക്ലോറില് ശ്രണിയുപയോഗിച്ച് പല ഫലനങ്ങളെയും അഭികേന്ദ്രസരണ നിബന്ധനകള്ക്കു വിധേയമായി ഘാതശ്രണികളായി വികസിപ്പിക്കാവുന്നതാണ്. ഫലനം f(x) ന്റെ മക്ലോറിന് ശ്രണി: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | ചില ഫലനങ്ങള്ക്ക് f (n)(x) പ്രത്യക്ഷത്തില് കണ്ടുപിടിക്കാന് എളുപ്പമല്ല. പുനരാവൃത്തി ബന്ധ(recurrence relation)ത്തിലൂടെയായിരിക്കും f (n)(x) പ്രത്യക്ഷപ്പെടുക. ഇത്തരം അവസരങ്ങളിലും f (n)(0) പ്രത്യേകം കണ്ടുപിടിച്ച് ഫലനത്തെ വികസിപ്പിക്കാവുന്നതാണ്. ഈ രീതിയുപയോഗിച്ച് (sin-1 x)2 നെ വികസിപ്പിക്കാം. | + | [[ചിത്രം:Vol6_619_6.jpg|300px]] |
| - | y = ( | + | |
| - | y1= 2y, (1- | + | ചില ഫലനങ്ങള്ക്ക് f <sup>(n)</sup>(x) പ്രത്യക്ഷത്തില് കണ്ടുപിടിക്കാന് എളുപ്പമല്ല. പുനരാവൃത്തി ബന്ധ(recurrence relation)ത്തിലൂടെയായിരിക്കും f <sup>(n)</sup>(x) പ്രത്യക്ഷപ്പെടുക. ഇത്തരം അവസരങ്ങളിലും f <sup>(n)</sup>(0) പ്രത്യേകം കണ്ടുപിടിച്ച് ഫലനത്തെ വികസിപ്പിക്കാവുന്നതാണ്. ഈ രീതിയുപയോഗിച്ച് (sin<sup>-1</sup> x)<sup>2</sup> നെ വികസിപ്പിക്കാം. |
| + | |||
| + | y = (sin<sup>-1</sup> x)<sup>2</sup> ആയിരിക്കട്ടെ. അവകലനം കൊണ്ട് [[ചിത്രം:Vol6_619_7.jpg|100px]] | ||
| + | y1= 2y, (1-x<sup>2</sup>) y<sub>2</sub> - xy<sub>1</sub> = 2 എന്നീ സമവാക്യങ്ങള് കിട്ടുന്നു. ലൈബ്നിറ്റ്സ് പ്രമേയമുപയോഗിച് n പ്രാവശ്യം അവകലിച്ചാല്, (1-x<sup>2</sup>) y<sub>n+2</sub> - (2n+1) xy<sub>n+1</sub> - n<sup>2</sup>yn = 0, x = 0, (y)<sub>0</sub> = 0, (y<sub>1</sub>)<sub>0</sub> = 0, (y<sub>2</sub>)<sub>0</sub> = 2, .... (y<sub>n+2</sub>) = n<sup>2</sup> (y<sub>n</sub>)<sub>0</sub> അതുകൊണ്ട് (y<sub>2n-1</sub>)<sub>0</sub> = 0, (y<sub>2n</sub>)<sub>0</sub> = 2.2<sup>2</sup> . 4<sup>2</sup> . 6<sup>2</sup> ... (2n-2)<sup>2</sup> (n≠1). മക്ലോറിന് ശ്രണിയില് വിലയിട്ടാല്, . | ||
| + | |||
| + | [[ചിത്രം:Vol6_619_8.jpg|300px]] | ||
=== അനന്തശ്രണികളും അനന്ത ഗുണനഫലങ്ങളും === | === അനന്തശ്രണികളും അനന്ത ഗുണനഫലങ്ങളും === | ||
"അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമ' എന്ന നിര്വചനമനുസരിച്ച്, നിശ്ചിതസമാകലം | "അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമ' എന്ന നിര്വചനമനുസരിച്ച്, നിശ്ചിതസമാകലം | ||
| + | |||
| + | [[ചിത്രം:Vol6_620_1.jpg|300px]] | ||
(nh = b-a ആകുമ്പോള്), a = 0, b = 1 ആയാല്, | (nh = b-a ആകുമ്പോള്), a = 0, b = 1 ആയാല്, | ||
| - | മുകളില് കൊടുത്ത സമവാക്യമുപയോഗിച്ച് അഭികേന്ദ്രസാരികളായ പല അനന്തശ്രണികളുടെയും അനന്തഗുണനഫലങ്ങളുടെയും "അഭികേന്ദ്രസീമ' കണ്ടുപിടിക്കാവുന്നതാണ്. വലതുവശത്തു കാണുന്ന അനന്തശ്രണിയുടെ തുക കണ്ടുപിടിക്കാന് | + | മുകളില് കൊടുത്ത സമവാക്യമുപയോഗിച്ച് അഭികേന്ദ്രസാരികളായ പല അനന്തശ്രണികളുടെയും അനന്തഗുണനഫലങ്ങളുടെയും "അഭികേന്ദ്രസീമ' കണ്ടുപിടിക്കാവുന്നതാണ്. വലതുവശത്തു കാണുന്ന അനന്തശ്രണിയുടെ തുക കണ്ടുപിടിക്കാന് |
| - | + | ||
| - | + | [[ചിത്രം:Vol6_620_2.jpg|300px]] | |
| + | |||
== കലനം നിത്യജീവിതത്തില്== | == കലനം നിത്യജീവിതത്തില്== | ||
17-ാം ശ.ത്തിന്റെ അവസാനത്തില് ജ്യോതിശ്ശാസ്ത്രം, ബലതന്ത്രം തുടങ്ങിയ ശാസ്ത്രശാഖകളിലെ വികാസം ന്യൂട്ടനും ലൈബ്നിറ്റ്സിനും കലനത്തിന്റെ മൗലിക തത്ത്വങ്ങള് ആവിഷ്കരിക്കാന് പ്രചോദനം നല്കി. ക്ലാസ്സിക് ഭൗതികശാസ്ത്രവികസനത്തിന് അടിസ്ഥാനമിട്ടത് അവകലനവും സമാകലനവും പിന്നീട് രൂപംകൊണ്ട അവകല സമീകരണങ്ങളുമാണ്. അവകലനം മാനവികശാസ്ത്രങ്ങളില് ഏറെ പ്രയോജനപ്പെടുത്തിയിട്ടുണ്ട്. തത്ക്ഷണികമായ വ്യതിയാനങ്ങള് അളക്കുന്നതിന് ഏറ്റവും പ്രയോജനകരമായ ഒരു ഉപാധിയാണ് അവകലജങ്ങള്. | 17-ാം ശ.ത്തിന്റെ അവസാനത്തില് ജ്യോതിശ്ശാസ്ത്രം, ബലതന്ത്രം തുടങ്ങിയ ശാസ്ത്രശാഖകളിലെ വികാസം ന്യൂട്ടനും ലൈബ്നിറ്റ്സിനും കലനത്തിന്റെ മൗലിക തത്ത്വങ്ങള് ആവിഷ്കരിക്കാന് പ്രചോദനം നല്കി. ക്ലാസ്സിക് ഭൗതികശാസ്ത്രവികസനത്തിന് അടിസ്ഥാനമിട്ടത് അവകലനവും സമാകലനവും പിന്നീട് രൂപംകൊണ്ട അവകല സമീകരണങ്ങളുമാണ്. അവകലനം മാനവികശാസ്ത്രങ്ങളില് ഏറെ പ്രയോജനപ്പെടുത്തിയിട്ടുണ്ട്. തത്ക്ഷണികമായ വ്യതിയാനങ്ങള് അളക്കുന്നതിന് ഏറ്റവും പ്രയോജനകരമായ ഒരു ഉപാധിയാണ് അവകലജങ്ങള്. | ||
ആധുനിക ലോകത്തില് നിത്യജീവിത സംവിധാനം ശാസ്ത്രപുരോഗതിയുമായി അഭേദ്യമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. പ്രത്യക്ഷമായോ പരോക്ഷമായോ ബന്ധമുള്ള എല്ലാ ശാസ്ത്രശാഖകളും അവയുടെ വികാസത്തില് കലനത്തോടു കടപ്പെട്ടിരിക്കുന്നു. കലനവുമായി ബന്ധപ്പെട്ട ശാസ്ത്രശാഖകള്ക്ക് ഉദാഹരണങ്ങളാണ് ബലതന്ത്രം, എന്ജിനീയറിങ്, കാലാവസ്ഥാശാസ്ത്രം മുതലായവ. | ആധുനിക ലോകത്തില് നിത്യജീവിത സംവിധാനം ശാസ്ത്രപുരോഗതിയുമായി അഭേദ്യമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. പ്രത്യക്ഷമായോ പരോക്ഷമായോ ബന്ധമുള്ള എല്ലാ ശാസ്ത്രശാഖകളും അവയുടെ വികാസത്തില് കലനത്തോടു കടപ്പെട്ടിരിക്കുന്നു. കലനവുമായി ബന്ധപ്പെട്ട ശാസ്ത്രശാഖകള്ക്ക് ഉദാഹരണങ്ങളാണ് ബലതന്ത്രം, എന്ജിനീയറിങ്, കാലാവസ്ഥാശാസ്ത്രം മുതലായവ. | ||
ഫലനങ്ങളുടെ സീമാന്തമൂല്യങ്ങളെക്കുറിച്ചാണ് കലനത്തില് പ്രതിപാദിക്കുന്നത്. പ്രായോഗികതലത്തില് ഒരു ഫലനത്തിന്റെ വര്ധനവിന്റെ തോതാണ് (rate) അതിന്റെ അവകലജഗുണാങ്കം. അതുകൊണ്ട് ഭൗതികശാസ്ത്രത്തില് അവകലനരീതികള് വളരെയധികം ഉപയോഗപ്പെടുന്നുണ്ട്. | ഫലനങ്ങളുടെ സീമാന്തമൂല്യങ്ങളെക്കുറിച്ചാണ് കലനത്തില് പ്രതിപാദിക്കുന്നത്. പ്രായോഗികതലത്തില് ഒരു ഫലനത്തിന്റെ വര്ധനവിന്റെ തോതാണ് (rate) അതിന്റെ അവകലജഗുണാങ്കം. അതുകൊണ്ട് ഭൗതികശാസ്ത്രത്തില് അവകലനരീതികള് വളരെയധികം ഉപയോഗപ്പെടുന്നുണ്ട്. | ||
| - | പരസ്പര ബന്ധമുള്ള രണ്ടു കാര്യങ്ങളില് ഒന്ന് സ്വതന്ത്രവും മറ്റേത് ആശ്രിതവും ആണെങ്കില് അവയുടെ മാറ്റം അവകലജം കൊണ്ട് സൂചിപ്പിക്കാം. പ്രവേഗം (velocity), ത്വരണം (acceleration) മുതലായ സങ്കല്പങ്ങള്ക്ക് കലനത്തിലൂടെ ഗണിതശാസ്ത്രരൂപം കിട്ടുന്നു. | + | |
| + | പരസ്പര ബന്ധമുള്ള രണ്ടു കാര്യങ്ങളില് ഒന്ന് സ്വതന്ത്രവും മറ്റേത് ആശ്രിതവും ആണെങ്കില് അവയുടെ മാറ്റം അവകലജം കൊണ്ട് സൂചിപ്പിക്കാം. പ്രവേഗം (velocity), ത്വരണം (acceleration) മുതലായ സങ്കല്പങ്ങള്ക്ക് കലനത്തിലൂടെ ഗണിതശാസ്ത്രരൂപം കിട്ടുന്നു. s ദൂരത്തെയും t സമയത്തെയും സൂചിപ്പിക്കുന്നുവെങ്കില് t യെ അപേക്ഷിച്ച് s ന്റെ അവകലജം s' വേഗത്തെയും s" ത്വരണത്തെയും കുറിക്കുന്നു. സെക്കന്ഡില്, ചലിക്കുന്ന ഒരു ബിന്ദുവിന്റെ സ്ഥിതിസദിശം (position vector) r ആയാല് ബിന്ദുവിന്റെ പ്രവേഗസദിശം N=dr/dt യും ത്വരണസദിശം d<sup>2</sup>r/dt<sup>2</sup> ഉം ആണ്. ഫലനങ്ങളുടെ ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കാന് കലനരീതിയാണ് സാധാരണയായി ഉപയോഗിക്കുന്നത്. സാമ്പത്തിക ശാസ്ത്രത്തിന്റെ പല മേഖലകളിലും കലന സങ്കല്പങ്ങള്ക്ക് വളരെ പ്രാധാന്യമുണ്ട്. ഉത്പാദനം, വിതരണം, വില, വിപണനം മുതലായവയുടെ അറ്റനിരക്ക് (തത്ക്ഷണിക | ||
നിരക്ക്) സൂചിപ്പിക്കാന് അവകലജം പ്രയോജനപ്പെടുന്നു. സമ്പദ് വ്യവസ്ഥയുടെ വിവിധ മാതൃകകള് ഗണിതശാസ്ത്രപ്രകാരം നിര്ണയിക്കുമ്പോഴും അവകലനതത്ത്വം ഉപയോഗിക്കാറുണ്ട്. എക്കണോമെട്രിക്സില് ഇത്തരം സമീപനം അംഗീകരിച്ചിരിക്കുന്നു. | നിരക്ക്) സൂചിപ്പിക്കാന് അവകലജം പ്രയോജനപ്പെടുന്നു. സമ്പദ് വ്യവസ്ഥയുടെ വിവിധ മാതൃകകള് ഗണിതശാസ്ത്രപ്രകാരം നിര്ണയിക്കുമ്പോഴും അവകലനതത്ത്വം ഉപയോഗിക്കാറുണ്ട്. എക്കണോമെട്രിക്സില് ഇത്തരം സമീപനം അംഗീകരിച്ചിരിക്കുന്നു. | ||
| - | |||
| + | അനന്തസൂക്ഷ്മങ്ങളുടെ "സങ്കലനം' സമാകലനപ്രക്രിയയിലൂടെയാണ് കലനത്തില് നിര്വഹിക്കുന്നത്. ഇലാസ്തികമായ ഒരു ചരടിനെ വലിച്ചു നീട്ടുമ്പോള് ചെയ്യേണ്ടിവരുന്ന പ്രവൃത്തി (work) കണക്കാക്കുവാന് കലനതത്ത്വങ്ങള് ഉപയോഗിക്കുന്നു. ചരടിന്റെ സാധാരണ നീളം Iഉം വലിച്ചുനീട്ടിയ നീളം xഉം ആയാല് "ഹൂക്ക് | ||
| + | |||
| + | [[ചിത്രം:Vol6_620_4.jpg|330px]] | ||
| + | |||
| + | എന്ന നീളത്തില് നിന്നും l<sub>2</sub>ലേക്കു വലിച്ചു നീട്ടുമ്പോള് ചെയ്യേണ്ടിവരുന്ന മൊത്തം പ്രവൃത്തി | ||
| + | |||
| + | [[ചിത്രം:Vol6_620_5.jpg|200px]] | ||
പ്രാരംഭിക ടെന്ഷന്, T2 അന്തിമ ടെന്ഷന്. | പ്രാരംഭിക ടെന്ഷന്, T2 അന്തിമ ടെന്ഷന്. | ||
ഇതേ രീതിയുപയോഗിച്ച് ജ്യാമിതീയ രൂപങ്ങളുടെ ഗുരുത്വകേന്ദ്രം, ജഡത്വ ആഘൂര്ണം (moment of inertia) മുതലായവ സമാകലനം കൊണ്ട് കണ്ടുപിടിക്കുന്നു. | ഇതേ രീതിയുപയോഗിച്ച് ജ്യാമിതീയ രൂപങ്ങളുടെ ഗുരുത്വകേന്ദ്രം, ജഡത്വ ആഘൂര്ണം (moment of inertia) മുതലായവ സമാകലനം കൊണ്ട് കണ്ടുപിടിക്കുന്നു. | ||
(പ്രാഫ. കെ.എസ്.വി. ഷേണായി, പ്രാഫ. കെ. ജയചന്ദ്രന്, സ.പ.) | (പ്രാഫ. കെ.എസ്.വി. ഷേണായി, പ്രാഫ. കെ. ജയചന്ദ്രന്, സ.പ.) | ||
Current revision as of 13:59, 9 ജൂലൈ 2014
കലനം
Calculus
ഫലനത്തിലെ അടിസ്ഥാന ക്രിയകളായ അവകലനം (Differentiation), സമാകലനം (Integration) എന്നിവയെക്കുറിച്ചും ഇവയുമായി ബന്ധപ്പെട്ട മറ്റു വസ്തുതകളെക്കുറിച്ചും പ്രതിപാദിക്കുന്ന ഗണിതശാസ്ത്രശാഖ. സീമ (limit)എന്ന ആശയവുമായി ബന്ധപ്പെട്ട ഗണിതശാസ്ത്രവിഭാഗമാണ് കലനം. കലനം ആധാരമായി വര്ത്തിക്കുന്ന ആധുനിക ഗണിത വിശ്ലേഷണത്തില് (Mathematical Analysis), സെീമ എന്ന സങ്കല്പത്തിന് മുഖ്യസ്ഥാനമാണുള്ളത്. സീമയുടെ വ്യത്യാസമനുസരിച്ച് അവകലനം, സമാകലനം എന്നീ രണ്ട് വിഭാഗങ്ങളായി കലനത്തെ വിഭജിച്ചിരിക്കുന്നു. ഫലനബന്ധമുള്ള രണ്ട് രാശികളുടെ വര്ധനവിന്റെ അനുപാതസീമയെക്കുറിച്ച് അവകലനത്തിലും അനന്തമായ എണ്ണത്തിലുള്ള ചെറിയ ഗുണനഫലങ്ങളുടെ തുകയുടെ സീമയെക്കുറിച്ച് സമാകലനത്തിലും പഠനം നടത്തുന്നു. അവകലന സമാകലന പ്രക്രിയകള് പ്രതിലോമങ്ങളായതുകൊണ്ട് സമാകലനത്തെ പ്രതിഅവകലജം (Anti derivative) എന്നും പറയാറുണ്ട്. ഒരു ചരത്തിന്റെ ഫലനത്തിന്റെ അവകലജ(derivative)ങ്ങളാണ് അവകലനത്തിന്റെ അടിസ്ഥാനാശയം.
അവകലനത്തിനും സമാകലനത്തിനും ഉപയോഗിക്കുന്ന സാങ്കേതിക രീതികളനുസരിച്ച് അവകലനം നിഗമനാത്മകവും (deductive) സമാകലനം ആഗമനാത്മകവും (inductive) ആണ്. ഈ രണ്ടു വിഭാഗങ്ങളില് ആഗമനാത്മക സ്വഭാവമുള്ള സമാകലനമാണ് ആദ്യം ആവിഷ്കരിക്കപ്പെട്ടത്. വക്രത്തിനു സ്പര്ശകം വരയ്ക്കുക, വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കുക തുടങ്ങിയ ചില ഒറ്റതിരിഞ്ഞ പ്രശ്നങ്ങളുടെ നിര്ധാരണം സംബന്ധിച്ച ഗണിതശാസ്ത്രാന്വേഷണങ്ങളില്നിന്നാണ് കലനം രൂപംകൊണ്ടത്. എന്നാല് പില്ക്കാലത്ത് ഇതിന്റെ അടിസ്ഥാന സങ്കല്പങ്ങളും രീതിയും പ്രായോഗികതലത്തിലുള്ള ഉപയോഗങ്ങളും വളരെ വികാസം പ്രാപിച്ചതിനാല് കലനം ഗണിതത്തിലെ വളരെ പ്രാധാന്യമുള്ള വിഷയമായി മാറിയിരിക്കുന്നു.
ചരിത്രം
എ.ഡി. 10-ാം നൂറ്റാണ്ടില്ത്തന്നെ അവകലനത്തിലെ ചില പ്രമേയങ്ങള് ഇന്ത്യന് ഗണിതശാസ്ത്രജ്ഞന്മാര്ക്ക് അറിയാമായിരുന്നു. മഞ്ജുളാചാര്യനും (932) അദ്ദേഹത്തിന്റെ കൃതിയുടെ വ്യാഖ്യാതാവായ പ്രശസ്തിധരനും (958), δ(sin θ) = cos θ δθ എന്ന സൂത്രവാക്യം അറിയാമായിരുന്നു എന്ന് പ്രാഫ. ബി.ബി. ദത്ത ചൂണ്ടിക്കാണിക്കുന്നു. അതുപോലെ f(x) മഹത്തമമാകുമ്പോള് ആണെന്ന് ഭാസ്കരാചാര്യനും (1150) ഗ്രഹിച്ചിരുന്നു. ഇന്നത്തെ രീതിയിലല്ലെങ്കിലും അവകലജം എന്ന ആശയത്തെപ്പറ്റി ആദ്യമായി ചിന്തിച്ച ഗണിതശാസ്ത്രജ്ഞന് ഭാസ്കരാചാര്യനാണ്. കലനം ഒരു ഗണിതശാസ്ത്രശാഖയായി രൂപം പ്രാപിച്ചത് അഞ്ചു നൂറ്റാണ്ടുകള്ക്കുശേഷമാണ്.
1612ല് ജ്യോതിശ്ശാസ്ത്രജ്ഞനായ കെപ്ലര് ദീര്ഘ വൃത്ത(ellipse)ത്തിന്റെ വിസ്തീര്ണം കണക്കുകൂട്ടി കണ്ടുപിടിച്ചു. യൂക്ലിഡ് ഉപയോഗിച്ചതില് നിന്നു വ്യത്യസ്തമായ രീതിയിലായിരുന്നു കെപ്ലര് വിസ്തീര്ണം കണ്ടുപിടിച്ചത്. ഒരു നിശ്ചിത വിസ്തീര്ണത്തെയോ വ്യാപ്തത്തെയോ അനന്തസൂക്ഷ്മങ്ങളായ ദീര്ഘചതുരങ്ങളായോ ഡിസ്ക്കുകളായോ ഭാഗിച്ചാണ് കെപ്ലര് മൊത്തം വിസ്തീര്ണവും വ്യാപ്തവും കണക്കാക്കിയത്. കെപ്ലറുടെ രീതി സ്വീകരിച്ച് 1635ല് ഗലീലിയോ, ഗലീലിയുടെ ശിഷ്യനായിരുന്ന ബൊണാവെന്റ്യുറ കാവലിറി "അഭാജ്യങ്ങളുടെ ജ്യാമിതി' എഴുതി. ഏകസമാനമല്ലാത്ത വ്യാപ്തങ്ങളുടെ ഗുരുത്വകേന്ദ്രം കണ്ടുപിടിക്കാന് അദ്ദേഹത്തിനു സാധിച്ചു. ഫെര്മ (1601-65) യുടെ ഗവേഷണം വിപരീത ദിശയിലായിരുന്നു. സ്പര്ശകങ്ങള് വരയ്ക്കുക, വക്രങ്ങളുടെ (ഫലനങ്ങളുടെ) മഹത്തമന്യൂനതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കുക തുടങ്ങിയ പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യാന് ഫെര്മയ്ക്കു കഴിഞ്ഞു (1629). 40 വര്ഷങ്ങള്ക്കുശേഷം ഐസക് ബറോ (Lectiones Opticae et Geometricae, 1669) ഒരു സീമാപ്രക്രിയയിലൂടെ അവകലജത്തെ നിര്വചിച്ചു. രണ്ടാംതര രാശികളെ ഉപേക്ഷിച്ചും a, e(ഇന്നത്തെ രീതിയില് δy, δx) ഇവ ഉള്ക്കൊള്ളാത്ത പദങ്ങളെ വിട്ടുകളഞ്ഞും അദ്ദേഹം yലും xലും ഉള്ള വ്യതിയാനങ്ങളുടെ അനുപാതം a/e കണ്ടുപിടിച്ചു. അങ്ങനെ അവകലനത്തിന്റെ ആധുനിക രീതിയോടടുത്തെത്താന് ഐസക് ബറോവിനു സാധിച്ചു. സ്പര്ശകങ്ങളെ സംബന്ധിച്ചും വിസ്തീര്ണത്തെ സംബന്ധിച്ചുമുള്ള പ്രതിലോമബന്ധം ആദ്യമായി മനസ്സിലാക്കിയത് അദ്ദേഹമായിരുന്നു.
ഈ പശ്ചാത്തലത്തിലാണ് ഐസക് ന്യൂട്ടനും (1642-1727) ഗോഡ്ഫ്രീദ് ഫൊണ് ലൈബ്നിറ്റ്സും (1646-1716) രംഗത്തെത്തുന്നത്. കലനത്തിന്റെ ക്രമാനുസൃതമായ ആവിഷ്കാരത്തില് പങ്കാളികളാവാന് അവര്ക്ക് സാധിച്ചു. ന്യൂട്ടന് സീമാപ്രക്രിയയിലൂടെ സമാകലനത്തെ കണക്കാക്കുന്ന പഴയരീതി ഉപേക്ഷിക്കുകയും സമാകലനത്തെ പ്രതി അവകലജമായി പരിഗണിക്കുകയും ചെയ്തു. 1666 മുതല് പ്രസിദ്ധീകരിക്കപ്പെട്ട മൂന്നു പ്രബന്ധങ്ങളില് കലനത്തിലുള്ള ന്യൂട്ടന്റെ സംഭാവനകള് ഉള്ക്കൊള്ളുന്നു. അദ്ദേഹം കാലത്തെ (time) അന്തിമമായ സ്വതന്ത്രചരമായി പരിഗണിക്കുകയും xന്റെ വര്ധമാനവേഗതയെ (ന്യൂട്ടന് ഇതിനെ "ഫ്ളക്ഷന്' എന്നു വിളിക്കുന്നു) x (=x ഡോട്ട്) എന്ന പ്രതീകം കൊണ്ടു കുറിക്കുകയും ചെയ്തു. xന്റെയും yന്റെയും അനുപാതമാണ് അവകലജ ഗുണാങ്കം (differential coefficient). തേന്റെ ആചാര്യനായ ഐസക് ബറോ ഉപയോഗിച്ച e, a എന്നീ അക്ഷരങ്ങള്ക്കുപകരം ന്യൂട്ടന് x0, y0 എന്നീ പ്രതീകങ്ങളാണ് ഉപയോഗി ച്ചത്. അദ്ദേഹം രണ്ടു ഫലനങ്ങളുടെ തുകയെയും ഫലനങ്ങളുടെ ഫലനത്തെയും അവകലിക്കാനുള്ള നിയമങ്ങള് കണ്ടുപിടിച്ചു. "n, ധന പൂര്ണസംഖ്യയാകുമ്പോള്, d/dx (xn) = nxn-1എന്ന സൂത്രവാക്യവും ന്യൂട്ടനാണ് കണ്ടുപിടിച്ചത്.
ലൈബ്നിറ്റ്സ് (Leibnitz), കലനത്തിന്റെ അടിസ്ഥാനതത്ത്വങ്ങള് സ്വതന്ത്രമായി കണ്ടുപിടിച്ച ഗണിതജ്ഞനാണ്. രണ്ടു ഫലനങ്ങളുടെ തുക, വ്യത്യാസം, ഗുണനഫലം, അനുപാതം എന്നിവയുടെ അവകലജങ്ങള് കണ്ടുപിടിച്ച അദ്ദേഹം അവകലന നിയമങ്ങളെ ക്രാഡീകരിച്ചു.m ധനപൂര്ണ സംഖ്യയാകുമ്പോള്, dxm=mxm-1dx എന്ന നിയമം ലൈബ്നിറ്റ്സ് സ്വതന്ത്രമായി ആവിഷ്കരിച്ചു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ "m-ാമത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള "ലൈബ്നിറ്റ്സ് നിയമം' പ്രസിദ്ധമാണ്. ആധുനിക പ്രതീകങ്ങളായ d/dx, ∫ എന്നിവയോടൊപ്പം കാല്കുലസ് ഡിഫറന്ഷ്യാലിസ് (calculus differentialis),കാല്ക്കുലസ് ഇന്റഗ്രാലിസ് (calculus integralis) തുടങ്ങിയ പേരുകളും ലൈബ്നിറ്റ്സ് കൊടുത്തിട്ടുള്ളവയാണ്. 1684ലാണ് ലൈബ്നിറ്റ്സിന്റെ കലനത്തെ സംബന്ധിച്ച ലേഖനം പ്രസിദ്ധീകരിക്കപ്പെട്ടത്. തുടര്ന്ന് 1686ല് സമാകലനത്തിലെ പ്രമേയങ്ങള് ഉള്ക്കൊള്ളുന്ന മറ്റൊരു ഗവേഷണപ്രബന്ധവും ലൈബ്നിറ്റ്സ് പ്രസിദ്ധീകരിച്ചു. ഐസക് ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നീ ശാസ്ത്രജ്ഞരെയാണ് അവകലനത്തിന്റെ ഉപജ്ഞാതാക്കളായി പാശ്ചാത്യ പണ്ഡിതന്മാര് കണക്കാക്കുന്നത്. ലൈബ്നിറ്റ്സിന്റെ ഗവേഷണം മുന്നോട്ടു കൊണ്ടുപോയത് ബെര്ണൂലി സഹോദരന്മാരായിരുന്നു. ശ്രദ്ധേയമായ "ഹോസ്പിറ്റല് നിയമം' ഉള്ക്കൊള്ളിച്ചുകൊണ്ടും 1696ല് ബെര്ണൂലിയുടെ ഗവേഷണ വിദ്യാര്ഥിയായ എല് ഹോസ്പിറ്റല് (Marquisde I'Hospital) കലനത്തെ സംബന്ധിച്ച ആദ്യത്തെ "ടെക്സ്റ്റ് ബുക്ക്' പ്രസിദ്ധീകരിച്ചു.
18-ാം ശ.ത്തിലെ ഗണിതശാസ്ത്ര പുരോഗതി കലനത്തെയും ബലതന്ത്രത്തില് (Mechanics)അതു ചെലുത്തിയ സ്വാധീനത്തെയും കേന്ദ്രീകരിച്ചായിരുന്നു. ഈ നൂറ്റാണ്ടില് കലനത്തിന്റെ ഉപജ്ഞാതാവായി ന്യൂട്ടന്, ലൈബ്നിറ്റ്സ് എന്നിവരില് ആരെ അംഗീകരിക്കണം എന്ന തര്ക്കത്തില് വ്യാപൃതരായിരുന്ന ബ്രിട്ടീഷ് ഗണിത ശാസ്ത്രജ്ഞര്ക്ക് ലൈബ്നിറ്റ്സിന്റെ രീതികളോടും പ്രതീകങ്ങളോടും താത്പര്യം തോന്നിയില്ല. ഇക്കാരണത്താല് അവരുടെ ഗവേഷണഫലങ്ങള് ടെയിലര്, മെക്ലാറിന് എന്നിവരുടെ പ്രമേയങ്ങളില് മാത്രം ഒതുങ്ങിനിന്നു. എന്നാല് യൂറോപ്പില് ഓയ്ലര്, ക്ലെയറാട്ട് തുടങ്ങിയവരുടെ ശ്രമങ്ങളുടെ ഫലമായി കലനതത്ത്വങ്ങളില് വളരെയേറെ പുരോഗതിയുണ്ടായി. ആംശിക അവകലജ(Partial derivative)ത്തെക്കുറിച്ചു മനസ്സിലാക്കാനും ഉച്ചതര വിമകളിലുള്ള സമഷ്ടി(space)യെക്കുറിച്ച് പഠിക്കുവാനും അവര്ക്കു സാധിച്ചു. അവകലന സമീകരണങ്ങളെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങള് രൂപം കൊണ്ടത് അക്കാലത്താണ്.
നൂതന വികാസങ്ങള്
കലനത്തില് ആധുനികതയുടെ തുടക്കം കുറിച്ചത് 19-ാം ശ.ത്തിലാണ്. 1823ല് പ്രസിദ്ധീകൃതമായ പ്രാമാണിക ഗ്രന്ഥത്തിലൂടെ (Resume Des Lecons Sur le Calcul Infinitesimal) ഫ്രഞ്ച് ഗണിതജ്ഞനായ അഗസ്തിന് എല്. കോഷി ഈ തുടക്കത്തിനു അടിസ്ഥാനമിട്ടു. അതോടെ ഗണിത വിശ്ലേഷണം ഒരു പ്രത്യേകശാഖയായി ഉരുത്തിരിഞ്ഞു. കൂടാതെ D(=d/dx) എന്ന അവകല സംകാരക(differential operator)ത്തിന്റെ ഉപയോഗത്തിലൂടെ കലനത്തിലെ പല പ്രശ്നങ്ങളും ബീജഗണിതരീതിയില് നിര്ധാരണം ചെയ്യുവാനും കോഷിക്കു കഴിഞ്ഞു. കാള് വെയര് സ്റ്റ്രാസ് (1815-97) ഈ ശാഖ വികസിപ്പിച്ചു.
ഈ നൂറ്റാണ്ടില് ഗണിതഗവേഷണത്തിന്റെ പല മേഖലകളിലൂടെ കലനം വികാസം പ്രാപിച്ചുകൊണ്ടിരിക്കുന്നു. റീമാന് സമാകലനത്തിനു ലെബേഗും സ്റ്റീല്ജീസും കൊടുത്ത പുതിയ വ്യാഖ്യാനം ഗണിതചരിത്രത്തില് ഒരപൂര്വ സംഭവമാണ്. സൂക്ഷ്മങ്ങളായ പണിയായുധങ്ങളെ സ്വരൂപിക്കുവാനും ശാസ്ത്രവികാസത്തെ അപ്രതീക്ഷിത ദിശകളിലേക്കു നയിക്കുവാനും സഹായിക്കുന്ന ഏറ്റവും ശക്തമായ ഒരു മാധ്യമമായി മാറിയിരിക്കുകയാണ് കലനസിദ്ധാന്തം.
പ്രാരംഭിക കലനത്തിലെ പ്രധാനപ്പെട്ട ആശയങ്ങളും പ്രക്രിയകളും പ്രയോഗവും മാത്രമേ ഈ ലേഖനത്തില് ഉള്ക്കൊള്ളിച്ചിട്ടുള്ളു. വികസിത കലന(advanced calculus)ത്തെിലെ പ്രധാന ആശയങ്ങളും പ്രയോഗങ്ങളും ഉപവിഭാഗങ്ങളും (ഫലനവിശ്ലേഷണം (Functional Analysis), സമ്മിശ്രവിശ്ലേഷണം (omplex Analysis), ടെന്സര് വിശ്ലേഷണം (Tensor Analysis), വിശ്ലേഷക ജ്യാമിതി (Analytic Geometry) തുടങ്ങിയവ.) വിശ്ലേഷണം (Analysis)എന്ന ഗണിതശാഖയുടെ ഭാഗമാണ്.
ഫലനത്തിന്റെ സീമയും സാതത്യവും
ഫലനത്തിന്റെ സീമയും സാതത്യവും (Limit and continuity of function). y = f (x) എന്ന ഫലനം സങ്കല്പിക്കുക. ഇവിടെ x എന്ന ചരം a എന്ന സംഖ്യയോട് ഏതെങ്കിലും വിധത്തില് അടുക്കുമ്പോള്, f (x) അടുക്കുന്നത് A യോടാണെങ്കില്, A യെxഎന്ന ചരം a യോടടുക്കുമ്പോഴുള്ള f (x) ന്റെ സീമ എന്നു പറയുന്നു. പ്രതീകാത്മകമായി സീമ f (x) = A എന്ന് എഴുതുന്നു. x, a യോടടുക്കുന്നത് രണ്ടുവിധത്തിലാകാം. സംഖ്യാരേഖയില് (Number line) a0 യുടെ വലതുവശത്തുള്ള വലിയ സംഖ്യകളില് നിന്നോ ഇടതുവശത്തുള്ള ചെറിയ സംഖ്യകളില് നിന്നോ x, a യോടടുക്കാം.
സീമയുടെ നിര്വചനം കൂടുതല് വ്യക്തമായി ഇങ്ങനെ പറയാം. x, a യോടടുക്കുമ്പോള് f(x) ന്റെ സീമ അ ആകണമെങ്കില്, തന്നിട്ടുള്ള ഏതെങ്കിലും ചെറിയ ധനസംഖ്യയായ ε (എപ്പ്സിലോണ്) സംഗതമായിx ന്റെ എല്ലാ വിലകള്ക്കും (x ≠ a), |f(x)-A|<ε ആകുമ്പോള് |x-a|<δആകത്തക്കവണ്ണം δ (ഡെല്റ്റ) എന്ന ചെറിയ ധനസംഖ്യ ഉണ്ടായിരിക്കണം. "x ന്റെ എല്ലാ വിലകള്ക്കും' എന്നതുകൊണ്ടും വലതു സീമയും ഇടതു സീമയും ഉണ്ടായിരിക്കണമെന്ന് അവ തുല്യമായിരിക്കണമെന്നും അര്ഥമാക്കുന്നു. അതായത് x→സീമa+ f(x)=A=x→സീമa- f(x) സീമാപ്രക്രിയയില് ഫലനത്തിന് x = a ആകുമ്പോഴുള്ള വില കണക്കിലെടുക്കുന്നില്ല. അതുകൊണ്ടാണ് x≠a എന്നു പറഞ്ഞത്.x=a ആകുമ്പോള് ഫലനത്തിനു മൂല്യം ഉണ്ടാകുകയോ ഉണ്ടാകാതിരിക്കുകയോ ചെയ്യാം. മൂല്യം ഉണ്ടെങ്കില്ത്തന്നെ അത് സീമയുടെ വിലയ്ക്ക് തുല്യമാകണമെന്നും ഇല്ല; ഫലനത്തിന്റെ മൂല്യവും ഫലനത്തിന്റെ സീമയും വ്യത്യസ്തങ്ങളായ സങ്കല്പങ്ങളാണ്. അതുപോലെ x,a യോടടുക്കുമ്പോള് (x→a)xന്റെ വില a യോടും ശരിക്കും "അടുത്തുവരുന്നു'. എന്നാല് x ഒരിക്കലും a യോടു തുല്യമാകുന്നില്ല.
ഒരു ഫലനത്തിന്റെ മൂല്യവും സീമയും തുല്യമാകുമ്പോള് ഫലനം സതതമാണെന്നു (continuous)പറയുന്നു. അതുകൊണ്ട് ഫലനസാതത്യത്തിന്റെ നിബന്ധനകള് x→സീമa+ f(x)=f(a)= x→സീമa- എന്നെഴുതുന്നു. ഇവയില് ഏതെങ്കിലും ഒരു നിബന്ധന ശരിയായില്ലെങ്കില് ഫലനം x=a യില് സതതമല്ല. ഒരു അന്തരാള(interval) ത്തിലെ എല്ലാ ബിന്ദുക്കളിലും സതതമായിരിക്കുന്ന ഫലനം ആ അന്തരാളത്തില് സതതമാണെന്നു പറയുന്നു.
അനന്തസൂക്ഷ്മങ്ങള് (Infinitesimals). സീമയുടെ (മുകളില് കൊടുത്ത) നിര്വചനത്തില്ഒരു സ്വേച്ഛാസ്ഥിരസംഖ്യ (arbitrary constant)യോണ്. അത് ഏതെങ്കിലും ചെറിയ സംഖ്യയാകാം. f(x)→A ആകുമ്പോള്, ε പൂജ്യത്തോടടുക്കുന്നു. അതുപോലെ δ യും ε നെ ആശ്രയിക്കുന്ന ഒരു സ്വേച്ഛാസ്ഥിര സംഖ്യയാണ്. x→a ആകുമ്പോള് δ യും പൂജ്യത്തോടടുക്കുന്നു. ഇങ്ങനെയുള്ള രാശികളെ (ε-ഉം δ-ഉം) അനന്ത സൂക്ഷ്മങ്ങളെന്നോ സീമാപൂജ്യങ്ങളെന്നോ (limiting zeros) പറയുന്നു. സീമാപൂജ്യങ്ങള് കേവല പൂജ്യ(absolute zeros)ങ്ങളല്ലാത്തതുകൊണ്ടും അവകൊണ്ടുള്ള ഹരണം അനുവദനീയമാണ്. മുകളില് കൊടുത്ത പ്രത്യേകസ്ഥിതിയില് ε,δ→0 ആകുമ്പോള്, ε/a' ഒരു നിശ്ചിത സംഖ്യ(fixed number)യോടടുക്കുകയാണെങ്കില്, ഈ സീമയെ അവകലജഗുണാങ്കം (differential coefficient)എന്നു പറയുന്നു.
അവകലനം
അനന്തസൂക്ഷ്മമായ അളവുകള് ക്രാഡീകരിക്കാനുള്ള മാര്ഗമാണ് സീമാതത്ത്വം ഉപയോഗിച്ച് കലനത്തില് പ്രതിപാദിക്കപ്പെടുന്നത്. അനന്തസൂക്ഷ്മങ്ങളായ δഉം εഉം യഥാക്രമം x ലും y = f(x) ഉള്ള സംഗത വ്യത്യാസങ്ങളാണ്. ഇവയെ Δx എന്നും Δy(ഡെല്റ്റ x, ഡെല്റ്റ y) എന്നും സാധാരണ കുറിക്കുന്നു. Δy/Δxനെ ഈ രാശികളുടെ വ്യത്യാസ ഭാഗഫലമെന്നു (difference quotient) വിളിക്കുന്നു. xന്റെ Δx എന്ന അന്തരാളത്തില് y ക്കുണ്ടാകുന്ന ശരാശരി വര്ധനവാണ് Δy/Δx. ഇവിടെ ![]() Δy/Δx ഉണ്ടെങ്കില് അതിനെ y യുടെ x കൊണ്ടുള്ള അവകലജ ഗുണാങ്കം അഥവാ അവകലജം എന്നു പറയുന്നു (differential coefficient of y with respect to x). ഈ സീമയെ കുറിക്കാന് dy/dx എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു.
Δy/Δx ഉണ്ടെങ്കില് അതിനെ y യുടെ x കൊണ്ടുള്ള അവകലജ ഗുണാങ്കം അഥവാ അവകലജം എന്നു പറയുന്നു (differential coefficient of y with respect to x). ഈ സീമയെ കുറിക്കാന് dy/dx എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു.
അവകലജത്തിന് ജ്യാമിതീയ വ്യാഖ്യാനം നല്കാവുന്നതാണ്. വിശ്ലേഷക ജ്യാമിതിയില് P(x,y), Q(x+Δy, y+Δx) എന്നീ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന രേഖയായ PQ വിന്റെ ചരിവുമാനം (slope) Δy/Δx ആണ്. ഇവിടെ കൊടുത്തിട്ടുള്ള ഗ്രാഫില് നിന്ന് Δy/Δx = tanθ. Q എന്ന ബിന്ദു, വക്രത്തിലൂടെ സഞ്ചരിച്ച് P യോടടുക്കുമ്പോള് Δx → 0, θ → Ψ . അതുകൊണ്ട് ![]() അതായത്, dy/dx=tanΨ.
അതായത്, dy/dx=tanΨ.
അങ്ങനെ y = f(x) എന്ന വക്രത്തിന്റെ (x, y) എന്ന ബിന്ദുവിലുള്ള ചരിവുമാനമാണ് dy/dx.
അതായത് സ്പര്ശക(tangent)ത്തേിന്റെ ചരിവുമാനമാണ് അവകലജം. അവകലജഗുണാങ്കത്തെ മറ്റൊരു വിധത്തിലും വ്യാഖ്യാനിക്കാം. മാറ്റത്തിന്റെ ക്ഷണികനിരക്ക് എന്നു അവകലജത്തെ നിര്വചിക്കാവുന്നതാണ്. xനുണ്ടാകുന്ന
മാറ്റമനുസരിച് yക്കുണ്ടാകുന്ന മാറ്റത്തിന്റെ തോതാണ് (rate of change)y യുടെ x കൊണ്ടുള്ള അവകലജഗുണാങ്കം. സെക്കന്ഡില് ദൂരം സെഞ്ചരിക്കുന്ന ഒരു കണത്തിന്റെ (particle) പ്രവേഗം (velocity), ത്വരണം (acceleration) എന്നിവയുടെ പരിമാണം കണ്ടുപിടിക്കാന് v=ds/dt, a=d2s/dt2 എന്നീ സൂത്രവാക്യങ്ങള് ഉപയോഗിക്കുന്നു. കൂടാതെ ചലിക്കുന്ന ഒരു കണത്തിന്റെ സെക്കന്ഡിലുള്ള കാര്ത്തീയ നിര്ദേശാങ്കങ്ങള് (x,y,z) ആയാല് അതിന്റെ പ്രവേഗ ഘടകങ്ങള് (velocity components) dx/dt, dy/dt, dz/dt ആണ്.
x = a എന്ന വിലയ്ക്കും y = f(x) എന്ന ഫലനം വര്ധിക്കുകയാണെങ്കില്,xന്റെ ഈ വിലയ്ക്ക് dy/dx ധനാത്മകമായിരിക്കും. അതുപോലെ ഫലനം കുറയുകയാണെങ്കില് dy/dx ഋണാത്മകമായിരിക്കും. x=a യ്ക്ക് dy/dxന്റെ വിലയെ കുറിക്കാന് (dy/dx)a എന്നെഴുതാം. (dy/dx)a=0 ആകുമ്പോള് x=a യ്ക്ക് y കൂടുകയോ കുറയുകയോ ചെയ്യുന്നില്ല. അപ്പോള് y യെ അചലബിന്ദു (stationary point)എന്നു വിളിക്കുന്നു. അചലബിന്ദുവില് വക്രത്തിനു വരയ്ക്കുന്ന സ്പര്ശകം x അക്ഷത്തിനു സമാന്തരമായിരിക്കും. ഫലനത്തിന്റെ മഹത്തമന്യൂനതമമൂല്യങ്ങള് കണ്ടുപിടിക്കാന് ഈ വസ്തുത ഉപയോഗിക്കുന്നു.
അവകലജ ഗുണാങ്കത്തിന്റെ നിര്വചനത്തില് നിന്ന് പ്രാരംഭികഫലനങ്ങളുടെ അവകലജങ്ങള് കണ്ടുപിടിക്കാം. xn, sin x, cos x, ex, log x, 1/x എന്നീ ഫലനങ്ങളുടെ അവകലജങ്ങള് യഥാക്രമം nxn-1, cos x, -sin x, ex, 1/x ആണ്. രണ്ടു ഫലനങ്ങളുടെ തുക, വ്യത്യാസം, ഗുണനഫലം, ഭാഗഫലം ഇവയുടെ അവകലജങ്ങള് കണ്ടുപിടിക്കാന് പ്രത്യേക നിയമങ്ങളുണ്ട്. ഗുണനഫലംu,vയുടെ അവകലജം, ![]() ഉം u/vയുടെ അവകലജം
ഉം u/vയുടെ അവകലജം  ഉം ആണ്. xഉം yഉം t എന്ന പ്രാചല (parameter) ത്തിന്റെ ഫലനങ്ങളാണെങ്കില്
ഉം ആണ്. xഉം yഉം t എന്ന പ്രാചല (parameter) ത്തിന്റെ ഫലനങ്ങളാണെങ്കില് ![]() അതുപോലെ yഉം zഉം xന്റെ ഫലനങ്ങളാണെങ്കില് y യുടെ z കൊണ്ടുള്ള അവകലജം
അതുപോലെ yഉം zഉം xന്റെ ഫലനങ്ങളാണെങ്കില് y യുടെ z കൊണ്ടുള്ള അവകലജം ![]() ആണ്.y, u ന്റെ ഫലനവും, u,x ന്റെ ഫലനവും ആയാല്
ആണ്.y, u ന്റെ ഫലനവും, u,x ന്റെ ഫലനവും ആയാല് ![]() (ശൃംഖലാനിയമം).y = uv ആയാല് ലോഗരിതീയ അവകലന രീതിയുപയോഗിച്ച് കണ്ടുപിടിക്കാവുന്നതാണ്.
(ശൃംഖലാനിയമം).y = uv ആയാല് ലോഗരിതീയ അവകലന രീതിയുപയോഗിച്ച് കണ്ടുപിടിക്കാവുന്നതാണ്.
ഉത്തരോത്തര അവകലനം
ഒരു ഫലനത്തിന്റെ അവകലജങ്ങളെ തുടര്ച്ചയായി അവകലിച്ചാല് ഉയര്ന്ന ക്രമത്തിലുള്ള അവകലജങ്ങള് കിട്ടും. ഈ പ്രക്രിയയെ ഉത്തരോത്തര അവകലനം എന്നു പറയുന്നു. n മത്തെ അവകലജത്തെ കുറിക്കാന് ![]() തുടങ്ങിയ പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ n മത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള സൂത്രവാക്യമാണ് "ലൈബ്നിറ്റ്സ് പ്രമേയം'. അതായത്, u, vഇവ
x ന്റെ ഫലനങ്ങളാണെങ്കില്,
തുടങ്ങിയ പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. രണ്ടു ഫലനങ്ങളുടെ ഗുണനഫലത്തിന്റെ n മത്തെ അവകലജം കണ്ടുപിടിക്കാനുള്ള സൂത്രവാക്യമാണ് "ലൈബ്നിറ്റ്സ് പ്രമേയം'. അതായത്, u, vഇവ
x ന്റെ ഫലനങ്ങളാണെങ്കില്,
ചില സാധാരണ ഫലനങ്ങളുടെ n-ാമത്തെ അവകലജത്തിന്റെ സൂത്രവാക്യങ്ങള് താഴെ കൊടുക്കുന്നു:
ആംശിക അവകലനം
ഒന്നില് ക്കൂടുതല് സ്വതന്ത്രചരങ്ങളുള്ള ഫലനങ്ങള്ക്ക് ആംശിക അവകലജങ്ങള് നിര്വചിക്കാവുന്നതാണ്. സ്വതന്ത്രചരങ്ങളില് ഏതെങ്കിലും ഒന്നുമാത്രം വ്യത്യാസപ്പെടുകയും മറ്റെല്ലാം സ്ഥിരമായിരിക്കുകയും ചെയ്യുമ്പോഴുള്ള വ്യത്യാസ ഭാഗഫലത്തിന്റെ (difference quotient) സീമയാണ് ആ ചരം കൊണ്ടുള്ള ആംശിക അവകലജം.u = f(x,y) രണ്ടു സ്വതന്ത്രചരങ്ങളുടെ ഫലനമായിരിക്കട്ടെ. അപ്പോള് ∂u/∂x, ∂u/∂y എന്നീ ആംശിക അവകലജങ്ങളെ
ഉത്തരോത്തര അവകലനംകൊണ്ട് ഉയര്ന്ന ക്രമങ്ങളിലുള്ള ആംശിക അവകലജങ്ങള് കിട്ടുന്നു. ![]() ഉം x, y എന്നിവയുടെ ഫലനങ്ങളാകയാല് അവയെ വീണ്ടും അവകലിക്കാം. അങ്ങനെ,
ഉം x, y എന്നിവയുടെ ഫലനങ്ങളാകയാല് അവയെ വീണ്ടും അവകലിക്കാം. അങ്ങനെ,
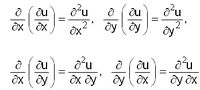 എന്നീ ഉയര്ന്ന ക്രമങ്ങളിലുള്ള അവകലജങ്ങള് കിട്ടുന്നു. സാധാരണ സ്ഥിതികളില്,
എന്നീ ഉയര്ന്ന ക്രമങ്ങളിലുള്ള അവകലജങ്ങള് കിട്ടുന്നു. സാധാരണ സ്ഥിതികളില്,
ഒരു ബീജീയ വ്യഞ്ജകത്തിലെ (algebraic expression) എല്ലാ പദങ്ങളുടെയും ഘാതം (degree) തുല്യമായിരുന്നാല് അതിനെ സമഘാതഫലനം (homogeneous function) എന്നു പറയുന്നു. x,y ചരങ്ങളുടെ 'n'-ാം ഘാതത്തിലുള്ള സമഘാത ഫലനം u (x,y) ആയാല് അതിനെu(x,y) = xn f(y/x)എന്നെഴുതാം.
x, yചരങ്ങളുടെ n-ാം ഘാതത്തിലുള്ള സമഘാത ഫലനം u(x,y) ആയാല് 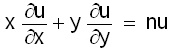 (ഓയ്ലര് പ്രമേയം). ഓയ്ലര് പ്രമേയത്തിന്റെ പൊതുരൂപം താഴെ കൊടുക്കുന്നു:
(ഓയ്ലര് പ്രമേയം). ഓയ്ലര് പ്രമേയത്തിന്റെ പൊതുരൂപം താഴെ കൊടുക്കുന്നു:
x1, x2, x3 ... ചരങ്ങളുടെ n-ാം ഘാതത്തിലുള്ള സമഘാതഫലനം u(x1, x2, x3 ...) ആയാല് ![]()
u(x, y) എന്ന ഫലനത്തില് xഉം yഉം എന്ന ചരത്തിന്റെ ഫലനങ്ങളാണെങ്കില് പൂര്ണ അവകലജം (total derivative) കണ്ടുപിടിക്കാന് ![]() എന്ന സൂത്രവാക്യം ഉപയോഗിക്കുന്നു.
എന്ന സൂത്രവാക്യം ഉപയോഗിക്കുന്നു.
മാധ്യമൂല്യ പ്രമേയങ്ങള് (Mean Value Theorems)
അവിച്ഛിന്നമായി വര്ധിച്ചുകൊണ്ടിരിക്കുന്ന വേഗതയോടെ പാഞ്ഞുപോകുന്ന ഒരു തീവണ്ടി അതിന്റെ യാത്രയ്ക്കിടയില് ഒരിടത്തെങ്കിലും ശരാശരി വേഗതയില് സഞ്ചരിക്കുമെന്നു വ്യക്തമാണ്. അതുപോലെ P, Q എന്നീ ബിന്ദുക്കളില്ക്കൂടി കടന്നുപോകുന്ന ഒരു വക്രത്തിന് ഈ ബിന്ദുക്കള്ക്കുള്ളില് എല്ലായിടത്തും നിയതമായ സ്പര്ശകങ്ങളുണ്ടെങ്കില്, ചാപം PQ വിനു സമാന്തരമായി സ്പര്ശകമുള്ള R എന്ന ഒരു ബിന്ദുവെങ്കിലും വക്രത്തിലുണ്ടായിരിക്കും. ഇതാണ് മാധ്യമൂല്യപ്രമേയത്തിന്റെ ജ്യാമിതീയ സ്വഭാവം. അവകലനത്തിലെ ഏറ്റവും പ്രധാനപ്പെട്ട പ്രമേയമാണിത്. വിശ്ലേഷണരീതിയില് പ്രമേയത്തെ ഇങ്ങനെ പ്രസ്താവിക്കാം: [a, b] എന്ന സംവൃത അന്തരാള(closed interval)ത്തില് f(x) സതതവും, (a, b) എന്ന വിവൃത അന്തരാളത്തില് f(x) അവകലനീയവുമായാല്, ![]() ആകത്തക്കവണ്ണം (a, b) യില് xന് c എന്ന ഒരു വിലയെങ്കിലും ഉണ്ടായിരിക്കും. "ലാഗ്രഞ്ചിന്റെ മാധ്യമൂല്യപ്രമേയം' എന്ന പേരില് ഇത് അറിയപ്പെടുന്നു. b - a = h ആയാല് c = a + θh (0 < θ < 1) എന്നെഴുതാം. അപ്പോള്, f(a+h) = f(a) + hf (a + θh). മാധ്യമൂല്യപ്രമേയത്തിന്റെ മറ്റൊരു രൂപമാണിത്.
ആകത്തക്കവണ്ണം (a, b) യില് xന് c എന്ന ഒരു വിലയെങ്കിലും ഉണ്ടായിരിക്കും. "ലാഗ്രഞ്ചിന്റെ മാധ്യമൂല്യപ്രമേയം' എന്ന പേരില് ഇത് അറിയപ്പെടുന്നു. b - a = h ആയാല് c = a + θh (0 < θ < 1) എന്നെഴുതാം. അപ്പോള്, f(a+h) = f(a) + hf (a + θh). മാധ്യമൂല്യപ്രമേയത്തിന്റെ മറ്റൊരു രൂപമാണിത്.
മാധ്യമൂല്യപ്രമേയത്തിന്റെ വ്യാപകരൂപമാണ് "ടെയിലര് പ്രമേയം' (Taylor's Theorem). ഈ പ്രമേയത്തെ ഇങ്ങനെ പ്രസ്താവിക്കാം: (a, a+h) എന്ന അന്തരാളത്തില് f (x)ഉം അതിന്റെ ആദ്യത്തെ (n 1) അവകലജങ്ങളും സതതമായിരിക്കുകയും, (a, a+h) അന്തരാളത്തില് x ന്റെ എല്ലാ വിലകള്ക്കും f (n)(x) ഉണ്ടായിരിക്കുകയും ചെയ്യുമ്പോള്,
മുകളില് കൊടുത്ത പ്രമേയങ്ങളില് f(x) ന്റെ എല്ലാ അവകലജങ്ങളും സതതവും n →∞,n പദങ്ങള് കഴിഞ്ഞുള്ള ശിഷ്ടം പൂജ്യത്തോടടുക്കുകയും ചെയ്യുന്നു എങ്കില് ടെയിലര് ശ്രണിയും മക്ലോറിന് ശ്രണിയും കിട്ടുന്നു:
മക്ലോറിന് ശ്രണിയുപയോഗിച്ച് sin x, cos x, tan x, ex തുടങ്ങിയ പല ഫലനങ്ങളെയും ഘാതശ്രണികളായി വികസിപ്പിക്കാനും അവയുടെ ഏകദേശവില കണ്ടുപിടിക്കാനും സാധിക്കുന്നു.
Δx വളരെ ചെറുതായതുകൊണ്ട് അതിന്റെ ഉയര്ന്ന ഘാതങ്ങള് അവഗണിക്കാവുന്നതാണ്. അപ്പോള് Δy=f'(x).Δx (ഏകദേശം) x ന്റെ മാപനത്തിലുള്ള പിശക് Δx ആയാല് y ന്റെ മാപനത്തിലുള്ള പിശക് Δy ആണ്. അതുകൊണ്ടും മുകളില് കൊടുത്തത് x, y എന്നിവയുടെ പിശകുകളുടെ ഏകദേശമാണ് (approximate error relation).
ഇതുവരെ അവകലജ ഗുണാങ്കമായ dy/dxനെ ഒരു പ്രതീകമായിട്ടാണ് ഗണിച്ചത്. എന്നാല് ചിലപ്പോള് dy ക്കും dx നും പ്രത്യേക അര്ഥ കല്പനകള് നടത്തി ഉപയോഗിക്കാറുണ്ട്. ഏതെങ്കിലും രണ്ടു ചെറിയ രാശികളായ dy, dx എന്നിവയുടെ അനുപാതം -dy/dx എന്ന അവകലജ ഗുണാങ്കമാണെങ്കില് dy, dx എന്നിവയെ യഥാക്രമം y യുടെയും x ന്റെയും അവകലങ്ങള് (differentials)എന്നു പറയുന്നു.
സമാകലനം
ഒരു തലത്തിലെ വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണം കണ്ടുപിടിക്കാനാണ് സമാകലനം ആദ്യകാലത്ത് ഉപയോഗിച്ചിരുന്നത്. അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമയായി റീമാന് (182666) സമാകലത്തെ (Integration) നിര്വചിച്ചു. പില്ക്കാലത്ത് ലെബേഗ് സമാകലനത്തിനു പുതിയ നിര്വചനം കൊടുത്തിട്ടുണ്ടെങ്കിലും റീമാന്റെ നിര്വചനം പ്രായോഗികതലത്തില് സുപ്രധാനമാണ്.
f(x) എന്ന ഫലനത്തിന്റെ x = a, x = b എന്നീ സീമകള്ക്കുള്ളിലുള്ള നിശ്ചിത സമാകലത്തെ (definite integral) 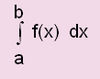
തീയ രീതിയില്, ഈ നിര്വചനമനുസരിച്ചുള്ള നിശ്ചിതസമാകലം വിസ്തീര്ണത്തെ (LMQP) കുറിക്കുന്നു. ഇവിടെ ചിത്രത്തില് ചെറിയ ദീര്ഘചതുരങ്ങളുടെ വീതി h→0, ദീര്ഘചതുരങ്ങളുടെ എണ്ണം (n) അനന്തത്തോടടുക്കുകയും ദീര്ഘചതുരങ്ങളുടെ മുകളിലുള്ള വക്രീയ ത്രികോണങ്ങളുടെ വിസ്തീര്ണങ്ങളുടെ തുക പൂജ്യത്തോടടുക്കുകയും ചെയ്യുന്നു.
മുകളില് കൊടുത്ത നിശ്ചിത സമാകലനത്തിന്റെ നിര്വചനം ഒരു സാമാന്യനിര്വചനത്തിന്റെ വിശേഷ രൂപമാണ്. നിശ്ചിതസമാകലത്തെ സംബന്ധിച്ച സാമാന്യ നിര്വചനം താഴെ കൊടുക്കുന്നു: (a, b) അന്തരാളത്തിലുള്ള
ഫലനം f(x) എടുക്കുക, അന്തരാളം (a,b) യെ (xr-1, xr) r = 1, 2, ... nഎന്ന n ഭാഗങ്ങളാക്കുക. ഈ ഉപഅന്തരാളങ്ങള് (sub-intervals) തുല്യമാകണമെന്നില്ല.r-ാമത്തെ
ത്തിലെ മൗലിക പ്രമേയമാണ്. ഇതില് നിന്ന്, സങ്കലനവും വ്യവകലനവുംപോലെ അവകലനവും സമാകലനവും പ്രതിലോമ ക്രിയകളാണെന്ന് വ്യക്തമാണ്. ഗ്രാഫികമായി ഈ പ്രമേയം പരിശോധിക്കാവുന്നതാണ്.
F(x) നെ f (x) ന്റെ പൂര്വഗം എന്നു പറയുന്നു.
ഒരു ഫലനത്തിന്റെ പ്രതിഅവകലജത്തിലെ രണ്ട് അംഗങ്ങള് തമ്മിലുള്ള വ്യത്യാസം ഒരു സ്വേച്ഛാ സ്ഥിരാങ്കമായിരിക്കും.
നിശ്ചിത സമാകലംപ്രാരംഭിക പ്രമേയങ്ങള്
f (x) യുഗ്മഫലനമാകുമ്പോള്, = 0, f (x) ഒറ്റഫലനമാകുമ്പോള്.
ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള്
ഉയര്ന്ന ക്രമങ്ങളിലുള്ള സമാകലങ്ങള് രണ്ടുവിധത്തിലാവാം. ഉത്തരോത്തര അവകലനത്തിനു സദൃശമായി ഒരു ഫലനത്തെ ഉത്തരോത്തരമായി n പ്രാവശ്യം സമാകലിച്ചാല് ഫലനത്തിന്റെ n-ാമത്തെ സമാകലം കിട്ടുന്നു. കൂടാതെ സാധാരണ സമാകലത്തിന്റെ പരിധി ഉയര്ന്ന വിമകളിലേക്കു വ്യാപിപ്പിച്ചാല് മറ്റൊരു തരത്തിലുള്ള സമാകലം കിട്ടുന്നു.
പുനരാവൃത്ത സമാകലം(Iterated integral)
f(x) എന്ന ഫലനത്തിന്റെ സമാകലനം F1(x) ആയിരിക്കട്ടെ. അതായത്
സമാകലനത്തിന്റെ ഓരോ ഘട്ടത്തിലുമുണ്ടാകുന്ന സമാകലന അചരം (constant of integration) അടുത്തഘട്ടത്തില് സമാകലിക്കപ്പെടുന്നു. അതുകൊണ് n-ആമത്തെ സമാകലത്തില്, Pn-1(x) = A1xn-1+ A2 xn-2 + ......... + A1 എന്ന ബഹുപദം കൂടി കിട്ടുന്നു.
ബഹുസമാകലം
(x, y) തലത്തിലുള്ള ഒരു വക്രം y = f(x) ആയിരിക്കട്ടെ. അപ്പോള് xന്റെ (a,b) എന്ന അന്തരാളത്തില് വക്രം ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണമാണ് ∫abf(x) dx ഈ സമാകലത്തിനു ഭൗതികമായ ഒരു അര്ഥകല്പന നടത്താവുന്നതാണ്.x അക്ഷത്തില് x = a, x = b എന്നീ ബിന്ദുക്കള്ക്കിടയിലുള്ളതും സാന്ദ്രത ρ=f(x) ആയതുമായ ഒരു ദണ്ഡിന്റെ ദ്രവ്യമാനമാണ് ഈ സമാകലം കുറിക്കുന്നത്. വിസ്തീര്ണത്തെ സംബന്ധിച്ച അര്ഥകല്പനയ്ക്കു സമാനമായ മറ്റൊരാശയമുപയോഗിച്ച് Z= f(x,y) എന്ന ഫലനത്തിന്റെ യുഗ്മസമാകലം (double integral) നിര്വചിക്കാവുന്നതാണ്. Z= f(x,y) എന്ന പ്രതലത്തിന്റെ (x,y) തലത്തിലുള്ള വിക്ഷേപം (projection), ഞ എന്ന വക്രമുള്ക്കൊള്ളുന്ന പ്രദേശമായിരിക്കട്ടെ. അപ്പോള് ഈ പ്രതലം ഉള്ക്കൊള്ളുന്ന സ്തംഭത്തിന്റെ വ്യാപ്തത്തെ കുറിക്കുന്ന സമാകലമാണ് ∫∫R f(x,y)dydx ചിത്രീകരിക്കാവുന്ന പ്രതലത്തെ പ്രതിനിധീകരിക്കുന്ന പ്രതലം Z = f(x,y) യും സമാകലനപരിധി, വിസ്തീര്ണവുമാണ്. ഞ ഒറ്റവക്രമോ (ഉദാ. ദീര്ഘവൃത്തം) രണ്ടോ അതിലധികമോ വക്രങ്ങള് ചേര്ന്നതോ ആകാം. സാന്ദ്രതാഫലനം ρ=f(x,y) ആകുമ്പോള് വക്രം R ഉള്ക്കൊള്ളുന്ന വിസ്തീര്ണത്തിന്റെ ദ്രവ്യമാനമായും ഈ സമാകലത്തെ കണക്കാക്കാം. യുഗ്മസമാകലത്തെ ഇരട്ട അനന്തശ്രണിയുടെ സീമയായും മറ്റൊരു വിധത്തില് വ്യാഖ്യാനിക്കാവുന്നതാണ്.
യുഗ്മസമാകലത്തിന്റെ മുല്യനിര്ണയനം
ഒരു യുഗ്മസമാകലത്തിന്റെ മൂല്യം നിര്ണയിക്കുവാന് ആദ്യം അതിനെ ഒരു ലഘുസമാകലമായി മാറ്റുന്നു. എന്നിട്ട് ലഘുസമാകലത്തെ സമാകലിക്കുന്നു. പ്രതീകാത്മകമായി ഈ പ്രക്രിയകളെ ഇങ്ങനെ എഴുതാം: ∫∫f(x,y)dy dx = [∫f(x,y)dy]dx,y യുടെയും x ന്റെയും നിശ്ചിതസീമകള്ക്കിടയി x നെ സ്ഥിരമായി സങ്കല്പിച്ചു (x ന്റെ വില x0 ആയിരിക്കട്ടെ. ചിത്രത്തില് x0 = OL) യുടെ മൂല്യം നിര്ണയിക്കുന്നു.x = x0 ആകുമ്പോള് y യുടെ സീമകള് വക്രം R ന്റെ സമീകരണത്തില് നിന്നു കിട്ടുന്നു (ചിത്രത്തില് x = x0 = OL ആകുമ്പോള്,y യുടെ വില y1ല് നിന്ന് y2ലേക്കു മാറുന്നു).
ഖരരൂപത്തെ x = x0 എന്ന തലം ഛേദിക്കുന്ന ലംബപരിച്ഛേദത്തെ F(x0) എന്ന ഫലനം പ്രതിനിധാനം ചെയ്യുന്നു.
x = x0, x = x0 + dx0 എന്നീ തലങ്ങള് ഉള്ക്കൊള്ളുന്ന നേര്ത്ത ലംബഖണ്ഡമാണ് F(x0) dx0. x0 നെ വര്ത്തമാന നിര്ദേശാങ്ക (current co-ordinate) ത്തിലേക്ക് മാറ്റി F(x) നെ യുക്തമായ സീമകള്ക്കുള്ളില് സമാകലിച്ചാല്
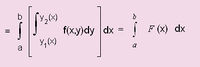 എന്ന ലഘു സമാകലം കിട്ടുന്നു.
എന്ന ലഘു സമാകലം കിട്ടുന്നു.
അങ്ങനെ ∫ ∫ f(x,y)dydx
ഉദാ: 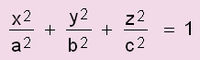 എന്ന ദീർഘവൃതജത്തിന്റെ (ellipsoid) (x,y) - തലത്തിലുള്ള വ്യാപ്തം കണക്കാക്കാം പ്രതലത്തിന്റെ സമീകരണത്തിൽ നിന്ന് z=f(x,y)=
എന്ന ദീർഘവൃതജത്തിന്റെ (ellipsoid) (x,y) - തലത്തിലുള്ള വ്യാപ്തം കണക്കാക്കാം പ്രതലത്തിന്റെ സമീകരണത്തിൽ നിന്ന് z=f(x,y)=
വിഷമ സമാകലങ്ങള്(Improper integrals)
റെീമാന്റെ നിര്വചനമനുസരിച്ച് സമാകലം  ല് സമാകലന അന്തരാളം (a, b) പരിമിതവും (finite) ഈ അന്തരാളത്തില് ഫലനം f(x) പരിബദ്ധവും (bounded) ആയിരിക്കണം. എന്നാല് ഇങ്ങനെ അല്ലാതെയും പ്രത്യേക സ്ഥിതികളെക്കൂടി ചേര്ത്ത് കോഷി, റീമാന്റെ നിര്വചനത്തെ പുതുക്കിയിട്ടുണ്ട്. പ്രത്യേക സ്ഥിതികള് താഴെപ്പറയുന്നവയാണ്:
ല് സമാകലന അന്തരാളം (a, b) പരിമിതവും (finite) ഈ അന്തരാളത്തില് ഫലനം f(x) പരിബദ്ധവും (bounded) ആയിരിക്കണം. എന്നാല് ഇങ്ങനെ അല്ലാതെയും പ്രത്യേക സ്ഥിതികളെക്കൂടി ചേര്ത്ത് കോഷി, റീമാന്റെ നിര്വചനത്തെ പുതുക്കിയിട്ടുണ്ട്. പ്രത്യേക സ്ഥിതികള് താഴെപ്പറയുന്നവയാണ്:
1. സമാകലന പരിധി അനന്തമായിരിക്കുന്ന അവസ്ഥ. അതായത് മ,യ ഇവയില് ഏതെങ്കിലും ഒന്നോ, രണ്ടും വെവ്വേറെയോ അനന്തമായിരിക്കും.
2. സീമകള് പരിമിതമാണെങ്കിലും ഫലനം f (x) പരിബദ്ധമായിരിക്കുകയില്ല; അതായത് f (x) ന് പരിമിതമായ അനന്ത അസാതത്യങ്ങള് (infinite discontinuities) ഉണ്ടായിരിക്കും.
ഇത്തരം സമാകലങ്ങളെ വിഷമ സമാകലങ്ങള് എന്നു പറയുന്നു. സമാകലന അന്തരാളത്തില് (a,b)ല് ഫലനം f(x) ന് x = c എന്ന ബിന്ദുവില് മാത്രം അനന്ത അസാതത്യം ഉണ്ടെന്നു സങ്കല്പിക്കുക. മറ്റെല്ലാ ബിന്ദുക്കളിലും ഫലനം പരിബദ്ധമാണ്. അപ്പോള് x = c എന്ന ബിന്ദുവിനെ (c-ε1,c+ε2) എന്ന ചെറിയ ഇടവേളയില് (ε1,ε2 സ്വേച്ഛാപരങ്ങളായ ചെറിയ സംഖ്യകളാണ്) ഒതുക്കിയാല് അന്തരാളം (a,b) യുടെ മറ്റു ഭാഗങ്ങളില് f(x) പരിബദ്ധമാണ്. അപ്പോള് , ![]() എന്നീ സമാകലങ്ങള്ക്ക് അസ്തിത്വമുണ്ട്. അവ ε1,ε2 എന്നിവയുടെഫലനങ്ങളാണ്. വലതുവശത്തെ സീമകള് ഉണ്ടെങ്കില്,
എന്നീ സമാകലങ്ങള്ക്ക് അസ്തിത്വമുണ്ട്. അവ ε1,ε2 എന്നിവയുടെഫലനങ്ങളാണ്. വലതുവശത്തെ സീമകള് ഉണ്ടെങ്കില്, ![]()
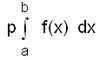 ഈ മൂല്യത്തെ സമാകലത്തിന്റെ പൊതുമൂല്യം എന്നു പറയുന്നു. പൊതു മൂല്യമുണ്ടെങ്കില് സമാകലം അഭികേന്ദ്രസാരി (convergent) ആണ്.
ഈ മൂല്യത്തെ സമാകലത്തിന്റെ പൊതുമൂല്യം എന്നു പറയുന്നു. പൊതു മൂല്യമുണ്ടെങ്കില് സമാകലം അഭികേന്ദ്രസാരി (convergent) ആണ്.
ε1=ε2ആകുമ്പോള് സമാകലത്തിന്റെ മുഖ്യമൂല്യം (principal value) കിട്ടുന്നു. മുഖ്യമൂല്യത്തെ കുറിക്കാന് കോഷി 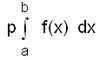 എന്ന പ്രതീകമുപയോഗിക്കുന്നു. സമാകലങ്ങള്ക്ക് പൊതുമൂല്യം എപ്പോഴും ഉണ്ടായിരിക്കണമെന്നില്ല. എന്നാല് പൊതുമൂല്യം ഉള്ളപ്പോള് അതു മുഖ്യമൂല്യം തന്നെയായിരിക്കും.
എന്ന പ്രതീകമുപയോഗിക്കുന്നു. സമാകലങ്ങള്ക്ക് പൊതുമൂല്യം എപ്പോഴും ഉണ്ടായിരിക്കണമെന്നില്ല. എന്നാല് പൊതുമൂല്യം ഉള്ളപ്പോള് അതു മുഖ്യമൂല്യം തന്നെയായിരിക്കും.
അസ്തിത്വമില്ലാത്തതിനാല് സമാകലത്തിനു പൊതുമൂല്യമില്ല. എന്നാല് ഈ സമാകലത്തിന്റെ മുഖ്യമൂല്യം പൂജ്യമാണ്.
വലതുവശത്തെ സീമകള് ഉണ്ടെങ്കില് സമാകലങ്ങള് അഭികേന്ദ്രസാരിയാണെന്നു പറയുന്നു. മൂന്നാമത്തെ സമാകലത്തിന്റെ മുഖ്യമൂല്യം 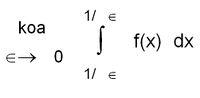 ആണ്.
ആണ്.
സവിശേഷതയുള്ള സമാകലങ്ങള്
സമാകലനംകൊണ്ട് ബീജീയം, ത്രികോണമിതീയം, ലോഗരിതീയം, ഹൈപ്പര് ജ്യാമിതീയം തുടങ്ങിയ ഫലനങ്ങള് ഉണ്ടാവുന്നു. എന്നാല് ഇത്തരത്തിലല്ലാത്ത സവിശേഷ സ്വഭാവമുള്ള പല ഫലനങ്ങളും സമാകലനം കൊണ്ടും കിട്ടാറുണ്ട്. അവയില് ചില ഫലനങ്ങളാണ് താഴെ പറയുന്നത്:
കലനം പ്രായോഗിക തലത്തില്
പ്രായോഗിക തലത്തില് കലനത്തിന്റെ ഉപയോഗം വ്യക്തമാക്കുന്ന ചില ഉദാഹരണങ്ങള് താഴെ കൊടുക്കുന്നു:
സ്പര്ശകങ്ങളും അഭിലംബങ്ങളും
(x1, y1) എന്ന ബിന്ദുവില് പ്രതിച്ഛേദിക്കുന്നy = f(x), y = g(x) എന്നീ വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം ഈ ബിന്ദുവില് വക്രങ്ങള്ക്കു വരയ്ക്കുന്ന സ്പര്ശകങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണമായി നിര്വചിച്ചിരിക്കുന്നു. അതുകൊണ്ടും വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം, ![]() ആണ്. പ്രതിച്ഛേദബിന്ദുവില് വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം 90° ആണെങ്കില് അവ, ലംബികമായി പ്രതിച്ഛേദിക്കുന്നു എന്നു പറയുന്നു. അപ്പോള്
ആണ്. പ്രതിച്ഛേദബിന്ദുവില് വക്രങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം 90° ആണെങ്കില് അവ, ലംബികമായി പ്രതിച്ഛേദിക്കുന്നു എന്നു പറയുന്നു. അപ്പോള്
1+f '(x1) g'(x1) = 0. വക്രങ്ങള് പരസ്പരം സ്പര്ശിക്കുമ്പോള് f '(x1) = g'(x1) എന്നു കിട്ടുന്നു.
വക്രത്തിനു P എന്ന ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകം PTഉം അഭിലംബം PGഉം x അക്ഷത്തെ T,G എന്നീ ബിന്ദുക്കളില് പ്രതിച്ഛേദിക്കുന്നു എന്നിരിക്കട്ടെ. കൂടാതെ Pല്ക്കൂടി x അക്ഷത്തിനു വരയ്ക്കുന്ന ലംബം PN ആയിരിക്കട്ടെ. അപ്പോള് PT, PG, TN, NG എന്നിവയെ യഥാക്രമം സ്പര്ശകം, അഭിലംബം, ഉപസ്പര്ശകം (subtangent), ഉപലംബം (subnormal) എന്നിവയുടെ ദൈര്ഘ്യമായി നിര്വചിച്ചിരിക്കുന്നു. ചിത്രത്തില് നിന്ന് ഇവ കണ്ടുപിടിക്കാവുന്നതാണ്. ഉദാ. ഉപലംബത്തിന്റെ ദൈര്ഘ്യം, .
അനന്ത സ്പര്ശകം
ഒരു വക്രത്തെ അനന്തത്തില് സ്പര്ശിക്കുന്നതും എന്നാല് അനന്തത്തിലല്ലാത്തതുമായ വാസ്തവിക രേഖയാണ് അനന്തസ്പര്ശകം. ഉദാ.xy = c2 (സമകോണീയ ഹൈപ്പര്ബോള) എന്ന വക്രത്തെ x അക്ഷവും y അക്ഷവും അനന്തത്തില് സ്പര്ശിക്കുന്നു. അതുകൊണ്ട് x,y അക്ഷങ്ങളാണ് xy = c2 എന്ന വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള്.
n-ാമത്തെ ഡിഗ്രിയിലുള്ള ഒരു ബീജീയവക്രത്തെ ![]() എന്ന് എഴുതാവുന്നതാണ്. ഈ വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാം.y = mx + δഎന്ന രേഖ ഈ വക്രത്തെ പ്രതിച്ഛേദിക്കുന്ന ബിന്ദുക്കളുടെ x നിര്ദേശാങ്കങ്ങള് കിട്ടുവാന് ഈ സമീകരണങ്ങളില്നിന്ന് y യെ ഒഴിവാക്കുന്നു. അപ്പോള്
എന്ന് എഴുതാവുന്നതാണ്. ഈ വക്രത്തിന്റെ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാം.y = mx + δഎന്ന രേഖ ഈ വക്രത്തെ പ്രതിച്ഛേദിക്കുന്ന ബിന്ദുക്കളുടെ x നിര്ദേശാങ്കങ്ങള് കിട്ടുവാന് ഈ സമീകരണങ്ങളില്നിന്ന് y യെ ഒഴിവാക്കുന്നു. അപ്പോള്
ഓരോ പദത്തെയും ടെയിലര് പ്രമേയമുപയോഗിച്ച് വികസിപ്പിച്ചാല്, xnΦ2(m) +x(n-1)[c Φ2(m)+ Φn-1(m)]+.. =0 . y = mx + c അനന്തസ്പര്ശിയാകുമ്പോള് മുകളില്ക്കൊടുത്ത സമീകരണത്തിന് രണ്ട് അനന്തമൂല്യങ്ങള് (inifinite roots) വേണ്ടിയിരിക്കുന്നു. അതുകൊണ്ട്, φn(m) =0, cφn'(m)+φn-1(m)=0 ആദ്യത്തെ സമീകരണത്തില് നിന്ന് m ന് n വിലകള് കിട്ടുന്നു. അവ m1, m2, ..., mn ആയിരിക്കട്ടെ. രണ്ടാമത്തെ സമീകരണത്തില് നിന്ന് ര യുടെ വിലകള് കിട്ടുന്നു. അതുകൊണ്ടും അനന്തസ്പര്ശകങ്ങളുടെ സമീകരണങ്ങള്, y = m1 x + c1, y = m2 x + c2, ..., y = mn x + cn ആണ്.
x,y അക്ഷങ്ങള്ക്കു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കണ്ടുപിടിക്കാന് താഴെ കൊടുക്കുന്ന പ്രവര്ത്തനസൂത്രങ്ങള് ഉപയോഗിക്കുന്നു. വക്രത്തിന്റെ സമീകരണത്തില് x ന്റെ ഏറ്റവും ഉയര്ന്ന ഡിഗ്രിയിലുള്ള പദത്തിന്റെ ഗുണാങ്കത്തെ പൂജ്യത്തോടു സമീകരിച്ചാല് x അക്ഷത്തിനു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കിട്ടും. അതുപോലെ y യുടെ ഏറ്റവും ഉയര്ന്ന ഡിഗ്രിയിലുള്ള പദത്തിന്റെ ഗുണാങ്കത്തെ പൂജ്യത്തോടു സമീകരിച്ചാല് y അക്ഷത്തിനു സമാന്തരമായ അനന്തസ്പര്ശകങ്ങള് കിട്ടും.
ഉച്ചതമങ്ങളും നിമ്നതമങ്ങളും
ഒരു വക്രത്തിന്റെ ഒരു ഖണ്ഡം പരിഗണിക്കുക. ആ വക്രഖണ്ഡത്തിന്റെ ഉച്ചതമവും നിമ്നതമവും കണ്ടുപിടിക്കാന് അവകലജങ്ങള് പ്രയോജനപ്പെടുന്നു. നിമ്നോന്നത ബിന്ദുക്കളില് y' എന്നത് പൂജ്യമായിരിക്കും.y" ന്റെ വില ഋണസംഖ്യയാണെങ്കില് ആ ബിന്ദു ഉച്ചതമത്തിന്റെയും ധനസംഖ്യയാണെങ്കില് നിമ്നതമത്തിന്റെയും ആയിരിക്കും.
ഉച്ചതമമൂല്യത്തില് വര്ധിച്ചുകൊണ്ടിരിക്കുന്ന ഒരു ഫലനത്തിന്റെ വര്ധനവ് നില്ക്കുകയും ഫലനം ക്രമേണ കുറയുകയും ചെയ്യുന്നു (ചിത്രത്തില് P എന്ന സ്ഥാനം). ഫലനം കുറയുന്നത് ചിലപ്പോള് പെട്ടെന്നാവുകയും ചെയ്യാം (ചിത്രത്തില് R എന്ന സ്ഥാനം). അതുപോലെ നിമ്നതമത്തില് കുറഞ്ഞുകൊണ്ടിരിക്കുന്ന ഫലനം വര്ധിക്കുവാന് ആരംഭിക്കുന്നു. രണ്ടിടത്തും ചരിവ് f '(x) ന്റെ ചിഹ്നം മാറുന്നു (ഫലനം വര്ധിക്കുമ്പോള് f '(x) ധനാത്മകവും കുറയുമ്പോള്
ഋണാത്മകവും ആണ്). ഒരു ഫലനത്തിന്റെ ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കാന് പ്രായോഗികമായി ഉപയോഗമുള്ള വസ്തുതയാണിത്. ഫലനം f(x), x = a യില് ഉച്ചതമമാകുമ്പോള് f ' (a) = 0, f " (a) < 0; അതുപോലെ നിമ്നതമമാകുമ്പോള് f '(a) = 0, f " (a) > 0.
ടെയിലര് പ്രമേയമുപയോഗിച്ച് ഒരു ഫലനം ഉച്ചതമവും നിമ്നതമവുമാകാനുള്ള ആവശ്യകവും പര്യാപ്തവുമായ നിബന്ധനകള് കണ്ടുപിടിക്കാവുന്നതാണ്.x = a യില് ഫലനം f(x) ഉച്ചതമമോ നിമ്നതമമോ ആകുമ്പോള്, വ ന്റെ ചെറിയ വിലകള്ക്ക്,
എന്നിവ ഒരേ ചിഹ്നത്തോടുകൂടിയതായിരിക്കും. ഇതില് നിന്ന് ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്കുള്ള പൊതുപ്രമേയം കിട്ടുന്നു:
f ' (a) = f " (a) = f (a) = ... = f n-1 (a) = 0, f (n) (a) ≠ 0 ആകുമ്പോള്, f(a) ഉച്ചതമമോ നിമ്നതമോ ആകണമെങ്കില് പൂജ്യമാകാത്ത ആദ്യത്തെ അവകലജം, അതായത് f(n)(a) ഇരട്ടക്രമത്തോടുകൂടിയതായിരിക്കണം. കൂടാതെ ഉച്ചതമമൂല്യത്തിന് f(n)(a) ഋണാത്മകവും നിമ്നതമ മൂല്യത്തിന് f(n)(a) ധനാത്മകവും ആകണം.
ഇവിടെ n = 2 ആകുമ്പോഴുള്ള പ്രത്യേക സ്ഥിതിയാണ് ഗ്രാഫിക് പരിഗണനയില് നിന്ന് മുന്പു ലഭിച്ച നിബന്ധനകള്. അതായത് ഉച്ചതമ മൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) < 0; നിമ്നതമമൂല്യങ്ങള്ക്ക് f ' (a) = 0, f " (a) > 0.
ഉദാ. തരംഗദൈര്ഘ്യം λ ഉള്ള തരംഗങ്ങള്ക്ക് ആഴത്തില് വെള്ളമുള്ളിടത്ത് വേഗത  യോട് ആനുപാതികമാണ് (a സ്ഥിരരാശി). എന്നാല് λ = a ആകുമ്പോള് വേഗത ന്യൂനതമമാകും.
യോട് ആനുപാതികമാണ് (a സ്ഥിരരാശി). എന്നാല് λ = a ആകുമ്പോള് വേഗത ന്യൂനതമമാകും.
പ്രതിബന്ധിത ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള്
(Constrained extrema). ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കേണ്ട ഫലനത്തിലെ രാശികള് എപ്പോഴും സ്വതന്ത്രമായിരിക്കണമെന്നില്ല. അവ തമ്മില് ഒരു ബന്ധം ഉണ്ടായിരിക്കും. അങ്ങനെയുള്ള അവസരങ്ങളില് ഉച്ചതമനിമ്നതമമൂല്യങ്ങള് കണ്ടുപിക്കാന് ലാഗ്രഞ്ചിന്റെ "അനിര്ധാരിത ഗുണനരീതി' (method of undetermined multipliers). ഉപയോഗിക്കാവുന്നതാണ്. u = f (x,y,z) എന്ന ഫലനത്തിലെ രാശികള് തമ്മിലുള്ള ബന്ധം φ(x,y,z) = 0 ആയിരിക്കട്ടെ. ഉച്ചതമനിമ്നതമമൂല്യങ്ങള്ക്ക്
അതുകൊണ്ട് രണ്ടാമത്തെ സമീകരണത്തെ കൊണ്ട് ഗുണിച്ചു ആദ്യത്തേതിനോട് കൂട്ടിയാല്,
കൂടാതെ φ(x,y,z) = 0. ഈ നാലു സമീകരണങ്ങളും നിര്ധാരണം ചെയ്താല് u അചലമായിരിക്കുമ്പോഴുള്ള (ഉച്ചതമോ നിമ്നതമമോ ആയിരിക്കുമ്പോഴുള്ളx, y, z ന്റെ മൂല്യങ്ങള് കിട്ടുന്നു. ഫലനം u = f(x,y,z) യഥാര്ഥത്തില് x,y,z മുകളില് കണ്ടുപിടിക്കുന്ന വിലകള്ക്ക് ഉച്ചതമമാകുമോ നിമ്നതമമാകുമോ എന്നറിയാന്, പരിഗണിക്കുന്ന പ്രശ്നത്തിന്റെ ഭൗതിക സാഹചര്യങ്ങള്കൂടി ഉപയോഗിക്കേണ്ടതാണ്.
വക്രത
വക്രങ്ങളുടെ ഒരു അവകല ഗുണധര്മമാണ് വക്രത. വക്രത്തിലെ ഏതെങ്കിലും ഒരു ബിന്ദുവില് വരയ്ക്കുന്ന സ്പര്ശകത്തിന്റെ ദിശ, ചാപ (arc) ത്തിനനുസരണമായി വ്യത്യാസപ്പെടുന്നതിന്റെ തോതാണ് വക്രത. സ്പര്ശകത്തിന്റെ ദിശയെ കുറിക്കുന്ന കോണം Ψ ഉം ചാപദൈര്ഘ്യം ξഉം ആയാല് വക്രത n=dΨ/dξആണ്. വക്രതയുടെ വ്യുത്ക്രമത്തെ 1/ρ വക്രതാവ്യാസാര്ധം(radius of curvature) എന്നു പറയുന്നു. ഒരു വൃത്തത്തിന്റെ വക്രതാവ്യാസാര്ധം അതിന്റെ വ്യാസാര്ധത്തോടു തുല്യമാണ്.
കാര്ത്തീയ സമീകരണംy = f(x) ഉള്ള ഒരു വക്രത്തിന്റെ വക്ര
ρ= 0 ആകുമ്പോള് വക്രം ശൂന്യവൃത്തമാകുകയും ((point circle), ρ= ∞ ആകുമ്പോള് വക്രം ഋജുരേഖയായി "അപഭ്രംശിക്കുക'യും (degenerate) ചെയ്യുന്നു. ചരിവുകോണം Ψ കൂടുമ്പോള്, ചാപദൈര്ഘ്യം ξ കൂടുകയോ കുറയുകയോ ചെയ്യുന്നതനുസരിച്ച് ρ<>0; അതായത് x വിലകള് കൂടുമ്പോള്, വക്രം ഇടത്തോട്ടോ വലത്തോട്ടോ തിരിയുന്നതനുസരിച്ച് fn മുകളിലോട്ടോ താഴോട്ടോ അവതലം (concave) ആകുന്നതനുസരിച്ച് ρ<>0 ആകുന്നു. ഉദാ. ഒരു വക്രത്തിന്റെ പ്രാചലികസമീകരണം (parametric equation) x = f(t), y =Φ (t) ആയിരിക്കട്ടെ.
വക്രത്തിലെ P(x,y) എന്ന ബിന്ദുവിലെ അഭിലംബത്തില് (വക്രത്തിന്റെ അവതല വശത്തുള്ള അഭിലംബത്തില്) PC = ρആകത്തക്കവണ്ണം C(x,y) എടുക്കുക. Cയെ വക്രതാകേന്ദ്രം (centre of curvature) എന്നു പറയുന്നു. വക്രതാകേന്ദ്രത്തിന്റെ നിര്ദേശാങ്കങ്ങള്,ആണ്.
വക്രതാകേന്ദ്രം (x,y) ന്റെ ബിന്ദുപഥത്തെ (locus) കേന്ദ്രജം (evolute) എന്നു പറയുന്നു. വക്രത്തിലെ ഏതെങ്കിലും രണ്ടുബിന്ദുക്കള് തമ്മിലുള്ള ചാപദൈര്ഘ്യം, ആ ബിന്ദുക്കളിലെ വക്രതാവ്യാസാര്ധങ്ങള് തമ്മിലുള്ള വ്യത്യാസമാണെന്നു തെളിയിക്കാവുന്നതാണ്.
എന്വെലപ് (Envelope)
xcosα+ysinα=1 ഒരു ഋജുരേഖയുടെ സമവാക്യമാണ്. α ക്ക് പല വിലകള് കൊടുത്താല് വ്യത്യസ്തങ്ങളായ രേഖകള് കിട്ടുന്നു. അങ്ങനെ α ക്കു പല വിലകള് കൊടുത്തുണ്ടാകുന്ന രേഖകളെല്ലാംകൂടി ഒരു രേഖാകുലം (family of straight lines) ആകുന്നു. ഇവിടെ αയെ പ്രാചലം (parameter) എന്നു പറയുന്നു. ഒരു പ്രാചലം മാത്രമുള്ള വക്രകുലത്തെ കുറിക്കാന് f(x,y,α)എന്നെഴുതാം.x2 + y2 = a2 ഒരു ഏകപ്രാചലവൃത്തകുലമാണ് (a പ്രാചലം). ഒരു വക്രം, തന്നിട്ടുള്ള വക്രകുലത്തിലെ എല്ലാ അംഗങ്ങളെയും സ്പര്ശിക്കുകയും അതിലെ ഓരോ ബിന്ദുവിനെയും വക്രകുലത്തിലെ ഏതെങ്കിലും ഒരംഗം സ്പര്ശിക്കപ്പെടുകയും ചെയ്യുന്നു എങ്കില് ആ വക്രത്തെ വക്രകുലത്തിന്റെ എന്വെലപ് എന്നു പറയുന്നു. ഉദാഹരണമായി, വിശ്ലേഷകജ്യാമിതിയില് നിന്ന് xcosα+ysinα=1 എന്ന രേഖാകുലം, വൃത്തം x2+y2 = 1 നെ സ്പര്ശിക്കുന്നു. കൂടാതെ ഈ വൃത്തത്തിലെ ഏതു ബിന്ദുവിലെയും സ്പര്ശകത്തിന്റെ സാമാന്യരൂപം ആണ്. അതുകൊണ്ട് ഈ രേഖാകുലത്തിന്റെ എന്വെലപ് x2 + y2 = 1 എന്ന വൃത്തമാണെന്ന് അനുമാനിക്കാം. ചിത്രത്തില് കാണുന്ന രേഖാകുലത്തിലെ തുടര്ച്ചയായ രണ്ടു അംഗങ്ങളുടെ അന്തിമമായ പ്രതിച്ഛേദ ബിന്ദുവിന്റെ (സീമാന്ത പ്രതിച്ഛേദ ബിന്ദു) ബിന്ദുപഥമാണ് എന്വെലപ്. ഈ ആശയമുപയോഗിച്ച് എന്വെലപ്പിനെ മറ്റൊരുവിധത്തില്
നിര്വചിക്കാം: f(x,y,α)എന്ന വക്രകുലത്തിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് α യെ
എന്നീ സമീകരണങ്ങളില് നിന്ന് വിലുപ്തമാക്കുന്നു (eliminate). ഉദാ. ![]() (m പ്രാചലം) ഒരു രേഖാകുലമാണ്. ഇതിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് പ്രാചലം m നെ,
(m പ്രാചലം) ഒരു രേഖാകുലമാണ്. ഇതിന്റെ എന്വെലപ് കണ്ടുപിടിക്കാന് പ്രാചലം m നെ, ![]() ,
, ![]() എന്നീ സമവാക്യങ്ങളില് നിന്നു വിലുപ്തമാക്കുന്നു. അപ്പോള്, കിട്ടുന്ന y2 = 4ax എന്ന പരാവളയം (parabola) ആണ് മുകളില് കൊടുത്ത രേഖാകുലത്തിന്റെ എന്വെലപ്.
ഒരു വക്രത്തിലെ വ്യത്യസ്ത ബിന്ദുക്കളിലെ വക്രതാ കേന്ദ്രങ്ങളുടെ ബിന്ദുപഥമാണ് കേന്ദ്രജം. ഈ ബിന്ദുക്കളിലെ അഭിലംബങ്ങളുടെ എന്വെലപ്പായും കേന്ദ്രജത്തെ പരിഗണിക്കാവുന്നതാണ്. പരാവളയം y2 = 4ax ന്റെ കേന്ദ്രജം "ബിന്ദുപഥ' കല്പന ഉപയോഗിച്ചും 'എന്വെലപ്' ഉപയോഗിച്ചും കണ്ടുപിടിക്കുന്നത് ഇപ്രകാരമാണ്.
എന്നീ സമവാക്യങ്ങളില് നിന്നു വിലുപ്തമാക്കുന്നു. അപ്പോള്, കിട്ടുന്ന y2 = 4ax എന്ന പരാവളയം (parabola) ആണ് മുകളില് കൊടുത്ത രേഖാകുലത്തിന്റെ എന്വെലപ്.
ഒരു വക്രത്തിലെ വ്യത്യസ്ത ബിന്ദുക്കളിലെ വക്രതാ കേന്ദ്രങ്ങളുടെ ബിന്ദുപഥമാണ് കേന്ദ്രജം. ഈ ബിന്ദുക്കളിലെ അഭിലംബങ്ങളുടെ എന്വെലപ്പായും കേന്ദ്രജത്തെ പരിഗണിക്കാവുന്നതാണ്. പരാവളയം y2 = 4ax ന്റെ കേന്ദ്രജം "ബിന്ദുപഥ' കല്പന ഉപയോഗിച്ചും 'എന്വെലപ്' ഉപയോഗിച്ചും കണ്ടുപിടിക്കുന്നത് ഇപ്രകാരമാണ്.
1.y2 = 4ax ലെ ഒരു ബിന്ദു (at2, 2at)എന്നെടുക്കാം. അപ്പോള് വക്രതാ കേന്ദ്രത്തിന്റെ നിര്ദേശാങ്കങ്ങള് x=2a+3at2, y=2at3 ആണ്. യെ വിലുപ്തമാക്കിയാല് കേന്ദ്രജത്തിന്റെ സമവാക്യം 27ay2 = 4(x-2a)3 എന്ന അര്ധ ത്രിഘാത പരാവളയം (semi cubical parabola) ആണെന്നു കാണാം.
2. പരാവളയത്തിലെ (at2, 2at)എന്ന ബിന്ദുവിലെ അഭിലംബംy + xt = 2at + at3 ആേണ്. കൊണ്ട് ആംശികമായി അവകലിച്ചാല്,x = 2a + 3at2. പ്രാചലം യെ വിലുപ്തമാക്കിയാല്, എന്വെലപ് 27 ay2 = 4 (x-2a)3 എന്നു കിട്ടുന്നു. ഇതാണ് മുകളില് കൊടുത്തപോലെ കേന്ദ്രജത്തിന്റെ സമവാക്യം.
അനിര്ധാര്യ രൂപങ്ങള്
ഫലനം f(x), xന്റെ പ്രത്യേക വിലകള്ക്ക് അനിര്ധാര്യരൂപം 0/0 ആകുമ്പോള്, സീമ എന്ന ആശയമുപയോഗിച്ച് ഫലനത്തിന് "സീമാന്തമൂല്യങ്ങള്' (limiting values) കൊടുക്കാവുന്നതാണ്. അനിര്ധാര്യ രൂപങ്ങള് മറ്റുവിധത്തിലുമാകാം. ∞/∞, ∞-∞, 00, 1∞, ∞0ഇവയൊക്കെ അനിര്ധാര്യ രൂപങ്ങളാണ്.
"ഹോസ്പിറ്റല് നിയമ'മനുസരിച്ച്, f(a) = 0, Φ(a)=0 ആകു
ഉദാ. . ബീജീയ ലഘുകരണം കൊണ്ട് ∞/∞, ∞x0, ∞-∞ തുടങ്ങിയ അനിര്ധാര്യരൂപങ്ങളെ എന്ന രൂപത്തിലേക്ക് മാറ്റാവുന്നതാണ്.
![]() എന്ന സര്വ സമവാക്യം (identity)∞-∞ എന്ന അനിര്ധാര്യരൂപത്തെ 0/0 ലേക്ക് മാറ്റുന്നതാണ്. അതുകൊണ്ട് ഇത്തരം സന്ദര്ഭങ്ങളില് ഹോസ്പിറ്റല് നിയമമുപയോഗിച്ച് ഫലനങ്ങളുടെ സീമകള് കണ്ടുപിടിക്കാം.
എന്ന സര്വ സമവാക്യം (identity)∞-∞ എന്ന അനിര്ധാര്യരൂപത്തെ 0/0 ലേക്ക് മാറ്റുന്നതാണ്. അതുകൊണ്ട് ഇത്തരം സന്ദര്ഭങ്ങളില് ഹോസ്പിറ്റല് നിയമമുപയോഗിച്ച് ഫലനങ്ങളുടെ സീമകള് കണ്ടുപിടിക്കാം.
അതുകൊണ്ട്, k = eº = 1.
സമീകരണങ്ങളുടെ ഏകദേശ മൂല്യങ്ങള്ന്യൂട്ടന്റെ രീതി
സമീകരണം f(x) = 0 ന് 'a' എന്ന സംഖ്യയ്ക്കടുത്ത് മൂല്യമുണ്ടെങ്കില് മൂല്യത്തിന്റെ ഏകദേശവില കണ്ടുപിടിക്കാവുന്നതാണ്. മൂല്യം a+h ആയാല് f(a+h) = 0; f(a) + hf '(a) = 0 (ഏകദേശം). ഇതില് നിന്ന്
പിടിക്കാവുന്നതാണ്. ഇങ്ങനെ തുടര്ന്നാല് ആവശ്യമുള്ള സൂക്ഷ്മതയോടെ ഏതു സമവാക്യത്തിന്റെയും ഏകദേശവില കിട്ടുന്നു. സമീകരണം x3 + 2x - 5 = 0 ന്റെ ഒരു മൂല്യത്തിന്റെ ഏകദേശവില 1.3 ആണ്. ന്യൂട്ടന്റെ രീതി ഉപയോഗിച്ചാല് അടുത്ത ഏകദേശവില 1.33 എന്നും കുറച്ചുകൂടി സൂക്ഷ്മമായ ഏകദേശവില 1.3283 എന്നും കിട്ടുന്നു.
ഫലനങ്ങളുടെ ശ്രണീ വികസനം
മെക്ലോറില് ശ്രണിയുപയോഗിച്ച് പല ഫലനങ്ങളെയും അഭികേന്ദ്രസരണ നിബന്ധനകള്ക്കു വിധേയമായി ഘാതശ്രണികളായി വികസിപ്പിക്കാവുന്നതാണ്. ഫലനം f(x) ന്റെ മക്ലോറിന് ശ്രണി:
ചില ഫലനങ്ങള്ക്ക് f (n)(x) പ്രത്യക്ഷത്തില് കണ്ടുപിടിക്കാന് എളുപ്പമല്ല. പുനരാവൃത്തി ബന്ധ(recurrence relation)ത്തിലൂടെയായിരിക്കും f (n)(x) പ്രത്യക്ഷപ്പെടുക. ഇത്തരം അവസരങ്ങളിലും f (n)(0) പ്രത്യേകം കണ്ടുപിടിച്ച് ഫലനത്തെ വികസിപ്പിക്കാവുന്നതാണ്. ഈ രീതിയുപയോഗിച്ച് (sin-1 x)2 നെ വികസിപ്പിക്കാം.
y = (sin-1 x)2 ആയിരിക്കട്ടെ. അവകലനം കൊണ്ട് ![]() y1= 2y, (1-x2) y2 - xy1 = 2 എന്നീ സമവാക്യങ്ങള് കിട്ടുന്നു. ലൈബ്നിറ്റ്സ് പ്രമേയമുപയോഗിച് n പ്രാവശ്യം അവകലിച്ചാല്, (1-x2) yn+2 - (2n+1) xyn+1 - n2yn = 0, x = 0, (y)0 = 0, (y1)0 = 0, (y2)0 = 2, .... (yn+2) = n2 (yn)0 അതുകൊണ്ട് (y2n-1)0 = 0, (y2n)0 = 2.22 . 42 . 62 ... (2n-2)2 (n≠1). മക്ലോറിന് ശ്രണിയില് വിലയിട്ടാല്, .
y1= 2y, (1-x2) y2 - xy1 = 2 എന്നീ സമവാക്യങ്ങള് കിട്ടുന്നു. ലൈബ്നിറ്റ്സ് പ്രമേയമുപയോഗിച് n പ്രാവശ്യം അവകലിച്ചാല്, (1-x2) yn+2 - (2n+1) xyn+1 - n2yn = 0, x = 0, (y)0 = 0, (y1)0 = 0, (y2)0 = 2, .... (yn+2) = n2 (yn)0 അതുകൊണ്ട് (y2n-1)0 = 0, (y2n)0 = 2.22 . 42 . 62 ... (2n-2)2 (n≠1). മക്ലോറിന് ശ്രണിയില് വിലയിട്ടാല്, .
അനന്തശ്രണികളും അനന്ത ഗുണനഫലങ്ങളും
"അനന്തമായ അനന്തസൂക്ഷ്മങ്ങളുടെ തുകയുടെ സീമ' എന്ന നിര്വചനമനുസരിച്ച്, നിശ്ചിതസമാകലം
(nh = b-a ആകുമ്പോള്), a = 0, b = 1 ആയാല്,
മുകളില് കൊടുത്ത സമവാക്യമുപയോഗിച്ച് അഭികേന്ദ്രസാരികളായ പല അനന്തശ്രണികളുടെയും അനന്തഗുണനഫലങ്ങളുടെയും "അഭികേന്ദ്രസീമ' കണ്ടുപിടിക്കാവുന്നതാണ്. വലതുവശത്തു കാണുന്ന അനന്തശ്രണിയുടെ തുക കണ്ടുപിടിക്കാന്
കലനം നിത്യജീവിതത്തില്
17-ാം ശ.ത്തിന്റെ അവസാനത്തില് ജ്യോതിശ്ശാസ്ത്രം, ബലതന്ത്രം തുടങ്ങിയ ശാസ്ത്രശാഖകളിലെ വികാസം ന്യൂട്ടനും ലൈബ്നിറ്റ്സിനും കലനത്തിന്റെ മൗലിക തത്ത്വങ്ങള് ആവിഷ്കരിക്കാന് പ്രചോദനം നല്കി. ക്ലാസ്സിക് ഭൗതികശാസ്ത്രവികസനത്തിന് അടിസ്ഥാനമിട്ടത് അവകലനവും സമാകലനവും പിന്നീട് രൂപംകൊണ്ട അവകല സമീകരണങ്ങളുമാണ്. അവകലനം മാനവികശാസ്ത്രങ്ങളില് ഏറെ പ്രയോജനപ്പെടുത്തിയിട്ടുണ്ട്. തത്ക്ഷണികമായ വ്യതിയാനങ്ങള് അളക്കുന്നതിന് ഏറ്റവും പ്രയോജനകരമായ ഒരു ഉപാധിയാണ് അവകലജങ്ങള്. ആധുനിക ലോകത്തില് നിത്യജീവിത സംവിധാനം ശാസ്ത്രപുരോഗതിയുമായി അഭേദ്യമായി ബന്ധപ്പെട്ടിരിക്കുന്നു. പ്രത്യക്ഷമായോ പരോക്ഷമായോ ബന്ധമുള്ള എല്ലാ ശാസ്ത്രശാഖകളും അവയുടെ വികാസത്തില് കലനത്തോടു കടപ്പെട്ടിരിക്കുന്നു. കലനവുമായി ബന്ധപ്പെട്ട ശാസ്ത്രശാഖകള്ക്ക് ഉദാഹരണങ്ങളാണ് ബലതന്ത്രം, എന്ജിനീയറിങ്, കാലാവസ്ഥാശാസ്ത്രം മുതലായവ. ഫലനങ്ങളുടെ സീമാന്തമൂല്യങ്ങളെക്കുറിച്ചാണ് കലനത്തില് പ്രതിപാദിക്കുന്നത്. പ്രായോഗികതലത്തില് ഒരു ഫലനത്തിന്റെ വര്ധനവിന്റെ തോതാണ് (rate) അതിന്റെ അവകലജഗുണാങ്കം. അതുകൊണ്ട് ഭൗതികശാസ്ത്രത്തില് അവകലനരീതികള് വളരെയധികം ഉപയോഗപ്പെടുന്നുണ്ട്.
പരസ്പര ബന്ധമുള്ള രണ്ടു കാര്യങ്ങളില് ഒന്ന് സ്വതന്ത്രവും മറ്റേത് ആശ്രിതവും ആണെങ്കില് അവയുടെ മാറ്റം അവകലജം കൊണ്ട് സൂചിപ്പിക്കാം. പ്രവേഗം (velocity), ത്വരണം (acceleration) മുതലായ സങ്കല്പങ്ങള്ക്ക് കലനത്തിലൂടെ ഗണിതശാസ്ത്രരൂപം കിട്ടുന്നു. s ദൂരത്തെയും t സമയത്തെയും സൂചിപ്പിക്കുന്നുവെങ്കില് t യെ അപേക്ഷിച്ച് s ന്റെ അവകലജം s' വേഗത്തെയും s" ത്വരണത്തെയും കുറിക്കുന്നു. സെക്കന്ഡില്, ചലിക്കുന്ന ഒരു ബിന്ദുവിന്റെ സ്ഥിതിസദിശം (position vector) r ആയാല് ബിന്ദുവിന്റെ പ്രവേഗസദിശം N=dr/dt യും ത്വരണസദിശം d2r/dt2 ഉം ആണ്. ഫലനങ്ങളുടെ ഉച്ചതമനിമ്നതമ മൂല്യങ്ങള് കണ്ടുപിടിക്കാന് കലനരീതിയാണ് സാധാരണയായി ഉപയോഗിക്കുന്നത്. സാമ്പത്തിക ശാസ്ത്രത്തിന്റെ പല മേഖലകളിലും കലന സങ്കല്പങ്ങള്ക്ക് വളരെ പ്രാധാന്യമുണ്ട്. ഉത്പാദനം, വിതരണം, വില, വിപണനം മുതലായവയുടെ അറ്റനിരക്ക് (തത്ക്ഷണിക നിരക്ക്) സൂചിപ്പിക്കാന് അവകലജം പ്രയോജനപ്പെടുന്നു. സമ്പദ് വ്യവസ്ഥയുടെ വിവിധ മാതൃകകള് ഗണിതശാസ്ത്രപ്രകാരം നിര്ണയിക്കുമ്പോഴും അവകലനതത്ത്വം ഉപയോഗിക്കാറുണ്ട്. എക്കണോമെട്രിക്സില് ഇത്തരം സമീപനം അംഗീകരിച്ചിരിക്കുന്നു.
അനന്തസൂക്ഷ്മങ്ങളുടെ "സങ്കലനം' സമാകലനപ്രക്രിയയിലൂടെയാണ് കലനത്തില് നിര്വഹിക്കുന്നത്. ഇലാസ്തികമായ ഒരു ചരടിനെ വലിച്ചു നീട്ടുമ്പോള് ചെയ്യേണ്ടിവരുന്ന പ്രവൃത്തി (work) കണക്കാക്കുവാന് കലനതത്ത്വങ്ങള് ഉപയോഗിക്കുന്നു. ചരടിന്റെ സാധാരണ നീളം Iഉം വലിച്ചുനീട്ടിയ നീളം xഉം ആയാല് "ഹൂക്ക്
എന്ന നീളത്തില് നിന്നും l2ലേക്കു വലിച്ചു നീട്ടുമ്പോള് ചെയ്യേണ്ടിവരുന്ന മൊത്തം പ്രവൃത്തി
പ്രാരംഭിക ടെന്ഷന്, T2 അന്തിമ ടെന്ഷന്. ഇതേ രീതിയുപയോഗിച്ച് ജ്യാമിതീയ രൂപങ്ങളുടെ ഗുരുത്വകേന്ദ്രം, ജഡത്വ ആഘൂര്ണം (moment of inertia) മുതലായവ സമാകലനം കൊണ്ട് കണ്ടുപിടിക്കുന്നു. (പ്രാഫ. കെ.എസ്.വി. ഷേണായി, പ്രാഫ. കെ. ജയചന്ദ്രന്, സ.പ.)