This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കപ്പി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Pulley) |
Mksol (സംവാദം | സംഭാവനകള്) (→Pulley) |
||
| (ഇടക്കുള്ള ഒരു പതിപ്പിലെ മാറ്റം ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 5: | വരി 5: | ||
== Pulley == | == Pulley == | ||
| - | മധ്യത്തിലൂടെ കടന്നുപോകുന്ന അച്ചുതണ്ടിനെ ആധാരമാക്കി തിരിയാന് കഴിയുന്നതും ചുറ്റും പൊഴിയുള്ളതും ആയ ഒരു ചക്രം. കപ്പിയുടെ അച്ചുതണ്ടിന് ആലംബമായുള്ള ചട്ടക്കൂടിനെ ബ്ലോക്ക് എന്നു പറയുന്നു. കപ്പി തിരിയുന്നത് അതിന്റെ അച്ചുതണ്ടിലാണ്. കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ എല്ലാ ബിന്ദുക്കളിലും | + | മധ്യത്തിലൂടെ കടന്നുപോകുന്ന അച്ചുതണ്ടിനെ ആധാരമാക്കി തിരിയാന് കഴിയുന്നതും ചുറ്റും പൊഴിയുള്ളതും ആയ ഒരു ചക്രം. കപ്പിയുടെ അച്ചുതണ്ടിന് ആലംബമായുള്ള ചട്ടക്കൂടിനെ ബ്ലോക്ക് എന്നു പറയുന്നു. കപ്പി തിരിയുന്നത് അതിന്റെ അച്ചുതണ്ടിലാണ്. കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ എല്ലാ ബിന്ദുക്കളിലും അനുഭവപ്പെടുന്ന വലിവുബലം തുല്യമാണെന്നതാണ് ഇതിന്റെ പ്രവര്ത്തനത്തിലെ അടിസ്ഥാന തത്ത്വം. ഈ തത്ത്വം ആവിഷ്കരിച്ചത് സൈമണ് സ്റ്റെവിന് എന്ന ശാസ്ത്രജ്ഞനാണ് (സു. 1610). |
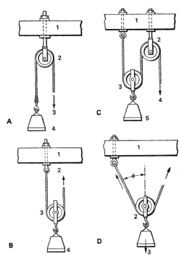
| - | [[ചിത്രം:Vol6p223_pully 1.jpg|thumb|]] | + | [[ചിത്രം:Vol6p223_pully 1.jpg|thumb|കപ്പി:A. സ്ഥിരക്കപ്പി 1. ദണ്ഡ്, 2. കപ്പി, 3. ബലം, 4. ഭാരം |
| + | B. ചലക്കപ്പി 1. ദണ്ഡ്, 2. ബലം, 3. കപ്പി, 4. ഭാരം | ||
| + | C. ചലിക്കുന്ന ഒറ്റക്കപ്പി 1. ദണ്ഡ്, 2-3. കപ്പി, 4. ബലം, 5. ഭാരം | ||
| + | D. ചലിക്കുന്ന ഒറ്റക്കപ്പി 1. ദണ്ഡ്, 2. കപ്പി, 3. ഭാരം]] | ||
ഉപയോഗിക്കുന്ന രീതിയെ അടിസ്ഥാനപ്പെടുത്തി കപ്പികളെ സ്ഥിരക്കപ്പി (immovable) എന്നും ചലക്കപ്പി (movable) എന്നും രണ്ടായി തരംതിരിക്കാം. കപ്പിയുടെ ബ്ലോക്ക് ഒരിടത്ത് സ്ഥിരമായി ഉറപ്പിച്ചിരിക്കുകയാണെങ്കില് അത്തരത്തിലുള്ളവയെ സ്ഥിരക്കപ്പികളെന്നും ഉറപ്പിക്കാത്തവയെ ചലക്കപ്പികളെന്നും പറയുന്നു. കിണറ്റില് നിന്നും വെള്ളം കോരുന്നതിഌം കൊടിമരത്തില് കൊടി ഉയര്ത്തുന്നതിഌം ഉപയോഗിക്കുന്ന കപ്പികള് സ്ഥിരക്കപ്പികള്ക്ക് ഉദാഹരണങ്ങളാണ്. | ഉപയോഗിക്കുന്ന രീതിയെ അടിസ്ഥാനപ്പെടുത്തി കപ്പികളെ സ്ഥിരക്കപ്പി (immovable) എന്നും ചലക്കപ്പി (movable) എന്നും രണ്ടായി തരംതിരിക്കാം. കപ്പിയുടെ ബ്ലോക്ക് ഒരിടത്ത് സ്ഥിരമായി ഉറപ്പിച്ചിരിക്കുകയാണെങ്കില് അത്തരത്തിലുള്ളവയെ സ്ഥിരക്കപ്പികളെന്നും ഉറപ്പിക്കാത്തവയെ ചലക്കപ്പികളെന്നും പറയുന്നു. കിണറ്റില് നിന്നും വെള്ളം കോരുന്നതിഌം കൊടിമരത്തില് കൊടി ഉയര്ത്തുന്നതിഌം ഉപയോഗിക്കുന്ന കപ്പികള് സ്ഥിരക്കപ്പികള്ക്ക് ഉദാഹരണങ്ങളാണ്. | ||
| - | '''സ്ഥിരക്കപ്പി.''' ഇതില് (ചിത്രം A) കപ്പിയുടെ പൊഴിയില്ക്കൂടി കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റത്ത് ഭാരം (W) തൂക്കിയിട്ടിരിക്കുന്നു. ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം (P) പ്രയോഗിക്കുമ്പോള് സ്ഥൈതികസന്തുലന (static equilibrium) | + | '''സ്ഥിരക്കപ്പി.''' ഇതില് (ചിത്രം A) കപ്പിയുടെ പൊഴിയില്ക്കൂടി കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റത്ത് ഭാരം (W) തൂക്കിയിട്ടിരിക്കുന്നു. ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം (P) പ്രയോഗിക്കുമ്പോള് സ്ഥൈതികസന്തുലന (static equilibrium) നിയമമനുസരിച്ച് ചക്രത്തിന്റെ ഇരുഭാഗത്തുമുള്ള ചരടിലെ വലിവ് തുല്യമായിരിക്കണം. അതായത്, ഭാരം പ്രയുക്തബലത്തിനു തുല്യമാണ്. അതുകൊണ്ട് ഘര്ഷണരഹിതമായ ഒരു കപ്പിയുടെ യാന്ത്രികലാഭം (W/P) ഒന്ന് ആയിരിക്കും. |
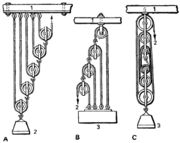
| - | [[ചിത്രം:Vol6p223_pully 2.jpg|thumb|]] | + | [[ചിത്രം:Vol6p223_pully 2.jpg|thumb|വ്യൂഹക്കപ്പികള്:A. 1. ദണ്ഡ്, 2. ഭാരം |
| - | '''ചലക്കപ്പി.''' ചലക്കപ്പിയിലും (ചിത്രം B) ചരടിന്റെ ഇരുഭാഗത്തുമുള്ള വലിവുബലങ്ങള് തുല്യമായിരിക്കും. എന്നാല് | + | B-C. 1. ദണ്ഡ്, 2. ബലം, 3. ഭാരം]] |
| + | '''ചലക്കപ്പി.''' ചലക്കപ്പിയിലും (ചിത്രം B) ചരടിന്റെ ഇരുഭാഗത്തുമുള്ള വലിവുബലങ്ങള് തുല്യമായിരിക്കും. എന്നാല് പ്രയുക്തബലത്തിനു സമമായ രണ്ടു തുല്യ ഉപരിബലം ഭാരത്തെ താങ്ങിയിരിക്കുന്നതിനാല് ഇത്തരം ക്രമീകരണങ്ങളില് ഉയര്ത്തേണ്ട ഭാരത്തിന്റെ പകുതി മൂല്യമുള്ള ബലം പ്രയോഗിച്ചാല് മതി. അതായത് ഒരു സ്ഥിരക്കപ്പികൊണ്ട് ഉയര്ത്തുവാന് കഴിയുന്ന ഭാരത്തിന്റെ ഇരട്ടിഭാരം, അത്ര തന്നെ ബലം പ്രയോഗിക്കുകയാണെങ്കില് ഒരു ചലക്കപ്പികൊണ്ട് ഉയര്ത്തുവാന് സാധിക്കും. തന്മൂലം യാന്ത്രികലാഭം രണ്ട് ആയിരിക്കും. | ||
സ്ഥിരക്കപ്പികളെ ചലക്കപ്പികളുമായി വ്യത്യസ്ത രീതികളില് ക്രമീകരിച്ചും ഉപയോഗിക്കുന്ന കപ്പികളുടെ എണ്ണം വര്ധിപ്പിച്ചും യാന്ത്രികലാഭം യഥേഷ്ടം വര്ധിപ്പിക്കാം. | സ്ഥിരക്കപ്പികളെ ചലക്കപ്പികളുമായി വ്യത്യസ്ത രീതികളില് ക്രമീകരിച്ചും ഉപയോഗിക്കുന്ന കപ്പികളുടെ എണ്ണം വര്ധിപ്പിച്ചും യാന്ത്രികലാഭം യഥേഷ്ടം വര്ധിപ്പിക്കാം. | ||
| വരി 17: | വരി 21: | ||
'''ചലിക്കുന്ന ഒറ്റക്കപ്പി.''' ഇതില് (ചിത്രം C) ഒരു സ്ഥിരക്കപ്പിയും ഒരു ചലക്കപ്പിയും ഉപയോഗിച്ചിരിക്കുന്നു. കപ്പികളിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡില് ഉറപ്പിച്ചിരിക്കുന്നു. സ്വതന്ത്രമായ മറ്റേ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ചരട് ഉറപ്പിച്ച ബിന്ദുവിലെ വലിവുബലം പ്രയുക്തബല(P)ത്തിഌം കപ്പി ഉറപ്പിച്ച ബിന്ദുവിലേത് 2Pക്കും തുല്യമായതിനാല് യാന്ത്രികബലം രണ്ട് ആയിത്തീരുന്നു. | '''ചലിക്കുന്ന ഒറ്റക്കപ്പി.''' ഇതില് (ചിത്രം C) ഒരു സ്ഥിരക്കപ്പിയും ഒരു ചലക്കപ്പിയും ഉപയോഗിച്ചിരിക്കുന്നു. കപ്പികളിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡില് ഉറപ്പിച്ചിരിക്കുന്നു. സ്വതന്ത്രമായ മറ്റേ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ചരട് ഉറപ്പിച്ച ബിന്ദുവിലെ വലിവുബലം പ്രയുക്തബല(P)ത്തിഌം കപ്പി ഉറപ്പിച്ച ബിന്ദുവിലേത് 2Pക്കും തുല്യമായതിനാല് യാന്ത്രികബലം രണ്ട് ആയിത്തീരുന്നു. | ||
| - | മുകളില് പ്രസ്താവിച്ച കപ്പികളിലെല്ലാം തന്നെ പ്രയുക്തബലം | + | മുകളില് പ്രസ്താവിച്ച കപ്പികളിലെല്ലാം തന്നെ പ്രയുക്തബലം ഭാരഭുജത്തിനു സമാന്തരമായ ദിശയില് പ്രയോഗിക്കുന്നു. എന്നാല് ചിത്രം D ല് കാണിച്ചപോലെ ഭാരദിശയുമായി f കോണം ഉണ്ടാക്കത്തക്കവിധം ചരട് വലിക്കുകയാണെങ്കില്, കുത്തനെ കീഴ്പോട്ടു പ്രയോഗിക്കപ്പെടുന്ന ഭാരം, P Cos Φ മൂല്യമുള്ള രണ്ടു തുല്യബലങ്ങള് എന്നിങ്ങനെ മൂന്നു ബലങ്ങള് കപ്പിയില് അനുഭവപ്പെടുന്നു. അതായത്, ഭാരം W = 2 P Cos Φ , അഥവാ W/P = 2 Cos Φ. ഇവിടെ Φ യുടെ വ്യത്യസ്ത മൂല്യങ്ങളനുസരിച്ച് യാന്ത്രികലാഭവും വ്യത്യാസപ്പെടുന്നതായി കാണാം; f പൂജ്യമാകുമ്പോള് ഉച്ചതമവും 60<sup>0</sup>ല് ഒന്നും 90<sup>0</sup> ആകുമ്പോള് നിമ്നതമവും ആണെന്നു കാണാം. |
രണ്ടോ അതിലധികമോ ചലക്കപ്പികള് ഉള്ക്കൊള്ളുന്ന വ്യൂഹത്തെ താഴെ ചിത്രങ്ങളില് കാണിച്ചിട്ടുള്ളതുപോലെ മൂന്നു തരത്തില് ക്രമീകരിക്കാം. എത്ര വലിയ ഭാരത്തെയും ഈ രീതി ഉപയോഗിച്ച് ഉയര്ത്താവുന്നതാണ്. | രണ്ടോ അതിലധികമോ ചലക്കപ്പികള് ഉള്ക്കൊള്ളുന്ന വ്യൂഹത്തെ താഴെ ചിത്രങ്ങളില് കാണിച്ചിട്ടുള്ളതുപോലെ മൂന്നു തരത്തില് ക്രമീകരിക്കാം. എത്ര വലിയ ഭാരത്തെയും ഈ രീതി ഉപയോഗിച്ച് ഉയര്ത്താവുന്നതാണ്. | ||
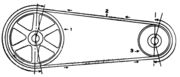
| - | [[ചിത്രം:Vol6p223_pully 3.jpg|thumb|]] | + | [[ചിത്രം:Vol6p223_pully 3.jpg|thumb|കപ്പികളും ബെൽറ്റും: 1. ചാലകക്കപ്പി, 2. ബെൽറ്റ് |
| + | 3. ചാലിതക്കപ്പി]] | ||
'''ഒന്നാം വ്യൂഹക്കപ്പികള്'''. ഈ സമ്പ്രദായത്തില്, ഇവിടെ (A) അഞ്ചു ചലക്കപ്പികള് ഉപയോഗിച്ചിരിക്കുന്നു. ആദ്യത്തെ ചലക്കപ്പിയുടെ ബ്ലോക്കിലാണ് ഭാരം തൂക്കിയിരിക്കുന്നത്. ഈ കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡിലും മറ്റേ അറ്റം രണ്ടാമത്തെ കപ്പിയുടെ ബ്ലോക്കിലും പിടിപ്പിച്ചിരിക്കുന്നു. ഇപ്രകാരം എല്ലാ കപ്പികളെയും ക്രമീകരിച്ചശേഷം ഒടുവിലത്തെ ചലക്കപ്പിയില് നിന്നുള്ള ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ഇവിടെ പ്രയുക്തബലം Dഉയര്ത്തേണ്ട ബലം B ആണെങ്കില് W = 25P അഥവാ W/P = 25. ഇവിടെ 5 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന് യാന്ത്രികലാഭം 2n ആയിരിക്കും. | '''ഒന്നാം വ്യൂഹക്കപ്പികള്'''. ഈ സമ്പ്രദായത്തില്, ഇവിടെ (A) അഞ്ചു ചലക്കപ്പികള് ഉപയോഗിച്ചിരിക്കുന്നു. ആദ്യത്തെ ചലക്കപ്പിയുടെ ബ്ലോക്കിലാണ് ഭാരം തൂക്കിയിരിക്കുന്നത്. ഈ കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡിലും മറ്റേ അറ്റം രണ്ടാമത്തെ കപ്പിയുടെ ബ്ലോക്കിലും പിടിപ്പിച്ചിരിക്കുന്നു. ഇപ്രകാരം എല്ലാ കപ്പികളെയും ക്രമീകരിച്ചശേഷം ഒടുവിലത്തെ ചലക്കപ്പിയില് നിന്നുള്ള ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ഇവിടെ പ്രയുക്തബലം Dഉയര്ത്തേണ്ട ബലം B ആണെങ്കില് W = 25P അഥവാ W/P = 25. ഇവിടെ 5 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന് യാന്ത്രികലാഭം 2n ആയിരിക്കും. | ||
'''രണ്ടാം വ്യൂഹക്കപ്പികള്.''' ഇതില് (B) ഏറ്റവും മുകളിലത്തെ കപ്പി ഉറപ്പിച്ചതും ബാക്കിയുള്ളവ ചലനസാധ്യതയുള്ളവയും ആകുന്നു. ഓരോ കപ്പിയിലൂടെയും കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ഭാരം തൂക്കിയിരിക്കുന്ന ഒരു ദൃഢദണ്ഡിനോടും മറ്റേ അറ്റം ഓരോ കപ്പിയുടെയും തൊട്ടു താഴെയുള്ള ഒരു കപ്പിയോടും ഘടിപ്പിച്ചിരിക്കുന്നു. ഇവിടെ ഓരോ കപ്പിയും യഥാക്രമം P, 2P, 4P, 8Pഎന്നീ ക്രമത്തിലുള്ള ബലങ്ങള് കൊണ്ട് ഭാരം (W) താങ്ങിയിരിക്കുന്നുവെങ്കില്, W = P + 2P + 4P + 8P = 15P = (24-1) P. ഇവിടെ 4 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന്െറ യാന്ത്രികലാഭം,2n-1 ആയിരിക്കും. | '''രണ്ടാം വ്യൂഹക്കപ്പികള്.''' ഇതില് (B) ഏറ്റവും മുകളിലത്തെ കപ്പി ഉറപ്പിച്ചതും ബാക്കിയുള്ളവ ചലനസാധ്യതയുള്ളവയും ആകുന്നു. ഓരോ കപ്പിയിലൂടെയും കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ഭാരം തൂക്കിയിരിക്കുന്ന ഒരു ദൃഢദണ്ഡിനോടും മറ്റേ അറ്റം ഓരോ കപ്പിയുടെയും തൊട്ടു താഴെയുള്ള ഒരു കപ്പിയോടും ഘടിപ്പിച്ചിരിക്കുന്നു. ഇവിടെ ഓരോ കപ്പിയും യഥാക്രമം P, 2P, 4P, 8Pഎന്നീ ക്രമത്തിലുള്ള ബലങ്ങള് കൊണ്ട് ഭാരം (W) താങ്ങിയിരിക്കുന്നുവെങ്കില്, W = P + 2P + 4P + 8P = 15P = (24-1) P. ഇവിടെ 4 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന്െറ യാന്ത്രികലാഭം,2n-1 ആയിരിക്കും. | ||
| - | '''മൂന്നാം വ്യൂഹക്കപ്പികള്'''. ഈ ക്രമീകരണത്തില് (C) 6 കപ്പികള്ക്കിടയിലൂടെ കടത്തിയിരിക്കുന്ന ചരടിന്റെ ഒരറ്റം ഉറപ്പിച്ചിരിക്കും; മറ്റേ അറ്റത്ത് ഭാരം തൂക്കുകയും ചെയ്യുന്നു. കപ്പികളില് 3 എണ്ണം ദൃഢദണ്ഡുമായി ഘടിപ്പിച്ചിരിക്കുന്നു. ബാക്കിയുള്ളവയ്ക്ക് ചലന സ്വാതന്ത്യ്രമുണ്ട്. ചരടിന്റെ ഓരോ ശാഖയിലും | + | '''മൂന്നാം വ്യൂഹക്കപ്പികള്'''. ഈ ക്രമീകരണത്തില് (C) 6 കപ്പികള്ക്കിടയിലൂടെ കടത്തിയിരിക്കുന്ന ചരടിന്റെ ഒരറ്റം ഉറപ്പിച്ചിരിക്കും; മറ്റേ അറ്റത്ത് ഭാരം തൂക്കുകയും ചെയ്യുന്നു. കപ്പികളില് 3 എണ്ണം ദൃഢദണ്ഡുമായി ഘടിപ്പിച്ചിരിക്കുന്നു. ബാക്കിയുള്ളവയ്ക്ക് ചലന സ്വാതന്ത്യ്രമുണ്ട്. ചരടിന്റെ ഓരോ ശാഖയിലും അനുഭവപ്പെടുന്ന വലിവുബലം പ്രയുക്തബലത്തിനു തുല്യമാകയാല് W = 6P, അതായത് W/P = 6 n കപ്പികളുണ്ടെങ്കില് W/P = n. അതായത്, യാന്ത്രികലാഭം n ആയിരിക്കും. |
'''കപ്പികളും ബെല്റ്റും'''. ഒരു ഷാഫ്റ്റില്നിന്നു മറ്റൊന്നിലേക്ക് ആഘൂര്ണബലം (force of rotation) കൈമാറുന്നതിന് ഇവ ഉപയോഗിക്കുന്നു (ചിത്രം). ചാലകക്കപ്പി (drive pulley)യില് നിന്നു ബെല്റ്റിലേക്കു കൈമാറുന്ന ആഘൂര്ണബലത്തെ കറങ്ങിക്കൊണ്ടിരിക്കുന്ന ബെല്റ്റ് മറ്റൊരു ചെറിയ ചാലിതക്കപ്പിയിലേക്കു (drive pulley) കൈമാറ്റം ചെയ്യുന്നു. | '''കപ്പികളും ബെല്റ്റും'''. ഒരു ഷാഫ്റ്റില്നിന്നു മറ്റൊന്നിലേക്ക് ആഘൂര്ണബലം (force of rotation) കൈമാറുന്നതിന് ഇവ ഉപയോഗിക്കുന്നു (ചിത്രം). ചാലകക്കപ്പി (drive pulley)യില് നിന്നു ബെല്റ്റിലേക്കു കൈമാറുന്ന ആഘൂര്ണബലത്തെ കറങ്ങിക്കൊണ്ടിരിക്കുന്ന ബെല്റ്റ് മറ്റൊരു ചെറിയ ചാലിതക്കപ്പിയിലേക്കു (drive pulley) കൈമാറ്റം ചെയ്യുന്നു. | ||
| - | കപ്പികള് ഉപയോഗിച്ച് കുറഞ്ഞ പ്രയത്നം കൊണ്ട് കൂടുതല് ഭാരം വലിക്കാന് സാധിക്കുന്നതിനാല് അവയെ പ്രായോഗികമായി വളരെ പ്രയോജനപ്പെടുത്തിവരുന്നു. കിണറ്റില് നിന്നു വെള്ളം കോരി | + | കപ്പികള് ഉപയോഗിച്ച് കുറഞ്ഞ പ്രയത്നം കൊണ്ട് കൂടുതല് ഭാരം വലിക്കാന് സാധിക്കുന്നതിനാല് അവയെ പ്രായോഗികമായി വളരെ പ്രയോജനപ്പെടുത്തിവരുന്നു. കിണറ്റില് നിന്നു വെള്ളം കോരി വലിച്ചെടുക്കാനുപയോഗിക്കുന്ന തുടി, ഭാരമുള്ള വസ്തുക്കള് പൊക്കിയെടുക്കാനുള്ള ക്രയിന് തുടങ്ങിയവ കപ്പിയുടെ പ്രയോജനത്തിനുദാഹരണങ്ങളാണ്. നോ: ഉത്തോലകം |
Current revision as of 12:23, 4 ജൂലൈ 2014
കപ്പി
Pulley
മധ്യത്തിലൂടെ കടന്നുപോകുന്ന അച്ചുതണ്ടിനെ ആധാരമാക്കി തിരിയാന് കഴിയുന്നതും ചുറ്റും പൊഴിയുള്ളതും ആയ ഒരു ചക്രം. കപ്പിയുടെ അച്ചുതണ്ടിന് ആലംബമായുള്ള ചട്ടക്കൂടിനെ ബ്ലോക്ക് എന്നു പറയുന്നു. കപ്പി തിരിയുന്നത് അതിന്റെ അച്ചുതണ്ടിലാണ്. കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ എല്ലാ ബിന്ദുക്കളിലും അനുഭവപ്പെടുന്ന വലിവുബലം തുല്യമാണെന്നതാണ് ഇതിന്റെ പ്രവര്ത്തനത്തിലെ അടിസ്ഥാന തത്ത്വം. ഈ തത്ത്വം ആവിഷ്കരിച്ചത് സൈമണ് സ്റ്റെവിന് എന്ന ശാസ്ത്രജ്ഞനാണ് (സു. 1610).
ഉപയോഗിക്കുന്ന രീതിയെ അടിസ്ഥാനപ്പെടുത്തി കപ്പികളെ സ്ഥിരക്കപ്പി (immovable) എന്നും ചലക്കപ്പി (movable) എന്നും രണ്ടായി തരംതിരിക്കാം. കപ്പിയുടെ ബ്ലോക്ക് ഒരിടത്ത് സ്ഥിരമായി ഉറപ്പിച്ചിരിക്കുകയാണെങ്കില് അത്തരത്തിലുള്ളവയെ സ്ഥിരക്കപ്പികളെന്നും ഉറപ്പിക്കാത്തവയെ ചലക്കപ്പികളെന്നും പറയുന്നു. കിണറ്റില് നിന്നും വെള്ളം കോരുന്നതിഌം കൊടിമരത്തില് കൊടി ഉയര്ത്തുന്നതിഌം ഉപയോഗിക്കുന്ന കപ്പികള് സ്ഥിരക്കപ്പികള്ക്ക് ഉദാഹരണങ്ങളാണ്.
സ്ഥിരക്കപ്പി. ഇതില് (ചിത്രം A) കപ്പിയുടെ പൊഴിയില്ക്കൂടി കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റത്ത് ഭാരം (W) തൂക്കിയിട്ടിരിക്കുന്നു. ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം (P) പ്രയോഗിക്കുമ്പോള് സ്ഥൈതികസന്തുലന (static equilibrium) നിയമമനുസരിച്ച് ചക്രത്തിന്റെ ഇരുഭാഗത്തുമുള്ള ചരടിലെ വലിവ് തുല്യമായിരിക്കണം. അതായത്, ഭാരം പ്രയുക്തബലത്തിനു തുല്യമാണ്. അതുകൊണ്ട് ഘര്ഷണരഹിതമായ ഒരു കപ്പിയുടെ യാന്ത്രികലാഭം (W/P) ഒന്ന് ആയിരിക്കും.
ചലക്കപ്പി. ചലക്കപ്പിയിലും (ചിത്രം B) ചരടിന്റെ ഇരുഭാഗത്തുമുള്ള വലിവുബലങ്ങള് തുല്യമായിരിക്കും. എന്നാല് പ്രയുക്തബലത്തിനു സമമായ രണ്ടു തുല്യ ഉപരിബലം ഭാരത്തെ താങ്ങിയിരിക്കുന്നതിനാല് ഇത്തരം ക്രമീകരണങ്ങളില് ഉയര്ത്തേണ്ട ഭാരത്തിന്റെ പകുതി മൂല്യമുള്ള ബലം പ്രയോഗിച്ചാല് മതി. അതായത് ഒരു സ്ഥിരക്കപ്പികൊണ്ട് ഉയര്ത്തുവാന് കഴിയുന്ന ഭാരത്തിന്റെ ഇരട്ടിഭാരം, അത്ര തന്നെ ബലം പ്രയോഗിക്കുകയാണെങ്കില് ഒരു ചലക്കപ്പികൊണ്ട് ഉയര്ത്തുവാന് സാധിക്കും. തന്മൂലം യാന്ത്രികലാഭം രണ്ട് ആയിരിക്കും.
സ്ഥിരക്കപ്പികളെ ചലക്കപ്പികളുമായി വ്യത്യസ്ത രീതികളില് ക്രമീകരിച്ചും ഉപയോഗിക്കുന്ന കപ്പികളുടെ എണ്ണം വര്ധിപ്പിച്ചും യാന്ത്രികലാഭം യഥേഷ്ടം വര്ധിപ്പിക്കാം.
ചലിക്കുന്ന ഒറ്റക്കപ്പി. ഇതില് (ചിത്രം C) ഒരു സ്ഥിരക്കപ്പിയും ഒരു ചലക്കപ്പിയും ഉപയോഗിച്ചിരിക്കുന്നു. കപ്പികളിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡില് ഉറപ്പിച്ചിരിക്കുന്നു. സ്വതന്ത്രമായ മറ്റേ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ചരട് ഉറപ്പിച്ച ബിന്ദുവിലെ വലിവുബലം പ്രയുക്തബല(P)ത്തിഌം കപ്പി ഉറപ്പിച്ച ബിന്ദുവിലേത് 2Pക്കും തുല്യമായതിനാല് യാന്ത്രികബലം രണ്ട് ആയിത്തീരുന്നു.
മുകളില് പ്രസ്താവിച്ച കപ്പികളിലെല്ലാം തന്നെ പ്രയുക്തബലം ഭാരഭുജത്തിനു സമാന്തരമായ ദിശയില് പ്രയോഗിക്കുന്നു. എന്നാല് ചിത്രം D ല് കാണിച്ചപോലെ ഭാരദിശയുമായി f കോണം ഉണ്ടാക്കത്തക്കവിധം ചരട് വലിക്കുകയാണെങ്കില്, കുത്തനെ കീഴ്പോട്ടു പ്രയോഗിക്കപ്പെടുന്ന ഭാരം, P Cos Φ മൂല്യമുള്ള രണ്ടു തുല്യബലങ്ങള് എന്നിങ്ങനെ മൂന്നു ബലങ്ങള് കപ്പിയില് അനുഭവപ്പെടുന്നു. അതായത്, ഭാരം W = 2 P Cos Φ , അഥവാ W/P = 2 Cos Φ. ഇവിടെ Φ യുടെ വ്യത്യസ്ത മൂല്യങ്ങളനുസരിച്ച് യാന്ത്രികലാഭവും വ്യത്യാസപ്പെടുന്നതായി കാണാം; f പൂജ്യമാകുമ്പോള് ഉച്ചതമവും 600ല് ഒന്നും 900 ആകുമ്പോള് നിമ്നതമവും ആണെന്നു കാണാം.
രണ്ടോ അതിലധികമോ ചലക്കപ്പികള് ഉള്ക്കൊള്ളുന്ന വ്യൂഹത്തെ താഴെ ചിത്രങ്ങളില് കാണിച്ചിട്ടുള്ളതുപോലെ മൂന്നു തരത്തില് ക്രമീകരിക്കാം. എത്ര വലിയ ഭാരത്തെയും ഈ രീതി ഉപയോഗിച്ച് ഉയര്ത്താവുന്നതാണ്.
ഒന്നാം വ്യൂഹക്കപ്പികള്. ഈ സമ്പ്രദായത്തില്, ഇവിടെ (A) അഞ്ചു ചലക്കപ്പികള് ഉപയോഗിച്ചിരിക്കുന്നു. ആദ്യത്തെ ചലക്കപ്പിയുടെ ബ്ലോക്കിലാണ് ഭാരം തൂക്കിയിരിക്കുന്നത്. ഈ കപ്പിയുടെ പൊഴിയിലൂടെ കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ദണ്ഡിലും മറ്റേ അറ്റം രണ്ടാമത്തെ കപ്പിയുടെ ബ്ലോക്കിലും പിടിപ്പിച്ചിരിക്കുന്നു. ഇപ്രകാരം എല്ലാ കപ്പികളെയും ക്രമീകരിച്ചശേഷം ഒടുവിലത്തെ ചലക്കപ്പിയില് നിന്നുള്ള ചരടിന്റെ സ്വതന്ത്രമായ അറ്റത്ത് ബലം പ്രയോഗിക്കുന്നു. ഇവിടെ പ്രയുക്തബലം Dഉയര്ത്തേണ്ട ബലം B ആണെങ്കില് W = 25P അഥവാ W/P = 25. ഇവിടെ 5 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന് യാന്ത്രികലാഭം 2n ആയിരിക്കും.
രണ്ടാം വ്യൂഹക്കപ്പികള്. ഇതില് (B) ഏറ്റവും മുകളിലത്തെ കപ്പി ഉറപ്പിച്ചതും ബാക്കിയുള്ളവ ചലനസാധ്യതയുള്ളവയും ആകുന്നു. ഓരോ കപ്പിയിലൂടെയും കടന്നുപോകുന്ന ചരടിന്റെ ഒരറ്റം ഭാരം തൂക്കിയിരിക്കുന്ന ഒരു ദൃഢദണ്ഡിനോടും മറ്റേ അറ്റം ഓരോ കപ്പിയുടെയും തൊട്ടു താഴെയുള്ള ഒരു കപ്പിയോടും ഘടിപ്പിച്ചിരിക്കുന്നു. ഇവിടെ ഓരോ കപ്പിയും യഥാക്രമം P, 2P, 4P, 8Pഎന്നീ ക്രമത്തിലുള്ള ബലങ്ങള് കൊണ്ട് ഭാരം (W) താങ്ങിയിരിക്കുന്നുവെങ്കില്, W = P + 2P + 4P + 8P = 15P = (24-1) P. ഇവിടെ 4 എന്നത് കപ്പികളുടെ എണ്ണത്തെ സൂചിപ്പിക്കുന്നതിനാല് n കപ്പികളുള്ള ഒരു വ്യൂഹത്തിന്െറ യാന്ത്രികലാഭം,2n-1 ആയിരിക്കും.
മൂന്നാം വ്യൂഹക്കപ്പികള്. ഈ ക്രമീകരണത്തില് (C) 6 കപ്പികള്ക്കിടയിലൂടെ കടത്തിയിരിക്കുന്ന ചരടിന്റെ ഒരറ്റം ഉറപ്പിച്ചിരിക്കും; മറ്റേ അറ്റത്ത് ഭാരം തൂക്കുകയും ചെയ്യുന്നു. കപ്പികളില് 3 എണ്ണം ദൃഢദണ്ഡുമായി ഘടിപ്പിച്ചിരിക്കുന്നു. ബാക്കിയുള്ളവയ്ക്ക് ചലന സ്വാതന്ത്യ്രമുണ്ട്. ചരടിന്റെ ഓരോ ശാഖയിലും അനുഭവപ്പെടുന്ന വലിവുബലം പ്രയുക്തബലത്തിനു തുല്യമാകയാല് W = 6P, അതായത് W/P = 6 n കപ്പികളുണ്ടെങ്കില് W/P = n. അതായത്, യാന്ത്രികലാഭം n ആയിരിക്കും.
കപ്പികളും ബെല്റ്റും. ഒരു ഷാഫ്റ്റില്നിന്നു മറ്റൊന്നിലേക്ക് ആഘൂര്ണബലം (force of rotation) കൈമാറുന്നതിന് ഇവ ഉപയോഗിക്കുന്നു (ചിത്രം). ചാലകക്കപ്പി (drive pulley)യില് നിന്നു ബെല്റ്റിലേക്കു കൈമാറുന്ന ആഘൂര്ണബലത്തെ കറങ്ങിക്കൊണ്ടിരിക്കുന്ന ബെല്റ്റ് മറ്റൊരു ചെറിയ ചാലിതക്കപ്പിയിലേക്കു (drive pulley) കൈമാറ്റം ചെയ്യുന്നു.
കപ്പികള് ഉപയോഗിച്ച് കുറഞ്ഞ പ്രയത്നം കൊണ്ട് കൂടുതല് ഭാരം വലിക്കാന് സാധിക്കുന്നതിനാല് അവയെ പ്രായോഗികമായി വളരെ പ്രയോജനപ്പെടുത്തിവരുന്നു. കിണറ്റില് നിന്നു വെള്ളം കോരി വലിച്ചെടുക്കാനുപയോഗിക്കുന്ന തുടി, ഭാരമുള്ള വസ്തുക്കള് പൊക്കിയെടുക്കാനുള്ള ക്രയിന് തുടങ്ങിയവ കപ്പിയുടെ പ്രയോജനത്തിനുദാഹരണങ്ങളാണ്. നോ: ഉത്തോലകം