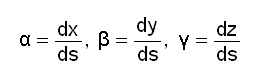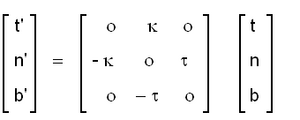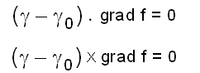This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അവകലജ്യാമിതി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→പ്രതലത്തിന്റെ മൂലരൂപങ്ങള്) |
Mksol (സംവാദം | സംഭാവനകള്) (→വക്രതാരേഖകള്) |
||
| (ഇടക്കുള്ള 4 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 2: | വരി 2: | ||
Differential Geometry | Differential Geometry | ||
| - | ഗണിതശാസ്ത്രശാഖ. അവകല(Differential calculus)ത്തിലെ രീതികളും സമവാക്യങ്ങളും ഉപയോഗിച്ച് ത്രിമാന | + | ഗണിതശാസ്ത്രശാഖ. അവകല(Differential calculus)ത്തിലെ രീതികളും സമവാക്യങ്ങളും ഉപയോഗിച്ച് ത്രിമാന യുക്ലീഡിയന് സ്പേസില് (Three Dimensional Euclidean) വക്രങ്ങളുടെയും പ്രതലങ്ങളുടെയും സവിശേഷതകളെക്കുറിച്ചുള്ള പഠനം. |
==ചരിത്രം== | ==ചരിത്രം== | ||
| - | ജര്മന് ശാസ്ത്രജ്ഞനായ ഗൗസ് (1777-1855) 1827-ല് പ്രസിദ്ധീകരിച്ച ഗവേഷണ പ്രബന്ധത്തിലാണ് ഈ വിഷയം ആദ്യമായി ചര്ച്ച ചെയ്യപ്പെട്ടിട്ടുള്ളത്. ത്രിമാന സ്പേസില് (Three Dimensional Euclidean Space) സമകോണീയ-കാര്ത്തീയ നിര്ദേശാങ്കങ്ങള് (Perpendicular Cartesian coordinates)x,y,z-ല് ഓരോന്നും u,v എന്ന രണ്ടു ചരങ്ങളുടെ ഫലനങ്ങളായിട്ടാണ് പ്രതലത്തെ ഗൌസ് നിര്വചിച്ചത്. ഈ ഫലനങ്ങള് പൊതുസ്വഭാവമുള്ളവയും സ്വതന്ത്രവുമായതിനാല് അവ പ്രതിനിധാനം ചെയ്തത് പ്രതലങ്ങളുടെ വ്യാപകരൂപം (general form) ആയിരുന്നു. ഗൗസിന്റെ പഠനം ശരിക്കും പ്രതലങ്ങളുടെ 'ത്രികോണമിതി'യില് ആദ്യത്തെ ചുവടുവയ്പാണ്. ഇതിനെത്തുടര്ന്ന് പ്രതലങ്ങളുടെ അവകലജ്യാമിതി റീമാന്, ഡിനി, അപ്പെല്, ദാര്ബൂ തുടങ്ങിയവരുടെ പ്രത്യേക ശ്രദ്ധയ്ക്കു വിഷയീഭവിച്ചു. ഈ ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ നിഗമനങ്ങള് 1887-ല് നാലുഭാഗങ്ങളുള്ള ഒരു ബൃഹദ്ഗ്രന്ഥമായി പ്രസിദ്ധീകൃതമായി. ഇതില് നിര്ദേശാങ്കങ്ങള് x<sup>i</sup> (i = 1,2,3,....n) ഉള്ള | + | ജര്മന് ശാസ്ത്രജ്ഞനായ ഗൗസ് (1777-1855) 1827-ല് പ്രസിദ്ധീകരിച്ച ഗവേഷണ പ്രബന്ധത്തിലാണ് ഈ വിഷയം ആദ്യമായി ചര്ച്ച ചെയ്യപ്പെട്ടിട്ടുള്ളത്. ത്രിമാന സ്പേസില് (Three Dimensional Euclidean Space) സമകോണീയ-കാര്ത്തീയ നിര്ദേശാങ്കങ്ങള് (Perpendicular Cartesian coordinates)x,y,z-ല് ഓരോന്നും u,v എന്ന രണ്ടു ചരങ്ങളുടെ ഫലനങ്ങളായിട്ടാണ് പ്രതലത്തെ ഗൌസ് നിര്വചിച്ചത്. ഈ ഫലനങ്ങള് പൊതുസ്വഭാവമുള്ളവയും സ്വതന്ത്രവുമായതിനാല് അവ പ്രതിനിധാനം ചെയ്തത് പ്രതലങ്ങളുടെ വ്യാപകരൂപം (general form) ആയിരുന്നു. ഗൗസിന്റെ പഠനം ശരിക്കും പ്രതലങ്ങളുടെ 'ത്രികോണമിതി'യില് ആദ്യത്തെ ചുവടുവയ്പാണ്. ഇതിനെത്തുടര്ന്ന് പ്രതലങ്ങളുടെ അവകലജ്യാമിതി റീമാന്, ഡിനി, അപ്പെല്, ദാര്ബൂ തുടങ്ങിയവരുടെ പ്രത്യേക ശ്രദ്ധയ്ക്കു വിഷയീഭവിച്ചു. ഈ ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ നിഗമനങ്ങള് 1887-ല് നാലുഭാഗങ്ങളുള്ള ഒരു ബൃഹദ്ഗ്രന്ഥമായി പ്രസിദ്ധീകൃതമായി. ഇതില് നിര്ദേശാങ്കങ്ങള് x<sup>i</sup> (i = 1,2,3,....n) ഉള്ള n-മാന സ്പേസിലെ ജ്യാമിതിയെക്കുറിച്ചുള്ള റീമാന്റെ (1826-1866) പഠനം ശ്രദ്ധേയമാണ്. ആധുനിക ജ്യാമിതികളില് റീമാന്റെ സിദ്ധാന്തങ്ങള് ഒരു പ്രത്യേക ഗണിതശാസ്ത്രവിഭാഗമായിത്തന്നെ രൂപംകൊണ്ടിട്ടുണ്ട്. ടെന്സര് കലനം (Tensor Calculus) ഉപയോഗിച്ചാണ് ഈ ജ്യാമിതി കൈകാര്യം ചെയ്യുന്നത്. ഗുരുത്വാകര്ഷണ നിയമങ്ങള് ആവിഷ്കരിക്കുവാന് കാലദേശ(Time and Space)ങ്ങളുടെ ഒരു ചതുര്മാന അവകലജ്യാമിതിയാണ് ഐന്സ്റ്റൈന് (1879-1955) ഉപയോഗിച്ചിട്ടുള്ളത്. ദാര്ബൂ ആവിഷ്കരിച്ച 'ദാര്ബൂ സമീകരണം' പ്രയോഗിച്ച് സമാംഗരൂപത്തിലുള്ള സമവാക്യങ്ങളുടെ അവകലജം (derivative) കണ്ടുപിടിക്കുവാന് സാധിക്കുന്നു. |
==പ്രാഥമിക തത്ത്വങ്ങള്== | ==പ്രാഥമിക തത്ത്വങ്ങള്== | ||
| വരി 15: | വരി 15: | ||
ആണ്. ഇങ്ങനെയുള്ള സ്പേസില് നിര്ദേശാങ്കങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യം ഓരോന്നും ഓരോ പ്രതലത്തെയും അത്തരത്തിലുള്ള രണ്ടു സമവാക്യങ്ങള് ഒരു വക്രത്തെയും കുറിക്കുന്നു. അവകലജ്യാമിതിയില് വക്രങ്ങളെയും പ്രതലങ്ങളെയും ചിത്രീകരിക്കുവാന് പ്രാചലങ്ങള് (Parameters) ഉപയോഗിക്കുന്നതു സൗകര്യപ്രദമാണ്. പ്രാചലങ്ങള് ഉപയോഗിക്കുന്ന രീതിയെ പ്രാചലചിത്രീകരണം (Parametric Representation) എന്നു പറയുന്നു. ഈ രീതിയനുസരിച്ച് ഒരു സ്പേസ്-വക്ര(Space-curve)ത്തിന്റെ സമവാക്യം x = x(t),y = y(t),z =z(t) ആണ്. ഇവിടെ t ഒരു പ്രാചലമാണ്. | ആണ്. ഇങ്ങനെയുള്ള സ്പേസില് നിര്ദേശാങ്കങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യം ഓരോന്നും ഓരോ പ്രതലത്തെയും അത്തരത്തിലുള്ള രണ്ടു സമവാക്യങ്ങള് ഒരു വക്രത്തെയും കുറിക്കുന്നു. അവകലജ്യാമിതിയില് വക്രങ്ങളെയും പ്രതലങ്ങളെയും ചിത്രീകരിക്കുവാന് പ്രാചലങ്ങള് (Parameters) ഉപയോഗിക്കുന്നതു സൗകര്യപ്രദമാണ്. പ്രാചലങ്ങള് ഉപയോഗിക്കുന്ന രീതിയെ പ്രാചലചിത്രീകരണം (Parametric Representation) എന്നു പറയുന്നു. ഈ രീതിയനുസരിച്ച് ഒരു സ്പേസ്-വക്ര(Space-curve)ത്തിന്റെ സമവാക്യം x = x(t),y = y(t),z =z(t) ആണ്. ഇവിടെ t ഒരു പ്രാചലമാണ്. | ||
| - | == | + | ==സ്പേസ് - വക്രങ്ങള്== |
| വരി 21: | വരി 21: | ||
| - | എന്ന സമവാക്യങ്ങള് കുറിക്കുന്ന സ്പേസ്-വക്രത്തില് ഏതെങ്കിലും ഒരു ബിന്ദുവായ P യുടെ സ്ഥിതിസദിശം ( | + | എന്ന സമവാക്യങ്ങള് കുറിക്കുന്ന സ്പേസ്-വക്രത്തില് ഏതെങ്കിലും ഒരു ബിന്ദുവായ P യുടെ സ്ഥിതിസദിശം (position vector) |
[[Image:page437for2.png|300px]] | [[Image:page437for2.png|300px]] | ||
| - | ആണ്. അതുകൊണ്ട് സ്പേസിലെ ഒരു വക്രത്തെ കുറിക്കുവാന് & | + | ആണ്. അതുകൊണ്ട് സ്പേസിലെ ഒരു വക്രത്തെ കുറിക്കുവാന് γ = γ (t) എന്ന് എഴുതുന്നു. ഇതിനെ വക്രത്തിന്റെ സദിശസമവാക്യം (vector equation) എന്നു പറയുന്നു. വക്രത്തിലുള്ള ഒരു നിശ്ചിതബിന്ദുവില്നിന്നുള്ള ചാപദൈര്ഘ്യം s ആയാല് P എന്ന ബിന്ദുവിലെ സ്പര്ശക(tangent)ത്തിന്റെ ദിശാ-കൊസൈനുകള് (direction cosines), |
[[Image:page437for3.png|300px]] | [[Image:page437for3.png|300px]] | ||
| വരി 31: | വരി 31: | ||
ആകുന്നു. സ്പേസില് സ്പര്ശകത്തിന്റെ ദിശ (direction) ഈ ദിശാ-കൊസൈനുകളെ ആശ്രയിച്ചിരിക്കുന്നു. | ആകുന്നു. സ്പേസില് സ്പര്ശകത്തിന്റെ ദിശ (direction) ഈ ദിശാ-കൊസൈനുകളെ ആശ്രയിച്ചിരിക്കുന്നു. | ||
| - | വക്രത്തിലുള്ള P,Q,R എന്ന ബിന്ദുക്കള് ഒരേതലത്തില് കിടക്കുന്നു എന്നു | + | വക്രത്തിലുള്ള P,Q,R എന്ന ബിന്ദുക്കള് ഒരേതലത്തില് കിടക്കുന്നു എന്നു സങ്കല്പിക്കുക. Q-ഉം, R-ഉം, P-യോട് അടുത്തടുത്തു വരുന്നതോടുകൂടി ഈ തലത്തിനുണ്ടാകുന്ന സീമാന്തസ്ഥാനം (limiting position) ആണ് വക്രത്തിന്റെ P എന്ന ബിന്ദുവിലെ ആശ്ലേഷതലം (Osculating plane). ഒരു വക്രത്തില് എല്ലാ ബിന്ദുക്കളും ഒരേ തലത്തില് കിടക്കുന്നു എങ്കില് അതിനെ സമതലവക്രം (Plane curve) എന്നു പറയുന്നു. ഒരു സമതലവക്രത്തിന്റെ ആശ്ലേഷതലം, വക്രം ഉള്ക്കൊള്ളുന്ന സമതലം തന്നെയാണ്. |
[[Image:page437.png|300px|left]] | [[Image:page437.png|300px|left]] | ||
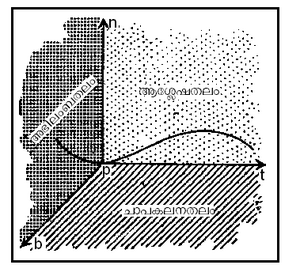
വക്രത്തില് ഒരു ബിന്ദുവിലെ സ്പര്ശകത്തിനു ലംബമായി അതേ ബിന്ദുവില്ക്കൂടിയുള്ള നേര്വരയാണ് അഭിലംബം (Normal); വക്രത്തിനും സ്പര്ശകത്തിനും പൊതുവായ ഒരു ബിന്ദുവില്ക്കൂടി സ്പര്ശകത്തിന് അനേകം അഭിലംബങ്ങള് വരയ്ക്കാം. ഈ അഭിലംബങ്ങളെല്ലാം ഒരേ തലത്തിലാണു കിടക്കുന്നത്. ഈ തലത്തെ അഭിലംബതലം (Normal plane) എന്നു പറയുന്നു. സ്പര്ശകം അഭിലംബതലത്തിനു ലംബമായിരിക്കും. ഒരു ബിന്ദുവിലുള്ള അനേകം അഭിലംബങ്ങളില് പ്രത്യേകം രണ്ടെണ്ണം പ്രധാനമാണ്. ആശ്ലേഷതലത്തില് കിടക്കുന്ന അഭിലംബത്തെ മുഖ്യാഭിലംബം (Principal normal) എന്നു പറയുന്നു; ഒരു ബിന്ദുവിലെ ആശ്ലേഷതലത്തിന്റെയും അഭിലംബതലത്തിന്റെയും പ്രതിച്ഛേദിരേഖ (line of intersection) ആണ് മുഖ്യാഭിലംബം. ആശ്ലേഷതലത്തിനു ലംബമായ അഭിലംബമാണ് ദ്വയാഭിലംബം (binormal). ഈ രേഖ മുഖ്യാഭിലംബത്തിനും സ്പര്ശരേഖയ്ക്കും ലംബമായ അഭിലംബമാണ്. അങ്ങനെ വക്രത്തില് ഓരോ ബിന്ദുവിലുമുള്ള അന്യോന്യം ലംബങ്ങളായ മൂന്നു സദിശങ്ങളാണ് സ്പര്ശരേഖയും മുഖ്യാഭിലംബവും ഉപാഭിലംബവും. ഇവയുടെ ദിശകളിലുള്ള ഏകകസദിശ(unit vector)ങ്ങളെ കുറിക്കുവാന് യഥാക്രമം t,n,b എന്ന പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. ഓരോ ബിന്ദുവിലും t,n,b എന്ന ഏകകസദിശങ്ങള് അന്യോന്യം ലംബങ്ങളായ മൂന്നു തലങ്ങള് സൃഷ്ടിക്കുന്നു. സദിശങ്ങള് t-ഉം n-ഉം ഉള്ള തലം ആശ്ലേഷതലവും n-ഉം b-ഉം ഉള്ള തലം അഭിലംബതലവും b-ഉം t-ഉം ഉള്ള തലം ചാപകലനതല(Rectifying plane)വും ആകുന്നു (ചിത്രം നോക്കുക). | വക്രത്തില് ഒരു ബിന്ദുവിലെ സ്പര്ശകത്തിനു ലംബമായി അതേ ബിന്ദുവില്ക്കൂടിയുള്ള നേര്വരയാണ് അഭിലംബം (Normal); വക്രത്തിനും സ്പര്ശകത്തിനും പൊതുവായ ഒരു ബിന്ദുവില്ക്കൂടി സ്പര്ശകത്തിന് അനേകം അഭിലംബങ്ങള് വരയ്ക്കാം. ഈ അഭിലംബങ്ങളെല്ലാം ഒരേ തലത്തിലാണു കിടക്കുന്നത്. ഈ തലത്തെ അഭിലംബതലം (Normal plane) എന്നു പറയുന്നു. സ്പര്ശകം അഭിലംബതലത്തിനു ലംബമായിരിക്കും. ഒരു ബിന്ദുവിലുള്ള അനേകം അഭിലംബങ്ങളില് പ്രത്യേകം രണ്ടെണ്ണം പ്രധാനമാണ്. ആശ്ലേഷതലത്തില് കിടക്കുന്ന അഭിലംബത്തെ മുഖ്യാഭിലംബം (Principal normal) എന്നു പറയുന്നു; ഒരു ബിന്ദുവിലെ ആശ്ലേഷതലത്തിന്റെയും അഭിലംബതലത്തിന്റെയും പ്രതിച്ഛേദിരേഖ (line of intersection) ആണ് മുഖ്യാഭിലംബം. ആശ്ലേഷതലത്തിനു ലംബമായ അഭിലംബമാണ് ദ്വയാഭിലംബം (binormal). ഈ രേഖ മുഖ്യാഭിലംബത്തിനും സ്പര്ശരേഖയ്ക്കും ലംബമായ അഭിലംബമാണ്. അങ്ങനെ വക്രത്തില് ഓരോ ബിന്ദുവിലുമുള്ള അന്യോന്യം ലംബങ്ങളായ മൂന്നു സദിശങ്ങളാണ് സ്പര്ശരേഖയും മുഖ്യാഭിലംബവും ഉപാഭിലംബവും. ഇവയുടെ ദിശകളിലുള്ള ഏകകസദിശ(unit vector)ങ്ങളെ കുറിക്കുവാന് യഥാക്രമം t,n,b എന്ന പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. ഓരോ ബിന്ദുവിലും t,n,b എന്ന ഏകകസദിശങ്ങള് അന്യോന്യം ലംബങ്ങളായ മൂന്നു തലങ്ങള് സൃഷ്ടിക്കുന്നു. സദിശങ്ങള് t-ഉം n-ഉം ഉള്ള തലം ആശ്ലേഷതലവും n-ഉം b-ഉം ഉള്ള തലം അഭിലംബതലവും b-ഉം t-ഉം ഉള്ള തലം ചാപകലനതല(Rectifying plane)വും ആകുന്നു (ചിത്രം നോക്കുക). | ||
| - | ഒരു | + | ഒരു സ്പേസ്വക്രത്തെ സംബന്ധിച്ചിടത്തോളം പ്രധാനപ്പെട്ട രണ്ടു ഗുണധര്മങ്ങളാണ് വക്രത(curvature)യും ടോര്ഷനും (torsion): dt/ds എന്ന സദിശത്തെ വക്രത്തിന്റെ P എന്ന ബിന്ദുവിലുള്ള വക്രതാസദിശം (curvature vector) എന്നും ഇതിന്റെ മൂല്യ(mangitude)ത്തെ വക്രത എന്നും പറയുന്നു. വക്രതാസദിശം ചാപദൈര്ഘ്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് സ്പര്ശരേഖയുടെ തിരിയലിന്റെ (ഘൂര്ണനത്തിന്റെ) നിരക്കാണ്. വക്രതയെ കുറിക്കാന് κ എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. വക്രത്തില് വക്രത ശൂന്യമാകുന്ന ബിന്ദുവാണ് അതിപരിവര്ത്തന ബിന്ദു (point of inflexion). db/ds എന്ന സദിശത്തെ വക്രത്തിന്റെ ടോര്ഷന് സദിശം (Torsion vector) എന്നു പറയുന്നു. ഇതു ചാപദൈര്ഘ്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് ദ്വയാഭിലംബം തിരിയുന്നതിന്റെ നിരക്കാണ്. ടോര്ഷന്സദിശത്തിന്റെ മൂല്യത്തെ ടോര്ഷന് എന്നു പറയുന്നു. ടോര്ഷനെ കുറിക്കാന് τ(tau) എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. ഒരു വക്രം സമതലവക്രമാകണമെങ്കില് എല്ലാ ബിന്ദുക്കളിലും ടോര്ഷന് ശൂന്യമാകണം; മറിച്ച് എല്ലാ ബിന്ദുക്കളിലും ടോര്ഷന് ശൂന്യമായ വക്രം സമതലവക്രമാണ്. സാധാരണ ρ=1/κഎന്നും σ=1/τഎന്നും എഴുതുന്നു. ρ-യെ വക്രതാത്രിജ്യ (radius of curvature) എന്നും τ-യെ ടോര്ഷന്ത്രിജ്യ (radius of torsion) എന്നും പറയുന്നു. |
ഒരു സിലിണ്ടറിന്റെ ഉപരിഭാഗത്ത്, സ്പര്ശരേഖ സ്പേസിലുള്ള ഏതെങ്കിലും നിശ്ചിത രേഖയുമായി ഒരു സ്ഥിരകോണം വരത്തക്കവണ്ണം വരയ്ക്കാവുന്ന വക്രത്തെ ഹെലിക്സ് (Helix) എന്നു പറയുന്നു. സ്പ്രിങ്ബാലന്സിലെ സ്പ്രിങ്, ഹെലിക്സിന്റെ രൂപത്തിലാണ്. വക്രതയും ടോര്ഷനും എല്ലാ ബിന്ദുക്കളിലും സ്ഥിരമായ ഹെലിക്സ് ആണ്. ഒരു വൃത്തീയ (circular) ഹെലിക്സില് | ഒരു സിലിണ്ടറിന്റെ ഉപരിഭാഗത്ത്, സ്പര്ശരേഖ സ്പേസിലുള്ള ഏതെങ്കിലും നിശ്ചിത രേഖയുമായി ഒരു സ്ഥിരകോണം വരത്തക്കവണ്ണം വരയ്ക്കാവുന്ന വക്രത്തെ ഹെലിക്സ് (Helix) എന്നു പറയുന്നു. സ്പ്രിങ്ബാലന്സിലെ സ്പ്രിങ്, ഹെലിക്സിന്റെ രൂപത്തിലാണ്. വക്രതയും ടോര്ഷനും എല്ലാ ബിന്ദുക്കളിലും സ്ഥിരമായ ഹെലിക്സ് ആണ്. ഒരു വൃത്തീയ (circular) ഹെലിക്സില് | ||
| വരി 58: | വരി 58: | ||
Surfaces | Surfaces | ||
| - | നിര്ദേശാങ്കങ്ങള് u,v എന്ന രണ്ടു സ്വതന്ത്ര പ്രാചലങ്ങളുടെ ഫലനങ്ങളായ ബിന്ദുപഥ(locus)ത്തിനെ പ്രതലം എന്നു പറയുന്നു. ഒരു പ്രതലത്തെ പ്രതിനിധാനം ചെയ്യുന്ന സമവാക്യങ്ങളെ x = x(u,v),y = y(u,v),z = z(u,v) എന്നെഴുതാം. ഈ പ്രതലത്തിന്റെ സദിശസമവാക്യം r= r(u,v) ആണ്. പ്രാചലങ്ങള് ഉപയോഗിച്ച് പ്രതലത്തെ ചിത്രീകരിക്കുന്ന സമവാക്യങ്ങളെ പ്രതലത്തിന്റെ ഗൗസിയന് രൂപം (Gaussian form) എന്നു പറയാറുണ്ട്. ബീജീയരീതികളുപയോഗിച്ച് u,v എന്ന പ്രാചലങ്ങളെ ഒഴിവാക്കിയാല് പ്രതലത്തിനു f(x,y,z) = 0 എന്ന രീതിയിലുള്ള ഒരു സമവാക്യം കിട്ടുന്നു. ഈ പ്രതലത്തില് & | + | നിര്ദേശാങ്കങ്ങള് u,v എന്ന രണ്ടു സ്വതന്ത്ര പ്രാചലങ്ങളുടെ ഫലനങ്ങളായ ബിന്ദുപഥ(locus)ത്തിനെ പ്രതലം എന്നു പറയുന്നു. ഒരു പ്രതലത്തെ പ്രതിനിധാനം ചെയ്യുന്ന സമവാക്യങ്ങളെ x = x(u,v),y = y(u,v),z = z(u,v) എന്നെഴുതാം. ഈ പ്രതലത്തിന്റെ സദിശസമവാക്യം r= r(u,v) ആണ്. പ്രാചലങ്ങള് ഉപയോഗിച്ച് പ്രതലത്തെ ചിത്രീകരിക്കുന്ന സമവാക്യങ്ങളെ പ്രതലത്തിന്റെ ഗൗസിയന് രൂപം (Gaussian form) എന്നു പറയാറുണ്ട്. ബീജീയരീതികളുപയോഗിച്ച് u,v എന്ന പ്രാചലങ്ങളെ ഒഴിവാക്കിയാല് പ്രതലത്തിനു f(x,y,z) = 0 എന്ന രീതിയിലുള്ള ഒരു സമവാക്യം കിട്ടുന്നു. ഈ പ്രതലത്തില് γ<sub>0</sub>സ്ഥിതി സദിശമുള്ള ഒരു ബിന്ദുവിലെ സ്പര്ശതല(tangent plane)ത്തിന്റെ സദിശസമവാക്യവും അഭിലംബരേഖയുടെ സമവാക്യവും ക്രമത്തില് താഴെ ചേര്ക്കുന്നു: |
[[Image:page438for3.png|200px]] | [[Image:page438for3.png|200px]] | ||
| വരി 65: | വരി 65: | ||
===വികസനീയ പ്രതലം=== | ===വികസനീയ പ്രതലം=== | ||
| - | സമതലങ്ങളുടെ ഏകരാശികുല(single parameter family | + | സമതലങ്ങളുടെ ഏകരാശികുല(single parameter family)ത്തിന്റെ ആവരണം ആണ് വികസനീയ പ്രതലം (Developable surface). ഇത്തരം പ്രതലങ്ങളെ മടക്കാതെയും ഒടിക്കാതെയും ഒരു സമതലത്തിന്മേല് നിവര്ത്തി വിരിക്കാവുന്നതാണ്. ഉദാഹരണമായി കോണ് (cone), വൃത്തസ്തംഭം (cylinder) എന്നീ ഘനരൂപങ്ങളുടെ ഉപരിതലം വികസനീയ പ്രതലമാണ്. സമതലത്തിലെന്നപോലെ ഒരു വികസനീയ പ്രതലത്തിന്റെ വക്രത എല്ലായിടത്തും ശൂന്യമായിരിക്കും. സാധാരണഗതിയില് ഒരു പ്രതലത്തിന്റെ സ്പര്ശതലം രണ്ടു പ്രാചലങ്ങളെ ആശ്രയിച്ചിരിക്കും. എന്നാല് വികസനീയ പ്രതലത്തിന്റെ സ്പര്ശതലത്തില് ഒരു പ്രാചലം മാത്രമേ കാണുകയുള്ളു. |
===പ്രതലത്തിന്റെ മൂലരൂപങ്ങള്=== | ===പ്രതലത്തിന്റെ മൂലരൂപങ്ങള്=== | ||
| വരി 87: | വരി 87: | ||
എന്നതിനെ പ്രതലത്തിന്റെ ദ്വിതീയ മൂലരൂപമെന്നും L,M,N എന്നിവയെ ദ്വിതീയ മൂലഗുണാങ്കങ്ങള് എന്നും പറയുന്നു. പ്രതലങ്ങളുടെ പഠനത്തില് ഈ ആറ് മൂലഗുണാങ്കങ്ങള്ക്കും അടിസ്ഥാനപരമായ പ്രാധാന്യമുണ്ട്. വക്രങ്ങളുടെ പഠനത്തില് വക്രതയ്ക്കും ടോര്ഷനുമുള്ള പ്രാധാന്യമാണ് പ്രതലങ്ങളുടെ സിദ്ധാന്തത്തില് ഇവയ്ക്കുള്ളത്. | എന്നതിനെ പ്രതലത്തിന്റെ ദ്വിതീയ മൂലരൂപമെന്നും L,M,N എന്നിവയെ ദ്വിതീയ മൂലഗുണാങ്കങ്ങള് എന്നും പറയുന്നു. പ്രതലങ്ങളുടെ പഠനത്തില് ഈ ആറ് മൂലഗുണാങ്കങ്ങള്ക്കും അടിസ്ഥാനപരമായ പ്രാധാന്യമുണ്ട്. വക്രങ്ങളുടെ പഠനത്തില് വക്രതയ്ക്കും ടോര്ഷനുമുള്ള പ്രാധാന്യമാണ് പ്രതലങ്ങളുടെ സിദ്ധാന്തത്തില് ഇവയ്ക്കുള്ളത്. | ||
| - | [[Image:page438for8.png| | + | [[Image:page438for8.png|100px]] |
ആയാല് ആ പ്രതലം ഒരു ഗോളത്തിന്റെ ഉപരിതലമാണ്. മുകളില് കൊടുത്ത രണ്ടു മൂലരൂപങ്ങള് കൂടാതെ പ്രതലത്തിനു മൂന്നാമതൊരു മൂലരൂപം കൂടിയുണ്ട്. | ആയാല് ആ പ്രതലം ഒരു ഗോളത്തിന്റെ ഉപരിതലമാണ്. മുകളില് കൊടുത്ത രണ്ടു മൂലരൂപങ്ങള് കൂടാതെ പ്രതലത്തിനു മൂന്നാമതൊരു മൂലരൂപം കൂടിയുണ്ട്. | ||
| വരി 96: | വരി 96: | ||
Curves on a Surface | Curves on a Surface | ||
| - | c ഒരു പ്രാചലമായാല്, f (u,v,c) = 0 എന്ന രൂപത്തിലുള്ള ഒരു സമവാക്യം കൊണ്ട് പ്രതലത്തിലെ ഒരു വക്രത്തെ നിര്ദേശിക്കാം. | + | c ഒരു പ്രാചലമായാല്, f (u,v,c) = 0 എന്ന രൂപത്തിലുള്ള ഒരു സമവാക്യം കൊണ്ട് പ്രതലത്തിലെ ഒരു വക്രത്തെ നിര്ദേശിക്കാം. c-യുടെ മൂല്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് പ്രതലത്തിലുള്ള വിഭിന്നവക്രങ്ങള് കിട്ടുന്നു. |
| - | അഭിലംബീയ പരിച്ഛേദവും അഭിലംബീയ വക്രതയും: പ്രതലത്തിലുള്ള P എന്ന ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഏതെങ്കിലും വക്രം C ആയാല് dt/ds ആണ് വക്രതാസദിശം k. k-യെ പ്രതലത്തിന് അഭിലംബമായും സ്പര്ശകമായും kn, kb എന്ന ഘടകങ്ങള് (component) ആയി വിഘടനം ചെയ്യാവുന്നതാണ്. സിനെ അഭിലംബീയ വക്രതാസദിശം (normal curvature vector) എന്നും | + | അഭിലംബീയ പരിച്ഛേദവും അഭിലംബീയ വക്രതയും: പ്രതലത്തിലുള്ള P എന്ന ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഏതെങ്കിലും വക്രം C ആയാല് dt/ds ആണ് വക്രതാസദിശം k. k-യെ പ്രതലത്തിന് അഭിലംബമായും സ്പര്ശകമായും kn, kb എന്ന ഘടകങ്ങള് (component) ആയി വിഘടനം ചെയ്യാവുന്നതാണ്. സിനെ അഭിലംബീയ വക്രതാസദിശം (normal curvature vector) എന്നും kb-യെ സ്പര്ശരേഖീയ വക്രതാസദിശം (അല്ലെങ്കില് ജിയോഡസിക വക്രതാസദിശം) എന്നും പറയുന്നു. |
| - | P എന്ന ബിന്ദുവിലെ അഭിലംബത്തില്ക്കൂടി പോകുന്ന തലം പ്രതലത്തെ ഛേദിക്കുന്ന പരിച്ഛേദത്തെ (section) അഭിലംബീയ പരിച്ഛേദം (normal section) എന്നു പറയുന്നു. പ്രതിച്ഛേദിവക്രത്തിന്റെ P എന്ന ബിന്ദുവിലെ വക്രതയാണ് അഭിലംബീയ വക്രത. ഒരേ സ്പര്ശരേഖയിലൂടെയുള്ള തിര്യക്ക് (oblique) പരിച്ഛേദത്തിന്റെയും അഭിലംബീയ പരിച്ഛേദത്തിന്റെയും വക്രതകള് യഥാക്രമം k,kn എന്നിവയും ഈ പരിച്ഛേദങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം യും ആയാല് 'മ്യൂണിയര് പ്രമേയം' (Meunier's Theorem) അനുസരിച്ച് | + | P എന്ന ബിന്ദുവിലെ അഭിലംബത്തില്ക്കൂടി പോകുന്ന തലം പ്രതലത്തെ ഛേദിക്കുന്ന പരിച്ഛേദത്തെ (section) അഭിലംബീയ പരിച്ഛേദം (normal section) എന്നു പറയുന്നു. പ്രതിച്ഛേദിവക്രത്തിന്റെ P എന്ന ബിന്ദുവിലെ വക്രതയാണ് അഭിലംബീയ വക്രത. ഒരേ സ്പര്ശരേഖയിലൂടെയുള്ള തിര്യക്ക് (oblique) പരിച്ഛേദത്തിന്റെയും അഭിലംബീയ പരിച്ഛേദത്തിന്റെയും വക്രതകള് യഥാക്രമം k,kn എന്നിവയും ഈ പരിച്ഛേദങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം Θ-യും ആയാല് 'മ്യൂണിയര് പ്രമേയം' (Meunier's Theorem) അനുസരിച്ച് kn=k cos Θ ആയിരിക്കും. |
===വക്രതാരേഖകള്=== | ===വക്രതാരേഖകള്=== | ||
| വരി 107: | വരി 107: | ||
ഒരു പ്രതലത്തില് P എന്ന ബിന്ദുവിലുള്ള ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകള് ഉള്ള അഭിലംബീയ പരിച്ഛേദങ്ങളാണ് ആ ബിന്ദുവിലെ മുഖ്യ പരിച്ഛേദങ്ങള്. ഇവ പരസ്പരം ലംബങ്ങളാണ്. പ്രതലത്തില് വരയ്ക്കുന്ന വക്രത്തിലുള്ള ഏതു ബിന്ദുവിനും ആ ബിന്ദുവിലെ മുഖ്യപരിച്ഛേദങ്ങളിലൊന്നിനും ഒരേ സ്പര്ശരേഖയുണ്ടെങ്കില് ആ വക്രത്തെ വക്രതാരേഖ എന്നു വിളിക്കുന്നു. ഗോളത്തിന്റെ ഉപരിതലത്തിലോ ഒരു സമതലത്തിലോ വരയ്ക്കുന്ന ഏതു വക്രവും ഒരു വക്രതാരേഖയാണ്. ഒരു കോണിന്റെ വക്രതാരേഖകള് അതിന്റെ ശീര്ഷം കേന്ദ്രമായുള്ള ഗോളങ്ങള് കോണിനെ പ്രതിച്ഛേദിക്കുന്ന വക്രങ്ങളാണ്. | ഒരു പ്രതലത്തില് P എന്ന ബിന്ദുവിലുള്ള ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകള് ഉള്ള അഭിലംബീയ പരിച്ഛേദങ്ങളാണ് ആ ബിന്ദുവിലെ മുഖ്യ പരിച്ഛേദങ്ങള്. ഇവ പരസ്പരം ലംബങ്ങളാണ്. പ്രതലത്തില് വരയ്ക്കുന്ന വക്രത്തിലുള്ള ഏതു ബിന്ദുവിനും ആ ബിന്ദുവിലെ മുഖ്യപരിച്ഛേദങ്ങളിലൊന്നിനും ഒരേ സ്പര്ശരേഖയുണ്ടെങ്കില് ആ വക്രത്തെ വക്രതാരേഖ എന്നു വിളിക്കുന്നു. ഗോളത്തിന്റെ ഉപരിതലത്തിലോ ഒരു സമതലത്തിലോ വരയ്ക്കുന്ന ഏതു വക്രവും ഒരു വക്രതാരേഖയാണ്. ഒരു കോണിന്റെ വക്രതാരേഖകള് അതിന്റെ ശീര്ഷം കേന്ദ്രമായുള്ള ഗോളങ്ങള് കോണിനെ പ്രതിച്ഛേദിക്കുന്ന വക്രങ്ങളാണ്. | ||
| - | മുഖ്യപരിച്ഛേദങ്ങളിലെ ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകളെ മുഖ്യവക്രതകള് എന്നു പറയുന്നു. ഇവയുടെ തുകയും ഗുണനഫലവും പ്രതലങ്ങളെ സംബന്ധിച്ചിടത്തോളം പ്രാധാന്യമുള്ള രാശികളാണ്. മുഖ്യവക്രതകളുടെ തുകയാണ് മാധ്യ (mean) വക്രത. അവയുടെ ഗുണനഫലത്തെയാണ് | + | മുഖ്യപരിച്ഛേദങ്ങളിലെ ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകളെ മുഖ്യവക്രതകള് എന്നു പറയുന്നു. ഇവയുടെ തുകയും ഗുണനഫലവും പ്രതലങ്ങളെ സംബന്ധിച്ചിടത്തോളം പ്രാധാന്യമുള്ള രാശികളാണ്. മുഖ്യവക്രതകളുടെ തുകയാണ് മാധ്യ (mean) വക്രത. അവയുടെ ഗുണനഫലത്തെയാണ് ഗൌസ്വക്രത എന്നുപറയുന്നത്. ഗോളത്തിന്റെ ഉപരിതലം ധനസ്ഥിരാങ്കം ഗൗസ്വക്രതയുള്ള പ്രതലത്തിന് ഉദാഹരണമാണ്. വികസനീയമായ ഒരു പ്രതലത്തിന്റെ ഗൗസ്വക്രത ശൂന്യമാണ്. സ്ഥിരഋണസംഖ്യ ഗൗസ്വക്രതയായുള്ള പ്രതലത്തെ കപടഗോളം (pseudo-sphere) എന്നു പറയുന്നു. ട്രാക്ട്രിക്സ് (tractrix) എന്ന വക്രം ഒരു പ്രത്യേക അക്ഷത്തില് പരിക്രമണം ചെയ്താലുണ്ടാകുന്ന പ്രതലം ഒരു കപടഗോളമാണ്. മാധ്യവക്രത ശൂന്യമായ പ്രതലത്തിനു മിനിമല് (minimal) പ്രതലം എന്നു പേര്. മാധ്യവക്രത h-ഉം ഗൗസ്വക്രത k-ഉം ആയാല് പ്രതലത്തിന്റെ മൂലരൂപങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യമാണ് |
| - | III - hII +kl=0 | + | III - hII + kl = 0 |
==ജിയോഡസിക്കുകള്== | ==ജിയോഡസിക്കുകള്== | ||
Current revision as of 05:36, 19 നവംബര് 2014
ഉള്ളടക്കം |
അവകലജ്യാമിതി
Differential Geometry
ഗണിതശാസ്ത്രശാഖ. അവകല(Differential calculus)ത്തിലെ രീതികളും സമവാക്യങ്ങളും ഉപയോഗിച്ച് ത്രിമാന യുക്ലീഡിയന് സ്പേസില് (Three Dimensional Euclidean) വക്രങ്ങളുടെയും പ്രതലങ്ങളുടെയും സവിശേഷതകളെക്കുറിച്ചുള്ള പഠനം.
ചരിത്രം
ജര്മന് ശാസ്ത്രജ്ഞനായ ഗൗസ് (1777-1855) 1827-ല് പ്രസിദ്ധീകരിച്ച ഗവേഷണ പ്രബന്ധത്തിലാണ് ഈ വിഷയം ആദ്യമായി ചര്ച്ച ചെയ്യപ്പെട്ടിട്ടുള്ളത്. ത്രിമാന സ്പേസില് (Three Dimensional Euclidean Space) സമകോണീയ-കാര്ത്തീയ നിര്ദേശാങ്കങ്ങള് (Perpendicular Cartesian coordinates)x,y,z-ല് ഓരോന്നും u,v എന്ന രണ്ടു ചരങ്ങളുടെ ഫലനങ്ങളായിട്ടാണ് പ്രതലത്തെ ഗൌസ് നിര്വചിച്ചത്. ഈ ഫലനങ്ങള് പൊതുസ്വഭാവമുള്ളവയും സ്വതന്ത്രവുമായതിനാല് അവ പ്രതിനിധാനം ചെയ്തത് പ്രതലങ്ങളുടെ വ്യാപകരൂപം (general form) ആയിരുന്നു. ഗൗസിന്റെ പഠനം ശരിക്കും പ്രതലങ്ങളുടെ 'ത്രികോണമിതി'യില് ആദ്യത്തെ ചുവടുവയ്പാണ്. ഇതിനെത്തുടര്ന്ന് പ്രതലങ്ങളുടെ അവകലജ്യാമിതി റീമാന്, ഡിനി, അപ്പെല്, ദാര്ബൂ തുടങ്ങിയവരുടെ പ്രത്യേക ശ്രദ്ധയ്ക്കു വിഷയീഭവിച്ചു. ഈ ഗണിതശാസ്ത്രജ്ഞന്മാരുടെ നിഗമനങ്ങള് 1887-ല് നാലുഭാഗങ്ങളുള്ള ഒരു ബൃഹദ്ഗ്രന്ഥമായി പ്രസിദ്ധീകൃതമായി. ഇതില് നിര്ദേശാങ്കങ്ങള് xi (i = 1,2,3,....n) ഉള്ള n-മാന സ്പേസിലെ ജ്യാമിതിയെക്കുറിച്ചുള്ള റീമാന്റെ (1826-1866) പഠനം ശ്രദ്ധേയമാണ്. ആധുനിക ജ്യാമിതികളില് റീമാന്റെ സിദ്ധാന്തങ്ങള് ഒരു പ്രത്യേക ഗണിതശാസ്ത്രവിഭാഗമായിത്തന്നെ രൂപംകൊണ്ടിട്ടുണ്ട്. ടെന്സര് കലനം (Tensor Calculus) ഉപയോഗിച്ചാണ് ഈ ജ്യാമിതി കൈകാര്യം ചെയ്യുന്നത്. ഗുരുത്വാകര്ഷണ നിയമങ്ങള് ആവിഷ്കരിക്കുവാന് കാലദേശ(Time and Space)ങ്ങളുടെ ഒരു ചതുര്മാന അവകലജ്യാമിതിയാണ് ഐന്സ്റ്റൈന് (1879-1955) ഉപയോഗിച്ചിട്ടുള്ളത്. ദാര്ബൂ ആവിഷ്കരിച്ച 'ദാര്ബൂ സമീകരണം' പ്രയോഗിച്ച് സമാംഗരൂപത്തിലുള്ള സമവാക്യങ്ങളുടെ അവകലജം (derivative) കണ്ടുപിടിക്കുവാന് സാധിക്കുന്നു.
പ്രാഥമിക തത്ത്വങ്ങള്
അവകലജ്യാമിതിക്ക് മിതീയ (Metric) അവകലജ്യാമിതി എന്നും പ്രക്ഷേപീയ (Projective) അവകലജ്യാമിതി എന്നും രണ്ട് ഉള്പ്പിരിവുകളുണ്ട്. വക്രങ്ങളുടെയും പ്രതലങ്ങളുടെയും ദൃഢചലനം (rigid motion) കൊണ്ട് നിശ്ചരം (invariant) ആയി വര്ത്തിക്കുന്ന സാമാന്യ മൂലക(general element) ങ്ങളുടെ സവിശേഷതകളെക്കുറിച്ചു പ്രതിപാദിക്കുന്ന വിഭാഗമാണ് മിതീയ അവകലജ്യാമിതി. ത്രിമാന യുക്ലീഡിയന് സ്പേസില് (x,y,z), (x + dx,y + dy,z + dz) എന്ന നിര്ദേശാങ്കങ്ങള് ഉള്ള രണ്ടു സമീപ ബിന്ദുക്കള് തമ്മിലുള്ള ദൂരത്തെ കുറിക്കുന്ന സമവാക്യം
dr2 =(dx)2+(dy)2+(dz)2
ആണ്. ഇങ്ങനെയുള്ള സ്പേസില് നിര്ദേശാങ്കങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യം ഓരോന്നും ഓരോ പ്രതലത്തെയും അത്തരത്തിലുള്ള രണ്ടു സമവാക്യങ്ങള് ഒരു വക്രത്തെയും കുറിക്കുന്നു. അവകലജ്യാമിതിയില് വക്രങ്ങളെയും പ്രതലങ്ങളെയും ചിത്രീകരിക്കുവാന് പ്രാചലങ്ങള് (Parameters) ഉപയോഗിക്കുന്നതു സൗകര്യപ്രദമാണ്. പ്രാചലങ്ങള് ഉപയോഗിക്കുന്ന രീതിയെ പ്രാചലചിത്രീകരണം (Parametric Representation) എന്നു പറയുന്നു. ഈ രീതിയനുസരിച്ച് ഒരു സ്പേസ്-വക്ര(Space-curve)ത്തിന്റെ സമവാക്യം x = x(t),y = y(t),z =z(t) ആണ്. ഇവിടെ t ഒരു പ്രാചലമാണ്.
സ്പേസ് - വക്രങ്ങള്
x = x(t), y = y(t),z = z(t)
എന്ന സമവാക്യങ്ങള് കുറിക്കുന്ന സ്പേസ്-വക്രത്തില് ഏതെങ്കിലും ഒരു ബിന്ദുവായ P യുടെ സ്ഥിതിസദിശം (position vector)
ആണ്. അതുകൊണ്ട് സ്പേസിലെ ഒരു വക്രത്തെ കുറിക്കുവാന് γ = γ (t) എന്ന് എഴുതുന്നു. ഇതിനെ വക്രത്തിന്റെ സദിശസമവാക്യം (vector equation) എന്നു പറയുന്നു. വക്രത്തിലുള്ള ഒരു നിശ്ചിതബിന്ദുവില്നിന്നുള്ള ചാപദൈര്ഘ്യം s ആയാല് P എന്ന ബിന്ദുവിലെ സ്പര്ശക(tangent)ത്തിന്റെ ദിശാ-കൊസൈനുകള് (direction cosines),
ആകുന്നു. സ്പേസില് സ്പര്ശകത്തിന്റെ ദിശ (direction) ഈ ദിശാ-കൊസൈനുകളെ ആശ്രയിച്ചിരിക്കുന്നു.
വക്രത്തിലുള്ള P,Q,R എന്ന ബിന്ദുക്കള് ഒരേതലത്തില് കിടക്കുന്നു എന്നു സങ്കല്പിക്കുക. Q-ഉം, R-ഉം, P-യോട് അടുത്തടുത്തു വരുന്നതോടുകൂടി ഈ തലത്തിനുണ്ടാകുന്ന സീമാന്തസ്ഥാനം (limiting position) ആണ് വക്രത്തിന്റെ P എന്ന ബിന്ദുവിലെ ആശ്ലേഷതലം (Osculating plane). ഒരു വക്രത്തില് എല്ലാ ബിന്ദുക്കളും ഒരേ തലത്തില് കിടക്കുന്നു എങ്കില് അതിനെ സമതലവക്രം (Plane curve) എന്നു പറയുന്നു. ഒരു സമതലവക്രത്തിന്റെ ആശ്ലേഷതലം, വക്രം ഉള്ക്കൊള്ളുന്ന സമതലം തന്നെയാണ്.
വക്രത്തില് ഒരു ബിന്ദുവിലെ സ്പര്ശകത്തിനു ലംബമായി അതേ ബിന്ദുവില്ക്കൂടിയുള്ള നേര്വരയാണ് അഭിലംബം (Normal); വക്രത്തിനും സ്പര്ശകത്തിനും പൊതുവായ ഒരു ബിന്ദുവില്ക്കൂടി സ്പര്ശകത്തിന് അനേകം അഭിലംബങ്ങള് വരയ്ക്കാം. ഈ അഭിലംബങ്ങളെല്ലാം ഒരേ തലത്തിലാണു കിടക്കുന്നത്. ഈ തലത്തെ അഭിലംബതലം (Normal plane) എന്നു പറയുന്നു. സ്പര്ശകം അഭിലംബതലത്തിനു ലംബമായിരിക്കും. ഒരു ബിന്ദുവിലുള്ള അനേകം അഭിലംബങ്ങളില് പ്രത്യേകം രണ്ടെണ്ണം പ്രധാനമാണ്. ആശ്ലേഷതലത്തില് കിടക്കുന്ന അഭിലംബത്തെ മുഖ്യാഭിലംബം (Principal normal) എന്നു പറയുന്നു; ഒരു ബിന്ദുവിലെ ആശ്ലേഷതലത്തിന്റെയും അഭിലംബതലത്തിന്റെയും പ്രതിച്ഛേദിരേഖ (line of intersection) ആണ് മുഖ്യാഭിലംബം. ആശ്ലേഷതലത്തിനു ലംബമായ അഭിലംബമാണ് ദ്വയാഭിലംബം (binormal). ഈ രേഖ മുഖ്യാഭിലംബത്തിനും സ്പര്ശരേഖയ്ക്കും ലംബമായ അഭിലംബമാണ്. അങ്ങനെ വക്രത്തില് ഓരോ ബിന്ദുവിലുമുള്ള അന്യോന്യം ലംബങ്ങളായ മൂന്നു സദിശങ്ങളാണ് സ്പര്ശരേഖയും മുഖ്യാഭിലംബവും ഉപാഭിലംബവും. ഇവയുടെ ദിശകളിലുള്ള ഏകകസദിശ(unit vector)ങ്ങളെ കുറിക്കുവാന് യഥാക്രമം t,n,b എന്ന പ്രതീകങ്ങള് ഉപയോഗിക്കുന്നു. ഓരോ ബിന്ദുവിലും t,n,b എന്ന ഏകകസദിശങ്ങള് അന്യോന്യം ലംബങ്ങളായ മൂന്നു തലങ്ങള് സൃഷ്ടിക്കുന്നു. സദിശങ്ങള് t-ഉം n-ഉം ഉള്ള തലം ആശ്ലേഷതലവും n-ഉം b-ഉം ഉള്ള തലം അഭിലംബതലവും b-ഉം t-ഉം ഉള്ള തലം ചാപകലനതല(Rectifying plane)വും ആകുന്നു (ചിത്രം നോക്കുക).
ഒരു സ്പേസ്വക്രത്തെ സംബന്ധിച്ചിടത്തോളം പ്രധാനപ്പെട്ട രണ്ടു ഗുണധര്മങ്ങളാണ് വക്രത(curvature)യും ടോര്ഷനും (torsion): dt/ds എന്ന സദിശത്തെ വക്രത്തിന്റെ P എന്ന ബിന്ദുവിലുള്ള വക്രതാസദിശം (curvature vector) എന്നും ഇതിന്റെ മൂല്യ(mangitude)ത്തെ വക്രത എന്നും പറയുന്നു. വക്രതാസദിശം ചാപദൈര്ഘ്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് സ്പര്ശരേഖയുടെ തിരിയലിന്റെ (ഘൂര്ണനത്തിന്റെ) നിരക്കാണ്. വക്രതയെ കുറിക്കാന് κ എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. വക്രത്തില് വക്രത ശൂന്യമാകുന്ന ബിന്ദുവാണ് അതിപരിവര്ത്തന ബിന്ദു (point of inflexion). db/ds എന്ന സദിശത്തെ വക്രത്തിന്റെ ടോര്ഷന് സദിശം (Torsion vector) എന്നു പറയുന്നു. ഇതു ചാപദൈര്ഘ്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് ദ്വയാഭിലംബം തിരിയുന്നതിന്റെ നിരക്കാണ്. ടോര്ഷന്സദിശത്തിന്റെ മൂല്യത്തെ ടോര്ഷന് എന്നു പറയുന്നു. ടോര്ഷനെ കുറിക്കാന് τ(tau) എന്ന പ്രതീകം ഉപയോഗിക്കുന്നു. ഒരു വക്രം സമതലവക്രമാകണമെങ്കില് എല്ലാ ബിന്ദുക്കളിലും ടോര്ഷന് ശൂന്യമാകണം; മറിച്ച് എല്ലാ ബിന്ദുക്കളിലും ടോര്ഷന് ശൂന്യമായ വക്രം സമതലവക്രമാണ്. സാധാരണ ρ=1/κഎന്നും σ=1/τഎന്നും എഴുതുന്നു. ρ-യെ വക്രതാത്രിജ്യ (radius of curvature) എന്നും τ-യെ ടോര്ഷന്ത്രിജ്യ (radius of torsion) എന്നും പറയുന്നു.
ഒരു സിലിണ്ടറിന്റെ ഉപരിഭാഗത്ത്, സ്പര്ശരേഖ സ്പേസിലുള്ള ഏതെങ്കിലും നിശ്ചിത രേഖയുമായി ഒരു സ്ഥിരകോണം വരത്തക്കവണ്ണം വരയ്ക്കാവുന്ന വക്രത്തെ ഹെലിക്സ് (Helix) എന്നു പറയുന്നു. സ്പ്രിങ്ബാലന്സിലെ സ്പ്രിങ്, ഹെലിക്സിന്റെ രൂപത്തിലാണ്. വക്രതയും ടോര്ഷനും എല്ലാ ബിന്ദുക്കളിലും സ്ഥിരമായ ഹെലിക്സ് ആണ്. ഒരു വൃത്തീയ (circular) ഹെലിക്സില്
( x = a cosθ, y = a sinθ,z = aθ)
വക്രതയും ടോര്ഷനും എല്ലാ ബിന്ദുക്കളിലും തുല്യമാണ്.
ഏതു സ്പേസ്-വക്രത്തിലും t,n,b എന്ന മൂലസദിശങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യങ്ങളാണ് താഴെ കൊടുക്കുന്നത്:
ഇവയെ സെററ്റ്-ഫ്രെനറ്റ് സമവാക്യങ്ങള് (Serret-Frenet equations) എന്നു പറയുന്നു. വക്രങ്ങളെക്കുറിച്ചുള്ള പഠനത്തില് ഇവയ്ക്കു മൌലികപ്രാധാന്യമുണ്ട്. മാട്രിക്സ് രീതിയില് ഈ സമവാക്യങ്ങളെ
എന്ന വിധത്തില് എഴുതാവുന്നതാണ്.
പൊതുവായ മുഖ്യാഭിലംബങ്ങള് ഉള്ള വക്രങ്ങളെ ബര്ട്രന്ഡ് വക്രങ്ങള് (Bertrand curves) എന്നു പറയുന്നു. ഇങ്ങനെയുള്ള വക്രങ്ങളില് ഏതു ബിന്ദുവിലും വക്രതയും ടോര്ഷനും തമ്മില് ഒരു ഏകഘാതബന്ധം (Linear relation) ഉണ്ട്.
പ്രതലങ്ങള്
Surfaces
നിര്ദേശാങ്കങ്ങള് u,v എന്ന രണ്ടു സ്വതന്ത്ര പ്രാചലങ്ങളുടെ ഫലനങ്ങളായ ബിന്ദുപഥ(locus)ത്തിനെ പ്രതലം എന്നു പറയുന്നു. ഒരു പ്രതലത്തെ പ്രതിനിധാനം ചെയ്യുന്ന സമവാക്യങ്ങളെ x = x(u,v),y = y(u,v),z = z(u,v) എന്നെഴുതാം. ഈ പ്രതലത്തിന്റെ സദിശസമവാക്യം r= r(u,v) ആണ്. പ്രാചലങ്ങള് ഉപയോഗിച്ച് പ്രതലത്തെ ചിത്രീകരിക്കുന്ന സമവാക്യങ്ങളെ പ്രതലത്തിന്റെ ഗൗസിയന് രൂപം (Gaussian form) എന്നു പറയാറുണ്ട്. ബീജീയരീതികളുപയോഗിച്ച് u,v എന്ന പ്രാചലങ്ങളെ ഒഴിവാക്കിയാല് പ്രതലത്തിനു f(x,y,z) = 0 എന്ന രീതിയിലുള്ള ഒരു സമവാക്യം കിട്ടുന്നു. ഈ പ്രതലത്തില് γ0സ്ഥിതി സദിശമുള്ള ഒരു ബിന്ദുവിലെ സ്പര്ശതല(tangent plane)ത്തിന്റെ സദിശസമവാക്യവും അഭിലംബരേഖയുടെ സമവാക്യവും ക്രമത്തില് താഴെ ചേര്ക്കുന്നു:
അനുക്രമമായ പ്രതലങ്ങളുടെ പ്രതിച്ഛേദിവക്രത്തിന്റെ സീമാന്തസ്ഥാനത്തെ അഭിലക്ഷണിക (Characteristic) വക്രം എന്നു പറയുന്നു. പ്രാചലത്തിന്റെ വില മാറിവരുമ്പോള് അനേകം അഭിലക്ഷണിക വക്രങ്ങള് കിട്ടുന്നു. പ്രാചലത്തിന്റെ എല്ലാ മൂല്യങ്ങള്ക്കുമുള്ള ഇത്തരം അഭിലക്ഷണിക വക്രങ്ങളുടെ പഥമാണ് പ്രതലങ്ങളുടെ ആവരണം (envelope). പ്രതലകുല(family of surfaces) ത്തിലുള്ള ഓരോ പ്രതലത്തെയും ആവരണം സ്പര്ശിക്കുന്നു.
വികസനീയ പ്രതലം
സമതലങ്ങളുടെ ഏകരാശികുല(single parameter family)ത്തിന്റെ ആവരണം ആണ് വികസനീയ പ്രതലം (Developable surface). ഇത്തരം പ്രതലങ്ങളെ മടക്കാതെയും ഒടിക്കാതെയും ഒരു സമതലത്തിന്മേല് നിവര്ത്തി വിരിക്കാവുന്നതാണ്. ഉദാഹരണമായി കോണ് (cone), വൃത്തസ്തംഭം (cylinder) എന്നീ ഘനരൂപങ്ങളുടെ ഉപരിതലം വികസനീയ പ്രതലമാണ്. സമതലത്തിലെന്നപോലെ ഒരു വികസനീയ പ്രതലത്തിന്റെ വക്രത എല്ലായിടത്തും ശൂന്യമായിരിക്കും. സാധാരണഗതിയില് ഒരു പ്രതലത്തിന്റെ സ്പര്ശതലം രണ്ടു പ്രാചലങ്ങളെ ആശ്രയിച്ചിരിക്കും. എന്നാല് വികസനീയ പ്രതലത്തിന്റെ സ്പര്ശതലത്തില് ഒരു പ്രാചലം മാത്രമേ കാണുകയുള്ളു.
പ്രതലത്തിന്റെ മൂലരൂപങ്ങള്
പ്രതലത്തിലുള്ള വക്രത്തിലെ ds എന്ന ഏകഘാത മൂലകാംശ(linear element)ത്തിന്റെ ചാപദൈര്ഘ്യം അളക്കുവാന്
എന്ന സൂത്രവാക്യം ഉപയോഗിക്കുന്നു. പ്രതീകങ്ങള് അല്പം മാറ്റിയാല് ഈ സൂത്രവാക്യത്തെ
എന്ന രീതിയില് എഴുതാവുന്നതാണ്.
I = Edu2 + 2 Fdudv + Gdv2
എന്ന വ്യഞ്ജക(expression)ത്തെ പ്രതലത്തിന്റെ പ്രഥമ മൂലരൂപം (first fundamental form) എന്നും രാശികള് E,F,G എന്നിവയെ പ്രഥമ മൂലഗുണാങ്കങ്ങള് എന്നും പറയുന്നു.
എന്നതിനെ പ്രതലത്തിന്റെ ദ്വിതീയ മൂലരൂപമെന്നും L,M,N എന്നിവയെ ദ്വിതീയ മൂലഗുണാങ്കങ്ങള് എന്നും പറയുന്നു. പ്രതലങ്ങളുടെ പഠനത്തില് ഈ ആറ് മൂലഗുണാങ്കങ്ങള്ക്കും അടിസ്ഥാനപരമായ പ്രാധാന്യമുണ്ട്. വക്രങ്ങളുടെ പഠനത്തില് വക്രതയ്ക്കും ടോര്ഷനുമുള്ള പ്രാധാന്യമാണ് പ്രതലങ്ങളുടെ സിദ്ധാന്തത്തില് ഇവയ്ക്കുള്ളത്.
ആയാല് ആ പ്രതലം ഒരു ഗോളത്തിന്റെ ഉപരിതലമാണ്. മുകളില് കൊടുത്ത രണ്ടു മൂലരൂപങ്ങള് കൂടാതെ പ്രതലത്തിനു മൂന്നാമതൊരു മൂലരൂപം കൂടിയുണ്ട്.
III = Adu2 + 2 Bdudv + Cdv2
പ്രതലവക്രങ്ങള്
Curves on a Surface
c ഒരു പ്രാചലമായാല്, f (u,v,c) = 0 എന്ന രൂപത്തിലുള്ള ഒരു സമവാക്യം കൊണ്ട് പ്രതലത്തിലെ ഒരു വക്രത്തെ നിര്ദേശിക്കാം. c-യുടെ മൂല്യം വ്യത്യാസപ്പെടുന്നതനുസരിച്ച് പ്രതലത്തിലുള്ള വിഭിന്നവക്രങ്ങള് കിട്ടുന്നു.
അഭിലംബീയ പരിച്ഛേദവും അഭിലംബീയ വക്രതയും: പ്രതലത്തിലുള്ള P എന്ന ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന ഏതെങ്കിലും വക്രം C ആയാല് dt/ds ആണ് വക്രതാസദിശം k. k-യെ പ്രതലത്തിന് അഭിലംബമായും സ്പര്ശകമായും kn, kb എന്ന ഘടകങ്ങള് (component) ആയി വിഘടനം ചെയ്യാവുന്നതാണ്. സിനെ അഭിലംബീയ വക്രതാസദിശം (normal curvature vector) എന്നും kb-യെ സ്പര്ശരേഖീയ വക്രതാസദിശം (അല്ലെങ്കില് ജിയോഡസിക വക്രതാസദിശം) എന്നും പറയുന്നു.
P എന്ന ബിന്ദുവിലെ അഭിലംബത്തില്ക്കൂടി പോകുന്ന തലം പ്രതലത്തെ ഛേദിക്കുന്ന പരിച്ഛേദത്തെ (section) അഭിലംബീയ പരിച്ഛേദം (normal section) എന്നു പറയുന്നു. പ്രതിച്ഛേദിവക്രത്തിന്റെ P എന്ന ബിന്ദുവിലെ വക്രതയാണ് അഭിലംബീയ വക്രത. ഒരേ സ്പര്ശരേഖയിലൂടെയുള്ള തിര്യക്ക് (oblique) പരിച്ഛേദത്തിന്റെയും അഭിലംബീയ പരിച്ഛേദത്തിന്റെയും വക്രതകള് യഥാക്രമം k,kn എന്നിവയും ഈ പരിച്ഛേദങ്ങള് ഉള്ക്കൊള്ളുന്ന കോണം Θ-യും ആയാല് 'മ്യൂണിയര് പ്രമേയം' (Meunier's Theorem) അനുസരിച്ച് kn=k cos Θ ആയിരിക്കും.
വക്രതാരേഖകള്
Lines of Curvature
ഒരു പ്രതലത്തില് P എന്ന ബിന്ദുവിലുള്ള ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകള് ഉള്ള അഭിലംബീയ പരിച്ഛേദങ്ങളാണ് ആ ബിന്ദുവിലെ മുഖ്യ പരിച്ഛേദങ്ങള്. ഇവ പരസ്പരം ലംബങ്ങളാണ്. പ്രതലത്തില് വരയ്ക്കുന്ന വക്രത്തിലുള്ള ഏതു ബിന്ദുവിനും ആ ബിന്ദുവിലെ മുഖ്യപരിച്ഛേദങ്ങളിലൊന്നിനും ഒരേ സ്പര്ശരേഖയുണ്ടെങ്കില് ആ വക്രത്തെ വക്രതാരേഖ എന്നു വിളിക്കുന്നു. ഗോളത്തിന്റെ ഉപരിതലത്തിലോ ഒരു സമതലത്തിലോ വരയ്ക്കുന്ന ഏതു വക്രവും ഒരു വക്രതാരേഖയാണ്. ഒരു കോണിന്റെ വക്രതാരേഖകള് അതിന്റെ ശീര്ഷം കേന്ദ്രമായുള്ള ഗോളങ്ങള് കോണിനെ പ്രതിച്ഛേദിക്കുന്ന വക്രങ്ങളാണ്.
മുഖ്യപരിച്ഛേദങ്ങളിലെ ഏറ്റവും കൂടുതലും ഏറ്റവും കുറവുമായ വക്രതകളെ മുഖ്യവക്രതകള് എന്നു പറയുന്നു. ഇവയുടെ തുകയും ഗുണനഫലവും പ്രതലങ്ങളെ സംബന്ധിച്ചിടത്തോളം പ്രാധാന്യമുള്ള രാശികളാണ്. മുഖ്യവക്രതകളുടെ തുകയാണ് മാധ്യ (mean) വക്രത. അവയുടെ ഗുണനഫലത്തെയാണ് ഗൌസ്വക്രത എന്നുപറയുന്നത്. ഗോളത്തിന്റെ ഉപരിതലം ധനസ്ഥിരാങ്കം ഗൗസ്വക്രതയുള്ള പ്രതലത്തിന് ഉദാഹരണമാണ്. വികസനീയമായ ഒരു പ്രതലത്തിന്റെ ഗൗസ്വക്രത ശൂന്യമാണ്. സ്ഥിരഋണസംഖ്യ ഗൗസ്വക്രതയായുള്ള പ്രതലത്തെ കപടഗോളം (pseudo-sphere) എന്നു പറയുന്നു. ട്രാക്ട്രിക്സ് (tractrix) എന്ന വക്രം ഒരു പ്രത്യേക അക്ഷത്തില് പരിക്രമണം ചെയ്താലുണ്ടാകുന്ന പ്രതലം ഒരു കപടഗോളമാണ്. മാധ്യവക്രത ശൂന്യമായ പ്രതലത്തിനു മിനിമല് (minimal) പ്രതലം എന്നു പേര്. മാധ്യവക്രത h-ഉം ഗൗസ്വക്രത k-ഉം ആയാല് പ്രതലത്തിന്റെ മൂലരൂപങ്ങളെ ബന്ധിപ്പിക്കുന്ന സമവാക്യമാണ്
III - hII + kl = 0
ജിയോഡസിക്കുകള്
Geodesics
പ്രതലത്തില് രണ്ടു ബിന്ദുക്കള് തമ്മിലുള്ള ഏറ്റവും കുറഞ്ഞ അകലം കുറിക്കുന്ന വക്രമാണ് ജിയോഡസിക് (Geodesic). വലിച്ചുമുറുക്കിയ ചരട് പ്രതലത്തിലുള്ള രണ്ടു ബിന്ദുക്കളില്ക്കൂടി കടന്നുപോകുന്ന വഴി ജിയോഡസിക് എന്ന വക്രത്തിലൂടെയാണ്. ചരടിന്റെ ഒരറ്റം പ്രതലത്തില് ഉറപ്പിച്ചു മറ്റേ അറ്റം പ്രതലത്തിലൂടെ ചലിപ്പിച്ചാല് ഒരു നിശ്ചിത ബിന്ദുവില്ക്കൂടി കടന്നുപോകുന്ന അനേകം ജിയോഡസിക്കുകള് കിട്ടുന്നു. ഇത്തരം വക്രങ്ങളുടെ ജിയോഡസിക് വക്രത ശൂന്യമാണ്. ഒരു ഗോളത്തിന്റെ ഉപരിതലത്തിലുള്ള ജിയോഡസിക്കുകള് ഗുരുവൃത്ത(Great circle)ങ്ങളാണ്; അതുപോലെ ഒരു വൃത്തസ്തംഭത്തിന്റെ ഉപരിതലത്തിലെ ജിയോഡസിക്കുകള് അതിന്മേല് വരയ്ക്കുന്ന ഹെലിക്സുകളും. ജിയോഡസിക്കില് ഏതു ബിന്ദുവിലെയും മുഖ്യാഭിലംബം പ്രതലത്തിലെ ആ ബിന്ദുവിലുള്ള അഭിലംബമായിരിക്കും. ഇത്തരം വക്രങ്ങളെ നിര്വചിക്കുവാന് ഈ ഗുണധര്മം ഉപയോഗിക്കാറുണ്ട്.
പ്രതലങ്ങളെക്കുറിച്ചുള്ള സിദ്ധാന്തം കൈകാര്യം ചെയ്യുവാന് പലപ്പോഴും ടെന്സറുകള് (tensors) ഉപയോഗിക്കുന്നതു സൗകര്യപ്രദമാണ്. ടെന്സര്വിശ്ലേഷണം ഉപയോഗിച്ച് ജിയോഡസിക്കുകളുടെ അവകല സമവാക്യങ്ങളും പ്രതലത്തിന്റെ മൂലരൂപങ്ങളും വളരെ സരളമായ രീതിയില് എഴുതാവുന്നതാണ്.
പ്രക്ഷേപീയ അവകലജ്യാമിതി
വക്രങ്ങളിലും പ്രതലങ്ങളിലും അളവ് എന്ന ആശയവുമായി ബന്ധപ്പെടാത്ത ഗുണങ്ങളെക്കുറിച്ചാണ് അവകലജ്യാമിതിയുടെ ഈ വിഭാഗത്തില് പ്രതിപാദിക്കുന്നത്. പലതരം വിന്യാസ(configuration)ങ്ങളുടെ പ്രക്ഷേപീയ രൂപാന്തരണം (projective transformation) കൊണ്ടു നിശ്ചരമായിരിക്കുന്ന അവകലഗുണധര്മങ്ങള് പ്രക്ഷേപീയ അവകലജ്യാമിതിയില് പ്രധാനമാണ്. ഈ ജ്യാമിതിയുടെ ഉപജ്ഞാതാക്കള് പ്രധാനമായി ഫുബിനി (Fubini), കാര്ട്ടന് (Cartan) തുടങ്ങിയ ഗണിതശാസ്ത്രജ്ഞന്മാരാണ്. നോ: അഫൈന് ജ്യാമിതി; ജ്യാമിതി; പ്രക്ഷേപീയജ്യാമിതി; മാട്രിക്സ് ആള്ജിബ്ര
(കെ. ജയചന്ദ്രന്)