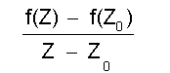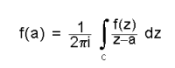This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
അനലിറ്റിക് ഫങ്ഷന്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
| (ഇടക്കുള്ള 4 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | = അനലിറ്റിക് ഫങ്ഷന് | + | = അനലിറ്റിക് ഫങ്ഷന് = |
| - | + | ||
Analytic function | Analytic function | ||
ഗണിതശാസ്ത്രശാഖയായ സമ്മിശ്രവിശ്ളേഷണ(complex analysis)ത്തിലെ ഗണിതപ്രാധാന്യമുള്ള ഫലനം. വിശ്ളേഷകഫലനം, ഹോളൊമോര്ഫികഫലനം (Holomorphic function), നിയമിതഫലനം (Regular function) എന്നീ പേരുകളിലും ഇതറിയപ്പെടുന്നു. | ഗണിതശാസ്ത്രശാഖയായ സമ്മിശ്രവിശ്ളേഷണ(complex analysis)ത്തിലെ ഗണിതപ്രാധാന്യമുള്ള ഫലനം. വിശ്ളേഷകഫലനം, ഹോളൊമോര്ഫികഫലനം (Holomorphic function), നിയമിതഫലനം (Regular function) എന്നീ പേരുകളിലും ഇതറിയപ്പെടുന്നു. | ||
| - | |||
'''ചരിത്രം'''. വിശ്ളേഷണഫലന സിദ്ധാന്ത(അനലിറ്റിക് ഫങ്ഷന്)ത്തിന്റെ ആദ്യകാല ഗവേഷകര് കോഷി, റീമാന്, വെയര്സ്റ്റ്രോസ് എന്നിവരാണ്. വ്യുത്പന്നം (derivative) അഥവാ അവകലജഗുണാങ്കം (differential coefficient) ഉള്ള ഫലനങ്ങളാണ് കോഷിസിദ്ധാന്തത്തിന്റെ അടിസ്ഥാനം. സമ്മിശ്രസമാകല(complex integration)ത്തിന്റെ ഉപാധിയിലൂടെയാണ് 1814-ല് കോഷി ഈ സിദ്ധാന്തത്തിനു രൂപംകൊടുത്തത്. ഗണിതശാസ്ത്രജ്ഞനായ ഗൂര്ഷ (Goursat) 1900-ത്തില് അതിനെ നവീകരിച്ചു. അനലിറ്റിക് ഫങ്ഷന്റെ ജ്യാമിതീയ പ്രാധാന്യമാണ് റീമാന് പഠന വിധേയമാക്കിയത്. ഘാതശ്രേണി (power series) ആണ് വെയര്സ്റ്റ്രോസ്തത്ത്വത്തിന്റെ അടിസ്ഥാനം. വിശ്ളേഷക-അവിച്ഛിന്നത(analytic continuum)യുടെ താത്ത്വിക വശങ്ങളിലാണ് വെയര്സ്റ്റ്രോസ് ശ്രദ്ധിച്ചത്. | '''ചരിത്രം'''. വിശ്ളേഷണഫലന സിദ്ധാന്ത(അനലിറ്റിക് ഫങ്ഷന്)ത്തിന്റെ ആദ്യകാല ഗവേഷകര് കോഷി, റീമാന്, വെയര്സ്റ്റ്രോസ് എന്നിവരാണ്. വ്യുത്പന്നം (derivative) അഥവാ അവകലജഗുണാങ്കം (differential coefficient) ഉള്ള ഫലനങ്ങളാണ് കോഷിസിദ്ധാന്തത്തിന്റെ അടിസ്ഥാനം. സമ്മിശ്രസമാകല(complex integration)ത്തിന്റെ ഉപാധിയിലൂടെയാണ് 1814-ല് കോഷി ഈ സിദ്ധാന്തത്തിനു രൂപംകൊടുത്തത്. ഗണിതശാസ്ത്രജ്ഞനായ ഗൂര്ഷ (Goursat) 1900-ത്തില് അതിനെ നവീകരിച്ചു. അനലിറ്റിക് ഫങ്ഷന്റെ ജ്യാമിതീയ പ്രാധാന്യമാണ് റീമാന് പഠന വിധേയമാക്കിയത്. ഘാതശ്രേണി (power series) ആണ് വെയര്സ്റ്റ്രോസ്തത്ത്വത്തിന്റെ അടിസ്ഥാനം. വിശ്ളേഷക-അവിച്ഛിന്നത(analytic continuum)യുടെ താത്ത്വിക വശങ്ങളിലാണ് വെയര്സ്റ്റ്രോസ് ശ്രദ്ധിച്ചത്. | ||
| - | |||
'''സമ്മിശ്രചരങ്ങളുടെ ഫലനം''' (function of complex variables). R, S എന്നീ രണ്ടു സമ്മിശ്ര സംഖ്യാഗണങ്ങള് (sets of complex numbers) ആദ്യത്തേതിലെ ഓരോ അംഗ(z)ത്തിനും രണ്ടാമത്തേതിലെ ഒരംഗത്തെ നിര്ദേശിക്കുന്ന നിയമം (f) ആണ്, ഇവിടെ 'ഫലനം' എന്നതുകൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നത്. ഫലനത്തിന്റെ ഡൊമെയിന് (domain) R-ഉം റെയിഞ്ച് (range) S-ഉം ആണ്. ഡൊമെയിന് ഒരു വിവൃത-ബന്ധിതം (open connected) ആയിരിക്കും. ഇത്തരം R-ഗണത്തെ റീജിയന് (region) എന്നു പറയുന്നു. R-റീജിയനില് f(z) നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു; Z എന്ന സമ്മിശ്രചരം Z0-നോടു സമീപിക്കുമ്പോള്, | '''സമ്മിശ്രചരങ്ങളുടെ ഫലനം''' (function of complex variables). R, S എന്നീ രണ്ടു സമ്മിശ്ര സംഖ്യാഗണങ്ങള് (sets of complex numbers) ആദ്യത്തേതിലെ ഓരോ അംഗ(z)ത്തിനും രണ്ടാമത്തേതിലെ ഒരംഗത്തെ നിര്ദേശിക്കുന്ന നിയമം (f) ആണ്, ഇവിടെ 'ഫലനം' എന്നതുകൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നത്. ഫലനത്തിന്റെ ഡൊമെയിന് (domain) R-ഉം റെയിഞ്ച് (range) S-ഉം ആണ്. ഡൊമെയിന് ഒരു വിവൃത-ബന്ധിതം (open connected) ആയിരിക്കും. ഇത്തരം R-ഗണത്തെ റീജിയന് (region) എന്നു പറയുന്നു. R-റീജിയനില് f(z) നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു; Z എന്ന സമ്മിശ്രചരം Z0-നോടു സമീപിക്കുമ്പോള്, | ||
| - | + | [[Image:p485b.png]] | |
| - | എന്ന അംശബന്ധം (ratio) ഒരു പരിമേയ സീമ(finite limit)യോടടുക്കുന്നു; എങ്കില് R-ലെ | + | എന്ന അംശബന്ധം (ratio) ഒരു പരിമേയ സീമ(finite limit)യോടടുക്കുന്നു; എങ്കില് R-ലെ Z<sub>0</sub> ബിന്ദുവില് f(Z) അവകലനീയം (differentiable) ആണ് എന്നു പറയുന്നു. Z<sub>0</sub>-ലേക്കു Z അടുക്കുന്ന രൂപരേഖ (contour) ഏതു തന്നെ ആയാലും f(Z) - f(Z<sub>0</sub>)/Z-Z<sub>0</sub>-ന്റെ സീമയ്ക്കു മാറ്റമുണ്ടാകാന് പാടില്ല. ഈ സീമയെ f(Z)-ന്റെ Z0 എന്ന ബിന്ദുവിലെ വ്യുത്പന്നം (derivative) f'(Z) എന്നു പറയുന്നു. R-ലുള്ള എല്ലാ ബിന്ദുക്കളിലും f'(Z)-നു അസ്തിത്വമുണ്ടെങ്കില് f(Z) എന്ന ഫലനം R എന്ന പ്രദേശത്തു വിശ്ളേഷകമാണെന്നു പറയുന്നു. n ഒരു ധനാത്മകപൂര്ണസംഖ്യ ആണെങ്കില് Zn പരിമിത (സമ്മിശ്ര) തലത്തില് വിശ്ളേഷകമാണ്. അതുകൊണ്ട് എല്ലാ ബഹുപദങ്ങളും (polynominals) വിശ്ളേഷകഫലനങ്ങളാണ്. |
f(Z) = u(x,y) + i v(x, y) സമ്മിശ്രതലത്തിലെ R-റീജിയനില് വിശ്ളേഷകമാണെന്നു കരുതിയാല് u(x,y), v(x, y) എന്നീ വാസ്തവികമൂല്യ ഫലനങ്ങള് (real valued functions) താഴെ പറയുന്ന സമവാക്യങ്ങള്ക്ക് അനുസൃതമായിരിക്കുമെന്നു കാണാം. | f(Z) = u(x,y) + i v(x, y) സമ്മിശ്രതലത്തിലെ R-റീജിയനില് വിശ്ളേഷകമാണെന്നു കരുതിയാല് u(x,y), v(x, y) എന്നീ വാസ്തവികമൂല്യ ഫലനങ്ങള് (real valued functions) താഴെ പറയുന്ന സമവാക്യങ്ങള്ക്ക് അനുസൃതമായിരിക്കുമെന്നു കാണാം. | ||
| - | + | [[Image:p485c.png]] | |
എന്നിവയെ കോഷി-റീമാന് സമവാക്യങ്ങള് (Cauchy-Riemann equations) എന്നു പറയുന്നു. ഇതില് പെടുന്ന ആംശികവ്യുത്പന്നങ്ങള് (partial derivatives), കോഷി-റീമാന് സമവാക്യങ്ങളെ തൃപ്തിപ്പെടുത്തുന്ന അവിച്ഛിന്ന ഫലനങ്ങള് (continuous functions) ആണെങ്കില് R-പ്രദേശത്ത് | എന്നിവയെ കോഷി-റീമാന് സമവാക്യങ്ങള് (Cauchy-Riemann equations) എന്നു പറയുന്നു. ഇതില് പെടുന്ന ആംശികവ്യുത്പന്നങ്ങള് (partial derivatives), കോഷി-റീമാന് സമവാക്യങ്ങളെ തൃപ്തിപ്പെടുത്തുന്ന അവിച്ഛിന്ന ഫലനങ്ങള് (continuous functions) ആണെങ്കില് R-പ്രദേശത്ത് | ||
| വരി 26: | വരി 23: | ||
എന്ന ഫലനം വിശ്ളേഷകമായിരിക്കും. | എന്ന ഫലനം വിശ്ളേഷകമായിരിക്കും. | ||
| + | '''ഘാതശ്രേണി''' (Power Series). Σ<sup>∞</sup> എന്ന ഘാതശ്രേണി, |z-a|യുടെ മൂല്യം pഎന്നൊരു വാസ്തവിക സംഖ്യയില് കുറഞ്ഞിരിക്കുമ്പോള്, അഭികേന്ദ്രസരണവും (convergent) കൂടുതലായിരിക്കുമ്പോള് അപകേന്ദ്രസരണവും (divergent) ആണെങ്കില് p, ആ ശ്രേണിയുടെ അഭികേന്ദ്രസരണ വ്യാസാര്ധം (radius of convergence) ആകുന്നു. തുല്യമായിരിക്കുമ്പോള് z-ബിന്ദുക്കളുടെ ബിന്ദുപഥം (locus) വൃത്തമാണ്. ഇതാണ് ശ്രേണിയുടെ അഭികേന്ദ്രസരണവൃത്തം (circle of convergence). ഈ വൃത്തത്തിന്മേലുള്ള ബിന്ദുക്കളില്, ശ്രേണി അഭികേന്ദ്രസരണമോ അപകേന്ദ്രസരണമോ ആകാം. p-യുടെ മൂല്യം കണ്ടുപിടിക്കാന് | ||
| - | + | 1/p =സീമ |an|<sup>1/n</sup> | |
| - | + | ||
| - | + | ||
എന്ന സമവാക്യം ഉപയോഗിക്കുന്നു (നോ: അങ്കനങ്ങള്, ഗണിത) ഈ വൃത്തത്തിനുള്ളില് ഘാതശ്രേണിയുടെ സങ്കലനഫലനം (sum function) f(z) ഒരു വിശ്ളേഷകഫലനമായിരിക്കും. | എന്ന സമവാക്യം ഉപയോഗിക്കുന്നു (നോ: അങ്കനങ്ങള്, ഗണിത) ഈ വൃത്തത്തിനുള്ളില് ഘാതശ്രേണിയുടെ സങ്കലനഫലനം (sum function) f(z) ഒരു വിശ്ളേഷകഫലനമായിരിക്കും. | ||
| - | |||
'''കോഷി സിദ്ധാന്തം''' (Cauchy Theory). വിശ്ളേഷകഫലനങ്ങളുടെ സവിശേഷതകളില് പലതും തെളിയിക്കുന്നത്, സമ്മിശ്ര സമാകലം ഉപയോഗിച്ചാണ്. പരിമേയമായ (finite) നിഷ്കോണചാപങ്ങ(smooth arcs)ളുടെ അവിച്ഛിന്ന ശൃംഖലയ്ക്ക് രൂപരേഖ (contour) എന്നു പറയുന്നു. | '''കോഷി സിദ്ധാന്തം''' (Cauchy Theory). വിശ്ളേഷകഫലനങ്ങളുടെ സവിശേഷതകളില് പലതും തെളിയിക്കുന്നത്, സമ്മിശ്ര സമാകലം ഉപയോഗിച്ചാണ്. പരിമേയമായ (finite) നിഷ്കോണചാപങ്ങ(smooth arcs)ളുടെ അവിച്ഛിന്ന ശൃംഖലയ്ക്ക് രൂപരേഖ (contour) എന്നു പറയുന്നു. | ||
| - | x= | + | x=ø;(t) ; y= ψ(t) |
| - | + | ||
| - | + | ||
| + | a≤t≤b എന്നിവ c എന്ന രൂപരേഖയെ നിര്വചിക്കുന്നു. ഇവിടെ ø(t), ψ(t) എന്നീ ഫലനങ്ങള് എന്ന വാസ്തവിക പ്രാചല(real parameter)ത്തിന്റെ ഭാഗിക-അവിച്ഛിന്ന ഫലനമാണ് (piecewise continuous function). c എന്ന രൂപരേഖയില് f(z) ഭാഗിക-അവിച്ഛിന്നഫലനമാണെന്നു കരുതുക. f(z)-ന്റെ, c-യിലെ രൂപരേഖാസമാകലം (contour integral) നിര്വചിക്കപ്പെടുന്നതിങ്ങനെയാണ്: | ||
| + | [[Image:p485d.png]] | ||
കോഷി-ഗൂര്ഷാപ്രമേയമനുസരിച്ച്, c എന്ന സംവൃത രൂപരേഖയിലും അതിനകത്തും f(z)വിശ്ളേഷകമാണെങ്കില് | കോഷി-ഗൂര്ഷാപ്രമേയമനുസരിച്ച്, c എന്ന സംവൃത രൂപരേഖയിലും അതിനകത്തും f(z)വിശ്ളേഷകമാണെങ്കില് | ||
| - | + | ∫<sub>c</sub> f(z)dz = 0 | |
| - | f(z)dz = 0 | + | |
വിശ്ളേഷകഫലന സിദ്ധാന്തത്തിലെ പലനിഗമനങ്ങള്ക്കും അടിസ്ഥാനം ഈ പ്രമേയമാണ്. c എന്ന രൂപരേഖയില് f(z)-ന്റെ രൂപരേഖാസമാകലമാണ് | വിശ്ളേഷകഫലന സിദ്ധാന്തത്തിലെ പലനിഗമനങ്ങള്ക്കും അടിസ്ഥാനം ഈ പ്രമേയമാണ്. c എന്ന രൂപരേഖയില് f(z)-ന്റെ രൂപരേഖാസമാകലമാണ് | ||
| - | + | [[Image:p486a.png]] | |
വിശ്ളേഷകഫലനത്തിന്റെ വ്യുത്പന്നങ്ങളും വിശ്ളേഷകമായിരിക്കും. | വിശ്ളേഷകഫലനത്തിന്റെ വ്യുത്പന്നങ്ങളും വിശ്ളേഷകമായിരിക്കും. | ||
| - | |||
'''വിശ്ളേഷകഫലനത്തിന്റെ ഘാതശ്രേണീവികാസം''' (Power series development of an Analytic function). സമ്മിശ്രതലത്തില് f(z) വിശ്ളേഷകമാകാതിരിക്കുന്ന ബിന്ദുവിനെയാണ് വിചിത്രത (singularity) എന്നു പറയുന്നത്. a എന്ന ബിന്ദുവിന്റെ 'സാമീപ്യ'ത്തില് f(z)-നു വേറെ വിചിത്രതകളില്ലെങ്കില് z = a-യെ f(z)-ന്റെ ഏകാന്തവിചിത്രത (isolated singularity) എന്നു പറയുന്നു. | '''വിശ്ളേഷകഫലനത്തിന്റെ ഘാതശ്രേണീവികാസം''' (Power series development of an Analytic function). സമ്മിശ്രതലത്തില് f(z) വിശ്ളേഷകമാകാതിരിക്കുന്ന ബിന്ദുവിനെയാണ് വിചിത്രത (singularity) എന്നു പറയുന്നത്. a എന്ന ബിന്ദുവിന്റെ 'സാമീപ്യ'ത്തില് f(z)-നു വേറെ വിചിത്രതകളില്ലെങ്കില് z = a-യെ f(z)-ന്റെ ഏകാന്തവിചിത്രത (isolated singularity) എന്നു പറയുന്നു. | ||
| + | |z-a|≤ r1, |z-a|≤r2 എന്നിവ രണ്ടു വൃത്തങ്ങളാണ്. കേന്ദ്രം x = a. r<sub>1</sub>നും r<sub>2</sub>നുമിടയ്ക്കുള്ള പ്രദേശം (c) വലയാകാരം (ring shaped) ആയിരിക്കും. c-യില് f(z) വിശ്ളേഷകമാണെങ്കില്, | ||
| + | f(z) = Σ<sup>∞</sup><sub>n=0</sup> | ||
| + | a<sub>n</sub>(z-a)<sup>n</sup> + &Sigma<sup>∞</sup> | ||
| + | <sub>n=1</sub>b<sub>n</sub>(z-a)<sup>-n</sup> | ||
| - | |||
| - | + | ഇവിടെ a<sub>n</sub>, b<sub>n</sub> എന്നിവ കണക്കാക്കാന് കഴിയും. b<sub>1</sub>, b<sub>2</sub> എന്നു തുടങ്ങിയവയെല്ലാം പൂജ്യം ആണെങ്കില്, z = a ഒരു അപനേയ വിചിത്രത (removable singularity) എന്നും, f(z)-ന്റെ ശ്രേണിയിലെ രണ്ടാംഭാഗം (മുഖ്യഭാഗം) ഒരു അനന്തശ്രേണിയാണെങ്കില് | |
| - | + | z = a ഒരു അനിവാര്യവിചിത്രത (essential singularity) എന്നും മുഖ്യ ഭാഗത്തില് പദങ്ങളുടെ എണ്ണം പരിമേയം (finite) ആണെങ്കില് x = a ഒരു ധ്രുവം (pole) എന്നും പറയുന്നു. z = a എന്ന ബിന്ദുവിലുള്ള f(z)-ന്റെ പരിശിഷ്ടം ആണ് b<sub>1</sub>. | |
| - | ഇവിടെ | + | |
| - | z = a ഒരു അനിവാര്യവിചിത്രത (essential singularity) എന്നും മുഖ്യ ഭാഗത്തില് പദങ്ങളുടെ എണ്ണം പരിമേയം (finite) ആണെങ്കില് x = a ഒരു ധ്രുവം (pole) എന്നും പറയുന്നു. z = a എന്ന ബിന്ദുവിലുള്ള f(z)-ന്റെ പരിശിഷ്ടം ആണ് | + | |
'''പരിശിഷ്ടപ്രമേയം''' (Residue Theorem). | '''പരിശിഷ്ടപ്രമേയം''' (Residue Theorem). | ||
| + | ∫<sub>c</sub>f(z)d(z) = 0 | ||
ആകണമെങ്കില് രൂപരേഖ (c)-യിലും അതിനകത്തും f(z) വിശ്ളേഷകമായിരിക്കണം. എന്നാല് c-യിലും c-യുടെ അകത്തു പരിമേയ വിചിത്രതകളൊഴിച്ചുള്ള (finite singularities) ബിന്ദുക്കളിലും f(z) വിശ്ളേഷകമാണെങ്കില്, | ആകണമെങ്കില് രൂപരേഖ (c)-യിലും അതിനകത്തും f(z) വിശ്ളേഷകമായിരിക്കണം. എന്നാല് c-യിലും c-യുടെ അകത്തു പരിമേയ വിചിത്രതകളൊഴിച്ചുള്ള (finite singularities) ബിന്ദുക്കളിലും f(z) വിശ്ളേഷകമാണെങ്കില്, | ||
| + | [[Image:p486c.png]] | ||
| - | + | ഇതില് R<sub>i</sub> രൂപരേഖയുടെ അകത്തുള്ള z = z<sub>i</sub> എന്ന വിചിത്രതയിലെ പരിശിഷ്ടം കുറിക്കുന്നു. ഇതാണ് കോഷിയുടെ പരിശിഷ്ടപ്രമേയം. ഈ പ്രമേയം ചില നിശ്ചിതസമാകലങ്ങളുടെ മൂല്യം നിര്ണയിക്കാനുപയോഗിക്കാറുണ്ട്. കൂടാതെ എലിപ്റ്റികഫലനസിദ്ധാന്ത(elliptic function theory)ത്തില് ഈ പ്രമേയത്തിനു വളരെ പ്രാധാന്യമുണ്ട്. നോ: അനാലിസിസ്, അവകലനം സമാകലനം, ഗണസിദ്ധാന്തം, ഫലനം (ഗണിതം), സമ്മിശ്രവിശ്ളേഷണം | |
| - | ഇതില് | + | |
(കെ. ജയചന്ദ്രന്) | (കെ. ജയചന്ദ്രന്) | ||
| + | [[Category:ഗണിതം]] | ||
Current revision as of 11:57, 8 ഏപ്രില് 2008
അനലിറ്റിക് ഫങ്ഷന്
Analytic function
ഗണിതശാസ്ത്രശാഖയായ സമ്മിശ്രവിശ്ളേഷണ(complex analysis)ത്തിലെ ഗണിതപ്രാധാന്യമുള്ള ഫലനം. വിശ്ളേഷകഫലനം, ഹോളൊമോര്ഫികഫലനം (Holomorphic function), നിയമിതഫലനം (Regular function) എന്നീ പേരുകളിലും ഇതറിയപ്പെടുന്നു.
ചരിത്രം. വിശ്ളേഷണഫലന സിദ്ധാന്ത(അനലിറ്റിക് ഫങ്ഷന്)ത്തിന്റെ ആദ്യകാല ഗവേഷകര് കോഷി, റീമാന്, വെയര്സ്റ്റ്രോസ് എന്നിവരാണ്. വ്യുത്പന്നം (derivative) അഥവാ അവകലജഗുണാങ്കം (differential coefficient) ഉള്ള ഫലനങ്ങളാണ് കോഷിസിദ്ധാന്തത്തിന്റെ അടിസ്ഥാനം. സമ്മിശ്രസമാകല(complex integration)ത്തിന്റെ ഉപാധിയിലൂടെയാണ് 1814-ല് കോഷി ഈ സിദ്ധാന്തത്തിനു രൂപംകൊടുത്തത്. ഗണിതശാസ്ത്രജ്ഞനായ ഗൂര്ഷ (Goursat) 1900-ത്തില് അതിനെ നവീകരിച്ചു. അനലിറ്റിക് ഫങ്ഷന്റെ ജ്യാമിതീയ പ്രാധാന്യമാണ് റീമാന് പഠന വിധേയമാക്കിയത്. ഘാതശ്രേണി (power series) ആണ് വെയര്സ്റ്റ്രോസ്തത്ത്വത്തിന്റെ അടിസ്ഥാനം. വിശ്ളേഷക-അവിച്ഛിന്നത(analytic continuum)യുടെ താത്ത്വിക വശങ്ങളിലാണ് വെയര്സ്റ്റ്രോസ് ശ്രദ്ധിച്ചത്.
സമ്മിശ്രചരങ്ങളുടെ ഫലനം (function of complex variables). R, S എന്നീ രണ്ടു സമ്മിശ്ര സംഖ്യാഗണങ്ങള് (sets of complex numbers) ആദ്യത്തേതിലെ ഓരോ അംഗ(z)ത്തിനും രണ്ടാമത്തേതിലെ ഒരംഗത്തെ നിര്ദേശിക്കുന്ന നിയമം (f) ആണ്, ഇവിടെ 'ഫലനം' എന്നതുകൊണ്ടു സൂചിപ്പിക്കപ്പെടുന്നത്. ഫലനത്തിന്റെ ഡൊമെയിന് (domain) R-ഉം റെയിഞ്ച് (range) S-ഉം ആണ്. ഡൊമെയിന് ഒരു വിവൃത-ബന്ധിതം (open connected) ആയിരിക്കും. ഇത്തരം R-ഗണത്തെ റീജിയന് (region) എന്നു പറയുന്നു. R-റീജിയനില് f(z) നിര്വചിക്കപ്പെട്ടിരിക്കുന്നു; Z എന്ന സമ്മിശ്രചരം Z0-നോടു സമീപിക്കുമ്പോള്,
എന്ന അംശബന്ധം (ratio) ഒരു പരിമേയ സീമ(finite limit)യോടടുക്കുന്നു; എങ്കില് R-ലെ Z0 ബിന്ദുവില് f(Z) അവകലനീയം (differentiable) ആണ് എന്നു പറയുന്നു. Z0-ലേക്കു Z അടുക്കുന്ന രൂപരേഖ (contour) ഏതു തന്നെ ആയാലും f(Z) - f(Z0)/Z-Z0-ന്റെ സീമയ്ക്കു മാറ്റമുണ്ടാകാന് പാടില്ല. ഈ സീമയെ f(Z)-ന്റെ Z0 എന്ന ബിന്ദുവിലെ വ്യുത്പന്നം (derivative) f'(Z) എന്നു പറയുന്നു. R-ലുള്ള എല്ലാ ബിന്ദുക്കളിലും f'(Z)-നു അസ്തിത്വമുണ്ടെങ്കില് f(Z) എന്ന ഫലനം R എന്ന പ്രദേശത്തു വിശ്ളേഷകമാണെന്നു പറയുന്നു. n ഒരു ധനാത്മകപൂര്ണസംഖ്യ ആണെങ്കില് Zn പരിമിത (സമ്മിശ്ര) തലത്തില് വിശ്ളേഷകമാണ്. അതുകൊണ്ട് എല്ലാ ബഹുപദങ്ങളും (polynominals) വിശ്ളേഷകഫലനങ്ങളാണ്.
f(Z) = u(x,y) + i v(x, y) സമ്മിശ്രതലത്തിലെ R-റീജിയനില് വിശ്ളേഷകമാണെന്നു കരുതിയാല് u(x,y), v(x, y) എന്നീ വാസ്തവികമൂല്യ ഫലനങ്ങള് (real valued functions) താഴെ പറയുന്ന സമവാക്യങ്ങള്ക്ക് അനുസൃതമായിരിക്കുമെന്നു കാണാം.
എന്നിവയെ കോഷി-റീമാന് സമവാക്യങ്ങള് (Cauchy-Riemann equations) എന്നു പറയുന്നു. ഇതില് പെടുന്ന ആംശികവ്യുത്പന്നങ്ങള് (partial derivatives), കോഷി-റീമാന് സമവാക്യങ്ങളെ തൃപ്തിപ്പെടുത്തുന്ന അവിച്ഛിന്ന ഫലനങ്ങള് (continuous functions) ആണെങ്കില് R-പ്രദേശത്ത്
f(z) = u(x,y) + iv (x,y)
എന്ന ഫലനം വിശ്ളേഷകമായിരിക്കും.
ഘാതശ്രേണി (Power Series). Σ∞ എന്ന ഘാതശ്രേണി, |z-a|യുടെ മൂല്യം pഎന്നൊരു വാസ്തവിക സംഖ്യയില് കുറഞ്ഞിരിക്കുമ്പോള്, അഭികേന്ദ്രസരണവും (convergent) കൂടുതലായിരിക്കുമ്പോള് അപകേന്ദ്രസരണവും (divergent) ആണെങ്കില് p, ആ ശ്രേണിയുടെ അഭികേന്ദ്രസരണ വ്യാസാര്ധം (radius of convergence) ആകുന്നു. തുല്യമായിരിക്കുമ്പോള് z-ബിന്ദുക്കളുടെ ബിന്ദുപഥം (locus) വൃത്തമാണ്. ഇതാണ് ശ്രേണിയുടെ അഭികേന്ദ്രസരണവൃത്തം (circle of convergence). ഈ വൃത്തത്തിന്മേലുള്ള ബിന്ദുക്കളില്, ശ്രേണി അഭികേന്ദ്രസരണമോ അപകേന്ദ്രസരണമോ ആകാം. p-യുടെ മൂല്യം കണ്ടുപിടിക്കാന്
1/p =സീമ |an|1/n
എന്ന സമവാക്യം ഉപയോഗിക്കുന്നു (നോ: അങ്കനങ്ങള്, ഗണിത) ഈ വൃത്തത്തിനുള്ളില് ഘാതശ്രേണിയുടെ സങ്കലനഫലനം (sum function) f(z) ഒരു വിശ്ളേഷകഫലനമായിരിക്കും.
കോഷി സിദ്ധാന്തം (Cauchy Theory). വിശ്ളേഷകഫലനങ്ങളുടെ സവിശേഷതകളില് പലതും തെളിയിക്കുന്നത്, സമ്മിശ്ര സമാകലം ഉപയോഗിച്ചാണ്. പരിമേയമായ (finite) നിഷ്കോണചാപങ്ങ(smooth arcs)ളുടെ അവിച്ഛിന്ന ശൃംഖലയ്ക്ക് രൂപരേഖ (contour) എന്നു പറയുന്നു.
x=ø;(t) ; y= ψ(t)
a≤t≤b എന്നിവ c എന്ന രൂപരേഖയെ നിര്വചിക്കുന്നു. ഇവിടെ ø(t), ψ(t) എന്നീ ഫലനങ്ങള് എന്ന വാസ്തവിക പ്രാചല(real parameter)ത്തിന്റെ ഭാഗിക-അവിച്ഛിന്ന ഫലനമാണ് (piecewise continuous function). c എന്ന രൂപരേഖയില് f(z) ഭാഗിക-അവിച്ഛിന്നഫലനമാണെന്നു കരുതുക. f(z)-ന്റെ, c-യിലെ രൂപരേഖാസമാകലം (contour integral) നിര്വചിക്കപ്പെടുന്നതിങ്ങനെയാണ്:
കോഷി-ഗൂര്ഷാപ്രമേയമനുസരിച്ച്, c എന്ന സംവൃത രൂപരേഖയിലും അതിനകത്തും f(z)വിശ്ളേഷകമാണെങ്കില്
∫c f(z)dz = 0 വിശ്ളേഷകഫലന സിദ്ധാന്തത്തിലെ പലനിഗമനങ്ങള്ക്കും അടിസ്ഥാനം ഈ പ്രമേയമാണ്. c എന്ന രൂപരേഖയില് f(z)-ന്റെ രൂപരേഖാസമാകലമാണ്
വിശ്ളേഷകഫലനത്തിന്റെ വ്യുത്പന്നങ്ങളും വിശ്ളേഷകമായിരിക്കും.
വിശ്ളേഷകഫലനത്തിന്റെ ഘാതശ്രേണീവികാസം (Power series development of an Analytic function). സമ്മിശ്രതലത്തില് f(z) വിശ്ളേഷകമാകാതിരിക്കുന്ന ബിന്ദുവിനെയാണ് വിചിത്രത (singularity) എന്നു പറയുന്നത്. a എന്ന ബിന്ദുവിന്റെ 'സാമീപ്യ'ത്തില് f(z)-നു വേറെ വിചിത്രതകളില്ലെങ്കില് z = a-യെ f(z)-ന്റെ ഏകാന്തവിചിത്രത (isolated singularity) എന്നു പറയുന്നു.
|z-a|≤ r1, |z-a|≤r2 എന്നിവ രണ്ടു വൃത്തങ്ങളാണ്. കേന്ദ്രം x = a. r1നും r2നുമിടയ്ക്കുള്ള പ്രദേശം (c) വലയാകാരം (ring shaped) ആയിരിക്കും. c-യില് f(z) വിശ്ളേഷകമാണെങ്കില്, f(z) = Σ∞n=0</sup> an(z-a)n + &Sigma∞ n=1bn(z-a)-n
ഇവിടെ an, bn എന്നിവ കണക്കാക്കാന് കഴിയും. b1, b2 എന്നു തുടങ്ങിയവയെല്ലാം പൂജ്യം ആണെങ്കില്, z = a ഒരു അപനേയ വിചിത്രത (removable singularity) എന്നും, f(z)-ന്റെ ശ്രേണിയിലെ രണ്ടാംഭാഗം (മുഖ്യഭാഗം) ഒരു അനന്തശ്രേണിയാണെങ്കില്
z = a ഒരു അനിവാര്യവിചിത്രത (essential singularity) എന്നും മുഖ്യ ഭാഗത്തില് പദങ്ങളുടെ എണ്ണം പരിമേയം (finite) ആണെങ്കില് x = a ഒരു ധ്രുവം (pole) എന്നും പറയുന്നു. z = a എന്ന ബിന്ദുവിലുള്ള f(z)-ന്റെ പരിശിഷ്ടം ആണ് b1.
പരിശിഷ്ടപ്രമേയം (Residue Theorem).
∫cf(z)d(z) = 0
ആകണമെങ്കില് രൂപരേഖ (c)-യിലും അതിനകത്തും f(z) വിശ്ളേഷകമായിരിക്കണം. എന്നാല് c-യിലും c-യുടെ അകത്തു പരിമേയ വിചിത്രതകളൊഴിച്ചുള്ള (finite singularities) ബിന്ദുക്കളിലും f(z) വിശ്ളേഷകമാണെങ്കില്,
ഇതില് Ri രൂപരേഖയുടെ അകത്തുള്ള z = zi എന്ന വിചിത്രതയിലെ പരിശിഷ്ടം കുറിക്കുന്നു. ഇതാണ് കോഷിയുടെ പരിശിഷ്ടപ്രമേയം. ഈ പ്രമേയം ചില നിശ്ചിതസമാകലങ്ങളുടെ മൂല്യം നിര്ണയിക്കാനുപയോഗിക്കാറുണ്ട്. കൂടാതെ എലിപ്റ്റികഫലനസിദ്ധാന്ത(elliptic function theory)ത്തില് ഈ പ്രമേയത്തിനു വളരെ പ്രാധാന്യമുണ്ട്. നോ: അനാലിസിസ്, അവകലനം സമാകലനം, ഗണസിദ്ധാന്തം, ഫലനം (ഗണിതം), സമ്മിശ്രവിശ്ളേഷണം
(കെ. ജയചന്ദ്രന്)