This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ദ്രവ ബലതന്ത്രം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
| (ഇടക്കുള്ള 7 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 55: | വരി 55: | ||
12. '''വിക്ഷുബ്ധ പ്രവാഹം''' (turbulent flow). തുടര്ച്ചയായ ചുഴികളോടെയുള്ള പ്രവാഹം. ഇതില്, ദ്രവകണങ്ങള് നിരന്തരമായി കൂടിക്കലരുന്നതിനാല് ഒരു നിശ്ചിത കണത്തിന്റെ കൃത്യമായ സ്ഥാനനിര്ണയനമോ പഥനിര്ണയനമോ സാധ്യമല്ല. അതിനാല് ഇത്തരം പ്രവാഹത്തെ സാംഖ്യികീയമായി (statistically) മാത്രം പരിഗണിക്കുന്നു. | 12. '''വിക്ഷുബ്ധ പ്രവാഹം''' (turbulent flow). തുടര്ച്ചയായ ചുഴികളോടെയുള്ള പ്രവാഹം. ഇതില്, ദ്രവകണങ്ങള് നിരന്തരമായി കൂടിക്കലരുന്നതിനാല് ഒരു നിശ്ചിത കണത്തിന്റെ കൃത്യമായ സ്ഥാനനിര്ണയനമോ പഥനിര്ണയനമോ സാധ്യമല്ല. അതിനാല് ഇത്തരം പ്രവാഹത്തെ സാംഖ്യികീയമായി (statistically) മാത്രം പരിഗണിക്കുന്നു. | ||
| - | [[Image:p580a.png| | + | [[Image:p580a.png|300px|left]] |
ഇവയില് ധാരാരേഖീയവും വിക്ഷുബ്ധവുമായ പ്രവാഹങ്ങളെയാണ് പ്രധാനമായും വേര്തിരിച്ചു പഠനവിധേയമാക്കുന്നത്. നെവിയര്-സ്റ്റോക്സ് സമീകരണങ്ങള് (Navier-Stokes equations) വഴി ധാരാരേഖീ പ്രവാഹത്തെ വിശദീകരിക്കാന് കഴിയുന്നു. വിക്ഷുബ്ധ പ്രവാഹത്തെക്കുറിച്ചുള്ള സമീകരണങ്ങള് കൂടുതല് സങ്കീര്ണങ്ങളാണ്. സാധാരണ ഒഴുക്കിന്റെ പ്രവേഗം വര്ധിക്കുമ്പോള് അത് അസ്ഥിരമായി മാറുകയും ധാരാരേഖീയത്തില്നിന്ന് വിക്ഷുബ്ധ അവസ്ഥയിലേക്കു വ്യതിയാനപ്പെടുകയും ചെയ്യുന്നു. ദ്രവകണങ്ങള് വളരെ അനിയമിത പഥങ്ങളിലൂടെ ഒഴുകാന് തുടങ്ങുകയും ചുഴികള് (eddies) രൂപപ്പെടുകയും ചെയ്യും. ദ്രവം ധാരാരേഖീ പ്രവാഹത്തില്നിന്ന് വിക്ഷുബ്ധ പ്രവാഹത്തിലേക്കു കടക്കുന്ന പ്രവേഗമൂല്യത്തെ ക്രാന്തിക പ്രവേഗം (critical velocity) എന്നു വിളിക്കുന്നു. ദ്രാവകങ്ങളുടെ കാര്യത്തില് രണ്ടിനം പ്രവാഹങ്ങളുടെയും പ്രധാന ലക്ഷണങ്ങള് താഴെ കൊടുക്കുന്നു. | ഇവയില് ധാരാരേഖീയവും വിക്ഷുബ്ധവുമായ പ്രവാഹങ്ങളെയാണ് പ്രധാനമായും വേര്തിരിച്ചു പഠനവിധേയമാക്കുന്നത്. നെവിയര്-സ്റ്റോക്സ് സമീകരണങ്ങള് (Navier-Stokes equations) വഴി ധാരാരേഖീ പ്രവാഹത്തെ വിശദീകരിക്കാന് കഴിയുന്നു. വിക്ഷുബ്ധ പ്രവാഹത്തെക്കുറിച്ചുള്ള സമീകരണങ്ങള് കൂടുതല് സങ്കീര്ണങ്ങളാണ്. സാധാരണ ഒഴുക്കിന്റെ പ്രവേഗം വര്ധിക്കുമ്പോള് അത് അസ്ഥിരമായി മാറുകയും ധാരാരേഖീയത്തില്നിന്ന് വിക്ഷുബ്ധ അവസ്ഥയിലേക്കു വ്യതിയാനപ്പെടുകയും ചെയ്യുന്നു. ദ്രവകണങ്ങള് വളരെ അനിയമിത പഥങ്ങളിലൂടെ ഒഴുകാന് തുടങ്ങുകയും ചുഴികള് (eddies) രൂപപ്പെടുകയും ചെയ്യും. ദ്രവം ധാരാരേഖീ പ്രവാഹത്തില്നിന്ന് വിക്ഷുബ്ധ പ്രവാഹത്തിലേക്കു കടക്കുന്ന പ്രവേഗമൂല്യത്തെ ക്രാന്തിക പ്രവേഗം (critical velocity) എന്നു വിളിക്കുന്നു. ദ്രാവകങ്ങളുടെ കാര്യത്തില് രണ്ടിനം പ്രവാഹങ്ങളുടെയും പ്രധാന ലക്ഷണങ്ങള് താഴെ കൊടുക്കുന്നു. | ||
<gallery> | <gallery> | ||
| വരി 64: | വരി 64: | ||
</gallery> | </gallery> | ||
പൊതുവേ, ഒരു പ്രവാഹം ധാരാരേഖീയമാണോ വിക്ഷുബ്ധമാണോ എന്ന് അതിന്റെ റെയ്നോള്ഡ്സ് നമ്പര് (Re) അടിസ്ഥാനമാക്കി നിര്ണയിക്കാനാകും. Re=ρLV/μഎന്ന സമീകരണം വഴി റെയ്നോള്ഡ്സ് നമ്പര് കണ്ടുപിടിക്കാം. ഇവിടെ ρ സാന്ദ്രതയെയും L നീളത്തെയും (ജ്യാമിതീയവും ലാക്ഷണികവുമായ നീളം) V പ്രവേഗത്തെയും μ ശ്യാനതയുടെ ഗുണാങ്കത്തെയും (coefficient of viscosity) പ്രതിനിധാനം ചെയ്യുന്നു. | പൊതുവേ, ഒരു പ്രവാഹം ധാരാരേഖീയമാണോ വിക്ഷുബ്ധമാണോ എന്ന് അതിന്റെ റെയ്നോള്ഡ്സ് നമ്പര് (Re) അടിസ്ഥാനമാക്കി നിര്ണയിക്കാനാകും. Re=ρLV/μഎന്ന സമീകരണം വഴി റെയ്നോള്ഡ്സ് നമ്പര് കണ്ടുപിടിക്കാം. ഇവിടെ ρ സാന്ദ്രതയെയും L നീളത്തെയും (ജ്യാമിതീയവും ലാക്ഷണികവുമായ നീളം) V പ്രവേഗത്തെയും μ ശ്യാനതയുടെ ഗുണാങ്കത്തെയും (coefficient of viscosity) പ്രതിനിധാനം ചെയ്യുന്നു. | ||
| - | + | <gallery> | |
| + | Image:1955 SUPERSONIC FLOW-7.jpg|അധിധ്വനിക പ്രവാഹം | ||
| + | Image:around a Subsonic Airfoil NAC.-6.png|അവധ്വനിക പ്രവാഹം | ||
| + | Image:1955 steady flow past a circular cylinder-9.jpg|സ്ഥിര പ്രവാഹം (സിലിണ്ടറിനു ചുറ്റും) | ||
| + | Image:1955 unsteady flow-8.png|അസ്ഥിര പ്രവാഹം (സിലിണ്ടറിനു ചുറ്റും) | ||
| + | Image:uniform flow (steady) in rain trench-10.png|ഏകസമാന പ്രവാഹം | ||
| + | Image:non uniiform flow-11.png|ഏകസമാനമല്ലാത്ത പ്രവാഹം | ||
| + | </gallery> | ||
Re മാനങ്ങളില്ലാത്ത (dimensionless) ഒരു ശുദ്ധ സംഖ്യ ആണ്. Re യുടെ മൂല്യം കുറഞ്ഞിരുന്നാല് പ്രവാഹം ധാരാരേഖീയവും, ക്രാന്തികമൂല്യം കടന്നുകഴിഞ്ഞാല് (Re > Re<sub>c</sub>)അത് വിക്ഷുബ്ധവുമായി മാറുന്നു.ρ,L,μ എന്നിവ സ്ഥിരമായിരുന്നാല് Re എന്നത് V യ്ക്ക് ആനുപാതികമായിമാത്രം മാറുന്നു എന്നു കാണാം. ഉരുണ്ടതും മിനുസമുള്ളതുമായ പൈപ്പുകളിലൂടെയുള്ള പ്രവാഹത്തില് Re<sub>c</sub>യുടെ മൂല്യം ഏകദേശം 2,000 ആയിരിക്കും. ഇവിടെ L പൈപ്പിന്റെ വ്യാസത്തിനു തുല്യമായ നീളമാണ്. മറിച്ച്, പരന്ന പ്രതലത്തിനു മുകളിലൂടെയുള്ള പ്രവാഹത്തില് Re<sub>c</sub> ഏകദേശം 5,00,000 ആണ്. | Re മാനങ്ങളില്ലാത്ത (dimensionless) ഒരു ശുദ്ധ സംഖ്യ ആണ്. Re യുടെ മൂല്യം കുറഞ്ഞിരുന്നാല് പ്രവാഹം ധാരാരേഖീയവും, ക്രാന്തികമൂല്യം കടന്നുകഴിഞ്ഞാല് (Re > Re<sub>c</sub>)അത് വിക്ഷുബ്ധവുമായി മാറുന്നു.ρ,L,μ എന്നിവ സ്ഥിരമായിരുന്നാല് Re എന്നത് V യ്ക്ക് ആനുപാതികമായിമാത്രം മാറുന്നു എന്നു കാണാം. ഉരുണ്ടതും മിനുസമുള്ളതുമായ പൈപ്പുകളിലൂടെയുള്ള പ്രവാഹത്തില് Re<sub>c</sub>യുടെ മൂല്യം ഏകദേശം 2,000 ആയിരിക്കും. ഇവിടെ L പൈപ്പിന്റെ വ്യാസത്തിനു തുല്യമായ നീളമാണ്. മറിച്ച്, പരന്ന പ്രതലത്തിനു മുകളിലൂടെയുള്ള പ്രവാഹത്തില് Re<sub>c</sub> ഏകദേശം 5,00,000 ആണ്. | ||
| - | + | <gallery Caption="രേഖീയവും വിക്ഷുബ്ധവുമായ പ്രവാഹങ്ങള്"> | |
| + | Image:san_tempabc.png | ||
| + | Image:laminar New-12 a.jpg|രേഖീയം | ||
| + | Image:laminar New-12b.jpg|വിക്ഷുബ്ധം | ||
| + | </gallery> | ||
പ്രവാഹം ഏതു തരത്തിലുള്ളതായാലും ശ്യാനത മൂലം യാന്ത്രികോര്ജം താപോര്ജമായി രൂപാന്തരപ്പെടും. പൈപ്പുകളിലൂടെയും മറ്റു വാഹികകളിലൂടെയുമുള്ള പ്രവാഹവുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യുമ്പോള് ഈ പ്രക്രിയകൂടി പ്രത്യേകം പരിഗണിക്കേണ്ടതുണ്ട്. | പ്രവാഹം ഏതു തരത്തിലുള്ളതായാലും ശ്യാനത മൂലം യാന്ത്രികോര്ജം താപോര്ജമായി രൂപാന്തരപ്പെടും. പൈപ്പുകളിലൂടെയും മറ്റു വാഹികകളിലൂടെയുമുള്ള പ്രവാഹവുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യുമ്പോള് ഈ പ്രക്രിയകൂടി പ്രത്യേകം പരിഗണിക്കേണ്ടതുണ്ട്. | ||
| - | + | <gallery> | |
| + | Image:1955Turbulence in the tip vortex from an airplane wing.jpg|വിക്ഷുബ്ധ പ്രവാഹം (വിമാനത്തിന്റെ പുറകില്) | ||
| + | Image:1955Laminar and turbulent water flow over the hull of a subm.jpg|രേഖീയവും വിക്ഷുബ്ധവും (അന്തര്വാഹിനിയുടെ സഞ്ചാരം) | ||
| + | </gallery> | ||
വിക്ഷുബ്ധത കഴിയുന്നത്ര കുറയ്ക്കത്തക്ക രീതിയിലാണ് വിമാനങ്ങളും മത്സരഓട്ടത്തിനുള്ള റേസിങ് കാറുകളും മറ്റും രൂപകല്പന ചെയ്യുന്നത്. എന്നാല് വിക്ഷുബ്ധത അഭിലഷണീയമായിത്തീരുന്ന സന്ദര്ഭങ്ങളും നിത്യജീവിതത്തിലുണ്ട്. ഇംഗ്ലണ്ടിനടുത്തുകൂടി ഒഴുകുന്ന ഉഷ്ണജലപ്രവാഹമാണ് 'ഗള്ഫ് സ്റ്റ്രീം'. ഇതിലെ ജലത്തിന്റെ ഒഴുക്ക് തീര്ത്തും ധാരാരേഖീയം മാത്രമായിരുന്നുവെങ്കില് ഇംഗ്ലണ്ട് ഇന്നത്തേതിനെക്കാള് കൂടുതല് തണുത്ത പ്രദേശമായി മാറുമായിരുന്നു. ദ്രവകണങ്ങളുടെ കൂടിക്കലരല് വര്ധിപ്പിച്ചുകൊണ്ട് ദ്രവ്യമാനം, സംവേഗം, ഊര്ജം എന്നിവയുടെ സ്ഥാനാന്തരണ നിരക്ക് കൂട്ടുന്നതിനും വിക്ഷുബ്ധത സഹായകമാകുന്നുണ്ട്. ഉദാഹരണമായി അടുക്കളയില് ഉപയോഗിക്കുന്ന മിക്സറില് (മിക്സി) ബ്ലേഡുകള്വഴി ജാറിനുള്ളില് വിക്ഷുബ്ധപ്രവാഹം ഉളവാക്കുകയാണു നാം ചെയ്യുന്നത്. മിക്സറില് മുട്ട ഏകസമാനമായി പതപ്പിച്ചെടുക്കാന് കഴിയുന്നത് ഈ ഗുണവിശേഷത്താലാണ്. | വിക്ഷുബ്ധത കഴിയുന്നത്ര കുറയ്ക്കത്തക്ക രീതിയിലാണ് വിമാനങ്ങളും മത്സരഓട്ടത്തിനുള്ള റേസിങ് കാറുകളും മറ്റും രൂപകല്പന ചെയ്യുന്നത്. എന്നാല് വിക്ഷുബ്ധത അഭിലഷണീയമായിത്തീരുന്ന സന്ദര്ഭങ്ങളും നിത്യജീവിതത്തിലുണ്ട്. ഇംഗ്ലണ്ടിനടുത്തുകൂടി ഒഴുകുന്ന ഉഷ്ണജലപ്രവാഹമാണ് 'ഗള്ഫ് സ്റ്റ്രീം'. ഇതിലെ ജലത്തിന്റെ ഒഴുക്ക് തീര്ത്തും ധാരാരേഖീയം മാത്രമായിരുന്നുവെങ്കില് ഇംഗ്ലണ്ട് ഇന്നത്തേതിനെക്കാള് കൂടുതല് തണുത്ത പ്രദേശമായി മാറുമായിരുന്നു. ദ്രവകണങ്ങളുടെ കൂടിക്കലരല് വര്ധിപ്പിച്ചുകൊണ്ട് ദ്രവ്യമാനം, സംവേഗം, ഊര്ജം എന്നിവയുടെ സ്ഥാനാന്തരണ നിരക്ക് കൂട്ടുന്നതിനും വിക്ഷുബ്ധത സഹായകമാകുന്നുണ്ട്. ഉദാഹരണമായി അടുക്കളയില് ഉപയോഗിക്കുന്ന മിക്സറില് (മിക്സി) ബ്ലേഡുകള്വഴി ജാറിനുള്ളില് വിക്ഷുബ്ധപ്രവാഹം ഉളവാക്കുകയാണു നാം ചെയ്യുന്നത്. മിക്സറില് മുട്ട ഏകസമാനമായി പതപ്പിച്ചെടുക്കാന് കഴിയുന്നത് ഈ ഗുണവിശേഷത്താലാണ്. | ||
ഓയ്ലര് സമീകരണങ്ങളുടെ (Euler equations) നിര്ധാരണങ്ങളാണ് ദ്രവ ബലതന്ത്രത്തില് കൂടുതലായും ഉപയോഗിക്കുന്നത്. വിക്ഷുബ്ധപ്രവാഹങ്ങളുടെ കാര്യത്തില്, പ്രത്യേകിച്ചും റെയ്നോള്ഡ്സ് സംഖ്യ വളരെ കൂടിയിരിക്കുമ്പോള്, ഗണിതനിര്ധാരണം സങ്കീര്ണവും അസാധുവുമായിത്തീരും. അതിവേഗ കമ്പ്യൂട്ടറുകളുടെ സഹായത്തോടെയുള്ള മാതൃകാപഠനങ്ങള് (Simulation studies) ആണ് ഇത്തരം സാഹചര്യങ്ങളില് പ്രയോജനപ്പെടുത്തുന്നത്. പൈപ്പുകള്, പമ്പുകള്, ഡാമുകള്, ടര്ബൈനുകള്, താപപ്രക്രിയാ പ്ലാന്റുകള് എന്നിവിടങ്ങളിലെ പ്രവാഹങ്ങള്; അന്തരീക്ഷത്തിലെയും സമുദ്രത്തിലെയും പ്രവാഹങ്ങള്; എയര്ക്രാഫ്റ്റ്, സ്പേയ്സ് ക്രാഫ്റ്റ് എന്നിവയുടെ ഫ്ലൈറ്റുകള്; പ്ലാസ്മാ പ്രവാഹങ്ങള് എന്നിവയെ വിശദീകരിക്കാന് ഈ സമീകരണങ്ങള് പ്രയോജനപ്പെടുത്തുന്നു. കൂടാതെ ചലനാവസ്ഥയിലുള്ള ഓട്ടോമൊബൈലുകള്, കപ്പലുകള്, തീവണ്ടികള് എന്നിവയ്ക്കും സ്ഥിരമായി നില്ക്കുന്ന പാലങ്ങള്, കെട്ടിടങ്ങള് എന്നിവയ്ക്കും ചുറ്റുമുള്ള ദ്രവപ്രവാഹം കണക്കുകൂട്ടാനും ഇതേ സമീകരണങ്ങള് തന്നെയാണ് ഉപയോഗപ്പെടുത്തുന്നത്. | ഓയ്ലര് സമീകരണങ്ങളുടെ (Euler equations) നിര്ധാരണങ്ങളാണ് ദ്രവ ബലതന്ത്രത്തില് കൂടുതലായും ഉപയോഗിക്കുന്നത്. വിക്ഷുബ്ധപ്രവാഹങ്ങളുടെ കാര്യത്തില്, പ്രത്യേകിച്ചും റെയ്നോള്ഡ്സ് സംഖ്യ വളരെ കൂടിയിരിക്കുമ്പോള്, ഗണിതനിര്ധാരണം സങ്കീര്ണവും അസാധുവുമായിത്തീരും. അതിവേഗ കമ്പ്യൂട്ടറുകളുടെ സഹായത്തോടെയുള്ള മാതൃകാപഠനങ്ങള് (Simulation studies) ആണ് ഇത്തരം സാഹചര്യങ്ങളില് പ്രയോജനപ്പെടുത്തുന്നത്. പൈപ്പുകള്, പമ്പുകള്, ഡാമുകള്, ടര്ബൈനുകള്, താപപ്രക്രിയാ പ്ലാന്റുകള് എന്നിവിടങ്ങളിലെ പ്രവാഹങ്ങള്; അന്തരീക്ഷത്തിലെയും സമുദ്രത്തിലെയും പ്രവാഹങ്ങള്; എയര്ക്രാഫ്റ്റ്, സ്പേയ്സ് ക്രാഫ്റ്റ് എന്നിവയുടെ ഫ്ലൈറ്റുകള്; പ്ലാസ്മാ പ്രവാഹങ്ങള് എന്നിവയെ വിശദീകരിക്കാന് ഈ സമീകരണങ്ങള് പ്രയോജനപ്പെടുത്തുന്നു. കൂടാതെ ചലനാവസ്ഥയിലുള്ള ഓട്ടോമൊബൈലുകള്, കപ്പലുകള്, തീവണ്ടികള് എന്നിവയ്ക്കും സ്ഥിരമായി നില്ക്കുന്ന പാലങ്ങള്, കെട്ടിടങ്ങള് എന്നിവയ്ക്കും ചുറ്റുമുള്ള ദ്രവപ്രവാഹം കണക്കുകൂട്ടാനും ഇതേ സമീകരണങ്ങള് തന്നെയാണ് ഉപയോഗപ്പെടുത്തുന്നത്. | ||
Current revision as of 09:17, 24 മാര്ച്ച് 2009
ദ്രവ ബലതന്ത്രം
Fluid mechanics
വിരാമാവസ്ഥയിലോ ചലനാവസ്ഥയിലോ ഉള്ള ദ്രവങ്ങളിന്മേല് ബലത്തിന്റെ പ്രഭാവത്തെക്കുറിച്ചുള്ള പഠനം. സ്വതന്ത്രമായി ഒഴുകാന് കഴിയുന്ന പദാര്ഥങ്ങളെയാണ് ദ്രവങ്ങള് (fluids) എന്നു വിവക്ഷിക്കുന്നത്. അതിനാല് ദ്രാവകങ്ങളെയും (liquids) വാതകങ്ങളെയും (gases) ദ്രവങ്ങളുടെ വിഭാഗത്തിലുള് പ്പെടുത്താം. ദ്രവ്യമാനം (mass), സംവേഗം (momentum), ഊര്ജം (energy) എന്നിവയുടെ അടിസ്ഥാന സംരക്ഷണ നിയമങ്ങള് ഖരപദാര്ഥങ്ങള്ക്കെന്നതുപോലെ ദ്രവങ്ങള്ക്കും ബാധകമാണ്. എങ്കിലും അവയുടെ ഗണിതീയരൂപങ്ങള്ക്കു വ്യത്യാസമുണ്ട്. അതിനാല് ദ്രവ ബലതന്ത്രം പ്രത്യേകമായൊരു ശാഖയായി പരിഗണിക്കപ്പെടുന്നു. ദ്രാവകങ്ങളുടെയും വാതകങ്ങളുടെയും പ്രവാഹവുമായി ബന്ധപ്പെട്ട് പ്രകൃതിയില് നാം കാണുന്ന ചില പ്രതിഭാസങ്ങളെ വിശദീകരിക്കുന്നതിനും വ്യവസായ-സാങ്കേതിക രംഗങ്ങളിലും ദ്രവ ബലതന്ത്ര തത്ത്വങ്ങള് ഉപയുക്തമാണ്. സിവില് എന്ജിനീയറിങ്, കെമിക്കല് എന്ജിനീയറിങ്, എയ്റോനോട്ടിക്സ്, അസ്റ്റ്രോനോട്ടിക്സ്, ജലവിജ്ഞാനം (Hydrology), സമുദ്രശാസ്ത്രം(Oceanography), കാലാവസ്ഥാശാസ്ത്രം (Meterology) എന്നീ മേഖലകളിലെല്ലാം ഈ ശാസ്ത്രശാഖയുടെ തത്ത്വങ്ങള് പ്രയോജനപ്പെടുത്തുന്നുണ്ട്.
വികാസ പരിണാമങ്ങള്. ബി.സി. 3-ാം ശ.-ത്തില് പ്രഖ്യാപിതങ്ങളായ ആര്ക്കിമിഡീസിന്റെ പ്ളവന നിയമങ്ങള് (laws of buoyancy) ആണ് ദ്രവ ബലതന്ത്രത്തിലെ ആദ്യപഠനങ്ങളായി അംഗീകരിക്കപ്പെട്ടിട്ടുള്ളത്. വിരാമാവസ്ഥ(rest)യിലെ ജലത്തെക്കുറിച്ചുള്ള പഠനമായ ഹൈഡ്രോസ്റ്റാറ്റിക്സ് ഒരു ശാസ്ത്രശാഖയായി ആദ്യം വികാസം പ്രാപിച്ചു. എന്നാല്, ചലനാവസ്ഥയിലെ ദ്രവങ്ങളെക്കുറിച്ചുള്ള പഠനം ദീര്ഘകാലത്തിനുശേഷം മാത്രമാണ് നടന്നിട്ടുള്ളത്. ദ്രവങ്ങളുടെ ഗുണധര്മങ്ങളായ ശ്യാനത (viscosity), ഇലാസ്തികത (elasticity) എന്നിവയെ തൃപ്തികരമായി വിശദീകരിക്കാന് കഴിയാതിരുന്നതായിരിക്കാം അതിനു കാരണം. സ്റ്റെവിന്, ടോറിസെല്ലി, പാസ്കല്, ന്യൂട്ടണ്, ഓയ്ലര്, ബെര്ണൗളി, നെവിയര്, സ്റ്റോക്സ്, റെയ്നോള്ഡ്സ്, പ്രണ്ഡല്, കാര്മന് എന്നീ ശാസ്ത്രജ്ഞരുടെ സംഭാവനകളാണ് പില്ക്കാലത്ത് ദ്രവ ബലതന്ത്രശാഖയെ പരിപോഷിപ്പിച്ചത്.
ദ്രവങ്ങളുടെ വ്യത്യസ്ത സ്ഥിതികളെ അടിസ്ഥാനമാക്കി ദ്രവബലതന്ത്രത്തെ പല ഉള്പ്പിരിവുകളായി തിരിച്ചാണ് ആധുനികകാലത്ത് പഠനം നടത്തുന്നത്. അവയില് പ്രധാനപ്പെട്ടവ
1. ഫ്ളൂയിഡ് സ്റ്റാറ്റിക്സ് (വിരാമാവസ്ഥയിലെ ദ്രവങ്ങളെക്കുറിച്ചുള്ള പഠനം),
2. ഫ്ളൂയിഡ് ഡൈനമിക്സ് (ഗതികാവസ്ഥയിലുള്ള ദ്രവങ്ങളെക്കുറിച്ചുള്ള പഠനം),
3. എയ്റോഡൈനമിക്സ് (വാതകങ്ങളുടെ പ്രവാഹത്തെക്കുറിച്ചുള്ള പഠനം),
4. ഗ്യാസ് ഡൈനമിക്സ് (ഗണ്യമായ സമ്മര്ദനീയതയുള്ള വാതകങ്ങളുടെ പ്രവാഹത്തെക്കുറിച്ചുള്ള പഠനം),
5. മാഗ്നറ്റോഹൈഡ്രോഡൈനമിക്സ് (അയോണീകൃതവാതകങ്ങളുടെ പ്രവാഹത്തെക്കുറിച്ചുള്ള പഠനം)
എന്നിവയാണ്.
ദ്രവങ്ങളുടെ ഗുണധര്മങ്ങള് (Properties of fluids). ഖരവസ്തുക്കളില്നിന്നു വ്യത്യസ്തമായി ദ്രവങ്ങളില് വളരെ എളുപ്പം വിരൂപണം (deformation) നടത്താന് കഴിയും. ദ്രവത്തെ ചലിപ്പിക്കാനും അവയുടെ സ്വതന്ത്രമായ ഒഴുക്ക് നിലനിര്ത്താനും വളരെ ചെറിയ ഒരു അപരൂപണ ബലത്തിന് (shearing force) സാധിക്കുന്നു. ദ്രാവകത്തെപ്പോലെ വാതകത്തെ ഒരു പാത്രത്തില്നിന്നു മറ്റൊന്നിലേക്കു പൂര്ണമായി പകരാന് കഴിയുകയില്ല. എന്നാല് അപരൂപണബലത്താല് വാതകത്തിനും വിരൂപണം സംഭവിക്കുന്നുണ്ട്.
പ്രയോഗിക്കപ്പെട്ട ബലത്താല് എളുപ്പത്തില് വിരൂപണം ചെയ്യപ്പെടുമെങ്കിലും ദ്രാവകവും വാതകവും ഈ ബലത്തെ പ്രതിരോധിക്കുന്നുണ്ട്. ശ്യാനതയാണ് ഈ പ്രതിരോധബലങ്ങളില് പ്രധാനം. വാതകങ്ങളുടെ ശ്യാനത ദ്രാവകങ്ങളുടേതിനെ അപേക്ഷിച്ച് വളരെ കുറഞ്ഞതാണ്. താപനില ഉയരുമ്പോള് അവയുടെ ശ്യാനതയും ചെറിയ തോതില് ഉയരുന്നു. എന്നാല്, താപനില കൂടുമ്പോള് ദ്രാവകങ്ങളുടെ ശ്യാനത കുറയുകയാണു ചെയ്യുന്നത്.
മര്ദവും സാന്ദ്രതയും ദ്രവത്തിന്റെ ബലതന്ത്ര ഗുണധര്മങ്ങള് (mechanical properties) ആയി പരിഗണിക്കപ്പെട്ടുപോരുന്നു (ഇവയെ താപഗതിക ഗുണധര്മങ്ങളായും പരിഗണിക്കാറുണ്ട്).
വിരാമാവസ്ഥയിലുള്ള ദ്രവങ്ങള്. ബാഹ്യബലങ്ങളുടെ മര്ദം വിരാമാവസ്ഥയിലുള്ള ദ്രവങ്ങളെ എങ്ങനെ ബാധിക്കുന്നു എന്ന് ഫ്ളൂയിഡ് സ്റ്റാറ്റിക്സില് പ്രതിപാദിക്കുന്നു. ഭൂഗുരുത്വത്താലുള്ള വസ്തുവിന്റെ ഭാരം, അന്തരീക്ഷമര്ദം, പിസ്റ്റണ് ഉപയോഗിച്ചു നല്കുന്ന ബലം എന്നിവയെല്ലാം ബാഹ്യബലങ്ങള്ക്ക് ഉദാഹരണങ്ങളാണ്. ഗുരുത്വബലത്തിന്റെ പ്രഭാവത്താല്, ആഴം കൂടുന്നതനുസരിച്ച് മര്ദവും വര്ധിക്കുന്നു. നിരീക്ഷിത ബിന്ദുവിന്റെ മുകളിലുള്ള ദ്രവത്തിന്റെ ഭാരംകൂടി കണക്കിലെടുക്കേണ്ടതുകൊണ്ടാണ് ഇപ്രകാരം സംഭവിക്കുന്നത്.
ഗതികാവസ്ഥയിലുള്ള ദ്രവങ്ങള്. ഒഴുക്കിന്റെ രീതിയും സംവഹന സംവിധാനത്തിന്റെ സ്വഭാവവുമനുസരിച്ച് ദ്രവങ്ങളുടെ പ്രവാഹത്തെ വിവിധ ഇനങ്ങളായി തിരിച്ച് പരിഗണിക്കുന്നു. ഇതാണ് ഫ്ളൂയിഡ് ഡൈനമിക്സിലെ പ്രതിപാദ്യം.
വിവിധയിനം പ്രവാഹങ്ങള്.
1. അസമ്മര്ദനീയ പ്രവാഹം (incompressible flow). സാന്ദ്രതയും (density) വിശിഷ്ട ഭാരവും (specific weight) സ്ഥിരമായിട്ടുള്ള ദ്രവത്തിന്റെ പ്രവാഹം. സാധാരണ താപനിലയിലും മര്ദത്തിലുമുള്ള ദ്രാവകങ്ങളുടെയും വാതകങ്ങളുടെയും പ്രവാഹം ഈ വിഭാഗത്തില് പരിഗണിക്കുന്നു.
2. സമ്മര്ദനീയ പ്രവാഹം (compressible flow). സാന്ദ്രതയും വിശിഷ്ട ഭാരവും സ്ഥിരമല്ലാത്ത ദ്രവങ്ങളുടെ പ്രവാഹം. വാതക ഗതികത്തിലെ പഠനങ്ങള് ഈ വിഭാഗത്തില് ഉള് പ്പെടുത്തിയിരിക്കുന്നു.
3. അടഞ്ഞ കുഴലിലെ പ്രവാഹം (closed conduit flow). പൈപ്പുകളിലൂടെയോ മറ്റ് അടഞ്ഞ ചാനലുകളിലൂടെയോ അന്തരീക്ഷമര്ദത്തിലല്ലാതെയുള്ള ദ്രാവകങ്ങളുടെ പ്രവാഹം.
4. തുറന്ന വാഹികയിലെ പ്രവാഹം (open channel flow). അന്തരീക്ഷ മര്ദത്തിലേക്കു തുറന്ന പ്രതലമുള്ള ദ്രാവകങ്ങളുടെ പ്രവാഹം.
5. അധിധ്വനിക പ്രവാഹം (supersonic flow). ഒരു നിര്ദിഷ്ട ദ്രവം അതിലൂടെയുള്ള ശബ്ദത്തിന്റെ വേഗതയെക്കാള് കൂടിയ വേഗതയില് പ്രവഹിക്കുന്ന അവസ്ഥ.
6. അവധ്വനിക പ്രവാഹം (subsonic flow). ദ്രവത്തിലൂടെയുള്ള ശബ്ദപ്രവേഗത്തെ അപേക്ഷിച്ച് കുറഞ്ഞ പ്രവേഗത്തിലുള്ള ദ്രവപ്രവാഹം.
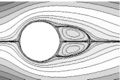
7. സ്ഥിര പ്രവാഹം (steady flow). ഒരു നിശ്ചിത സമയത്തേക്ക് സ്ഥിരമായി നില്ക്കുന്ന രീതിയിലുള്ള പ്രവാഹം.
8. അസ്ഥിര പ്രവാഹം (unsteady flow). സമയം മാറുന്നതനുസരിച്ച് വ്യത്യാസപ്പെടുന്നയിനം പ്രതിരൂപ(pattern)ത്തോടുകൂടിയ പ്രവാഹം. ഉദാ. തരംഗ ചലനം.
9. ഏകസമാന പ്രവാഹം (non uniform flow). നിശ്ചിത ദൂരത്തിനുള്ളില് സ്ഥിരപ്രവേഗത്തോടെയുള്ള പ്രവാഹം. ഉദാ. സ്ഥിര വ്യാസമുള്ള പൈപ്പ്ലൈനിലെ പ്രവാഹം.
10. ഏകസമാനമല്ലാത്ത പ്രവാഹം (uniform flow). പ്രവാഹപാതയിലെ ഓരോ ബിന്ദുവിലും പ്രവേഗമാറ്റത്തോടെയുള്ള പ്രവാഹം.
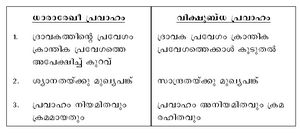
11. ധാരാരേഖീ പ്രവാഹം (streamline or laminar flow). ദ്രാവകത്തിലെ ഓരോ സ്തരവും മറ്റൊന്നിനുമേല് മൃദുവായി (smooth), വിക്ഷോഭത്തിന് ഇടനല്കാതെ തെന്നിനീങ്ങുന്നതാണ് ധാരാരേഖീ പ്രവാഹം. ഒഴുക്കിന്റെ വേഗം ഒരു നിശ്ചിത അളവില് (ക്രാന്തിക പ്രവേഗം) കുറഞ്ഞിരുന്നാല് മാത്രമേ പ്രവാഹം ധാരാരേഖീയമാകൂ.
12. വിക്ഷുബ്ധ പ്രവാഹം (turbulent flow). തുടര്ച്ചയായ ചുഴികളോടെയുള്ള പ്രവാഹം. ഇതില്, ദ്രവകണങ്ങള് നിരന്തരമായി കൂടിക്കലരുന്നതിനാല് ഒരു നിശ്ചിത കണത്തിന്റെ കൃത്യമായ സ്ഥാനനിര്ണയനമോ പഥനിര്ണയനമോ സാധ്യമല്ല. അതിനാല് ഇത്തരം പ്രവാഹത്തെ സാംഖ്യികീയമായി (statistically) മാത്രം പരിഗണിക്കുന്നു.
ഇവയില് ധാരാരേഖീയവും വിക്ഷുബ്ധവുമായ പ്രവാഹങ്ങളെയാണ് പ്രധാനമായും വേര്തിരിച്ചു പഠനവിധേയമാക്കുന്നത്. നെവിയര്-സ്റ്റോക്സ് സമീകരണങ്ങള് (Navier-Stokes equations) വഴി ധാരാരേഖീ പ്രവാഹത്തെ വിശദീകരിക്കാന് കഴിയുന്നു. വിക്ഷുബ്ധ പ്രവാഹത്തെക്കുറിച്ചുള്ള സമീകരണങ്ങള് കൂടുതല് സങ്കീര്ണങ്ങളാണ്. സാധാരണ ഒഴുക്കിന്റെ പ്രവേഗം വര്ധിക്കുമ്പോള് അത് അസ്ഥിരമായി മാറുകയും ധാരാരേഖീയത്തില്നിന്ന് വിക്ഷുബ്ധ അവസ്ഥയിലേക്കു വ്യതിയാനപ്പെടുകയും ചെയ്യുന്നു. ദ്രവകണങ്ങള് വളരെ അനിയമിത പഥങ്ങളിലൂടെ ഒഴുകാന് തുടങ്ങുകയും ചുഴികള് (eddies) രൂപപ്പെടുകയും ചെയ്യും. ദ്രവം ധാരാരേഖീ പ്രവാഹത്തില്നിന്ന് വിക്ഷുബ്ധ പ്രവാഹത്തിലേക്കു കടക്കുന്ന പ്രവേഗമൂല്യത്തെ ക്രാന്തിക പ്രവേഗം (critical velocity) എന്നു വിളിക്കുന്നു. ദ്രാവകങ്ങളുടെ കാര്യത്തില് രണ്ടിനം പ്രവാഹങ്ങളുടെയും പ്രധാന ലക്ഷണങ്ങള് താഴെ കൊടുക്കുന്നു.
പൊതുവേ, ഒരു പ്രവാഹം ധാരാരേഖീയമാണോ വിക്ഷുബ്ധമാണോ എന്ന് അതിന്റെ റെയ്നോള്ഡ്സ് നമ്പര് (Re) അടിസ്ഥാനമാക്കി നിര്ണയിക്കാനാകും. Re=ρLV/μഎന്ന സമീകരണം വഴി റെയ്നോള്ഡ്സ് നമ്പര് കണ്ടുപിടിക്കാം. ഇവിടെ ρ സാന്ദ്രതയെയും L നീളത്തെയും (ജ്യാമിതീയവും ലാക്ഷണികവുമായ നീളം) V പ്രവേഗത്തെയും μ ശ്യാനതയുടെ ഗുണാങ്കത്തെയും (coefficient of viscosity) പ്രതിനിധാനം ചെയ്യുന്നു.
Re മാനങ്ങളില്ലാത്ത (dimensionless) ഒരു ശുദ്ധ സംഖ്യ ആണ്. Re യുടെ മൂല്യം കുറഞ്ഞിരുന്നാല് പ്രവാഹം ധാരാരേഖീയവും, ക്രാന്തികമൂല്യം കടന്നുകഴിഞ്ഞാല് (Re > Rec)അത് വിക്ഷുബ്ധവുമായി മാറുന്നു.ρ,L,μ എന്നിവ സ്ഥിരമായിരുന്നാല് Re എന്നത് V യ്ക്ക് ആനുപാതികമായിമാത്രം മാറുന്നു എന്നു കാണാം. ഉരുണ്ടതും മിനുസമുള്ളതുമായ പൈപ്പുകളിലൂടെയുള്ള പ്രവാഹത്തില് Recയുടെ മൂല്യം ഏകദേശം 2,000 ആയിരിക്കും. ഇവിടെ L പൈപ്പിന്റെ വ്യാസത്തിനു തുല്യമായ നീളമാണ്. മറിച്ച്, പരന്ന പ്രതലത്തിനു മുകളിലൂടെയുള്ള പ്രവാഹത്തില് Rec ഏകദേശം 5,00,000 ആണ്.
പ്രവാഹം ഏതു തരത്തിലുള്ളതായാലും ശ്യാനത മൂലം യാന്ത്രികോര്ജം താപോര്ജമായി രൂപാന്തരപ്പെടും. പൈപ്പുകളിലൂടെയും മറ്റു വാഹികകളിലൂടെയുമുള്ള പ്രവാഹവുമായി ബന്ധപ്പെട്ട പ്രശ്നങ്ങള് നിര്ധാരണം ചെയ്യുമ്പോള് ഈ പ്രക്രിയകൂടി പ്രത്യേകം പരിഗണിക്കേണ്ടതുണ്ട്.
വിക്ഷുബ്ധത കഴിയുന്നത്ര കുറയ്ക്കത്തക്ക രീതിയിലാണ് വിമാനങ്ങളും മത്സരഓട്ടത്തിനുള്ള റേസിങ് കാറുകളും മറ്റും രൂപകല്പന ചെയ്യുന്നത്. എന്നാല് വിക്ഷുബ്ധത അഭിലഷണീയമായിത്തീരുന്ന സന്ദര്ഭങ്ങളും നിത്യജീവിതത്തിലുണ്ട്. ഇംഗ്ലണ്ടിനടുത്തുകൂടി ഒഴുകുന്ന ഉഷ്ണജലപ്രവാഹമാണ് 'ഗള്ഫ് സ്റ്റ്രീം'. ഇതിലെ ജലത്തിന്റെ ഒഴുക്ക് തീര്ത്തും ധാരാരേഖീയം മാത്രമായിരുന്നുവെങ്കില് ഇംഗ്ലണ്ട് ഇന്നത്തേതിനെക്കാള് കൂടുതല് തണുത്ത പ്രദേശമായി മാറുമായിരുന്നു. ദ്രവകണങ്ങളുടെ കൂടിക്കലരല് വര്ധിപ്പിച്ചുകൊണ്ട് ദ്രവ്യമാനം, സംവേഗം, ഊര്ജം എന്നിവയുടെ സ്ഥാനാന്തരണ നിരക്ക് കൂട്ടുന്നതിനും വിക്ഷുബ്ധത സഹായകമാകുന്നുണ്ട്. ഉദാഹരണമായി അടുക്കളയില് ഉപയോഗിക്കുന്ന മിക്സറില് (മിക്സി) ബ്ലേഡുകള്വഴി ജാറിനുള്ളില് വിക്ഷുബ്ധപ്രവാഹം ഉളവാക്കുകയാണു നാം ചെയ്യുന്നത്. മിക്സറില് മുട്ട ഏകസമാനമായി പതപ്പിച്ചെടുക്കാന് കഴിയുന്നത് ഈ ഗുണവിശേഷത്താലാണ്.
ഓയ്ലര് സമീകരണങ്ങളുടെ (Euler equations) നിര്ധാരണങ്ങളാണ് ദ്രവ ബലതന്ത്രത്തില് കൂടുതലായും ഉപയോഗിക്കുന്നത്. വിക്ഷുബ്ധപ്രവാഹങ്ങളുടെ കാര്യത്തില്, പ്രത്യേകിച്ചും റെയ്നോള്ഡ്സ് സംഖ്യ വളരെ കൂടിയിരിക്കുമ്പോള്, ഗണിതനിര്ധാരണം സങ്കീര്ണവും അസാധുവുമായിത്തീരും. അതിവേഗ കമ്പ്യൂട്ടറുകളുടെ സഹായത്തോടെയുള്ള മാതൃകാപഠനങ്ങള് (Simulation studies) ആണ് ഇത്തരം സാഹചര്യങ്ങളില് പ്രയോജനപ്പെടുത്തുന്നത്. പൈപ്പുകള്, പമ്പുകള്, ഡാമുകള്, ടര്ബൈനുകള്, താപപ്രക്രിയാ പ്ലാന്റുകള് എന്നിവിടങ്ങളിലെ പ്രവാഹങ്ങള്; അന്തരീക്ഷത്തിലെയും സമുദ്രത്തിലെയും പ്രവാഹങ്ങള്; എയര്ക്രാഫ്റ്റ്, സ്പേയ്സ് ക്രാഫ്റ്റ് എന്നിവയുടെ ഫ്ലൈറ്റുകള്; പ്ലാസ്മാ പ്രവാഹങ്ങള് എന്നിവയെ വിശദീകരിക്കാന് ഈ സമീകരണങ്ങള് പ്രയോജനപ്പെടുത്തുന്നു. കൂടാതെ ചലനാവസ്ഥയിലുള്ള ഓട്ടോമൊബൈലുകള്, കപ്പലുകള്, തീവണ്ടികള് എന്നിവയ്ക്കും സ്ഥിരമായി നില്ക്കുന്ന പാലങ്ങള്, കെട്ടിടങ്ങള് എന്നിവയ്ക്കും ചുറ്റുമുള്ള ദ്രവപ്രവാഹം കണക്കുകൂട്ടാനും ഇതേ സമീകരണങ്ങള് തന്നെയാണ് ഉപയോഗപ്പെടുത്തുന്നത്.