This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ദിഗ്ഭ്രംശം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(New page: =ദിഗ്ഭ്രംശം= Parallax ഒരേ വസ്തുവിനെ രണ്ട് വ്യത്യസ്ത സ്ഥാനങ്ങളില്നിന്നു ന...) |
(→ദിഗ്ഭ്രംശം) |
||
| (ഇടക്കുള്ള 3 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 3: | വരി 3: | ||
Parallax | Parallax | ||
| + | ഒരേ വസ്തുവിനെ രണ്ട് വ്യത്യസ്ത സ്ഥാനങ്ങളില്നിന്നു നോക്കുമ്പോള് തോന്നുന്ന (apparent) കോണീയ വ്യതിയാനം (angular displacement). പ്രപഞ്ചത്തിലെ രണ്ട് വ്യത്യസ്ത സ്ഥാനങ്ങളില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് ജ്യോതിര്ഗോളങ്ങളുടെ ദിശയ്ക്കുണ്ടാകുന്ന വ്യത്യാസത്തെ ജ്യോതിശ്ശാസ്ത്രത്തില് ദിഗ്ഭ്രംശമായി കണക്കാക്കുന്നു. നിരീക്ഷണ ബിന്ദുക്കള്ക്കിടയിലുള്ള അകലത്തെ | ||
| + | അടിസ്ഥാനമാക്കി ജ്യോതിര്ഗോളങ്ങളിലേക്കുള്ള ദൂരം നിര്ണയിക്കാനാവും. ട്രയാംഗുലേഷന് എന്നാണ് ഈ രീതി അറിയപ്പെടുന്നത്. നിരീക്ഷണ ബിന്ദുക്കള്ക്കിടയിലുള്ള അകലത്തെ ആധാരരേഖ (base line) എന്നു വിളിക്കുന്നു. ആധാരരേഖയെ അടിസ്ഥാനമാക്കി സാധാരണയായി രണ്ടുതരം ദിഗ്ഭ്രംശങ്ങളാണുള്ളത്: ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശവും വാര്ഷിക ദിഗ്ഭ്രംശവും. ഭൗമവ്യാസാര്ധം ഒരു ഖഗോളവസ്തുവില് (celestial body) സമ്മുഖമാക്കുന്ന (subtend) കോണളവാണ് ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശം (Geocentric parallax). സമീപ നക്ഷത്രങ്ങള്ക്കുപോലും ഇത് തികച്ചും നിസ്സാരമായിരിക്കുമെന്നതിനാല് സൗരയൂഥത്തിനുള്ളില് വരുന്ന വസ്തുക്കളുടെ അകലം നിര്ണയിക്കുന്നതിനു മാത്രമേ ഈ രീതി ഉപയോഗിക്കാറുള്ളൂ. ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശം ഏറ്റവും കൂടുതലായുള്ളത് ചന്ദ്രനാണ്. സൂര്യനില്നിന്ന് ഭൂമിയിലേക്കുള്ള ശരാശരി അകലം ഒരു സൗര മാത്ര (Astronomical Unit-AU) ആയി കണക്കാക്കപ്പെടുന്നതിനാല് ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശത്തില് ഏറ്റവും പ്രാധാന്യമര്ഹിക്കുന്ന ദിഗ്ഭ്രംശം സൂര്യന്റേതാണ്. വിദൂര ജ്യോതിര്ഗോളങ്ങളുടെ ദൂരം നിര്ണയിക്കുമ്പോള് ആധാരരേഖയുടെ നീളവും കൂടണം. ഭൂമിയുടെ വ്യാസം അടിസ്ഥാനരേഖയാക്കി എടുത്താല്പ്പോലും നക്ഷത്രങ്ങളുടെ സ്ഥാനം നിര്ണയിക്കാനാവില്ല. ഇവിടെ ഭൂപ്രദക്ഷിണപഥത്തിന്റെ വ്യാസം ഉപയോഗിച്ചാണ് ദിഗ്ഭ്രംശം കണക്കാക്കുന്നത്. ഭൂമിയോട് താരതമ്യേന അടുത്തായി വരുന്ന നക്ഷത്രങ്ങളുടെ ദൂരം ഈ രീതി (വാര്ഷിക ദിഗ്ഭ്രംശം) ഉപയോഗിച്ച് നിര്ണയിക്കാം. ഖഗോളീയ ദിഗ്ഭ്രംശം കണക്കാക്കുമ്പോള് ഒരു സൌരമാത്ര ആണ് ഏകകമാക്കുന്നത്. പാര്സെക് (parsec) ആണ് ഖഗോളീയ ദിഗ്ഭ്രംശം അളക്കാനുപയോഗിക്കുന്ന ഏകകം. പാരലാക്സ് സെക്കന്ഡ് (parallax second) എന്നതിന്റെ ചുരുക്കരൂപമാണ് പാര്സെക് എന്നത് (പാര്സെക് - ഒരു ആര്ക് സെക്കന്ഡ് വാര്ഷിക ദിഗ്ഭ്രംശമുള്ള ഒരു നക്ഷത്രത്തിന്റെ ദൂരമാണ് ഈ ഏകകം). ഒരു നക്ഷത്രത്തിന്റെ വാര്ഷിക ദിഗ്ഭ്രംശം 1/10 സെക്കന്ഡ് ആണെങ്കില് ആ നക്ഷത്രം 10 പാര്സെക് | ||
| + | |||
| + | [[Image:p384.png|300px|left]] | ||
| - | |||
| - | |||
അകലെ സ്ഥിതിചെയ്യുന്നുവെന്നാണ് അര്ഥമാക്കുന്നത്. ഒരു പാര്സെക് എന്നത് 3.26 പ്രകാശവര്ഷത്തിനു തുല്യമാണ്. അതായത്, പ്രകാശം സെക്കന്ഡില് 3 ലക്ഷം കി.മീ. വേഗത്തില് 3.26 വര്ഷംകൊണ്ട് സഞ്ചരിക്കുന്ന ദൂരം. ഭൂമിയുടെ ഏറ്റവും അടുത്തുള്ള നക്ഷത്രമായ പ്രോക്സിമ സെന്റൌറിയുടെ ദിഗ്ഭ്രംശം 0.76 ആര്ക്ക് സെ. ആണ്. അതിനാല് ഭൂമിയില്നിന്ന് ഇത് | അകലെ സ്ഥിതിചെയ്യുന്നുവെന്നാണ് അര്ഥമാക്കുന്നത്. ഒരു പാര്സെക് എന്നത് 3.26 പ്രകാശവര്ഷത്തിനു തുല്യമാണ്. അതായത്, പ്രകാശം സെക്കന്ഡില് 3 ലക്ഷം കി.മീ. വേഗത്തില് 3.26 വര്ഷംകൊണ്ട് സഞ്ചരിക്കുന്ന ദൂരം. ഭൂമിയുടെ ഏറ്റവും അടുത്തുള്ള നക്ഷത്രമായ പ്രോക്സിമ സെന്റൌറിയുടെ ദിഗ്ഭ്രംശം 0.76 ആര്ക്ക് സെ. ആണ്. അതിനാല് ഭൂമിയില്നിന്ന് ഇത് | ||
| വരി 20: | വരി 22: | ||
[[Image:p384a.png|300px|right]] | [[Image:p384a.png|300px|right]] | ||
| + | |||
ഖഗോളീയ ദിഗ്ഭ്രംശം ആദ്യമായി നിര്ണയിച്ചത് 1838-ലാണ്. എന്നാല് വിശ്വസനീയമായ അളവുകള് 20-ാം ശ.-ത്തിലാണ് ലഭ്യമായത്. വലിയ ദൂരദര്ശിനികളുടെ ആവിര്ഭാവവും ഫോട്ടോഗ്രഫിക് സങ്കേതങ്ങള് ജ്യോതിശ്ശാസ്ത്രരംഗത്ത് പ്രയോഗിച്ചുതുടങ്ങിയതും ഇതിനു സഹായകമായി. | ഖഗോളീയ ദിഗ്ഭ്രംശം ആദ്യമായി നിര്ണയിച്ചത് 1838-ലാണ്. എന്നാല് വിശ്വസനീയമായ അളവുകള് 20-ാം ശ.-ത്തിലാണ് ലഭ്യമായത്. വലിയ ദൂരദര്ശിനികളുടെ ആവിര്ഭാവവും ഫോട്ടോഗ്രഫിക് സങ്കേതങ്ങള് ജ്യോതിശ്ശാസ്ത്രരംഗത്ത് പ്രയോഗിച്ചുതുടങ്ങിയതും ഇതിനു സഹായകമായി. | ||
Current revision as of 11:14, 20 മാര്ച്ച് 2009
ദിഗ്ഭ്രംശം
Parallax
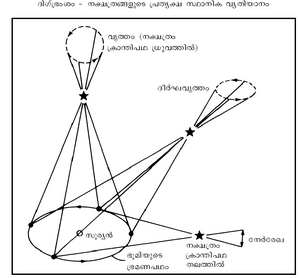
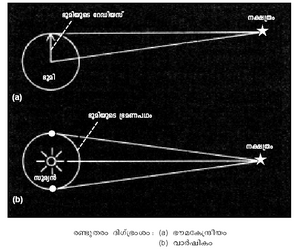
ഒരേ വസ്തുവിനെ രണ്ട് വ്യത്യസ്ത സ്ഥാനങ്ങളില്നിന്നു നോക്കുമ്പോള് തോന്നുന്ന (apparent) കോണീയ വ്യതിയാനം (angular displacement). പ്രപഞ്ചത്തിലെ രണ്ട് വ്യത്യസ്ത സ്ഥാനങ്ങളില് നിന്ന് നിരീക്ഷിക്കുമ്പോള് ജ്യോതിര്ഗോളങ്ങളുടെ ദിശയ്ക്കുണ്ടാകുന്ന വ്യത്യാസത്തെ ജ്യോതിശ്ശാസ്ത്രത്തില് ദിഗ്ഭ്രംശമായി കണക്കാക്കുന്നു. നിരീക്ഷണ ബിന്ദുക്കള്ക്കിടയിലുള്ള അകലത്തെ അടിസ്ഥാനമാക്കി ജ്യോതിര്ഗോളങ്ങളിലേക്കുള്ള ദൂരം നിര്ണയിക്കാനാവും. ട്രയാംഗുലേഷന് എന്നാണ് ഈ രീതി അറിയപ്പെടുന്നത്. നിരീക്ഷണ ബിന്ദുക്കള്ക്കിടയിലുള്ള അകലത്തെ ആധാരരേഖ (base line) എന്നു വിളിക്കുന്നു. ആധാരരേഖയെ അടിസ്ഥാനമാക്കി സാധാരണയായി രണ്ടുതരം ദിഗ്ഭ്രംശങ്ങളാണുള്ളത്: ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശവും വാര്ഷിക ദിഗ്ഭ്രംശവും. ഭൗമവ്യാസാര്ധം ഒരു ഖഗോളവസ്തുവില് (celestial body) സമ്മുഖമാക്കുന്ന (subtend) കോണളവാണ് ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശം (Geocentric parallax). സമീപ നക്ഷത്രങ്ങള്ക്കുപോലും ഇത് തികച്ചും നിസ്സാരമായിരിക്കുമെന്നതിനാല് സൗരയൂഥത്തിനുള്ളില് വരുന്ന വസ്തുക്കളുടെ അകലം നിര്ണയിക്കുന്നതിനു മാത്രമേ ഈ രീതി ഉപയോഗിക്കാറുള്ളൂ. ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശം ഏറ്റവും കൂടുതലായുള്ളത് ചന്ദ്രനാണ്. സൂര്യനില്നിന്ന് ഭൂമിയിലേക്കുള്ള ശരാശരി അകലം ഒരു സൗര മാത്ര (Astronomical Unit-AU) ആയി കണക്കാക്കപ്പെടുന്നതിനാല് ഭൗമകേന്ദ്ര ദിഗ്ഭ്രംശത്തില് ഏറ്റവും പ്രാധാന്യമര്ഹിക്കുന്ന ദിഗ്ഭ്രംശം സൂര്യന്റേതാണ്. വിദൂര ജ്യോതിര്ഗോളങ്ങളുടെ ദൂരം നിര്ണയിക്കുമ്പോള് ആധാരരേഖയുടെ നീളവും കൂടണം. ഭൂമിയുടെ വ്യാസം അടിസ്ഥാനരേഖയാക്കി എടുത്താല്പ്പോലും നക്ഷത്രങ്ങളുടെ സ്ഥാനം നിര്ണയിക്കാനാവില്ല. ഇവിടെ ഭൂപ്രദക്ഷിണപഥത്തിന്റെ വ്യാസം ഉപയോഗിച്ചാണ് ദിഗ്ഭ്രംശം കണക്കാക്കുന്നത്. ഭൂമിയോട് താരതമ്യേന അടുത്തായി വരുന്ന നക്ഷത്രങ്ങളുടെ ദൂരം ഈ രീതി (വാര്ഷിക ദിഗ്ഭ്രംശം) ഉപയോഗിച്ച് നിര്ണയിക്കാം. ഖഗോളീയ ദിഗ്ഭ്രംശം കണക്കാക്കുമ്പോള് ഒരു സൌരമാത്ര ആണ് ഏകകമാക്കുന്നത്. പാര്സെക് (parsec) ആണ് ഖഗോളീയ ദിഗ്ഭ്രംശം അളക്കാനുപയോഗിക്കുന്ന ഏകകം. പാരലാക്സ് സെക്കന്ഡ് (parallax second) എന്നതിന്റെ ചുരുക്കരൂപമാണ് പാര്സെക് എന്നത് (പാര്സെക് - ഒരു ആര്ക് സെക്കന്ഡ് വാര്ഷിക ദിഗ്ഭ്രംശമുള്ള ഒരു നക്ഷത്രത്തിന്റെ ദൂരമാണ് ഈ ഏകകം). ഒരു നക്ഷത്രത്തിന്റെ വാര്ഷിക ദിഗ്ഭ്രംശം 1/10 സെക്കന്ഡ് ആണെങ്കില് ആ നക്ഷത്രം 10 പാര്സെക്
അകലെ സ്ഥിതിചെയ്യുന്നുവെന്നാണ് അര്ഥമാക്കുന്നത്. ഒരു പാര്സെക് എന്നത് 3.26 പ്രകാശവര്ഷത്തിനു തുല്യമാണ്. അതായത്, പ്രകാശം സെക്കന്ഡില് 3 ലക്ഷം കി.മീ. വേഗത്തില് 3.26 വര്ഷംകൊണ്ട് സഞ്ചരിക്കുന്ന ദൂരം. ഭൂമിയുടെ ഏറ്റവും അടുത്തുള്ള നക്ഷത്രമായ പ്രോക്സിമ സെന്റൌറിയുടെ ദിഗ്ഭ്രംശം 0.76 ആര്ക്ക് സെ. ആണ്. അതിനാല് ഭൂമിയില്നിന്ന് ഇത്
1/0.76 അല്ലെങ്കില് 1.3 പാര്സെക് (4.3 പ്രകാശവര്ഷം) അകലത്തില് സ്ഥിതിചെയ്യുന്നു എന്നു കണക്കാക്കുന്നു. മറ്റു ചില നക്ഷത്രങ്ങളുടെ ശരാശരി ദിഗ്ഭ്രംശം ചുവടെ ചേര്ക്കുന്നു.
സിറിയസ് - 0.37
പ്രോസിയോണ് - 0.29
ആള്ട്ടേര് (തിരുവോണം) - 0.2
വേഗ (അഭിജിത്ത്) - 0.13
ഖഗോളീയ ദിഗ്ഭ്രംശം ആദ്യമായി നിര്ണയിച്ചത് 1838-ലാണ്. എന്നാല് വിശ്വസനീയമായ അളവുകള് 20-ാം ശ.-ത്തിലാണ് ലഭ്യമായത്. വലിയ ദൂരദര്ശിനികളുടെ ആവിര്ഭാവവും ഫോട്ടോഗ്രഫിക് സങ്കേതങ്ങള് ജ്യോതിശ്ശാസ്ത്രരംഗത്ത് പ്രയോഗിച്ചുതുടങ്ങിയതും ഇതിനു സഹായകമായി.