This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഡയറക്ട്രിക്സ്
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(New page: ഡയറക്ട്രിക്സ് ഉശൃലരൃശഃ കോണിക (രീിശര)വുമായി ബന്ധപ്പെട്ട ഒരു നിശ്ചിത ...) |
(→ഡയറക്ട്രിക്സ്) |
||
| (ഇടക്കുള്ള 2 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 1: | വരി 1: | ||
| - | ഡയറക്ട്രിക്സ് | + | =ഡയറക്ട്രിക്സ് = |
| + | Directrix | ||
| - | + | കോണിക (conic)വുമായി ബന്ധപ്പെട്ട ഒരു നിശ്ചിത രേഖ. x y തലത്തില്‍ ഒരു നിശ്ചിത ബിന്ദു(fixed point)വില്‍ നിന്നും ഒരു നിശ്ചിതരേഖയില്‍ നിന്നും ഉള്ള ദൂരങ്ങളുടെ അനുപാതം സ്ഥിരസംഖ്യ വരത്തക്കവിധം ഒരു ബിന്ദു സഞ്ചരിച്ചാല്‍ ആ ബിന്ദുവിന്റെ ബിന്ദുപഥമാണ് (locus) കോണികം എന്ന വക്രം. നിശ്ചിത ബിന്ദുവിനെ കോണികത്തിന്റെ ഫോക്കസ് (focus) എന്നും നിശ്ചിത രേഖയെ ഡയറക്ട്രിക്സ് (directrix) എന്നും വിളിക്കുന്നു. | |
| - | + | x y തലത്തിലുള്ള ഏതെങ്കിലും ബിന്ദു P യും, S ഒരു നിശ്ചിത ബിന്ദുവും, Pയില്‍ നിന്ന് ഒരു നിശ്ചിതരേഖയിലേക്കുള്ള ലംബദൂരം PM ഉം ആയിരിക്കട്ടെ. അപ്പോള്‍ <math>\frac{SP}{PM}</math> = സ്ഥിരസംഖ്യ വരത്തക്കവണ്ണം P സഞ്ചരിച്ചാല്‍, P യുടെ ബിന്ദുപഥമാണ് കോണികം. സ്ഥിരസംഖ്യയെ കോണികത്തിന്റെ ഉല്‍ക്കേന്ദ്രത (eccentricity) എന്നു പറയുന്നു. ഉല്‍ക്കേന്ദ്രതയെ കുറിക്കാന്‍ e എന്ന പ്രതീകമുപയോഗിക്കുന്നു. e<1 ആകുമ്പോള്‍ കോണികം എലിപ്സും (ellipse), e =1ആകുമ്പോള്‍ പരാബൊള(parabola)യും, e>1ആകുമ്പോള്‍ ഹൈപര്‍ബൊള(hyperbola)യും ആകുന്നു. | |
| - | + | മാനക സമീകരണം (standard equation) y<sup>2</sup> = 4ax ആയ പരാബൊളയുടെ ഡയറക്ട്രിക്സിന്റെ സമീകരണം x+a = 0 ആണ്. <math>\frac{x^2}{a^2}-\frac{y^2}{b^2}=1</math> എന്ന എലിപ്സിന് രണ്ടു ഡയറക്ട്രിക്സുകള്‍ ഉണ്ട്. അവയുടെ സമീകരണങ്ങള്‍ <math>x= \plusmn\frac{a}{e}</math>. അതുപോലെ <math> \frac{x^2}{a^2}-\frac{y^2}{b^2}=1</math>എന്ന ഹൈപര്‍ബൊളയുടെ ഡയറക്ട്രിക്സുകളുടെ സമീകരണം <math>x=\plusmn\frac{a}{e}</math> ആണ്. | |
| - | + | (പ്രൊഫ. കെ. ജയചന്ദ്രന്‍) | |
| - | + | ||
| - | + | ||
Current revision as of 05:51, 10 ഡിസംബര്‍ 2008
ഡയറക്ട്രിക്സ്
Directrix
കോണിക (conic)വുമായി ബന്ധപ്പെട്ട ഒരു നിശ്ചിത രേഖ. x y തലത്തില്‍ ഒരു നിശ്ചിത ബിന്ദു(fixed point)വില്‍ നിന്നും ഒരു നിശ്ചിതരേഖയില്‍ നിന്നും ഉള്ള ദൂരങ്ങളുടെ അനുപാതം സ്ഥിരസംഖ്യ വരത്തക്കവിധം ഒരു ബിന്ദു സഞ്ചരിച്ചാല്‍ ആ ബിന്ദുവിന്റെ ബിന്ദുപഥമാണ് (locus) കോണികം എന്ന വക്രം. നിശ്ചിത ബിന്ദുവിനെ കോണികത്തിന്റെ ഫോക്കസ് (focus) എന്നും നിശ്ചിത രേഖയെ ഡയറക്ട്രിക്സ് (directrix) എന്നും വിളിക്കുന്നു.
x y തലത്തിലുള്ള ഏതെങ്കിലും ബിന്ദു P യും, S ഒരു നിശ്ചിത ബിന്ദുവും, Pയില്‍ നിന്ന് ഒരു നിശ്ചിതരേഖയിലേക്കുള്ള ലംബദൂരം PM ഉം ആയിരിക്കട്ടെ. അപ്പോള്‍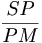 
= സ്ഥിരസംഖ്യ വരത്തക്കവണ്ണം P സഞ്ചരിച്ചാല്‍, P യുടെ ബിന്ദുപഥമാണ് കോണികം. സ്ഥിരസംഖ്യയെ കോണികത്തിന്റെ ഉല്‍ക്കേന്ദ്രത (eccentricity) എന്നു പറയുന്നു. ഉല്‍ക്കേന്ദ്രതയെ കുറിക്കാന്‍ e എന്ന പ്രതീകമുപയോഗിക്കുന്നു. e<1 ആകുമ്പോള്‍ കോണികം എലിപ്സും (ellipse), e =1ആകുമ്പോള്‍ പരാബൊള(parabola)യും, e>1ആകുമ്പോള്‍ ഹൈപര്‍ബൊള(hyperbola)യും ആകുന്നു.
മാനക സമീകരണം (standard equation) y2 = 4ax ആയ പരാബൊളയുടെ ഡയറക്ട്രിക്സിന്റെ സമീകരണം x+a = 0 ആണ്.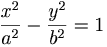 
എന്ന എലിപ്സിന് രണ്ടു ഡയറക്ട്രിക്സുകള്‍ ഉണ്ട്. അവയുടെ സമീകരണങ്ങള്‍ 
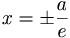. അതുപോലെ 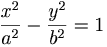എന്ന ഹൈപര്‍ബൊളയുടെ ഡയറക്ട്രിക്സുകളുടെ സമീകര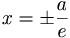ണം ആണ്.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്‍)
