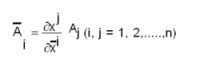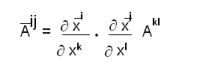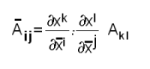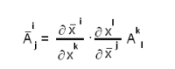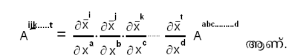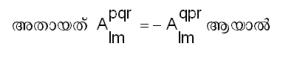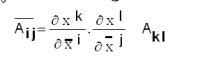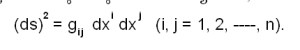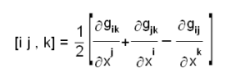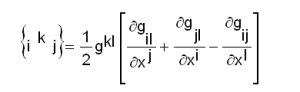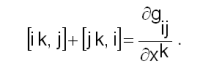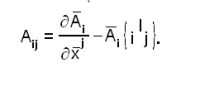This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ടെന്സര് വിശ്ളേഷണം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→രണ്ടാം ക്രമത്തിലുള്ള ടെന്സറുകള്) |
(→രണ്ടാം ക്രമത്തിലുള്ള ടെന്സറുകള്) |
||
| (ഇടക്കുള്ള 22 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 54: | വരി 54: | ||
===രണ്ടാം ക്രമത്തിലുള്ള ടെന്സറുകള്=== | ===രണ്ടാം ക്രമത്തിലുള്ള ടെന്സറുകള്=== | ||
| - | |||
i,j ഇവ 1, 2, ....., n എന്നീ മൂല്യങ്ങള് സ്വീകരിച്ചാല് A<sup>ij</sup> എന്ന പ്രതീകത്തില്നിന്ന് n<sup>2</sup> ഫലങ്ങള് ലഭിക്കുന്നു. | i,j ഇവ 1, 2, ....., n എന്നീ മൂല്യങ്ങള് സ്വീകരിച്ചാല് A<sup>ij</sup> എന്ന പ്രതീകത്തില്നിന്ന് n<sup>2</sup> ഫലങ്ങള് ലഭിക്കുന്നു. | ||
'''നിര്വചനങ്ങള് :''' | '''നിര്വചനങ്ങള് :''' | ||
| - | x നിര്ദേശാങ്കവ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് A<sup>ij</sup>യും (i,j = 1, 2, .....,n) നിര്ദേശാങ്കവ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് <math>\bar{A} | + | x നിര്ദേശാങ്കവ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് A<sup>ij</sup>യും (i,j = 1, 2, .....,n) നിര്ദേശാങ്കവ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് <math>\bar{A}</math><sup>ij</sup> യും ആയിരിക്കുകയും അവ തമ്മില് |
[[Image:pno265formula4.png]] | [[Image:pno265formula4.png]] | ||
| വരി 67: | വരി 66: | ||
x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് A<sub>ij</sub> യും | x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് A<sub>ij</sub> യും | ||
| - | (i,j = 1, 2, ....., n)<math> | + | (i,j = 1, 2, ....., n)<math>\bar{X}</math> വ്യൂഹത്തില് അതിന്റെ |
| - | ഘടകങ്ങള് <math> | + | ഘടകങ്ങള് <math>\bar{A}</math><sub>ij</sub> ആയിരിക്കുകയും അവ തമ്മില് |
[[Image:pno265formula5.png]] | [[Image:pno265formula5.png]] | ||
| വരി 74: | വരി 73: | ||
എന്ന നിയമപ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ രണ്ടാം ക്രമത്തിലുള്ള ഒരു സഹചര ടെന്സര് (covariant tensor of second order) എന്നു പറയുന്നു. | എന്ന നിയമപ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ രണ്ടാം ക്രമത്തിലുള്ള ഒരു സഹചര ടെന്സര് (covariant tensor of second order) എന്നു പറയുന്നു. | ||
| - | x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് <math>A^i_j യും (i,j= 1, 2, .... | + | x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് <math>A^i_j</math> യും<math> (i,j= 1, 2, .... |
| - | ..., n) | + | ..., n)\bar{X}</math> വ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് <math>\bar{A}</math><sup>i</sup><sub>j</sub> യും ആയിരിക്കുകയും അവ തമ്മില് |
[[Image:pno265formula6.png]] | [[Image:pno265formula6.png]] | ||
| വരി 99: | വരി 98: | ||
രണ്ടു പ്രതിചര സൂചകങ്ങളേയോ (contravariant indices) അല്ലെങ്കില് രണ്ടു സഹചര സൂചകങ്ങളേയോ പരസ്പരം മാറ്റുമ്പോള് ടെന്സറിന്റെ ഘടകങ്ങള്ക്കു മാറ്റം സംഭവിക്കുന്നില്ലെങ്കില് ആ ടെന്സറിനെ ആ സൂചകങ്ങളിലുള്ള സമമിത ടെന്സര് എന്നു പറയുന്നു. | രണ്ടു പ്രതിചര സൂചകങ്ങളേയോ (contravariant indices) അല്ലെങ്കില് രണ്ടു സഹചര സൂചകങ്ങളേയോ പരസ്പരം മാറ്റുമ്പോള് ടെന്സറിന്റെ ഘടകങ്ങള്ക്കു മാറ്റം സംഭവിക്കുന്നില്ലെങ്കില് ആ ടെന്സറിനെ ആ സൂചകങ്ങളിലുള്ള സമമിത ടെന്സര് എന്നു പറയുന്നു. | ||
| - | + | [[Image:pno265formula9.png]] | |
| - | + | ടെന്സര് p യിലും q വിലും വിഷമ സമമിതമാണ് | |
| - | + | ഒരേ വരിയിലെ രണ്ടു സൂചകങ്ങള് പരസ്പരം മാറ്റുമ്പോള് ഘടകങ്ങള്ക്ക് ചിഹ്നത്തില് മാറ്റം വരുന്നെങ്കില് ആ ടെന്സറിനെ വിഷമ സമമിത ടെന്സര് എന്നു പറയുന്നു. | |
| - | + | [[Image:pno265formula10.png]] | |
| + | |||
| + | ടെന്സര് p യിലും q വിലും വിഷമ സമമിതമാണ്. | ||
| - | + | ==ടെന്സര് ബീജഗണിതം== | |
| - | + | ടെന്സര് ബീജഗണിതമുപയോഗിച്ച് തന്നിട്ടുള്ള ടെന്സറുകളില്നിന്ന് പുതിയ ടെന്സറുകള്ക്ക് രൂപം കൊടുക്കാം. ടെന്സറുകളെ സംബന്ധിച്ച ചില ബീജഗണിത സംക്രിയകള് (algebraic operations) താഴെ കൊടുക്കുന്നു. | |
| - | + | ===ടെന്സറുകളുടെ സങ്കലനവും വ്യവകലനവും=== | |
| - | + | ഒരേ ക്രമത്തിലും (order) ഇനത്തിലും (type)പെട്ട രണ്ടു ടെന്സറുകളുടെ തുക (അല്ലെങ്കില് വ്യത്യാസം) അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്. | |
| - | + | ഒരേ ക്രമത്തിലും ഇനത്തിലും പെട്ട രണ്ടു ടെന്സറുകള് A<sub>ij</sub> യും B<sub>ij</sub> യും ആയിരിക്കട്ടെ. അവയുടെ രൂപാന്തരണ നിയമം താഴെ കൊടുക്കുന്നതായിരിക്കട്ടെ. | |
| - | + | [[Image:pno265formula11.png]] | |
| - | + | [[Image:pno266formula1.png]] | |
| - | + | C<sub>ij</sub> രൂപാന്തരപ്പെടുന്നത് A<sub>ij</sub> യും B<sub>ij</sub> യും രൂപാന്തരപ്പെടുന്ന അതേ രീതിയിലാണ്. അതുകൊണ്ട് ഇശഷ അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്. | |
| - | + | ഇതുപോലെ ഒരേ ക്രമത്തിലും ഇനത്തിലും പെട്ട രണ്ടു ടെന്സറുകളുടെ വ്യത്യാസവും അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്. | |
| - | + | രണ്ടാം ക്രമത്തിലുള്ള ഒരു ടെന്സറിനെ ഒരു സമമിത ടെന്സറിന്റേയും വിഷമ സമമിത ടെന്സറിന്റേയും തുകയായി എഴുതാവുന്നതാണ്. | |
| - | + | ===ബാഹ്യഗുണനം (Outer product)=== | |
| + | രണ്ടു ടെന്സറുകള് ഗുണിക്കുമ്പോള് മറ്റൊരു ടെന്സര് ലഭിക്കുന്നു. ഇതിന്റെ ക്രമം ആദ്യത്തെ രണ്ടു ടെന്സറുകളുടെ ക്രമങ്ങളുടെ തുകയാണ്. പ്രതിചര ക്രമം (contra variant order)s ഉം സഹചര ക്രമം (covariant order) t യും ആയ ഒരു ടെന്സറും പ്രതിചര ക്രമം p യും സഹചര ക്രമം q ഉം ആയ മറ്റൊരു ടെന്സറും ഗുണിക്കുമ്പോള് കിട്ടുന്നത് പ്രതിചര ക്രമം s + p യും സഹചര ക്രമം t + q ഉം ആയ ഒരു മിശ്ര ടെന്സറാണ്. ഈ ടെന്സറിനെ തന്നിട്ടുള്ള ടെന്സറുകളുടെ ബാഹ്യഗുണനഫലം എന്നു വിളിക്കുന്നു. ടെന്സറുകളുടെ ബാഹ്യഗുണനം, ഗുണനക്രമവിനിമേയ നിയമവും (commutative law of multipllication) വിതരണ നിയമവും അനുസരിക്കുന്നു. | ||
| - | + | ===സങ്കോചനം (Contraction)=== | |
| + | ക്രമം r ആയ ഒരു മിശ്ര ടെന്സറില് നിന്ന് ക്രമം r-2 ആയ ഒരു ടെന്സര് നിര്മിക്കുന്ന പ്രക്രിയ (process)യെ സങ്കോചനം എന്നു പറയുന്നു. ഉദാഹരണമായി C<sup>lm</sup><sub>pqr</sub> എന്ന l = p ടെന്സറില് എന്ന് എഴുതിയാല് കിട്ടുന്ന C<sup>pm</sup><sub>pqr</sub> എന്ന രാശി ഒരു ടെന്സര് ആണ്. സങ്കോചനഫലമായി ലഭിക്കുന്ന ടെന്സറിന്റെ ക്രമം സങ്കോചന പ്രക്രിയയ്ക്കു വിധേയമായ ടെന്സറിന്റെ ക്രമത്തേക്കാള് രണ്ട് കുറവായിരിക്കും. | ||
| - | + | ===ആന്തരിക ഗുണനഫലം (Inner product)=== | |
| + | തന്നിട്ടുള്ള രണ്ടു ടെന്സറുകളുടെ ബാഹ്യ ഗുണനഫലമായി കിട്ടുന്ന ടെന്സറില് സങ്കോചനം നടത്തിയാല് അവയുടെ ആന്തരിക ഗുണനഫലം കിട്ടുന്നു. ടെന്സറുകളുടെ ബാഹ്യഗുണനവും സങ്കോചനവും ടെന്സര് സംക്രിയകള് ആയതിനാല് ആന്തരിക ഗുണനഫലവും ഒരു ടെന്സര് ആയിരിക്കും. | ||
| - | + | ===മെട്രിക് ടെന്സര് (Metric tensor)=== | |
| + | ഒരു വക്രരേഖീയ (curvilinear) വ്യൂഹത്തെ ആസ്പദമാക്കിയുള്ള <math>x^i,x^i + dx^i</math> എന്നീ സമീപസ്ഥ ബിന്ദുക്കള് തമ്മിലുള്ള ദൂരത്തെ കുറിക്കുന്ന സമവാക്യമാണ്, | ||
| - | + | [[Image:pno266formula2.png]] | |
| - | + | ഇതില് g<sub>ij</sub> രണ്ടാം ക്രമത്തിലുള്ള ഒരു സഹചര ടെന്സറാണ്. ഇതിനെ മെട്രിക് ടെന്സര് അല്ലെങ്കില് ഒന്നാം മൗലിക ടെന്സര് (first fundamental tensor) എന്നു പറയുന്നു. g<sub>ij</sub> = g<sub>ji</sub> ആയതുകൊണ്ട് g<sub>ij</sub> ഒരു സമമിത ടെന്സറാണ്. | |
| - | + | ===സംയുഗ്മി മെട്രിക് ടെന്സര് (Conjugate metric tensor)=== | |
| - | + | g = |g<sub>ij</sub>|≠ 0 എന്ന സാരണികത്തില് (determinant) g<sub>ij</sub> യുടെ സഹഘടകം (co-factor)G<sub>ij</sub> ആയിരിക്കട്ടെ. g<sub>ij</sub>യുമായി ബന്ധപ്പെട്ട ഗണം g<sup>ij</sup> ഇപ്രകാരം നിര്വചിക്കുന്നു: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | <math>g^ij = \frac{G_ij}{g}</math> | ||
| + | g<sub>ij</sub> രണ്ടാം ക്രമത്തിലുള്ള ഒരു പ്രതിചര ടെന്സറാണ്. | ||
| - | + | ==ടെന്സര് അവകലനം== | |
| - | + | ===ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള് (Christoffel symbols)=== | |
| - | + | മെട്രിക് ടെന്സര് g<sub>ij</sub> യില്നിന്നു നിര്മിക്കുന്ന രണ്ടു ഫലനങ്ങളാണ് ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള്. | |
| - | + | [[Image:pno266formula4.png]] | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | എന്ന വ്യംജകത്തെ (expression) ഒന്നാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നം (Christoffel of the first kind) എന്നും | |
| - | + | [[Image:pno267formula1.png]] | |
| - | + | എന്ന വ്യംജകത്തെ രണ്ടാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നം എന്നും വിളിക്കുന്നു. ഇവയില്നിന്നും ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള് തമ്മിലുള്ള ബന്ധം | |
| - | + | [[Image:pno267formula2.png]] | |
| - | + | ===മെട്രിക് ടെന്സറിന്റെ അവകലജം=== | |
| - | + | g<sub>ij</sub> എന്ന മെട്രിക് ടെന്സറിന്റെ അവകലജം ക്രിസ്റ്റോഫല് ചിഹ്നം ഉപയോഗിച്ചെഴുതാം. ഒന്നാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നത്തിന്റെ നിര്വചനത്തില്നിന്ന്, | |
| - | + | [[Image:pno266formulaaa.png]] | |
| - | + | ===സഹചര സദിശത്തിന്റെ അവകലജം=== | |
| + | A<sub>i</sub> എന്ന സഹചര സദിശത്തിന്റെ x<sup>j</sup> കൊണ്ടുള്ള സഹചര അവകലജമാണ് (covariant derivative) | ||
| - | + | [[Image:pno266formulabbb.png]] | |
| - | + | (പ്രൊ. കെ. ജയചന്ദ്രന്) | |
Current revision as of 07:28, 5 നവംബര് 2008
ഉള്ളടക്കം |
ടെന്സര് വിശ്ലേഷണം
Tensor Analysis
പ്രയുക്ത ഗണിതത്തിന്റെ ഒരു ആധുനിക ശാഖ. നിര്ദിഷ്ടമായ രൂപാന്തരണ(transformation) നിയമങ്ങളനുസരിച്ച് മാറ്റംവരുന്ന ഘടകങ്ങളോടുകൂടിയ സത്ത(entity)യാണ് ടെന്സര്. ടെന്സറുകളെക്കുറിച്ചുള്ള പഠനമാണ് ടെന്സര് വിശ്ലേഷണം. ആപേക്ഷികതാസിദ്ധാന്തം, ഇലാസ്തികതാസിദ്ധാന്തം, അവകലജ്യാമിതി തുടങ്ങിയ ഗണിതശാഖകളില് ടെന്സര് വിശ്ലേഷണത്തിന് വളരെയേറെ പ്രാധാന്യമുണ്ട്. ബഹിരാകാശ പഠനത്തിലേര്പ്പെട്ട ശാസ്ത്രജ്ഞര്ക്കും എന്ജിനീയര്മാര്ക്കും അവരുടെ ഗവേഷണത്തില് ടെന്സര് വിശ്ലേഷണം ഗണിതശാസ്ത്രപരമായ പശ്ചാത്തലമൊരുക്കുന്നു.
സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം ആവിഷ്കരിക്കാന് ഐന്സ്റ്റൈന് ടെന്സറുകള് ഉപയോഗിച്ചുതുടങ്ങിയതോടെയാണ് ശാസ്ത്രലോകത്തിന്റെ ശ്രദ്ധയില് ഈ ഗണിതശാഖയ്ക്ക് പ്രത്യേക പ്രാധാന്യവും പരിഗണനയും ലഭിച്ചത്. ഇതിനുശേഷം മറ്റു ശാസ്ത്രശാഖകളിലും ഈ വിഷയം ഉപയോഗിച്ചുതുടങ്ങി. ഇറ്റാലിയന് ഗണിതശാസ്ത്രജ്ഞനായ റിക്കി (Ricci:18531925) ആയിരുന്നു ഈ ഗണിതശാഖ ആവിഷ്കരിച്ചത് (1887). അതിനുശേഷം ഈ വിഷയത്തില് കൂടുതല് ഗവേഷണം നടത്തിയത് അദ്ദേഹത്തിന്റെ ശിഷ്യനായ ലെവി-സിവിറ്റ (Levi-civita:18731941) ആണ്.
ടെന്സര്
Tensor
ഒരു സദിശ(vector)ത്തിന്റെ n-വിമീയ സ്പേസിലുള്ള പൊതുരൂപമാണ് ടെന്സര്. നാം സാധാരണ ഉപയോഗിക്കുന്ന അദിശങ്ങള് (scalars) പൂജ്യം ക്രമവും (പൂജ്യം റാങ്കും) സദിശങ്ങള് (vector) ഒന്നാം ക്രമവും (ഒന്നാം റാങ്കും) ഉള്ള ടെന്സറുകളാണ്.
ടെന്സറുകളെക്കുറിച്ചു മനസ്സിലാക്കാന് ചില പ്രത്യേക സങ്കേതങ്ങളും ചിഹ്നനസമ്പ്രദായവും ആവശ്യമായിവരുന്നു.
സങ്കലന സങ്കേതം
Summation convention
സങ്കലന സമ്പ്രദായത്തിന്റെ ഒരു ചുരുക്കെഴുത്താണ് ഐന്സ്റ്റൈന് ആവിഷ്ക്കരിച്ച ഈ രീതി.a1x1 + ...... + anxn അതായത് 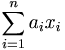 എന്ന വ്യംജകം (expression) എടുക്കുക. ടെന്സര് വിശ്ലേഷണത്തില് x1,X2,....,x2എന്നീ ചരങ്ങളുടെ കീഴ്ക്കുറി (subscript) മാറ്റി മേല്ക്കുറി (superscript) ആയിx1,x2,....,xn എന്നെഴുതുന്നു. അതായത്
എന്ന വ്യംജകം (expression) എടുക്കുക. ടെന്സര് വിശ്ലേഷണത്തില് x1,X2,....,x2എന്നീ ചരങ്ങളുടെ കീഴ്ക്കുറി (subscript) മാറ്റി മേല്ക്കുറി (superscript) ആയിx1,x2,....,xn എന്നെഴുതുന്നു. അതായത് 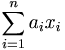 എന്ന വ്യംജകത്തെ
എന്ന വ്യംജകത്തെ 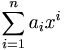 എന്നെഴുതുന്നു. ഇതിനെ വീണ്ടും ചുരുക്കി aixi എന്നെഴുതാം. ഇതില് ശ സൂചിപ്പിക്കുന്ന വിലകള് 1, 2, 3,......., nഇവയാണ്. അതുകൊണ്ട് a1x1 + a2x2 + ..... + anxn = aixi വലതുവശത്തുള്ള അങ്കനസമ്പ്രദായത്തെ സങ്കലന സങ്കേതമെന്നു പറയുന്നു. ഉദാഹരണത്തിന്, n ചരങ്ങള് x1,x2,....,xnഇവയുടെ ഫലനം f ആയിരിക്കട്ടെ. അതായത് f = f(x1,x2,..........,xn)
എന്നെഴുതുന്നു. ഇതിനെ വീണ്ടും ചുരുക്കി aixi എന്നെഴുതാം. ഇതില് ശ സൂചിപ്പിക്കുന്ന വിലകള് 1, 2, 3,......., nഇവയാണ്. അതുകൊണ്ട് a1x1 + a2x2 + ..... + anxn = aixi വലതുവശത്തുള്ള അങ്കനസമ്പ്രദായത്തെ സങ്കലന സങ്കേതമെന്നു പറയുന്നു. ഉദാഹരണത്തിന്, n ചരങ്ങള് x1,x2,....,xnഇവയുടെ ഫലനം f ആയിരിക്കട്ടെ. അതായത് f = f(x1,x2,..........,xn)
ക്രോനെക്കര് ഡെല്റ്റ (ഗൃീിലരസലൃ റലഹമേ)
i,j എന്ന രണ്ടു സൂചകങ്ങളുള്ളതും i യും j യും തുല്യമായിരിക്കുമ്പോള് മൂല്യം ഒന്നും, i യും j യും വ്യത്യസ്തമായിരിക്കുമ്പോള് മൂല്യം പൂജ്യവും ആയ രാശിയെ (quantity) ക്രോനെക്കര് ഡെല്റ്റ എന്നു വിളിക്കുന്നു. ഇതിനെ കുറിക്കാന് 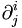 എന്ന പ്രതീകമാണ് ഉപയോഗിക്കുന്നത്.
എന്ന പ്രതീകമാണ് ഉപയോഗിക്കുന്നത്.
ഭൗതികശാസ്ത്രനിയമങ്ങളെ സൗകര്യപൂര്വം ഗണിതത്തിന്റെ ഭാഷയില് ആവിഷ്ക്കരിക്കുന്നതിന് ഒരു നിര്ദേശാങ്ക വ്യൂഹം (co-ordinate system) ആവശ്യമാണ്. ഒരു പ്രത്യേക നിര്ദേശാങ്കവ്യൂഹത്തെ അവലംബിച്ചല്ല ഭൗതിക നിയമങ്ങളുടെ സാധുത നിലനില്ക്കുന്നത്. അതുകൊണ്ട് ഭൗതിക നിയമങ്ങള് നിര്ദേശാങ്ക രൂപാന്തരണത്തില് (transformation of co-ordinate) നിശ്ചര (invariant) മായിരിക്കും. നിര്ദേശാങ്ക രൂപാന്തരണത്തിന് ടെന്സര് വിശ്ലേഷണത്തില് അടിസ്ഥാനപരമായ പ്രാധാന്യമുണ്ട്.
പ്രതിചര സദിശം, സഹചര സദിശം
ചില പ്രധാന നിര്വചനങ്ങള് പരിശോധിക്കാം. പ്രതിചര സദിശം (Contravariant vector)
x നിര്ദേശാങ്കവ്യൂഹത്തില് ഒരു സത്ത(entity)യുടെ ഘടകങ്ങള് (components)Ai ഉം (i = 1, 2, ....,n)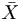 നിര്ദേശാങ്കവ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള്
നിര്ദേശാങ്കവ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് 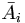 ഉം ആയിരിക്കട്ടെ. അവ തമ്മില്
ഉം ആയിരിക്കട്ടെ. അവ തമ്മില്
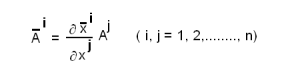
എന്ന നിയമപ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ (സത്തയെ) ഒരു പ്രതിചര സദിശം എന്നു പറയുന്നു. പ്രതിചര സദിശത്തെ ഒന്നാം ക്രമത്തിലുള്ള പ്രതിചര ടെന്സര് (contravariant tensor of order one) എന്നും വിളിക്കുന്നു.
ഉദാഹരണത്തിന് അവകലജങ്ങള് (differentials)dxi ഒരു പ്രതിചര സദിശമാണ് (സങ്കലന സങ്കേതമനുസരിച്ച് 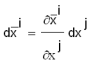 ആയതുകൊണ്ട്).
ആയതുകൊണ്ട്).
സഹചര സദിശം (co-variant vector)
x നിര്ദേശാങ്ക വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് Ai ഉം (i = 1, 2, ....,n) വ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് 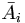 ഉം ആയിരിക്കുകയും അവ തമ്മില്
ഉം ആയിരിക്കുകയും അവ തമ്മില്
എന്ന രൂപാന്തരണ സമീകരണ പ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ (സത്തയെ) ഒരു സഹചര സദിശം എന്നുവിളിക്കുന്നു. (സഹചര സദിശത്തിന്റെ ഘടകങ്ങള് സൂചിപ്പിക്കാന് കീഴ്ക്കുറി (subscript) ഉപയോഗിക്കുന്നു. സഹചര സദിശത്തെ ഒന്നാം ക്രമത്തിലുള്ള സഹചര ടെന്സര് എന്നു പറയുന്നു. ഉദാഹരണത്തിന് ആംശിക അവകലജങ്ങള് (partial derivatives)
നിര്ദേശാങ്ക രൂപാന്തരണത്തില് മാറ്റം സംഭവിക്കാത്ത ഒരേ ഒരു ഘടകത്തോടുകൂടിയ സത്തയെ നിശ്ചരം (invariant) അല്ലെങ്കില് അദിശം (scalar) എന്നു പറയുന്നു.
രണ്ടാം ക്രമത്തിലുള്ള ടെന്സറുകള്
i,j ഇവ 1, 2, ....., n എന്നീ മൂല്യങ്ങള് സ്വീകരിച്ചാല് Aij എന്ന പ്രതീകത്തില്നിന്ന് n2 ഫലങ്ങള് ലഭിക്കുന്നു.
നിര്വചനങ്ങള് :
x നിര്ദേശാങ്കവ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് Aijയും (i,j = 1, 2, .....,n) നിര്ദേശാങ്കവ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് 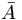 ij യും ആയിരിക്കുകയും അവ തമ്മില്
ij യും ആയിരിക്കുകയും അവ തമ്മില്
എന്ന നിയമപ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ രണ്ടാം ക്രമത്തിലുള്ള ഒരു പ്രതിചര ടെന്സര് (covariant tensor of second order) എന്നു പറയുന്നു.
x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് Aij യും
(i,j = 1, 2, ....., n)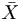 വ്യൂഹത്തില് അതിന്റെ
ഘടകങ്ങള്
വ്യൂഹത്തില് അതിന്റെ
ഘടകങ്ങള് 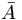 ij ആയിരിക്കുകയും അവ തമ്മില്
ij ആയിരിക്കുകയും അവ തമ്മില്
എന്ന നിയമപ്രകാരം ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ രണ്ടാം ക്രമത്തിലുള്ള ഒരു സഹചര ടെന്സര് (covariant tensor of second order) എന്നു പറയുന്നു.
x വ്യൂഹത്തില് ഒരു സത്തയുടെ ഘടകങ്ങള് 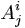 യും
യും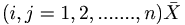 വ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള്
വ്യൂഹത്തില് അതിന്റെ ഘടകങ്ങള് 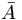 ij യും ആയിരിക്കുകയും അവ തമ്മില്
ij യും ആയിരിക്കുകയും അവ തമ്മില്
എന്ന നിയമംകൊണ്ട് ബന്ധപ്പെട്ടിരിക്കുകയും ചെയ്താല് അതിനെ രണ്ടാം ക്രമത്തിലുള്ള ഒരു മിശ്ര ടെന്സര് (mixed tensor of second order) എന്നു പറയുന്നു.
ഉദാഹരണത്തിന് ക്രോനെക്കര് ഡെല്റ്റ രണ്ടാം ക്രമത്തിലുള്ള ഒരു മിശ്ര ടെന്സര് ആണ്.
ഇതേ വിധത്തില് ഉയര്ന്ന ക്രമത്തിലുള്ള പ്രതിചര, സഹചര, മിശ്ര ടെന്സറുകള്
ഉദാഹരണത്തിന് ക്രമം p ഉള്ള പ്രതിചര ടെന്സറിന്റെ രൂപാന്തരണ നിയമം
കാര്ട്ടീഷ്യന് ടെന്സര് (Cartesian tensor)
കാര്ട്ടീഷ്യന് നിര്ദേശാങ്ക വ്യൂഹങ്ങളില് മാത്രമുള്ള രൂപാന്തരണങ്ങളില് ടെന്സര് നിയമം അനുസരിക്കുന്ന സത്തകളെ കാര്ട്ടീഷ്യന് ടെന്സര് എന്നു പറയുന്നു. ഇത്തരം ടെന്സറുകളില് പ്രതിചര ഘടകങ്ങളും (contravariant components) സഹചര ഘടകങ്ങളും തമ്മില് വ്യത്യാസമില്ല.
സമമിത (symmetric) ടെന്സറും വിഷമ - സമമിത (skew symmetric) ടെന്സറും
രണ്ടു പ്രതിചര സൂചകങ്ങളേയോ (contravariant indices) അല്ലെങ്കില് രണ്ടു സഹചര സൂചകങ്ങളേയോ പരസ്പരം മാറ്റുമ്പോള് ടെന്സറിന്റെ ഘടകങ്ങള്ക്കു മാറ്റം സംഭവിക്കുന്നില്ലെങ്കില് ആ ടെന്സറിനെ ആ സൂചകങ്ങളിലുള്ള സമമിത ടെന്സര് എന്നു പറയുന്നു.
ടെന്സര് p യിലും q വിലും വിഷമ സമമിതമാണ്
ഒരേ വരിയിലെ രണ്ടു സൂചകങ്ങള് പരസ്പരം മാറ്റുമ്പോള് ഘടകങ്ങള്ക്ക് ചിഹ്നത്തില് മാറ്റം വരുന്നെങ്കില് ആ ടെന്സറിനെ വിഷമ സമമിത ടെന്സര് എന്നു പറയുന്നു.
ടെന്സര് p യിലും q വിലും വിഷമ സമമിതമാണ്.
ടെന്സര് ബീജഗണിതം
ടെന്സര് ബീജഗണിതമുപയോഗിച്ച് തന്നിട്ടുള്ള ടെന്സറുകളില്നിന്ന് പുതിയ ടെന്സറുകള്ക്ക് രൂപം കൊടുക്കാം. ടെന്സറുകളെ സംബന്ധിച്ച ചില ബീജഗണിത സംക്രിയകള് (algebraic operations) താഴെ കൊടുക്കുന്നു.
ടെന്സറുകളുടെ സങ്കലനവും വ്യവകലനവും
ഒരേ ക്രമത്തിലും (order) ഇനത്തിലും (type)പെട്ട രണ്ടു ടെന്സറുകളുടെ തുക (അല്ലെങ്കില് വ്യത്യാസം) അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്.
ഒരേ ക്രമത്തിലും ഇനത്തിലും പെട്ട രണ്ടു ടെന്സറുകള് Aij യും Bij യും ആയിരിക്കട്ടെ. അവയുടെ രൂപാന്തരണ നിയമം താഴെ കൊടുക്കുന്നതായിരിക്കട്ടെ.
Cij രൂപാന്തരപ്പെടുന്നത് Aij യും Bij യും രൂപാന്തരപ്പെടുന്ന അതേ രീതിയിലാണ്. അതുകൊണ്ട് ഇശഷ അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്.
ഇതുപോലെ ഒരേ ക്രമത്തിലും ഇനത്തിലും പെട്ട രണ്ടു ടെന്സറുകളുടെ വ്യത്യാസവും അതേ ക്രമത്തിലും ഇനത്തിലും പെട്ട ടെന്സറാണ്.
രണ്ടാം ക്രമത്തിലുള്ള ഒരു ടെന്സറിനെ ഒരു സമമിത ടെന്സറിന്റേയും വിഷമ സമമിത ടെന്സറിന്റേയും തുകയായി എഴുതാവുന്നതാണ്.
ബാഹ്യഗുണനം (Outer product)
രണ്ടു ടെന്സറുകള് ഗുണിക്കുമ്പോള് മറ്റൊരു ടെന്സര് ലഭിക്കുന്നു. ഇതിന്റെ ക്രമം ആദ്യത്തെ രണ്ടു ടെന്സറുകളുടെ ക്രമങ്ങളുടെ തുകയാണ്. പ്രതിചര ക്രമം (contra variant order)s ഉം സഹചര ക്രമം (covariant order) t യും ആയ ഒരു ടെന്സറും പ്രതിചര ക്രമം p യും സഹചര ക്രമം q ഉം ആയ മറ്റൊരു ടെന്സറും ഗുണിക്കുമ്പോള് കിട്ടുന്നത് പ്രതിചര ക്രമം s + p യും സഹചര ക്രമം t + q ഉം ആയ ഒരു മിശ്ര ടെന്സറാണ്. ഈ ടെന്സറിനെ തന്നിട്ടുള്ള ടെന്സറുകളുടെ ബാഹ്യഗുണനഫലം എന്നു വിളിക്കുന്നു. ടെന്സറുകളുടെ ബാഹ്യഗുണനം, ഗുണനക്രമവിനിമേയ നിയമവും (commutative law of multipllication) വിതരണ നിയമവും അനുസരിക്കുന്നു.
സങ്കോചനം (Contraction)
ക്രമം r ആയ ഒരു മിശ്ര ടെന്സറില് നിന്ന് ക്രമം r-2 ആയ ഒരു ടെന്സര് നിര്മിക്കുന്ന പ്രക്രിയ (process)യെ സങ്കോചനം എന്നു പറയുന്നു. ഉദാഹരണമായി Clmpqr എന്ന l = p ടെന്സറില് എന്ന് എഴുതിയാല് കിട്ടുന്ന Cpmpqr എന്ന രാശി ഒരു ടെന്സര് ആണ്. സങ്കോചനഫലമായി ലഭിക്കുന്ന ടെന്സറിന്റെ ക്രമം സങ്കോചന പ്രക്രിയയ്ക്കു വിധേയമായ ടെന്സറിന്റെ ക്രമത്തേക്കാള് രണ്ട് കുറവായിരിക്കും.
ആന്തരിക ഗുണനഫലം (Inner product)
തന്നിട്ടുള്ള രണ്ടു ടെന്സറുകളുടെ ബാഹ്യ ഗുണനഫലമായി കിട്ടുന്ന ടെന്സറില് സങ്കോചനം നടത്തിയാല് അവയുടെ ആന്തരിക ഗുണനഫലം കിട്ടുന്നു. ടെന്സറുകളുടെ ബാഹ്യഗുണനവും സങ്കോചനവും ടെന്സര് സംക്രിയകള് ആയതിനാല് ആന്തരിക ഗുണനഫലവും ഒരു ടെന്സര് ആയിരിക്കും.
മെട്രിക് ടെന്സര് (Metric tensor)
ഒരു വക്രരേഖീയ (curvilinear) വ്യൂഹത്തെ ആസ്പദമാക്കിയുള്ള xi,xi + dxi എന്നീ സമീപസ്ഥ ബിന്ദുക്കള് തമ്മിലുള്ള ദൂരത്തെ കുറിക്കുന്ന സമവാക്യമാണ്,
ഇതില് gij രണ്ടാം ക്രമത്തിലുള്ള ഒരു സഹചര ടെന്സറാണ്. ഇതിനെ മെട്രിക് ടെന്സര് അല്ലെങ്കില് ഒന്നാം മൗലിക ടെന്സര് (first fundamental tensor) എന്നു പറയുന്നു. gij = gji ആയതുകൊണ്ട് gij ഒരു സമമിത ടെന്സറാണ്.
സംയുഗ്മി മെട്രിക് ടെന്സര് (Conjugate metric tensor)
g = |gij|≠ 0 എന്ന സാരണികത്തില് (determinant) gij യുടെ സഹഘടകം (co-factor)Gij ആയിരിക്കട്ടെ. gijയുമായി ബന്ധപ്പെട്ട ഗണം gij ഇപ്രകാരം നിര്വചിക്കുന്നു:
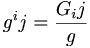
gij രണ്ടാം ക്രമത്തിലുള്ള ഒരു പ്രതിചര ടെന്സറാണ്.
ടെന്സര് അവകലനം
ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള് (Christoffel symbols)
മെട്രിക് ടെന്സര് gij യില്നിന്നു നിര്മിക്കുന്ന രണ്ടു ഫലനങ്ങളാണ് ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള്.
എന്ന വ്യംജകത്തെ (expression) ഒന്നാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നം (Christoffel of the first kind) എന്നും
എന്ന വ്യംജകത്തെ രണ്ടാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നം എന്നും വിളിക്കുന്നു. ഇവയില്നിന്നും ക്രിസ്റ്റോഫല് ചിഹ്നങ്ങള് തമ്മിലുള്ള ബന്ധം
മെട്രിക് ടെന്സറിന്റെ അവകലജം
gij എന്ന മെട്രിക് ടെന്സറിന്റെ അവകലജം ക്രിസ്റ്റോഫല് ചിഹ്നം ഉപയോഗിച്ചെഴുതാം. ഒന്നാം തരത്തിലുള്ള ക്രിസ്റ്റോഫല് ചിഹ്നത്തിന്റെ നിര്വചനത്തില്നിന്ന്,
സഹചര സദിശത്തിന്റെ അവകലജം
Ai എന്ന സഹചര സദിശത്തിന്റെ xj കൊണ്ടുള്ള സഹചര അവകലജമാണ് (covariant derivative)
(പ്രൊ. കെ. ജയചന്ദ്രന്)