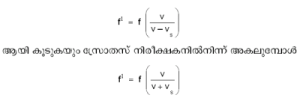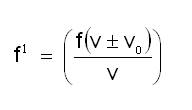This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഡോപ്ളര്‍ പ്രഭാവം
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
(→ഡോപ്ലര്‍ പ്രഭാവം) |
(→ഡോപ്ലര്‍ പ്രഭാവം) |
||
| (ഇടക്കുള്ള 14 പതിപ്പുകളിലെ മാറ്റങ്ങള്‍ ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 27: | വരി 27: | ||
[[Image:p103b.png|400px]] | [[Image:p103b.png|400px]] | ||
| - | + | [[Image:p103c.png|300px|right]] | |
| - | + | ശബ്ദപ്രവേഗത്തേക്കാള്‍ കൂടിയ വേഗതയിലാണ് ശബ്ദസ്രോതസ്സിന്റെ ചലനമെങ്കില്‍ തരംഗങ്ങള്‍ അതിവ്യാപനം (overlap) ചെയ്ത് V ആകൃതിയില്‍ ഞെരുങ്ങിയ ഒരു തരംഗാഗ്രം (wavefront) രൂപീകൃതമാകും. | |
ഇടതിങ്ങിയ ഈ വായു ഒരു 'ഷോക്ക് വേവ് കോണ്‍' ആയി രൂപംപൂണ്ട് 'സോണിക് ബൂം' ആയി നിരീക്ഷകനെ കടന്നുപോകും. സൂപ്പര്‍സോണിക് വിമാനത്തില്‍നിന്നു ശ്രവിക്കുന്ന ശബ്ദത്തിന് ഈ മാറ്റമാണു സംഭവിക്കുന്നത്. | ഇടതിങ്ങിയ ഈ വായു ഒരു 'ഷോക്ക് വേവ് കോണ്‍' ആയി രൂപംപൂണ്ട് 'സോണിക് ബൂം' ആയി നിരീക്ഷകനെ കടന്നുപോകും. സൂപ്പര്‍സോണിക് വിമാനത്തില്‍നിന്നു ശ്രവിക്കുന്ന ശബ്ദത്തിന് ഈ മാറ്റമാണു സംഭവിക്കുന്നത്. | ||
'''b. സ്രോതസ് സ്ഥിരാവസ്ഥയിലും നിരീക്ഷകന്‍ ചലനാവസ്ഥയിലും.''' എല്ലാ ദിശകളിലേക്കും ഒരുപോലെ ശബ്ദവീചികള്‍ അയയ്ക്കുന്ന ഒരു സ്ഥിരസ്രോതസ്സാണ് S എന്നു കരുതുക. ഉദാ. സൈറണ്‍. നിരീക്ഷകന്‍ A എന്ന സ്ഥലത്തു നിന്ന് സ്രോതസ്സിലേക്ക് അടുത്താല്‍ ഡോപ്ലര്‍ പ്രഭാവം മൂലം ആവൃത്തി കൂടി ഉച്ചതയേറിയ ശബ്ദം കേള്‍ക്കുന്നു. സ്രോതസ്സിനെ കടന്ന് B-യിലേക്ക് അകലുമ്പോള്‍ ആവൃത്തി കുറഞ്ഞ് ശബ്ദത്തിന്റെ ഉച്ചതയും കുറയുന്നു. | '''b. സ്രോതസ് സ്ഥിരാവസ്ഥയിലും നിരീക്ഷകന്‍ ചലനാവസ്ഥയിലും.''' എല്ലാ ദിശകളിലേക്കും ഒരുപോലെ ശബ്ദവീചികള്‍ അയയ്ക്കുന്ന ഒരു സ്ഥിരസ്രോതസ്സാണ് S എന്നു കരുതുക. ഉദാ. സൈറണ്‍. നിരീക്ഷകന്‍ A എന്ന സ്ഥലത്തു നിന്ന് സ്രോതസ്സിലേക്ക് അടുത്താല്‍ ഡോപ്ലര്‍ പ്രഭാവം മൂലം ആവൃത്തി കൂടി ഉച്ചതയേറിയ ശബ്ദം കേള്‍ക്കുന്നു. സ്രോതസ്സിനെ കടന്ന് B-യിലേക്ക് അകലുമ്പോള്‍ ആവൃത്തി കുറഞ്ഞ് ശബ്ദത്തിന്റെ ഉച്ചതയും കുറയുന്നു. | ||
| - | [[Image:p103d.png]] | + | [[Image:p103d.png|200px|centre]] |
| - | [[Image:p103e.png| | + | |
| - | + | എന്ന സമീകരണം വഴി മാറ്റംവന്ന ആവൃത്തി കണ്ടുപിടിക്കാം.[[Image:p103e.png|300px|thumb|ഡോപ്ലര്‍ പ്രഭാവം ശബ്ദത്തില്‍:സ്രോതസ് സ്ഥിരാവസ്ഥയിലും നിരീക്ഷകന്‍ ചലനാവസ്ഥയിലും|left]]ഇവിടെ +ചിഹ്നം നിരീക്ഷകന്‍ സ്രോതസ്സിലേക്ക് അടുക്കുമ്പോഴും -ചിഹ്നം സ്രോതസ്സില്‍നിന്ന് അകലുമ്പോഴും പ്രതിസ്ഥാപിക്കേണ്ടതാണ്. | |
'''2. ഡോപ്ലര്‍ പ്രഭാവം പ്രകാശത്തില്‍.''' ശബ്ദതരംഗങ്ങളിലെന്നപോലെ, വൈദ്യുതകാന്തതരംഗങ്ങളായ പ്രകാശത്തിലും ഡോപ്ലര്‍ പ്രഭാവം സംഭവിക്കുന്നുണ്ട്. പ്രഭാവത്തില്‍ സമാനസ്വഭാവമുണ്ടെങ്കിലും ഇവിടെ ഡോപ്ലര്‍ നീക്കം (Doppler shift) നിര്‍ണയിക്കാന്‍ ഉപയോഗിക്കുന്ന സൂത്രവാക്യം (formula) വ്യത്യസ്തമാണ്. | '''2. ഡോപ്ലര്‍ പ്രഭാവം പ്രകാശത്തില്‍.''' ശബ്ദതരംഗങ്ങളിലെന്നപോലെ, വൈദ്യുതകാന്തതരംഗങ്ങളായ പ്രകാശത്തിലും ഡോപ്ലര്‍ പ്രഭാവം സംഭവിക്കുന്നുണ്ട്. പ്രഭാവത്തില്‍ സമാനസ്വഭാവമുണ്ടെങ്കിലും ഇവിടെ ഡോപ്ലര്‍ നീക്കം (Doppler shift) നിര്‍ണയിക്കാന്‍ ഉപയോഗിക്കുന്ന സൂത്രവാക്യം (formula) വ്യത്യസ്തമാണ്. | ||
| വരി 44: | വരി 44: | ||
ആയിരിക്കും. അതായത് നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം കുറയുകയും (ആവൃത്തി കൂടുകയും) സ്പെക്ട്രരേഖ വയലറ്റുഭാഗത്തേക്കു നീങ്ങുകയും ചെയ്യുന്നു. മറിച്ച്, സ്രോതസ് നിരീക്ഷകനില്‍നിന്ന് അകന്നുപോവുകയാണെങ്കില്‍ നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം വര്‍ധിച്ച് (ആവൃത്തി കുറഞ്ഞ്) സ്പെക്ട്രരേഖ ചുവപ്പുഭാഗത്തേക്കു നീങ്ങും. [[Image:p104a.png]] | ആയിരിക്കും. അതായത് നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം കുറയുകയും (ആവൃത്തി കൂടുകയും) സ്പെക്ട്രരേഖ വയലറ്റുഭാഗത്തേക്കു നീങ്ങുകയും ചെയ്യുന്നു. മറിച്ച്, സ്രോതസ് നിരീക്ഷകനില്‍നിന്ന് അകന്നുപോവുകയാണെങ്കില്‍ നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം വര്‍ധിച്ച് (ആവൃത്തി കുറഞ്ഞ്) സ്പെക്ട്രരേഖ ചുവപ്പുഭാഗത്തേക്കു നീങ്ങും. [[Image:p104a.png]] | ||
എന്നതായിരിക്കും പുതിയ തരംഗദൈര്‍ഘ്യം. | എന്നതായിരിക്കും പുതിയ തരംഗദൈര്‍ഘ്യം. | ||
| + | |||
| + | [[Image:p104b.png|400px|right]] | ||
നിരീക്ഷണങ്ങളില്‍നിന്ന് മിക്ക ഗാലക്സികളുടേയും നെബുലകളുടേയും നക്ഷത്രങ്ങളുടേയും ദൃശ്യസ്പെക്ട്രം ചുവപ്പുഭാഗത്തേക്കു നീങ്ങുന്നതായാണു കാണുന്നത്. ഇതിനെ ചുവപ്പു നീക്കം (red shift) എന്നു വിശേഷിപ്പിക്കുന്നു. | നിരീക്ഷണങ്ങളില്‍നിന്ന് മിക്ക ഗാലക്സികളുടേയും നെബുലകളുടേയും നക്ഷത്രങ്ങളുടേയും ദൃശ്യസ്പെക്ട്രം ചുവപ്പുഭാഗത്തേക്കു നീങ്ങുന്നതായാണു കാണുന്നത്. ഇതിനെ ചുവപ്പു നീക്കം (red shift) എന്നു വിശേഷിപ്പിക്കുന്നു. | ||
| - | + | ||
അനേകം പ്രകാശവര്‍ഷം അകലെയുള്ള ഗാലക്സികളുടെ ഇത്തരം ചുവപ്പു നീക്കം ഗാലക്സികള്‍ തമ്മില്‍ അകലുകയാണ് എന്നു തെളിയിക്കുന്നു. ഇത് 'പ്രപഞ്ചം വികസിച്ചുകൊണ്ടിരിക്കുന്നു' (Expanding Universe) എന്ന ആശയത്തെ പിന്താങ്ങുന്നു. | അനേകം പ്രകാശവര്‍ഷം അകലെയുള്ള ഗാലക്സികളുടെ ഇത്തരം ചുവപ്പു നീക്കം ഗാലക്സികള്‍ തമ്മില്‍ അകലുകയാണ് എന്നു തെളിയിക്കുന്നു. ഇത് 'പ്രപഞ്ചം വികസിച്ചുകൊണ്ടിരിക്കുന്നു' (Expanding Universe) എന്ന ആശയത്തെ പിന്താങ്ങുന്നു. | ||
| വരി 64: | വരി 66: | ||
ദൂരദര്‍ശിനിയില്‍ക്കൂടി വീക്ഷിക്കുമ്പോള്‍ വേര്‍തിരിഞ്ഞു കാണാന്‍ കഴിയാതെ ഒരു പ്രകാശബിന്ദുവായി മാത്രം കാണപ്പെടുന്ന യുഗ്മതാരകള്‍ അഥവാ ഇരട്ട നക്ഷത്രങ്ങള്‍ (double stars) ഉണ്ട്. ഡോപ്ലര്‍ തത്ത്വം അനുസരിച്ച് ഇവ ഇരട്ടയാണെന്നു കണ്ടുപിടിക്കാനാകും. ഇത്തരം നക്ഷത്രങ്ങളുടെ പ്രകാശരേഖകള്‍ കാലികമായി ഇരട്ടയായും ഒറ്റയായും പ്രത്യക്ഷപ്പെടും. | ദൂരദര്‍ശിനിയില്‍ക്കൂടി വീക്ഷിക്കുമ്പോള്‍ വേര്‍തിരിഞ്ഞു കാണാന്‍ കഴിയാതെ ഒരു പ്രകാശബിന്ദുവായി മാത്രം കാണപ്പെടുന്ന യുഗ്മതാരകള്‍ അഥവാ ഇരട്ട നക്ഷത്രങ്ങള്‍ (double stars) ഉണ്ട്. ഡോപ്ലര്‍ തത്ത്വം അനുസരിച്ച് ഇവ ഇരട്ടയാണെന്നു കണ്ടുപിടിക്കാനാകും. ഇത്തരം നക്ഷത്രങ്ങളുടെ പ്രകാശരേഖകള്‍ കാലികമായി ഇരട്ടയായും ഒറ്റയായും പ്രത്യക്ഷപ്പെടും. | ||
| - | [[Image:p104c.png]] | + | [[Image:p104c.png|400px|left]] |
A,B എന്നിവ യുഗ്മ നക്ഷത്രങ്ങളുടെ ആദ്യസ്ഥാനങ്ങളാണെന്നു കരുതുക. A സൂര്യനില്‍നിന്ന് അകന്നുപോകുമ്പോള്‍ B സൂര്യനോട് അടുക്കുകയായിരിക്കും. അവ യഥാക്രമം A1,B1 എന്നീ സ്ഥാനങ്ങളിലെത്തുമ്പോള്‍ ഒറ്റവര മാത്രമായിരിക്കും സ്പെക്ട്രോ മീറ്ററില്‍ പ്രത്യക്ഷപ്പെടുന്നത്. | A,B എന്നിവ യുഗ്മ നക്ഷത്രങ്ങളുടെ ആദ്യസ്ഥാനങ്ങളാണെന്നു കരുതുക. A സൂര്യനില്‍നിന്ന് അകന്നുപോകുമ്പോള്‍ B സൂര്യനോട് അടുക്കുകയായിരിക്കും. അവ യഥാക്രമം A1,B1 എന്നീ സ്ഥാനങ്ങളിലെത്തുമ്പോള്‍ ഒറ്റവര മാത്രമായിരിക്കും സ്പെക്ട്രോ മീറ്ററില്‍ പ്രത്യക്ഷപ്പെടുന്നത്. | ||
ഡോപ്ലര്‍ തത്ത്വപ്രകാരം എയര്‍ക്രാഫ്റ്റുകള്‍, മിസ്സൈലുകള്‍, ഉപഗ്രഹങ്ങള്‍ എന്നിവയുടെ സ്ഥാനനിര്‍ണയനം നടത്താന്‍ കഴിയും. | ഡോപ്ലര്‍ തത്ത്വപ്രകാരം എയര്‍ക്രാഫ്റ്റുകള്‍, മിസ്സൈലുകള്‍, ഉപഗ്രഹങ്ങള്‍ എന്നിവയുടെ സ്ഥാനനിര്‍ണയനം നടത്താന്‍ കഴിയും. | ||
| - | [[Image:p104d.png]] | + | |
| + | [[Image:p104d.png|400px|right]] | ||
ഇവിടെ ഉച്ചാവൃത്തിയുള്ള റേഡിയോ തരംഗങ്ങള്‍ അയച്ച് ടാര്‍ജറ്റില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ ഡോപ്ലര്‍ നീക്കം നിരീക്ഷിക്കുന്നു. ടാര്‍ജറ്റ് അടുക്കുന്നോ അകലുന്നോ എന്നും അതിന്റെ വേഗത എത്രയെന്നും ഇതില്‍നിന്നു മനസ്സിലാക്കാം. ഡോപ്ളര്‍ തത്ത്വത്തെ അടിസ്ഥാനപ്പെടുത്തിയാണ് ഡോപ്ലര്‍ റഡാര്‍ സംവിധാനം ചെയ്തിരിക്കുന്നത്. ചിത്രത്തില്‍ നിന്നും, അകന്നുകൊണ്ടിരിക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കൂടുന്നു എന്നും അടുക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കുറയുന്നു എന്നും കാണാം. അന്തര്‍വാഹിനി (submarine) പോലെ സമുദ്രാന്തര്‍ഭാഗത്തുള്ള വസ്തുക്കളുടേയും കൃത്യമായ സ്ഥാനം ഇതുപോലെ നിര്‍ണയിക്കാനാകും. | ഇവിടെ ഉച്ചാവൃത്തിയുള്ള റേഡിയോ തരംഗങ്ങള്‍ അയച്ച് ടാര്‍ജറ്റില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ ഡോപ്ലര്‍ നീക്കം നിരീക്ഷിക്കുന്നു. ടാര്‍ജറ്റ് അടുക്കുന്നോ അകലുന്നോ എന്നും അതിന്റെ വേഗത എത്രയെന്നും ഇതില്‍നിന്നു മനസ്സിലാക്കാം. ഡോപ്ളര്‍ തത്ത്വത്തെ അടിസ്ഥാനപ്പെടുത്തിയാണ് ഡോപ്ലര്‍ റഡാര്‍ സംവിധാനം ചെയ്തിരിക്കുന്നത്. ചിത്രത്തില്‍ നിന്നും, അകന്നുകൊണ്ടിരിക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കൂടുന്നു എന്നും അടുക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കുറയുന്നു എന്നും കാണാം. അന്തര്‍വാഹിനി (submarine) പോലെ സമുദ്രാന്തര്‍ഭാഗത്തുള്ള വസ്തുക്കളുടേയും കൃത്യമായ സ്ഥാനം ഇതുപോലെ നിര്‍ണയിക്കാനാകും. | ||
Current revision as of 07:02, 16 ജൂണ്‍ 2008
ഡോപ്ലര്‍ പ്രഭാവം
Doppler effect
തരംഗസ്രോതസ്സും നിരീക്ഷകനും തമ്മില്‍ ആപേക്ഷിക ചലനം ഉള്ളപ്പോള്‍ നിരീക്ഷിത തരംഗത്തിന്റെ ആവൃത്തി (frequency) യില്‍ അനുഭവപ്പെടുന്ന മാറ്റം. ശബ്ദതരംഗങ്ങളുടേയും പ്രകാശതരംഗങ്ങളുടേയും കാര്യത്തില്‍ ഈ ഭൗതിക പ്രതിഭാസം നിരീക്ഷിക്കാം. ആപേക്ഷിക ചലനം പല തരത്തിലാകാം:
i. സ്രോതസ് സ്ഥിരാവസ്ഥയിലും നിരീക്ഷകന്‍ ചലനാവസ്ഥയിലും
ii. സ്രോതസ് ചലനാവസ്ഥയിലും നിരീക്ഷകന്‍ സ്ഥിരാവസ്ഥയിലും
iii. സ്രോതസ്സും നിരീക്ഷകനും ചലനാവസ്ഥയില്‍.
ആപേക്ഷിക ദൂരം കുറയുമ്പോള്‍ തരംഗത്തിന്റെ ആവൃത്തി കൂടുകയും (തരംഗദൈര്‍ഘ്യം കുറയുകയും) ദൂരം കൂടുമ്പോള്‍ ആവൃത്തി കുറയുകയും (തരംഗദൈര്‍ഘ്യം കൂടുകയും) ചെയ്യും എന്നതാണ് ഡോപ്ലര്‍ തത്ത്വം. ശബ്ദത്തിന്റെ കാര്യത്തില്‍ ഉച്ചത (pitch)യില്‍ വരുന്ന ഏറ്റക്കുറച്ചിലായും പ്രകാശത്തിലാണെങ്കില്‍ നിറംമാറ്റമായും ആണ് ഡോപ്ലര്‍ പ്രഭാവം നമുക്കനുഭവപ്പെടുക. 1842-ല്‍ ക്രിസ്റ്റ്യന്‍ യൊഹാന്‍ ഡോപ്ലര്‍ എന്ന ആസ്റ്റ്രിയന്‍ ശാസ്ത്രജ്ഞനാണ് ഈ പ്രതിഭാസത്തിന് ശാസ്ത്രീയ വ്യാഖ്യാനം നല്‍കിയത്.
1.ഡോപ്ലര്‍ പ്രഭാവം ശബ്ദത്തില്‍
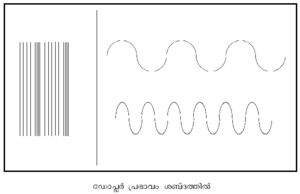
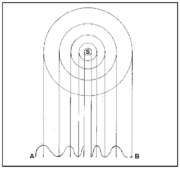
a.സ്രോതസ് ചലനാവസ്ഥയിലും നിരീക്ഷകന്‍ സ്ഥിരാവസ്ഥയിലും.
തീവണ്ടിപ്പാളത്തിനടുത്തു നില്ക്കുന്ന ഒരാള്‍ക്ക് തീവണ്ടി അടുത്തുവരുന്തോറും അതിന്റെ വിസിലിന്റെ ഉച്ചത കൂടിവരുന്നതായും വണ്ടി കടന്നുപോയിക്കഴിയുമ്പോള്‍ ഉച്ചത പെട്ടെന്നു കുറയുന്നതായും അനുഭവപ്പെടും. ഡോപ്ലര്‍ പ്രഭാവത്തിന് ഉത്തമോദാഹരണമാണിത്. വണ്ടി സമീപിക്കുന്തോറും വിസിലില്‍ നിന്നു പുറപ്പെടുന്ന ശബ്ദതരംഗത്തിന്റെ സംപീഡനങ്ങളും (compressions) വിരളനങ്ങളും (rarefactions) തമ്മില്‍ കൂടുതല്‍ അടുക്കുന്നു. അപ്പോള്‍ ശ്രോതാവ് ഓരോ സെക്കന്‍ഡിലും സ്വീകരിക്കുന്ന ശബ്ദതരംഗങ്ങളുടെ എണ്ണം യഥാര്‍ഥത്തില്‍ ഉത്സര്‍ജിക്കപ്പെടുന്നതിനേക്കാള്‍ കൂടുതലായിരിക്കും. അതായത് കേള്‍ക്കുന്ന ശബ്ദത്തിന്റെ ആവൃത്തി വര്‍ധിക്കുന്നു; ഉച്ചത കൂടിയ ശബ്ദമായിട്ട് ഈ മാറ്റം അനുഭവപ്പെടുകയും ചെയ്യുന്നു. തരംഗദൈര്‍ഘ്യവും ആവൃത്തിയും പ്രതിലോമാനുപാതികമായതിനാല്‍ ഇവിടെ ശബ്ദതരംഗങ്ങളുടെ തരംഗദൈര്‍ഘ്യം (wavelength) കുറയുന്നു എന്നു പറയാം. വണ്ടി അകലുമ്പോള്‍ ശബ്ദതരംഗത്തിന്റെ വികാസം കൂടുന്നു. യൂണിറ്റ് സമയത്ത് (ഒരു സെക്കന്‍ഡില്‍) ശ്രോതാവു സ്വീകരിക്കുന്ന ശബ്ദതരംഗങ്ങളുടെ എണ്ണം കുറയുന്നു. അതായത് ആവൃത്തി കുറഞ്ഞ് ഉച്ചതയും കുറയുന്നു.
സ്രോതസ്സിന്റെ ആവൃത്തി f-ഉം അതിന്റെ ചലന പ്രവേഗം vs-ഉം ശബ്ദത്തിന്റെ വായുവിലുള്ള പ്രവേഗം v-യും ആയാല്‍, സ്രോതസ് നിരീക്ഷകനിലേക്ക് അടുക്കുമ്പോള്‍ പുതിയ ആവൃത്തി
ആയി കുറയുകയും ചെയ്യുന്നു.
ഉദാഹരണമായി 400 ഹെര്‍ട്സ് (Hz) ആവൃത്തിയില്‍ വിസില്‍ മുഴക്കിക്കൊണ്ട് ഒരു തീവണ്ടി മണിക്കൂറില്‍ 96 കി.മീ. (27 മീ./സെ.) വേഗതയില്‍ റെയില്‍വേ സ്റ്റേഷനില്‍ നില്ക്കുന്ന ഒരാളെ കടന്നു പോകുന്നു എന്നു സങ്കല്പിക്കുക. ശബ്ദപ്രവേഗം = 346 മീ./സെ. വണ്ടി അടുത്തേക്കു വരുമ്പോള്‍ ശ്രവിക്കുന്ന ആവൃത്തി
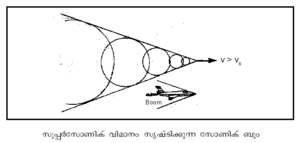
ശബ്ദപ്രവേഗത്തേക്കാള്‍ കൂടിയ വേഗതയിലാണ് ശബ്ദസ്രോതസ്സിന്റെ ചലനമെങ്കില്‍ തരംഗങ്ങള്‍ അതിവ്യാപനം (overlap) ചെയ്ത് V ആകൃതിയില്‍ ഞെരുങ്ങിയ ഒരു തരംഗാഗ്രം (wavefront) രൂപീകൃതമാകും.
ഇടതിങ്ങിയ ഈ വായു ഒരു 'ഷോക്ക് വേവ് കോണ്‍' ആയി രൂപംപൂണ്ട് 'സോണിക് ബൂം' ആയി നിരീക്ഷകനെ കടന്നുപോകും. സൂപ്പര്‍സോണിക് വിമാനത്തില്‍നിന്നു ശ്രവിക്കുന്ന ശബ്ദത്തിന് ഈ മാറ്റമാണു സംഭവിക്കുന്നത്.
b. സ്രോതസ് സ്ഥിരാവസ്ഥയിലും നിരീക്ഷകന്‍ ചലനാവസ്ഥയിലും. എല്ലാ ദിശകളിലേക്കും ഒരുപോലെ ശബ്ദവീചികള്‍ അയയ്ക്കുന്ന ഒരു സ്ഥിരസ്രോതസ്സാണ് S എന്നു കരുതുക. ഉദാ. സൈറണ്‍. നിരീക്ഷകന്‍ A എന്ന സ്ഥലത്തു നിന്ന് സ്രോതസ്സിലേക്ക് അടുത്താല്‍ ഡോപ്ലര്‍ പ്രഭാവം മൂലം ആവൃത്തി കൂടി ഉച്ചതയേറിയ ശബ്ദം കേള്‍ക്കുന്നു. സ്രോതസ്സിനെ കടന്ന് B-യിലേക്ക് അകലുമ്പോള്‍ ആവൃത്തി കുറഞ്ഞ് ശബ്ദത്തിന്റെ ഉച്ചതയും കുറയുന്നു.
2. ഡോപ്ലര്‍ പ്രഭാവം പ്രകാശത്തില്‍. ശബ്ദതരംഗങ്ങളിലെന്നപോലെ, വൈദ്യുതകാന്തതരംഗങ്ങളായ പ്രകാശത്തിലും ഡോപ്ലര്‍ പ്രഭാവം സംഭവിക്കുന്നുണ്ട്. പ്രഭാവത്തില്‍ സമാനസ്വഭാവമുണ്ടെങ്കിലും ഇവിടെ ഡോപ്ലര്‍ നീക്കം (Doppler shift) നിര്‍ണയിക്കാന്‍ ഉപയോഗിക്കുന്ന സൂത്രവാക്യം (formula) വ്യത്യസ്തമാണ്.
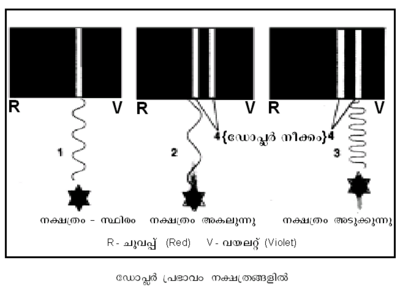
പ്രകാശിക(Optic)ത്തില്‍, സ്പെക്ട്രോസ്കോപ്പിക നിരീക്ഷണത്തിലൂടെ ഡോപ്ലര്‍ പ്രഭാവം വ്യക്തമായി തെളിയുന്നു. വിദൂര ഗാലക്സികളില്‍ നിന്നോ നക്ഷത്രങ്ങളില്‍നിന്നോ വരുന്ന പ്രകാശരശ്മികളുടെ പഠനത്തില്‍ നിന്ന് അവയുടെ ചലനസ്വഭാവത്തെക്കുറിച്ചു പഠിക്കാന്‍ കഴിയും. നിര്‍ദിഷ്ട തരംഗദൈര്‍ഘ്യമുള്ള ഒരേ സ്രോതസ്സുതന്നെ സ്ഥിരമായിരിക്കുമ്പോഴും ചലിച്ചുകൊണ്ടിരിക്കുമ്പോഴും സ്പെക്ട്രോമീറ്ററില്‍ക്കൂടി നാം വീക്ഷിക്കുന്നു എന്നു കരുതുക. ചലിക്കുന്ന സ്രോതസ്സില്‍ സ്പെക്ട്രരേഖകള്‍ക്ക് ചുവപ്പിന്റെ അറ്റത്തേക്കോ വയലറ്റിന്റെ അറ്റത്തേക്കോ വിസ്ഥാപനം (displacement) ഉള്ളതായിക്കാണാം. ഈ നീക്കത്തെയാണ് ഡോപ്ലര്‍ നീക്കം എന്നു വിവക്ഷിക്കുന്നത്.
ഉദാഹരണമായി നിരീക്ഷകന്‍ ഒരിടത്തു നിന്നുകൊണ്ട് അടുത്തുകൊണ്ടിരിക്കുന്ന ഒരു പ്രകാശ സ്രോതസ്സിനെ വീക്ഷിക്കുന്നു എന്നു കരുതുക. λ അതിന്റെ തരംഗദൈര്‍ഘ്യവും v പ്രവേഗവും c പ്രകാശവേഗവും ആയാല്‍ നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം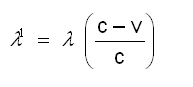 
ആയിരിക്കും. അതായത് നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം കുറയുകയും (ആവൃത്തി കൂടുകയും) സ്പെക്ട്രരേഖ വയലറ്റുഭാഗത്തേക്കു നീങ്ങുകയും ചെയ്യുന്നു. മറിച്ച്, സ്രോതസ് നിരീക്ഷകനില്‍നിന്ന് അകന്നുപോവുകയാണെങ്കില്‍ നിരീക്ഷിത തരംഗദൈര്‍ഘ്യം വര്‍ധിച്ച് (ആവൃത്തി കുറഞ്ഞ്) സ്പെക്ട്രരേഖ ചുവപ്പുഭാഗത്തേക്കു നീങ്ങും. 
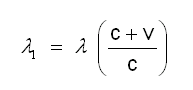എന്നതായിരിക്കും പുതിയ തരംഗദൈര്‍ഘ്യം.
നിരീക്ഷണങ്ങളില്‍നിന്ന് മിക്ക ഗാലക്സികളുടേയും നെബുലകളുടേയും നക്ഷത്രങ്ങളുടേയും ദൃശ്യസ്പെക്ട്രം ചുവപ്പുഭാഗത്തേക്കു നീങ്ങുന്നതായാണു കാണുന്നത്. ഇതിനെ ചുവപ്പു നീക്കം (red shift) എന്നു വിശേഷിപ്പിക്കുന്നു.
അനേകം പ്രകാശവര്‍ഷം അകലെയുള്ള ഗാലക്സികളുടെ ഇത്തരം ചുവപ്പു നീക്കം ഗാലക്സികള്‍ തമ്മില്‍ അകലുകയാണ് എന്നു തെളിയിക്കുന്നു. ഇത് 'പ്രപഞ്ചം വികസിച്ചുകൊണ്ടിരിക്കുന്നു' (Expanding Universe) എന്ന ആശയത്തെ പിന്താങ്ങുന്നു.
ഡോപ്ലര്‍ പ്രഭാവത്തിന് ശബ്ദത്തിലും പ്രകാശത്തിലും ഉള്ള വ്യത്യാസങ്ങള്‍. അടിസ്ഥാനപരമായി മൂന്നു വ്യത്യാസങ്ങളാണ് ഇവ തമ്മിലുള്ളത്.
1.പ്രകാശികത്തില്‍, സ്രോതസ്സാണോ നിരീക്ഷകനാണോ ആപേക്ഷിക ചലനത്തില്‍ എന്നുള്ളതിനെ ആശ്രയിച്ചല്ല തരംഗത്തിന്റെ ആവൃത്തിമാറ്റം. ശബ്ദത്തില്‍, ഈ രണ്ടു വ്യത്യസ്ത സാഹചര്യങ്ങളിലും ആവൃത്തിമാറ്റം വ്യത്യസ്തമാണ്.
2.സ്രോതസ്സിനേയും നിരീക്ഷകനേയും തമ്മില്‍ ബന്ധിപ്പിക്കുന്ന നേര്‍രേഖയ്ക്ക് 90º യില്‍ (at right angle) സ്രോതസ്സോ നിരീക്ഷകനോ ചലിക്കുന്നു എന്നു കരുതുക. ഇവിടെ ശബ്ദത്തില്‍ ഡോപ്ലര്‍ പ്രഭാവം (ആവൃത്തി മാറ്റം)ഉണ്ടാകുന്നില്ല. എന്നാല്‍ പ്രകാശത്തില്‍ ഡോപ്ലര്‍ പ്രഭാവം സംഭവിക്കുന്നു.
3. തരംഗം സഞ്ചരിക്കുന്ന മാധ്യമവും ചലനാവസ്ഥയിലാണ് എങ്കില്‍ നിരീക്ഷിത പ്രകാശത്തില്‍ ആവൃത്തിയെ അത് ബാധിക്കുന്നില്ല. എന്നാല്‍ ശബ്ദത്തിലെ നിരീക്ഷിത ആവൃത്തിയെ അതു ബാധിക്കുന്നു.
ഡോപ്ലര്‍ പ്രഭാവം കൊണ്ടുള്ള പ്രായോഗിക പ്രയോജനങ്ങള്‍. തരംഗസ്പെക്ട്രത്തിലെ ഫ്രോണ്‍ഹോഫര്‍ രേഖകളുടെ വിസ്ഥാപനം അളന്ന്, ഭൂമിയെ അപേക്ഷിച്ച് വിവിധ നക്ഷത്രങ്ങള്‍, ഗ്രഹങ്ങള്‍, ഗാലക്സികള്‍, നെബുലകള്‍ എന്നിവയുടെ പ്രയാണസ്വഭാവം (അകലുന്നോ അടുക്കുന്നോ എന്ന്), ചലന പ്രവേഗം എന്നിവ നിര്‍ണയിക്കാം.സ്രോതസ് ഭ്രമണം ചെയ്യുന്നെങ്കില്‍ അതിന്റെ ദിശ, കറക്കത്തിന്റെ വേഗത എന്നിവയും മനസ്സിലാക്കാം.
ഒരേ സ്രോതസ്സില്‍ നിന്നുള്ള പ്രകാശ സ്പെക്ട്രം വളരെ നാള്‍ ഛായാഗ്രഹണം ചെയ്താല്‍ ഒരു മാനചിത്രം (map) ഉണ്ടാക്കാന്‍ കഴിയും. ഓരോ നിശ്ചിത രേഖയ്ക്കും വരുന്ന ഡോപ്ലര്‍ നീക്കം ആധാരമാക്കി തയ്യാറാക്കുന്ന ഈ മാനചിത്രത്തില്‍ നിന്നും ചലിക്കുന്ന സ്രോതസ്സിന്റെ ഏതു സമയത്തുമുള്ള പഥവും അവസ്ഥയും അടയാളപ്പെടുത്താം. സൗരസ്പെക്ട്ര ഛായാഗ്രഹണത്തില്‍ സൂര്യന്റെ പശ്ചിമാംഗത്തിനു സംഗതമായ ഫോണ്‍ഹോഫര്‍ രേഖകള്‍ പൂര്‍വാംഗത്തിലുള്ളവയെ അപേക്ഷിച്ച് വയലറ്റ് നിറത്തിലേക്കു നീങ്ങിയതായി കാണാം. സൂര്യന്‍ പടിഞ്ഞാറു നിന്ന് കിഴക്കോട്ട് ഭ്രമണം ചെയ്യുന്നുവെന്ന് ഇതു തെളിയിക്കുന്നു.
ശനിഗ്രഹത്തിന്റെ വലയങ്ങളുടെ ഡോപ്ലര്‍ പ്രഭാവം നിരീക്ഷിക്കുമ്പോള്‍ അതിന്റെ ഉള്‍വലയം ബാഹ്യവലയത്തേക്കാള്‍ വേഗത്തില്‍ കറങ്ങുന്നതായി കാണുന്നു. ഇത് ശനിയുടെ വലയങ്ങള്‍ ഘനാകാരമല്ല; അസന്തതമായ (discontinuous) ഒരു കൂട്ടം ഉപഗ്രഹങ്ങള്‍ അടങ്ങിയതാണ് എന്നു കാണിക്കുന്നു.
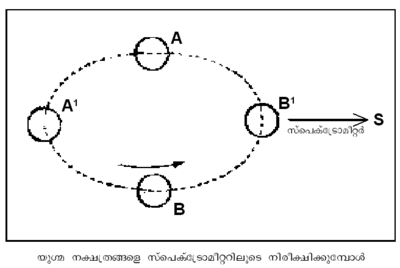
ദൂരദര്‍ശിനിയില്‍ക്കൂടി വീക്ഷിക്കുമ്പോള്‍ വേര്‍തിരിഞ്ഞു കാണാന്‍ കഴിയാതെ ഒരു പ്രകാശബിന്ദുവായി മാത്രം കാണപ്പെടുന്ന യുഗ്മതാരകള്‍ അഥവാ ഇരട്ട നക്ഷത്രങ്ങള്‍ (double stars) ഉണ്ട്. ഡോപ്ലര്‍ തത്ത്വം അനുസരിച്ച് ഇവ ഇരട്ടയാണെന്നു കണ്ടുപിടിക്കാനാകും. ഇത്തരം നക്ഷത്രങ്ങളുടെ പ്രകാശരേഖകള്‍ കാലികമായി ഇരട്ടയായും ഒറ്റയായും പ്രത്യക്ഷപ്പെടും.
A,B എന്നിവ യുഗ്മ നക്ഷത്രങ്ങളുടെ ആദ്യസ്ഥാനങ്ങളാണെന്നു കരുതുക. A സൂര്യനില്‍നിന്ന് അകന്നുപോകുമ്പോള്‍ B സൂര്യനോട് അടുക്കുകയായിരിക്കും. അവ യഥാക്രമം A1,B1 എന്നീ സ്ഥാനങ്ങളിലെത്തുമ്പോള്‍ ഒറ്റവര മാത്രമായിരിക്കും സ്പെക്ട്രോ മീറ്ററില്‍ പ്രത്യക്ഷപ്പെടുന്നത്.
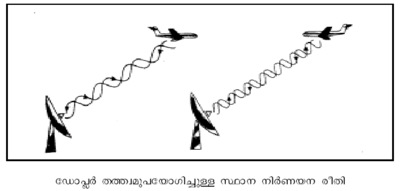
ഡോപ്ലര്‍ തത്ത്വപ്രകാരം എയര്‍ക്രാഫ്റ്റുകള്‍, മിസ്സൈലുകള്‍, ഉപഗ്രഹങ്ങള്‍ എന്നിവയുടെ സ്ഥാനനിര്‍ണയനം നടത്താന്‍ കഴിയും.
ഇവിടെ ഉച്ചാവൃത്തിയുള്ള റേഡിയോ തരംഗങ്ങള്‍ അയച്ച് ടാര്‍ജറ്റില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ ഡോപ്ലര്‍ നീക്കം നിരീക്ഷിക്കുന്നു. ടാര്‍ജറ്റ് അടുക്കുന്നോ അകലുന്നോ എന്നും അതിന്റെ വേഗത എത്രയെന്നും ഇതില്‍നിന്നു മനസ്സിലാക്കാം. ഡോപ്ളര്‍ തത്ത്വത്തെ അടിസ്ഥാനപ്പെടുത്തിയാണ് ഡോപ്ലര്‍ റഡാര്‍ സംവിധാനം ചെയ്തിരിക്കുന്നത്. ചിത്രത്തില്‍ നിന്നും, അകന്നുകൊണ്ടിരിക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കൂടുന്നു എന്നും അടുക്കുന്ന വിമാനത്തില്‍ തട്ടി പ്രതിഫലിക്കുന്ന സിഗ്നലുകളുടെ തരംഗദൈര്‍ഘ്യം കുറയുന്നു എന്നും കാണാം. അന്തര്‍വാഹിനി (submarine) പോലെ സമുദ്രാന്തര്‍ഭാഗത്തുള്ള വസ്തുക്കളുടേയും കൃത്യമായ സ്ഥാനം ഇതുപോലെ നിര്‍ണയിക്കാനാകും.
