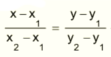This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ജ്യാമിതി
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(→കോണികങ്ങള് (Conics)) |
(→ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതി) |
||
| (ഇടക്കുള്ള 35 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 21: | വരി 21: | ||
=====ഗ്രീക്കുകാരുടെ സമീപനം===== | =====ഗ്രീക്കുകാരുടെ സമീപനം===== | ||
| - | ജ്യാമിതിയുടെ പ്രാഥമിക പാഠങ്ങള് ഉള്ക്കൊണ്ട് ധൈഷണികമായ തലത്തിലേക്ക് ആദ്യമായി അന്വേഷണമാരംഭിച്ചതു ഗ്രീക്കുകാരാണ്. അവരുടെ ഗണിതീയ സിദ്ധാന്തങ്ങള് രചിക്കപ്പെട്ടത് ബി.സി. 600-200 കാലയളവിലാണ്. ഗ്രീക്കു ഗണിതശാസ്ത്രജ്ഞരില് പലരും തത്ത്വചിന്തകര് കൂടിയായിരുന്നു. പ്രകൃതിയുടെ രൂപകല്പന ജ്യാമിതീയമാണെന്ന് അവര് വിശ്വസിച്ചു. 'ഈശ്വരന് അനശ്വരമായി ജ്യാമിതീകരിക്കുന്നു (God eternally geometrizes)' എന്ന പ്ലേറ്റോയുടെ സാക്ഷ്യപ്പെടുത്തല് ഗ്രീക്കുകാരുടെ ഗണിതസങ്കല്പം വ്യക്തമാക്കുന്നു. സ്വയംസിദ്ധങ്ങളായ പ്രസ്താവനകളില് നിന്നു കാര്യകാരണസഹിതം നിഗമനങ്ങളിലെത്തുക എന്നതായിരുന്നു അവരുടെ രീതി. സ്വയംസിദ്ധങ്ങളായ ഇത്തരം പ്രസ്താവനകളാണ് അഭിഗൃഹീതങ്ങള് (axioms). ഉദാ. ഒരു ഋജുരേഖ എതിര്ദിശകളിലേക്ക് അനന്തമായി നീണ്ടുപോകുന്നു; സന്നിപതിക്കുന്ന(coincide)രൂപങ്ങള് സര്വസമ (congruent)ങ്ങളാണ്. എലിമെന്റ്സ് എന്ന ഗ്രന്ഥത്തില് യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) ഇത്തരം അഭിഗൃഹീതങ്ങളുപയോഗിച്ച് അഞ്ഞൂറോളം പ്രമേയങ്ങള് അവതരിപ്പിച്ചിട്ടുണ്ട്. യൂക്ലീഡിയന് ജ്യാമിതിയില് അക്കാലത്ത് അറിയാമായിരുന്ന ബീജഗണിതവും കാണാം. ഉദാ. x< | + | ജ്യാമിതിയുടെ പ്രാഥമിക പാഠങ്ങള് ഉള്ക്കൊണ്ട് ധൈഷണികമായ തലത്തിലേക്ക് ആദ്യമായി അന്വേഷണമാരംഭിച്ചതു ഗ്രീക്കുകാരാണ്. അവരുടെ ഗണിതീയ സിദ്ധാന്തങ്ങള് രചിക്കപ്പെട്ടത് ബി.സി. 600-200 കാലയളവിലാണ്. ഗ്രീക്കു ഗണിതശാസ്ത്രജ്ഞരില് പലരും തത്ത്വചിന്തകര് കൂടിയായിരുന്നു. പ്രകൃതിയുടെ രൂപകല്പന ജ്യാമിതീയമാണെന്ന് അവര് വിശ്വസിച്ചു. 'ഈശ്വരന് അനശ്വരമായി ജ്യാമിതീകരിക്കുന്നു (God eternally geometrizes)' എന്ന പ്ലേറ്റോയുടെ സാക്ഷ്യപ്പെടുത്തല് ഗ്രീക്കുകാരുടെ ഗണിതസങ്കല്പം വ്യക്തമാക്കുന്നു. സ്വയംസിദ്ധങ്ങളായ പ്രസ്താവനകളില് നിന്നു കാര്യകാരണസഹിതം നിഗമനങ്ങളിലെത്തുക എന്നതായിരുന്നു അവരുടെ രീതി. സ്വയംസിദ്ധങ്ങളായ ഇത്തരം പ്രസ്താവനകളാണ് അഭിഗൃഹീതങ്ങള് (axioms). ഉദാ. ഒരു ഋജുരേഖ എതിര്ദിശകളിലേക്ക് അനന്തമായി നീണ്ടുപോകുന്നു; സന്നിപതിക്കുന്ന(coincide)രൂപങ്ങള് സര്വസമ (congruent)ങ്ങളാണ്. എലിമെന്റ്സ് എന്ന ഗ്രന്ഥത്തില് യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) ഇത്തരം അഭിഗൃഹീതങ്ങളുപയോഗിച്ച് അഞ്ഞൂറോളം പ്രമേയങ്ങള് അവതരിപ്പിച്ചിട്ടുണ്ട്. യൂക്ലീഡിയന് ജ്യാമിതിയില് അക്കാലത്ത് അറിയാമായിരുന്ന ബീജഗണിതവും കാണാം. ഉദാ. x<sup>2</sup> – 8x + 7 = 0എന്ന ദ്വിഘാത സമവാക്യത്തിന്റെ നിര്ധാരണമൂല്യം സംഖ്യയ്ക്കു പകരം ഒരു രേഖാഖണ്ഡമായി കൊടുത്തിരിക്കുന്നു. |
| - | ഗ്രീക്ക് ജ്യാമിതി കൈകാര്യം ചെയ്ത പ്രധാനാശയങ്ങള് സര്വസമത (congruence), സമരൂപത (similarity), തുല്യത (equivalence) എന്നിവയാണ്. അലക്സാന്ഡ്രിയന് കാലഘട്ടത്തില് (ബി.സി. 4-ാം ശ.) ഗ്രീക്ക് ഗണിതത്തിനു പ്രായോഗികമായ ഒരടിത്തറ കൈവന്നു. ഇക്കാലത്താണ് ആര്ക്കിമെഡിസ് π (പൈ)യുടെ വില നും [[ചിത്രം: | + | ഗ്രീക്ക് ജ്യാമിതി കൈകാര്യം ചെയ്ത പ്രധാനാശയങ്ങള് സര്വസമത (congruence), സമരൂപത (similarity), തുല്യത (equivalence) എന്നിവയാണ്. അലക്സാന്ഡ്രിയന് കാലഘട്ടത്തില് (ബി.സി. 4-ാം ശ.) ഗ്രീക്ക് ഗണിതത്തിനു പ്രായോഗികമായ ഒരടിത്തറ കൈവന്നു. ഇക്കാലത്താണ് ആര്ക്കിമെഡിസ് π (പൈ)യുടെ വില [[ചിത്രം:Jymithi.png|25px]] നും [[ചിത്രം:Pg918 scr.png|25px]]നും ഇടയ്ക്കാണെന്നു കണ്ടുപിടിച്ചത്. എ.ഡി. 18-ാം ശ. വരെ ഗണിതശാസ്ത്രത്തില് മുഖ്യസ്ഥാനം ഗ്രീക്കുകാരുടെ ക്ലാസ്സിക് ജ്യാമിതിക്കായിരുന്നു. |
====ജ്യാമിതിയിലെ ആധുനികത==== | ====ജ്യാമിതിയിലെ ആധുനികത==== | ||
| വരി 39: | വരി 39: | ||
ത്രിവിമീയ സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കാന് 3 സംഖ്യകള് ഉപയോഗിക്കുന്നു. x, y, z നിര്ദേശാങ്കങ്ങളായ ബിന്ദുവിന് മൂലബിന്ദുവില് നിന്നുള്ള അകലം [[ചിത്രം:SR3.png]] ആണ്. x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup> = r<sup>2</sup> എന്നത് ഗോളത്തിന്റെയും ax + by + cz + d = 0 എന്നത് സമതലത്തിന്റെയും സമീകരണങ്ങളാണ്. | ത്രിവിമീയ സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കാന് 3 സംഖ്യകള് ഉപയോഗിക്കുന്നു. x, y, z നിര്ദേശാങ്കങ്ങളായ ബിന്ദുവിന് മൂലബിന്ദുവില് നിന്നുള്ള അകലം [[ചിത്രം:SR3.png]] ആണ്. x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup> = r<sup>2</sup> എന്നത് ഗോളത്തിന്റെയും ax + by + cz + d = 0 എന്നത് സമതലത്തിന്റെയും സമീകരണങ്ങളാണ്. | ||
| - | |||
| - | |||
=====അവകല ജ്യാമിതി (Differential Geometry)===== | =====അവകല ജ്യാമിതി (Differential Geometry)===== | ||
| - | ഈ ശാഖയില് അവകലഗണിത (Differential Calculus)ത്തിലെ ആശയങ്ങള് വ്യാപകമായി ഉപയോഗിക്കുന്നു. ഇതില് വക്രങ്ങളുടെ | + | ഈ ശാഖയില് അവകലഗണിത (Differential Calculus)ത്തിലെ ആശയങ്ങള് വ്യാപകമായി ഉപയോഗിക്കുന്നു. ഇതില് വക്രങ്ങളുടെ മൗലിക ഗുണധര്മങ്ങളായ ചരിവ് (slope), വക്രത (curvature) എന്നിവയ്ക്കു പുറമേ സ്പേസ് വക്രങ്ങള്, അവ ഉള്ക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ വിസ്തീര്ണമുള്ള പ്രതലങ്ങള്, ജിയോഡസിക്കുകള് എന്നിവയെക്കുറിച്ചു പ്രതിപാദിക്കുന്നു. ഫ്രഞ്ച് ഗണിതജ്ഞന് ഗാസ്പാര്ഡ് മോംഗ്, ജര്മന് ഗണിതശാസ്ത്രജ്ഞന് കാള് ഫ്രീഡ്റിക് ഗൗസ് എന്നിവരാണ് ഈ വിഭാഗത്തിലെ ആദ്യകാല ഗവേഷകര്. അവകലജ്യാമിതി 19-ഉം 20-ഉം ശ.-ങ്ങളില് സജാതീയ (Affine), പ്രക്ഷേപീയ (Projective), സമാകല (integral) ജ്യാമിതികളിലേക്കു വികസിക്കുകയും ചെയ്തിട്ടുണ്ട്. |
=====വിവരണാത്മക ജ്യാമിതി (Descriptive Geometry)===== | =====വിവരണാത്മക ജ്യാമിതി (Descriptive Geometry)===== | ||
| വരി 53: | വരി 51: | ||
അഭിഗൃഹീതങ്ങളെ ആധാരമാക്കി രചിച്ച, നൂറ്റാണ്ടുകള് പഴക്കമുള്ള ജ്യാമിതീയ ശാഖയാണ് യൂക്ലീഡിയന് ജ്യാമിതി. യൂക്ലിഡിന്റെ 5-ാം ആക്സിയം 'സമാന്തര ആക്സിയം (axiom on parallels)' എന്നറിയപ്പെടുന്നത് ഇതാണ്. | അഭിഗൃഹീതങ്ങളെ ആധാരമാക്കി രചിച്ച, നൂറ്റാണ്ടുകള് പഴക്കമുള്ള ജ്യാമിതീയ ശാഖയാണ് യൂക്ലീഡിയന് ജ്യാമിതി. യൂക്ലിഡിന്റെ 5-ാം ആക്സിയം 'സമാന്തര ആക്സിയം (axiom on parallels)' എന്നറിയപ്പെടുന്നത് ഇതാണ്. | ||
| + | |||
| + | [[ചിത്രം:SR6.png]] | ||
'n എന്ന നേര്വര l, m എന്നീ നേര്വരകളെ ഖണ്ഡിക്കുമ്പോള് നേര്വരയുടെ ഒരു വശത്തുണ്ടാകുന്ന അന്തഃകോണങ്ങളുടെ ആകെത്തുക 180°-യില് കുറവാണെങ്കില്, n എന്ന നേര്വരയുടെ ഏതു വശത്താണോ അന്തഃകോണങ്ങള്, ആ വശത്ത് l,m എന്നീ നേര്വരകള് കൂട്ടിമുട്ടും'. | 'n എന്ന നേര്വര l, m എന്നീ നേര്വരകളെ ഖണ്ഡിക്കുമ്പോള് നേര്വരയുടെ ഒരു വശത്തുണ്ടാകുന്ന അന്തഃകോണങ്ങളുടെ ആകെത്തുക 180°-യില് കുറവാണെങ്കില്, n എന്ന നേര്വരയുടെ ഏതു വശത്താണോ അന്തഃകോണങ്ങള്, ആ വശത്ത് l,m എന്നീ നേര്വരകള് കൂട്ടിമുട്ടും'. | ||
| വരി 62: | വരി 62: | ||
'l എന്നതു തന്നിട്ടുള്ള നേര്വരയും, P അതില് ഇല്ലാത്ത ഒരു ബിന്ദുവും ആണെങ്കില് അവയുടെ തലത്തില് P യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ ഒരൊറ്റ നേര്വര m മാത്രമേയുള്ളു'. സമാന്തരരേഖകളെക്കുറിച്ച് എളുപ്പത്തില് ഒരവബോധം ഉളവാക്കിയ ഈ ആക്സിയവും ഇതിനുശേഷം വച്ച എല്ലാ പകര ആക്സിയങ്ങളും നിരാകരിക്കപ്പെട്ടു. | 'l എന്നതു തന്നിട്ടുള്ള നേര്വരയും, P അതില് ഇല്ലാത്ത ഒരു ബിന്ദുവും ആണെങ്കില് അവയുടെ തലത്തില് P യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ ഒരൊറ്റ നേര്വര m മാത്രമേയുള്ളു'. സമാന്തരരേഖകളെക്കുറിച്ച് എളുപ്പത്തില് ഒരവബോധം ഉളവാക്കിയ ഈ ആക്സിയവും ഇതിനുശേഷം വച്ച എല്ലാ പകര ആക്സിയങ്ങളും നിരാകരിക്കപ്പെട്ടു. | ||
| - | സമാന്തര ആക്സിയത്തില് നിന്നും തികച്ചും വിഭിന്നമായ ഒരു ആക്സിയവുമായി ഗൗസ് രംഗത്തുവന്നു. 'l എന്നത് ഒരു നേര്വരയും P-യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ അസംഖ്യം നേര്വരകളുണ്ട്'. ഈ ആക്സിയവും യൂക്ലിഡിന്റെ മറ്റ് 9 ആക്സിയങ്ങളും ഉപയോഗിച്ച് അദ്ദേഹം പല പുതിയ പ്രമേയങ്ങളും തെളിയിച്ചു. ഈ ജ്യാമിതിക്ക് ഗൗസ് 'അയൂക്ലീഡിയന് ജ്യാമിതി' എന്നു പേരിട്ടു. ഈ ജ്യാമിതിയനുസരിച്ച് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ ആകെത്തുക | + | സമാന്തര ആക്സിയത്തില് നിന്നും തികച്ചും വിഭിന്നമായ ഒരു ആക്സിയവുമായി ഗൗസ് രംഗത്തുവന്നു. 'l എന്നത് ഒരു നേര്വരയും P-യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ അസംഖ്യം നേര്വരകളുണ്ട്'. ഈ ആക്സിയവും യൂക്ലിഡിന്റെ മറ്റ് 9 ആക്സിയങ്ങളും ഉപയോഗിച്ച് അദ്ദേഹം പല പുതിയ പ്രമേയങ്ങളും തെളിയിച്ചു. ഈ ജ്യാമിതിക്ക് ഗൗസ് 'അയൂക്ലീഡിയന് ജ്യാമിതി' എന്നു പേരിട്ടു. ഈ ജ്യാമിതിയനുസരിച്ച് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ ആകെത്തുക 180°-യില് കുറവാണ്. പ്രഥമവീക്ഷണത്തില് ഇത് അബദ്ധജടിലമാണെന്നു തോന്നിയേക്കാം. ത്രികോണത്തിന്റെ വിസ്തൃതിയനുസരിച്ച് കോണങ്ങളുടെ ആകെത്തുകയിലും വ്യത്യാസം വരുന്നു. വിസ്തീര്ണം പൂജ്യത്തെ സമീപിക്കുമ്പോള് തുക 180°-യോട് അടുക്കും. സാധാരണ നാം ഉപയോഗിക്കുന്ന ത്രികോണങ്ങള് ചെറുതായിരിക്കും. അളക്കാനുപയോഗിക്കുന്ന ഉപകരണങ്ങളുടെ പിശകുകള് (errors) കൂടി പരിഗണിക്കുമ്പോള് തുക 180°-യോട് അടുത്തുമാത്രമേ വരൂ എന്നു കാണാം. ഇതുതന്നെയാണ് ഗൗസ് സിദ്ധാന്തിക്കുന്നതും. അയൂക്ലീഡിയന് ജ്യാമിതിയെ സംബന്ധിച്ച നിഗമനങ്ങളൊന്നും തന്നെ ഗൗസ് സ്വന്തം ജീവിതകാലത്ത് പ്രസിദ്ധീകരിച്ചില്ല. റഷ്യയിലെ നിക്കൊളായ് ലൊബാഷ്യേവ്സ്കിയുടെയും ഹംഗറിയിലെ യാനോസ്ബൊള്യായുടെയും പേരിലാണ് അയൂക്ലീഡിയന് ജ്യാമിതി പൊതുവെ അറിയപ്പെടുന്നത്. ലൊബാഷ്യേവ്സ്കി 1931-ലും ബൊള്യായി 1936-ലും സ്വതന്ത്രമായി ഗവേഷണഫലങ്ങള് പ്രസിദ്ധീകരിക്കുകയായിരുന്നു. ഇന്ന് ഹൈപര്ബൊളിക ജ്യാമിതി എന്ന പേരിലും ഈ ശാഖ അറിയപ്പെടുന്നു. |
=====റീമാനിയന് ജ്യാമിതി (Riemanian Geometry)===== | =====റീമാനിയന് ജ്യാമിതി (Riemanian Geometry)===== | ||
| വരി 134: | വരി 134: | ||
[[ചിത്രം:JYOTH SR576.png]] | [[ചിത്രം:JYOTH SR576.png]] | ||
| - | ഇവിടെ | + | ഇവിടെ [[ചിത്രം:For 1.png|150px]] |
ലഘൂകരിച്ചാല് c<sup>2</sup> = a<sup>2</sup>+ b<sup>2</sup> എന്നു കിട്ടുന്നു. | ലഘൂകരിച്ചാല് c<sup>2</sup> = a<sup>2</sup>+ b<sup>2</sup> എന്നു കിട്ടുന്നു. | ||
| വരി 166: | വരി 166: | ||
x, y തലത്തിലെ P എന്ന ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങളാണ് (x, y). ഈ ബിന്ദുവിനെ P (x, y) എന്നു കുറിക്കുന്നു. (x, y) ഇവയെ കാര്ട്ടീഷ്യന് നിര്ദേശാങ്കങ്ങള് (cartesian co-ordinates) എന്നു പറയുന്നു. മൂലബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് (0, 0). P (x<sub>1</sub>,y<sub>1</sub>), Q (x<sub>2</sub>, y<sub>2</sub>) എന്നിവ രണ്ടു ബിന്ദുക്കളാണെങ്കില് PQ എന്ന രേഖാഖണ്ഡത്തിന്റെ നീളം പിഥഗറസ് പ്രമേയമുപയോഗിച്ച് കണ്ടുപിടിക്കാം. | x, y തലത്തിലെ P എന്ന ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങളാണ് (x, y). ഈ ബിന്ദുവിനെ P (x, y) എന്നു കുറിക്കുന്നു. (x, y) ഇവയെ കാര്ട്ടീഷ്യന് നിര്ദേശാങ്കങ്ങള് (cartesian co-ordinates) എന്നു പറയുന്നു. മൂലബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് (0, 0). P (x<sub>1</sub>,y<sub>1</sub>), Q (x<sub>2</sub>, y<sub>2</sub>) എന്നിവ രണ്ടു ബിന്ദുക്കളാണെങ്കില് PQ എന്ന രേഖാഖണ്ഡത്തിന്റെ നീളം പിഥഗറസ് പ്രമേയമുപയോഗിച്ച് കണ്ടുപിടിക്കാം. | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Src870for.png]] |
=====നേര്വരകള്===== | =====നേര്വരകള്===== | ||
| വരി 177: | വരി 177: | ||
ചരിവുമാനങ്ങള് m<sub>1</sub>, m<sub>2</sub> ആയ രണ്ടു രേഖകള് ഛേദിക്കുമ്പോഴുണ്ടാകുന്ന കോണം θ | ചരിവുമാനങ്ങള് m<sub>1</sub>, m<sub>2</sub> ആയ രണ്ടു രേഖകള് ഛേദിക്കുമ്പോഴുണ്ടാകുന്ന കോണം θ | ||
| - | ആയാല് [[ചിത്രം: | + | ആയാല് [[ചിത്രം:Scr870 for2.png|100px]] എന്നു തെളിയിക്കാം. ഇതില്നിന്ന്, രണ്ടു രേഖകള് സമാന്തരമാണെങ്കില് m<sub>1</sub> = m<sub>2</sub>; ലംബങ്ങളായാല് m<sub>1</sub> m<sub>2</sub> = –1. ഏതു നേര്വരയുടെയും സാമാന്യ സമീകരണം ax + by + c = 0 |
ആണ്. | ആണ്. | ||
=====വൃത്തം===== | =====വൃത്തം===== | ||
| - | യൂക്ലീഡിയന് ജ്യാമിതിയില് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നു സ്ഥിരദൂരത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദുപഥം (locus) ആണ് വൃത്തം. നിശ്ചിത ബിന്ദുവിനെ വൃത്തത്തിന്റെ കേന്ദ്രം എന്നും സ്ഥിരദൂരത്തെ ആരം (radius) എന്നും പറയുന്നു. കേന്ദ്രം (h,k)യും ആരം r-ഉം ആയി വരയ്ക്കുന്ന വൃത്തത്തിന്റെ സമീകരണമാണ് (x – h)<sup>2</sup> + (y – k)<sup>2</sup> = r<sup>2</sup>. എല്ലാ വൃത്തങ്ങളുടെയും സമീകരണത്തിന്റെ പൊതുവായ രൂപമാണ് x<sup>2</sup> + y<sup>2</sup> + 2gx + 2fy + c = 0 എന്നത്. ഈ വൃത്തത്തിന്റെ കേന്ദ്രം | + | യൂക്ലീഡിയന് ജ്യാമിതിയില് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നു സ്ഥിരദൂരത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദുപഥം (locus) ആണ് വൃത്തം. നിശ്ചിത ബിന്ദുവിനെ വൃത്തത്തിന്റെ കേന്ദ്രം എന്നും സ്ഥിരദൂരത്തെ ആരം (radius) എന്നും പറയുന്നു. കേന്ദ്രം (h,k)യും ആരം r-ഉം ആയി വരയ്ക്കുന്ന വൃത്തത്തിന്റെ സമീകരണമാണ് (x – h)<sup>2</sup> + (y – k)<sup>2</sup> = r<sup>2</sup>. എല്ലാ വൃത്തങ്ങളുടെയും സമീകരണത്തിന്റെ പൊതുവായ രൂപമാണ് x<sup>2</sup> + y<sup>2</sup> + 2gx + 2fy + c = 0 എന്നത്. ഈ വൃത്തത്തിന്റെ കേന്ദ്രം = (–g, –f); ആരം [[ചിത്രം:Scr870for3.png|100px]]. വൃത്തത്തിന്റെ പ്രധാനമായ ഒരു സവിശേഷത അതിന്റെ പരിധിയിലുള്ള ഏതൊരു ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന സ്പര്ശരേഖ(tangent)യും അതേ ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന ആരവും പരസ്പരം ലംബങ്ങളായിരിക്കും എന്നുള്ളതാണ്. |
[[ചിത്രം:Jyoth Sr 120.png]] | [[ചിത്രം:Jyoth Sr 120.png]] | ||
| വരി 198: | വരി 198: | ||
'''പരാബൊള'''. പരാബൊളയുടെ ഉള്കേന്ദ്രത e = 1 ആയതുകൊണ്ട് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നും നിശ്ചിതരേഖയില് നിന്നും തുല്യ അകലത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദു പഥമാണ് ഈ വക്രം. സമീകരണത്തിന്റെ മാനകരൂപം (standard form) y<sup>2</sup> = 4ax; ശീര്ഷം (0, 0) സമമിതി അക്ഷം x-അക്ഷം; നിയതരേഖയുടെ സമീകരണം x + a = 0 (x അക്ഷത്തിന്റെ ഇടതുവശത്തു y അക്ഷത്തിനു സമാന്തരമായി a ദൂരത്തിലുളളത്). | '''പരാബൊള'''. പരാബൊളയുടെ ഉള്കേന്ദ്രത e = 1 ആയതുകൊണ്ട് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നും നിശ്ചിതരേഖയില് നിന്നും തുല്യ അകലത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദു പഥമാണ് ഈ വക്രം. സമീകരണത്തിന്റെ മാനകരൂപം (standard form) y<sup>2</sup> = 4ax; ശീര്ഷം (0, 0) സമമിതി അക്ഷം x-അക്ഷം; നിയതരേഖയുടെ സമീകരണം x + a = 0 (x അക്ഷത്തിന്റെ ഇടതുവശത്തു y അക്ഷത്തിനു സമാന്തരമായി a ദൂരത്തിലുളളത്). | ||
| + | [[ചിത്രം:Parabola.png|200px]] | ||
| + | '''എലിപ്സ്'''. ഉള്കേന്ദ്രത e < 1 ആയ കോണികമാണ് എലിപ്സ്. വലിച്ചുനീട്ടിയ ഒരു വൃത്തത്തെപ്പോലെയാണ് ഇതിന്റെ ആകൃതി. മാനക സമീകരണം [[ചിത്രം:Jyoth 4.png]] രണ്ടു ഫോക്കസ്സുകള് S(æ;0), S<sup>1</sup> (-æ,0); രണ്ടു നിയതരേഖകള് [[ചിത്രം:Jyot SR5.png]]. ചിത്രത്തില് എലിപ്സിന്റെ ദീര്ഘ അക്ഷം (major axis) = A'A = 2a; ലഘു അക്ഷം (minor axis) = B'B = 2b. P എന്നത് എലിപ്സിലുള്ള ഏതെങ്കിലും ബിന്ദുവായാല് SP + S'P = 2a എന്നു കിട്ടുന്നു. അതായത് രണ്ടു നിശ്ചിത ബിന്ദുക്കളില് നിന്നുള്ള ദൂരങ്ങളുടെ തുക സ്ഥിരസംഖ്യയാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ പഥമാണ് എലിപ്സ്. ജ്യോതിശ്ശാസ്ത്രപരമായി ഈ വക്രത്തിനു വളരെ പ്രാധാന്യമുണ്ട്. കെപ്ളറുടെ നിയമമനുസരിച്ച് സൂര്യനു ചുറ്റുമുള്ള ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം എലിപ്സുകളാണ്; സൂര്യന്റെ സ്ഥിരസ്ഥാനം ഒരു ഫോക്കസ്സിലും. | ||
| - | + | [[ചിത്രം:Elips.png|300px]] | |
| + | '''ഹൈപര്ബൊള'''. ഹൈപര്ബൊളയുടെ ഉള്കേന്ദ്രത e > 1. മാനക സമീകരണം [[ചിത്രം:Jya SR1.png]] രണ്ടു ഫോക്കസ്സുകള് S (æ, 0), S<sup>2</sup> (–æ,0); A'A = 2a, B'B = 2b. | ||
| + | [[ചിത്രം:Herbola.png|250px]] | ||
| - | + | A'A-യെ അനുപ്രസ്ഥ അക്ഷം (transverse axis) എന്നും B'B-യെ സംയുഗ്മി അക്ഷം (conjugate axis) എന്നും പറയുന്നു. രണ്ടു നിയതരേഖകള് [[ചിത്രം:Jyothi SR2.png]]. കോണികങ്ങളില് ഹൈപര്ബൊളയ്ക്കു മാത്രമേ അനന്തസ്പര്ശികള് (asymptotes)ഉള്ളു. | |
| - | + | ||
| - | + | ||
=====ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതി===== | =====ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതി===== | ||
ഈ ശാഖയില് 3 നിര്ദേശാങ്കങ്ങള് ഉപയോഗിച്ച് സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കുന്നു. ചിത്രം (15) നോക്കുക. | ഈ ശാഖയില് 3 നിര്ദേശാങ്കങ്ങള് ഉപയോഗിച്ച് സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കുന്നു. ചിത്രം (15) നോക്കുക. | ||
| - | |||
| - | |||
[[ചിത്രം:Jyoth SR16.png]] | [[ചിത്രം:Jyoth SR16.png]] | ||
| - | + | ബിന്ദു P-യെ P (x, y, z) എന്നെഴുതുന്നു. ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതിയില് തലം, രേഖ, ഗോളം, കോണ്, സിലിണ്ടര് തുടങ്ങിയവയുടെ ഗുണധര്മങ്ങള് അപഗ്രഥിക്കുന്നു. ത്രിവിമീയ ജ്യാമിതിയില് P (x, y, z) എന്ന സമീകരണം ഒരു തല(plane)ത്തെ കുറിക്കുന്നു. ത്രിവിമീയ സ്പേസില് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നു സ്ഥിരദൂരത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദുപഥമാണ് ഗോളം. ഗോളത്തിന്റെ മാനക സമീകരണം x<sup>2</sup> + y<sup>2</sup> + z<sup>2</sup> + 2ux + 2vy + 2wz + d = 0. x, y, z ചരങ്ങളിലുള്ള F (x, y, z) = 0 എന്ന സമീകരണം പൊതുവായി ഒരു പ്രതല (surface)ത്തെയാണു പ്രതിനിധീകരിക്കുന്നത്. | |
| - | + | ||
| - | ബിന്ദു P-യെ P (x, y, z) എന്നെഴുതുന്നു. ത്രിവിമീയ | + | |
| - | + | ||
| - | + | ||
[[ചിത്രം:Jyth Sr14.png]] | [[ചിത്രം:Jyth Sr14.png]] | ||
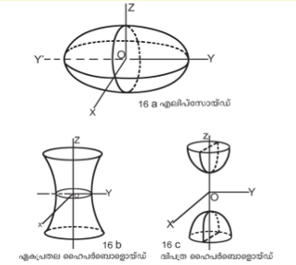
| + | ഒരു പ്രതലം എന്നു പറയുമ്പോള് അതില് വ്യത്യസ്ത ഘനരൂപങ്ങള് ഉള്പ്പെടുന്നു. ഗോളം, കോണ്, സിലിണ്ടര്, എലിപ്സോയ്ഡ്, ഹൈപര്ബൊളോയ്ഡ് ഇവയൊക്കെ പ്രതലങ്ങളാണ്. ശീര്ഷം മൂലബിന്ദുവായ കോണിന്റെ സാമാന്യരൂപം ഒരു പ്രത്യേക നിബന്ധനയ്ക്ക് വിധേയമായി ax<sup>2</sup> + by<sup>2</sup> + cz<sup>2</sup> + 2fyz + 2gzx + 2hxy = 0 എന്നെഴുതാം. ഈ നിബന്ധനയാണ് abc + 2fgh - af<sup>2</sup> - bg<sup>2</sup> - ch<sup>2</sup> ≠ 0 . Ax<sup>2</sup> + By<sup>2</sup> + Cz<sup>2</sup> = 1 എന്ന രൂപത്തിലെഴുതുന്ന പ്രതലങ്ങളെ കേന്ദ്രീയ കോണികജങ്ങള് (central quadrics) എന്നു വിളിക്കുന്നു. ഓരോ നിര്ദേശാങ്കത്തിനും ഇവ സമമിതമാണ്. | ||
| - | + | ഇവയില് എലിപ്സോയ്ഡും, [[ചിത്രം:For00 1.png]]ഏകപ്രതല ഹൈപര്ബൊളോയ്ഡും | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | ഇവയില് എലിപ്സോയ്ഡും , | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[ചിത്രം:Jyoth sr13.png]] | [[ചിത്രം:Jyoth sr13.png]] | ||
| - | + | ===അയൂക്ലീഡിയന് ജ്യാമിതി ( Non-EuclideanGeometry)=== | |
| - | + | യൂക്ലിഡിന്റെ ആക്സിയങ്ങളില് അഞ്ചാമത്തെതായ സമാന്തര ആക്സിയം ഒഴിവാക്കിക്കൊണ്ട് നിര്മിക്കപ്പെട്ട എല്ലാ ജ്യാമിതികളും അയൂക്ലീഡിയന് വിഭാഗത്തില്പ്പെടുന്നു. ഹൈപര്ബൊളിക ജ്യാമിതിയും എലിപ്റ്റിക ജ്യാമിതിയും അയൂക്ലീഡിയന് ജ്യാമിതികളാണ്. ആക്സിയങ്ങളുടെ സ്വീകാര രീതിയനുസരിച്ച് ഇവയെ യഥാക്രമം 'ലൊബാഷ്യേവ്സ്കിയന് ജ്യാമിതി' എന്നും 'റീമാനിയന് ജ്യാമിതി' എന്നും വിളിക്കുന്നു. | |
| - | അയൂക്ലീഡിയന് ജ്യാമിതി ( Non-EuclideanGeometry) | + | |
| - | + | ||
| - | + | ||
=====ഹൈപര്ബൊളിക ജ്യാമിതി===== | =====ഹൈപര്ബൊളിക ജ്യാമിതി===== | ||
'ഒരു നേര്വരയ്ക്കു സമാന്തരമായി അതിലില്ലാത്ത ഒരു ബിന്ദുവില്ക്കൂടി ചുരുങ്ങിയത് രണ്ടു വരകളെങ്കിലും വരയ്ക്കാം' എന്ന ആക്സിയമാണ് ഇതില് പകരം ആക്സിയമായി സ്വീകരിച്ചിരിക്കുന്നത്. ഈ ജ്യാമിതിയില് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക 0°-ക്കും 180°-ക്കും ഇടയില് ഏതു വിലയും ആകാം. മറ്റൊരു പ്രമേയമാണ് തുല്യ അകലമുള്ള രണ്ടു സമാന്തരരേഖകള് ഇല്ല എന്നത്. ഹൈപര്ബൊളിക ജ്യാമിതിയില് ഒരു ത്രികോണത്തിന്റെ വിസ്തീര്ണം കുറഞ്ഞുവരുന്തോറും അതിലെ കോണങ്ങളുടെ തുക കൂടുകയും വിസ്തീര്ണം പൂജ്യത്തെ സമീപിക്കുമ്പോള് കോണങ്ങളുടെ തുക 180° യോടടുക്കുകയും ചെയ്യുന്നു. ത്രികോണം ABC-യില്, കോണങ്ങള് റേഡിയന് അളവില് α, β, γ ആയാല് ത്രികോണത്തിന്റെ വിസ്തീര്ണം K = k (π - α - β - γ) ആണ്. ഇതില് നിന്ന് K < k π എന്നു കിട്ടുന്നു. അതായത് ത്രികോണങ്ങളുടെ വിസ്തീര്ണം പരിബദ്ധം (bounded) ആണ്. ത്രികോണങ്ങളെ സംബന്ധിച്ച് വിസ്മയം പകരുന്ന ഒരു അയൂക്ലീഡിയന് ഗുണധര്മമാണിത്. | 'ഒരു നേര്വരയ്ക്കു സമാന്തരമായി അതിലില്ലാത്ത ഒരു ബിന്ദുവില്ക്കൂടി ചുരുങ്ങിയത് രണ്ടു വരകളെങ്കിലും വരയ്ക്കാം' എന്ന ആക്സിയമാണ് ഇതില് പകരം ആക്സിയമായി സ്വീകരിച്ചിരിക്കുന്നത്. ഈ ജ്യാമിതിയില് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക 0°-ക്കും 180°-ക്കും ഇടയില് ഏതു വിലയും ആകാം. മറ്റൊരു പ്രമേയമാണ് തുല്യ അകലമുള്ള രണ്ടു സമാന്തരരേഖകള് ഇല്ല എന്നത്. ഹൈപര്ബൊളിക ജ്യാമിതിയില് ഒരു ത്രികോണത്തിന്റെ വിസ്തീര്ണം കുറഞ്ഞുവരുന്തോറും അതിലെ കോണങ്ങളുടെ തുക കൂടുകയും വിസ്തീര്ണം പൂജ്യത്തെ സമീപിക്കുമ്പോള് കോണങ്ങളുടെ തുക 180° യോടടുക്കുകയും ചെയ്യുന്നു. ത്രികോണം ABC-യില്, കോണങ്ങള് റേഡിയന് അളവില് α, β, γ ആയാല് ത്രികോണത്തിന്റെ വിസ്തീര്ണം K = k (π - α - β - γ) ആണ്. ഇതില് നിന്ന് K < k π എന്നു കിട്ടുന്നു. അതായത് ത്രികോണങ്ങളുടെ വിസ്തീര്ണം പരിബദ്ധം (bounded) ആണ്. ത്രികോണങ്ങളെ സംബന്ധിച്ച് വിസ്മയം പകരുന്ന ഒരു അയൂക്ലീഡിയന് ഗുണധര്മമാണിത്. | ||
| - | |||
| - | |||
=====എലിപ്റ്റിക ജ്യാമിതി===== | =====എലിപ്റ്റിക ജ്യാമിതി===== | ||
1854-ല് റീമാന് രൂപം കൊടുത്ത അയൂക്ലീഡിയ ജ്യാമിതിയാണിത്. യൂക്ല ഡിന്റെ സമാന്തര ആക്സിയത്തിനു ബദലായി 'സമാന്തര രേഖകള് ഇല്ല' എന്ന ആക്സിയം റീമാന് സ്വീകരിച്ചു. | 1854-ല് റീമാന് രൂപം കൊടുത്ത അയൂക്ലീഡിയ ജ്യാമിതിയാണിത്. യൂക്ല ഡിന്റെ സമാന്തര ആക്സിയത്തിനു ബദലായി 'സമാന്തര രേഖകള് ഇല്ല' എന്ന ആക്സിയം റീമാന് സ്വീകരിച്ചു. | ||
| - | |||
| - | |||
റീമാനിയന് ജ്യാമിതിയെക്കുറിച്ചു സാമാന്യമായി മനസ്സിലാക്കാന് സ്പേസില് ഒരു വക്രപ്രതലവും (curved surface)) അതില് ഒരു ബിന്ദുവും ബിന്ദുവില്ക്കൂടി പോകുന്ന വക്രപ്രതലത്തിന്റെ സ്പര്ശതലവും (tangent plane) സങ്കല്പിക്കുക. ഈ പ്രതലത്തിന്റെ രണ്ടു ബിന്ദുക്കളെ യോജിപ്പിക്കുമ്പോള് കിട്ടുന്ന 'നേര്വര' ഈ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന ഏറ്റവും നീളം കുറഞ്ഞ വക്രം (ജിയോഡസിക്ക്) ആയിരിക്കട്ടെ. അപ്പോള് പ്രതലത്തിലെ ബിന്ദുക്കള് രണ്ടു വിധത്തിലുള്ളവയാണ്: | റീമാനിയന് ജ്യാമിതിയെക്കുറിച്ചു സാമാന്യമായി മനസ്സിലാക്കാന് സ്പേസില് ഒരു വക്രപ്രതലവും (curved surface)) അതില് ഒരു ബിന്ദുവും ബിന്ദുവില്ക്കൂടി പോകുന്ന വക്രപ്രതലത്തിന്റെ സ്പര്ശതലവും (tangent plane) സങ്കല്പിക്കുക. ഈ പ്രതലത്തിന്റെ രണ്ടു ബിന്ദുക്കളെ യോജിപ്പിക്കുമ്പോള് കിട്ടുന്ന 'നേര്വര' ഈ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന ഏറ്റവും നീളം കുറഞ്ഞ വക്രം (ജിയോഡസിക്ക്) ആയിരിക്കട്ടെ. അപ്പോള് പ്രതലത്തിലെ ബിന്ദുക്കള് രണ്ടു വിധത്തിലുള്ളവയാണ്: | ||
| - | |||
| - | |||
ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം ഗോളാകൃതി പോലെയാവുകയും പ്രതലത്തിലെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലത്തിന്റെ ഒരു വശത്തുമാത്രം പ്രതലം ഉണ്ടായിരിക്കുകയും ചെയ്യുന്ന അവസ്ഥ. പ്രതലത്തിലെ ഇത്തരം ബിന്ദുക്കളെ എലിപ്റ്റിക ബിന്ദുക്കള് എന്നു പറയുന്നു. | ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം ഗോളാകൃതി പോലെയാവുകയും പ്രതലത്തിലെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലത്തിന്റെ ഒരു വശത്തുമാത്രം പ്രതലം ഉണ്ടായിരിക്കുകയും ചെയ്യുന്ന അവസ്ഥ. പ്രതലത്തിലെ ഇത്തരം ബിന്ദുക്കളെ എലിപ്റ്റിക ബിന്ദുക്കള് എന്നു പറയുന്നു. | ||
| - | |||
| - | |||
[[ചിത്രം:Jyoth Sr12.png]] | [[ചിത്രം:Jyoth Sr12.png]] | ||
| - | |||
| - | |||
ഇവിടെ സ്പര്ശതലം ഒരല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് അതു പ്രതലത്തെ എലിപ്റ്റിക വക്രത്തിന്റെ ആകൃതിയില് ഛേദിക്കുന്നു. ചിത്രം (17) നോക്കുക. | ഇവിടെ സ്പര്ശതലം ഒരല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് അതു പ്രതലത്തെ എലിപ്റ്റിക വക്രത്തിന്റെ ആകൃതിയില് ഛേദിക്കുന്നു. ചിത്രം (17) നോക്കുക. | ||
| - | |||
| - | |||
ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം രണ്ടുവശവും ഉയര്ന്ന് നടുക്കു കുഴിഞ്ഞിരിക്കുകയും (മോഡയുടെ പാര്ശ്വതലം പോലെ) പ്രതലത്തിന്റെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലം പ്രതലത്തെ രണ്ടായി ഛേദിക്കുകയും ചെയ്യുന്ന അവസ്ഥ. | ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം രണ്ടുവശവും ഉയര്ന്ന് നടുക്കു കുഴിഞ്ഞിരിക്കുകയും (മോഡയുടെ പാര്ശ്വതലം പോലെ) പ്രതലത്തിന്റെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലം പ്രതലത്തെ രണ്ടായി ഛേദിക്കുകയും ചെയ്യുന്ന അവസ്ഥ. | ||
| - | |||
| - | |||
[[ചിത്രം:Jyoth img1.png|200px]] | [[ചിത്രം:Jyoth img1.png|200px]] | ||
| - | |||
| - | |||
ഇവിടെ സ്പര്ശതലം അല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് പ്രതലത്തെ ഹൈപര്ബൊളയുടെ വക്രത്തിന്റെ ആകൃതിയില് രണ്ടായി ഛേദിക്കുന്നു. പ്രതലത്തിലുള്ള ഇത്തരം ബിന്ദുക്കളെ ഹൈപര്ബൊളിക ബിന്ദുക്കള് എന്നു പറയുന്നു. ചിത്രം (18) നോക്കുക. | ഇവിടെ സ്പര്ശതലം അല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് പ്രതലത്തെ ഹൈപര്ബൊളയുടെ വക്രത്തിന്റെ ആകൃതിയില് രണ്ടായി ഛേദിക്കുന്നു. പ്രതലത്തിലുള്ള ഇത്തരം ബിന്ദുക്കളെ ഹൈപര്ബൊളിക ബിന്ദുക്കള് എന്നു പറയുന്നു. ചിത്രം (18) നോക്കുക. | ||
| - | |||
| - | |||
സ്പേസിലെ ജ്യാമിതി വിഭാവന ചെയ്യുന്ന പ്രത്യേകതകള് റീമാന്റെ പഠനങ്ങള്ക്കനുയോജ്യമാണ്. റീമാന്റെ ജ്യാമിതിയില് എല്ലാ ദൂരങ്ങളും ഒരു ധനസ്ഥിരാങ്കത്തിനു തുല്യമോ അതില് കുറവോ ആയിരിക്കും. അതുകൊണ്ട് മറ്റ് ജ്യാമിതികളില് നിന്നു വ്യത്യസ്തങ്ങളായ പല ഗുണധര്മങ്ങളും ഈ ജ്യാമിതിയിലുണ്ട്. ഉദാ. ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക എപ്പോഴും 180° യില് കൂടുതലായിരിക്കും. ചതുര്ഭുജത്തിലെ നാലു കോണുകളുടെ തുക 360° യിലും അധികമാണ്. ത്രികോണം ABC യില് കോണങ്ങള് ആയാല് അതിന്റെ വിസ്തീര്ണം K കണ്ടുപിടിക്കാനുള്ള റീമാന്റെ ഫോര്മുലയാണ് [[ചിത്രം:Jyoth sr11.png]]. ഇതില് നിന്നു ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യത്തോടടുക്കുമ്പോള് കോണങ്ങളുടെ തുക ക്രമേണ കുറഞ്ഞ് 180°-യോടടുക്കുന്നു എന്നു വ്യക്തമാണ്. ഇറ്റലിക്കാരായ റിക്കി (Gregorio Ricci: 18531925) യും ലെവി-സിവിറ്റ (Tullio Levi-Civita: 18731941)യും റീമാന്റെ അയുക്ളീഡിയന് ജ്യാമിതിയില് പില്ക്കാലത്തു കൂടുതല് പഠനങ്ങള് നടത്തിയവരാണ്. | സ്പേസിലെ ജ്യാമിതി വിഭാവന ചെയ്യുന്ന പ്രത്യേകതകള് റീമാന്റെ പഠനങ്ങള്ക്കനുയോജ്യമാണ്. റീമാന്റെ ജ്യാമിതിയില് എല്ലാ ദൂരങ്ങളും ഒരു ധനസ്ഥിരാങ്കത്തിനു തുല്യമോ അതില് കുറവോ ആയിരിക്കും. അതുകൊണ്ട് മറ്റ് ജ്യാമിതികളില് നിന്നു വ്യത്യസ്തങ്ങളായ പല ഗുണധര്മങ്ങളും ഈ ജ്യാമിതിയിലുണ്ട്. ഉദാ. ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക എപ്പോഴും 180° യില് കൂടുതലായിരിക്കും. ചതുര്ഭുജത്തിലെ നാലു കോണുകളുടെ തുക 360° യിലും അധികമാണ്. ത്രികോണം ABC യില് കോണങ്ങള് ആയാല് അതിന്റെ വിസ്തീര്ണം K കണ്ടുപിടിക്കാനുള്ള റീമാന്റെ ഫോര്മുലയാണ് [[ചിത്രം:Jyoth sr11.png]]. ഇതില് നിന്നു ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യത്തോടടുക്കുമ്പോള് കോണങ്ങളുടെ തുക ക്രമേണ കുറഞ്ഞ് 180°-യോടടുക്കുന്നു എന്നു വ്യക്തമാണ്. ഇറ്റലിക്കാരായ റിക്കി (Gregorio Ricci: 18531925) യും ലെവി-സിവിറ്റ (Tullio Levi-Civita: 18731941)യും റീമാന്റെ അയുക്ളീഡിയന് ജ്യാമിതിയില് പില്ക്കാലത്തു കൂടുതല് പഠനങ്ങള് നടത്തിയവരാണ്. | ||
| - | |||
| - | |||
(പ്രൊഫ. കെ. ജയചന്ദ്രന്) | (പ്രൊഫ. കെ. ജയചന്ദ്രന്) | ||
Current revision as of 13:51, 19 ഏപ്രില് 2016
ജ്യാമിതി
Geometry
സ്പേസിന്റെയും അതിലുള്ള വസ്തുക്കളുടെയും ഗുണധര്മങ്ങളെക്കുറിച്ചു പ്രതിപാദിക്കുന്ന ഗണിതശാസ്ത്രശാഖ. 'ജ്യ' (ഭൂമി), 'മെട്രോണ്' (അളവ്) എന്നീ ഗ്രീക്കു പദങ്ങളില് നിന്നാണ് ജ്യാമിതി എന്നര്ഥം വരുന്ന ജ്യോമട്രി എന്ന ഇംഗ്ലീഷ് സംജ്ഞ രൂപംകൊണ്ടത്. ജ്യാമിതിക്കു പല വിഭാഗങ്ങളും ഇന്നു നിലവിലുണ്ട്. സമതല ജ്യാമിതി (Plane Geometry), ഘന ജ്യാമിതി (Solid Geometry) തുടങ്ങിയ ക്ലാസ്സിക്കല് പഠനവിഭാഗങ്ങളും, അമൂര്ത്തങ്ങളായ ആശയങ്ങളും ചിന്താധാരകളും ഉള്ക്കൊള്ളുന്ന ടോപോളജി (Tropology) പോലുള്ള ആധുനിക വിഭാഗങ്ങളും ഇതിലുള്പ്പെടുന്നു.
ആമുഖം
പ്രാചീന നാഗരികതകളുടെ പ്രായോഗികാവശ്യങ്ങളുമായി ബന്ധപ്പെട്ടാണു ജ്യാമിതി ഉരുത്തിരിഞ്ഞത്. ആദ്യകാലത്ത് ഈജിപ്തിലും മെസപ്പൊട്ടേമിയയിലും ഭൂമി അളക്കാന് സര്വേക്ഷണം ചെയ്യുന്നവര് ജ്യാമിതി ഉപയോഗിച്ചുതുടങ്ങി. പിന്നീട് ഗ്രീക്കുകാരുടെ സംഭാവനകളിലൂടെ ജ്യാമിതി ഒരു ശാസ്ത്രമായി വളര്ന്നു.
ഒരു നേര്വരയ്ക്കു ചെറിയ തോതിലാണെങ്കിലും ഒരു വീതി യും സങ്കീര്ണമായ തന്മാത്രീയ ഘടനയുമുണ്ട്. എന്നാല് ഗണിതശാസ്ത്രപരമായ അവലോകനത്തില് ഇവയൊക്കെ അവഗണിച്ച് രേഖയുടെ നീളവും ഋജുത്വ (straightness) വും മാത്രം കണക്കിലെടുക്കുന്നു. അതുപോലെ ഒരു റബ്ബര് പന്തിന്റെ ആകൃതിയിലുള്ള ഏറ്റക്കുറച്ചിലുകള് അവഗണിച്ച് അതിനെ ഗണിതശാസ്ത്രപരമായ ഒരു ഗോളമായി കരുതുന്നു. ചുരുക്കത്തില് ഭൗതിക പദാര്ഥങ്ങളുടെ മാതൃകാരൂപം (idealised shape) ആണ് ജ്യാമിതിയില് പരിഗണിക്കുന്നത്.
ജ്യാമിതിയുടെ വികാസം
ആദ്യകാലത്ത് കൃഷിഭൂമിയുടെ അരികളവ്, വിസ്തീര്ണം എന്നിവയുടെ നിര്ണയത്തിനും പാര്പ്പിടങ്ങള്, ആരാധനാലയങ്ങള്, പിരമിഡുകള്, തോടുകള് എന്നിവയുടെ നിര്മാണത്തിനും ജ്യാമിതീയരൂപങ്ങളുടെ നീളം, വിസ്തീര്ണം, ഉള്ളളവ് എന്നിവയെക്കുറിച്ചുള്ള സാമാന്യമായ അറിവു വേണ്ടിവന്നു. പില്ക്കാലത്ത്, വിസ്തൃതങ്ങളായ ഭൂപ്രദേശങ്ങളുടെ സര്വേ, ഭൂപട നിര്മാണം, ഭൂമിയുടെ ആകൃതി നിര്ണയനം, ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥപഠനം ഇവയൊക്കെ ജ്യാമിതീയ പഠനങ്ങളെ വിപുലമാക്കി.
പ്രാചീന ജ്യാമിതി (Ancient Geometry)
ഈജിപ്തുകാര്, ബാബിലോണിയക്കാര്
ഈജിപ്ത്, ബാബിലോണിയ, ഇന്ത്യ, ചൈന എന്നീ രാജ്യങ്ങള് പുരാതന കാലത്തുതന്നെ ഗണിതശാസ്ത്രപരമായ നേട്ടങ്ങള് കൈവരിച്ചിരുന്നു. ബി.സി. 4000-300 കാലഘട്ടത്ത് ഈജിപ്തുകാരും ബാബിലോണിയക്കാരും ത്രികോണം, ദീര്ഘചതുരം, വൃത്തം എന്നിവയുടെ സവിശേഷതകള് സംബന്ധിച്ച ജ്യാമിതീയ വിശകലനം നടത്തിയതിന്റെ ചരിത്രരേഖകള് ലഭ്യമാണ്. ഇവരുടെ നാഗരികതകള് മുഖ്യമായും കൃഷിയിലധിഷ്ഠിതമായിരുന്നു. അതിനാല് കൃഷിസ്ഥലങ്ങളുടെ അളന്നുതിരിക്കലിലും അവയുടെ ചുറ്റളവും വിസ്തീര്ണവും കണക്കുകൂട്ടുന്നതിലും അവര് ശ്രദ്ധ ചെലുത്തി. നൈല്നദിയിലെ വെള്ളപ്പൊക്കത്തില് കൃഷിഭൂമി നഷ്ടപ്പെട്ടവര്ക്ക് അവരുടെ ഭൂമിയുടെ വിസ്തീര്ണമനുസരിച്ച് കൃഷിസ്ഥലങ്ങള് പുനര്നിര്ണയം ചെയ്തുകൊടുക്കേണ്ടി വന്നു. ജ്യാമിതിയുടെ തുടക്കം ഇതില് നിന്നാണ് എന്നു ബി.സി. 5-ാം ശ.-ലെ ഗ്രീക്കു ചരിത്രകാരനായ ഹെറൊഡോട്ടസ് രേഖപ്പെടുത്തിയിട്ടുണ്ട്. ബാബിലോണിയയില് ജലസേചനത്തിനു യൂഫ്രട്ടിസ്, ടൈഗ്രിസ് എന്നീ നദികളില് നിന്നു വലിയ തോടുകള്വഴി ജലം കൊണ്ടുവന്നിരുന്നു. ഈ തോടുകള് നിര്മിക്കാന് കുഴിച്ചെടുക്കേണ്ട മണ്ണിന്റെ വ്യാപ്തം നിര്ണയിക്കേണ്ടിവന്നു. ആരാധനാലയങ്ങള്, പിരമിഡുകള് എന്നിവയുടെ നിര്മിതിക്കു വിസ്തീര്ണം, വ്യാപ്തം എന്നിവയെ സംബന്ധിച്ച സാമാന്യമായ അറിവ് ആവശ്യമായി വന്നു. ഇവയൊക്കെ ജ്യാമിതിയുടെ തുടക്കത്തിനും പുരോഗതിക്കും നിദാനമായി. അഹ്മെസ് പാപ്പിറസ് (ബി.സി.1650) എന്ന പ്രാചീന ഈജിപ്ഷ്യന് ഗ്രന്ഥത്തില് ജ്യാമിതിയിലെ കുറെ പ്രശ്നങ്ങളും അവയുടെ നിര്ധാരണവും അടങ്ങിയിട്ടുണ്ട്.
ഗ്രീക്കുകാരുടെ സമീപനം
ജ്യാമിതിയുടെ പ്രാഥമിക പാഠങ്ങള് ഉള്ക്കൊണ്ട് ധൈഷണികമായ തലത്തിലേക്ക് ആദ്യമായി അന്വേഷണമാരംഭിച്ചതു ഗ്രീക്കുകാരാണ്. അവരുടെ ഗണിതീയ സിദ്ധാന്തങ്ങള് രചിക്കപ്പെട്ടത് ബി.സി. 600-200 കാലയളവിലാണ്. ഗ്രീക്കു ഗണിതശാസ്ത്രജ്ഞരില് പലരും തത്ത്വചിന്തകര് കൂടിയായിരുന്നു. പ്രകൃതിയുടെ രൂപകല്പന ജ്യാമിതീയമാണെന്ന് അവര് വിശ്വസിച്ചു. 'ഈശ്വരന് അനശ്വരമായി ജ്യാമിതീകരിക്കുന്നു (God eternally geometrizes)' എന്ന പ്ലേറ്റോയുടെ സാക്ഷ്യപ്പെടുത്തല് ഗ്രീക്കുകാരുടെ ഗണിതസങ്കല്പം വ്യക്തമാക്കുന്നു. സ്വയംസിദ്ധങ്ങളായ പ്രസ്താവനകളില് നിന്നു കാര്യകാരണസഹിതം നിഗമനങ്ങളിലെത്തുക എന്നതായിരുന്നു അവരുടെ രീതി. സ്വയംസിദ്ധങ്ങളായ ഇത്തരം പ്രസ്താവനകളാണ് അഭിഗൃഹീതങ്ങള് (axioms). ഉദാ. ഒരു ഋജുരേഖ എതിര്ദിശകളിലേക്ക് അനന്തമായി നീണ്ടുപോകുന്നു; സന്നിപതിക്കുന്ന(coincide)രൂപങ്ങള് സര്വസമ (congruent)ങ്ങളാണ്. എലിമെന്റ്സ് എന്ന ഗ്രന്ഥത്തില് യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) ഇത്തരം അഭിഗൃഹീതങ്ങളുപയോഗിച്ച് അഞ്ഞൂറോളം പ്രമേയങ്ങള് അവതരിപ്പിച്ചിട്ടുണ്ട്. യൂക്ലീഡിയന് ജ്യാമിതിയില് അക്കാലത്ത് അറിയാമായിരുന്ന ബീജഗണിതവും കാണാം. ഉദാ. x2 – 8x + 7 = 0എന്ന ദ്വിഘാത സമവാക്യത്തിന്റെ നിര്ധാരണമൂല്യം സംഖ്യയ്ക്കു പകരം ഒരു രേഖാഖണ്ഡമായി കൊടുത്തിരിക്കുന്നു.
ഗ്രീക്ക് ജ്യാമിതി കൈകാര്യം ചെയ്ത പ്രധാനാശയങ്ങള് സര്വസമത (congruence), സമരൂപത (similarity), തുല്യത (equivalence) എന്നിവയാണ്. അലക്സാന്ഡ്രിയന് കാലഘട്ടത്തില് (ബി.സി. 4-ാം ശ.) ഗ്രീക്ക് ഗണിതത്തിനു പ്രായോഗികമായ ഒരടിത്തറ കൈവന്നു. ഇക്കാലത്താണ് ആര്ക്കിമെഡിസ് π (പൈ)യുടെ വില ![]() നും
നും ![]() നും ഇടയ്ക്കാണെന്നു കണ്ടുപിടിച്ചത്. എ.ഡി. 18-ാം ശ. വരെ ഗണിതശാസ്ത്രത്തില് മുഖ്യസ്ഥാനം ഗ്രീക്കുകാരുടെ ക്ലാസ്സിക് ജ്യാമിതിക്കായിരുന്നു.
നും ഇടയ്ക്കാണെന്നു കണ്ടുപിടിച്ചത്. എ.ഡി. 18-ാം ശ. വരെ ഗണിതശാസ്ത്രത്തില് മുഖ്യസ്ഥാനം ഗ്രീക്കുകാരുടെ ക്ലാസ്സിക് ജ്യാമിതിക്കായിരുന്നു.
ജ്യാമിതിയിലെ ആധുനികത
പ്രക്ഷേപീയ ജ്യാമിതി (Projective Geometry)
ആധുനിക ജ്യാമിതിയുടെ ഒരു പ്രധാന ശാഖയാണിത്. പ്രകൃതിയിലെ ജ്യാമിതീയ രൂപമുള്ള വസ്തുക്കള്ക്കു പ്രക്ഷേപ(projection)ത്തിലൂടെയുണ്ടാകുന്ന മാറ്റമാണ് ഇതില് പഠനവിധേയമാക്കുന്നത്. ത്രിവിമീയ വസ്തുക്കളെ ദ്വിവിമീയ കാന്വാസില് പകര്ത്താന് ചിത്രമെഴുത്തുകാര് നടത്തിയ ശ്രമങ്ങളില് നിന്നാണ് ഈ ജ്യാമിതിയുടെ തുടക്കം. 14-ാം ശ.-ത്തിലെ നവോത്ഥാന (renaissance)ത്തോടെ കൂടുതല് യഥാതഥ(realistic)മായ ഒരു ശൈലി ചിത്രകാരന്മാര് സ്വീകരിച്ചു. അവര് അവതരിപ്പിച്ച പ്രക്ഷേപം, ഛേദം (section) എന്നിവയെക്കുറിച്ചുള്ള ആശയങ്ങള് ഗണിതശാസ്ത്രജ്ഞര്ക്കു മൗലികപ്രാധാന്യമുള്ള ഒരു ജ്യാമിതീയ പ്രശ്നമായിരുന്നു. പ്രക്ഷേപത്തിലൂടെ ജ്യാമിതീയാകൃതിയുടെ ഛേദത്തിനു മാറ്റം സംഭവിക്കുന്നുണ്ടെങ്കിലും അതിന്റെ മറ്റു ഗുണധര്മങ്ങള്ക്ക് ഒരു മാറ്റവും സംഭവിക്കുന്നില്ല എന്ന് അവര് മനസ്സിലാക്കി.
ജെറാള്ഡ് ദെസാര്ഗ്യു (1591-1661), ബ്ലെയ്സ് പാസ്കല് (1623-62), ഗാസ്പാര്ഡ് മോംഗ് (1746-1818), പോണ്സലെ (1788-1867) എന്നിവരെല്ലാം പ്രക്ഷേപീയ ജ്യാമിതിയില് പഠനം നടത്തിയവരാണ്.
ജ്യാമിതിയും ബീജഗണിതവും
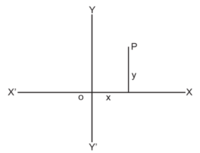
17-ഉം 18-ഉം ശ.-ങ്ങളിലെ ശാസ്ത്രീയ പുരോഗതി കൂടുതല് സങ്കീര്ണമായ ജ്യാമിതീയ പ്രശ്നങ്ങള് കൈകാര്യം ചെയ്യാനിടയാക്കി. കോപ്പര്നിക്കസിന്റെയും കെപ്ലറുടെയും ജ്യോതിശ്ശാസ്ത്ര നിഗമനങ്ങളനുസരിച്ച്, സൂര്യനെ ചുറ്റിയുള്ള ഗ്രഹങ്ങളുടെ പഥം നിര്ണയിക്കപ്പെട്ടതോടെ കോണിക പരിച്ഛേദങ്ങളെ(conic sections) കുറിച്ചുള്ള പഠനം സജീവമായി. പീരങ്കിയില് നിന്നു കുതിച്ചുപായുന്ന വെടിയുണ്ട സഞ്ചരിക്കുന്നത് ഒരു പ്രക്ഷേപ്യ(projectile)ത്തിന്റെ പഥത്തിലൂടെയാണെന്നു മനസ്സിലായതോടെ ഈ ജ്യാമിതീയ പഥത്തെക്കുറിച്ചു കൂടുതല് അറിയേണ്ട ആവശ്യം വന്നുചേര്ന്നു. ഇത്തരം ജ്യാമിതീയ പ്രശ്നങ്ങളില് ബീജഗണിതത്തിന്റെ ഉപയോഗം കണ്ടെത്തിയത് ഫ്രഞ്ചു ഗണിതജ്ഞരായ ദെക്കാര്ത്തെ (1596-1650)യും ഫെര്മ (1601-65)യുമായിരുന്നു. ഇവരാണ് അനലിറ്റിക്ക് ജ്യോമട്രി (കാര്ട്ടീഷ്യന് ജ്യോമട്രി)യുടെ ഉപജ്ഞാതാക്കള്. ഇതില് ജ്യാമിതീയാശയങ്ങളെ ബീജഗണിതവുമായി സമന്വയിപ്പിച്ച് വക്രങ്ങളുടെ സമവാക്യങ്ങള് (equations) എഴുതുന്നു. സമതലത്തിലുള്ള ഒരു ബിന്ദുവിനെക്കുറിക്കാന് സംഖ്യകളുടെ ക്രമിതയുഗ്മവും (ordered pair) സ്പേസിലാണെങ്കില് ക്രമിത ത്രികവും (ordered triplet) ഉപയോഗിക്കുന്നു. ഉദാ. (x, y) ഒരു ബിന്ദുവിനെ കുറിക്കുന്നു എങ്കില് ആദ്യസംഖ്യ x നിര്ദേശാങ്കം: ബിന്ദുവിന് y അക്ഷത്തില് നിന്നുള്ള അകലം; രണ്ടാം സംഖ്യ y - നിര്ദേശാങ്കം: ബിന്ദുവിന് x അക്ഷത്തില് നിന്നുള്ള അകലം. മൂലബിന്ദു(origin)വില് നിന്ന് (x,y) എന്ന ബിന്ദുവിന്റെ അകലമാണ് ![]() . കേന്ദ്രം മൂലബിന്ദുവും ആരം (radius)r- ഉം ആയ ഒരു വൃത്തത്തിലെ ഏതെങ്കിലും ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് (x,y) ആയാല് x2 + y2 = r2 എന്നു കിട്ടുന്നു. നിര്ദേശാങ്കങ്ങളുടെ പരസ്പരബന്ധം കുറിക്കുന്ന ഈ ബീജിയ സമവാക്യമാണു വൃത്തത്തിന്റെ സമവാക്യം അഥവാ സമീകരണം (equation). ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നും ഒരു നിര്ദിഷ്ടരേഖയില് നിന്നുമുള്ള അകലങ്ങളുടെ അനുപാതം സ്ഥിരസംഖ്യയാകത്തക്കവണ്ണം ഒരു ബിന്ദു ചലിച്ചാല് അതിന്റെ ബിന്ദുപഥത്തെ കോണികം (conic) അല്ലെങ്കില് കോണികപരിച്ഛേദം (conic section) എന്നു പറയുന്നു. നിശ്ചിത ബിന്ദു കോണികത്തിന്റെ ഫോക്കസും നിര്ദിഷ്ടരേഖ ഡയറിട്രിക്സും ആണ്. സ്ഥിരസംഖ്യയായ അനുപാതമാണ് കോണികത്തിന്റെ ഉള്കേന്ദ്രത(eccentricity). ഈ ഉള്കേന്ദ്രത ഒന്നോ, ഒന്നില് കുറവോ, ഒന്നില് കൂടുതലോ ആകുന്നതനുസരിച്ചു കിട്ടുന്ന വക്രങ്ങളെ യഥാക്രമം പരാബൊള, എലിപ്സ്, ഹൈപര്ബൊള എന്നു വിളിക്കുന്നു. പീരങ്കിയില് നിന്നു ചീറിപ്പായുന്ന വെടിയുണ്ടയുടെ പഥം പരാബൊളയാണ്. സൗരയൂഥത്തിലെ ഗ്രഹങ്ങള് സൂര്യനെ ചുറ്റുന്ന പഥം ദീര്ഘവൃത്തം (ellipse) ആണ്. സൂര്യന് ദീര്ഘവൃത്തത്തിന്റെ ഒരു ഫോക്കസില് സ്ഥിതിചെയ്യുന്നു.
. കേന്ദ്രം മൂലബിന്ദുവും ആരം (radius)r- ഉം ആയ ഒരു വൃത്തത്തിലെ ഏതെങ്കിലും ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് (x,y) ആയാല് x2 + y2 = r2 എന്നു കിട്ടുന്നു. നിര്ദേശാങ്കങ്ങളുടെ പരസ്പരബന്ധം കുറിക്കുന്ന ഈ ബീജിയ സമവാക്യമാണു വൃത്തത്തിന്റെ സമവാക്യം അഥവാ സമീകരണം (equation). ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നും ഒരു നിര്ദിഷ്ടരേഖയില് നിന്നുമുള്ള അകലങ്ങളുടെ അനുപാതം സ്ഥിരസംഖ്യയാകത്തക്കവണ്ണം ഒരു ബിന്ദു ചലിച്ചാല് അതിന്റെ ബിന്ദുപഥത്തെ കോണികം (conic) അല്ലെങ്കില് കോണികപരിച്ഛേദം (conic section) എന്നു പറയുന്നു. നിശ്ചിത ബിന്ദു കോണികത്തിന്റെ ഫോക്കസും നിര്ദിഷ്ടരേഖ ഡയറിട്രിക്സും ആണ്. സ്ഥിരസംഖ്യയായ അനുപാതമാണ് കോണികത്തിന്റെ ഉള്കേന്ദ്രത(eccentricity). ഈ ഉള്കേന്ദ്രത ഒന്നോ, ഒന്നില് കുറവോ, ഒന്നില് കൂടുതലോ ആകുന്നതനുസരിച്ചു കിട്ടുന്ന വക്രങ്ങളെ യഥാക്രമം പരാബൊള, എലിപ്സ്, ഹൈപര്ബൊള എന്നു വിളിക്കുന്നു. പീരങ്കിയില് നിന്നു ചീറിപ്പായുന്ന വെടിയുണ്ടയുടെ പഥം പരാബൊളയാണ്. സൗരയൂഥത്തിലെ ഗ്രഹങ്ങള് സൂര്യനെ ചുറ്റുന്ന പഥം ദീര്ഘവൃത്തം (ellipse) ആണ്. സൂര്യന് ദീര്ഘവൃത്തത്തിന്റെ ഒരു ഫോക്കസില് സ്ഥിതിചെയ്യുന്നു.
ത്രിവിമീയ സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കാന് 3 സംഖ്യകള് ഉപയോഗിക്കുന്നു. x, y, z നിര്ദേശാങ്കങ്ങളായ ബിന്ദുവിന് മൂലബിന്ദുവില് നിന്നുള്ള അകലം ![]() ആണ്. x2 + y2 + z2 = r2 എന്നത് ഗോളത്തിന്റെയും ax + by + cz + d = 0 എന്നത് സമതലത്തിന്റെയും സമീകരണങ്ങളാണ്.
ആണ്. x2 + y2 + z2 = r2 എന്നത് ഗോളത്തിന്റെയും ax + by + cz + d = 0 എന്നത് സമതലത്തിന്റെയും സമീകരണങ്ങളാണ്.
അവകല ജ്യാമിതി (Differential Geometry)
ഈ ശാഖയില് അവകലഗണിത (Differential Calculus)ത്തിലെ ആശയങ്ങള് വ്യാപകമായി ഉപയോഗിക്കുന്നു. ഇതില് വക്രങ്ങളുടെ മൗലിക ഗുണധര്മങ്ങളായ ചരിവ് (slope), വക്രത (curvature) എന്നിവയ്ക്കു പുറമേ സ്പേസ് വക്രങ്ങള്, അവ ഉള്ക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ വിസ്തീര്ണമുള്ള പ്രതലങ്ങള്, ജിയോഡസിക്കുകള് എന്നിവയെക്കുറിച്ചു പ്രതിപാദിക്കുന്നു. ഫ്രഞ്ച് ഗണിതജ്ഞന് ഗാസ്പാര്ഡ് മോംഗ്, ജര്മന് ഗണിതശാസ്ത്രജ്ഞന് കാള് ഫ്രീഡ്റിക് ഗൗസ് എന്നിവരാണ് ഈ വിഭാഗത്തിലെ ആദ്യകാല ഗവേഷകര്. അവകലജ്യാമിതി 19-ഉം 20-ഉം ശ.-ങ്ങളില് സജാതീയ (Affine), പ്രക്ഷേപീയ (Projective), സമാകല (integral) ജ്യാമിതികളിലേക്കു വികസിക്കുകയും ചെയ്തിട്ടുണ്ട്.
വിവരണാത്മക ജ്യാമിതി (Descriptive Geometry)
ശില്പികളും എന്ജിനീയര്മാരും ഉപയോഗം കണ്ടെത്തുന്ന ജ്യാമിതീയ വിഭാഗമാണിത്. ഗാസ്പാര്ഡ് മോംഗാണ് ഇതിന്റെ ഉപജ്ഞാതാവ്. പ്രക്ഷേപം എന്ന തത്ത്വമുപയോഗിച്ച് ചിത്രങ്ങള് വരയ്ക്കേണ്ട രീതി ഇതില് ചര്ച്ച ചെയ്യുന്നു. കെട്ടിടനിര്മിതിയില് പ്ലാന്, എലിവേഷന് എന്നിവ തയ്യാറാക്കാന് ഇതുപകരിക്കുന്നു. ദര്ശനകോടി (perspective), ലംബിക പ്രക്ഷേപം (orthographic projection) എന്നിവ വിവരണാത്മക ജ്യാമിതിയിലെ പ്രധാന ആശയങ്ങളാണ്. ചിത്രകാരന്മാരായ ലിയോനാര്ഡോ ഡാവിഞ്ചിയും ആല്ബ്രെഹ്ത് ഡൂററും ഈ രംഗത്തു പ്രവര്ത്തിച്ചവരാണ്.
അയൂക്ലീഡിയന് പശ്ചാത്തലം (The non-Euclidean background)
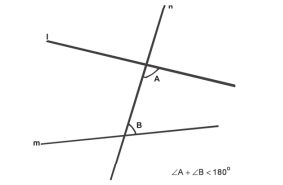
അഭിഗൃഹീതങ്ങളെ ആധാരമാക്കി രചിച്ച, നൂറ്റാണ്ടുകള് പഴക്കമുള്ള ജ്യാമിതീയ ശാഖയാണ് യൂക്ലീഡിയന് ജ്യാമിതി. യൂക്ലിഡിന്റെ 5-ാം ആക്സിയം 'സമാന്തര ആക്സിയം (axiom on parallels)' എന്നറിയപ്പെടുന്നത് ഇതാണ്.
'n എന്ന നേര്വര l, m എന്നീ നേര്വരകളെ ഖണ്ഡിക്കുമ്പോള് നേര്വരയുടെ ഒരു വശത്തുണ്ടാകുന്ന അന്തഃകോണങ്ങളുടെ ആകെത്തുക 180°-യില് കുറവാണെങ്കില്, n എന്ന നേര്വരയുടെ ഏതു വശത്താണോ അന്തഃകോണങ്ങള്, ആ വശത്ത് l,m എന്നീ നേര്വരകള് കൂട്ടിമുട്ടും'.
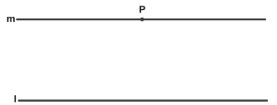
പല യൂക്ലീഡിയന് പ്രമേയങ്ങളും തെളിയിക്കുന്നത് ഈ ആക്സിയം ഉപയോഗിച്ചാണ്. ഉദാ. ഒരു ത്രികോണത്തിലെ 3 കോണങ്ങളുടെ തുക 180° ആയിരിക്കും. സ്വയംസിദ്ധമല്ല എന്ന കാരണത്താല് 18-ാം ശ.-ത്തിനുശേഷം ഗണിതജ്ഞര്ക്കു സമാന്തര ആക്സിയത്തില് പൊരുത്തക്കേടു തോന്നി. പ്ലേഫെയര് ഇതിനു പകരം പുതിയൊരു ആക്സിയം നിര്ദേശിച്ചു.
'l എന്നതു തന്നിട്ടുള്ള നേര്വരയും, P അതില് ഇല്ലാത്ത ഒരു ബിന്ദുവും ആണെങ്കില് അവയുടെ തലത്തില് P യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ ഒരൊറ്റ നേര്വര m മാത്രമേയുള്ളു'. സമാന്തരരേഖകളെക്കുറിച്ച് എളുപ്പത്തില് ഒരവബോധം ഉളവാക്കിയ ഈ ആക്സിയവും ഇതിനുശേഷം വച്ച എല്ലാ പകര ആക്സിയങ്ങളും നിരാകരിക്കപ്പെട്ടു.
സമാന്തര ആക്സിയത്തില് നിന്നും തികച്ചും വിഭിന്നമായ ഒരു ആക്സിയവുമായി ഗൗസ് രംഗത്തുവന്നു. 'l എന്നത് ഒരു നേര്വരയും P-യില്ക്കൂടി പോകുന്നതും l-നോടു കൂട്ടിമുട്ടാത്തതുമായ അസംഖ്യം നേര്വരകളുണ്ട്'. ഈ ആക്സിയവും യൂക്ലിഡിന്റെ മറ്റ് 9 ആക്സിയങ്ങളും ഉപയോഗിച്ച് അദ്ദേഹം പല പുതിയ പ്രമേയങ്ങളും തെളിയിച്ചു. ഈ ജ്യാമിതിക്ക് ഗൗസ് 'അയൂക്ലീഡിയന് ജ്യാമിതി' എന്നു പേരിട്ടു. ഈ ജ്യാമിതിയനുസരിച്ച് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ ആകെത്തുക 180°-യില് കുറവാണ്. പ്രഥമവീക്ഷണത്തില് ഇത് അബദ്ധജടിലമാണെന്നു തോന്നിയേക്കാം. ത്രികോണത്തിന്റെ വിസ്തൃതിയനുസരിച്ച് കോണങ്ങളുടെ ആകെത്തുകയിലും വ്യത്യാസം വരുന്നു. വിസ്തീര്ണം പൂജ്യത്തെ സമീപിക്കുമ്പോള് തുക 180°-യോട് അടുക്കും. സാധാരണ നാം ഉപയോഗിക്കുന്ന ത്രികോണങ്ങള് ചെറുതായിരിക്കും. അളക്കാനുപയോഗിക്കുന്ന ഉപകരണങ്ങളുടെ പിശകുകള് (errors) കൂടി പരിഗണിക്കുമ്പോള് തുക 180°-യോട് അടുത്തുമാത്രമേ വരൂ എന്നു കാണാം. ഇതുതന്നെയാണ് ഗൗസ് സിദ്ധാന്തിക്കുന്നതും. അയൂക്ലീഡിയന് ജ്യാമിതിയെ സംബന്ധിച്ച നിഗമനങ്ങളൊന്നും തന്നെ ഗൗസ് സ്വന്തം ജീവിതകാലത്ത് പ്രസിദ്ധീകരിച്ചില്ല. റഷ്യയിലെ നിക്കൊളായ് ലൊബാഷ്യേവ്സ്കിയുടെയും ഹംഗറിയിലെ യാനോസ്ബൊള്യായുടെയും പേരിലാണ് അയൂക്ലീഡിയന് ജ്യാമിതി പൊതുവെ അറിയപ്പെടുന്നത്. ലൊബാഷ്യേവ്സ്കി 1931-ലും ബൊള്യായി 1936-ലും സ്വതന്ത്രമായി ഗവേഷണഫലങ്ങള് പ്രസിദ്ധീകരിക്കുകയായിരുന്നു. ഇന്ന് ഹൈപര്ബൊളിക ജ്യാമിതി എന്ന പേരിലും ഈ ശാഖ അറിയപ്പെടുന്നു.
റീമാനിയന് ജ്യാമിതി (Riemanian Geometry)
ഗൗസിന്റെ ശിഷ്യനായ ഫ്രീഡ്റിഹ് ബെണ്ഹാര്ഡ് റീമാന് (1826-66) യൂക്ലിഡിന്റെ പല ആക്സിയങ്ങളെയും ചോദ്യം ചെയ്തു. ഒരു നേര്വര അനന്തമായി നീണ്ടുപോകുന്നു എന്ന യൂക്ലീഡിയന് ആക്സിയത്തിനെതിരായി ഭൗതിക സ്പേസിലെ ഒരു നേര്വര ഒരിക്കലും അനന്തതയിലേക്കു പോകുന്നതായി അനുഭവപ്പെടുന്നില്ല എന്നദ്ദേഹം പ്രസ്താവിച്ചു. ഒരു രേഖ അവസാനിക്കുന്നില്ല എന്നതുമാത്രമാണ് ഭൗതിക സത്യം. ഉദാ. ഭൂമധ്യരേഖ. അതായത് ഒരു രേഖ അവസാനമില്ലാത്തതാണെന്നോ (endless) പരിബദ്ധമാണെന്നോ (unbounded) പറയാമെന്നു മാത്രം. സമാന്തരരേഖകളില്ലെന്നു സങ്കല്പിച്ച് യൂക്ലീഡിയന് ജ്യാമിതിയിലെ ആക്സിയം മാറ്റിയെഴുതി റീമാന് നിര്മിച്ച മറ്റൊരു അയൂക്ളീഡിയന് ജ്യാമിതിയാണ് ദീര്ഘവൃത്തീയ ജ്യാമിതി(Elliptic Geometry). ഈ ജ്യാമിതിപ്രകാരം ഒരു ത്രികോണത്തിലെ 3 കോണങ്ങളുടെ ആകെത്തുക 180° യില് കൂടുതലാണ്. ദൂരം (distance) എന്നത് മാറിക്കൊണ്ടിരിക്കുന്ന ഒരു ചരരാശി (variable) ആണെന്നാണ് റീമാന്റെ കാഴ്ചപ്പാട്. കലന(Calculus)ത്തിന്റെ സാധ്യതകളും അവകലജ്യാമിതിയുടെ രീതികളും റീമാനിയന് ജ്യാമിതിയില് അവലംബിച്ചിരിക്കുന്നു. ഈ ജ്യാമിതീയ വിഭാഗത്തിനു പ്രാധാന്യം കൈവന്നത് 1915-ല് ആല്ബര്ട്ട് ഐന്സ്റ്റൈന് ആപേക്ഷികസിദ്ധാന്തം അവതരിപ്പിച്ചതോടെയാണ്. ഐന്സ്റ്റൈന് ഉപയോഗിച്ച ചതുര്വിമീയ സ്പേസ്-റ്റൈം ജ്യാമിതിയില് ദൂരങ്ങളെ സംബന്ധിച്ച ഫോര്മുല റീമാനിയന് ജ്യാമിതിയിലെന്നപോലെ ഒരു ചരരാശിയാണ്.
ടോപോളജി
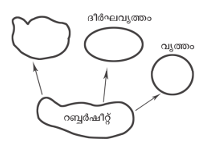
ജ്യാമിതിയുടെ ശാഖയായ ടോപോളജി 19-ാം ശ.-ത്തിലാണു രൂപപ്പെട്ടത്. ഓയ്ലര് (Euler), റീമാന്, പ്വാന്കറെ, കാന്റര് തുടങ്ങിയ ഗണിതശാസ്ത്രജ്ഞര് ഈ ശാഖയില് സംഭാവനകള് നല്കിയിട്ടുണ്ട്. വിരൂപണം (deformation) കൊണ്ട്, അതായത് വലിച്ചുനീട്ടല്, വളയ്ക്കല്, ചുക്കിച്ചുളിയല് മുതലായവകൊണ്ട്, വസ്തുവിന്റെ മാറ്റം വരാത്ത ഗുണധര്മങ്ങളുടെ പഠനമാണു ടോപോളജി. 'റബ്ബര്ഷീറ്റ് ജ്യോമട്രി' എന്ന പേരിലും ഇതറിയപ്പെടുന്നു.
ചിത്രം (3)-ല് വിരലുകൊണ്ട് റബ്ബര്ഷീറ്റില് ഉണ്ടാക്കിയിരിക്കുന്ന വിരൂപണങ്ങള് ശ്രദ്ധിക്കുക. ഇത്തരം വിരൂപണത്തില് അവശ്യം പാലിക്കേണ്ട വ്യവസ്ഥകള് നിഷ്കര്ഷിച്ചിട്ടുണ്ട്.
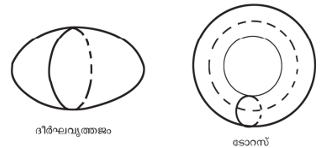
ടോപോളജിയില് ജ്യാമിതീയ രൂപങ്ങളുടെ വളരെ സാമാന്യമായ ഗുണധര്മങ്ങള് മാത്രമേ പഠനവിധേയമാക്കുന്നുള്ളു. യൂക്ലീഡിയന് ജ്യാമിതിയുമായുള്ള സുപ്രധാനമായ ഒരു വ്യത്യാസമാണിത്. ടോപോളജിയില് ഒരു വൃത്തത്തെ ദീര്ഘവൃത്തം കൊണ്ടോ ഗോളത്തെ അണ്ഡാകൃതിയിലുള്ള രൂപം കൊണ്ടോ പ്രതിസ്ഥാപിക്കാം. എന്നാല് ഗോളവും സൈക്കിള്ട്യൂബ് പോലുള്ള ടോറസ് (torus) എന്ന പ്രതലവും തമ്മില് അന്തരമുണ്ട്. വിരൂപണപ്രക്രിയകള്കൊണ്ടു കിട്ടുന്ന രൂപമാറ്റങ്ങള് ടോപോളജീയമായി തുല്യമാനമെന്നോ (topologically equivalent) ഹോമിയോമോര്ഫികമെന്നോ പറയുന്നു. വൃത്തവും ചതുരവും ടോപോളജീയമായി തുല്യമാനമാണ്. എന്നാല് ഒരു വൃത്തത്തെ വളച്ചൊടിച്ചോ ചുക്കിച്ചുളിച്ചോ കിട്ടുന്ന എട്ട് (8) എന്ന അക്കത്തിന്റെ ആകൃതി വൃത്താകൃതിയുമായി ടോപോളജീയമായി തുല്യമാനമല്ല.
ഗോളത്തിന്റെയോ ദീര്ഘവൃത്തജത്തിന്റെയോ പുറത്ത് ഒരു സംവൃതവക്രം വരയ്ക്കുമ്പോള് അതിനുള്ളില് എപ്പോഴും വിസ്തീര്ണമുള്ള ഒരു ഭാഗം വേര്തിരിയുന്നു. എന്നാല് ഒരു ടോറസിനു പുറത്ത് വിസ്തീര്ണമുള്ള ഭാഗം വേര്തിരിയാത്ത രണ്ടു സംവൃതവക്രങ്ങള് വരയ്ക്കാവുന്നതാണ് (ചിത്രം 4). അതുകൊണ്ട് ഗോളവും (ദീര്ഘവൃത്തവും) ടോറസും ടോപോളജീയമായി തുല്യമാനമല്ല.
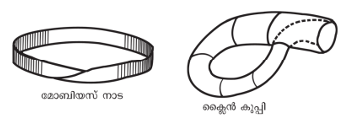
നമുക്കു ചുറ്റുമുള്ള ഭൗതികവസ്തുക്കളുടെ ചിത്രണമായ യൂക്ലീഡിയന് ജ്യാമിതിയില് എല്ലാ വസ്തുക്കള്ക്കും രണ്ടു വശമുണ്ട്. അതായത് ഒരു അകവശവും ഒരു പുറവശവും. എന്നാല് ഒരു വശം മാത്രമുള്ള പ്രതലങ്ങളെ ടോപോളജിസ്റ്റുകള് അവതരിപ്പിക്കുന്നു.
ചിത്രം (5)ലെ മോബിയസ് നാടയും ക്ളൈന്കുപ്പിയും ഒരു വശം മാത്രമുള്ള പ്രതലങ്ങളാണ്.
ടോപോളജിക്കുള്ള ഒരു മുഖവുര മാത്രമേ ഇവിടെ കൊടുത്തിട്ടുള്ളു. ഗണിതശാസ്ത്രത്തില് സ്പേസ് എന്ന വാക്ക് വളരെ അമൂര്ത്ത(abstract)മായ ഒരാശയത്തെയാണ് കുറിക്കുന്നത്. 19-ാം ശ.-ത്തിന്റെ അവസാനത്തോടെ പലതരത്തിലുള്ള സ്പേസുകളും അവയുടെ ഗുണധര്മങ്ങളും ആവിഷ്കരിക്കപ്പെട്ടു. ആധുനിക ഗണിതം സമ്മിശ്രവും അമൂര്ത്തവുമായി മാറിക്കൊണ്ടിരിക്കുമ്പോള് അമൂര്ത്തങ്ങളായ ആശയങ്ങള്ക്കു മുന്തൂക്കം ലഭിക്കുന്നു. എല്ലാവിധ സ്പേസുകളുടെയും പൊതുവായ ഗുണധര്മങ്ങള് കണക്കിലെടുത്ത് ജ്യാമിതീയാശയങ്ങള് ഉപയോഗിച്ച് സ്പേസുകളുടെ ഒരു അടിസ്ഥാനസിദ്ധാന്തത്തിനു ഫ്രഞ്ചുഗണിതജ്ഞനായ മോറിസ് ഫ്രെഷറ്റ് (1878-1973) രൂപം കൊടുത്തിട്ടുണ്ട്. 'അമൂര്ത്ത സ്പേസുകളുടെ സിദ്ധാന്തം (The theory of abstract spaces)' എന്ന പേരില് ഇതറിയപ്പെടുന്നു. ഫലനസ്പേസുകള് അനന്തവിമീയങ്ങളാണ്. ഫലനത്തെക്കുറിച്ചുള്ള സിദ്ധാന്തങ്ങളില് ജ്യാമിതീയമായ ഉള്ക്കാഴ്ച അവയുടെ സങ്കീര്ണസ്വഭാവത്തിന് അയവു വരുത്തുന്നതിനാല് സ്പേസുകളുടെ പഠനം എളുപ്പമാകുന്നു. ആധുനിക ഗണിതജ്ഞരുടെ വീക്ഷണത്തില് ഹോമിയോ മോര്ഫിക രൂപാന്തരണം കൊണ്ട് മാറ്റമില്ലാതെ തുടരുന്ന (നിശ്ചരമാകുന്ന) സ്പേസിലെ ഗുണധര്മങ്ങളെക്കുറിച്ചുള്ള പഠനമാണു ടോപോളജി.
യൂക്ലീഡിയന് ജ്യാമിതി (Euclidean Geometry)
ഗ്രീക്കു ഗണിതജ്ഞരുടെ സുപ്രധാന നേട്ടങ്ങളിലൊന്ന് നിഗമനങ്ങളിലൂടെ അവര് അവതരിപ്പിച്ച ജ്യാമിതിയാണ്. യൂക്ളീഡിന്റെ എലിമെന്റ്സ് എന്ന ഗ്രന്ഥം ജ്യാമിതീയ പഠനങ്ങളുടെ പ്രമാണഗ്രന്ഥമാണ്. 13 ഭാഗങ്ങളാണ് ഈ ഗ്രന്ഥത്തിനുള്ളത്. നേര്വര, ബിന്ദു, വൃത്തം, സമതലം, ഘനരൂപം എന്നിവയെക്കുറിച്ച് അറിയേണ്ട പല വിവരങ്ങളും തെളിവുകള് സഹിതം ഇതിലുണ്ട്. 5 ആക്സിയങ്ങളും 5 പൊതുതത്ത്വങ്ങളും ആധാരമാക്കിയുള്ള, ബുദ്ധിപൂര്വകമായ ചിന്താധാരയുടെ പരിണതഫലമാണ് യൂക്ലിഡിന്റെ പ്രമേയങ്ങള്.
യൂക്ലിഡിന്റെ ആക്സിയങ്ങള്
1. ഒരു ബിന്ദുവില് നിന്നു മറ്റൊരു ബിന്ദുവിലേക്ക് ഒരു നേര്വര വരയ്ക്കാം.
2. ഒരു നേര്വരയില്ക്കൂടി തുടര്ച്ചയായി സാന്തമായ ഒരു നേര്വര വരയ്ക്കാം.
3. ഒരു വൃത്തത്തിന്റെ കേന്ദ്രവും അതിലുള്ള ഒരു ബിന്ദുവും തന്നാല് വൃത്തം വരയ്ക്കാം.
4. എല്ലാ മട്ടകോണങ്ങളും തുല്യമായിരിക്കും.
5. ഒരു നേര്വര രണ്ടു നേര്വരകളെ ഖണ്ഡിക്കുമ്പോള് നേര്വരയുടെ ഒരു വശത്തുണ്ടാകുന്ന അന്തഃകോണങ്ങളുടെ ആകെത്തുക 180° യില് കുറവാണെങ്കില്, നേര്വരയുടെ ഏതു വശത്താണോ അന്തഃകോണങ്ങള്, ആ വശത്ത് രണ്ടു നേര്വരകളും സന്ധിക്കും.
യൂക്ലിഡിന്റെ പൊതുതത്ത്വങ്ങള്:
1. ഒരു വസ്തുവിനോടു തുല്യങ്ങളായ വസ്തുക്കളെല്ലാം അന്യോന്യം തുല്യങ്ങളാണ്.
2. തുല്യങ്ങളോടു തുല്യങ്ങള് കൂട്ടുമ്പോഴുണ്ടാകുന്ന തുകകള് തുല്യങ്ങളാണ്.
3. തുല്യങ്ങളില് നിന്നു തുല്യങ്ങള് കുറച്ചാലുണ്ടാകുന്ന ഫലങ്ങള് തുല്യങ്ങളായിരിക്കും.
4. സംപതിക്കുന്ന (coincide) വസ്തുക്കള് തുല്യങ്ങളായിരിക്കും.
5. പൂര്ണങ്ങള് ഭാഗങ്ങളെക്കാള് വലുതാണ്.
സമതല ജ്യാമിതി (Plane Geometry)
എലിമെന്റ്സിലെ 13 ഭാഗങ്ങളില് ആദ്യ ആറുഭാഗങ്ങള് സമതലജ്യാമിതിയെക്കുറിച്ചും പിന്നീടുള്ള 4 ഭാഗങ്ങള് സംഖ്യകളുടെയും ദൂരങ്ങളുടെയും ഗുണധര്മങ്ങളെക്കുറിച്ചും അവസാന 3 എണ്ണം ഘനജ്യാമിതിയെക്കുറിച്ചും പ്രതിപാദിക്കുന്നു. ജ്യാമിതീയ സങ്കല്പങ്ങള്ക്ക് അടിസ്ഥാനമിടുന്ന ബിന്ദു, രേഖ, തലം, വൃത്തം, പ്രതലം തുടങ്ങിയവയെ നിര്വചിച്ചുകൊണ്ടാണു യൂക്ലിഡ് പ്രമേയങ്ങളിലേക്കു കടക്കുന്നത്. ഇന്ന് ഈ പദങ്ങള്ക്കു നിര്വചനം കൊടുക്കാറില്ല.
സമതലജ്യാമിതിയില് രേഖാഖണ്ഡം (line segment), കോണം (angle), ത്രികോണം (triangle), ബഹുഭുജം (polygon), കോണിക പരിച്ഛേദം (conic section) എന്നിവയെക്കുറിച്ചുള്ള യൂക്ലിഡിന്റെ പഠനങ്ങള് പ്രാധാന്യമര്ഹിക്കുന്നു. ഒരു ഋജുരേഖയില് തന്നിട്ടുള്ള രണ്ടു ബിന്ദുക്കള്ക്കിടയിലുള്ള എല്ലാ ബിന്ദുക്കളും രേഖാഖണ്ഡത്തില് ഉള്പ്പെടുന്നു. രേഖാഖണ്ഡത്തിന് രണ്ട് അറ്റബിന്ദുക്കള് ഉണ്ട് എന്നതും അതു രേഖയെപ്പോലെ രണ്ടുവശങ്ങളിലേക്കും നീണ്ടുപോകുന്നില്ല എന്നതുമാണ് രേഖാഖണ്ഡവും രേഖയും തമ്മിലുള്ള വ്യത്യാസം. രശ്മി (ray) ആകട്ടെ ഒരു ബിന്ദുവില് തുടങ്ങുകയും ഒരു ദിശയിലേക്കു നീണ്ടുപോകുകയും ചെയ്യുന്നു. രണ്ടു രശ്മികള്ക്കു പൊതുവായ ഒരു അറ്റബിന്ദു ഉണ്ടെങ്കില്, അവയിലെ അറ്റബിന്ദു ഉള്പ്പെടെയുള്ള ബിന്ദുക്കളുടെ ഗണമാണ് കോണം (angle). സമീപസ്ഥകോണങ്ങള് തുല്യമാകത്തക്കവണ്ണം രണ്ടു രേഖകള് കൂട്ടിമുട്ടുമ്പോള്, ഈ കോണങ്ങളെ ലംബകോണങ്ങള് അഥവാ മട്ടകോണങ്ങള് (right angles) എന്നു പറയുന്നു. ഇതിന്റെ ഡിഗ്രിയിലുള്ള അളവ് 90° യും റേഡിയനിലുള്ളത് ![]() ഉം ആകുന്നു. 3 അസമരേഖാ (non-collinear) ബിന്ദുക്കളും അവയെ യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡങ്ങളും ചേര്ന്നതാണ് ത്രികോണം. ഇതിലെ കോണങ്ങളുടെ ആകെത്തുക 180° ആണ്. 4 വശങ്ങളുള്ള ബഹുഭുജത്തെ ചതുര്ഭുജം (quadrilateral) എന്നു പറയുന്നു.
ഉം ആകുന്നു. 3 അസമരേഖാ (non-collinear) ബിന്ദുക്കളും അവയെ യോജിപ്പിക്കുന്ന രേഖാഖണ്ഡങ്ങളും ചേര്ന്നതാണ് ത്രികോണം. ഇതിലെ കോണങ്ങളുടെ ആകെത്തുക 180° ആണ്. 4 വശങ്ങളുള്ള ബഹുഭുജത്തെ ചതുര്ഭുജം (quadrilateral) എന്നു പറയുന്നു.
ഒരു സമതലം ലംബവൃത്തീയ കോണികപ്രതലത്തെ (right circular cone ) പ്രതിച്ഛേദിക്കുമ്പോള് കിട്ടുന്ന വക്രങ്ങളെ കോണിക പരിച്ഛേദങ്ങള് (conic sections) എന്നു പറയുന്നു.കോണികപ്രതലത്തിന്റെ അക്ഷത്തിനു ലംബമായി സമതലം പ്രതിച്ഛേദിക്കുമ്പോള് കിട്ടുന്നതാണു വൃത്തം. സമതലം, കോണിക പ്രതലത്തിന്റെ രണ്ടു പകുതികളെയും (nappens) ഒന്നിച്ചു പ്രതിച്ഛേദിക്കുമ്പോള് ഹൈപര്ബൊള കിട്ടുന്നു. എന്നാല് സമതലം, കോണിക പ്രതലത്തിന്റെ ഒരു പകുതിക്കു സമാന്തരമാണെങ്കില് അതു മറ്റേ പകുതിയെ പ്രതിച്ഛേദിക്കുന്ന വക്രമാണു പരാബൊള. സമതലം, കോണികപ്രതലത്തിന്റെ ഒരു പകുതിക്കു സമാന്തരമോ അക്ഷത്തിനു ലംബമോ അല്ലെങ്കില് കിട്ടുന്ന പ്രതിച്ഛേദ വക്രമാണ് എലിപ്സ്.
പ്രമേയങ്ങളും തെളിവുകളും
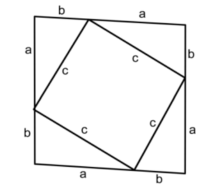
എലിമെന്റ്സിലെ ആദ്യഭാഗത്തിലെ 47-ാം പ്രമേയമായ പിഥഗറസ് പ്രമേയം യൂക്ലിഡിന്റെ പ്രമേയങ്ങളില് പ്രാധാന്യമര്ഹിക്കുന്നു. ഒരു മട്ടത്രികോണത്തില്, കര്ണത്തിന്റെ വര്ഗം മറ്റു രണ്ടു വശങ്ങളുടെ വര്ഗങ്ങളുടെ തുകയ്ക്കു തുല്യമാണ് എന്നതാണ് ഈ പ്രമേയം. അമേരിക്കന് ഗണിതജ്ഞനായ ലൂമിസ്, പിഥഗറസ് പ്രമേയത്തിന്റെ 366 വ്യത്യസ്ത തെളിവുകള് സമാഹരിച്ചിട്ടുണ്ട്. ഇതില് ഏറ്റവും ലഘുവായ ഒരു തെളിവ് ചിത്രം 7-ല് കൊടുത്തിരിക്കുന്നു.
ലഘൂകരിച്ചാല് c2 = a2+ b2 എന്നു കിട്ടുന്നു.
നിര്മിതികള്
റൂളറും കോമ്പസസും മാത്രം ഉപയോഗിച്ച ജ്യാമിതീയ നിര്മിതികളിലായിരുന്നു ഗ്രീക്കുകാര്ക്കു താത്പര്യമുണ്ടായിരുന്നത്. എന്നാല് ഇവകൊണ്ട് ഉത്തരം കിട്ടാത്ത 3 നിര്മാണപ്രശ്നങ്ങള് നിലനിന്നു: (1) ക്യൂബ് ഇരട്ടിപ്പിക്കല്, (2) വൃത്തത്തെ സമചതുരമാക്കല്, (3) കോണത്തിന്റെ സമത്രിഭാജനം.
അതായത് ![]() ഇവ എങ്ങനെ വരയ്ക്കാം എന്നുള്ളതാണ് ഈ പ്രശ്നങ്ങള്. ഇന്ന്, ആധുനിക ബീജഗണിതവും വിശ്ലേഷണവും ഉപയോഗിച്ച് ഈ നിര്മിതികള് അസാധ്യമാണെന്ന് തെളിയിക്കപ്പെട്ടിട്ടുണ്ട്.
ഇവ എങ്ങനെ വരയ്ക്കാം എന്നുള്ളതാണ് ഈ പ്രശ്നങ്ങള്. ഇന്ന്, ആധുനിക ബീജഗണിതവും വിശ്ലേഷണവും ഉപയോഗിച്ച് ഈ നിര്മിതികള് അസാധ്യമാണെന്ന് തെളിയിക്കപ്പെട്ടിട്ടുണ്ട്.
ഘന ജ്യാമിതി (Solid Geometry)
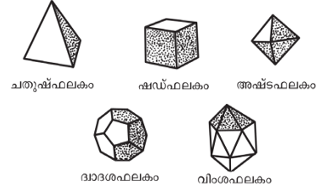
എലിമെന്റ്സിന്റെ അവസാന 3 ഭാഗങ്ങള് ഘനജ്യാമിതിയിലെ സമതലം, പിരമിഡ്, കോണ്, സിലിണ്ടര്, ബഹുഫലകം (polyhedron) തുടങ്ങിയവയെക്കുറിച്ചുള്ള പ്രമേയങ്ങള് ഉള്ക്കൊള്ളുന്നുണ്ട്. ബഹുഭുജങ്ങള് പാര്ശ(face)ങ്ങളായുള്ള ഘനരൂപങ്ങളാണ് ബഹുഫലകങ്ങള്. ചിത്രം (8)-ല് അവ വിശദമായി ചേര്ത്തിരിക്കുന്നു.
ഭൗതിക സ്പേസില് ആകെ 5 സമബഹുഫലകങ്ങള് മാത്രമേ ഉള്ളൂ. അവയെ 'പ്ലേറ്റോണിക് ഘനരൂപങ്ങള്' എന്നു വിളിക്കുന്നു. എലിമെന്റ്സ് അവസാനിക്കുന്നത് അവയുടെ നിര്മിതിയെക്കുറിച്ചുള്ള പ്രതിപാദനത്തോടെയാണ്.
അമൂര്ത്തമായ യൂക്ലീഡിയന് ജ്യാമിതി
19-ാം ശ.-ത്തിന്റെ അവസാനത്തോടെ നൂറ്റാണ്ടുകള് പഴക്കമുള്ള യൂക്ലീഡിയന് ജ്യാമിതിയില് പുതുമകള് ഉള്ക്കൊള്ളിക്കാന് തുടങ്ങി. 1899-ല് ജര്മന് ഗണിതശാസ്ത്രകാരനായ ഹില്ബെര്ട്ട് പ്രസിദ്ധീകരിച്ച ഗ്രന്ഥത്തോടെ യൂക്ലിഡിന്റെ ക്ലാസ്സിക്കല് ജ്യോമട്രി പൂര്ണമായി നവീകരിക്കപ്പെട്ടു. നിര്വചിക്കാത്ത 6 പദങ്ങളുള്ക്കൊള്ളുന്ന 21 ആക്സിയങ്ങളോടെ തുടങ്ങി ജ്യാമിതിയെ അമൂര്ത്തവത്കരിച്ച അദ്ദേഹത്തിന്റെ ചിന്താപദ്ധതിക്ക് അംഗീകാരം ലഭിച്ചത് 20-ാം ശ.-ത്തിലാണ്.
വിശ്ലേഷക ജ്യാമിതി (Analytical Geometry)
യൂക്ലീഡിയന് ജ്യാമിതിയില് ബീജഗണിത ആശയങ്ങള് സന്നിവേശിപ്പിച്ച് വിശ്ലേഷക ജ്യാമിതി രൂപപ്പെടുത്തിയത് ഫ്രഞ്ചു ഗണിതശാസ്ത്രജ്ഞനായ ദെക്കാര്ത്തെയും ഫെര്മയും ആണ്. സ്പേസിലുള്ള ഒരു ബിന്ദുവിന്റെ സ്ഥാനം നിര്ണയിക്കാന് സംഖ്യകള് ഉപയോഗിക്കാമെന്നുള്ളതാണ് വിശ്ലേഷക ജ്യാമിതിയുടെ അടിസ്ഥാനസങ്കല്പം.
സമതല വിശ്ലേഷക ജ്യാമിതിയില് സമതലത്തെ പരസ്പരം ലംബമായ x, y അക്ഷങ്ങള് 4 ആയി ഭാഗിക്കുന്നു. ഓരോ ഭാഗത്തിനും ചതുര്ത്ഥാംശം (quadrant) എന്നു പറയുന്നു.
x, y തലത്തിലെ P എന്ന ബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങളാണ് (x, y). ഈ ബിന്ദുവിനെ P (x, y) എന്നു കുറിക്കുന്നു. (x, y) ഇവയെ കാര്ട്ടീഷ്യന് നിര്ദേശാങ്കങ്ങള് (cartesian co-ordinates) എന്നു പറയുന്നു. മൂലബിന്ദുവിന്റെ നിര്ദേശാങ്കങ്ങള് (0, 0). P (x1,y1), Q (x2, y2) എന്നിവ രണ്ടു ബിന്ദുക്കളാണെങ്കില് PQ എന്ന രേഖാഖണ്ഡത്തിന്റെ നീളം പിഥഗറസ് പ്രമേയമുപയോഗിച്ച് കണ്ടുപിടിക്കാം.
നേര്വരകള്
വിശ്ലേഷക ജ്യാമിതിയില് നേര്വരകളെ സമീകരണങ്ങള് (equations)കൊണ്ടു കുറിക്കുന്നു. x അക്ഷത്തിലെ ബിന്ദുക്കളുടെ y - നിര്ദേശാങ്കം പൂജ്യം ആയിരിക്കും. അതുകൊണ്ട് x അക്ഷത്തെ y = 0 എന്ന സമീകരണംകൊണ്ടു പ്രതിനിധീകരിക്കുന്നു. y - അക്ഷത്തിന്റെ സമീകരണമാണ് x = 0. x, y അക്ഷങ്ങള്ക്കു സമാന്തരങ്ങളായ രേഖകളുടെ സമീകരണങ്ങളാണ് y = K, x = K (K സ്ഥിരസംഖ്യ).
ഒരു നേര്വര x - അക്ഷത്തെ ഛേദിക്കുമ്പോഴുണ്ടാകുന്ന ധനാത്മക കോണം θ ആയാല് tanθയെ നേര്വരയുടെ ചരിവുമാനം (slope) എന്നു പറയുന്നു. ഉദാ. θ = 60° ആയാല് വരയുടെ ചരിവുമാനം ![]() ആണ്. ഒരു രേഖയുടെ ചരിവുമാനം m-ഉം y അന്തഃഖണ്ഡം c-യും ആയാല് ആ രേഖയുടെ സമീകരണം y = mx + c ആണ്. അതായത് രേഖയിലുള്ള ഏതെങ്കിലും ബിന്ദു (x,y) ആണെങ്കില് x-ഉം y-യും തമ്മില് y = mx + c എന്ന നിബന്ധനയ്ക്കു വിധേയമായിരിക്കുന്നു. ഇങ്ങനെയുള്ള നിബന്ധനയെയാണ് സമീകരണം എന്നു പറയുന്നത്. (x1, y1), (x2, y2) എന്നീ ബിന്ദുക്കളിലൂടെ കടന്നുപോകുന്ന നേര്വരയുടെ സമീകരണമാണ്.
ആണ്. ഒരു രേഖയുടെ ചരിവുമാനം m-ഉം y അന്തഃഖണ്ഡം c-യും ആയാല് ആ രേഖയുടെ സമീകരണം y = mx + c ആണ്. അതായത് രേഖയിലുള്ള ഏതെങ്കിലും ബിന്ദു (x,y) ആണെങ്കില് x-ഉം y-യും തമ്മില് y = mx + c എന്ന നിബന്ധനയ്ക്കു വിധേയമായിരിക്കുന്നു. ഇങ്ങനെയുള്ള നിബന്ധനയെയാണ് സമീകരണം എന്നു പറയുന്നത്. (x1, y1), (x2, y2) എന്നീ ബിന്ദുക്കളിലൂടെ കടന്നുപോകുന്ന നേര്വരയുടെ സമീകരണമാണ്.
ചരിവുമാനങ്ങള് m1, m2 ആയ രണ്ടു രേഖകള് ഛേദിക്കുമ്പോഴുണ്ടാകുന്ന കോണം θ
ആയാല് ![]() എന്നു തെളിയിക്കാം. ഇതില്നിന്ന്, രണ്ടു രേഖകള് സമാന്തരമാണെങ്കില് m1 = m2; ലംബങ്ങളായാല് m1 m2 = –1. ഏതു നേര്വരയുടെയും സാമാന്യ സമീകരണം ax + by + c = 0
ആണ്.
എന്നു തെളിയിക്കാം. ഇതില്നിന്ന്, രണ്ടു രേഖകള് സമാന്തരമാണെങ്കില് m1 = m2; ലംബങ്ങളായാല് m1 m2 = –1. ഏതു നേര്വരയുടെയും സാമാന്യ സമീകരണം ax + by + c = 0
ആണ്.
വൃത്തം
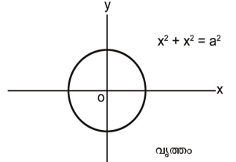
യൂക്ലീഡിയന് ജ്യാമിതിയില് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നു സ്ഥിരദൂരത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദുപഥം (locus) ആണ് വൃത്തം. നിശ്ചിത ബിന്ദുവിനെ വൃത്തത്തിന്റെ കേന്ദ്രം എന്നും സ്ഥിരദൂരത്തെ ആരം (radius) എന്നും പറയുന്നു. കേന്ദ്രം (h,k)യും ആരം r-ഉം ആയി വരയ്ക്കുന്ന വൃത്തത്തിന്റെ സമീകരണമാണ് (x – h)2 + (y – k)2 = r2. എല്ലാ വൃത്തങ്ങളുടെയും സമീകരണത്തിന്റെ പൊതുവായ രൂപമാണ് x2 + y2 + 2gx + 2fy + c = 0 എന്നത്. ഈ വൃത്തത്തിന്റെ കേന്ദ്രം = (–g, –f); ആരം ![]() . വൃത്തത്തിന്റെ പ്രധാനമായ ഒരു സവിശേഷത അതിന്റെ പരിധിയിലുള്ള ഏതൊരു ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന സ്പര്ശരേഖ(tangent)യും അതേ ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന ആരവും പരസ്പരം ലംബങ്ങളായിരിക്കും എന്നുള്ളതാണ്.
. വൃത്തത്തിന്റെ പ്രധാനമായ ഒരു സവിശേഷത അതിന്റെ പരിധിയിലുള്ള ഏതൊരു ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന സ്പര്ശരേഖ(tangent)യും അതേ ബിന്ദുവിലൂടെ വരയ്ക്കുന്ന ആരവും പരസ്പരം ലംബങ്ങളായിരിക്കും എന്നുള്ളതാണ്.
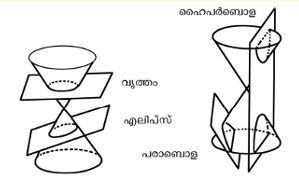
കോണികങ്ങള് (Conics)
ഒരു ലംബവൃത്തീയ കോണിനെ ഒരു സമതലം വ്യത്യസ്ത കോണങ്ങളില് ഛേദിക്കുമ്പോള് കിട്ടുന്ന ഏതൊരു വക്രത്തിനെയും കോണികം എന്നു പറയുന്നു. ഇവ മൂന്നുവിധമുണ്ട്. പരാബൊള, എലിപ്സ്, ഹൈപര്ബൊള.
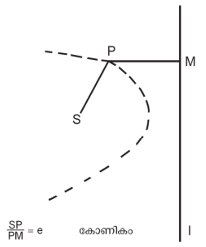
ചിത്രം 11-ല് S ഒരു നിശ്ചിത ബിന്ദുവും I ഒരു നിശ്ചിത രേഖയും P ചലിക്കുന്ന ഒരു ബിന്ദുവും ആണെന്നിരിക്കട്ടെ. P-യില് നിന്ന് I രേഖയിലേക്കുള്ള ലംബമാണ് PM. ബിന്ദു P ചലിക്കുന്നത് ![]() (സ്ഥിരാങ്കം) എന്ന നിബന്ധനയ്ക്കു വിധേയമായാണ്. അപ്പോള് P-യുടെ ബിന്ദുപഥത്തെ കോണികം എന്നു പറയുന്നു. ഇവിടെ S ഫോക്കസും I നിയതരേഖ (directrix))യും e ഉള്കേന്ദ്രത (eccentricity)യും ആണ്.
(സ്ഥിരാങ്കം) എന്ന നിബന്ധനയ്ക്കു വിധേയമായാണ്. അപ്പോള് P-യുടെ ബിന്ദുപഥത്തെ കോണികം എന്നു പറയുന്നു. ഇവിടെ S ഫോക്കസും I നിയതരേഖ (directrix))യും e ഉള്കേന്ദ്രത (eccentricity)യും ആണ്.
e = 1 ആയാല് കിട്ടുന്ന വക്രമാണു പരാബൊള. e < 1 ആയാല് എലിപ്സും e > 1 ആയാല് ഹൈപര്ബൊളയും കിട്ടുന്നു.
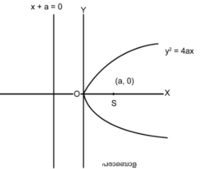
പരാബൊള. പരാബൊളയുടെ ഉള്കേന്ദ്രത e = 1 ആയതുകൊണ്ട് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നും നിശ്ചിതരേഖയില് നിന്നും തുല്യ അകലത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദു പഥമാണ് ഈ വക്രം. സമീകരണത്തിന്റെ മാനകരൂപം (standard form) y2 = 4ax; ശീര്ഷം (0, 0) സമമിതി അക്ഷം x-അക്ഷം; നിയതരേഖയുടെ സമീകരണം x + a = 0 (x അക്ഷത്തിന്റെ ഇടതുവശത്തു y അക്ഷത്തിനു സമാന്തരമായി a ദൂരത്തിലുളളത്).
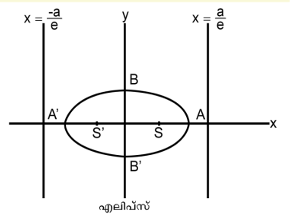
എലിപ്സ്. ഉള്കേന്ദ്രത e < 1 ആയ കോണികമാണ് എലിപ്സ്. വലിച്ചുനീട്ടിയ ഒരു വൃത്തത്തെപ്പോലെയാണ് ഇതിന്റെ ആകൃതി. മാനക സമീകരണം ![]() രണ്ടു ഫോക്കസ്സുകള് S(æ;0), S1 (-æ,0); രണ്ടു നിയതരേഖകള്
രണ്ടു ഫോക്കസ്സുകള് S(æ;0), S1 (-æ,0); രണ്ടു നിയതരേഖകള് ![]() . ചിത്രത്തില് എലിപ്സിന്റെ ദീര്ഘ അക്ഷം (major axis) = A'A = 2a; ലഘു അക്ഷം (minor axis) = B'B = 2b. P എന്നത് എലിപ്സിലുള്ള ഏതെങ്കിലും ബിന്ദുവായാല് SP + S'P = 2a എന്നു കിട്ടുന്നു. അതായത് രണ്ടു നിശ്ചിത ബിന്ദുക്കളില് നിന്നുള്ള ദൂരങ്ങളുടെ തുക സ്ഥിരസംഖ്യയാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ പഥമാണ് എലിപ്സ്. ജ്യോതിശ്ശാസ്ത്രപരമായി ഈ വക്രത്തിനു വളരെ പ്രാധാന്യമുണ്ട്. കെപ്ളറുടെ നിയമമനുസരിച്ച് സൂര്യനു ചുറ്റുമുള്ള ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം എലിപ്സുകളാണ്; സൂര്യന്റെ സ്ഥിരസ്ഥാനം ഒരു ഫോക്കസ്സിലും.
. ചിത്രത്തില് എലിപ്സിന്റെ ദീര്ഘ അക്ഷം (major axis) = A'A = 2a; ലഘു അക്ഷം (minor axis) = B'B = 2b. P എന്നത് എലിപ്സിലുള്ള ഏതെങ്കിലും ബിന്ദുവായാല് SP + S'P = 2a എന്നു കിട്ടുന്നു. അതായത് രണ്ടു നിശ്ചിത ബിന്ദുക്കളില് നിന്നുള്ള ദൂരങ്ങളുടെ തുക സ്ഥിരസംഖ്യയാകത്തക്കവണ്ണം സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ പഥമാണ് എലിപ്സ്. ജ്യോതിശ്ശാസ്ത്രപരമായി ഈ വക്രത്തിനു വളരെ പ്രാധാന്യമുണ്ട്. കെപ്ളറുടെ നിയമമനുസരിച്ച് സൂര്യനു ചുറ്റുമുള്ള ഗ്രഹങ്ങളുടെ സഞ്ചാരപഥം എലിപ്സുകളാണ്; സൂര്യന്റെ സ്ഥിരസ്ഥാനം ഒരു ഫോക്കസ്സിലും.
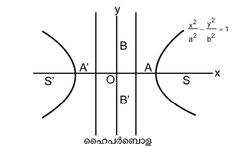
ഹൈപര്ബൊള. ഹൈപര്ബൊളയുടെ ഉള്കേന്ദ്രത e > 1. മാനക സമീകരണം ![]() രണ്ടു ഫോക്കസ്സുകള് S (æ, 0), S2 (–æ,0); A'A = 2a, B'B = 2b.
രണ്ടു ഫോക്കസ്സുകള് S (æ, 0), S2 (–æ,0); A'A = 2a, B'B = 2b.
A'A-യെ അനുപ്രസ്ഥ അക്ഷം (transverse axis) എന്നും B'B-യെ സംയുഗ്മി അക്ഷം (conjugate axis) എന്നും പറയുന്നു. രണ്ടു നിയതരേഖകള് ![]() . കോണികങ്ങളില് ഹൈപര്ബൊളയ്ക്കു മാത്രമേ അനന്തസ്പര്ശികള് (asymptotes)ഉള്ളു.
. കോണികങ്ങളില് ഹൈപര്ബൊളയ്ക്കു മാത്രമേ അനന്തസ്പര്ശികള് (asymptotes)ഉള്ളു.
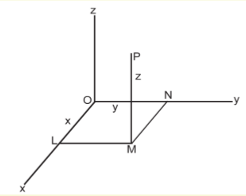
ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതി
ഈ ശാഖയില് 3 നിര്ദേശാങ്കങ്ങള് ഉപയോഗിച്ച് സ്പേസില് ഒരു ബിന്ദുവിനെ പ്രതിനിധീകരിക്കുന്നു. ചിത്രം (15) നോക്കുക.
ബിന്ദു P-യെ P (x, y, z) എന്നെഴുതുന്നു. ത്രിവിമീയ വിശ്ലേഷക ജ്യാമിതിയില് തലം, രേഖ, ഗോളം, കോണ്, സിലിണ്ടര് തുടങ്ങിയവയുടെ ഗുണധര്മങ്ങള് അപഗ്രഥിക്കുന്നു. ത്രിവിമീയ ജ്യാമിതിയില് P (x, y, z) എന്ന സമീകരണം ഒരു തല(plane)ത്തെ കുറിക്കുന്നു. ത്രിവിമീയ സ്പേസില് ഒരു നിശ്ചിത ബിന്ദുവില് നിന്നു സ്ഥിരദൂരത്തില് സഞ്ചരിക്കുന്ന ബിന്ദുവിന്റെ ബിന്ദുപഥമാണ് ഗോളം. ഗോളത്തിന്റെ മാനക സമീകരണം x2 + y2 + z2 + 2ux + 2vy + 2wz + d = 0. x, y, z ചരങ്ങളിലുള്ള F (x, y, z) = 0 എന്ന സമീകരണം പൊതുവായി ഒരു പ്രതല (surface)ത്തെയാണു പ്രതിനിധീകരിക്കുന്നത്.
ഒരു പ്രതലം എന്നു പറയുമ്പോള് അതില് വ്യത്യസ്ത ഘനരൂപങ്ങള് ഉള്പ്പെടുന്നു. ഗോളം, കോണ്, സിലിണ്ടര്, എലിപ്സോയ്ഡ്, ഹൈപര്ബൊളോയ്ഡ് ഇവയൊക്കെ പ്രതലങ്ങളാണ്. ശീര്ഷം മൂലബിന്ദുവായ കോണിന്റെ സാമാന്യരൂപം ഒരു പ്രത്യേക നിബന്ധനയ്ക്ക് വിധേയമായി ax2 + by2 + cz2 + 2fyz + 2gzx + 2hxy = 0 എന്നെഴുതാം. ഈ നിബന്ധനയാണ് abc + 2fgh - af2 - bg2 - ch2 ≠ 0 . Ax2 + By2 + Cz2 = 1 എന്ന രൂപത്തിലെഴുതുന്ന പ്രതലങ്ങളെ കേന്ദ്രീയ കോണികജങ്ങള് (central quadrics) എന്നു വിളിക്കുന്നു. ഓരോ നിര്ദേശാങ്കത്തിനും ഇവ സമമിതമാണ്.
ഇവയില് എലിപ്സോയ്ഡും, ![]() ഏകപ്രതല ഹൈപര്ബൊളോയ്ഡും
ഏകപ്രതല ഹൈപര്ബൊളോയ്ഡും
അയൂക്ലീഡിയന് ജ്യാമിതി ( Non-EuclideanGeometry)
യൂക്ലിഡിന്റെ ആക്സിയങ്ങളില് അഞ്ചാമത്തെതായ സമാന്തര ആക്സിയം ഒഴിവാക്കിക്കൊണ്ട് നിര്മിക്കപ്പെട്ട എല്ലാ ജ്യാമിതികളും അയൂക്ലീഡിയന് വിഭാഗത്തില്പ്പെടുന്നു. ഹൈപര്ബൊളിക ജ്യാമിതിയും എലിപ്റ്റിക ജ്യാമിതിയും അയൂക്ലീഡിയന് ജ്യാമിതികളാണ്. ആക്സിയങ്ങളുടെ സ്വീകാര രീതിയനുസരിച്ച് ഇവയെ യഥാക്രമം 'ലൊബാഷ്യേവ്സ്കിയന് ജ്യാമിതി' എന്നും 'റീമാനിയന് ജ്യാമിതി' എന്നും വിളിക്കുന്നു.
ഹൈപര്ബൊളിക ജ്യാമിതി
'ഒരു നേര്വരയ്ക്കു സമാന്തരമായി അതിലില്ലാത്ത ഒരു ബിന്ദുവില്ക്കൂടി ചുരുങ്ങിയത് രണ്ടു വരകളെങ്കിലും വരയ്ക്കാം' എന്ന ആക്സിയമാണ് ഇതില് പകരം ആക്സിയമായി സ്വീകരിച്ചിരിക്കുന്നത്. ഈ ജ്യാമിതിയില് ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക 0°-ക്കും 180°-ക്കും ഇടയില് ഏതു വിലയും ആകാം. മറ്റൊരു പ്രമേയമാണ് തുല്യ അകലമുള്ള രണ്ടു സമാന്തരരേഖകള് ഇല്ല എന്നത്. ഹൈപര്ബൊളിക ജ്യാമിതിയില് ഒരു ത്രികോണത്തിന്റെ വിസ്തീര്ണം കുറഞ്ഞുവരുന്തോറും അതിലെ കോണങ്ങളുടെ തുക കൂടുകയും വിസ്തീര്ണം പൂജ്യത്തെ സമീപിക്കുമ്പോള് കോണങ്ങളുടെ തുക 180° യോടടുക്കുകയും ചെയ്യുന്നു. ത്രികോണം ABC-യില്, കോണങ്ങള് റേഡിയന് അളവില് α, β, γ ആയാല് ത്രികോണത്തിന്റെ വിസ്തീര്ണം K = k (π - α - β - γ) ആണ്. ഇതില് നിന്ന് K < k π എന്നു കിട്ടുന്നു. അതായത് ത്രികോണങ്ങളുടെ വിസ്തീര്ണം പരിബദ്ധം (bounded) ആണ്. ത്രികോണങ്ങളെ സംബന്ധിച്ച് വിസ്മയം പകരുന്ന ഒരു അയൂക്ലീഡിയന് ഗുണധര്മമാണിത്.
എലിപ്റ്റിക ജ്യാമിതി
1854-ല് റീമാന് രൂപം കൊടുത്ത അയൂക്ലീഡിയ ജ്യാമിതിയാണിത്. യൂക്ല ഡിന്റെ സമാന്തര ആക്സിയത്തിനു ബദലായി 'സമാന്തര രേഖകള് ഇല്ല' എന്ന ആക്സിയം റീമാന് സ്വീകരിച്ചു.
റീമാനിയന് ജ്യാമിതിയെക്കുറിച്ചു സാമാന്യമായി മനസ്സിലാക്കാന് സ്പേസില് ഒരു വക്രപ്രതലവും (curved surface)) അതില് ഒരു ബിന്ദുവും ബിന്ദുവില്ക്കൂടി പോകുന്ന വക്രപ്രതലത്തിന്റെ സ്പര്ശതലവും (tangent plane) സങ്കല്പിക്കുക. ഈ പ്രതലത്തിന്റെ രണ്ടു ബിന്ദുക്കളെ യോജിപ്പിക്കുമ്പോള് കിട്ടുന്ന 'നേര്വര' ഈ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന ഏറ്റവും നീളം കുറഞ്ഞ വക്രം (ജിയോഡസിക്ക്) ആയിരിക്കട്ടെ. അപ്പോള് പ്രതലത്തിലെ ബിന്ദുക്കള് രണ്ടു വിധത്തിലുള്ളവയാണ്:
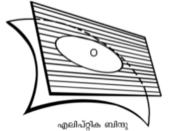
ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം ഗോളാകൃതി പോലെയാവുകയും പ്രതലത്തിലെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലത്തിന്റെ ഒരു വശത്തുമാത്രം പ്രതലം ഉണ്ടായിരിക്കുകയും ചെയ്യുന്ന അവസ്ഥ. പ്രതലത്തിലെ ഇത്തരം ബിന്ദുക്കളെ എലിപ്റ്റിക ബിന്ദുക്കള് എന്നു പറയുന്നു.
ഇവിടെ സ്പര്ശതലം ഒരല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് അതു പ്രതലത്തെ എലിപ്റ്റിക വക്രത്തിന്റെ ആകൃതിയില് ഛേദിക്കുന്നു. ചിത്രം (17) നോക്കുക.
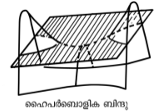
ബിന്ദുക്കളുടെ സാമീപ്യമുള്ക്കൊള്ളുന്ന പ്രതലം രണ്ടുവശവും ഉയര്ന്ന് നടുക്കു കുഴിഞ്ഞിരിക്കുകയും (മോഡയുടെ പാര്ശ്വതലം പോലെ) പ്രതലത്തിന്റെ ഒരു ബിന്ദുവിന്റെ സ്പര്ശതലം പ്രതലത്തെ രണ്ടായി ഛേദിക്കുകയും ചെയ്യുന്ന അവസ്ഥ.
ഇവിടെ സ്പര്ശതലം അല്പം സമാന്തരമായി താഴ്ത്തുമ്പോള് പ്രതലത്തെ ഹൈപര്ബൊളയുടെ വക്രത്തിന്റെ ആകൃതിയില് രണ്ടായി ഛേദിക്കുന്നു. പ്രതലത്തിലുള്ള ഇത്തരം ബിന്ദുക്കളെ ഹൈപര്ബൊളിക ബിന്ദുക്കള് എന്നു പറയുന്നു. ചിത്രം (18) നോക്കുക.
സ്പേസിലെ ജ്യാമിതി വിഭാവന ചെയ്യുന്ന പ്രത്യേകതകള് റീമാന്റെ പഠനങ്ങള്ക്കനുയോജ്യമാണ്. റീമാന്റെ ജ്യാമിതിയില് എല്ലാ ദൂരങ്ങളും ഒരു ധനസ്ഥിരാങ്കത്തിനു തുല്യമോ അതില് കുറവോ ആയിരിക്കും. അതുകൊണ്ട് മറ്റ് ജ്യാമിതികളില് നിന്നു വ്യത്യസ്തങ്ങളായ പല ഗുണധര്മങ്ങളും ഈ ജ്യാമിതിയിലുണ്ട്. ഉദാ. ഒരു ത്രികോണത്തിലെ കോണങ്ങളുടെ തുക എപ്പോഴും 180° യില് കൂടുതലായിരിക്കും. ചതുര്ഭുജത്തിലെ നാലു കോണുകളുടെ തുക 360° യിലും അധികമാണ്. ത്രികോണം ABC യില് കോണങ്ങള് ആയാല് അതിന്റെ വിസ്തീര്ണം K കണ്ടുപിടിക്കാനുള്ള റീമാന്റെ ഫോര്മുലയാണ് ![]() . ഇതില് നിന്നു ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യത്തോടടുക്കുമ്പോള് കോണങ്ങളുടെ തുക ക്രമേണ കുറഞ്ഞ് 180°-യോടടുക്കുന്നു എന്നു വ്യക്തമാണ്. ഇറ്റലിക്കാരായ റിക്കി (Gregorio Ricci: 18531925) യും ലെവി-സിവിറ്റ (Tullio Levi-Civita: 18731941)യും റീമാന്റെ അയുക്ളീഡിയന് ജ്യാമിതിയില് പില്ക്കാലത്തു കൂടുതല് പഠനങ്ങള് നടത്തിയവരാണ്.
. ഇതില് നിന്നു ത്രികോണത്തിന്റെ വിസ്തീര്ണം പൂജ്യത്തോടടുക്കുമ്പോള് കോണങ്ങളുടെ തുക ക്രമേണ കുറഞ്ഞ് 180°-യോടടുക്കുന്നു എന്നു വ്യക്തമാണ്. ഇറ്റലിക്കാരായ റിക്കി (Gregorio Ricci: 18531925) യും ലെവി-സിവിറ്റ (Tullio Levi-Civita: 18731941)യും റീമാന്റെ അയുക്ളീഡിയന് ജ്യാമിതിയില് പില്ക്കാലത്തു കൂടുതല് പഠനങ്ങള് നടത്തിയവരാണ്.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്)