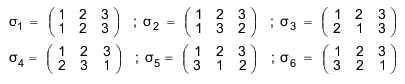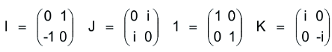This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

11:31, 14 ഡിസംബര്‍ 2015-നു നിലവിലുണ്ടായിരുന്ന രൂപം

ഗ്രൂപ്പ് സിദ്ധാന്തം

Group Theory

അമൂര്‍ത്ത ബീജഗണിത (Abstract Algebra) ത്തിലെ ഒരു പ്രധാന ശാഖ. ഒരു ഗ്രൂപ്പിന്റെ ഏത് രണ്ടംഗങ്ങളെയും ചില വ്യവസ്ഥകള്‍ പാലിക്കുന്ന ക്രിയയ്ക്ക് വിധേയമാക്കാന്‍ സാധിക്കും. ഈ ക്രിയ സങ്കലനമോ ഗുണനമോ വേറെ ക്രിയയോ ആകാം.

ആമുഖം

ഗ്രൂപ്പ് സിദ്ധാന്തം എ.ഡി. 20-ാം ശ.-ത്തിലാണ് പ്രാധാന്യം നേടിയത്. പ്രാചീന സംസ്കാരങ്ങളില്‍ത്തന്നെ സമമിതി (symmetry) എന്ന ആശയം ഉണ്ടായിരുന്നു. ഈജിപ്തിലെ ഭിത്തികളിലെ കലാത്മകമായ ചിത്രങ്ങളില്‍ 'സമമിതി' എന്ന ആശയം പ്രകടമായിട്ടുണ്ട്. ഈ 'സമമിതി'കളെ ഗ്രൂപ്പെന്ന സങ്കല്പംകൊണ്ട് വ്യക്തമാക്കാം. യൂക്ലിഡ് (ബി.സി. 3-ാം ശ.) എന്ന സുപ്രസിദ്ധ ഗണിതശാസ്ത്രജ്ഞന്‍ ബഹുഭുജങ്ങള്‍ (polygons), സമബഹുഫലകങ്ങള്‍ (regular polyhedra) എന്നിവയെപ്പറ്റി പഠിച്ചിട്ടുണ്ട്. പക്ഷേ, ഗ്രൂപ്പ് എന്ന ആശയം എ.ഡി. 18-ാം ശ.-ത്തിലാണ് ആദ്യമായി ഉടലെടുത്തത്. ജോസഫ് ലൂയി ലഗ്റാഞ്ജ് (എ.ഡി. 1736-1813) ഗ്രൂപ്പുകളെപ്പറ്റി പരാമര്‍ശിച്ചിട്ടുണ്ട്. അതിനുശേഷം അഗസ്റ്റിന്‍ ലൂയി കാഷി (1789-1857) ക്രമചയങ്ങളുടെ ഗ്രൂപ്പുകളെ പരിഗണിച്ചു. എന്നാല്‍, ഗ്രൂപ്പുകള്‍ക്ക് പ്രാധാന്യം ഉണ്ടാകാന്‍ ഒരു പ്രത്യേക കാരണമുണ്ടായിരുന്നു. ബീജഗണിതത്തില്‍ 4-ാം ഘാതം വരെയുള്ള സമീകരണങ്ങളെ കരണികള്‍ ഉപയോഗിച്ച് നിര്‍ധാരണം ചെയ്യാം. അതായത്, സങ്കലനം, വ്യവകലനം, ഗുണനം, ഹരണം, ഘാതം, മൂലം ഇവ ഉപയോഗിച്ച് നിര്‍ധാരണമൂല്യത്തെ സൂചിപ്പിക്കാന്‍ സാധിക്കും. പക്ഷേ, 5-ാം ഘാതത്തിലെ സമീകരണത്തിന് അത് സാധ്യമല്ല. ആബെല്‍ (1802-29) എന്ന നോര്‍വീജിയന്‍ ഗണിതശാസ്ത്രജ്ഞന്‍ ഇത് തെളിയിച്ചു. എന്തുകൊണ്ടാണ് ഇത് സാധ്യമാകാത്തത് എന്നുള്ള കാര്യം ഗ്രൂപ്പ് സിദ്ധാന്തം ഉപയോഗിച്ച് ഇവാരിസ്ത് ഗാല്‍വ (1811-32) എന്ന ഗണിതജ്ഞന്‍ അനന്യസാധാരണമായ രീതിയില്‍ വിശദമാക്കി. അതിനുശേഷമാണ് ഗ്രൂപ്പ് സിദ്ധാന്തത്തിന്റെ നൈസര്‍ഗികമായ പ്രാധാന്യം ഗണിതശാസ്ത്രജ്ഞന്മാര്‍ മനസ്സിലാക്കുകയും ഗ്രൂപ്പ് സിദ്ധാന്തം പഠനത്തിന് വിധേയമാക്കുകയും ചെയ്തത്. ഇപ്പോള്‍ അമൂര്‍ത്തബീജഗണിതത്തിന്റെ ലളിതവും അടിസ്ഥാനപരവുമായ ഒരു ശാഖയാണ് ഗ്രൂപ്പ് സിദ്ധാന്തം. ഗണിതത്തിന്റെ പല ശാഖകളിലും, ഭൗതികം, രസതന്ത്രംപോലുള്ള ഇതര ശാസ്ത്രങ്ങളിലും, ഗ്രൂപ്പ് സിദ്ധാന്തം പ്രയോജനപ്പെടുത്താവുന്നതാണ്.

ഗ്രൂപ്പുകള്‍

ബീജഗണിതത്തിലെ ഒരു ആധാര തത്ത്വമാണ് ദ്വിചരക്രിയ (Binary operation). X ഒരു അശൂന്യഗണം (non-empty) എന്നിരിക്കട്ടെ. X-ലെ ഏത് രണ്ടംഗങ്ങള്‍ക്കും സംഗതമായി (corresponding to) ഗണത്തിലെ ഒരംഗം നിര്‍വചിക്കുന്നതിനെയാണ് ദ്വിചരക്രിയ എന്നുപറയുന്നത്. അതായത്. X x X-ല്‍ നിന്നും X-ലേക്കുള്ള ഒരു ഫലനമാണ് ദ്വിചരക്രിയ. ഉദാഹരണമായി N = {1,2,3, ...} എന്നിരിക്കട്ടെ. N-ല്‍ സങ്കലനം എന്ന ക്രിയ നിര്‍വചിക്കാം. '+' എന്ന ചിഹ്നംകൊണ്ടാണ് അതിനെ സൂചിപ്പിക്കുന്നത്.

N-ലെ a,b എന്ന ഏത് അംഗങ്ങള്‍ക്കും a + b എന്ന സങ്കലനഫലമുണ്ട്. അതുപോലെ N-ലെ a,b എന്ന ഏത് അംഗങ്ങള്‍ക്കും 'x' എന്ന ഗുണനം നിര്‍വചിക്കാം. മ,യ ഇവയുടെ ഗുണനഫലം മഃയ ആണ്.

A = {1, 2, 3} എന്നിരിക്കട്ടെ. A - ക്ക് 6 ക്രമചയങ്ങള്‍ ഉണ്ട്. ഈ ക്രമചയങ്ങളെ എന്ന രീതിയില്‍ സൂചിപ്പിക്കാം. ഇവിടെ a₁, a₂, a₃ എന്നിവ ഏതെങ്കിലും ക്രമത്തില്‍ എഴുതപ്പെട്ട 1,2,3 എന്ന സഖ്യകളാണ്. ഇങ്ങനെ കിട്ടുന്ന ക്രമചയങ്ങള്‍ ഇപ്രകാരമാണ്.

σ, τ എന്നീ ക്രമചയങ്ങളുടെ ഗുണനഫലമായ എന്ന ക്രമചയത്തെ ഇങ്ങനെ നിര്‍വചിക്കാം. ആദ്യം എന്ന ക്രമചയത്തെ നിര്‍വചിക്കുക. പിന്നീട് എന്ന ക്രമചയം നിര്‍വചിക്കുക. അപ്പോള്‍ കിട്ടുന്ന ക്രമചയമാണ് .

ഉദാഹരണമായി എന്നുകിട്ടും.

ദ്വിചരക്രിയയെ +, ⦁, *, ⊕ എന്നീ ചിഹ്നങ്ങള്‍കൊണ്ടോ അല്ലെങ്കില്‍ സാന്നിധ്യംകൊണ്ടോ സൂചിപ്പിക്കാവുന്നതാണ്. സാധാരണയായി സാന്നിധ്യം കൊണ്ടാണ് സൂചിപ്പിക്കുന്നത്. അതായത് a, b ഇവയുടെ ദ്വിചരക്രിയമൂലം കിട്ടുന്ന ഫലത്തെ വേറെ ചിഹ്നങ്ങളൊന്നും കൂടാതെ, ab എന്നു മാത്രം. X, ഒരു ദ്വിചരക്രിയയുള്ള ഗണമെന്ന് സങ്കല്പിക്കുക. a, b, c ε X എന്നിരിക്കട്ടെ. a (bc) = (ab) c ആണെങ്കില്‍, ദ്വിചരക്രിയയെ സാഹചര്യക്രിയ എന്നുപറയുന്നു. ദ്വിചരക്രിയ സാഹചര്യ നിയമം (Associative law) അനുസരിക്കുന്നു എന്നു പറയും.

ഒരു ദ്വിചരക്രിയ നിര്‍വചിക്കപ്പെട്ടിട്ടുള്ള അശൂന്യഗണത്തെ ഗ്രൂപ്പോയ്ഡ് എന്നുപറയും. അത് സാഹചര്യനിയമം അനുസരിക്കുകയാണെങ്കില്‍ അതിനെ അര്‍ധഗ്രൂപ്പ് എന്നു പറയാം. യൂക്ലിഡിയന്‍ ത്രിവിമേയ സദിശങ്ങള്‍ സദിശഗുണനം എന്ന ക്രിയയോടുകൂടിയ ഗ്രൂപ്പോയ്ഡ് ആണ്. എണ്ണല്‍ സംഖ്യകളുടെ ഗണം സങ്കലനത്തോടുകൂടിയ ഒരു അര്‍ധഗ്രൂപ്പ് (semi group) ആണ്.

S ഒരു ദ്വിചരക്രിയയോടുകൂടിയ ഗണമെന്നിരിക്കട്ടെ. S-ലെ a എന്ന ഓരോ അംഗത്തിനും ae = a (ea = a) എന്ന വ്യവസ്ഥ അനുസരിക്കുന്ന e എന്ന അംഗം S-ല്‍ ഉണ്ടെങ്കില്‍ അതിനെ ദക്ഷിണ (വാമ) തത്സമകം [right (left) identity] എന്നുപറയും. ഒരു വാമ ദക്ഷിണ തത്സമകത്തെ (left right identity) തത്സമകം എന്നുപറയും. a എന്ന അംഗത്തിന് aa^-1 = e, (a^-1a = e) എന്ന വ്യവസ്ഥ അനുസരിക്കുന്ന a^-1 എന്ന അംഗമുണ്ടെങ്കില്‍, അതിനെ ദക്ഷിണ (വാമ) വ്യുത്ക്രമം [right (left) inverse] എന്നു പറയാം. ഇവിടെ ല ഒരു വാമതത്സമകമോ ദക്ഷിണ തത്സമകമോ ആകാം. ഒരു വാമ, ദക്ഷിണ വ്യുത്ക്രമത്തെ വ്യുത്ക്രമം (inverse) എന്നു പറയുന്നു.

ഒരു തത്സമകത്തോടു കൂടിയ അര്‍ധഗ്രൂപ്പിന് മോണോയ്ഡ് എന്നു പറയും. എണ്ണല്‍സംഖ്യകളുടെ ഗണം ഗുണനക്രിയയോടുകൂടിയ മോണോയ്ഡ് ആണ്. അതിന്റെ തത്സമകം '1' എന്ന അംഗമാണ്.

മുകളില്‍ വിവരിച്ചിട്ടുള്ള തത്ത്വങ്ങളുടെ അടിസ്ഥാനത്തില്‍ ഒരു ഗ്രൂപ്പിനെ നിര്‍വചിക്കാം.

താഴെ പറയുന്ന വ്യവസ്ഥകള്‍ അനുസരിക്കുന്ന G എന്ന അശൂന്യഗണത്തെ ഗ്രൂപ്പ് എന്നു പറയുന്നു.

G₁ : G ഒരു അര്‍ധഗ്രൂപ്പാണ്.

G₂ : G-യില്‍ ഒരു തത്സമകം ഉണ്ട്. അതായത് a എന്ന G-യിലെ ഏത് അംഗത്തിനും ae = ea = a എന്ന വ്യവസ്ഥ പാലിക്കുന്ന e എന്ന അംഗം ഉണ്ട്.

G₃ : G-യിലെ ഓരോ അംഗത്തിനും വ്യുത്ക്രമം ഉണ്ട്. അതായത് G-യിലെ a എന്ന ഏത് അംഗത്തിനും aa^-1 = a^-1a = e എന്ന വ്യവസ്ഥ പാലിക്കുന്ന a^-1 എന്ന അംഗം ഉണ്ട്.

യഥാര്‍ഥത്തില്‍ ഈ വ്യവസ്ഥകളില്‍ അയവു വരുത്താവുന്നതാണ്. താഴെക്കൊടുത്തിട്ടുള്ള പ്രമേയ (theorem)ത്തില്‍ നിന്നു അത് വ്യക്തമാകും.

പ്രമേയം 2.1. G എന്ന അര്‍ധഗ്രൂപ്പില്‍ താഴെ പറയുന്ന വ്യവസ്ഥകള്‍ തുല്യമാണ്.

AG₁ : G ഒരു ഗ്രൂപ്പാണ്;

AG₂ : G - യില്‍ ഒരു വാമ തത്സമകവും, ഓരോ അംഗത്തിനും ഒരു വാമ വ്യുത്ക്രമവും ഉണ്ട്;

AG₃ : G -യില്‍ ഒരു ദക്ഷിണ തത്സമകവും ഓരോ അംഗത്തിനും ഒരു ദക്ഷിണ വ്യുത്ക്രമവും ഉണ്ട്.

ഗ്രൂപ്പിലെ തത്സമകം ഏകമാത്രം (unique) ആണ്. e, e' രണ്ട് തത്സമകങ്ങള്‍ എന്നിരിക്കട്ടെ. അപ്പോള്‍,

e = e.e' (e' തത്സമകമായതുകൊണ്ട്)

= e' (e' തത്സമകമായതുകൊണ്ട്) എന്നു കിട്ടും.

അതുപോലെ ഓരോ അംഗത്തിനും വ്യുത്ക്രമവും ഏകമാത്രമാണ്. a എന്ന അംഗത്തിന് a', a എന്ന രണ്ടു വ്യുത്ക്രമങ്ങള്‍ ഉണ്ടെന്ന് സങ്കല്പിക്കുക. അപ്പോള്‍,

a' = a' e

= a' (aa) ; aa തത്സമകമായതുകൊണ്ട്)

= a (a'a തത്സമകമായതുകൊണ്ട്) എന്നു കിട്ടും.

ദ്വിചരക്രിയ നിര്‍വചിക്കപ്പെട്ടിട്ടുള്ള ഒരു ഗണം ഗ്രൂപ്പാണെന്ന് തെളിയിക്കാന്‍ അയവു വരുത്തിയ വ്യവസ്ഥകള്‍ സഹായകരമായിരിക്കും. പക്ഷേ, ഗ്രൂപ്പിന്റെ സവിശേഷതകള്‍ പറയുമ്പോള്‍ അയവുവരുത്താത്ത, കര്‍ശന നിബന്ധനകള്‍ പ്രയോജനപ്രദമായിരിക്കും.

ഗ്രൂപ്പിന് പല സവിശേഷതകള്‍ ഉണ്ട്. രണ്ട് പ്രധാന സവിശേഷതകള്‍ താഴെപ്പറയുന്ന പ്രമേയത്തില്‍ ചേര്‍ക്കുന്നു.

പ്രമേയം 2.2 (i). G ഒരു ഗ്രൂപ്പെന്നും, a, b, c G -യിലെ അംഗങ്ങളെന്നുമിരിക്കട്ടെ. അപ്പോള്‍ ab = ac എങ്കില്‍ b = c ആയിരിക്കും. ba = ca എങ്കില്‍ b = c ആയിരിക്കും.

(ii) ax = b എന്ന സമീകരണത്തിന് ഏകമാത്ര നിര്‍ധാരണമൂല്യം ഉണ്ടായിരിക്കും; ya = b എന്ന സമീകരണത്തിന് ഏകമാത്ര നിര്‍ധാരണമൂല്യം ഉണ്ടായിരിക്കും.

(i) -ലെ സവിശേഷതകളെ ക്രമേണ വാമ (left) ദക്ഷിണ (right) നിരാസ നിയമങ്ങള്‍ (cancellation laws) എന്നു പറയുന്നു.

ഒരു ഗ്രൂപ്പില്‍ a, b എന്ന ഏത് അംഗങ്ങളും ab = ba എന്ന നിയമം അനുസരിക്കുകയാണെങ്കില്‍ അതിനെ ക്രമവിനിമേയ ഗ്രൂപ്പ് (commutative group) അല്ലെങ്കില്‍ ആബെല്‍ ഗ്രൂപ്പ് എന്നു പറയുന്നു.

ഗണിതശാസ്ത്രത്തിലും ഇതരശാസ്ത്രങ്ങളിലും വളരെ സാധാരണയായി കണ്ടുവരുന്ന ഒരു ബീജീയഘടന (Algebraic structure) ആണ് ഗ്രൂപ്പ്. ചില ഉദാഹരണങ്ങള്‍ താഴെ കൊടുത്തിരിക്കുന്നു.

ഉദാഹരണങ്ങള്‍

i. Z = {0, 1, 2, ..., n, ...} സങ്കലനത്തോടുകൂടിയ ഒരു ഗ്രൂപ്പാണ്. '0' തത്സമകവും n എന്ന അംഗത്തിന്റെ വ്യുത്ക്രമം -n ഉം ആണ്. ഇത് ഒരു ആബെല്‍ ഗ്രൂപ്പാണ്.

ii. പൂജ്യം ഉള്‍പ്പെടുത്താത്ത വാസ്തവിക സംഖ്യകളുടെ ഗണം ഒരു ഗുണനാത്മകമായ ഗ്രൂപ്പാണ്. '1' അതിന്റെ തത്സമകവും a എന്ന സഖ്യയുടെ വ്യുത്ക്രമം യും ആണ്. ഇത് ഒരു ആബെല്‍ ഗ്രൂപ്പാണ്.

iii. Z എന്ന പൂര്‍ണസംഖ്യകളുടെ ഗണത്തില്‍ ≡ എന്ന ഒരു ബന്ധം ഇപ്രകാരം നിര്‍വചിക്കുക.

a, b എന്ന Z -ന്റെ അംഗങ്ങളെ n എന്ന അംഗംകൊണ്ട് ഹരിക്കുമ്പോള്‍ ശിഷ്ടങ്ങള്‍ തുല്യമാണെങ്കില്‍

a b (മോഡ് n) ആണ്.

'a സര്‍വസമം b മോഡുലോ n' എന്നാണ് ഇത് വായിക്കുക. ഇത് ഒരു തുല്യതാബന്ധം (Equivalance relation) ആണ്. ഈ ബന്ധം Z-നെ n വര്‍ഗങ്ങളായി വിഭജനം ചെയ്യുന്നു. ഇങ്ങനെ (0), (1), ..., (n-1) എന്ന n വര്‍ഗങ്ങള്‍ കിട്ടും. ഇപ്രകാരം Zn = {(0), (1), ... (n-1)} എന്ന ഗണം ഉണ്ടാക്കുന്നു. (a), (b) ഇവ Z_n -ലെ അംഗങ്ങളാണെങ്കില്‍, (a) + (b) = (a + b) എന്നു നിര്‍വചിക്കാന്‍ സാധിക്കും. (0) തത്സമകമാണ്. K + (n - k) = (0) ആയതുകൊണ്ട് (K) യുടെ വ്യുത്ക്രമം (n-k) ആണ്. Z ഒരു ആബെല്‍ ഗ്രൂപ്പാണ്.

iv. എന്ന രൂപത്തിലുള്ള വാസ്തവിക സംഖ്യകളാല്‍ നിര്‍മിതമായ എല്ലാ അവിചിത്ര (Non-singular) മാട്രിക്സുകളുടെയും ഗണം M₂ എന്നിരിക്കട്ടെ. മാട്രിക്സുകളുടെ ഗുണനത്തെ ഇപ്രകാരം നിര്‍വചിക്കാം.

ഈ ഗുണനം സാഹചര്യനിയമം പാലിക്കുന്ന ഒന്നാണ്. അവിചിത്ര മാട്രിക്സുകളുടെ ഗുണനഫലം അവിചിത്രമാണ്. എന്ന മാട്രിക്സ് M₂ -വിന്റ തത്സമകമാണ്. 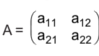എന്ന മാട്രിക്സിന് വ്യുത്ക്രമമാണ്. ഇങ്ങനെ M₂ ഒരു ഗ്രൂപ്പാണെന്ന് കിട്ടുന്നു. M₂ ഒരു ആബെല്‍ ഗ്രൂപ്പല്ല.

(v) S = {1, 2, 3, ..., n} എന്നിരിക്കട്ടെ. S -ന്റെ ക്രമചയങ്ങളുടെ ഗണത്തെ S_n എന്നു സൂചിപ്പിക്കാം. σ, τ ഇവ രണ്ട് ക്രമചയങ്ങളാണെന്ന് സങ്കല്പിക്കുക.എന്നതിനെ ആദ്യം -യും പിന്നീട് -യും നിര്‍വചിക്കുമ്പോള്‍ കിട്ടുന്ന ക്രമചയമെന്ന് നിര്‍വചിക്കാം. ക്രമചയങ്ങളുടെ ഈ ഗുണനം സാഹചര്യനിയമം പാലിക്കും.

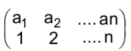എന്ന ക്രമചയം തത്സമകമായിരിക്കും. എന്ന ക്രമചയത്തിന് എന്ന ക്രമചയം വ്യുത്ക്രമമായിരിക്കും. ഇങ്ങനെ S_n ഒരു ഗ്രൂപ്പാണെന്ന് കിട്ടുന്നു. ഈ ഗ്രൂപ്പിന് n - ഘാത സമമിത ഗ്രൂപ്പ് (permutation group of ordern) എന്നു പറയും.

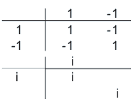
vi. C 4 = {1, -1, i, -i} എന്ന സങ്കീര്‍ണസംഖ്യകള്‍ (Complex numbers)ക്ക് ഗുണനം നിര്‍വചിക്കാം. ഗുണനഫലത്തെ ഒരു പട്ടികയില്‍ സൂചിപ്പിക്കുന്നു.

പ്രസ്തുത ഗുണനം സാഹചര്യനിയമം അനുസരിക്കുന്നു. '1' തത്സമകമാണ്. ഓരോ അംഗത്തിനും വ്യുത്ക്രമം ഉണ്ടെന്നുള്ളത് പട്ടികയില്‍ നിന്നും വ്യക്തമാണ്. ഇങ്ങനെ C₄ ഒരു ഗ്രൂപ്പാണെന്ന് കിട്ടുന്നു.

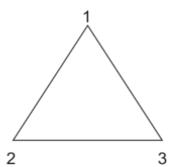
vii. 1 2 3 ഒരു സമഭുജത്രികോണമെന്നിരിക്കട്ടെ. ഈ ത്രികോണത്തിന്റെ സമമിതികളുടെ ഗണം G എന്നിരിക്കട്ടെ. ഈ ത്രികോണത്തെ ചില രീതികളില്‍ ചലിപ്പിക്കുമ്പോള്‍ 'ഒന്നുപോലുള്ള' സ്ഥിതികള്‍ കിട്ടും. '1' എന്ന ബിന്ദുവിനെ ബന്ധിപ്പിച്ച് 2-നെയും 3-നെയും പരസ്പരം മാറ്റുക. ഇതുപോലെ 2-നെ ബന്ധിപ്പിച്ച് 3-നെയും 1-നെയും മാറ്റുക. 3-നെ ബന്ധിപ്പിച്ച് 1-നെയും 2-നെയും പരസ്പരം മാറ്റുക. ഇങ്ങനെ σ₁, σ₂, σ₃, എന്ന മൂന്ന് രീതിയിലുള്ള ചലനങ്ങള്‍ കിട്ടും. ത്രികോണത്തെ 120° അപ്രദക്ഷിണ (anticlockwise)മായി ചുറ്റുക. അതായത്, 3, 1-ന്റെ സ്ഥാനത്തും 1, 2-ന്റെ സ്ഥാനത്തും 2, 3-ന്റെ സ്ഥാനത്തും വരത്തക്കവിധം ത്രികോണത്തെ ചലിപ്പിക്കുക. ഇതുപോലെ 240°, 360° ചുറ്റുമ്പോഴും ത്രികോണം പൂര്‍വസദൃശമായ സ്ഥിതിയെ പ്രാപിക്കും. ഇങ്ങനെ τ₁, τ ₂ , τ₃ എന്ന മൂന്നു ചലനങ്ങള്‍ കിട്ടും.

G = σ₁ , σ ₂ , σ ₃ , τ₁ , τ ₂ , τ ₃ , എന്നിരിക്കട്ടെ. രണ്ട് ചലനങ്ങള്‍ തുടര്‍ന്ന് ഉണ്ടാകുമ്പോള്‍ കിട്ടുന്ന ചലനം G-യിലെ ഒരംഗമായിരിക്കും. ചലനങ്ങളുടെ ഈ ഗുണനം സാഹചര്യനിയമം അനുസരിക്കും. 360° (0°) ചുറ്റുന്ന 'ചലനം' തത്സമകമാണ്. ഓരോ ചലനത്തിനും വ്യുത്ക്രമചലനമുണ്ട്. ഇങ്ങനെ G ഒരു ഗ്രൂപ്പാണെന്ന് കിട്ടുന്നു.

viii. അടുത്തതായി ഒരു സമചതുരത്തിന്റെ സമമിതികളെപ്പറ്റി പഠിക്കാം.

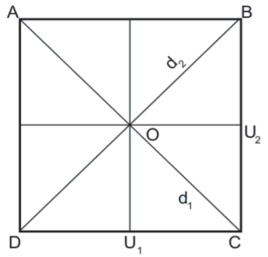
A B C D ഒരു സമചതുരമാണ്. U₁, സമചതുരത്തിന്റെ മധ്യബിന്ദുവില്‍ക്കൂടി സഞ്ചരിക്കുന്ന AD, BC ഇവയ്ക്കു സമാന്തരമായ രേഖ. അതുപോലെ U₂ സമചതുരത്തിന്റെ മധ്യബിന്ദുവില്‍ക്കൂടി സഞ്ചരിക്കുന്ന AB, CD ഇവയ്ക്കു സമാന്തരമായ രേഖ. d₁ , d₂ എന്നിവ വികര്‍ണങ്ങള്‍ (diago-nals). സമചതുരത്തെ പൂര്‍വസ്ഥിതിയിലേക്ക് നയിക്കുന്ന 8 ചലനങ്ങള്‍ ഇനി പറയുന്നവയാണ്.

i. U₁ ന് ആപേക്ഷികമായുള്ള σ₁ എന്ന പ്രതിഫലനം (Reflection).

ii. U₂ വിന് ആപേക്ഷികമായുള്ള σ₂ എന്ന പ്രതിഫലനം.

iii. d₁ ന് ആപേക്ഷികമായുള്ള σ₃ എന്ന പ്രതിഫലനം.

iv. d₂ വിന് ആപേക്ഷികമായുള്ള σ₄ എന്ന പ്രതിഫലനം.

v. S₁ = 90° അളവില്‍ സമചതുരത്തിന്റെ അപ്രദക്ഷിണ ഘൂര്‍ണനം (anticlockwise rotation).

vi. S₂ = 180° അളവില്‍ സമചതുരത്തിന്റെ അപ്രദക്ഷിണ ഘൂര്‍ണനം.

vii. S₃ = 270° അളവില്‍ സമചതുരത്തിന്റെ അപ്രദക്ഷിണ ഘൂര്‍ണനം.

viii. S₄ = 360° അളവില്‍ സമചതുരത്തിന്റെ അപ്രദക്ഷിണ ഘൂര്‍ണനം.

7-ാമത്തെ ഉദാഹരണത്തിലെന്നപോലെ ഇവിടെയും ദ്വിചരക്രിയ നിര്‍വചിക്കാം. 8 ചലനങ്ങളുടെ ഗണം ഒരു ഗ്രൂപ്പാണ്. 360° ചുറ്റുന്നത് (S₄) ഇതിന്റെ തത്സമകമാണ്. ഓരോ ചലനത്തിനും വ്യുത്ക്രമം ഉണ്ട്. അങ്ങനെ ഈ ചലനങ്ങളുടെ ഗണം ഒരു ഗ്രൂപ്പാണ്.

പൊതുവായി n ഭുജങ്ങളുള്ള ഒരു സമഭുജബഹുഭുജത്തിന്റെ സമമിതികളെ ആസ്പദമാക്കി 2n അംഗങ്ങളുള്ള ഒരു ഗ്രൂപ്പ് നിര്‍വചിക്കാം. ഇതിനെ ഡൈഹീഡ്രല്‍ ഗ്രൂപ്പ് എന്നുപറയുന്നു.

ix. ഒരു ഗണത്തിന്റെ എല്ലാ ആച്ഛാദക ഏകൈക ഫലനങ്ങളു (epimorphic 1-1 mappings)ടെയും ഗണം, ഫലനങ്ങളുടെ ഗുണനത്തോടുകൂടിയ ഒരു ഗ്രൂപ്പാണ്.

x. ഒരു പ്രധാനപ്പെട്ട ഗ്രൂപ്പാണ് ക്വാട്ടേര്‍ണിയന്‍ ഗ്രൂപ്പ് (Quaternion group).

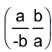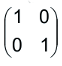a, b സങ്കീര്‍ണ സംഖ്യകള്‍ എന്നിരിക്കട്ടെ. എന്ന രൂപത്തില്‍ എഴുതാവുന്ന എല്ലാ മാട്രിക്സുകളുടെയും ഗണത്തെ D എന്നു സൂചിപ്പിക്കുക. ഇങ്ങനെയുള്ള മാട്രിക്സുകളെ ഗുണിക്കുമ്പോള്‍ ഇതേ രൂപത്തിലുള്ള മാട്രിക്സാണ് കിട്ടുന്നത്. മാട്രിക്സ് ഗുണനം സാഹചര്യനിയമം അനുസരിക്കും. ഈ തരത്തിലുള്ള മാട്രിക്സിന്റെ ഡിറ്റര്‍മിനന്റ് ആകണമെങ്കില്‍ a = 0, b = 0 എന്നു വേണം. എന്ന മാട്രിക്സ് D-യിലെ അംഗമാണ്. ഇത് തത്സമകമായിരിക്കും. D-യിലെ ഓരോ അംഗത്തിനും വ്യുത്ക്രമം ഉണ്ട്. ഇങ്ങനെ D ഒരു ഗ്രൂപ്പാണെന്ന് കിട്ടും.

ഇതിന്റെ കൂടെ വേറൊരു ഗ്രൂപ്പിനെയും കണ്ടെത്താം.

എന്നിരിക്കട്ടെ.

IJ=K, K=I, KI=J, JI=-K, KJ=-I, IK=-J, I²=J²=K²= -1 { ± 1, ± I, ±J, ±K}, 8 ഇങ്ങനെ അംഗങ്ങളുള്ള ഒരു ഗ്രൂപ്പാണെന്ന് തെളിയിക്കാം. ഇത്തരം ഗ്രൂപ്പുകളെ ക്വാട്ടേര്‍ണിയന്‍ ഗ്രൂപ്പ് എന്ന് പറയുന്നു. 8 അംഗങ്ങളുള്ള ക്വാട്ടേര്‍ണിയന്‍ ഗ്രൂപ്പിനെ Q₈ എന്ന് സൂചിപ്പിക്കാം.

ഉപഗ്രൂപ്പുകള്‍ സഹഗണങ്ങള്‍

Subgroups cosets

G ഒരു ഗ്രൂപ്പാണെന്ന് സങ്കല്പിക്കുക. H, G -യുടെ ഉപഗണമെന്നിരിക്കട്ടെ. G -യിലെ ദ്വിചരക്രിയ പ്രേരിപ്പിക്കുന്ന ക്രിയയ്ക്ക് ആപേക്ഷികമായി H ഒരു ഗ്രൂപ്പാണെങ്കില്‍ H-നെ G -യുടെ ഉപഗ്രൂപ്പ് എന്നുപറയുന്നു.

ഉദാഹരണങ്ങള്‍. Z {0, ± 1, ± 2, ..., ± n, ...} എന്നിരിക്കട്ടെ. K ഒരു പൂര്‍ണ സംഖ്യയാണെങ്കില്‍ എന്നത് Z-ന്റെ ഉപഗ്രൂപ്പാണ്.

ഉപഗ്രൂപ്പുകളെക്കുറിച്ചുള്ള പ്രധാന പ്രമേയം ചുവടെ ചേര്‍ക്കുന്നു.

പ്രമേയം 3.1. ഏ ഒരു ഗ്രൂപ്പാണെന്നിരിക്കട്ടെ. H അതിന്റെ ഒരു അശൂന്യഗണ (non-empty set) മെന്ന് സങ്കല്പിക്കുക. ഓരോ s, t ε S നും s, t ε S, s^-1 ε S എങ്കിലും, എങ്കില്‍ മാത്രവും (if and only if), H ഒരു ഉപഗ്രൂപ്പാണ്.

ഒരു ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പുകളുടെ ഒരു പരിമിതവര്‍ഗത്തിന്റെ സംഗമം (intersection) ഉപഗ്രൂപ്പാണ്. എന്നാല്‍ ഉപഗ്രൂപ്പുകളുടെ യോഗം (union) ഉപഗ്രൂപ്പാകണമെന്നില്ല.

G ഒരു ഗ്രൂപ്പാണെന്ന് സങ്കല്പിക്കുക. S അതിന്റെ ഉപഗണമെന്നിരിക്കട്ടെ. S ഉള്‍ക്കൊള്ളുന്ന ഏറ്റവും ചെറിയ ഉപഗ്രൂപ്പിനെ, S ജനിപ്പിക്കുന്ന ഉപഗ്രൂപ്പ് എന്നു പറയുന്നു. ഇതിനെ < S > എന്ന് സൂചിപ്പിക്കുന്നു. S ഒരു ഏകാംഗഗണമാണെങ്കില്‍ < S > നെ ചക്രിയഉപഗ്രൂപ്പ് (cyclic subgroup) എന്നു പറയും. അതായത്. എങ്കില്‍ H = {a⁰. , a, a²...} ഒരു ചക്രിയ ഉപഗ്രൂപ്പാണ്. ഒരു ഗ്രൂപ്പിന്റെ എല്ലാ അംഗങ്ങളെയും ഒരു അംഗത്തിന്റെ ഘാതങ്ങളായി എഴുതാന്‍ സാധിക്കുമെങ്കില്‍ അതിനെ ചക്രിയഗ്രൂപ്പ് എന്നു പറയും. ഉദാഹരണമായി 1, ω, ω² എന്നിവ 1-ന്റെ ഘനമൂലങ്ങള്‍ (cube roots) എന്നു സങ്കല്പിക്കുക.ഒരു ചക്രിയഗ്രൂപ്പാണ്. C-യിലെ അംഗങ്ങളെ ' ω' യുടെ ഘാതങ്ങളായി എഴുതാം. അല്ലെങ്കില്‍ -ന്റെ ഘാതങ്ങളായി എഴുതാം. C = <ω> = ω²ഗ്രൂപ്പിനെ ജനിപ്പിക്കുന്ന അംഗത്തെ ജനകം (generator) എന്നു പറയുന്നു. ഇവിടെ ω, ω² ഇവ രണ്ടും ജനകങ്ങളാണ്. ഇത് ഒരു പരിമിതഗ്രൂപ്പ് (finite group) ആണ്. അനന്ത ചക്രിയ ഗ്രൂപ്പിന് ഉദാഹരണമായി Z ={0,±1, ±2,.....±n,....} എന്ന ഗ്രൂപ്പിനെ പറയാം. ഇവിടെ ജനകമായി '1'-നെ കരുതാം. അല്ലെങ്കില്‍ -1-നെ.

G എന്ന ഗ്രൂപ്പിലെ ഒരംഗം g എന്നിരിക്കട്ടെ. <g> യിലെ അംഗസംഖ്യയെ g-യുടെ തരം (order) എന്നുപറയും. g-യുടെ തരം n ആണെങ്കില്‍ gⁿ = e എന്നാകത്തക്കവിധമുള്ള ഏറ്റവും ചെറിയ ധനപൂര്‍ണസംഖ്യ n ആയിരിക്കും. ഇതിനെ o(g) = n എന്നു സൂചിപ്പിക്കാം. <g> ഒരു അനന്തഗ്രൂപ്പാണെങ്കില്‍ 0(g) = 𝜶 എന്ന് എഴുതാം. G എന്ന ഒരു ഗ്രൂപ്പിന്റെ അംഗസംഖ്യയെ അതിന്റെ തരം എന്നു പറയാം. ഇതിനെ o(G) എന്നു സൂചിപ്പിക്കും. G അനന്തഗ്രൂപ്പാണെങ്കില്‍ o(G) = എന്ന എഴുതാം.

H, G എന്ന ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പാണെന്ന് സങ്കല്പിക്കുക. g G എന്നിരിക്കട്ടെ. അപ്പോള്‍ gH = {gh: h H} എന്ന ഗണത്തെ g-യാല്‍ ഉണ്ടായ H-ന്റെ വാമസഹഗണം (left coset) എന്നും Hg = {hg : h H} എന്ന ഗണത്തെ g-യാല്‍ ഉണ്ടായ H-ന്റെ ദക്ഷിണ സഹഗണം (right coset) എന്നുപറയാം.

ഉദാഹരണമായിഎന്ന ഗ്രൂപ്പിനെ പരിഗണിക്കുക.

3Z = { 0, ±3, ±6, ...,±3n...} അതിന്റെ ഉപഗ്രൂപ്പാണ്.

3Z = { 0, ±3, ±6, ...,±3n...}

3Z + 1 = { .., -8, -5, -2, 1, 4, 7, 10,...}

3Z + 2 = { ..., -7, - 4, -1, 2, 5, 8, 11,...} എന്നീ മൂന്നും വാമ (ദക്ഷിണ) സഹഗണങ്ങളാണ്. Z ആബെല്‍ ഗ്രൂപ്പായതുകൊണ്ട് ഓരോ വാമസഹഗണവും ദക്ഷിണസഹഗണം ആണ്.

പരിമിത ഗ്രൂപ്പുകളെ സംബന്ധിക്കുന്ന പ്രമേയങ്ങളില്‍ പ്രധാനപ്പെട്ടതാണ് ലഗ്റാഞ്ജിന്റെ പ്രമേയം.

പ്രമേയം 3.2. G എന്ന പരിമിത ഗ്രൂപ്പിന്റെ ഒരു ഉപഗ്രൂപ്പാണ് H എന്നിരിക്കട്ടെ. അപ്പോള്‍ o(H), o(G) യുടെ ഭാജകം (divisior) ആയിരിക്കും.

ഉദാഹരണമായി G = {1, -1, i, -i} എന്നിരിക്കട്ടെ. അപ്പോള്‍ H = {1, -1} G -യുടെ ഒരു ഉപഗ്രൂപ്പാണ്. 0(G) = 4, 0(H) = 2.2, 4-ന്റെ ഭാജകമാണ്.

പ്രമേയം 3.3. G ഒരു ഗ്രൂപ്പെന്നിരിക്കട്ടെ. H അതിന്റെ ഉപഗ്രൂപ്പാണെന്ന് സങ്കല്പിക്കുക. L, H-ന്റെ വാമസഹഗണങ്ങളുടെ ഗണവും; R, H-ന്റെ ദക്ഷിണസഹഗണങ്ങളുടെ ഗണവുമാണെങ്കില്‍ Φ : L → Rഎന്ന ഒരു ഏകൈകസാംഗത്വം (one-to-one corres- pondence) ഉണ്ടായിരിക്കും.

G പരിമിതമാണെങ്കില്‍, H എന്ന ഉപഗ്രൂപ്പിന്റെ സഹഗണങ്ങളുടെ എണ്ണത്തെ H-ന്റെ സൂചിക (index) എന്നുപറയും.

ചില ചിഹ്നങ്ങള്‍. അടുത്ത വിഭാഗത്തിലേക്ക് കടക്കുന്നതിനുമുമ്പ് ചില ƒ : G → Hചിഹ്നങ്ങളുടെ ആവശ്യമുണ്ട്. ƒ ഒരു ഫലനം എന്നിരിക്കട്ടെ. G -യിലെ x എന്ന ഓരോ അംഗത്തിനും സംഗതമായി ƒƒ എന്ന ഏകമാത്രമായ (unique) അംഗമുണ്ട്. G -യുടെ പ്രതിബിംബമാണ്. ഇതിനെ ƒƒ ƒ (G)= 1_m ƒഎന്നു സൂചിപ്പിക്കാം.

സമാകാരിതയും നോര്‍മല്‍ ഉപഗ്രൂപ്പുകളും

(Homo-morphism and Normal subgroups)

ആദ്യം നമുക്ക് ഒരുദാഹരണം നോക്കാം. G = {1, 1} ഒരു ഗ്രൂപ്പാണ്. ഇവിടെ ക്രിയ ഗുണനമാണ്. A = {1, 2, 3} എന്ന ഗണത്തിന്റെ ക്രമചയങ്ങളുടെ ഗ്രൂപ്പിലും രണ്ടംഗങ്ങള്‍ ഉണ്ട്. ഇവിടെ ക്രിയ ക്രമചയങ്ങളുടെ ഗുണനമാണ്. എന്നാല്‍ ഒരു കാര്യം വ്യക്തമാണ്. എന്ന ക്രമചയം 1-നെ പോലെയും, എന്ന ക്രമചയം 1-നെ പ്പോലെയുമാണ് പെരുമാറുന്നത്. ബീജീയഘടനകള്‍ എന്ന രീതിയില്‍ രണ്ടു ഗ്രൂപ്പുകളും തമ്മില്‍ ഒരു വ്യത്യാസവുമില്ല. രണ്ടിന്റെയും കെയ്ലി പട്ടികകള്‍ (cayley tables) ഇപ്രകാരമാണ്.

രണ്ട് ഗ്രൂപ്പുകളും ഒരു അമൂര്‍ത്തഗ്രൂപ്പിന്റെ രണ്ടു രീതിയിലുള്ള മൂര്‍ത്തിമത്തായ ആവിഷ്കാരങ്ങളുമാണ്. ഈ സ്ഥിതിവിശേഷത്തെ സര്‍വസമാകാരിത (isomorphism) എന്നുപറയുന്നു. എന്നാല്‍ സമാകാരിത (homomorphism) എന്ന തത്ത്വം കുറേക്കൂടി അയവു വരുത്തിയ ഒന്നാണ്. മുകളില്‍ പറഞ്ഞ ഉദാഹരണത്തില്‍ ƒƒ : G → S₂ എന്ന ഫലനം ഇപ്രകാരം നിര്‍വചിക്കുക ƒ (1) = i, ƒ(-1) = σ. ƒG-യിലെ g,h എന്ന ഏത് അംഗങ്ങള്‍ക്കും ƒ(gh)= ƒ(g) ƒ(h) എന്നു കിട്ടും. ഇവിടെ ƒ ƒ എന്ന ഫലനം ഏകൈകമാണ്.

G, H എന്നിവ ഗ്രൂപ്പുകളാണെന്ന് സങ്കല്പിക്കുക. ഓരോ x, y εG -ക്കും, എന്നാകത്തക്കവിധമുള്ള ƒ ƒ : G → H എന്ന ഫലനത്തെ സമാകാരിത എന്നു പറയുന്നു. ƒ ƒ ഒരു ആച്ഛാദക ഫലനം (surjection) ആണെങ്കില്‍ ƒ ƒ നെ ഒരു അധിസമാകാരിത (epimorphism) എന്നും, ƒ ƒ ഏകൈകമാണെങ്കില്‍ ഏകൈക സമാകാരിത (monomorphism)എന്നും രണ്ടുമാണെങ്കില്‍ സര്‍വസമാകാരിത (isomorphism) എന്നും ƒ : G → G പറയും. ƒ എന്ന സമാകാരിതയെ അന്തഃസമാകാരിത (ലിറീാീൃുവശാ) എന്നും, അത് സര്‍വസമാകാരിതയാണെങ്കില്‍ സ്വസമാകാരിത (മൌീാീൃുവശാ) എന്നുമാണ് പറയുന്നത്. ഏ-ക്ക് ഒ സമാകാരി എന്നതിനെ ഏ ~ ഒ എന്നും സര്‍വസമാകാരി എന്നതിനെ എന്നും സൂചിപ്പിക്കാം.

  ഉദാഹരണങ്ങള്‍. വളരെ ലളിതമായ രണ്ട് ഉദാഹരണങ്ങളാണ് ആദ്യം ചേര്‍ത്തിരിക്കുന്നത്.
   ശ. ഏ ഒരു ഗ്രൂപ്പെന്നിരിക്കട്ടെ. ല അതിന്റെ തത്സമകം എന്ന് സങ്കല്പിക്കുക. ഓരോ -ക്കും ƒ(ഴ) = ല എന്നാകത്തക്കവിധം  നിര്‍വചിക്കുക. അപ്പോള്‍ ƒ ഒരു സമാകാരിതയാണ്.
   ശശ. ഓരോ -ക്കും ശ(ഴ) = ഴ എന്നാകത്തക്കവിധം ശ:   നിര്‍വചിക്കുക. അപ്പോള്‍ ശ ഒരു സര്‍വസമാകാരിതയാണ്.
   ശശശ. ഏ ഒരു ഗ്രൂപ്പെന്നിരിക്കട്ടെ. ഓരോ -ക്കും സംഗതമായി ƒഴ(ഃ) = ഴ1 ഃ ഴ എന്നാകത്തക്കവിധം ƒഴ:  നിര്‍വചിക്കുക. അപ്പോള്‍ ƒഴ ഒരു സര്‍വസമാകാരിതയായിരിക്കും.
   ശ്. വാസ്തവിക സംഖ്യകള്‍കൊണ്ട് നിര്‍മിക്കപ്പെട്ട             എന്ന 2 ഃ 2 മാട്രിക്സുകളുടെ ഗണമായ ങ2 മാട്രിക്സ് സങ്കലനത്തോടുകൂടിയ ഒരു ഗ്രൂപ്പാണ്. ƒ:ങ2ഞ : (മശഷ)  മ11 + മ12 എന്ന് നിര്‍വചിക്കുക. അപ്പോള്‍ ƒ ഒരു സമാകാരിതയാണ്.
   ്. വാസ്തവിക സംഖ്യകള്‍കൊണ്ട് നിര്‍മിക്കപ്പെട്ട                എന്ന രൂപത്തിലുള്ള അവിചിത്രമാട്രിക്സുകളുടെ ഗണമായ ഏഘ2(ഞ) ഗുണനത്തോടുകൂടിയ ഒരു ഗ്രൂപ്പാണ്. ƒധ(മശഷ)പ = ക മശഷ ക എന്ന രീതിയില്‍ ƒശഏഘ2(ഞ)ഞ0} നിര്‍വചിക്കുക. അപ്പോള്‍ ƒ, ഏഘ2(ഞ)-ല്‍ നിന്നും ഞ0} എന്ന ഗുണനത്തോടുകൂടിയ ഗ്രൂപ്പിലേക്കുള്ള സമാകാരിതയാണ്.
  ഇനി സമാകാരിതയുടെ പഠനത്തിന് ഉതകുന്ന ചില തത്ത്വങ്ങളെപ്പറ്റി പഠിക്കാം. ഏ ഒരു ഗ്രൂപ്പാണെന്നിരിക്കട്ടെ. ച എന്ന ഏ-യുടെ ഉപഗ്രൂപ്പ്, ഏ-യിലെ ഓരോ ഃ-നും ഃച = ിത എന്ന വ്യവസ്ഥ അനുസരിക്കുകയാണെങ്കില്‍ ച-നെ ഒരു നോര്‍മല്‍ ഉപഗ്രൂപ്പ് എന്നു പറയും.
   ƒ : ഏ  ഒ  ഒരു സമാകാരിതയാണെന്നിരിക്കട്ടെ. ഗലൃƒ = ഃ  ഏ: ƒ(ഃ) = ല}-യെ ƒ-ന്റെ കെര്‍ണല്‍ (ഗലൃിമഹ) എന്നു പറയുന്നു. കെര്‍ണലിനെയും നോര്‍മല്‍ ഉപഗ്രൂപ്പുകളെയും ബന്ധിപ്പിക്കുന്ന പ്രമേയം ഇപ്രകാരമാണ്.
  പ്രമേയം 4.1. ഒരു സമാകാരിതയുടെ കെര്‍ണല്‍ നോര്‍മല്‍ ഉപഗ്രൂപ്പാണ്. ഏ ഒരു ഗ്രൂപ്പും ച അതിന്റെ നോര്‍മല്‍ ഗ്രൂപ്പാണെന്നും സങ്കല്പിക്കുക. അപ്പോള്‍, ഓരോ-ക്കും ഃച, ചഃ എന്ന സഹഗണങ്ങളെ വാമ, ദക്ഷിണ എന്ന വിശേഷണങ്ങള്‍ കൂടാതെ സഹഗണങ്ങള്‍ എന്നു പറയാം. ഃ, ്യഏ എങ്കില്‍ ചഃച്യ = ച ച്യഃ = ച്യഃ. അതുകൊണ്ട് (ചഃ) (ച്യ) = ച്യഃ എന്നു നിര്‍വചിക്കാം. അങ്ങനെ ഏ/ച എന്ന ഖണ്ഡഗണ(ൂൌീശേലി ലെ)ത്തില്‍ ഒരു ദ്വിചരക്രിയ നിര്‍വചിക്കാന്‍ സാധിക്കും. ഇത് സാഹചര്യനിയമം അനുസരിക്കും. ച ഇതിന്റെ തത്സമകമായിരിക്കും. ചഃന്റെ വ്യുത്ക്രമം  ചഃ1 ആണ്. ഇങ്ങനെ ഏ/ച എന്ന ഖണ്ഡഗ്രൂപ്പ് (ൂൌീശേലി ഴൃീൌു) നിര്‍വചിക്കാം. ഏ/ച-നെ ഏ-യുടെ ച-മോഡുലോ ഗ്രൂപ്പ് എന്നു പറയുന്നു.
   ഏഏ/ച, ഃചഃ ഒരു സമാകാരിതയാണ്. ഇതിനെ ഏ-യില്‍ നിന്നും ഏ/ച-ലേക്കുള്ള നിസര്‍ഗ സമാകാരിത (ിമൌൃമഹ വീാീാീൃുവശാ) എന്നുപറയുന്നു. വേറൊരു രീതിയില്‍ പറഞ്ഞാല്‍ ഏ/ഗലൃƒ ഒരു ഖണ്ഡ ഗ്രൂപ്പാണ്.
  പ്രമേയം 4.2. ഒരു സമാകാരിതയാണെങ്കില്‍
  ഒരു സര്‍വസമാകാരിതയാണ്.
  പ്രമേയം 4.3. ഏ ഒരു ഗ്രൂപ്പാണെന്നും ച ഒരു നോര്‍മല്‍ ഉപഗ്രൂപ്പാണെന്നുമിരിക്കട്ടെ. അപ്പോള്‍ ച-നെ ഉള്‍ക്കൊള്ളുന്ന ഏ/ച-ന്റെ ഉപഗ്രൂപ്പുകളുടെ ഗണത്തിന് ഒന്നിനൊന്നു സാംഗത്യമുണ്ട്. നോര്‍മല്‍ ഉപഗ്രൂപ്പുകള്‍ക്ക് സംഗതമായി നോര്‍മല്‍ ഉപഗ്രൂപ്പുകള്‍ വരും.
  പ്രമേയം 4.4. ഏ ഒരു ഗ്രൂപ്പെന്നും, ച, ഒ ഇവ ഏ-യുടെ നോര്‍മല്‍ ഉപഗ്രൂപ്പുകളുമെന്നിരിട്ടെ. അപ്പോള്‍ ഏ/ഒ  (ഏ/ച) / (ഒ/ച)
  പ്രമേയം 4.5. ഒ, ഏ എന്ന ഒരു ഗ്രൂപ്പിന്റെ ഉപഗ്രൂപ്പാണെന്നിരിക്കട്ടെ. ച, ഏ-യുടെ നോര്‍മല്‍ ഉപഗ്രൂപ്പാണെന്ന് സങ്കല്പിക്കുക. അപ്പോള്‍ ഒച, ഏ-യുടെ ഉപഗ്രൂപ്പാണ്. കൂടാതെ,  ആകുന്നു.
  ഇനി ചക്രിയ ഗ്രൂപ്പുകളുടെ സവിശേഷതയെപ്പറ്റി ഒരു പ്രമേയം ചേര്‍ക്കുന്നു.