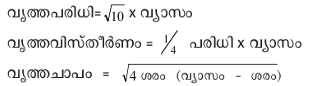This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
ഗണിതാനുയോഗം
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
(പുതിയ താള്: ==ഗണിതാനുയോഗം== ജൈന വൈദികഗ്രന്ഥങ്ങളില് ഗണിതതത്ത്വങ്ങള് പ്ര...) |
(→ഗണിതാനുയോഗം) |
||
| വരി 5: | വരി 5: | ||
ഗണിതത്തിലെ അടിസ്ഥാനക്രിയകളില് ഗുണനത്തിനും ഹരണത്തിനും ഉപയോഗിക്കുന്ന രണ്ടു രീതികളെക്കുറിച്ച് ഉമാശ്വതി പറയുന്നുണ്ട്: ഒന്ന് ഇപ്പോള് സാമാന്യമായി പ്രചാരത്തിലുള്ളതും മറ്റേത് ഘടകങ്ങളുപയോഗിച്ച് ഗുണിക്കുന്ന രീതിയുമാണ്. വിസ്താരകലന(mensuration)ത്തിന് ജൈനര് 'രജ്ജു' എന്ന പദം ഉപയോഗിക്കുന്നു. വൃത്തത്തിന്റെ ഗുണധര്മങ്ങളെ കുറിക്കുന്ന അനേകം സൂത്രവാക്യങ്ങള് തത്ത്വാര്ഥാധിഗമസൂത്രഭാഷ്യത്തില് രേഖപ്പെടുത്തിയിട്ടുണ്ട്. അവയില് ചിലത് താഴെ കൊടുക്കുന്നു: | ഗണിതത്തിലെ അടിസ്ഥാനക്രിയകളില് ഗുണനത്തിനും ഹരണത്തിനും ഉപയോഗിക്കുന്ന രണ്ടു രീതികളെക്കുറിച്ച് ഉമാശ്വതി പറയുന്നുണ്ട്: ഒന്ന് ഇപ്പോള് സാമാന്യമായി പ്രചാരത്തിലുള്ളതും മറ്റേത് ഘടകങ്ങളുപയോഗിച്ച് ഗുണിക്കുന്ന രീതിയുമാണ്. വിസ്താരകലന(mensuration)ത്തിന് ജൈനര് 'രജ്ജു' എന്ന പദം ഉപയോഗിക്കുന്നു. വൃത്തത്തിന്റെ ഗുണധര്മങ്ങളെ കുറിക്കുന്ന അനേകം സൂത്രവാക്യങ്ങള് തത്ത്വാര്ഥാധിഗമസൂത്രഭാഷ്യത്തില് രേഖപ്പെടുത്തിയിട്ടുണ്ട്. അവയില് ചിലത് താഴെ കൊടുക്കുന്നു: | ||
| - | + | [[ചിത്രം:Page_751for.png]] | |
ഇതില് ആദ്യത്തെ സൂത്രവാക്യത്തില്നിന്ന് π(പൈ)യുടെ വിലയായി √10 എന്ന സംഖ്യയാണ് എടുത്തിട്ടുള്ളതെന്ന് വ്യക്തമാണ്. സൂര്യപ്രജ്ഞപ്തിയില് π-യുടെ ഈ വിലയും ഇത്രത്തോളം കൃത്യമല്ലാത്ത മൂന്ന് എന്ന വിലയും ഉപയോഗിക്കുന്നുണ്ട്. ബൃഹത് സംഖ്യകളെക്കുറിച്ചും അനന്തത (infinity)യെക്കുറിച്ചും സുവ്യക്തമായ ഒരു സമീപനം അവര്ക്കുണ്ടായിരുന്നു. ജൈനരുടെ എണ്ണാവുന്ന ഏറ്റവും വലിയസംഖ്യ ആധുനികഗണിതത്തിലെ അലഫ് സംഖ്യയെ (ഗ്രീക്ക് അക്ഷരം 'അലഫ് സീറോ') ഓര്മിപ്പിക്കുന്നു. അനന്തത എന്ന ആശയത്തിന് അഞ്ചു മുഖങ്ങളുണ്ടെന്ന് അവര് കരുതിയിരുന്നു: ഏകദിശാഭിമുഖമായ അനന്തത (infinite in one direction), ദ്വിദിശാഭിമുഖമായ അനന്തത, വിസ്തീര്ണങ്ങളുടെ അനന്തത, സര്വാനന്തത (infinite every-where) നിതാന്താനന്തത (infinite perpectually) എന്നിങ്ങനെയാണവ. | ഇതില് ആദ്യത്തെ സൂത്രവാക്യത്തില്നിന്ന് π(പൈ)യുടെ വിലയായി √10 എന്ന സംഖ്യയാണ് എടുത്തിട്ടുള്ളതെന്ന് വ്യക്തമാണ്. സൂര്യപ്രജ്ഞപ്തിയില് π-യുടെ ഈ വിലയും ഇത്രത്തോളം കൃത്യമല്ലാത്ത മൂന്ന് എന്ന വിലയും ഉപയോഗിക്കുന്നുണ്ട്. ബൃഹത് സംഖ്യകളെക്കുറിച്ചും അനന്തത (infinity)യെക്കുറിച്ചും സുവ്യക്തമായ ഒരു സമീപനം അവര്ക്കുണ്ടായിരുന്നു. ജൈനരുടെ എണ്ണാവുന്ന ഏറ്റവും വലിയസംഖ്യ ആധുനികഗണിതത്തിലെ അലഫ് സംഖ്യയെ (ഗ്രീക്ക് അക്ഷരം 'അലഫ് സീറോ') ഓര്മിപ്പിക്കുന്നു. അനന്തത എന്ന ആശയത്തിന് അഞ്ചു മുഖങ്ങളുണ്ടെന്ന് അവര് കരുതിയിരുന്നു: ഏകദിശാഭിമുഖമായ അനന്തത (infinite in one direction), ദ്വിദിശാഭിമുഖമായ അനന്തത, വിസ്തീര്ണങ്ങളുടെ അനന്തത, സര്വാനന്തത (infinite every-where) നിതാന്താനന്തത (infinite perpectually) എന്നിങ്ങനെയാണവ. | ||
(പ്രൊഫ. കെ. ജയചന്ദ്രന്) | (പ്രൊഫ. കെ. ജയചന്ദ്രന്) | ||
Current revision as of 06:13, 16 ഓഗസ്റ്റ് 2015
ഗണിതാനുയോഗം
ജൈന വൈദികഗ്രന്ഥങ്ങളില് ഗണിതതത്ത്വങ്ങള് പ്രതിപാദിക്കുന്ന ഭാഗം. അങ്കഗണിതത്തിലെ അടിസ്ഥാനക്രിയകള്, ജ്യാമിതി, വിസ്താരകലനം, ഭിന്നങ്ങള്, സമീകരണം, ക്രമചയങ്ങള് (Permutations), സഞ്ചയങ്ങള് (Combinations) മുതലായവ പല വിഷയങ്ങളെക്കുറിച്ചും ഗണിതാനുയോഗത്തില് പ്രതിപാദിക്കുന്നുണ്ട്. ജൈനമതസ്ഥാപകനായ മഹാവീരന് ഗണിതത്തില് നിപുണനായിരുന്നു. ജൈനഗണിതത്തെപ്പറ്റി അറിവു ലഭിക്കുന്നത് ഭാഷ്യങ്ങളെ അവലംബിച്ചാണ്. വൈദികഗ്രന്ഥങ്ങളില് ഗണിതശാസ്ത്രം ഉള്ക്കൊള്ളുന്ന പ്രധാനപ്പെട്ട കൃതികളാണ് സൂര്യപ്രജ്ഞപ്തി (ബി.സി. 500), ചന്ദ്രപ്രജ്ഞപ്തി, സ്ഥാനാംഗസൂത്രം, ഭഗവതീസൂത്രം, ഉത്തരാധ്യായനസൂത്രം എന്നിവ. ഇവയില് സൂര്യപ്രജ്ഞപ്തിയിലും ചന്ദ്രപ്രജ്ഞപ്തിയിലും ഗണിതത്തോടൊപ്പം ജ്യോതിശ്ശാത്രത്തെക്കുറിച്ചും പ്രതിപാദിക്കുന്നു. മതഗ്രന്ഥങ്ങളായ ഭഗവതീസൂത്രത്തിലും (ബി.സി. 100) ഉത്തരാധ്യായനസൂത്രത്തിലും (എ.ഡി.100) സ്ഥാനാംഗസൂത്രത്തിലെന്നപോലെ ഗണിതത്തെയും ജ്യോതിശ്ശാസ്ത്രത്തെയും കുറിച്ചുള്ള ലഘുവായ ചില വസ്തുതകള് ഉള്ക്കൊള്ളുന്നു. ജൈനന്മാരുടെ മതഗ്രന്ഥങ്ങളില് തത്ത്വാര്ഥാദിഗമസൂത്രഭാഷ്യം പ്രധാനപ്പെട്ട ഒരു കൃതിയാണ്. ഇതിന്റെ കര്ത്താവ് ബി.സി. രണ്ടാം ശതകത്തില് ജീവിച്ചിരുന്ന ഉമാശ്വതിയാണ്. തത്ത്വശാസ്ത്രജ്ഞവിശാരദനായ ഉമാശ്വതി ഗണിതശാസ്ത്രജ്ഞനായി അറിയപ്പെടുന്നില്ലെങ്കിലും അദ്ദേഹത്തിന്റെ കൃതിയില് ഗണിതീയ സൂത്രവാക്യങ്ങളെക്കുറിച്ച് പ്രസ്താവമുണ്ട്. ഉമാശ്വതി കുസുമപുരത്ത് (പാറ്റ്ന) ഒരു ഗണിതവിദ്യാലയം സ്ഥാപിച്ചിരുന്നു. നൂറ്റാണ്ടുകള് പഴക്കമുള്ള ഈ വിദ്യാലയത്തിലാണ് ആര്യഭടന് പഠനം നടത്തിയത്.
ഗണിതത്തിലെ അടിസ്ഥാനക്രിയകളില് ഗുണനത്തിനും ഹരണത്തിനും ഉപയോഗിക്കുന്ന രണ്ടു രീതികളെക്കുറിച്ച് ഉമാശ്വതി പറയുന്നുണ്ട്: ഒന്ന് ഇപ്പോള് സാമാന്യമായി പ്രചാരത്തിലുള്ളതും മറ്റേത് ഘടകങ്ങളുപയോഗിച്ച് ഗുണിക്കുന്ന രീതിയുമാണ്. വിസ്താരകലന(mensuration)ത്തിന് ജൈനര് 'രജ്ജു' എന്ന പദം ഉപയോഗിക്കുന്നു. വൃത്തത്തിന്റെ ഗുണധര്മങ്ങളെ കുറിക്കുന്ന അനേകം സൂത്രവാക്യങ്ങള് തത്ത്വാര്ഥാധിഗമസൂത്രഭാഷ്യത്തില് രേഖപ്പെടുത്തിയിട്ടുണ്ട്. അവയില് ചിലത് താഴെ കൊടുക്കുന്നു:
ഇതില് ആദ്യത്തെ സൂത്രവാക്യത്തില്നിന്ന് π(പൈ)യുടെ വിലയായി √10 എന്ന സംഖ്യയാണ് എടുത്തിട്ടുള്ളതെന്ന് വ്യക്തമാണ്. സൂര്യപ്രജ്ഞപ്തിയില് π-യുടെ ഈ വിലയും ഇത്രത്തോളം കൃത്യമല്ലാത്ത മൂന്ന് എന്ന വിലയും ഉപയോഗിക്കുന്നുണ്ട്. ബൃഹത് സംഖ്യകളെക്കുറിച്ചും അനന്തത (infinity)യെക്കുറിച്ചും സുവ്യക്തമായ ഒരു സമീപനം അവര്ക്കുണ്ടായിരുന്നു. ജൈനരുടെ എണ്ണാവുന്ന ഏറ്റവും വലിയസംഖ്യ ആധുനികഗണിതത്തിലെ അലഫ് സംഖ്യയെ (ഗ്രീക്ക് അക്ഷരം 'അലഫ് സീറോ') ഓര്മിപ്പിക്കുന്നു. അനന്തത എന്ന ആശയത്തിന് അഞ്ചു മുഖങ്ങളുണ്ടെന്ന് അവര് കരുതിയിരുന്നു: ഏകദിശാഭിമുഖമായ അനന്തത (infinite in one direction), ദ്വിദിശാഭിമുഖമായ അനന്തത, വിസ്തീര്ണങ്ങളുടെ അനന്തത, സര്വാനന്തത (infinite every-where) നിതാന്താനന്തത (infinite perpectually) എന്നിങ്ങനെയാണവ.
(പ്രൊഫ. കെ. ജയചന്ദ്രന്)