This site is not complete. The work to converting the volumes of സര്വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോണികജങ്ങള്
സര്വ്വവിജ്ഞാനകോശം സംരംഭത്തില് നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Conicoids) |
(→Conicoids) |
||
| (ഇടക്കുള്ള 3 പതിപ്പുകളിലെ മാറ്റങ്ങള് ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 4: | വരി 4: | ||
== Conicoids == | == Conicoids == | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Page77scree.png|thumb|250px|thumb]] |
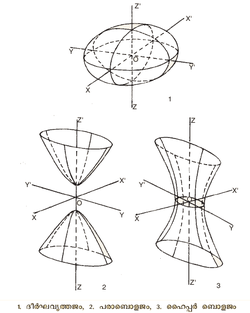
എല്ലാ സമതലഛേദങ്ങളും കോണികങ്ങളായുള്ള ത്രിമാന പ്രതലങ്ങള്. ഉദാ. ഗോളം, കോണ്, ദീര്ഘവൃത്തജം (ellipsoid), പരാബൊളജം (paraboloid), ഹൈപ്പര്ബൊളജം (hyperboloid). | എല്ലാ സമതലഛേദങ്ങളും കോണികങ്ങളായുള്ള ത്രിമാന പ്രതലങ്ങള്. ഉദാ. ഗോളം, കോണ്, ദീര്ഘവൃത്തജം (ellipsoid), പരാബൊളജം (paraboloid), ഹൈപ്പര്ബൊളജം (hyperboloid). | ||
| - | + | ax<sup>2</sup> + 2hxy + by<sup>2</sup> + 2gx + 2fy + c = 0 എന്ന ദ്വിഘാത സമവാക്യം ഒരു ജോടി നേര്രേഖകളെയോ, ഒരു വൃത്തത്തെയോ മറ്റു കോണിക ഖണ്ഡങ്ങളെയോ പ്രതിനിധാനം ചെയ്യുന്നു. അതുപോലെ ax<sup>2</sup> + by<sup>2</sup> + cz<sup>2</sup> + 2hxy + 2fyz + 2gzx + 2ux + 2vy + 2wz + d = 0 എന്ന ത്രിചര ദ്വിഘാത സമവാക്യം ഒരുജോടി സമതലങ്ങളെയോ, ഒരു ഗോളത്തെയോ മറ്റു കോണികജങ്ങളെയോ പ്രതിനിധാനം ചെയ്യുന്നു. രണ്ടു ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള് ഒരു സമതലത്തിലുള്ള രേഖകളേയും മൂന്നു ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള് ത്രിമാനത്തിലുള്ള പ്രതലങ്ങളേയും കുറിക്കുന്നു. | |
| - | രണ്ട് ഏകഘാതവാക്യങ്ങളുടെ ഗുണിതമാണെങ്കില് മേല്പറഞ്ഞ ത്രിചര ദ്വിഘാതവാക്യം രണ്ടു സമതലങ്ങളെ കുറിക്കുന്നു. | + | രണ്ട് ഏകഘാതവാക്യങ്ങളുടെ ഗുണിതമാണെങ്കില് മേല്പറഞ്ഞ ത്രിചര ദ്വിഘാതവാക്യം രണ്ടു സമതലങ്ങളെ കുറിക്കുന്നു. x<sup>2</sup>, y<sup>2</sup>, z<sup>2</sup> എന്നിവയുടെ ഗുണനാങ്കങ്ങള് തുല്യമായിരിക്കുകയും xy, yz, zx എന്നിവയുടെ ഗുണനാങ്കങ്ങള് ഓരോന്നും പൂജ്യമായിരിക്കുകയുമാണെങ്കില് , അതായത് സമവാക്യം ax<sup>2</sup> + ay<sup>2</sup> +az<sup>2</sup> + 2ux + 2vy + 2wz + d = 0 എന്നായിത്തീര്ന്നാല് അത് ഒരു ഗോളത്തെ സൂചിപ്പിക്കുന്നു. ഇതു രണ്ടുമല്ലെങ്കില് രൂപാന്തരണം കൊണ്ട്, ത്രിചര ദ്വിഘാത സമവാക്യത്തെ Ax<sup>2</sup> + By<sup>2</sup> = Cz എന്നോ |
| - | + | Ax<sup>2</sup> + By<sup>2</sup> + Cz<sup>2</sup> = 0 എന്നോ അല്ലെങ്കില് Ax<sup>2</sup> + By<sup>2</sup>+Cz<sup>2</sup> = 1 എന്നോ മാറ്റാം. | |
| - | + | Ax<sup>2</sup> + By<sup>2</sup> = Cz എന്ന സമവാക്യം പ്രതിനിധാനം ചെയ്യുന്ന കോണികജത്തിന്റെ സമതലഛേദങ്ങള് ദീര്ഘവൃത്തമോ (അല്ലെങ്കില് ബഹിര്വലയമോ) പരാവലയമോ ആയിരിക്കും. അതിനാല് ഈ സമവാക്യം സൂചിപ്പിക്കുന്ന കോണികജത്തെ എലിപ്റ്റിക് (അഥവാ ഹൈപ്പര്ബൊളിക്) പരാബൊളോയ്ഡ് എന്നു വിളിക്കുന്നു. Ax<sup>2,/sup> + By<sup>2</sup> + Cz<sup>2</sup> = 0 എന്നത് ഒരു കോണിന്റെ സമവാക്യമാണ്. | |
| - | (അഥവാ ഹൈപ്പര്ബൊളിക്) പരാബൊളോയ്ഡ് എന്നു വിളിക്കുന്നു. | + | |
| - | + | Ax<sup>2</sup> + By<sup>2</sup> + Cz<sup>2</sup> = 1 എന്ന സമവാക്യം പ്രതിനിധാനം ചെയ്യുന്ന കോണികജത്തിന്റെ സമതലഛേദങ്ങള് ഒന്നുകില് എല്ലാം ദീര്ഘവൃത്തങ്ങളായിരിക്കും; അല്ലെങ്കില് ദീര്ഘവൃത്തവും ബഹിര്വലയങ്ങളുമായിരിക്കും. അവയ്ക്ക് യഥാക്രമം എലിപ്സോയ്ഡ് എന്നോ ഹൈപ്പര്ബൊളോയ്ഡ് എന്നോ പറയുന്നു. ഹൈപ്പര് ബൊളോയ്ഡ് രണ്ടു തരമുണ്ട് - ഒരു ഷീറ്റുള്ള ഹൈപ്പര് ബൊളോയ്ഡും രണ്ടു ഷീറ്റുള്ള ഹൈപ്പര്ബൊളോയ്ഡും. | |
കോണികങ്ങള് (conics) അവയുടെ സമമിതിഅക്ഷ(axes of symmetry)ങ്ങളെ ആധാരമാക്കി പരിക്രമണം ചെയ്യുമ്പോള് കിട്ടുന്ന കോണികജങ്ങള്ക്ക് പരിക്രമണകോണികജങ്ങള് (conicoids of revolution) എന്ന് പറയുന്നു. പരിക്രമണ കോണികജങ്ങളുടെ സമതലഛേദങ്ങള് വൃത്തങ്ങളോ മറ്റു കോണികങ്ങളോ ആയിരിക്കും. നോ. അനലിറ്റിക്കല് ജ്യോമട്രി | കോണികങ്ങള് (conics) അവയുടെ സമമിതിഅക്ഷ(axes of symmetry)ങ്ങളെ ആധാരമാക്കി പരിക്രമണം ചെയ്യുമ്പോള് കിട്ടുന്ന കോണികജങ്ങള്ക്ക് പരിക്രമണകോണികജങ്ങള് (conicoids of revolution) എന്ന് പറയുന്നു. പരിക്രമണ കോണികജങ്ങളുടെ സമതലഛേദങ്ങള് വൃത്തങ്ങളോ മറ്റു കോണികങ്ങളോ ആയിരിക്കും. നോ. അനലിറ്റിക്കല് ജ്യോമട്രി | ||
(ഡോ.എസ്. പരമേശ്വരന്) | (ഡോ.എസ്. പരമേശ്വരന്) | ||
Current revision as of 17:14, 2 ഓഗസ്റ്റ് 2015
കോണികജങ്ങള്
Conicoids
എല്ലാ സമതലഛേദങ്ങളും കോണികങ്ങളായുള്ള ത്രിമാന പ്രതലങ്ങള്. ഉദാ. ഗോളം, കോണ്, ദീര്ഘവൃത്തജം (ellipsoid), പരാബൊളജം (paraboloid), ഹൈപ്പര്ബൊളജം (hyperboloid).
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0 എന്ന ദ്വിഘാത സമവാക്യം ഒരു ജോടി നേര്രേഖകളെയോ, ഒരു വൃത്തത്തെയോ മറ്റു കോണിക ഖണ്ഡങ്ങളെയോ പ്രതിനിധാനം ചെയ്യുന്നു. അതുപോലെ ax2 + by2 + cz2 + 2hxy + 2fyz + 2gzx + 2ux + 2vy + 2wz + d = 0 എന്ന ത്രിചര ദ്വിഘാത സമവാക്യം ഒരുജോടി സമതലങ്ങളെയോ, ഒരു ഗോളത്തെയോ മറ്റു കോണികജങ്ങളെയോ പ്രതിനിധാനം ചെയ്യുന്നു. രണ്ടു ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള് ഒരു സമതലത്തിലുള്ള രേഖകളേയും മൂന്നു ചരങ്ങളുള്ള ദ്വിഘാത സമവാക്യങ്ങള് ത്രിമാനത്തിലുള്ള പ്രതലങ്ങളേയും കുറിക്കുന്നു.
രണ്ട് ഏകഘാതവാക്യങ്ങളുടെ ഗുണിതമാണെങ്കില് മേല്പറഞ്ഞ ത്രിചര ദ്വിഘാതവാക്യം രണ്ടു സമതലങ്ങളെ കുറിക്കുന്നു. x2, y2, z2 എന്നിവയുടെ ഗുണനാങ്കങ്ങള് തുല്യമായിരിക്കുകയും xy, yz, zx എന്നിവയുടെ ഗുണനാങ്കങ്ങള് ഓരോന്നും പൂജ്യമായിരിക്കുകയുമാണെങ്കില് , അതായത് സമവാക്യം ax2 + ay2 +az2 + 2ux + 2vy + 2wz + d = 0 എന്നായിത്തീര്ന്നാല് അത് ഒരു ഗോളത്തെ സൂചിപ്പിക്കുന്നു. ഇതു രണ്ടുമല്ലെങ്കില് രൂപാന്തരണം കൊണ്ട്, ത്രിചര ദ്വിഘാത സമവാക്യത്തെ Ax2 + By2 = Cz എന്നോ Ax2 + By2 + Cz2 = 0 എന്നോ അല്ലെങ്കില് Ax2 + By2+Cz2 = 1 എന്നോ മാറ്റാം.
Ax2 + By2 = Cz എന്ന സമവാക്യം പ്രതിനിധാനം ചെയ്യുന്ന കോണികജത്തിന്റെ സമതലഛേദങ്ങള് ദീര്ഘവൃത്തമോ (അല്ലെങ്കില് ബഹിര്വലയമോ) പരാവലയമോ ആയിരിക്കും. അതിനാല് ഈ സമവാക്യം സൂചിപ്പിക്കുന്ന കോണികജത്തെ എലിപ്റ്റിക് (അഥവാ ഹൈപ്പര്ബൊളിക്) പരാബൊളോയ്ഡ് എന്നു വിളിക്കുന്നു. Ax2,/sup> + By2 + Cz2 = 0 എന്നത് ഒരു കോണിന്റെ സമവാക്യമാണ്.
Ax2 + By2 + Cz2 = 1 എന്ന സമവാക്യം പ്രതിനിധാനം ചെയ്യുന്ന കോണികജത്തിന്റെ സമതലഛേദങ്ങള് ഒന്നുകില് എല്ലാം ദീര്ഘവൃത്തങ്ങളായിരിക്കും; അല്ലെങ്കില് ദീര്ഘവൃത്തവും ബഹിര്വലയങ്ങളുമായിരിക്കും. അവയ്ക്ക് യഥാക്രമം എലിപ്സോയ്ഡ് എന്നോ ഹൈപ്പര്ബൊളോയ്ഡ് എന്നോ പറയുന്നു. ഹൈപ്പര് ബൊളോയ്ഡ് രണ്ടു തരമുണ്ട് - ഒരു ഷീറ്റുള്ള ഹൈപ്പര് ബൊളോയ്ഡും രണ്ടു ഷീറ്റുള്ള ഹൈപ്പര്ബൊളോയ്ഡും.
കോണികങ്ങള് (conics) അവയുടെ സമമിതിഅക്ഷ(axes of symmetry)ങ്ങളെ ആധാരമാക്കി പരിക്രമണം ചെയ്യുമ്പോള് കിട്ടുന്ന കോണികജങ്ങള്ക്ക് പരിക്രമണകോണികജങ്ങള് (conicoids of revolution) എന്ന് പറയുന്നു. പരിക്രമണ കോണികജങ്ങളുടെ സമതലഛേദങ്ങള് വൃത്തങ്ങളോ മറ്റു കോണികങ്ങളോ ആയിരിക്കും. നോ. അനലിറ്റിക്കല് ജ്യോമട്രി
(ഡോ.എസ്. പരമേശ്വരന്)