This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam
കോണ്‍
സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്
Mksol (സംവാദം | സംഭാവനകള്) (→Cone) |
(→Cone) |
||
| (ഇടക്കുള്ള ഒരു പതിപ്പിലെ മാറ്റം ഇവിടെ കാണിക്കുന്നില്ല.) | |||
| വരി 4: | വരി 4: | ||
== Cone == | == Cone == | ||
| - | [[ചിത്രം: | + | [[ചിത്രം:Screenpage74.png|200px|right]] |
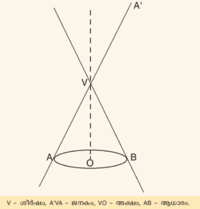
ഒരു മട്ടത്രികോണ(right angled triangle)ത്തിന്റെ ഏതെങ്കിലും ലഘുവശത്തെ അക്ഷമാക്കി ത്രികോണം ചുറ്റുമ്പോള്‍ ഉളവാകുന്ന ഘനരൂപം. സാമാന്യമായി ഒരു സമതലവും കോണീയരൂപത്തിലുള്ള ഒരു വക്രതലവും ചേര്‍ന്ന ഘനരൂപത്തിന്‌ കോണ്‍ എന്നുപറയുന്നു. ഒരു നേര്‍വര ഏതെങ്കിലുമൊരു സമതലവക്രത്തെ ഖണ്ഡിക്കുന്നവിധം സമതലത്തിനു പുറത്തുള്ള ഒരു സ്ഥിരബിന്ദുവില്‍ തിരിയുമ്പോഴുണ്ടാകുന്ന തലത്തെയാണ്‌ കോണ്‍ എന്നുവിളിക്കുന്നത്‌. പ്രാചീന ഗ്രീക്കു ഗണിതശാസ്‌ത്രജ്ഞനായ അപ്പളോണിയസ്‌ (ബി.സി. 260-200) 8 ഭാഗങ്ങളായി രചിച്ച കോണിക്‌ സെക്ഷന്‍സ്‌ എന്ന പ്രമുഖ ഗണിതശാസ്‌ത്ര ഗ്രന്ഥത്തില്‍ കോണിന്‌ നല്‌കിയ നിര്‍വചനമാണിത്‌. ഇവിടെ നേര്‍വരയെ ജനകം (generator) എന്നും ബിന്ദുവിനെ ശീര്‍ഷം (vertex) എന്നും വിളിക്കുന്നു. | ഒരു മട്ടത്രികോണ(right angled triangle)ത്തിന്റെ ഏതെങ്കിലും ലഘുവശത്തെ അക്ഷമാക്കി ത്രികോണം ചുറ്റുമ്പോള്‍ ഉളവാകുന്ന ഘനരൂപം. സാമാന്യമായി ഒരു സമതലവും കോണീയരൂപത്തിലുള്ള ഒരു വക്രതലവും ചേര്‍ന്ന ഘനരൂപത്തിന്‌ കോണ്‍ എന്നുപറയുന്നു. ഒരു നേര്‍വര ഏതെങ്കിലുമൊരു സമതലവക്രത്തെ ഖണ്ഡിക്കുന്നവിധം സമതലത്തിനു പുറത്തുള്ള ഒരു സ്ഥിരബിന്ദുവില്‍ തിരിയുമ്പോഴുണ്ടാകുന്ന തലത്തെയാണ്‌ കോണ്‍ എന്നുവിളിക്കുന്നത്‌. പ്രാചീന ഗ്രീക്കു ഗണിതശാസ്‌ത്രജ്ഞനായ അപ്പളോണിയസ്‌ (ബി.സി. 260-200) 8 ഭാഗങ്ങളായി രചിച്ച കോണിക്‌ സെക്ഷന്‍സ്‌ എന്ന പ്രമുഖ ഗണിതശാസ്‌ത്ര ഗ്രന്ഥത്തില്‍ കോണിന്‌ നല്‌കിയ നിര്‍വചനമാണിത്‌. ഇവിടെ നേര്‍വരയെ ജനകം (generator) എന്നും ബിന്ദുവിനെ ശീര്‍ഷം (vertex) എന്നും വിളിക്കുന്നു. | ||
വിശ്ലേഷകജ്യാമിതി(Analytical geometry)യില്‍ കോണീയതല(Conical surface)ത്തെയാണ്‌ കോണ്‍ എന്നുപറയുന്നത്‌. കോണ്‍ ശീര്‍ഷത്തിന്റെ രണ്ടുവശവും അനന്തദൂരത്തേക്കു വ്യാപിച്ചുകിടക്കുന്നതായും ഗണിതശാസ്‌ത്രജ്ഞന്മാര്‍ സങ്കല്‍പ്പിക്കുന്നു. ഈ സങ്കല്‍പ്പകോണിന്റെ ഒരുവശത്തുള്ള ഖണ്ഡത്തെയാണ്‌ സാമാന്യമായി കോണ്‍ എന്നുപറയുന്നത്‌. ഒരു സാമാന്യകോണിന്‌ ശീര്‍ഷവും ആധാര(base)വും വേണം. ശീര്‍ഷം ഒന്നേയുള്ളൂ. ഒരു സമതലം (ശീര്‍ഷത്തിന്റെ ഒരു വശത്തുള്ള) കോണീയതലത്തെ ഖണ്ഡിക്കുമ്പോള്‍ കിട്ടുന്ന (സംവൃതവക്രരേഖ ഉള്‍ക്കൊള്ളുന്ന) ഭാഗമാണ്‌ ആധാരം. ശീര്‍ഷത്തിലൂടെ പോകുന്ന ഏതെങ്കിലും നേര്‍വരയുമായി ജനകം സദാ തുല്യമായ കോണം (angle) ഉണ്ടാക്കുന്നെങ്കില്‍, അപ്രകാരമുളവാകുന്ന കോണിനെ ഭ്രമണകോണ്‍ (Cone of revolution) എന്നും ആ നേര്‍വരയെ ഭ്രമണാക്ഷം എന്നും പറയുന്നു. | വിശ്ലേഷകജ്യാമിതി(Analytical geometry)യില്‍ കോണീയതല(Conical surface)ത്തെയാണ്‌ കോണ്‍ എന്നുപറയുന്നത്‌. കോണ്‍ ശീര്‍ഷത്തിന്റെ രണ്ടുവശവും അനന്തദൂരത്തേക്കു വ്യാപിച്ചുകിടക്കുന്നതായും ഗണിതശാസ്‌ത്രജ്ഞന്മാര്‍ സങ്കല്‍പ്പിക്കുന്നു. ഈ സങ്കല്‍പ്പകോണിന്റെ ഒരുവശത്തുള്ള ഖണ്ഡത്തെയാണ്‌ സാമാന്യമായി കോണ്‍ എന്നുപറയുന്നത്‌. ഒരു സാമാന്യകോണിന്‌ ശീര്‍ഷവും ആധാര(base)വും വേണം. ശീര്‍ഷം ഒന്നേയുള്ളൂ. ഒരു സമതലം (ശീര്‍ഷത്തിന്റെ ഒരു വശത്തുള്ള) കോണീയതലത്തെ ഖണ്ഡിക്കുമ്പോള്‍ കിട്ടുന്ന (സംവൃതവക്രരേഖ ഉള്‍ക്കൊള്ളുന്ന) ഭാഗമാണ്‌ ആധാരം. ശീര്‍ഷത്തിലൂടെ പോകുന്ന ഏതെങ്കിലും നേര്‍വരയുമായി ജനകം സദാ തുല്യമായ കോണം (angle) ഉണ്ടാക്കുന്നെങ്കില്‍, അപ്രകാരമുളവാകുന്ന കോണിനെ ഭ്രമണകോണ്‍ (Cone of revolution) എന്നും ആ നേര്‍വരയെ ഭ്രമണാക്ഷം എന്നും പറയുന്നു. | ||
| - | ഒരു സാമാന്യകോണിന്റെ വ്യാപ്‌തം ആയിരിക്കും | + | ഒരു സാമാന്യകോണിന്റെ വ്യാപ്‌തം ആയിരിക്കും [[ചിത്രം:Formula01.png]] (A = ആധാരത്തിന്റെ വിസ്‌തീര്‍ണം, h = കോണിന്റെ ഉന്നതി); കോണ്‍ ലംബവൃത്തീയ(right circular)മാണെങ്കില്‍ വ്യാപ്‌തം [[ചിത്രം:Formula2.png]]ആയിരിക്കും (r = ആധാരവൃത്തത്തിന്റെ ആരം, h = ചരിവുനീളം) നോ. കോണികങ്ങള്‍ |
| - | + | ||
| - | (A = ആധാരത്തിന്റെ വിസ്‌തീര്‍ണം, h = കോണിന്റെ ഉന്നതി); കോണ്‍ ലംബവൃത്തീയ(right circular)മാണെങ്കില്‍ വ്യാപ്‌തം | + | |
Current revision as of 15:55, 2 ഓഗസ്റ്റ്‌ 2015
കോണ്‍
Cone
ഒരു മട്ടത്രികോണ(right angled triangle)ത്തിന്റെ ഏതെങ്കിലും ലഘുവശത്തെ അക്ഷമാക്കി ത്രികോണം ചുറ്റുമ്പോള്‍ ഉളവാകുന്ന ഘനരൂപം. സാമാന്യമായി ഒരു സമതലവും കോണീയരൂപത്തിലുള്ള ഒരു വക്രതലവും ചേര്‍ന്ന ഘനരൂപത്തിന്‌ കോണ്‍ എന്നുപറയുന്നു. ഒരു നേര്‍വര ഏതെങ്കിലുമൊരു സമതലവക്രത്തെ ഖണ്ഡിക്കുന്നവിധം സമതലത്തിനു പുറത്തുള്ള ഒരു സ്ഥിരബിന്ദുവില്‍ തിരിയുമ്പോഴുണ്ടാകുന്ന തലത്തെയാണ്‌ കോണ്‍ എന്നുവിളിക്കുന്നത്‌. പ്രാചീന ഗ്രീക്കു ഗണിതശാസ്‌ത്രജ്ഞനായ അപ്പളോണിയസ്‌ (ബി.സി. 260-200) 8 ഭാഗങ്ങളായി രചിച്ച കോണിക്‌ സെക്ഷന്‍സ്‌ എന്ന പ്രമുഖ ഗണിതശാസ്‌ത്ര ഗ്രന്ഥത്തില്‍ കോണിന്‌ നല്‌കിയ നിര്‍വചനമാണിത്‌. ഇവിടെ നേര്‍വരയെ ജനകം (generator) എന്നും ബിന്ദുവിനെ ശീര്‍ഷം (vertex) എന്നും വിളിക്കുന്നു.
വിശ്ലേഷകജ്യാമിതി(Analytical geometry)യില്‍ കോണീയതല(Conical surface)ത്തെയാണ്‌ കോണ്‍ എന്നുപറയുന്നത്‌. കോണ്‍ ശീര്‍ഷത്തിന്റെ രണ്ടുവശവും അനന്തദൂരത്തേക്കു വ്യാപിച്ചുകിടക്കുന്നതായും ഗണിതശാസ്‌ത്രജ്ഞന്മാര്‍ സങ്കല്‍പ്പിക്കുന്നു. ഈ സങ്കല്‍പ്പകോണിന്റെ ഒരുവശത്തുള്ള ഖണ്ഡത്തെയാണ്‌ സാമാന്യമായി കോണ്‍ എന്നുപറയുന്നത്‌. ഒരു സാമാന്യകോണിന്‌ ശീര്‍ഷവും ആധാര(base)വും വേണം. ശീര്‍ഷം ഒന്നേയുള്ളൂ. ഒരു സമതലം (ശീര്‍ഷത്തിന്റെ ഒരു വശത്തുള്ള) കോണീയതലത്തെ ഖണ്ഡിക്കുമ്പോള്‍ കിട്ടുന്ന (സംവൃതവക്രരേഖ ഉള്‍ക്കൊള്ളുന്ന) ഭാഗമാണ്‌ ആധാരം. ശീര്‍ഷത്തിലൂടെ പോകുന്ന ഏതെങ്കിലും നേര്‍വരയുമായി ജനകം സദാ തുല്യമായ കോണം (angle) ഉണ്ടാക്കുന്നെങ്കില്‍, അപ്രകാരമുളവാകുന്ന കോണിനെ ഭ്രമണകോണ്‍ (Cone of revolution) എന്നും ആ നേര്‍വരയെ ഭ്രമണാക്ഷം എന്നും പറയുന്നു.
ഒരു സാമാന്യകോണിന്റെ വ്യാപ്‌തം ആയിരിക്കും 
(A = ആധാരത്തിന്റെ വിസ്‌തീര്‍ണം, h = കോണിന്റെ ഉന്നതി); കോണ്‍ ലംബവൃത്തീയ(right circular)മാണെങ്കില്‍ വ്യാപ്‌തം 
ആയിരിക്കും (r = ആധാരവൃത്തത്തിന്റെ ആരം, h = ചരിവുനീളം) നോ. കോണികങ്ങള്‍
