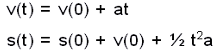This site is not complete. The work to converting the volumes of സര്‍വ്വവിജ്ഞാനകോശം is on progress. Please bear with us
Please contact webmastersiep@yahoo.com for any queries regarding this website.
Reading Problems? see Enabling Malayalam

സര്‍വ്വവിജ്ഞാനകോശം സംരംഭത്തില്‍ നിന്ന്

15:48, 19 ജൂലൈ 2015-നു നിലവിലുണ്ടായിരുന്ന രൂപം

കൈനമാറ്റിക്സ്

Kinematics

ഭൗതികപദാര്‍ഥങ്ങളുടെ ചലനത്തെ ആസ്പദമാക്കിയുള്ള പഠനശാഖ. ഇതില്‍ പദാര്‍ഥങ്ങളുടെ ചലനത്തിന്റെ ഹേതുവോ ഫലമോ പരിഗണിക്കാറില്ല. ചലനത്തിന്റെ കാരണവും ഫലവും കണക്കിലെടുത്തുകൊണ്ടുള്ള ചലനപഠനമാണ് ഗതികം (dynamics).

ചലിക്കുന്ന പദാര്‍ഥത്തിന് ഘടനയില്ലെന്ന സങ്കല്പത്തില്‍ അതിനെ ഒരു സ്ഥാനം കൊണ്ടു സൂചിപ്പിക്കുകയാണ് ചെയ്യുന്നത്. സ്ഥാനം ഏതെങ്കിലുമൊരു നിര്‍ദേശാങ്കരീതി (co-ordinate system) കൊണ്ട് നിശ്ചിതമായിരിക്കും (സമയത്തിനനുസരിച്ച് സ്ഥാനം മാറുമ്പോള്‍ സ്ഥാനത്തെ സമയത്തിന്റെ ഒരു ധര്‍മ(function)മായി കണക്കാക്കാവുന്നതാണ്). ഇതനുസരിച്ച് പദാര്‍ഥം അതിന്റെ സഞ്ചാരപഥം (trajectory) നിര്‍ദേശിച്ചു കൊണ്ടു നിര്‍വചിക്കപ്പെടുന്നു. ഏറ്റവും സരളമായ നിര്‍ദേശാങ്കരീതി കാര്‍ട്ടീഷ്യന്‍ ത്രിമാനപദ്ധതി (Cartesian three dimensional system) ആണ്.

കൈനമാറ്റിക്സിലെ മൂന്നു മൌലികഘടകങ്ങളാണ് വിസ്ഥാപനം (displacement), പ്രവേഗം അഥവാ വിസ്ഥാപനമാറ്റത്തിന്റെ നിരക്ക് (velocity), പ്രവേഗമാറ്റത്തിന്റെ നിരക്ക് (ത്വരണം - accelaration) എന്നിവ. സമയമാറ്റത്തിനനുസരിച്ച് ത്വരണവും വിസ്ഥാപനവും സൂചിപ്പിക്കുന്ന സമീകരണങ്ങളാണ് ഇവിടെ ചേര്‍ക്കുന്നത്.

ഇവിടെ aത്വരണത്തെയും v പ്രവേഗത്തെയും s വിസ്ഥാപനത്തെയും t സമയത്തെയും \frac{d}{dt}; മാറ്റത്തെയും അഭിവ്യഞ്ജിപ്പിക്കുന്ന ചിഹ്നങ്ങളാണ്. സ്ഥിരനിരക്കിലാണ് പദാര്‍ഥം ചലിക്കുന്നതെങ്കില്‍

ഇങ്ങനെ പ്രവേഗം, ത്വരണം, വിസ്ഥാപനം എന്നിവയെ ബന്ധപ്പെടുത്തുന്ന സമീകരങ്ങള്‍ കലനം വഴി കണ്ടു പിടിക്കാവുന്നതാണ്. ഇവിടെ v(t), s(t) എന്നിവ (പ്രവേഗവും വിസ്ഥാപനവും) സമയത്തിന്റെ ധര്‍മങ്ങളാണെന്നു കാണാം.v(t), s(0) പ്രാരംഭപ്രവേഗവും പ്രാരംഭവിസ്ഥാപനവുമാണ്. ഈ നിയമങ്ങളനുസരിച്ച് ചലിക്കുന്ന പദാര്‍ഥത്തിന്റെ സഞ്ചാരപഥം പരാബോളയാണെന്ന് അവസാനത്തെ സമീകരണത്തില്‍ നിന്നും വ്യക്തമാകുന്നു. ഭൂമിയില്‍ നിന്നു തൊടുക്കുന്ന പ്രൊജക്റ്റൈലുകളുടെയും സ്ഥിരവൈദ്യുതമണ്ഡലങ്ങളില്‍ വൈദ്യുതാധാനമായ പദാര്‍ഥങ്ങളുടെയും സഞ്ചാരപഥങ്ങള്‍ ഈ നിയമത്തിനു വിധേയമായിരിക്കും. വ്യാസത്തിനു മാറ്റമില്ലാത്ത സ്ഥിരമായ വൃത്തപഥത്തിലാണ് പദാര്‍ഥം സ്ഥിരവേഗത്തില്‍ ചലിക്കുന്നതെങ്കില്‍ പ്രവേഗത്തിന്റെ ദിശയ്ക്കു മാറ്റമുള്ളതിനാല്‍ ചലനം ത്വരിതപ്പെടുന്നതാണ്. ഇവിടെ ത്വരണം ആയിരിക്കും.

v പ്രവേഗത്തെയും r വൃത്തത്തിന്റെ വ്യാസാര്‍ധത്തെയും സൂചിപ്പിക്കുന്നു. വൃത്തകേന്ദ്രത്തിലേക്കാണ് ഈ ത്വരണത്തിന്റെ ദര്‍ശനം. പരസ്പരദൂരത്തിനു മാറ്റമില്ലാത്ത കണങ്ങളുടെ സംഘാതത്തെയാണ് ദൃഢപദാര്‍ഥം എന്നു പറയുന്നത്. അതുകൊണ്ട് ദൃഢ പദാര്‍ഥത്തിന്റെ ചലനവും കൈനമാറ്റിക്സില്‍ പ്രതിപാദിച്ചുവരുന്നു. പരസ്പരദൂരം സ്ഥിരമായിരിക്കുകയെന്ന വ്യവസ്ഥയോടെ കണങ്ങളുടെ ചലനം പഠനവിധേയമാക്കുമ്പോള്‍ ആ ദൃഢപദാര്‍ഥത്തിന്റെ തന്നെ ചലനവും പഠനവിധേയമായിത്തീരുന്നതാണ്. പദാര്‍ഥത്തിന്റെ ദ്രവ്യകേന്ദ്രം ഒരു ദ്രവ്യബിന്ദു എന്ന പോലെ ചലിക്കുന്നു. സംവിധാനത്തിന്റെ തന്നെ മാറ്റം കോണീയ പ്രവേഗ (angular velocity) ത്തിലൂടെയാണ് സാധിക്കുന്നത്. ദ്രവ്യകേന്ദ്രം സ്ഥിരമായി നില്ക്കുമ്പോള്‍ പദാര്‍ഥം ഘൂര്‍ണനം (rotation) ചെയ്യുന്നു. ലംബീയ നിര്‍ദേശാങ്കങ്ങള്‍ (right angular co-ordinates) കൊണ്ട് സൂചിപ്പിക്കപ്പെടുന്ന കണികാസ്ഥാനങ്ങള്‍ മറ്റേതു സാമാന്യവത്കൃത (generalised) നിര്‍ദേശാങ്കങ്ങള്‍ ഉപയോഗിച്ചും പ്രകടിപ്പിക്കാവുന്നതാണ്.

കണികാസ്ഥാനങ്ങളെ സ്ഥിരമായ നിര്‍ദേശാങ്ക പദ്ധതിയുടെ അടിസ്ഥാനത്തില്‍ കൈകാര്യം ചെയ്യുന്നതുപോലെതന്നെ പദ്ധതിയുടെ മാറ്റത്തിലൂടെയും കൈകാര്യം ചെയ്യാവുന്നതാണ്. അതായത് ഒരു പദ്ധതിയില്‍ നിന്ന് മറ്റൊരു പദ്ധതിയിലേക്ക് അടിസ്ഥാനം മാറ്റിയാല്‍ ചലനത്തിനും സ്ഥാനത്തോടൊപ്പം മാറ്റം വരുന്നതാണ്.